1. Introduction
The distributed modelling of snow and ice mass balance is of scientific and practical interest, since it permits us to better understand the processes involved in glacier hydrology and to predict glacier runoff under possible future climatic scenarios. In addition, distributed glacier mass-balance modelling is an important component of modern multilevel glacier monitoring, since it allows us to interconnect different levels of observations (length change, mass balance, inventories) and to extrapolate data in space and time (Reference Machguth, Paul, Hoelzle and HaeberliMachguth and others, 2006a).
Glaciers typically exhibit a complex distribution of the energy and mass balance, originating from the interaction of climate with local topography and regulated by different feedbacks. A number of investigations with automatic weather stations (AWS) and distributed measurements on glaciers have significantly improved our knowledge of the physical processes involved in accumulation and ablation (e.g. Reference Hock and HolmgrenHock and Holmgren, 1996;Reference Greuell, Knap and SmeetsGreuell and others, 1997; Reference Brock, Willis and SharpBrock and others, 2000; Reference OerlemansOerlemans, 2000; Reference Andreassen, Van den Broeke, Giesen and OerlemansAndreassen and others, 2008), but have also highlighted the peculiarities of the glacier boundary layer. Incorporating this knowledge into ‘operational’ models is still a problem. Specifically, large uncertainties may affect the estimations of input variables in most applications over glaciers, since the climate stations are usually located in the lower parts of the basins and outside the influence of glaciers. This is even more evident in fully distributed applications, which require a realistic distribution of input variables in space and time (Reference Charbonneau, Lardeau and ObledCharbonneau and others, 1981;Reference Machguth, Paul, Hoelzle and HaeberliMachguth and others, 2006a). Scaling issues, over-parameterization, lack of adequate data for internal validation and equifinality may eventually hamper the applicability of models to ungauged catchments, despite the good knowledge achieved for individual processes (Reference BloschlBloschl, 1999;Reference Refsgaard, Anderson and BatesRefsgaard, 2001; Reference SavenijeSavenije, 2001;Reference Sivapalan, Anderson and McDonnellSivapalan, 2006).
Most research on glaciers has focused on energy fluxes and melt processes. Snow accumulation has been less studied, mainly due to its high spatial variability, which requires adequate experimental data to be investigated. Hence, accumulation is often dealt with by vertical precipitation gradients, neglecting processes of preferential deposition and redistribution which dominate at high altitude and over glaciers (Reference KuhnKuhn, 2003;Reference Lehning, Lowe, Ryser and RadeschallLehning and others, 2008). The result is a ubiquitous linear increase of snow water equivalent (w.e.) with elevation, which is not supported by field evidence (Reference Machguth, Paul, Hoelzle and HaeberliMachguth and others, 2006b;Reference Plattner, Braun and BrenningPlattner and others, 2006;Reference Escher-Vetter, Kuhn and WeberEscher-Vetter and others, 2009). Instrumental errors also affect the estimation of precipitation inputs and gradients in alpine terrain (Reference Adam and LettenmaierAdam and Lettenmaier, 2003; Reference Verbunt, Gurtz, Jasper, Lang, Warmerdam and ZappaVerbunt and others, 2003; Carturan and others, in press). The correction factors for instrumental errors and the precipitation gradients can be tuned to match field observations, but this can lead to distortions in model calibration. These approximations strongly impact melt calculations as well, since large differences exist between snow and ice albedo. Therefore, major improvement in glacier mass- balance modelling can be achieved by focusing on accumulation processes (Reference Machguth, Paul, Hoelzle and HaeberliMachguth and others, 2006b; Reference Paul, Machguth, Hoelzle, Salzmann, Haeberli, Orlove, Wiegandt and LuckmanPaul and others, 2008, Reference Paul, Escher-Vetter and Machguth2009).
The complexity of the modelling approach must deal with these constraints and must also fit with the purposes of its application and with the temporal and spatial resolution required in simulations (Reference Kirnbauer, Bloschl and GutknechtKirnbauer and others, 1994;Reference HockHock and Jansson, 2005). Among usable modelling approaches, the so-called ‘enhanced temperature-index’ melt models constitute a good compromise between model simplicity, parsimony of input data, and the capability to account for dominant processes in snow and ice mass balance. Based on the observation that the net shortwave solar radiation is the dominant source of melt energy in most glaciers (Reference Willis, Arnold and BrockWillis and others, 2002), these models improve the classical temperature-index method, based only on air temperature, by introducing shortwave solar radiation to account for the spatial and temporal variability of the melt energy. The clear- sky solar radiation can be calculated using a digital terrain model (DTM), and can be used as an energy index without including additional climatic variables besides air temperature and precipitation. This modelling approach is particularly suited to applications in areas with limited availability of meteorological input data, but its robustness and transferability are still topics of discussion, due to its dependence on empirical parameters (Reference Carenzo, Pellicciotti, Rimkus and BurlandoCarenzo and others, 2009). Three main types of melt algorithms have been proposed in the literature for applications on glaciers: (1) simple multiplicative formulation with only one melt factor (Reference Cazorzi and Dalla FontanaCazorzi and Dalla Fontana, 1996;Reference Cazorzi, Carturan and Dalla FontanaCazorzi and others, 2005);(2) multiplicative formulation with thermal and shortwave radiation factors (Reference HockHock, 1999); and (3) additive formulation with thermal and shortwave radiation factors (Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others, 2005).
This paper deals with the implementation and application of an ‘enhanced temperature-index’ mass-balance model, and is focused on two main aspects:
-
1. improvement of the simulation of snow accumulation, accounting for preferential deposition and redistribution processes by means of topographic indexes calculated from a DTM
-
2. comparison of three existing melt algorithms, aimed at identifying possible best solutions.
The fully distributed model was applied over a 6year period on a watershed of the Eastern Italian Alps, where direct mass-balance data were available for calibration and validation on two glaciers with different characteristics. The purpose was to assess the performance of this modelling approach in the absence of meteorological observations from glacier areas. Thus, the input data for simulations (hourly temperature and precipitation) came from two weather stations located outside the influence of glaciers.
2. Study-Area Description and Data Collection
La Mare and Careser glaciers are located in the upper part of Val de la Mare, Eastern Italian Alps (Fig. 1). This is a 68.3km2 experimental watershed where detailed studies of climate-change effects on the cryosphere and hydrology are carried out. The highest summit is Monte Cevedale (3769 m a.s.l.), while the outlet altitude is 1158m a.s.l. The catchment lies in the southern part of the Ortles-Cevedale massif, near the inner dry Alpine zone (Reference SchwarbSchwarb, 2000).
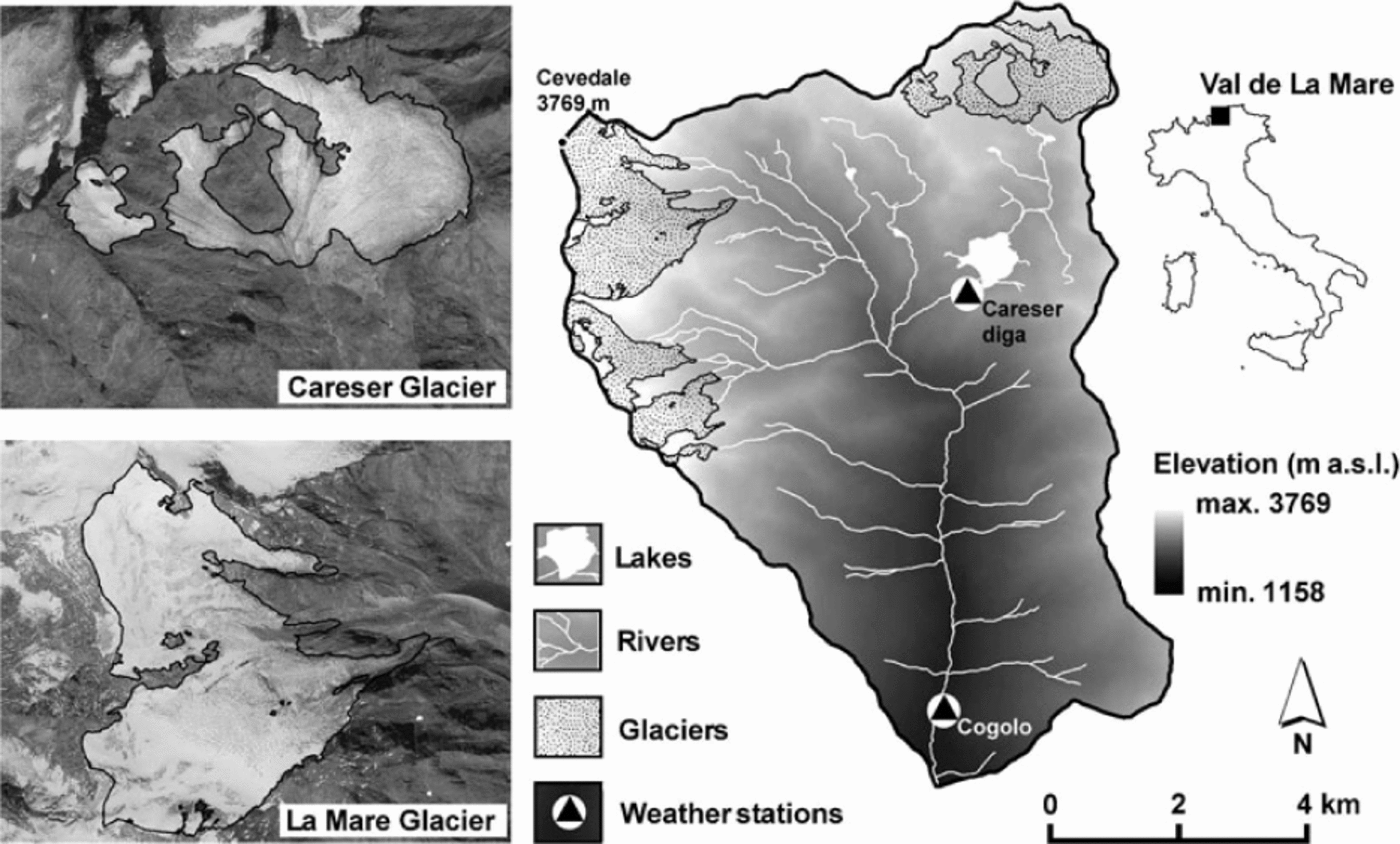
Fig. 1. Geographical setting of Val de la Mare and of Careser and La Mare glaciers. Monte Cevedale coordinates are 46°28’08 N, 10°36’03"E.
Two weather stations have operated since the 1920s in Val de la Mare (Fig. 1): Careser Diga (2605 m a.s.l.) and Cogolo (1200 m a.s.l.), recording 2 m air temperature and precipitation. Since the 1990s they have recorded hourly data. For Careser Diga, daily observations of snow depth and fresh-snow height are also available. At this station the mean 1979-2009 annual precipitation (corrected for gauge errors; see Section 3.3) is 1233 mm and the mean annual air temperature is -0.4°C. In the accumulation season, precipitation is mainly brought by synoptic disturbances and southerly winds, while thermal convection and thunderstorms prevail during summer. Post-event snow redistribution during the accumulation season typically occurs with strong northwesterly winds.
The two glaciers are very different. Careser glacier (28703279 m a.s.l.) is flat and mainly exposed to the south. La Mare (2650-3769 m a.s.l.) is mainly exposed to the east and is steeper. On both glaciers, topographic shading is of minor importance. The hypsometry of the two ice bodies controls the current deglaciation phase. Careser glacier has no accumulation area and exhibits rapid mass loss and fragmentation, while La Mare glacier still has an accumulation area and shows ‘active’ retreat (Reference ZanonZanon, 1982;Reference Carturan and SeppiCarturan and Seppi, 2007, Reference Carturan and Seppi2009). The physical characteristics and the availability of comprehensive mass-balance observations from 2004 to 2009 make these glaciers highly suitable for the purposes of this study. The mass balance was negative for both glaciers in this period, but weather conditions displayed good interannual variability (Table 1), which is appropriate for assessing the model performance.
Table 1. Mean precipitation and temperature anomalies in the accumulation and ablation seasons from 2004 to 2009 at the Careser Diga weather station (reference period 1979-2009)

2.1 Mass-balance measurements on Careser and La Mare glaciers
A long-term mass-balance monitoring programme exists for both glaciers. Measurements started in 1967 (the longest series in Italy) on Careser, and similar observations were begun in 2003 on La Mare, but data prior to 2004 are too scarce for modelling purposes (Reference ZanonZanon, 1982;Reference Carturan and SeppiCarturan and Seppi, 2007;Reference Carturan and SeppiCarturan and others, 2009a). Measurements were carried out according to the ‘direct glaciological’ method (Reference Østrem and BrugmanØstrem and Brugman, 1991). Snow accumulation was sampled in May using snow depth soundings and snow density measurements in pits. Ablation was measured using aluminium stakes in the ablation area, and by repeated snow depth sounding and snow pits in the accumulation area. The snow cover and transient snow line were also monitored during summer, using GPS tracking and repeated photographs.
The monitoring network was kept as unchanged as possible. However, the rapid retreat of glaciers implied the relocation of some ablation stakes. Other typical contingencies related to this kind of measurement and harsh glacial environment (e.g. loss of ablation stakes due to fresh-snow burial or melt-out, bad weather, avalanche or crevasse danger, etc.) led to slight differences in sample size and location from year to year. Additional constraints affected the measurement of seasonal components of mass balance (winter and summer balance) in the case of prolonged ice ablation during the accumulation season.
In this work, we use mass-balance point data to implement our model and to assess its performance. Typical errors reported in the literature for individual measurements are 0.1-0.3 mw.e. a-1 for snow accumulation and 0.1- 0.4mw.e. a-1 for ablation (Reference Cogley and AdamsCogley and Adams, 1998; Reference Gerbaux, Genthon, Etchevers, Vincent and DedieuGerbaux and others, 2005;Reference Thibert, Blanc, Vincent and EckertThibert and others, 2008;Reference Huss, Bauder and FunkHuss and others, 2009).
3. Model Structure
In this section we describe the general structure of the model (Section 3.1), the simulation of snow accumulation (Section 3.2) and the application of the model to our study area, including the preparation of input data and the parameter initialization, calibration and validation (Section 3.3).
3.1. The energy index snow-and-ice model (EISModel)
The EISModel derives from the grid-distributed model described by Reference Cazorzi and Dalla FontanaCazorzi and Dalla Fontana (1996). It simulates accumulation and melt processes at hourly intervals and only requires as inputs a DTM of the watershed and precipitation and 2 m air-temperature data from at least one weather station. In the present work, hourly data were used.
For each pixel, X, and for each hour, t, at elevation EL X (ma.s.l.), the 2 m air temperature, TX,t , is computed by an hourly lapse rate, LR t (°Cm-1):
where T s1,t is the 2 m air temperature at the reference weather station (s1) with elevation ELs1. LR t can be assigned as a constant value or can be calculated for each time-step by the model from at least two weather stations at different altitudes (see Section 3.3).
The precipitation data at the gauging stations s (s1, s2,...sn) are extrapolated at the pixel elevation using a precipitation linear increase factor (PLIF;% km-1) to account for the typical increase of precipitation with altitude. PLIF can be assigned as a constant value or calculated by the model from at least two weather stations at different altitudes (see Section 3.3).
When the temperature at the pixel elevation exceeds the snow/rain threshold, T snow, the rainfall increases the liquid content of the snowpack, LQW (mm);otherwise the snowfall increases the water equivalent of snow, WEs (mm):
SRF X (snow redistribution factor) accounts for preferential deposition and redistribution of snow due to wind drift and gravity. Its significance and calculation method are described in detail in Section 3.2.
Snow and ice melt are assumed to occur when the air temperature exceeds the threshold temperature for melt, T melt = 0°C. The melt rate, MLT X,t (mmh-1), is calculated as a function of T X,t and clear-sky shortwave radiation, CSR X,t (W m-2). The model calculates CSR X,t based on the DTM, accounting for the effects of the surrounding relief which determines the local sunrise and sunset times and shadowing (Reference OkeOke, 1987;Reference Dubayah, Dozier and DavisDubayah and others, 1990;Reference DeWalle and RangoDeWalle and Rango, 2008). In this paper, we compare three melt algorithms proposed in the literature, which have been successfully used on glacier applications. The Reference Cazorzi and Dalla FontanaCazorzi and Dalla Fontana (1996) algorithm is
The Reference HockHock (1999) algorithm is

and the Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others (2005) algorithm is
where α X,t is the surface albedo, and RTMF, TMF and RMF are empirical coefficients, namely, radiation-temperature melt factor (mm h-1 °C-1 W-1 m2), temperature melt factor (mm h”‘ °C-1) and radiation melt factor (mm h-1 W-1 m2), respectively. These three coefficients are the calibration parameters of the model. Henceforth we call the algorithms in Eqns (4), (5) and (6) ‘multiplicative’, ‘extended’ and ‘additive’, respectively.
The extended and multiplicative algorithms have been modified as suggested by Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others (2005), by incorporating surface albedo. The multiplicative algorithm derives from a classical degree-day model with the melt factor here corrected, in space and time, by the net fraction of CSR. Reference HockHock (1999) extended the multiplicative algorithm by adding a simple degree-day term. The additive algorithm, on the other hand, derives from an extreme simplification of the energy equation, aimed at preserving some physical significance while using air temperature as the unique meteorological input to calculate melt. These differences affect melt calculations in a significant way. In particular, a different sensitivity to air temperature is reported in the literature (e.g. Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others, 2005) and possible compensation effects are expected to exist with respect to air-temperature extrapolations from weather stations.
The albedo is related to the ‘thermal history’ of the surface layer of the snowpack (Reference Brock, Willis and SharpBrock and others, 2000), which can be represented by the positive temperature sum (ST, updated hourly) since the formation of the snow layer. The model calculates snow albedo using a stack algorithm at the pixel scale. At every snowfall (PX,t >0.5 mm), a new snow layer is created and set active with a fresh-snow albedo. When the air temperature exceeds the melting point, the positive temperature sum assigned to the surface layer, σ, is increased as follows:
The snow albedo is calculated as
where β1 and β2 are the parameters of the decay function, both given as inputs (see Section 3.3). The thermal sum and the albedo values are stored when a new layer overlaps. The ‘active’ layer is the upper layer and, when it melts completely, the thermal history and albedo calculations restart from the stored values of the underlying layer, if its albedo is lower than the final albedo of the depleted layer. If, on the contrary, it is higher, the albedo and thermal history of the depleted layer are assigned to the new active layer. The glacier ice albedo is assumed to be constant in time and can be given in input as a single uniform value or as a spatially variable map. At the beginning of the winter season (normally 1 October at mid-latitude in the Northern Hemisphere), the residual snow is considered to be firn and converted to a single layer.
During the night, CSR X,t is zero and Eqns (5) and (6) automatically calculate melt as a function only of air temperature, while Eqn (4) will always calculate a melt rate of zero. To overcome this, the nocturnal melt rate is calculated as
using a TMF with the same units and significance described above.
When melt is generated by rainfall (TX,t >0°C and PX,t >0.2 mm), the energy flux at the surface is dominated by the longwave radiation and turbulent heat exchanges (Reference AndersonAnderson, 1968). In this case a temperature-index function, derived from an extreme simplification of the energy budget (Reference AndersonAnderson, 1973), is used to calculate the melt rate:
where 0.0125°C-1 is the amount of melt (mmw.e.) per 1 mm of rainfall at 1 8C, and RF is a rainfall melt factor (mm °C-1 h-1).
The snowpack is assumed to be constantly at the melting point and its ‘cold content’ is not modelled. However, the threshold temperature for melt, T melt = 0°C, is used to refreeze a fraction of liquid water in low-temperature conditions, as follows:
and

where FRZ is a freezing factor (mm °C-1 h-1) and TX,t is air temperature. The final w.e. of the snowpack includes both ice and liquid water retained inside it.
Glacier ice temperature is also assumed to be constant at the melting point, but no refreezing of meltwater is calculated inside it.
3.2. Snow accumulation
Observation of the snow-cover distribution during the ablation season reveals a typical pattern that repeats nearly unchanged from year to year. This is observed both over glaciers and in ice-free terrain above the tree limit. Our observations on Careser and La Mare glaciers confirm this behaviour, which results from the control exerted by local topography on snow accumulation and ablation. Numerous authors have recognized the persistence of topographic control on snow distribution (e.g. Reference Elder, Dozier and MichaelsenElder and others, 1991; Reference Luce, Tarboton and CooleyLuce and others, 1998;Reference Grayson and BloschlGrayson and Bloschl, 2001;Reference Erickson, Williams and WinstralErickson and others, 2005;Reference Sturm and WagnerSturm and Wagner, 2010).
The topography influences snow accumulation since it regulates the spatial distribution of precipitation (i.e. vertical and horizontal gradients) and the wind-driven processes of snow preferential deposition and redistribution (Reference Bloschl, Kirnbauer and GutknechtBloschl and others, 1991;Reference Machguth, Paul, Hoelzle and HaeberliMachguth and others, 2006b;Reference Lehning, Lowe, Ryser and RadeschallLehning and others, 2008;Reference Dadic, Mott, Lehning and BurlandoDadic and others, 2010). During precipitation events, enhanced deposition occurs on the lee side of mountain ridges, while reduced deposition takes place on the windward side. Post-event winds typically erode snow from wind-exposed sites (e.g. ridges and convex areas) and accumulate it on wind-sheltered areas. In addition, snow is transferred by gravity from steep slopes to the underlying flatter areas, in the avalanche runout zones.
In this work, topographic indexes calculated from the DTM were used to account for wind and avalanche redistribution and, indirectly, for preferential deposition. A snow redistribution factor (SRF) is calculated offline from (1) a relative elevation attribute (REAr), which accounts for wind exposure (Reference Carturan and SeppiCarturan and others, 2009b), and (2) a gravitative mass transport and deposition (MTD) algorithm proposed by Reference GruberGruber (2007). The REAr is the difference between the DTM and a smoother DTMs, calculated as the average elevation of each pixel within an assigned radius, r (m). The indexed REAr (REAindex) can be >1 (dips), <1 (peaks, crests) or 1 (flat areas). In MTD the mass transport is driven along the flow paths derived from the DTM, and is controlled by a slope limit, by the available mass and by the maximum deposition, a local variable.
The empirical parameters that control SRF are (1) r (averaging radius of REAr), (2) REAindex range, (3) I/Dlim ratio (snow-input/snow-deposition limit ratio for MTD) and (4) βlim (slope limit for MTD). Additional effects of wind and avalanches are not calculated. Therefore, in the areas of gravitational redistribution, snowdrift is not calculated and vice versa. The final SRF grid expresses the local accumulation anomaly for solid precipitation. This grid is applied as a local multiplier for precipitation, when air temperature does not exceed the snow/rain threshold (Eqn (3)). Similar approaches have been proposed, for example, by Reference Tarboton, Chowdhury and JacksonTarboton and others (1995), Reference Huss, Bauder and FunkHuss and others (2009) and Reference Farinotti, Magnusson, Huss and BauderFarinotti and others (2010).
3.3. Model set-up, calibration and validation
A DTM with a grid size of 10m was derived from a lidar aerial survey carried out in September 2006. It was used to calculate the snow redistribution parameters and as input for mass-balance calculations.
Air-temperature and precipitation data from Careser Diga (2605 m a.s.l.) and Cogolo (1200ma.s.l.) (Fig. 1) were first checked for missing values and inhomogeneities. Rain- gauge undercatch errors were adjusted using a correction procedure that accounts for the aggregation phase of the precipitation, the wind speed and the wind exposure of gauge sites (Reference SevrukSevruk, 1986;Reference Spreafico, Weingartner and LeinbundgutSpreafico and others, 1992; Carturan and others, in press). At Careser Diga the correction factor for snow (1.6 on average) was calculated from the w.e. of fresh snow.
The precipitation was extrapolated from Careser Diga by a monthly variable vertical precipitation gradient, PLIF (%km-1), referred to Careser Diga elevation. PLIF was calculated offline from monthly sums of corrected precipitation at the two weather stations (0-62% km-1; the minimum was set to 0%km-1 to avoid null or negative precipitation at high altitude). It was not adjusted to fit observed accumulation over the glaciers, since it is not a calibration parameter. Horizontal gradients of precipitation were assumed to be negligible in the study area. In this work, a monthly resolution was used to account for the temporal variability of vertical precipitation gradients (e.g. Reference SchwarbSchwarb, 2000;Reference KuhnKuhn, 2003). Higher time resolutions were tested but did not improve calculations.
The air-temperature data of Cogolo were not used in mass-balance calculations, since this station lies in the valley bottom and is subject to thermal inversions. A fixed standard lapse rate of-6.5°Ckm-1 was used to extrapolate air temperature from Careser Diga, in the absence of information concerning the distribution of air temperature over the two glaciers.
The initialization parameters were mostly calculated from the meteorological dataset and from experimental data. In a few cases they were taken from the literature (Table 2). The average rain/snow threshold temperature and the parameters for the calculation of clear-sky global radiation (atmosphere diffusivity and optical depth) were determined by direct observations at Careser Diga. Distributed measurements of albedo, mostly over ice, were carried out on both glaciers using a portable albedometer during the 2007 and 2008 summer seasons. In addition, higher time-resolution data were acquired over snow by a data logger at an experimental site on La Mare glacier (Reference Carturan and SeppiCarturan and others, 2009c). These data were used to calculate the parameters of the decay function of snow albedo (A and /32 in Eqn (8)), and to initialize the spatial distribution of ice albedo by a map that expresses its inverse linear relationship with elevation (r =0.75; Fig. 2). A similar dependence was found by other authors (e.g. Reference OerlemansOerlemans, 1992;Reference Koelemeijer, Oerlemans and TjemkesKoelemeijer and others, 1993) and is related to a gradual increase in surface concentration of dust and debris towards the glacier front. In unsampled areas at high altitude, we assumed a constant. ice albedo of 0.32, the measured value at the highest sampled point (3242 m a.s.l.). Temporal variations of ice albedo were not modelled. Firn was exposed for short periods in small areas of La Mare glacier. It was quite dark and showed an average albedo of 0.19 (range 0.14-0.30), so firn was not distinguished from ice in model initialization.
Table 2. EISModel initialization parameters: bold type indicates parameters derived from experimental data; normal type indicates parameters obtained from the literature

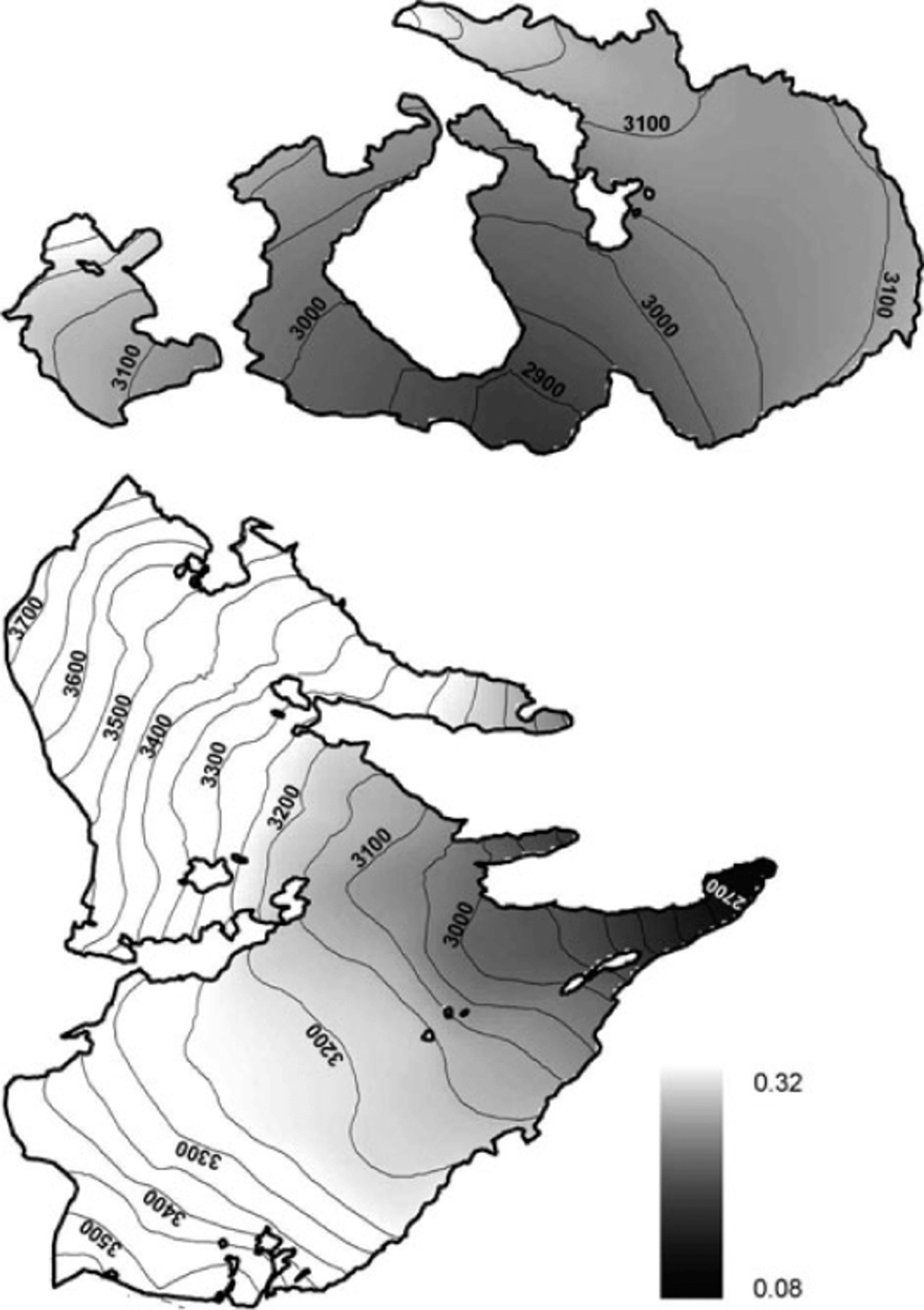
Fig. 2. Ice albedo distribution calculated from field measurements on Careser and La Mare glaciers.
Snow redistribution was optimized by comparing different SRF maps (Section 3.2;calculated by different combinations of parameters) with normalized data of snow w.e. measured on glaciers at the end of the 2007/08 accumulation season. The snow redistribution across the glacier margin was taken into account by including a buffer of 200m outside the glacier perimeter in SRF calculations. For the 2007/08 accumulation season the snow accumulation data could be directly compared to precipitation without computing ablation, since winter melt and liquid precipitation were negligible and accumulation measurements were carried out before the onset of the ablation season. Normalized data of snow w.e. were calculated with respect to the extrapolated precipitation from Careser Diga in the 2007/08 accumulation season (average PLIF = 32.5% km-1), and the accuracy of the different SRF maps was assessed using the Reference Nash and SutcliffeNash and Sutcliffe (1970) efficiency index (Ef). Too few snow w.e. data were available in avalanche areas for a quantitative optimization of MTD parameters. Hence in these areas the redistribution parameters were adjusted according to direct observations and mapping of recent avalanches and summer snow cover.
The calibration parameters (TMF, RTMF, RMF) were optimized by comparing simulation outputs with cumulated mass-balance measurements at single points in the three years 2004-06, maximizing Ef. The model was independently validated using cumulated mass balances at individual points in the three years 2007-09. In addition, we compared measured and modelled temporal behaviour of mass balance, seasonal components and summer snow-cover maps. All these evaluations were made with unchanged parameters (initialization and calibration parameters reported in Tables 2-4). The snow w.e. was initialized for each model run by means of measured data, while the ice w.e. was initialized with an arbitrary constant value of 50 m (i.e. larger than the observed maximum net ablation over the 6 years). The start and end dates of the model runs (calibration, validation and seasonal components) are reported in Table 5.
Table 3. Optimal values for the SRF parameters

Table 4. Melt factors and statistics of EISModel calibration (2004–06) and validation (2007–09). Ef is the efficiency index. Root-mean-square error (RMSE) and mean error (ME) are expressed in mm a–1

Table 5. Start and end dates of the model runs executed on Careser and La Mare glaciers. Date format is dd-mm-yyyy

4. Results
4.1. Snow redistribution
Figure 3 shows the snow distribution pattern at the end of the 2007/08 accumulation season and the snow-cover pattern in the following summer. Very similar patterns were observed throughout the observation period (2004-09). The exceptionally low snow cover in mid-August 2003, attributable to a strong positive temperature anomaly (Reference ScharSchar and others, 2004), is added in Figure 3b to show the areas with maximum net accumulation. Remarkable differences between the two glaciers are observed. The snow distribution is complex and affected by redistribution on La Mare glacier, while it looks more uniform on Careser glacier, with a few exceptions at the glacier margins. The timing of snowmelt is also very different and largely depends on the hypsometric distribution of area vs altitude.

Fig. 3. (a) Spatial distribution of normalized snow w.e. data at the beginning of May 2008, on Careser and La Mare glaciers. (b) Observed snow-cover extent on different dates during summer 2008 and in August 2003. Date format is dd-mm-yyyy.
In Figure 4 we show the Nash and Sutcliffe indexes obtained with various DTM resolutions and different combinations of parameters controlling snow redistribution by wind. A REAindex range of 0.1-1.9 was found to provide the best results, irrespective of other parameters. Figure 4a (Careser and La Mare glacier datasets) shows a strong dependence of efficiency on REAr radius and on DTM resolution, with the best results provided by low REAr radius and high DTM resolution. However, these results are biased by the different sample sizes of the two glaciers (156 soundings on Careser glacier and 83 on La Mare glacier). As noted before (Fig. 3), La Mare glacier is far more affected by snow redistribution than Careser glacier, and it is likely more suitable for adjusting SRF parameters. The results of the same analysis, using the only subset of La Mare glacier, are shown in Figure 4b. In this case we found an optimal radius of 60 m for REAr and a lower sensitivity to the DTM resolution, since on La Mare glacier the redistribution effects prevail over ‘noise effects’ (which increase with DTM resolution and are typical of areas where wind redistribution is of secondary importance).

Fig. 4. Efficiency of different SRF maps (REAindex range = 0.1–1.9), with varying r (averaging radius of REAr) and DTM cell size, in the 2007/08 accumulation season: (a) Careser and La Mare glaciers; (b) La Mare glacier alone.
The data collected in avalanche deposits were too few for a similar analysis of the gravitative redistribution. In this case, βlim and I/Dlim were optimized in order to match the observed avalanche paths. The resulting optimal values for the SRF parameters are reported in Table 3, and the corresponding SRF map is shown in Figure 5, where yellow to deep red indicates snow erosion and light blue to purple indicates snow accumulation. The impact of snow redistribution is clear in Figure 6. On Careser glacier the improvements were more evident where snow redistribution is expected to occur (e.g. near the margins and over the ice ridge in the northeastern part of the glacier). On La Mare glacier the enhancements were more widespread, even if underestimations persisted in the upper part of the glacier.

Fig. 5. The SRF map used in simulations.

Fig. 6. Spatial distribution of differences between extrapolated winter precipitation from Careser Diga and snow w.e. measured at the beginning of May 2008: (a) without redistribution; (b) with redistribution through SRF.
4.2. Mass-balance modeling
The surfaces in Figure 7 show the results of the calibration procedure for the three melt algorithms. A ‘ridge’ of high Ef values, rather than a clear peak, is observable for all three algorithms, indicating the presence of many combinations of parameters which provide nearly identical results in terms of model efficiency. Figure 8 displays the results of EISModel calibrations and validations, and Table 4 reports the corresponding statistics. The temporal behaviour of mass balance is given in Figures 9 and 10, which compare modelled and measured cumulated values at seven ablation stakes (numbered 1–7 in Fig. 8f).
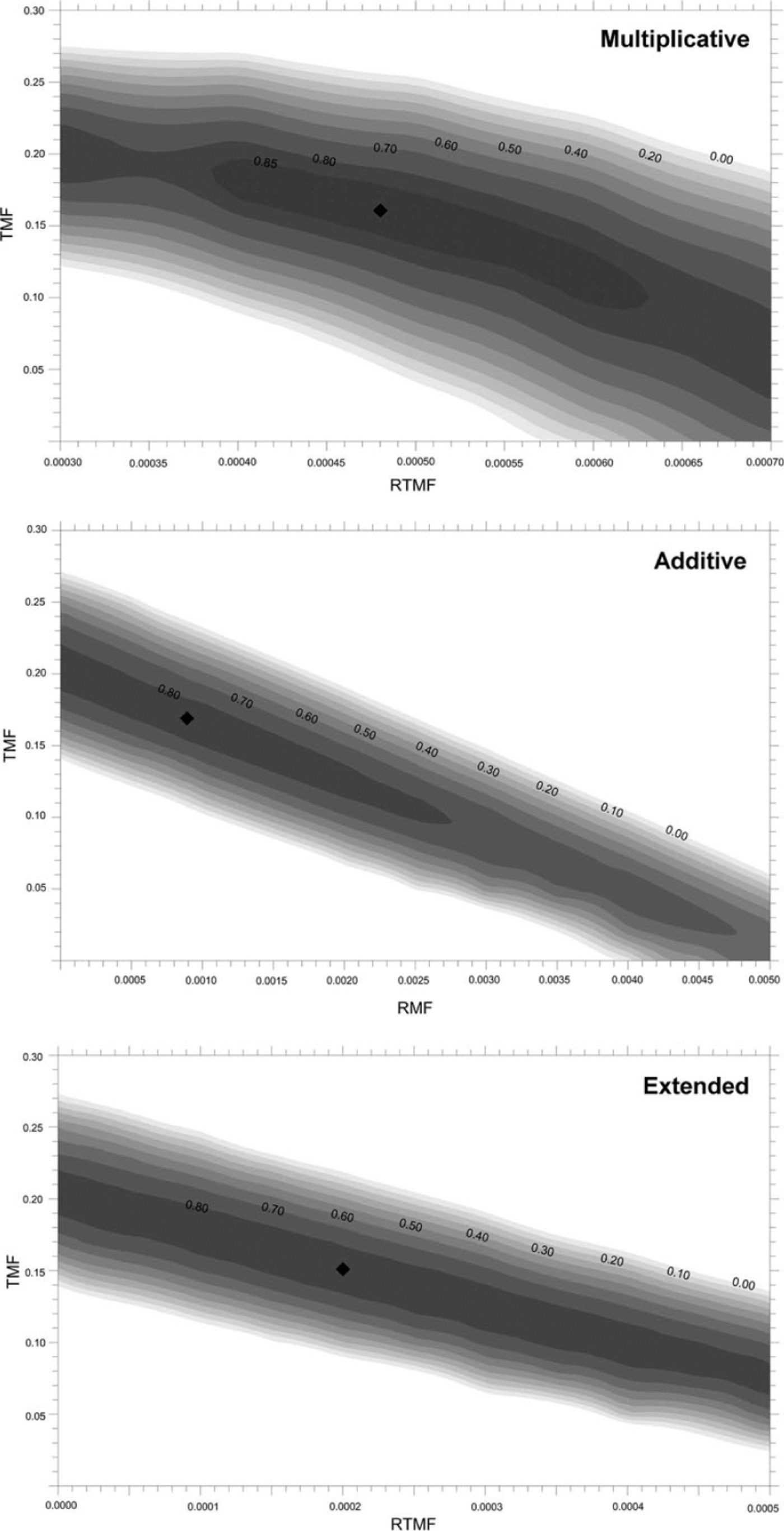
Fig. 7. Ef index for different combinations of calibration parameters (grey shades). Calibration values are highlighted by a black rhombus.

Fig. 8. Spatial distribution of simulation errors and measured vs simulated mass balances with the multiplicative (a, b), additive (c, d) and extended (e, f) melt algorithms.
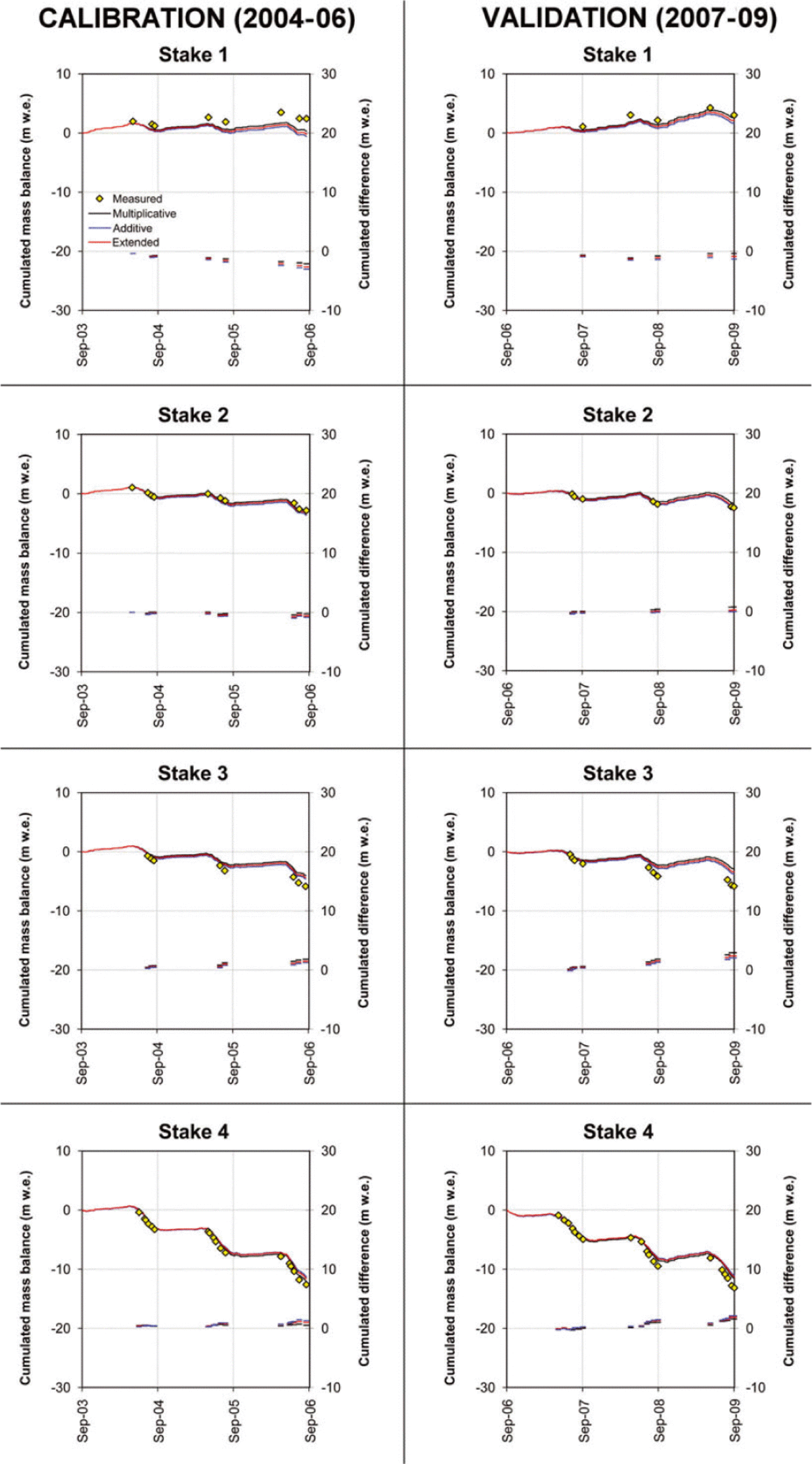
Fig. 9. Measured and modelled cumulative mass balance at four ablation stakes on La Mare glacier (numbered 1-4 in Fig. 8f).
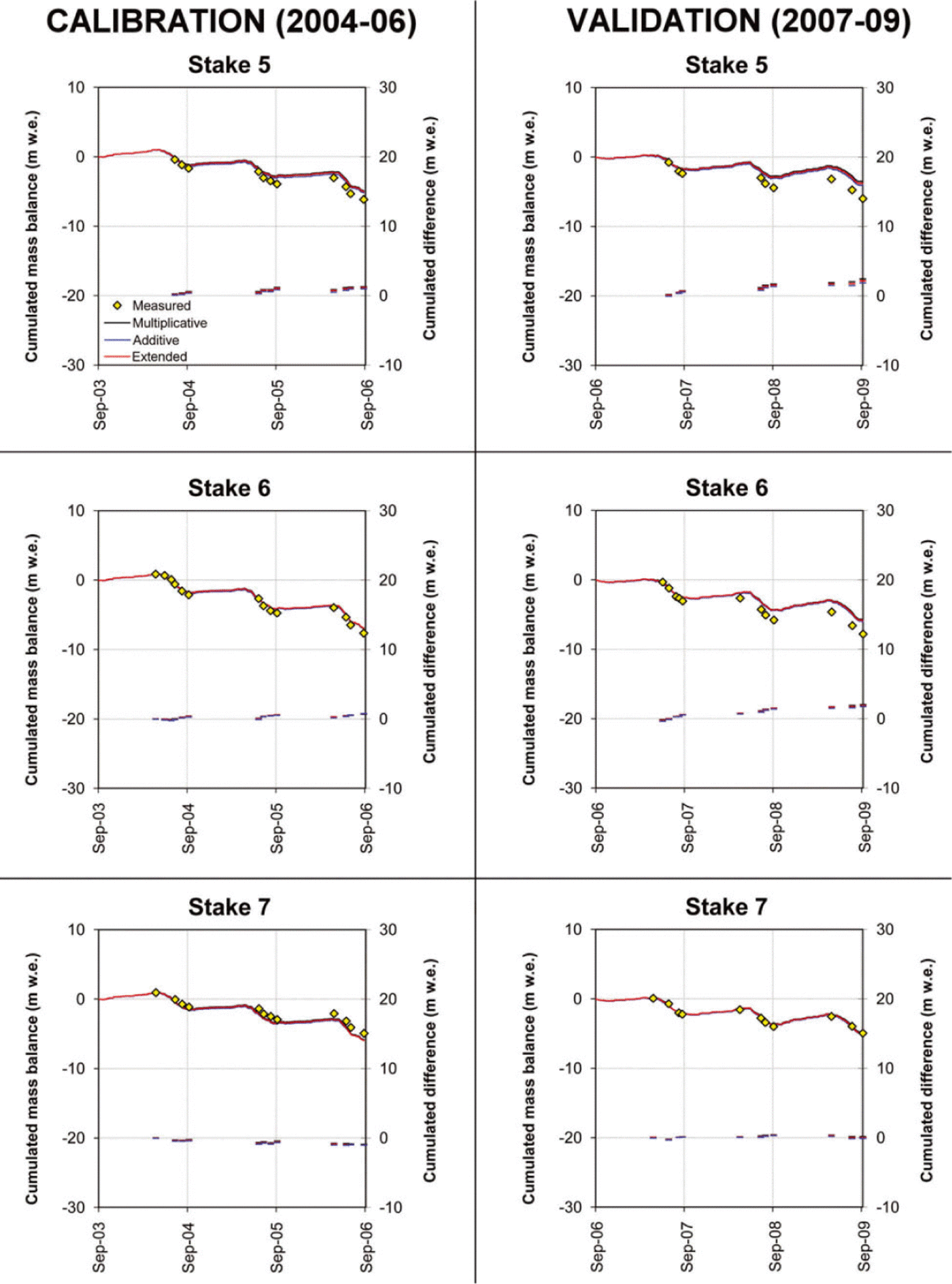
Fig. 10. Measured and modelled cumulative mass balance at three ablation stakes on Careser glacier (numbered 5–7 in Fig. 8f).
The three melt algorithms captured quite well thespatial and temporal variability of the mass balance in the investigated glaciers, providing comparable performances. The multiplicative algorithm matched slightly better the observed vertical gradient of mass balance, but the other two formulations were more efficient in the validation period. The overall Ef index (average of calibration and validation values) was 0.819, 0.809 and 0.790 for the additive, extended and multiplicative melt algorithms, respectively.
An interesting outcome of calibration is the clustering of simulation errors in well-defined areas. A prevalence of mass-balance overestimations in the calibration period is observable in the central and lower part of La Mare glacier and in the western part of Careser glacier, while the mass balance was underestimated in the eastern flat area of Careser glacier and in the upper point (accumulation area) of La Mare glacier. In the validation period the calibrated melt factors were generally too low, with the exception of the eastern area of Careser and of the points near or above the equilibriumline altitude of La Mare glacier. The temporal behaviour of the three melt algorithms was nearly identical (Figs 9 and 10), with a few exceptions in 2006 and 2009 on La Mare glacier.
The analysis of the seasonal components of mass-balance simulations is summarized in Tables 6 and 7 and Figures 11 and 12. The three algorithms gave very similar results in the accumulation season;the multiplicative and the extended algorithm results were nearly identical, while the additive algorithm slightly underestimated the accumulation. In 2006 a possible underestimation of vertical precipitation gradients led to a general underestimation of accumulation. The comparison with the ‘extended (without SRF)’ simulation in Table 6 and Figure 11 shows how the model performance is improved by including the snow redistribution procedure. Overall we observe a tendency to overestimate the low accumulation rates and to underestimate the high accumulation rates.
Table 6. Accuracy of snow w.e. simulations in May. Ef is the efficiency index. RMSE and ME are expressed in mm w.e.

Table 7. Accuracy of summer balance simulations. Ef is the efficiency index. RMSE and ME are expressed in mm w.e.

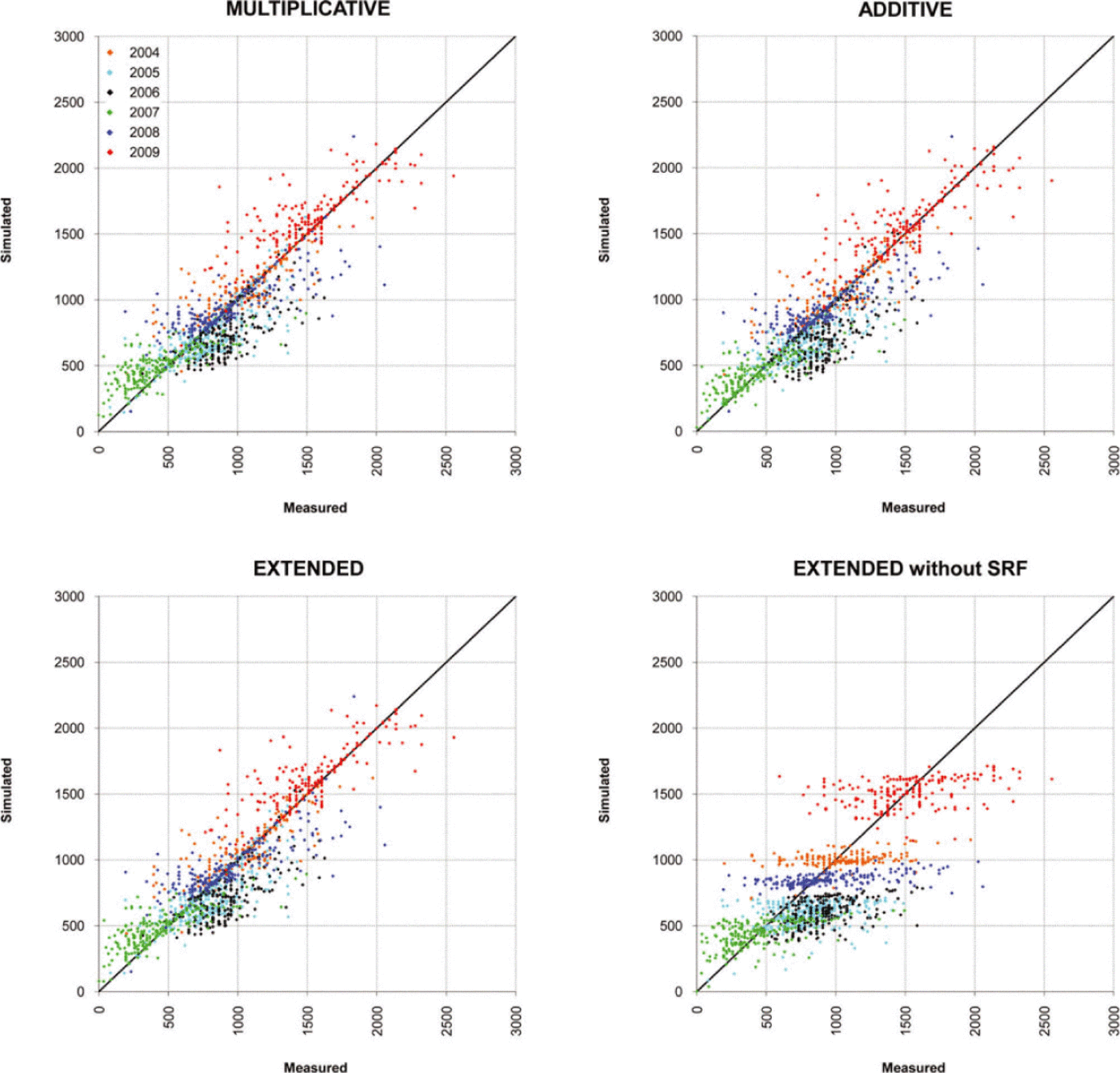
Fig. 11. Measured vs simulated snow w.e. values in May from 2004 to 2009 on Careser and La Mare glaciers. Summary statistics are reported in Table 6.

Fig. 12. Measured vs simulated summer balances from 2004 to 2009 on Careser and La Mare glaciers. Summary statistics are reported in Table 7.
The best performance in simulating summer balance was achieved using the multiplicative melt algorithm (Table 7; Fig. 12). In particular, this algorithm slightly better captured the vertical gradient of mass balance (better alignment of simulated vs observed couples with the 1 : 1 line in Fig. 12), which was somewhat underestimated by the additive and extended algorithms. This overestimation of the low melt rates and underestimation of the high melt rates was observable both in space (e.g. lower and upper areas of La Mare glacier) and in time (e.g. 2004 and 2006 in Table 7), and was more remarkable for the additive formulation. Significant overestimations of the summer balance (too low melt rates) occurred in 2008, with comparable magnitude by the three formulations.
Figure 13 compares observed and simulated snow-cover maps in summer 2004, using the multiplicative melt algorithm. A fairly good correspondence was found between observations and simulations over both glaciers. Snow melted slightly earlier than observed in the eastern part of Careser glacier and later in the western part of Careser glacier and on La Mare glacier. This behaviour confirms the results obtained at the ablation stakes (Fig. 8). Other exceptions were found on high-altitude unsampled areas of La Mare glacier, where the simulated snow cover in late summer was more continuous than observed. In most cases these discrepancies must be attributed to the systematic under- or overestimation of ablation on specific areas, as was assessed at ablation stakes, but snow redistribution and precipitation gradients may also have played a role.

Fig. 13. Comparison of simulated (multiplicative melt algorithm) vs observed snow-cover maps in summer 2004.
5. Discussion
The snow redistribution procedure implemented in the EISModel, though very simple, significantly improved the simulation of snow accumulation on the investigated glaciers, with respect to an extrapolation of precipitation data using only vertical precipitation gradients (Figs 6a and b and 11; Table 6). The improvements were more decisive on La Mare glacier and in areas of Careser glacier where redistribution is more active (i.e. near the margins and in the northeastern ridge). The comparison of observed snow cover with simulations in summer 2004 confirms that the redistribution procedure also works well in unsampled areas. The use of a unique SRF map throughout the 6 year period implies the general assumption of a stationary distribution pattern of snow, dominated by local topography and insensitive to weather conditions and snowpack characteristics (i.e. wind speed and direction, precipitation gradients, erodibility of snow surface, internal layering, etc.). Nevertheless, calculations did not seem to be much affected by this assumption (see Table 6), with the exception of winter 2006. In this case the vertical precipitation gradient calculated between Careser Diga and Cogolo was too low, leading to underestimation of precipitation over the glaciers. The redistribution procedure, as it was implemented, does not capture snow accumulation on the lee side of obstacles and sudden slope changes (e.g. on the tongue of La Mare glacier). Moreover, uncertainties affect inaccessible or unsampled areas like avalanche deposits and high-elevation crests or steep slopes. Underestimation of accumulation persisted in the highest sampled area of La Mare glacier (Fig. 6b). In this high-accumulation area, some tests revealed better results with higher REAr radiuses (~100m instead of 60 m), possibly due to increasing wind speeds and longer paths of drifted snow at high elevation than at lower elevation. However, more data are needed, especially at high altitude, to confirm a possible direct relationship between elevation and optimal radius of REAr.
In general, the distribution of mass balance in the two investigated glaciers appears well captured by the model, irrespective of the melt algorithm used. The three different formulations provided very similar results (Figs 8-12; Tables 4, 6 and 7), and the multiplicative algorithm obtained the better statistics in simulating the seasonal components of mass balance and in the calibration period. In particular, a closer inspection of the results reveals a slightly better performance of this algorithm in capturing the vertical gradient of mass balance. On the other hand, it was less efficient during the validation period, with respect to the additive algorithm and the extended algorithm.
This behaviour must be attributed to the different structure of melt formulations (Eqns (4-6)). A higher sensitivity to air temperature must be expected for the extended and for the multiplicative algorithms, compared to the additive algorithm where the temperature-dependent and -independent components are separated (Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others, 2005). This higher sensitivity of the multiplicative formulation led to a stronger decrease in model efficiency from calibration to validation periods, which showed different weather characteristics (Table 1). On the other hand, it likely compensated some unavoidable inaccuracies in the extrapolation of air temperature over the glaciers, as discussed hereafter, providing a more realistic vertical gradient of mass balance.
The examination of mass-balance results can be useful to both improve the knowledge of dominant processes and enhance the robustness of the model. In particular, the presence of systematic errors clustered into specific areas of Careser and La Mare glaciers is remarkable (Figs 8 and 13). On Careser glacier the ablation is underestimated on eastfacing slopes and overestimated in west-facing areas during the calibration period (2004-06). The distribution of simulation errors in the validation period (2007-09) confirms this behaviour, and suggests the existence of uncaptured processes which are neither local nor accidental. On La Mare glacier their spatial distribution is less organized, suggesting more local sources of error.
Inaccuracies in the simulation of melt processes in most cases explain the observed simulation errors, while wrong calculations of accumulation were of minor importance and not systematic (Figs 9 and 10;Tables 6 and 7). Possible excessive simplifications or assumptions must be regarded as the main cause of these discrepancies. Among them, the assumptions regarding air temperature and shortwave radiation distribution, as discussed hereafter, seem to play a crucial role, even though they are reasonable and widely used in the literature.
The 2 m air temperature was calculated by a moist adiabatic lapse rate (-6.5°Ckm-1), from a weather station located outside the thermal influence of glaciers. The glacier cooling effect (Reference BraithwaiteBraithwaite, 2008) was not explicitly simulated. Therefore it was accounted for by calibration parameters and this corresponds to assuming it as a linear function of the extrapolated temperature. The actual air- temperature distribution, however, was likely more complex as evidenced by experiments carried out with AWS over glaciers (e.g. Reference Greuell, Knap and SmeetsGreuell and others, 1997;Reference Greuell and BOhmGreuell and Bohm, 1998;Reference Strasser, Corripio, Pellicciotti, Burlando, Brock and FunkStrasser and others, 2004). In particular, the 2 m air- temperature lapse rate tends to be lower over melting glaciers with respect to the moist adiabatic lapse rate. The temperature distribution is also affected by the local prevalence of cooling due to loss of sensible heat (gentle slopes) or prevalence of adiabatic heating of descending air (steep slopes), heat released from rock outcrops, interaction of glacier wind with valley winds and coupling of the glacier microclimate to the synoptic-scale weather conditions (Reference OerlemansOerlemans, 2001, Reference Oerlemans2010).
The assumptions regarding the 2 m air temperature may have caused an overestimation of ablation in the eastern flat area of Careser glacier, where the cooling effect is expected to be more effective with respect to other (steeper) areas. A local warming effect could be responsible for mass-balance overestimations in the central part of La Mare glacier (ablation stake 3 in Fig. 8f), which is located downstream of a steep glaciated slope which could be responsible for local adiabatic heating due to the glacier wind (Reference Strasser, Corripio, Pellicciotti, Burlando, Brock and FunkStrasser and others, 2004), possibly enhanced by the nearby rock outcrops. In the lower part of La Mare glacier, underestimation of ablation prevailed and a lower air-temperature lapse rate would have even worsened calculations. There, a local warming effect by nearby unglaciated slopes and/or valley winds very likely occurred.
The synoptic-scale weather conditions may also have influenced the air-temperature distribution. In particular, some types of weather (e.g. persistent anticyclones with high temperatures and low wind speeds in the free atmosphere) could have favoured a more efficient cooling effect by the glacier surfaces, with respect to other weather conditions. In this case, estimating 2 m air temperatures from measurements taken outside the thermal influence of the glaciers and at lower altitudes may have led to overestimations, especially during daytime (Reference Stenning, Banfield and YoungStenning and others, 1981;Reference OerlemansOerlemans, 2010). Thus, the temporal variability of the glacier cooling effect possibly played a role in controlling melt rates.
Clear-sky radiation (CSR) was calculated and used as an index of melt energy. It only depends on astronomical and terrain characteristics, so the actual distribution of melt energy may have been very different from simulations. Firstly, global radiation typically increases with elevation, due to cloud characteristics and multiple reflection between clouds and snow-covered slopes (Reference Greuell, Knap and SmeetsGreuell and others, 1997; Reference Marty, Philipona, Frohlich and OhmuraMarty and others, 2002). Secondly, the atmospheric disturbances can greatly reduce the shortwave radiation inputs and significantly impact melt modelling (Reference Pellicciotti, Raschle, Huerlimann, Carenzo and BurlandoPellicciotti and others, 2011). In addition, the diurnal cycle of cloud cover during the ablation season is another important process controlling the actual melt energy supply. During summer a daily recursive cloud formation cycle is often recognizable in many alpine areas (Reference Gray and JacobsonGray and Jacobson, 1977;Reference Bergman and SalbyBergman and Salby, 1996;Reference Kondragunta and GruberKondragunta and Gruber, 1996): the sky is almost clear in the morning and becomes progressively cloudier in the afternoon, under the effect of thermal convection. Therefore the areas exposed to the east tend to receive a larger portion of clear-sky shortwave radiation than the areas exposed to the west. The thermal convection can also trigger the formation of ‘orographic’ clouds, which form and persist over the same area in the absence of atmospheric disturbances.
The spatial distribution of simulation anomalies (Figs 8 and 13) is consistent with a diurnal cycle of cloud cover, whose persistence during the 2007 and 2008 ablation seasons was verified by global radiation measurements at the Careser Diga weather station (~40% average reduction in fraction of clear-sky global radiation from 07:00 to 19:00). However, the shading of persistent orographic clouds in some areas and the multiple reflection between scattered clouds and glaciated slopes in others could also have played a role.
Other simplifications involve ice albedo which, based on field measurements, was set dependent on altitude and constant in time (Section 3.3). Some authors have reported a decay of ice albedo leading to a positive feedback in deglaciation (e.g. Reference Paul, Machguth and KaabPaul and others, 2005;Reference OerlemansOerlemans, 2010), but this behaviour was hardly parameterizable for Careser and La Mare glaciers.
Using fixed melt factors implies a steadiness of the relative importance of energy-balance components used to calculate ablation (shortwave net radiation and temperature- dependent part of the energy flux), while field evidence showed significant differences between different sites on different glaciers and in periods with heterogeneous weather conditions (Reference HockHock, 2005; Reference Carenzo, Pellicciotti, Rimkus and BurlandoCarenzo and others, 2009;Reference OerlemansOerlemans, 2010).
The prevailing overestimations of mass balance in the validation period may have been related to different weather conditions from those during the calibration period. However, further investigations are required to understand possible links between the synoptic circulation and variables connected to the energy and mass balance on these glaciers. On the other hand, the feedback related to surface albedo certainly played a role, since underestimations of the snow accumulation prevailed in the calibration period, while overestimations mainly occurred in the validation period (Table 6). This implied the calculation of lower melt factors during calibration, which turned out to be excessively low in the following 3 years.
6. Conclusions
The availability of a comprehensive dataset of mass-balance measurements for two neighbouring glaciers in the eastern Italian Alps allowed us to implement and test a mass- balance model, across 6 consecutive years. The distributed dataset is characterized by a high spatial and temporal variability of physical and weather conditions and constitutes a severe test for modelling assumptions. An ‘enhanced temperature-index’ modelling approach was used, focusing on snow redistribution processes and comparing three different melt algorithms proposed in recent literature. The purpose was to assess the performance and possible limits of this modelling approach in the absence of meteorological observations on the glaciers.
The proposed snow redistribution procedure only uses the DTM and accounts for the attitude of each gridcell to accumulate snow, based on its degree of wind exposure and location along avalanche paths. A map of snow redistribution was calculated from the DTM and was used in mass- balance calculations as a multiplicative factor for solid precipitation. This procedure, while simple, significantly improved the simulation of accumulation processes. However, it must be noted that precipitation data need to be properly pre-processed to be extrapolated from gauging stations to high-altitude, ungauged areas (i.e. correction for gauge errors and calculation of precipitation gradients). There is still room for refinements, by acquiring more data at high elevation or over inaccessible areas (e.g. by remote sensing), in order to improve knowledge of redistribution processes and precipitation gradients.
The mass-balance simulation was satisfactory, with all three algorithms tested, which gave very similar results. The multiplicative formulation was more efficient in calibration and in simulation of the seasonal components, since it better captured the vertical gradient of mass balance, due to its higher sensitivity to air temperature. However, this characteristic became a drawback in validation since the other two algorithms were somewhat more stable.
Simulation errors were clustered in specific areas. In particular, the mass balance was underestimated in west- exposed sites and overestimated in east-exposed sites and at the tongue of the lowest-reaching glacier. In addition, the melt factors calibrated in the first 3 years of simulation were too low for the last 3 years of independent validation. Wrong melt simulations were more decisive than inaccuracies in accumulation modelling, in most cases.
Possible reasons for inaccuracies in mass-balance calculations must be sought in the modelling approach (sensitivity to air temperature, spatial and temporal variability of melt factors) and in assumptions concerning air temperature and incoming shortwave radiation over glaciers. As far as air temperature is concerned, we assumed a moist adiabatic lapse rate and a uniform cooling effect, while the incoming shortwave radiation was surrogated by a fixed portion of the clear-sky radiation. A number of possible deviations from these assumptions, compatible with the spatial distribution of simulation errors, have been discussed. The most interesting to evaluate are: (1) the temporal and spatial variability of the glacier cooling effect, (2) the interaction with valley winds and local heating by rock outcrops and deglaciated slopes and (3) the temporal and spatial distribution of cloud cover. It is worth noting that possible inaccuracies in the calculation of air temperature over glaciers may have been partly or totally compensated by the different sensitivity to air temperature of the three melt algorithms.
Further considerations aimed at establishing which of the melt algorithms works better on Careser and La Mare glaciers would not provide conclusive and unequivocal responses. The uncertainty affecting the calculation of air temperature and incoming shortwave radiation over the glaciers from off-site weather data partly masks the peculiar behaviour of each algorithm. The model performance will probably benefit from even simpler parameterizations of the cloud cover (temporal variability, diurnal cycle, orographic clouds) and of air temperature (spatial and temporal variability of the glacier cooling effect). Therefore a quantitative assessment of these variables and of their relative importance by automatic instrumentation would be very valuable. Experiments are planned in the next few years to enhance the focus on the dominant processes regulating the mass-balance distribution and the current deglaciation phase on this area.
Finally, it must be noted that a more complete knowledge of these processes is an essential prerequisite not only for simple modelling schemes such as temperature-index approaches, but also for more complex and physically based models, in order to avoid equifinality and distortions in parameter calibrations.
Acknowledgements
We thank the Comitato Glaciologico Trentino - SAT, ENEL SPA, Provincia Autonoma di Trento, Museo Tridentino di Scienze Naturali, Universita di Trento, for support during the fieldwork and for providing the meteorological data. We extend special thanks to the friends, students and mountain guides who have contributed to data surveys. This work was supported by the Universita degli Studi di Padova (UNIPD) 2007 project: ‘Climate change effects on the cryosphere and hydrology of a high-altitude watersheds’.






















