Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-16T16:11:54.488Z Has data issue: false hasContentIssue false
  • English
  • Français

Rational points on hyperelliptic curves having a marked non-Weierstrass point

Part of: Arithmetic algebraic geometry

Published online by Cambridge University Press:  09 October 2017

Arul Shankar  and
Xiaoheng Wang
Arul Shankar
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Ontario, Canada email [email protected]
Xiaoheng Wang
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, Ontario, Canada email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider the family of hyperelliptic curves over 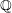$\mathbb{Q}$ having a fixed genus $n$ and a marked rational non-Weierstrass point. We show that when 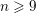$n\geqslant 9$, a positive proportion of these curves have exactly two rational points, and that this proportion tends to one as $n$ tends to infinity. We study rational points on these curves by first obtaining results on the 2-Selmer groups of their Jacobians. In this direction, we prove that the average size of the 2-Selmer groups of the Jacobians of curves in our family is bounded above by 6, which implies a bound of 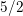$5/2$ on the average rank of these Jacobians. Our results are natural extensions of Poonen and Stoll [Most odd degree hyperelliptic curves have only one rational point, Ann. of Math. (2) 180 (2014), 1137–1166] and Bhargava and Gross [The average size of the 2-Selmer group of Jacobians of hyperelliptic curves having a rational Weierstrass point, in Automorphic representations and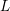$L$-functions, Tata Inst. Fundam. Res. Stud. Math., vol. 22 (Tata Institute of Fundamental Research, Mumbai, 2013), 23–91], where the analogous results are proved for the family of hyperelliptic curves with a marked rational Weierstrass point.

Keywords

rational points on curveshyperelliptic curvesranks of abelian varietiesSelmer groups

MSC classification

Primary: 11G30: Curves of arbitrary genus or genus $ne 1$ over global fields
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 1 , January 2018 , pp. 188 - 222
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bektemirov, B., Mazur, B., Stein, W. and Watkins, M., Average ranks of elliptic curves: tension between data and conjecture , Bull. Amer. Math. Soc. (N.S.) 44 (2007), 233–254 (electronic).Google Scholar
Bhargava, M., The density of discriminants of quartic rings and fields , Ann. of Math. (2) 162 (2005), 1031–1063.CrossRefGoogle Scholar
Bhargava, M., The density of discriminants of quintic rings and fields , Ann. of Math. (2) 172 (2010), 1559–1591.CrossRefGoogle Scholar
Bhargava, M., Most hyperelliptic over $\mathbb{Q}$ curves have no rational points, Preprint (2013), arXiv:1308.0395.Google Scholar
Bhargava, M. and Gross, B., The average size of the 2-Selmer group of Jacobians of hyperelliptic curves having a rational Weierstrass point , in Automorphic representations and L-functions, Tata Inst. Fundam. Res. Stud. Math., vol. 22 (Tata Institute of Fundamental Research, Mumbai, 2013), 23–91.Google Scholar
Bhargava, M. and Gross, B., Arithmetic invariant theory , in Symmetry: representation theory and its applications, Progress in Mathematics, vol. 257 (Birkhäuser, New York, 2014), 33–54.Google Scholar
Bhargava, M. and Shankar, A., Binary quartic forms having bounded invariants, and the boundedness of the average rank of elliptic curves , Ann. of Math. (2) 181 (2015), 191–242.CrossRefGoogle Scholar
Bhargava, M., Shankar, A. and Wang, X., Squarefree values of polynomial discriminants I, Preprint (2016), arXiv:1611.09806.Google Scholar
Borel, A., Ensembles fondamentaux pour les groupes arithmétiques , in Colloque sur la Théorie des Groupes Algébriques, Bruxelles (1962), 23–40.Google Scholar
Bosch, S., Lutkebohmert, W. and Raynaud, M., Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), vol. 21 (Springer, Berlin, 1990).Google Scholar
Chabauty, C., Sur les points rationnels des courbes algébriques de genre supérieur à l’unité , C. R. Acad. Sci. Paris 212 (1941), 882–885.Google Scholar
Coleman, R., Effective Chabauty , Duke Math. J. 52 (1985), 765–770.CrossRefGoogle Scholar
Davenport, H., On a principle of Lipschitz , J. Lond. Math. Soc. 26 (1951), 179–183. Corrigendum: ‘On a principle of Lipschitz’, J. Lond. Math. Soc. 39 (1964), 580.Google Scholar
Denef, J. and van den Dries, L., p-adic and real subanalytic sets , Ann. of Math. (2) 128 (1988), 79–138.CrossRefGoogle Scholar
Langlands, R. P., The volume of the fundamental domain for some arithmetical subgroups of Chevalley groups , in Algebraic groups and discontinuous subgroups, Proceedings of Symposia in Pure Mathematics, vol. 9 (American Mathematical Society, Providence, RI, 1966), 143–148.Google Scholar
Platonov, V. and Rapinchuk, A., Algebraic groups and number theory, Pure and Applied Mathematics, vol. 139 (Academic Press, Boston, MA, 1994). Translated from the 1991 Russian original by Rachel Rowen.Google Scholar
Poonen, B. and Schaefer, E., Explicit descent for Jacobians of cyclic covers of the projective line , J. Reine Angew. Math. 488 (1997), 141–188.Google Scholar
Poonen, B. and Stoll, M., Most odd degree hyperelliptic curves have only one rational point , Ann. of Math. (2) 180 (2014), 1137–1166.CrossRefGoogle Scholar
Serre, J. P., A course in arithmetic, Graduate Texts in Mathematics, vol. 7 (Springer, New York, 1973).Google Scholar
Stoll, M., Implementing 2-descent for Jacobians of hyperelliptic curves , Acta Arithmetica XCVIII.3 (2001), 245–277.Google Scholar
Wang, X., Maximal linear spaces contained in the base loci of pencils of quadrics, Preprint (2013), arXiv:1302.2385.Google Scholar
Wang, X., Pencils of quadrics and Jacobians of hyperelliptic curves, PhD thesis, Harvard University (2013).Google Scholar