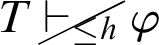
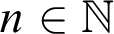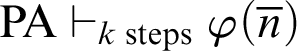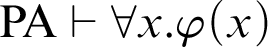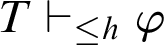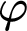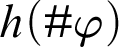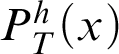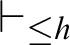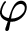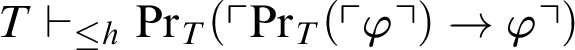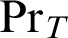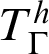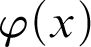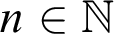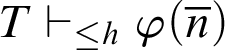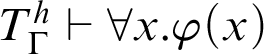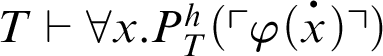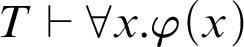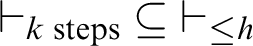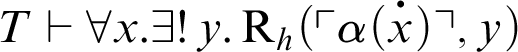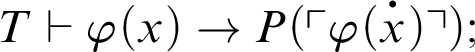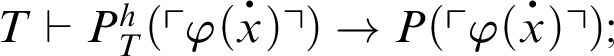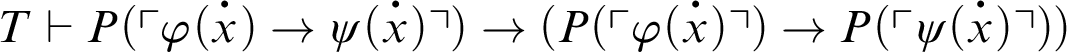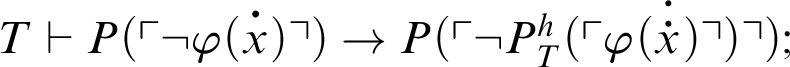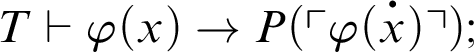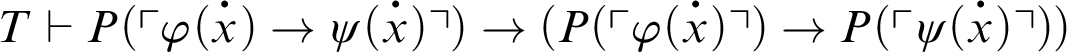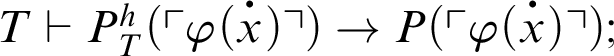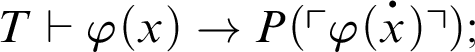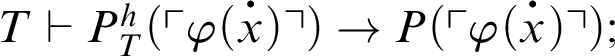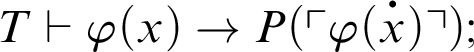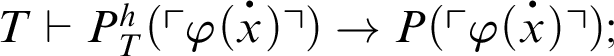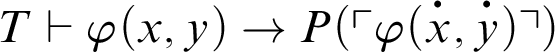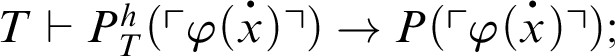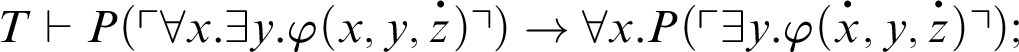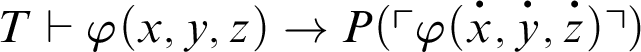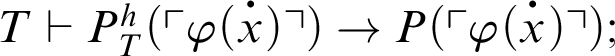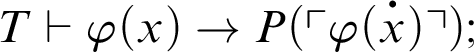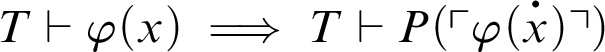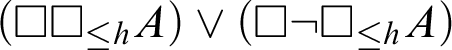1 Preliminaries
Let T be a fixed theory of arithmetic which is a consistent primitive-recursive extension of Robinson’s
![]() $\mathop {\text {Q}} \nolimits $
.
$\mathop {\text {Q}} \nolimits $
.
Following [Reference Ritchie and Young14], we say that a partial function
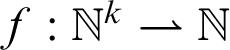 $f:\mathbb {N}^k\rightharpoonup \mathbb {N}$
is strongly representable in T if there is a formula
$f:\mathbb {N}^k\rightharpoonup \mathbb {N}$
is strongly representable in T if there is a formula
![]() $\varphi (x_0,\ldots ,x_{k-1},y)$
such thatFootnote
1
$\varphi (x_0,\ldots ,x_{k-1},y)$
such thatFootnote
1
-
(i) For all
 $m_0,\ldots ,m_{k-1},n\in \mathbb {N}$
,
$m_0,\ldots ,m_{k-1},n\in \mathbb {N}$
,
 $f(m_0,\ldots ,m_{k-1})\simeq n\iff T \vdash \varphi (\overline {m_0},\ldots ,\overline {m_{k-1}},\overline {n})$
;
$f(m_0,\ldots ,m_{k-1})\simeq n\iff T \vdash \varphi (\overline {m_0},\ldots ,\overline {m_{k-1}},\overline {n})$
; -
(ii)
 $T \vdash \forall x_0\cdots \forall x_{k-1}.\exists ! y.\varphi (x_0,\ldots ,x_{k-1},y)$
.
$T \vdash \forall x_0\cdots \forall x_{k-1}.\exists ! y.\varphi (x_0,\ldots ,x_{k-1},y)$
.
If a function f is strongly representable by a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (x,y)$
in T, then f is provably recursive in T (see [Reference Rathjen, Sieg and Zalta13] for a definition of this last concept). Every theory of arithmetic which is a consistent primitive-recursive extension of
$\varphi (x,y)$
in T, then f is provably recursive in T (see [Reference Rathjen, Sieg and Zalta13] for a definition of this last concept). Every theory of arithmetic which is a consistent primitive-recursive extension of
![]() $\mathop {\text {Q}} \nolimits $
can strongly represent every (partial) recursive function (not necessarily by a
$\mathop {\text {Q}} \nolimits $
can strongly represent every (partial) recursive function (not necessarily by a
![]() $\Sigma _1$
-formula; see [Reference Ritchie and Young14]).
$\Sigma _1$
-formula; see [Reference Ritchie and Young14]).
For a standard Gödelization
![]() $\ulcorner \cdot \urcorner $
of the underlying language, we use Feferman’s dot notation [Reference Smorynski16, p. 837]: Let
$\ulcorner \cdot \urcorner $
of the underlying language, we use Feferman’s dot notation [Reference Smorynski16, p. 837]: Let
![]() $\mathop {\text {sub}} \nolimits (x,y)$
be a function-symbol such that, for every term t,
$\mathop {\text {sub}} \nolimits (x,y)$
be a function-symbol such that, for every term t,
![]() $T\vdash \mathop {\text {sub}} \nolimits (\ulcorner \varphi \urcorner ,\ulcorner t\urcorner )=\ulcorner \varphi (t)\urcorner $
, and let
$T\vdash \mathop {\text {sub}} \nolimits (\ulcorner \varphi \urcorner ,\ulcorner t\urcorner )=\ulcorner \varphi (t)\urcorner $
, and let
![]() $\mathop {\text {num}} \nolimits (x)$
be a function-symbol which represents the numerals in T. With
$\mathop {\text {num}} \nolimits (x)$
be a function-symbol which represents the numerals in T. With
![]() $\mathop {\text {s}} \nolimits (x,y):=\mathop {\text {sub}} \nolimits (x,\mathop {\text {num}} \nolimits (y))$
we denote
$\mathop {\text {s}} \nolimits (x,y):=\mathop {\text {sub}} \nolimits (x,\mathop {\text {num}} \nolimits (y))$
we denote
![]() $\mathop {\text {s}} \nolimits (\ulcorner \varphi (x)\urcorner ,y)$
by
$\mathop {\text {s}} \nolimits (\ulcorner \varphi (x)\urcorner ,y)$
by
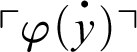 .
.
![]() $P(x)$
is a provability predicate in T if for all formulas
$P(x)$
is a provability predicate in T if for all formulas
![]() $\varphi $
,
$\varphi $
,
![]() $T\vdash P(\ulcorner \varphi \urcorner )$
if, and only if,
$T\vdash P(\ulcorner \varphi \urcorner )$
if, and only if,
![]() $\varphi $
is a theorem of T. Furthermore,
$\varphi $
is a theorem of T. Furthermore,
![]() $S(x)$
is a notion of provability in T if, for every formula
$S(x)$
is a notion of provability in T if, for every formula
![]() $\varphi $
,
$\varphi $
,
![]() $T\vdash S(\ulcorner \varphi \urcorner )$
implies that
$T\vdash S(\ulcorner \varphi \urcorner )$
implies that
![]() $\varphi $
is provable in T. For a provability predicate
$\varphi $
is provable in T. For a provability predicate
![]() $P(x)$
, we define
$P(x)$
, we define
![]() $\mathop {\text {Con}} \nolimits _P:=\neg P(\ulcorner \perp \urcorner )$
.
$\mathop {\text {Con}} \nolimits _P:=\neg P(\ulcorner \perp \urcorner )$
.
We say a formula is
![]() $\Sigma _n$
when it is equivalent in T to a
$\Sigma _n$
when it is equivalent in T to a
![]() $\Sigma _n$
-formula.
$\Sigma _n$
-formula.
For a (partial) recursive function h, the notation
![]() $T\vdash _{\leq h}\varphi $
expresses that
$T\vdash _{\leq h}\varphi $
expresses that
![]() $h(\#\varphi )$
is defined and
$h(\#\varphi )$
is defined and
![]() $\varphi $
is provable in T with a proof whose code is at most
$\varphi $
is provable in T with a proof whose code is at most
![]() $h(\#\varphi )$
. This notion generalises the approach followed in [Reference Lindström9, pp. 33–35].
$h(\#\varphi )$
. This notion generalises the approach followed in [Reference Lindström9, pp. 33–35].
![]() $\vdash _{\leq h}$
depends heavily on the chosen Gödelization: different codings give rise to different notions. For the rest the concrete Gödelization is assumed to be a fixed one.
$\vdash _{\leq h}$
depends heavily on the chosen Gödelization: different codings give rise to different notions. For the rest the concrete Gödelization is assumed to be a fixed one.
Given T, the theory
![]() $K_T$
extends T by the following axiom schema:
$K_T$
extends T by the following axiom schema:
Axiom K. If f is a total recursive function such that, for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() ${f(n)\neq 0}$
, and
${f(n)\neq 0}$
, and
![]() ${\mathop {\text {R}} \nolimits }(x,y)$
is a formula that strongly represents f in T, then
${\mathop {\text {R}} \nolimits }(x,y)$
is a formula that strongly represents f in T, then
![]() $K_T \vdash \forall x.\neg {\mathop {\text {R}} \nolimits }(x,0)$
.
$K_T \vdash \forall x.\neg {\mathop {\text {R}} \nolimits }(x,0)$
.
This schema can be restricted to a smaller class of functions in such a way that
![]() $K_T$
is recursively enumerable (for instance by considering the class of all primitive recursive functions [Reference Liu10]).
$K_T$
is recursively enumerable (for instance by considering the class of all primitive recursive functions [Reference Liu10]).
2 Introduction
According to [Reference Friedman5], Kreisel’s conjecture is the statement:
 $$ \begin{align*} \text{If, for all }n\in \mathbb{N}, \mathop{\text{PA}} \nolimits\vdash_{k \text{ steps}} \varphi(\overline{n}), \text{then }\mathop{\text{PA}} \nolimits\vdash \forall x.\varphi(x). \end{align*} $$
$$ \begin{align*} \text{If, for all }n\in \mathbb{N}, \mathop{\text{PA}} \nolimits\vdash_{k \text{ steps}} \varphi(\overline{n}), \text{then }\mathop{\text{PA}} \nolimits\vdash \forall x.\varphi(x). \end{align*} $$
Kreisel’s conjecture has been studied for different systems, with partial solutions for specific theories of arithmetic other than
![]() $\mathop {\text {PA}} \nolimits $
—see, for instance, [Reference Baaz, Pudlák, Clote and Krajićek1, Reference Miyatake11, Reference Parikh12]; for a detailed account on the conjecture we refer to [Reference Cavagnetto2].
$\mathop {\text {PA}} \nolimits $
—see, for instance, [Reference Baaz, Pudlák, Clote and Krajićek1, Reference Miyatake11, Reference Parikh12]; for a detailed account on the conjecture we refer to [Reference Cavagnetto2].
In this paper we present results similar to Kreisel’s conjecture for
![]() $\vdash _{\leq h}$
, which are not restricted to
$\vdash _{\leq h}$
, which are not restricted to
![]() $\mathop {\text {PA}} \nolimits $
. It is an interesting feature of our approach that it does not depend so heavily on the particular axiomatisation of T that one chooses. In some sense, it can be seen as a uniform approach, since it applies to any consistent, primitive-recursive extension of
$\mathop {\text {PA}} \nolimits $
. It is an interesting feature of our approach that it does not depend so heavily on the particular axiomatisation of T that one chooses. In some sense, it can be seen as a uniform approach, since it applies to any consistent, primitive-recursive extension of
![]() $\mathop {\text {Q}} \nolimits $
.
$\mathop {\text {Q}} \nolimits $
.
For h be a total recursive function, the adapted Kreisel’s conjecture for
![]() $\vdash _{\leq h}$
is:
$\vdash _{\leq h}$
is:
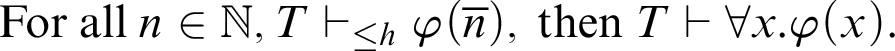 $$ \begin{align*} \text{For all }n\in \mathbb{N}, T\vdash_{\leq h} \varphi(\overline{n}), \text{ then } T\vdash \forall x.\varphi(x). \end{align*} $$
$$ \begin{align*} \text{For all }n\in \mathbb{N}, T\vdash_{\leq h} \varphi(\overline{n}), \text{ then } T\vdash \forall x.\varphi(x). \end{align*} $$
Theorem 2.1. The adapted Kreisel’s conjecture for
![]() $\vdash _{\leq h}$
is false.
$\vdash _{\leq h}$
is false.
Proof Let
![]() $\mathop {\text {Proof}} \nolimits (x,y)$
be a standard proof predicate of T that expresses that x is a proof of y (see [Reference Smorynski16, p. 838] for details). Let h be the function defined by:
$\mathop {\text {Proof}} \nolimits (x,y)$
be a standard proof predicate of T that expresses that x is a proof of y (see [Reference Smorynski16, p. 838] for details). Let h be the function defined by:
 $$ \begin{align*}h(m):=\begin{cases}\mu k[k \text{ is the code of a proof of the formula coded by }m \text{ in } T],\\ & \hspace{-160pt}\text{if } m=\neg \mathop{\text{Proof}} \nolimits(\overline{n}, \ulcorner\perp\urcorner), \text{for some }n,\\ 0, & \hspace{-160pt}\text{otherwise,} \end{cases} \end{align*} $$
$$ \begin{align*}h(m):=\begin{cases}\mu k[k \text{ is the code of a proof of the formula coded by }m \text{ in } T],\\ & \hspace{-160pt}\text{if } m=\neg \mathop{\text{Proof}} \nolimits(\overline{n}, \ulcorner\perp\urcorner), \text{for some }n,\\ 0, & \hspace{-160pt}\text{otherwise,} \end{cases} \end{align*} $$
where
![]() $\mu $
denotes the minimisation function (see [Reference Smorynski16, p. 833] for further details on minimisation). It is clear that h is a (total) recursive function. By construction, for all
$\mu $
denotes the minimisation function (see [Reference Smorynski16, p. 833] for further details on minimisation). It is clear that h is a (total) recursive function. By construction, for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
 $T \vdash _{\leq h} \neg \mathop {\text {Proof}} \nolimits (\overline {n}, \ulcorner \perp \urcorner )$
. If the adapted Kreisel’s conjecture for
$T \vdash _{\leq h} \neg \mathop {\text {Proof}} \nolimits (\overline {n}, \ulcorner \perp \urcorner )$
. If the adapted Kreisel’s conjecture for
![]() $\vdash _{\leq h}$
was true, it would follow
$\vdash _{\leq h}$
was true, it would follow
![]() $T\vdash \forall x.\neg \mathop {\text {Proof}} \nolimits (x, \ulcorner \perp \urcorner )$
, contradicting the second incompleteness theorem (see [Reference Smorynski16, p. 828] for further information).
$T\vdash \forall x.\neg \mathop {\text {Proof}} \nolimits (x, \ulcorner \perp \urcorner )$
, contradicting the second incompleteness theorem (see [Reference Smorynski16, p. 828] for further information).
It is not known whether the theorem still holds if one restricts oneself to primitive-recursive functions.
The result is in accordance with [Reference Hrubeš6], where several reasons are given to believe that Kreisel’s conjecture is, in fact, false.
Even though the adapted Kreisel’s conjecture for
![]() $\vdash _{\leq h}$
is false, it is worth studying variants and weakenings of it. For example, one could ask for an extension
$\vdash _{\leq h}$
is false, it is worth studying variants and weakenings of it. For example, one could ask for an extension
![]() $T^h$
of T such that Kreisel’s conjecture holds adapted to
$T^h$
of T such that Kreisel’s conjecture holds adapted to
![]() $T^h$
: given a total recursive function h, if, for all
$T^h$
: given a total recursive function h, if, for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
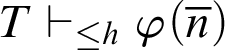 $T\vdash _{\leq h} \varphi (\overline {n})$
, then
$T\vdash _{\leq h} \varphi (\overline {n})$
, then
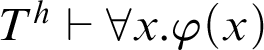 $T^h\vdash \forall x.\varphi (x)$
.
$T^h\vdash \forall x.\varphi (x)$
.
One immediate solution would be to add the true sentence
![]() $\forall x.\varphi (x)$
as an axiom to T. We will, however, construct a theory
$\forall x.\varphi (x)$
as an axiom to T. We will, however, construct a theory
![]() $T^h$
, avoiding the trivial a priori addition of
$T^h$
, avoiding the trivial a priori addition of
![]() $\forall x.\varphi (x)$
as an axiom. The approach is of interest, because it allows to establish relations between different concepts.
$\forall x.\varphi (x)$
as an axiom. The approach is of interest, because it allows to establish relations between different concepts.
We will also study versions of the conjecture for theories that satisfy certain derivability conditions. We exhibit conditions for a theory to satisfy the following implication:
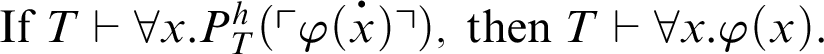
This corresponds to an arithmetization of Kreisel’s conjecture.
Finally, we prove, for certain theories, the existence of a total recursive function h such that
![]() $\vdash _{k \text { steps}}~\subseteq ~\vdash _{\leq h}$
.
$\vdash _{k \text { steps}}~\subseteq ~\vdash _{\leq h}$
.
3 On the notion of provability
 $\vdash _{\leq h}$
$\vdash _{\leq h}$
In this section, we study the notion
![]() $\vdash _{\leq h}$
and some of its properties. We start with a result that guarantees that
$\vdash _{\leq h}$
and some of its properties. We start with a result that guarantees that
![]() $\vdash _{\leq h}$
is representable in T.
$\vdash _{\leq h}$
is representable in T.
Theorem 3.1. Given a total recursive function h, there is a notion of provability
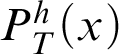 $P^h_T(x)$
that represents
$P^h_T(x)$
that represents
![]() $\vdash _{\leq h}$
in T such that if, for all
$\vdash _{\leq h}$
in T such that if, for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
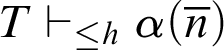 $T\vdash _{\leq h} \alpha (\overline {n})$
, then
$T\vdash _{\leq h} \alpha (\overline {n})$
, then
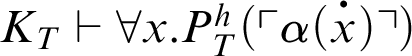 .
.
Proof Let h be an arbitrary, but fixed total recursive function. We define
![]() $f_h$
by:
$f_h$
by:
 $$ \begin{align*}\!\!\!\!\!f_h(n):=\!\begin{cases} \mu m\leq h(n)[m \text{ is the code of a proof of the formula coded by }n],\\ & \hspace{-250pt}\text{if }n \text{ is a code of a formula and there is such an }m,\\ 0, & \hspace{-250pt}\text{otherwise}.\end{cases} \end{align*} $$
$$ \begin{align*}\!\!\!\!\!f_h(n):=\!\begin{cases} \mu m\leq h(n)[m \text{ is the code of a proof of the formula coded by }n],\\ & \hspace{-250pt}\text{if }n \text{ is a code of a formula and there is such an }m,\\ 0, & \hspace{-250pt}\text{otherwise}.\end{cases} \end{align*} $$
![]() $f_h$
is a total recursive function, thus
$f_h$
is a total recursive function, thus
![]() $f_h$
can be strongly representable by a formula
$f_h$
can be strongly representable by a formula
![]() $\mathop {\text {R}} \nolimits _h(x,y)$
in T. Given
$\mathop {\text {R}} \nolimits _h(x,y)$
in T. Given
![]() $n,m\in \mathbb {N}$
, it is clear that
$n,m\in \mathbb {N}$
, it is clear that
![]() $m\leq h(n)$
is the smallest code of a proof of the formula coded by n if, and only if,
$m\leq h(n)$
is the smallest code of a proof of the formula coded by n if, and only if,
![]() $T\vdash \mathop {\text {R}} \nolimits _h(\overline {n},\overline {m})\land \overline {m}\neq 0$
. Thus, we can define the provability predicate
$T\vdash \mathop {\text {R}} \nolimits _h(\overline {n},\overline {m})\land \overline {m}\neq 0$
. Thus, we can define the provability predicate
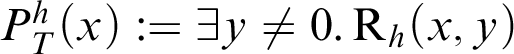 $P^h_T(x):=\exists y\neq 0.\mathop {\text {R}} \nolimits _h(x,y)$
.
$P^h_T(x):=\exists y\neq 0.\mathop {\text {R}} \nolimits _h(x,y)$
.
Assume that, for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
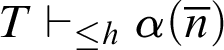 $T\vdash _{\leq h} \alpha (\overline {n})$
. Let
$T\vdash _{\leq h} \alpha (\overline {n})$
. Let
![]() $g_h$
be the function defined by:
$g_h$
be the function defined by:
![]() $g_h(n):=f_h(\#\alpha (\overline {n}))$
.
$g_h(n):=f_h(\#\alpha (\overline {n}))$
.
![]() $g_h$
is a total recursive function. Furthermore,
$g_h$
is a total recursive function. Furthermore,
![]() $g_h$
is strongly representable by the formula
$g_h$
is strongly representable by the formula
 since:
since:
-
(i) If
 $g_h(n)=m$
, then
$g_h(n)=m$
, then
 $f_h(\#\alpha (\overline {n}))=m$
, and thus
$f_h(\#\alpha (\overline {n}))=m$
, and thus
 $T\vdash \mathop {\text {R}} \nolimits _h(\ulcorner \alpha (\overline {n})\urcorner ,\overline {m})$
, i.e.,
$T\vdash \mathop {\text {R}} \nolimits _h(\ulcorner \alpha (\overline {n})\urcorner ,\overline {m})$
, i.e.,
 $T\vdash {\textrm {S}}_h(\overline {n},\overline {m})$
;
$T\vdash {\textrm {S}}_h(\overline {n},\overline {m})$
; -
(ii) As
 $T\vdash \forall x.\exists !y.\mathop {\text {R}} \nolimits _h(x,y)$
it follows that
$T\vdash \forall x.\exists !y.\mathop {\text {R}} \nolimits _h(x,y)$
it follows that
 , i.e.,
, i.e.,
 $T\vdash \forall x.\exists !y.{\textrm {S}}_h(x,y)$
.
$T\vdash \forall x.\exists !y.{\textrm {S}}_h(x,y)$
.
By hypothesis, for all
![]() $n \in \mathbb {N}$
, there is
$n \in \mathbb {N}$
, there is
![]() $m\leq h(\#\alpha (\overline {n}))$
such that m is the code of a proof of
$m\leq h(\#\alpha (\overline {n}))$
such that m is the code of a proof of
![]() $\alpha (\overline {n})$
in T. Hence, for all
$\alpha (\overline {n})$
in T. Hence, for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $g_h(n)\neq 0$
. As
$g_h(n)\neq 0$
. As
![]() ${\textrm {S}}_h(x,y)$
strongly represents
${\textrm {S}}_h(x,y)$
strongly represents
![]() $g_h$
, we have by hypothesis that
$g_h$
, we have by hypothesis that
![]() $K_T \vdash \forall x.\neg {\textrm {S}}_h(x,0)$
. From
$K_T \vdash \forall x.\neg {\textrm {S}}_h(x,0)$
. From
![]() $T\vdash \forall x.\exists !y.{\textrm {S}}_h(x,y)$
follows that
$T\vdash \forall x.\exists !y.{\textrm {S}}_h(x,y)$
follows that
![]() $T\vdash \forall x.\exists y.{\textrm {S}}_h(x,y)$
. Together with
$T\vdash \forall x.\exists y.{\textrm {S}}_h(x,y)$
. Together with
![]() $K_T \vdash \forall x.\neg {\textrm {S}}_h(x,0)$
, it follows that
$K_T \vdash \forall x.\neg {\textrm {S}}_h(x,0)$
, it follows that
![]() $K_T \vdash \forall x.\exists y\neq 0.{\textrm {S}}_h(x,y)$
, i.e.,
$K_T \vdash \forall x.\exists y\neq 0.{\textrm {S}}_h(x,y)$
, i.e.,
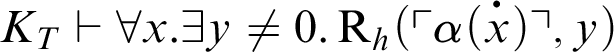 . So,
. So,
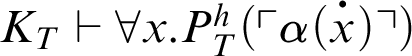 .
.
We show that, for all formulas
![]() $\varphi $
,
$\varphi $
,
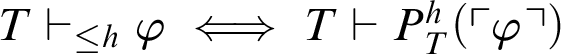 $T \vdash _{\leq h} \varphi \iff T \vdash P^h_T(\ulcorner \varphi \urcorner )$
. Suppose that
$T \vdash _{\leq h} \varphi \iff T \vdash P^h_T(\ulcorner \varphi \urcorner )$
. Suppose that
![]() $T \vdash _{\leq h} \varphi $
. For
$T \vdash _{\leq h} \varphi $
. For
![]() $m:=f_h(\#\varphi )$
, we have that
$m:=f_h(\#\varphi )$
, we have that
![]() $m\neq 0$
. Thus,
$m\neq 0$
. Thus,
![]() $T\vdash \mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,\overline {m})\land \overline {m}\neq 0$
, and so
$T\vdash \mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,\overline {m})\land \overline {m}\neq 0$
, and so
![]() $T \vdash \exists y\neq 0.\mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,y)$
. Hence,
$T \vdash \exists y\neq 0.\mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,y)$
. Hence,
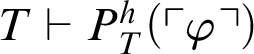 $T \vdash P^h_T(\ulcorner \varphi \urcorner )$
. Now suppose that
$T \vdash P^h_T(\ulcorner \varphi \urcorner )$
. Now suppose that
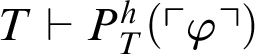 $T \vdash P^h_T(\ulcorner \varphi \urcorner )$
. Let
$T \vdash P^h_T(\ulcorner \varphi \urcorner )$
. Let
![]() $m:=f_h(\# \varphi )$
. If
$m:=f_h(\# \varphi )$
. If
![]() $m\neq 0$
, then
$m\neq 0$
, then
![]() $T \vdash _{\leq h} \varphi $
. Suppose, towards a contradiction, that
$T \vdash _{\leq h} \varphi $
. Suppose, towards a contradiction, that
![]() $m=0$
. We have that
$m=0$
. We have that
![]() $T\vdash \exists y\neq 0.\mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,y)$
and
$T\vdash \exists y\neq 0.\mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,y)$
and
![]() $T\vdash \mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,0)$
. As
$T\vdash \mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,0)$
. As
![]() $T\vdash \forall x.\exists !y.\mathop {\text {R}} \nolimits _h(x,y)$
we arrive at a contradiction. So,
$T\vdash \forall x.\exists !y.\mathop {\text {R}} \nolimits _h(x,y)$
we arrive at a contradiction. So,
![]() $m\neq 0$
, as desired.
$m\neq 0$
, as desired.
The next result follows immediately from the proof of the last theorem.
Corollary 3.1. Given a total recursive function h, and a formula
![]() $\varphi $
, we have that
$\varphi $
, we have that
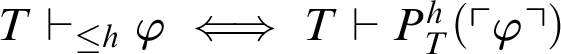 $T \vdash _{\leq h} \varphi \iff T \vdash P^h_T(\ulcorner \varphi \urcorner )$
.
$T \vdash _{\leq h} \varphi \iff T \vdash P^h_T(\ulcorner \varphi \urcorner )$
.
The provability predicate
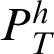 $P^h_T$
is provably decidable, in the following sense:
$P^h_T$
is provably decidable, in the following sense:
Theorem 3.2. Given a total recursive function h, for every formula
![]() $\varphi $
, we have that
$\varphi $
, we have that
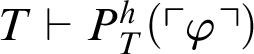 $T\vdash P^h_T(\ulcorner \varphi \urcorner )$
or
$T\vdash P^h_T(\ulcorner \varphi \urcorner )$
or
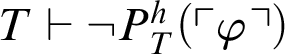 $T\vdash \neg P^h_T(\ulcorner \varphi \urcorner )$
.
$T\vdash \neg P^h_T(\ulcorner \varphi \urcorner )$
.
Proof Suppose that
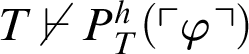 . By the previous result,
. By the previous result,
![]() . This means that
. This means that
![]() $f_h(\# \varphi )=0$
. As
$f_h(\# \varphi )=0$
. As
![]() $\mathop {\text {R}} \nolimits _h(x,y)$
strongly represents the function
$\mathop {\text {R}} \nolimits _h(x,y)$
strongly represents the function
![]() $f_h$
, it follows that
$f_h$
, it follows that
![]() $T\vdash \mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,0)$
. Since
$T\vdash \mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,0)$
. Since
![]() $T\vdash \forall x.\exists !y.\mathop {\text {R}} \nolimits _h(x,y)$
, we can conclude that
$T\vdash \forall x.\exists !y.\mathop {\text {R}} \nolimits _h(x,y)$
, we can conclude that
![]() $T \vdash \forall y. (\mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,y)\rightarrow y=0)$
, and so,
$T \vdash \forall y. (\mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,y)\rightarrow y=0)$
, and so,
![]() $T \vdash \neg \exists y. (y\neq 0 \land \mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,y))$
, i.e.,
$T \vdash \neg \exists y. (y\neq 0 \land \mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,y))$
, i.e.,
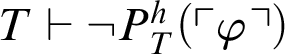 $T \vdash \neg P^h_T(\ulcorner \varphi \urcorner )$
.
$T \vdash \neg P^h_T(\ulcorner \varphi \urcorner )$
.
The next result corresponds to an arithmetization of the previous statement.
Theorem 3.3. Given a provability predicate
![]() $P(x)$
and a total recursive function h, we have for every formula
$P(x)$
and a total recursive function h, we have for every formula
![]() $\varphi $
that
$\varphi $
that
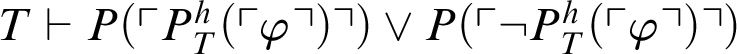 $T\vdash P(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner ) \lor P(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner )\urcorner )$
.
$T\vdash P(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner ) \lor P(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner )\urcorner )$
.
Proof From Theorem 3.2, it follows
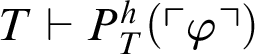 $T\vdash P^h_T(\ulcorner \varphi \urcorner )$
or
$T\vdash P^h_T(\ulcorner \varphi \urcorner )$
or
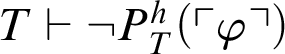 $T\vdash \neg P^h_T(\ulcorner \varphi \urcorner )$
. If
$T\vdash \neg P^h_T(\ulcorner \varphi \urcorner )$
. If
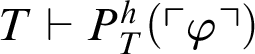 $T\vdash P^h_T(\ulcorner \varphi \urcorner )$
, then
$T\vdash P^h_T(\ulcorner \varphi \urcorner )$
, then
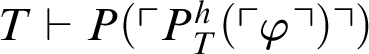 $T\vdash P(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner )$
, and so
$T\vdash P(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner )$
, and so
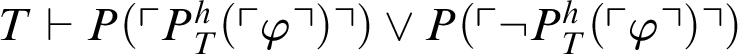 $T\vdash P(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner ) \lor P(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner )\urcorner )$
. If
$T\vdash P(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner ) \lor P(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner )\urcorner )$
. If
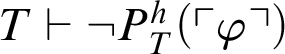 $T\vdash \neg P^h_T(\ulcorner \varphi \urcorner )$
, then
$T\vdash \neg P^h_T(\ulcorner \varphi \urcorner )$
, then
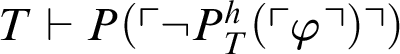 $T\vdash P(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner )\urcorner )$
; hence
$T\vdash P(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner )\urcorner )$
; hence
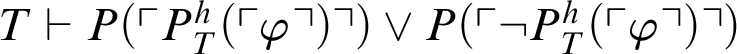 $T\vdash P(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner ) \lor P(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner )\urcorner )$
. In sum,
$T\vdash P(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner ) \lor P(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner )\urcorner )$
. In sum,
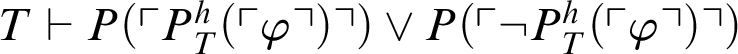 $T\vdash P(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner ) \lor P(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner )\urcorner )$
.
$T\vdash P(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner ) \lor P(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner )\urcorner )$
.
We now prove that there is no h such that
![]() $\vdash _{\leq h}$
coincides with
$\vdash _{\leq h}$
coincides with
![]() $\vdash $
.
$\vdash $
.
Theorem 3.4. For every total recursive function h, there is a formula
![]() $\varphi $
such that
$\varphi $
such that
![]() $T\vdash \varphi $
, but
$T\vdash \varphi $
, but
![]() .
.
Proof Let h be a fixed total recursive function. Let
![]() $\varphi $
be the sentence obtained from the application of the diagonalisation lemma [Reference Smith15, p. 169] to the formula
$\varphi $
be the sentence obtained from the application of the diagonalisation lemma [Reference Smith15, p. 169] to the formula
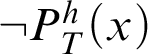 $\neg P^h_T(x)$
. Then,
$\neg P^h_T(x)$
. Then,
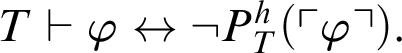 $$ \begin{align} T\vdash \varphi\leftrightarrow \neg P^h_T(\ulcorner \varphi\urcorner). \end{align} $$
$$ \begin{align} T\vdash \varphi\leftrightarrow \neg P^h_T(\ulcorner \varphi\urcorner). \end{align} $$
Suppose, towards a contradiction, that
![]() $T \vdash _{\leq h} \varphi $
. Thus,
$T \vdash _{\leq h} \varphi $
. Thus,
![]() $T\vdash \varphi $
. By Corollary 3.1 we have that
$T\vdash \varphi $
. By Corollary 3.1 we have that
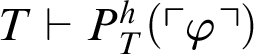 $T\vdash P^h_T(\ulcorner \varphi \urcorner )$
, and so, by (I),
$T\vdash P^h_T(\ulcorner \varphi \urcorner )$
, and so, by (I),
![]() $T\vdash \neg \varphi $
, which contradicts
$T\vdash \neg \varphi $
, which contradicts
![]() $T\vdash \varphi $
. Hence,
$T\vdash \varphi $
. Hence,
![]() . From Theorem 3.2 it follows that
. From Theorem 3.2 it follows that
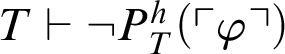 $T\vdash \neg P^h_T(\ulcorner \varphi \urcorner )$
, i.e.,
$T\vdash \neg P^h_T(\ulcorner \varphi \urcorner )$
, i.e.,
![]() $T\vdash \varphi $
.
$T\vdash \varphi $
.
The next fact will play a major role for the discussion of Kreisel’s conjecture.
Theorem 3.5. Given a total recursive function h, for every formula
![]() $\varphi $
,
$\varphi $
,
 $T\vdash P^h_T(\ulcorner \varphi \urcorner )\rightarrow \varphi $
.
$T\vdash P^h_T(\ulcorner \varphi \urcorner )\rightarrow \varphi $
.
Proof Let
![]() $\varphi $
be an arbitrary formula. From Theorem 3.2,
$\varphi $
be an arbitrary formula. From Theorem 3.2,
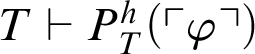 $T\vdash P^h_T(\ulcorner \varphi \urcorner )$
or
$T\vdash P^h_T(\ulcorner \varphi \urcorner )$
or
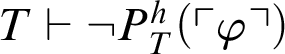 $T\vdash \neg P^h_T(\ulcorner \varphi \urcorner )$
. First, suppose that
$T\vdash \neg P^h_T(\ulcorner \varphi \urcorner )$
. First, suppose that
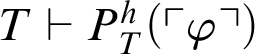 $T\vdash P^h_T(\ulcorner \varphi \urcorner )$
. Then, by Corollary 3.1, we conclude
$T\vdash P^h_T(\ulcorner \varphi \urcorner )$
. Then, by Corollary 3.1, we conclude
![]() $T\vdash _{\leq h} \varphi $
, from where we get
$T\vdash _{\leq h} \varphi $
, from where we get
![]() $T\vdash \varphi $
. Thus,
$T\vdash \varphi $
. Thus,
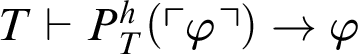 $T\vdash P^h_T(\ulcorner \varphi \urcorner )\rightarrow \varphi $
. Second, suppose that
$T\vdash P^h_T(\ulcorner \varphi \urcorner )\rightarrow \varphi $
. Second, suppose that
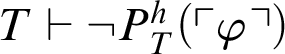 $T\vdash \neg P^h_T(\ulcorner \varphi \urcorner )$
. Then, by logic,
$T\vdash \neg P^h_T(\ulcorner \varphi \urcorner )$
. Then, by logic,
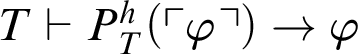 $T\vdash P^h_T(\ulcorner \varphi \urcorner )\rightarrow \varphi $
. In all,
$T\vdash P^h_T(\ulcorner \varphi \urcorner )\rightarrow \varphi $
. In all,
 $T\vdash P^h_T(\ulcorner \varphi \urcorner )\rightarrow \varphi $
.
$T\vdash P^h_T(\ulcorner \varphi \urcorner )\rightarrow \varphi $
.
Theorem 3.6. Let h be a primitive-recursive function and
![]() $P(x)$
be a provability predicate such that
$P(x)$
be a provability predicate such that
![]() $:$
$:$
-
C1 For all
 $\Sigma _1$
-formulas
$\Sigma _1$
-formulas
 $\varphi $
,
$\varphi $
,
 $T\vdash \varphi \rightarrow P(\ulcorner \varphi \urcorner );$
$T\vdash \varphi \rightarrow P(\ulcorner \varphi \urcorner );$
-
C2 For all formulas
 $\varphi $
and
$\varphi $
and
 $\psi $
,
$\psi $
,
 $T\vdash \varphi \rightarrow \psi \implies T\vdash P(\ulcorner \varphi \urcorner )\rightarrow P(\ulcorner \psi \urcorner )$
.
$T\vdash \varphi \rightarrow \psi \implies T\vdash P(\ulcorner \varphi \urcorner )\rightarrow P(\ulcorner \psi \urcorner )$
.
Then, for every formula
![]() $\varphi $
,
$\varphi $
,
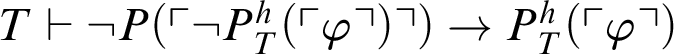 $T\vdash \neg P(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner ) \urcorner )\rightarrow P^h_T(\ulcorner \varphi \urcorner )$
.
$T\vdash \neg P(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner ) \urcorner )\rightarrow P^h_T(\ulcorner \varphi \urcorner )$
.
Proof If h is primitive-recursive, then
![]() $\mathop {\text {R}} \nolimits _h(x,y)$
can be picked as being a
$\mathop {\text {R}} \nolimits _h(x,y)$
can be picked as being a
![]() $\Sigma _1$
-formula. Clearly,
$\Sigma _1$
-formula. Clearly,
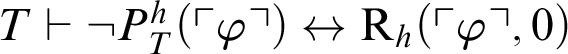 $T\vdash \neg P^h_T(\ulcorner \varphi \urcorner )\leftrightarrow \mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,0)$
. From C2 we get that
$T\vdash \neg P^h_T(\ulcorner \varphi \urcorner )\leftrightarrow \mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,0)$
. From C2 we get that
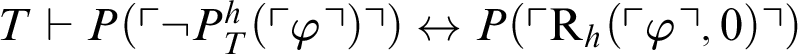 $T\vdash P(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner ) \urcorner )\leftrightarrow P(\ulcorner \mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,0)\urcorner )$
. From C1,
$T\vdash P(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner ) \urcorner )\leftrightarrow P(\ulcorner \mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,0)\urcorner )$
. From C1,
![]() $T\vdash \mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,0)\rightarrow P(\ulcorner \mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,0)\urcorner )$
, so
$T\vdash \mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,0)\rightarrow P(\ulcorner \mathop {\text {R}} \nolimits _h(\ulcorner \varphi \urcorner ,0)\urcorner )$
, so
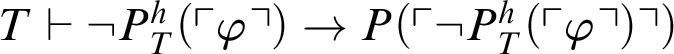 $T\vdash \neg P^h_T(\ulcorner \varphi \urcorner )\rightarrow P(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner )\urcorner )$
, as wanted.
$T\vdash \neg P^h_T(\ulcorner \varphi \urcorner )\rightarrow P(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner )\urcorner )$
, as wanted.
Let
![]() $\mathop {\text {Pr}} \nolimits _T(x):=\exists y.\mathop {\text {Proof}} \nolimits (x,y)$
denote the standard provability predicate in T [Reference Smorynski16, p. 826] and
$\mathop {\text {Pr}} \nolimits _T(x):=\exists y.\mathop {\text {Proof}} \nolimits (x,y)$
denote the standard provability predicate in T [Reference Smorynski16, p. 826] and
![]() $\mathop {\text {Con}} \nolimits _T:=\neg \mathop {\text {Pr}} \nolimits _T(\ulcorner \perp \urcorner )$
.
$\mathop {\text {Con}} \nolimits _T:=\neg \mathop {\text {Pr}} \nolimits _T(\ulcorner \perp \urcorner )$
.
Theorem 3.7. Given a primitive-recursive function h, for every formula
![]() $\varphi $
,
$\varphi $
,
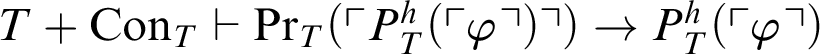 $T+\mathop {\text {Con}} \nolimits _{T}\vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner )\rightarrow P^h_T(\ulcorner \varphi \urcorner )$
.
$T+\mathop {\text {Con}} \nolimits _{T}\vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner )\rightarrow P^h_T(\ulcorner \varphi \urcorner )$
.
Proof It is clear that
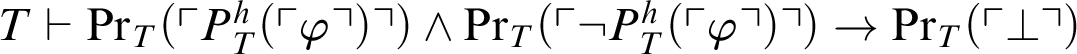 $T \vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner )\land \mathop {\text {Pr}} \nolimits _T(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner ) \urcorner )\rightarrow \mathop {\text {Pr}} \nolimits _T(\ulcorner \perp \urcorner )$
. Thus,
$T \vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner )\land \mathop {\text {Pr}} \nolimits _T(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner ) \urcorner )\rightarrow \mathop {\text {Pr}} \nolimits _T(\ulcorner \perp \urcorner )$
. Thus,
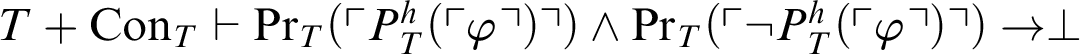 $T+\mathop {\text {Con}} \nolimits _{T}\vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner )\land \mathop {\text {Pr}} \nolimits _T(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner ) \urcorner )\rightarrow \perp $
. Hence,
$T+\mathop {\text {Con}} \nolimits _{T}\vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner )\land \mathop {\text {Pr}} \nolimits _T(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner ) \urcorner )\rightarrow \perp $
. Hence,
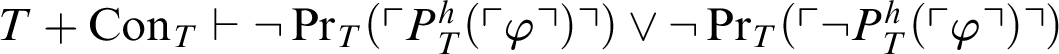 $T+\mathop {\text {Con}} \nolimits _{T}\vdash \neg \mathop {\text {Pr}} \nolimits _T(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner )\lor \neg \mathop {\text {Pr}} \nolimits _T(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner ) \urcorner )$
, i.e.,
$T+\mathop {\text {Con}} \nolimits _{T}\vdash \neg \mathop {\text {Pr}} \nolimits _T(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner )\lor \neg \mathop {\text {Pr}} \nolimits _T(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner ) \urcorner )$
, i.e.,
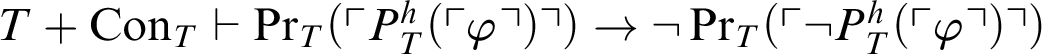 $T+\mathop {\text {Con}} \nolimits _{T}\vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner )\rightarrow \neg \mathop {\text {Pr}} \nolimits _T(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner ) \urcorner )$
. By the previous result we conclude that
$T+\mathop {\text {Con}} \nolimits _{T}\vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner )\rightarrow \neg \mathop {\text {Pr}} \nolimits _T(\ulcorner \neg P^h_T(\ulcorner \varphi \urcorner ) \urcorner )$
. By the previous result we conclude that
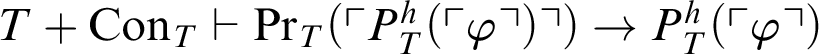 $T+\mathop {\text {Con}} \nolimits _{T}\vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner )\rightarrow P^h_T(\ulcorner \varphi \urcorner )$
.
$T+\mathop {\text {Con}} \nolimits _{T}\vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner P^h_T(\ulcorner \varphi \urcorner )\urcorner )\rightarrow P^h_T(\ulcorner \varphi \urcorner )$
.
4 Montagna’s conjecture
Löb’s theorem [Reference Lindström9, pp. 28–29] expresses that for all formulas
![]() $\varphi $
, if
$\varphi $
, if
![]() $T \vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi $
, then
$T \vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi $
, then
![]() $T\vdash \varphi $
. More generally, for all formulas
$T\vdash \varphi $
. More generally, for all formulas
![]() $\varphi $
,
$\varphi $
,
If one analyses the proof of Löb’s theorem, it indicates that one can prove
![]() $\mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi $
only if one has already proved
$\mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi $
only if one has already proved
![]() $\varphi $
. It indicates, moreover, that
$\varphi $
. It indicates, moreover, that
![]() $\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )$
is only provable, if
$\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )$
is only provable, if
![]() $\varphi $
is proven in the first place. This intuition can be related to a problem proposed by Montagna in [Reference Clote, Krajićek, Clote and Krajićek3, p. 9]: “Does
$\varphi $
is proven in the first place. This intuition can be related to a problem proposed by Montagna in [Reference Clote, Krajićek, Clote and Krajićek3, p. 9]: “Does
 $\mathop {\text {PA}} \nolimits \vdash _{k \text { steps}} \mathop {\text {Pr}} \nolimits _{\mathop {\text {PA}} \nolimits }(\ulcorner \varphi \urcorner )\rightarrow \varphi $
imply
$\mathop {\text {PA}} \nolimits \vdash _{k \text { steps}} \mathop {\text {Pr}} \nolimits _{\mathop {\text {PA}} \nolimits }(\ulcorner \varphi \urcorner )\rightarrow \varphi $
imply
![]() $\mathop {\text {PA}} \nolimits \vdash _{k \text { steps}} \varphi $
?” Let us consider a variant of this question: “Does
$\mathop {\text {PA}} \nolimits \vdash _{k \text { steps}} \varphi $
?” Let us consider a variant of this question: “Does
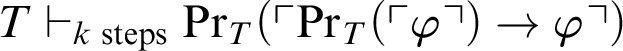 $T\vdash _{k \text { steps}} \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )$
imply
$T\vdash _{k \text { steps}} \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )$
imply
![]() $T\vdash _{k \text { steps}} \varphi $
?” We prove that the adapted question to the provability notion
$T\vdash _{k \text { steps}} \varphi $
?” We prove that the adapted question to the provability notion
![]() $\vdash _{\leq h}$
is false: “
$\vdash _{\leq h}$
is false: “
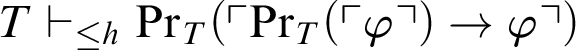 $T\vdash _{\leq h}\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )$
does not imply
$T\vdash _{\leq h}\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )$
does not imply
![]() $T \vdash _{\leq h} \varphi $
.”
$T \vdash _{\leq h} \varphi $
.”
Theorem 4.1. For every primitive-recursive function
![]() $g(x,y)$
with
$g(x,y)$
with
![]() $g(x,y)>y$
, there are a sentence
$g(x,y)>y$
, there are a sentence
![]() $\varphi $
and a number
$\varphi $
and a number
![]() $n_0$
such that
$n_0$
such that
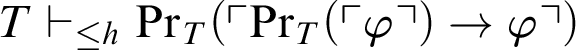 $T\vdash _{\leq h}\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )$
, but
$T\vdash _{\leq h}\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )$
, but
![]() , where
, where
![]() $h:=\lambda x. g(x,n_0)$
.
$h:=\lambda x. g(x,n_0)$
.
Proof We follow closely the proof of Theorem 14 from [Reference Lindström9, p. 34]. Let
![]() $\mathop {\text {g}} \nolimits $
be a function-symbol that represents the primitive-recursive function g. By the diagonalization lemma, there is a sentence
$\mathop {\text {g}} \nolimits $
be a function-symbol that represents the primitive-recursive function g. By the diagonalization lemma, there is a sentence
![]() $\varphi $
such that
$\varphi $
such that
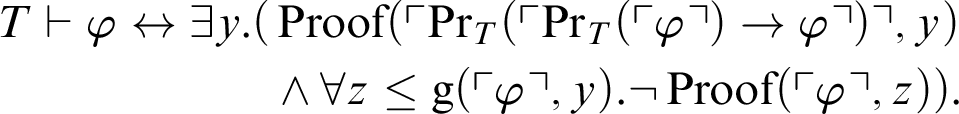 $$ \begin{align*} T \vdash \varphi\leftrightarrow \exists y. (&\mathop{\text{Proof}} \nolimits(\ulcorner\mathop{\text{Pr}} \nolimits_T(\ulcorner \mathop{\text{Pr}} \nolimits_T(\ulcorner \varphi\urcorner)\rightarrow \varphi \urcorner)\urcorner,y)\\ &\land \forall z\leq \mathop{\text{g}} \nolimits(\ulcorner \varphi\urcorner,y). \neg\mathop{\text{Proof}} \nolimits(\ulcorner \varphi\urcorner,z)). \end{align*} $$
$$ \begin{align*} T \vdash \varphi\leftrightarrow \exists y. (&\mathop{\text{Proof}} \nolimits(\ulcorner\mathop{\text{Pr}} \nolimits_T(\ulcorner \mathop{\text{Pr}} \nolimits_T(\ulcorner \varphi\urcorner)\rightarrow \varphi \urcorner)\urcorner,y)\\ &\land \forall z\leq \mathop{\text{g}} \nolimits(\ulcorner \varphi\urcorner,y). \neg\mathop{\text{Proof}} \nolimits(\ulcorner \varphi\urcorner,z)). \end{align*} $$
By construction,
![]() $T+\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )\urcorner )+\neg \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\vdash \varphi $
. As T is
$T+\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )\urcorner )+\neg \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\vdash \varphi $
. As T is
![]() $\Sigma _1$
-complete,
$\Sigma _1$
-complete,
![]() $T+\varphi \vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )$
. Thus, we can conclude that
$T+\varphi \vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )$
. Thus, we can conclude that
![]() $T+\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )\urcorner )\vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )$
. By Löb’s theorem, it follows that
$T+\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )\urcorner )\vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )$
. By Löb’s theorem, it follows that
![]() $T\vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )\urcorner )\leftrightarrow \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\urcorner )$
. Hence,
$T\vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )\urcorner )\leftrightarrow \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\urcorner )$
. Hence,
![]() $T+ \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\urcorner )\vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )$
. Again by Löb’s theorem, it follows that
$T+ \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\urcorner )\vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )$
. Again by Löb’s theorem, it follows that
![]() $T\vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )$
, and consequently
$T\vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )$
, and consequently
![]() $T \vdash \varphi $
and
$T \vdash \varphi $
and
![]() $T\vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )$
. This means that
$T\vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )$
. This means that
![]() $\varphi $
is true. Let
$\varphi $
is true. Let
![]() $n_0$
satisfy the true existential property of
$n_0$
satisfy the true existential property of
![]() $\varphi $
. Then,
$\varphi $
. Then,
![]() $n_0$
is the code of a proof of
$n_0$
is the code of a proof of
![]() $\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )$
. By hypothesis on g, it follows that
$\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )$
. By hypothesis on g, it follows that
![]() $n_0< g(\#\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner ),n_0)=h(\#\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner ))$
, ergo
$n_0< g(\#\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner ),n_0)=h(\#\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner ))$
, ergo
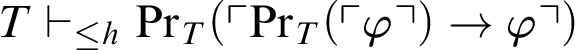 $T\vdash _{\leq h} \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )$
. From the fact that
$T\vdash _{\leq h} \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )$
. From the fact that
![]() $\varphi $
is true one can conclude that for all
$\varphi $
is true one can conclude that for all
![]() $z\leq g(\#\varphi ,n_0)$
, z is not the code of a proof of
$z\leq g(\#\varphi ,n_0)$
, z is not the code of a proof of
![]() $\varphi $
. This means that
$\varphi $
. This means that
![]() .
.
If a formula
![]() $\varphi $
is provable in T, we define
$\varphi $
is provable in T, we define
Moreover, if
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are formulas, we stipulate that
$\psi $
are formulas, we stipulate that
![]() $\varphi <_{T} \psi $
if
$\varphi <_{T} \psi $
if
![]() $T \vdash \varphi \land \psi $
and
$T \vdash \varphi \land \psi $
and
![]() ${\|\varphi \|}_{T}<{\|\psi \|}_{T}$
. The following result confirms that the mentioned intuition that a proof of
${\|\varphi \|}_{T}<{\|\psi \|}_{T}$
. The following result confirms that the mentioned intuition that a proof of
![]() $\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )$
should encompass, in a way, a proof of
$\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )$
should encompass, in a way, a proof of
![]() $\varphi $
fails.
$\varphi $
fails.
Theorem 4.2. There is a formula
![]() $\varphi $
such that
$\varphi $
such that
Proof By the diagonalization lemma, there is a sentence
![]() $\varphi $
such that
$\varphi $
such that
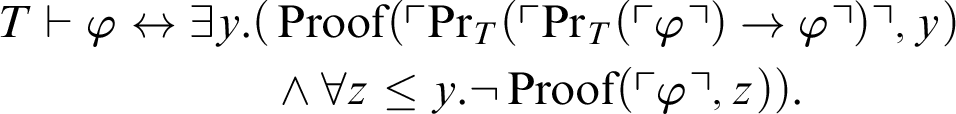 $$ \begin{align*} T \vdash \varphi\leftrightarrow \exists y. (&\mathop{\text{Proof}} \nolimits(\ulcorner\mathop{\text{Pr}} \nolimits_T(\ulcorner \mathop{\text{Pr}} \nolimits_T(\ulcorner \varphi\urcorner)\rightarrow \varphi \urcorner)\urcorner,y)\\ &\land \forall z\leq y. \neg\mathop{\text{Proof}} \nolimits(\ulcorner \varphi\urcorner,z)). \end{align*} $$
$$ \begin{align*} T \vdash \varphi\leftrightarrow \exists y. (&\mathop{\text{Proof}} \nolimits(\ulcorner\mathop{\text{Pr}} \nolimits_T(\ulcorner \mathop{\text{Pr}} \nolimits_T(\ulcorner \varphi\urcorner)\rightarrow \varphi \urcorner)\urcorner,y)\\ &\land \forall z\leq y. \neg\mathop{\text{Proof}} \nolimits(\ulcorner \varphi\urcorner,z)). \end{align*} $$
Applying the same reasoning as in the previous proof, it follows that
![]() $T \vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )\land \varphi $
; in particular
$T \vdash \mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )\land \varphi $
; in particular
![]() $\varphi $
is true. Take
$\varphi $
is true. Take
![]() $n_0$
as being the natural number that is guaranteed to exist from the true formula
$n_0$
as being the natural number that is guaranteed to exist from the true formula
![]() $\varphi $
. It is straightforward that
$\varphi $
. It is straightforward that
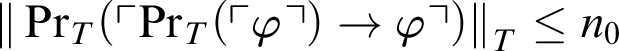 ${\|\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )\|}_{T}\leq n_0$
. As
${\|\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )\|}_{T}\leq n_0$
. As
![]() $\varphi $
is true, it follows that for all
$\varphi $
is true, it follows that for all
![]() $z\leq n_0$
, z is not the code of a proof of
$z\leq n_0$
, z is not the code of a proof of
![]() $\varphi $
. Hence,
$\varphi $
. Hence,
![]() $n_0< {\|\varphi \|}_{T}$
, and so
$n_0< {\|\varphi \|}_{T}$
, and so
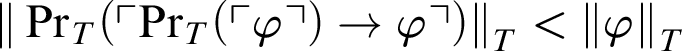 ${\|\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )\|}_{T}<{\|\varphi \|}_{T}$
. In all,
${\|\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )\|}_{T}<{\|\varphi \|}_{T}$
. In all,
![]() $\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner ) <_{T} \varphi $
.
$\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner ) <_{T} \varphi $
.
5 Variants of Kreisel’s conjecture
In this section we present some partial results related to Kreisel’s conjecture, namely variants of the conjecture for provability predicates in the present of different derivability conditions. In this section, the theory T does not need to be r.e.
Theorem 5.1. Let h be a primitive-recursive function and T be such that there is a provability predicate
![]() $P(x)$
satisfying
$P(x)$
satisfying
![]() $:$
$:$
-
C1 If
 $\varphi (x)$
is a
$\varphi (x)$
is a
 $\Sigma _n$
-formula, then
$\Sigma _n$
-formula, then

-
C2

-
C3 For all formulas
 $\varphi (x)$
and
$\varphi (x)$
and
 $\psi (x)$
,
$\psi (x)$
,
 .
.
If
![]() $\varphi (x)$
is a
$\varphi (x)$
is a
![]() $\Pi _n$
-formula such that
$\Pi _n$
-formula such that
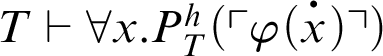 , then
, then
![]() $T+\mathop {\text {Con}} \nolimits _P\vdash \forall x. \varphi (x)$
.
$T+\mathop {\text {Con}} \nolimits _P\vdash \forall x. \varphi (x)$
.
Proof As
![]() $\varphi (x)$
is
$\varphi (x)$
is
![]() $\Pi _n$
, by C1, we have
$\Pi _n$
, by C1, we have
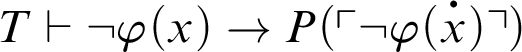 . Thus,
. Thus,
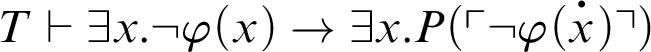 . By C2,
. By C2,
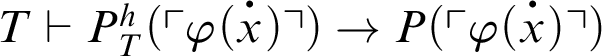 . Hence,
. Hence,
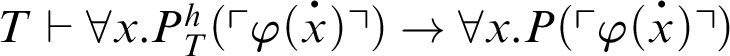 . So,
. So,
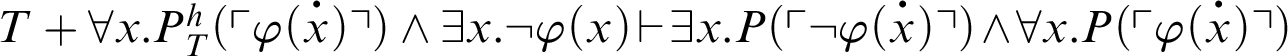 . By C3,
. By C3,
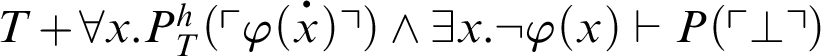 , i.e.,
, i.e.,
 .
.
The condition
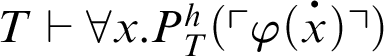 corresponds to an arithmetization of the antecedent of a version of Kreisel’s conjecture. Thus, the result is weaker than Kreisel’s conjecture. If
corresponds to an arithmetization of the antecedent of a version of Kreisel’s conjecture. Thus, the result is weaker than Kreisel’s conjecture. If
![]() $T\vdash \mathop {\text {Con}} \nolimits _P$
, then the previous result can be proved inside T. The next result is a particular case of the previous theorem.
$T\vdash \mathop {\text {Con}} \nolimits _P$
, then the previous result can be proved inside T. The next result is a particular case of the previous theorem.
Corollary 5.1. Let h be a primitive-recursive function. If
![]() $\varphi (x)$
is a
$\varphi (x)$
is a
![]() $\Pi _1$
-formula such that
$\Pi _1$
-formula such that
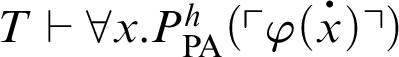 , then
, then
![]() $\mathop {\text {PA}} \nolimits +\mathop {\text {Con}} \nolimits _{\mathop {\text {PA}} \nolimits }\vdash \forall x. \varphi (x)$
.
$\mathop {\text {PA}} \nolimits +\mathop {\text {Con}} \nolimits _{\mathop {\text {PA}} \nolimits }\vdash \forall x. \varphi (x)$
.
Proof The corollary follows immediately from the fact that
![]() $\mathop {\text {Pr}} \nolimits _{\mathop {\text {PA}} \nolimits }$
satisfies C1 and C2 of the previous theorem [Reference Kurahashi7].
$\mathop {\text {Pr}} \nolimits _{\mathop {\text {PA}} \nolimits }$
satisfies C1 and C2 of the previous theorem [Reference Kurahashi7].
Theorem 5.2. Let h be a primitive-recursive function and T be such that there is a provability predicate
![]() $P(x)$
satisfying
$P(x)$
satisfying
![]() $:$
$:$
-
C1 For all formulas
 $\varphi (x)$
,
$\varphi (x)$
,

-
C2 If
 $\varphi (x)$
is a
$\varphi (x)$
is a
 $\Sigma _n$
-formula, then
$\Sigma _n$
-formula, then

-
C3 For all formulas
 $\varphi (x)$
and
$\varphi (x)$
and
 $\psi (x)$
,
$\psi (x)$
,
 .
.
If
![]() $\varphi (x)$
is a
$\varphi (x)$
is a
![]() $\Pi _n$
-formula such that
$\Pi _n$
-formula such that
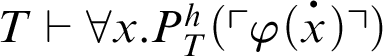 , then
, then
![]() $T+\mathop {\text {Con}} \nolimits _P\vdash \forall x. \varphi (x)$
.
$T+\mathop {\text {Con}} \nolimits _P\vdash \forall x. \varphi (x)$
.
Proof As
![]() $\neg \varphi (x)$
is
$\neg \varphi (x)$
is
![]() $\Sigma _n$
, by C2
$\Sigma _n$
, by C2
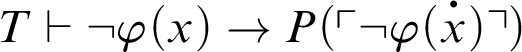 . Thus,
. Thus,
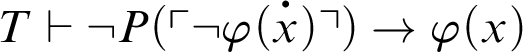 . By C3, we have that
. By C3, we have that
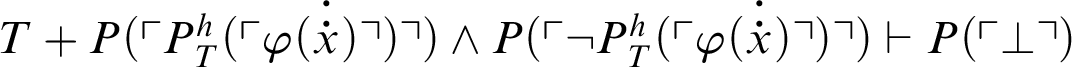 , since
, since
![]() $\neg \varphi :=\varphi \rightarrow {\perp }$
. Hence,
$\neg \varphi :=\varphi \rightarrow {\perp }$
. Hence,
 . Together with C1 we get that
. Together with C1 we get that
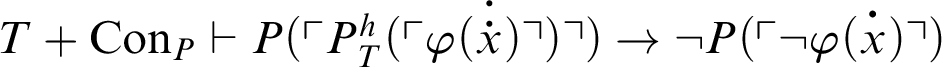 , but, by what was previously concluded, one gets that
, but, by what was previously concluded, one gets that
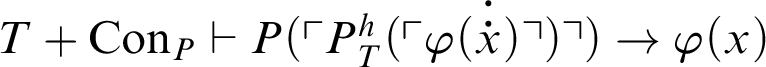 . Suppose that
. Suppose that
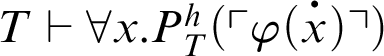 . As h is primitive-recursive, we have that
. As h is primitive-recursive, we have that
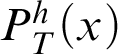 $P^h_T(x)$
is
$P^h_T(x)$
is
![]() $\Sigma _1$
. Ergo, by C2,
$\Sigma _1$
. Ergo, by C2,
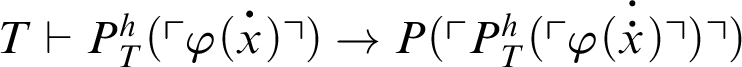 . By assumption, it follows that
. By assumption, it follows that
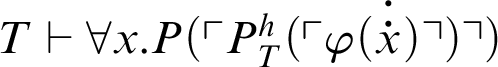 ; therefore,
; therefore,
![]() $T\vdash \forall x. \varphi (x)$
.
$T\vdash \forall x. \varphi (x)$
.
In the next result, we drop the assumption that h is primitive-recursive, but we need to strengthen condition C1.
Theorem 5.3. Let T be such that there is a provability predicate
![]() $P(x)$
satisfying
$P(x)$
satisfying
![]() $:$
$:$
-
C1 For all formulas
 $\varphi (x)$
,
$\varphi (x)$
,

-
C2 If
 $\varphi (x)$
is a
$\varphi (x)$
is a
 $\Sigma _n$
-formula, then
$\Sigma _n$
-formula, then

-
C3 For all formulas
 $\varphi (x)$
and
$\varphi (x)$
and
 $\psi (x)$
,
$\psi (x)$
,
 .
.
If
![]() $\varphi (x)$
is a
$\varphi (x)$
is a
![]() $\Pi _n$
-formula such that
$\Pi _n$
-formula such that
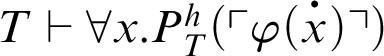 , then
, then
![]() $T+\mathop {\text {Con}} \nolimits _P\vdash \forall x. \varphi (x)$
.
$T+\mathop {\text {Con}} \nolimits _P\vdash \forall x. \varphi (x)$
.
Proof As
![]() $\varphi (x)$
is
$\varphi (x)$
is
![]() $\Pi _n$
, by C2,
$\Pi _n$
, by C2,
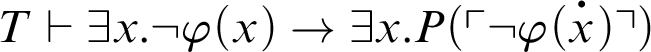 . As
. As
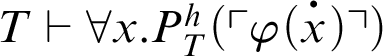 , it follows, by C1, that
, it follows, by C1, that
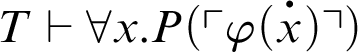 . This, together with the fact that
. This, together with the fact that
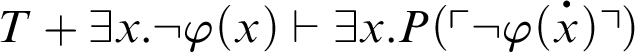 , yields
, yields
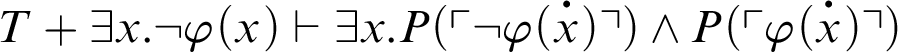 . As
. As
![]() $\neg \varphi :=\varphi \rightarrow {\perp }$
, it follows by C3 that
$\neg \varphi :=\varphi \rightarrow {\perp }$
, it follows by C3 that
![]() $T+\exists x.\neg \varphi (x)\vdash \exists x. P(\ulcorner \perp \urcorner )$
, i.e.,
$T+\exists x.\neg \varphi (x)\vdash \exists x. P(\ulcorner \perp \urcorner )$
, i.e.,
![]() $T+\exists x.\neg \varphi (x)\vdash P(\ulcorner \perp \urcorner )$
. Hence,
$T+\exists x.\neg \varphi (x)\vdash P(\ulcorner \perp \urcorner )$
. Hence,
![]() $T+\mathop {\text {Con}} \nolimits _P\vdash \forall x. \varphi (x)$
.
$T+\mathop {\text {Con}} \nolimits _P\vdash \forall x. \varphi (x)$
.
Feferman, in [Reference Feferman4], requires an intensionally correct arithmetization of provability to satisfy several conditions including C1, C2, and C3.
Corollary 5.2. Let T be such that there is a provability predicate
![]() $P(x)$
satisfying
$P(x)$
satisfying
![]() $:$
$:$
-
C1 For all formulas
 $\varphi (x)$
,
$\varphi (x)$
,

-
C2 If
 $\varphi (x)$
is a
$\varphi (x)$
is a
 $\Sigma _1$
-formula, then
$\Sigma _1$
-formula, then

-
C3 For all formulas
 $\varphi (x)$
and
$\varphi (x)$
and
 $\psi (x)$
,
$\psi (x)$
,

-
C4
 $T\vdash \mathop {\text {Con}} \nolimits _P$
.
$T\vdash \mathop {\text {Con}} \nolimits _P$
.
If
![]() $\varphi (x)$
is a
$\varphi (x)$
is a
![]() $\Pi _1$
-formula such that
$\Pi _1$
-formula such that
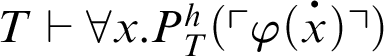 , then
, then
![]() $T\vdash \forall x. \varphi (x)$
.
$T\vdash \forall x. \varphi (x)$
.
Proof Follows immediately from the previous theorem.
By [Reference Feferman4, Reference Kurahashi8], there is a provability predicate that satisfies C2, C3, and C4. Furthermore, if
![]() $P(x)$
is a provability predicate that satisfies C2 and C4, then
$P(x)$
is a provability predicate that satisfies C2 and C4, then
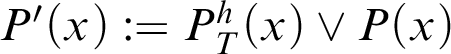 $P'(x):=P^h_T(x)\lor P(x)$
is a provability predicate that satisfies C1, C2, and C4. For this reason, we believe that any sufficiently strong theory T satisfies all the previous conditions.
$P'(x):=P^h_T(x)\lor P(x)$
is a provability predicate that satisfies C1, C2, and C4. For this reason, we believe that any sufficiently strong theory T satisfies all the previous conditions.
Using the theory
![]() $K_T$
we can go even further:
$K_T$
we can go even further:
Corollary 5.3. Let T be a theory in the conditions of the previous result. If
![]() $\varphi (x)$
is a
$\varphi (x)$
is a
![]() $\Pi _1$
-formula such that, for all
$\Pi _1$
-formula such that, for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
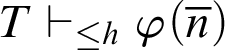 $T\vdash _{\leq h} \varphi (\overline {n})$
, then
$T\vdash _{\leq h} \varphi (\overline {n})$
, then
![]() $K_T\vdash \forall x. \varphi (x)$
.
$K_T\vdash \forall x. \varphi (x)$
.
Proof By the proof of Corollary 5.2, it can be concluded that
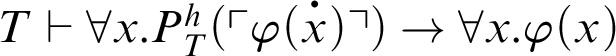 . Thus, the result follows from Theorem 3.1.
. Thus, the result follows from Theorem 3.1.
A result similar to Theorem 5.3, for some
![]() $\Sigma $
-formulas, holds in the presence of the stronger schema
$\Sigma $
-formulas, holds in the presence of the stronger schema
:
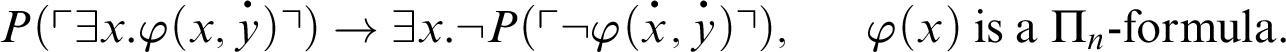
Theorem 5.4. Let T be such that there is a provability predicate
![]() $P(x)$
satisfying
$P(x)$
satisfying
![]() $:$
$:$
-
C1 For all formulas
 $\varphi (x)$
,
$\varphi (x)$
,

-
C2 For all
 $\Sigma _{n}$
-formulas
$\Sigma _{n}$
-formulas
 $\varphi (x,y)$
,
$\varphi (x,y)$
,
 .
.
Suppose that
![]() $\varphi (x)$
is a
$\varphi (x)$
is a
![]() $\Pi _n$
-formula. If
$\Pi _n$
-formula. If
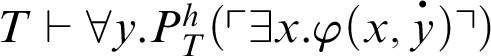 , then
, then
![]() .
.
Proof Suppose that
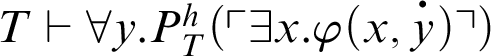 . By C1, we have
. By C1, we have
 . Hence,
. Hence,
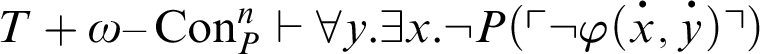 , i.e.,
, i.e.,
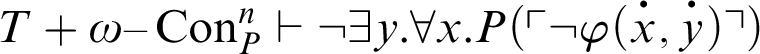 . Furthermore, by C2, we have
. Furthermore, by C2, we have
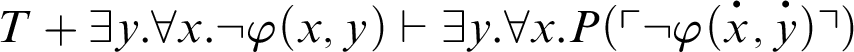 . Therefore,
. Therefore,
![]() , and so,
, and so,
![]() .
.
If
, then everything is provable in T. We can yet get a stronger result, but, like before, we need a stronger schema. Let
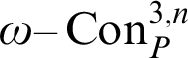
be the following schema:
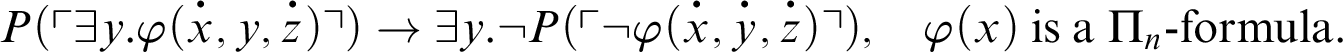
Theorem 5.5. Let T be such that there is a provability predicate
![]() $P(x)$
satisfying
$P(x)$
satisfying
![]() $:$
$:$
-
C1 For all formulas
 $\varphi (x)$
,
$\varphi (x)$
,

-
C2 For all
 $\Pi _n$
-formulas
$\Pi _n$
-formulas
 $\varphi (x,y,z)$
,
$\varphi (x,y,z)$
,

-
C3 For all
 $\Sigma _n$
-formulas
$\Sigma _n$
-formulas
 $\varphi (x,y,z)$
,
$\varphi (x,y,z)$
,
 .
.
Suppose that
![]() $\varphi (x)$
is a
$\varphi (x)$
is a
![]() $\Pi _n$
-formula. If
$\Pi _n$
-formula. If
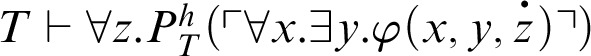 , then
, then
 .
.
Proof
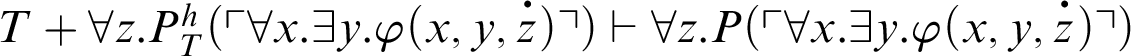 , by C1. From C2,
, by C1. From C2,
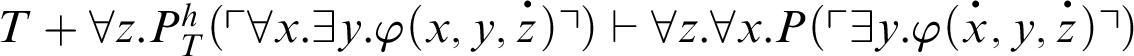 . This means that
. This means that
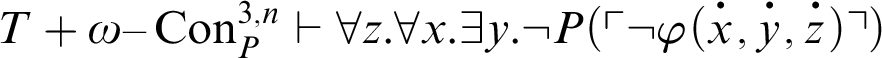 , i.e.,
, i.e.,
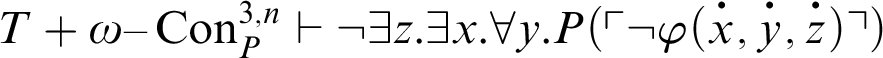 . As
. As
![]() $\varphi (x,y,z)$
is
$\varphi (x,y,z)$
is
![]() $\Pi _n$
, by C3,
$\Pi _n$
, by C3,
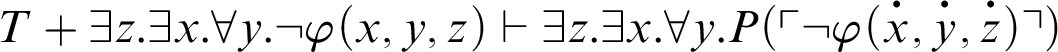 . Altogether,
. Altogether,
 .
.
By Theorem 3.5, we have that the Local Reflection Principle (see [Reference Smorynski16, p. 845]) of
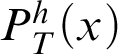 $P^h_T(x)$
is provable in T, i.e.,
$P^h_T(x)$
is provable in T, i.e.,
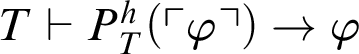 $T\vdash P^h_T(\ulcorner \varphi \urcorner )\rightarrow \varphi $
. In fact, we have the following result.
$T\vdash P^h_T(\ulcorner \varphi \urcorner )\rightarrow \varphi $
. In fact, we have the following result.
Theorem 5.6. Suppose that h is primitive-recursive. Let T be such that there is a provability predicate
![]() $P(x)$
satisfying
$P(x)$
satisfying
![]() $:$
$:$
-
C1 For all formulas
 $\varphi (x)$
,
$\varphi (x)$
,

-
C2 For all
 $\Sigma _1$
-formulas
$\Sigma _1$
-formulas
 $\varphi (x)$
,
$\varphi (x)$
,

-
C3 For all formulas
 $\varphi (x)$
and
$\varphi (x)$
and
 $\psi (x)$
,
$\psi (x)$
,

-
C4
 $T\vdash \mathop {\text {Con}} \nolimits _P;$
$T\vdash \mathop {\text {Con}} \nolimits _P;$
-
C5 For all formulas
 $\varphi (x)$
,
$\varphi (x)$
,
 .
.
Then,
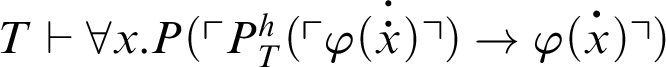 .
.
Proof As h is primitive-recursive, we know that
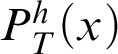 $P^h_T(x)$
and
$P^h_T(x)$
and
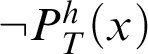 $\neg P^h_T(x)$
are
$\neg P^h_T(x)$
are
![]() $\Sigma _1$
-formulas. By C2,
$\Sigma _1$
-formulas. By C2,
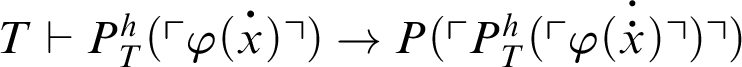 , so
, so
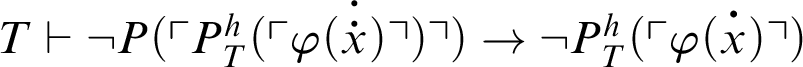 . It holds that
. It holds that
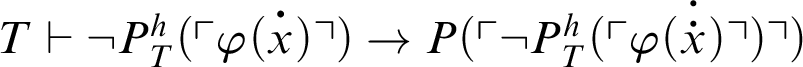 . So,
. So,
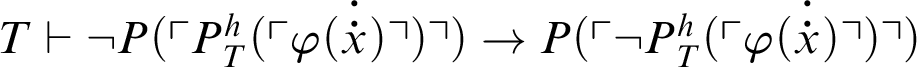 , i.e.,
, i.e.,
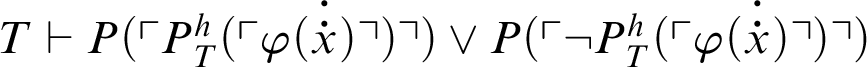 .
.
From logic,
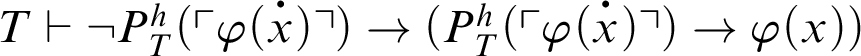 . Hence, by C5,
. Hence, by C5,
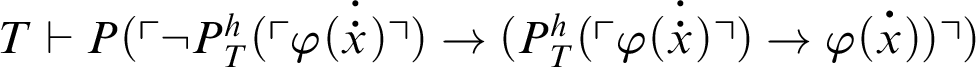 ; thus, by C3,
; thus, by C3,
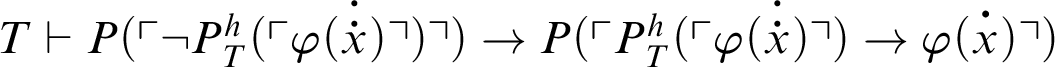 .
.
From C1,
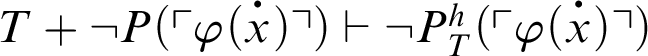 . By C2,
. By C2,
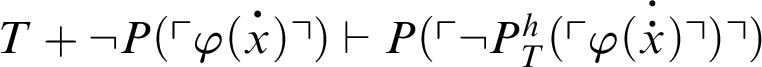 . Ergo we have
. Ergo we have
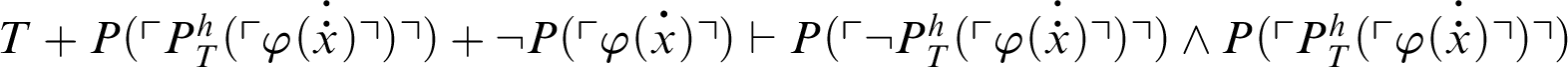 . From C3 and C4, it follows that
. From C3 and C4, it follows that
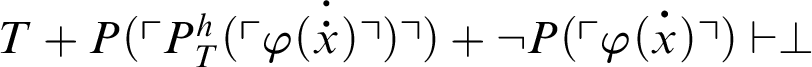 , i.e.,
, i.e.,
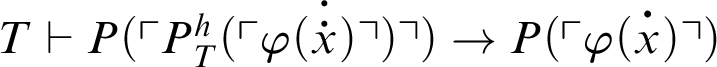 . From logic,
. From logic,
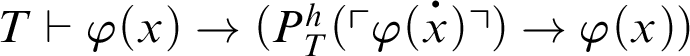 ; thus, by C5 and C3,
; thus, by C5 and C3,
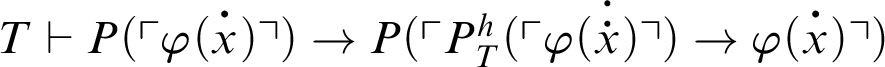 . Hence,
. Hence,
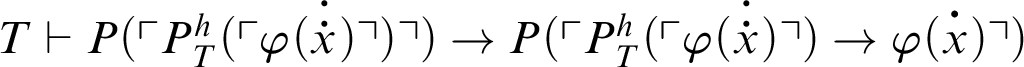 .
.
So we have
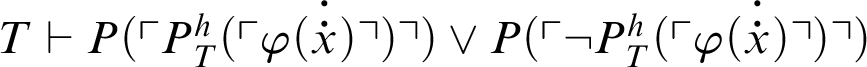 and also
and also
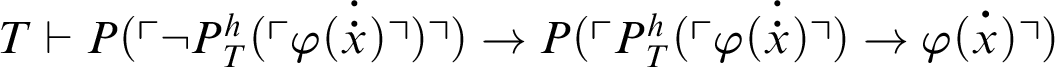 . From before, we have
. From before, we have
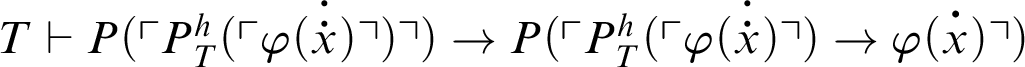 , and thus the result follows.
, and thus the result follows.
Inspired by the previous fact, one can consider the uniform reflection principle schema,
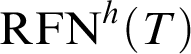 $\mathop {\text {RFN}} \nolimits ^h(T)$
, for the provability notion
$\mathop {\text {RFN}} \nolimits ^h(T)$
, for the provability notion
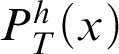 $P^h_T(x)$
(see [Reference Smorynski16, p. 845]):
$P^h_T(x)$
(see [Reference Smorynski16, p. 845]):

With
![]() $\Gamma $
being an arbitrary class of formulas (for example,
$\Gamma $
being an arbitrary class of formulas (for example,
![]() $\Sigma _n$
,
$\Sigma _n$
,
![]() $\Pi _n$
, or even
$\Pi _n$
, or even
![]() $\Delta _n$
), we denote by
$\Delta _n$
), we denote by
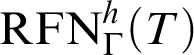 $\mathop {\text {RFN}} \nolimits ^h_\Gamma (T)$
the previous schema restricted to
$\mathop {\text {RFN}} \nolimits ^h_\Gamma (T)$
the previous schema restricted to
![]() $\Gamma $
-formulas and define
$\Gamma $
-formulas and define
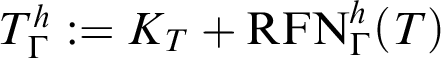 ${T}^h_\Gamma :=K_T+\mathop {\text {RFN}} \nolimits ^h_\Gamma (T)$
. There is a deep relation between
${T}^h_\Gamma :=K_T+\mathop {\text {RFN}} \nolimits ^h_\Gamma (T)$
. There is a deep relation between
![]() $\omega $
-consistency and reflection principles [Reference Smorynski16, p. 853]: Restrictions to
$\omega $
-consistency and reflection principles [Reference Smorynski16, p. 853]: Restrictions to
![]() $\Pi $
-formulas of the uniform reflexion principle for the standard provability predicate are equivalent to restrictions of the schema
$\Pi $
-formulas of the uniform reflexion principle for the standard provability predicate are equivalent to restrictions of the schema
from above to
![]() $\Sigma $
-formulas. Note that we are adding
$\Sigma $
-formulas. Note that we are adding
![]() $\omega $
-consistency and not
$\omega $
-consistency and not
![]() $\omega $
-completeness; hence Kreisel’s conjecture—which follows immediately from
$\omega $
-completeness; hence Kreisel’s conjecture—which follows immediately from
![]() $\omega $
-completeness—is not being trivialised.
$\omega $
-completeness—is not being trivialised.
Now we presented another adapted version of Kreisel’s conjecture.
Theorem 5.7. Let h be a total recursive function and
![]() $\varphi (x)$
be a
$\varphi (x)$
be a
![]() $\Gamma $
-formula such t hat, for all
$\Gamma $
-formula such t hat, for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
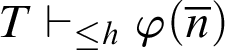 $T\vdash _{\leq h} \varphi (\overline {n})$
. Then,
$T\vdash _{\leq h} \varphi (\overline {n})$
. Then,
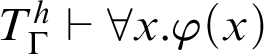 ${T}^h_\Gamma \vdash \forall x.\varphi (x)$
.
${T}^h_\Gamma \vdash \forall x.\varphi (x)$
.
Proof Let h be a total recursive function and
![]() $\varphi (x)$
be a
$\varphi (x)$
be a
![]() $\Gamma $
-formula such that, for all
$\Gamma $
-formula such that, for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
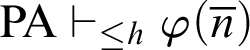 $\mathop {\text {PA}} \nolimits \vdash _{\leq h} \varphi (\overline {n})$
. By Theorem 3.1, we have that
$\mathop {\text {PA}} \nolimits \vdash _{\leq h} \varphi (\overline {n})$
. By Theorem 3.1, we have that
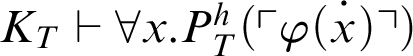 $K_T\vdash \forall x.P^h_T(\ulcorner \varphi (\overset {\boldsymbol {\cdot }}{x})\urcorner )$
. Thus, by
$K_T\vdash \forall x.P^h_T(\ulcorner \varphi (\overset {\boldsymbol {\cdot }}{x})\urcorner )$
. Thus, by
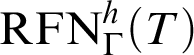 $\mathop {\text {RFN}} \nolimits ^h_\Gamma (T)$
, it follows that
$\mathop {\text {RFN}} \nolimits ^h_\Gamma (T)$
, it follows that
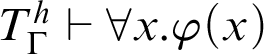 ${T}^h_\Gamma \vdash \forall x.\varphi (x)$
.
${T}^h_\Gamma \vdash \forall x.\varphi (x)$
.
Note that there are no particular reasons to believe that the theory
![]() $K_T$
is effectively axiomatisable. This is something worth studying.
$K_T$
is effectively axiomatisable. This is something worth studying.
Furthermore, one could consider a modal logic with modalities
![]() $\square $
(interpreted by
$\square $
(interpreted by
![]() ${\mathop {\text {Pr}} \nolimits }_{\mathop {\text {PA}} \nolimits }(\cdot )$
) and
${\mathop {\text {Pr}} \nolimits }_{\mathop {\text {PA}} \nolimits }(\cdot )$
) and
![]() $\square _{\leq h}$
(with
$\square _{\leq h}$
(with
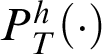 $P^h_T(\cdot )$
as an intended interpretation) and, at least, the usual axioms of
$P^h_T(\cdot )$
as an intended interpretation) and, at least, the usual axioms of
![]() $\square $
and the properties of
$\square $
and the properties of
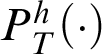 $P^h_T(\cdot )$
. For example, as modal versions of Theorems 3.3, 3.5, and 3.6, one could add the following axioms:
$P^h_T(\cdot )$
. For example, as modal versions of Theorems 3.3, 3.5, and 3.6, one could add the following axioms:
-
Ax.1
 $(\square \square _{\leq h} A)\lor (\square \neg \square _{\leq h} A)$
;
$(\square \square _{\leq h} A)\lor (\square \neg \square _{\leq h} A)$
; -
Ax.2
 $\square _{\leq h} A \rightarrow A$
;
$\square _{\leq h} A \rightarrow A$
; -
Ax.3
 $\neg \square \neg \square _{\leq h} A \rightarrow \square _{\leq h} A$
.
$\neg \square \neg \square _{\leq h} A \rightarrow \square _{\leq h} A$
.
6 On
 $\vdash _{{k\ \mathrm {steps}}}$
and
$\vdash _{{k\ \mathrm {steps}}}$
and
 $\vdash _{\leq h}$
$\vdash _{\leq h}$
From [Reference Clote, Krajićek, Clote and Krajićek3, p. 8], we know the following fact:
Theorem 6.1. If T is a finitely axiomatised theory, then there is a total recursive function
![]() $f(k,\#\varphi )$
such that
$f(k,\#\varphi )$
such that
With this theorem, one can establish a relation between
![]() $\vdash _{k \text { steps}}$
and
$\vdash _{k \text { steps}}$
and
![]() $\vdash _{\leq h}$
.
$\vdash _{\leq h}$
.
Theorem 6.2. Given k, if T is a finitely axiomatised theory, then the function
 $$ \begin{align*} g_k(\#\varphi):=\begin{cases} 1, & T\vdash_{k \text{ steps}} \varphi,\\ 0, & \text{otherwise}\end{cases} \end{align*} $$
$$ \begin{align*} g_k(\#\varphi):=\begin{cases} 1, & T\vdash_{k \text{ steps}} \varphi,\\ 0, & \text{otherwise}\end{cases} \end{align*} $$
is recursive.
Proof Let k be fixed. We will intuitively describe the algorithm that computes the function
![]() $g_k$
. Consider the input
$g_k$
. Consider the input
![]() $\#\varphi $
. Compute, by Theorem 6.2,
$\#\varphi $
. Compute, by Theorem 6.2,
![]() $f(k,\#\varphi )$
. If
$f(k,\#\varphi )$
. If
![]() $\varphi $
is provable with at most k steps, then it must be provable using at most
$\varphi $
is provable with at most k steps, then it must be provable using at most
![]() $f(k,\#\varphi )$
symbols. In such a hypothetical proof, clearly there are, at most,
$f(k,\#\varphi )$
symbols. In such a hypothetical proof, clearly there are, at most,
![]() $f(k,\#\varphi )$
different variables. Furthermore, the variables, besides the ones that occur in
$f(k,\#\varphi )$
different variables. Furthermore, the variables, besides the ones that occur in
![]() $\varphi $
, can be arbitrarily chosen, i.e., if one performs a change of variables in the proof without changing the variables occurring in
$\varphi $
, can be arbitrarily chosen, i.e., if one performs a change of variables in the proof without changing the variables occurring in
![]() $\varphi $
, one maintains the soundness of the proof and the number of steps in it. This means that it is enough to consider a finite set of variables consisting of: the variables in
$\varphi $
, one maintains the soundness of the proof and the number of steps in it. This means that it is enough to consider a finite set of variables consisting of: the variables in
![]() $\varphi $
and
$\varphi $
and
![]() $f(k,\#\varphi )$
other variables. Then, the algorithm considers all possible finite strings constructed using the finite set consisting of: the logical connectives, quantifiers, parenthesis, a blank symbol (to separate the steps in a proof), and the variables of the finite set that was mentioned. By vanishing over all the (finite) possible strings, the algorithm tests if any of them is a proof of
$f(k,\#\varphi )$
other variables. Then, the algorithm considers all possible finite strings constructed using the finite set consisting of: the logical connectives, quantifiers, parenthesis, a blank symbol (to separate the steps in a proof), and the variables of the finite set that was mentioned. By vanishing over all the (finite) possible strings, the algorithm tests if any of them is a proof of
![]() $\varphi $
with at most k steps. If there is any, it outputs
$\varphi $
with at most k steps. If there is any, it outputs
![]() $1$
; otherwise it ought to output
$1$
; otherwise it ought to output
![]() $0$
. Thus, the algorithm outputs
$0$
. Thus, the algorithm outputs
![]() $1$
exactly when
$1$
exactly when
![]() $\varphi $
is provable with at most k steps.
$\varphi $
is provable with at most k steps.
Theorem 6.3. Given k, if T is a finitely axiomatised theory, then there is a total recursive function
![]() $h_k$
such that
$h_k$
such that
Proof Let
![]() $g_k$
be as in Theorem 6.2. It is immediate that the function
$g_k$
be as in Theorem 6.2. It is immediate that the function
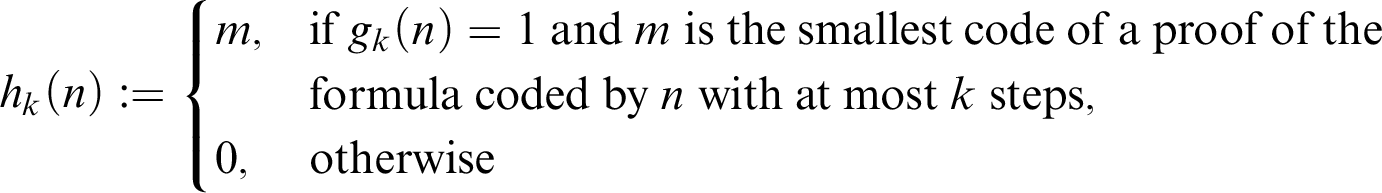 $$ \begin{align*} h_k(n):=\begin{cases} m, & \text{if }g_k(n)=1 \text{ and } m \text{ is the smallest code of a proof of the}\\ &\text{formula coded by }n \text{ with at most }k \text{ steps,}\\ 0, & \text{otherwise} \end{cases} \end{align*} $$
$$ \begin{align*} h_k(n):=\begin{cases} m, & \text{if }g_k(n)=1 \text{ and } m \text{ is the smallest code of a proof of the}\\ &\text{formula coded by }n \text{ with at most }k \text{ steps,}\\ 0, & \text{otherwise} \end{cases} \end{align*} $$
is total recursive. We show that
![]() $T\vdash _{k \text { steps}} \varphi \implies T\vdash _{\leq h_k} \varphi $
. If
$T\vdash _{k \text { steps}} \varphi \implies T\vdash _{\leq h_k} \varphi $
. If
![]() $T\vdash _{k \text { steps}}$
, then
$T\vdash _{k \text { steps}}$
, then
![]() $g_k(n)=1$
and so
$g_k(n)=1$
and so
![]() $h_k(\#\varphi )$
is the code of a proof of
$h_k(\#\varphi )$
is the code of a proof of
![]() $\varphi $
with at most k steps; by definition,
$\varphi $
with at most k steps; by definition,
![]() $T\vdash _{\leq h_k} \varphi $
.
$T\vdash _{\leq h_k} \varphi $
.
There are two immediate consequences of the previous result.
Corollary 6.1. Suppose that T is a finitely axiomatised theory satisfying the conditions of Corollary 5.3 for the function
![]() $h_k$
and that
$h_k$
and that
![]() $\varphi (x)$
is a
$\varphi (x)$
is a
![]() $\Pi _1$
-formula. If for all
$\Pi _1$
-formula. If for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
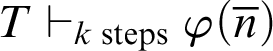 $T\vdash _{k \text { steps}} \varphi (\overline {n})$
, then
$T\vdash _{k \text { steps}} \varphi (\overline {n})$
, then
![]() $K_T\vdash \forall x. \varphi (x)$
.
$K_T\vdash \forall x. \varphi (x)$
.
Proof Follows from the previous theorem and from Corollary 5.3.
Corollary 6.2. Suppose that T is a finitely axiomatised theory and that
![]() $\varphi (x)$
be a
$\varphi (x)$
be a
![]() $\Gamma $
-formula. If, for all
$\Gamma $
-formula. If, for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
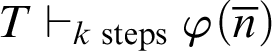 $T\vdash _{k \text { steps}} \varphi (\overline {n})$
, then
$T\vdash _{k \text { steps}} \varphi (\overline {n})$
, then
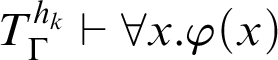 ${T}^{h_k}_\Gamma \vdash \forall x.\varphi (x)$
.
${T}^{h_k}_\Gamma \vdash \forall x.\varphi (x)$
.
We finish with an open problem.
Problem Is there a total recursive function h such that, for all formulas
![]() $\varphi $
,
$\varphi $
,
![]() $\mathop {\text {PA}} \nolimits \vdash _{k \text { steps}} \varphi \implies \mathop {\text {PA}} \nolimits \vdash _{\leq h} \varphi $
?
$\mathop {\text {PA}} \nolimits \vdash _{k \text { steps}} \varphi \implies \mathop {\text {PA}} \nolimits \vdash _{\leq h} \varphi $
?
7 Conclusion
Kreisel’s conjecture is the fundamental problem of k-steps-provability. As mentioned in the introduction, there are some solutions under specific conditions. Usually they rely on properties of the considered formulas or properties of the theory. In this paper, we presented a novel approach to the conjecture, where we abstracted from the concrete formalization.
We introduced a notion of provability
![]() $\vdash _{\leq h}$
expressing that
$\vdash _{\leq h}$
expressing that
![]() $T \vdash _{\leq h} \varphi $
holds if there is a proof of
$T \vdash _{\leq h} \varphi $
holds if there is a proof of
![]() $\varphi $
in T whose code is at most
$\varphi $
in T whose code is at most
![]() $h(\#\varphi )$
. This is clearly an intensional notion. We studied the representation of
$h(\#\varphi )$
. This is clearly an intensional notion. We studied the representation of
![]() $\vdash _{\leq h}$
inside the theory T using the formula
$\vdash _{\leq h}$
inside the theory T using the formula
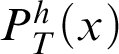 $P^h_T(x)$
and several of its properties. Montagna’s conjecture (“Does
$P^h_T(x)$
and several of its properties. Montagna’s conjecture (“Does
 $\mathop {\text {PA}} \nolimits \vdash _{k \text { steps}} \mathop {\text {Pr}} \nolimits _{\mathop {\text {PA}} \nolimits }(\ulcorner \varphi \urcorner )\rightarrow \varphi $
imply
$\mathop {\text {PA}} \nolimits \vdash _{k \text { steps}} \mathop {\text {Pr}} \nolimits _{\mathop {\text {PA}} \nolimits }(\ulcorner \varphi \urcorner )\rightarrow \varphi $
imply
![]() $\mathop {\text {PA}} \nolimits \vdash _{k \text { steps}} \varphi $
?”) was analysed for the notion
$\mathop {\text {PA}} \nolimits \vdash _{k \text { steps}} \varphi $
?”) was analysed for the notion
![]() $\vdash _{\leq h}$
.
$\vdash _{\leq h}$
.
We also considered variants of Kreisel’s conjecture for provability predicates with different derivability conditions. From the results, we like to highlight Theorem 5.4 that, using a form of
![]() $\omega $
-consistency (
$\omega $
-consistency (
![]() ) and under certain derivability conditions, allows to conclude
) and under certain derivability conditions, allows to conclude
![]() from
from
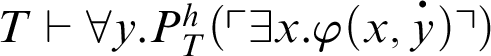 .
.
The paper finishes with connections between
![]() $\vdash _{k \text { steps}}$
and
$\vdash _{k \text { steps}}$
and
![]() $\vdash _{\leq h}$
, in particular, two forms of Kreisel’s conjecture for
$\vdash _{\leq h}$
, in particular, two forms of Kreisel’s conjecture for
![]() $\vdash _{\leq h}$
(Corollaries 6.1 and 6.2).
$\vdash _{\leq h}$
(Corollaries 6.1 and 6.2).
Acknowledgments
This work was funded by the following FCT-projects: Centro de Matemática e Aplicações (UIDB/00297/2020) and Bolsa de Doutoramento (SFRH/BD/143756/2019). The second author was also supported by the Udo Keller Foundation.