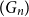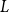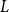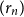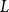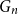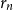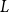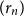1. Introduction
The field of graph convergence studies asymptotic properties of large graphs. The goal is to define a well-behaved notion of a limit structure that describes the limit behaviour of a convergent sequence of graphs. Several different approaches are studied. The two most prominent types of convergence are defined as sequences of dense [Reference Borgs, Chayes, Lovász, Sós and Vesztergombi2, Reference Lovász and Szegedy9, Reference Lovász8] and sparse graphs [Reference Benjamini and Schramm1, Reference Elek4]. The recently introduced notion of structural convergence by Nešetřil and Ossona de Mendez offers a generalising framework for these cases using ideas from analysis, model theory, and probability [Reference Nešetřil and de Mendez10, Reference Nešetřil and de Mendez11].
Structural convergence is a framework of convergence for general relational structures; however, we follow the usual approach that we restrict to the language of graphs and rooted graphs without loss of generality. Our arguments remain valid in the general case (e.g. as in [Reference Christofides and Král’3]). The Stone pairing of a first-order formula
![]() $\phi$
in the language of graphs and a finite graph
$\phi$
in the language of graphs and a finite graph
![]() $G$
, denoted by
$G$
, denoted by
![]() $\langle \phi, G \rangle$
, is the probability that
$\langle \phi, G \rangle$
, is the probability that
![]() $\phi$
is satisfied by a tuple of vertices of
$\phi$
is satisfied by a tuple of vertices of
![]() $G$
selected uniformly at random (for a sentence
$G$
selected uniformly at random (for a sentence
![]() $\phi$
, we set
$\phi$
, we set
![]() $\langle \phi, G \rangle = 1$
if
$\langle \phi, G \rangle = 1$
if
![]() $G \models \phi$
, and
$G \models \phi$
, and
![]() $\langle \phi, G \rangle = 0$
otherwise). A sequence of finite graphs
$\langle \phi, G \rangle = 0$
otherwise). A sequence of finite graphs
![]() $(G_n)$
is said to be
$(G_n)$
is said to be
![]() $\mathrm{FO}$
-convergent if the sequence
$\mathrm{FO}$
-convergent if the sequence
![]() $(\langle \phi, G_n \rangle )$
of probabilities converges for each formula
$(\langle \phi, G_n \rangle )$
of probabilities converges for each formula
![]() $\phi$
. The limit structure
$\phi$
. The limit structure
![]() $L$
, called modelling, is a graph on a standard Borel space with a probability measure
$L$
, called modelling, is a graph on a standard Borel space with a probability measure
![]() $\nu$
satisfying that all the first-order definable sets are measurable. The value
$\nu$
satisfying that all the first-order definable sets are measurable. The value
![]() $\langle \phi, L \rangle$
is defined as the measure of the set
$\langle \phi, L \rangle$
is defined as the measure of the set
![]() ${\phi }({L})$
, the set of solutions of
${\phi }({L})$
, the set of solutions of
![]() $\phi$
in
$\phi$
in
![]() $L$
, using the appropriate power of the measure
$L$
, using the appropriate power of the measure
![]() $\nu$
. A modelling
$\nu$
. A modelling
![]() $L$
is a limit of an
$L$
is a limit of an
![]() $\mathrm{FO}$
-convergent sequence
$\mathrm{FO}$
-convergent sequence
![]() $(G_n)$
if
$(G_n)$
if
![]() $\lim _n \langle \phi, G_n \rangle = \langle \phi, L \rangle$
for each formula
$\lim _n \langle \phi, G_n \rangle = \langle \phi, L \rangle$
for each formula
![]() $\phi$
. A modelling limit does not exist for each
$\phi$
. A modelling limit does not exist for each
![]() $\mathrm{FO}$
-convergent sequence of finite graphs. It is known to exist for all sequences of graphs from a class
$\mathrm{FO}$
-convergent sequence of finite graphs. It is known to exist for all sequences of graphs from a class
![]() $\mathcal{C}$
if and only if
$\mathcal{C}$
if and only if
![]() $\mathcal{C}$
is a nowhere dense class [Reference Nešetřil and de Mendez12].
$\mathcal{C}$
is a nowhere dense class [Reference Nešetřil and de Mendez12].
The authors of this framework asked in [Reference Nešetřil and de Mendez10] the following question: given a sequence
![]() $(G_n)$
converging to a modelling
$(G_n)$
converging to a modelling
![]() $L$
and a vertex of
$L$
and a vertex of
![]() $r$
of
$r$
of
![]() $L$
, is there a sequence of vertices
$L$
, is there a sequence of vertices
![]() $(r_n)$
such that the graphs
$(r_n)$
such that the graphs
![]() $G_n$
rooted at
$G_n$
rooted at
![]() $r_n$
converge to
$r_n$
converge to
![]() $L$
rooted at
$L$
rooted at
![]() $r$
? Christofides and Král’ [Reference Christofides and Král’3] provided an example that the answer is negative in general. However, they also proved that it is always possible to find such a sequence
$r$
? Christofides and Král’ [Reference Christofides and Král’3] provided an example that the answer is negative in general. However, they also proved that it is always possible to find such a sequence
![]() $(r_n)$
for almost all choices of the vertex
$(r_n)$
for almost all choices of the vertex
![]() $r$
. That is, if the root of
$r$
. That is, if the root of
![]() $L$
is chosen at random (according to the measure
$L$
is chosen at random (according to the measure
![]() $\nu$
), the vertices
$\nu$
), the vertices
![]() $(r_n)$
exist with probability
$(r_n)$
exist with probability
![]() $1$
[Reference Christofides and Král’3].
$1$
[Reference Christofides and Král’3].
In this paper, we refine the original problem by considering the root
![]() $r$
to be an algebraic vertex of
$r$
to be an algebraic vertex of
![]() $L$
. That is,
$L$
. That is,
![]() $r$
belongs to a finite definable set of
$r$
belongs to a finite definable set of
![]() $L$
[Reference Tent and Ziegler15]. We prove that the sequence of roots
$L$
[Reference Tent and Ziegler15]. We prove that the sequence of roots
![]() $(r_n)$
always exists under such a condition. Our main result reads as follows:
$(r_n)$
always exists under such a condition. Our main result reads as follows:
Theorem 1.
Let
![]() $(G_n)$
be an
$(G_n)$
be an
![]() $\mathrm{FO}$
-convergent sequence of graphs with a modelling limit
$\mathrm{FO}$
-convergent sequence of graphs with a modelling limit
![]() $L$
and
$L$
and
![]() $r$
be an algebraic vertex of
$r$
be an algebraic vertex of
![]() $L$
. Then there is a sequence
$L$
. Then there is a sequence
![]() $(r_n)$
,
$(r_n)$
,
![]() $r_n \in V(G_n)$
, such that
$r_n \in V(G_n)$
, such that
![]() $(G_n, r_n)$
$(G_n, r_n)$
![]() $\mathrm{FO}$
-converges to
$\mathrm{FO}$
-converges to
![]() $(L,r)$
.
$(L,r)$
.
Note that Theorem1 deals with full
![]() $\mathrm{FO}$
-convergence and not just convergence with respect to sentences (called elementary convergence), for which it is a trivial statement (see the case of
$\mathrm{FO}$
-convergence and not just convergence with respect to sentences (called elementary convergence), for which it is a trivial statement (see the case of
![]() $p=0$
in Lemma 3).
$p=0$
in Lemma 3).
In Section 5, we formulate the example from [Reference Christofides and Král’3] in our context to indicate that Theorem1 is, in a way, best possible. Moreover, we give a simple probabilistic construction of an
![]() $\mathrm{FO}$
-convergent sequence of graphs that does not admit an
$\mathrm{FO}$
-convergent sequence of graphs that does not admit an
![]() $\mathrm{FO}$
-convergent rooting when restricting the roots to a certain definable set.
$\mathrm{FO}$
-convergent rooting when restricting the roots to a certain definable set.
This article is an extended version of the proceeding paper [Reference Hartman, Hons and Nešetřil5].
2. Notation and tools
We use
![]() $\mathbb{N} = \{1, 2, \dots \}, \mathbb{N}_0 = \mathbb{N} \cup \{0\}$
and
$\mathbb{N} = \{1, 2, \dots \}, \mathbb{N}_0 = \mathbb{N} \cup \{0\}$
and
![]() $[n] = \{1, 2, \dots, n\}, [n]_0 = [n] \cup \{0\}$
. All graphs are finite except modelings, which are of size continuum. The vertex set of a graph
$[n] = \{1, 2, \dots, n\}, [n]_0 = [n] \cup \{0\}$
. All graphs are finite except modelings, which are of size continuum. The vertex set of a graph
![]() $G$
is denoted by
$G$
is denoted by
![]() $V(G)$
. The set of formulas in
$V(G)$
. The set of formulas in
![]() $p$
free variables in the language of graphs is denoted by
$p$
free variables in the language of graphs is denoted by
![]() $\mathrm{FO}_p$
, and
$\mathrm{FO}_p$
, and
![]() $\mathrm{FO} = \bigcup _{p \in \mathbb{N}_0} \mathrm{FO}_p$
is the set of all formulas. Tuples of vertices, free variables, etc., are denoted by boldface letters, for example,
$\mathrm{FO} = \bigcup _{p \in \mathbb{N}_0} \mathrm{FO}_p$
is the set of all formulas. Tuples of vertices, free variables, etc., are denoted by boldface letters, for example,
![]() $\boldsymbol{x} = (x_1, \dots, x_p)$
. Multiset is a set that allows multiplicities of its elements. The power set of a set
$\boldsymbol{x} = (x_1, \dots, x_p)$
. Multiset is a set that allows multiplicities of its elements. The power set of a set
![]() $X$
is denoted by
$X$
is denoted by
![]() $2^{X}$
.
$2^{X}$
.
Let
![]() $G$
be an arbitrary graph and
$G$
be an arbitrary graph and
![]() $r$
one of its vertices. By
$r$
one of its vertices. By
![]() $(G,r)$
, we denote the graph
$(G,r)$
, we denote the graph
![]() $G$
rooted at
$G$
rooted at
![]() $r$
. Formally, considering
$r$
. Formally, considering
![]() $G$
as a structure in the language of graphs, we add a new constant ‘Root’ to the vocabulary and interpret it as
$G$
as a structure in the language of graphs, we add a new constant ‘Root’ to the vocabulary and interpret it as
![]() $r$
. We refer to the extended language as the language of rooted graphs. The set of formulas in the extended language is denoted by
$r$
. We refer to the extended language as the language of rooted graphs. The set of formulas in the extended language is denoted by
![]() $\mathrm{FO}^+$
. Note that
$\mathrm{FO}^+$
. Note that
![]() $\mathrm{FO}_p \subseteq \mathrm{FO}^+_p$
. The observation that a rooted modelling is again a modelling was a motivation for the original problem of [Reference Nešetřil and de Mendez10].
$\mathrm{FO}_p \subseteq \mathrm{FO}^+_p$
. The observation that a rooted modelling is again a modelling was a motivation for the original problem of [Reference Nešetřil and de Mendez10].
Let
![]() $L$
be a modelling. A formula
$L$
be a modelling. A formula
![]() $\phi \in \mathrm{FO}_p$
is algebraic in
$\phi \in \mathrm{FO}_p$
is algebraic in
![]() $L$
if
$L$
if
![]() ${\phi }({L})$
is finite, where
${\phi }({L})$
is finite, where
![]() ${\phi }({L}) = \{\boldsymbol{v} \in V(L)^p \;:\; L \models \phi (\boldsymbol{v})\}$
is the set of solutions of
${\phi }({L}) = \{\boldsymbol{v} \in V(L)^p \;:\; L \models \phi (\boldsymbol{v})\}$
is the set of solutions of
![]() $\phi$
in
$\phi$
in
![]() $L$
. A vertex of
$L$
. A vertex of
![]() $L$
is algebraic if it satisfies an algebraic formula [Reference Tent and Ziegler15].
$L$
is algebraic if it satisfies an algebraic formula [Reference Tent and Ziegler15].
We recall Newton’s identities (also known as Girard-Newton formulas) that connect sums of powers with symmetric polynomials. One of the identities states that for a given
![]() $a_1, \dots, a_n \in{\mathbb{R}}$
, the coefficients of the polynomial
$a_1, \dots, a_n \in{\mathbb{R}}$
, the coefficients of the polynomial
![]() $p(x) = \prod _{i=1}^n (x - a_i)$
can be obtained by basic arithmetic operations from values
$p(x) = \prod _{i=1}^n (x - a_i)$
can be obtained by basic arithmetic operations from values
![]() $z_1, \dots, z_n$
, where
$z_1, \dots, z_n$
, where
![]() $z_k = \sum _{i=1}^n a_i^k$
[Reference Stanley and Fomin14].
$z_k = \sum _{i=1}^n a_i^k$
[Reference Stanley and Fomin14].
It is a folklore that the roots of a polynomial continuously depend on the coefficients of the polynomial: for a polynomial
![]() $p(x) = \prod _{i=1}^n (x - a_i) = \sum _{j=0}^n c_j x^j$
and
$p(x) = \prod _{i=1}^n (x - a_i) = \sum _{j=0}^n c_j x^j$
and
![]() $\varepsilon \gt 0$
, there is
$\varepsilon \gt 0$
, there is
![]() $\delta \gt 0$
such that each polynomial
$\delta \gt 0$
such that each polynomial
![]() $q(x) = \sum _{j=0}^n d_j x^j$
with
$q(x) = \sum _{j=0}^n d_j x^j$
with
![]() $|c_j - d_j| \lt \delta$
can decomposed as
$|c_j - d_j| \lt \delta$
can decomposed as
![]() $\prod _{i=1}^n (x - b_i)$
satisfying
$\prod _{i=1}^n (x - b_i)$
satisfying
![]() $|a_i - b_i| \lt \varepsilon$
. All the coefficients and roots are complex [Reference Whitney16].
$|a_i - b_i| \lt \varepsilon$
. All the coefficients and roots are complex [Reference Whitney16].
These classical tools will be used in the proof of Theorem1 and particularly in the key Lemma 6 in Section 4. From Newton’s identities, it follows that the sums
![]() $z_1, \dots, z_n$
determine the values
$z_1, \dots, z_n$
determine the values
![]() $a_1, \dots, a_n$
up to a permutation, which is the fact we utilise. The continuous dependence of roots on coefficients is used for polynomials created via Newton’s identities with real values. Then the statement reads as follows: for each
$a_1, \dots, a_n$
up to a permutation, which is the fact we utilise. The continuous dependence of roots on coefficients is used for polynomials created via Newton’s identities with real values. Then the statement reads as follows: for each
![]() $a_1, \dots, a_n \in{\mathbb{R}}$
and
$a_1, \dots, a_n \in{\mathbb{R}}$
and
![]() $\varepsilon \gt 0$
, there is
$\varepsilon \gt 0$
, there is
![]() $\delta \gt 0$
such that for each
$\delta \gt 0$
such that for each
![]() $b_1, \dots, b_n \in{\mathbb{R}}$
with
$b_1, \dots, b_n \in{\mathbb{R}}$
with
![]() $\left |\sum _{i=1}^n a_i^k - \sum _{i=1}^n b_i^k \right | \lt \delta$
for all
$\left |\sum _{i=1}^n a_i^k - \sum _{i=1}^n b_i^k \right | \lt \delta$
for all
![]() $k = 1, \dots, n$
holds that there is a permutation
$k = 1, \dots, n$
holds that there is a permutation
![]() $\pi$
satisfying
$\pi$
satisfying
![]() $|a_i - b_{\pi (i)}| \lt \varepsilon$
.
$|a_i - b_{\pi (i)}| \lt \varepsilon$
.
3. Rooting in algebraic sets
We prove Theorem1 in the following equivalent form.
Theorem 2.
Let
![]() $(G_n)$
be an
$(G_n)$
be an
![]() $\mathrm{FO}$
-convergent sequence of graphs with a modelling limit
$\mathrm{FO}$
-convergent sequence of graphs with a modelling limit
![]() $L$
and
$L$
and
![]() $\xi (x)$
be an algebraic formula in
$\xi (x)$
be an algebraic formula in
![]() $L$
. Then there is a sequence
$L$
. Then there is a sequence
![]() $(r_n)$
,
$(r_n)$
,
![]() $r_n \in V(G_n)$
, and a vertex
$r_n \in V(G_n)$
, and a vertex
![]() $r \in{\xi }({L})$
such that
$r \in{\xi }({L})$
such that
![]() $(G_n, r_n)$
$(G_n, r_n)$
![]() $\mathrm{FO}$
-converges to
$\mathrm{FO}$
-converges to
![]() $(L,r)$
.
$(L,r)$
.
Obviously, Theorem2 is implied by Theorem1. The converse follows from the fact that
![]() $\xi$
has only finitely many solutions in
$\xi$
has only finitely many solutions in
![]() $L$
and we can root them iteratively one by one until we reach
$L$
and we can root them iteratively one by one until we reach
![]() $r$
.
$r$
.
Fix a sequence
![]() $(G_n)$
that
$(G_n)$
that
![]() $\mathrm{FO}$
-converges to a modelling
$\mathrm{FO}$
-converges to a modelling
![]() $L$
and a formula
$L$
and a formula
![]() $\xi$
that is algebraic in
$\xi$
that is algebraic in
![]() $L$
for the rest of the paper. Without loss of generality, assume that
$L$
for the rest of the paper. Without loss of generality, assume that
![]() ${\xi }({L})$
is an inclusion-minimal definable set in
${\xi }({L})$
is an inclusion-minimal definable set in
![]() $L$
and
$L$
and
![]() $|{\xi }({G_n})| = |{\xi }({L})|$
for each
$|{\xi }({G_n})| = |{\xi }({L})|$
for each
![]() $n$
. We prove Theorem2 in three steps. First, we consider a single formula
$n$
. We prove Theorem2 in three steps. First, we consider a single formula
![]() $\phi$
in the language of rooted graphs and show that we can find the roots
$\phi$
in the language of rooted graphs and show that we can find the roots
![]() $(r_n)$
and
$(r_n)$
and
![]() $r$
such that
$r$
such that
![]() $\lim \langle \phi, (G_n, r_n) \rangle = \langle \phi, (L, r) \rangle$
. Then we consider an arbitrary finite collection of formulas
$\lim \langle \phi, (G_n, r_n) \rangle = \langle \phi, (L, r) \rangle$
. Then we consider an arbitrary finite collection of formulas
![]() $\phi _1, \dots, \phi _k$
and construct a single formula
$\phi _1, \dots, \phi _k$
and construct a single formula
![]() $\psi$
with the property that convergence of
$\psi$
with the property that convergence of
![]() $\langle \psi, (G_n, r_n) \rangle$
to
$\langle \psi, (G_n, r_n) \rangle$
to
![]() $\langle \psi, (L, r) \rangle$
implies convergence of each
$\langle \psi, (L, r) \rangle$
implies convergence of each
![]() $\langle \phi _i, (G_n, r_n) \rangle$
to
$\langle \phi _i, (G_n, r_n) \rangle$
to
![]() $\langle \phi _i, (L, r) \rangle$
. Finally, a routine use of compactness extends the previous to all formulas, which proves the theorem.
$\langle \phi _i, (L, r) \rangle$
. Finally, a routine use of compactness extends the previous to all formulas, which proves the theorem.
3.1 Single formula
For a formula
![]() $\phi (\boldsymbol{x}) \in \mathrm{FO}^+_p$
, let
$\phi (\boldsymbol{x}) \in \mathrm{FO}^+_p$
, let
![]() $\phi ^-(\boldsymbol{x}, y) \in \mathrm{FO}_{p+1}$
be the formula created from
$\phi ^-(\boldsymbol{x}, y) \in \mathrm{FO}_{p+1}$
be the formula created from
![]() $\phi$
by replacing each occurrence of the term ‘Root’ by ‘
$\phi$
by replacing each occurrence of the term ‘Root’ by ‘
![]() $y$
’ (we assume that
$y$
’ (we assume that
![]() $y$
does not appear in
$y$
does not appear in
![]() $\phi$
).
$\phi$
).
Lemma 3.
For a given
![]() $\phi \in \mathrm{FO}^+_p$
, there is a sequence
$\phi \in \mathrm{FO}^+_p$
, there is a sequence
![]() $(r_n)$
,
$(r_n)$
,
![]() $r_n \in{\xi }({G_n})$
, and a vertex
$r_n \in{\xi }({G_n})$
, and a vertex
![]() $r \in{\xi }({L})$
such that
$r \in{\xi }({L})$
such that
![]() $\lim \langle \phi, (G_n, r_n) \rangle = \langle \phi, (L,r) \rangle$
.
$\lim \langle \phi, (G_n, r_n) \rangle = \langle \phi, (L,r) \rangle$
.
Proof. If
![]() $p = 0$
, then either the sentence
$p = 0$
, then either the sentence
![]() $(\forall y)(\xi (y) \rightarrow \phi ^-(y))$
or
$(\forall y)(\xi (y) \rightarrow \phi ^-(y))$
or
![]() $(\forall y)(\xi (y) \rightarrow \neg \phi ^-(y))$
is satisfied in
$(\forall y)(\xi (y) \rightarrow \neg \phi ^-(y))$
is satisfied in
![]() $L$
(using the assumption that
$L$
(using the assumption that
![]() ${\xi }({L})$
is an inclusion-minimal definable set); hence, it holds in each
${\xi }({L})$
is an inclusion-minimal definable set); hence, it holds in each
![]() $G_n$
from a certain index on. Therefore, an arbitrary choice of
$G_n$
from a certain index on. Therefore, an arbitrary choice of
![]() $r_n \in{\xi }({G_n})$
and
$r_n \in{\xi }({G_n})$
and
![]() $r \in{\xi }({L})$
meets the conclusion.
$r \in{\xi }({L})$
meets the conclusion.
Assume that
![]() $p \geq 1$
. Let
$p \geq 1$
. Let
![]() $\nu$
be the measure associated with the modelling
$\nu$
be the measure associated with the modelling
![]() $L$
. Define
$L$
. Define
![]() $f_L\;:\; V(L)^p \to 2^{{\xi }({L})}$
to be the function that sends
$f_L\;:\; V(L)^p \to 2^{{\xi }({L})}$
to be the function that sends
![]() $\boldsymbol{v}$
to the set
$\boldsymbol{v}$
to the set
![]() $\{u \in{\xi }({L}) \;:\; L \models \phi ^-(\boldsymbol{v}, u)\}$
. Consider the pushforward measure
$\{u \in{\xi }({L}) \;:\; L \models \phi ^-(\boldsymbol{v}, u)\}$
. Consider the pushforward measure
![]() $\mu _L$
on
$\mu _L$
on
![]() $2^{{\xi }({L})}$
of the
$2^{{\xi }({L})}$
of the
![]() $p$
-th power of
$p$
-th power of
![]() $\nu$
by
$\nu$
by
![]() $f_L$
(note that for each
$f_L$
(note that for each
![]() $u \in \xi (L)$
is the set
$u \in \xi (L)$
is the set
![]() $f_L^{-1}({u})$
measurable). Viewing
$f_L^{-1}({u})$
measurable). Viewing
![]() $2^{{\xi }({L})}$
as a lattice, we are mostly interested in the measure of the filter generated by atoms of
$2^{{\xi }({L})}$
as a lattice, we are mostly interested in the measure of the filter generated by atoms of
![]() $2^{{\xi }({L})}$
. Let
$2^{{\xi }({L})}$
. Let
![]() $X^\uparrow = \{Y \in 2^{{\xi }({L})} \;:\; X \subseteq Y\}$
denote the filter generated by
$X^\uparrow = \{Y \in 2^{{\xi }({L})} \;:\; X \subseteq Y\}$
denote the filter generated by
![]() $X \in 2^{{\xi }({L})}$
. Observe that for
$X \in 2^{{\xi }({L})}$
. Observe that for
![]() $u \in{\xi }({L})$
, we have
$u \in{\xi }({L})$
, we have
![]() $\mu _L(\{u\}^\uparrow ) = \langle \phi, (L, u) \rangle$
. Suppose that
$\mu _L(\{u\}^\uparrow ) = \langle \phi, (L, u) \rangle$
. Suppose that
![]() $|{\xi }({L})| = t$
and define an ordering
$|{\xi }({L})| = t$
and define an ordering
![]() $R_L = (u_1, u_2, \dots, u_t)$
of
$R_L = (u_1, u_2, \dots, u_t)$
of
![]() $\xi (L)$
such that
$\xi (L)$
such that
![]() $\mu _L(R_L) = (\mu _L(\{u_i\}^\uparrow ))_{i \in [t]}$
satisfies
$\mu _L(R_L) = (\mu _L(\{u_i\}^\uparrow ))_{i \in [t]}$
satisfies
![]() $\mu _L(\{u_1\}^\uparrow ) \geq \mu _L(\{u_2\}^\uparrow ) \geq \dots \geq \mu _L(\{u_t\}^\uparrow )$
. Define similarly for each
$\mu _L(\{u_1\}^\uparrow ) \geq \mu _L(\{u_2\}^\uparrow ) \geq \dots \geq \mu _L(\{u_t\}^\uparrow )$
. Define similarly for each
![]() $n$
the function
$n$
the function
![]() $f_n \;:\; V(G_n)^p \to 2^{{\xi }({G_n})}$
, measure
$f_n \;:\; V(G_n)^p \to 2^{{\xi }({G_n})}$
, measure
![]() $\mu _n$
(as the pushforward of the uniform measure), and the
$\mu _n$
(as the pushforward of the uniform measure), and the
![]() $t$
-tuple
$t$
-tuple
![]() $R_n$
.
$R_n$
.
We prove that the sequence of vectors
![]() $\big (\mu _n(R_n)\big ) \subset ([0,1]^t, \|\cdot \|_\infty )$
converges to
$\big (\mu _n(R_n)\big ) \subset ([0,1]^t, \|\cdot \|_\infty )$
converges to
![]() $\mu _L(R_L)$
. Then an arbitrary choice of an index
$\mu _L(R_L)$
. Then an arbitrary choice of an index
![]() $i \in [t]$
yields the sequence
$i \in [t]$
yields the sequence
![]() $(r_n)$
and vertex
$(r_n)$
and vertex
![]() $r$
as the
$r$
as the
![]() $i$
-th elements of the tuples
$i$
-th elements of the tuples
![]() $R_n$
and
$R_n$
and
![]() $R_L$
, respectively.
$R_L$
, respectively.
Let us argue that the convergence
![]() $\big (\mu _n(R_n)\big ) \to \mu _L(R_L)$
follows from Lemma 6. We first apply the lemma for the set
$\big (\mu _n(R_n)\big ) \to \mu _L(R_L)$
follows from Lemma 6. We first apply the lemma for the set
![]() $M ={\xi }({L})$
, that is,
$M ={\xi }({L})$
, that is,
![]() $m = t$
, and the probability distribution
$m = t$
, and the probability distribution
![]() $\mu = \mu _L$
to show that the values of
$\mu = \mu _L$
to show that the values of
![]() $\mu _L(R_L)$
can be computed from probabilities
$\mu _L(R_L)$
can be computed from probabilities
![]() $\langle \psi _{k,\ell }, L \rangle, \ell \in [t]_0, k \in \left [ \binom{t}{\ell } \right ]$
for certain formulas
$\langle \psi _{k,\ell }, L \rangle, \ell \in [t]_0, k \in \left [ \binom{t}{\ell } \right ]$
for certain formulas
![]() $\psi _{k,\ell } \in \mathrm{FO}$
.
$\psi _{k,\ell } \in \mathrm{FO}$
.
This can be done as follows. By definition,
![]() $\Pr [F_\ell ^k]$
is the probability that the intersection of
$\Pr [F_\ell ^k]$
is the probability that the intersection of
![]() $k$
independently chosen
$k$
independently chosen
![]() $\mu _L$
-random subsets
$\mu _L$
-random subsets
![]() $S_i$
of
$S_i$
of
![]() ${\xi }({L})$
has size at least
${\xi }({L})$
has size at least
![]() $\ell$
. To compute the probability, we sample each set
$\ell$
. To compute the probability, we sample each set
![]() $S_i = f_L(\boldsymbol{v}_i) = \{u \in{\xi }({L}) \;:\; L \models \phi ^-(\boldsymbol{v}_i, u)\}$
by taking an independent
$S_i = f_L(\boldsymbol{v}_i) = \{u \in{\xi }({L}) \;:\; L \models \phi ^-(\boldsymbol{v}_i, u)\}$
by taking an independent
![]() $\nu$
-random
$\nu$
-random
![]() $p$
-tuple
$p$
-tuple
![]() $\boldsymbol{v}_i \in V(L)^p$
, and we verify that the intersection
$\boldsymbol{v}_i \in V(L)^p$
, and we verify that the intersection
![]() $\bigcap _{i=1}^k S_i \subseteq \xi (L)$
contains at least
$\bigcap _{i=1}^k S_i \subseteq \xi (L)$
contains at least
![]() $\ell$
distinct elements
$\ell$
distinct elements
![]() $y_1, \dots, y_\ell$
. Therefore,
$y_1, \dots, y_\ell$
. Therefore,
![]() $\Pr [F_\ell ^k]$
is equal to
$\Pr [F_\ell ^k]$
is equal to
![]() $\langle \psi _{k,\ell }, L \rangle$
for the
$\langle \psi _{k,\ell }, L \rangle$
for the
![]() $\mathrm{FO}$
-formulas
$\mathrm{FO}$
-formulas
![]() $\psi _{k,\ell }(\boldsymbol{x}_1, \dots, \boldsymbol{x}_k) \in \mathrm{FO}_{k \cdot p}$
of the form
$\psi _{k,\ell }(\boldsymbol{x}_1, \dots, \boldsymbol{x}_k) \in \mathrm{FO}_{k \cdot p}$
of the form
 \begin{equation*} (\exists y_1, \dots, y_\ell ) \left ( \bigwedge _{i = 1}^\ell \xi (y_i) \land \bigwedge _{1 \leq i \lt j \leq \ell } y_i \not = y_j \land \bigwedge _{i = 1}^k \bigwedge _{j = 1}^\ell \phi ^-(\boldsymbol{x}_i, y_j) \right ), \end{equation*}
\begin{equation*} (\exists y_1, \dots, y_\ell ) \left ( \bigwedge _{i = 1}^\ell \xi (y_i) \land \bigwedge _{1 \leq i \lt j \leq \ell } y_i \not = y_j \land \bigwedge _{i = 1}^k \bigwedge _{j = 1}^\ell \phi ^-(\boldsymbol{x}_i, y_j) \right ), \end{equation*}
where, by definition of
![]() $\langle \cdot, \cdot \rangle$
, the independent
$\langle \cdot, \cdot \rangle$
, the independent
![]() $\nu$
-random
$\nu$
-random
![]() $p$
-tuples
$p$
-tuples
![]() $\boldsymbol{v}_i \in V(L)^p$
are assigned to the disjoint
$\boldsymbol{v}_i \in V(L)^p$
are assigned to the disjoint
![]() $p$
-tuples of variables
$p$
-tuples of variables
![]() $\boldsymbol{x}_i$
. Moreover, we have directly from the definition that the values of the multiset
$\boldsymbol{x}_i$
. Moreover, we have directly from the definition that the values of the multiset
![]() $A_1$
from the conclusion of Lemma 6 are exactly the values of
$A_1$
from the conclusion of Lemma 6 are exactly the values of
![]() $\mu _L(R_L)$
.
$\mu _L(R_L)$
.
Similarly, by applying Lemma 6 for
![]() $M ={\xi }({G_n})$
and
$M ={\xi }({G_n})$
and
![]() $\mu = \mu _n$
, we obtain that
$\mu = \mu _n$
, we obtain that
![]() $\mu _n(R_n)$
depends only on
$\mu _n(R_n)$
depends only on
![]() $\langle \psi _{k,\ell }, G_n \rangle, \ell \in [t]_0, k \in \left [ \binom{t}{\ell } \right ]$
. Furthermore, since the dependency is continuous, and
$\langle \psi _{k,\ell }, G_n \rangle, \ell \in [t]_0, k \in \left [ \binom{t}{\ell } \right ]$
. Furthermore, since the dependency is continuous, and
![]() $\langle \psi _{k,\ell }, G_n \rangle \to \langle \psi _{k,\ell }, L \rangle$
for each
$\langle \psi _{k,\ell }, G_n \rangle \to \langle \psi _{k,\ell }, L \rangle$
for each
![]() $k, \ell \in \mathbb{N}$
by
$k, \ell \in \mathbb{N}$
by
![]() $\mathrm{FO}$
-convergence of
$\mathrm{FO}$
-convergence of
![]() $(G_n)$
to
$(G_n)$
to
![]() $L$
, we infer that the vectors
$L$
, we infer that the vectors
![]() $\big (\mu _n(R_n)\big )$
indeed converge to
$\big (\mu _n(R_n)\big )$
indeed converge to
![]() $\mu _L(R_L)$
.
$\mu _L(R_L)$
.
3.2 Finite collection of formulas
In this part, we use Lemma 3 to prove an analogous statement for a finite collection of formulas.
Lemma 4.
For given formulas
![]() $\phi _1, \dots, \phi _k$
, there is a sequence
$\phi _1, \dots, \phi _k$
, there is a sequence
![]() $(r_n)$
,
$(r_n)$
,
![]() $r_n \in{\xi }({G_n})$
, and a vertex
$r_n \in{\xi }({G_n})$
, and a vertex
![]() $r \in{\xi }({L})$
such that
$r \in{\xi }({L})$
such that
![]() $\lim \langle \phi _i, (G_n, r_n) \rangle = \langle \phi _i, (L,r) \rangle$
for each
$\lim \langle \phi _i, (G_n, r_n) \rangle = \langle \phi _i, (L,r) \rangle$
for each
![]() $\phi _i$
.
$\phi _i$
.
Proof. Since for sentences any choice of
![]() $(r_n)$
and
$(r_n)$
and
![]() $r$
works, we assume that neither of
$r$
works, we assume that neither of
![]() $\phi _1, \dots, \phi _k$
is a sentence.
$\phi _1, \dots, \phi _k$
is a sentence.
Consider an inclusion-maximal set
![]() $I \subseteq [k]$
for which there is
$I \subseteq [k]$
for which there is
![]() $v \in{\xi }({L})$
such that every
$v \in{\xi }({L})$
such that every
![]() $i \in I$
satisfies
$i \in I$
satisfies
![]() $\langle \phi _i, (L,v) \rangle \gt 0$
. Denote
$\langle \phi _i, (L,v) \rangle \gt 0$
. Denote
![]() $|I|$
by
$|I|$
by
![]() $k'$
. If
$k'$
. If
![]() $I = \emptyset$
, we can choose
$I = \emptyset$
, we can choose
![]() $(r_n)$
and
$(r_n)$
and
![]() $r$
arbitrarily; hence, assume otherwise. For
$r$
arbitrarily; hence, assume otherwise. For
![]() $i \in I$
, set
$i \in I$
, set
![]() $A_i = \{\langle \phi _i, (L,u) \rangle \;:\; u \in{\xi }({L}) \} \cap (0, 1]$
. Take a vector
$A_i = \{\langle \phi _i, (L,u) \rangle \;:\; u \in{\xi }({L}) \} \cap (0, 1]$
. Take a vector
![]() $\boldsymbol{e} \in \mathbb{N}^{k'}$
of exponents with the property that for each distinct
$\boldsymbol{e} \in \mathbb{N}^{k'}$
of exponents with the property that for each distinct
![]() $\boldsymbol{a}, \boldsymbol{b} \in \textrm{X}_{i \in I} A_i$
, we have
$\boldsymbol{a}, \boldsymbol{b} \in \textrm{X}_{i \in I} A_i$
, we have
![]() $\prod _{i \in I} a_i^{e_i} \not = \prod _{i \in I} b_i^{e_i}$
. Such a vector exists as each
$\prod _{i \in I} a_i^{e_i} \not = \prod _{i \in I} b_i^{e_i}$
. Such a vector exists as each
![]() $A_i$
is finite and contains only positive values. The set of bad choices of rational exponents that make the values for particular
$A_i$
is finite and contains only positive values. The set of bad choices of rational exponents that make the values for particular
![]() $\boldsymbol{a}, \boldsymbol{b}$
coincide form a
$\boldsymbol{a}, \boldsymbol{b}$
coincide form a
![]() $(k'-1)$
-dimensional hyperplane in
$(k'-1)$
-dimensional hyperplane in
![]() $\mathbb{Q}^{k'}$
. We can surely avoid finitely many of such hyperplanes (one for each choice of
$\mathbb{Q}^{k'}$
. We can surely avoid finitely many of such hyperplanes (one for each choice of
![]() $\boldsymbol{a}$
and
$\boldsymbol{a}$
and
![]() $\boldsymbol{b}$
) to find a good vector of positive rational exponents and scale them to integers.
$\boldsymbol{b}$
) to find a good vector of positive rational exponents and scale them to integers.
Use Lemma 3 for the formula
![]() $\psi$
of the form
$\psi$
of the form
 \begin{equation*} \bigwedge _{i \in I} \bigwedge _{j=1}^{e_i} \phi _i(\boldsymbol{x}_{i,j}), \end{equation*}
\begin{equation*} \bigwedge _{i \in I} \bigwedge _{j=1}^{e_i} \phi _i(\boldsymbol{x}_{i,j}), \end{equation*}
where all the tuples
![]() $\boldsymbol{x}_{i,j}$
are pairwise disjoint, to obtain roots
$\boldsymbol{x}_{i,j}$
are pairwise disjoint, to obtain roots
![]() $(r_n)$
and
$(r_n)$
and
![]() $r$
. In particular, we can take the vertex
$r$
. In particular, we can take the vertex
![]() $r$
such that
$r$
such that
![]() $\langle \psi, (L,r) \rangle \gt 0$
(due to our choice of
$\langle \psi, (L,r) \rangle \gt 0$
(due to our choice of
![]() $I$
).
$I$
).
We have
![]() $\lim \langle \phi _i, (G_n, r_n) \rangle = \langle \phi _i, (L, r) \rangle \gt 0$
for each
$\lim \langle \phi _i, (G_n, r_n) \rangle = \langle \phi _i, (L, r) \rangle \gt 0$
for each
![]() $i \in I$
as
$i \in I$
as
using our selection of exponents
![]() $\boldsymbol{e}$
.
$\boldsymbol{e}$
.
Also, it holds that
![]() $\lim \langle \phi _j, (G_n, r_n) \rangle = \langle \phi _j, (L,r) \rangle = 0$
for each
$\lim \langle \phi _j, (G_n, r_n) \rangle = \langle \phi _j, (L,r) \rangle = 0$
for each
![]() $j \not \in I$
: for the formula
$j \not \in I$
: for the formula
![]() $\chi = \bigwedge _{i \in I \cup \{j\}} \phi _i(\boldsymbol{x}_i)$
, we have
$\chi = \bigwedge _{i \in I \cup \{j\}} \phi _i(\boldsymbol{x}_i)$
, we have
![]() $\lim \langle \chi, (G_n,r_n) \rangle = \langle \chi, (L,r) \rangle = 0$
due to the maximality of
$\lim \langle \chi, (G_n,r_n) \rangle = \langle \chi, (L,r) \rangle = 0$
due to the maximality of
![]() $I$
(this is for any choice of
$I$
(this is for any choice of
![]() $(r_n)$
and
$(r_n)$
and
![]() $r$
). We have
$r$
). We have
and as for some
![]() $\varepsilon \gt 0$
, there is
$\varepsilon \gt 0$
, there is
![]() $n_0$
such that
$n_0$
such that
![]() $\langle \phi _i, (G_n,r_n) \rangle \gt \varepsilon$
for each
$\langle \phi _i, (G_n,r_n) \rangle \gt \varepsilon$
for each
![]() $i \in I$
and
$i \in I$
and
![]() $n \geq n_0$
, the factor
$n \geq n_0$
, the factor
![]() $\langle \phi _j, (G_n,r_n) \rangle$
must tend to
$\langle \phi _j, (G_n,r_n) \rangle$
must tend to
![]() $0$
.
$0$
.
We remark that the rationalisation of the fact that the sequence
![]() $\big (\langle \phi _j, (G_n, r_n) \rangle \big )$
for
$\big (\langle \phi _j, (G_n, r_n) \rangle \big )$
for
![]() $j \not \in I$
even converge is the reason why we are proving Theorem2 instead of Theorem1. That is, we are using the fact that we can choose the set
$j \not \in I$
even converge is the reason why we are proving Theorem2 instead of Theorem1. That is, we are using the fact that we can choose the set
![]() $I$
(and the root
$I$
(and the root
![]() $r$
for the formula
$r$
for the formula
![]() $\psi$
) such that any rooting
$\psi$
) such that any rooting
![]() $(r_n)$
makes the sequence
$(r_n)$
makes the sequence
![]() $\langle \chi, (G_n, r_n) \rangle$
converge to
$\langle \chi, (G_n, r_n) \rangle$
converge to
![]() $0$
.
$0$
.
3.3 All formulas
Fix an arbitrary ordering
![]() $\phi _1, \phi _2, \dots$
of
$\phi _1, \phi _2, \dots$
of
![]() $\mathrm{FO}^+$
. We call a collection of sequences of roots
$\mathrm{FO}^+$
. We call a collection of sequences of roots
![]() $(r_n^i)$
,
$(r_n^i)$
,
![]() $r_n^i \in{\xi }({G_n})$
, and
$r_n^i \in{\xi }({G_n})$
, and
![]() $r^i \in{\xi }({L})$
extending if for all indices
$r^i \in{\xi }({L})$
extending if for all indices
![]() $j \leq i \in \mathbb{N}$
satisfies that
$j \leq i \in \mathbb{N}$
satisfies that
![]() $\lim \langle \phi _j, (G_n, r_n^i) \rangle = \langle \phi _j, (L,r^i) \rangle$
and, moreover, for any
$\lim \langle \phi _j, (G_n, r_n^i) \rangle = \langle \phi _j, (L,r^i) \rangle$
and, moreover, for any
![]() $i' \geq i$
, it holds
$i' \geq i$
, it holds
![]() $\langle \phi _j, (L,r^i) \rangle = \langle \phi _j, (L,r^{i'}) \rangle$
. We prove the existence of such a collection and then extract the desired sequence
$\langle \phi _j, (L,r^i) \rangle = \langle \phi _j, (L,r^{i'}) \rangle$
. We prove the existence of such a collection and then extract the desired sequence
![]() $(r_n)$
and vertex
$(r_n)$
and vertex
![]() $r$
by diagonalization.
$r$
by diagonalization.
Lemma 5.
There exists an extending collection of sequences of roots
![]() $(r_n^i)$
,
$(r_n^i)$
,
![]() $r_n^i \in{\xi }({G_n})$
, and
$r_n^i \in{\xi }({G_n})$
, and
![]() $r^i \in{\xi }({L})$
.
$r^i \in{\xi }({L})$
.
Proof. Let
![]() $S_j$
be the set of possible limit values of
$S_j$
be the set of possible limit values of
![]() $\langle \phi _j, (G_n, r_n) \rangle$
, that is, the values of
$\langle \phi _j, (G_n, r_n) \rangle$
, that is, the values of
![]() $\mu _L(R_L)$
from Lemma 3. Let
$\mu _L(R_L)$
from Lemma 3. Let
![]() $T = (V,E)$
be an infinite rooted tree defined as follows:
$T = (V,E)$
be an infinite rooted tree defined as follows:
![]() $V = \bigcup V_\ell$
, where
$V = \bigcup V_\ell$
, where
![]() $V_\ell$
is the set of vertices on the level
$V_\ell$
is the set of vertices on the level
![]() $\ell$
defined as the Cartesian product of the sets
$\ell$
defined as the Cartesian product of the sets
![]() $S_j$
for
$S_j$
for
![]() $j \leq \ell$
, that is, a vertex on the
$j \leq \ell$
, that is, a vertex on the
![]() $\ell$
-th level is a vector with possible limit probabilities for
$\ell$
-th level is a vector with possible limit probabilities for
![]() $\phi _1, \dots, \phi _\ell$
. The only element in
$\phi _1, \dots, \phi _\ell$
. The only element in
![]() $V_0$
, the empty set, is the root of the tree. We put an edge between
$V_0$
, the empty set, is the root of the tree. We put an edge between
![]() $\boldsymbol{a} \in V_\ell$
and
$\boldsymbol{a} \in V_\ell$
and
![]() $\boldsymbol{b} \in V_{\ell +1}$
if
$\boldsymbol{b} \in V_{\ell +1}$
if
![]() $a_j = b_j$
for all
$a_j = b_j$
for all
![]() $j \leq \ell$
, and there are vertices
$j \leq \ell$
, and there are vertices
![]() $x_n \in{\xi }({G_n}), x \in{\xi }({L})$
such that
$x_n \in{\xi }({G_n}), x \in{\xi }({L})$
such that
for each
![]() $j \leq \ell +1$
. Observe that if
$j \leq \ell +1$
. Observe that if
![]() $\boldsymbol{a}\boldsymbol{b} \in E$
, then
$\boldsymbol{a}\boldsymbol{b} \in E$
, then
![]() $\boldsymbol{b}$
is connected to the root (all edges of the path are witnessed by the vertices
$\boldsymbol{b}$
is connected to the root (all edges of the path are witnessed by the vertices
![]() $(x_n)$
and
$(x_n)$
and
![]() $x$
).
$x$
).
By Lemma 4, there is at least one vertex in each set
![]() $V_\ell$
connected to the root. Thus, by König’s lemma, the tree contains an infinite path
$V_\ell$
connected to the root. Thus, by König’s lemma, the tree contains an infinite path
![]() $\emptyset = \boldsymbol{a}_0, \boldsymbol{a}_1, \boldsymbol{a}_2, \dots$
(all degrees are bounded as each
$\emptyset = \boldsymbol{a}_0, \boldsymbol{a}_1, \boldsymbol{a}_2, \dots$
(all degrees are bounded as each
![]() $S_j$
is finite). The sequence
$S_j$
is finite). The sequence
![]() $(r_n^i)$
and vertex
$(r_n^i)$
and vertex
![]() $r^i$
are defined as the vertices
$r^i$
are defined as the vertices
![]() $(x_n)$
and
$(x_n)$
and
![]() $x$
witnessing the edge from
$x$
witnessing the edge from
![]() $\boldsymbol{a}_{i-1}$
to
$\boldsymbol{a}_{i-1}$
to
![]() $\boldsymbol{a}_i$
.
$\boldsymbol{a}_i$
.
Now we are ready to give the proof of Theorem2.
Proof of Theorem
2. Let
![]() $(r_n^i)$
and
$(r_n^i)$
and
![]() $r^i$
for
$r^i$
for
![]() $i \in \mathbb{N}$
be the vertices from collection of extending sequences from Lemma 5 above. Let
$i \in \mathbb{N}$
be the vertices from collection of extending sequences from Lemma 5 above. Let
![]() $\alpha _i = \langle \phi _i, (L,r^i) \rangle$
, and let
$\alpha _i = \langle \phi _i, (L,r^i) \rangle$
, and let
![]() $N_i$
to be an index satisfying
$N_i$
to be an index satisfying
-
(i)
 $\langle \phi _j, (G_n, r_n^i) \rangle \in (\alpha _j - 2^{-i}, \alpha _j + 2^{-i})$
for each
$\langle \phi _j, (G_n, r_n^i) \rangle \in (\alpha _j - 2^{-i}, \alpha _j + 2^{-i})$
for each
 $n \geq N_i$
and
$n \geq N_i$
and
 $j \leq i$
,
$j \leq i$
, -
(ii)
 $N_i \gt N_j$
for each
$N_i \gt N_j$
for each
 $j \lt i$
.
$j \lt i$
.
Set
![]() $r_n = r_n^i$
, where
$r_n = r_n^i$
, where
![]() $i$
is the minimal positive integer satisfying that
$i$
is the minimal positive integer satisfying that
![]() $n \lt N_{i+1}$
. For the vertex
$n \lt N_{i+1}$
. For the vertex
![]() $r$
, we can set an arbitrary vertex from
$r$
, we can set an arbitrary vertex from
![]() ${\xi }({L})$
that appears infinitely many times as
${\xi }({L})$
that appears infinitely many times as
![]() $r^i$
.
$r^i$
.
It remains to verify that for an arbitrary formula
![]() $\phi _j$
, we have
$\phi _j$
, we have
![]() $\lim \langle \phi _j, (G_n, r_n) \rangle = \alpha _j = \langle \phi _j, (L, r) \rangle$
. Obviously, the second equality holds as
$\lim \langle \phi _j, (G_n, r_n) \rangle = \alpha _j = \langle \phi _j, (L, r) \rangle$
. Obviously, the second equality holds as
![]() $r = r^i$
for some
$r = r^i$
for some
![]() $i \geq j$
. For the first equality, fix
$i \geq j$
. For the first equality, fix
![]() $\varepsilon \gt 0$
and set
$\varepsilon \gt 0$
and set
![]() $k$
to be a positive integer satisfying
$k$
to be a positive integer satisfying
![]() $2^{-k} \lt \varepsilon$
and
$2^{-k} \lt \varepsilon$
and
![]() $k \geq \max \{j, 2\}$
. Then for
$k \geq \max \{j, 2\}$
. Then for
![]() $n \geq N_k$
, we have
$n \geq N_k$
, we have
![]() $\langle \phi _j, (G_n, r_n) \rangle = \langle \phi _j, (G_n, r_n^i) \rangle \in (\alpha _j - 2^{-i}, \alpha _j + 2^{-i})$
for some
$\langle \phi _j, (G_n, r_n) \rangle = \langle \phi _j, (G_n, r_n^i) \rangle \in (\alpha _j - 2^{-i}, \alpha _j + 2^{-i})$
for some
![]() $i \geq k$
. Thus
$i \geq k$
. Thus
![]() $\langle \phi _j, (G_n, r_n) \rangle \in (\alpha _j - \varepsilon, \alpha _j + \varepsilon )$
, which concludes the proof.
$\langle \phi _j, (G_n, r_n) \rangle \in (\alpha _j - \varepsilon, \alpha _j + \varepsilon )$
, which concludes the proof.
4. A lemma about finite Boolean lattices
Let
![]() $M$
be a finite set of size
$M$
be a finite set of size
![]() $m$
. We are going to work with a probability space that allows us to consider random subsets
$m$
. We are going to work with a probability space that allows us to consider random subsets
![]() $S_i$
of
$S_i$
of
![]() $M$
with
$M$
with
![]() $\mathbb{P}[S_i = X] = \mu (\{X\})$
for each
$\mathbb{P}[S_i = X] = \mu (\{X\})$
for each
![]() $X \subseteq M$
, where
$X \subseteq M$
, where
![]() $\mu$
is a probability distribution on
$\mu$
is a probability distribution on
![]() $2^{M}$
. Let
$2^{M}$
. Let
![]() $S_1, S_2, \dots, S_k$
be independently chosen random subsets of
$S_1, S_2, \dots, S_k$
be independently chosen random subsets of
![]() $M$
with distribution
$M$
with distribution
![]() $\mu$
, denote by
$\mu$
, denote by
![]() $E_X^k$
the event
$E_X^k$
the event
![]() $X \subseteq \bigcap _{i=1}^k S_i$
and by
$X \subseteq \bigcap _{i=1}^k S_i$
and by
![]() $F_\ell ^k$
the event
$F_\ell ^k$
the event
![]() $|\bigcap _{i=1}^k S_i| \geq \ell$
. Let
$|\bigcap _{i=1}^k S_i| \geq \ell$
. Let
![]() $X^\uparrow$
stand for the filter
$X^\uparrow$
stand for the filter
![]() $\{Y \in 2^{M} \;:\; X \subseteq Y\}$
and
$\{Y \in 2^{M} \;:\; X \subseteq Y\}$
and
![]() $\mathcal{M}_\ell$
denote the row of
$\mathcal{M}_\ell$
denote the row of
![]() $\ell$
-element sets, that is, the set
$\ell$
-element sets, that is, the set
![]() $\{X \subseteq M \;:\; |X|= \ell \}$
. For
$\{X \subseteq M \;:\; |X|= \ell \}$
. For
![]() $\ell \in [m]_0$
, we define the multiset
$\ell \in [m]_0$
, we define the multiset
![]() $A_\ell = \{ \mu (X^\uparrow ) \;:\; X \in \mathcal{M}_\ell \}$
.
$A_\ell = \{ \mu (X^\uparrow ) \;:\; X \in \mathcal{M}_\ell \}$
.
Lemma 6.
The values of
![]() $\mathbb{P}[F_\ell ^k]$
for
$\mathbb{P}[F_\ell ^k]$
for
![]() $\ell \in [m]_0$
and
$\ell \in [m]_0$
and
![]() $k \in \left [ \binom{m}{\ell } \right ]$
continuously determine the multisets
$k \in \left [ \binom{m}{\ell } \right ]$
continuously determine the multisets
![]() $A_\ell$
for all
$A_\ell$
for all
![]() $\ell \in [m]_0$
.
$\ell \in [m]_0$
.
That is, for each
![]() $\varepsilon \gt 0$
, there is
$\varepsilon \gt 0$
, there is
![]() $\delta \gt 0$
such that changing each
$\delta \gt 0$
such that changing each
![]() $\mathbb{P}[F_\ell ^k]$
by at most
$\mathbb{P}[F_\ell ^k]$
by at most
![]() $\delta$
induces a change of each value in
$\delta$
induces a change of each value in
![]() $A_\ell$
by at most
$A_\ell$
by at most
![]() $\varepsilon$
.
$\varepsilon$
.
Proof. We proceed by downward induction on
![]() $\ell$
. For
$\ell$
. For
![]() $\ell = m$
, we have
$\ell = m$
, we have
![]() $\mu (M^\uparrow ) = \mathbb{P}[F_m^1]$
.
$\mu (M^\uparrow ) = \mathbb{P}[F_m^1]$
.
Now fix
![]() $\ell \lt m$
and suppose that all
$\ell \lt m$
and suppose that all
![]() $A_{\ell '}$
for
$A_{\ell '}$
for
![]() $\ell ' \gt \ell$
are known. We have that
$\ell ' \gt \ell$
are known. We have that
 \begin{equation*} \mathbb {P}[F_\ell ^k] = \mathbb {P} \left [ \bigcup _{X \in \mathcal {M}_\ell } E_X^k \right ] . \end{equation*}
\begin{equation*} \mathbb {P}[F_\ell ^k] = \mathbb {P} \left [ \bigcup _{X \in \mathcal {M}_\ell } E_X^k \right ] . \end{equation*}
We apply the inclusion-exclusion principle to the union of events. Observe that for
![]() $\mathcal{I} \subseteq 2^{M}$
, we have
$\mathcal{I} \subseteq 2^{M}$
, we have
![]() $\bigcap _{X \in \mathcal{I}} E_X^k = E_{\bigcup \mathcal{I}}^k$
, where
$\bigcap _{X \in \mathcal{I}} E_X^k = E_{\bigcup \mathcal{I}}^k$
, where
![]() $\bigcup \mathcal{I}$
stands for
$\bigcup \mathcal{I}$
stands for
![]() $\bigcup _{X \in \mathcal{I}} X$
.
$\bigcup _{X \in \mathcal{I}} X$
.
 \begin{equation*} \mathbb {P} \left [ \bigcup _{X \in \mathcal {M}_\ell } E_X^k \right ] = \sum _{j=1}^{\binom {m}{\ell }} (\!-\!1)^{j-1} \sum _{\mathcal {I} \subseteq \mathcal {M}_\ell \;:\; |\mathcal {I}| = j} \mathbb {P} \left [ E_{\bigcup \mathcal {I}}^k \right ] \end{equation*}
\begin{equation*} \mathbb {P} \left [ \bigcup _{X \in \mathcal {M}_\ell } E_X^k \right ] = \sum _{j=1}^{\binom {m}{\ell }} (\!-\!1)^{j-1} \sum _{\mathcal {I} \subseteq \mathcal {M}_\ell \;:\; |\mathcal {I}| = j} \mathbb {P} \left [ E_{\bigcup \mathcal {I}}^k \right ] \end{equation*}
Now we gather the terms with the same set
![]() $Y = \bigcup \mathcal{I}$
together. Let
$Y = \bigcup \mathcal{I}$
together. Let
![]() $C(j,\ell, r)$
be number of covers of the set
$C(j,\ell, r)$
be number of covers of the set
![]() $[r]$
by
$[r]$
by
![]() $j$
distinct subsets of size
$j$
distinct subsets of size
![]() $\ell$
and define
$\ell$
and define
 \begin{equation*} D(\ell, r) = \sum _{j=1}^{\binom {r}{\ell }} (\!-\!1)^{j-1} C(j,\ell, r) . \end{equation*}
\begin{equation*} D(\ell, r) = \sum _{j=1}^{\binom {r}{\ell }} (\!-\!1)^{j-1} C(j,\ell, r) . \end{equation*}
Then we have
 \begin{align*} \sum _{j=1}^{\binom{m}{\ell }} (\!-\!1)^{j-1} \sum _{\mathcal{I} \subseteq \mathcal{M}_\ell \;:\; |\mathcal{I}| = j} \mathbb{P} \left [ E_{\bigcup \mathcal{I}}^k \right ] = \sum _{r=\ell }^m (\!-\!1)^{r-\ell } \sum _{Y \in \mathcal{M}_r} D(\ell, r) \mathbb{P} [ E_Y^k ] . \end{align*}
\begin{align*} \sum _{j=1}^{\binom{m}{\ell }} (\!-\!1)^{j-1} \sum _{\mathcal{I} \subseteq \mathcal{M}_\ell \;:\; |\mathcal{I}| = j} \mathbb{P} \left [ E_{\bigcup \mathcal{I}}^k \right ] = \sum _{r=\ell }^m (\!-\!1)^{r-\ell } \sum _{Y \in \mathcal{M}_r} D(\ell, r) \mathbb{P} [ E_Y^k ] . \end{align*}
Moving the known terms to the left-hand side, using that
![]() $D(\ell, \ell ) = 1$
and
$D(\ell, \ell ) = 1$
and
![]() $\mathbb{P}[E_Y^k] = \mu (Y^\uparrow )^k$
, we obtain
$\mathbb{P}[E_Y^k] = \mu (Y^\uparrow )^k$
, we obtain
 \begin{equation} \mathbb{P}[F_\ell ^k] - \sum _{r=\ell +1}^m (\!-\!1)^{r-\ell } \sum _{Y \in \mathcal{M}_r} D(\ell, r) \mu (Y^\uparrow )^k = \sum _{Y \in \mathcal{M}_\ell } \mu (Y^\uparrow )^k, \end{equation}
\begin{equation} \mathbb{P}[F_\ell ^k] - \sum _{r=\ell +1}^m (\!-\!1)^{r-\ell } \sum _{Y \in \mathcal{M}_r} D(\ell, r) \mu (Y^\uparrow )^k = \sum _{Y \in \mathcal{M}_\ell } \mu (Y^\uparrow )^k, \end{equation}
from which we determine the multiset
![]() $A_\ell$
using Newton’s identities. The identities are applicable as Equation (1) holds for all
$A_\ell$
using Newton’s identities. The identities are applicable as Equation (1) holds for all
![]() $k \in \left [ \binom{m}{\ell } \right ]$
, and all the values on the left-hand side are known by induction hypothesis (strictly speaking, we know the values
$k \in \left [ \binom{m}{\ell } \right ]$
, and all the values on the left-hand side are known by induction hypothesis (strictly speaking, we know the values
![]() $\mu (Y^\uparrow )^k$
only up to a permutation of
$\mu (Y^\uparrow )^k$
only up to a permutation of
![]() $\mathcal{M}_r$
, but the formula is symmetric).
$\mathcal{M}_r$
, but the formula is symmetric).
Finally, we argue that the values in
![]() $A_\ell$
continuously depend on
$A_\ell$
continuously depend on
![]() $\mathbb{P}[F_\ell ^k]$
. This is proved by induction. The case
$\mathbb{P}[F_\ell ^k]$
. This is proved by induction. The case
![]() $\ell = m$
is obvious. For
$\ell = m$
is obvious. For
![]() $\ell \lt m$
, the left-hand side of (1) is a continuous function of values
$\ell \lt m$
, the left-hand side of (1) is a continuous function of values
![]() $\mathbb{P}[F_\ell ^k]$
and
$\mathbb{P}[F_\ell ^k]$
and
![]() $\mu (Y^\uparrow )^k$
for
$\mu (Y^\uparrow )^k$
for
![]() $Y \in \mathcal{M}_r$
,
$Y \in \mathcal{M}_r$
,
![]() $r \gt \ell$
. The later terms continuously depend on
$r \gt \ell$
. The later terms continuously depend on
![]() $\mathbb{P}[F_\ell ^k]$
by induction hypothesis. Obtaining the values in
$\mathbb{P}[F_\ell ^k]$
by induction hypothesis. Obtaining the values in
![]() $A_\ell$
via Newton’s identities is also a continuous process as the complex roots of a complex polynomial continuously depend on its coefficients.
$A_\ell$
via Newton’s identities is also a continuous process as the complex roots of a complex polynomial continuously depend on its coefficients.
5. Examples
The original example with bipartite graphs of Christofides and Král’ [Reference Christofides and Král’3] implies that if the root
![]() $r$
of a modelling does not belong to a finite definable set, the desired sequence of roots
$r$
of a modelling does not belong to a finite definable set, the desired sequence of roots
![]() $(r_n)$
needs not to exist. Moreover, observe that the root
$(r_n)$
needs not to exist. Moreover, observe that the root
![]() $r$
lies in a countable definable set (vertices from the smaller part
$r$
lies in a countable definable set (vertices from the smaller part
![]() $B$
can be distinguished by the property that they have no twin,that is, another vertex with the same neighbourhood). Therefore, the finiteness of the definable set is the weakest sufficient condition for the sequence
$B$
can be distinguished by the property that they have no twin,that is, another vertex with the same neighbourhood). Therefore, the finiteness of the definable set is the weakest sufficient condition for the sequence
![]() $(r_n)$
to exist regarding the cardinality of definable sets containing
$(r_n)$
to exist regarding the cardinality of definable sets containing
![]() $r$
.
$r$
.
Here we give a simple probabilistic construction for the following statement.
Proposition 7.
There exists an
![]() $\mathrm{FO}$
-convergent sequence of graphs
$\mathrm{FO}$
-convergent sequence of graphs
![]() $(G_n)$
and a formula
$(G_n)$
and a formula
![]() $\xi (x)$
(satisfying
$\xi (x)$
(satisfying
![]() $G_n \models (\exists x)\xi (x)$
for all
$G_n \models (\exists x)\xi (x)$
for all
![]() $n$
) with the property that there are no roots
$n$
) with the property that there are no roots
![]() $(r_n)$
,
$(r_n)$
,
![]() $r_n \in{\xi }({G_n})$
, such that the sequence
$r_n \in{\xi }({G_n})$
, such that the sequence
![]() $(G_n, r_n)$
is
$(G_n, r_n)$
is
![]() $\mathrm{FO}$
-convergent.
$\mathrm{FO}$
-convergent.
Note that necessarily
![]() $\lim \langle \xi, G_n \rangle = 0$
; otherwise, the roots exist by the result Christofides and Král’ [Reference Christofides and Král’3]. Moreover, the sequence
$\lim \langle \xi, G_n \rangle = 0$
; otherwise, the roots exist by the result Christofides and Král’ [Reference Christofides and Král’3]. Moreover, the sequence
![]() $|{\xi }({G_n})|$
has to be unbounded; otherwise, the roots exist by Theorem2 (see the second paragraph the last section).
$|{\xi }({G_n})|$
has to be unbounded; otherwise, the roots exist by Theorem2 (see the second paragraph the last section).
It is an interesting question whether the sequence in Proposition 7 can be chosen from a nowhere dense class [Reference Nešetřil and de Mendez13].
5.1 Proof of Proposition 7
First, we describe the example with bipartite graphs with distinguished parts (i.e. marked by distinct unary symbols), and then we show how to remove the marks to obtain a sequence of simple graphs.
Let
![]() $L = \{E,A,B\}$
be a language with one binary relation
$L = \{E,A,B\}$
be a language with one binary relation
![]() $E$
and two unary relations
$E$
and two unary relations
![]() $A, B$
. Let
$A, B$
. Let
![]() $T$
be the theory of bipartite graph with vertices in the first part marked by the symbol
$T$
be the theory of bipartite graph with vertices in the first part marked by the symbol
![]() $A$
and vertices in the other part marked by the symbol
$A$
and vertices in the other part marked by the symbol
![]() $B$
. We denote the parts of
$B$
. We denote the parts of
![]() $G$
, a model of
$G$
, a model of
![]() $T$
, by
$T$
, by
![]() $A$
and
$A$
and
![]() $B$
, by abuse of notation.
$B$
, by abuse of notation.
We say that a graph
![]() $G$
has bipartite
$G$
has bipartite
![]() $k$
-extension property if it satisfies the following:
$k$
-extension property if it satisfies the following:
-
1. For any disjoint
 $X, Y \subseteq A$
,
$X, Y \subseteq A$
,
 $Z \subseteq B$
with
$Z \subseteq B$
with
 $|X|+|Y|+|Z| \leq k-1$
, there exists
$|X|+|Y|+|Z| \leq k-1$
, there exists
 $v \in B \setminus Z$
such that
$v \in B \setminus Z$
such that
 $\forall x \in X \;:\; vx \in E$
and
$\forall x \in X \;:\; vx \in E$
and
 $\forall y \in Y \;:\; vy \not \in E$
.
$\forall y \in Y \;:\; vy \not \in E$
. -
2. For any disjoint
 $X, Y \subseteq B$
,
$X, Y \subseteq B$
,
 $Z \subseteq A$
with
$Z \subseteq A$
with
 $|X|+|Y|+|Z| \leq k-1$
, there exists
$|X|+|Y|+|Z| \leq k-1$
, there exists
 $v \in A \setminus Z$
such that
$v \in A \setminus Z$
such that
 $\forall x \in X \;:\; vx \in E$
and
$\forall x \in X \;:\; vx \in E$
and
 $\forall y \in Y \;:\; vy \not \in E$
.
$\forall y \in Y \;:\; vy \not \in E$
.
A countable model of
![]() $T$
that has bipartite
$T$
that has bipartite
![]() $k$
-extension property for every
$k$
-extension property for every
![]() $k \in \mathbb{N}$
is called a bipartite Rado graph whose properties are reminiscent of the Rado graph [Reference Hodges7] (also known as the countable random graph). A standard back-and-forth argument shows that there is only one bipartite Rado graph
$k \in \mathbb{N}$
is called a bipartite Rado graph whose properties are reminiscent of the Rado graph [Reference Hodges7] (also known as the countable random graph). A standard back-and-forth argument shows that there is only one bipartite Rado graph
![]() $\mathcal{BR}$
up to isomorphism and it is ultrahomogeneous. Moreover, if
$\mathcal{BR}$
up to isomorphism and it is ultrahomogeneous. Moreover, if
![]() $(G_n)$
is a sequence of models of
$(G_n)$
is a sequence of models of
![]() $T$
with increasing size of parts and for each
$T$
with increasing size of parts and for each
![]() $k \in \mathbb{N}$
, there is an index
$k \in \mathbb{N}$
, there is an index
![]() $n_k$
such that for
$n_k$
such that for
![]() $n \geq n_k$
, the graph
$n \geq n_k$
, the graph
![]() $G_n$
has the bipartite
$G_n$
has the bipartite
![]() $k$
-extension property, then
$k$
-extension property, then
![]() $(G_n)$
elementarily converges to
$(G_n)$
elementarily converges to
![]() $\mathcal{BR}$
. We recall that if a sequence
$\mathcal{BR}$
. We recall that if a sequence
![]() $(G_n)$
elementarily converges to a an ultrahomogeneous structure, the question of
$(G_n)$
elementarily converges to a an ultrahomogeneous structure, the question of
![]() $\mathrm{FO}$
-convergence reduces to convergence with respect to only quantifier-free formulas, so-called
$\mathrm{FO}$
-convergence reduces to convergence with respect to only quantifier-free formulas, so-called
![]() $\mathrm{QF}$
-convergence [Reference Nešetřil and de Mendez10, Lemma 2.28].
$\mathrm{QF}$
-convergence [Reference Nešetřil and de Mendez10, Lemma 2.28].
Let
![]() $G_n(p) = (A_n \cup B_n, E_n)$
,
$G_n(p) = (A_n \cup B_n, E_n)$
,
![]() $p \in (0,1)$
, be a model of
$p \in (0,1)$
, be a model of
![]() $T$
with parts of size
$T$
with parts of size
![]() $n^2$
and
$n^2$
and
![]() $n$
with the edge between each pair
$n$
with the edge between each pair
![]() $u \in A_n, v \in B_n$
with probability
$u \in A_n, v \in B_n$
with probability
![]() $p$
, independently of all the other pairs. A direct computation yields that for each
$p$
, independently of all the other pairs. A direct computation yields that for each
![]() $k \in \mathbb{N}$
, the probability that
$k \in \mathbb{N}$
, the probability that
![]() $G_n(p)$
does not possess the bipartite
$G_n(p)$
does not possess the bipartite
![]() $k$
-extension property decays exponentially with
$k$
-extension property decays exponentially with
![]() $n$
. Therefore, using Borel–Cantelli lemma, the sequence
$n$
. Therefore, using Borel–Cantelli lemma, the sequence
![]() $(G_n(p))$
elementarily converges to
$(G_n(p))$
elementarily converges to
![]() $\mathcal{BR}$
almost surely.
$\mathcal{BR}$
almost surely.
Observe that
![]() $(G_n(p))$
is always
$(G_n(p))$
is always
![]() $\mathrm{QF}$
-convergent as almost all
$\mathrm{QF}$
-convergent as almost all
![]() $t$
-tuples of vertices induce an independent set. This also implies that the sequence
$t$
-tuples of vertices induce an independent set. This also implies that the sequence
![]() $(H_n)$
formed by interlacing
$(H_n)$
formed by interlacing
![]() $(G_n(p))$
and
$(G_n(p))$
and
![]() $(G_n(q))$
for some
$(G_n(q))$
for some
![]() $0 \lt p \lt q \lt 1$
is almost surely
$0 \lt p \lt q \lt 1$
is almost surely
![]() $\mathrm{FO}$
-convergent.
$\mathrm{FO}$
-convergent.
We claim that for any sequence of roots
![]() $(r_n)$
from the smaller components
$(r_n)$
from the smaller components
![]() $B_n$
, the sequence
$B_n$
, the sequence
![]() $(H_n, r_n)$
does not converge. Fix
$(H_n, r_n)$
does not converge. Fix
![]() $\varepsilon \gt 0$
and consider the event ‘
$\varepsilon \gt 0$
and consider the event ‘
![]() $\forall u \in B \;:\; \deg u \in pn^2 \pm \varepsilon$
’. This event holds for all except finitely many graphs of
$\forall u \in B \;:\; \deg u \in pn^2 \pm \varepsilon$
’. This event holds for all except finitely many graphs of
![]() $(G_n(p))$
by Chernoff bounds and Borel–Cantelli lemma. Therefore, the proportion of neighbours of roots
$(G_n(p))$
by Chernoff bounds and Borel–Cantelli lemma. Therefore, the proportion of neighbours of roots
![]() $r_n$
from
$r_n$
from
![]() $H_n$
oscillates between
$H_n$
oscillates between
![]() $pn^2 \pm \varepsilon$
and
$pn^2 \pm \varepsilon$
and
![]() $qn^2 \pm \varepsilon$
. Therefore, using
$qn^2 \pm \varepsilon$
. Therefore, using
![]() $\varepsilon = (q-p)/3$
, the sequence
$\varepsilon = (q-p)/3$
, the sequence
![]() $(H_n, r_n)$
is almost surely not
$(H_n, r_n)$
is almost surely not
![]() $\mathrm{FO}$
-convergent as witnessed by the formula
$\mathrm{FO}$
-convergent as witnessed by the formula
![]() $\phi (x)\;:\; x \sim \mathrm{Root}$
.
$\phi (x)\;:\; x \sim \mathrm{Root}$
.
If we want to remove the marks, we can attach, for example, a triangle to each vertex of the smaller part and a pentagon to each vertex of the larger part (i.e. preserving the property that the parts are definable). This operation can be formalised as a gadget construction, where the marks are considered to be the replaced edges by the gadgets triangle and pentagon, which in these cases preserves
![]() $\mathrm{FO}$
-convergence [Reference Hartman, Hons and Nešetřil6, Theorem 5.3, Corollary 5.5].
$\mathrm{FO}$
-convergence [Reference Hartman, Hons and Nešetřil6, Theorem 5.3, Corollary 5.5].
6. Concluding remarks
An iterative use of Theorem1 or 2 allows us to gain complete control over the algebraic elements as we can consider each of them separately. Note that it is also possible to root solutions of algebraic formulas with multiple free variables (i.e.
![]() $p$
-tuples instead of singletons) since the projection to each coordinate yields an algebraic set.
$p$
-tuples instead of singletons) since the projection to each coordinate yields an algebraic set.
We would like to point out that Theorem2 remains valid for
![]() $\mathrm{FO}$
-convergent sequences
$\mathrm{FO}$
-convergent sequences
![]() $(G_n)$
without a modelling limit. The proofs are analogous except that the set
$(G_n)$
without a modelling limit. The proofs are analogous except that the set
![]() $I$
in Lemma 4 is defined as an inclusion-maximal set for which there are roots
$I$
in Lemma 4 is defined as an inclusion-maximal set for which there are roots
![]() $(r_n)$
with the property that
$(r_n)$
with the property that
![]() $\lim \langle \bigwedge _{i \in I} \phi _i(\boldsymbol{x}_i), (G_n, r_n) \rangle \gt 0$
.
$\lim \langle \bigwedge _{i \in I} \phi _i(\boldsymbol{x}_i), (G_n, r_n) \rangle \gt 0$
.
It can be shown that the sequence of random bipartite graphs constructed for Proposition 7 admits (almost surely) a modelling limit. This together with a rich context will be the subject of a forthcoming paper.
Besides the original problem in [Reference Nešetřil and de Mendez10], our motivation was the study of structural convergence of sequences created via gadget construction; see [Reference Hartman, Hons and Nešetřil6]. Using the result of this paper, we conclude that
![]() $\mathrm{FO}$
-convergence is preserved by gadget construction if the gadgets replace only finitely many edges (under additional natural assumptions).
$\mathrm{FO}$
-convergence is preserved by gadget construction if the gadgets replace only finitely many edges (under additional natural assumptions).
In the typical case, the modelling
![]() $L$
is of size continuum, and the set of algebraic vertices (which is at most countable) has measure
$L$
is of size continuum, and the set of algebraic vertices (which is at most countable) has measure
![]() $0$
. Hence, our results reveal only a negligible portion of vertices of
$0$
. Hence, our results reveal only a negligible portion of vertices of
![]() $L$
for which the roots
$L$
for which the roots
![]() $(r_n)$
exist, which shows that there is still room for further research.
$(r_n)$
exist, which shows that there is still room for further research.
Acknowledgements
Supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (ERC Synergy Grant DYNASNET, grant agreement no. 810115).