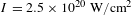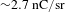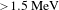1 Introduction
Intensive experimental and theoretical investigations have been dedicated to the optimization of relativistic electron parameters in relation to ion acceleration[Reference Macchi, Sgattoni, Sinigardi, Borghesi and Passoni1, Reference Steinke, Henig, Schnürer, Sokollik, Nickles, Jung, Kiefer, Hörlein, Schreiber, Tajima, Yan, Hegelich, Meyer-ter-Vehn, Sandner and Habs2], creation of warm dense or high-energy-density matter states[Reference Riley3, Reference Bailly-Grandvaux, Santos, Bellei, Forestier-Colleoni, Fujioka, Giuffrida, Honrubia, Batani, Bouillaud, Chevrot, Cross, Crowston, Dorard, Dubois, Ehret, Gregori, Hulin, Kojima, Loyez, Marques, Morace, Nicolai, Roth, Sakata, Schaumann, Serres, Servel, Tikhonchuk, Woolsey and Zhang4], generation of high harmonic or X-ray sources[Reference Teubner and Gibbon5] and the fast ignition approach to inertial confinement fusion[Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell and Perry6, Reference Kodama, Norreys, Mima, Dangor, Evans, Fujita, Kitagawa, Krushelnick, Miyakoshi, Miyanaga, Norimatsu, Rose, Shozaki, Shigemori, Sunahara, Tampo, Tanaka, Toyama, Yamanaka and Zepf7]. Novel interaction conditions and target configurations have been constantly explored[Reference Prencipe, Fuchs, Pascarelli, Schumacher, Stephens, Alexander, Briggs, Büscher, Cernaianu, Choukourov, Marco, Erbe, Fassbender, Fiquet, Fitzsimmons, Gheorghiu, Hund, Huang, Harmand, Hartley, Irman, Kluge, Konopkova, Kraft, Kraus, Leca, Margarone, Metzkes, Nagai, Nazarov, Lutoslawski, Papp, Passoni, Pelka, Perin, Schulz, Smid, Spindloe, Steinke, Torchio, Vass, Wiste, Zaffino, Zeil, Schramm and Cowan8]. Recently, structured targets have been intensively studied as it was shown that they are able to enhance the level of laser light absorption[Reference Cerchez, Swantusch, Toncian, Zhu, Prasad, Toncian, Rödel, Jäckel, Paulus, Andreev and Willi9] and the radiation yield (HHG, THz, X-ray)[Reference Cerchez, Giesecke, Peth, Toncian, Albertazzi, Fuchs, Willi and Toncian10, Reference Giesecke, Peth, Toncian, Willi and Cerchez11] or to improve the physical parameters of electron and ion beams via excitation of surface plasmons (plasma waves)[Reference Sgattoni, Fedeli, Cantono, Ceccotti and Macchi12–Reference Fedeli, Formenti, Cialfi, Sgattoni, Cantono and Passoni14]. Surface plasma waves (SPWs) are localized electron oscillation modes that can be excited at the vacuum–plasma interface by a laser field that irradiates a periodically modulated surface[Reference Pitarke, Silkin, Chulkov and Echenique15, Reference Stockman16]. Using the dielectric constants of the media, 
$\unicode[STIX]{x1D716}_{1}=1$ (vacuum) and 
$\unicode[STIX]{x1D716}_{2}(\unicode[STIX]{x1D714})=1-(\unicode[STIX]{x1D714}_{p}/\unicode[STIX]{x1D714})^{2}$ (plasma), the dispersion relation of an SPW reads as: 
$k_{\text{SPW}}(\unicode[STIX]{x1D714})=\unicode[STIX]{x1D714}/c\sqrt{\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D716}_{2}/(\unicode[STIX]{x1D716}_{1}+\unicode[STIX]{x1D716}_{2})}=\unicode[STIX]{x1D714}/c\sqrt{(1-\unicode[STIX]{x1D702})/(2-\unicode[STIX]{x1D702})}$. Here, the factor 
$\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D714}_{p}/\unicode[STIX]{x1D714})^{2}=n_{e}/n_{c}$ represents the plasma parameter, 
$\unicode[STIX]{x1D714}_{p}=\sqrt{n_{e}e^{2}/m_{e}\unicode[STIX]{x1D716}_{0}}$ is the plasma frequency and 
$n_{c}=m_{e}\unicode[STIX]{x1D716}_{0}\unicode[STIX]{x1D714}_{L}^{2}/e^{2}$ is the plasma critical density. An electromagnetic wave of frequency 
$\unicode[STIX]{x1D714}$ and wave vector 
$k_{L}$, incident at an angle 
$\unicode[STIX]{x1D6FC}$ onto a periodically structured target (grating) of periodicity 
$\unicode[STIX]{x1D706}_{g}$, can excite resonantly an SPW if the phase matching condition is fulfilled: 
$k_{\Vert ,L}\equiv \frac{\unicode[STIX]{x1D714}}{c}\cdot \sin \unicode[STIX]{x1D6FC}=k_{\text{SPW}}\pm q\frac{2\unicode[STIX]{x1D70B}}{\unicode[STIX]{x1D706}_{g}}$ (
$q$ – integer number). Thus, for a given value of laser and grating periodicities, and in the limit of the linear regime (neglecting thermal, collisional and/or relativistic effects, inhomogeneous preplasma conditions, etc.), the condition leads to the expression of a resonance angle as 
$\sin \unicode[STIX]{x1D6FC}=[(1-\unicode[STIX]{x1D702})/(2-\unicode[STIX]{x1D702})]^{1/2}-\unicode[STIX]{x1D706}_{L}/\unicode[STIX]{x1D706}_{g}$ for 
$q=1$. The electron acceleration by the evanescent field of an SPW has been theoretically and experimentally investigated[Reference Sgattoni, Fedeli, Cantono, Ceccotti and Macchi12, Reference Fedeli, Sgattoni, Cantono, Garzella, Réau, Prencipe, Passoni, Raynaud, Kveton, Proska, Macchi and Ceccotti17–Reference Raynaud, Kupersztych, Riconda, Adam and Heron21], and the studies demonstrate that the SPW excitation for the resonant condition has a direct impact on the electron acceleration process leading to improved physical parameters such as enhanced flux and charge density of the electrons, a higher electron maximum energy, and a higher absorption efficiency[Reference Fedeli, Formenti, Cialfi, Sgattoni, Cantono and Passoni14, Reference Raynaud, Kupersztych, Riconda, Adam and Heron21–Reference Cantono, Sgattoni, Fedeli, Garzella, Reau, Riconda, Macchi and Ceccotti23]. Moreover, in the resonant regime, SPWs are a very efficient route to transfer the laser energy via hot electrons to secondary sources including high harmonic generation[Reference Cantono, Fedeli, Sgattoni, Denoeud, Chopineau, Reau, Ceccotti and Macchi24] or ion acceleration[Reference Ceccotti, Floquet, Sgattoni, Bigongiari, Klimo, Raynaud, Riconda, Heron, Baffigi, Labate, Gizzi, Vassura, Fuchs, Passoni, Květon, Novotny, Possolt, Prokůpek, Proška, Pšikal, Štolcová, Velyhan, Bougeard, D’Oliveira, Tcherbakoff, Réau, Martin and Macchi25] and to optimize the physical properties of these sources[Reference Macchi13, Reference Fedeli, Sgattoni, Cantono, Garzella, Réau, Prencipe, Passoni, Raynaud, Kveton, Proska, Macchi and Ceccotti17, Reference Bigongiari, Raynaud, Riconda and Héron22, Reference Cantono, Sgattoni, Fedeli, Garzella, Reau, Riconda, Macchi and Ceccotti23, Reference Ceccotti, Floquet, Sgattoni, Bigongiari, Klimo, Raynaud, Riconda, Heron, Baffigi, Labate, Gizzi, Vassura, Fuchs, Passoni, Květon, Novotny, Possolt, Prokůpek, Proška, Pšikal, Štolcová, Velyhan, Bougeard, D’Oliveira, Tcherbakoff, Réau, Martin and Macchi25, Reference Bagchi, Kiran, Wang, Sheng, Bhuyan, Krishnamurthy and Kumar26].
High field plasmonics is one of the new research fields that have synergetically benefited from the advances in laser technology. The possibility of attaining laser radiation fields at intensities exceeding 
$10^{18}~\text{W}/\text{cm}^{2}$ brought plasmonics into a new regime where relativistic and nonlinear effects start to dominate the dynamics of SPWs[Reference Sgattoni, Fedeli, Cantono, Ceccotti and Macchi12, Reference Kauranen and Zayats27]. By investigating the high field plasmonics at laser intensities exceeding 
$10^{20}~\text{W}/\text{cm}^{2}$ (
$a_{0}\gg 1$), nonlinear interaction of the radiation field with the plasma and relativistic effects have to be considered as they can influence the SPW equation of dispersion. Nonlinear optical effects in the high field regime can be excited via localized strong electromagnetic fields or by the control of the dielectric properties of the media[Reference Kauranen and Zayats27]. Experimentally[Reference Fedeli, Sgattoni, Cantono, Garzella, Réau, Prencipe, Passoni, Raynaud, Kveton, Proska, Macchi and Ceccotti17], it was proven that SPWs excited on grating targets (GTs) by intense laser pulses of intensity 
${\sim}10^{19}~\text{W}/\text{cm}^{2}$ corresponding to a relativistic parameter of 
$a_{0}=0.85\cdot [I\unicode[STIX]{x1D706}^{2}/10^{18}~\text{W}/(\text{cm}^{2}\cdot \unicode[STIX]{x03BC}\text{m}^{2})]^{1/2}\simeq 2{-}3$ are able to efficiently accelerate hot electrons (few MeVs) along the target surface in a narrow cone. The strongest electron emission along the target surface was found for 
$\unicode[STIX]{x1D6FC}=30^{\circ }$, the laser incidence angle on the target for a step-like plasma density profile. This angle corresponds to the resonance angle in the SPW linear model for the studied interaction conditions.
Furthermore, despite all possible cleaning techniques, the pedestal of very high intensity laser pulses is able to generate a preplasma of finite expansion and of scale length 
$L_{n}=n_{e}/\unicode[STIX]{x2202}_{x}n_{e}$, at the vacuum–target interface. Recently, experiments performed in the regime of 
$a_{0}=3$ and presented in Ref. [Reference Cantono, Fedeli, Sgattoni, Denoeud, Chopineau, Reau, Ceccotti and Macchi24] showed that the maximum energy of the surface electrons peaks at the resonance angle of 
$30^{\circ }$ in the case of a step plasma density profile (
$L_{n}=0$) or at 
$35^{\circ }$ incidence angle in the presence of a finite preplasma of scale length of 
$L_{n}=0.1\unicode[STIX]{x1D706}_{L}$. The results were considered as an indication of a shift in the resonance angle. In addition, in the same experimental observations, an enhancement of the high harmonic emission was seen. Thus, in this more complex picture, one has to consider the propagation of the radiation field in a variable plasma density profile caused by plasma expansion and/or radiation pressure effects. A model of the surface plasmon excitation that includes relativistic and ponderomotive nonlinearities was discussed in Ref. [Reference Liu, Tripathi, Shao and Liu28], aiming to explain the target normal sheath acceleration of protons at high intensity and in the presence of a preformed plasma on gratings. The model demonstrates that in these conditions, an SPW with a larger amplitude than the transmitted laser amplitude can be excited and leads to stronger target normal sheath acceleration of protons. However, no experimental evidence of electrons accelerated via SPW excitation in the high intensity regime (
$a_{0}>10$) has been reported, where the roles of the preformed plasma and the relativistic effects have been discussed.
Here, we present an experimental and theoretical study of high energy surface electrons via SPW acceleration from periodically modulated targets (gratings) irradiated by high intensity and high-contrast laser pulses. Our results indicate that the acceleration process of high energy electrons along GTs at laser intensities above 
$10^{20}~\text{W}/\text{cm}^{2}$ is not only dependent on the laser intensity but also on the presence of a preformed plasma. The surface electron beam accelerated using GTs with a longitudinal periodicity twice the laser wavelength irradiated by a femtosecond laser pulse at an intensity of 
$I=2.5\times 10^{20}~\text{W}/\text{cm}^{2}$ corresponding to a relativistic parameter of 
$a_{0}\simeq 10$ was measured for two relevant incidence angles, 
$\unicode[STIX]{x1D6FC}=30^{\circ }$ and 
$45^{\circ }$. Our results were compared with the classical model[Reference Pitarke, Silkin, Chulkov and Echenique15, Reference Kaw and McBride20] which predicts the resonant excitation of the SPWs at a laser incidence angle of 
$30^{\circ }$ and consequently, the maximum efficiency of the surface fast electron (SFE) acceleration. The total charge flux of the SFEs, however, measured in our interaction condition at 
$\unicode[STIX]{x1D6FC}=45^{\circ }$ was larger by a factor of 3.5 than detected at 
$\unicode[STIX]{x1D6FC}=30^{\circ }$. Detailed two-dimensional (2D) numerical simulations and a novel analytical model that includes a two-wave nonlinear diffraction approximation[Reference Andreev, Platonov and Salomaa29] with more realistic initial preplasma conditions indicate a shift of the resonance angle, in good agreement with the experimental data. Our theoretical studies suggest the possibility of employing the effects of the high laser field and the preplasma to increase the effectiveness of the SPWs on accelerating SFEs with high flux. These combined interaction conditions could be exploited in the generation of SPWs in the relativistic regime and could open the route to the study of electron beam generation via high field plasmonics.
2 Experimental arrangement and methods
Figure 1. (a) A schematic of the experimental setup showing the interaction geometry. A laser pulse is focused at an incident angle of 
$\unicode[STIX]{x1D6FC}$ onto a GT with a periodical modulation of 
$\unicode[STIX]{x1D706}_{g}=1667~\text{nm}$ and of vertical amplitude 
$h_{g}=80~\text{nm}$. The spatial distribution of surface electrons is recorded by image plate (IP) stacks. 
$\unicode[STIX]{x1D719}$ and 
$\unicode[STIX]{x1D703}$ are the azimuthal and polar angles, respectively, used to describe spatially the electrons. (b) The side-on view of experimental setup. Three IP stacks (shown in purple color) are arranged around the interaction point to detect the high energy electrons emitted within an angular range of 
$\unicode[STIX]{x1D719}$ between 
$0^{\circ }$ and 
$180^{\circ }$, and an electron spectrometer is oriented along the target surface direction to measure the energy spectra of the surface fast electrons. (c) The IP stack consists of IPs and aluminum filters of different thicknesses, allowing the electron spatial distribution for different energies to be obtained.
The experiments were carried out at the Ti:sapphire Arcturus laser facility of the Heinrich-Heine-University Düsseldorf[Reference Cerchez, Prasad, Aurand, Giesecke, Spickermann, Brauckmann, Aktan, Swantusch, Toncian, Toncian and Willi30, Reference Willi, Behmke, Gezici, Hidding, Jung, Königstein, Pipahl, Osterholz, Pretzler, Pukhov, Toncian, Toncian, Heyer, Jäckel, Kübel, Paulus, Rödel, Schlenvoigt, Ziegler, Büscher, Feyt, Lehrach, Ohm, Oswald, Raab, Ruzzo, Seltmann and Zhang31]. The laser system can deliver pulses with energies up to 
$7~\text{J}$ at the central wavelength of 
$\unicode[STIX]{x1D706}_{L}=800~\text{nm}$ and a pulse duration of 
$30~\text{fs}$ (FWHM) in p-polarization. The beam was focused by an off-axis F/2 parabola at an incidence angle 
$\unicode[STIX]{x1D6FC}$ and to a focal spot of 
$6~\unicode[STIX]{x03BC}\text{m}$ in diameter which contains 50% of the laser energy resulting in an intensity of 
$I=2.5\times 10^{20}~\text{W}/\text{cm}^{2}$. The targets used in the experiment were either holographic gold gratings with a sinusoidal profile or flat gold targets. The targets substrate was glass of 
$5~\text{mm}$ in thickness overcoated by a 
$1~\unicode[STIX]{x03BC}\text{m}$ gold layer. The gratings have a groove spacing 
$\unicode[STIX]{x1D706}_{g}=1667~\text{nm}$ and the peak-to-valley amplitude of the grooves (
$h_{g}$) was 
$80~\text{nm}$, measured by an atomic force microscope. A schematic view of the experimental setup is shown in Figure 1(a). The SFE spatial distribution was detected by means of an image plate (Fujifilm BAS-TR) stack placed at 
$60~\text{mm}$ from the interaction point, at a plane perpendicular to the target surface and incidence plane. In order to record the full angular distribution of the high energy electrons, additional measurements were performed by surrounding the interaction point with three image plate (IP) stacks of similar design. The geometry of this arrangement is depicted in Figure 1(b). The azimuthal 
$\unicode[STIX]{x1D719}$ and polar 
$\unicode[STIX]{x1D703}$ angles are used to describe the spatial electron distribution. The IP stack detector consists of four layers of IPs of 
$80~\text{mm}\times 80~\text{mm}$ in size separated by Al filters (Figure 1(c)). This arrangement enables the simultaneous detection of the spatial profile of the electron beam for several energies. A 1.5-mm-thick Al filter was used to protect the IP plates with a transmission of 
$2\%$ for X-rays with energies below 
$15~\text{keV}$ and electrons with energies 
${\leqslant}800~\text{keV}$. The last IP recorded electrons with energies higher than 
$1.7~\text{MeV}$. The IPs were scanned with a CR35BIO scanner and the data were evaluated following the calibration method described in Refs. [Reference Ingenito, Andreoli, Batani, Boutoux, Cipriani, Consoli, Cristofari, Curcio, Angeli, Giorgio, Ducret, Forestier-Colleoni, Hulin, Jakubowska and Rabhi32–Reference Tanaka34]. The scanner pixel resolution was set to 
$25~\unicode[STIX]{x03BC}\text{m}$ and the gray level (GL) used the photostimulable luminescence (PSL) formula (
$\text{PSL}=0.0004\cdot \text{GL}-0.0024$) of the scanner CR35BIO for BAS-TR image plates[Reference Ingenito, Andreoli, Batani, Boutoux, Cipriani, Consoli, Cristofari, Curcio, Angeli, Giorgio, Ducret, Forestier-Colleoni, Hulin, Jakubowska and Rabhi32]. An electron spectrometer oriented along the target surface direction at 
$\unicode[STIX]{x1D719}=3^{\circ }$ was employed to measure the energy spectra of the SFEs with IPs as a detector. The spectrometer consisted of a pair of 
$5~\text{cm}$ long permanent magnets of 
$0.28~\text{T}$ and was used for detecting electrons with energies higher than 
$330~\text{keV}$.
Figure 2. (a) The temporal profile of the laser pulse after compression (blue line). The red dashed line is the estimated laser contrast improvement due to a plasma mirror (PM) system. (b) Results of the one-dimensional (1D) hydrocode MULTI-fs simulation of the electron density prior to the arrival of the main pulse for two different contrasts (with and without PM) are shown. The gray rectangle on the right-hand side depicts the initial position of the solid target before the interaction.
The surface modulations of GTs are very sensitive to the preplasma generated by the rising edge of the laser pulse as only tens of nanometers of preplasma will fill the surface structures. A double stage pulse cleaning system which includes an XPW module[Reference Ricci, Jullien, Rousseau, Liu, Houard, Ramirez, Papadopoulos, Pellegrina, Georges, Druon, Forget and Lopez-Martens35] and a plasma mirror (PM) arrangement[Reference Ziener, Foster, Divall, Hooker, Hutchinson, Langley and Neely36, Reference Dromey, Kar, Zepf and Foster37] improves the prepulse-to-pulse laser contrast up to 
$10^{-12}$ in the 100s of ps range[Reference Cerchez, Prasad, Aurand, Giesecke, Spickermann, Brauckmann, Aktan, Swantusch, Toncian, Toncian and Willi30] and the temporal profile of the laser pulse is shown in Figure 2(a). The graph shows the temporal profile of the laser pulse after the vacuum compressor measured by a SEQUOIA third-order cross-correlator[38] (blue line). The red dashed line indicates the estimated laser contrast improvement due to the PM system[Reference Behmke, Bruegge, Rödel, Cerchez, Hemmers, Heyer, Jäckel, Kübel, Paulus, Pretzler, Pukhov, Toncian, Toncian and Willi39]. For the experimental conditions used, the scale length of the preplasma created prior to the main laser peak was estimated by 1D hydrocode MULTI-fs simulations to be in the range of a few 10s of 
$~\text{nm}$ (i.e., 
$L_{n}<\unicode[STIX]{x1D706}_{L}/10$), a value in agreement with our previous experimental results[Reference Cerchez, Swantusch, Toncian, Zhu, Prasad, Toncian, Rödel, Jäckel, Paulus, Andreev and Willi9–Reference Giesecke, Peth, Toncian, Willi and Cerchez11, Reference Behmke, Bruegge, Rödel, Cerchez, Hemmers, Heyer, Jäckel, Kübel, Paulus, Pretzler, Pukhov, Toncian, Toncian and Willi39] (Figure 2(b)).
3 Experimental results
Figure 3. Electron spatial distributions recorded for a GT (
$\unicode[STIX]{x1D706}_{g}=1667~\text{nm}$) and an FT at (a), (c) 
$\unicode[STIX]{x1D6FC}=30^{\circ }$ and (b), (d) 
$45^{\circ }$, respectively. The IPs raw data correspond to electron energies 
${\geqslant}1.5~\text{MeV}$ and the color bar expresses the number of electrons. In the diagrams (e) and (f) are presented the angular distributions of fast electrons produced in the incidence plane at full azimuthal angle 
$\unicode[STIX]{x1D719}=0^{\circ }{-}180^{\circ }$ from the GT (green line) and the FT (black line) irradiated by a laser pulse of high contrast at the angle of incidence of 
$\unicode[STIX]{x1D6FC}=30^{\circ }$ and 
$\unicode[STIX]{x1D6FC}=45^{\circ }$ with electron energies 
${\geqslant}1.5~\text{MeV}$, respectively. In the diagram (g) similar measurements performed for low-contrast conditions at an incidence angle of 
$45^{\circ }$ for both targets, GT and FT are shown.
The spatial distributions of the SFEs collected by the 3rd IP of the stack detector (corresponding to electron energies 
${\geqslant}1.5~\text{MeV}$) accelerated along the surface of the GT for two incidence angles, 
$\unicode[STIX]{x1D6FC}=30^{\circ }$ and 
$45^{\circ }$, are shown in Figures 3(a) and 3(b). Both values are relevant to study and compare the effect of the SPWs on the efficiency of electron acceleration in the classical, linear regime and in our experimental conditions. Prominently, two preferential spatial distribution directions can be recognized, (I) in the incidence plane up to 
$\unicode[STIX]{x1D719}=40^{\circ }$ and, (II) in the surface plane up to 
$\unicode[STIX]{x1D703}\doteq \pm 30^{\circ }$. The spatial distribution of the surface electrons in the incidence plane (I) is similar to the previous results reported in Ref. [Reference Fedeli, Sgattoni, Cantono, Garzella, Réau, Prencipe, Passoni, Raynaud, Kveton, Proska, Macchi and Ceccotti17]. The distribution in the surface plane (II) shows a novel spatial feature in our interaction conditions and it was observed for both incidence angles (Figures 3(a) and 3(b)). The results reveal an enhanced flux of SFEs emitted at 
$\unicode[STIX]{x1D6FC}=45^{\circ }$ compared to 
$\unicode[STIX]{x1D6FC}=30^{\circ }$. The charge of the recorded electrons with energies larger than 
$1.5~\text{MeV}$ emitted in the full angle interval covered by the IPs (
$\unicode[STIX]{x1D719}=[0^{\circ },50^{\circ }]$ and 
$\unicode[STIX]{x1D703}=[-30^{\circ },30^{\circ }]$) by the GT irradiated at 
$\unicode[STIX]{x1D6FC}=45^{\circ }$ is estimated to be about 
${\sim}0.26~\text{nC}$, i.e., 
$3.5$ times larger compared to the data obtained in the case of 
$\unicode[STIX]{x1D6FC}=30^{\circ }$. The highest electron flux was detected around the emission direction defined by 
$\unicode[STIX]{x1D719}=5^{\circ }$ with a flux of about 
$2.7~\text{nC/sr}$ for 
$\unicode[STIX]{x1D6FC}=45^{\circ }$, while in the case of the 
$30^{\circ }$ incidence angle, the flux was smaller by a factor 3. For comparison, the spatial distribution of the surface electrons emitted by the flat target (FT) and recorded at similar experimental conditions is shown in Figures 3(c) and 3(d). The estimated error of the SFE flux measured experimentally was in the range of 20%–30%. This value was obtained from the scatter of about six measurements recorded for each target and laser condition. The effectiveness of accelerating SFEs at high flux along the target surface by GTs in competition to other acceleration mechanisms was analyzed by recording the full angular distribution 
$\unicode[STIX]{x1D719}=0^{\circ }{-}180^{\circ }$ by IP stacks surrounding the interaction spot. The results are shown in Figure 3(e) (
$\unicode[STIX]{x1D6FC}=30^{\circ }$) and Figure 3(f) (
$\unicode[STIX]{x1D6FC}=45^{\circ }$) for the highest laser contrast condition (by employing a PM module) in comparison to FT in similar interaction conditions. The number of electrons per radian is obtained by adding the electron counts over all polar directions in the incidence plane. For the best contrast, the largest fraction of electrons using GTs propagates along the target surface direction, with a peak in the azimuthal interval 
$\unicode[STIX]{x1D719}=3^{\circ }{-}5^{\circ }$ for both incidence angles studied here. In contrast, in the case of FT, no electrons with energies higher than 1.5 MeV are found for 
$\unicode[STIX]{x1D6FC}=30^{\circ }$ and the number of SFEs was smaller by a factor 6 for 
$\unicode[STIX]{x1D6FC}=45^{\circ }$ (compared to GTs, in the same angular interval). Depending on the incidence angle, electrons are seen for both targets close to the specular direction and/or along the target normal direction which is a signature of vacuum heating and 
$\overrightarrow{j}\times \overrightarrow{B}$ mechanisms. However, the electron beam at the front of the target has a lower divergence and flux compared with SFEs. For comparison for interactions with laser pulses of low contrast, the results are shown in Figure 3(g), for the incidence angle of 
$\unicode[STIX]{x1D6FC}=45^{\circ }$. In this case, the scale length of the preformed plasma is expected to be in the order of 
$1.5~\unicode[STIX]{x03BC}\text{m}$ and the plasma completely fills in the GT surface modulations (see the previous comments and the simulation results shown in Figure 2(b)). In the case of low contrast, GT and FT exhibit similar angular distributions of high energy electrons which are mainly accelerated between the laser specular direction and target surface. The acceleration directions of high energy electrons are influenced by the primary acceleration mechanisms, by the target surface condition and by the electric and magnetic field structure developed in the interaction area. Thus, the angular distribution of high energy electrons accelerated at the target front could have a complex structure and, in the case of flat targets, depends on the interaction conditions (laser intensity, incidence angle and plasma scale length). The acceleration direction of the electrons can also be affected by the combined scalar and vector potential fields existing at the target–vacuum interface[Reference Chen, Sheng and Zhang40–Reference Li, Yuan, Xu, Zheng, Sheng, Chen, Ma, Liang, Yu, Zhang, Liu, Wang, Wei, Zhao, Jin and Zhang42]. However, in the case of low contrast, the total number of high energy electrons is larger by a factor of about 2 for GTs than for FTs.
Figure 4. In the chart (a), the total numbers of electrons (
$\unicode[STIX]{x1D719}=0^{\circ }{-}180^{\circ }$) including the SFEs (
$\unicode[STIX]{x1D719}=0^{\circ }{-}10^{\circ }$) with energies larger than 
$1.5~\text{MeV}$ using GT (
$\unicode[STIX]{x1D706}_{g}=1667~\text{nm}$) and FT at 
$\unicode[STIX]{x1D6FC}=30^{\circ }$ (blue colors) and 
$\unicode[STIX]{x1D6FC}=45^{\circ }$ (magenta colors) for different interaction conditions are shown. Abbreviations ‘l’ and ‘h’ stand for low- and high-contrast conditions, respectively, while ‘p’ stands for the case when the grating’s grooves were parallel with the incident laser plane. In all other cases discussed before, the grooves were orientated perpendicularly to the incidence plane. (b) A typical electron energy spectrum of the fast electrons recorded at the high-contrast conditions at 
$\unicode[STIX]{x1D719}=3^{\circ }$ from the GT tangent direction (
$\unicode[STIX]{x1D706}_{g}=1667~\text{nm}$) and for 
$\unicode[STIX]{x1D6FC}=45^{\circ }$.
An overview of the SFE fractions of the total number of accelerated electrons is shown in Figure 4(a) for different interaction conditions. In the case of GTs and for an incidence angle of 
$30^{\circ }$, the SFEs represent 12.5% of the total number of electrons, while in the case of 
$\unicode[STIX]{x1D6FC}=45^{\circ }$, almost 
$25\%$ of electrons are accelerated along the target surface in a narrow cone of 
$\unicode[STIX]{x1D719}=0^{\circ }{-}10^{\circ }$. For the GT of 
$\unicode[STIX]{x1D706}_{g}=1667~\text{nm}\approx 2\unicode[STIX]{x1D706}_{L}$ and characterized by a step-like density profile (
$\unicode[STIX]{x1D702}\rightarrow \infty$), the linear model indicates that the resonance condition is fulfilled when the laser is incident at 
$\unicode[STIX]{x1D6FC}\approx 30^{\circ }$, while for our experimental conditions, a higher charge of high energy electrons was measured at 
$\unicode[STIX]{x1D6FC}=45^{\circ }$. The generation of the preplasma leads to a decrease of the maximum plasma density (i.e., of the factor 
$\unicode[STIX]{x1D702}$) and, as previous studies indicate, this might lead to an increase of the optimal incidence angle of the laser pulse for the electron acceleration[Reference Liu, Tripathi, Shao and Liu28].
In addition, the energy distribution of the fast electrons emitted along the target surface was measured using the magnetic spectrometer placed at 
$4~\text{cm}$ from the interaction point. The effective temperature of the fast electrons obtained from the energy spectra is 
$1.8\pm 0.03~\text{MeV}$ for targets irradiated with high-contrast laser pulses. We also investigated the fast electron generation for low-contrast laser pulses with an estimated scale length of the preplasma of 
$1.5~\unicode[STIX]{x03BC}\text{m}$, which is larger than the wavelength of the laser pulse. Under these conditions, only a small number of electrons are emitted along the target surface direction with an effective temperature of only 
$0.5\pm 0.02~\text{MeV}$. Similarly, a low flux of SFEs was recorded for FTs for both high- and low-contrast conditions. A typical SFE spectrum for the GT of 
$\unicode[STIX]{x1D706}_{g}=1667~\text{nm}$ for the high-contrast condition and for 
$\unicode[STIX]{x1D6FC}=45^{\circ }$ is shown in Figure 4(b).
4 Numerical particle-in-cell simulations of surface electron acceleration
The dynamics of surface electron acceleration by laser grating interaction was numerically investigated by using the 2D particle-in-cell (PIC) code EPOCH[Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evan, Schmitz, Bell and Ridgers43]. In the simulations, the GT was assumed to have a sinusoidal profile with a thickness of 
$14~\unicode[STIX]{x03BC}\text{m}$ and 4 times ionized gold which corresponds to 
$n_{e}=139n_{c}$ (where 
$n_{c}$ is the critical density). For the study of the preplasma effect in the interaction, an exponential decay of the target density with a characteristic length 
$L_{n}$ was modeled at the front of the target. The target was irradiated at different angles of incidence and preplasma conditions. The ionization was modeled using field ionization. The numerical box size was 
$50~\unicode[STIX]{x03BC}\text{m}\times 50~\unicode[STIX]{x03BC}\text{m}$, which was large enough to minimize the boundary effects. The spatial resolution was 
$50$ points per wavelength (
$\unicode[STIX]{x1D706}_{L}=0.8~\unicode[STIX]{x03BC}\text{m}$) in each direction and 45 particles per cell were used. The diameter of the laser focal spot was set to 
$5~\unicode[STIX]{x03BC}\text{m}$. Other parameters followed the experimental conditions. For comparison, in Figure 5 the magnetic field components 
$B_{z}$ (perpendicular to the simulation plane 
$XY$) in the case of the laser interaction with a flat surface target (Figure 5(a)) and a GT 
$\unicode[STIX]{x1D706}_{g}=2\unicode[STIX]{x1D706}_{L}$ at 
$\unicode[STIX]{x1D6FC}=45^{\circ }$ incidence angle (Figure 5(b)) are shown. A preplasma of 
$L_{n}=60~\text{nm}$ scale length was modeled at the front of the target. The snapshots are recorded at 
$t=74.5~\text{fs}=28T_{L}$ after the peak of the laser reaches the target. In the case of the FT, the field corresponds mainly to the laser reflected beam. In the simulation for the GT irradiated for similar conditions, a strong field component is observed at the vacuum–target interface which propagates with a velocity close to the speed of light indicating the excitation of the SPW. Moreover, different diffraction orders of the laser fundamental and higher order harmonics are visible in the reflected field[Reference Cerchez, Swantusch, Toncian, Zhu, Prasad, Toncian, Rödel, Jäckel, Paulus, Andreev and Willi9, Reference Cerchez, Giesecke, Peth, Toncian, Albertazzi, Fuchs, Willi and Toncian10].
Figure 5. Snapshots of 2D PIC simulations showing the magnetic field components 
$B_{z}$ at 
$t=28\cdot T_{L}$ for the two targets: FT in (a) and GT (
$\unicode[STIX]{x1D706}_{g}=2\unicode[STIX]{x1D706}_{L}$) in (b). Laser is incident at 
$\unicode[STIX]{x1D6FC}=45^{\circ }$ and its direction is marked by the red arrow. The initial target surface position is indicated by the dotted line and a preplasma of scale length 
$L_{n}=60~\text{nm}$ was modeled at the front of the target.
Figure 6 shows the simulation results of the number of SFEs with energies larger than 
$1.5~\text{MeV}$ within the interval 
$\unicode[STIX]{x1D719}=[0^{\circ },10^{\circ }]$ for different laser incident angles in the interval 
$\unicode[STIX]{x1D6FC}=20^{\circ }{-}55^{\circ }$. In order to identify the effect of the interaction conditions on the efficiency of the SFE acceleration, the simulations were performed considering four different values for the preplasma scale length, i.e., 
$L_{n}=0$ (step density plasma profile), 
$30~\text{nm}$, 
$50~\text{nm}$ and 
$60~\text{nm}$, as well as for two laser intensity regimes: high intensity 
$I=2.5\times 10^{20}~\text{W}/\text{cm}^{2}$ (
$a_{0}=10$) and low intensity 
$I=2.5\times 10^{18}~\text{W}/\text{cm}^{2}$ (
$a_{0}=1$).
Figure 6. The 2D PIC simulation results show the number of SFEs within the angular interval 
$\unicode[STIX]{x1D719}=[0^{\circ },10^{\circ }]$ as a function of the incidence angle for three relevant interaction conditions. Two distinct intensity regimes were considered, described by ‘high I’: 
$I=2.5\times 10^{20}~\text{W}/\text{cm}^{2}$ and ‘low I’: 
$I=2.5\times 10^{18}~\text{W}/\text{cm}^{2}$. The effect of the preformed plasma on the number of SFEs in the high intensity regime was studied for different values of the preplasma scale length: 
$L_{n}=0~\text{nm}$, 
$30~\text{nm}$, 
$50~\text{nm}$ and 
$60~\text{nm}$. For a direct comparison to the experimental data, electrons with energies 
${\geqslant}1.5~\text{MeV}$ were considered. For better visibility, the results in case of 
$L_{n}=30~\text{nm}$ (low 
$I$) and 
$L_{n}=0~\text{nm}$ (high 
$I$) are shown on a different scale (right-hand side axis).
For the interaction of a low intensity pulse with the GT having a preplasma of 
$30~\text{nm}$, the number of SFE peaks at 
$\unicode[STIX]{x1D6FC}=35^{\circ }$ (Figure 6 right 
$y$-axis). In the case of a GT with a step density profile (
$L_{n}=0$) irradiated by a laser pulse at high intensity of 
$2.5\times 10^{20}~\text{W}/\text{cm}^{2}$ (right 
$y$-axis), the peak is seen at 
$\unicode[STIX]{x1D6FC}=32^{\circ }$ and the electron number is increased by almost a factor of 4 compared to the low intensity regime. Note that the optimum incident angle of 
$30^{\circ }$ corresponds to the resonance condition of SPW excitation in the linear regime. However, when a preplasma of 
$30~\text{nm}$ scale length at the front of the target and a laser intensity of 
$2.5\times 10^{20}~\text{W}/\text{cm}^{2}$ are used, the number of SFEs increases by almost two orders of magnitude (left 
$y$-axis) compared to the step density profile case. For the same high laser intensity, results indicate that in the presence of few 10s of nm preplasma, the number of SFEs shows a similar dependence on the incidence angle, namely it peaks at a certain incidence angle, which is larger compared to the linear model prediction. Thus, for the interaction conditions corresponding to 
$L_{n}=30~\text{nm}$, 
$50~\text{nm}$ and 
$60~\text{nm}$, the optimum incidence angle for the SFE number is 
$37^{\circ }$, 
$45^{\circ }$ and 
$50^{\circ }$, respectively. Hence the peak angle shift is larger for larger preplasma scale lengths. The existence of a steep plasma density profile with a finite scale length generates a new condition for SPW excitation and leads to a shift of the optimum angle for the electron acceleration. The investigations are limited to preplasma scale lengths 
$L_{n}<h=80~\text{nm}$, where 
$h$ is the peak-to-valley vertical amplitude of the gratings’ grooves. Above this limit (
$L_{n}>80~\text{nm}$), the preplasma expansion overrides the target periodical modulations, the excitation of the SPWs is suppressed and the number of SFEs from the GT reaches a similar level as in the case of an FT. This effect was observed both experimentally and numerically. One may note that in the case of high intensity the grating surface suffers a denting of less than 
$100~\text{nm}$ due to the light pressure. The grating structure survives up to the laser peak intensity, while the grating surface starts to degrade during the second half of the laser pulse toward the end of the interaction. The surface denting can lead to a maximum variation of the incidence angle of about 
$\pm 2^{\circ }$. The denting had however no detectable effect on the surface electron acceleration.
The PIC simulations performed for different scale lengths emphasize the effect of the finite preplasma on the optimum angular shift from the resonant value as well as the sensitivity of the optimum angle on the small variation of the preplasma scale length (in the order of 
$10~\text{nm}$). As hydrodynamics simulations offer just an estimation of the preplasma expansion, an agreement of the simulation results with the experimental data should be considered valid more for a variation of plasma scale lengths and not for a fixed scale length. We also studied numerically the effect of the preplasma scale length on the efficiency of the SFEs for the high intensity regime (
$I=10^{20}~\text{W}/\text{cm}^{2}$), and the results are shown in Figure 7(a). Different simulations were performed to investigate such as, for comparison, a GT (
$\unicode[STIX]{x1D706}_{g}=1667~\text{nm}$) and an FT irradiated by laser pulses at 
$30^{\circ }$ and 
$45^{\circ }$ incidence angles. For each configuration, three relevant preplasma scale lengths were considered: 
$L_{n}=0~\text{nm}$ (step density profile), 
$L_{n}=30~\text{nm}$ and 
$L_{n}=100~\text{nm}$ (value larger than the grating surface vertical modulations). In the case of a GT without a preformed preplasma, the results indicate a larger number of SFEs at 
$30^{\circ }$ compared with 
$45^{\circ }$. When a finite preplasma with a scale length 
$L_{n}<h$ is modeled at the front of the target, the configuration with 
$\unicode[STIX]{x1D6FC}=45^{\circ }$ becomes more efficient as the SFE flux is by 3.6 times larger than in the case of 
$\unicode[STIX]{x1D6FC}=30^{\circ }$. For both preplasma values, the GT is superior to the flat target with respect to the number of the accelerated SFEs. At 
$L_{n}=100~\text{nm}>h$, the grating effect cannot be distinguished from the FT case indicating that both targets are similarly efficient in generating SFEs. Due to the extended preplasma, targets with a flat surface have a higher absorption rate of the laser energy (in the range of 
$L_{n}/\unicode[STIX]{x1D706}_{L}<1$), which influences directly the number of accelerated high energy electrons. This was also observed by many previous experimental and numerical studies (see, for example, Refs. [Reference Ma, Sawada, Patel, Chen, Divol, Higginson, Kemp, Key, Larson, Pape, Link, Macphee, Mclean, Ping, Stephens, Wilks and Beg44–Reference Ivanov, Shulyapov, Ksenofontov, Tsymbalov, Volkov, Savel’ev, Brantov, Bychenkov, Turinge, Lapik, Rusakov, Djilkibaev and Nedorezov46]). At the same time, for a preplasma expansion larger than the surface vertical modulations (
$L_{n}>h$), it is expected that the preplasma fills in the GT modulations and flattens the surface. For these conditions, simulation results show that both targets have in general a similar overall behavior with respect to the number of SFEs. For different applications employing high energy electrons such as staged acceleration schemes or radiation sources based on backscattering geometries, physical parameters of the SFEs accelerated by GTs can be of high relevance. While a high flux of energetic electrons in the specular direction can be obtained for an FT and a small scale length, this experimental configuration is not attractive as the reflected laser can damage the upstream laser amplification stages or detectors, for example. In the case of GTs, high energy electrons are accelerated via SPW along the target surface with lower divergence which could represent an advantage in various applications as discussed above. However, a direct comparison of the simulation results for a long preplasma 
$L_{n}=100~\text{nm}>h$ with the experimental data using low-contrast pulses is limited. The reason is that in the experiment with low-contrast conditions the target has at the front a preplasma with a much longer scale length (estimated as 
$L_{n}>\unicode[STIX]{x1D706}_{L}$). Moreover, the 2D simulations cannot reproduce the three-dimensional (3D) effects including laser focusing, surface rippling and denting. In particular, denting is more pronounced in a preplasma with long scale lengths.
Figure 7. (a) The effect of the preplasma scale length on the number of SFEs for FTs and GTs at 
$30^{\circ }$ and 
$45^{\circ }$ laser incidence angles. 2D simulation results are shown for SFEs with energies 
$E>1.5~\text{MeV}$ accelerated along the target surface within the angular range 
$\unicode[STIX]{x1D711}=[0^{\circ },10^{\circ }]$, for three preplasma scale lengths 
$L_{n}=0,30$ and 
$100~\text{nm}$. For all configurations the laser intensity is 
$I=10^{20}~\text{W}/\text{cm}^{2}$. (b) Simulation results show the angular distributions of the electron energies 
$E>1.5~\text{MeV}$ for GT (green line) and FT (black line) for a preplasma scale length of 
$L_{n}=30~\text{nm}$. Here the incidence angle was 
$45^{\circ }$ and the laser intensity was the same as in (a).
The angular distributions of the electrons were numerically investigated and the results for GT and FT with the simulation conditions 
$I=10^{20}~\text{W}/\text{cm}^{2}$ and 
$L=30~\text{nm}$ are presented in Figure 7(b). In both cases, the electrons are accelerated mainly in two directions, close to the specular direction and along the target surface, similar with the experimental findings. The flux of the SFEs accelerated by the GT is by a factor of 
$11$ larger compared to the FT while the total number of electrons for the FT is 
$33.5\%$ of the number of electrons for the GT. For direct comparison between the experimental results, shown in Figure 3(f), and numerical ones presented in Figure 7(b), one may note that, in the simulations the high energy electron beams have in both acceleration directions a lower divergence compared to the experimental case. As mentioned before, this difference originates from the fact that the simulations, which are performed in a 2D geometry cannot account for the real 3D interaction geometry which can lead to a broader emission cone in both, polar and azimuthal angles.
5 Theoretical modeling of the SPW excitation
Figure 8. (a) The approach of the analytical model is schematically shown. (b) The dependence of the longitudinal (along the target surface) normalized electric field component 
$E_{z}/E_{i}$ on the angle of laser incidence (
$\unicode[STIX]{x1D6FC}$) is presented, at different laser intensities: high 
$I$: 
$3\times 10^{20}~\text{W}/\text{cm}^{2}$; low 
$I$: 
$3\times 10^{18}~\text{W}/\text{cm}^{2}$. For each intensity regime, two values of the plasma parameter 
$\unicode[STIX]{x1D702}_{\text{eff}}$, 
$40$ and 
$80$ have been considered with the same plasma inhomogeneity. Data are averaged over the angle interval 
$\pm 5^{\circ }$. (c) The analytical calculation of the resonance angle as a function of the laser intensity corresponding to four different plasma parameters: 
$\unicode[STIX]{x1D702}_{\text{eff}}=20$ (magenta), 
$30$ (green), 
$40$ (blue) and 
$=100$ (purple) for a grating of 
$\unicode[STIX]{x1D706}_{g}=1667~\text{nm}$.
In consideration of these results, we revised the linear model of SPWs and its simple scaling of Refs. [Reference Pitarke, Silkin, Chulkov and Echenique15, Reference Riconda, Raynaud, Vialis and Grech18, Reference Kaw and McBride20, Reference Raynaud, Kupersztych, Riconda, Adam and Heron21] and presumed a finite value of the plasma parameter 
$\unicode[STIX]{x1D702}=n_{e}/n_{c}$. The condition is closer to the real experimental conditions as, at these high intensities (
$I>10^{20}~\text{W}/\text{cm}^{2}$), a preplasma with 
$L_{n}/\unicode[STIX]{x1D706}_{L}\ll 1$ but not zero is generated. We aim to calculate the transformation of the laser electric field to the plasma wave field and we assume the oblique incidence of a p-polarized laser field of amplitude 
$E_{i}$ and wave vector 
$k=\unicode[STIX]{x1D714}/c$ onto an overdense plasma (
$\unicode[STIX]{x1D702}>1$). The schematic of the interaction geometry considered in the model is shown in Figure 8(a). We calculate the electric field components in the two-‘wave’ approximation (reflected and surface ones) diffraction theory (see, for example, Ref. [Reference Andreev, Platonov and Salomaa29]). In this approximation, the fields in vacuum can be written as
$$\begin{eqnarray}\displaystyle E_{x} & {\approx} & \displaystyle E_{i}\sin \unicode[STIX]{x1D6FC}\exp (-ik_{x}x+ik_{z}z)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{q=0,\unicode[STIX]{x1D705}}E_{q}\exp [i(k_{z}+q)z+\unicode[STIX]{x1D6E4}_{q}x]+\text{c.c.},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{z} & {\approx} & \displaystyle E_{i}\cos \unicode[STIX]{x1D6FC}\exp (-ik_{x}x+ik_{z}z)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{q=0,\unicode[STIX]{x1D705}}\frac{i\unicode[STIX]{x1D6E4}_{q}}{k_{z}+q}E_{q}\exp [i(k_{z}+q)z+\unicode[STIX]{x1D6E4}_{q}x]+\text{c.c.},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$where
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{q}^{2}=-\unicode[STIX]{x1D714}^{2}/c^{2}+(k_{z}+q)^{2}.\end{eqnarray}$$ The first term corresponds to the incident field, 
$q=0$ is the reflected field and 
$q=\unicode[STIX]{x1D705}=2\unicode[STIX]{x1D70B}/\unicode[STIX]{x1D706}_{g}$ corresponds to the surface wave field with the wave vector 
$k_{z}+\unicode[STIX]{x1D705}$. The electric fields in the plasma are defined as
$$\begin{eqnarray}\displaystyle & \displaystyle E_{x}^{p}\approx \mathop{\sum }_{q=0,\unicode[STIX]{x1D705}}E_{q}^{p}\exp [i(k_{z}+q)z+\unicode[STIX]{x1D6FE}_{q}x]+\text{c.c.}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle E_{z}^{p}\approx \mathop{\sum }_{q=0,\unicode[STIX]{x1D705}}\frac{i\unicode[STIX]{x1D6FE}_{q}}{k_{z}+q}E_{q}^{p}\exp [i(k_{z}+q)z+\unicode[STIX]{x1D6FE}_{q}x]+\text{c.c.}, & \displaystyle\end{eqnarray}$$ where 
$\unicode[STIX]{x1D6FE}_{q}^{2}=\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D700}(\unicode[STIX]{x1D714})/c^{2}+(k_{z}+q)^{2}\cong -\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D700}(\unicode[STIX]{x1D714})/c^{2}$ assuming 
$\unicode[STIX]{x1D702}>1$. To calculate the amplitudes of spatial harmonics, we use the boundary conditions at the plasma surface
$x=f(z)=(h/2)\cdot \sin (\unicode[STIX]{x1D705}z)$ with the peak-to-valley depths 
$h<\unicode[STIX]{x1D706}_{L}$ but 
$h\geqslant L_{s}=c/\unicode[STIX]{x1D714}\sqrt{\unicode[STIX]{x1D702}}$, where 
$L_{s}$ is the skin layer depth. We expand the exponential functions with a Fourier series and, in the limit of a two-wave approximation, we take into account only two harmonics: 
$\exp (ik_{z}z)$ and 
$\exp [i(k_{z}+\unicode[STIX]{x1D705})z]$. Equations (1)–(4) have four unknown quantities in view of continuity of the fields at the boundaries. It is worth emphasizing that this system of equations depends on the amplitude 
$h$, essentially in a nonlinear manner (as Bessel functions with argument 
${\sim}h/L_{s}$). The nonlinearity starts to affect when the surface oscillation amplitude becomes of the order of the skin layer. The solutions of the system of equations can be retrieved analytically or numerically. The simulations indicate that the preplasma parameters play a key role during the excitation of SPW. In our model we consider the case when the electron density profile at the vacuum interface is affected by a prepulse of duration 
$t_{\text{pp}}$ leading to the formation of an electron layer with a constant density. In order to account for the preplasma, we considered for the vacuum and preplasma different dielectric constants 
$\unicode[STIX]{x1D716}_{1}=1$ and 
$\unicode[STIX]{x1D716}_{2}=\unicode[STIX]{x1D702}_{\text{eff}}$. The density of the second layer was obtained from the mass conservation law, supposing that the mass of the Debye layer, initially of length 
$r_{D}$, was extended up to 
$L_{\text{eff}}$. Thus, the density of the preplasma layer can be expressed as
$$\begin{eqnarray}\unicode[STIX]{x1D702}_{\text{eff}}\approx \unicode[STIX]{x1D702}\frac{r_{D}}{\unicode[STIX]{x1D6FE}_{e}L_{\text{eff}}}.\end{eqnarray}$$ The layer thickness 
$L_{\text{eff}}=c_{s}\cdot t_{\text{pp}}$ (
$c_{s}$ is ion sound velocity) was determined from numerical calculations. Here, 
$\unicode[STIX]{x1D6FE}_{e}=T_{e}/mc^{2}=\sqrt{1+a_{0}^{2}}$ is the electron relativistic factor. Using the new form of the plasma parameter, one can notice that both parameters, the plasma density profile and the high laser intensity can affect the optimum angle.
We paid close attention to the SFEs which are driven by the tangential component 
$E_{z}$ of the surface wave. Figure 8(b) shows the solution for 
$E_{z}$ in vacuum as a function of the incidence angle 
$\unicode[STIX]{x1D6FC}$ at different laser intensities and for two values of the parameter 
$\unicode[STIX]{x1D702}_{\text{eff}}$ (40 and 80). The angular dependence clearly shows that at low intensities and high value of 
$\unicode[STIX]{x1D702}_{\text{eff}}=80$, the resonance peak occurs at 
$\unicode[STIX]{x1D6FC}=30^{\circ }$, which follows the linear SPW model. When the laser intensity is increased to 
$3\times 10^{20}~\text{W}/\text{cm}^{2}$, the electric field peaks in this case at 
$\unicode[STIX]{x1D6FC}=32.5^{\circ }$ with 
$E_{z}=0.42E_{i}$. In the case of a lower preplasma parameter of 
$\unicode[STIX]{x1D702}_{\text{eff}}=40$ and high laser intensity, the normalized electrical field increases up to 
$0.66E_{i}$. In this case the peak emission is at an incidence angle of 
$\unicode[STIX]{x1D6FC}=46^{\circ }$. At low laser intensities, the optimum angular shift from the linear resonance value is rather small (a few degrees). Moreover, in the relativistic regime and over three orders of magnitude of laser intensity, we calculated the dependence of the optimum angle on the laser intensity for different values of the plasma parameter (
$\unicode[STIX]{x1D702}_{\text{eff}}=20$, 
$30$, 
$40$ and 
$100$ for a grating of 
$\unicode[STIX]{x1D706}_{g}=1667~\text{nm}$) and the results are shown in Figure 8(c). From this dependence, one can clearly see that an increase of the resonant angle, in comparison to the linear case, is possible if the laser intensity increases above the relativistic limit (
$I\geqslant 10^{18}~\text{W}/\text{cm}^{2}$) and the plasma density decreases. If one considers a very dense (solid) plasma with a step density profile, the angle shift is quite weak.
6 Summary
In summary, we presented the first experimental evidence showing the efficiency of electron acceleration by SPWs excited by laser pulses at intensities larger than 
$10^{20}~\text{W}/\text{cm}^{2}$ on grating surfaces. The results indicate that the SFE acceleration process is affected by the presence of a steep, but finite, preformed plasma. In these particular interaction conditions, it was observed that the optimum angle is larger than predicted by the linear SPW model as shown by an increase of the electron acceleration efficiency. Experimentally, we found for a grating of 
$\unicode[STIX]{x1D706}_{g}=1667~\text{nm}$ that the SFE flux is greater by a factor of 
$3.5$ at a laser incidence larger than the angle predicted by the linear SPW theory. These results are interpreted rather well by an analytical model which considers high intensity and inhomogeneous plasma effects. The SPW excitation by high field laser radiation suggests the possibility of a substantial increase of the high energy electron flux by optimizing the preplasma conditions. We may conclude that our theoretical studies (analytical and numerical) indicate the essential contributions of both parameters, the high intensity field and a finite preplasma, on the resonant SPW excitation in the relativistic regime.
Acknowledgement
Computational support and infrastructure were provided by the Centre for Information and Media Technology (ZIM) of the University of Düsseldorf (Germany).
Open access
