A model of vaccination use and livestock introductions

A theoretical model of the relationship between livestock introductions, disease outcomes, and vaccinations is developed next as a foundation for deriving hypotheses and to guide estimation. Herd replacement and dynamics and disease management decisions under drought and disease risk have been modeled separately in the literature (Fafchamps, Udry, and Czukas Reference Fafchamps, Udry and Czukas1998; Marsh et al. Reference Marsh, Yoder, Deboch, McElwain and Palmer2016; Ahmed et al. Reference Ahmed, Call, Quinlan and Yoder2018). Our theoretical model extends this literature by providing an integrated framework of disease management and herd maintenance decisions under disease risk.

We assume that households act as if to maximize net herd returns by utilizing quasi-fixed inputs such as available labor and accessible land, livestock vaccination investments, and herd introductions, where herd introductions can be both a response to disease losses and a source of disease introductions into the herd. Although not a focus of this article, we also account for drought losses because they can be substantial in these environments, and we capture them in our data.

For the theoretical model, we assume one livestock type and combine disease-related deaths and/or abortions into a general concept of livestock loss, but we later separate these for estimation. To support our analysis based on cross-sectional data in a parsimonious framework, we develop a static, partial agricultural household model (assuming separability between consumption and production decisions (as in Carter Reference Carter1988, Taylor and Adelman Reference Taylor and Adelman2003, Ahmed et al. Reference Ahmed, Call, Quinlan and Yoder2018) that focuses on how the potential for livestock disease or drought loss provides an incentive to both vaccinate to reduce loss and introduce animals for loss replacement and/or for portfolio management. The household's net returns from livestock are characterized as follows:

(1) $$\mathop {\max }\limits_{l, v, n} {\rm \;\pi } = p( {y( {l\semicolon \;k} ) + n} ) ( {1-{\rm \delta }( {v, \;n\semicolon \;g, \;{\rm \rho }, \;{\rm \gamma }} ) } ) -mn-cv-wl-r, \;$$

where p is the marginal value of an animal to the household in terms of its productivity in the herd, y is the “initial” herd size prior to introductions and losses, which might be thought of as a target or preferred herd size in the absence of livestock losses. Labor available for husbandry, l, and carrying capacity, k, are quasi-fixed with respect to herd size decisions, and therefore, y is quasi-fixed in the model.

The loss rate, δ( ⋅ ) ∈ [0, 1], is the fraction of animal units lost by drought and disease through abortions and/or death. Vaccinations, v, reduce losses at a decreasing rate (δ_v < 0, δ_vv > 0), reflecting the standard assumption of diminishing marginal benefit of input use. Introductions to the herd via purchase or gifts, denoted by n, are assumed to increase mortality at an increasing rate (δ_n > 0, δ_nn > 0), reflecting compounding disease contagion with increased new contacts (e.g., Anderson and May Reference Anderson and May1992). Furthermore, the marginal value of vaccinations increases with an increase in introductions (δ_vn = δ_nv > 0), where subscripts indicate partial derivatives. These interaction effects reflect the increase in the marginal benefit of vaccines in terms of disease control when the potential risk of disease transmission increases. The loss rate is also assumed to be positively associated with a background disease burden, ρ, (δ_ρ > 0); general grazing/feeding practices, g, (δ_g > 0) that we take as quasi-fixed and related to land tenure and cultural norms such as communal or zero grazing (as in Ahmed et al. Reference Ahmed, Call, Quinlan and Yoder2018); and rainfall, γ, which we assume reduces losses, i.e., δ_γ < 0 (based on the evidence that droughts adversely affect livestock health and mortality [Fafchamps, Udry, and Czukas Reference Fafchamps, Udry and Czukas1998; Ahmed et al. Reference Ahmed, Yoder, de Glanville, Davis, Kibona, Mmbaga, Lankester, Swai and Cleaveland2019]). General livestock grazing practices, g, and introductions, n, capture interherd contact, which is related to disease prevalence in the region (Bronsvoort et al. Reference Bronsvoort, Nfon, Hamman, Tanya, Kitching and Morgan2004; Rufael et al. Reference Rufael, Catley, Bogale, Sahle and Shiferaw2008; Schoonman and Swai Reference Schoonman and Swai2010; Ahmed et al. Reference Ahmed, Call, Quinlan and Yoder2018).

The marginal cost of an introduction is m (e.g., the market price of an animal), c is the marginal cost of vaccination, w is the cost of labor, and r represents any purely fixed costs such as land or capital rent applicable to the livestock enterprise.

The first-order necessary conditions for maximizing with respect to the choice variables v, n, and l are as follows:

(2)$$\displaystyle{{\partial {\rm \pi }} \over {\partial v}} = {-}p{\rm \delta }_v( {y + n} ) = c{\rm \;}$$

(3)$$\;\displaystyle{{\partial {\rm \pi }} \over {\partial n}} = p( {1-{\rm \delta }} ) -p{\rm \delta }_n( {y + n} ) = m{\rm \;}$$

(4)$$\displaystyle{{\partial {\rm \pi }} \over {\partial l}} = py_l( {1-{\rm \delta }} ) = w.{\rm \;}$$

Equation 2 implies that households choose to vaccinate to the point that the marginal benefit of vaccinations in terms of loss mitigation,−pδ_v(y + n), equals the marginal cost of vaccinations, c. Equation 3 implies that households will supplement after-loss herd size with introductions as long as the purchase cost is no greater than the in-herd value net of disease losses to introductions (p(1 − δ)) plus the marginal cost of disease transmission due to herd introduction, −pδ_n(y + n). Equation 4 implies that households choose to allocate labor for livestock management to the point that the marginal revenue product, py _l(1 − δ), is equal to the marginal cost of labor, w.Footnote ¹

Given exogenous factors θ =  (p, m, c, w, g, ρ, k, γ), the first-order conditions (equations 2 and 3) implicitly define the optimal demand functions for vaccinations, v* = v(θ), and introductions, n* = n(θ), which, in turn, imply an endogenous damage rate δ* = δ(v*, n*;g, ρ, γ) ≡ δ(θ). Background disease risk ρ, weather γ, and general grazing practices g have both direct effects on loss rates and indirect effects through vaccination and reintroduction demands. One might expect, for example, that a higher background disease risk ρ would instigate more vaccination through its effect on the value of the marginal product of vaccination, which would partially offset the disease losses due to background disease risk. To the extent that communal grazing heightens herd interactions and disease transmission, herd loss and subsequent animal acquisition for replacement may lead to an additional (indirect) herd infection risk.

Livestock loss from illness is L* = δ*(y* + n*) and depends on endogenous introductions and vaccination use. The value of disease losses would be pL* = pδ*(y* + n*). Equation 4 implicitly defines the optimal demand function for labor, l* = l(θ).

Our hypotheses and implications for empirical strategies follow. Vaccinations reduce disease losses by $\;( \partial L^{\rm \ast }/\partial v^{\rm \ast }) = p{\rm \delta }_{\rm v}( {y^\ast{ + } n^\ast } ) < 0$, and this value is larger when the value of the herd is large, suggesting the following hypotheses:

The marginal effect of herd introductions n* on losses L* evaluated at $v^\ast , \;{\kern 1pt} l^\ast$, and n* is represented by$\;( \partial L^{\rm \ast }/\partial n^{\rm \ast }) = {\rm \delta }_n( {y^\ast{ + } n^\ast } ) + {\rm \delta }^\ast > 0, \;$ suggesting

While the hypotheses derived from the model are intuitive, this model highlights two issues that are important for guiding empirical methodology. First, v* = v(θ) and introductions n* = n(θ) are endogenous choices, driven by exogenous biophysical and economic factors. Disease losses L* = L(v*, n*, l*;g, ρ, k, γ) are directly affected by management decisions and a set of exogenous household characteristics and disease conditions and indirectly affected by management decisions by a broader set of exogenous variables. Second, the hypotheses each reflect model-based correlations between two endogenous variables conditional on exogenous factors. Thus, while we utilize regression methods to control for exogenous factors in assessing relationships, our regression results relating directly to hypotheses 1 through 3 should not be interpreted as implying direct causality in any given direction.

The endogeneity of vaccinations and introductions as factors affecting disease losses has important implications for formulating an econometric estimation strategy, but because the specifics of the available data also inform the estimation strategy, a description of the data is, therefore, provided next.

Data

Data were collected as part of the “Social, Economic and Environmental Drivers of Zoonotic Disease in Tanzania” (SEEDZ) project (Ahmed et al. Reference Ahmed, Yoder, de Glanville, Davis, Kibona, Mmbaga, Lankester, Swai and Cleaveland2019; de Glanville et al. Reference de Glanville, Davis, Allan, Buza, Claxton and Crump2020). A cross-sectional survey was conducted across six districts in Arusha Region (Arusha, Karatu, Longido, Meru, Monduli, and Ngorongoro Districts) and four districts in Manyara Region (Babati Rural, Babati Urban, Mbulu, and Simanjiro Districts) between January and December 2016. A multistage sampling design was used. Villages were selected from a spatially referenced list of all villages in the study area (from the Tanzanian National Bureau of Statistics [NBS]) using a generalized random tessellation stratified sampling approach (Stevens and Olsen Reference Stevens and Olsen2004). Within each village, two to three subvillages were randomly selected, and data collection was performed at a central point within each village (up to 10 households were included in each subvillage based on the willingness to participate). In total, data were collected from 404 households in 49 subvillages, and the dataset was made up of one record (observation) per household collected from a questionnaire survey conducted with the household head. Some observations were dropped in our analysis due to missing data from an incomplete survey response, so the analysis was based on 386 observations.

Table 1 describes the variables used in the analysis, and Table 2 provides summary statistics. Vaccinations (v in our theoretical model) are the count of vaccine types used for different diseases within a household (variable names are presented in italics throughout). The diseases covered by these vaccinations include anthrax, foot-and-mouth disease, lumpy skin disease, black quarter, East Coast fever (ECF), contagious bovine pleuro-pneumonia (CBPP), peste des petits ruminants, and Rift Valley fever.Footnote ² Vaccinations range from zero to three in our data, which implies that although vaccinations are being used, they do not cover the wide range of livestock diseases faced by households. Of the households in our sample, 81.5 percent reported having not vaccinated their livestock in the last 12 months, 16 percent reported using one type of vaccine, 2.5 percent reported using 2, and 1 percent reported using three. The most frequently used vaccines were for CBPP and anthrax, followed by vaccines for lumpy skin disease and foot-and-mouth disease.

Table 1. Data description

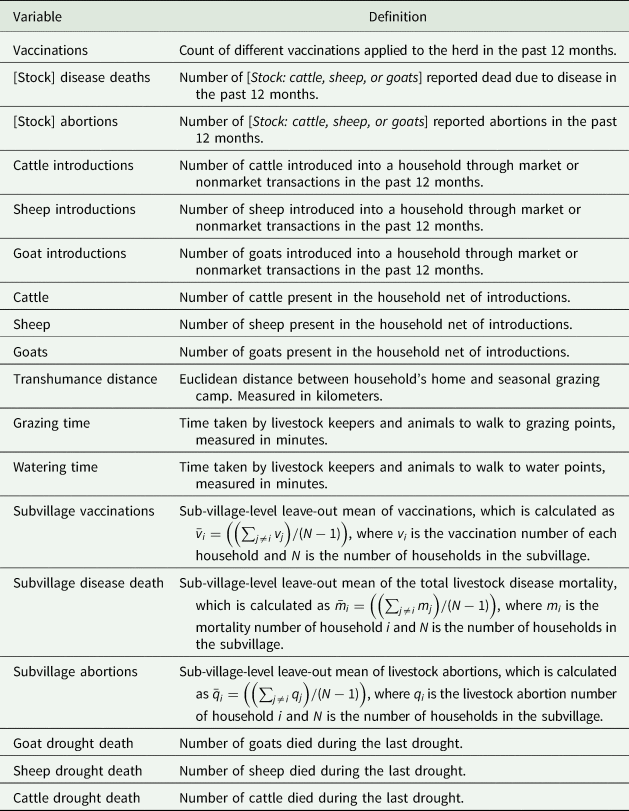
Table 2. Summary statistics (N = 386)

The low adoption rates of livestock vaccines in Tanzania (and Africa more broadly) can be attributed to several supply, demand, and informational factors. First, the available vaccines in Tanzania may not completely protect against disease (Railey et al. Reference Railey, Lembo, Palmer, Shirima and Marsh2018). Second, due to limited disease surveillance and awareness of the etiology of many adverse animal health outcomes in Tanzania, available vaccines (that are generally produced outside the country) may not protect against those diseases that cause the greatest actual losses. Third, the vaccine distribution system is marred by poor transport infrastructure (Waithanji, Mtimet, and Muindi Reference Waithanji, Mtimet and Muindi2019). In addition, vaccine cost, poor access, and a lack of information may limit the demand for vaccines (Homewood et al. Reference Homewood, Trench, Randall, Lynen and Bishop2006; Railey and Marsh Reference Railey and Marsh2019; Railey et al. Reference Railey, Lankester, Lembo, Reeve, Shirima and Marsh2019).

Our analytical model focuses on general disease losses L* = L(v*, n*, l*;g, ρ, k, γ). Our data distinguish between livestock abortions and other livestock deaths for three species—cattle, sheep, and goats. Average Cattle, Sheep, and Goat Disease Deaths in the past 12 months in the sample are 1.5, 4.2, and 5.4, respectively. Mean deaths due to drought are 2.8, 2.4, and 2.6 for cattle, sheep, and goats in the preceding year, respectively. The disease and drought-related death measures are based on respondent recall. The average numbers of Cattle, Sheep, and Goat Livestock Abortions reported in the past 12 months by the household are 0.59, 1.12, and 2.10, respectively (Table 2).

Cattle, Sheep, and Goat Introductions (represented by n) are count variables for the number of livestock of each type introduced into the herd from any source in the past 12 months. Sources of animal introductions include purchases from the livestock market, borrowing, and gifts from informal networks of kin in our sample. Cattle, Sheep, and Goat Introductions means are 1.61, 0.78, and 1.5, respectively (Table 2).

The mean gross herd size (net of introductions, y, in our model) is 54, 61, and 64 for cattle, sheep, and goats, respectively, and is represented by the variables Cattle, Sheep, and Goats.

We utilize a set of variables relating to grazing and watering practices, which we hypothesize may affect disease transmission through interherd contact. On average, in our sample, households cover about 10 km of Transhumance Distance seasonally to find suitable grazing areas, and they travel, on average, for about an hour daily for grazing and watering purposes (Grazing Time and Watering Time, respectively). To capture the village-level disease environment within which each household resides, we create Sub-Village Vaccination, Sub-Village Disease Deaths, and Sub-Village Abortion rates. Table 1 provides information on how these subvillage averages for vaccinations, disease deaths, and abortions are created. These variables help as exogenous instruments in the identification of our endogenous variables.

Estimation

To test our hypotheses and estimate the relationships between management practices and disease outcomes, we estimate (i) the effect of disease prevention (vaccinations) on disease-related deaths and (ii) the effect of herd accumulation on abortions and disease-related deaths. Vaccinations and herd introductions are endogenous variables. A standard two-stage instrumental variable approach is, therefore, used (Greene Reference Greene2011). In stage 1, reduced form equations for vaccinations (v) and Cattle, Sheep, and Goat Introductions (n) are estimated first based on control variables and including additional exogenous variables in the equation. In stage 2, the predicted values from these first-stage regressions are included in the outcome regressions as instruments in place of the original endogenous variables. This process, in principle, purges correlation between endogenous regressors and the regression disturbance that is the source of bias.

Vaccinations and disease deaths

Our aim is to estimate the relationship between Vaccinations (v) and Cattle, Sheep, and Goat Disease Deaths (d). Households may choose to vaccinate their animals when the disease burden is high, and therefore, there may be bidirectional causality between vaccinations and disease-related losses. Furthermore, vaccinations are a management decision and may depend on several unobserved factors. Therefore, we use instrumental variables to obtain consistent estimates that minimize the bias introduced by the potential endogeneity of these decisions. Therefore, the first-stage regression equation that describes vaccine demand is as follows:

(5)$$v = f_v( {{\boldsymbol X}_1, \;\;Z_1, \;\;Z_2} ) + {\rm \varepsilon }_v\;$$

where f _v( ⋅ ) can be interpreted as a predicted value conditional on its regressors and ɛ_v as a random error. X₁ contains household-level variables like preexisting herd size and grazing practices of the household. The Sub-Village Vaccination average (Z ₁) is the exogenous variable calculated as the subvillage vaccination rate averaged over all households in the sample except the household represented in a given record. This “leave-out” vaccination rate is hypothesized to correlate with household's vaccination decisions but is assumed to affect only dependent variables through its effect on vaccinations (v). Z ₁ accounts for sub-village-level exogenous factors affecting the local supply of vaccinations and factors affecting general vaccination demand in the subvillage (e.g., general information and acceptance of vaccinations in the area).Footnote ³ Z ₂ is the subvillage disease death that captures regional disease burden.Footnote ⁴

The second-stage regression equation for livestock deaths is as follows:

(6)$$d_i = f_{d_i}( {v^\ast , \;{\boldsymbol X}_1, \;\;Z_2} ) + {\rm \varepsilon }_{d_i}\;$$

where d _i represents disease-related deaths for each livestock species i ∈ (Cattle, Sheep, Goats): one regression for each species. X₁ is the control variables, as described above, and Z ₂ is the subvillage disease death average that controls for regional disease burdens.Footnote ⁵

Functional forms f _v(.) and $f_{{\rm d}_i}(. )$ are chosen from the Poisson/Negative binomial family, since v and d _i are all count variables. Because predicted values from first-stage regressions are included in the second-stage regressions, the covariance matrix for each second-stage equation is adjusted to obtain unbiased standard errors.Footnote ⁶

Herd introductions and disease losses

In addition to estimating the effect of vaccinations on deaths, we estimate the relationship between Cattle, Sheep, and Goat Introductions (n), Cattle, Sheep, and Goat Disease Deaths (d), and Cattle, Sheep, and Goat Abortions (a). Households may choose to introduce more animals in their herd to maintain herd size if they have lost animals due to a disease, but these introductions may also introduce pathogens that can cause disease. There may, therefore, be bidirectional causality between introductions and disease-related losses. To account for this, we use instrumental variables to minimize the bias introduced by the potential endogeneity of these decisions.

The first-stage regression equation that describes herd introduction demand is as follows:

(7)$$n_i = f_{n_i}( {{\boldsymbol X}_1, \;\;Z_2, \;\;{\boldsymbol Z}_3} ) + {\rm \varepsilon }_{n_i}$$

where n _i ∈ n represents the introductions for each livestock species i ∈ (Cattle, Sheep, Goats). X₁ contains household-level variables including preexisting herd size and grazing practices of the household. Z ₂ is the subvillage disease outcome that captures regional disease burden. Z₃ captures the livestock deaths that occurred due to a drought. These drought-related deaths are used as exogenous instruments that are assumed to affect disease-related losses only through herd introductions. A concern regarding our instrument here is that the incidence of drought may affect animals’ ability to fight off disease, as animals become malnourished and are expected to be less healthy during a drought. This likely positive correlation between the instrument and the outcome variables means that we will potentially overestimate the impact of herd introductions on disease-related outcomes. In that sense, we will likely obtain the upper bound of the effect of introductions on disease-related outcomes. Functional form $f_{n_i}(. )$ is chosen from the Poisson/Negative binomial family, since variables contained in each n _i ∈ n are count variables.

Predictions n^* from regression equation 7 are used as regressors in a pair of second-stage regressions for death and abortion outcomes:

(8a)$$d_i = f_{d_i}( {{\boldsymbol n}^{\boldsymbol \ast }, \;{\boldsymbol X}_1, \;\;Z_2} ) + {\rm \varepsilon }_{d_i}$$

(8b)$$a_i = f_{a_i}( {{\boldsymbol n}^{\boldsymbol \ast }, \;{\boldsymbol X}_1, \;\;Z_2} ) + {\rm \varepsilon }_{a_i}$$

where d _i and a _i are deaths and abortions for each livestock species i ∈ (Cattle, Sheep, Goats), respectively. X₁ is the control variable, as described above, and Z ₂ is the subvillage disease outcome average that controls for regional disease burden. The functional forms are again chosen from the Poisson/Negative binomial family, since d _i and a _i are count variables.Footnote ⁷ Because predicted values from first-stage regressions are included in the second-stage regressions, the covariance matrix for each second-stage equation is adjusted to obtain unbiased standard errors, as described in footnote 7.