1 Introduction
The homotopy groups of a simply connected
![]() $CW$
-complex Y of finite type have the form
$CW$
-complex Y of finite type have the form
 $$\begin{align*}\pi_i(Y)\cong \left(\mathop{\oplus}_{d_i}\mathbb{Z}\right)\oplus \mathop{\oplus}\limits_{\substack{\mathrm{prime}~p\\t \in \mathbb{Z}^+}}\left(\mathop{\oplus}\limits_{k_{p,t}} \mathbb{Z}/p^t\right), \end{align*}$$
$$\begin{align*}\pi_i(Y)\cong \left(\mathop{\oplus}_{d_i}\mathbb{Z}\right)\oplus \mathop{\oplus}\limits_{\substack{\mathrm{prime}~p\\t \in \mathbb{Z}^+}}\left(\mathop{\oplus}\limits_{k_{p,t}} \mathbb{Z}/p^t\right), \end{align*}$$
where
![]() $d_i$
and
$d_i$
and
![]() $k_{p,t}$
are the rank of the free summands and the
$k_{p,t}$
are the rank of the free summands and the
![]() $\mathbb {Z}/p^t$
-summands of
$\mathbb {Z}/p^t$
-summands of
![]() $\pi _i(Y),$
respectively. Denote
$\pi _i(Y),$
respectively. Denote
![]() $\mathrm{rank}_{0}(\pi _i(Y)):=d_i$
and
$\mathrm{rank}_{0}(\pi _i(Y)):=d_i$
and
![]() $\mathrm{rank}_{\mathbb {Z}/p^t}(\pi _i(Y)):=k_{p,t}$
.
$\mathrm{rank}_{\mathbb {Z}/p^t}(\pi _i(Y)):=k_{p,t}$
.
In the remarkable work [Reference Félix, Halperin and ThomasFHT], Félix, Halperin, and Thomas proved an asymptotic formula for the ranks
![]() $\mathrm{rank}_{0}(\pi _i(Y))$
of the free part of the homotopy groups. In particular, they showed that if Y is finite and
$\mathrm{rank}_{0}(\pi _i(Y))$
of the free part of the homotopy groups. In particular, they showed that if Y is finite and
![]() $\mathrm{rank}_{0}(\pi _i(Y))\neq 0$
for infinitely many
$\mathrm{rank}_{0}(\pi _i(Y))\neq 0$
for infinitely many
![]() $i\in \mathbb {Z}^{+}$
, then there is a constant
$i\in \mathbb {Z}^{+}$
, then there is a constant
![]() $\delta>1$
such that for N large enough
$\delta>1$
such that for N large enough
 $$\begin{align*}\sum_{i=N+2}^{N+\mathrm{dim}(Y)} \mathrm{rank}_{0}(\pi_i(Y))\geq \delta^{N}, \end{align*}$$
$$\begin{align*}\sum_{i=N+2}^{N+\mathrm{dim}(Y)} \mathrm{rank}_{0}(\pi_i(Y))\geq \delta^{N}, \end{align*}$$
which they interpret as a strong “regularity” property for the ranks
![]() $\mathrm{rank}_{0}(\pi _i(Y))$
of the free part of the homotopy groups. Concerning the ranks
$\mathrm{rank}_{0}(\pi _i(Y))$
of the free part of the homotopy groups. Concerning the ranks
![]() $\mathrm{rank}_{\mathbb {Z}/p^t}(\pi _i(Y))$
of the torsion part of the homotopy groups, they further raised the following natural question, which was rephrased in an explicit form by Wu and the second author in [Reference Huang and WuHW, Question 1.8].
$\mathrm{rank}_{\mathbb {Z}/p^t}(\pi _i(Y))$
of the torsion part of the homotopy groups, they further raised the following natural question, which was rephrased in an explicit form by Wu and the second author in [Reference Huang and WuHW, Question 1.8].
Question 1.1 Are there “regularity” properties of the torsion subgroups of the homotopy groups
![]() $\pi _i(Y)$
as
$\pi _i(Y)$
as
![]() $i\rightarrow \infty $
?
$i\rightarrow \infty $
?
In this paper, we study the above question by providing estimates for the ranks
![]() $\mathrm{rank}_{\mathbb {Z}/p^t}(\pi _i(Y))$
in certain cases. In particular, we give quantitative refinements of results of the authors and Wu, from the papers [Reference BoydeBoy1, Reference BoydeBoy2, Reference Huang and WuHW]. The methods of these papers implied more than were stated in the theorems: the statements were always that the volume of p-torsion in the homotopy groups of various spaces grows exponentially, but actually the methods were completely constructive, and with more work one can extract concrete exponential lower bounds. The extraction of these lower bounds is the business of this paper.
$\mathrm{rank}_{\mathbb {Z}/p^t}(\pi _i(Y))$
in certain cases. In particular, we give quantitative refinements of results of the authors and Wu, from the papers [Reference BoydeBoy1, Reference BoydeBoy2, Reference Huang and WuHW]. The methods of these papers implied more than were stated in the theorems: the statements were always that the volume of p-torsion in the homotopy groups of various spaces grows exponentially, but actually the methods were completely constructive, and with more work one can extract concrete exponential lower bounds. The extraction of these lower bounds is the business of this paper.
The proof of each of our main theorems (1.2 and 1.7) begins with the combinatorics of free Lie algebras, which have been well understood since long before Félix, Halperin, and Thomas’s celebrated theorem. We use in particular some results of Babenko [Reference BabenkoBab] and Lambrechts [Reference LambrechtsLam], both of which are more general. From this common beginning, the proof of each theorem is then complicated in a different way; we elaborate briefly after each theorem statement.
Recent work of Burklund and Senger [Reference BurklundBS] has greatly advanced our understanding of these phenomena: they finish a story begun by Henn [Reference HennHen] and Iriye [Reference IriyeIri] and show that the radii of convergence of the p-local “homotopy” and “loop-homology” power series are equal. Again, we discuss each of our theorems in light of this.
1.1 Results via homology
We first give our quantitative refinement of the main result of [Reference BoydeBoy2]. To state the results, for any integer
![]() $q\geq 2$
, define a function
$q\geq 2$
, define a function
 $$\begin{align*}f_q(x)= \bigg(1 - \frac{x}{x-1} \frac{1}{\varphi}\bigg) \cdot \frac{1}{x} \varphi^{x} - c x \varphi^{\frac{x}{2}} - \kappa \lvert \psi \rvert^x \end{align*}$$
$$\begin{align*}f_q(x)= \bigg(1 - \frac{x}{x-1} \frac{1}{\varphi}\bigg) \cdot \frac{1}{x} \varphi^{x} - c x \varphi^{\frac{x}{2}} - \kappa \lvert \psi \rvert^x \end{align*}$$
for
![]() $x\geq 2$
, where:
$x\geq 2$
, where:
-
•
 $\varphi $
is the unique positive real root of the degree
$\varphi $
is the unique positive real root of the degree
 $q+1$
polynomial
$q+1$
polynomial
 $P(z)=z^{q+1} - z - 1$
,
$P(z)=z^{q+1} - z - 1$
, -
•
 $\psi $
is the root of
$\psi $
is the root of
 $\frac {P(z)}{(z - \varphi )}$
for which the absolute value
$\frac {P(z)}{(z - \varphi )}$
for which the absolute value
 $\lvert \varphi \rvert $
is maximized (i.e., the “second largest root of
$\lvert \varphi \rvert $
is maximized (i.e., the “second largest root of
 $P(z)$
after
$P(z)$
after
 $\varphi $
in absolute value”),
$\varphi $
in absolute value”), -
•
 $c= 2(q+2)(1+ \varphi )$
, and
$c= 2(q+2)(1+ \varphi )$
, and -
•
 $\kappa = (q+1)\left(1+ \frac {1}{\lvert \psi \rvert }\right)$
.
$\kappa = (q+1)\left(1+ \frac {1}{\lvert \psi \rvert }\right)$
.
We have the properties:
-
•
 $2^{\frac {1}{q+1}}< \varphi < 1 + \frac {1}{q}$
, and
$2^{\frac {1}{q+1}}< \varphi < 1 + \frac {1}{q}$
, and -
• for any
 $\varepsilon>0$
, once x is large enough we have
$\varepsilon>0$
, once x is large enough we have  $$\begin{align*}f_q(x) \geq (1- \varepsilon) \bigg(1 - \frac{1}{\varphi}\bigg) \cdot \frac{1}{x} \varphi^{x}> (1- \varepsilon) \bigg(1 - 2^{-\frac{1}{q+1}}\bigg) \cdot \frac{1}{x} 2^{\frac{x}{q+1}}. \end{align*}$$
$$\begin{align*}f_q(x) \geq (1- \varepsilon) \bigg(1 - \frac{1}{\varphi}\bigg) \cdot \frac{1}{x} \varphi^{x}> (1- \varepsilon) \bigg(1 - 2^{-\frac{1}{q+1}}\bigg) \cdot \frac{1}{x} 2^{\frac{x}{q+1}}. \end{align*}$$
We will use the function
![]() $f_q(x)$
with its properties freely in this subsection.
$f_q(x)$
with its properties freely in this subsection.
Let
![]() $P^{q+1}(p^r)$
be the Moore space defined as the mapping cone of the degree
$P^{q+1}(p^r)$
be the Moore space defined as the mapping cone of the degree
![]() $p^r$
map
$p^r$
map
![]() $S^{q}\rightarrow S^q$
. The following theorem provides an asymptotic formula for the p-local homotopy groups under a homological condition.
$S^{q}\rightarrow S^q$
. The following theorem provides an asymptotic formula for the p-local homotopy groups under a homological condition.
Theorem 1.2 Let Y be a simply connected
![]() $CW$
-complex, let
$CW$
-complex, let
![]() $p \neq 2$
be prime, and let
$p \neq 2$
be prime, and let
![]() $s \leq r \in \mathbb {Z}^+$
. If there exists a map
$s \leq r \in \mathbb {Z}^+$
. If there exists a map
for some
![]() $q\geq 2$
, such that the induced map
$q\geq 2$
, such that the induced map
is an injection, then we have the bound
In particular, for any
![]() $\varepsilon>0$
, once N is large enough we have
$\varepsilon>0$
, once N is large enough we have
 $$\begin{align*}\sum_{t=s}^r \mathrm{rank}_{{\mathbb{Z}/p^t}}(\pi_{N+1}(Y))>(1- \varepsilon) \bigg(1 - 2^{-\frac{1}{q+1}}\bigg) \cdot \frac{1}{N} 2^{\frac{N}{q+1}}. \end{align*}$$
$$\begin{align*}\sum_{t=s}^r \mathrm{rank}_{{\mathbb{Z}/p^t}}(\pi_{N+1}(Y))>(1- \varepsilon) \bigg(1 - 2^{-\frac{1}{q+1}}\bigg) \cdot \frac{1}{N} 2^{\frac{N}{q+1}}. \end{align*}$$
Algebraically, Theorem 1.2 depends on the structure of the module of boundaries in a free Lie algebra over a finite field. It is the need to take boundaries which complicates the story relative to Babenko and Lambrechts’s work. This is dealt with in Section 2.3, using a result of Cohen, Moore, and Neisendorfer [Reference Cohen, Moore and NeisendorferCMN].
Using [Reference BoydeBoy2, Proposition 10.12], the hypotheses of Theorem 1.2 simplify in the case that
![]() $Y=\Sigma X$
is a suspension, as follows:
$Y=\Sigma X$
is a suspension, as follows:
Theorem 1.3 Let X be a connected
![]() $CW$
-complex, let
$CW$
-complex, let
![]() $p \neq 2$
be prime, and let
$p \neq 2$
be prime, and let
![]() $s \leq r \in \mathbb {Z}^+$
. Suppose that
$s \leq r \in \mathbb {Z}^+$
. Suppose that
![]() $H_*(X; {\mathbb {Z}/p^s})$
has finite type. If there exists a map
$H_*(X; {\mathbb {Z}/p^s})$
has finite type. If there exists a map
for some
![]() $q\geq 2$
, such that
$q\geq 2$
, such that
is an injection, then we have the bound
In particular, for any
![]() $\varepsilon>0$
, once N is large enough we have
$\varepsilon>0$
, once N is large enough we have
The spaces X and Y in Theorems 1.2 and 1.3 can be infinite. The asymptotic formulae in both theorems bound the ranks of the p-local homotopy groups from below by an exponential function. In particular, they strengthen a recent result of the first author on local hyperbolicity [Reference BoydeBoy2, Theorems 1.5 and 1.6].
Note also that if
![]() $s=r$
, then the sum appearing on the left-hand side in the conclusions of Theorems 1.2 and 1.3 simplifies to
$s=r$
, then the sum appearing on the left-hand side in the conclusions of Theorems 1.2 and 1.3 simplifies to
![]() $\mathrm{rank}_{{\mathbb {Z}/p^r}}(\pi _{N+1}(\Sigma X)),$
and this simplification will apply in all the examples.
$\mathrm{rank}_{{\mathbb {Z}/p^r}}(\pi _{N+1}(\Sigma X)),$
and this simplification will apply in all the examples.
Theorem 1.3 has interesting applications. For instance, the Hurewicz theorem immediately gives the following example, which refines [Reference BoydeBoy2, Corollary 2.4]. We caution the reader to bear in mind that when a space X satisfies the hypotheses of Theorem 1.3, the conclusions of that theorem refer to the suspension
![]() $\Sigma X$
, rather than to X itself.
$\Sigma X$
, rather than to X itself.
Example 1.4 Let X be a connected
![]() $CW$
-complex, and let
$CW$
-complex, and let
![]() $p \neq 2$
be prime. Suppose that
$p \neq 2$
be prime. Suppose that
![]() $H_*(X; {\mathbb {Z}/p^r})$
has finite type and that the lowest-dimensional nontrivial reduced integral homology group contains a
$H_*(X; {\mathbb {Z}/p^r})$
has finite type and that the lowest-dimensional nontrivial reduced integral homology group contains a
![]() $\mathbb {Z}/p^r$
-summand. Then X satisfies the hypotheses of Theorem 1.3 with
$\mathbb {Z}/p^r$
-summand. Then X satisfies the hypotheses of Theorem 1.3 with
![]() $s=r$
and
$s=r$
and
![]() $q=\mathrm {conn}(X)+2$
.
$q=\mathrm {conn}(X)+2$
.
The identity map on a Moore space automatically satisfies the hypotheses of Theorem 1.2 (alternatively, apply Example 1.4), so we obtain the following.
Example 1.5 Let p be an odd prime and
![]() $q \geq 2$
. Then
$q \geq 2$
. Then
![]() $P^{q}(p^r)$
satisfies the hypotheses of Theorem 1.2 with
$P^{q}(p^r)$
satisfies the hypotheses of Theorem 1.2 with
![]() $s=r$
and
$s=r$
and
![]() $\mu $
equal to the identity map on
$\mu $
equal to the identity map on
![]() $\Sigma P^{q}(p^r) = P^{q+1}(p^r)$
. It follows that
$\Sigma P^{q}(p^r) = P^{q+1}(p^r)$
. It follows that
This strengthens a result of Wu and the second author on the
![]() $\mathbb {Z}/p^r$
-hyperbolicity of
$\mathbb {Z}/p^r$
-hyperbolicity of
![]() $P^{q+1}(p^r)$
[Reference Huang and WuHW, Theorem 1.6].
$P^{q+1}(p^r)$
[Reference Huang and WuHW, Theorem 1.6].
It is enlightening to compare this result from what could be deduced already from Burklund and Senger’s work [Reference BurklundBS]. It follows from their Corollary A.5 that the radius of convergence of the series
![]() $\sum _{N=1}^\infty \dim _{{\mathbb {Z}/p}}(\pi _N(P^{q+1}(p^r)) \otimes {\mathbb {Z}/p}) \cdot t^N$
is precisely
$\sum _{N=1}^\infty \dim _{{\mathbb {Z}/p}}(\pi _N(P^{q+1}(p^r)) \otimes {\mathbb {Z}/p}) \cdot t^N$
is precisely
![]() $\frac {1}{\varphi }$
. Since
$\frac {1}{\varphi }$
. Since
![]() $P^{q+1}(p^r)$
is rationally elliptic (being rationally contractible), this power series really is describing the torsion. Example 1.5 adds information in two ways: first, by giving a concrete function as a lower bound for all N, and second, by saying something about summands isomorphic to
$P^{q+1}(p^r)$
is rationally elliptic (being rationally contractible), this power series really is describing the torsion. Example 1.5 adds information in two ways: first, by giving a concrete function as a lower bound for all N, and second, by saying something about summands isomorphic to
![]() ${\mathbb {Z}/p^r}$
in particular, rather than p-torsion in general.
${\mathbb {Z}/p^r}$
in particular, rather than p-torsion in general.
Another interesting consequence of Example 1.4 is a torsion bound for an Eilenberg–MacLane space after suspension. In particular, the following immediate consequence gives a quantitative refinement of [Reference BoydeBoy2, Example 2.5].
Example 1.6 Let p be an odd prime and
![]() $q \geq 2$
. Then
$q \geq 2$
. Then
![]() $K(\mathbb {Z}/p^r, q-1)$
is
$K(\mathbb {Z}/p^r, q-1)$
is
![]() $(q-2)$
-connected, and the least-dimensional nontrivial homology group is
$(q-2)$
-connected, and the least-dimensional nontrivial homology group is
![]() $H_{q-1}(K(\mathbb {Z}/p^r, q-1)) \cong \mathbb {Z}/p^r$
. By Example 1.4,
$H_{q-1}(K(\mathbb {Z}/p^r, q-1)) \cong \mathbb {Z}/p^r$
. By Example 1.4,
![]() $K(\mathbb {Z}/p^r, q-1)$
satisfies the hypotheses of Theorem 1.3 with
$K(\mathbb {Z}/p^r, q-1)$
satisfies the hypotheses of Theorem 1.3 with
![]() $s=r$
.
$s=r$
.
1.2 Results via K-theory
Denote by
the rank of the p-torsion summands of
![]() $\pi _{i}(\Sigma X)$
. Our other main result refines the main theorem of [Reference BoydeBoy1] to a quantitative statement under a K-theoretical condition is the following.
$\pi _{i}(\Sigma X)$
. Our other main result refines the main theorem of [Reference BoydeBoy1] to a quantitative statement under a K-theoretical condition is the following.
Theorem 1.7 (Weak version of Theorem 3.3)
Let p be an odd prime, and let X be a path connected space having the p-local homotopy type of a finite
![]() $CW$
-complex. Suppose that there exists a map
$CW$
-complex. Suppose that there exists a map
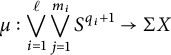 $$ \begin{align*} \mu : \bigvee_{i=1}^\ell \bigvee_{j=1}^{m_i} S^{q_i+1} \to \Sigma X \end{align*} $$
$$ \begin{align*} \mu : \bigvee_{i=1}^\ell \bigvee_{j=1}^{m_i} S^{q_i+1} \to \Sigma X \end{align*} $$
with
![]() $1 \leq q_1 < q_2 < \dots < q_\ell $
, such that the map
$1 \leq q_1 < q_2 < \dots < q_\ell $
, such that the map
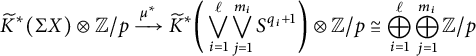 $$ \begin{align*} \widetilde{K}^*(\Sigma X) \otimes {\mathbb{Z}/p} \xrightarrow{\mu^*} \widetilde{K}^*\bigg(\bigvee_{i=1}^\ell \bigvee_{j=1}^{m_i} S^{q_i+1}\bigg) \otimes {\mathbb{Z}/p} \cong \bigoplus_{i=1}^\ell \bigoplus_{j=1}^{m_i} {\mathbb{Z}/p} \end{align*} $$
$$ \begin{align*} \widetilde{K}^*(\Sigma X) \otimes {\mathbb{Z}/p} \xrightarrow{\mu^*} \widetilde{K}^*\bigg(\bigvee_{i=1}^\ell \bigvee_{j=1}^{m_i} S^{q_i+1}\bigg) \otimes {\mathbb{Z}/p} \cong \bigoplus_{i=1}^\ell \bigoplus_{j=1}^{m_i} {\mathbb{Z}/p} \end{align*} $$
is a surjection.
Then, for any
![]() $\varepsilon>0$
, once the multiple
$\varepsilon>0$
, once the multiple
![]() $M=mg'$
of
$M=mg'$
of
is large enough we have
where
![]() $\varphi $
is the unique positive real root of the degree
$\varphi $
is the unique positive real root of the degree
![]() $q_\ell $
polynomial
$q_\ell $
polynomial
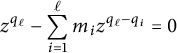 $$ \begin{align*}z^{q_\ell} - \sum_{i=1}^\ell m_i z^{q_\ell - q_i} = 0\end{align*} $$
$$ \begin{align*}z^{q_\ell} - \sum_{i=1}^\ell m_i z^{q_\ell - q_i} = 0\end{align*} $$
(in particular,
![]() $\varphi \geq (\sum _{i=1}^\ell m_i)^{\frac {1}{q_\ell }} = (\sum _{i=1}^\ell m_i)^{\frac {1}{\max (q_1, \dots , q_\ell )}}$
),
$\varphi \geq (\sum _{i=1}^\ell m_i)^{\frac {1}{q_\ell }} = (\sum _{i=1}^\ell m_i)^{\frac {1}{\max (q_1, \dots , q_\ell )}}$
),
![]() $\mathrm {conn}(X)$
is the p-local connectivity of X, and
$\mathrm {conn}(X)$
is the p-local connectivity of X, and
![]() $\dim (X)$
is the rational cohomological dimension of X.
$\dim (X)$
is the rational cohomological dimension of X.
A stronger estimate is provided by Theorem 3.3 with Remark 3.4 at the end of the paper. In particular, the asymptotic formulae in both theorems bound the ranks of the p-local homotopy groups from below by an exponential function. Unlike with Theorem 1.2, it is not necessary to take boundaries to prove Theorem 1.7, but the topological picture is difficult. The difficulty arises ultimately from an interaction between the James construction and the Adams operations, which as far as the authors know originates in the paper [Reference SelickSel] of Selick on which [Reference BoydeBoy1] is modeled, and manifests combinatorially as Condition (*) in the last section. This condition means that the “Lie algebra” one is ultimately able to find a copy of in homotopy groups “lags”—appearing in higher dimensions than one might expect. In the end, this shows up as, for example, the factor of
![]() $\left(\frac {\mathrm{{conn}(X)+1}}{\dim (X)+1}\right)$
in the exponent in Theorem 1.7.
$\left(\frac {\mathrm{{conn}(X)+1}}{\dim (X)+1}\right)$
in the exponent in Theorem 1.7.
Theorem 1.7 has interesting applications. For instance, let
![]() $\mathrm{Gr}_k(\mathbb {C}^n)$
be the Grassmannian of k-dimensional complex linear subspaces of
$\mathrm{Gr}_k(\mathbb {C}^n)$
be the Grassmannian of k-dimensional complex linear subspaces of
![]() $\mathbb {C}^n$
, which is simply connected and of complex dimension
$\mathbb {C}^n$
, which is simply connected and of complex dimension
![]() $k(n-k)$
. Recall
$k(n-k)$
. Recall
![]() $\mathrm{Gr}_1(\mathbb {C}^n)\cong \mathbb {C}P^{n-1}$
. In [Reference BoydeBoy1, Example 2.6], it is shown that when
$\mathrm{Gr}_1(\mathbb {C}^n)\cong \mathbb {C}P^{n-1}$
. In [Reference BoydeBoy1, Example 2.6], it is shown that when
![]() $n\geq 3$
and
$n\geq 3$
and
![]() $0<k<n$
there is a map
$0<k<n$
there is a map
which induces a surjection on
![]() $\widetilde {K}^\ast (~)\otimes \mathbb {Z}/p$
for all odd primes p. Applying Theorem 1.7, we must find the positive root of
$\widetilde {K}^\ast (~)\otimes \mathbb {Z}/p$
for all odd primes p. Applying Theorem 1.7, we must find the positive root of
![]() $z^4-z^2-1$
, which is
$z^4-z^2-1$
, which is
![]() $\sqrt {\frac {1+ \sqrt {5}}{2}}$
. Tidying the resulting formula a little, we obtain the following corollary, which strengthens [Reference BoydeBoy1, Examples 2.5 and 2.6].
$\sqrt {\frac {1+ \sqrt {5}}{2}}$
. Tidying the resulting formula a little, we obtain the following corollary, which strengthens [Reference BoydeBoy1, Examples 2.5 and 2.6].
Corollary 1.8 Let p be an odd prime,
![]() $n\geq 3$
and
$n\geq 3$
and
![]() $0<k<n$
. Then, for any
$0<k<n$
. Then, for any
![]() $\varepsilon>0$
, once m is large enough we have
$\varepsilon>0$
, once m is large enough we have
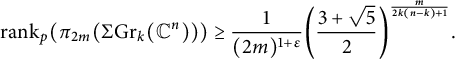 $$\begin{align*} \mathrm{rank}_{p}(\pi_{2m}(\Sigma \mathrm{Gr}_k(\mathbb{C}^n)))\geq \frac{1}{(2m)^{1+\varepsilon}}\bigg(\frac{3+\sqrt{5}}{2}\bigg)^{\frac{m}{2k(n-k)+1}}. \end{align*}$$
$$\begin{align*} \mathrm{rank}_{p}(\pi_{2m}(\Sigma \mathrm{Gr}_k(\mathbb{C}^n)))\geq \frac{1}{(2m)^{1+\varepsilon}}\bigg(\frac{3+\sqrt{5}}{2}\bigg)^{\frac{m}{2k(n-k)+1}}. \end{align*}$$
Similarly, let
![]() $H_{n, \ell }$
be the Milnor hypersurface defined by
$H_{n, \ell }$
be the Milnor hypersurface defined by
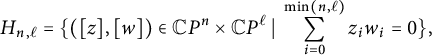 $$\begin{align*}H_{n, \ell}=\{([z], [w])\in \mathbb{C}P^n\times \mathbb{C}P^\ell~|~ \sum\limits_{i=0}^{\mathrm{min}(n, \ell)} z_iw_i=0\}, \end{align*}$$
$$\begin{align*}H_{n, \ell}=\{([z], [w])\in \mathbb{C}P^n\times \mathbb{C}P^\ell~|~ \sum\limits_{i=0}^{\mathrm{min}(n, \ell)} z_iw_i=0\}, \end{align*}$$
which is simply connected and of complex dimension
![]() $n+\ell -1$
. In [Reference BoydeBoy1, Example 2.7], it is showed that when
$n+\ell -1$
. In [Reference BoydeBoy1, Example 2.7], it is showed that when
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $\ell \geq 3$
there is a map
$\ell \geq 3$
there is a map
which induces a surjection on
![]() $\widetilde {K}^\ast (~)\otimes \mathbb {Z}/p$
for all odd primes p. Therefore, the following corollary follows immediately from Theorem 1.7, which strengthens [Reference BoydeBoy1, Example 2.7].
$\widetilde {K}^\ast (~)\otimes \mathbb {Z}/p$
for all odd primes p. Therefore, the following corollary follows immediately from Theorem 1.7, which strengthens [Reference BoydeBoy1, Example 2.7].
Corollary 1.9 Let p be an odd prime,
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $\ell \geq 3$
. Then, for any
$\ell \geq 3$
. Then, for any
![]() $\varepsilon>0$
, once m is large enough we have
$\varepsilon>0$
, once m is large enough we have
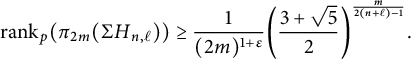 $$\begin{align*} \mathrm{rank}_{p}(\pi_{2m}(\Sigma H_{n, \ell}))\geq \frac{1}{(2m)^{1+\varepsilon}}\bigg(\frac{3+\sqrt{5}}{2}\bigg)^{\frac{m}{2(n+\ell)-1}}. \end{align*}$$
$$\begin{align*} \mathrm{rank}_{p}(\pi_{2m}(\Sigma H_{n, \ell}))\geq \frac{1}{(2m)^{1+\varepsilon}}\bigg(\frac{3+\sqrt{5}}{2}\bigg)^{\frac{m}{2(n+\ell)-1}}. \end{align*}$$
Consider the nth unitary group
![]() $U(n)$
which is connected and of real dimension
$U(n)$
which is connected and of real dimension
![]() $n^2$
. In [Reference BoydeBoy1, Example 2.8], it is showed that when
$n^2$
. In [Reference BoydeBoy1, Example 2.8], it is showed that when
![]() $n\geq 3$
there is a map
$n\geq 3$
there is a map
which induces a surjection on
![]() $\widetilde {K}^\ast (~)\otimes \mathbb {Z}/p$
for all odd primes p. It is clear that this map can be lifted to the special unitary group
$\widetilde {K}^\ast (~)\otimes \mathbb {Z}/p$
for all odd primes p. It is clear that this map can be lifted to the special unitary group
![]() $SU(n)$
, which is
$SU(n)$
, which is
![]() $2$
-connected and of real dimension
$2$
-connected and of real dimension
![]() $n^2-1$
. Therefore, the following corollary follows immediately from Theorem 1.7, which strengthens [Reference BoydeBoy1, Example 2.8].
$n^2-1$
. Therefore, the following corollary follows immediately from Theorem 1.7, which strengthens [Reference BoydeBoy1, Example 2.8].
Corollary 1.10 Let p be an odd prime and
![]() $n\geq 3$
. Then, for any
$n\geq 3$
. Then, for any
![]() $\varepsilon>0$
, once m is large enough we have
$\varepsilon>0$
, once m is large enough we have
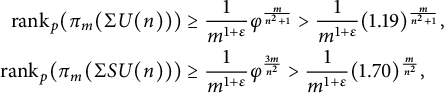 $$\begin{align*}\begin{aligned} \mathrm{rank}_{p}(\pi_{m}(\Sigma U(n)))&\geq \frac{1}{m^{1+\varepsilon}}\varphi^{\frac{m}{n^2+1}}>\frac{1}{m^{1+\varepsilon}} (1.19)^{\frac{m}{n^2+1}}, \\ \mathrm{rank}_{p}(\pi_{m}(\Sigma SU(n)))&\geq \frac{1}{m^{1+\varepsilon}}\varphi^{\frac{3m}{n^2}}>\frac{1}{m^{1+\varepsilon}} (1.70)^{\frac{m}{n^2}}, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \mathrm{rank}_{p}(\pi_{m}(\Sigma U(n)))&\geq \frac{1}{m^{1+\varepsilon}}\varphi^{\frac{m}{n^2+1}}>\frac{1}{m^{1+\varepsilon}} (1.19)^{\frac{m}{n^2+1}}, \\ \mathrm{rank}_{p}(\pi_{m}(\Sigma SU(n)))&\geq \frac{1}{m^{1+\varepsilon}}\varphi^{\frac{3m}{n^2}}>\frac{1}{m^{1+\varepsilon}} (1.70)^{\frac{m}{n^2}}, \end{aligned} \end{align*}$$
where
![]() $\varphi $
is the unique positive real root of
$\varphi $
is the unique positive real root of
![]() $z^5-z^2-1=0$
.
$z^5-z^2-1=0$
.
The structure of this paper is as follows: Section 2 treats the algebra and combinatorics. Section 2.2 treats free Lie algebras without a differential, and Section 2.3 studies the module of boundaries in the differential case. These results are then used to prove the main theorems in Section 3.
2 Algebra
2.1 Complex arithmetic
Lemma 2.1 Let S be a finite set of positive integers, let
![]() $g = \gcd (S)$
, and let
$g = \gcd (S)$
, and let
![]() $\eta \in \mathbb {C}$
be nonzero. Then
$\eta \in \mathbb {C}$
be nonzero. Then
![]() $\eta ^g$
is a positive real if and only if
$\eta ^g$
is a positive real if and only if
![]() $\eta ^i$
is a positive real for all
$\eta ^i$
is a positive real for all
![]() $i \in S$
.
$i \in S$
.
Proof The “only if” direction follows from the fact that g divides each member of S. For the “if” direction, Bezout’s Lemma gives
![]() $\alpha _i \in \mathbb {Z}$
for each
$\alpha _i \in \mathbb {Z}$
for each
![]() $i \in S$
such that
$i \in S$
such that
![]() ${\sum _i \alpha _i \cdot i = g}$
. Thus, if each
${\sum _i \alpha _i \cdot i = g}$
. Thus, if each
![]() $\eta ^i$
is a positive real, we get
$\eta ^i$
is a positive real, we get
which is a product of powers of positive reals, hence also a positive real.
Lemma 2.2 Let
![]() $c_0, \dots , c_{k-1} \in \mathbb {Z}_{\geq 0}$
, with
$c_0, \dots , c_{k-1} \in \mathbb {Z}_{\geq 0}$
, with
![]() $c_0 \geq 1$
. The polynomial
$c_0 \geq 1$
. The polynomial
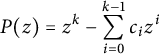 $$ \begin{align*}P(z) = z^{k} - \sum_{i=0}^{k-1} c_i z^i\end{align*} $$
$$ \begin{align*}P(z) = z^{k} - \sum_{i=0}^{k-1} c_i z^i\end{align*} $$
has precisely one positive real root,
![]() $\varphi $
, which occurs with multiplicity one, and satisfies
$\varphi $
, which occurs with multiplicity one, and satisfies
![]() $\varphi \geq 1$
. The other roots
$\varphi \geq 1$
. The other roots
![]() $\eta $
satisfy
$\eta $
satisfy
![]() $|\eta | \leq \varphi $
, with equality holding if and only if
$|\eta | \leq \varphi $
, with equality holding if and only if
![]() $\eta $
is the product of
$\eta $
is the product of
![]() $\varphi $
with a gth root of unity, where
$\varphi $
with a gth root of unity, where
![]() $g=\gcd (\{i \mid c_i \neq 0\}\cup \{k\})$
.
$g=\gcd (\{i \mid c_i \neq 0\}\cup \{k\})$
.
Proof The number of sign changes between consecutive coefficients in P is 1, so P has precisely one positive real root by Descartes’ rule of signs. Call this root
![]() $\varphi $
. Rearranging, we have
$\varphi $
. Rearranging, we have
![]() $\varphi ^k = \sum _{i=0}^{k-1} c_i \varphi ^i$
. Since
$\varphi ^k = \sum _{i=0}^{k-1} c_i \varphi ^i$
. Since
![]() $c_0 \geq 1$
, we must have
$c_0 \geq 1$
, we must have
![]() $\varphi ^k \geq 1$
, so
$\varphi ^k \geq 1$
, so
![]() $\varphi \geq 1$
.
$\varphi \geq 1$
.
Suppose that
![]() $\eta \in \mathbb {C}$
is a root of P. Taking modulus and applying the triangle inequality, we obtain
$\eta \in \mathbb {C}$
is a root of P. Taking modulus and applying the triangle inequality, we obtain
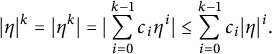 $$ \begin{align*}| \eta | ^{k} = | \eta^{k} | = | \sum_{i=0}^{k-1} c_i \eta^i | \leq \sum_{i=0}^{k-1} c_i |\eta|^ i.\end{align*} $$
$$ \begin{align*}| \eta | ^{k} = | \eta^{k} | = | \sum_{i=0}^{k-1} c_i \eta^i | \leq \sum_{i=0}^{k-1} c_i |\eta|^ i.\end{align*} $$
Equality holds in the above if and only if (1)
![]() $\eta ^i$
is a nonnegative real for all i for which
$\eta ^i$
is a nonnegative real for all i for which
![]() $c_i \neq 0$
, and (2)
$c_i \neq 0$
, and (2)
![]() $|\eta |$
is a root of P. By Lemma 2.1, the first condition is equivalent to
$|\eta |$
is a root of P. By Lemma 2.1, the first condition is equivalent to
![]() $\eta ^g$
being a nonnegative real, where
$\eta ^g$
being a nonnegative real, where
![]() $g = \gcd \{i \ \lvert \ c_i \neq 0 \}$
. The second condition is equivalent to
$g = \gcd \{i \ \lvert \ c_i \neq 0 \}$
. The second condition is equivalent to
![]() $|\eta | = \varphi $
, since
$|\eta | = \varphi $
, since
![]() $|\eta |$
is a nonnegative real. The root
$|\eta |$
is a nonnegative real. The root
![]() $\varphi $
satisfies these conditions, and the other solutions are obtained as the product of
$\varphi $
satisfies these conditions, and the other solutions are obtained as the product of
![]() $\varphi $
with the gth roots of unity.
$\varphi $
with the gth roots of unity.
If the inequality is strict then we have
![]() $P(|\eta |) < 0$
. Since the value of the polynomial
$P(|\eta |) < 0$
. Since the value of the polynomial
![]() $P(|z|)$
is positive for sufficiently large
$P(|z|)$
is positive for sufficiently large
![]() $|z|$
, and
$|z|$
, and
![]() $\varphi $
is the unique positive real root,
$\varphi $
is the unique positive real root,
![]() $P(|z|)>0$
for any
$P(|z|)>0$
for any
![]() $|z|>\varphi $
. It follows that
$|z|>\varphi $
. It follows that
![]() $|\eta | < \varphi $
, as required.
$|\eta | < \varphi $
, as required.
For a polynomial
![]() $P(z)$
of degree k, let
$P(z)$
of degree k, let
![]() $\eta _1, \dots , \eta _k$
be the roots of P, with multiplicity. The Nth Newton sum of P is the complex number
$\eta _1, \dots , \eta _k$
be the roots of P, with multiplicity. The Nth Newton sum of P is the complex number
![]() $\eta _1^N+ \dots + \eta _k^N$
. If P has real coefficients, then the roots occur in conjugate pairs and the Newton sums take real values. Lemma 2.2 controls the Newton sums quite tightly. In particular, the next lemma explains that when
$\eta _1^N+ \dots + \eta _k^N$
. If P has real coefficients, then the roots occur in conjugate pairs and the Newton sums take real values. Lemma 2.2 controls the Newton sums quite tightly. In particular, the next lemma explains that when
![]() $N=gn$
is g-divisible they are well approximated asymptotically by
$N=gn$
is g-divisible they are well approximated asymptotically by
![]() $g \varphi ^{gn}$
, and when N is not g-divisible they are approximated by zero with the same error.
$g \varphi ^{gn}$
, and when N is not g-divisible they are approximated by zero with the same error.
Lemma 2.3 Let
![]() $c_0, \dots , c_{k-1} \in \mathbb {Z}_{\geq 0}$
, with
$c_0, \dots , c_{k-1} \in \mathbb {Z}_{\geq 0}$
, with
![]() $c_0 \geq 1$
. Let
$c_0 \geq 1$
. Let
![]() $\eta _1, \dots , \eta _k$
be the complex roots of the polynomial
$\eta _1, \dots , \eta _k$
be the complex roots of the polynomial
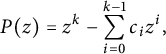 $$ \begin{align*}P(z) = z^{k} - \sum_{i=0}^{k-1} c_i z^i,\end{align*} $$
$$ \begin{align*}P(z) = z^{k} - \sum_{i=0}^{k-1} c_i z^i,\end{align*} $$
with multiplicity. As
![]() $N \to \infty $
, the Newton sums of
$N \to \infty $
, the Newton sums of
![]() $P(z)$
satisfy:
$P(z)$
satisfy:
-
• For N not divisible by g we have
 $$ \begin{align*}\lvert \eta_1^{N} + \dots + \eta_k^{N} \rvert \leq (k-g)|\psi|^{N}.\end{align*} $$
$$ \begin{align*}\lvert \eta_1^{N} + \dots + \eta_k^{N} \rvert \leq (k-g)|\psi|^{N}.\end{align*} $$
-
• When
 $N=gn$
is g-divisible we have
$N=gn$
is g-divisible we have  $$ \begin{align*}\lvert g \varphi^{gn} - (\eta_1^{gn} + \dots + \eta_k^{gn}) \rvert \leq (k-g)|\psi|^{gn},\end{align*} $$
$$ \begin{align*}\lvert g \varphi^{gn} - (\eta_1^{gn} + \dots + \eta_k^{gn}) \rvert \leq (k-g)|\psi|^{gn},\end{align*} $$
where
![]() $\varphi $
is the unique positive real root of
$\varphi $
is the unique positive real root of
![]() $P(z)$
,
$P(z)$
,
![]() $\psi $
is the second largest root in absolute value, and
$\psi $
is the second largest root in absolute value, and
![]() $g=\gcd (\{i \mid c_i \neq 0\}\cup \{k\})$
.
$g=\gcd (\{i \mid c_i \neq 0\}\cup \{k\})$
.
By definition,
![]() $|\psi | < \varphi $
. This means that this lemma implies for example that
$|\psi | < \varphi $
. This means that this lemma implies for example that
![]() $(\eta _1^{gn} + \dots + \eta _k^{gn}) \sim g \varphi ^{gn}$
as
$(\eta _1^{gn} + \dots + \eta _k^{gn}) \sim g \varphi ^{gn}$
as
![]() $n \to \infty $
.
$n \to \infty $
.
Proof By Lemma 2.2, roots of
![]() $P(z)$
come in two kinds: those which are the product of
$P(z)$
come in two kinds: those which are the product of
![]() $\varphi $
with a gth root of unity, and those roots
$\varphi $
with a gth root of unity, and those roots
![]() $\eta $
with
$\eta $
with
![]() $|\eta | < \varphi $
(hence
$|\eta | < \varphi $
(hence
![]() $|\eta | \leq | \psi |$
). The important point is that each root of the first kind occurs with multiplicity precisely 1.
$|\eta | \leq | \psi |$
). The important point is that each root of the first kind occurs with multiplicity precisely 1.
To see this, apply Lemma 2.2 to the polynomial
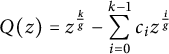 $$ \begin{align*}Q(z) = z^{\frac{k}{g}} - \sum_{i=0}^{k-1} c_i z^{\frac{i}{g}}\end{align*} $$
$$ \begin{align*}Q(z) = z^{\frac{k}{g}} - \sum_{i=0}^{k-1} c_i z^{\frac{i}{g}}\end{align*} $$
obtained by dividing all powers by g, and use the fact that roots of
![]() $P(z)$
are precisely the gth roots of the roots of
$P(z)$
are precisely the gth roots of the roots of
![]() $Q(z)$
.
$Q(z)$
.
Then, without loss of generality assume
![]() $\eta _1$
, …,
$\eta _1$
, …,
![]() $\eta _g$
are the roots of the first kind, so that
$\eta _g$
are the roots of the first kind, so that
![]() $\lvert \eta _1 \rvert = \dots = \lvert \eta _g \rvert = \varphi $
. From elementary complex analysis or group theory, we have that
$\lvert \eta _1 \rvert = \dots = \lvert \eta _g \rvert = \varphi $
. From elementary complex analysis or group theory, we have that
 $\eta _1^N + \dots + \eta _g^N = \begin {cases} g \varphi ^N, & g \mid N, \\ 0, & g \nmid N, \end {cases}$
and the result then follows from the triangle inequality.
$\eta _1^N + \dots + \eta _g^N = \begin {cases} g \varphi ^N, & g \mid N, \\ 0, & g \nmid N, \end {cases}$
and the result then follows from the triangle inequality.
2.2 Free Lie algebras
We write the generating set X of a free Lie algebra
![]() $L=L(X)$
over
$L=L(X)$
over
![]() $\mathbb {Z}$
as follows. Write
$\mathbb {Z}$
as follows. Write
![]() $q_1 < \dots < q_\ell $
for the distinct degrees which contain an element of X. Write
$q_1 < \dots < q_\ell $
for the distinct degrees which contain an element of X. Write
![]() $x_{i,1}, x_{i,2}, \dots , x_{i,m_i}$
for the distinct generators in degree
$x_{i,1}, x_{i,2}, \dots , x_{i,m_i}$
for the distinct generators in degree
![]() $q_i$
, so that in particular, the number of generators in degree
$q_i$
, so that in particular, the number of generators in degree
![]() $q_i$
is
$q_i$
is
![]() $m_i$
. Hilton [Reference HiltonHil] showed that L is free as a
$m_i$
. Hilton [Reference HiltonHil] showed that L is free as a
![]() $\mathbb {Z}$
-module.
$\mathbb {Z}$
-module.
Let
![]() $\mu : \mathbb {Z}_{> 0} \longrightarrow \{-1, 0, 1\}$
be the Möbius inversion function, defined by
$\mu : \mathbb {Z}_{> 0} \longrightarrow \{-1, 0, 1\}$
be the Möbius inversion function, defined by
 $$ \begin{align*}\mu(s) = \begin{cases} 1, & s=1, \\ 0, & s>1 \textrm{ is not square-free,} \\ (-1)^{\ell}, & s>1 \textrm{ is a product of } \ell \textrm{ distinct primes.} \end{cases}\end{align*} $$
$$ \begin{align*}\mu(s) = \begin{cases} 1, & s=1, \\ 0, & s>1 \textrm{ is not square-free,} \\ (-1)^{\ell}, & s>1 \textrm{ is a product of } \ell \textrm{ distinct primes.} \end{cases}\end{align*} $$
Given a polynomial
![]() $P(z) = a_0 + a_1 z + \dots + a_k z^k$
with
$P(z) = a_0 + a_1 z + \dots + a_k z^k$
with
![]() $ a_0\neq 0$
, the reciprocal of
$ a_0\neq 0$
, the reciprocal of
![]() $P(z)$
is
$P(z)$
is
![]() $a_k + a_{k-1} z + \dots + a_0 z^k$
. For given
$a_k + a_{k-1} z + \dots + a_0 z^k$
. For given
![]() $P(z)$
, let
$P(z)$
, let
![]() $\eta _1, \dots , \eta _k$
be the complex roots of the reciprocal of
$\eta _1, \dots , \eta _k$
be the complex roots of the reciprocal of
![]() $P(z)$
, with multiplicity (so
$P(z)$
, with multiplicity (so
![]() $P(z)=a_0 \prod _{i=1}^k (1-\eta _i z)$
). Write
$P(z)=a_0 \prod _{i=1}^k (1-\eta _i z)$
). Write
for the Nth Newton sum in the zeros of the reciprocal.
The following theorem is due to Babenko. Relative to his statement, we have changed variable using the fact that, for fixed N,
![]() $d \mapsto \frac {N}{d}$
is a self-bijection of the set of divisors of N.
$d \mapsto \frac {N}{d}$
is a self-bijection of the set of divisors of N.
Theorem 2.4 [Reference BabenkoBab, Proposition 1]
Let L be the free graded Lie algebra over
![]() $\mathbb {Z}$
on a finite set of generators
$\mathbb {Z}$
on a finite set of generators
![]() $\{x_{i,j}\}$
, with notation as above. Then
$\{x_{i,j}\}$
, with notation as above. Then
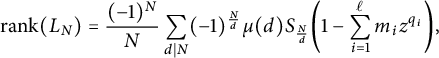 $$ \begin{align*} \mathrm{rank}(L_N)=\frac{(-1)^N}{N} \sum_{d \mid N} (-1)^{\frac{N}{d}} \mu(d) S_{\frac{N}{d}}\bigg(1- \sum_{i=1}^{\ell} m_i z^{q_i}\bigg), \end{align*} $$
$$ \begin{align*} \mathrm{rank}(L_N)=\frac{(-1)^N}{N} \sum_{d \mid N} (-1)^{\frac{N}{d}} \mu(d) S_{\frac{N}{d}}\bigg(1- \sum_{i=1}^{\ell} m_i z^{q_i}\bigg), \end{align*} $$
where the sum is taken over the divisors d of N.
Our next theorem is essentially a result of Lambrechts [Reference LambrechtsLam, Proposition 1] in the special case of free Lie algebras. Our derivation of this result from Babenko’s is essentially the same as Lambrechts’s, but the situation is simpler and slightly more is true. The point of the theorem is that when
![]() $g \mid N$
,
$g \mid N$
,
![]() $\mathrm{rank}(L_N)$
is well-approximated by
$\mathrm{rank}(L_N)$
is well-approximated by
![]() $\frac {g}{N} \varphi ^{N}$
with an error term given by a sum of exponentials in smaller bases.
$\frac {g}{N} \varphi ^{N}$
with an error term given by a sum of exponentials in smaller bases.
Theorem 2.5 Let L be the free graded Lie algebra over
![]() $\mathbb {Z}$
on a finite set of generators X. As before, write
$\mathbb {Z}$
on a finite set of generators X. As before, write
![]() $q_1 < \dots < q_\ell $
for the distinct degrees which contain an element of X, and let
$q_1 < \dots < q_\ell $
for the distinct degrees which contain an element of X, and let
![]() $g= \gcd (q_i)$
. Let
$g= \gcd (q_i)$
. Let
![]() $m_i$
be the number of generators in degree
$m_i$
be the number of generators in degree
![]() $q_i$
.
$q_i$
.
-
• If
 $g \nmid N$
, then
$g \nmid N$
, then
 $\mathrm{rank}(L_N) = 0$
.
$\mathrm{rank}(L_N) = 0$
. -
• If
 $g \mid N$
, then
$g \mid N$
, then
 $\lvert \mathrm{rank}(L_N) - \frac {g}{N} \varphi ^{N} \rvert \leq \frac {q_{\ell }}{N}|\psi |^{N}+g \varphi ^{\frac {N}{2}}+q_{\ell }|\psi |^{\frac {N}{2}}$
,
$\lvert \mathrm{rank}(L_N) - \frac {g}{N} \varphi ^{N} \rvert \leq \frac {q_{\ell }}{N}|\psi |^{N}+g \varphi ^{\frac {N}{2}}+q_{\ell }|\psi |^{\frac {N}{2}}$
,
where
![]() $\varphi $
is the unique positive real root of the degree
$\varphi $
is the unique positive real root of the degree
![]() $q_\ell $
polynomial
$q_\ell $
polynomial
 $$ \begin{align*}P(z)=z^{q_{\ell}} - \sum_{i=1}^\ell m_i z^{q_\ell - q_i} = 0,\end{align*} $$
$$ \begin{align*}P(z)=z^{q_{\ell}} - \sum_{i=1}^\ell m_i z^{q_\ell - q_i} = 0,\end{align*} $$
and
![]() $\psi $
is the second largest root in absolute value. In particular,
$\psi $
is the second largest root in absolute value. In particular,
![]() $\varphi \geq (\sum _{i=1}^\ell m_i)^{\frac {1}{q_\ell }}$
.
$\varphi \geq (\sum _{i=1}^\ell m_i)^{\frac {1}{q_\ell }}$
.
If
![]() $P(z)$
has no roots which are strictly smaller than
$P(z)$
has no roots which are strictly smaller than
![]() $\varphi $
in absolute value (i.e., “
$\varphi $
in absolute value (i.e., “
![]() $\psi $
does not exist”) then terms involving
$\psi $
does not exist”) then terms involving
![]() $\psi $
may be disregarded: precisely, the inequality in the second claim may be replaced by
$\psi $
may be disregarded: precisely, the inequality in the second claim may be replaced by
![]() $\lvert \mathrm{rank}(L_N) - \frac {g}{N} \varphi ^{N} \rvert \leq g \varphi ^{\frac {N}{2}}$
.
$\lvert \mathrm{rank}(L_N) - \frac {g}{N} \varphi ^{N} \rvert \leq g \varphi ^{\frac {N}{2}}$
.
Proof The first claim follows immediately from the fact that L is concentrated in degrees divisible by g.
We will now prove the second claim. The point is that the Babenko’s formula of Theorem 2.4 is dominated by the
![]() $d=1$
term. Let N be divisible by g. By Theorem 2.4 (using that
$d=1$
term. Let N be divisible by g. By Theorem 2.4 (using that
![]() $\mu (1)=1$
), we have
$\mu (1)=1$
), we have
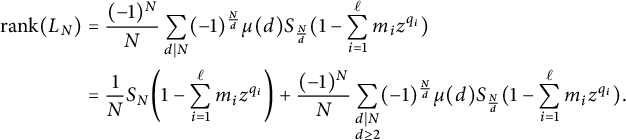 $$ \begin{align*} \begin{aligned} \mathrm{rank}(L_N) &=\frac{(-1)^N}{N} \sum_{d \mid N} (-1)^{\frac{N}{d}} \mu(d) S_{\frac{N}{d}}(1- \sum_{i=1}^{\ell} m_i z^{q_i}) \\ &= \frac{1}{N}S_{N}\bigg(1- \sum_{i=1}^{\ell} m_i z^{q_i}\bigg) + \frac{(-1)^N}{N} \sum_{\substack{d \mid N \\ d \geq 2}} (-1)^{\frac{N}{d}} \mu(d) S_{\frac{N}{d}}(1- \sum_{i=1}^{\ell} m_i z^{q_i}). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathrm{rank}(L_N) &=\frac{(-1)^N}{N} \sum_{d \mid N} (-1)^{\frac{N}{d}} \mu(d) S_{\frac{N}{d}}(1- \sum_{i=1}^{\ell} m_i z^{q_i}) \\ &= \frac{1}{N}S_{N}\bigg(1- \sum_{i=1}^{\ell} m_i z^{q_i}\bigg) + \frac{(-1)^N}{N} \sum_{\substack{d \mid N \\ d \geq 2}} (-1)^{\frac{N}{d}} \mu(d) S_{\frac{N}{d}}(1- \sum_{i=1}^{\ell} m_i z^{q_i}). \end{aligned} \end{align*} $$
We name these two terms, writing
![]() $S_N=S_{N}(1- \sum _{i=1}^{\ell } m_i z^{q_i})$
to simplify notation. Let
$S_N=S_{N}(1- \sum _{i=1}^{\ell } m_i z^{q_i})$
to simplify notation. Let
and let
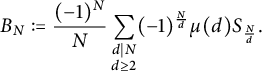 $$ \begin{align*}B_N := \frac{(-1)^N}{N} \sum_{\substack{d \mid N \\ d \geq 2}} (-1)^{\frac{N}{d}} \mu(d) S_{\frac{N}{d}}.\end{align*} $$
$$ \begin{align*}B_N := \frac{(-1)^N}{N} \sum_{\substack{d \mid N \\ d \geq 2}} (-1)^{\frac{N}{d}} \mu(d) S_{\frac{N}{d}}.\end{align*} $$
By Lemma 2.3 (with
![]() $n = \frac {N}{g}$
), we have
$n = \frac {N}{g}$
), we have
![]() $\lvert S_N - g \varphi ^{N} \rvert \leq (q_\ell - g) |\psi |^N \leq q_\ell |\psi |^N$
for
$\lvert S_N - g \varphi ^{N} \rvert \leq (q_\ell - g) |\psi |^N \leq q_\ell |\psi |^N$
for
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
as in the theorem statement. It therefore suffices to show that
$\psi $
as in the theorem statement. It therefore suffices to show that
![]() $\lvert B_N \rvert \leq g \varphi ^{\frac {N}{2}} + q_{\ell }|\psi |^{\frac {N}{2}}.$
$\lvert B_N \rvert \leq g \varphi ^{\frac {N}{2}} + q_{\ell }|\psi |^{\frac {N}{2}}.$
Since
![]() $\lvert \mu (d) \rvert \leq 1$
, we have by Lemma 2.3 that
$\lvert \mu (d) \rvert \leq 1$
, we have by Lemma 2.3 that
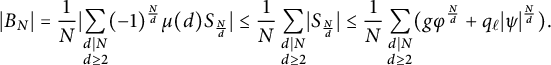 $$ \begin{align*}\lvert B_N \rvert = \frac{1}{N} \lvert \sum_{\substack{d \mid N \\ d \geq 2}} (-1)^{\frac{N}{d}} \mu(d) S_{\frac{N}{d}} \rvert \leq \frac{1}{N} \sum_{\substack{d \mid N \\ d \geq 2}} \lvert S_{\frac{N}{d}} \rvert \leq \frac{1}{N} \sum_{\substack{d \mid N \\ d \geq 2}}( g \varphi^{\frac{N}{d}} + q_{\ell}|\psi|^{\frac{N}{d}}).\end{align*} $$
$$ \begin{align*}\lvert B_N \rvert = \frac{1}{N} \lvert \sum_{\substack{d \mid N \\ d \geq 2}} (-1)^{\frac{N}{d}} \mu(d) S_{\frac{N}{d}} \rvert \leq \frac{1}{N} \sum_{\substack{d \mid N \\ d \geq 2}} \lvert S_{\frac{N}{d}} \rvert \leq \frac{1}{N} \sum_{\substack{d \mid N \\ d \geq 2}}( g \varphi^{\frac{N}{d}} + q_{\ell}|\psi|^{\frac{N}{d}}).\end{align*} $$
The number of terms in this summation is at most the number of divisors of N, which is at most N. The term is a sum of exponentials in positive bases, hence is strictly increasing, and in particular, for
![]() $d \geq 2,$
we have the termwise bound
$d \geq 2,$
we have the termwise bound
![]() $g \varphi ^{\frac {N}{d}} + q_{\ell }|\psi |^{\frac {N}{d}} \leq g \varphi ^{\frac {N}{2}} + q_{\ell }|\psi |^{\frac {N}{2}}$
. Putting this together gives
$g \varphi ^{\frac {N}{d}} + q_{\ell }|\psi |^{\frac {N}{d}} \leq g \varphi ^{\frac {N}{2}} + q_{\ell }|\psi |^{\frac {N}{2}}$
. Putting this together gives
as required.
Lastly, we check that
![]() $\varphi \geq (\sum _{i=1}^\ell m_i)^{\frac {1}{q_\ell }}$
. Since the polynomial
$\varphi \geq (\sum _{i=1}^\ell m_i)^{\frac {1}{q_\ell }}$
. Since the polynomial
![]() $P(z) = z^{q_{\ell }} - \sum _{i=1}^\ell m_i z^{q_\ell - q_i}$
has a unique positive root by Lemma 2.2, it suffices to check that
$P(z) = z^{q_{\ell }} - \sum _{i=1}^\ell m_i z^{q_\ell - q_i}$
has a unique positive root by Lemma 2.2, it suffices to check that
![]() $P((\sum _{i=1}^\ell m_i)^{\frac {1}{q_\ell }})$
is nonpositive. For each i,
$P((\sum _{i=1}^\ell m_i)^{\frac {1}{q_\ell }})$
is nonpositive. For each i,
![]() $\frac {q_\ell - q_i}{q_\ell }$
lies between 1 and 0, so for any
$\frac {q_\ell - q_i}{q_\ell }$
lies between 1 and 0, so for any
![]() $x \geq 1,$
we have
$x \geq 1,$
we have
![]() $x^{\frac {q_\ell - q_i}{q_\ell }} \geq 1$
. It follows that
$x^{\frac {q_\ell - q_i}{q_\ell }} \geq 1$
. It follows that
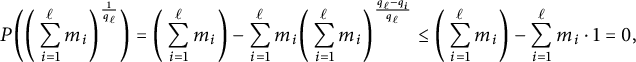 $$ \begin{align*} P\bigg(\bigg(\sum_{i=1}^\ell m_i\bigg)^{\frac{1}{q_\ell}}\bigg) = \bigg(\sum_{i=1}^\ell m_i\bigg) - \sum_{i=1}^\ell m_i \bigg(\sum_{i=1}^\ell m_i\bigg)^{\frac{q_\ell - q_i}{q_\ell}} \leq \bigg(\sum_{i=1}^\ell m_i\bigg) - \sum_{i=1}^\ell m_i \cdot 1 = 0, \end{align*} $$
$$ \begin{align*} P\bigg(\bigg(\sum_{i=1}^\ell m_i\bigg)^{\frac{1}{q_\ell}}\bigg) = \bigg(\sum_{i=1}^\ell m_i\bigg) - \sum_{i=1}^\ell m_i \bigg(\sum_{i=1}^\ell m_i\bigg)^{\frac{q_\ell - q_i}{q_\ell}} \leq \bigg(\sum_{i=1}^\ell m_i\bigg) - \sum_{i=1}^\ell m_i \cdot 1 = 0, \end{align*} $$
as required.
2.3 Free Lie algebras with differentials
Free Lie algebras over
![]() ${\mathbb {Z}/p^r}$
are obtained by tensoring the corresponding free Lie algebra over
${\mathbb {Z}/p^r}$
are obtained by tensoring the corresponding free Lie algebra over
![]() $\mathbb {Z}$
with
$\mathbb {Z}$
with
![]() ${\mathbb {Z}/p^r}$
, since this gives the correct universal property.
${\mathbb {Z}/p^r}$
, since this gives the correct universal property.
In this subsection, we consider
![]() $L=L(x,y)=L(x,dx)$
, the free differential Lie algebra over
$L=L(x,y)=L(x,dx)$
, the free differential Lie algebra over
![]() ${\mathbb {Z}/p^r}$
on the acyclic rank 2 free differential
${\mathbb {Z}/p^r}$
on the acyclic rank 2 free differential
![]() ${\mathbb {Z}/p^r}$
-module on generators x and y (
${\mathbb {Z}/p^r}$
-module on generators x and y (
![]() $dx = y$
). Suppose that
$dx = y$
). Suppose that
![]() $\deg (x)=q+1$
, so
$\deg (x)=q+1$
, so
![]() $\deg (y)=q$
. By Theorem 2.5, since
$\deg (y)=q$
. By Theorem 2.5, since
![]() $\gcd (q,q+1)=1$
, we know that
$\gcd (q,q+1)=1$
, we know that
where
![]() $\varphi $
is the unique positive real root of the degree
$\varphi $
is the unique positive real root of the degree
![]() $q+1$
polynomial
$q+1$
polynomial
The size of the error in this approximation is exponential in base depending on the second largest root
![]() $\psi $
(in absolute value), and
$\psi $
(in absolute value), and
![]() $\sqrt {\varphi }$
.
$\sqrt {\varphi }$
.
In this subsection, we are instead interested in
![]() $B := \textrm {Im}(d) \subset L$
, the module of boundaries. Our aim is to prove Theorem 2.11. The argument will go as follows. It is known (Theorem 2.7) that the differential on L is “almost acyclic.” A counting argument using the fact that
$B := \textrm {Im}(d) \subset L$
, the module of boundaries. Our aim is to prove Theorem 2.11. The argument will go as follows. It is known (Theorem 2.7) that the differential on L is “almost acyclic.” A counting argument using the fact that
![]() $\mathrm{rank}(L_N) \sim \frac {1}{N} \varphi ^{N}$
then shows that the rank of the module of boundaries must be asymptotically a fixed fraction of that of
$\mathrm{rank}(L_N) \sim \frac {1}{N} \varphi ^{N}$
then shows that the rank of the module of boundaries must be asymptotically a fixed fraction of that of
![]() $L_N$
.
$L_N$
.
We will first reduce to the case
![]() $r=1$
by means of the following lemma, which is proven in [Reference BoydeBoy2] as Lemma 7.10.
$r=1$
by means of the following lemma, which is proven in [Reference BoydeBoy2] as Lemma 7.10.
Lemma 2.6 Let
![]() $\varphi : M \longrightarrow N$
be a map of
$\varphi : M \longrightarrow N$
be a map of
![]() ${\mathbb {Z}/p^r}$
-modules, with N free. Then
${\mathbb {Z}/p^r}$
-modules, with N free. Then
![]() $\mathrm{rank}_{{\mathbb {Z}/p^r}}(\mathrm {Im}(\varphi )) = \mathrm{rank}_{{\mathbb {Z}/p}}(\mathrm {Im}(\varphi \otimes {\mathbb {Z}/p}))$
.
$\mathrm{rank}_{{\mathbb {Z}/p^r}}(\mathrm {Im}(\varphi )) = \mathrm{rank}_{{\mathbb {Z}/p}}(\mathrm {Im}(\varphi \otimes {\mathbb {Z}/p}))$
.
Now assume
![]() $r=1$
. Let u be an even-dimensional class in a graded differential Lie algebra L over
$r=1$
. Let u be an even-dimensional class in a graded differential Lie algebra L over
![]() ${\mathbb {Z}/p}$
for
${\mathbb {Z}/p}$
for
![]() $p \neq 2$
. Following [Reference Cohen, Moore and NeisendorferCMN], let
$p \neq 2$
. Following [Reference Cohen, Moore and NeisendorferCMN], let
and let
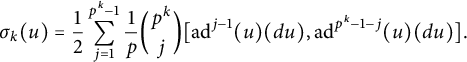 $$ \begin{align*}\sigma_k(u) = \frac{1}{2} \sum_{j=1}^{p^k-1} \frac{1}{p}{p^k \choose j}[\mathrm{ad}^{j-1}(u)(du), \mathrm{ad}^{p^k-1-j}(u)(du)].\end{align*} $$
$$ \begin{align*}\sigma_k(u) = \frac{1}{2} \sum_{j=1}^{p^k-1} \frac{1}{p}{p^k \choose j}[\mathrm{ad}^{j-1}(u)(du), \mathrm{ad}^{p^k-1-j}(u)(du)].\end{align*} $$
From our point of view, the point of the next theorem is that free differential Lie algebras are almost acyclic.
Theorem 2.7 [Reference Cohen, Moore and NeisendorferCMN, Proposition 4.9]
Let V be an acyclic differential
![]() ${\mathbb {Z}/p}$
-vector space. Write
${\mathbb {Z}/p}$
-vector space. Write
![]() $L(V) \cong HL(V) \oplus K$
, for an acyclic module K. If K has an acyclic basis, that is, a basis
$L(V) \cong HL(V) \oplus K$
, for an acyclic module K. If K has an acyclic basis, that is, a basis
where
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
range over index sets
$\beta $
range over index sets
![]() $\mathscr {I}$
and
$\mathscr {I}$
and
![]() $\mathscr {J}$
, respectively, and we have
$\mathscr {J}$
, respectively, and we have
then
![]() $HL(V)$
has a basis
$HL(V)$
has a basis
The theorem implies that the differential on L can be modified slightly to make it acyclic. Namely, define a new differential
![]() $\overline {d} : L(V) \to L(V)$
by setting
$\overline {d} : L(V) \to L(V)$
by setting
![]() $\overline {d} = d$
on K, and letting
$\overline {d} = d$
on K, and letting
![]() $\overline {d}(\tau _k(x_\alpha )) = \sigma _k(x_\alpha )$
,
$\overline {d}(\tau _k(x_\alpha )) = \sigma _k(x_\alpha )$
,
![]() $\overline {d}(\sigma _k(x_\alpha )) = 0$
. Of course,
$\overline {d}(\sigma _k(x_\alpha )) = 0$
. Of course,
![]() $\overline {d}$
will no longer satisfy the Leibniz rule, but it will still be a vector space endomorphism of degree
$\overline {d}$
will no longer satisfy the Leibniz rule, but it will still be a vector space endomorphism of degree
![]() $-1$
which satisfies
$-1$
which satisfies
![]() $\overline {d}^2=0$
.
$\overline {d}^2=0$
.
Now, let
![]() $\overline {B} := \mathrm {Im}(\overline {d}) \subset L$
, and let
$\overline {B} := \mathrm {Im}(\overline {d}) \subset L$
, and let
![]() $\sigma \subset L$
be the subspace spanned by the elements
$\sigma \subset L$
be the subspace spanned by the elements
![]() $\sigma _k(x)$
, for some even degree
$\sigma _k(x)$
, for some even degree
![]() $x \in L$
and
$x \in L$
and
![]() $k \in \mathbb {Z}^+$
. By definition of
$k \in \mathbb {Z}^+$
. By definition of
![]() $\overline {d}$
, we then have the following corollary.
$\overline {d}$
, we then have the following corollary.
Corollary 2.8 We have
![]() $\overline {B}_N \cong B_N \oplus \sigma _N$
.
$\overline {B}_N \cong B_N \oplus \sigma _N$
.
The next lemma justifies the approximation by providing a crude upper bound on
![]() $\sigma _N$
.
$\sigma _N$
.
Lemma 2.9 We have the bound
where
![]() $c_1 = 2(q+2)\varphi ^{\frac {2}{p}}$
.
$c_1 = 2(q+2)\varphi ^{\frac {2}{p}}$
.
Proof By definition,
![]() $\sigma _N$
is spanned by classes
$\sigma _N$
is spanned by classes
![]() $\sigma _k(x_\alpha )$
, and we have
$\sigma _k(x_\alpha )$
, and we have
![]() $\deg (\sigma _k(x_\alpha )) = p^k \deg (x_\alpha )-2$
. We therefore have
$\deg (\sigma _k(x_\alpha )) = p^k \deg (x_\alpha )-2$
. We therefore have
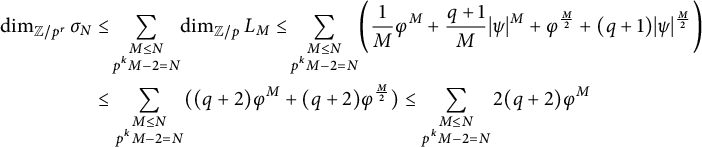 $$ \begin{align*} \dim_{{\mathbb{Z}/p^r}} \sigma_N &\leq \!\sum_{\substack{M \leq N \\ p^k M - 2 =N}}\! \dim_{{\mathbb{Z}/p}} L_M \leq \!\sum_{\substack{M \leq N \\ p^k M - 2 =N}} \!\bigg(\frac{1}{M} \varphi^M + \frac{q+1}{M} |\psi|^{M} + \varphi^{\frac{M}{2}} + (q+1)|\psi|^{\frac{M}{2}}\bigg)\\&\leq \sum_{\substack{M \leq N \\ p^k M - 2 =N}} ( (q+2) \varphi^{M} +(q+2)\varphi^{\frac{M}{2}}) \leq \sum_{\substack{M \leq N \\ p^k M - 2 =N}} 2(q+2) \varphi^{M} \end{align*} $$
$$ \begin{align*} \dim_{{\mathbb{Z}/p^r}} \sigma_N &\leq \!\sum_{\substack{M \leq N \\ p^k M - 2 =N}}\! \dim_{{\mathbb{Z}/p}} L_M \leq \!\sum_{\substack{M \leq N \\ p^k M - 2 =N}} \!\bigg(\frac{1}{M} \varphi^M + \frac{q+1}{M} |\psi|^{M} + \varphi^{\frac{M}{2}} + (q+1)|\psi|^{\frac{M}{2}}\bigg)\\&\leq \sum_{\substack{M \leq N \\ p^k M - 2 =N}} ( (q+2) \varphi^{M} +(q+2)\varphi^{\frac{M}{2}}) \leq \sum_{\substack{M \leq N \\ p^k M - 2 =N}} 2(q+2) \varphi^{M} \end{align*} $$
by Theorem 2.5 (we use
![]() $|\psi | < \varphi $
, and then drop the factors of
$|\psi | < \varphi $
, and then drop the factors of
![]() $\frac {1}{M}$
, to obtain a bound which is strictly increasing even for small M). This summation contains fewer than N terms, and since the value of a given term is increasing in M, the size of the largest term is controlled by
$\frac {1}{M}$
, to obtain a bound which is strictly increasing even for small M). This summation contains fewer than N terms, and since the value of a given term is increasing in M, the size of the largest term is controlled by
![]() $M = \frac {N+2}{p^k} \leq \frac {N+2}{p}$
, so
$M = \frac {N+2}{p^k} \leq \frac {N+2}{p}$
, so
as required.
We next estimate the size of
![]() $\dim \overline {B}_N$
.
$\dim \overline {B}_N$
.
Lemma 2.10 Let
![]() $\psi $
be the second largest (in absolute value) root of
$\psi $
be the second largest (in absolute value) root of
![]() $z^{q+1}-z-1$
after
$z^{q+1}-z-1$
after
![]() $\varphi $
. We have
$\varphi $
. We have
where
![]() $\kappa = (q+1)(1+ \frac {1}{\lvert \psi \rvert })$
and
$\kappa = (q+1)(1+ \frac {1}{\lvert \psi \rvert })$
and
![]() $c_2 = (q+2)(1+ \frac {1}{\sqrt {\varphi }}) \leq 2(q+2)$
.
$c_2 = (q+2)(1+ \frac {1}{\sqrt {\varphi }}) \leq 2(q+2)$
.
Proof Since
![]() $\overline {d}$
is acyclic, we have
$\overline {d}$
is acyclic, we have
![]() $\overline {B}_N = \mathrm {Ker}(\overline {d}: L_N \to L_{N-1})$
. The First Isomorphism Theorem then gives that
$\overline {B}_N = \mathrm {Ker}(\overline {d}: L_N \to L_{N-1})$
. The First Isomorphism Theorem then gives that
![]() , and since
, and since
![]() $\overline {B}_{N-1} \subset L_{N-1}$
, we get
$\overline {B}_{N-1} \subset L_{N-1}$
, we get
Theorem 2.5 gives (since
![]() $g=1$
and
$g=1$
and
![]() $|\psi | < \varphi $
)
$|\psi | < \varphi $
)
and
Combining these inequalities gives the result.
We are now ready to state and prove the main theorem of this subsection.
Theorem 2.11 Let
![]() $L \otimes {\mathbb {Z}/p^r}$
be the free differential graded Lie algebra over
$L \otimes {\mathbb {Z}/p^r}$
be the free differential graded Lie algebra over
![]() ${\mathbb {Z}/p^r}$
on two generators x and y satisfying
${\mathbb {Z}/p^r}$
on two generators x and y satisfying
![]() $y= d x$
. Let
$y= d x$
. Let
![]() $q = \deg (y)$
, so that
$q = \deg (y)$
, so that
![]() $\deg (x) = q+1$
. Let
$\deg (x) = q+1$
. Let
![]() $B = \textrm {Im} (d) \subset L \otimes {\mathbb {Z}/p^r}$
be the submodule of boundaries. Then we have the bound
$B = \textrm {Im} (d) \subset L \otimes {\mathbb {Z}/p^r}$
be the submodule of boundaries. Then we have the bound
where
![]() $\varphi> 1$
is the unique positive real root of the degree n polynomial
$\varphi> 1$
is the unique positive real root of the degree n polynomial
![]() $\psi $
is the second largest root in absolute value,
$\psi $
is the second largest root in absolute value,
![]() $c= 2(q+2)(1+ \varphi )$
, and
$c= 2(q+2)(1+ \varphi )$
, and
![]() $\kappa = (q+1)(1+ \frac {1}{\lvert \psi \rvert })$
. We have the bounds
$\kappa = (q+1)(1+ \frac {1}{\lvert \psi \rvert })$
. We have the bounds
![]() $2^{\frac {1}{q+1}}< \varphi < 1 + \frac {1}{q}$
.
$2^{\frac {1}{q+1}}< \varphi < 1 + \frac {1}{q}$
.
3 Topology
3.1 Homology
We now prove Theorem 1.2.
Proof of Theorem 1.2
In the proof of Theorem 1.5 of [Reference BoydeBoy2] it is shown that there exists a commutative diagram (the details of the definitions of the maps need not concern us here):

In the diagram,
![]() $L(x,dx) \otimes {\mathbb {Z}/p^s}$
is the free differential Lie algebra (with
$L(x,dx) \otimes {\mathbb {Z}/p^s}$
is the free differential Lie algebra (with
![]() $dx=y$
,
$dx=y$
,
![]() $\deg (x) = q+1$
,
$\deg (x) = q+1$
,
![]() $\deg (y) = q$
). The top-left entry
$\deg (y) = q$
). The top-left entry
![]() $L'(x,dx)$
is a certain module over
$L'(x,dx)$
is a certain module over
![]() ${\mathbb {Z}/p^r}$
which is “almost” a free differential Lie algebra.
${\mathbb {Z}/p^r}$
which is “almost” a free differential Lie algebra.
We now use various results from [Reference BoydeBoy2]. By the remark immediately before Corollary 8.9 of that paper, the image of the left-hand vertical map
![]() $\theta \circ d$
is precisely the module of boundaries
$\theta \circ d$
is precisely the module of boundaries
![]() $BL$
. By Lemma 9.6, the map
$BL$
. By Lemma 9.6, the map
![]() $\Phi _H^{r,s}$
is an injection, and the induced map on homology,
$\Phi _H^{r,s}$
is an injection, and the induced map on homology,
![]() $(\Omega \mu )_*$
, is an injection by assumption. It follows by commutativity that the image in the bottom-right,
$(\Omega \mu )_*$
, is an injection by assumption. It follows by commutativity that the image in the bottom-right,
![]() $I := \mathrm {Im}(h \circ \rho ^s \circ (\Omega \mu )_* \circ \beta ^r \circ \Phi _\pi ^{r,r})$
, is isomorphic to
$I := \mathrm {Im}(h \circ \rho ^s \circ (\Omega \mu )_* \circ \beta ^r \circ \Phi _\pi ^{r,r})$
, is isomorphic to
![]() $BL$
.
$BL$
.
The point is then that the homotopy groups of Y surject onto I, hence must be just as large. More precisely, we obtain that
by Lemma 7.8 of [Reference BoydeBoy2] applied to the part of the diagram consisting of

The loops on Y is just a degree shift on homotopy groups, so the result follows by Theorem 2.11 of this paper.
3.2 K-theory
In this subsection, the following linear inequality relating integers j and N will arise often. We will refer to it as Condition (*). Here, X is a fixed space,
![]() $\mathrm {conn}(X)$
is the p-local connectivity of X, and
$\mathrm {conn}(X)$
is the p-local connectivity of X, and
![]() $\dim (X)$
is the largest d for which
$\dim (X)$
is the largest d for which
![]() $H^d(X; \mathbb {Q}) \neq 0$
.
$H^d(X; \mathbb {Q}) \neq 0$
.
 $$ \begin{align} j> \frac{1}{2(p-1)}\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}-1\right)N+\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}\right)(\mathrm{conn}(X)+2)-1). \end{align} $$
$$ \begin{align} j> \frac{1}{2(p-1)}\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}-1\right)N+\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}\right)(\mathrm{conn}(X)+2)-1). \end{align} $$
The next theorem refines and slightly generalizes Theorem 1.4 of [Reference BoydeBoy1].
Theorem 3.1 Let p be an odd prime, and let X be a path connected space having the p-local homotopy type of a finite
![]() $CW$
-complex. Suppose that there exists a map
$CW$
-complex. Suppose that there exists a map
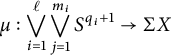 $$ \begin{align*}\mu : \bigvee_{i=1}^\ell \bigvee_{j=1}^{m_i} S^{q_i+1} \to \Sigma X\end{align*} $$
$$ \begin{align*}\mu : \bigvee_{i=1}^\ell \bigvee_{j=1}^{m_i} S^{q_i+1} \to \Sigma X\end{align*} $$
with
![]() $1 \leq q_1 < q_2 < \dots < q_\ell $
, such that the map
$1 \leq q_1 < q_2 < \dots < q_\ell $
, such that the map
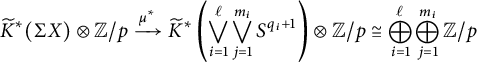 $$ \begin{align*}\widetilde{K}^*(\Sigma X) \otimes {\mathbb{Z}/p} \xrightarrow{\mu^*} \widetilde{K}^*\left(\bigvee_{i=1}^\ell \bigvee_{j=1}^{m_i} S^{q_i+1}\right) \otimes {\mathbb{Z}/p} \cong \bigoplus_{i=1}^\ell \bigoplus_{j=1}^{m_i} {\mathbb{Z}/p}\end{align*} $$
$$ \begin{align*}\widetilde{K}^*(\Sigma X) \otimes {\mathbb{Z}/p} \xrightarrow{\mu^*} \widetilde{K}^*\left(\bigvee_{i=1}^\ell \bigvee_{j=1}^{m_i} S^{q_i+1}\right) \otimes {\mathbb{Z}/p} \cong \bigoplus_{i=1}^\ell \bigoplus_{j=1}^{m_i} {\mathbb{Z}/p}\end{align*} $$
is a surjection.
Then, for any N, j such that
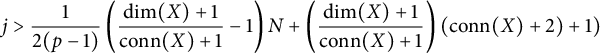 $$ \begin{align*}j> \frac{1}{2(p-1)}\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}-1\right)N+\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}\right)(\mathrm{conn}(X)+2)+1)\end{align*} $$
$$ \begin{align*}j> \frac{1}{2(p-1)}\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}-1\right)N+\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}\right)(\mathrm{conn}(X)+2)+1)\end{align*} $$
(i.e., such that Condition (*) holds) we have
where L is as in Theorem 2.5 (the free Lie algebra on generators corresponding to the spheres in the wedge),
![]() $\mathrm {conn}(X)$
is the p-local connectivity of X,
$\mathrm {conn}(X)$
is the p-local connectivity of X,
![]() $\dim (X)$
is the dimension of X as measured by rational cohomology, and
$\dim (X)$
is the dimension of X as measured by rational cohomology, and
![]() $g=\gcd (q_1, \dots , q_\ell )$
.
$g=\gcd (q_1, \dots , q_\ell )$
.
Proof This is essentially a more careful restatement of Theorem 1.4 of [Reference BoydeBoy1]. Some of the arguments of that paper are given only for a wedge of two spheres, but all of them apply verbatim to any finite wedge. Construction 7.15 of that paper gives (in slightly different language) a diagram of the form

for some module
![]() $E_*$
whose definition need not concern us.
$E_*$
whose definition need not concern us.
Theorem 7.16 of that paper then says that the horizontal map is an injection, and hence, just as in the proof of Theorem 1.2, the conclusion holds, provided that there exists some
![]() $\ell \in \mathbb {Z}_{\geq 0}$
such that
$\ell \in \mathbb {Z}_{\geq 0}$
such that
![]() $\ell ^{j(p-1)+\frac {N-1}{2}}> \lambda _\ell ^k$
, for an integer k which may be taken to be
$\ell ^{j(p-1)+\frac {N-1}{2}}> \lambda _\ell ^k$
, for an integer k which may be taken to be
![]() $\lceil \frac {N+1}{\mathrm{{conn}(X)+1}} \rceil $
, where
$\lceil \frac {N+1}{\mathrm{{conn}(X)+1}} \rceil $
, where
![]() $\lambda _\ell $
is the largest eigenvalue of the Adams operation
$\lambda _\ell $
is the largest eigenvalue of the Adams operation
![]() $\psi ^\ell $
on
$\psi ^\ell $
on
![]() $\widetilde {K}^*(X)$
.
$\widetilde {K}^*(X)$
.
The inequality therefore rearranges to
![]() $j> \frac {1}{p-1}\left(\lceil \frac {N+1}{\mathrm{{conn}(X)+1}} \rceil \frac {\log (\lambda _\ell )}{\log (\ell )}- \frac {N-1}{2}\right).$
In [Reference Adams and AtiyahAA], it is shown that
$j> \frac {1}{p-1}\left(\lceil \frac {N+1}{\mathrm{{conn}(X)+1}} \rceil \frac {\log (\lambda _\ell )}{\log (\ell )}- \frac {N-1}{2}\right).$
In [Reference Adams and AtiyahAA], it is shown that
![]() $\lambda _\ell = \ell ^{\lceil \frac {\dim (X)}{2} \rceil }$
, so we may simplify to
$\lambda _\ell = \ell ^{\lceil \frac {\dim (X)}{2} \rceil }$
, so we may simplify to
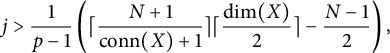 $$ \begin{align*}j> \frac{1}{p-1}\left(\lceil \frac{N+1}{\mathrm{conn}(X)+1} \rceil \lceil \frac{\dim(X)}{2} \rceil - \frac{N-1}{2}\right),\end{align*} $$
$$ \begin{align*}j> \frac{1}{p-1}\left(\lceil \frac{N+1}{\mathrm{conn}(X)+1} \rceil \lceil \frac{\dim(X)}{2} \rceil - \frac{N-1}{2}\right),\end{align*} $$
which is implied by Condition (*), using the fact that, for an integer
![]() $z,$
we have
$z,$
we have
![]() $\lceil \frac {z}{2}\rceil \leq \frac {z+1}{2}$
. This completes the proof.
$\lceil \frac {z}{2}\rceil \leq \frac {z+1}{2}$
. This completes the proof.
The next step is a simple application of Bezout’s Lemma.
Lemma 3.2 Let
![]() $\alpha , \beta \in \mathbb {Z}$
with
$\alpha , \beta \in \mathbb {Z}$
with
![]() $\alpha , \beta> 0$
, and let
$\alpha , \beta> 0$
, and let
![]() $a,b \in \mathbb {R}$
with
$a,b \in \mathbb {R}$
with
![]() $a>0$
. Consider the set of linear combinations
$a>0$
. Consider the set of linear combinations
Let
![]() $g' = \gcd (\alpha , \beta )$
. There exists a constant B, independent of n, such that for each n, all multiples of
$g' = \gcd (\alpha , \beta )$
. There exists a constant B, independent of n, such that for each n, all multiples of
![]() $g'$
which are at least
$g'$
which are at least
![]() $\min (S_n)+B$
are contained in
$\min (S_n)+B$
are contained in
![]() $S_i$
for some i which is close to n in the sense that
$S_i$
for some i which is close to n in the sense that
![]() $n \leq i < n+\beta (\beta + 1)$
. Furthermore, there exists a suitable B satisfying the bound
$n \leq i < n+\beta (\beta + 1)$
. Furthermore, there exists a suitable B satisfying the bound
![]() $B \leq \beta ^2 (\alpha + a (1 + \beta ))+ \beta $
, and hence, any
$B \leq \beta ^2 (\alpha + a (1 + \beta ))+ \beta $
, and hence, any
![]() $B \geq \beta ^2 (\alpha + a (1 + \beta )) + \beta $
is also suitable.
$B \geq \beta ^2 (\alpha + a (1 + \beta )) + \beta $
is also suitable.
If
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are fixed (and j and n are allowed to vary), then it is a familiar fact that the set of integers of the form
$\beta $
are fixed (and j and n are allowed to vary), then it is a familiar fact that the set of integers of the form
![]() $n \alpha + j \beta $
is precisely the multiples of
$n \alpha + j \beta $
is precisely the multiples of
![]() $g'$
. Our statement is essentially just a more complicated version of this.
$g'$
. Our statement is essentially just a more complicated version of this.
Proof First, consider the set
![]() $S_n$
. If an integer j satisfies
$S_n$
. If an integer j satisfies
![]() $j> an+b$
(so that
$j> an+b$
(so that
![]() $n \alpha + j \beta $
lies in
$n \alpha + j \beta $
lies in
![]() $S_n$
), then increasing the parameter j certainly does not violate this condition. Therefore, adding a positive multiple of
$S_n$
), then increasing the parameter j certainly does not violate this condition. Therefore, adding a positive multiple of
![]() $\beta $
to an element of
$\beta $
to an element of
![]() $S_n$
yields another element of
$S_n$
yields another element of
![]() $S_n$
. In particular,
$S_n$
. In particular,
![]() $S_n$
already contains all integers which are obtained by increasing
$S_n$
already contains all integers which are obtained by increasing
![]() $\min (S_n)$
by a multiple of
$\min (S_n)$
by a multiple of
![]() $\beta $
. These values are by construction linear combinations of
$\beta $
. These values are by construction linear combinations of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, so they are all multiples of
$\beta $
, so they are all multiples of
![]() $g'$
.
$g'$
.
It remains, then, to show that by increasing n “just a little,” we can “fill in” the intermediate multiples of
![]() $g'$
. We will do so by “giving ourselves enough room,” in the sense of an ad-hoc quantity which we now define. Define the excess of
$g'$
. We will do so by “giving ourselves enough room,” in the sense of an ad-hoc quantity which we now define. Define the excess of
![]() $(j,n)$
to be
$(j,n)$
to be
![]() $j - (an+b)$
. The condition
$j - (an+b)$
. The condition
![]() $j> an+b$
is then equivalent to
$j> an+b$
is then equivalent to
![]() $(j,n)$
having positive excess.
$(j,n)$
having positive excess.
By Bezout’s Lemma, let
![]() $x> 0 $
and
$x> 0 $
and
![]() $y \geq 0$
be the solution of
$y \geq 0$
be the solution of
![]() $x \alpha - y \beta = g'$
with smallest nonnegative y. We have
$x \alpha - y \beta = g'$
with smallest nonnegative y. We have
![]() $0 < x \leq \frac {g'}{\alpha }+ \beta $
and
$0 < x \leq \frac {g'}{\alpha }+ \beta $
and
![]() $0 \leq y \leq \alpha $
. Given an expression
$0 \leq y \leq \alpha $
. Given an expression
![]() $n \alpha + j \beta $
, replacing n by
$n \alpha + j \beta $
, replacing n by
![]() $n+x$
and j by
$n+x$
and j by
![]() $j-y$
increases the value of the linear combination
$j-y$
increases the value of the linear combination
![]() $n \alpha + j \beta $
by
$n \alpha + j \beta $
by
![]() $g'$
, and reduces the excess by the constant
$g'$
, and reduces the excess by the constant
![]() $ax+y$
. We will use this to fill in the remaining multiples of
$ax+y$
. We will use this to fill in the remaining multiples of
![]() $g'$
.
$g'$
.
Let
![]() $j_0$
realize the smallest member of
$j_0$
realize the smallest member of
![]() $S_n$
, in the sense that
$S_n$
, in the sense that
![]() $\min (S_n) = n \alpha + j_0 \beta $
. Now, take any
$\min (S_n) = n \alpha + j_0 \beta $
. Now, take any
![]() $j \geq j_0 + \frac {\beta }{g'}(ax+y)$
. The excess of
$j \geq j_0 + \frac {\beta }{g'}(ax+y)$
. The excess of
![]() $(n,j_0)$
was positive, so the excess of
$(n,j_0)$
was positive, so the excess of
![]() $(n,j)$
is greater than
$(n,j)$
is greater than
![]() $\frac {\beta }{g'}(ax+y)$
. We may therefore add
$\frac {\beta }{g'}(ax+y)$
. We may therefore add
![]() $(x,-y)$
to
$(x,-y)$
to
![]() $(n,j)$
up to
$(n,j)$
up to
![]() $\frac {\beta }{g'}$
times while retaining a positive excess (and keeping j nonnegative). This shows that all multiples of
$\frac {\beta }{g'}$
times while retaining a positive excess (and keeping j nonnegative). This shows that all multiples of
![]() $g'$
lying between
$g'$
lying between
![]() $n \alpha + j \beta $
and
$n \alpha + j \beta $
and
![]() $n \alpha + (j+1) \beta $
are contained in
$n \alpha + (j+1) \beta $
are contained in
![]() $S_i$
for some i satisfying
$S_i$
for some i satisfying
![]() $n \leq i < n+ \frac {\beta }{g'} x$
, and we may perform this procedure for any
$n \leq i < n+ \frac {\beta }{g'} x$
, and we may perform this procedure for any
![]() $j \geq j_0 + \frac {\beta }{g'}(ax+y)$
. In particular, all multiples of
$j \geq j_0 + \frac {\beta }{g'}(ax+y)$
. In particular, all multiples of
![]() $g'$
which are at least
$g'$
which are at least
![]() $\min (S_n)+\beta (\frac {\beta }{g'}(ax+y)+1)$
are contained in
$\min (S_n)+\beta (\frac {\beta }{g'}(ax+y)+1)$
are contained in
![]() $S_i$
for some i satisfying
$S_i$
for some i satisfying
![]() $n \leq i < n+ \frac {\beta }{g'} x$
. The extra
$n \leq i < n+ \frac {\beta }{g'} x$
. The extra
![]() $+1$
here is because j must be an integer. This is essentially the result, and it remains only to establish that we may take the constants as in the statement.
$+1$
here is because j must be an integer. This is essentially the result, and it remains only to establish that we may take the constants as in the statement.
Now,
![]() $\frac {g'}{\alpha } \leq 1$
, so
$\frac {g'}{\alpha } \leq 1$
, so
![]() $x \leq 1 + \beta $
, and
$x \leq 1 + \beta $
, and
![]() $\frac {\beta }{g'}x \leq \beta x \leq \beta (1+ \beta )$
. This establishes the bounds on i. The bound on B follows from these inequalities, together with
$\frac {\beta }{g'}x \leq \beta x \leq \beta (1+ \beta )$
. This establishes the bounds on i. The bound on B follows from these inequalities, together with
![]() $y \leq \alpha $
. This completes the proof.
$y \leq \alpha $
. This completes the proof.
We now prove the following strong version of Theorem 1.7.
Theorem 3.3 Let p be an odd prime, and let X be a path connected space having the p-local homotopy type of a finite
![]() $CW$
-complex. Suppose that there exists a map
$CW$
-complex. Suppose that there exists a map
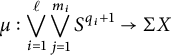 $$ \begin{align*}\mu : \bigvee_{i=1}^\ell \bigvee_{j=1}^{m_i} S^{q_i+1} \to \Sigma X\end{align*} $$
$$ \begin{align*}\mu : \bigvee_{i=1}^\ell \bigvee_{j=1}^{m_i} S^{q_i+1} \to \Sigma X\end{align*} $$
with
![]() $1 \leq q_1 < q_2 < \dots < q_\ell $
, such that the map
$1 \leq q_1 < q_2 < \dots < q_\ell $
, such that the map
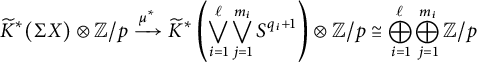 $$ \begin{align*}\widetilde{K}^*(\Sigma X) \otimes {\mathbb{Z}/p} \xrightarrow{\mu^*} \widetilde{K}^*\left(\bigvee_{i=1}^\ell \bigvee_{j=1}^{m_i} S^{q_i+1}\right) \otimes {\mathbb{Z}/p} \cong \bigoplus_{i=1}^\ell \bigoplus_{j=1}^{m_i} {\mathbb{Z}/p}\end{align*} $$
$$ \begin{align*}\widetilde{K}^*(\Sigma X) \otimes {\mathbb{Z}/p} \xrightarrow{\mu^*} \widetilde{K}^*\left(\bigvee_{i=1}^\ell \bigvee_{j=1}^{m_i} S^{q_i+1}\right) \otimes {\mathbb{Z}/p} \cong \bigoplus_{i=1}^\ell \bigoplus_{j=1}^{m_i} {\mathbb{Z}/p}\end{align*} $$
is a surjection.
Then there exist constants
![]() $\tau ,\theta>0$
such that for multiples
$\tau ,\theta>0$
such that for multiples
![]() $M=mg'$
of
$M=mg'$
of
we have
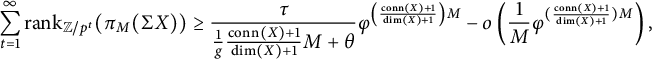 $$ \begin{align*}\sum_{t=1}^\infty \mathrm{rank}_{{\mathbb{Z}/p^t}}(\pi_{M}(\Sigma X))\geq \frac{\tau}{\frac{1}{g}\frac{\mathrm{conn}(X)+1}{\dim(X)+1}M + \theta} \varphi^{\left(\frac{\mathrm{conn}(X)+1}{\dim(X)+1}\right)M}-o\left(\frac{1}{M}\varphi^{(\frac{\mathrm{conn}(X)+1}{\dim(X)+1})M}\right),\end{align*} $$
$$ \begin{align*}\sum_{t=1}^\infty \mathrm{rank}_{{\mathbb{Z}/p^t}}(\pi_{M}(\Sigma X))\geq \frac{\tau}{\frac{1}{g}\frac{\mathrm{conn}(X)+1}{\dim(X)+1}M + \theta} \varphi^{\left(\frac{\mathrm{conn}(X)+1}{\dim(X)+1}\right)M}-o\left(\frac{1}{M}\varphi^{(\frac{\mathrm{conn}(X)+1}{\dim(X)+1})M}\right),\end{align*} $$
where
![]() $\varphi $
is the unique positive real root of the degree
$\varphi $
is the unique positive real root of the degree
![]() $q_\ell $
polynomial
$q_\ell $
polynomial
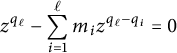 $$ \begin{align*}z^{q_\ell} - \sum_{i=1}^\ell m_i z^{q_\ell - q_i} = 0\end{align*} $$
$$ \begin{align*}z^{q_\ell} - \sum_{i=1}^\ell m_i z^{q_\ell - q_i} = 0\end{align*} $$
(in particular,
![]() $\varphi \geq (\sum _{i=1}^\ell m_i)^{\frac {1}{q_\ell }} = (\sum _{i=1}^\ell m_i)^{\frac {1}{\max (q_1, \dots , q_\ell )}}$
),
$\varphi \geq (\sum _{i=1}^\ell m_i)^{\frac {1}{q_\ell }} = (\sum _{i=1}^\ell m_i)^{\frac {1}{\max (q_1, \dots , q_\ell )}}$
),
![]() $\mathrm {conn}(X)$
is the p-local connectivity of X,
$\mathrm {conn}(X)$
is the p-local connectivity of X,
![]() $\dim (X)$
is the rational cohomological dimension of X, and
$\dim (X)$
is the rational cohomological dimension of X, and
![]() $g=\gcd (q_1, \dots , q_\ell )$
.
$g=\gcd (q_1, \dots , q_\ell )$
.
Proof Let
![]() $S_n$
be the set of dimensions M for which Theorem 3.1 tells us that
$S_n$
be the set of dimensions M for which Theorem 3.1 tells us that
![]() $\sum _{t=1}^\infty \mathrm {rank}_{{\mathbb {Z}/p^t}}(\pi _{M}(\Sigma X)) \geq \dim _{{\mathbb {Z}/p}}(L_{ng} \otimes {\mathbb {Z}/p^r})$
. That is,
$\sum _{t=1}^\infty \mathrm {rank}_{{\mathbb {Z}/p^t}}(\pi _{M}(\Sigma X)) \geq \dim _{{\mathbb {Z}/p}}(L_{ng} \otimes {\mathbb {Z}/p^r})$
. That is,
where
![]() $a=\frac {g}{2(p-1)}\left(\frac {\dim (X)+1}{\mathrm{{conn}(X)+1}}-1\right)$
and
$a=\frac {g}{2(p-1)}\left(\frac {\dim (X)+1}{\mathrm{{conn}(X)+1}}-1\right)$
and
![]() $b = \frac {1}{2(p-1)}\left(\frac {\dim (X)+1}{\mathrm{{conn}(X)+1}}(\mathrm {conn}(X)+2)+1\right)$
.
$b = \frac {1}{2(p-1)}\left(\frac {\dim (X)+1}{\mathrm{{conn}(X)+1}}(\mathrm {conn}(X)+2)+1\right)$
.
By Lemma 3.2, there exists a constant B, which may be taken to be
![]() $4(p-1)^2 (g + a (1 + 2(p-1)))+ 2(p-1)$
such that, for each
$4(p-1)^2 (g + a (1 + 2(p-1)))+ 2(p-1)$
such that, for each
![]() $M=mg' \geq \min (S_n) + B$
, we have
$M=mg' \geq \min (S_n) + B$
, we have
![]() $\sum _{t=1}^\infty \mathrm {rank}_{{\mathbb {Z}/p^t}}(\pi _{M}(\Sigma X)) \geq \dim _{{\mathbb {Z}/p}}(L_{ig} \otimes {\mathbb {Z}/p^r})$
for some i with
$\sum _{t=1}^\infty \mathrm {rank}_{{\mathbb {Z}/p^t}}(\pi _{M}(\Sigma X)) \geq \dim _{{\mathbb {Z}/p}}(L_{ig} \otimes {\mathbb {Z}/p^r})$
for some i with
![]() $n \leq i < n + 8(p-1)^2$
. By Theorem 2.5,
$n \leq i < n + 8(p-1)^2$
. By Theorem 2.5,
Regardless of whether
![]() $|\psi |> 1$
, we have
$|\psi |> 1$
, we have
![]() $|\psi |^{\frac {ig}{2}} < 1 + |\psi |^{ig} < 2 + |\psi |^{(n+8(p-1)^2)g}$
, so the inequality implies
$|\psi |^{\frac {ig}{2}} < 1 + |\psi |^{ig} < 2 + |\psi |^{(n+8(p-1)^2)g}$
, so the inequality implies
It remains only to find the dependency of n upon M, and convert this expression into one in terms of M.
The smallest member of
![]() $S_n$
is obtained by taking the smallest
$S_n$
is obtained by taking the smallest
![]() $j=j_n$
satisfying Condition (*). By definition
$j=j_n$
satisfying Condition (*). By definition
![]() $j_n$
is the smallest integer with
$j_n$
is the smallest integer with
![]() $j_n> an+b$
, so
$j_n> an+b$
, so
![]() $j_n \leq an+b + 1$
. Thus,
$j_n \leq an+b + 1$
. Thus,
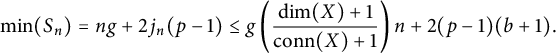 $$ \begin{align*}\min(S_n)=ng+2j_n(p-1) \leq g\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}\right)n+2(p-1)(b+1).\end{align*} $$
$$ \begin{align*}\min(S_n)=ng+2j_n(p-1) \leq g\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}\right)n+2(p-1)(b+1).\end{align*} $$
To conclude, for given
![]() $M=mg'$
, let
$M=mg'$
, let
![]() $n=n(M)$
be the largest nonnegative integer satisfying
$n=n(M)$
be the largest nonnegative integer satisfying
![]() $M \geq g(\frac {\dim (X)+1}{\mathrm{{conn}(X)+1}})n+2(p-1)(b+1)+B$
. Rearranging gives
$M \geq g(\frac {\dim (X)+1}{\mathrm{{conn}(X)+1}})n+2(p-1)(b+1)+B$
. Rearranging gives
![]() $n \leq \frac {M-(2(p-1)(b+1)+B)}{g} (\frac {\mathrm{{conn}(X)+1}}{\dim (X)+1})$
. Since n is the largest such integer, it is at least one less than this expression. Applying the bounds
$n \leq \frac {M-(2(p-1)(b+1)+B)}{g} (\frac {\mathrm{{conn}(X)+1}}{\dim (X)+1})$
. Since n is the largest such integer, it is at least one less than this expression. Applying the bounds
![]() $n \leq i < n + 8(p-1)^2$
, now gives that
$n \leq i < n + 8(p-1)^2$
, now gives that
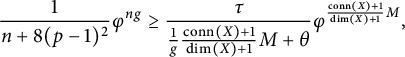 $$ \begin{align*}\frac{1}{n+8(p-1)^2} \varphi^{ng} \geq \frac{\tau}{\frac{1}{g}\frac{\mathrm{conn}(X)+1}{\dim(X)+1}M + \theta} \varphi^{\frac{\mathrm{conn}(X)+1}{\dim(X)+1}M},\end{align*} $$
$$ \begin{align*}\frac{1}{n+8(p-1)^2} \varphi^{ng} \geq \frac{\tau}{\frac{1}{g}\frac{\mathrm{conn}(X)+1}{\dim(X)+1}M + \theta} \varphi^{\frac{\mathrm{conn}(X)+1}{\dim(X)+1}M},\end{align*} $$
for constants
![]() $\theta $
and
$\theta $
and
![]() $\tau $
, and shows that the other terms of the inequality † are
$\tau $
, and shows that the other terms of the inequality † are
![]() $o(\frac {1}{M}\varphi ^{\frac {\mathrm{{conn}(X)+1}}{\dim (X)+1}})$
, as required.
$o(\frac {1}{M}\varphi ^{\frac {\mathrm{{conn}(X)+1}}{\dim (X)+1}})$
, as required.
Remark 3.4 In this remark, we give the constants and error term for Theorem 3.3, and collect the other constants appearing in the proof.
The positive integers
![]() $q_1, \dots , q_\ell $
are given in the hypotheses of Theorem 3.3 (or Theorem 2.5). Then
$q_1, \dots , q_\ell $
are given in the hypotheses of Theorem 3.3 (or Theorem 2.5). Then
and
The space X and the prime
![]() $p \neq 2$
are given in the hypotheses of Theorem 3.3,
$p \neq 2$
are given in the hypotheses of Theorem 3.3,
![]() $\dim (X)$
is the rational dimension of X, and
$\dim (X)$
is the rational dimension of X, and
![]() $\mathrm {conn}(X)$
is its p-local connectivity.
$\mathrm {conn}(X)$
is its p-local connectivity.
The constants appearing in the proof of Theorem 3.3 are then
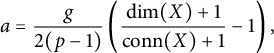 $$ \begin{align*}a=\frac{g}{2(p-1)}\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}-1\right),\end{align*} $$
$$ \begin{align*}a=\frac{g}{2(p-1)}\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}-1\right),\end{align*} $$
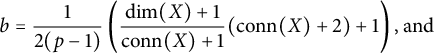 $$ \begin{align*}b = \frac{1}{2(p-1)}\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}(\mathrm{conn}(X)+2)+1\right) \textrm{, and} \end{align*} $$
$$ \begin{align*}b = \frac{1}{2(p-1)}\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}(\mathrm{conn}(X)+2)+1\right) \textrm{, and} \end{align*} $$
It then follows from the proof that the constants
![]() $\theta $
and
$\theta $
and
![]() $\tau $
of Theorem 3.3 may be taken as follows:
$\tau $
of Theorem 3.3 may be taken as follows:
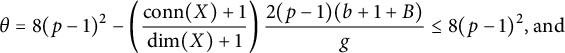 $$ \begin{align*}\theta = 8(p-1)^2 - \left(\frac{\mathrm{conn}(X)+1}{\dim(X)+1}\right)\frac{2(p-1)(b+1+B)}{g} \leq 8(p-1)^2 \textrm{, and}\end{align*} $$
$$ \begin{align*}\theta = 8(p-1)^2 - \left(\frac{\mathrm{conn}(X)+1}{\dim(X)+1}\right)\frac{2(p-1)(b+1+B)}{g} \leq 8(p-1)^2 \textrm{, and}\end{align*} $$
where, as usual,
![]() $\varphi $
is the unique positive root of the polynomial
$\varphi $
is the unique positive root of the polynomial
![]() $P(z) = z^{q_\ell } - \sum _{i=1}^\ell m_i z^{q_\ell - q_i} = 0.$
$P(z) = z^{q_\ell } - \sum _{i=1}^\ell m_i z^{q_\ell - q_i} = 0.$
The error term in the bound Theorem 3.3 is an unpleasant expression, and we restrict ourselves to noting that it is negative, and of the form
for constants
![]() $c_i$
, where
$c_i$
, where
![]() $\psi $
is the second largest root of
$\psi $
is the second largest root of
![]() $P(z)$
, in absolute value. The deviation of the bound from being a pleasant expression is therefore exponential in bases determined by the roots of
$P(z)$
, in absolute value. The deviation of the bound from being a pleasant expression is therefore exponential in bases determined by the roots of
![]() $P(z)$
.
$P(z)$
.
Acknowledgment
This paper was written while G.B. was an EPSRC Doctoral Prize postdoc at the University of Southampton. He would like to thank Naomi Andrew, George Davenport, Lawk Mineh, and Stephen Theriault for their many helpful conversations. Both authors would like to thank the referee for their careful proofreading and numerous helpful comments, both on technical points and on exposition.




