Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-10T21:28:43.735Z Has data issue: false hasContentIssue false
  • English
  • Français

Surgeries on iterated torus knots bounding rational homology 4-balls

Part of: Curves Differential topology

Published online by Cambridge University Press:  23 June 2023

Lisa Lokteva
Lisa Lokteva*
Affiliation:
School of Mathematics and Statistics, University of Glasgow, Glasgow, Scotland, UK([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that all large enough positive integral surgeries on algebraic knots bound a 4-manifold with a negative definite plumbing tree, which we describe explicitly. Then we apply the lattice embedding obstruction coming from Donaldson’s Theorem to classify the ones of the form 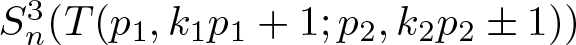$S^3_n(T(p_1,k_1p_1+1; p_2, k_2p_2\pm 1))$ that also bound rational homology 4-balls.

Keywords

rational ballslattice embeddingssurgeries on iterated torus knotssurgeries on algebraic knotsplumbing graphnegative definite fillingalgebraic knotrational homology 4-ballcuspidal singularity

MSC classification

Primary: 57R65: Surgery and handlebodies 14H20: Singularities, local rings
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 2 , May 2023 , pp. 557 - 578
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aceto, P., Rational homology cobordisms of plumbed manifolds, Algebr. Geom. Topol. 20(3) (2020), 1073–1126.10.2140/agt.2020.20.1073CrossRefGoogle Scholar
Aceto, P. and Golla, M., Dehn surgeries and rational homology balls, Algebr. Geom. Topol. 17(1) (2017), 487–527.10.2140/agt.2017.17.487CrossRefGoogle Scholar
Aceto, P., Golla, M., Larson, K. and Lecuona, A. G., Surgeries on torus knots, rational balls, and cabling. arXiv e-prints, arXiv:2008.06760 (2020).Google Scholar
Bodnár, J., Classification of rational unicuspidal curves with two Newton pairs, Acta Math. Hungar. 148(2) (2016), 294–299.10.1007/s10474-015-0576-8CrossRefGoogle Scholar
Casson, A. J. and Harer, J. L., Some homology lens spaces which bound rational homology balls, Pacific J. Math. 96(1) (1981), 23–36.10.2140/pjm.1981.96.23CrossRefGoogle Scholar
Donaldson, S. K., An application of gauge theory to four dimensional topology, J. Differential Geom. 18(2) (1983), 279–315.10.4310/jdg/1214437665CrossRefGoogle Scholar
Eisenbud, D. and Neumann, W., Three-dimensional link theory and invariants of plane curve singularities, in Annals of Mathematics Studies, Volume 110 (Princeton University Press, Princeton, NJ, 1985).Google Scholar
Gordon, C. M., Dehn surgery and satellite knots, Trans. Amer. Math. Soc. 275(2) (1983), 687–708.10.1090/S0002-9947-1983-0682725-0CrossRefGoogle Scholar
Kirby, R., Problems in low-dimensional topology, in Geometric Topology, Volume 2, (American Mathematical Society, Providence, R.I, 1997). AMS/IP Stud. Adv.Math.Google Scholar
Lecuona, A. G., On the slice-ribbon conjecture for Montesinos knots, Trans. Amer. Math. Soc. 364(1) (2012), 233–285.10.1090/S0002-9947-2011-05385-7CrossRefGoogle Scholar
Lecuona, A. G. and Lisca, P., Stein fillable Seifert fibered 3-manifolds, Algebr. Geom. Topol. 11(2) (2011), 625–642.10.2140/agt.2011.11.625CrossRefGoogle Scholar
Lisca, P., Lens spaces, rational balls and the ribbon conjecture, Geom. Topol. 11 (2007), 429–472.10.2140/gt.2007.11.429CrossRefGoogle Scholar
Lisca, P., Sums of lens spaces bounding rational balls, Algebr. Geom. Topol. 7 (2007), 2141–2164.10.2140/agt.2007.7.2141CrossRefGoogle Scholar
Neumann, W. D., A calculus for plumbing applied to the topology of complex surface singularities and degenerating complex curves, Trans. Amer. Math. Soc. 268(2) (1981), 299–344.10.1090/S0002-9947-1981-0632532-8CrossRefGoogle Scholar
Neumann, W. D., On bilinear forms represented by trees, Bull. Aust. Math. Soc. 40(2) (1989), 303–321.10.1017/S0004972700004391CrossRefGoogle Scholar
Owens, B. and Strle, S., Dehn surgeries and negative-definite four-manifolds, Selecta Math. (N.S.) 18(4) (2012), 839–854.10.1007/s00029-012-0086-2CrossRefGoogle Scholar
Riemenschneider, O., Deformationen von Quotientensingularitäten (nach zyklischen Gruppen), Math. Ann. 209 (1974), 211–248.10.1007/BF01351850CrossRefGoogle Scholar
Simone, J., Classification of torus bundles that bound rational homology circles. arXiv:2006.14986 (2020).Google Scholar
Simone, J., Using rational homology circles to construct rational homology balls, Topology Appl. 291 (2021), .10.1016/j.topol.2021.107626CrossRefGoogle Scholar