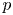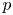1. Introduction
Let ![]() $p$ be a prime number,
$p$ be a prime number, ![]() $\mathbb {A}_{\mathbb {Q}}^{\infty }$ the finite adèles of
$\mathbb {A}_{\mathbb {Q}}^{\infty }$ the finite adèles of ![]() $\mathbb {Q}$,
$\mathbb {Q}$, ![]() $\mathbb {A}^{\infty,p}_{\mathbb {Q}}$ the finite prime-to-
$\mathbb {A}^{\infty,p}_{\mathbb {Q}}$ the finite prime-to-![]() $p$ adèles, and
$p$ adèles, and ![]() $\mathbb {Z}_p$ the ring of
$\mathbb {Z}_p$ the ring of ![]() $p$-adic integers. Let
$p$-adic integers. Let ![]() $\mathbb {C}_p$ be the
$\mathbb {C}_p$ be the ![]() $p$-adic completion of an algebraic closure of
$p$-adic completion of an algebraic closure of ![]() $\mathbb {Q}_p$, and
$\mathbb {Q}_p$, and ![]() $G_{\mathbb {Q}_p}=\operatorname {Gal}(\mathbb {C}_p/\mathbb {Q}_p)$ the absolute Galois group. From now on, we fix a neat compact open subgroup
$G_{\mathbb {Q}_p}=\operatorname {Gal}(\mathbb {C}_p/\mathbb {Q}_p)$ the absolute Galois group. From now on, we fix a neat compact open subgroup ![]() $K^p\subset \operatorname {GL}_2(\mathbb {A}^{\infty,p}_{\mathbb {Q}})$. Given an open compact subgroup
$K^p\subset \operatorname {GL}_2(\mathbb {A}^{\infty,p}_{\mathbb {Q}})$. Given an open compact subgroup ![]() $K_p\subset \operatorname {GL}_2(\mathbb {Q}_p)$, we denote by
$K_p\subset \operatorname {GL}_2(\mathbb {Q}_p)$, we denote by ![]() $Y_{K_p}^{{\rm alg}}$ the modular curve over
$Y_{K_p}^{{\rm alg}}$ the modular curve over ![]() $\operatorname {Spec} \mathbb {Q}_p$ of level
$\operatorname {Spec} \mathbb {Q}_p$ of level ![]() $K^pK_p\subset \operatorname {GL}_2(\mathbb {A}^{\infty }_{\mathbb {Q}})=\operatorname {GL}_2(\mathbb {A}^{\infty,p}_{\mathbb {Q}})\times \operatorname {GL}_2(\mathbb {Q}_p)$, and by
$K^pK_p\subset \operatorname {GL}_2(\mathbb {A}^{\infty }_{\mathbb {Q}})=\operatorname {GL}_2(\mathbb {A}^{\infty,p}_{\mathbb {Q}})\times \operatorname {GL}_2(\mathbb {Q}_p)$, and by ![]() $X_{K_p}^{{\rm alg}}$ its compactification by adding cusps. Let
$X_{K_p}^{{\rm alg}}$ its compactification by adding cusps. Let ![]() $Y_{K_p}$ and
$Y_{K_p}$ and ![]() $X_{K_p}$ be the rigid analytic varieties attached to the modular curves, seen as adic spaces over
$X_{K_p}$ be the rigid analytic varieties attached to the modular curves, seen as adic spaces over ![]() $\operatorname {Spa}(\mathbb {Q}_p, \mathbb {Z}_p)$ (cf. [Reference HuberHub96]). Letting
$\operatorname {Spa}(\mathbb {Q}_p, \mathbb {Z}_p)$ (cf. [Reference HuberHub96]). Letting ![]() $D= X_{K_p}\backslash Y_{K_p}$ be the cusp divisor, we endow
$D= X_{K_p}\backslash Y_{K_p}$ be the cusp divisor, we endow ![]() $X_{K_p}$ with the
$X_{K_p}$ with the ![]() $\log$-structure defined by
$\log$-structure defined by ![]() $D$.
$D$.
Given a fine and saturated (fs) ![]() $\log$ adic space
$\log$ adic space ![]() $Z$ and
$Z$ and ![]() $?\in \{{\rm an},{\rm \acute {e}t},{\rm k\acute {e}t},{\rm pro\acute {e}t},{\rm prok\acute {e}t}\}$, we denote by
$?\in \{{\rm an},{\rm \acute {e}t},{\rm k\acute {e}t},{\rm pro\acute {e}t},{\rm prok\acute {e}t}\}$, we denote by ![]() $Z_{?}$ its analytic, étale, Kummer-étale, proétale and pro-Kummer-étale sites, respectively (see [Reference ScholzeSch13] and [Reference Diao, Lan, Liu and ZhuDLLZ23b]).
$Z_{?}$ its analytic, étale, Kummer-étale, proétale and pro-Kummer-étale sites, respectively (see [Reference ScholzeSch13] and [Reference Diao, Lan, Liu and ZhuDLLZ23b]).
In [Reference FaltingsFal87], Faltings described the Hodge–Tate decomposition of the étale cohomology (with coefficients) of the modular curve ![]() $Y_{K_p }$. More precisely, let
$Y_{K_p }$. More precisely, let ![]() $E$ be the universal elliptic curve over
$E$ be the universal elliptic curve over ![]() $Y_{K_p}$. This admits an extension to a semi-abelian adic space
$Y_{K_p}$. This admits an extension to a semi-abelian adic space ![]() $E^{sm}$ over
$E^{sm}$ over ![]() $X_{K_p}$ (cf. [Reference Deligne and RapoportDR73]). Let
$X_{K_p}$ (cf. [Reference Deligne and RapoportDR73]). Let ![]() $e: X_{K_p}\rightarrow E^{sm}$ be the unit section,
$e: X_{K_p}\rightarrow E^{sm}$ be the unit section, ![]() $\omega _E= e^* \Omega ^1_{ E^{sm}/X}$ the modular sheaf and
$\omega _E= e^* \Omega ^1_{ E^{sm}/X}$ the modular sheaf and ![]() $T_p E =\varprojlim _{n} E[p^n]$ the Tate module over
$T_p E =\varprojlim _{n} E[p^n]$ the Tate module over ![]() $Y_{K_p}$. We have the following theorem.
$Y_{K_p}$. We have the following theorem.
Theorem 1.0.1 (Faltings)
Let ![]() $k\geq 0$. There exists a Galois and Hecke equivariant isomorphism
$k\geq 0$. There exists a Galois and Hecke equivariant isomorphism
called the Eichler–Shimura decomposition.
The first result of this paper is a new proof of Faltings's Eichler–Shimura decomposition using Bernstein–Gelfand–Gelfand (BGG) methods and the Hodge–Tate period map. Our proof is the proétale analogue of the BGG decomposition for the de Rham cohomology of Faltings and Chai [Reference Faltings and ChaiFC90, Ch. 5 and Theorem 5.5]. Let us develop the ideas behind it.
Let ![]() $X_{\infty }:= \varprojlim _{K_p} X_{K_p}$ be Scholze's perfectoid modular curve and
$X_{\infty }:= \varprojlim _{K_p} X_{K_p}$ be Scholze's perfectoid modular curve and ![]() ${\pi _{\operatorname {HT}}: X_{\infty }\rightarrow \mathbb {P}^1_{\mathbb {Q}_p}}$ the Hodge–Tate period map [Reference ScholzeSch15]. The morphism
${\pi _{\operatorname {HT}}: X_{\infty }\rightarrow \mathbb {P}^1_{\mathbb {Q}_p}}$ the Hodge–Tate period map [Reference ScholzeSch15]. The morphism ![]() $\pi _{\operatorname {HT}}$ is
$\pi _{\operatorname {HT}}$ is ![]() $\operatorname {GL}_2(\mathbb {Q}_p)$-equivariant, where we see
$\operatorname {GL}_2(\mathbb {Q}_p)$-equivariant, where we see ![]() $\mathbb {P}^1_{\mathbb {Q}_p}$ as the left quotient of
$\mathbb {P}^1_{\mathbb {Q}_p}$ as the left quotient of ![]() $\operatorname {GL}_2$ by the upper triangular Borel
$\operatorname {GL}_2$ by the upper triangular Borel ![]() $\mathbf {B}$. Let
$\mathbf {B}$. Let ![]() $\pi _{K_p}: X_{\infty }\rightarrow X_{K_p}$ be the natural map. We can see
$\pi _{K_p}: X_{\infty }\rightarrow X_{K_p}$ be the natural map. We can see ![]() $X_{\infty }$ as a pro-Kummer-étale
$X_{\infty }$ as a pro-Kummer-étale ![]() $K_p$-torsor over
$K_p$-torsor over ![]() $X_{K_p}$. We let
$X_{K_p}$. We let ![]() $\widehat {\mathscr {O}}_{X_{K_p}}$ denote the
$\widehat {\mathscr {O}}_{X_{K_p}}$ denote the ![]() $p$-adic completion of the structural sheaf over
$p$-adic completion of the structural sheaf over ![]() $X_{K_p, {\rm prok\acute {e}t}}$. Let
$X_{K_p, {\rm prok\acute {e}t}}$. Let ![]() $\mathbb {Z}_p(1)= \varprojlim _{n} \mu _{p^n}$ be the Tate twist and
$\mathbb {Z}_p(1)= \varprojlim _{n} \mu _{p^n}$ be the Tate twist and ![]() $\widehat {\mathscr {O}}_{X_{K_p}}(i)$ the
$\widehat {\mathscr {O}}_{X_{K_p}}(i)$ the ![]() $i$th twist of
$i$th twist of ![]() $\widehat {\mathscr {O}}_{X_{K_p}}$. By [Reference Diao, Lan, Liu and ZhuDLLZ23b, Theorem 4.6.1],
$\widehat {\mathscr {O}}_{X_{K_p}}$. By [Reference Diao, Lan, Liu and ZhuDLLZ23b, Theorem 4.6.1], ![]() $T_pE$ admits a natural extension to the pro-Kummer-étale site of
$T_pE$ admits a natural extension to the pro-Kummer-étale site of ![]() $X_{K_p}$ which we denote in the same way. From now on, we fix the level
$X_{K_p}$ which we denote in the same way. From now on, we fix the level ![]() $K_p$ and write
$K_p$ and write ![]() $Y=Y_{K_p}$ and
$Y=Y_{K_p}$ and ![]() $X=X_{K_p}$.
$X=X_{K_p}$.
The map ![]() $\pi _{\operatorname {HT}}$ is defined from the Hodge–Tate exact sequence
$\pi _{\operatorname {HT}}$ is defined from the Hodge–Tate exact sequence
which is the variation in families of the Hodge–Tate decomposition for elliptic curves (cf. [Reference TateTat67]). More precisely, let ![]() $\Psi : \mathbb {Z}_p^2\xrightarrow {\sim } T_pE$ be the universal trivialization over
$\Psi : \mathbb {Z}_p^2\xrightarrow {\sim } T_pE$ be the universal trivialization over ![]() $X_{\infty }$; then (2) defines a line subbundle of
$X_{\infty }$; then (2) defines a line subbundle of ![]() $\mathscr {O}_{X_{\infty }}^{\oplus 2}$ which induces the map
$\mathscr {O}_{X_{\infty }}^{\oplus 2}$ which induces the map ![]() $\pi _{\operatorname {HT}}$.
$\pi _{\operatorname {HT}}$.
The ![]() $\operatorname {GL}_2(\mathbb {Q}_p)$-equivariance of
$\operatorname {GL}_2(\mathbb {Q}_p)$-equivariance of ![]() $\pi _{\operatorname {HT}}$ recovers (2) from a short exact sequence of
$\pi _{\operatorname {HT}}$ recovers (2) from a short exact sequence of ![]() $\operatorname {GL}_2$-equivariant sheaves over
$\operatorname {GL}_2$-equivariant sheaves over ![]() $\mathbb {P}^1_{\mathbb {Q}_p}$. Indeed, the presentation
$\mathbb {P}^1_{\mathbb {Q}_p}$. Indeed, the presentation ![]() $\mathbb {P}^1_{\mathbb {Q}_p}= \mathbf {B} \backslash\!\operatorname {GL}_2$ induces an equivalence between algebraic
$\mathbb {P}^1_{\mathbb {Q}_p}= \mathbf {B} \backslash\!\operatorname {GL}_2$ induces an equivalence between algebraic ![]() $\mathbf {B}$-representations and
$\mathbf {B}$-representations and ![]() $\operatorname {GL}_2$-equivariant vector bundles over
$\operatorname {GL}_2$-equivariant vector bundles over ![]() $\mathbb {P}^1_{\mathbb {Q}_p}$. More explicitly, let
$\mathbb {P}^1_{\mathbb {Q}_p}$. More explicitly, let ![]() $V$ be a
$V$ be a ![]() $\mathbf {B}$-representation; then one defines the vector bundle
$\mathbf {B}$-representation; then one defines the vector bundle ![]() $\mathcal {V}= \operatorname {GL}_2 \times ^{\mathbf {B}} V = \mathbf {B}\backslash (\operatorname {GL}_2\times V)$, where in the right-hand side term
$\mathcal {V}= \operatorname {GL}_2 \times ^{\mathbf {B}} V = \mathbf {B}\backslash (\operatorname {GL}_2\times V)$, where in the right-hand side term ![]() $\operatorname {GL}_2 \times V$, the group
$\operatorname {GL}_2 \times V$, the group ![]() $\mathbf{B}$ acts diagonally. Let
$\mathbf{B}$ acts diagonally. Let ![]() $\mathscr {F}$ be a
$\mathscr {F}$ be a ![]() $K_p$-equivariant sheaf over
$K_p$-equivariant sheaf over ![]() $\mathbb {P}^1_{\mathbb {Q}_p}$; we shall identify
$\mathbb {P}^1_{\mathbb {Q}_p}$; we shall identify ![]() $\pi _{\operatorname {HT}}^*(\mathscr {F})$ with the pro-Kummer-étale sheaf over
$\pi _{\operatorname {HT}}^*(\mathscr {F})$ with the pro-Kummer-étale sheaf over ![]() $X_{K_p}$ obtained by descent from the
$X_{K_p}$ obtained by descent from the ![]() $K_p$-equivariant pullback over
$K_p$-equivariant pullback over ![]() $X_{\infty }$.
$X_{\infty }$.
Let ![]() $\mathbf {T}\subset \mathbf {B}$ be the diagonal torus and let
$\mathbf {T}\subset \mathbf {B}$ be the diagonal torus and let ![]() $\kappa =(k_1,k_2) \in X^*(\mathbf {T})$ be a character. We denote by
$\kappa =(k_1,k_2) \in X^*(\mathbf {T})$ be a character. We denote by ![]() $\mathbb {Q}_p(\kappa )$ the representation defined by
$\mathbb {Q}_p(\kappa )$ the representation defined by ![]() $\kappa$ and consider it as a
$\kappa$ and consider it as a ![]() $\mathbf {B}$-representation by letting the unipotent radical act trivially. We say that
$\mathbf {B}$-representation by letting the unipotent radical act trivially. We say that ![]() $\kappa =(k_1,k_2)$ is dominant if
$\kappa =(k_1,k_2)$ is dominant if ![]() $k_1\geq k_2$. Given a dominant character
$k_1\geq k_2$. Given a dominant character ![]() $\kappa$, we let
$\kappa$, we let ![]() $V_{\kappa }= \operatorname {Sym}^{k_1-k_2}\operatorname {St}\otimes \det ^{k_2}$ be the irreducible representation of
$V_{\kappa }= \operatorname {Sym}^{k_1-k_2}\operatorname {St}\otimes \det ^{k_2}$ be the irreducible representation of ![]() $\operatorname {GL}_2$ of highest weight
$\operatorname {GL}_2$ of highest weight ![]() $\kappa$, and we denote by
$\kappa$, and we denote by ![]() $V_{\kappa,{\rm \acute {e}t}}$ the associated pro-Kummer-étale sheaf obtained by descent from
$V_{\kappa,{\rm \acute {e}t}}$ the associated pro-Kummer-étale sheaf obtained by descent from ![]() $X_{\infty }$. Let
$X_{\infty }$. Let ![]() $W=\{1,w_0\}$ be the Weyl group of
$W=\{1,w_0\}$ be the Weyl group of ![]() $\operatorname {GL}_2$. We denote by
$\operatorname {GL}_2$. We denote by ![]() $\mathscr {L}(\kappa )$ the
$\mathscr {L}(\kappa )$ the ![]() $\operatorname {GL}_2$-equivariant sheaf over
$\operatorname {GL}_2$-equivariant sheaf over ![]() $\mathbb {P}^1_{\mathbb {Q}_p}$ given by
$\mathbb {P}^1_{\mathbb {Q}_p}$ given by ![]() $\mathbf {B}\backslash ( \operatorname {GL}_2\times w_0(\kappa ))$. The standard representation
$\mathbf {B}\backslash ( \operatorname {GL}_2\times w_0(\kappa ))$. The standard representation ![]() $\operatorname {St}$ has a
$\operatorname {St}$ has a ![]() $\mathbf {B}$-filtration
$\mathbf {B}$-filtration
By construction, the pullback of (3) by ![]() $\pi _{\operatorname {HT}}$ is equal to the Hodge–Tate exact sequence (2). In particular,
$\pi _{\operatorname {HT}}$ is equal to the Hodge–Tate exact sequence (2). In particular, ![]() $\pi _{\operatorname {HT}}^*( \operatorname {St} \otimes \mathscr {O}_{\mathbb {P}^1_{\mathbb {Q}_p}})= T_p E \otimes \widehat {\mathscr {O}}_X$ and
$\pi _{\operatorname {HT}}^*( \operatorname {St} \otimes \mathscr {O}_{\mathbb {P}^1_{\mathbb {Q}_p}})= T_p E \otimes \widehat {\mathscr {O}}_X$ and ![]() $\pi _{\operatorname {HT}}( \mathscr {L}(\kappa ))= \omega _E^{k_1-k_2}\otimes _{\mathscr {O}_X} \widehat {\mathscr {O}}_X(k_2)$. A natural question arises, namely, how to describe the pullbacks by
$\pi _{\operatorname {HT}}( \mathscr {L}(\kappa ))= \omega _E^{k_1-k_2}\otimes _{\mathscr {O}_X} \widehat {\mathscr {O}}_X(k_2)$. A natural question arises, namely, how to describe the pullbacks by ![]() $\pi _{\operatorname {HT}}$ of the
$\pi _{\operatorname {HT}}$ of the ![]() $\operatorname {GL}_2$-equivariant vector bundles over
$\operatorname {GL}_2$-equivariant vector bundles over ![]() $\mathbb {P}^1_{\mathbb {Q}_p}$. We already know that the pullbacks of those vector bundles constructed from characters of
$\mathbb {P}^1_{\mathbb {Q}_p}$. We already know that the pullbacks of those vector bundles constructed from characters of ![]() $\mathbf {T}$ are related to modular sheaves, and it remains to understand the
$\mathbf {T}$ are related to modular sheaves, and it remains to understand the ![]() $\operatorname {GL}_2$-equivariant sheaves constructed from non-semi-simple representations of
$\operatorname {GL}_2$-equivariant sheaves constructed from non-semi-simple representations of ![]() $\mathbf {B}$.
$\mathbf {B}$.
Let ![]() $\mathscr {O}(\mathbf {B})$ be the ring of algebraic functions of
$\mathscr {O}(\mathbf {B})$ be the ring of algebraic functions of ![]() $\mathbf {B}$ endowed with the right regular action; note that any algebraic representation of
$\mathbf {B}$ endowed with the right regular action; note that any algebraic representation of ![]() $\mathbf {B}$ occurs in
$\mathbf {B}$ occurs in ![]() $\mathscr {O}(\mathbf {B})$. The presentation
$\mathscr {O}(\mathbf {B})$. The presentation ![]() $\mathbf {B}= \mathbf {T}\ltimes \mathbf {N}$ as a semidirect product gives an isomorphism
$\mathbf {B}= \mathbf {T}\ltimes \mathbf {N}$ as a semidirect product gives an isomorphism ![]() $\mathscr {O}(\mathbf {B})= \mathscr {O}(\mathbf {T})\otimes \mathscr {O}(\mathbf {N})$, where
$\mathscr {O}(\mathbf {B})= \mathscr {O}(\mathbf {T})\otimes \mathscr {O}(\mathbf {N})$, where ![]() $\mathbf {B}$ acts on the first factor by the right regular action of
$\mathbf {B}$ acts on the first factor by the right regular action of ![]() $\mathbf {T}$, and it acts on the second factor under the formula
$\mathbf {T}$, and it acts on the second factor under the formula ![]() $(n,b)\mapsto t_{b}^{-1}nt_{b} n_b$, with
$(n,b)\mapsto t_{b}^{-1}nt_{b} n_b$, with ![]() $(n,b)\in \mathbf {N}\times \mathbf {B}$ and
$(n,b)\in \mathbf {N}\times \mathbf {B}$ and ![]() $b=(t_b,n_b)\in \mathbf {T}\ltimes \mathbf {N}$. We have the following theorem.
$b=(t_b,n_b)\in \mathbf {T}\ltimes \mathbf {N}$. We have the following theorem.
Theorem 1.0.2 (Theorem 4.1.2)
Let ![]() $\underline {\mathscr {O}}(\mathbf {N})$ be the
$\underline {\mathscr {O}}(\mathbf {N})$ be the ![]() $\operatorname {GL}_2$-equivariant quasi-coherent sheaf over
$\operatorname {GL}_2$-equivariant quasi-coherent sheaf over ![]() $\mathbb {P}^1_{\mathbb {Q}_p}$ associated to
$\mathbb {P}^1_{\mathbb {Q}_p}$ associated to ![]() $\mathscr {O}(\mathbf {N})$. Let
$\mathscr {O}(\mathbf {N})$. Let ![]() $\mathscr {O}\!\mathbb {B}_{{\rm dR},\log }$ be the geometric de Rham period sheaf of [Reference ScholzeSch13] and [Reference Diao, Lan, Liu and ZhuDLLZ23b], and let
$\mathscr {O}\!\mathbb {B}_{{\rm dR},\log }$ be the geometric de Rham period sheaf of [Reference ScholzeSch13] and [Reference Diao, Lan, Liu and ZhuDLLZ23b], and let ![]() $\mathscr {O}\!\mathbb {C}_{\log }= \operatorname {gr}^0 \mathscr {O}\!\mathbb {B}_{{\rm dR},\log }$ be the Hodge–Tate sheaf. We have a natural isomorphism of pro-Kummer-étale sheaves over
$\mathscr {O}\!\mathbb {C}_{\log }= \operatorname {gr}^0 \mathscr {O}\!\mathbb {B}_{{\rm dR},\log }$ be the Hodge–Tate sheaf. We have a natural isomorphism of pro-Kummer-étale sheaves over ![]() $X$,
$X$,
As a corollary one obtains the Eichler–Shimura decompositions.
Theorem 1.0.3 (Theorem 4.1.4)
Let ![]() $\kappa =(k_1,k_2)$ be a dominant character and set
$\kappa =(k_1,k_2)$ be a dominant character and set ![]() $\alpha = (1,-1)\in X^*(\mathbf {T})$. Let
$\alpha = (1,-1)\in X^*(\mathbf {T})$. Let ![]() $\operatorname {BGG}(\kappa )$ be the dual BGG complex of weight
$\operatorname {BGG}(\kappa )$ be the dual BGG complex of weight ![]() $\kappa$ (Proposition 2.4.3),
$\kappa$ (Proposition 2.4.3),
We denote by ![]() $\underline {\operatorname {BGG}(\kappa )}$ the associated
$\underline {\operatorname {BGG}(\kappa )}$ the associated ![]() $\operatorname {GL}_2$-equivariant complex over
$\operatorname {GL}_2$-equivariant complex over ![]() $\mathbb {P}^1_{\mathbb {Q}_p}$. Then the pullback of
$\mathbb {P}^1_{\mathbb {Q}_p}$. Then the pullback of ![]() $\underline {\operatorname {BGG}(\kappa )}$ by
$\underline {\operatorname {BGG}(\kappa )}$ by ![]() $\pi _{\operatorname {HT}}$ is the short exact sequence
$\pi _{\operatorname {HT}}$ is the short exact sequence
Furthermore, let ![]() $\lambda : X_{\mathbb {C}_p,{\rm prok\acute {e}t}}\rightarrow X_{ \mathbb {C}_p,{\rm an}}$ be the projection of sites. Then
$\lambda : X_{\mathbb {C}_p,{\rm prok\acute {e}t}}\rightarrow X_{ \mathbb {C}_p,{\rm an}}$ be the projection of sites. Then
Taking ![]() $H^1$-cohomology in the analytic site of
$H^1$-cohomology in the analytic site of ![]() $X_{\mathbb {C}_p}$, we recover the Eichler–Shimura decomposition of Theorem 1.0.1.
$X_{\mathbb {C}_p}$, we recover the Eichler–Shimura decomposition of Theorem 1.0.1.
The proof of Theorem 1.0.2 follows from the isomorphism between Faltings extension ![]() $\operatorname {gr}^1 \mathscr {O}\!\mathbb {B}_{{\rm dR},\log }^+$ and the sheaf
$\operatorname {gr}^1 \mathscr {O}\!\mathbb {B}_{{\rm dR},\log }^+$ and the sheaf ![]() $T_pE \otimes \widehat {\mathscr {O}}_X \otimes \omega _E$. This isomorphism was known to Faltings, and used in his original proof of Theorem 1.0.1. Our new proof provides a more explicit definition of the Eichler–Shimura maps in terms of cocycles and can be generalized to any Shimura variety. Moreover, using this method, one easily deduces the degeneration of the spectral sequence appearing in [Reference FaltingsFal87], as well as its natural splitting using simple properties of the dual BGG resolution. It is worth mentioning that the isomorphism between the twist of the Tate module and the Faltings extension was used by Lue Pan in [Reference PanPan22] to compute the relative Sen operator of the modular curve.
$T_pE \otimes \widehat {\mathscr {O}}_X \otimes \omega _E$. This isomorphism was known to Faltings, and used in his original proof of Theorem 1.0.1. Our new proof provides a more explicit definition of the Eichler–Shimura maps in terms of cocycles and can be generalized to any Shimura variety. Moreover, using this method, one easily deduces the degeneration of the spectral sequence appearing in [Reference FaltingsFal87], as well as its natural splitting using simple properties of the dual BGG resolution. It is worth mentioning that the isomorphism between the twist of the Tate module and the Faltings extension was used by Lue Pan in [Reference PanPan22] to compute the relative Sen operator of the modular curve.
The second goal of this paper is the interpolation of the Eichler–Shimura decomposition (1). The ![]() $H^0$-map of the overconvergent Eichler–Shimura maps was previously constructed by Andreatta, Iovita and Stevens in [Reference Andreatta, Iovita and StevensAIS15]. The strategy followed in this paper is close to the construction of the Eichler–Shimura map for Shimura curves in [Reference Chojecki, Hansen and JohanssonCHJ17]. Roughly speaking, we take pullbacks by
$H^0$-map of the overconvergent Eichler–Shimura maps was previously constructed by Andreatta, Iovita and Stevens in [Reference Andreatta, Iovita and StevensAIS15]. The strategy followed in this paper is close to the construction of the Eichler–Shimura map for Shimura curves in [Reference Chojecki, Hansen and JohanssonCHJ17]. Roughly speaking, we take pullbacks by ![]() $\pi _{\operatorname {HT}}$ of certain locally analytic sheaves over
$\pi _{\operatorname {HT}}$ of certain locally analytic sheaves over ![]() $\mathbb {P}^1_{\mathbb {Q}_p}$. In this way, we interpolate all the terms appearing in the Hodge–Tate exact sequence (2): we get overconvergent modular sheaves whose cohomology is the object of study in higher Coleman theory developed by Boxer and Pilloni [Reference Boxer and PilloniBP21, Reference Boxer and PilloniBP22]. The interpolation of the symmetric powers of the Tate module will be given by locally analytic principal series or locally analytic distributions as in [Reference Ash and StevensAS08]. Finally, the Hodge–Tate maps
$\mathbb {P}^1_{\mathbb {Q}_p}$. In this way, we interpolate all the terms appearing in the Hodge–Tate exact sequence (2): we get overconvergent modular sheaves whose cohomology is the object of study in higher Coleman theory developed by Boxer and Pilloni [Reference Boxer and PilloniBP21, Reference Boxer and PilloniBP22]. The interpolation of the symmetric powers of the Tate module will be given by locally analytic principal series or locally analytic distributions as in [Reference Ash and StevensAS08]. Finally, the Hodge–Tate maps ![]() $\operatorname {HT}$ and
$\operatorname {HT}$ and ![]() $\operatorname {HT}^\vee$ can be put in families, obtaining the
$\operatorname {HT}^\vee$ can be put in families, obtaining the ![]() $\operatorname {dlog}$ map of [Reference Andreatta, Iovita and StevensAIS15] as a particular case.
$\operatorname {dlog}$ map of [Reference Andreatta, Iovita and StevensAIS15] as a particular case.
Let us sketch the main steps of the construction. Let ![]() $n\geq 1$ be an integer and let
$n\geq 1$ be an integer and let
 \[ \operatorname{Iw}_n:= \biggl(
\begin{matrix} \mathbb{Z}_p^{\times} & \mathbb{Z}_p \\ p^n
\mathbb{Z}_p & \mathbb{Z}_p^\times \end{matrix} \biggr)
\]
\[ \operatorname{Iw}_n:= \biggl(
\begin{matrix} \mathbb{Z}_p^{\times} & \mathbb{Z}_p \\ p^n
\mathbb{Z}_p & \mathbb{Z}_p^\times \end{matrix} \biggr)
\]
be the Iwahori group modulo ![]() $p^n$. From now on, we will take
$p^n$. From now on, we will take ![]() $X=X_{\operatorname {Iw}_n}$. Let
$X=X_{\operatorname {Iw}_n}$. Let ![]() $\epsilon \geq \delta \geq n$ be rational numbers and
$\epsilon \geq \delta \geq n$ be rational numbers and ![]() $(R,R^+)$ a uniform Tate algebra over
$(R,R^+)$ a uniform Tate algebra over ![]() $\mathbb {Q}_p$ which we may assume to be sheafy (i.e. such that the pre-sheaf of rational functions in
$\mathbb {Q}_p$ which we may assume to be sheafy (i.e. such that the pre-sheaf of rational functions in ![]() $\operatorname {Spa}(R,R^+)$ is an actual sheaf). Let
$\operatorname {Spa}(R,R^+)$ is an actual sheaf). Let ![]() $T=\mathbf {T}(\mathbb {Z}_p)$ denote the
$T=\mathbf {T}(\mathbb {Z}_p)$ denote the ![]() $\mathbb {Z}_p$-points of the diagonal torus and
$\mathbb {Z}_p$-points of the diagonal torus and ![]() $\chi =(\chi _1,\chi _2): T\rightarrow R^{+,\times }$ a
$\chi =(\chi _1,\chi _2): T\rightarrow R^{+,\times }$ a ![]() $\delta$-analytic character (cf. Lemma 2.2.5). We let
$\delta$-analytic character (cf. Lemma 2.2.5). We let ![]() $R\widehat {\otimes }\widehat {\mathscr {O}}_X$ be the
$R\widehat {\otimes }\widehat {\mathscr {O}}_X$ be the ![]() $p$-adically complete tensor product of
$p$-adically complete tensor product of ![]() $R$ and the completed sheaf
$R$ and the completed sheaf ![]() $\widehat {\mathscr {O}}_X$. Given a character
$\widehat {\mathscr {O}}_X$. Given a character ![]() $\lambda : \mathbb {Z}_p^\times \to R^{+,\times }$, we denote by
$\lambda : \mathbb {Z}_p^\times \to R^{+,\times }$, we denote by ![]() $R(\lambda )$ the
$R(\lambda )$ the ![]() $G_{\mathbb {Q}_p}$-module induced by the composition
$G_{\mathbb {Q}_p}$-module induced by the composition ![]() $G_{\mathbb {Q}_p}\xrightarrow {\chi _{{\rm cyc}}} \mathbb {Z}_p^\times \xrightarrow {\lambda } R^{\times }$. Finally, we write
$G_{\mathbb {Q}_p}\xrightarrow {\chi _{{\rm cyc}}} \mathbb {Z}_p^\times \xrightarrow {\lambda } R^{\times }$. Finally, we write ![]() $\widehat {\mathscr {O}}_X(\lambda ):= R(\lambda )\widehat {\otimes }\widehat {\mathscr {O}}_X$.
$\widehat {\mathscr {O}}_X(\lambda ):= R(\lambda )\widehat {\otimes }\widehat {\mathscr {O}}_X$.
We begin with the construction of all the sheaves over ![]() $\mathbb {P}^1_{\mathbb {Q}_p}$: for
$\mathbb {P}^1_{\mathbb {Q}_p}$: for ![]() $w\in W=\{1,w_0\}$ we define a family of overconvergent neighbourhoods
$w\in W=\{1,w_0\}$ we define a family of overconvergent neighbourhoods ![]() $\{U_w(\epsilon )\operatorname {Iw}_n\}_{\epsilon \geq n}$ of
$\{U_w(\epsilon )\operatorname {Iw}_n\}_{\epsilon \geq n}$ of ![]() $w\operatorname {Iw}_n$ in
$w\operatorname {Iw}_n$ in ![]() $\mathbb {P}^1_{\mathbb {Q}_p}$. The affinoid spaces
$\mathbb {P}^1_{\mathbb {Q}_p}$. The affinoid spaces ![]() $U_w(\epsilon )\operatorname {Iw}_n$ admit sections of the quotient map
$U_w(\epsilon )\operatorname {Iw}_n$ admit sections of the quotient map ![]() $\operatorname {GL}_2\rightarrow \mathbb {P}^1_{\mathbb {Q}_p}$. In particular, the natural
$\operatorname {GL}_2\rightarrow \mathbb {P}^1_{\mathbb {Q}_p}$. In particular, the natural ![]() $\mathbf {T}$-torsor
$\mathbf {T}$-torsor ![]() $\mathbf {N}\backslash\!\operatorname {GL}_2\rightarrow \mathbb {P}^1_{\mathbb {Q}_p}$, where
$\mathbf {N}\backslash\!\operatorname {GL}_2\rightarrow \mathbb {P}^1_{\mathbb {Q}_p}$, where ![]() $\mathbf {N}$ is the unipotent radical of
$\mathbf {N}$ is the unipotent radical of ![]() $\mathbf {B}$, has a trivialization over
$\mathbf {B}$, has a trivialization over ![]() $U_{w}(\epsilon )\operatorname {Iw}_n$. We define a
$U_{w}(\epsilon )\operatorname {Iw}_n$. We define a ![]() $R\widehat {\otimes } \mathscr {O}_{\mathbb {P}^1_{\mathbb {Q}_p}}$ line bundle
$R\widehat {\otimes } \mathscr {O}_{\mathbb {P}^1_{\mathbb {Q}_p}}$ line bundle ![]() $\mathscr {L}(\chi )$ in the analytic site of
$\mathscr {L}(\chi )$ in the analytic site of ![]() $U_w(\epsilon )\operatorname {Iw}_n$ in the same way we have defined the line bundles
$U_w(\epsilon )\operatorname {Iw}_n$ in the same way we have defined the line bundles ![]() $\mathscr {L}(\kappa )$ for
$\mathscr {L}(\kappa )$ for ![]() $\kappa \in X^*(\mathbf {T})$. Then we define the space of
$\kappa \in X^*(\mathbf {T})$. Then we define the space of ![]() $\delta$-analytic principal series of weight
$\delta$-analytic principal series of weight ![]() $\chi$ to be the
$\chi$ to be the ![]() $R$-Banach space
$R$-Banach space
We define the ![]() $\delta$-analytic distributions
$\delta$-analytic distributions ![]() $D^{\delta }_{\chi }$ to be the continuous dual of
$D^{\delta }_{\chi }$ to be the continuous dual of ![]() $A^{\delta }_{\chi }$ endowed with the weak topology. The space
$A^{\delta }_{\chi }$ endowed with the weak topology. The space ![]() $A^{\delta }_{\chi }$ has a natural action of
$A^{\delta }_{\chi }$ has a natural action of ![]() $\operatorname {Iw}_n$, so that it defines a constant
$\operatorname {Iw}_n$, so that it defines a constant ![]() $\operatorname {Iw}_n$-equivariant sheaf on
$\operatorname {Iw}_n$-equivariant sheaf on ![]() $\mathbb {P}^1_{\mathbb {Q}_p}$. We let
$\mathbb {P}^1_{\mathbb {Q}_p}$. We let ![]() $A^{\delta }_{\chi,{\rm \acute {e}t}}$ and
$A^{\delta }_{\chi,{\rm \acute {e}t}}$ and ![]() $D_{\chi,{\rm \acute {e}t}}^{\delta }$ denote the pro-Kummer-étale sheaves over
$D_{\chi,{\rm \acute {e}t}}^{\delta }$ denote the pro-Kummer-étale sheaves over ![]() $X$ obtained by descent from the topological
$X$ obtained by descent from the topological ![]() $K_p$-equivariant sheaves over
$K_p$-equivariant sheaves over ![]() $X_{\infty }$.
$X_{\infty }$.
In Proposition 2.4.4 we construct maps
 \begin{gather*} R(\chi)
\xrightarrow{\iota} A^{\delta}_{\chi} \text{ equivariant
for the action of } \mathbf{B}(\mathbb{Z}_p)\cap
\operatorname{Iw}_n,\\
A^{\delta}_{\chi}\xrightarrow{\operatorname{ev}_{w_0}}
R(\chi) \text{ equivariant for the action of } w_0^{-1}
\mathbf{B}(\mathbb{Z}_p)w_0 \cap \operatorname{Iw}_n,
\end{gather*}
\begin{gather*} R(\chi)
\xrightarrow{\iota} A^{\delta}_{\chi} \text{ equivariant
for the action of } \mathbf{B}(\mathbb{Z}_p)\cap
\operatorname{Iw}_n,\\
A^{\delta}_{\chi}\xrightarrow{\operatorname{ev}_{w_0}}
R(\chi) \text{ equivariant for the action of } w_0^{-1}
\mathbf{B}(\mathbb{Z}_p)w_0 \cap \operatorname{Iw}_n,
\end{gather*}
with ![]() $\iota$ being the highest weight vector, and
$\iota$ being the highest weight vector, and ![]() $\operatorname {ev}_{w_0}$ the evaluation at
$\operatorname {ev}_{w_0}$ the evaluation at ![]() $w_0$. We prove that these maps give rise morphisms of
$w_0$. We prove that these maps give rise morphisms of ![]() $\operatorname {Iw}_n$-equivariant sheaves
$\operatorname {Iw}_n$-equivariant sheaves
 \begin{equation} \begin{gathered} \mathscr{L}(w_0(\chi)) \rightarrow A^{\delta}_{\chi}\widehat{\otimes}_{\mathbb{Q}_p} \mathscr{O}_{\mathbb{P}^1_{\mathbb{Q}_p}} \text{ over } U_{1}(\epsilon)\operatorname{Iw}_n,\\ A^{\delta}_{\chi}\widehat{\otimes}_{\mathbb{Q}_p} \mathscr{O}_{\mathbb{P}^1_{\mathbb{Q}_p}} \rightarrow \mathscr{L}(\chi) \text{ over } U_{w_0}(\epsilon)\operatorname{Iw}_n. \end{gathered} \end{equation}
\begin{equation} \begin{gathered} \mathscr{L}(w_0(\chi)) \rightarrow A^{\delta}_{\chi}\widehat{\otimes}_{\mathbb{Q}_p} \mathscr{O}_{\mathbb{P}^1_{\mathbb{Q}_p}} \text{ over } U_{1}(\epsilon)\operatorname{Iw}_n,\\ A^{\delta}_{\chi}\widehat{\otimes}_{\mathbb{Q}_p} \mathscr{O}_{\mathbb{P}^1_{\mathbb{Q}_p}} \rightarrow \mathscr{L}(\chi) \text{ over } U_{w_0}(\epsilon)\operatorname{Iw}_n. \end{gathered} \end{equation} The next step is to translate all the previous constructions to the modular curve ![]() $X$. We start by defining the strict neighbourhoods of the
$X$. We start by defining the strict neighbourhoods of the ![]() $w$-ordinary locus
$w$-ordinary locus ![]() $\{X_{w}(\epsilon )\}_{\epsilon >n}$; they are equal to
$\{X_{w}(\epsilon )\}_{\epsilon >n}$; they are equal to ![]() $\pi _{\operatorname {Iw}_n}( \pi _{\operatorname {HT}}^{-1}(U_w(\epsilon )\operatorname {Iw}_n) )$. The second object we descend to
$\pi _{\operatorname {Iw}_n}( \pi _{\operatorname {HT}}^{-1}(U_w(\epsilon )\operatorname {Iw}_n) )$. The second object we descend to ![]() $X$ are the overconvergent modular sheaves
$X$ are the overconvergent modular sheaves ![]() $\omega _E^{\chi }$; they are
$\omega _E^{\chi }$; they are ![]() $R\widehat {\otimes } \mathscr {O}_{X}$-line bundles in the étale or analytic site of
$R\widehat {\otimes } \mathscr {O}_{X}$-line bundles in the étale or analytic site of ![]() $X_{w}(\epsilon )$. We refer to [Reference Boxer and PilloniBP21] for the general construction of these sheaves. The dictionary provided by
$X_{w}(\epsilon )$. We refer to [Reference Boxer and PilloniBP21] for the general construction of these sheaves. The dictionary provided by ![]() $\pi _{\operatorname {HT}}$ then gives (see Corollary 3.2.11)
$\pi _{\operatorname {HT}}$ then gives (see Corollary 3.2.11)
We continue with the pullback of the ![]() $\delta$-analytic principal series and distributions, seen as
$\delta$-analytic principal series and distributions, seen as ![]() $\operatorname {Iw}_n$-equivariant sheaves over
$\operatorname {Iw}_n$-equivariant sheaves over ![]() $\mathbb {P}^1_{\mathbb {Q}_p}$. By definition one has
$\mathbb {P}^1_{\mathbb {Q}_p}$. By definition one has ![]() $\pi _{\operatorname {HT}}^*(A_{\chi }^{\delta }\widehat {\otimes } \mathscr {O}_{\mathbb {P}^1_{\mathbb {Q}_p}})= A^{\delta }_{\chi,{\rm \acute {e}t}}\widehat {\otimes } \widehat {\mathscr {O}}_X$ (and similarly for
$\pi _{\operatorname {HT}}^*(A_{\chi }^{\delta }\widehat {\otimes } \mathscr {O}_{\mathbb {P}^1_{\mathbb {Q}_p}})= A^{\delta }_{\chi,{\rm \acute {e}t}}\widehat {\otimes } \widehat {\mathscr {O}}_X$ (and similarly for ![]() $D^{\delta }_{\chi }$). Finally, we pullback the maps (4) obtaining overconvergent Hodge–Tate maps of pro-Kummer-étale sheaves
$D^{\delta }_{\chi }$). Finally, we pullback the maps (4) obtaining overconvergent Hodge–Tate maps of pro-Kummer-étale sheaves
 \begin{gather*} \omega_E^{w_0(\chi)} \widehat{\otimes} \widehat{\mathscr{O}}_X(\chi_1) \xrightarrow{\operatorname{HT}^\vee} A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes} \widehat{\mathscr{O}}_X \text{ over } X_{1}(\epsilon),\\ A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X \xrightarrow{\operatorname{HT}} \omega_E^{\chi} \widehat{\otimes} \widehat{\mathscr{O}}_X(\chi_2) \text{ over } X_{w_0}(\epsilon) \end{gather*}
\begin{gather*} \omega_E^{w_0(\chi)} \widehat{\otimes} \widehat{\mathscr{O}}_X(\chi_1) \xrightarrow{\operatorname{HT}^\vee} A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes} \widehat{\mathscr{O}}_X \text{ over } X_{1}(\epsilon),\\ A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X \xrightarrow{\operatorname{HT}} \omega_E^{\chi} \widehat{\otimes} \widehat{\mathscr{O}}_X(\chi_2) \text{ over } X_{w_0}(\epsilon) \end{gather*}
(and similarly for ![]() $D^{\delta }_{\chi }$). Taking pro-Kummer-étale cohomology, one obtains the following theorem.
$D^{\delta }_{\chi }$). Taking pro-Kummer-étale cohomology, one obtains the following theorem.
Theorem 1.0.4 (Theorem 4.2.2)
There are overconvergent Eichler–Shimura maps
satisfying the following properties.
(i) The composition
 $ES_{A}\circ ES^{\vee }_{A}$ is zero.
$ES_{A}\circ ES^{\vee }_{A}$ is zero.(ii) Assume that
 $\mathcal {V}=\operatorname {Spa}(R,R^+)$ is an affinoid subspace of the weight space
$\mathcal {V}=\operatorname {Spa}(R,R^+)$ is an affinoid subspace of the weight space  $\mathcal {W}_T$ of
$\mathcal {W}_T$ of  $T=\mathbf {T}(\mathbb {Z}_p)$, and let
$T=\mathbf {T}(\mathbb {Z}_p)$, and let  $\kappa =(k_1,k_2)\in \mathcal {V}$ be a dominant weight of
$\kappa =(k_1,k_2)\in \mathcal {V}$ be a dominant weight of  $\mathbf {T}$. Let
$\mathbf {T}$. Let  $\alpha =(1,-1)\in X^*(\mathbf {T})$ and let
$\alpha =(1,-1)\in X^*(\mathbf {T})$ and let  $\chi =\chi ^{{\rm un}}_{\mathcal {V}}$ be the universal character of
$\chi =\chi ^{{\rm un}}_{\mathcal {V}}$ be the universal character of  $\mathcal {V}$. Then we have the following commutative diagram.
$\mathcal {V}$. Then we have the following commutative diagram.

(iii) The maps of (ii) are Galois and
 $U_p^t$-equivariant with respect to the good normalizations of the
$U_p^t$-equivariant with respect to the good normalizations of the  $U_p^t$-operators. In particular, the above diagram restricts to the finite slope part with respect to the
$U_p^t$-operators. In particular, the above diagram restricts to the finite slope part with respect to the  $U_p^t$-action.
$U_p^t$-action.(iv) Let
 $h< k_1-k_2+1$. There exists an open affinoid
$h< k_1-k_2+1$. There exists an open affinoid  $\mathcal {V}'\subset \mathcal {V}$ containing
$\mathcal {V}'\subset \mathcal {V}$ containing  $\kappa$ such that the
$\kappa$ such that the  $(\leq h)$-slope part of the restriction of (6) to
$(\leq h)$-slope part of the restriction of (6) to  $\mathcal {V}'$ is a short exact sequence of finite free
$\mathcal {V}'$ is a short exact sequence of finite free  $\mathbb {C}_p\widehat {\otimes }_{\mathbb {Q}_p} \mathscr {O}(\mathcal {V}')$-modules.
$\mathbb {C}_p\widehat {\otimes }_{\mathbb {Q}_p} \mathscr {O}(\mathcal {V}')$-modules.(v) Keep the hypothesis of (iv), and let
 $\chi$ be the universal character of
$\chi$ be the universal character of  $\mathcal {V}'$. Let
$\mathcal {V}'$. Let  $\widetilde {\chi }= \chi _1-\chi _2+1 : \mathbb {Z}_p^\times \rightarrow R^{+,\times }$, and
$\widetilde {\chi }= \chi _1-\chi _2+1 : \mathbb {Z}_p^\times \rightarrow R^{+,\times }$, and  $b= {d}/{dt}|_{t=1} \widetilde {\chi }(t)$. Then we have a Galois equivariant split after inverting
$b= {d}/{dt}|_{t=1} \widetilde {\chi }(t)$. Then we have a Galois equivariant split after inverting  $b$
$b$
 \[ H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X)^{\leq h}_{b} =[H^1_{1,c}(X_{\mathbb{C}_p}, \omega_E^{w_0(\chi)})^{\leq h}_{\epsilon}(\chi_1)]_b \oplus [H^0_{w_0}(X_{\mathbb{C}_p}, \omega_E^{\chi+\alpha})^{\leq h}_{\epsilon}(\chi_2-1)]_b. \]
\[ H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X)^{\leq h}_{b} =[H^1_{1,c}(X_{\mathbb{C}_p}, \omega_E^{w_0(\chi)})^{\leq h}_{\epsilon}(\chi_1)]_b \oplus [H^0_{w_0}(X_{\mathbb{C}_p}, \omega_E^{\chi+\alpha})^{\leq h}_{\epsilon}(\chi_2-1)]_b. \]
Remark 1.0.5
(i) The group
 $H^0_w(X_{\mathbb {C}_p}, -)_{\epsilon }$ is the overconvergent cohomology and
$H^0_w(X_{\mathbb {C}_p}, -)_{\epsilon }$ is the overconvergent cohomology and  $H^1_{w,c}(X_{\mathbb {C}_p},-)_{\epsilon }$ the overconvergent cohomology with compact support around the
$H^1_{w,c}(X_{\mathbb {C}_p},-)_{\epsilon }$ the overconvergent cohomology with compact support around the  $w$-ordinary locus of
$w$-ordinary locus of  $X$ (see [Reference Boxer and PilloniBP22] and Definition 3.2.12 below).
$X$ (see [Reference Boxer and PilloniBP22] and Definition 3.2.12 below).(ii) A similar statement holds for the distribution sheaves
 $D^{\delta }_{\chi,{\rm \acute {e}t}}$, in this case the overconvergent Eichler–Shimura map of [Reference Andreatta, Iovita and StevensAIS15] is
$D^{\delta }_{\chi,{\rm \acute {e}t}}$, in this case the overconvergent Eichler–Shimura map of [Reference Andreatta, Iovita and StevensAIS15] is  $ES_{D}$.
$ES_{D}$.(iii) We also prove the theorem for the proétale cohomology with compact support of
 $A_{\chi,{\rm \acute {e}t}}^{\delta }$ and
$A_{\chi,{\rm \acute {e}t}}^{\delta }$ and  $D_{\chi,{\rm \acute {e}t}}^{\delta }$.
$D_{\chi,{\rm \acute {e}t}}^{\delta }$.(iv) Note that if
 $\kappa =(k_1,k_2)$ with
$\kappa =(k_1,k_2)$ with  $k_1+1\neq k_2$ (i.e. when the Hodge–Tate weights are not equal), one can choose
$k_1+1\neq k_2$ (i.e. when the Hodge–Tate weights are not equal), one can choose  $\mathcal {V}'$ small enough such that
$\mathcal {V}'$ small enough such that  $b\neq 0$.
$b\neq 0$.
We finish with the compatibility of the oveconvergent Eichler–Shimura maps (6) with the Poincaré and Serre pairings. One can define a Poincaré pairing between the overconvergent proétale cohomologies
where the left-hand side term is the proétale cohomology with compact support. On the other hand, one also has Serre pairings between overconvergent coherent cohomologies
 \begin{equation} \begin{aligned} & \langle -, -\rangle_S: H^1_{w,c}(X, \omega_E^{-\chi}(-D))_{\epsilon}\times H^{0}_{w}(X,\omega_E^{\chi+\alpha})_{\epsilon} \rightarrow \mathscr{O}(\mathcal{V}'),\\ & \langle -, -\rangle_S: H^1_{w,c}(X, \omega_E^{w_0(\chi)})_{\epsilon}\times H^{0}_{w}(X,\omega_E^{-w_0(\chi)+\alpha}(-D))_{\epsilon} \rightarrow \mathscr{O}(\mathcal{V}'). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & \langle -, -\rangle_S: H^1_{w,c}(X, \omega_E^{-\chi}(-D))_{\epsilon}\times H^{0}_{w}(X,\omega_E^{\chi+\alpha})_{\epsilon} \rightarrow \mathscr{O}(\mathcal{V}'),\\ & \langle -, -\rangle_S: H^1_{w,c}(X, \omega_E^{w_0(\chi)})_{\epsilon}\times H^{0}_{w}(X,\omega_E^{-w_0(\chi)+\alpha}(-D))_{\epsilon} \rightarrow \mathscr{O}(\mathcal{V}'). \end{aligned} \end{equation}We have the following theorem.
Theorem 1.0.6 (Theorem 4.2.3)
(i) The Poincaré and Serre pairings (7) and (8) are compatible with the
 $U_p$-operators and the overconvergent Eichler–Shimura maps.
$U_p$-operators and the overconvergent Eichler–Shimura maps.(ii) Let
 $\mathcal {W}_T$ be the weight space of
$\mathcal {W}_T$ be the weight space of  $T=\mathbf {T}(\mathbb {Z}_p)$, let
$T=\mathbf {T}(\mathbb {Z}_p)$, let  $\mathcal {V}\subset \mathcal {W}_T$ be an open affinoid and
$\mathcal {V}\subset \mathcal {W}_T$ be an open affinoid and  $\chi$ the universal character of
$\chi$ the universal character of  $\mathcal {V}$. Let
$\mathcal {V}$. Let  $\kappa =(k_1,k_2)\in \mathcal {V}$ be a dominant weight and fix
$\kappa =(k_1,k_2)\in \mathcal {V}$ be a dominant weight and fix  $h< k_1-k_2+1$. There exists an open affinoid
$h< k_1-k_2+1$. There exists an open affinoid  $\mathcal {V}'\subset \mathcal {V}$ containing
$\mathcal {V}'\subset \mathcal {V}$ containing  $\kappa$ such that the
$\kappa$ such that the  $(\leq h)$-parts of the pairings (7) and (8) are perfect pairings of finite free
$(\leq h)$-parts of the pairings (7) and (8) are perfect pairings of finite free  $\mathbb {C}_p\widehat {\otimes } \mathscr {O}(\mathcal {V}')$-modules compatible with the Eichler–Shimura decomposition.
$\mathbb {C}_p\widehat {\otimes } \mathscr {O}(\mathcal {V}')$-modules compatible with the Eichler–Shimura decomposition.
The outline of the paper is as follows. In § 2 we develop the overconvergent theory over the flag variety. We define the affinoid subspaces ![]() $U_w(\epsilon )\operatorname {Iw}_n$ and the sheaves
$U_w(\epsilon )\operatorname {Iw}_n$ and the sheaves ![]() $\mathscr {L}(\chi )$. We construct the
$\mathscr {L}(\chi )$. We construct the ![]() $\delta$-analytic principal series
$\delta$-analytic principal series ![]() $A^{\delta }_{\chi }$ and the maps (4). We recall some facts of the BGG theory for irreducible representations of
$A^{\delta }_{\chi }$ and the maps (4). We recall some facts of the BGG theory for irreducible representations of ![]() $\operatorname {GL}_2$; in particular, we define the dual BGG complex
$\operatorname {GL}_2$; in particular, we define the dual BGG complex ![]() $\operatorname {BGG}(\kappa )$.
$\operatorname {BGG}(\kappa )$.
Then in § 3, we translate all the previous constructions from ![]() $\mathbb {P}^1_{\mathbb {Q}_p}$ to the modular curves via
$\mathbb {P}^1_{\mathbb {Q}_p}$ to the modular curves via ![]() $\pi _{\operatorname {HT}}$. We define the strict neighbourhoods of the
$\pi _{\operatorname {HT}}$. We define the strict neighbourhoods of the ![]() $w$-ordinary locus, the overconvergent modular sheaves and the overconvergent Hodge–Tate maps. We give the good normalizations of the Hecke operators and show that the Hodge–Tate maps are compatible with the normalized
$w$-ordinary locus, the overconvergent modular sheaves and the overconvergent Hodge–Tate maps. We give the good normalizations of the Hecke operators and show that the Hodge–Tate maps are compatible with the normalized ![]() $U_p$-correspondence.
$U_p$-correspondence.
Finally, in § 4, we show how to obtain the classical Eichler–Shimura decomposition from the dual BGG complex, proving Theorems 1.0.3 and 1.0.1, in the process we also prove the theorem for the cohomology with compact support. Next, we construct the overconvergent Eichler–Shimura maps and obtain Theorem 1.0.4. Finally, we show the compatibility of Poincaré and Serre duality for the overconvergent Eichler–Shimura maps, obtaining Theorem 1.0.6.
Notation
Throughout this paper we fix a prime number ![]() $p$, we fix an algebraic closure of
$p$, we fix an algebraic closure of ![]() $\mathbb {Q}_p$ and denote by
$\mathbb {Q}_p$ and denote by ![]() $\mathbb {C}_p$ its
$\mathbb {C}_p$ its ![]() $p$-adic completion. We will work with adic spaces over
$p$-adic completion. We will work with adic spaces over ![]() $\operatorname {Spa}(\mathbb {Q}_p,\mathbb {Z}_p)$ which are either locally topologically of finite type over a non-archimedean extension
$\operatorname {Spa}(\mathbb {Q}_p,\mathbb {Z}_p)$ which are either locally topologically of finite type over a non-archimedean extension ![]() $K$ of
$K$ of ![]() $\mathbb {Q}_p$, or perfectoid spaces.
$\mathbb {Q}_p$, or perfectoid spaces.
Let ![]() $X$ be a log adic space over
$X$ be a log adic space over ![]() $\mathbb {Q}_p$; we will work with the proétale and pro-Kummer-étale site of
$\mathbb {Q}_p$; we will work with the proétale and pro-Kummer-étale site of ![]() $X$ as introduced in [Reference ScholzeSch13] and [Reference Diao, Lan, Liu and ZhuDLLZ23a, Reference Diao, Lan, Liu and ZhuDLLZ23b]. We denote by
$X$ as introduced in [Reference ScholzeSch13] and [Reference Diao, Lan, Liu and ZhuDLLZ23a, Reference Diao, Lan, Liu and ZhuDLLZ23b]. We denote by ![]() $X_{?}$, with
$X_{?}$, with ![]() $?\in \{{\rm an}, {\rm \acute {e}t},{\rm k\acute {e}t},{\rm pro\acute {e}t},{\rm prok\acute {e}t}\}$, the analytic, étale, Kummer-étale, proétale and pro-Kummer-étale sites of
$?\in \{{\rm an}, {\rm \acute {e}t},{\rm k\acute {e}t},{\rm pro\acute {e}t},{\rm prok\acute {e}t}\}$, the analytic, étale, Kummer-étale, proétale and pro-Kummer-étale sites of ![]() $X$, respectively. A space without an underlying log structure will be endowed with the trivial one. Fibre products are always fibre products of fs log adic spaces unless otherwise specified (cf. [Reference Diao, Lan, Liu and ZhuDLLZ23b, Proposition 2.3.27]).
$X$, respectively. A space without an underlying log structure will be endowed with the trivial one. Fibre products are always fibre products of fs log adic spaces unless otherwise specified (cf. [Reference Diao, Lan, Liu and ZhuDLLZ23b, Proposition 2.3.27]).
Finally, we will denote by ![]() $\mathscr {O}_{X}^{(+)}$ the uncompleted structural sheaves over
$\mathscr {O}_{X}^{(+)}$ the uncompleted structural sheaves over ![]() $X_{{\rm prok\acute {e}t}}$, and by
$X_{{\rm prok\acute {e}t}}$, and by ![]() $\widehat {\mathscr {O}}_X^{(+)}$ their
$\widehat {\mathscr {O}}_X^{(+)}$ their ![]() $p$-adic completion, omitting the index
$p$-adic completion, omitting the index ![]() $X$ if the space is clear in the context. Let
$X$ if the space is clear in the context. Let ![]() $V$ be a topological
$V$ be a topological ![]() $\mathbb {Z}_p$-module. By an abuse of notation we also denote by
$\mathbb {Z}_p$-module. By an abuse of notation we also denote by ![]() $V$ the pro-Kummer-étale sheaf over
$V$ the pro-Kummer-étale sheaf over ![]() $X_{{\rm prok\acute {e}t}}$ whose points at an object
$X_{{\rm prok\acute {e}t}}$ whose points at an object ![]() $U$ are equal to the space of continuous functions
$U$ are equal to the space of continuous functions ![]() $\mathrm {Cont}(|U|, V)$, where
$\mathrm {Cont}(|U|, V)$, where ![]() $|U|$ is the underlying topological space attached to
$|U|$ is the underlying topological space attached to ![]() $U$.
$U$.
2. Overconvergent sheaves over the flag variety
Let ![]() $\operatorname {GL}_2$ be the algebraic group of invertible
$\operatorname {GL}_2$ be the algebraic group of invertible ![]() $2\times 2$ matrices. Let
$2\times 2$ matrices. Let ![]() $\mathbf {B}$ and
$\mathbf {B}$ and ![]() $\mathbf {T}$ respectively be the upper triangular Borel and the diagonal torus of
$\mathbf {T}$ respectively be the upper triangular Borel and the diagonal torus of ![]() $\operatorname {GL}_2$, and let
$\operatorname {GL}_2$, and let ![]() $\mathbf {N}\subset \mathbf {B}$ be the unipotent radical consisting of upper triangular unipotent matrices. We also let
$\mathbf {N}\subset \mathbf {B}$ be the unipotent radical consisting of upper triangular unipotent matrices. We also let ![]() $\overline {\mathbf {B}}$ and
$\overline {\mathbf {B}}$ and ![]() $\overline {\mathbf {N}}$ be the lower triangular Borel and its unipotent radical, respectively. Let
$\overline {\mathbf {N}}$ be the lower triangular Borel and its unipotent radical, respectively. Let ![]() $W=\{1,w_0\}$ be the Weyl group of
$W=\{1,w_0\}$ be the Weyl group of ![]() $\operatorname {GL}_2$. Given
$\operatorname {GL}_2$. Given ![]() $n\geq 1$, we let
$n\geq 1$, we let ![]() $\operatorname {Iw}_n\subset \operatorname {GL}_2(\mathbb {Z}_p)$ denote the Iwahori subgroup of level
$\operatorname {Iw}_n\subset \operatorname {GL}_2(\mathbb {Z}_p)$ denote the Iwahori subgroup of level ![]() $p^n$, that is, the subgroup of invertible matrices
$p^n$, that is, the subgroup of invertible matrices ![]() $\big (\begin {smallmatrix} a & b \\ c & d\end {smallmatrix} \big )$ such that
$\big (\begin {smallmatrix} a & b \\ c & d\end {smallmatrix} \big )$ such that ![]() $c \equiv 0\ \mathrm {mod}~p^n$. We let
$c \equiv 0\ \mathrm {mod}~p^n$. We let ![]() $\operatorname {FL}= \mathbf {B}\backslash\!\operatorname {GL}_2$ be the flag variety and
$\operatorname {FL}= \mathbf {B}\backslash\!\operatorname {GL}_2$ be the flag variety and ![]() $\operatorname {\mathscr {F}\!\ell }$ its analytification to an adic space over
$\operatorname {\mathscr {F}\!\ell }$ its analytification to an adic space over ![]() $\operatorname {Spa}(\mathbb {Q}_p, \mathbb {Z}_p)$. From now on, we see all the previous schemes as living over
$\operatorname {Spa}(\mathbb {Q}_p, \mathbb {Z}_p)$. From now on, we see all the previous schemes as living over ![]() $\mathbb {Q}_p$.
$\mathbb {Q}_p$.
The goal of this section is to introduce a family of ![]() $\operatorname {Iw}_n$-stable overconvergent neighbourhoods of the
$\operatorname {Iw}_n$-stable overconvergent neighbourhoods of the ![]() $\operatorname {Iw}_n$-orbit of
$\operatorname {Iw}_n$-orbit of ![]() $w\in W$ in
$w\in W$ in ![]() $\operatorname {\mathscr {F}\!\ell }$. Then we introduce some
$\operatorname {\mathscr {F}\!\ell }$. Then we introduce some ![]() $\operatorname {Iw}_n$-equivariant line bundles which play the role of the overconvergent modular sheaves over
$\operatorname {Iw}_n$-equivariant line bundles which play the role of the overconvergent modular sheaves over ![]() $\operatorname {\mathscr {F}\!\ell }$. Finally, we construct some weight vector morphisms, which will be translated into the overconvergent Hodge–Tate maps over the modular curve.
$\operatorname {\mathscr {F}\!\ell }$. Finally, we construct some weight vector morphisms, which will be translated into the overconvergent Hodge–Tate maps over the modular curve.
For future reference we make the following convention.
Convention 2.0.7 Let ![]() $\mathbf {H}$ be an algebraic group scheme over
$\mathbf {H}$ be an algebraic group scheme over ![]() $\operatorname {Spec} \mathbb {Z}_p$. We denote by
$\operatorname {Spec} \mathbb {Z}_p$. We denote by ![]() $\mathcal {H}^0$ the rigid generic fibre of the
$\mathcal {H}^0$ the rigid generic fibre of the ![]() $p$-adic completion of
$p$-adic completion of ![]() $\mathbf {H}$, and by
$\mathbf {H}$, and by ![]() $\mathcal {H}$ the analytification of the schematic generic fibre of
$\mathcal {H}$ the analytification of the schematic generic fibre of ![]() $\mathbf {H}$ (see [Reference HuberHub96]). Given a rational number
$\mathbf {H}$ (see [Reference HuberHub96]). Given a rational number ![]() $\delta >0$, we let
$\delta >0$, we let ![]() $\mathcal {H}(\delta )\subset \mathcal {H}^0\subset \mathcal {H}$ denote the open subgroup whose
$\mathcal {H}(\delta )\subset \mathcal {H}^0\subset \mathcal {H}$ denote the open subgroup whose ![]() $(R,R^+)$-points are
$(R,R^+)$-points are
We call ![]() $\mathcal {H}(\delta )$ the
$\mathcal {H}(\delta )$ the ![]() $\delta$-neighbourhood of the identity in
$\delta$-neighbourhood of the identity in ![]() $\mathcal {H}$.
$\mathcal {H}$.
It will be useful to introduce some particular open subgroups of ![]() $\operatorname {\mathcal {G}\!\mathcal {L}}_2$.
$\operatorname {\mathcal {G}\!\mathcal {L}}_2$.
Definition 2.0.8 Let ![]() $\epsilon \geq \delta$ be positive rational numbers.
$\epsilon \geq \delta$ be positive rational numbers.
(i) We let
 \[ \operatorname{\mathcal{G}\!\mathcal{L}}_2(\epsilon,\delta):= \mathcal{N}(\delta)\times \mathcal{T}(\delta) \times \overline{\mathcal{N}}(\epsilon)\subset \operatorname{\mathcal{G}\!\mathcal{L}}_2. \]
\[ \operatorname{\mathcal{G}\!\mathcal{L}}_2(\epsilon,\delta):= \mathcal{N}(\delta)\times \mathcal{T}(\delta) \times \overline{\mathcal{N}}(\epsilon)\subset \operatorname{\mathcal{G}\!\mathcal{L}}_2. \]
(ii) Suppose that
 $\delta \geq n$. The
$\delta \geq n$. The  $\delta$-neighbourhood of
$\delta$-neighbourhood of  $\operatorname {Iw}_n$ in
$\operatorname {Iw}_n$ in  $\operatorname {\mathcal {G}\!\mathcal {L}}_2$ is the open subgroup
We refer to
$\operatorname {\mathcal {G}\!\mathcal {L}}_2$ is the open subgroup
We refer to \[ \operatorname{\mathcal{I}\!w}_n({\delta}):= \operatorname{Iw}_n \operatorname{\mathcal{G}\!\mathcal{L}}_2(\delta)= \operatorname{\mathcal{G}\!\mathcal{L}}_2(\delta)\operatorname{Iw}_n. \]
\[ \operatorname{\mathcal{I}\!w}_n({\delta}):= \operatorname{Iw}_n \operatorname{\mathcal{G}\!\mathcal{L}}_2(\delta)= \operatorname{\mathcal{G}\!\mathcal{L}}_2(\delta)\operatorname{Iw}_n. \]
 $\operatorname {\mathcal {I}\!w}_n(\delta )$ as an affinoid Iwahori subgroup of
$\operatorname {\mathcal {I}\!w}_n(\delta )$ as an affinoid Iwahori subgroup of  $\operatorname {\mathcal {G}\!\mathcal {L}}_2$.
$\operatorname {\mathcal {G}\!\mathcal {L}}_2$.(iii) We let
 $T$,
$T$,  $B$,
$B$,  $N$, etc. denote the
$N$, etc. denote the  $\mathbb {Z}_p$-points of
$\mathbb {Z}_p$-points of  $\mathbf {T}$,
$\mathbf {T}$,  $\mathbf {B}$,
$\mathbf {B}$,  $\mathbf {N}$, etc. Let
$\mathbf {N}$, etc. Let  $n\geq 1$. We define the following subgroups of
$n\geq 1$. We define the following subgroups of  $T$,
$T$,  $N$ and
$N$ and  $\overline {N}$
$\overline {N}$
 \[ T_n= \biggl( \begin{matrix} 1+p^n \mathbb{Z}_p & 0 \\ 0 & 1+p^n \mathbb{Z}_p \end{matrix} \biggr), \quad N_n=\biggl( \begin{matrix} 1 & p^n \mathbb{Z}_p \\ 0 & 1 \end{matrix} \biggr), \quad \overline{N}_n = \biggl( \begin{matrix} 1 & 0 \\ p^n \mathbb{Z}_p & 1 \end{matrix} \biggr). \]
\[ T_n= \biggl( \begin{matrix} 1+p^n \mathbb{Z}_p & 0 \\ 0 & 1+p^n \mathbb{Z}_p \end{matrix} \biggr), \quad N_n=\biggl( \begin{matrix} 1 & p^n \mathbb{Z}_p \\ 0 & 1 \end{matrix} \biggr), \quad \overline{N}_n = \biggl( \begin{matrix} 1 & 0 \\ p^n \mathbb{Z}_p & 1 \end{matrix} \biggr). \]
2.1  $\operatorname {GL}_2$-equivariant sheaves over the flag variety
$\operatorname {GL}_2$-equivariant sheaves over the flag variety
In this subsection we fix notation for the representation theory of ![]() $\operatorname {GL}_2$. Let
$\operatorname {GL}_2$. Let ![]() $X^*(\mathbf {T})$ be the character group of the diagonal torus; we identify
$X^*(\mathbf {T})$ be the character group of the diagonal torus; we identify ![]() $X^*(\mathbf {T}) \cong \mathbb {Z}^2$ via the presentation
$X^*(\mathbf {T}) \cong \mathbb {Z}^2$ via the presentation
A weight ![]() $\kappa \in X^*(\mathbf {T})$, written as
$\kappa \in X^*(\mathbf {T})$, written as ![]() $\kappa = (k_1,k_2)$, is said to be dominant if
$\kappa = (k_1,k_2)$, is said to be dominant if ![]() $k_1\geq k_2$. We denote by
$k_1\geq k_2$. We denote by ![]() $X^*(\mathbf {T})^+$ the cone of dominant weights. Given
$X^*(\mathbf {T})^+$ the cone of dominant weights. Given ![]() $\kappa \in X^*(\mathbf {T})^+$, we let
$\kappa \in X^*(\mathbf {T})^+$, we let ![]() $V_{\kappa }$ denote the irreducible algebraic representation of
$V_{\kappa }$ denote the irreducible algebraic representation of ![]() $\operatorname {GL}_2$ of highest weight
$\operatorname {GL}_2$ of highest weight ![]() $\kappa$. Letting
$\kappa$. Letting ![]() $\operatorname {St}$ and
$\operatorname {St}$ and ![]() $\det$ respectively be the standard and the determinant representations of
$\det$ respectively be the standard and the determinant representations of ![]() $\operatorname {GL}_2$, explicitly one has that
$\operatorname {GL}_2$, explicitly one has that ![]() $V_{\kappa } \cong \operatorname {Sym}^{k_1-k_2} \operatorname {St} \otimes \det ^{k_2}$.
$V_{\kappa } \cong \operatorname {Sym}^{k_1-k_2} \operatorname {St} \otimes \det ^{k_2}$.
Since ![]() $\operatorname {FL}= \mathbf {B}\backslash\!\operatorname {GL}_2$, there is an equivalence between the category of algebraic representations of
$\operatorname {FL}= \mathbf {B}\backslash\!\operatorname {GL}_2$, there is an equivalence between the category of algebraic representations of ![]() $\mathbf {B}$ and the category of
$\mathbf {B}$ and the category of ![]() $\operatorname {GL}_2$-equivariant vector bundles over
$\operatorname {GL}_2$-equivariant vector bundles over ![]() $\operatorname {FL}$. Explicitly, given
$\operatorname {FL}$. Explicitly, given ![]() $W$ a representation of
$W$ a representation of ![]() $\mathbf {B}$, one forms the
$\mathbf {B}$, one forms the ![]() $\operatorname {GL}_2$-equivariant vector bundle
$\operatorname {GL}_2$-equivariant vector bundle
where in the right-hand-side term the group ![]() $\mathbf {B}$ acts diagonally.
$\mathbf {B}$ acts diagonally.
Definition 2.1.1 Let ![]() $\kappa \in X^*(\mathbf {T})$. We define
$\kappa \in X^*(\mathbf {T})$. We define ![]() $\mathscr {L}(\kappa )$ to be the
$\mathscr {L}(\kappa )$ to be the ![]() $\operatorname {GL}_2$-equivariant line bundle given by
$\operatorname {GL}_2$-equivariant line bundle given by ![]() $\operatorname {GL}_w \times ^{\mathbf {B}} w_0(\kappa )$.
$\operatorname {GL}_w \times ^{\mathbf {B}} w_0(\kappa )$.
Remark 2.1.2 (i) The line bundle ![]() $\mathcal {L}(\kappa )$ can be described in the following way. Let
$\mathcal {L}(\kappa )$ can be described in the following way. Let ![]() $\widetilde {\operatorname {FL}}= \mathbf {N}\backslash\!\operatorname {GL}_2$ be the natural
$\widetilde {\operatorname {FL}}= \mathbf {N}\backslash\!\operatorname {GL}_2$ be the natural ![]() $\mathbf {T}$-torsor over
$\mathbf {T}$-torsor over ![]() $\operatorname {FL}$ and
$\operatorname {FL}$ and ![]() $\pi : \widetilde {\operatorname {FL}} \to \operatorname {FL}$ the projection map. Then
$\pi : \widetilde {\operatorname {FL}} \to \operatorname {FL}$ the projection map. Then ![]() $\pi _* \mathscr {O}_{\widetilde {\operatorname {FL}}}$ is endowed with a left regular action of
$\pi _* \mathscr {O}_{\widetilde {\operatorname {FL}}}$ is endowed with a left regular action of ![]() $\mathbf {T}$. One can construct the line bundle
$\mathbf {T}$. One can construct the line bundle ![]() $\mathcal {L}(\kappa )$ as the following isotypic component:
$\mathcal {L}(\kappa )$ as the following isotypic component:
The previous description shows that
(ii) The convention on the weight is made such that, if ![]() $\kappa$ is dominant, then
$\kappa$ is dominant, then ![]() $\Gamma (\operatorname {FL}, \mathcal {L}(\kappa ))$ is isomorphic to
$\Gamma (\operatorname {FL}, \mathcal {L}(\kappa ))$ is isomorphic to ![]() $V_{\kappa }$ as a
$V_{\kappa }$ as a ![]() $\operatorname {GL}_2$-representation.
$\operatorname {GL}_2$-representation.
2.2 Overconvergent line bundles over the flag variety
In order to define the overconvergent line bundles we first need to introduce some affinoid neighbourhoods of ![]() $w\in W$.
$w\in W$.
Definition 2.2.1 Let ![]() $\epsilon >0$ be a rational number,
$\epsilon >0$ be a rational number, ![]() $w \in W$ and
$w \in W$ and ![]() $w\operatorname {\mathcal {G}\!\mathcal {L}}_2(\epsilon )$ the
$w\operatorname {\mathcal {G}\!\mathcal {L}}_2(\epsilon )$ the ![]() $\epsilon$-neighbourhood of
$\epsilon$-neighbourhood of ![]() $w$ in
$w$ in ![]() $\operatorname {\mathcal {G}\!\mathcal {L}}_2$. We denote by
$\operatorname {\mathcal {G}\!\mathcal {L}}_2$. We denote by ![]() $U_w(\epsilon )$ its image in
$U_w(\epsilon )$ its image in ![]() $\operatorname {\mathscr {F}\!\ell }$.
$\operatorname {\mathscr {F}\!\ell }$.
Lemma 2.2.2
(i) The collection
 $\{U_{w}(\epsilon )\}_{\epsilon > 0}$ is a basis of open affinoid neighbourhoods of
$\{U_{w}(\epsilon )\}_{\epsilon > 0}$ is a basis of open affinoid neighbourhoods of  $w\in \operatorname {\mathscr {F}\!\ell }$. Moreover, we have a natural isomorphism
$w\in \operatorname {\mathscr {F}\!\ell }$. Moreover, we have a natural isomorphism
 \begin{align*} \overline{\mathcal{N}}(\epsilon) w \xrightarrow{\sim} U_{w}(\epsilon). \end{align*}
\begin{align*} \overline{\mathcal{N}}(\epsilon) w \xrightarrow{\sim} U_{w}(\epsilon). \end{align*}
(ii) The Iwahori subgroups admit Iwahori decompositions
 \[ \operatorname{\mathcal{I}\!w}_n(\epsilon)= (\overline{N}_n\overline{\mathcal{N}}(\epsilon))\times (T\mathcal{T}(\epsilon))\times (N \mathcal{N}(\epsilon)). \]
\[ \operatorname{\mathcal{I}\!w}_n(\epsilon)= (\overline{N}_n\overline{\mathcal{N}}(\epsilon))\times (T\mathcal{T}(\epsilon))\times (N \mathcal{N}(\epsilon)). \]
(iii) Let
 $\epsilon \geq \delta \geq n \geq 1$. We have decompositions
$\epsilon \geq \delta \geq n \geq 1$. We have decompositions
 \begin{gather*} \operatorname{\mathcal{G}\!\mathcal{L}}_2(\epsilon,\delta) \operatorname{Iw}_n = (N\mathcal{N}(\delta))\times(T \mathcal{T}(\delta))\times(\overline{N}_n \overline{\mathcal{N}}(\epsilon) ),\\ \operatorname{\mathcal{G}\!\mathcal{L}}_2(\epsilon,\delta) w_0 \operatorname{Iw}_n= (N_n \mathcal{N}(\delta))\times (T\mathcal{T}(\delta)) \times( \overline{N} \overline{\mathcal{N}}(\epsilon) )w_0. \end{gather*}
\begin{gather*} \operatorname{\mathcal{G}\!\mathcal{L}}_2(\epsilon,\delta) \operatorname{Iw}_n = (N\mathcal{N}(\delta))\times(T \mathcal{T}(\delta))\times(\overline{N}_n \overline{\mathcal{N}}(\epsilon) ),\\ \operatorname{\mathcal{G}\!\mathcal{L}}_2(\epsilon,\delta) w_0 \operatorname{Iw}_n= (N_n \mathcal{N}(\delta))\times (T\mathcal{T}(\delta)) \times( \overline{N} \overline{\mathcal{N}}(\epsilon) )w_0. \end{gather*}
Proof. The collection ![]() $\{U_w(\epsilon )\}_{\epsilon >0}$ is a basis of neighbourhoods of
$\{U_w(\epsilon )\}_{\epsilon >0}$ is a basis of neighbourhoods of ![]() $w$ since
$w$ since ![]() $\operatorname {\mathscr {F}\!\ell }$ is a locally spectral space and
$\operatorname {\mathscr {F}\!\ell }$ is a locally spectral space and ![]() $\bigcap _{\epsilon >0} U_w(\epsilon )=\{w\}$. The isomorphism
$\bigcap _{\epsilon >0} U_w(\epsilon )=\{w\}$. The isomorphism ![]() $U_w(\epsilon )\cong \overline {\mathcal {N}}(\epsilon )w$ is obvious. Next we prove (ii); part (iii) is proved in a similar way. It suffices to show the equality at
$U_w(\epsilon )\cong \overline {\mathcal {N}}(\epsilon )w$ is obvious. Next we prove (ii); part (iii) is proved in a similar way. It suffices to show the equality at ![]() $(R,R^+)$-points, with
$(R,R^+)$-points, with ![]() $(R,R^+)$ a uniform affinoid
$(R,R^+)$ a uniform affinoid ![]() $\mathbb {Q}_p$-algebra. By definition we have
$\mathbb {Q}_p$-algebra. By definition we have
 \[
\operatorname{\mathcal{I}\!w}_n(\epsilon)= \biggl(
\begin{matrix} \mathbb{Z}_p^\times(1+p^\epsilon
\mathbb{D}^1_{\mathbb{Q}_p}) & \mathbb{Z}_p+p^\epsilon
\mathbb{D}^1_{\mathbb{Q}_p} \\ p^n\mathbb{Z}_p+p^\epsilon
\mathbb{D}^1_{\mathbb{Q}_p} &
\mathbb{Z}_p^\times(1+p^\epsilon
\mathbb{D}^1_{\mathbb{Q}_p}) \end{matrix} \biggr),
\]
\[
\operatorname{\mathcal{I}\!w}_n(\epsilon)= \biggl(
\begin{matrix} \mathbb{Z}_p^\times(1+p^\epsilon
\mathbb{D}^1_{\mathbb{Q}_p}) & \mathbb{Z}_p+p^\epsilon
\mathbb{D}^1_{\mathbb{Q}_p} \\ p^n\mathbb{Z}_p+p^\epsilon
\mathbb{D}^1_{\mathbb{Q}_p} &
\mathbb{Z}_p^\times(1+p^\epsilon
\mathbb{D}^1_{\mathbb{Q}_p}) \end{matrix} \biggr),
\]
where ![]() $\mathbb {D}^1_{\mathbb {Q}_p}=
\operatorname {Spa}(\mathbb {Q}_p\langle T \rangle, \mathbb
{Z}_p \langle T \rangle
)$ is the
closed affinoid disc. Then
$\mathbb {D}^1_{\mathbb {Q}_p}=
\operatorname {Spa}(\mathbb {Q}_p\langle T \rangle, \mathbb
{Z}_p \langle T \rangle
)$ is the
closed affinoid disc. Then
 \[
\operatorname{\mathcal{I}\!w}_n(\epsilon)(R,R^+)= \biggl(
\begin{matrix} \mathbb{Z}_p^\times(1+p^\epsilon R^+) &
\mathbb{Z}_p+p^\epsilon R^+ \\ p^n\mathbb{Z}_p+p^\epsilon
R^+ & \mathbb{Z}_p^\times(1+p^\epsilon R^+) \end{matrix}
\biggr) \]
\[
\operatorname{\mathcal{I}\!w}_n(\epsilon)(R,R^+)= \biggl(
\begin{matrix} \mathbb{Z}_p^\times(1+p^\epsilon R^+) &
\mathbb{Z}_p+p^\epsilon R^+ \\ p^n\mathbb{Z}_p+p^\epsilon
R^+ & \mathbb{Z}_p^\times(1+p^\epsilon R^+) \end{matrix}
\biggr) \]
Let ![]() $g\in \operatorname {\mathcal {I}\!w}_n(\epsilon )(R,R^+)$. Writing
$g\in \operatorname {\mathcal {I}\!w}_n(\epsilon )(R,R^+)$. Writing
and solving the equations, one finds ![]() $x_3\in p^n \mathbb {Z}_p+ p^{\epsilon }R^+$,
$x_3\in p^n \mathbb {Z}_p+ p^{\epsilon }R^+$, ![]() $x_1$ and
$x_1$ and ![]() $x_4\in \mathbb {Z}_p^\times (1+p^{\epsilon }R^+)$, and
$x_4\in \mathbb {Z}_p^\times (1+p^{\epsilon }R^+)$, and ![]() $x_2\in \mathbb {Z}_p+ p^\epsilon R^+$ which gives (ii).
$x_2\in \mathbb {Z}_p+ p^\epsilon R^+$ which gives (ii).
Remark 2.2.3 Let us identify ![]() $\operatorname {\mathscr {F}\!\ell } \cong \mathbb {P}^1_{\mathbb {Q}_p}$ by taking
$\operatorname {\mathscr {F}\!\ell } \cong \mathbb {P}^1_{\mathbb {Q}_p}$ by taking ![]() $[0:1]\in \mathbb {P}^1_{\mathbb {Q}_p}$ as the marked point, and where
$[0:1]\in \mathbb {P}^1_{\mathbb {Q}_p}$ as the marked point, and where ![]() $\operatorname {GL}_2$ acts by
$\operatorname {GL}_2$ acts by
Let ![]() $T= {x}/{y}$ be the canonical coordinate and
$T= {x}/{y}$ be the canonical coordinate and ![]() $\epsilon = p^{-n}$. In the notation of [Reference Andreatta and IovitaAI22, § 4.2] we have
$\epsilon = p^{-n}$. In the notation of [Reference Andreatta and IovitaAI22, § 4.2] we have
 \begin{align*} U_1(\epsilon) &= U_{0,0}^{(n)} = \{[x:y]\in \mathbb{P}^1_{\mathbb{Q}_p} : |T/ p^n|\leq 1\} ,\\ U_{w_0}(\epsilon) & = U_{\infty}^{(n)} = \{[x:y]\in \mathbb{P}^1_{\mathbb{Q}_p} : |1/(p^nT)|\leq 1\}. \end{align*}
\begin{align*} U_1(\epsilon) &= U_{0,0}^{(n)} = \{[x:y]\in \mathbb{P}^1_{\mathbb{Q}_p} : |T/ p^n|\leq 1\} ,\\ U_{w_0}(\epsilon) & = U_{\infty}^{(n)} = \{[x:y]\in \mathbb{P}^1_{\mathbb{Q}_p} : |1/(p^nT)|\leq 1\}. \end{align*}
Lemma 2.2.4 describes the dynamics of the element ![]() $\varpi = \operatorname {diag} (1,p)$ over
$\varpi = \operatorname {diag} (1,p)$ over ![]() $\operatorname {\mathscr {F}\!\ell }$. This action has only two fixed points represented by the elements of
$\operatorname {\mathscr {F}\!\ell }$. This action has only two fixed points represented by the elements of ![]() $W$, and expands or shrinks neighbourhoods of
$W$, and expands or shrinks neighbourhoods of ![]() $1$ and
$1$ and ![]() $w_0$, respectively.
$w_0$, respectively.
Lemma 2.2.4 Let ![]() $\varpi = \operatorname {diag}(1,p)$. The following assertions hold.
$\varpi = \operatorname {diag}(1,p)$. The following assertions hold.
(i)
 $U_1(\epsilon )\varpi = U_1(\epsilon -1)$ and
$U_1(\epsilon )\varpi = U_1(\epsilon -1)$ and  $U_{w_0}(\epsilon )\varpi = U_{w_0}(\epsilon +1)$.
$U_{w_0}(\epsilon )\varpi = U_{w_0}(\epsilon +1)$.(ii) Let
 $\epsilon \geq n \geq 1$. Then
$\epsilon \geq n \geq 1$. Then  $U_1(\epsilon )\operatorname {Iw}_n \varpi = U_1(\epsilon -1)\operatorname {Iw}_{n-1}$ and
$U_1(\epsilon )\operatorname {Iw}_n \varpi = U_1(\epsilon -1)\operatorname {Iw}_{n-1}$ and  $U_{w_0}(\epsilon )\operatorname {Iw}_n \varpi =U_{w_0}(\epsilon +1) N_1$.
$U_{w_0}(\epsilon )\operatorname {Iw}_n \varpi =U_{w_0}(\epsilon +1) N_1$.
Proof. The proof follows from Lemma 2.2.2 and the computation
Let ![]() $\Gamma$ be a finite
$\Gamma$ be a finite ![]() $\mathbb {Z}_p$-module. Abstractly,
$\mathbb {Z}_p$-module. Abstractly, ![]() $\Gamma$ is isomorphic to
$\Gamma$ is isomorphic to ![]() $\mathbb {Z}_p^s\bigoplus \Gamma _{\mathrm {tor}}$ where
$\mathbb {Z}_p^s\bigoplus \Gamma _{\mathrm {tor}}$ where ![]() $s\in \mathbb {N}$ and
$s\in \mathbb {N}$ and ![]() $\Gamma _{\mathrm {tor}}\subset \Gamma$ is the torsion subgroup; we call such an isomorphism a chart of
$\Gamma _{\mathrm {tor}}\subset \Gamma$ is the torsion subgroup; we call such an isomorphism a chart of ![]() $\Gamma$. Let
$\Gamma$. Let ![]() $\mathcal {V}=\operatorname {Spa}(R,R^+)$ be an affinoid adic space with
$\mathcal {V}=\operatorname {Spa}(R,R^+)$ be an affinoid adic space with ![]() $R$ an uniform Tate
$R$ an uniform Tate ![]() $\mathbb {Q}_p$-algebra, and
$\mathbb {Q}_p$-algebra, and ![]() $\chi : \Gamma \to R^{+,\times }$ a continuous character.
$\chi : \Gamma \to R^{+,\times }$ a continuous character.
Lemma 2.2.5 [Reference UrbanUrb11, Lemma 3.4.6]
Let ![]() $\psi : \Gamma \cong \mathbb {Z}_p^s\times \Gamma _{\mathrm {tor}}$ be a chart. There exists
$\psi : \Gamma \cong \mathbb {Z}_p^s\times \Gamma _{\mathrm {tor}}$ be a chart. There exists ![]() $\delta >0$ such that
$\delta >0$ such that ![]() $\chi$ extends to a character
$\chi$ extends to a character
We say that ![]() $\chi$ is a
$\chi$ is a ![]() $\delta$-analytic character of
$\delta$-analytic character of ![]() $\Gamma$ with respect to the chart
$\Gamma$ with respect to the chart ![]() $\psi$.
$\psi$.
Remark 2.2.6 In the following we will take ![]() $\Gamma = T$, and we say that
$\Gamma = T$, and we say that ![]() $\chi$ is
$\chi$ is ![]() $\delta$-analytic if it extends to a character of
$\delta$-analytic if it extends to a character of ![]() $T\mathcal {T}(\delta )$. Let
$T\mathcal {T}(\delta )$. Let ![]() $\mathfrak {W}_T = \operatorname {Spf} \mathbb {Z}_p[[T]]$ be the weight space of
$\mathfrak {W}_T = \operatorname {Spf} \mathbb {Z}_p[[T]]$ be the weight space of ![]() $T$ and
$T$ and ![]() $\mathcal {W}_T$ its rigid generic fibre, in practice we will take
$\mathcal {W}_T$ its rigid generic fibre, in practice we will take ![]() $\mathcal {V}= \operatorname {Spa}(R,R^+)\subset \mathcal {W}_T$ an affinoid subspace and
$\mathcal {V}= \operatorname {Spa}(R,R^+)\subset \mathcal {W}_T$ an affinoid subspace and ![]() $\chi = \chi _{\mathrm {univ}}$ the universal character over
$\chi = \chi _{\mathrm {univ}}$ the universal character over ![]() $\mathcal {V}$.
$\mathcal {V}$.
Definition 2.2.7 Let ![]() $\epsilon \geq \delta \geq n \geq 1$,
$\epsilon \geq \delta \geq n \geq 1$, ![]() $w\in W$, and
$w\in W$, and ![]() $\widetilde {\operatorname {\mathscr {F}\!\ell }}= \mathcal {N}\backslash\!\operatorname {\mathcal {G}\!\mathcal {L}}_2$ the natural
$\widetilde {\operatorname {\mathscr {F}\!\ell }}= \mathcal {N}\backslash\!\operatorname {\mathcal {G}\!\mathcal {L}}_2$ the natural ![]() $\mathcal {T}$-torsor over
$\mathcal {T}$-torsor over ![]() $\operatorname {\mathscr {F}\!\ell }$.
$\operatorname {\mathscr {F}\!\ell }$.
(i) We define the following neighbourhood of
 $w$ in
$w$ in  $\widetilde {\operatorname {\mathscr {F}\!\ell }}$:
Let
$\widetilde {\operatorname {\mathscr {F}\!\ell }}$:
Let \[ \widetilde{U}_{w}(\epsilon,\delta)= \mathcal{N}(\delta) \backslash\! \operatorname{\mathcal{G}\!\mathcal{L}}_2(\epsilon,\delta) w. \]
\[ \widetilde{U}_{w}(\epsilon,\delta)= \mathcal{N}(\delta) \backslash\! \operatorname{\mathcal{G}\!\mathcal{L}}_2(\epsilon,\delta) w. \]
 $\operatorname {pr}: \widetilde {U}_w(\epsilon,\delta )\operatorname {Iw}_n \to U_w(\epsilon )\operatorname {Iw}_n$ denote the natural projection, Lemma 2.2.2(iii) implies that
$\operatorname {pr}: \widetilde {U}_w(\epsilon,\delta )\operatorname {Iw}_n \to U_w(\epsilon )\operatorname {Iw}_n$ denote the natural projection, Lemma 2.2.2(iii) implies that  $\operatorname {pr}$ is a trivial
$\operatorname {pr}$ is a trivial  $T\mathcal {T(\delta )}$-torsor.
$T\mathcal {T(\delta )}$-torsor.(ii) Let
 $\chi : T \to R^\times$ be a
$\chi : T \to R^\times$ be a  $\delta$-analytic character. We define the
$\delta$-analytic character. We define the  $\mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}\widehat {\otimes } R$-line bundle
In other words,
$\mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}\widehat {\otimes } R$-line bundle
In other words, \[ \mathcal{L}(\chi)= \operatorname{pr}_* \mathscr{O}_{\widetilde{U}_w(\epsilon, \delta) }\widehat{\otimes} R [-w_0(\chi)]. \]
\[ \mathcal{L}(\chi)= \operatorname{pr}_* \mathscr{O}_{\widetilde{U}_w(\epsilon, \delta) }\widehat{\otimes} R [-w_0(\chi)]. \]
 $\mathcal {L}(\chi )$ is the line bundle whose sections over
$\mathcal {L}(\chi )$ is the line bundle whose sections over  $U\subset U_w(\epsilon )\operatorname {Iw}_n$ are
$U\subset U_w(\epsilon )\operatorname {Iw}_n$ are
 \[ \mathcal{L}(\chi)(U)= \{f \in \mathscr{O}_{\operatorname{\mathscr{F}\!\ell}}(\operatorname{pr}^{-1}(U))\widehat{\otimes }R : f(tx) = w_0(\chi)(t)f(x), \text{ for } t\in T\mathcal{T}(\delta)\}. \]
\[ \mathcal{L}(\chi)(U)= \{f \in \mathscr{O}_{\operatorname{\mathscr{F}\!\ell}}(\operatorname{pr}^{-1}(U))\widehat{\otimes }R : f(tx) = w_0(\chi)(t)f(x), \text{ for } t\in T\mathcal{T}(\delta)\}. \]
Remark 2.2.8 Let ![]() $\varpi = \operatorname {diag}(1,p)$,
$\varpi = \operatorname {diag}(1,p)$, ![]() $c= \operatorname {diag}(p,p)$, and
$c= \operatorname {diag}(p,p)$, and ![]() $\Lambda = \langle \varpi, c\rangle \subset \mathbf {T}(\mathbb {Q}_p)$. The natural map
$\Lambda = \langle \varpi, c\rangle \subset \mathbf {T}(\mathbb {Q}_p)$. The natural map ![]() $\widetilde {\operatorname {\mathscr {F}\!\ell }}\to \Lambda \backslash \widetilde {\operatorname {\mathscr {F}\!\ell }}$ identifies
$\widetilde {\operatorname {\mathscr {F}\!\ell }}\to \Lambda \backslash \widetilde {\operatorname {\mathscr {F}\!\ell }}$ identifies ![]() $\widetilde {U}_w(\epsilon,\delta )$ with an open affinoid of the quotient, namely, the
$\widetilde {U}_w(\epsilon,\delta )$ with an open affinoid of the quotient, namely, the ![]() $\Lambda$ orbit of
$\Lambda$ orbit of ![]() $\widetilde {U}_w(\epsilon,\delta )$ in
$\widetilde {U}_w(\epsilon,\delta )$ in ![]() $\widetilde {\operatorname {\mathscr {F}\!\ell }}$ is the disjoint union
$\widetilde {\operatorname {\mathscr {F}\!\ell }}$ is the disjoint union
By construction, the sheaves ![]() $\mathcal {L}(\chi )$ are independent of
$\mathcal {L}(\chi )$ are independent of ![]() $\delta$ and
$\delta$ and ![]() $\epsilon$. They fit in a
$\epsilon$. They fit in a ![]() $U_p$-correspondence as follows. Let
$U_p$-correspondence as follows. Let ![]() $\varpi = \operatorname {diag}(1,p)$ and consider the double coset
$\varpi = \operatorname {diag}(1,p)$ and consider the double coset ![]() $\operatorname {Iw}_n \varpi \operatorname {Iw}_n$. Then one has that
$\operatorname {Iw}_n \varpi \operatorname {Iw}_n$. Then one has that
 \[ \operatorname{Iw}_n \varpi \operatorname{Iw}_n=\bigsqcup_{a=0}^{p-1} \operatorname{Iw}_n \biggl( \begin{matrix} 1 & -a \\ 0 & p \end{matrix} \biggr). \]
\[ \operatorname{Iw}_n \varpi \operatorname{Iw}_n=\bigsqcup_{a=0}^{p-1} \operatorname{Iw}_n \biggl( \begin{matrix} 1 & -a \\ 0 & p \end{matrix} \biggr). \]
Let us denote ![]() $U_{p,a}=\big (\begin {smallmatrix} 1 & -a \\ 0 & p \end {smallmatrix} \big )$.
$U_{p,a}=\big (\begin {smallmatrix} 1 & -a \\ 0 & p \end {smallmatrix} \big )$.
Definition 2.2.9 We define the ![]() $U_p$-correspondence of
$U_p$-correspondence of ![]() $\widetilde {\operatorname {\mathscr {F}\!\ell }}$ (respectively, the normalized
$\widetilde {\operatorname {\mathscr {F}\!\ell }}$ (respectively, the normalized ![]() $U_p$-correspondence of
$U_p$-correspondence of ![]() $\Lambda \backslash \widetilde {\operatorname {\mathscr {F}\!\ell }}$) to be the diagram
$\Lambda \backslash \widetilde {\operatorname {\mathscr {F}\!\ell }}$) to be the diagram

(respectively, for ![]() $\Lambda \backslash \widetilde {\operatorname {\mathscr {F}\!\ell }}$), where
$\Lambda \backslash \widetilde {\operatorname {\mathscr {F}\!\ell }}$), where ![]() $\widetilde {\operatorname {\mathscr {F}\!\ell }}_a= \widetilde {\operatorname {\mathscr {F}\!\ell }}$,
$\widetilde {\operatorname {\mathscr {F}\!\ell }}_a= \widetilde {\operatorname {\mathscr {F}\!\ell }}$, ![]() $p_1|_{ \widetilde {\operatorname {\mathscr {F}\!\ell }}_a}= \operatorname {id}_{ \operatorname {\mathscr {F}\!\ell }}$, and
$p_1|_{ \widetilde {\operatorname {\mathscr {F}\!\ell }}_a}= \operatorname {id}_{ \operatorname {\mathscr {F}\!\ell }}$, and ![]() $p_2 |_{\operatorname {\mathscr {F}\!\ell }_a} = R_{U_{p,a}^{-1}}$ is right multiplication by
$p_2 |_{\operatorname {\mathscr {F}\!\ell }_a} = R_{U_{p,a}^{-1}}$ is right multiplication by ![]() $U_{p,a}^{-1}$.
$U_{p,a}^{-1}$.
Remark 2.2.10 The correspondence (10) is equivariant for the natural action of ![]() $\operatorname {Iw}_n$, namely, the group acts by right multiplication on the bottom spaces, and it acts on the disjoint union
$\operatorname {Iw}_n$, namely, the group acts by right multiplication on the bottom spaces, and it acts on the disjoint union ![]() $\bigsqcup _{a=0}^{p-1}\widetilde {\operatorname {\mathscr {F}\!\ell }}$ as follows. Let
$\bigsqcup _{a=0}^{p-1}\widetilde {\operatorname {\mathscr {F}\!\ell }}$ as follows. Let ![]() $\gamma \in \operatorname {Iw}_n$ and
$\gamma \in \operatorname {Iw}_n$ and ![]() $a,a'\in \{0,\ldots, p-1\}$ such that
$a,a'\in \{0,\ldots, p-1\}$ such that
Then, given ![]() $x\in \operatorname {\mathscr {F}\!\ell }_a$, we define
$x\in \operatorname {\mathscr {F}\!\ell }_a$, we define ![]() $x\cdot \gamma$ to be
$x\cdot \gamma$ to be ![]() $x\gamma \in \operatorname {\mathscr {F}\!\ell }_{a'}$. This action satisfies the following properties.
$x\gamma \in \operatorname {\mathscr {F}\!\ell }_{a'}$. This action satisfies the following properties.
(i) The map
 $p_1$ is
$p_1$ is  $\operatorname {Iw}_n$-equivariant.
$\operatorname {Iw}_n$-equivariant.(ii) The map
 $p_2$ preserves
$p_2$ preserves  $\operatorname {Iw}_n$-orbits, that is, the composition
$\operatorname {Iw}_n$-orbits, that is, the composition  $\bigsqcup _{a=0}^{p-1}\widetilde {\operatorname {\mathscr {F}\!\ell }}\xrightarrow {p_2}\widetilde {\operatorname {\mathscr {F}\!\ell }}/\operatorname {Iw}_n$ onto the quotient stackFootnote 1 factors through
$\bigsqcup _{a=0}^{p-1}\widetilde {\operatorname {\mathscr {F}\!\ell }}\xrightarrow {p_2}\widetilde {\operatorname {\mathscr {F}\!\ell }}/\operatorname {Iw}_n$ onto the quotient stackFootnote 1 factors through  $(\bigsqcup _{a=0}^{p-1} \widetilde {\operatorname {\mathscr {F}\!\ell }})/\operatorname {Iw}_n$.
$(\bigsqcup _{a=0}^{p-1} \widetilde {\operatorname {\mathscr {F}\!\ell }})/\operatorname {Iw}_n$.
The previous points show that we have a correspondence of stacks

In § 3 we will relate this diagram to the ![]() $U_p$-correspondence of modular curves.
$U_p$-correspondence of modular curves.
The following lemma describes the dynamics of the correspondence on neighbourhoods of ![]() $1$ and
$1$ and ![]() $w_0$.
$w_0$.
Lemma 2.2.11 The following assertions hold.
(i)
 $p_2 (p_1^{-1}( \widetilde {U}_{w_0}(\epsilon,\delta )\operatorname {Iw}_n)) \supset \widetilde {U}_{w_0}(\epsilon -1,\delta )\operatorname {Iw}_n$.
$p_2 (p_1^{-1}( \widetilde {U}_{w_0}(\epsilon,\delta )\operatorname {Iw}_n)) \supset \widetilde {U}_{w_0}(\epsilon -1,\delta )\operatorname {Iw}_n$.(ii)
 $p_2 (p_1^{-1}(\widetilde {U}_{1}(\epsilon,\delta )\operatorname {Iw}_n )) \subset \widetilde {U}_1(\epsilon +1, \delta )\operatorname {Iw}_n$.
$p_2 (p_1^{-1}(\widetilde {U}_{1}(\epsilon,\delta )\operatorname {Iw}_n )) \subset \widetilde {U}_1(\epsilon +1, \delta )\operatorname {Iw}_n$.(iii)
 $p_1 (p_2^{-1}(\widetilde {U}_{w_0}(\epsilon, \delta ) \operatorname {Iw}_n ))\subset \widetilde {U}_{w_0}(\epsilon +1,\delta )\operatorname {Iw}_n$.
$p_1 (p_2^{-1}(\widetilde {U}_{w_0}(\epsilon, \delta ) \operatorname {Iw}_n ))\subset \widetilde {U}_{w_0}(\epsilon +1,\delta )\operatorname {Iw}_n$.(iv)
 $p_1 (p_2^{-1}(\widetilde {U}_{1}(\epsilon, \delta ) \operatorname {Iw}_n)) \supset \widetilde {U}_{1}(\epsilon -1, \delta )\operatorname {Iw}_n$.
$p_1 (p_2^{-1}(\widetilde {U}_{1}(\epsilon, \delta ) \operatorname {Iw}_n)) \supset \widetilde {U}_{1}(\epsilon -1, \delta )\operatorname {Iw}_n$.
Proof. These assertions follow from the definition of the correspondence and Lemma 2.2.4.
Definition 2.2.12
(i) Let
 $\kappa \in X^*(\mathbf {T})$. We define the
$\kappa \in X^*(\mathbf {T})$. We define the  $U_{p,\kappa }$- and
$U_{p,\kappa }$- and  $U_{p,\kappa }^t$-correspondences of
$U_{p,\kappa }^t$-correspondences of  $\mathscr {L}(\kappa )$
to be the maps constructed by taking
$\mathscr {L}(\kappa )$
to be the maps constructed by taking \[ U_{p,\kappa}: p_{2}^* \mathscr{L}(\kappa) \to p_1^* \mathscr{L}(\chi)\quad\text{and}\quad U_{p,\kappa}^t: p_{1}^* \mathscr{L}(\kappa) \to p_2^*\mathscr{L}(\chi), \]
\[ U_{p,\kappa}: p_{2}^* \mathscr{L}(\kappa) \to p_1^* \mathscr{L}(\chi)\quad\text{and}\quad U_{p,\kappa}^t: p_{1}^* \mathscr{L}(\kappa) \to p_2^*\mathscr{L}(\chi), \]
 $(-w_0(\kappa ))$-isotypic components of the structural sheaves of diagram (10).
$(-w_0(\kappa ))$-isotypic components of the structural sheaves of diagram (10).(ii) Let
 $\chi$ be a
$\chi$ be a  $\delta$-analytic character of
$\delta$-analytic character of  $T$. We define the normalized
$T$. We define the normalized  $U_p$- and
$U_p$- and  $U_p^t$-correspondences of
$U_p^t$-correspondences of  $\mathscr {L}(\chi )$,
to be the maps constructed by taking
$\mathscr {L}(\chi )$,
to be the maps constructed by taking \[ U_{p}: p_{2}^* \mathscr{L}(\chi) \to p_1^* \mathscr{L}(\chi) \quad \text{and}\quad U_{p}^t: p_{1}^* \mathscr{L}(\chi) \to p_2^*\mathscr{L}(\chi), \]
\[ U_{p}: p_{2}^* \mathscr{L}(\chi) \to p_1^* \mathscr{L}(\chi) \quad \text{and}\quad U_{p}^t: p_{1}^* \mathscr{L}(\chi) \to p_2^*\mathscr{L}(\chi), \]
 $(-w_0(\chi ))$-isotypic components of the structural sheaves of the diagrams
obtained from the normalized diagram (10) and Lemma 2.2.11.
$(-w_0(\chi ))$-isotypic components of the structural sheaves of the diagrams
obtained from the normalized diagram (10) and Lemma 2.2.11.
Remark 2.2.13 Let ![]() $\kappa$ be a classical weight. The relation between the classical and the normalized
$\kappa$ be a classical weight. The relation between the classical and the normalized ![]() $U_p$-operators for
$U_p$-operators for ![]() $\mathscr {L}(\kappa )$ is given by the formulas
$\mathscr {L}(\kappa )$ is given by the formulas
 \begin{gather*} U_p= \frac{1}{w_0(\kappa)(\varpi^{-1})}U_{p,\kappa}\quad\text{and}\quad U_p^{t}= \frac{1}{w_0(\kappa)(\varpi)} U_{p,\kappa}^t \quad\text{over } U_1(\epsilon)\operatorname{Iw}_n,\\ U_p= \frac{1}{\kappa (\varpi^{-1})} U_{p,\kappa}\quad\text{and}\quad U_p^{t}= \frac{1}{\kappa(\varpi)} U_{p,\kappa}^t \quad\text{over } U_{w_0}(\epsilon)\operatorname{Iw}_n. \end{gather*}
\begin{gather*} U_p= \frac{1}{w_0(\kappa)(\varpi^{-1})}U_{p,\kappa}\quad\text{and}\quad U_p^{t}= \frac{1}{w_0(\kappa)(\varpi)} U_{p,\kappa}^t \quad\text{over } U_1(\epsilon)\operatorname{Iw}_n,\\ U_p= \frac{1}{\kappa (\varpi^{-1})} U_{p,\kappa}\quad\text{and}\quad U_p^{t}= \frac{1}{\kappa(\varpi)} U_{p,\kappa}^t \quad\text{over } U_{w_0}(\epsilon)\operatorname{Iw}_n. \end{gather*}
2.3 Analytic principal series and distributions
In this subsection we introduce some non-archimedean spaces interpolating the finite-dimensional representations of ![]() $\operatorname {GL}_2$. Let
$\operatorname {GL}_2$. Let ![]() $\mathcal {V}= \operatorname {Spa}(R,R^+)$ be a uniform affinoid adic space over
$\mathcal {V}= \operatorname {Spa}(R,R^+)$ be a uniform affinoid adic space over ![]() $\mathbb {Q}_p$ and
$\mathbb {Q}_p$ and ![]() $\chi : T \to R^{+,\times }$ a
$\chi : T \to R^{+,\times }$ a ![]() $\delta$-analytic character.
$\delta$-analytic character.
Definition 2.3.1 Let ![]() $\delta \geq n$.
$\delta \geq n$.
(i) We define the
 $\delta$-analytic principal series of weight
$\delta$-analytic principal series of weight  $\chi$ to be the
$\chi$ to be the  $\operatorname {Iw}_n$-module
seen as a Banach space over
$\operatorname {Iw}_n$-module
seen as a Banach space over \[ A_{\chi}^{\delta}= \Gamma(U_{w_0}(\delta)\operatorname{Iw}_n, \mathscr{L}(\chi)), \]
\[ A_{\chi}^{\delta}= \Gamma(U_{w_0}(\delta)\operatorname{Iw}_n, \mathscr{L}(\chi)), \]
 $R$. Equivalently, we have that
$R$. Equivalently, we have that
 \[ A_{\chi}^{\delta}=\{f: w_0 \operatorname{\mathcal{I}\!w}_n(\epsilon,\delta)\to \mathbb{A}^1_{R} | f(bw_0 x)= w_0(\chi)(b) f(w_0x),\text{ for } b\in \mathcal{B}\cap w_0 \operatorname{\mathcal{I}\!w}_n(\epsilon,\delta) w_0^{-1} \}. \]
\[ A_{\chi}^{\delta}=\{f: w_0 \operatorname{\mathcal{I}\!w}_n(\epsilon,\delta)\to \mathbb{A}^1_{R} | f(bw_0 x)= w_0(\chi)(b) f(w_0x),\text{ for } b\in \mathcal{B}\cap w_0 \operatorname{\mathcal{I}\!w}_n(\epsilon,\delta) w_0^{-1} \}. \]
(ii) We define the
 $\delta$-analytic distributions of weight
$\delta$-analytic distributions of weight  $\chi$ to be the continuous weak dual
$\chi$ to be the continuous weak dual
 \[ D_{\chi}^{\delta}= \text{Hom}^0_{R}(A^{\delta}_{\chi}, R). \]
\[ D_{\chi}^{\delta}= \text{Hom}^0_{R}(A^{\delta}_{\chi}, R). \]
Remark 2.3.2 It will come in handy to define lattices in the principal series and distributions, namely, let ![]() $\mathscr {L}^+(\chi )= f_* \mathscr {O}^+_{\widetilde {U}_{w}(\epsilon,\delta )\operatorname {Iw}_n}[-w_0(\chi )]$,
$\mathscr {L}^+(\chi )= f_* \mathscr {O}^+_{\widetilde {U}_{w}(\epsilon,\delta )\operatorname {Iw}_n}[-w_0(\chi )]$, ![]() $A_{\chi }^{\delta,+}= \Gamma (U_{w_0}(\epsilon )\operatorname {Iw}_n, \mathscr {L}^+(\chi ))$, and
$A_{\chi }^{\delta,+}= \Gamma (U_{w_0}(\epsilon )\operatorname {Iw}_n, \mathscr {L}^+(\chi ))$, and ![]() $D_{\chi }^{\delta,+}= \text {font Hom}_{R^+}(A^{\delta,+}_{\chi },R^+)$. The space
$D_{\chi }^{\delta,+}= \text {font Hom}_{R^+}(A^{\delta,+}_{\chi },R^+)$. The space ![]() $N\mathcal {N}(\delta )$ is a disjoint union of closed discs; in particular,
$N\mathcal {N}(\delta )$ is a disjoint union of closed discs; in particular, ![]() $\mathscr {O}^+(N\mathcal {N}(\delta ))$ is an orthonormalizable
$\mathscr {O}^+(N\mathcal {N}(\delta ))$ is an orthonormalizable ![]() $\mathbb {Z}_p$-algebra. Let
$\mathbb {Z}_p$-algebra. Let ![]() $\{e_i\}_{i\in I }$ be an orthonormalizable basis of
$\{e_i\}_{i\in I }$ be an orthonormalizable basis of ![]() $\mathscr {O}^+(N\mathcal {N}(\delta ))$. Using the Iwahori decomposition, one has isomorphisms of
$\mathscr {O}^+(N\mathcal {N}(\delta ))$. Using the Iwahori decomposition, one has isomorphisms of ![]() $R^+$-modules
$R^+$-modules
 \[ A^{\delta,+}_{\chi} \cong \underset{i\in I}{\widehat{\bigoplus}} R^+ e_i \quad\text{and}\quad D^{\delta,+}_{\chi} \cong \prod_{i\in I} R^+ e_{i}^{\vee}. \]
\[ A^{\delta,+}_{\chi} \cong \underset{i\in I}{\widehat{\bigoplus}} R^+ e_i \quad\text{and}\quad D^{\delta,+}_{\chi} \cong \prod_{i\in I} R^+ e_{i}^{\vee}. \]
Remark 2.3.3 It is easy to compare the ![]() $\delta$-analytic principal series and distributions defined above with those used in [Reference Andreatta, Iovita and StevensAIS15]. Let
$\delta$-analytic principal series and distributions defined above with those used in [Reference Andreatta, Iovita and StevensAIS15]. Let ![]() $\chi : T\rightarrow R^{+,\times }$ be a
$\chi : T\rightarrow R^{+,\times }$ be a ![]() $\delta$-analytic character written as
$\delta$-analytic character written as ![]() $\chi =(\chi _1,\chi _2)$. Consider the set
$\chi =(\chi _1,\chi _2)$. Consider the set ![]() $\mathbb {Z}_p^\times \times \mathbb {Z}_p$ endowed with right multiplication by
$\mathbb {Z}_p^\times \times \mathbb {Z}_p$ endowed with right multiplication by ![]() $\operatorname {Iw}_n$ and left multiplication by
$\operatorname {Iw}_n$ and left multiplication by ![]() $\mathbb {Z}_p^\times$. We let
$\mathbb {Z}_p^\times$. We let ![]() $A^{\delta,+}_{\chi _1-\chi _2}$ be the space of functions
$A^{\delta,+}_{\chi _1-\chi _2}$ be the space of functions ![]() $f: \mathbb {Z}_p^\times \times \mathbb {Z}_p\rightarrow R^{+,\times }$ satisfying the following conditions.
$f: \mathbb {Z}_p^\times \times \mathbb {Z}_p\rightarrow R^{+,\times }$ satisfying the following conditions.
(i)
 $f|_{1\times \mathbb {Z}_p}$ extends to an analytic function of
$f|_{1\times \mathbb {Z}_p}$ extends to an analytic function of  $\mathbb {Z}_p+ p^\delta \mathbb {D}^1_{\mathbb {Q}_p}$.
$\mathbb {Z}_p+ p^\delta \mathbb {D}^1_{\mathbb {Q}_p}$.(ii)
 $f(tx)=(\chi _1-\chi _2)(t)f(x)$ for
$f(tx)=(\chi _1-\chi _2)(t)f(x)$ for  $t\in \mathbb {Z}_p^\times$ and
$t\in \mathbb {Z}_p^\times$ and  $x\in \mathbb {Z}_p^\times \times \mathbb {Z}_p$.
$x\in \mathbb {Z}_p^\times \times \mathbb {Z}_p$.
Note that ![]() $\mathbb {Z}_p^\times \times \mathbb {Z}_p$ endowed with the action of
$\mathbb {Z}_p^\times \times \mathbb {Z}_p$ endowed with the action of ![]() $\operatorname {Iw}_n$ and
$\operatorname {Iw}_n$ and ![]() $\mathbb {Z}_p^\times$ is isomorphic to the quotient
$\mathbb {Z}_p^\times$ is isomorphic to the quotient
Thus, we have an isomorphism
Remark 2.3.4 Let ![]() $\delta '>\delta \geq n$. The inclusion
$\delta '>\delta \geq n$. The inclusion ![]() $U_{w_0}(\delta ')\operatorname {Iw}_n \subset U_{w_0}(\delta )\operatorname {Iw}_n$ induces maps
$U_{w_0}(\delta ')\operatorname {Iw}_n \subset U_{w_0}(\delta )\operatorname {Iw}_n$ induces maps ![]() $A_{\chi }^{\delta,+}\to A_{\chi }^{\delta ',+}$ and
$A_{\chi }^{\delta,+}\to A_{\chi }^{\delta ',+}$ and ![]() $D_{\chi }^{\delta ',+}\to D_{\chi }^{\delta,+}$. Furthermore, let
$D_{\chi }^{\delta ',+}\to D_{\chi }^{\delta,+}$. Furthermore, let ![]() $\widehat {A}^{\delta,+}_{\chi }$ be the completion of
$\widehat {A}^{\delta,+}_{\chi }$ be the completion of ![]() $A^{\delta,+}_{\chi }$ in
$A^{\delta,+}_{\chi }$ in ![]() $A^{\delta ',+}_{\chi }$. Since the inclusion of affinoids above is strict, one has that
$A^{\delta ',+}_{\chi }$. Since the inclusion of affinoids above is strict, one has that
endowed with the product topology. Let ![]() $D_{\chi }^{\delta,b,+}$ be the continuous
$D_{\chi }^{\delta,b,+}$ be the continuous ![]() $R^+$-dual of
$R^+$-dual of ![]() $\widehat {A}_{\chi }^{\delta,+}$ endowed with the
$\widehat {A}_{\chi }^{\delta,+}$ endowed with the ![]() $p$-adic topology. Then the arrow
$p$-adic topology. Then the arrow ![]() $D_{\chi }^{\delta ',+} \to D_{\chi }^{\delta,+}$ factors through
$D_{\chi }^{\delta ',+} \to D_{\chi }^{\delta,+}$ factors through ![]() $D_{\chi }^{\delta,b,+}$. Moreover, we have that
$D_{\chi }^{\delta,b,+}$. Moreover, we have that
 \[ D^{\delta,b,+}_{\chi} \cong \underset{i\in I}{\widehat{\bigoplus}} R^+ e_i^{\vee}. \]
\[ D^{\delta,b,+}_{\chi} \cong \underset{i\in I}{\widehat{\bigoplus}} R^+ e_i^{\vee}. \]
The previous discussion shows that the directed (respectively, inverse) systems ![]() $\{A_{\chi }^{\delta,+}\}_{\delta \geq n}$ and
$\{A_{\chi }^{\delta,+}\}_{\delta \geq n}$ and ![]() $\{\widehat {A}_{\chi }^{\delta,+}\}_{\delta \geq n}$ (respectively,
$\{\widehat {A}_{\chi }^{\delta,+}\}_{\delta \geq n}$ (respectively, ![]() $\{D_{\chi }^{\delta,+}\}_{\delta \geq n}$ and
$\{D_{\chi }^{\delta,+}\}_{\delta \geq n}$ and ![]() $\{D_{\chi }^{\delta,b,+}\}_{\delta \geq n}$) are isomorphic as systems of topological
$\{D_{\chi }^{\delta,b,+}\}_{\delta \geq n}$) are isomorphic as systems of topological ![]() $R^+$-modules.
$R^+$-modules.
For future reference we will prove a devisage of ![]() $A_{\chi }^{\delta }$ and
$A_{\chi }^{\delta }$ and ![]() $D^{\delta }_{\chi }$ in terms of finite
$D^{\delta }_{\chi }$ in terms of finite ![]() $\operatorname {Iw}_n$-modules. We need the following lemma.
$\operatorname {Iw}_n$-modules. We need the following lemma.
Lemma 2.3.5 Let ![]() $(F,\mathcal {O}_F)$ be a non-archimedean field. Let
$(F,\mathcal {O}_F)$ be a non-archimedean field. Let ![]() $\mathcal {H}=\operatorname {Spa}(A,A^+)$ be an affinoid adic analytic group over
$\mathcal {H}=\operatorname {Spa}(A,A^+)$ be an affinoid adic analytic group over ![]() $F$, and
$F$, and ![]() $Z=\operatorname {Spa}(R,R^+)$ be an affinoid adic space topologically of finite type over
$Z=\operatorname {Spa}(R,R^+)$ be an affinoid adic space topologically of finite type over ![]() $\operatorname {Spa}(F,\mathcal {O}_F)$. Let
$\operatorname {Spa}(F,\mathcal {O}_F)$. Let ![]() $\Theta : \mathcal {H}\times Z \rightarrow Z$ be an action of
$\Theta : \mathcal {H}\times Z \rightarrow Z$ be an action of ![]() $\mathcal {H}$ over
$\mathcal {H}$ over ![]() $Z$. Then for all
$Z$. Then for all ![]() $N>0$ there exists a neighbourhood
$N>0$ there exists a neighbourhood ![]() $1\in U \subset \mathcal {H}$ such that for all
$1\in U \subset \mathcal {H}$ such that for all ![]() $g\in U$,
$g\in U$, ![]() $z\in Z$ and
$z\in Z$ and ![]() $f\in \mathscr {O}^+(Z)$, we have
$f\in \mathscr {O}^+(Z)$, we have ![]() $|f(z)-f(gz)|\leq |p|^{N}$.
$|f(z)-f(gz)|\leq |p|^{N}$.
Proof. As ![]() $\mathscr {O}^+(Z)=R^+$ is topologically of finite type over
$\mathscr {O}^+(Z)=R^+$ is topologically of finite type over ![]() $\mathcal {O}_F$, it suffices to prove the proposition for a single
$\mathcal {O}_F$, it suffices to prove the proposition for a single ![]() $f\in R^+$. Let
$f\in R^+$. Let ![]() $\Theta ^*: R^+\rightarrow (A^+\widehat {\otimes }_{\mathcal {O}_K} R^+)^+$ be the pullback of the multiplication map. Let
$\Theta ^*: R^+\rightarrow (A^+\widehat {\otimes }_{\mathcal {O}_K} R^+)^+$ be the pullback of the multiplication map. Let ![]() $V\subset \mathcal {H}\times Z$ be the open affinoid subspace defined by the equation
$V\subset \mathcal {H}\times Z$ be the open affinoid subspace defined by the equation
As ![]() $V$ contains
$V$ contains ![]() $1\times Z$ and this is a quasi-compact closed subset of
$1\times Z$ and this is a quasi-compact closed subset of ![]() $\mathcal {H}\times Z$, there exists
$\mathcal {H}\times Z$, there exists ![]() $1\in U_f\subset U$ such that
$1\in U_f\subset U$ such that ![]() $U_f\times Z \subset V$. Therefore, for all
$U_f\times Z \subset V$. Therefore, for all ![]() $g\in U_f$ and
$g\in U_f$ and ![]() $z\in Z$ we have
$z\in Z$ we have ![]() $|f(z)-f(gz)|\leq |p|^{N}$.
$|f(z)-f(gz)|\leq |p|^{N}$.
Corollary 2.3.6 Let ![]() $s\geq 1$. There exists an open subgroup
$s\geq 1$. There exists an open subgroup ![]() $H\subset \operatorname {Iw}_n$, depending on
$H\subset \operatorname {Iw}_n$, depending on ![]() $s$, which acts trivially on
$s$, which acts trivially on ![]() $A^{\delta,+}_{\chi }/p^s$. In particular, we can write
$A^{\delta,+}_{\chi }/p^s$. In particular, we can write ![]() $A^{\delta,+}_{\chi }/p^s$ as a colimit of finite
$A^{\delta,+}_{\chi }/p^s$ as a colimit of finite ![]() $R/p^s[\operatorname {Iw}_n]$-modules (dually, we can write
$R/p^s[\operatorname {Iw}_n]$-modules (dually, we can write ![]() $D^{\delta,+}_{\chi }/p^s$ as a projective limit of finite
$D^{\delta,+}_{\chi }/p^s$ as a projective limit of finite ![]() $R/p^s[\operatorname {Iw}_n]$-modules).
$R/p^s[\operatorname {Iw}_n]$-modules).
Proof. The affinoid group ![]() $\operatorname {\mathcal {I}\!w}_n(\delta )$ acts on the space
$\operatorname {\mathcal {I}\!w}_n(\delta )$ acts on the space ![]() $\widetilde {U}_{w_0}(\delta,\delta )$ by right multiplication. The corollary follows by Lemma 2.3.5 since
$\widetilde {U}_{w_0}(\delta,\delta )$ by right multiplication. The corollary follows by Lemma 2.3.5 since ![]() $A^{\delta,+}_{\chi }$ is by definition an isotypic component of the global functions of
$A^{\delta,+}_{\chi }$ is by definition an isotypic component of the global functions of ![]() $\widetilde {U}_{w_0}(\delta,\delta )$. Dually, consider the map
$\widetilde {U}_{w_0}(\delta,\delta )$. Dually, consider the map ![]() $D_{\chi }^{\delta,+}\to D_{\chi }^{\delta -1,+}$ and define
$D_{\chi }^{\delta,+}\to D_{\chi }^{\delta -1,+}$ and define ![]() $\operatorname {Fil}^s D_{\chi }^{\delta,+}= D_{\chi }^{\delta,+}\cap p^{s} D_{\chi }^{\delta -1,+}$. Then the quotients
$\operatorname {Fil}^s D_{\chi }^{\delta,+}= D_{\chi }^{\delta,+}\cap p^{s} D_{\chi }^{\delta -1,+}$. Then the quotients ![]() $D_{\chi }^{\delta,+}/ \operatorname {Fil}^s D_{\chi }^{\delta,+}$ are finite
$D_{\chi }^{\delta,+}/ \operatorname {Fil}^s D_{\chi }^{\delta,+}$ are finite ![]() $R^+/p^s$-modules and the weak topology of
$R^+/p^s$-modules and the weak topology of ![]() $D_{\chi }^{\delta,+}$ is the same as the inverse limit topology (see [Reference Andreatta, Iovita and StevensAIS15, Proposition 3.10])
$D_{\chi }^{\delta,+}$ is the same as the inverse limit topology (see [Reference Andreatta, Iovita and StevensAIS15, Proposition 3.10])
The corollary follows.
Definition 2.3.7 Let ![]() $V$ be a Banach space over
$V$ be a Banach space over ![]() $\mathbb {Q}_p$ and
$\mathbb {Q}_p$ and ![]() $V^+\subset V$ a lattice. We define the completed tensor products
$V^+\subset V$ a lattice. We define the completed tensor products
Next, let us explain how ![]() $A^{\delta }_{\chi }$ and
$A^{\delta }_{\chi }$ and ![]() $D^{\delta }_{\chi }$ interpolate the finite-dimensional representations of
$D^{\delta }_{\chi }$ interpolate the finite-dimensional representations of ![]() $\operatorname {GL}_2$.
$\operatorname {GL}_2$.
Proposition 2.3.8 Let ![]() $\kappa \in X^*(\mathbf {T})$ be a dominant weight and
$\kappa \in X^*(\mathbf {T})$ be a dominant weight and ![]() $\delta \geq n$. There is a natural
$\delta \geq n$. There is a natural ![]() $\operatorname {Iw}_n$-equivariant inclusion
$\operatorname {Iw}_n$-equivariant inclusion ![]() $V_\kappa \rightarrow A_\kappa ^{\delta }$. Dually, there is a natural
$V_\kappa \rightarrow A_\kappa ^{\delta }$. Dually, there is a natural ![]() $\operatorname {Iw}_n$-equivariant surjective map
$\operatorname {Iw}_n$-equivariant surjective map ![]() $D^{\delta }_{\kappa }\rightarrow V_{\kappa }^{\vee }=V_{-w_0(\kappa )}$.
$D^{\delta }_{\kappa }\rightarrow V_{\kappa }^{\vee }=V_{-w_0(\kappa )}$.
Proof. The second map is just the dual of the first, and the arrow ![]() $V_{\kappa } \to A^{\delta }_{\kappa }$ arises from the global sections functor applied to the inclusion
$V_{\kappa } \to A^{\delta }_{\kappa }$ arises from the global sections functor applied to the inclusion ![]() $U_{w_0}(\delta )\operatorname {Iw}_n \subset \operatorname {\mathscr {F}\!\ell }$ and to the line bundle
$U_{w_0}(\delta )\operatorname {Iw}_n \subset \operatorname {\mathscr {F}\!\ell }$ and to the line bundle ![]() $\mathscr {L}(\kappa )$.
$\mathscr {L}(\kappa )$.
Finally, let us briefly discuss the ![]() $U_p$-correspondence of the principal series and distributions. We let
$U_p$-correspondence of the principal series and distributions. We let ![]() $A_{\chi }^{\delta } \widehat {\otimes } \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$ and
$A_{\chi }^{\delta } \widehat {\otimes } \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$ and ![]() $D_{\chi }^{\delta } \widehat {\otimes } \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$ be the constant
$D_{\chi }^{\delta } \widehat {\otimes } \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$ be the constant ![]() $\operatorname {Iw}_n$-equivariant quasi-coherent sheaves over
$\operatorname {Iw}_n$-equivariant quasi-coherent sheaves over ![]() $\operatorname {\mathscr {F}\!\ell }$ induced by
$\operatorname {\mathscr {F}\!\ell }$ induced by ![]() $A_{\chi }^{\delta }$ and
$A_{\chi }^{\delta }$ and ![]() $D_{\chi }^{\delta }$. We have isomorphisms of
$D_{\chi }^{\delta }$. We have isomorphisms of ![]() $\mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$-sheaves
$\mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$-sheaves
 \[ A^{\delta}_{\chi}\widehat{\otimes} \mathscr{O}_{\operatorname{\mathscr{F}\!\ell}} = \underset{i\in I}{\widehat{\bigoplus}} \big(R\widehat{\otimes } \mathscr{O}_{\operatorname{\mathscr{F}\!\ell}}\big) e_i\quad\text{and}\quad D^{\delta}_{\chi}\widehat{\otimes} \mathscr{O}_{\operatorname{\mathscr{F}\!\ell}} = \prod_{i\in I} \big(R^+\widehat{\otimes } \mathscr{O}_{\operatorname{\mathscr{F}\!\ell}}^+\big) e_i^{\vee}\biggl[\frac{1}{p}\biggr]. \]
\[ A^{\delta}_{\chi}\widehat{\otimes} \mathscr{O}_{\operatorname{\mathscr{F}\!\ell}} = \underset{i\in I}{\widehat{\bigoplus}} \big(R\widehat{\otimes } \mathscr{O}_{\operatorname{\mathscr{F}\!\ell}}\big) e_i\quad\text{and}\quad D^{\delta}_{\chi}\widehat{\otimes} \mathscr{O}_{\operatorname{\mathscr{F}\!\ell}} = \prod_{i\in I} \big(R^+\widehat{\otimes } \mathscr{O}_{\operatorname{\mathscr{F}\!\ell}}^+\big) e_i^{\vee}\biggl[\frac{1}{p}\biggr]. \]
By Remark 2.2.8 one can endow ![]() $A^{\delta }_{\chi }$ with an action of
$A^{\delta }_{\chi }$ with an action of ![]() $\varpi$ commuting with
$\varpi$ commuting with ![]() $\operatorname {Iw}_n$ (dually, one can endow
$\operatorname {Iw}_n$ (dually, one can endow ![]() $D^{\delta }_{\chi }$ with an action of
$D^{\delta }_{\chi }$ with an action of ![]() $\varpi ^{-1}$). Moreover, the multiplication by
$\varpi ^{-1}$). Moreover, the multiplication by ![]() $\varpi$ on
$\varpi$ on ![]() $A^{\delta }_{\chi }$ (respectively,
$A^{\delta }_{\chi }$ (respectively, ![]() $D^{\delta }_{\chi }$) factors through
$D^{\delta }_{\chi }$) factors through ![]() $A^{\delta -1}_{\chi }$ (respectively,
$A^{\delta -1}_{\chi }$ (respectively, ![]() $D^{\delta +1}_{\chi }$) in accordance with Lemma 2.2.4. Using this action and diagram (10), one defines maps
$D^{\delta +1}_{\chi }$) in accordance with Lemma 2.2.4. Using this action and diagram (10), one defines maps
(see [Reference Andreatta and IovitaAI22, §§ 3.5.2 and 4.5] for more details). We highlight that the previous ![]() $U_p$-correspondence is compatible with the maps of Proposition 2.3.8, after normalizing the action of
$U_p$-correspondence is compatible with the maps of Proposition 2.3.8, after normalizing the action of ![]() $\varpi$ and
$\varpi$ and ![]() $c$ on
$c$ on ![]() $V_{\kappa }$ (see Remark 2.2.13 and the first remark of [Reference Ash and StevensAS08, § 3.11]).
$V_{\kappa }$ (see Remark 2.2.13 and the first remark of [Reference Ash and StevensAS08, § 3.11]).
2.4 The dual BGG complex and the weight vector maps
Let ![]() $W=\{1,w_0\}$ be the Weyl group of
$W=\{1,w_0\}$ be the Weyl group of ![]() $\operatorname {GL}_2$ and
$\operatorname {GL}_2$ and ![]() $\mathbf {B} w_0 \mathbf {N}\subset \operatorname {GL}_2$ the big cell. We have a commutative diagram of torsors as follows.
$\mathbf {B} w_0 \mathbf {N}\subset \operatorname {GL}_2$ the big cell. We have a commutative diagram of torsors as follows.

Let ![]() $\kappa \in X^*(\mathbf {T})$ be a character and
$\kappa \in X^*(\mathbf {T})$ be a character and ![]() $\mathscr {L}(\kappa )$ the associated
$\mathscr {L}(\kappa )$ the associated ![]() $\operatorname {GL}_2$-equivariant line bundle over
$\operatorname {GL}_2$-equivariant line bundle over ![]() $\operatorname {FL}$ (see Definition 2.1.1). Recall that, if
$\operatorname {FL}$ (see Definition 2.1.1). Recall that, if ![]() $\kappa$ is dominant, the global sections of
$\kappa$ is dominant, the global sections of ![]() $\mathscr {L}(\kappa )$ are isomorphic to
$\mathscr {L}(\kappa )$ are isomorphic to ![]() $V_{\kappa }$.
$V_{\kappa }$.
Definition 2.4.1 We define the ![]() $(\mathfrak {g}, \mathbf {B})$-representation
$(\mathfrak {g}, \mathbf {B})$-representation ![]() $V(\kappa ):= \Gamma (\mathbf {B}\backslash \mathbf {B}w_0 \mathbf {N}, \mathscr {L}(\kappa ))$, where the action of
$V(\kappa ):= \Gamma (\mathbf {B}\backslash \mathbf {B}w_0 \mathbf {N}, \mathscr {L}(\kappa ))$, where the action of ![]() $(\mathfrak {g},\mathbf {B})$ is induced by the right regular action on the big cell.
$(\mathfrak {g},\mathbf {B})$ is induced by the right regular action on the big cell.
As a ![]() $\mathbf {B}$-module,
$\mathbf {B}$-module, ![]() $V(\kappa )$ is a twist of the algebra of regular functions of
$V(\kappa )$ is a twist of the algebra of regular functions of ![]() $\mathbf {N}$. Indeed, there is an isomorphism of affine schemes
$\mathbf {N}$. Indeed, there is an isomorphism of affine schemes ![]() $\mathbf {B} \backslash \mathbf {B} w_0 \mathbf {N} \cong \mathbf {N}$, and one has
$\mathbf {B} \backslash \mathbf {B} w_0 \mathbf {N} \cong \mathbf {N}$, and one has
where the action of ![]() $\mathbf {B}=\mathbf {T} \ltimes \mathbf {N}$ on
$\mathbf {B}=\mathbf {T} \ltimes \mathbf {N}$ on ![]() $\mathscr {O}(\mathbf {N})$ is induced from the map
$\mathscr {O}(\mathbf {N})$ is induced from the map ![]() $(n,b)\mapsto t_{b}^{-1}n t_{b} n_b$ for
$(n,b)\mapsto t_{b}^{-1}n t_{b} n_b$ for ![]() $(n,b)\in \mathbf {N}\times \mathbf {B}$ and
$(n,b)\in \mathbf {N}\times \mathbf {B}$ and ![]() $b= (t_b,n_b)\in \mathbf {T} \ltimes \mathbf {N}$.
$b= (t_b,n_b)\in \mathbf {T} \ltimes \mathbf {N}$.
Remark 2.4.2 The ![]() $(\mathfrak {g}, \mathbf {B})$-module
$(\mathfrak {g}, \mathbf {B})$-module ![]() $V(\kappa )$ is in fact the admissible dual of the Verma module of highest weight
$V(\kappa )$ is in fact the admissible dual of the Verma module of highest weight ![]() $-w_0(\kappa )$ (see § 3.10 of [Reference Ash and StevensAS08]).
$-w_0(\kappa )$ (see § 3.10 of [Reference Ash and StevensAS08]).
Let ![]() $\kappa$ be a dominant weight. Taking the global sections of
$\kappa$ be a dominant weight. Taking the global sections of ![]() $\mathscr {L}(\kappa )$ in the bottom arrow of diagram (13), one obtains a map
$\mathscr {L}(\kappa )$ in the bottom arrow of diagram (13), one obtains a map
Writing ![]() $\kappa =(k_1,k_2)\in \mathbb {Z}^2$, and
$\kappa =(k_1,k_2)\in \mathbb {Z}^2$, and ![]() $\mathbb {G}_a\cong \mathbf {N}$ via
$\mathbb {G}_a\cong \mathbf {N}$ via ![]() $X \mapsto \big (\!\begin {smallmatrix} 1 & X \\ 0 & 1 \end {smallmatrix}\! \big )$, the map of
$X \mapsto \big (\!\begin {smallmatrix} 1 & X \\ 0 & 1 \end {smallmatrix}\! \big )$, the map of ![]() $V_{\kappa }$ in
$V_{\kappa }$ in ![]() $V(\kappa )$ is identified in (14) with the inclusion
$V(\kappa )$ is identified in (14) with the inclusion ![]() $\mathbb {Q}_p[X]_{k_1-k_2}\subset \mathbb {Q}_p[X]\cong \mathscr {O}(\mathbf {N})$ of polynomials of degree at most
$\mathbb {Q}_p[X]_{k_1-k_2}\subset \mathbb {Q}_p[X]\cong \mathscr {O}(\mathbf {N})$ of polynomials of degree at most ![]() $k_1-k_2$. We have the following proposition.
$k_1-k_2$. We have the following proposition.
Proposition 2.4.3 Let ![]() $\alpha =(1,-1)\in \mathbb {Z}^2 \cong X^*(\mathbf {T})$ and let
$\alpha =(1,-1)\in \mathbb {Z}^2 \cong X^*(\mathbf {T})$ and let ![]() $\kappa =(k_1,k_2)$ be a dominant weight. There is a short exact sequence of
$\kappa =(k_1,k_2)$ be a dominant weight. There is a short exact sequence of ![]() $(\mathfrak {g}, \mathbf {B})$-representations
$(\mathfrak {g}, \mathbf {B})$-representations
called the dual BGG complex of weight ![]() $\kappa$. As such it is identified with the short exact sequence
$\kappa$. As such it is identified with the short exact sequence
where ![]() $\mathbb {Q}_p[X] = \mathscr {O}(\mathbf {N})$.
$\mathbb {Q}_p[X] = \mathscr {O}(\mathbf {N})$.
Proof. We have a weight decomposition of ![]() $V(\kappa )$ with respect to
$V(\kappa )$ with respect to ![]() $\mathbf {T}$,
$\mathbf {T}$,
where ![]() $(\kappa -n\alpha )\mathbb {Q}_p$ is identified with
$(\kappa -n\alpha )\mathbb {Q}_p$ is identified with ![]() $\kappa \otimes \mathbb {Q}_p X^{n}$ under the isomorphism (14). As
$\kappa \otimes \mathbb {Q}_p X^{n}$ under the isomorphism (14). As ![]() $V_{\kappa }$ is the irreducible representation of highest weight
$V_{\kappa }$ is the irreducible representation of highest weight ![]() $\kappa$, it has a weight decomposition
$\kappa$, it has a weight decomposition ![]() $V_{\kappa }\cong \bigoplus _{0\leq n \leq k_1-k_2} (\kappa -n\alpha ) \mathbb {Q}_p$. This shows that
$V_{\kappa }\cong \bigoplus _{0\leq n \leq k_1-k_2} (\kappa -n\alpha ) \mathbb {Q}_p$. This shows that ![]() $V_\kappa \subset V(\kappa )$ is identified with the inclusion
$V_\kappa \subset V(\kappa )$ is identified with the inclusion ![]() $\kappa \otimes \mathbb {Q}_p[X]_{\leq k_1-k_2}\subset \kappa \otimes \mathbb {Q}_p[X]$. As
$\kappa \otimes \mathbb {Q}_p[X]_{\leq k_1-k_2}\subset \kappa \otimes \mathbb {Q}_p[X]$. As ![]() $\kappa \otimes X^{k_1-k_2+1}$ has weight
$\kappa \otimes X^{k_1-k_2+1}$ has weight ![]() $(w_0(\kappa )-\alpha )$, the isomorphism of
$(w_0(\kappa )-\alpha )$, the isomorphism of ![]() $\operatorname {BGG}(\kappa )$ with (15) as
$\operatorname {BGG}(\kappa )$ with (15) as ![]() $\mathbf {B}$-representations is clear.
$\mathbf {B}$-representations is clear.
The representation ![]() $V_{\kappa }$ has a
$V_{\kappa }$ has a ![]() $\mathbf {B}$-filtration whose highest and lowest weight vectors are
$\mathbf {B}$-filtration whose highest and lowest weight vectors are ![]() $\mathbb {Q}_p(\kappa ) \to V_{\kappa }$ and
$\mathbb {Q}_p(\kappa ) \to V_{\kappa }$ and ![]() $V_{\kappa } \to \mathbb {Q}_p(w_0(\kappa ))$, respectively. Taking the associated
$V_{\kappa } \to \mathbb {Q}_p(w_0(\kappa ))$, respectively. Taking the associated ![]() $\operatorname {GL}_2$-equivariant vector bundles over
$\operatorname {GL}_2$-equivariant vector bundles over ![]() $\operatorname {FL}$, one finds morphisms
$\operatorname {FL}$, one finds morphisms ![]() $\Psi _{-w_0(\kappa )}^{\vee }: \mathscr {L}(w_0(\kappa )) \to \mathscr {O}_{\operatorname {FL}} \otimes V_{\kappa }$ and
$\Psi _{-w_0(\kappa )}^{\vee }: \mathscr {L}(w_0(\kappa )) \to \mathscr {O}_{\operatorname {FL}} \otimes V_{\kappa }$ and ![]() $\Psi _{\kappa }: \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }} \otimes V_{\kappa } \to \mathscr {L}(\kappa )$. In Propositions 2.4.4 and 2.4.5 we interpolate these maps on neighbourhoods of
$\Psi _{\kappa }: \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }} \otimes V_{\kappa } \to \mathscr {L}(\kappa )$. In Propositions 2.4.4 and 2.4.5 we interpolate these maps on neighbourhoods of ![]() $w\in W$.
$w\in W$.
Proposition 2.4.4 Let ![]() $\epsilon \geq \delta \geq n$. Let
$\epsilon \geq \delta \geq n$. Let ![]() $(R,R^+)$ be a uniform Tate
$(R,R^+)$ be a uniform Tate ![]() $\mathbb {Q}_p$-algebra and
$\mathbb {Q}_p$-algebra and ![]() $\chi : T=\mathbf {T}(\mathbb {Z}_p)\rightarrow R^{\times,+}$ a
$\chi : T=\mathbf {T}(\mathbb {Z}_p)\rightarrow R^{\times,+}$ a ![]() $\delta$-analytic character.
$\delta$-analytic character.
(i) There is a
 $\mathcal {B}\cap \operatorname {\mathcal {I}\!w}_n(\delta )$-equivariant map
$\mathcal {B}\cap \operatorname {\mathcal {I}\!w}_n(\delta )$-equivariant map  $\iota : R(\chi ) \rightarrow A^{\delta }_{\chi }$ (the highest weight vector map). It induces a morphism of
$\iota : R(\chi ) \rightarrow A^{\delta }_{\chi }$ (the highest weight vector map). It induces a morphism of  $\operatorname {Iw}_n$-equivariant sheaves over
$\operatorname {Iw}_n$-equivariant sheaves over  $U_{1}(\epsilon )\operatorname {Iw}_n$,
Dually, we have equivariant maps
$U_{1}(\epsilon )\operatorname {Iw}_n$,
Dually, we have equivariant maps \[ \Psi^{A,\vee}_{-w_0(\chi)}: \mathscr{L}(w_0(\chi)) \rightarrow A_{\chi}^{\delta}\widehat{\otimes} \mathscr{O}_{U_{1}(\epsilon)\operatorname{Iw}_n}. \]
\[ \Psi^{A,\vee}_{-w_0(\chi)}: \mathscr{L}(w_0(\chi)) \rightarrow A_{\chi}^{\delta}\widehat{\otimes} \mathscr{O}_{U_{1}(\epsilon)\operatorname{Iw}_n}. \]
 $D^{\delta }_{\chi }\rightarrow R(-\chi )$ and
$D^{\delta }_{\chi }\rightarrow R(-\chi )$ and  $\Psi ^{D}_{-w_0(\chi )} :D_{\chi }^{\delta }\widehat {\otimes } \mathscr {O}_{U_{1}(\epsilon )\operatorname {Iw}_n} \rightarrow \mathscr {L}(-w_0(\chi ))$.
$\Psi ^{D}_{-w_0(\chi )} :D_{\chi }^{\delta }\widehat {\otimes } \mathscr {O}_{U_{1}(\epsilon )\operatorname {Iw}_n} \rightarrow \mathscr {L}(-w_0(\chi ))$.(ii) There is a
 $\overline {\mathcal {B}}\cap \operatorname {\mathcal {I}\!w}_n(\delta )$-equivariant map
$\overline {\mathcal {B}}\cap \operatorname {\mathcal {I}\!w}_n(\delta )$-equivariant map  $\operatorname {ev}_{w_0}: A^{\delta }_{\chi }\rightarrow R(\chi )$ (the lowest weight vector quotient). Moreover, it induces a morphism of
$\operatorname {ev}_{w_0}: A^{\delta }_{\chi }\rightarrow R(\chi )$ (the lowest weight vector quotient). Moreover, it induces a morphism of  $\operatorname {Iw}_n$-equivariant sheaves over
$\operatorname {Iw}_n$-equivariant sheaves over  $U_{w_0}(\epsilon )\operatorname {Iw}_n$,
Dually, we have equivariant maps
$U_{w_0}(\epsilon )\operatorname {Iw}_n$,
Dually, we have equivariant maps \[ \Psi^{A}_{\chi} :A^{\delta}_{\chi} \widehat{\otimes} \mathscr{O}_{U_{w_0}(\epsilon)\operatorname{Iw}_n} \rightarrow \mathscr{L}(\chi). \]
\[ \Psi^{A}_{\chi} :A^{\delta}_{\chi} \widehat{\otimes} \mathscr{O}_{U_{w_0}(\epsilon)\operatorname{Iw}_n} \rightarrow \mathscr{L}(\chi). \]
 $R(-\chi ) \rightarrow D^{\delta }_{\chi }$ and
$R(-\chi ) \rightarrow D^{\delta }_{\chi }$ and  $\Psi ^{D,\vee }_{\chi }:\mathscr {L}(-\chi ) \rightarrow D^{\delta }_{\chi } \widehat {\otimes } \mathscr {O}_{U_{w_0}(\epsilon )\operatorname {Iw}_n}$.
$\Psi ^{D,\vee }_{\chi }:\mathscr {L}(-\chi ) \rightarrow D^{\delta }_{\chi } \widehat {\otimes } \mathscr {O}_{U_{w_0}(\epsilon )\operatorname {Iw}_n}$.
Moreover, the morphisms of sheaves above are compatible with the ![]() $U_p$-correspondence (10).
$U_p$-correspondence (10).
Proof. It is enough to prove the statements for the principal series. Recall that ![]() $A^{\delta }_{\chi }= \mathscr {O}_{\widetilde {U}_{w_0}(\epsilon, \delta )}[-w_0(\chi )]$, where one takes isotypic components with respect to the left regular action of
$A^{\delta }_{\chi }= \mathscr {O}_{\widetilde {U}_{w_0}(\epsilon, \delta )}[-w_0(\chi )]$, where one takes isotypic components with respect to the left regular action of ![]() $T\mathcal {T}(\delta )$.
$T\mathcal {T}(\delta )$.
(i) By Lemma 2.2.2(iii) we have an isomorphism of
 $R$-modules
$R$-modules  $A_{\chi }^{\delta } \cong \mathscr {O}( \overline {N} \overline {\mathcal {N}}(\delta ) w_0)$; this shows that the
$A_{\chi }^{\delta } \cong \mathscr {O}( \overline {N} \overline {\mathcal {N}}(\delta ) w_0)$; this shows that the  $N\mathcal {N}(\delta )$-invariants of
$N\mathcal {N}(\delta )$-invariants of  $A_{\chi }^{\delta }$ are isomorphic to the
$A_{\chi }^{\delta }$ are isomorphic to the  $\mathcal {B}\cap \operatorname {\mathcal {I}\!w}_{n}(\delta )$-module
$\mathcal {B}\cap \operatorname {\mathcal {I}\!w}_{n}(\delta )$-module  $R(\chi )$, and thus provides the first arrow. The map
$R(\chi )$, and thus provides the first arrow. The map  $\Psi ^{A,\vee }_{-w_0(\chi )}: \mathscr {L}(w_0(\chi )) \to A^{\delta }_{\chi }\widehat {\otimes } \mathscr {O}_{U_{1}(\epsilon )\operatorname {Iw}_n}$ is constructed from the arrow
$\Psi ^{A,\vee }_{-w_0(\chi )}: \mathscr {L}(w_0(\chi )) \to A^{\delta }_{\chi }\widehat {\otimes } \mathscr {O}_{U_{1}(\epsilon )\operatorname {Iw}_n}$ is constructed from the arrow  $R(\chi )\to A^{\delta }_{\chi }$ via the presentation
$R(\chi )\to A^{\delta }_{\chi }$ via the presentation  $U_{w_0}(\epsilon )\operatorname {Iw}_n= \mathcal {B}\cap \operatorname {\mathcal {I}\!w}_{n}(\delta ) \backslash\!\operatorname {\mathcal {G}\!\mathcal {L}}_{2}(\epsilon,\delta ) \operatorname {Iw}_n$. Indeed, one has that
$U_{w_0}(\epsilon )\operatorname {Iw}_n= \mathcal {B}\cap \operatorname {\mathcal {I}\!w}_{n}(\delta ) \backslash\!\operatorname {\mathcal {G}\!\mathcal {L}}_{2}(\epsilon,\delta ) \operatorname {Iw}_n$. Indeed, one has that
 \[ \mathscr{L}(w_0(\chi))= \operatorname{\mathcal{G}\!\mathcal{L}}_{2}(\epsilon,\delta)w_0\operatorname{Iw}_n\times^{\mathcal{B}} R(\chi) \text{ and } A_{\chi}^{\delta}\widehat{\otimes} \mathscr{O}_{U_{1}(\epsilon)\operatorname{Iw}_n}= \operatorname{\mathcal{G}\!\mathcal{L}}_{2}(\epsilon,\delta)w_0\operatorname{Iw}_n \times^{\mathcal{B}} A_{\chi}^{\delta}. \]
\[ \mathscr{L}(w_0(\chi))= \operatorname{\mathcal{G}\!\mathcal{L}}_{2}(\epsilon,\delta)w_0\operatorname{Iw}_n\times^{\mathcal{B}} R(\chi) \text{ and } A_{\chi}^{\delta}\widehat{\otimes} \mathscr{O}_{U_{1}(\epsilon)\operatorname{Iw}_n}= \operatorname{\mathcal{G}\!\mathcal{L}}_{2}(\epsilon,\delta)w_0\operatorname{Iw}_n \times^{\mathcal{B}} A_{\chi}^{\delta}. \]
(ii) By Lemma 2.2.2 we have the presentation
Then a straightforward computation shows that the evaluation map \[ \widetilde{U}_{w_0}(\epsilon, \delta)\operatorname{Iw}_n = N_n\mathcal{N}(\delta) \backslash ( N_n \mathcal{N}(\delta) \times T \mathcal{T}(\delta) \times \overline{N} \overline{\mathcal{N}}(\epsilon) w_0). \]
\[ \widetilde{U}_{w_0}(\epsilon, \delta)\operatorname{Iw}_n = N_n\mathcal{N}(\delta) \backslash ( N_n \mathcal{N}(\delta) \times T \mathcal{T}(\delta) \times \overline{N} \overline{\mathcal{N}}(\epsilon) w_0). \]
 $\operatorname {ev}_{w_0}: A_{\chi }^{\delta } \to R(\chi )$ is
$\operatorname {ev}_{w_0}: A_{\chi }^{\delta } \to R(\chi )$ is  $\overline {\mathcal {B}} \cap \operatorname {\mathcal {I}\!w}_n(\delta )$-equivariant. The arrow
$\overline {\mathcal {B}} \cap \operatorname {\mathcal {I}\!w}_n(\delta )$-equivariant. The arrow  $\Psi ^{A}_{\chi }: A_{\chi }^{\delta } \widehat {\otimes }\mathscr {O}_{U_{w_0}(\epsilon )\operatorname {Iw}_n} \to \mathscr {L}(\chi )$ is just the natural map induced by the global sections since
$\Psi ^{A}_{\chi }: A_{\chi }^{\delta } \widehat {\otimes }\mathscr {O}_{U_{w_0}(\epsilon )\operatorname {Iw}_n} \to \mathscr {L}(\chi )$ is just the natural map induced by the global sections since  $A_{\chi }^{\delta }= \Gamma (U_{w_0}(\epsilon )\operatorname {Iw}_n, \mathscr {L}(\chi ))$. Notice that it factors through the co-invariants of
$A_{\chi }^{\delta }= \Gamma (U_{w_0}(\epsilon )\operatorname {Iw}_n, \mathscr {L}(\chi ))$. Notice that it factors through the co-invariants of  $A_{\chi }^{\delta }$ by the action of
$A_{\chi }^{\delta }$ by the action of  $\overline {N}_n \overline {\mathcal {N}}(\delta )$.
$\overline {N}_n \overline {\mathcal {N}}(\delta )$.
By definition of the ![]() $U_p$-correspondence, it is enough to show that the maps
$U_p$-correspondence, it is enough to show that the maps ![]() $\Psi ^{A,\vee }_{-w_0(\chi )}$ and
$\Psi ^{A,\vee }_{-w_0(\chi )}$ and ![]() $\Psi ^{A}_{\chi }$ are equivariant for the action of
$\Psi ^{A}_{\chi }$ are equivariant for the action of ![]() $\varpi = \operatorname {diag}(1,p)$; this is clear since the multiplication by
$\varpi = \operatorname {diag}(1,p)$; this is clear since the multiplication by ![]() $\varpi$ on
$\varpi$ on ![]() $\mathscr {L}(\chi )$ and
$\mathscr {L}(\chi )$ and ![]() $A_{\chi }^{\delta }$ is induced by the right multiplication of
$A_{\chi }^{\delta }$ is induced by the right multiplication of ![]() $\varpi$ on
$\varpi$ on ![]() $\Lambda \backslash \widetilde {\operatorname {\mathscr {F}\!\ell }}$ (see Remark 2.2.8 and Definition 2.2.12).
$\Lambda \backslash \widetilde {\operatorname {\mathscr {F}\!\ell }}$ (see Remark 2.2.8 and Definition 2.2.12).
Proposition 2.4.5 Let ![]() $\kappa \in X^*(\mathbf {T})$ be a dominant character. There are commutative diagrams of
$\kappa \in X^*(\mathbf {T})$ be a dominant character. There are commutative diagrams of ![]() $\operatorname {Iw}_n$-equivariant sheaves
$\operatorname {Iw}_n$-equivariant sheaves

A dual statement holds for ![]() $D^{\delta }_{\kappa }$. Moreover, these diagrams are compatible with the (normalized)
$D^{\delta }_{\kappa }$. Moreover, these diagrams are compatible with the (normalized) ![]() $U_p$-correspondence (Definition 2.2.9).
$U_p$-correspondence (Definition 2.2.9).
Proof. The commutativity of the diagrams is obvious from the definition of the maps ![]() $\Psi ^{A}_{\kappa }$ and
$\Psi ^{A}_{\kappa }$ and ![]() $\Psi ^{A,\vee }_{-w_0(\kappa )}$ of Proposition 2.4.4, and the fact that
$\Psi ^{A,\vee }_{-w_0(\kappa )}$ of Proposition 2.4.4, and the fact that ![]() $\Psi ^{\vee }_{-w_0(\kappa )}$ and
$\Psi ^{\vee }_{-w_0(\kappa )}$ and ![]() $\Psi _{\kappa }$ are induced by the invariants and co-invariants for the action of
$\Psi _{\kappa }$ are induced by the invariants and co-invariants for the action of ![]() $\mathbf {N}$ on
$\mathbf {N}$ on ![]() $V_{\kappa }$, respectively. The compatibility with the (normalized)
$V_{\kappa }$, respectively. The compatibility with the (normalized) ![]() $U_p$-correspondence follows from the fact that the (normalized) action of
$U_p$-correspondence follows from the fact that the (normalized) action of ![]() $\varpi$ on any of the sheaves involved is induced by the right multiplication on
$\varpi$ on any of the sheaves involved is induced by the right multiplication on ![]() $\Lambda \backslash \widetilde {\operatorname {\mathscr {F}\!\ell }}$ (see Remark 2.2.8 and Definition 2.2.12).
$\Lambda \backslash \widetilde {\operatorname {\mathscr {F}\!\ell }}$ (see Remark 2.2.8 and Definition 2.2.12).
Remark 2.4.6 In [Reference Andreatta and IovitaAI22, §§ 4.7 and 4.8] the authors define some filtrations attached to the sheaves of modular symbols over the modular curves; it turns out that these can be constructed directly from the flag variety. Indeed, Andreatta and Iovita use the formalism of vector bundles with marked sections to define the filtrations (see [Reference Andreatta and IovitaAI21, Corollary 2.6]), and the data of a vector bundle with marked section lives over affinoid neighbourhoods of ![]() $w\in W$. For example, let
$w\in W$. For example, let ![]() $\operatorname {St}$ be the standard representation of
$\operatorname {St}$ be the standard representation of ![]() $\operatorname {GL}_2$ and
$\operatorname {GL}_2$ and ![]() $\operatorname {St}^+\subset \operatorname {St}$ its natural lattice, and let us denote by
$\operatorname {St}^+\subset \operatorname {St}$ its natural lattice, and let us denote by ![]() $e_1,e_2$ the canonical basis of
$e_1,e_2$ the canonical basis of ![]() $\operatorname {St}^+$. Over
$\operatorname {St}^+$. Over ![]() $U_1(\epsilon )$ the natural map
$U_1(\epsilon )$ the natural map ![]() $\mathscr {L}^+(0,1)\to \operatorname {St}^+ \otimes \mathscr {O}_{U_1(\epsilon )}$ induces an isomorphism
$\mathscr {L}^+(0,1)\to \operatorname {St}^+ \otimes \mathscr {O}_{U_1(\epsilon )}$ induces an isomorphism ![]() $\mathscr {L}^+(0,1)/p^\epsilon = e_1\otimes \mathscr {O}^+_{U_1(\epsilon)}/p^\epsilon$. Therefore, we have the data of a vector bundle with marked sections
$\mathscr {L}^+(0,1)/p^\epsilon = e_1\otimes \mathscr {O}^+_{U_1(\epsilon)}/p^\epsilon$. Therefore, we have the data of a vector bundle with marked sections ![]() $(\operatorname {St}^+\otimes \mathscr {O}_{U_1(\epsilon )}, \mathscr {L}(0,1), e_1)$. The previous discussion shows in particular that the map of [Reference Andreatta and IovitaAI22, Proposition 4.15 ii.] is
$(\operatorname {St}^+\otimes \mathscr {O}_{U_1(\epsilon )}, \mathscr {L}(0,1), e_1)$. The previous discussion shows in particular that the map of [Reference Andreatta and IovitaAI22, Proposition 4.15 ii.] is ![]() $\Psi ^{D}_{\chi }$.
$\Psi ^{D}_{\chi }$.
Following the work of Pan [Reference PanPan22], there is a better way to study the filtrations above. Let ![]() $\mathfrak {gl}_2^0= \mathfrak {gl}_2 \otimes \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$ be the constant Lie algebroid over
$\mathfrak {gl}_2^0= \mathfrak {gl}_2 \otimes \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$ be the constant Lie algebroid over ![]() $\operatorname {\mathscr {F}\!\ell }$, and let
$\operatorname {\mathscr {F}\!\ell }$, and let ![]() $\mathfrak {n}^0 \subset \mathfrak {gl}_2^0$ be the
$\mathfrak {n}^0 \subset \mathfrak {gl}_2^0$ be the ![]() $\operatorname {GL}_2$-equivariant line bundle whose fibre at a point
$\operatorname {GL}_2$-equivariant line bundle whose fibre at a point ![]() $x\in \operatorname {\mathscr {F}\!\ell }$ is
$x\in \operatorname {\mathscr {F}\!\ell }$ is ![]() $\mathfrak {n}^0(x)= \operatorname {Lie} x \mathbf {N} x^{-1}$, that is, the Lie algebra of the unipotent group fixing
$\mathfrak {n}^0(x)= \operatorname {Lie} x \mathbf {N} x^{-1}$, that is, the Lie algebra of the unipotent group fixing ![]() $x$. Then
$x$. Then ![]() $\mathfrak {n}^0$ is an ideal of
$\mathfrak {n}^0$ is an ideal of ![]() $\mathfrak {gl}_2^0$, and the natural action of
$\mathfrak {gl}_2^0$, and the natural action of ![]() $\mathfrak {n}^0$ on
$\mathfrak {n}^0$ on ![]() $A^{\delta }_{\chi } \widehat {\otimes } \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$ induced by derivations of
$A^{\delta }_{\chi } \widehat {\otimes } \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$ induced by derivations of ![]() $\mathfrak {gl}_2^0$ defines the filtrations of Andreatta and Iovita.
$\mathfrak {gl}_2^0$ defines the filtrations of Andreatta and Iovita.
3. Overconvergent sheaves over the modular curve
Let ![]() $\mathbb {A}^{\infty }_\mathbb {Q}$ and
$\mathbb {A}^{\infty }_\mathbb {Q}$ and ![]() $\mathbb {A}^{\infty,p}_{\mathbb {Q}_p}$ be the rings of finite and finite prime-to-
$\mathbb {A}^{\infty,p}_{\mathbb {Q}_p}$ be the rings of finite and finite prime-to-![]() $p$ adèles of
$p$ adèles of ![]() $\mathbb {Q}$, respectively. From now on, we fix a neat compact open subgroup
$\mathbb {Q}$, respectively. From now on, we fix a neat compact open subgroup ![]() $K^p\subset \operatorname {GL}_2(\mathbb {A}^{\infty,p}_{\mathbb {Q}})$. Letting
$K^p\subset \operatorname {GL}_2(\mathbb {A}^{\infty,p}_{\mathbb {Q}})$. Letting ![]() $n\geq 0$, we denote by
$n\geq 0$, we denote by ![]() $\Gamma (p^n)$,
$\Gamma (p^n)$, ![]() $\Gamma _1(p^n)$ and
$\Gamma _1(p^n)$ and ![]() $\Gamma _0(p^n)$ the principal congruence subgroups
$\Gamma _0(p^n)$ the principal congruence subgroups
 \begin{gather*} \Gamma(p^n)=\{g\in
\operatorname{GL}_2(\mathbb{Z}_p) : g\equiv 1\ \mathrm{mod}\ p^n\} ,\\ \Gamma_1(p^n)=\biggl \{g\in
\operatorname{GL}_2(\mathbb{Z}_p) : g\equiv \biggl(
\begin{matrix} 1 & * \\ 0 & 1 \end{matrix} \biggr)\ \mathrm{mod}\ p^n\biggr \},\\
\Gamma_0(p^n)=\biggl \{g\in
\operatorname{GL}_2(\mathbb{Z}_p) : g\equiv \biggl(
\begin{matrix} * & * \\ 0 & * \end{matrix} \biggr)\ \mathrm{mod}\ p^n\biggr\}.
\end{gather*}
\begin{gather*} \Gamma(p^n)=\{g\in
\operatorname{GL}_2(\mathbb{Z}_p) : g\equiv 1\ \mathrm{mod}\ p^n\} ,\\ \Gamma_1(p^n)=\biggl \{g\in
\operatorname{GL}_2(\mathbb{Z}_p) : g\equiv \biggl(
\begin{matrix} 1 & * \\ 0 & 1 \end{matrix} \biggr)\ \mathrm{mod}\ p^n\biggr \},\\
\Gamma_0(p^n)=\biggl \{g\in
\operatorname{GL}_2(\mathbb{Z}_p) : g\equiv \biggl(
\begin{matrix} * & * \\ 0 & * \end{matrix} \biggr)\ \mathrm{mod}\ p^n\biggr\}.
\end{gather*}
Let ![]() $K_p\subset \operatorname {GL}_2(\mathbb {Q}_p)$ be a compact open subgroup. We denote by
$K_p\subset \operatorname {GL}_2(\mathbb {Q}_p)$ be a compact open subgroup. We denote by ![]() $Y_{K_p}^{{\rm alg}}$ and
$Y_{K_p}^{{\rm alg}}$ and ![]() $X_{K_p}^{{\rm alg}}$ the affine and compact modular curves of level
$X_{K_p}^{{\rm alg}}$ the affine and compact modular curves of level ![]() $K^pK_p$ over
$K^pK_p$ over ![]() $\operatorname {Spec} \mathbb {Q}_p$ (cf. [Reference Deligne and RapoportDR73]). We let
$\operatorname {Spec} \mathbb {Q}_p$ (cf. [Reference Deligne and RapoportDR73]). We let ![]() $Y^{{\rm alg}}(p^n)$,
$Y^{{\rm alg}}(p^n)$, ![]() $Y^{{\rm alg}}_1(p^n)$ and
$Y^{{\rm alg}}_1(p^n)$ and ![]() $Y^{{\rm alg}}_0(p^n)$ be the modular curves of level
$Y^{{\rm alg}}_0(p^n)$ be the modular curves of level ![]() $K^p\Gamma (p^n)$,
$K^p\Gamma (p^n)$, ![]() $K^p\Gamma _1(p^n)$ and
$K^p\Gamma _1(p^n)$ and ![]() $K^p\Gamma _0(p^n)$, respectively (and similarly for the compact modular curves). We let
$K^p\Gamma _0(p^n)$, respectively (and similarly for the compact modular curves). We let ![]() $Y_{K_p}$ and
$Y_{K_p}$ and ![]() $X_{K_p}$ denote their
$X_{K_p}$ denote their ![]() $p$-adic analytification to adic spaces over
$p$-adic analytification to adic spaces over ![]() $\operatorname {Spa}(\mathbb {Q}_p, \mathbb {Z}_p)$ (see [Reference HuberHub96]). We endow
$\operatorname {Spa}(\mathbb {Q}_p, \mathbb {Z}_p)$ (see [Reference HuberHub96]). We endow ![]() $X_{K_p}$ with the log structure defined by the cusp divisor
$X_{K_p}$ with the log structure defined by the cusp divisor ![]() $D= X_{K_p}\backslash Y_{K_p}$.
$D= X_{K_p}\backslash Y_{K_p}$.
Let ![]() $E^{{\rm alg}}/Y_{K_p}^{{\rm alg}}$ be the universal elliptic curve and
$E^{{\rm alg}}/Y_{K_p}^{{\rm alg}}$ be the universal elliptic curve and ![]() $E^{{\rm alg},{\rm sm}}/X_{K_p}^{{\rm alg}}$ its extension to a semi-abelian scheme. Let
$E^{{\rm alg},{\rm sm}}/X_{K_p}^{{\rm alg}}$ its extension to a semi-abelian scheme. Let ![]() $e: X_{K_p}^{{\rm alg}}\rightarrow E^{{\rm alg}, {\rm sm}}$ be the unit section and
$e: X_{K_p}^{{\rm alg}}\rightarrow E^{{\rm alg}, {\rm sm}}$ be the unit section and ![]() $\omega _E=e^* \Omega ^1_{E^{{\rm alg}, {\rm sm}}/X^{{\rm alg}}}$ the modular sheaf. Given an integer
$\omega _E=e^* \Omega ^1_{E^{{\rm alg}, {\rm sm}}/X^{{\rm alg}}}$ the modular sheaf. Given an integer ![]() $k\in \mathbb {Z}$, we denote by
$k\in \mathbb {Z}$, we denote by ![]() $\omega _E^{k}=\omega _E^{\otimes k}$ the modular sheaf of weight
$\omega _E^{k}=\omega _E^{\otimes k}$ the modular sheaf of weight ![]() $k$. We define the modular torsor to be the
$k$. We define the modular torsor to be the ![]() $\mathcal {T}$-torsor over
$\mathcal {T}$-torsor over ![]() $X_{K_p}$ defined by
$X_{K_p}$ defined by
Let ![]() $E[p^n]/Y_{K_p}$ be the étale local system of
$E[p^n]/Y_{K_p}$ be the étale local system of ![]() $p^n$-torsion points of the universal elliptic curve. By [Reference Diao, Lan, Liu and ZhuDLLZ23b, Theorem 4.6.1], the sheaf
$p^n$-torsion points of the universal elliptic curve. By [Reference Diao, Lan, Liu and ZhuDLLZ23b, Theorem 4.6.1], the sheaf ![]() $E[p^n]$ has a natural extension to a Kummer-étale local system over
$E[p^n]$ has a natural extension to a Kummer-étale local system over ![]() $X_{K_p}$, which by an abuse of notation we also write as
$X_{K_p}$, which by an abuse of notation we also write as ![]() $E[p^n]$. We let
$E[p^n]$. We let ![]() $T_pE = \varprojlim _{n} E[p^n]$ be the Tate module of
$T_pE = \varprojlim _{n} E[p^n]$ be the Tate module of ![]() $E$, seen as a pro-Kummer-étale local system over
$E$, seen as a pro-Kummer-étale local system over ![]() $X_{K_p}$. Given a dominant weight
$X_{K_p}$. Given a dominant weight ![]() $\kappa \in X^*(\mathbf {T})^+$, we let
$\kappa \in X^*(\mathbf {T})^+$, we let ![]() $V_{\kappa, {\rm \acute {e}t}}$ denote the pro-Kummer-étale local system over
$V_{\kappa, {\rm \acute {e}t}}$ denote the pro-Kummer-étale local system over ![]() $X_{K_p}$ attached to the
$X_{K_p}$ attached to the ![]() $K_p$-representation
$K_p$-representation ![]() $V_{\kappa }$. We let
$V_{\kappa }$. We let ![]() $R\Gamma _{{\rm pro\acute {e}t}}(Y_{\mathbb {C}_p}, V_{\kappa,{\rm \acute {e}t}})$ and
$R\Gamma _{{\rm pro\acute {e}t}}(Y_{\mathbb {C}_p}, V_{\kappa,{\rm \acute {e}t}})$ and ![]() $R\Gamma _{{\rm pro\acute {e}t},c}( Y_{\mathbb {C}_p}, V_{\kappa,{\rm \acute {e}t}})$ respectively be the étale cohomology and the étale cohomology with compact support of
$R\Gamma _{{\rm pro\acute {e}t},c}( Y_{\mathbb {C}_p}, V_{\kappa,{\rm \acute {e}t}})$ respectively be the étale cohomology and the étale cohomology with compact support of ![]() $V_{\kappa,{\rm \acute {e}t}}$.
$V_{\kappa,{\rm \acute {e}t}}$.
3.1 The Hodge–Tate period map
Let ![]() $\mathbb {Q}_p^{{\rm cyc}}$ be the
$\mathbb {Q}_p^{{\rm cyc}}$ be the ![]() $p$-adic completion of the
$p$-adic completion of the ![]() $p$-adic cyclotomic field
$p$-adic cyclotomic field ![]() $\mathbb {Q}_p(\mu _{p^\infty})$. Scholze proved in [Reference ScholzeSch15] that the inverse limit
$\mathbb {Q}_p(\mu _{p^\infty})$. Scholze proved in [Reference ScholzeSch15] that the inverse limit ![]() $X(p^\infty )=\varprojlim _n X(p^n)$ has a natural interpretation as a perfectoid space. Furthermore, he constructed a Hodge–Tate period map
$X(p^\infty )=\varprojlim _n X(p^n)$ has a natural interpretation as a perfectoid space. Furthermore, he constructed a Hodge–Tate period map ![]() $\pi _{\operatorname {HT}}: X(p^\infty )\rightarrow \mathbb {P}^1_{\mathbb {Q}_p}$ parametrizing the Hodge–Tate filtration of elliptic curves at geometric points; let us briefly recall how it is constructed. The Hodge–Tate exact sequence is the following short exact sequence of pro-Kummer-étale sheaves over
$\pi _{\operatorname {HT}}: X(p^\infty )\rightarrow \mathbb {P}^1_{\mathbb {Q}_p}$ parametrizing the Hodge–Tate filtration of elliptic curves at geometric points; let us briefly recall how it is constructed. The Hodge–Tate exact sequence is the following short exact sequence of pro-Kummer-étale sheaves over ![]() $X_{K_p}$:
$X_{K_p}$:
On the other hand, the perfectoid space ![]() $X(p^{\infty })$ parametrizes trivializations of
$X(p^{\infty })$ parametrizes trivializations of ![]() $T_pE$. If
$T_pE$. If ![]() $\psi : \mathbb {Z}_p^2 \cong T_pE$ denotes the universal trivialization of the Tate module, the pullback of (17) by
$\psi : \mathbb {Z}_p^2 \cong T_pE$ denotes the universal trivialization of the Tate module, the pullback of (17) by ![]() $\psi$ gives rise a line subbundle of
$\psi$ gives rise a line subbundle of ![]() $\mathscr {O}_{X(p^{\infty })}^{\oplus 2}$ which defines the map
$\mathscr {O}_{X(p^{\infty })}^{\oplus 2}$ which defines the map ![]() $\pi _{\operatorname {HT}}: X(p^{\infty }) \to \operatorname {\mathscr {F}\!\ell }= \mathbb {P}^1_{\mathbb {Q}_p}$. Let us summarize the previous discussion and some properties of
$\pi _{\operatorname {HT}}: X(p^{\infty }) \to \operatorname {\mathscr {F}\!\ell }= \mathbb {P}^1_{\mathbb {Q}_p}$. Let us summarize the previous discussion and some properties of ![]() $\pi _{\operatorname {HT}}$ in the following theorem.
$\pi _{\operatorname {HT}}$ in the following theorem.
Theorem 3.1.1 [Reference ScholzeSch15, Theorem III.3.18]
There exists a perfectoid space ![]() $X(p^\infty )$ over
$X(p^\infty )$ over ![]() $\mathbb {Q}_p^{{\rm cyc}}$ satisfying the tilde limit property [Reference Scholze and WeinsteinSW13, Definition 2.4.1]
$\mathbb {Q}_p^{{\rm cyc}}$ satisfying the tilde limit property [Reference Scholze and WeinsteinSW13, Definition 2.4.1]
Moreover, let ![]() $[x:y] \in \operatorname {\mathscr {F}\!\ell }= \mathbb {P}^1_{\mathbb {Q}_p}$ denote the projective coordinates of the projective space. There is a
$[x:y] \in \operatorname {\mathscr {F}\!\ell }= \mathbb {P}^1_{\mathbb {Q}_p}$ denote the projective coordinates of the projective space. There is a ![]() $\operatorname {GL}_2(\mathbb {Q}_p)$-equivariant Hodge–Tate period map
$\operatorname {GL}_2(\mathbb {Q}_p)$-equivariant Hodge–Tate period map
such that for any open rational subset ![]() $U$ of
$U$ of ![]() $U_1= \{[x:y] | |x/y|\leq 1\}$ or
$U_1= \{[x:y] | |x/y|\leq 1\}$ or ![]() $U_{\infty }= \{[x:y] | |y/x|\leq 1\}$ of
$U_{\infty }= \{[x:y] | |y/x|\leq 1\}$ of ![]() $\operatorname {\mathscr {F}\!\ell }$, the inverse image
$\operatorname {\mathscr {F}\!\ell }$, the inverse image ![]() $\pi ^{-1}_{\operatorname {HT}}(U)\subset X(p^\infty )$ is an affinoid perfectoid subspace, and there exist
$\pi ^{-1}_{\operatorname {HT}}(U)\subset X(p^\infty )$ is an affinoid perfectoid subspace, and there exist ![]() $n\gg 0$ and an open affinoid
$n\gg 0$ and an open affinoid ![]() $V_n\subset X(p^n)$ whose inverse image to
$V_n\subset X(p^n)$ whose inverse image to ![]() $X(p^\infty )$ is equal to
$X(p^\infty )$ is equal to ![]() $\pi _{\operatorname {HT}}^{-1}(U)$.
$\pi _{\operatorname {HT}}^{-1}(U)$.
Another feature of the Hodge–Tate period map is that it encodes the modular sheaves in terms of ![]() $\operatorname {GL}_2$-equivariant line bundles over
$\operatorname {GL}_2$-equivariant line bundles over ![]() $\operatorname {\mathscr {F}\!\ell }$. More precisely, letting
$\operatorname {\mathscr {F}\!\ell }$. More precisely, letting ![]() $\operatorname {St}$ be the standard representation, we have an exact sequence of
$\operatorname {St}$ be the standard representation, we have an exact sequence of ![]() $\mathbf {B}$-modules
$\mathbf {B}$-modules
Taking the associated ![]() $\operatorname {GL}_2$-equivariant vector bundles over
$\operatorname {GL}_2$-equivariant vector bundles over ![]() $\operatorname {\mathscr {F}\!\ell }$, we have a short exact sequence
$\operatorname {\mathscr {F}\!\ell }$, we have a short exact sequence
Now the map ![]() $\pi _{\operatorname {HT}}$ induces a
$\pi _{\operatorname {HT}}$ induces a ![]() $\operatorname {GL}_2(\mathbb {Q}_p)$-equivariant morphism of ringed sites
$\operatorname {GL}_2(\mathbb {Q}_p)$-equivariant morphism of ringed sites
In particular, we can take pullbacks of ![]() $\operatorname {GL}_2$-equivariant
$\operatorname {GL}_2$-equivariant ![]() $\mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$-vector bundles over
$\mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$-vector bundles over ![]() $\operatorname {\mathscr {F}\!\ell }$ to
$\operatorname {\mathscr {F}\!\ell }$ to ![]() $\operatorname {GL}_2(\mathbb {Q}_p)$-equivariant
$\operatorname {GL}_2(\mathbb {Q}_p)$-equivariant ![]() $\widehat {\mathscr {O}}_X$-vector bundles over
$\widehat {\mathscr {O}}_X$-vector bundles over ![]() $X(p^{\infty })_{{\rm prok\acute {e}t}}$.
$X(p^{\infty })_{{\rm prok\acute {e}t}}$.
Convention 3.1.2 Given a ![]() $K_p$-equivariant sheaf
$K_p$-equivariant sheaf ![]() $\mathscr {F}$ over
$\mathscr {F}$ over ![]() $\operatorname {\mathscr {F}\!\ell }$, we will identify
$\operatorname {\mathscr {F}\!\ell }$, we will identify ![]() $\pi _{\operatorname {HT}}^*(\mathscr {F})$ with the pro-Kummer-étale sheaf over
$\pi _{\operatorname {HT}}^*(\mathscr {F})$ with the pro-Kummer-étale sheaf over ![]() $X_{K_p}$ defined by descent from the
$X_{K_p}$ defined by descent from the ![]() $K_p$-equivariant sheaf over
$K_p$-equivariant sheaf over ![]() $X(p^{\infty })_{{\rm prok\acute {e}t}}$.
$X(p^{\infty })_{{\rm prok\acute {e}t}}$.
Remark 3.1.3 Essentially by definition, the pullback of (18) by ![]() $\pi _{\operatorname {HT}}$ is the Hodge–Tate exact sequence (17). Our convention differs from that of [Reference Andreatta and IovitaAI22, § 4.3], where the pullback of the standard representation by
$\pi _{\operatorname {HT}}$ is the Hodge–Tate exact sequence (17). Our convention differs from that of [Reference Andreatta and IovitaAI22, § 4.3], where the pullback of the standard representation by ![]() $\pi _{\operatorname {HT}}$ is identified with the dual of
$\pi _{\operatorname {HT}}$ is identified with the dual of ![]() $T_pE$.
$T_pE$.
Let ![]() $\kappa \in X^*(\mathbf {T})^+$ be a dominant weight and
$\kappa \in X^*(\mathbf {T})^+$ be a dominant weight and ![]() $V_{\kappa }$ the irreducible representation of
$V_{\kappa }$ the irreducible representation of ![]() $\operatorname {GL}_2$ of highest weight
$\operatorname {GL}_2$ of highest weight ![]() $\kappa$. Treating
$\kappa$. Treating ![]() $V_{\kappa }$ as a constant
$V_{\kappa }$ as a constant ![]() $\operatorname {GL}_2(\mathbb {Q}_p)$-equivariant sheaf over
$\operatorname {GL}_2(\mathbb {Q}_p)$-equivariant sheaf over ![]() $\operatorname {\mathscr {F}\!\ell }$, one has that
$\operatorname {\mathscr {F}\!\ell }$, one has that ![]() $\pi _{\operatorname {HT}}^*(V_{\kappa })= V_{\kappa, {\rm \acute {e}t}}$ as pro-Kummer-étale sheaves. This implies that the pullback by
$\pi _{\operatorname {HT}}^*(V_{\kappa })= V_{\kappa, {\rm \acute {e}t}}$ as pro-Kummer-étale sheaves. This implies that the pullback by ![]() $\pi _{\operatorname {HT}}$ of the
$\pi _{\operatorname {HT}}$ of the ![]() $\operatorname {GL}_2$-equivariant vector bundle
$\operatorname {GL}_2$-equivariant vector bundle ![]() $V_{\kappa }\otimes \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$ is equal to
$V_{\kappa }\otimes \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$ is equal to ![]() $V_{\kappa, {\rm \acute {e}t}}\otimes \widehat {\mathscr {O}}_X$. Concerning the
$V_{\kappa, {\rm \acute {e}t}}\otimes \widehat {\mathscr {O}}_X$. Concerning the ![]() $\operatorname {GL}_2$-equivariant line bundles over
$\operatorname {GL}_2$-equivariant line bundles over ![]() $\operatorname {\mathscr {F}\!\ell }$, one has the following result (cf. [Reference Caraiani and ScholzeCS17, Proposition 2.3.9]).
$\operatorname {\mathscr {F}\!\ell }$, one has the following result (cf. [Reference Caraiani and ScholzeCS17, Proposition 2.3.9]).
Proposition 3.1.4 Let ![]() $\kappa =(k_1,k_2) \in X^*(\mathbf {T})$ be an algebraic weight and
$\kappa =(k_1,k_2) \in X^*(\mathbf {T})$ be an algebraic weight and ![]() $\mathscr {L}(\kappa )$ the
$\mathscr {L}(\kappa )$ the ![]() $\operatorname {GL}_2$-equivariant line bundle over
$\operatorname {GL}_2$-equivariant line bundle over ![]() $\operatorname {\mathscr {F}\!\ell }$ of weight
$\operatorname {\mathscr {F}\!\ell }$ of weight ![]() $\kappa$. There is a natural isomorphism of pro-Kummer-étale sheaves over
$\kappa$. There is a natural isomorphism of pro-Kummer-étale sheaves over ![]() $X_{K_p}$,
$X_{K_p}$,
Equivalently, let ![]() $\widetilde {\operatorname {\mathscr {F}\!\ell }}= \mathcal {N} \backslash\!\operatorname {\mathcal {G}\!\mathcal {L}}_2$ and
$\widetilde {\operatorname {\mathscr {F}\!\ell }}= \mathcal {N} \backslash\!\operatorname {\mathcal {G}\!\mathcal {L}}_2$ and ![]() $\pi _{K_p}:X(p^{\infty }) \to X_{K_p}$. We have an isomorphism of
$\pi _{K_p}:X(p^{\infty }) \to X_{K_p}$. We have an isomorphism of ![]() $\operatorname {GL}_2(\mathbb {Q}_p)$-equivariant
$\operatorname {GL}_2(\mathbb {Q}_p)$-equivariant ![]() $\mathcal {T}$-torsors over
$\mathcal {T}$-torsors over ![]() $X(p^{\infty })$,
$X(p^{\infty })$,
where ![]() $\mathcal {T}_{{\rm mod}}(-1,0)$ is a Tate twist in the first component of the modular torsor (16).
$\mathcal {T}_{{\rm mod}}(-1,0)$ is a Tate twist in the first component of the modular torsor (16).
Proof. We only need to show the isomorphism of torsors; this follows from Remark 2.1.2(i) and the definition of the modular torsor. In fact, since the pullback of (18) is the Hodge–Tate exact sequence, one has that ![]() $\pi _{\operatorname {HT}}^*(\mathscr {L}(1,0))= \omega _E^1\otimes \widehat {\mathscr {O}}_X$ and
$\pi _{\operatorname {HT}}^*(\mathscr {L}(1,0))= \omega _E^1\otimes \widehat {\mathscr {O}}_X$ and ![]() $\pi _{\operatorname {HT}}^*(\mathscr {L}(0,1))= \omega _E^{-1}\otimes \widehat {\mathscr {O}}(1)$, and the proposition follows since
$\pi _{\operatorname {HT}}^*(\mathscr {L}(0,1))= \omega _E^{-1}\otimes \widehat {\mathscr {O}}(1)$, and the proposition follows since ![]() $\mathscr {L}(\kappa )= \mathscr {L}(1,0)^{\otimes k_1}\otimes \mathscr {L}(0,1)^{\otimes k_2}$.
$\mathscr {L}(\kappa )= \mathscr {L}(1,0)^{\otimes k_1}\otimes \mathscr {L}(0,1)^{\otimes k_2}$.
3.2 Overconvergent modular forms
Throughout the rest of this section we fix ![]() $n\geq 1$ and write
$n\geq 1$ and write ![]() $X_{\infty }=X(p^{\infty })$ and
$X_{\infty }=X(p^{\infty })$ and ![]() $X= X_0(p^n)$. Let
$X= X_0(p^n)$. Let ![]() $\pi _{\operatorname {Iw}_n}: X_{\infty }\to X$ be the natural projection and
$\pi _{\operatorname {Iw}_n}: X_{\infty }\to X$ be the natural projection and ![]() $\pi _{\operatorname {HT}}: X_{\infty }\to \operatorname {\mathscr {F}\!\ell } \cong \mathbb {P}^1_{\mathbb {Q}_p}$ the Hodge–Tate period map. Let
$\pi _{\operatorname {HT}}: X_{\infty }\to \operatorname {\mathscr {F}\!\ell } \cong \mathbb {P}^1_{\mathbb {Q}_p}$ the Hodge–Tate period map. Let ![]() $\overline {X}^{{\rm ord}}_{\infty }= \pi _{\operatorname {HT}}^{-1}(\operatorname {\mathscr {F}\!\ell }(\mathbb {Q}_p))$ be the closure of the ordinary locus at infinite level [Reference ScholzeSch15, Lemma III.3.6.], and
$\overline {X}^{{\rm ord}}_{\infty }= \pi _{\operatorname {HT}}^{-1}(\operatorname {\mathscr {F}\!\ell }(\mathbb {Q}_p))$ be the closure of the ordinary locus at infinite level [Reference ScholzeSch15, Lemma III.3.6.], and ![]() $\overline {X}^{{\rm ord}} = \pi _{\operatorname {Iw}_n}(\overline {X}^{{\rm ord}}_{\infty })$ the closure of the ordinary locus of
$\overline {X}^{{\rm ord}} = \pi _{\operatorname {Iw}_n}(\overline {X}^{{\rm ord}}_{\infty })$ the closure of the ordinary locus of ![]() $X$.
$X$.
Let ![]() $C^{{\rm can}}_n\subset E[p^n]$ be the canonical subgroup over
$C^{{\rm can}}_n\subset E[p^n]$ be the canonical subgroup over ![]() $\overline {X}^{{\rm ord}}$ and
$\overline {X}^{{\rm ord}}$ and ![]() $w\in W=\{1,w_0\}$. We let
$w\in W=\{1,w_0\}$. We let ![]() $\overline {X}^{{\rm ord}}_{w}\subset \overline {X}^{{\rm ord}}$ denote the
$\overline {X}^{{\rm ord}}_{w}\subset \overline {X}^{{\rm ord}}$ denote the ![]() $w$-ordinary locus, that is, the ordinary locus where
$w$-ordinary locus, that is, the ordinary locus where ![]() $C_n^{{\rm can}}$ has relative position
$C_n^{{\rm can}}$ has relative position ![]() $w$ with respect to the universal subgroup
$w$ with respect to the universal subgroup ![]() $H_n\subset E[p^n]$. In other words,
$H_n\subset E[p^n]$. In other words, ![]() $\overline {X}_{1}^{{\rm ord}}$ is the ordinary locus where
$\overline {X}_{1}^{{\rm ord}}$ is the ordinary locus where ![]() $C_n^{{\rm can}}= H_n$ and
$C_n^{{\rm can}}= H_n$ and ![]() $\overline {X}_{w_0}^{{\rm ord}}$ the locus where
$\overline {X}_{w_0}^{{\rm ord}}$ the locus where ![]() $C_n^{{\rm can}}\cap H_n=0$. We can also write
$C_n^{{\rm can}}\cap H_n=0$. We can also write ![]() $\overline {X}^{{\rm ord}}_{w}=\pi _{\operatorname {Iw}_n}(\pi _{\operatorname {HT}}^{-1}(w\operatorname {Iw}_n))$.
$\overline {X}^{{\rm ord}}_{w}=\pi _{\operatorname {Iw}_n}(\pi _{\operatorname {HT}}^{-1}(w\operatorname {Iw}_n))$.
Let ![]() $\epsilon \geq n \geq 1$ and
$\epsilon \geq n \geq 1$ and ![]() $w\in W=\{1,w_0\}$. In § 2.2 we defined affinoid neighbourhoods
$w\in W=\{1,w_0\}$. In § 2.2 we defined affinoid neighbourhoods ![]() $\{U_w(\epsilon )\operatorname {Iw}_n\}_{\epsilon \geq n}$ of
$\{U_w(\epsilon )\operatorname {Iw}_n\}_{\epsilon \geq n}$ of ![]() $w\in \operatorname {\mathscr {F}\!\ell }$. By Theorem 3.1.1 their pullback to
$w\in \operatorname {\mathscr {F}\!\ell }$. By Theorem 3.1.1 their pullback to ![]() $X_{\infty }$ is an affinoid perfectoid arising from some finite level modular curve
$X_{\infty }$ is an affinoid perfectoid arising from some finite level modular curve ![]() $X_{K_p}$. Furthermore, as
$X_{K_p}$. Furthermore, as ![]() $\pi _{\operatorname {HT}}^{-1}(U_w(\epsilon )\operatorname {Iw}_n)$ is
$\pi _{\operatorname {HT}}^{-1}(U_w(\epsilon )\operatorname {Iw}_n)$ is ![]() $\operatorname {Iw}_n$-stable, we can take
$\operatorname {Iw}_n$-stable, we can take ![]() $K_p=\operatorname {Iw}_n$. The previous discussion leads to the following definition.
$K_p=\operatorname {Iw}_n$. The previous discussion leads to the following definition.
Definition 3.2.1 There exists a unique open affinoid subspace ![]() $X_{w}(\epsilon )\subset X$ such that
$X_{w}(\epsilon )\subset X$ such that ![]() $\pi _{\operatorname {Iw}_n}^{-1}(X_{w}(\epsilon ))= \pi _{\operatorname {HT}}^{-1}(U_w(\epsilon )\operatorname {Iw}_n)$.
$\pi _{\operatorname {Iw}_n}^{-1}(X_{w}(\epsilon ))= \pi _{\operatorname {HT}}^{-1}(U_w(\epsilon )\operatorname {Iw}_n)$.
Remark 3.2.2 The following properties are deduced from Lemma 2.2.2.
(i)
 $X_{w}(\epsilon ') \subset X_{w}(\epsilon )$ is a strict immersion for
$X_{w}(\epsilon ') \subset X_{w}(\epsilon )$ is a strict immersion for  $\epsilon '>\epsilon$.
$\epsilon '>\epsilon$.(ii)
 $\{X_{w}(\epsilon )\}_{\epsilon \geq n}$ is a basis of strict neighbourhoods of
$\{X_{w}(\epsilon )\}_{\epsilon \geq n}$ is a basis of strict neighbourhoods of  $\overline {X}^{{\rm ord}}_{w}$, namely,
$\overline {X}^{{\rm ord}}_{w}$, namely,  $\bigcap _{\epsilon \geq n} X_{w}(\epsilon )= \overline {X}^{{\rm ord}}_w$.
$\bigcap _{\epsilon \geq n} X_{w}(\epsilon )= \overline {X}^{{\rm ord}}_w$.
The affine modular curve ![]() $Y\subset X$ parametrizes triples
$Y\subset X$ parametrizes triples ![]() $(E,H_n, \psi _N)$ where
$(E,H_n, \psi _N)$ where ![]() $E$ is an elliptic curve
$E$ is an elliptic curve ![]() $E$,
$E$, ![]() $\psi _N$ is some prime-to-
$\psi _N$ is some prime-to-![]() $p$ level structure, and
$p$ level structure, and ![]() $H_n\subset E[p^n]$ is a cyclic subgroup of order
$H_n\subset E[p^n]$ is a cyclic subgroup of order ![]() $p^n$. Let
$p^n$. Let ![]() $\varpi =\operatorname {diag}(1,p)$. In the following we study the dynamics of the
$\varpi =\operatorname {diag}(1,p)$. In the following we study the dynamics of the ![]() $U_p$-correspondence (cf. [Reference Boxer and PilloniBP22, § 5.3]).
$U_p$-correspondence (cf. [Reference Boxer and PilloniBP22, § 5.3]).
Definition 3.2.3 The ![]() $U_p$-correspondence of
$U_p$-correspondence of ![]() $X$ is the finite flat correspondence
$X$ is the finite flat correspondence ![]() $C$ fitting into the diagram
$C$ fitting into the diagram

and parametrizing tuples ![]() $(E,H_n, \psi _{N},H')$ where
$(E,H_n, \psi _{N},H')$ where ![]() $(E,H_n,\psi _N)$ defines a point in
$(E,H_n,\psi _N)$ defines a point in ![]() $X$, and
$X$, and ![]() $H'\subset E[p]$ is a cyclic subgroup of order
$H'\subset E[p]$ is a cyclic subgroup of order ![]() $p$ such that
$p$ such that ![]() $H_n\cap H'=0$. We define
$H_n\cap H'=0$. We define ![]() $p_1(E, H_n,\psi _N,H')=(E, H_n, \psi _N)$ and
$p_1(E, H_n,\psi _N,H')=(E, H_n, \psi _N)$ and ![]() $p_2(E, H_n ,\psi _N,H')= (E/H',\overline {H}_n ,\overline {\psi }_N)$, where
$p_2(E, H_n ,\psi _N,H')= (E/H',\overline {H}_n ,\overline {\psi }_N)$, where ![]() $\overline {\psi }_N$ and
$\overline {\psi }_N$ and ![]() $\overline {H}_n$ are the images of
$\overline {H}_n$ are the images of ![]() $\psi _N$ and
$\psi _N$ and ![]() $H_n$ in the quotient
$H_n$ in the quotient ![]() $E/H'$. Let
$E/H'$. Let ![]() $\pi : p_1^*E\rightarrow p_2^*E$ be the universal isogeny over
$\pi : p_1^*E\rightarrow p_2^*E$ be the universal isogeny over ![]() $C$ and
$C$ and ![]() $\pi ^\vee : p_2^* E\rightarrow p_1^* E$ its dual. For a subspace
$\pi ^\vee : p_2^* E\rightarrow p_1^* E$ its dual. For a subspace ![]() $Z\subset X$ let us denote
$Z\subset X$ let us denote ![]() $U_p(Z)= p_1(p^{-1}_2(Z))$ and
$U_p(Z)= p_1(p^{-1}_2(Z))$ and ![]() $U_p^{t}(Z)= p_2(p_1^{-1}(Z))$.
$U_p^{t}(Z)= p_2(p_1^{-1}(Z))$.
The following lemma uses the same strategy as [Reference Andreatta and IovitaAI22, § 4.5]. Notice, however, that the convention on ![]() $\pi _{\operatorname {HT}}$ differs (see Remark 3.1.3).
$\pi _{\operatorname {HT}}$ differs (see Remark 3.1.3).
Lemma 3.2.4 Let ![]() $\epsilon \geq n$. The following assertions hold.
$\epsilon \geq n$. The following assertions hold.
(i)
 $U_p^t(X_{1}(\epsilon )) \subset X_{1}(\epsilon +1)$ and
$U_p^t(X_{1}(\epsilon )) \subset X_{1}(\epsilon +1)$ and  $U_p(X_{1}(\epsilon )) \supset X_{1}(\epsilon -1)$ if
$U_p(X_{1}(\epsilon )) \supset X_{1}(\epsilon -1)$ if  $\epsilon \geq n+1$.
$\epsilon \geq n+1$.(ii)
 $U_p(X_{w_0}(\epsilon )) \subset X_{w_0}(\epsilon +1)$ and
$U_p(X_{w_0}(\epsilon )) \subset X_{w_0}(\epsilon +1)$ and  $U_p^t( X_{w_0}(\epsilon )) \supset X_{w_0}(\epsilon -1)$ if
$U_p^t( X_{w_0}(\epsilon )) \supset X_{w_0}(\epsilon -1)$ if  $\epsilon \geq n+1$.
$\epsilon \geq n+1$.
Proof. The perfectoid modular curve ![]() $X_{\infty }$ parametrizes triples
$X_{\infty }$ parametrizes triples ![]() $(E,\psi _N, (e_1,e_2))$ where
$(E,\psi _N, (e_1,e_2))$ where ![]() $E$ is an elliptic curve,
$E$ is an elliptic curve, ![]() $\psi _N$ a prime-to-
$\psi _N$ a prime-to-![]() $p$ level structure, and
$p$ level structure, and ![]() $(e_1,e_2)$ a basis of
$(e_1,e_2)$ a basis of ![]() $T_pE$. Let
$T_pE$. Let ![]() $C_{\infty }=X_{\infty }\times _{X,p_1} C$. The perfectoid curve
$C_{\infty }=X_{\infty }\times _{X,p_1} C$. The perfectoid curve ![]() $C_{\infty }$ parametrizes
$C_{\infty }$ parametrizes ![]() $(E, \psi _N,(e_1,e_2), H' )$, where
$(E, \psi _N,(e_1,e_2), H' )$, where ![]() $(E,\psi _N, (e_1,e_2))\in X_\infty$ and
$(E,\psi _N, (e_1,e_2))\in X_\infty$ and ![]() $H'\subset E[p^n]$ is a cyclic subgroup of order
$H'\subset E[p^n]$ is a cyclic subgroup of order ![]() $p$ such that
$p$ such that ![]() $\langle \overline {e}_1 \rangle \cap H'=0\ \mathrm {mod}~p$. Write
$\langle \overline {e}_1 \rangle \cap H'=0\ \mathrm {mod}~p$. Write ![]() $C_{\infty }= \bigsqcup _{a\in \mathbb {F}_p} C_{\infty,a}$, with
$C_{\infty }= \bigsqcup _{a\in \mathbb {F}_p} C_{\infty,a}$, with ![]() $C_{\infty,a}$ the locus where
$C_{\infty,a}$ the locus where ![]() $H'=\langle \overline { e}_2+a \overline {e}_1\rangle$. Note that the map
$H'=\langle \overline { e}_2+a \overline {e}_1\rangle$. Note that the map ![]() $p_1:C_{\infty,a}\rightarrow X_{\infty }$ is an isomorphism for all
$p_1:C_{\infty,a}\rightarrow X_{\infty }$ is an isomorphism for all ![]() $a$. We have a diagram
$a$. We have a diagram

with ![]() $p_1(E,\psi _N, (e_1,e_2), H')=(E,\psi _N, (e_1,e_2))$ and
$p_1(E,\psi _N, (e_1,e_2), H')=(E,\psi _N, (e_1,e_2))$ and ![]() $p_2(E,\psi _N, (e_1,e_2), H')= (E/H', \overline {\psi }_N, (\pi (e_1), \tilde {e}_2))$, such that the restriction of
$p_2(E,\psi _N, (e_1,e_2), H')= (E/H', \overline {\psi }_N, (\pi (e_1), \tilde {e}_2))$, such that the restriction of ![]() $p_2$ to
$p_2$ to ![]() $C_{\infty,a}$ is given by
$C_{\infty,a}$ is given by ![]() $\tilde {e}_2= ({1}/{p})(\pi (e_2)+a\pi (e_1))$ for
$\tilde {e}_2= ({1}/{p})(\pi (e_2)+a\pi (e_1))$ for ![]() $0 \leq a < p$ lifting
$0 \leq a < p$ lifting ![]() $a$. Let
$a$. Let ![]() $U_{p,a}:=\big ( \begin {smallmatrix} 1 & -a \\ 0 & p \end {smallmatrix} \big )$. Composing with the Hodge–Tate period map
$U_{p,a}:=\big ( \begin {smallmatrix} 1 & -a \\ 0 & p \end {smallmatrix} \big )$. Composing with the Hodge–Tate period map ![]() $\pi _{\operatorname {HT}}: X_{\infty }\rightarrow \operatorname {\mathscr {F}\!\ell }$, we have a commutative diagram of correspondences (see diagram (10))
$\pi _{\operatorname {HT}}: X_{\infty }\rightarrow \operatorname {\mathscr {F}\!\ell }$, we have a commutative diagram of correspondences (see diagram (10))

where the map ![]() $p_{2,a}: \operatorname {\mathscr {F}\!\ell }_a \to \operatorname {\mathscr {F}\!\ell }$ is the right multiplication by
$p_{2,a}: \operatorname {\mathscr {F}\!\ell }_a \to \operatorname {\mathscr {F}\!\ell }$ is the right multiplication by ![]() $U_{p,a}^{-1}$. Indeed, if
$U_{p,a}^{-1}$. Indeed, if ![]() $e_1,e_2$ is the canonical basis of the standard representation of
$e_1,e_2$ is the canonical basis of the standard representation of ![]() $\operatorname {GL}_2$ we have that
$\operatorname {GL}_2$ we have that ![]() $p_{2,a}^*(e_1)=e_1$ and
$p_{2,a}^*(e_1)=e_1$ and ![]() $p_{2,a}^*(e_2)= ({1}/{p}) (e_2+ae_1)$. The lemma follows by Lemma 2.2.11 and the definition of the affinoids
$p_{2,a}^*(e_2)= ({1}/{p}) (e_2+ae_1)$. The lemma follows by Lemma 2.2.11 and the definition of the affinoids ![]() $X_w(\epsilon )$.
$X_w(\epsilon )$.
Remark 3.2.5 Taking ![]() $\operatorname {Iw}_n$-quotients in (20), one obtains the morphism of correspondences
$\operatorname {Iw}_n$-quotients in (20), one obtains the morphism of correspondences

where the bottom correspondence is that of (11). Therefore, the ![]() $U_p$-correspondence of
$U_p$-correspondence of ![]() $X$ is simply the pullback of the
$X$ is simply the pullback of the ![]() $U_p$-correspondence of the stack
$U_p$-correspondence of the stack ![]() $\operatorname {\mathscr {F}\!\ell }/\operatorname {Iw}_n$.
$\operatorname {\mathscr {F}\!\ell }/\operatorname {Iw}_n$.
Let ![]() $\mathcal {T}^{0} \subset \mathcal {T}$ be the affinoid bounded torus given by the generic fibre of the
$\mathcal {T}^{0} \subset \mathcal {T}$ be the affinoid bounded torus given by the generic fibre of the ![]() $p$-adic completion of
$p$-adic completion of ![]() $\mathbf {T}$. Let
$\mathbf {T}$. Let ![]() $\mathcal {T}_{{\rm mod},{\rm \acute {e}t}}$ be the base change of
$\mathcal {T}_{{\rm mod},{\rm \acute {e}t}}$ be the base change of ![]() $\mathcal {T}_{{\rm mod}}$ to a
$\mathcal {T}_{{\rm mod}}$ to a ![]() $\mathcal {T}$-torsor over the étale site of
$\mathcal {T}$-torsor over the étale site of ![]() $X$. In order to construct overconvergent modular sheaves we have to find refinements of the torsor
$X$. In order to construct overconvergent modular sheaves we have to find refinements of the torsor ![]() $\mathcal {T}_{{\rm mod}}$. It turns out that the torsor
$\mathcal {T}_{{\rm mod}}$. It turns out that the torsor ![]() $\mathcal {T}_{{\rm mod}}$ admits an integral reduction to an étale torsor.
$\mathcal {T}_{{\rm mod}}$ admits an integral reduction to an étale torsor.
Theorem 3.2.6 [Reference Boxer and PilloniBP22, § 4.6]
Let ![]() $\widetilde {\operatorname {\mathscr {F}\!\ell }}^0= \mathcal {N}^0 \backslash\!\operatorname {\mathcal {G}\!\mathcal {L}}_2^{0}$ be the natural
$\widetilde {\operatorname {\mathscr {F}\!\ell }}^0= \mathcal {N}^0 \backslash\!\operatorname {\mathcal {G}\!\mathcal {L}}_2^{0}$ be the natural ![]() $\operatorname {\mathcal {G}\!\mathcal {L}}_2^0$-equivariant
$\operatorname {\mathcal {G}\!\mathcal {L}}_2^0$-equivariant ![]() $\mathcal {T}^0$-torsor over
$\mathcal {T}^0$-torsor over ![]() $\operatorname {\mathscr {F}\!\ell }$. There exists an étale
$\operatorname {\mathscr {F}\!\ell }$. There exists an étale ![]() $\mathcal {T}^0$-torsor
$\mathcal {T}^0$-torsor ![]() $\mathcal {T}^0_{{\rm mod},{\rm \acute {e}t}}$ over
$\mathcal {T}^0_{{\rm mod},{\rm \acute {e}t}}$ over ![]() $X$ such that
$X$ such that
Remark 3.2.7 The existence of the integral torsor holds in greater generality for any Shimura variety. The theorem follows from the fact that ![]() $\pi _{\operatorname {HT}}^*(\widetilde {\operatorname {\mathscr {F}\!\ell }}^0)$ is a
$\pi _{\operatorname {HT}}^*(\widetilde {\operatorname {\mathscr {F}\!\ell }}^0)$ is a ![]() $\operatorname {GL}(\mathbb {Z}_p)$-equivariant open subspace of the twisted torsor
$\operatorname {GL}(\mathbb {Z}_p)$-equivariant open subspace of the twisted torsor ![]() $\pi _{\operatorname {Iw}_n}(\mathcal {T}_{{\rm mod}}) (-1,0)$ over
$\pi _{\operatorname {Iw}_n}(\mathcal {T}_{{\rm mod}}) (-1,0)$ over ![]() $X_{\infty }$, and it follows that this open subspace descends to some finite level providing, locally étale on
$X_{\infty }$, and it follows that this open subspace descends to some finite level providing, locally étale on ![]() $X$, an integral trivialization of
$X$, an integral trivialization of ![]() $\mathcal {T}_{{\rm mod}}$.
$\mathcal {T}_{{\rm mod}}$.
The following definition is justified by the proof of Theorem 3.2.6 (see [Reference Boxer and PilloniBP21, Proposition 4.6.12] or [Reference Boxer and PilloniBP22, Proposition 5.15]).
Definition 3.2.8 Let ![]() $\epsilon \geq \delta \geq n \geq 1$ and
$\epsilon \geq \delta \geq n \geq 1$ and ![]() $w\in W=\{1,w_0\}$. Consider the
$w\in W=\{1,w_0\}$. Consider the ![]() $\operatorname {Iw}_n$-equivariant
$\operatorname {Iw}_n$-equivariant ![]() $T\mathcal {T}(\delta )$-torsor of Definition 2.2.7,
$T\mathcal {T}(\delta )$-torsor of Definition 2.2.7,
The restriction of ![]() $\mathcal {T}_{{\rm mod},{\rm \acute {e}t}}^0$ to
$\mathcal {T}_{{\rm mod},{\rm \acute {e}t}}^0$ to ![]() $X_{w}(\epsilon )$ admits a reduction to an étale
$X_{w}(\epsilon )$ admits a reduction to an étale ![]() $T\mathcal {T}(\delta )$-torsor
$T\mathcal {T}(\delta )$-torsor ![]() $\mathcal {T}_{{\rm mod}}(\delta )$ determined by the equality
$\mathcal {T}_{{\rm mod}}(\delta )$ determined by the equality
as open subspaces of ![]() $\pi _{\operatorname {HT}}^*(\widetilde {\operatorname {\mathscr {F}\!\ell }})=\pi _{\operatorname {Iw}_n}^*( \mathcal {T})(-1,0)$.
$\pi _{\operatorname {HT}}^*(\widetilde {\operatorname {\mathscr {F}\!\ell }})=\pi _{\operatorname {Iw}_n}^*( \mathcal {T})(-1,0)$.
Definition 3.2.9 Let ![]() $(R,R^+)$ be a uniform affinoid Tate
$(R,R^+)$ be a uniform affinoid Tate ![]() $\mathbb {Q}_p$-algebra, and
$\mathbb {Q}_p$-algebra, and ![]() $\chi : T=\mathbf {T}(\mathbb {Z}_p)\rightarrow R^{+,\times }$ a
$\chi : T=\mathbf {T}(\mathbb {Z}_p)\rightarrow R^{+,\times }$ a ![]() $\delta$-analytic character. Let
$\delta$-analytic character. Let ![]() $\mathscr {O}_{\mathcal {T}_{{\rm mod}}(\delta )}$ be the algebra of regular functions of
$\mathscr {O}_{\mathcal {T}_{{\rm mod}}(\delta )}$ be the algebra of regular functions of ![]() $\mathcal {T}_{{\rm mod}}(\delta )$, seen as an étale Banach
$\mathcal {T}_{{\rm mod}}(\delta )$, seen as an étale Banach ![]() $\mathscr {O}_X$-algebra over
$\mathscr {O}_X$-algebra over ![]() $X_w(\epsilon )$. The sheaf of overconvergent modular forms of weight
$X_w(\epsilon )$. The sheaf of overconvergent modular forms of weight ![]() $\chi$ is given by
$\chi$ is given by
 \begin{align*} \omega_E^{\chi} & = \mathscr{O}_{\mathcal{T}_{\rm mod}(\delta)} \widehat{\otimes }R [-w_0(\chi)] \\ & = \{f \in \mathscr{O}_{\mathcal{T}_{\rm mod}(\delta)} \widehat{\otimes} R : f(tx) = w_0(\chi)(t) f(x) \text{ for } t\in T\mathcal{T}(\delta)\}. \end{align*}
\begin{align*} \omega_E^{\chi} & = \mathscr{O}_{\mathcal{T}_{\rm mod}(\delta)} \widehat{\otimes }R [-w_0(\chi)] \\ & = \{f \in \mathscr{O}_{\mathcal{T}_{\rm mod}(\delta)} \widehat{\otimes} R : f(tx) = w_0(\chi)(t) f(x) \text{ for } t\in T\mathcal{T}(\delta)\}. \end{align*}
Remark 3.2.10 In [Reference Boxer and PilloniBP21, Proposition 4.6.15] it is shown that the torsor ![]() $\mathcal {T}_{{\rm mod}}(\delta )$ is trivial in a finite étale covering of
$\mathcal {T}_{{\rm mod}}(\delta )$ is trivial in a finite étale covering of ![]() $X_w(\epsilon )$. This implies that the étale sheaf
$X_w(\epsilon )$. This implies that the étale sheaf ![]() $\omega _{E}^{\chi }$ is locally in the étale topology an orthonormalizable
$\omega _{E}^{\chi }$ is locally in the étale topology an orthonormalizable ![]() $\mathscr {O}_X$-sheaf, and equal to the pullback to the étale site of an
$\mathscr {O}_X$-sheaf, and equal to the pullback to the étale site of an ![]() $\mathscr {O}_{X_w(\epsilon )}\widehat {\otimes }R$-line bundle over the analytic site of
$\mathscr {O}_{X_w(\epsilon )}\widehat {\otimes }R$-line bundle over the analytic site of ![]() $X_w(\epsilon )$.
$X_w(\epsilon )$.
From Definition 3.2.8 we deduce the following overconvergent analogue of Proposition 3.1.4.
Corollary 3.2.11 Let ![]() $(R,R^+)$ and
$(R,R^+)$ and ![]() $\delta$ be as in Definition 3.2.9, and write
$\delta$ be as in Definition 3.2.9, and write ![]() $\chi =(\chi _1,\chi _2)$. Let
$\chi =(\chi _1,\chi _2)$. Let ![]() $\chi _{{\rm cyc}}: G_{\mathbb {Q}_p}\rightarrow \mathbb {Z}_p^\times$ be the cyclotomic character and
$\chi _{{\rm cyc}}: G_{\mathbb {Q}_p}\rightarrow \mathbb {Z}_p^\times$ be the cyclotomic character and ![]() $\chi _2\circ \chi _{{\rm cyc}}: G_{\mathbb {Q}_p}\rightarrow R^{+,\times }$ its composition with
$\chi _2\circ \chi _{{\rm cyc}}: G_{\mathbb {Q}_p}\rightarrow R^{+,\times }$ its composition with ![]() $\chi _2$. We set
$\chi _2$. We set ![]() $\widehat {\mathscr {O}}_{X}(\chi _2):= R( \chi _2\circ \chi _{{\rm cyc}}) \widehat {\otimes } \widehat {\mathscr {O}}_X$. There is a Galois equivariant isomorphism of pro-Kummer-étale sheaves over
$\widehat {\mathscr {O}}_{X}(\chi _2):= R( \chi _2\circ \chi _{{\rm cyc}}) \widehat {\otimes } \widehat {\mathscr {O}}_X$. There is a Galois equivariant isomorphism of pro-Kummer-étale sheaves over ![]() $X_{w}(\epsilon )$,
$X_{w}(\epsilon )$,
We can finally define the overconvergent modular forms and the overconvergent cohomology classes appearing in higher Coleman theory. We refer to [Reference UrbanUrb11] for the notion of perfect Banach complexes and compact operators of perfect Banach complexes. See [Sta20, Tag 0A39] for the definition of cohomology with supports in a closed subspace.
Definition 3.2.12 Let ![]() $w\in W=\{1,w_0\}$ and let
$w\in W=\{1,w_0\}$ and let ![]() $\mathscr {F}$ be a sheaf over
$\mathscr {F}$ be a sheaf over ![]() $X_w(\epsilon )_{{\rm an}}$. Denote
$X_w(\epsilon )_{{\rm an}}$. Denote ![]() $X_w(>\epsilon ):= \bigcup _{\epsilon '>\epsilon } X_w(\epsilon )$. We define the cohomology complexes
$X_w(>\epsilon ):= \bigcup _{\epsilon '>\epsilon } X_w(\epsilon )$. We define the cohomology complexes
Set ![]() $H^0_w(X,\mathscr {F}):=H^0( R\Gamma _w(X, \mathscr {F})_{\epsilon })$ and
$H^0_w(X,\mathscr {F}):=H^0( R\Gamma _w(X, \mathscr {F})_{\epsilon })$ and ![]() $H^1_{w,c}(X,\mathscr {F})=H^1(R\Gamma _{w,c}(X, \mathscr {F})_{\epsilon })$. When
$H^1_{w,c}(X,\mathscr {F})=H^1(R\Gamma _{w,c}(X, \mathscr {F})_{\epsilon })$. When ![]() $\mathscr {F}= \omega _E^{\chi }$, we call
$\mathscr {F}= \omega _E^{\chi }$, we call ![]() $H^0_w(X, \omega _E^{\chi })_{\epsilon }$ and
$H^0_w(X, \omega _E^{\chi })_{\epsilon }$ and ![]() $H^1_{w,c}(X, \omega _W^{\chi })_{\epsilon }$ the space of overconvergent modular forms and the overconvergent cohomology with compact support of weight
$H^1_{w,c}(X, \omega _W^{\chi })_{\epsilon }$ the space of overconvergent modular forms and the overconvergent cohomology with compact support of weight ![]() $\chi$, respectively.
$\chi$, respectively.
3.2.1 Hecke operators
We end this subsection with the definition of the ![]() $U_p$-operators for the overconvergent modular forms. First, let us recall the definition for the classical modular sheaves. Let
$U_p$-operators for the overconvergent modular forms. First, let us recall the definition for the classical modular sheaves. Let ![]() $X \xleftarrow {p_1} C\xrightarrow {p_2} X$ be the
$X \xleftarrow {p_1} C\xrightarrow {p_2} X$ be the ![]() $U_p$-correspondence. We let
$U_p$-correspondence. We let ![]() $\pi : p_1^*E \rightarrow p_2^* E$ be the universal isogeny over
$\pi : p_1^*E \rightarrow p_2^* E$ be the universal isogeny over ![]() $C$ and
$C$ and ![]() $\pi ^{\vee }: p_2^* E \rightarrow p_1^* E$ its dual. We denote by
$\pi ^{\vee }: p_2^* E \rightarrow p_1^* E$ its dual. We denote by ![]() $\pi ^*: p_2^* \omega _E \rightarrow p_1^* \omega _E$ and
$\pi ^*: p_2^* \omega _E \rightarrow p_1^* \omega _E$ and ![]() $\pi _*: p_1^* \omega _E^{-1}\rightarrow p_2^* \omega _E^{-1}$ the pullback and pushforward maps of
$\pi _*: p_1^* \omega _E^{-1}\rightarrow p_2^* \omega _E^{-1}$ the pullback and pushforward maps of ![]() $\pi$ (respectively, for
$\pi$ (respectively, for ![]() $\pi ^\vee$). For a quasi-coherent sheaf
$\pi ^\vee$). For a quasi-coherent sheaf ![]() $\mathscr {F}$ over
$\mathscr {F}$ over ![]() $X$ we let
$X$ we let ![]() $\operatorname {Tr}_{p_i}: p_{i,*} p^*_i \mathscr {F}\rightarrow \mathscr {F}$ be the trace map of
$\operatorname {Tr}_{p_i}: p_{i,*} p^*_i \mathscr {F}\rightarrow \mathscr {F}$ be the trace map of ![]() $p_i$. Let
$p_i$. Let ![]() $\kappa = (k_1,k_2)\in X^*(\mathbf {T})$ be a character of
$\kappa = (k_1,k_2)\in X^*(\mathbf {T})$ be a character of ![]() $\mathbf {T}$, and recall that we have made the convention
$\mathbf {T}$, and recall that we have made the convention ![]() $\omega _E^{\kappa }= \omega _E^{k_1}\otimes \omega _E^{-k_2}= \omega _E^{k_1-k_2}$.
$\omega _E^{\kappa }= \omega _E^{k_1}\otimes \omega _E^{-k_2}= \omega _E^{k_1-k_2}$.
Definition 3.2.13 The Hecke operator ![]() $U_{p,\kappa }$ acting over
$U_{p,\kappa }$ acting over ![]() $R\Gamma _{{\rm an}}(X, \omega _E^{\kappa })$ is the composition
$R\Gamma _{{\rm an}}(X, \omega _E^{\kappa })$ is the composition
We define the ![]() $U^{t}_{p,\kappa }$ operator by shifting the roles of
$U^{t}_{p,\kappa }$ operator by shifting the roles of ![]() $p_1$ and
$p_1$ and ![]() $p_2$, and by composing with the map
$p_2$, and by composing with the map ![]() $( \pi ^{\vee,*})^{\otimes k_1}\otimes (\pi _*)^{\otimes k_2}$.
$( \pi ^{\vee,*})^{\otimes k_1}\otimes (\pi _*)^{\otimes k_2}$.
Remark 3.2.14 The ![]() $U_{p,\kappa }$ above is equal to the operator
$U_{p,\kappa }$ above is equal to the operator ![]() $p^{-k_1}U_{p,k_1-k_2}^{{\rm naive}}$ of [Reference Boxer and PilloniBP22]. Indeed,
$p^{-k_1}U_{p,k_1-k_2}^{{\rm naive}}$ of [Reference Boxer and PilloniBP22]. Indeed, ![]() $(\pi ^{\vee,*,-1})^{\otimes k_1}= p^{-k_1}( \pi ^*)^{\otimes k_1}$ and
$(\pi ^{\vee,*,-1})^{\otimes k_1}= p^{-k_1}( \pi ^*)^{\otimes k_1}$ and ![]() $(\pi _*^{-1})^{\otimes k_2}= (\pi ^*)^{\otimes - k_2}$. In other words,
$(\pi _*^{-1})^{\otimes k_2}= (\pi ^*)^{\otimes - k_2}$. In other words, ![]() $U_{p,k}^{{\rm naive}}=U_{p, (0,-k)}$.
$U_{p,k}^{{\rm naive}}=U_{p, (0,-k)}$.
Let us explain the normalization of the Hecke operator ![]() $U_{p,\kappa }$ of the previous definition. It turns out that it is induced from the
$U_{p,\kappa }$ of the previous definition. It turns out that it is induced from the ![]() $U_{p,\kappa }$-correspondence of the sheaf
$U_{p,\kappa }$-correspondence of the sheaf ![]() $\mathscr {L}(\kappa )$ over
$\mathscr {L}(\kappa )$ over ![]() $\operatorname {\mathscr {F}\!\ell }$ (see Definition 2.2.12(i)). Recall that the Hodge–Tate exact sequence
$\operatorname {\mathscr {F}\!\ell }$ (see Definition 2.2.12(i)). Recall that the Hodge–Tate exact sequence
is the pullback by ![]() $\pi _{\operatorname {HT}}$ of the exact sequence of
$\pi _{\operatorname {HT}}$ of the exact sequence of ![]() $\operatorname {GL}_2$-equivariant vector bundles
$\operatorname {GL}_2$-equivariant vector bundles
By the proof of Lemma 3.2.4, the ![]() $U_p$-correspondence of
$U_p$-correspondence of ![]() $X$ at level
$X$ at level ![]() $X_{\infty }$ commutes with the
$X_{\infty }$ commutes with the ![]() $U_p$-correspondence of
$U_p$-correspondence of ![]() $\operatorname {\mathscr {F}\!\ell }$ defined in (10). Then the natural
$\operatorname {\mathscr {F}\!\ell }$ defined in (10). Then the natural ![]() $U_p$-correspondence of
$U_p$-correspondence of ![]() $\pi _{\operatorname {HT}}^* \operatorname {St} \otimes \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}= T_pE \otimes \mathscr {O}_{X_{\infty }}$ induced by the
$\pi _{\operatorname {HT}}^* \operatorname {St} \otimes \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}= T_pE \otimes \mathscr {O}_{X_{\infty }}$ induced by the ![]() $\operatorname {GL}_2(\mathbb {Q}_p)$-equivariant structure of
$\operatorname {GL}_2(\mathbb {Q}_p)$-equivariant structure of ![]() $\operatorname {St}$ is compatible with the natural
$\operatorname {St}$ is compatible with the natural ![]() $U_p$-correspondence of
$U_p$-correspondence of ![]() $\pi _{\operatorname {HT}}^*(\mathcal {L}(0,1))= \omega _E^{-1}\otimes \mathscr {O}_{X_{\infty }}(1)$ and
$\pi _{\operatorname {HT}}^*(\mathcal {L}(0,1))= \omega _E^{-1}\otimes \mathscr {O}_{X_{\infty }}(1)$ and ![]() $\pi _{\operatorname {HT}}^*(\mathcal {L}(1,0))= \omega _E\otimes \mathscr {O}_{X_\infty }$. But the correspondence of
$\pi _{\operatorname {HT}}^*(\mathcal {L}(1,0))= \omega _E\otimes \mathscr {O}_{X_\infty }$. But the correspondence of ![]() $T_pE$ is just the natural isogeny
$T_pE$ is just the natural isogeny ![]() $\pi : p_1^* (T_pE) \to p_2^*( T_pE)$ and we have the following commutative diagram.
$\pi : p_1^* (T_pE) \to p_2^*( T_pE)$ and we have the following commutative diagram.

Then the natural ![]() $U_p$ correspondences of
$U_p$ correspondences of ![]() $\omega _E\otimes \mathscr {O}_{X_\infty }$ and
$\omega _E\otimes \mathscr {O}_{X_\infty }$ and ![]() $\omega _E^{-1}\otimes \mathscr {O}_{X_\infty }(1)$, defined by
$\omega _E^{-1}\otimes \mathscr {O}_{X_\infty }(1)$, defined by ![]() $\mathscr {L}(1,0)$ and
$\mathscr {L}(1,0)$ and ![]() $\mathscr {L}(0,1)$ respectively, are given by the maps
$\mathscr {L}(0,1)$ respectively, are given by the maps
With the previous explanation in mind, we can now define the ![]() $U_p$-correspondence for the overconvergent modular forms. We refer to [Reference Boxer and PilloniBP22, Proposition 5.8] for the details.
$U_p$-correspondence for the overconvergent modular forms. We refer to [Reference Boxer and PilloniBP22, Proposition 5.8] for the details.
Definition 3.2.15 Consider the ![]() $U_p$-correspondence (19) and its restriction to the overconvergent neighbourhoods of
$U_p$-correspondence (19) and its restriction to the overconvergent neighbourhoods of ![]() $\overline {X}_w^{{\rm ord}}$ (see Lemma 3.2.4):
$\overline {X}_w^{{\rm ord}}$ (see Lemma 3.2.4):

(i) We define the maps
to be the unique maps whose base changes to \[ U_p:p_2^* \omega_E^{\chi} \to p_1^* \omega_E^{\chi}\quad\text{and}\quad U_p^t:p_1^* \omega_E^{\chi} \to p_2^* \omega_E^{\chi} \]
\[ U_p:p_2^* \omega_E^{\chi} \to p_1^* \omega_E^{\chi}\quad\text{and}\quad U_p^t:p_1^* \omega_E^{\chi} \to p_2^* \omega_E^{\chi} \]
 $\widehat {\mathscr {O}}_X$-modules coincide with the pullback by
$\widehat {\mathscr {O}}_X$-modules coincide with the pullback by  $\pi _{\operatorname {HT}}$ of the
$\pi _{\operatorname {HT}}$ of the  $U_p$-correspondence of Definition 2.2.12(ii).
$U_p$-correspondence of Definition 2.2.12(ii).(ii) The
 $U_p$ operator on
$U_p$ operator on  $R\Gamma _1(X, \omega _E^{\chi })_{\epsilon }$ and
$R\Gamma _1(X, \omega _E^{\chi })_{\epsilon }$ and  $R\Gamma _{w_0,c}(X, \omega _E^{\chi })_{\epsilon }$ is the one induced by the map
$R\Gamma _{w_0,c}(X, \omega _E^{\chi })_{\epsilon }$ is the one induced by the map  $U_p$ above.
$U_p$ above.(iii) The
 $U_p^t$ operator on
$U_p^t$ operator on  $R\Gamma _{w_0}(X, \omega _E^{\chi })_{\epsilon }$ and
$R\Gamma _{w_0}(X, \omega _E^{\chi })_{\epsilon }$ and  $R\Gamma _{1,c}(X, \omega _E^{\chi })_{\epsilon }$ is the one induced by the map
$R\Gamma _{1,c}(X, \omega _E^{\chi })_{\epsilon }$ is the one induced by the map  $U_p^t$ above.
$U_p^t$ above.
In order to state the classicality result we need to normalize the ![]() $U_p$-operators.
$U_p$-operators.
Definition 3.2.16 Let ![]() $(R,R^+)$ be a uniform Tate
$(R,R^+)$ be a uniform Tate ![]() $\mathbb {Q}_p$-algebra and
$\mathbb {Q}_p$-algebra and ![]() $\chi : T\rightarrow R^{+,\times }$ be a
$\chi : T\rightarrow R^{+,\times }$ be a ![]() $\delta$-analytic character. Let
$\delta$-analytic character. Let ![]() $\kappa \in X^*(\mathbf {T})$. We define normalizations of
$\kappa \in X^*(\mathbf {T})$. We define normalizations of ![]() $U_p$ and
$U_p$ and ![]() $U_p^t$:
$U_p^t$:
 \begin{align*} U_p^{\mathrm{good}}= \begin{cases} \dfrac{1}{p} U_{p} & \text{ over } R\Gamma_1(X,\omega_E^{\chi})_{\epsilon}, \\ U_{p} & \text{ over } R\Gamma_{w_0,c}(X,\omega_E^{\chi})_{\epsilon}, \\ p^{-\min\{ 1-k_1,-k_2\}} U_{p,\kappa} & \text{ over } R\Gamma_{\rm an}(X, \omega^k), \end{cases} \\ U_p^{t,\mathrm{good}}= \begin{cases} \dfrac{1}{p} U_{p}^t & \text{ over } R\Gamma_{w_0}(X,\omega_E^{\chi})_{\epsilon}, \\ U_{p}^t & \text{ over } R\Gamma_{1,c}(X,\omega_E^{\chi})_{\epsilon}, \\ p^{-\min\{1-k_1,-k_2\}}U_{p,\kappa}^{t} & \text{ over } R\Gamma_{\rm an}(X, \omega^\kappa_E). \end{cases} \end{align*}
\begin{align*} U_p^{\mathrm{good}}= \begin{cases} \dfrac{1}{p} U_{p} & \text{ over } R\Gamma_1(X,\omega_E^{\chi})_{\epsilon}, \\ U_{p} & \text{ over } R\Gamma_{w_0,c}(X,\omega_E^{\chi})_{\epsilon}, \\ p^{-\min\{ 1-k_1,-k_2\}} U_{p,\kappa} & \text{ over } R\Gamma_{\rm an}(X, \omega^k), \end{cases} \\ U_p^{t,\mathrm{good}}= \begin{cases} \dfrac{1}{p} U_{p}^t & \text{ over } R\Gamma_{w_0}(X,\omega_E^{\chi})_{\epsilon}, \\ U_{p}^t & \text{ over } R\Gamma_{1,c}(X,\omega_E^{\chi})_{\epsilon}, \\ p^{-\min\{1-k_1,-k_2\}}U_{p,\kappa}^{t} & \text{ over } R\Gamma_{\rm an}(X, \omega^\kappa_E). \end{cases} \end{align*}
We shall need the following classicality theorem for overconvergent cohomologies.
Theorem 3.2.17 [Reference Boxer and PilloniBP22, Theorem 5.13]
Let ![]() $\kappa =(k_1,k_2)\in X^*(\mathbf {T})$ be an algebraic weight.
$\kappa =(k_1,k_2)\in X^*(\mathbf {T})$ be an algebraic weight.
(i) The
 $U_p^{\mathrm {good}}$ operator has non-negative slopes on
$U_p^{\mathrm {good}}$ operator has non-negative slopes on  $H^0_1(X,\omega _E^{\kappa })_{\epsilon }$ and
$H^0_1(X,\omega _E^{\kappa })_{\epsilon }$ and  $H^1_{w_0,c}(X,\omega _E^{\kappa })_{\epsilon }$.
$H^1_{w_0,c}(X,\omega _E^{\kappa })_{\epsilon }$.(ii) The
 $U_p^{t,\mathrm {good}}$ operator has non-negative slopes on
$U_p^{t,\mathrm {good}}$ operator has non-negative slopes on  $H^0_{w_0}(X,\omega _E^\kappa )_{\epsilon }$ and
$H^0_{w_0}(X,\omega _E^\kappa )_{\epsilon }$ and  $H^1_{1,c}(X,\omega _E^\kappa )_{\epsilon }$.
$H^1_{1,c}(X,\omega _E^\kappa )_{\epsilon }$.
Furthermore, we have isomorphisms of small-slope cohomologies
 \begin{align*}
H^0_1(X,\omega_E^\kappa)_{\epsilon}^{U_p^{\mathrm{good}}<
k_1-k_2-1} &= H^0_{\rm an}(X,
\omega_E^{\kappa})^{U_p^{\mathrm{good}}<
k_1 -k_2-1}, \\
H^1_{w_0,c}(X,\omega_E^\kappa)_{\epsilon}^{U_p^{\mathrm{good}}<1+k_2-k_1}
&=H^1_{\rm an}(X,
\omega_E^{\kappa})^{U_p^{\mathrm{good}}<1+k_2-k_1},\\
H^0_{w_0}(X,\omega_E^\kappa)_{\epsilon}^{U_p^{t,\mathrm{good}}<
k_1-k_2-1}&= H^0_{\rm an}(X,
\omega_E^{\kappa})^{U_p^{t,\mathrm{good}}<
k_1-k_2-1}, \\
H^1_{1,c}(X,\omega_E^\kappa)_{\epsilon}^{U_p^{t,\mathrm{good}}<1+k_2-k_1}
&= H^1_{\rm an}(X,
\omega_E^{\kappa})^{U_p^{t,\mathrm{good}}<1+k_2-k_1}
. \end{align*}
\begin{align*}
H^0_1(X,\omega_E^\kappa)_{\epsilon}^{U_p^{\mathrm{good}}<
k_1-k_2-1} &= H^0_{\rm an}(X,
\omega_E^{\kappa})^{U_p^{\mathrm{good}}<
k_1 -k_2-1}, \\
H^1_{w_0,c}(X,\omega_E^\kappa)_{\epsilon}^{U_p^{\mathrm{good}}<1+k_2-k_1}
&=H^1_{\rm an}(X,
\omega_E^{\kappa})^{U_p^{\mathrm{good}}<1+k_2-k_1},\\
H^0_{w_0}(X,\omega_E^\kappa)_{\epsilon}^{U_p^{t,\mathrm{good}}<
k_1-k_2-1}&= H^0_{\rm an}(X,
\omega_E^{\kappa})^{U_p^{t,\mathrm{good}}<
k_1-k_2-1}, \\
H^1_{1,c}(X,\omega_E^\kappa)_{\epsilon}^{U_p^{t,\mathrm{good}}<1+k_2-k_1}
&= H^1_{\rm an}(X,
\omega_E^{\kappa})^{U_p^{t,\mathrm{good}}<1+k_2-k_1}
. \end{align*}
3.3 Overconvergent modular symbols
Let ![]() $(R,R^+)$ be a uniform affinoid Tate algebra over
$(R,R^+)$ be a uniform affinoid Tate algebra over ![]() $\mathbb {Q}_p$, and
$\mathbb {Q}_p$, and ![]() $\chi : T \to R^{+,\times }$ a
$\chi : T \to R^{+,\times }$ a ![]() $\delta$-analytic character. Let
$\delta$-analytic character. Let ![]() $A_{\chi }^{\delta }$ and
$A_{\chi }^{\delta }$ and ![]() $D_{\chi }^{\delta }=\text {Hom}^0_{R}(A^{\delta }_{\chi }, R)$ be the principal series and distributions of Definition 2.3.1. These are topological
$D_{\chi }^{\delta }=\text {Hom}^0_{R}(A^{\delta }_{\chi }, R)$ be the principal series and distributions of Definition 2.3.1. These are topological ![]() $\mathbb {Q}_p$-vector spaces,
$\mathbb {Q}_p$-vector spaces, ![]() $A^{\delta }_{\chi }$ being a Banach space and
$A^{\delta }_{\chi }$ being a Banach space and ![]() $D_{\chi }^{\delta }$ endowed with the weak topology. Consider the constant
$D_{\chi }^{\delta }$ endowed with the weak topology. Consider the constant ![]() $\operatorname {Iw}_n$-equivariant quasi-coherent sheaves
$\operatorname {Iw}_n$-equivariant quasi-coherent sheaves ![]() $A_{\chi }^{\delta } \widehat {\otimes } \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$ and
$A_{\chi }^{\delta } \widehat {\otimes } \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$ and ![]() $D_{\chi }^{\delta }\widehat {\otimes } \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$ over
$D_{\chi }^{\delta }\widehat {\otimes } \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$ over ![]() $\operatorname {\mathscr {F}\!\ell }$, where the completed tensor products are as in Definition 2.3.7. Their pullbacks by
$\operatorname {\mathscr {F}\!\ell }$, where the completed tensor products are as in Definition 2.3.7. Their pullbacks by ![]() $\pi _{\operatorname {HT}}$ are identified with pro-Kummer-étale sheaves
$\pi _{\operatorname {HT}}$ are identified with pro-Kummer-étale sheaves ![]() $A_{\chi, {\rm \acute {e}t}}^{\delta }\widehat {\otimes } \widehat {\mathscr {O}}_X$ and
$A_{\chi, {\rm \acute {e}t}}^{\delta }\widehat {\otimes } \widehat {\mathscr {O}}_X$ and ![]() $D_{\chi,{\rm \acute {e}t}}^{\delta } \widehat {\otimes } \widehat {\mathscr {O}}_X$, where
$D_{\chi,{\rm \acute {e}t}}^{\delta } \widehat {\otimes } \widehat {\mathscr {O}}_X$, where ![]() $A_{\chi, {\rm \acute {e}t}}^{\delta }$ and
$A_{\chi, {\rm \acute {e}t}}^{\delta }$ and ![]() $D_{\chi,{\rm \acute {e}t}}^{\delta }$ are the sheaves over
$D_{\chi,{\rm \acute {e}t}}^{\delta }$ are the sheaves over ![]() $X_{{\rm prok\acute {e}t}}$ obtained by descent from the
$X_{{\rm prok\acute {e}t}}$ obtained by descent from the ![]() $\operatorname {Iw}_n$-equivariant constant sheaves over
$\operatorname {Iw}_n$-equivariant constant sheaves over ![]() $X_{\infty }$ induced by the corresponding topological
$X_{\infty }$ induced by the corresponding topological ![]() $\operatorname {Iw}_n$-modules.
$\operatorname {Iw}_n$-modules.
Before introducing the spaces of overconvergent modular symbols, let us define the proétale cohomology with compact support.
Definition 3.3.1 Let ![]() $\mathscr {F}$ be a proétale sheaf over
$\mathscr {F}$ be a proétale sheaf over ![]() $Y=Y_0(p^n)$, and let
$Y=Y_0(p^n)$, and let ![]() $j_{{\rm prok\acute {e}t}}: Y_{{\rm pro\acute {e}t}}\to X_{{\rm prok\acute {e}t}}$ be the natural morphism of sites. The proétale cohomology with compact support of
$j_{{\rm prok\acute {e}t}}: Y_{{\rm pro\acute {e}t}}\to X_{{\rm prok\acute {e}t}}$ be the natural morphism of sites. The proétale cohomology with compact support of ![]() $\mathscr {F}$ is the complex
$\mathscr {F}$ is the complex
Remark 3.3.2 Let ![]() $j_{{\rm pro\acute {e}t}}: Y_{{\rm pro\acute {e}t}}\to X_{{\rm pro\acute {e}t}}$ be the natural morphism of sites and let
$j_{{\rm pro\acute {e}t}}: Y_{{\rm pro\acute {e}t}}\to X_{{\rm pro\acute {e}t}}$ be the natural morphism of sites and let ![]() $\mathbb {L}$ be a proétale
$\mathbb {L}$ be a proétale ![]() $\mathbb {Z}_p$-local system over
$\mathbb {Z}_p$-local system over ![]() $Y$. The proétale cohomology with compact support of
$Y$. The proétale cohomology with compact support of ![]() $\mathbb {L}$ is usually defined as
$\mathbb {L}$ is usually defined as ![]() $R\Gamma _{{\rm pro\acute {e}t}, c}(Y_{\mathbb {C}_p}, \mathbb {L}):= R\Gamma _{{\rm pro\acute {e}t}}(X_{\mathbb {C}_p}, j_{{\rm pro\acute {e}t},!} \mathbb {L})$. On the other hand, [Reference Diao, Lan, Liu and ZhuDLLZ23b, Lemma 4.4.27] implies that this cohomology can be computed in the pro-Kummer-étale site, that is, that we have a quasi-isomorphism
$R\Gamma _{{\rm pro\acute {e}t}, c}(Y_{\mathbb {C}_p}, \mathbb {L}):= R\Gamma _{{\rm pro\acute {e}t}}(X_{\mathbb {C}_p}, j_{{\rm pro\acute {e}t},!} \mathbb {L})$. On the other hand, [Reference Diao, Lan, Liu and ZhuDLLZ23b, Lemma 4.4.27] implies that this cohomology can be computed in the pro-Kummer-étale site, that is, that we have a quasi-isomorphism
In other words, if ![]() $\mathscr {F}=\mathbb {L}$ is a proétale local system over
$\mathscr {F}=\mathbb {L}$ is a proétale local system over ![]() $Y$. The cohomology with compact support of Definition 3.3.1 coincides with the classical one.
$Y$. The cohomology with compact support of Definition 3.3.1 coincides with the classical one.
Definition 3.3.3 We define the overconvergent modular symbols as the cohomology complexes
We also define the overconvergent modular symbols with compact support in the obvious way.
Remark 3.3.4 By purity on ![]() $p$-torsion local systems [Reference Diao, Lan, Liu and ZhuDLLZ23b, Theorem 6.4.1] and the devisage of
$p$-torsion local systems [Reference Diao, Lan, Liu and ZhuDLLZ23b, Theorem 6.4.1] and the devisage of ![]() $A_{\chi }^{\delta,+}$ and
$A_{\chi }^{\delta,+}$ and ![]() $D_{\chi }^{\delta,+}$ of Corollary 2.3.6, one has quasi-isomorphisms
$D_{\chi }^{\delta,+}$ of Corollary 2.3.6, one has quasi-isomorphisms
 \begin{align*} R\Gamma_{\rm pro\acute{e}t}(Y_{\mathbb{C}_p}, A^{\delta}_{\chi,\rm \acute{e}t}) & = R\Gamma_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, A^{\delta}_{\chi,\rm \acute{e}t}),\\ R\Gamma_{\rm pro\acute{e}t}(Y_{\mathbb{C}_p}, D^{\delta}_{\chi,\rm \acute{e}t}) & = R\Gamma_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, D^{\delta}_{\chi, \rm \acute{e}t}). \end{align*}
\begin{align*} R\Gamma_{\rm pro\acute{e}t}(Y_{\mathbb{C}_p}, A^{\delta}_{\chi,\rm \acute{e}t}) & = R\Gamma_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, A^{\delta}_{\chi,\rm \acute{e}t}),\\ R\Gamma_{\rm pro\acute{e}t}(Y_{\mathbb{C}_p}, D^{\delta}_{\chi,\rm \acute{e}t}) & = R\Gamma_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, D^{\delta}_{\chi, \rm \acute{e}t}). \end{align*}
The primitive comparison theorem also applies for the modular symbols as follows.
Lemma 3.3.5 Let ![]() $\iota :D \subset X$ be the cusp divisor endowed with the log structure induced by
$\iota :D \subset X$ be the cusp divisor endowed with the log structure induced by ![]() $X$. Let
$X$. Let ![]() $\iota : D_{{\rm prok\acute {e}t}}\to X_{{\rm prok\acute {e}t}}$ be the natural morphism, and let
$\iota : D_{{\rm prok\acute {e}t}}\to X_{{\rm prok\acute {e}t}}$ be the natural morphism, and let ![]() $\widehat {\mathscr {I}}^+= \ker ( \widehat {\mathscr {O}}_{X}^+ \to \iota _* \widehat {\mathscr {O}}^+_{D})$ be the ideal defining the cusps. Then
$\widehat {\mathscr {I}}^+= \ker ( \widehat {\mathscr {O}}_{X}^+ \to \iota _* \widehat {\mathscr {O}}^+_{D})$ be the ideal defining the cusps. Then ![]() $(j_{{\rm prok\acute {e}t},!}A^{\delta,+}_{\chi,{\rm \acute {e}t}})\widehat {\otimes } \widehat {\mathscr {O}}^+_X= A^{\delta,+}_{\chi,{\rm \acute {e}t}}\widehat {\otimes }\widehat {\mathscr {I}}^+$. Furthermore, we have almost quasi-isomorphisms
$(j_{{\rm prok\acute {e}t},!}A^{\delta,+}_{\chi,{\rm \acute {e}t}})\widehat {\otimes } \widehat {\mathscr {O}}^+_X= A^{\delta,+}_{\chi,{\rm \acute {e}t}}\widehat {\otimes }\widehat {\mathscr {I}}^+$. Furthermore, we have almost quasi-isomorphisms
 \begin{equation} \begin{aligned}
R\Gamma_{\rm prok\acute{e}t}(X_{\mathbb{C}_p},
A^{\delta,+}_{\chi,\rm \acute{e}t})\widehat{\otimes}
\mathcal{O}_{\mathbb{C}_p} & =^{a}
R\Gamma_{\rm prok\acute{e}t}(X_{\mathbb{C}_p},
A^{\delta,+}_{\chi,\rm \acute{e}t} \widehat{\otimes}
\widehat{\mathscr{O}}^+_X),\\
R\Gamma_{\rm prok\acute{e}t}(X_{\mathbb{C}_p},
j_{\rm prok\acute{e}t,!}
A^{\delta,+}_{\chi,\rm \acute{e}t})\widehat{\otimes}
\mathcal{O}_{\mathbb{C}_p} & =^{a}
R\Gamma_{\rm prok\acute{e}t}(X_{\mathbb{C}_p},
A^{\delta,+}_{\chi,\rm \acute{e}t} \widehat{\otimes}
\widehat{\mathscr{I}}^+). \end{aligned}
\end{equation}
\begin{equation} \begin{aligned}
R\Gamma_{\rm prok\acute{e}t}(X_{\mathbb{C}_p},
A^{\delta,+}_{\chi,\rm \acute{e}t})\widehat{\otimes}
\mathcal{O}_{\mathbb{C}_p} & =^{a}
R\Gamma_{\rm prok\acute{e}t}(X_{\mathbb{C}_p},
A^{\delta,+}_{\chi,\rm \acute{e}t} \widehat{\otimes}
\widehat{\mathscr{O}}^+_X),\\
R\Gamma_{\rm prok\acute{e}t}(X_{\mathbb{C}_p},
j_{\rm prok\acute{e}t,!}
A^{\delta,+}_{\chi,\rm \acute{e}t})\widehat{\otimes}
\mathcal{O}_{\mathbb{C}_p} & =^{a}
R\Gamma_{\rm prok\acute{e}t}(X_{\mathbb{C}_p},
A^{\delta,+}_{\chi,\rm \acute{e}t} \widehat{\otimes}
\widehat{\mathscr{I}}^+). \end{aligned}
\end{equation}
An analogous statement holds for the sheaf ![]() $D_{\chi,{\rm \acute {e}t}}^{\delta }$.
$D_{\chi,{\rm \acute {e}t}}^{\delta }$.
Proof. We only give the proof for ![]() $A_{\chi,{\rm \acute {e}t}}^{\delta,+}$, the other being identical. By Corollary 2.3.6 we can write
$A_{\chi,{\rm \acute {e}t}}^{\delta,+}$, the other being identical. By Corollary 2.3.6 we can write ![]() $A_{\chi,{\rm \acute {e}t}}^{\delta,+}= R\varprojlim _{i}( \varinjlim _{j} \mathbb {L}_{i,j})$, where
$A_{\chi,{\rm \acute {e}t}}^{\delta,+}= R\varprojlim _{i}( \varinjlim _{j} \mathbb {L}_{i,j})$, where ![]() $\mathbb {L}_{i,j}$ are finite Kummer-étale local systems over
$\mathbb {L}_{i,j}$ are finite Kummer-étale local systems over ![]() $X$. Then, by the primitive comparison theorem for finite local systems, one has that
$X$. Then, by the primitive comparison theorem for finite local systems, one has that
 \begin{align*} R\Gamma_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, A^{\delta,+}_{\chi,\rm \acute{e}t})\widehat{\otimes} \mathcal{O}_{\mathbb{C}_p} & = R\varprojlim_{i} \operatorname{hocolim}_{j} (R\Gamma_{\rm k\acute{e}t}(X_{\mathbb{C}_p}, \mathbb{L}_{i,j}) \otimes \mathcal{O}_{\mathbb{C}_p})\\ & =^{a} R\varprojlim_{i} \operatorname{hocolim}_{j} (R\Gamma_{\rm k\acute{e}t}(X_{\mathbb{C}_p}, \mathbb{L}_{i,j}\otimes \mathscr{O}^+_X))\\ & = R\Gamma_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, A^{\delta,+}_{\chi,\rm \acute{e}t} \widehat{\otimes} \widehat{\mathscr{O}}^+_X). \end{align*}
\begin{align*} R\Gamma_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, A^{\delta,+}_{\chi,\rm \acute{e}t})\widehat{\otimes} \mathcal{O}_{\mathbb{C}_p} & = R\varprojlim_{i} \operatorname{hocolim}_{j} (R\Gamma_{\rm k\acute{e}t}(X_{\mathbb{C}_p}, \mathbb{L}_{i,j}) \otimes \mathcal{O}_{\mathbb{C}_p})\\ & =^{a} R\varprojlim_{i} \operatorname{hocolim}_{j} (R\Gamma_{\rm k\acute{e}t}(X_{\mathbb{C}_p}, \mathbb{L}_{i,j}\otimes \mathscr{O}^+_X))\\ & = R\Gamma_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, A^{\delta,+}_{\chi,\rm \acute{e}t} \widehat{\otimes} \widehat{\mathscr{O}}^+_X). \end{align*}
To prove the case of cohomology with compact support we need the following observation. Consider the exact sequence of Kummer-étale sheaves over ![]() $X$,
$X$,
Tensoring with ![]() $\mathscr {O}^+_X$ and taking projective limits on
$\mathscr {O}^+_X$ and taking projective limits on ![]() $s$, one obtains the short exact sequence
$s$, one obtains the short exact sequence
Therefore, tensoring with ![]() $A^{\delta,+}_{\chi,{\rm \acute {e}t}}$, one gets a short exact sequence
$A^{\delta,+}_{\chi,{\rm \acute {e}t}}$, one gets a short exact sequence
It is easy to see that (23) is the (completed) ![]() $\widehat {\mathscr {O}}^+_X$-scalar extension of the short exact sequence
$\widehat {\mathscr {O}}^+_X$-scalar extension of the short exact sequence
In particular, from the previous two short exact sequences one deduces that ![]() $j_{{\rm prok\acute {e}t},!}A_{\chi,{\rm \acute {e}t}}^{\delta,+}\widehat {\otimes } \widehat {\mathscr {O}}_X^+= A_{\chi,{\rm \acute {e}t}}^{\delta,+}\widehat {\otimes }\widehat {\mathscr {I}}^+$. Moreover, the second almost equality of (22) holds after taking pro-Kummer-étale cohomology of the triangle (23), by applying the primitive comparison theorem for both
$j_{{\rm prok\acute {e}t},!}A_{\chi,{\rm \acute {e}t}}^{\delta,+}\widehat {\otimes } \widehat {\mathscr {O}}_X^+= A_{\chi,{\rm \acute {e}t}}^{\delta,+}\widehat {\otimes }\widehat {\mathscr {I}}^+$. Moreover, the second almost equality of (22) holds after taking pro-Kummer-étale cohomology of the triangle (23), by applying the primitive comparison theorem for both ![]() $X$ and
$X$ and ![]() $D$ (see [Reference Lan, Liu and ZhuLLZ23, Theorem 2.2.1]).
$D$ (see [Reference Lan, Liu and ZhuLLZ23, Theorem 2.2.1]).
Next, we define the ![]() $U_p$-operators for overconvergent modular symbols. These are obtained by pulling back the maps of (12).
$U_p$-operators for overconvergent modular symbols. These are obtained by pulling back the maps of (12).
Definition 3.3.6 Consider the ![]() $U_p$-correspondence
$U_p$-correspondence ![]() $C$ of
$C$ of ![]() $X$. The
$X$. The ![]() $U^t_p$ and
$U^t_p$ and ![]() $U_p$-correspondences of
$U_p$-correspondences of ![]() $A^{\delta }_{\chi,{\rm \acute {e}t}}$ and
$A^{\delta }_{\chi,{\rm \acute {e}t}}$ and ![]() $D_{\chi,{\rm \acute {e}t}}^{\delta }$ are the morphisms
$D_{\chi,{\rm \acute {e}t}}^{\delta }$ are the morphisms
defined by the pullback of (12) by ![]() $\pi _{\operatorname {HT}}$.
$\pi _{\operatorname {HT}}$.
We shall need the following classicality result (see [Reference Ash and StevensAS08, Theorem 6.4.1] and [Reference Andreatta, Iovita and StevensAIS15, Theorem 3.16]).
Theorem 3.3.7 Let ![]() $\kappa =(k_1,k_2)\in X^*(\mathbf {T})^+$ be a dominant weight. The maps
$\kappa =(k_1,k_2)\in X^*(\mathbf {T})^+$ be a dominant weight. The maps ![]() $D^{\delta }_{\kappa } \rightarrow V_{-w_0(\kappa )}$ and
$D^{\delta }_{\kappa } \rightarrow V_{-w_0(\kappa )}$ and ![]() $V_\kappa \rightarrow A^\delta _\kappa$ induce isomorphisms of the
$V_\kappa \rightarrow A^\delta _\kappa$ induce isomorphisms of the ![]() $(< k_1-k_2+1)$-slope part for the action of the (normalized)
$(< k_1-k_2+1)$-slope part for the action of the (normalized) ![]() $U_p$-operators
$U_p$-operators
 \begin{align*} H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, D^\delta_{\kappa,\rm \acute{e}t}) ^{U_p< k_1-k_2+1} \xrightarrow{\sim} H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, V_{-w_0(\kappa), \rm \acute{e}t})^{U_p< k_1-k_2+1} ,\\ H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, V_{\kappa,\rm \acute{e}t})^{U_p^t< k_1-k_2+1}\xrightarrow{\sim} H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, A^\delta_{\kappa,\rm \acute{e}t})^{U_p^t< k_1-k_2+1}. \end{align*}
\begin{align*} H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, D^\delta_{\kappa,\rm \acute{e}t}) ^{U_p< k_1-k_2+1} \xrightarrow{\sim} H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, V_{-w_0(\kappa), \rm \acute{e}t})^{U_p< k_1-k_2+1} ,\\ H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, V_{\kappa,\rm \acute{e}t})^{U_p^t< k_1-k_2+1}\xrightarrow{\sim} H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, A^\delta_{\kappa,\rm \acute{e}t})^{U_p^t< k_1-k_2+1}. \end{align*}
A similar result holds for the cohomology with compact support.
Remark 3.3.8 In [Reference Ash and StevensAS08], Theorem 3.3.7 is proved only for the cohomology of distributions. However, the same strategy works for the principal series and the cohomology with compact support. In particular, the bounds of the classicality theorem are motivated by [Reference Ash and StevensAS08, Theorem 3.11.1].
3.4 Overconvergent Hodge–Tate maps
We end this section with the definition of overconvergent Hodge–Tate maps interpolating the morphisms ![]() $\operatorname {HT}^k:\operatorname {Sym}^k T_pE \otimes \widehat {\mathscr {O}}_X \rightarrow \omega _E^{k}\otimes _{\mathscr {O}_X}\widehat {\mathscr {O}}_X$ and
$\operatorname {HT}^k:\operatorname {Sym}^k T_pE \otimes \widehat {\mathscr {O}}_X \rightarrow \omega _E^{k}\otimes _{\mathscr {O}_X}\widehat {\mathscr {O}}_X$ and ![]() $\operatorname {HT}^{k,\vee }: \omega _E^{-k}\otimes _{\mathscr {O}_X}\widehat {\mathscr {O}}_X(k)\rightarrow \operatorname {Sym}^k T_pE \otimes \widehat {\mathscr {O}}_X$.
$\operatorname {HT}^{k,\vee }: \omega _E^{-k}\otimes _{\mathscr {O}_X}\widehat {\mathscr {O}}_X(k)\rightarrow \operatorname {Sym}^k T_pE \otimes \widehat {\mathscr {O}}_X$.
Definition 3.4.1 Let ![]() $\epsilon \geq \delta \geq n$,
$\epsilon \geq \delta \geq n$, ![]() $(R,R^+)$ a uniform affinoid Tate
$(R,R^+)$ a uniform affinoid Tate ![]() $\mathbb {Q}_p$-algebra and
$\mathbb {Q}_p$-algebra and ![]() $\chi =(\chi _1,\chi _2): T=\mathbf {T}(\mathbb {Z}_p)\rightarrow R^{+,\times }$ a
$\chi =(\chi _1,\chi _2): T=\mathbf {T}(\mathbb {Z}_p)\rightarrow R^{+,\times }$ a ![]() $\delta$-analytic character.
$\delta$-analytic character.
(i) We define the map of pro-Kummer-étale sheaves over
 $X_{1}(\epsilon )$,
as the pullback of the highest weight vector map
$X_{1}(\epsilon )$,
as the pullback of the highest weight vector map \[ \operatorname{HT}^{A,\vee}_{-w_0(\chi)}: \omega_E^{w_0(\chi)}\otimes_{R\widehat{\otimes} \mathscr{O}_X} \widehat{\mathscr{O}}_X(\chi_1) \rightarrow A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X, \]
\[ \operatorname{HT}^{A,\vee}_{-w_0(\chi)}: \omega_E^{w_0(\chi)}\otimes_{R\widehat{\otimes} \mathscr{O}_X} \widehat{\mathscr{O}}_X(\chi_1) \rightarrow A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X, \]
 $\Psi ^{A,\vee }_{-w_0(\chi )}:\mathscr {L}(w_0(\chi ))\rightarrow A^{\delta }_{\chi }\widehat {\otimes } \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$ over
$\Psi ^{A,\vee }_{-w_0(\chi )}:\mathscr {L}(w_0(\chi ))\rightarrow A^{\delta }_{\chi }\widehat {\otimes } \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }}$ over  $U_1(\epsilon )\operatorname {Iw}_n\subset \operatorname {\mathscr {F}\!\ell }$ by
$U_1(\epsilon )\operatorname {Iw}_n\subset \operatorname {\mathscr {F}\!\ell }$ by  $\pi _{\operatorname {HT}}$ (cf. Proposition 2.4.4). We let
$\pi _{\operatorname {HT}}$ (cf. Proposition 2.4.4). We let  $\operatorname {HT}_{-w_0(\chi )}^{D}: D^{\delta }_{\chi,{\rm \acute {e}t}}\widehat {\otimes }\widehat {\mathscr {O}}_X \rightarrow \omega _E^{-w_0(\chi )}\otimes \widehat {\mathscr {O}}_X(-\chi _1)$ be the dual of
$\operatorname {HT}_{-w_0(\chi )}^{D}: D^{\delta }_{\chi,{\rm \acute {e}t}}\widehat {\otimes }\widehat {\mathscr {O}}_X \rightarrow \omega _E^{-w_0(\chi )}\otimes \widehat {\mathscr {O}}_X(-\chi _1)$ be the dual of  $\operatorname {HT}^{A,\vee }_{-w_0(\chi )}$.
$\operatorname {HT}^{A,\vee }_{-w_0(\chi )}$.(ii) We define the map of pro-Kummer-étale sheaves over
 $X_{w_0}(\epsilon )$,
as the pullback by
$X_{w_0}(\epsilon )$,
as the pullback by \[ \operatorname{HT}^{A}_{\chi}: A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X \rightarrow \omega_E^{\chi}\otimes \widehat{\mathscr{O}}_X(\chi_2), \]
\[ \operatorname{HT}^{A}_{\chi}: A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X \rightarrow \omega_E^{\chi}\otimes \widehat{\mathscr{O}}_X(\chi_2), \]
 $\pi _{\operatorname {HT}}$ of the lowest weight vector map
$\pi _{\operatorname {HT}}$ of the lowest weight vector map  $A^{\delta }_{\chi }\widehat {\otimes } \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }} \rightarrow \mathscr {L}(\chi )$ over
$A^{\delta }_{\chi }\widehat {\otimes } \mathscr {O}_{\operatorname {\mathscr {F}\!\ell }} \rightarrow \mathscr {L}(\chi )$ over  $U_{w_0}(\epsilon )\operatorname {Iw}_n\subset \operatorname {\mathscr {F}\!\ell }$. We let
$U_{w_0}(\epsilon )\operatorname {Iw}_n\subset \operatorname {\mathscr {F}\!\ell }$. We let  $\operatorname {HT}^{D, \vee }_{\chi }: \omega _E^{-\chi }\otimes \widehat {\mathscr {O}}_X (-\chi _2) \rightarrow D^{\delta }_{\chi,{\rm \acute {e}t}}\widehat {\otimes }\widehat {\mathscr {O}}_X$ be the dual of
$\operatorname {HT}^{D, \vee }_{\chi }: \omega _E^{-\chi }\otimes \widehat {\mathscr {O}}_X (-\chi _2) \rightarrow D^{\delta }_{\chi,{\rm \acute {e}t}}\widehat {\otimes }\widehat {\mathscr {O}}_X$ be the dual of  $\operatorname {HT}^{A}_{\chi }$.
$\operatorname {HT}^{A}_{\chi }$.
Lemma 3.4.2 The overconvergent Hodge–Tate maps of Definition 3.4.1 are compatible with the ![]() $U_p$-correspondences of Definitions 3.2.15 and 3.3.6. Moreover, they are compatible with the normalized
$U_p$-correspondences of Definitions 3.2.15 and 3.3.6. Moreover, they are compatible with the normalized ![]() $U_p$-correspondences of the sheaves
$U_p$-correspondences of the sheaves ![]() $V_{\kappa, {\rm \acute {e}t}}$ for
$V_{\kappa, {\rm \acute {e}t}}$ for ![]() $\kappa \in X^*(\mathbf {T})^+$ (see Remark 2.2.13).
$\kappa \in X^*(\mathbf {T})^+$ (see Remark 2.2.13).
4.  $p$-adic Eichler–Shimura maps
$p$-adic Eichler–Shimura maps
Throughout this section we fix a neat compact open subgroup ![]() $K^p\subset \operatorname {GL}_2(\mathbb {A}_{\mathbb {Q}}^{\infty,p})$, and, given
$K^p\subset \operatorname {GL}_2(\mathbb {A}_{\mathbb {Q}}^{\infty,p})$, and, given ![]() $K_p\subset \operatorname {GL}_2(\mathbb {Q}_p)$, we let
$K_p\subset \operatorname {GL}_2(\mathbb {Q}_p)$, we let ![]() $Y=Y_{K_p}$ and
$Y=Y_{K_p}$ and ![]() $X=X_{K_p}$ denote the affine and compact modular curves of level
$X=X_{K_p}$ denote the affine and compact modular curves of level ![]() $K_p$, respectively. We let
$K_p$, respectively. We let ![]() $D= X\backslash Y$ be the cusp divisor. Let
$D= X\backslash Y$ be the cusp divisor. Let ![]() $f: E^{sm} \rightarrow X$ be the semi-abelian scheme extending the universal elliptic curve over
$f: E^{sm} \rightarrow X$ be the semi-abelian scheme extending the universal elliptic curve over ![]() $Y$, and
$Y$, and ![]() $\overline {E}$ be its relative compactification to a log smooth adic space over
$\overline {E}$ be its relative compactification to a log smooth adic space over ![]() $X$ (cf. [Reference Deligne and RapoportDR73]). We denote by
$X$ (cf. [Reference Deligne and RapoportDR73]). We denote by ![]() $\operatorname {DR}_X(\overline {E})$ the relative log de Rham complex of
$\operatorname {DR}_X(\overline {E})$ the relative log de Rham complex of ![]() $\overline {E}$ over
$\overline {E}$ over ![]() $X$, and by
$X$, and by ![]() $\mathscr {H}^1_{{\rm dR}}:= R^1 f_{{\rm an},*}(\operatorname {DR}_X(\overline {E}))$ the first relative de Rham cohomology group. The sheaf
$\mathscr {H}^1_{{\rm dR}}:= R^1 f_{{\rm an},*}(\operatorname {DR}_X(\overline {E}))$ the first relative de Rham cohomology group. The sheaf ![]() $\mathscr {H}^{1}_{{\rm dR}}$ is endowed with a log connection
$\mathscr {H}^{1}_{{\rm dR}}$ is endowed with a log connection
and a Hodge filtration ![]() $0\to \omega _E \to \mathscr {H}^1_{dR} \to \omega _E^{-1}\to 0$ with
$0\to \omega _E \to \mathscr {H}^1_{dR} \to \omega _E^{-1}\to 0$ with ![]() $\operatorname {Fil}^0 \mathscr {H}^1_{{\rm dR}}= \mathscr {H}^1_{{\rm dR}}$,
$\operatorname {Fil}^0 \mathscr {H}^1_{{\rm dR}}= \mathscr {H}^1_{{\rm dR}}$, ![]() $\operatorname {Fil}^1 \mathscr {H}^1_{{\rm dR}}=\omega _E$ and
$\operatorname {Fil}^1 \mathscr {H}^1_{{\rm dR}}=\omega _E$ and ![]() $\operatorname {Fil}^2\mathscr {H}^1_{{\rm dR}}=0$, satisfying Griffiths transversality. This last section is dedicated to the construction of the Eichler–Shimura decomposition for the étale cohomology of the modular curves. We first provide a new proof of Faltings's Eichler–Shimura decomposition of the cohomology of the local systems
$\operatorname {Fil}^2\mathscr {H}^1_{{\rm dR}}=0$, satisfying Griffiths transversality. This last section is dedicated to the construction of the Eichler–Shimura decomposition for the étale cohomology of the modular curves. We first provide a new proof of Faltings's Eichler–Shimura decomposition of the cohomology of the local systems ![]() $V_{\kappa, {\rm \acute {e}t}}$ (cf. [Reference FaltingsFal87]). Our method uses the Hodge–Tate period map and the dual BGG resolution of Proposition 2.4.3. Next, we use the overconvergent Hodge–Tate maps of Definition 3.4.1 to define overconvergent Eichler–Shimura maps. We shall recover the results of [Reference Andreatta, Iovita and StevensAIS15] as well as a new map from the
$V_{\kappa, {\rm \acute {e}t}}$ (cf. [Reference FaltingsFal87]). Our method uses the Hodge–Tate period map and the dual BGG resolution of Proposition 2.4.3. Next, we use the overconvergent Hodge–Tate maps of Definition 3.4.1 to define overconvergent Eichler–Shimura maps. We shall recover the results of [Reference Andreatta, Iovita and StevensAIS15] as well as a new map from the ![]() $H^1$-cohomology with compact support of overconvergent modular forms to overconvergent modular symbols. Finally, we show that the overconvergent Eichler–Shimura maps are compatible with the Poincaré and Serre duality pairings, and that, for small slope, we have a perfect pairing.
$H^1$-cohomology with compact support of overconvergent modular forms to overconvergent modular symbols. Finally, we show that the overconvergent Eichler–Shimura maps are compatible with the Poincaré and Serre duality pairings, and that, for small slope, we have a perfect pairing.
4.1 A proétale Eichler–Shimura decomposition
Let ![]() $\kappa =(k_1,k_2)\in X^*(\mathbf {T})^+$ be a dominant weight,
$\kappa =(k_1,k_2)\in X^*(\mathbf {T})^+$ be a dominant weight, ![]() $V_{\kappa }$ the irreducible representation of highest weight
$V_{\kappa }$ the irreducible representation of highest weight ![]() $\kappa$, and
$\kappa$, and ![]() $V_{\kappa,{\rm \acute {e}t}}$ the pro-Kummer-étale local system over
$V_{\kappa,{\rm \acute {e}t}}$ the pro-Kummer-étale local system over ![]() $X$ defined by
$X$ defined by ![]() $V_{\kappa }$. Let
$V_{\kappa }$. Let ![]() $\alpha =(1,-1)\in X^*(\mathbf {T})$. Let us recall a theorem of Faltings.
$\alpha =(1,-1)\in X^*(\mathbf {T})$. Let us recall a theorem of Faltings.
Theorem 4.1.1 [Reference FaltingsFal87, Theorem 6]
There are Hecke and Galois equivariant isomorphisms
 \begin{align*} H^1_{\rm pro\acute{e}t}(Y_{\mathbb{C}_p}, V_{\kappa,\rm \acute{e}t})\otimes_{\mathbb{Z}_p} \mathbb{C}_p & = H^1_{\rm an}(X_{\mathbb{C}_p}, \omega_E^{w_0(\kappa)})(k_1) \oplus H^0_{\rm an}(X_{\mathbb{C}_p}, \omega_E^{\kappa+\alpha})(k_2-1),\\ H^1_{\rm pro\acute{e}t,c}(Y_{\mathbb{C}_p}, V_{\kappa,\rm \acute{e}t})\otimes_{\mathbb{Z}_p} \mathbb{C}_p & = H^{1}_{\rm an}( X_{\mathbb{C}_p}, \omega_E^{w_0(\kappa)}(-D))(k_1) \oplus H^0_{\rm an}(X_{\mathbb{C}_p}, \omega_E^{\kappa+\alpha}(-D))(k_2-1). \end{align*}
\begin{align*} H^1_{\rm pro\acute{e}t}(Y_{\mathbb{C}_p}, V_{\kappa,\rm \acute{e}t})\otimes_{\mathbb{Z}_p} \mathbb{C}_p & = H^1_{\rm an}(X_{\mathbb{C}_p}, \omega_E^{w_0(\kappa)})(k_1) \oplus H^0_{\rm an}(X_{\mathbb{C}_p}, \omega_E^{\kappa+\alpha})(k_2-1),\\ H^1_{\rm pro\acute{e}t,c}(Y_{\mathbb{C}_p}, V_{\kappa,\rm \acute{e}t})\otimes_{\mathbb{Z}_p} \mathbb{C}_p & = H^{1}_{\rm an}( X_{\mathbb{C}_p}, \omega_E^{w_0(\kappa)}(-D))(k_1) \oplus H^0_{\rm an}(X_{\mathbb{C}_p}, \omega_E^{\kappa+\alpha}(-D))(k_2-1). \end{align*}
Let ![]() $\mathbb {B}_{{\rm dR}}^+$ be the de Rham period sheaf of
$\mathbb {B}_{{\rm dR}}^+$ be the de Rham period sheaf of ![]() $X_{{\rm prok\acute {e}t}}$,
$X_{{\rm prok\acute {e}t}}$, ![]() $\theta : \mathbb {B}_{{\rm dR}}^+\to \widehat {\mathscr {O}}_X$ the Fontaine map, and
$\theta : \mathbb {B}_{{\rm dR}}^+\to \widehat {\mathscr {O}}_X$ the Fontaine map, and ![]() $\xi \in \ker \theta$ a local generator of the kernel; we set
$\xi \in \ker \theta$ a local generator of the kernel; we set ![]() $\mathbb {B}_{{\rm dR}}:= \mathbb {B}^+_{{\rm dR}}[ {1}/{\xi }]$. Let
$\mathbb {B}_{{\rm dR}}:= \mathbb {B}^+_{{\rm dR}}[ {1}/{\xi }]$. Let ![]() $\mathscr {O}\!\mathbb {B}_{{\rm dR},\log }^+$ be the geometric de Rham period sheaf and
$\mathscr {O}\!\mathbb {B}_{{\rm dR},\log }^+$ be the geometric de Rham period sheaf and ![]() $\mathscr {O}\!\mathbb {B}_{{\rm dR},\log }=\mathscr {O}\!\mathbb {B}_{{\rm dR},\log }^+[{1}/{\xi }]$, we denote by
$\mathscr {O}\!\mathbb {B}_{{\rm dR},\log }=\mathscr {O}\!\mathbb {B}_{{\rm dR},\log }^+[{1}/{\xi }]$, we denote by ![]() $\mathscr {O}\!\mathbb {C}_{\log }$ the sheaf
$\mathscr {O}\!\mathbb {C}_{\log }$ the sheaf ![]() $\operatorname {gr}^0(\mathscr {O}\!\mathbb {B}_{{\rm dR},\log })$. We refer to [Reference ScholzeSch13] and [Reference Diao, Lan, Liu and ZhuDLLZ23a] for the definition of the period sheaves.
$\operatorname {gr}^0(\mathscr {O}\!\mathbb {B}_{{\rm dR},\log })$. We refer to [Reference ScholzeSch13] and [Reference Diao, Lan, Liu and ZhuDLLZ23a] for the definition of the period sheaves.
The main ingredient of our proof of Theorem 4.1.1 is an explicit relation between the Faltings extension ![]() $\operatorname {gr}^1 \mathscr {O}\!\mathbb {B}_{{\rm dR},\log }^+$ and the Tate module
$\operatorname {gr}^1 \mathscr {O}\!\mathbb {B}_{{\rm dR},\log }^+$ and the Tate module ![]() $T_pE$. This arises naturally in the study of pullbacks of
$T_pE$. This arises naturally in the study of pullbacks of ![]() $\operatorname {GL}_2$-equivariant vector bundles of
$\operatorname {GL}_2$-equivariant vector bundles of ![]() $\operatorname {\mathscr {F}\!\ell }$ by
$\operatorname {\mathscr {F}\!\ell }$ by ![]() $\pi _{\operatorname {HT}}$. Recall that
$\pi _{\operatorname {HT}}$. Recall that ![]() $\operatorname {FL}= \mathbf {B} \backslash\!\operatorname {GL}_2$, so that we have an equivalence of categories between
$\operatorname {FL}= \mathbf {B} \backslash\!\operatorname {GL}_2$, so that we have an equivalence of categories between ![]() $\operatorname {GL}_2$-equivariant vector bundles over
$\operatorname {GL}_2$-equivariant vector bundles over ![]() $\operatorname {\mathscr {F}\!\ell }$ and algebraic representations of
$\operatorname {\mathscr {F}\!\ell }$ and algebraic representations of ![]() $\mathbf {B}$. Let
$\mathbf {B}$. Let ![]() $\mathscr {O}(\mathbf {B})$ be the ring of algebraic functions of
$\mathscr {O}(\mathbf {B})$ be the ring of algebraic functions of ![]() $\mathbf {B}$ endowed with the right regular action; note that any finite representation of
$\mathbf {B}$ endowed with the right regular action; note that any finite representation of ![]() $\mathbf {B}$ occurs in
$\mathbf {B}$ occurs in ![]() $\mathscr {O}(\mathbf {B})$. Writing
$\mathscr {O}(\mathbf {B})$. Writing ![]() $\mathbf {B}= \mathbf {T} \ltimes \mathbf {N}$ as a product of the diagonal torus and its unipotent radical, one has that
$\mathbf {B}= \mathbf {T} \ltimes \mathbf {N}$ as a product of the diagonal torus and its unipotent radical, one has that ![]() $\mathscr {O}(\mathbf {B})=\mathscr {O}(\mathbf {T}) \otimes \mathscr {O}(\mathbf {N})$. The action of
$\mathscr {O}(\mathbf {B})=\mathscr {O}(\mathbf {T}) \otimes \mathscr {O}(\mathbf {N})$. The action of ![]() $\mathbf {B}$ on
$\mathbf {B}$ on ![]() $\mathscr {O}(\mathbf {T})$ factors through
$\mathscr {O}(\mathbf {T})$ factors through ![]() $\mathbf {T}$, so that this ring can be decomposed in terms of characters of the torus. By Proposition 3.1.4 we already know what the pullback by
$\mathbf {T}$, so that this ring can be decomposed in terms of characters of the torus. By Proposition 3.1.4 we already know what the pullback by ![]() $\pi _{\operatorname {HT}}$ of the quasi-coherent sheaf associated to
$\pi _{\operatorname {HT}}$ of the quasi-coherent sheaf associated to ![]() $\mathscr {O}(\mathbf {T})$ is; it admits an explicit description in terms of modular sheaves. On the other hand, the action of
$\mathscr {O}(\mathbf {T})$ is; it admits an explicit description in terms of modular sheaves. On the other hand, the action of ![]() $\mathbf {B}$ on
$\mathbf {B}$ on ![]() $\mathscr {O}(\mathbf {N})$ is determined by the right action
$\mathscr {O}(\mathbf {N})$ is determined by the right action ![]() $(n,b)\mapsto t_{b}^{-1}nt_b n_b$, where
$(n,b)\mapsto t_{b}^{-1}nt_b n_b$, where ![]() $n\in \mathbf {N}$ and
$n\in \mathbf {N}$ and ![]() $b=(t_b,n_b)\in \mathbf {B}=\mathbf {T} \ltimes \mathbf {N}$. Let
$b=(t_b,n_b)\in \mathbf {B}=\mathbf {T} \ltimes \mathbf {N}$. Let ![]() $\underline {\mathscr {O}}(\mathbf {N})$ be the
$\underline {\mathscr {O}}(\mathbf {N})$ be the ![]() $\operatorname {GL}_2$-equivariant quasi-coherent sheaf over
$\operatorname {GL}_2$-equivariant quasi-coherent sheaf over ![]() $\operatorname {\mathscr {F}\!\ell }$ attached to
$\operatorname {\mathscr {F}\!\ell }$ attached to ![]() $\mathscr {O}(\mathbf {N})$.
$\mathscr {O}(\mathbf {N})$.
Theorem 4.1.2 ([Reference FaltingsFal87, Theorem 5] and [Reference PanPan22, Theorem 4.2.2])
There is a natural isomorphism of pro-Kummer-étale sheaves over ![]() $X$,
$X$,
Furthermore, let ![]() $\mathscr {O}(\mathbf {N})^{\leq 1}\subset \mathscr {O}(\mathbf {N})$ be the subrepresentation consisting on polynomials of degree at most
$\mathscr {O}(\mathbf {N})^{\leq 1}\subset \mathscr {O}(\mathbf {N})$ be the subrepresentation consisting on polynomials of degree at most ![]() $1$. We have an isomorphism as
$1$. We have an isomorphism as ![]() $\mathbf {B}$-representations
$\mathbf {B}$-representations ![]() $\mathscr {O}(\mathbf {N})^{\leq 1} = \operatorname {St} \otimes \mathbb {Q}_p(-1,0)$; in particular,
$\mathscr {O}(\mathbf {N})^{\leq 1} = \operatorname {St} \otimes \mathbb {Q}_p(-1,0)$; in particular, ![]() $\pi _{\operatorname {HT}}^*(\underline {\mathscr {O}}(\mathbf {N})^{\leq 1})= T_pE \otimes \widehat {\mathscr {O}}_X(-1)\otimes \omega _E$. Moreover, there is an isomorphism of extensions
$\pi _{\operatorname {HT}}^*(\underline {\mathscr {O}}(\mathbf {N})^{\leq 1})= T_pE \otimes \widehat {\mathscr {O}}_X(-1)\otimes \omega _E$. Moreover, there is an isomorphism of extensions

where ![]() $KS$ is the Kodaira–Spencer isomorphism.
$KS$ is the Kodaira–Spencer isomorphism.
Proof. It is enough to show the second statement, namely, that if ![]() $\pi _{\operatorname {HT}}^*( \underline {\mathscr {O}}(\mathbf {N})^{\leq 1}) =T_pE\otimes \widehat {\mathscr {O}}(-1)\otimes \omega _E= \operatorname {gr}^1 \mathscr {O}\!\mathbb {B}_{{\rm dR},\log }^+(-1)$, one has
$\pi _{\operatorname {HT}}^*( \underline {\mathscr {O}}(\mathbf {N})^{\leq 1}) =T_pE\otimes \widehat {\mathscr {O}}(-1)\otimes \omega _E= \operatorname {gr}^1 \mathscr {O}\!\mathbb {B}_{{\rm dR},\log }^+(-1)$, one has
Let ![]() $\mathscr {F}$ be a sheaf endowed with an integral log connection
$\mathscr {F}$ be a sheaf endowed with an integral log connection ![]() $\nabla$; we denote by
$\nabla$; we denote by ![]() $\operatorname {DR}(\mathscr {F}, \nabla )$ the log de Rham complex of
$\operatorname {DR}(\mathscr {F}, \nabla )$ the log de Rham complex of ![]() $\mathscr {F}$. Let
$\mathscr {F}$. Let ![]() $f:\overline {E}\to X$ be the compactification of the elliptic curve as a log smooth adic space over
$f:\overline {E}\to X$ be the compactification of the elliptic curve as a log smooth adic space over ![]() $X$. We have a quasi-isomorphism of complexes over
$X$. We have a quasi-isomorphism of complexes over ![]() $\overline {E}_{{\rm prok\acute {e}t}}$,
$\overline {E}_{{\rm prok\acute {e}t}}$,
Taking ![]() $R^1 f_{{\rm prok\acute {e}t},*}$ one obtains by [Reference Diao, Lan, Liu and ZhuDLLZ23a, Theorem 3.2.7 (5)] or [Reference ScholzeSch13, Theorem 8.8]
$R^1 f_{{\rm prok\acute {e}t},*}$ one obtains by [Reference Diao, Lan, Liu and ZhuDLLZ23a, Theorem 3.2.7 (5)] or [Reference ScholzeSch13, Theorem 8.8]
Let ![]() $\mathbb {M}:= T_pE(-1)\otimes \mathbb {B}_{{\rm dR},X}^+ =(T_pE(-1) \otimes \mathscr {O}\! \mathbb {B}_{{\rm dR},\log,X}^+)^{\nabla =0}$ and
$\mathbb {M}:= T_pE(-1)\otimes \mathbb {B}_{{\rm dR},X}^+ =(T_pE(-1) \otimes \mathscr {O}\! \mathbb {B}_{{\rm dR},\log,X}^+)^{\nabla =0}$ and ![]() $\mathbb {M}_0 = ( \mathscr {H}_{{\rm dR}}^1\otimes \mathscr {O}\! \mathbb {B}_{{\rm dR},\log, X}^+)^{\nabla =0}$. Both
$\mathbb {M}_0 = ( \mathscr {H}_{{\rm dR}}^1\otimes \mathscr {O}\! \mathbb {B}_{{\rm dR},\log, X}^+)^{\nabla =0}$. Both ![]() $\mathbb {M}_0$ and
$\mathbb {M}_0$ and ![]() $\mathbb {M}$ are
$\mathbb {M}$ are ![]() $\mathbb {B}_{{\rm dR},X}^+$-lattices of
$\mathbb {B}_{{\rm dR},X}^+$-lattices of ![]() $T_pE(-1)\otimes \mathbb {B}_{{\rm dR},X}$. The Hodge filtration of
$T_pE(-1)\otimes \mathbb {B}_{{\rm dR},X}$. The Hodge filtration of ![]() $\mathscr {H}^{1}_{{\rm dR}}$ is concentrated in degrees
$\mathscr {H}^{1}_{{\rm dR}}$ is concentrated in degrees ![]() $0$ and
$0$ and ![]() $1$, and is equal to
$1$, and is equal to
This implies that ![]() $\xi \mathbb {M} \subset \mathbb {M}_0\subset \mathbb {M}$, and that
$\xi \mathbb {M} \subset \mathbb {M}_0\subset \mathbb {M}$, and that ![]() $(\operatorname {Fil}^1( \mathscr {H}^1_{{\rm dR}} \otimes \mathscr {O}\! \mathbb {B}^+_{{\rm dR},\log,X} ))^{\nabla =0}= \xi \mathbb {M}$. Then Proposition 7.9 of [Reference ScholzeSch13] implies that
$(\operatorname {Fil}^1( \mathscr {H}^1_{{\rm dR}} \otimes \mathscr {O}\! \mathbb {B}^+_{{\rm dR},\log,X} ))^{\nabla =0}= \xi \mathbb {M}$. Then Proposition 7.9 of [Reference ScholzeSch13] implies that
 \begin{gather*} \mathbb{M}_0/ \xi \mathbb{M} = \operatorname{gr}^0 \mathscr{H}^1_{\rm dR}\otimes \widehat{\mathscr{O}}_X = \omega_{E}^{-1}\otimes \widehat{\mathscr{O}}_{X},\\ \mathbb{M}/\mathbb{M}_0 = \operatorname{gr}^{1} \mathscr{H}^1_{\rm dR} \otimes \widehat{\mathscr{O}}_X(-1)= \omega_E\otimes \widehat{\mathscr{O}}_X(-1). \end{gather*}
\begin{gather*} \mathbb{M}_0/ \xi \mathbb{M} = \operatorname{gr}^0 \mathscr{H}^1_{\rm dR}\otimes \widehat{\mathscr{O}}_X = \omega_{E}^{-1}\otimes \widehat{\mathscr{O}}_{X},\\ \mathbb{M}/\mathbb{M}_0 = \operatorname{gr}^{1} \mathscr{H}^1_{\rm dR} \otimes \widehat{\mathscr{O}}_X(-1)= \omega_E\otimes \widehat{\mathscr{O}}_X(-1). \end{gather*}
In particular,
is just the Hodge–Tate exact sequence of ![]() $T_pE\otimes \widehat {\mathscr {O}}_X$ (note the multiplication by
$T_pE\otimes \widehat {\mathscr {O}}_X$ (note the multiplication by ![]() $\xi$ induced by the Tate twist in (24)), and
$\xi$ induced by the Tate twist in (24)), and
is the Hodge exact sequence of ![]() $\mathscr {H}_{dR}^1\otimes \widehat {\mathscr {O}}_X$.
$\mathscr {H}_{dR}^1\otimes \widehat {\mathscr {O}}_X$.
Consider the map of short exact sequences

and let ![]() $\tilde {\theta }: \mathscr {O}\!\mathbb {B}_{{\rm dR},\log,X}^+ \rightarrow \widehat {\mathscr {O}}_X$ be Fontaine's map.
$\tilde {\theta }: \mathscr {O}\!\mathbb {B}_{{\rm dR},\log,X}^+ \rightarrow \widehat {\mathscr {O}}_X$ be Fontaine's map.
Taking the first graded piece in the upper short exact sequence, one finds
 \[ 0 \rightarrow \xi\mathbb{M}/\xi^2\mathbb{M} \rightarrow \frac{\mathbb{M}\otimes (\ker \tilde{\theta})}{ \mathbb{M}\otimes (\ker \tilde{\theta})^2} \xrightarrow{\overline{\nabla}} \frac{\mathbb{M}\otimes \mathscr{O}\!\mathbb{B}^+_{\rm dR,\log,X}}{\mathbb{M}\otimes (\ker \tilde{\theta})} \otimes \Omega^1_X(\log) \rightarrow 0. \]
\[ 0 \rightarrow \xi\mathbb{M}/\xi^2\mathbb{M} \rightarrow \frac{\mathbb{M}\otimes (\ker \tilde{\theta})}{ \mathbb{M}\otimes (\ker \tilde{\theta})^2} \xrightarrow{\overline{\nabla}} \frac{\mathbb{M}\otimes \mathscr{O}\!\mathbb{B}^+_{\rm dR,\log,X}}{\mathbb{M}\otimes (\ker \tilde{\theta})} \otimes \Omega^1_X(\log) \rightarrow 0. \]
Since ![]() $\xi \mathbb {M}\subset \mathbb {M}_0$, taking the intersection with the image of the lower short exact sequence in (25), one obtains a short exact sequence
$\xi \mathbb {M}\subset \mathbb {M}_0$, taking the intersection with the image of the lower short exact sequence in (25), one obtains a short exact sequence
 \begin{equation} 0\,{\rightarrow}\, \frac{\xi
\mathbb{M}}{\xi^2\mathbb{M}} \,{\rightarrow}\,
\frac{\mathbb{M}_0\otimes (\ker\tilde{\theta}) + \xi
\mathbb{M}\otimes
\mathscr{O}\!\mathbb{B}_{\rm dR,\log,X}^+ }{\mathbb{M}_0 \otimes (\ker
\tilde{\theta})^2 \,{+}\, \xi \mathbb{M}\otimes (\ker
\tilde{\theta}) } \xrightarrow{\nabla} \frac{\mathbb{M}_0
\otimes
\mathscr{O}\!\mathbb{B}_{\rm dR,\log,X}^+}{\mathbb{M}_0 \otimes (\ker
\tilde{\theta})\,{+}\, \xi \mathbb{M}\otimes
\mathscr{O}\!\mathbb{B}_{\rm dR,\log,X}^+}\otimes \Omega^1_X(\log) \,{\rightarrow}\, 0.
\end{equation}
\begin{equation} 0\,{\rightarrow}\, \frac{\xi
\mathbb{M}}{\xi^2\mathbb{M}} \,{\rightarrow}\,
\frac{\mathbb{M}_0\otimes (\ker\tilde{\theta}) + \xi
\mathbb{M}\otimes
\mathscr{O}\!\mathbb{B}_{\rm dR,\log,X}^+ }{\mathbb{M}_0 \otimes (\ker
\tilde{\theta})^2 \,{+}\, \xi \mathbb{M}\otimes (\ker
\tilde{\theta}) } \xrightarrow{\nabla} \frac{\mathbb{M}_0
\otimes
\mathscr{O}\!\mathbb{B}_{\rm dR,\log,X}^+}{\mathbb{M}_0 \otimes (\ker
\tilde{\theta})\,{+}\, \xi \mathbb{M}\otimes
\mathscr{O}\!\mathbb{B}_{\rm dR,\log,X}^+}\otimes \Omega^1_X(\log) \,{\rightarrow}\, 0.
\end{equation}
The quotient term of the short exact sequence (26) is equal to ![]() $\mathbb {M}_0/ \xi \mathbb {M}\otimes \Omega ^1_X(\log )= \omega _E^{-1}\otimes \Omega ^1_X(\log )\otimes \widehat {\mathscr {O}}_X$. The middle term of the short exact sequence is equal to
$\mathbb {M}_0/ \xi \mathbb {M}\otimes \Omega ^1_X(\log )= \omega _E^{-1}\otimes \Omega ^1_X(\log )\otimes \widehat {\mathscr {O}}_X$. The middle term of the short exact sequence is equal to
Note that the restriction of ![]() $\overline {\nabla }$ to
$\overline {\nabla }$ to ![]() $\omega _E \otimes \widehat {\mathscr {O}}_X$ is the Kodaira–Spencer map by definition. Indeed, if
$\omega _E \otimes \widehat {\mathscr {O}}_X$ is the Kodaira–Spencer map by definition. Indeed, if ![]() $\nabla : \mathscr {H}^1_{dR}\rightarrow \mathscr {H}^1_{dR}\otimes \Omega ^1_{X}(\log )$ is the connection, taking the first graded piece we get the map
$\nabla : \mathscr {H}^1_{dR}\rightarrow \mathscr {H}^1_{dR}\otimes \Omega ^1_{X}(\log )$ is the connection, taking the first graded piece we get the map
Therefore, we have constructed a short exact sequence
Thus, as ![]() $KS$ is an isomorphism so is
$KS$ is an isomorphism so is ![]() $\alpha$, and we have a commutative diagram
$\alpha$, and we have a commutative diagram

which finishes the proof.
Remark 4.1.3 The previous proposition is the key tool necessary to compute the relative Sen operator for the modular curve in Pan's locally analytic vectors (cf. [Reference PanPan22]).
We deduce the Eichler–Shimura decompositions for the local systems ![]() $V_{\kappa,{\rm \acute {e}t}}$.
$V_{\kappa,{\rm \acute {e}t}}$.
Theorem 4.1.4 Let ![]() $\alpha =(1,-1)$. Let
$\alpha =(1,-1)$. Let ![]() $\kappa =(k_1,k_2)\in X^*(\mathbf {T})^+$ be a dominant weight and
$\kappa =(k_1,k_2)\in X^*(\mathbf {T})^+$ be a dominant weight and ![]() $\operatorname {BGG}(\kappa )$ the BGG complex of Proposition 2.4.3:
$\operatorname {BGG}(\kappa )$ the BGG complex of Proposition 2.4.3:
Let ![]() $\underline {\operatorname {BGG}(\kappa )}$ be the
$\underline {\operatorname {BGG}(\kappa )}$ be the ![]() $\operatorname {GL}_2$-equivariant complex of sheaves defined by
$\operatorname {GL}_2$-equivariant complex of sheaves defined by ![]() $\operatorname {BGG}(\kappa )$. We have a quasi-isomorphism of complexes over
$\operatorname {BGG}(\kappa )$. We have a quasi-isomorphism of complexes over ![]() $X_{{\rm prok\acute {e}t}}$,
$X_{{\rm prok\acute {e}t}}$,
Moreover, let ![]() $\lambda : X_{\mathbb {C}_p, {\rm prok\acute {e}t}} \to X_{\mathbb {C}_p, {\rm an}}$ be the projection of sites. Let
$\lambda : X_{\mathbb {C}_p, {\rm prok\acute {e}t}} \to X_{\mathbb {C}_p, {\rm an}}$ be the projection of sites. Let ![]() $\iota : D_{{\rm prok\acute {e}t}}\to X_{{\rm prok\acute {e}t}}$ be the natural morphism, and
$\iota : D_{{\rm prok\acute {e}t}}\to X_{{\rm prok\acute {e}t}}$ be the natural morphism, and ![]() $\widehat {\mathscr {I}}= \ker (\widehat {\mathscr {O}}_X \to \iota _* \widehat {\mathscr {O}}_D)$. We have
$\widehat {\mathscr {I}}= \ker (\widehat {\mathscr {O}}_X \to \iota _* \widehat {\mathscr {O}}_D)$. We have
 \begin{align*} R\lambda_{*} (V_{\kappa,\rm \acute{e}t}\otimes \widehat{\mathscr{O}}_{X})&= \omega_E^{w_0(\kappa)}\otimes \mathbb{C}_p(k_1)[0]\oplus \omega_E^{\kappa+\alpha} \otimes \mathbb{C}_p(k_2-1)[-1], \\ R\lambda_{*} (V_{\kappa,\rm \acute{e}t}\otimes \widehat{\mathscr{I}}_{X}) & = \omega_E^{w_0(\kappa)}(-D)\otimes \mathbb{C}(k_1)[0]\oplus \omega_E^{\kappa+\alpha}(-D) \otimes \mathbb{C} (k_2-1)[-1]. \end{align*}
\begin{align*} R\lambda_{*} (V_{\kappa,\rm \acute{e}t}\otimes \widehat{\mathscr{O}}_{X})&= \omega_E^{w_0(\kappa)}\otimes \mathbb{C}_p(k_1)[0]\oplus \omega_E^{\kappa+\alpha} \otimes \mathbb{C}_p(k_2-1)[-1], \\ R\lambda_{*} (V_{\kappa,\rm \acute{e}t}\otimes \widehat{\mathscr{I}}_{X}) & = \omega_E^{w_0(\kappa)}(-D)\otimes \mathbb{C}(k_1)[0]\oplus \omega_E^{\kappa+\alpha}(-D) \otimes \mathbb{C} (k_2-1)[-1]. \end{align*}
Then, taking the ![]() $H^1$-cohomology over
$H^1$-cohomology over ![]() $X_{\mathbb {C}_p,{\rm an}}$, one obtains Theorem 4.1.1.
$X_{\mathbb {C}_p,{\rm an}}$, one obtains Theorem 4.1.1.
Proof. Note that ![]() $V(\kappa )= \kappa \otimes V(0)$ as a
$V(\kappa )= \kappa \otimes V(0)$ as a ![]() $\mathbf {B}$-module, thus the first part of the theorem follows from Theorem 4.1.2 and Proposition 3.1.4. On the other hand, by [Reference Diao, Lan, Liu and ZhuDLLZ23a, Lemma 3.3.2] we know that
$\mathbf {B}$-module, thus the first part of the theorem follows from Theorem 4.1.2 and Proposition 3.1.4. On the other hand, by [Reference Diao, Lan, Liu and ZhuDLLZ23a, Lemma 3.3.2] we know that ![]() $R \lambda _* \mathscr {O}\!\mathbb {C}_{\log } = \mathscr {O}_{X_{\mathbb {C}_p}}$ and
$R \lambda _* \mathscr {O}\!\mathbb {C}_{\log } = \mathscr {O}_{X_{\mathbb {C}_p}}$ and ![]() $R\lambda _* ( \mathscr {O}\!\mathbb {C}_{\log }\otimes \iota _* \widehat {\mathscr {O}}_D )= \iota _* \mathscr {O}_D$, in particular that
$R\lambda _* ( \mathscr {O}\!\mathbb {C}_{\log }\otimes \iota _* \widehat {\mathscr {O}}_D )= \iota _* \mathscr {O}_D$, in particular that ![]() $R\lambda _* (\mathscr {O}\!\mathbb {C}_{\log } \otimes \widehat {\mathscr {I}})= \mathscr {O}(-D)$. Therefore,
$R\lambda _* (\mathscr {O}\!\mathbb {C}_{\log } \otimes \widehat {\mathscr {I}})= \mathscr {O}(-D)$. Therefore,
 \begin{equation}
\begin{aligned}
R \lambda_*(V_{\kappa,\rm \acute{e}t}\otimes
\widehat{\mathscr{O}}_X)&=[\omega_E^{w_0(\kappa)}\otimes \mathbb{C}_p(k_1) \rightarrow \omega_E^{\kappa+\alpha}
\otimes \mathbb{C}_p(k_2-1)],\\
R\lambda_*(V_{\kappa,\rm \acute{e}t}\otimes
\widehat{\mathscr{I}})&=[\omega_E^{w_0(\kappa)}(-D)\otimes \mathbb{C}_p(k_1)\to \omega_E^{\kappa+\alpha}(-D)\otimes
\mathbb{C}_p(k_2-1)]. \end{aligned} \end{equation}
\begin{equation}
\begin{aligned}
R \lambda_*(V_{\kappa,\rm \acute{e}t}\otimes
\widehat{\mathscr{O}}_X)&=[\omega_E^{w_0(\kappa)}\otimes \mathbb{C}_p(k_1) \rightarrow \omega_E^{\kappa+\alpha}
\otimes \mathbb{C}_p(k_2-1)],\\
R\lambda_*(V_{\kappa,\rm \acute{e}t}\otimes
\widehat{\mathscr{I}})&=[\omega_E^{w_0(\kappa)}(-D)\otimes \mathbb{C}_p(k_1)\to \omega_E^{\kappa+\alpha}(-D)\otimes
\mathbb{C}_p(k_2-1)]. \end{aligned} \end{equation}
But the arrows of (27) are ![]() $0$ since the sheaf
$0$ since the sheaf ![]() $\omega _E^{w_0(\kappa )}\otimes \mathbb {C}_p(k_1)$ already factors through
$\omega _E^{w_0(\kappa )}\otimes \mathbb {C}_p(k_1)$ already factors through ![]() $V_{\kappa,{\rm \acute {e}t}}\otimes \widehat {\mathscr {O}}_X$ via
$V_{\kappa,{\rm \acute {e}t}}\otimes \widehat {\mathscr {O}}_X$ via ![]() $\operatorname {HT}^{\vee }_{-w_0(\kappa )}: \omega _E^{w_0(\kappa )}\otimes \widehat {\mathscr {O}}_X(k_1)\to V_{\kappa, {\rm \acute {e}t}}\otimes \widehat {\mathscr {O}}_X$. The theorem follows.
$\operatorname {HT}^{\vee }_{-w_0(\kappa )}: \omega _E^{w_0(\kappa )}\otimes \widehat {\mathscr {O}}_X(k_1)\to V_{\kappa, {\rm \acute {e}t}}\otimes \widehat {\mathscr {O}}_X$. The theorem follows.
Remark 4.1.5 In [Reference Lan, Liu and ZhuLLZ23], Lan, Liu and Zhu gave another proof of the Eichler–Shimura decomposition for arbitrary Shimura varieties (also called BGG decomposition; see [Reference Lan, Liu and ZhuLLZ23, Theorem 6.2.3]). Their proof uses the ![]() $p$-adic Riemann–Hilbert correspondence and the BGG decomposition in terms of Verma modules; they then apply Faltings's strategy to construct a complex of
$p$-adic Riemann–Hilbert correspondence and the BGG decomposition in terms of Verma modules; they then apply Faltings's strategy to construct a complex of ![]() $\mathcal {D}$-modules quasi-isomorphic to the de Rham complex of the corresponding vector bundle with connection. In our situation, we use the dual BGG decomposition and the associated
$\mathcal {D}$-modules quasi-isomorphic to the de Rham complex of the corresponding vector bundle with connection. In our situation, we use the dual BGG decomposition and the associated ![]() $\operatorname {GL}_2$-equivariant sheaves over
$\operatorname {GL}_2$-equivariant sheaves over ![]() $\operatorname {\mathscr {F}\!\ell }$ instead. Our key ingredient to compute the proétale cohomology of
$\operatorname {\mathscr {F}\!\ell }$ instead. Our key ingredient to compute the proétale cohomology of ![]() $V_{\kappa }\otimes \widehat {\mathscr {O}}_X$ is Theorem 4.1.2, which serves as a dictionary between vector bundles over
$V_{\kappa }\otimes \widehat {\mathscr {O}}_X$ is Theorem 4.1.2, which serves as a dictionary between vector bundles over ![]() $\operatorname {\mathscr {F}\!\ell }$ and
$\operatorname {\mathscr {F}\!\ell }$ and ![]() $\widehat {\mathscr {O}}_X$-vector bundles over
$\widehat {\mathscr {O}}_X$-vector bundles over ![]() $X$.
$X$.
We finish this section with the compatibility of the Eichler–Shimura decomposition with Poincaré and Serre duality.
Proposition 4.1.6 [Reference Lan, Liu and ZhuLLZ23, Theorem 6.2.3]
Let ![]() $\operatorname {Tr}_P: H^2_{{\rm pro\acute {e}t},c}(Y_{\mathbb {C}_p}, \mathbb {Q}_p(1))\to \mathbb {Q}_p$ and
$\operatorname {Tr}_P: H^2_{{\rm pro\acute {e}t},c}(Y_{\mathbb {C}_p}, \mathbb {Q}_p(1))\to \mathbb {Q}_p$ and ![]() $\operatorname {Tr}_S: H^1_{{\rm an}}(X_{\mathbb {C}_p}, \Omega ^1_X)\to \mathbb {C}_p$ respectively be the Poincaré and Serre traces. Then the Poincaré pairing
$\operatorname {Tr}_S: H^1_{{\rm an}}(X_{\mathbb {C}_p}, \Omega ^1_X)\to \mathbb {C}_p$ respectively be the Poincaré and Serre traces. Then the Poincaré pairing
and the Serre pairing
(respectively, for ![]() $\omega ^{w_0(\kappa )}_E(-D)$ and
$\omega ^{w_0(\kappa )}_E(-D)$ and ![]() $\omega _E^{-w_0(\kappa )}$) are compatible with the Eichler–Shimura decomposition.
$\omega _E^{-w_0(\kappa )}$) are compatible with the Eichler–Shimura decomposition.
4.2 The overconvergent Eichler–Shimura maps
Let ![]() $n\geq 1$ be a fixed integer. In this subsection we will work with
$n\geq 1$ be a fixed integer. In this subsection we will work with ![]() $Y=Y_0(p^n)$ and
$Y=Y_0(p^n)$ and ![]() $X=X_0(p^n)$, the modular curves of level
$X=X_0(p^n)$, the modular curves of level ![]() $K^p\operatorname {Iw}_n$. Let
$K^p\operatorname {Iw}_n$. Let ![]() $\epsilon \geq \delta \geq n$ be rational numbers,
$\epsilon \geq \delta \geq n$ be rational numbers, ![]() $(R,R^+)$ a uniform affinoid Tate
$(R,R^+)$ a uniform affinoid Tate ![]() $\mathbb {Q}_p$-algebra and
$\mathbb {Q}_p$-algebra and ![]() $\chi =(\chi _1,\chi _2): T\rightarrow R^{+,\times }$ a
$\chi =(\chi _1,\chi _2): T\rightarrow R^{+,\times }$ a ![]() $\delta$-analytic character. Let
$\delta$-analytic character. Let ![]() $w\in W=\{1,w_0\}$ be an element in the Weyl group of
$w\in W=\{1,w_0\}$ be an element in the Weyl group of ![]() $\operatorname {GL}_2$ and
$\operatorname {GL}_2$ and ![]() $X_{w}(\epsilon )$ the
$X_{w}(\epsilon )$ the ![]() $\epsilon$-neighbourhood of the
$\epsilon$-neighbourhood of the ![]() $w$-ordinary locus (cf. Definition 3.2.1). Let
$w$-ordinary locus (cf. Definition 3.2.1). Let ![]() $\omega _E^{\chi }$ be the sheaf of overconvergent modular forms of weight
$\omega _E^{\chi }$ be the sheaf of overconvergent modular forms of weight ![]() $\chi$ over
$\chi$ over ![]() $X_{w}(\epsilon )$ (cf. Definition 3.2.9), and let
$X_{w}(\epsilon )$ (cf. Definition 3.2.9), and let ![]() $A_{\chi,{\rm \acute {e}t}}^{\delta }$ and
$A_{\chi,{\rm \acute {e}t}}^{\delta }$ and ![]() $D_{\chi,{\rm \acute {e}t}}^{\delta }$ be the pro-Kummer-étale sheaves of
$D_{\chi,{\rm \acute {e}t}}^{\delta }$ be the pro-Kummer-étale sheaves of ![]() $\delta$-analytic principal series and distributions over
$\delta$-analytic principal series and distributions over ![]() $X$ (cf. § 3.3). We can finally state the main theorem of this section, but first we need the following lemma.
$X$ (cf. § 3.3). We can finally state the main theorem of this section, but first we need the following lemma.
Lemma 4.2.1 Let ![]() $\alpha =(1,-1)\in X^*(\mathbf {T})$. The overconvergent Hodge–Tate morphisms of Definition 3.4.1 give rise to Galois and
$\alpha =(1,-1)\in X^*(\mathbf {T})$. The overconvergent Hodge–Tate morphisms of Definition 3.4.1 give rise to Galois and ![]() $U_p^t$-equivariant maps of cohomology groups (see Definition 3.2.16 for the good normalizations)
$U_p^t$-equivariant maps of cohomology groups (see Definition 3.2.16 for the good normalizations)
 \begin{equation} \begin{gathered} H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X )\xrightarrow{ES_{A}} H^0_{w_0}(X_{\mathbb{C}_p}, \omega_E^{\chi+\alpha})_{\epsilon}(\chi_2-1),\\ H^1_{1,c}(X_{\mathbb{C}_p}, \omega_E^{w_0(\chi)})_{\epsilon}(\chi_1)\xrightarrow{ES^{\vee}_{A}} H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes} \widehat{\mathscr{O}}_X ). \end{gathered} \end{equation}
\begin{equation} \begin{gathered} H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X )\xrightarrow{ES_{A}} H^0_{w_0}(X_{\mathbb{C}_p}, \omega_E^{\chi+\alpha})_{\epsilon}(\chi_2-1),\\ H^1_{1,c}(X_{\mathbb{C}_p}, \omega_E^{w_0(\chi)})_{\epsilon}(\chi_1)\xrightarrow{ES^{\vee}_{A}} H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes} \widehat{\mathscr{O}}_X ). \end{gathered} \end{equation}
Dually, we have Galois and ![]() $U_p$-equivariant maps of cohomology groups
$U_p$-equivariant maps of cohomology groups
 \begin{gather*} H^1_{w_0,c}(X_{\mathbb{C}_p}, \omega_E^{-\chi})_{\epsilon}(-\chi_2) \xrightarrow{ES^\vee_{D}} H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, D^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X),\\ H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, D^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X)\xrightarrow{ES_{D}} H^0_{1}(X_{\mathbb{C}_p}, \omega_E^{-w_0(\chi)+ \alpha} )_{\epsilon}(-\chi_1-1). \end{gather*}
\begin{gather*} H^1_{w_0,c}(X_{\mathbb{C}_p}, \omega_E^{-\chi})_{\epsilon}(-\chi_2) \xrightarrow{ES^\vee_{D}} H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, D^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X),\\ H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, D^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X)\xrightarrow{ES_{D}} H^0_{1}(X_{\mathbb{C}_p}, \omega_E^{-w_0(\chi)+ \alpha} )_{\epsilon}(-\chi_1-1). \end{gather*}
An analogous statement holds by exchanging ![]() $A^{\delta }_{\chi,{\rm \acute {e}t}}$ (respectively,
$A^{\delta }_{\chi,{\rm \acute {e}t}}$ (respectively, ![]() $D^{\delta }_{\chi,{\rm \acute {e}t} }$) with
$D^{\delta }_{\chi,{\rm \acute {e}t} }$) with ![]() $j_{{\rm prok\acute {e}t},!} A^{\delta }_{\chi,et}$ (respectively,
$j_{{\rm prok\acute {e}t},!} A^{\delta }_{\chi,et}$ (respectively, ![]() $j_{{\rm prok\acute {e}t},!}D^{\delta }_{\chi,{\rm \acute {e}t}}$), and
$j_{{\rm prok\acute {e}t},!}D^{\delta }_{\chi,{\rm \acute {e}t}}$), and ![]() $\omega ^{\chi }_E$ with
$\omega ^{\chi }_E$ with ![]() $\omega ^{\chi }_{E}(-D)$.
$\omega ^{\chi }_{E}(-D)$.
Proof. Let ![]() $\lambda :X_{\mathbb {C}_p, {\rm prok\acute {e}t}}\rightarrow X_{\mathbb {C}_p, {\rm an}}$ be the natural projection. First, let us show that
$\lambda :X_{\mathbb {C}_p, {\rm prok\acute {e}t}}\rightarrow X_{\mathbb {C}_p, {\rm an}}$ be the natural projection. First, let us show that
 \begin{equation} \begin{aligned}
R\lambda_{*} (\omega_E^{\chi}\widehat{\otimes
}\widehat{\mathscr{O}}_X) &= \omega_E^{\chi}[0] \oplus
\omega_E^{\chi+\alpha}\otimes \mathbb{C}_p(-1)[-1],\\
R\lambda_{*} (\omega_E^{\chi}\widehat{\otimes
}\widehat{\mathscr{I}} ) &= \omega_E^{\chi}(-D)[0] \oplus
\omega_E^{\chi+\alpha}(-D)\otimes\mathbb{C}_p (-1)[-1].
\end{aligned} \end{equation}
\begin{equation} \begin{aligned}
R\lambda_{*} (\omega_E^{\chi}\widehat{\otimes
}\widehat{\mathscr{O}}_X) &= \omega_E^{\chi}[0] \oplus
\omega_E^{\chi+\alpha}\otimes \mathbb{C}_p(-1)[-1],\\
R\lambda_{*} (\omega_E^{\chi}\widehat{\otimes
}\widehat{\mathscr{I}} ) &= \omega_E^{\chi}(-D)[0] \oplus
\omega_E^{\chi+\alpha}(-D)\otimes\mathbb{C}_p (-1)[-1].
\end{aligned} \end{equation}
By Remark 3.2.10, the sheaf ![]() $\omega _E^{\chi,+}$ is an orthonormalizable
$\omega _E^{\chi,+}$ is an orthonormalizable ![]() $\mathscr {O}^+_{X,{\rm \acute {e}t}}\widehat {\otimes }R^+$ sheaf locally for the étale topology of
$\mathscr {O}^+_{X,{\rm \acute {e}t}}\widehat {\otimes }R^+$ sheaf locally for the étale topology of ![]() $X$. Let
$X$. Let ![]() $\nu : X_{\mathbb {C}_p,{\rm prok\acute {e}t}}\rightarrow X_{\mathbb {C}_p,{\rm k\acute {e}t}}$ be the natural projection of sites. Then, locally étale, we can write
$\nu : X_{\mathbb {C}_p,{\rm prok\acute {e}t}}\rightarrow X_{\mathbb {C}_p,{\rm k\acute {e}t}}$ be the natural projection of sites. Then, locally étale, we can write ![]() $\omega _E^{\chi,+}\widehat {\otimes }\widehat {\mathscr {O}}_X= \widehat {\bigoplus }_i \widehat {\mathscr {O}}^+_X \widehat {\otimes } R^+ e_i$. We get that
$\omega _E^{\chi,+}\widehat {\otimes }\widehat {\mathscr {O}}_X= \widehat {\bigoplus }_i \widehat {\mathscr {O}}^+_X \widehat {\otimes } R^+ e_i$. We get that
 \begin{align*} R\nu_{ *} (\omega_E^{\chi}\widehat{\otimes}\widehat{\mathscr{O}}_X) & = R\nu_{*} (\omega_E^{\chi,+} \widehat{\otimes}\widehat{\mathscr{O}}_X^+) \biggl[\frac{1}{p}\biggr]\\ & = R \varprojlim_s R\nu_{*} ( \bigoplus_i (\mathscr{O}^+_X/p^s\otimes R^+) e_i) \biggl[\frac{1}{p}\biggr]\\ & = R\varprojlim_s \bigoplus_i( R\nu_{*} \widehat{\mathscr{O}}_X^+/p^s\otimes R^+)e_i \biggl[\frac{1}{p}\biggr]\\ & = \omega_E^{\chi} \widehat{\otimes}_{R\widehat{\otimes} \widehat{\mathscr{O}}_X} R \nu_{*} (\widehat{\mathscr{O}}_X\widehat{\otimes}R). \end{align*}
\begin{align*} R\nu_{ *} (\omega_E^{\chi}\widehat{\otimes}\widehat{\mathscr{O}}_X) & = R\nu_{*} (\omega_E^{\chi,+} \widehat{\otimes}\widehat{\mathscr{O}}_X^+) \biggl[\frac{1}{p}\biggr]\\ & = R \varprojlim_s R\nu_{*} ( \bigoplus_i (\mathscr{O}^+_X/p^s\otimes R^+) e_i) \biggl[\frac{1}{p}\biggr]\\ & = R\varprojlim_s \bigoplus_i( R\nu_{*} \widehat{\mathscr{O}}_X^+/p^s\otimes R^+)e_i \biggl[\frac{1}{p}\biggr]\\ & = \omega_E^{\chi} \widehat{\otimes}_{R\widehat{\otimes} \widehat{\mathscr{O}}_X} R \nu_{*} (\widehat{\mathscr{O}}_X\widehat{\otimes}R). \end{align*}
Since ![]() $R$ is a
$R$ is a ![]() $\mathbb {Q}_p$-Banach space, it has a orthonormalizable basis over
$\mathbb {Q}_p$-Banach space, it has a orthonormalizable basis over ![]() $\mathbb {Q}_p$, and the same reasoning as before shows that
$\mathbb {Q}_p$, and the same reasoning as before shows that ![]() $\omega _E^{\chi } \widehat {\otimes }_{R\widehat {\otimes } \widehat {\mathscr {O}}_X} R \nu _{*} (\widehat {\mathscr {O}}_X\widehat {\otimes }R)= \omega _E^\chi \widehat {\otimes }_{\widehat {\mathscr {O}}_X} R\nu _* \widehat {\mathscr {O}}_X$. On the other hand, by Theorem 4.1.4 we know that
$\omega _E^{\chi } \widehat {\otimes }_{R\widehat {\otimes } \widehat {\mathscr {O}}_X} R \nu _{*} (\widehat {\mathscr {O}}_X\widehat {\otimes }R)= \omega _E^\chi \widehat {\otimes }_{\widehat {\mathscr {O}}_X} R\nu _* \widehat {\mathscr {O}}_X$. On the other hand, by Theorem 4.1.4 we know that ![]() $R \nu _* \widehat {\mathscr {O}}_X= \mathscr {O}_{X,{\rm k\acute {e}t}}[0] \oplus \omega _E^{\alpha }(-1)[-1]$. Lemma 5.5 of [Reference ScholzeSch13] and Lemma 6.17 of [Reference Diao, Lan, Liu and ZhuDLLZ23b] imply that the integral structure obtained by
$R \nu _* \widehat {\mathscr {O}}_X= \mathscr {O}_{X,{\rm k\acute {e}t}}[0] \oplus \omega _E^{\alpha }(-1)[-1]$. Lemma 5.5 of [Reference ScholzeSch13] and Lemma 6.17 of [Reference Diao, Lan, Liu and ZhuDLLZ23b] imply that the integral structure obtained by ![]() $R\nu _{*}(\widehat {\mathscr {O}}^+_X)$ defines the same topology as that given by
$R\nu _{*}(\widehat {\mathscr {O}}^+_X)$ defines the same topology as that given by ![]() $\mathscr {O}^+_{X,{\rm k\acute {e}t}}[0]\oplus \omega _E^{\alpha,+}(-1)[-1]$ (in fact, the lemmas cited show that both complexes differ just by bounded torsion when evaluated at affinoids). Therefore,
$\mathscr {O}^+_{X,{\rm k\acute {e}t}}[0]\oplus \omega _E^{\alpha,+}(-1)[-1]$ (in fact, the lemmas cited show that both complexes differ just by bounded torsion when evaluated at affinoids). Therefore,
over the Kummer-étale site of ![]() $X_{w}(\epsilon )$. Finally, let
$X_{w}(\epsilon )$. Finally, let ![]() $\mu :X_{\mathbb {C}_p,{\rm k\acute {e}t}}\rightarrow X_{\mathbb {C}_p,{\rm an}}$ be the projection map. In order to descend to the analytic site we recall that
$\mu :X_{\mathbb {C}_p,{\rm k\acute {e}t}}\rightarrow X_{\mathbb {C}_p,{\rm an}}$ be the projection map. In order to descend to the analytic site we recall that ![]() $\omega _E^{\chi }$ is a projective Banach sheaf over
$\omega _E^{\chi }$ is a projective Banach sheaf over ![]() $X_{w}(\epsilon )$ (cf. [Reference Boxer and PilloniBP22, § 5.5.2]). Thus, it is a direct summand of an orthonormalizable Banach sheaf
$X_{w}(\epsilon )$ (cf. [Reference Boxer and PilloniBP22, § 5.5.2]). Thus, it is a direct summand of an orthonormalizable Banach sheaf ![]() $\widehat {\bigoplus }_i \mathscr {O}_X$ over
$\widehat {\bigoplus }_i \mathscr {O}_X$ over ![]() $X_{w}(\epsilon )$. But we know that the Kummer-étale cohomology of
$X_{w}(\epsilon )$. But we know that the Kummer-étale cohomology of ![]() $\mathscr {O}^+_{X}$ in affinoids admitting a Kummer-étale map to a torus
$\mathscr {O}^+_{X}$ in affinoids admitting a Kummer-étale map to a torus ![]() $\mathbb {T}= \operatorname {Spa}(\mathbb {Q}_p\langle T^{\pm 1} \rangle, \mathbb {Z}_p\langle T^{\pm 1}\rangle )$ or a disc
$\mathbb {T}= \operatorname {Spa}(\mathbb {Q}_p\langle T^{\pm 1} \rangle, \mathbb {Z}_p\langle T^{\pm 1}\rangle )$ or a disc ![]() $\mathbb {D}=\operatorname {Spa}(\mathbb {Q}_p\langle U\rangle, \mathbb {Z}_p\langle U \rangle )$ has bounded torsion (by computing the cohomology via the pullback of the perfectoid torus or disc, and using Lemma 5.5 of [Reference ScholzeSch13] or Lemma 6.1.7 of [Reference Diao, Lan, Liu and ZhuDLLZ23b] again). An argument similar to that before using derived limits shows that
$\mathbb {D}=\operatorname {Spa}(\mathbb {Q}_p\langle U\rangle, \mathbb {Z}_p\langle U \rangle )$ has bounded torsion (by computing the cohomology via the pullback of the perfectoid torus or disc, and using Lemma 5.5 of [Reference ScholzeSch13] or Lemma 6.1.7 of [Reference Diao, Lan, Liu and ZhuDLLZ23b] again). An argument similar to that before using derived limits shows that ![]() $R\mu _{*} (\widehat {\bigoplus }_i \mathscr {O}_{X,{\rm k\acute {e}t}}) =\widehat {\bigoplus }_i \mathscr {O}_{X,{\rm an}}$, whence
$R\mu _{*} (\widehat {\bigoplus }_i \mathscr {O}_{X,{\rm k\acute {e}t}}) =\widehat {\bigoplus }_i \mathscr {O}_{X,{\rm an}}$, whence ![]() $R\mu _{*} \omega _E^{\chi }= \omega _E^{\chi }$. Finally, to prove the second equality of (29), it is enough to show the analogous property for
$R\mu _{*} \omega _E^{\chi }= \omega _E^{\chi }$. Finally, to prove the second equality of (29), it is enough to show the analogous property for ![]() $\omega ^{\chi }_E\widehat {\otimes }\iota _* \widehat {\mathscr {O}}_D$, which follows from the previous argument applied to the log adic space defined by the cusps (notice that even if
$\omega ^{\chi }_E\widehat {\otimes }\iota _* \widehat {\mathscr {O}}_D$, which follows from the previous argument applied to the log adic space defined by the cusps (notice that even if ![]() $D$ is a disjoint union of points, the log structure is not trivial!).
$D$ is a disjoint union of points, the log structure is not trivial!).
Next, we construct the overconvergent Eichler–Shimura maps; we only explain the procedure for the sheaf ![]() $A_{\chi,{\rm \acute {e}t}}^{\delta }$ and the pro-Kummer-étale cohomology; the case of
$A_{\chi,{\rm \acute {e}t}}^{\delta }$ and the pro-Kummer-étale cohomology; the case of ![]() $D_{\chi,{\rm \acute {e}t}}^{\delta }$ or the cohomology with compact support follows the same steps. Consider the overconvergent Hodge–Tate maps of Definition 3.4.1,
$D_{\chi,{\rm \acute {e}t}}^{\delta }$ or the cohomology with compact support follows the same steps. Consider the overconvergent Hodge–Tate maps of Definition 3.4.1,
 \begin{gather*} \operatorname{HT}^{A,\vee}_{-w_0(\chi)}: \omega_E^{w_0(\chi)}\widehat{\otimes } \widehat{\mathscr{O}}_X(\chi_1) \rightarrow A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X \text{ over } X_{1}(\epsilon ),\\ \operatorname{HT}^{A}_{\chi}: A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X \rightarrow \omega_E^{\chi}\widehat{\otimes} \widehat{\mathscr{O}}_X(\chi_2) \text{ over } X_{w_0}(\epsilon). \end{gather*}
\begin{gather*} \operatorname{HT}^{A,\vee}_{-w_0(\chi)}: \omega_E^{w_0(\chi)}\widehat{\otimes } \widehat{\mathscr{O}}_X(\chi_1) \rightarrow A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X \text{ over } X_{1}(\epsilon ),\\ \operatorname{HT}^{A}_{\chi}: A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X \rightarrow \omega_E^{\chi}\widehat{\otimes} \widehat{\mathscr{O}}_X(\chi_2) \text{ over } X_{w_0}(\epsilon). \end{gather*}
Taking the projection from the pro-Kummer-étale site to the analytic site, one gets maps
 \begin{gather*} \omega_E^{w_0(\chi)}\widehat{\otimes } R\lambda_{*} \widehat{\mathscr{O}}_X(\chi_1) \rightarrow R\lambda_{*}(A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes} \widehat{\mathscr{O}}_X) \text{ over } X_{1}(\epsilon ),\\ R\lambda_{*}(A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes} \widehat{\mathscr{O}}_X) \rightarrow \omega_E^{\chi} \widehat{\otimes} R \lambda_{*}\widehat{\mathscr{O}}_X(\chi_2) \text{ over } X_{w_0}(\epsilon). \end{gather*}
\begin{gather*} \omega_E^{w_0(\chi)}\widehat{\otimes } R\lambda_{*} \widehat{\mathscr{O}}_X(\chi_1) \rightarrow R\lambda_{*}(A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes} \widehat{\mathscr{O}}_X) \text{ over } X_{1}(\epsilon ),\\ R\lambda_{*}(A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes} \widehat{\mathscr{O}}_X) \rightarrow \omega_E^{\chi} \widehat{\otimes} R \lambda_{*}\widehat{\mathscr{O}}_X(\chi_2) \text{ over } X_{w_0}(\epsilon). \end{gather*}
Taking the overconvergent cohomologies of Definition 3.2.12 and using (29), we obtain maps
 \begin{align} \begin{gathered} R\Gamma_{1,c}(X_{\mathbb{C}_p}, \omega_E^{w_0(\chi)})_{\epsilon}(\chi_1) \rightarrow R\Gamma_{1,c}(X_{\mathbb{C}_p}, R\lambda_{*}(A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes} \widehat{\mathscr{O}}_X))_{\epsilon},\\ R\Gamma_{w_0}(X_{\mathbb{C}_p}, R\lambda_{*}(A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X))_{\epsilon} \rightarrow R\Gamma_{w_0}(X_{\mathbb{C}_p}, \omega_E^{\chi+\alpha}))_{\epsilon}(\chi_2-1)[-1]. \end{gathered} \end{align}
\begin{align} \begin{gathered} R\Gamma_{1,c}(X_{\mathbb{C}_p}, \omega_E^{w_0(\chi)})_{\epsilon}(\chi_1) \rightarrow R\Gamma_{1,c}(X_{\mathbb{C}_p}, R\lambda_{*}(A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes} \widehat{\mathscr{O}}_X))_{\epsilon},\\ R\Gamma_{w_0}(X_{\mathbb{C}_p}, R\lambda_{*}(A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}\widehat{\mathscr{O}}_X))_{\epsilon} \rightarrow R\Gamma_{w_0}(X_{\mathbb{C}_p}, \omega_E^{\chi+\alpha}))_{\epsilon}(\chi_2-1)[-1]. \end{gathered} \end{align}On the other hand, we have restriction and corestriction maps
Taking ![]() $H^1$-cohomology in (30), and composing with the morphisms of (31), one obtains the maps in (28). The Galois equivariance is clear as the Hodge–Tate maps are defined over
$H^1$-cohomology in (30), and composing with the morphisms of (31), one obtains the maps in (28). The Galois equivariance is clear as the Hodge–Tate maps are defined over ![]() $X_{w}(\epsilon )\subset X$. The compatibility with respect to the good normalization of the
$X_{w}(\epsilon )\subset X$. The compatibility with respect to the good normalization of the ![]() $U_p$-operators follows from Lemma 3.4.2 and the fact that
$U_p$-operators follows from Lemma 3.4.2 and the fact that ![]() $U_{p,\alpha }^{\mathrm {good}}= U_{p,\alpha }$ for the correspondence associated to
$U_{p,\alpha }^{\mathrm {good}}= U_{p,\alpha }$ for the correspondence associated to ![]() $\omega ^{\alpha }_E$ (see Definition 3.2.16).
$\omega ^{\alpha }_E$ (see Definition 3.2.16).
Theorem 4.2.2 Let ![]() $\epsilon \geq \delta \geq n$,
$\epsilon \geq \delta \geq n$, ![]() $(R,R^+)$ be a uniform affinoid Tate
$(R,R^+)$ be a uniform affinoid Tate ![]() $\mathbb {Q}_p$-algebra and
$\mathbb {Q}_p$-algebra and ![]() $\chi : T=\mathbf {T}(\mathbb {Z}_p)\rightarrow R^{+,\times }$ be a
$\chi : T=\mathbf {T}(\mathbb {Z}_p)\rightarrow R^{+,\times }$ be a ![]() $\delta$-analytic character. The following assertions hold.
$\delta$-analytic character. The following assertions hold.
(i) The composition of the Eichler–Shimura maps
 $ES_{A}\circ ES^{\vee }_{A}$ is zero. Consider the following sequence:
(32)
$ES_{A}\circ ES^{\vee }_{A}$ is zero. Consider the following sequence:
(32) \begin{align} & 0\rightarrow
H^1_{1,c}(X_{\mathbb{C}_p},
\omega_E^{w_0(\chi)})_{\epsilon}(\chi_1)
\xrightarrow{ES_{A}^{\vee}}
H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p},
A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}
\widehat{\mathscr{O}}_X)\nonumber\\ & \qquad
\xrightarrow{ES_{A}} H^0_{w_0}(X_{\mathbb{C}_p},
\omega_E^{\chi+\alpha})_{\epsilon}(\chi_2-1)\rightarrow 0.
\end{align}
\begin{align} & 0\rightarrow
H^1_{1,c}(X_{\mathbb{C}_p},
\omega_E^{w_0(\chi)})_{\epsilon}(\chi_1)
\xrightarrow{ES_{A}^{\vee}}
H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p},
A^{\delta}_{\chi,\rm \acute{e}t}\widehat{\otimes}
\widehat{\mathscr{O}}_X)\nonumber\\ & \qquad
\xrightarrow{ES_{A}} H^0_{w_0}(X_{\mathbb{C}_p},
\omega_E^{\chi+\alpha})_{\epsilon}(\chi_2-1)\rightarrow 0.
\end{align}
(ii) Assume that
 $\mathcal {V}=\operatorname {Spa}(R,R^+)$ is an affinoid subspace of the weight space
$\mathcal {V}=\operatorname {Spa}(R,R^+)$ is an affinoid subspace of the weight space  $\mathcal {W}_T$ of
$\mathcal {W}_T$ of  $T$, and let
$T$, and let  $\kappa =(k_1,k_2)\in \mathcal {V}$ be a dominant weight of
$\kappa =(k_1,k_2)\in \mathcal {V}$ be a dominant weight of  $\mathbf {T}$. Let
$\mathbf {T}$. Let  $\alpha =(1,-1)\in X^*(\mathbf {T})$ and let
$\alpha =(1,-1)\in X^*(\mathbf {T})$ and let  $\chi =\chi ^{{\rm un}}_{\mathcal {V}}$ be the universal character of
$\chi =\chi ^{{\rm un}}_{\mathcal {V}}$ be the universal character of  $\mathcal {V}$. The following diagram commutes.
$\mathcal {V}$. The following diagram commutes.

(iii) The maps of (ii) are Galois and
 $U_p^t$-equivariant with respect to the good normalizations of the Hecke operator (Definition 3.2.16). In particular, the diagram above restricts to the finite slope part with respect to the action of
$U_p^t$-equivariant with respect to the good normalizations of the Hecke operator (Definition 3.2.16). In particular, the diagram above restricts to the finite slope part with respect to the action of  $U_p^t$.
$U_p^t$.(iv) Let
 $h< k_1-k_2+1$. There exists an open affinoid
$h< k_1-k_2+1$. There exists an open affinoid  $\mathcal {V}'\subset \mathcal {V}$ containing
$\mathcal {V}'\subset \mathcal {V}$ containing  $\kappa$ such that the
$\kappa$ such that the  $(\leq h)$-slope part of the restriction of (32) to
$(\leq h)$-slope part of the restriction of (32) to  $\mathcal {V}'$ is a short exact sequence of finite free
$\mathcal {V}'$ is a short exact sequence of finite free  $\mathbb {C}_p\widehat {\otimes }_{\mathbb {Q}_p} \mathscr {O}(\mathcal {V}')$-modules.
$\mathbb {C}_p\widehat {\otimes }_{\mathbb {Q}_p} \mathscr {O}(\mathcal {V}')$-modules.(v) Retain the hypothesis of (iv), and let
 $\chi$ be the universal character of
$\chi$ be the universal character of  $\mathcal {V}'$. Let
$\mathcal {V}'$. Let  $\widetilde {\chi }= \chi _1-\chi _2+1 : \mathbb {Z}_p^\times \rightarrow R^{+,\times }$ and
$\widetilde {\chi }= \chi _1-\chi _2+1 : \mathbb {Z}_p^\times \rightarrow R^{+,\times }$ and  $b= {d}/{dt}|_{t=1} \widetilde {\chi }(t)$. Then we have a Galois equivariant split after inverting
$b= {d}/{dt}|_{t=1} \widetilde {\chi }(t)$. Then we have a Galois equivariant split after inverting  $b$:
Analogous statements hold for the cohomology with compact support and for the sheaf
$b$:
Analogous statements hold for the cohomology with compact support and for the sheaf \[ H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, \mathcal{A}^{\delta}_{\chi}\widehat{\otimes}\widehat{\mathscr{O}}_X)^{\leq h}_{b} =[H^1_{1,c}(X_{\mathbb{C}_p}, \omega_E^{w_0(\chi)})^{\leq h}_{\epsilon}(\chi_1)]_b \oplus [H^0_{w_0}(X_{\mathbb{C}_p}, \omega_E^{\chi+\alpha})^{\leq h}_{\epsilon}(\chi_2-1)]_b. \]
\[ H^1_{\rm prok\acute{e}t}(X_{\mathbb{C}_p}, \mathcal{A}^{\delta}_{\chi}\widehat{\otimes}\widehat{\mathscr{O}}_X)^{\leq h}_{b} =[H^1_{1,c}(X_{\mathbb{C}_p}, \omega_E^{w_0(\chi)})^{\leq h}_{\epsilon}(\chi_1)]_b \oplus [H^0_{w_0}(X_{\mathbb{C}_p}, \omega_E^{\chi+\alpha})^{\leq h}_{\epsilon}(\chi_2-1)]_b. \]
 $D_{\chi,{\rm \acute {e}t}}^{\delta }$.
$D_{\chi,{\rm \acute {e}t}}^{\delta }$.
Proof. Part (i) follows from the fact that the composition of the restriction and corestriction maps (31) is zero.
Parts (ii) and (iii) follow from Lemma 4.2.1, and the compatibility of the formation of ![]() $A^{\delta }_{\chi,{\rm \acute {e}t}}$ and
$A^{\delta }_{\chi,{\rm \acute {e}t}}$ and ![]() $\omega _{E}^{\chi }$ with the character
$\omega _{E}^{\chi }$ with the character ![]() $\chi$. The commutation of the lower diagram is a direct consequence of the constructions and Corollary 2.4.5.
$\chi$. The commutation of the lower diagram is a direct consequence of the constructions and Corollary 2.4.5.
For part (iv) we follow the same arguments as [Reference Andreatta, Iovita and StevensAIS15]. The finite-slope theory (cf. [Reference UrbanUrb11, Reference BuzzardBuz07]) implies that there is an affinoid open subspace ![]() $\mathcal {V}'\subset \mathcal {V}$ containing
$\mathcal {V}'\subset \mathcal {V}$ containing ![]() $\kappa$ such that the
$\kappa$ such that the ![]() $(\leq h)$-part of the sequence (32) restricted to
$(\leq h)$-part of the sequence (32) restricted to ![]() $\mathcal {V}'$ is a sequence of finite free
$\mathcal {V}'$ is a sequence of finite free ![]() $\mathbb {C}_p \widehat {\otimes }_{\mathbb {Q}_p}\mathscr {O}(\mathcal {V}')$-modules. Moreover, by classicality (Theorems 3.2.17 and 3.3.7) and the classical Eichler–Shimura decomposition (Theorem 4.1.1), we can take
$\mathbb {C}_p \widehat {\otimes }_{\mathbb {Q}_p}\mathscr {O}(\mathcal {V}')$-modules. Moreover, by classicality (Theorems 3.2.17 and 3.3.7) and the classical Eichler–Shimura decomposition (Theorem 4.1.1), we can take ![]() $\mathcal {V}'$ such that the
$\mathcal {V}'$ such that the ![]() $(\leq h)$-slope of the sequence (32) is short and exact.
$(\leq h)$-slope of the sequence (32) is short and exact.
Finally, we briefly sketch the argument for part (v). Let ![]() $\mathcal {V}'$ be as in (iv), let
$\mathcal {V}'$ be as in (iv), let ![]() $R=\mathscr {O}(\mathcal {V}')$, and consider the short exact sequence of the
$R=\mathscr {O}(\mathcal {V}')$, and consider the short exact sequence of the ![]() $(\leq h)$-slope of (32). Taking basis of the finite free
$(\leq h)$-slope of (32). Taking basis of the finite free ![]() $\mathbb{C}_p \widehat{\otimes} R$-modules of (32) and tensoring with the Tate twist
$\mathbb{C}_p \widehat{\otimes} R$-modules of (32) and tensoring with the Tate twist ![]() $R(1-\chi _2)$, we are left to prove that the localization by
$R(1-\chi _2)$, we are left to prove that the localization by ![]() $b$ of
$b$ of ![]() $H^1(G_{\mathbb {Q}_p}, \mathbb {C}_p \widehat {\otimes } R(\chi _1-\chi _2+1))$ vanishes. By almost étale descent one has
$H^1(G_{\mathbb {Q}_p}, \mathbb {C}_p \widehat {\otimes } R(\chi _1-\chi _2+1))$ vanishes. By almost étale descent one has
We identify ![]() $\operatorname {Gal}(\mathbb {Q}_p^{{\rm cyc}}/\mathbb {Q}_p)$ with
$\operatorname {Gal}(\mathbb {Q}_p^{{\rm cyc}}/\mathbb {Q}_p)$ with ![]() $\mathbb {Z}_p^\times$ via
$\mathbb {Z}_p^\times$ via ![]() $\chi _{{\rm cyc}}$. By Sen theory, to show that (33) is of
$\chi _{{\rm cyc}}$. By Sen theory, to show that (33) is of ![]() $b$-torsion it is enough to prove that
$b$-torsion it is enough to prove that ![]() $H^1(\operatorname {Lie} \mathbb {Z}_p^\times, R(\chi _1-\chi _2+1))_b=0$, but this is clear as
$H^1(\operatorname {Lie} \mathbb {Z}_p^\times, R(\chi _1-\chi _2+1))_b=0$, but this is clear as ![]() $H^1(\operatorname {Lie} \mathbb {Z}_p^\times, R(\chi _1-\chi _2+1))\cong R/ b R$.
$H^1(\operatorname {Lie} \mathbb {Z}_p^\times, R(\chi _1-\chi _2+1))\cong R/ b R$.
4.2.1 Previous works in the literature
Here we briefly discuss some previous works and their connection with Theorem 4.2.2. Our main result is the complement of the work of Andreatta, Iovita and Stevens; they constructed the map ![]() $ES_{D}$ from
$ES_{D}$ from ![]() $H^1_{{\rm pro\acute {e}t}}(Y_{\mathbb {C}_p}, D^{\delta }_{\chi,{\rm \acute {e}t}})\widehat {\otimes }\mathbb {C}_p$ to the space of overconvergent modular forms of weight
$H^1_{{\rm pro\acute {e}t}}(Y_{\mathbb {C}_p}, D^{\delta }_{\chi,{\rm \acute {e}t}})\widehat {\otimes }\mathbb {C}_p$ to the space of overconvergent modular forms of weight ![]() $-w_0(\chi )$ (cf. [Reference Andreatta, Iovita and StevensAIS15, Theorem 6.1]). Our theorem constructs a new map from the overconvergent
$-w_0(\chi )$ (cf. [Reference Andreatta, Iovita and StevensAIS15, Theorem 6.1]). Our theorem constructs a new map from the overconvergent ![]() $H^1$-cohomology with supports of higher Coleman theory [Reference Boxer and PilloniBP22], to the space of modular symbols defined by the distributions. In addition, we have discussed the dual picture with the principal series, and with the proétale cohomology with compact support instead.
$H^1$-cohomology with supports of higher Coleman theory [Reference Boxer and PilloniBP22], to the space of modular symbols defined by the distributions. In addition, we have discussed the dual picture with the principal series, and with the proétale cohomology with compact support instead.
On the other hand, the first work on the subject which uses the perfectoid modular curve to construct the ![]() $ES_{D}$ map goes back to Chojecki, Hansen and Johansson. Additionally, they constructed the map for Shimura curves, and they translated a theorem analogous to Theorem 4.2.2 in terms of the eigencurve (see [Reference Chojecki, Hansen and JohanssonCHJ17, Theorem 5.14]).
$ES_{D}$ map goes back to Chojecki, Hansen and Johansson. Additionally, they constructed the map for Shimura curves, and they translated a theorem analogous to Theorem 4.2.2 in terms of the eigencurve (see [Reference Chojecki, Hansen and JohanssonCHJ17, Theorem 5.14]).
The work of Sean Howe [Reference HoweHow21] studies natural pairings between some local cohomologies attached to the flag variety ![]() $\operatorname {\mathscr {F}\!\ell }= \mathbb {P}^1_{\mathbb {Q}_p}$ and overconvergent modular forms; these take values in the locally analytic vectors of the completed cohomology of the modular curve. The local cohomologies are the cohomology with supports
$\operatorname {\mathscr {F}\!\ell }= \mathbb {P}^1_{\mathbb {Q}_p}$ and overconvergent modular forms; these take values in the locally analytic vectors of the completed cohomology of the modular curve. The local cohomologies are the cohomology with supports ![]() $\varprojlim _{\epsilon } H^1_{\overline {U_w(\epsilon )}}(\mathbb {P}^1_{\mathbb {Q}_p}, \mathscr {L}(\chi ))$ or the overconvergent cohomology
$\varprojlim _{\epsilon } H^1_{\overline {U_w(\epsilon )}}(\mathbb {P}^1_{\mathbb {Q}_p}, \mathscr {L}(\chi ))$ or the overconvergent cohomology ![]() $\varinjlim _{\epsilon } H^1(U_w(\epsilon ), \mathscr {L}(\chi ))$ (see [Reference HoweHow21, Lemma 4.3.1 and Remark 1.2.12]; in the notation of [Reference HoweHow21] one has
$\varinjlim _{\epsilon } H^1(U_w(\epsilon ), \mathscr {L}(\chi ))$ (see [Reference HoweHow21, Lemma 4.3.1 and Remark 1.2.12]; in the notation of [Reference HoweHow21] one has ![]() $0=[0:1]$, which is represented by
$0=[0:1]$, which is represented by ![]() $1\in \operatorname {GL}_2$). It is expected that these pairings provide a more geometric interpretation of the
$1\in \operatorname {GL}_2$). It is expected that these pairings provide a more geometric interpretation of the ![]() $ES_{A}^{\vee }$ map of Theorem 4.2.2, namely, they are closely related to the description the of completed cohomology of Lue Pan that we briefly explain next.
$ES_{A}^{\vee }$ map of Theorem 4.2.2, namely, they are closely related to the description the of completed cohomology of Lue Pan that we briefly explain next.
In his recent work [Reference PanPan22], Lue Pan gives an exhausting description of the ![]() $\chi$-isotypic part of the locally analytic vectors of the completed cohomology for the action of the Borel algebra
$\chi$-isotypic part of the locally analytic vectors of the completed cohomology for the action of the Borel algebra ![]() $\mathrm {Lie} \mathbf {B}$ (see [Reference PanPan22, Theorem 1.0.1]). His method uses a new tool in
$\mathrm {Lie} \mathbf {B}$ (see [Reference PanPan22, Theorem 1.0.1]). His method uses a new tool in ![]() $p$-adic Hodge theory which is the geometric Sen operator; then, using the dictionary between representation theory over
$p$-adic Hodge theory which is the geometric Sen operator; then, using the dictionary between representation theory over ![]() $\operatorname {\mathscr {F}\!\ell }$ and proétale sheaves over the modular curve provided by
$\operatorname {\mathscr {F}\!\ell }$ and proétale sheaves over the modular curve provided by ![]() $\pi _{\operatorname {HT}}$, he shows that the completed cohomology can be decomposed in terms of overconvergent modular forms. The intersection between locally analytic vectors of completed cohomology and Theorem 4.2.2 lies in the fact that the cohomology group
$\pi _{\operatorname {HT}}$, he shows that the completed cohomology can be decomposed in terms of overconvergent modular forms. The intersection between locally analytic vectors of completed cohomology and Theorem 4.2.2 lies in the fact that the cohomology group ![]() $H^1_{{\rm pro\acute {e}t}}(Y_{\mathbb {C}_p}, A^{\delta }_{\chi,{\rm \acute {e}t}})$ is a subspace of the locally analytic completed cohomology, consisting on those
$H^1_{{\rm pro\acute {e}t}}(Y_{\mathbb {C}_p}, A^{\delta }_{\chi,{\rm \acute {e}t}})$ is a subspace of the locally analytic completed cohomology, consisting on those ![]() $\delta$-analytic cohomology classes admitting an action of
$\delta$-analytic cohomology classes admitting an action of ![]() $\operatorname {Iw}_n$, such that
$\operatorname {Iw}_n$, such that ![]() $\mathbf {B}(\mathbb {Z}_p)\cap \operatorname {Iw}_n$ acts via
$\mathbf {B}(\mathbb {Z}_p)\cap \operatorname {Iw}_n$ acts via ![]() $-\chi$. Finally, the maps
$-\chi$. Finally, the maps ![]() $ES_A^{\vee }$ and
$ES_A^{\vee }$ and ![]() $ES_{A}$ are instances of the spaces
$ES_{A}$ are instances of the spaces ![]() $M_{\mu,1}$ and
$M_{\mu,1}$ and ![]() $M_{\mu,w}$ appearing in [Reference PanPan22, Theorem 5.4.2].
$M_{\mu,w}$ appearing in [Reference PanPan22, Theorem 5.4.2].
4.2.2 The pairings
We end this section with the compatibility of the overconvergent Eichler–Shimura maps and Poincaré and Serre duality. Let ![]() $\epsilon \geq \delta \geq n$, and let
$\epsilon \geq \delta \geq n$, and let ![]() $(R,R^+)$ and
$(R,R^+)$ and ![]() $\chi$ be as in previous sections. By definition there is a natural pairing between the
$\chi$ be as in previous sections. By definition there is a natural pairing between the ![]() $\delta$-principal series and distributions
$\delta$-principal series and distributions
It is easy to see that it induces a Poincaré pairing
where the first arrow is a Yoneda pairing, and the last arrow is induced by the Poincaré trace ![]() $H^1_{{\rm pro\acute {e}t},c}(Y_{\mathbb {C}_p}, \mathbb {Z}_p(1))\xrightarrow {\operatorname {Tr}_P} \mathbb {Z}_p$.
$H^1_{{\rm pro\acute {e}t},c}(Y_{\mathbb {C}_p}, \mathbb {Z}_p(1))\xrightarrow {\operatorname {Tr}_P} \mathbb {Z}_p$.
On the other hand, in [Reference Boxer and PilloniBP22] the authors have defined overconvergent Serre pairings in families
compatible with the classical Serre pairings. The pairings are constructed by taking the Yoneda's product
and composing with the Serre trace map of ![]() $X$,
$X$,
Theorem 4.2.3 Retain the notation of Theorem 4.2.2. The following assertions hold.
(i) The Poincaré and Serre pairings of overconvergent cohomologies are compatible with the good normalizations of the
 $U_p$-operators (Definition 3.2.16). Moreover, they are compatible with the classical Eichler–Shimura maps of Theorem 4.1.1.
$U_p$-operators (Definition 3.2.16). Moreover, they are compatible with the classical Eichler–Shimura maps of Theorem 4.1.1.(ii) Let
 $\mathcal {W}_T$ be the weight space of
$\mathcal {W}_T$ be the weight space of  $T= \mathbf {T}(\mathbb {Z}_p)$, let
$T= \mathbf {T}(\mathbb {Z}_p)$, let  $\mathcal {V}\subset \mathcal {W}_T$ be an open affinoid, and let
$\mathcal {V}\subset \mathcal {W}_T$ be an open affinoid, and let  $\chi =\chi ^{{\rm un}}_{\mathcal {V}}$ be the universal character of
$\chi =\chi ^{{\rm un}}_{\mathcal {V}}$ be the universal character of  $\mathcal {V}$. Let
$\mathcal {V}$. Let  $\kappa =(k_1,k_2)\in \mathcal {V}$ be a classical weight and fix
$\kappa =(k_1,k_2)\in \mathcal {V}$ be a classical weight and fix  $h< k_1-k_2+1$. There exists an open affinoid
$h< k_1-k_2+1$. There exists an open affinoid  $\mathcal {V}'\subset \mathcal {V}$ containing
$\mathcal {V}'\subset \mathcal {V}$ containing  $\kappa$ such that we have perfect pairings of finite free
$\kappa$ such that we have perfect pairings of finite free  $\mathbb {C}_p\widehat {\otimes } \mathscr {O}(\mathcal {V}')$-modules
and
$\mathbb {C}_p\widehat {\otimes } \mathscr {O}(\mathcal {V}')$-modules
and \[ \langle -,- \rangle_P: H^1_{\rm pro\acute{e}t,c}(Y_{\mathbb{C}_p}, D^{\delta}_{\chi,\rm \acute{e}t}(1))^{\leq h}\times H^1_{\rm pro\acute{e}t}(Y_{\mathbb{C}_p}, A^{\delta}_{\chi,\rm \acute{e}t} )^{\leq h} \rightarrow \mathscr{O}(\mathcal{V}') \]
compatible with the overconvergent Eichler–Shimura maps.
\[ \langle -,- \rangle_P: H^1_{\rm pro\acute{e}t,c}(Y_{\mathbb{C}_p}, D^{\delta}_{\chi,\rm \acute{e}t}(1))^{\leq h}\times H^1_{\rm pro\acute{e}t}(Y_{\mathbb{C}_p}, A^{\delta}_{\chi,\rm \acute{e}t} )^{\leq h} \rightarrow \mathscr{O}(\mathcal{V}') \]
compatible with the overconvergent Eichler–Shimura maps. \begin{gather*} \langle -, -\rangle_S: H^1_{w,c}(X_{\mathbb{C}_p}, \omega_E^{-\chi}(-D))^{\leq h}_{\epsilon}\times H^{0}_{w}(X_{\mathbb{C}_p},\omega_E^{\chi+\alpha})^{\leq h}_{\epsilon} \rightarrow \mathbb{C}_p\widehat{\otimes} \mathscr{O}(\mathcal{V}'),\\ \langle -, -\rangle_S: H^1_{w,c}(X_{\mathbb{C}_p}, \omega_E^{w_0(\chi)})^{\leq h}_{\epsilon}\times H^{0}_{w}(X_{\mathbb{C}_p},\omega_E^{-w_0(\chi)+\alpha}(-D))^{\leq h}_{\epsilon} \rightarrow \mathbb{C}_p\widehat{\otimes} \mathscr{O}(\mathcal{V}') , \end{gather*}
\begin{gather*} \langle -, -\rangle_S: H^1_{w,c}(X_{\mathbb{C}_p}, \omega_E^{-\chi}(-D))^{\leq h}_{\epsilon}\times H^{0}_{w}(X_{\mathbb{C}_p},\omega_E^{\chi+\alpha})^{\leq h}_{\epsilon} \rightarrow \mathbb{C}_p\widehat{\otimes} \mathscr{O}(\mathcal{V}'),\\ \langle -, -\rangle_S: H^1_{w,c}(X_{\mathbb{C}_p}, \omega_E^{w_0(\chi)})^{\leq h}_{\epsilon}\times H^{0}_{w}(X_{\mathbb{C}_p},\omega_E^{-w_0(\chi)+\alpha}(-D))^{\leq h}_{\epsilon} \rightarrow \mathbb{C}_p\widehat{\otimes} \mathscr{O}(\mathcal{V}') , \end{gather*}
Proof. The Hecke operators are compatible with the pairings by their definition via finite flat correspondences (see Definitions 3.2.15 and 3.3.6).
In the following we forget the Galois action. Let ![]() $\lambda : X_{\mathbb {C}_p, {\rm prok\acute {e}t}} \rightarrow X_{\mathbb {C}_p, {\rm an}}$ be the projection of sites. We have the following commutative diagram of Yoneda's products.
$\lambda : X_{\mathbb {C}_p, {\rm prok\acute {e}t}} \rightarrow X_{\mathbb {C}_p, {\rm an}}$ be the projection of sites. We have the following commutative diagram of Yoneda's products.

On the other hand, we also have compatible pairings provided by the Faltings extension (cf. [Reference ScholzeSch13, Corollary 6.14])

The compatibility of Poincaré and Serre traces [Reference Lan, Liu and ZhuLLZ23, Theorem 4.4.1(4)] implies part (i). Part (ii) follows along the same lines of the proof of Theorem 4.2.2 using the fact that the pairings are perfect for the classical Eichler–Shimura decomposition.
Acknowledgements
None of this work would have been possible without the support of my advisor V. Pilloni, and I want to express my deep gratitude for the many hours he dedicated to explaining to me the theory of overconvergent modular forms. I want to thank Professors A. Iovita and F. Andreatta for very fruitful exchanges during the spring of 2020, and the opportunity to give a talk on this subject in the workshop on higher Coleman theory in December of the same year. I want to thank G. Boxer, D. Junger, J. R. Jacinto and J.-F. Wu for corrections to and comments on an earlier version of this paper. Finally, I want to thank the anonymous referees for the many suggestions and corrections that improved the presentation of this paper. This work was written while the author was a PhD student at the ENS de Lyon.