1. Introduction
An important component of ice forecasting models is the ice interaction. This interaction is especially pronounced in regions with narrow land constrictions such as the Day of Bothnia and the Great Lakes of the United States of America. Ice forecast models for these regions have generally made use of linear vis-cous rheologies (Udin and Ullerstig 1977, Leppäranta 1981), with, in some cases, reduction of the wind-stress field in regions of ice convergence (Udin and Ullerstig 1977) in order to produce a more stationary ice-motion field. While these linear models have improved ice forecasts, there are a number of cases where, if it is taken into account, the non-linear nature of ice interaction can substantially modify ice dynamics and build-up simulations.
To determine the ramifications of assuming a nonlinear ice interaction in forecast models we have carried out a series of idealized simulations using the nonlinear viscous-plastic sea ice model developed by Reference HiblerHibler (1979), This model was initially developed for the simulation of the circulation and thickness of sea ice over a seasonal cycle. Using this model it was possible to reproduce many of the observed features of the circulation of and thickness build-up of the Arctic ice cover. In addition, recent studies have shown the use of the model for simulating large-scale fluctuations of Arctic and Antarctic sea ice (Hibler and Ackley 1982, Hibler and Walsh 1982). A key feature of this model is a nonlinear viscous plastic rheology. This rheology describes an ice interaction in which the ice resists compression and shearing in a manner independent of rate, while having effectively no resistance to dilation,
The purpose of this paper is to summarize a version of this model suitable for short-term (several days) mesoscale ice forecasts, and to examine aspects of this higher resolution model relevant to ice dynamics and build-up.
To investigate the behavior of this model several different approaches have been employed. To gain understanding and perspective on the nonlinear model behavior, a series of simulations employing idealized geometry and forcing are carried out. To aid in interpreting these idealized simulations, analytic solutions of certain idealized cases are also constructed. Finally, to establish the utility of the model for actual forecasts, simulations employing observed drift and forcing data have been carried out for the Bay of Bothnia. A detailed description of these studies is available in report form (Hibler and others in press). The present paper presents some of the more important idealized results from this study relevant to ice build-up.
2. Model Description
The model basically consists of a momentum balance coupled to equations describing the evolution of ice thickness. Since we are only concerned here with forecasts over a few days, we will consider only the evolution of the compactness and thickness of ice without thermodynamic growth and decay terms. For purposes of forecasting ice motion, the ice strength supplies a critical coupling between the momentum balance and the compactness. Basically, with the ice strength coupled to the fraction of open water, changes in ice compactness can induce significant changes in ice velocity over times as short as a few hours. In this paper, the nature of these variations in ice velocity due to changes in compactness are examined.
2(a). Momentum balance
The momentum balance includes inertial terms, Coriolis force, wind and water stresses and, most important for this paper, ice interaction. In Cartesian coordinates the momentum balance is
where D/Dt = ∂/∂t + u·Δ the substantial time derivative, is a unit vector normal to the surface, k is the ice velocity, f is the Coriolis parameter, m is the ice mass per unit area, Ta and Ty are forces due to air and water stresses, H is the dynamic height of the sea surface, g is the acceleration due to gravity, and I is the force due to variation in internal ice stress. The air and water stresses are determined by integral boundary layers (see e.g. Reference McPhee and PritchardMcPhee 1980), assuming constant turning angles:
and
where Ug is the geostrophic wind, Uw is the geo-strophic ocean current, ф and θ are air and water turning angles, Ca and Cw are air and water drag coefficients, and pa and p5 are air and water densities.
To simplify analysis in these idealized simu-lations, Uw and H have been set equal to zero and the term for momentum advection ignored, (It should be noted, however, that, depending on the location, these current terms may be important in ice-forecasting applications.) As a consequence the momentum balance employed here is
For modeling the ice interaction the ice is con-sidered to ;
obey a nonlinear viscous constitutive law given by
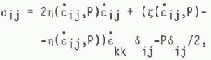
where oij is the two-dimensional stress tensor, ε ij the straln-rate tensor, P/2 a pressure term equal toone half of the ice strength P (taken to be a functionof the ice-thickness characteristics as discussedlater), and ~ and n are nonlinear bulk andshear viscosities. The internal ice stress I isrelated to this constitutive law by
For calculations performed here the dependence of ç and n on εij and P is taken so that the stress state lies on an elliptical yield curve passing through the origin with no-stress conditions applying for pure divergence (Reference HiblerHibler 1979).
2(b). Compactness evolution and ice strength
The main prognostic parameter in the model is the compactness A. Since for forecast purposes we are only concerned with changes of A over, at most, a few days, we neglect thermodynamic terms and consider only the evolution of the ice compactness and thickness due to mechanical effects:
and
where A is the fraction of the area covered by ice, and h is the mean ice thickness averaged over a whole grid cell. Inclusion of thermodynamic terms can make some difference for forecasts longer than a few days. However, within the approximation of the two-level model, for short-term forecasts (<36 h), errors due to the neglect of thermodynamics are felt to be about the same order of magnitude as errors in the initialization of the compactness fields.
We further specify that A<1, which essentially means that once the open water is removed, further convergence of the ice takes place by ice thickening. This is equivalent to adding a term for mechanical redistribution to Equation (4). To relate the ice strength to the compactness (and ice thickness) the following relation is used:
Where P* and C are constants Note that by allowing h and A to go zero, a free ice edge may be treated.
3. Numerical Considerations
To solve Equations (2) to (6) numerically a time-marching procedure using finite difference techniques is employed. A computer code for this procedure is documented by Reference HiblerHibler (1980). The numerical procedure employed here used this computer code with only minor modifications (terms for momentum advection set equal to zero, smaller time steps, a smaller value for maximum viscosity, and a value of zero for minimum viscosity (Table 1)). In this time-marching scheme an implicit method using relaxation techniques is used to solve the momentum balance, while an explicit procedure is used for the equations for ice evolution. In this explicit solution second-order centered differences are used for the advection terms, together with a modified Euler procedure to center the advec-tion terms in the center of the time step. In addi-tion, to control nonlinear instabilities, a small diffusion term is added to the continuity equations. Details of this solution technique and a description of the finite differences are given in Reference HiblerHibler (1979).
Table 1. NUMERICAL PARAMETERS USED IM THE STANDARD SIMULATIONS
In the momentum balance portion of the solution a linearized momentum balance is solved at each time step by relaxation. The viscosities used in the momentum balance are based on the deformation field from the previous time step. Using these viscosities a new velocity field is obtained, a new set of viscosities are estimated, and another linearized equation solved. We will refer to each of these relaxation solutions as an “iterative time step”. By carrying out several iterative time steps at each “physical time step”, ideal plastic flow may be approached. In the simulations presented here, two iterative time steps are carried out at each physical time step. The main numerical features that change as smaller scales are simulated are the number of relaxation loops needed to solve the linearized momentum balance and the number of iterative time steps needed to fully attain plastic flow. To investigate the dependence of the solutions on these features a series of simulations over a region 143 by 148 km with fixed land boundaries and fixed geostrophic wind in the x-direction were carried out. A complete description of these tests is given by Hibler and others (in press). The main conclusion of these tests relevant to mesoscale ice forecasting was that half-hour time steps allowed adequate time for plastic adjustment for application with winds at 3-h intervals.
The main formal stability requirement for the coupled system of equations is a Courant-Friedrichs-Lewy criterion on the advection terms (i.e. 
). Since ice velocities are normally less than -1 m s A this restriction is relatively mild and would, for example, allow time steps of up to 6 h on a grid of 20 km. However, a more restrictive condition is to take time steps short enough to allow the nonlinear aspects of the model to evolve properly, as mentioned above. Since the solution time for the equations of ice evolution is short, it is convenient for forecasting purposes to simply reduce the time steps for the whole system. Tests of the coupled system tend to support the results for momentum balance only, and indicate the simulation results to be relatively independent of time-step magnitude for time steps less than 0.5 h, unless very rapidly varying winds are employed.
4. Response Characteristics of Coupled System
In forecast applications near coasts or in constrained regions the evolution of the ice-thickness characteristics has a critical modifying effect on the dynamical behavior. These modifications can be substantial over time scales as short as a few hours. As a consequence the coupled system of equations must be considered in actual forecast situations. To examine the behavior of this coupled system we consider in this section a series of solutions for idealized geometries. To understand this system of equations it is useful first to analyze analytically the behavior of a simplified one-dimensional system. For this purpose we first consider the momentum balance only and then the complete system.
4(a). Analytic analysis of the momentum balance for a one-dimensional system
Consider the one-dimensional case of the momentum balance employing only a linear water drag term Cu, an external constant wind stress F, and a one-dimensional ice interaction stress c:
Consider the region bounded by no slip walls at x = 0 and x = L. For our plastic rheology we will assume that o = -P for ?u/? x<0 and σ = 0 for ?u/?x>0. These assumptions define a rigid plastic rheology with no tensile strength. A solution for this case may be constructed by noticing (i) that for any converging deformation σ = -P, (ii) for no deformation 0> σ >-P, and (iii) the maximum force would be expected to take place at the right-hand boundary since the wind stress has built up at this point. With these considerations in mind we see first that if F L<P no motion of any kind will occur and the system will be rigid. If on the other hand F L>P then a solution of Equation (7) can occur for a σ satisfying the above plastic assumptions and σ(L) = -P. Integrating Equation (7) from x to L we have
However, we also must have ?u/?x = 0 except at the boundary, otherwise σ (X) = -P and Equation (7) cannot be satisfied. Therefore u is a constant, as is F, and we obtain
The value of u0 may be obtained by noting that the total force acting on the moving rigid block is -Cu0L + FL - P, and since there is no acceleration
Another way to see this is to note that σ (x=0) since divergence is occurring there and we nave assumed no tensile strength. The validity of this solution was also verified numerically.
4(b). Analysis of coupled behavior for an idealized one-dimensional system
As in the momentum balance only, consider a one-dimensional system having a linear water drag, rigid plastic interaction and constant wind stress F from left to right. The initial condition consists of a compactness A of 0.9. For the coupling of P to A let us consider P discontinuously changing at A = 1 as follows
where P>P1 Because of this discontinuous change the local momentum balance will not be modified by any changes in compactness until the compactness goes to 1. Based on the analysis of the momentum balance only, presented earlier, all deformation takes place at a right-hand boundary; consequently, at some arbitrary time At after the initiation of motion we would expect the geometry in Figure 1 to apply. By the earlier analysis of momentum balance, for (P-P 1 < FL3 all velocities in the L3 region (compactness of 1) will be zero. Also by this analysis, the velocities in the L2 region will be given by
so that as L2 becomes smaller Ugwill slow down unless P1 = 0. Since, with the L3 region motionless, all the deformation is occurring at the L2, L3 boundary it is clear that the Lg, L3 boundary will propagate outward (to the left) at a speed of U22/0.1. However, note that for L3 large enough (i.e. 13(P-P1)/F) the L3 region will start moving again with a speed
Fig. 1. Geometry of idealized compactness conditions.
When this occurs, the propagation of the ridging front will slow down to [Ug-U3)/0,l. Also, once all the ice is converted to 100% compactness, the speed will then slowly decrease as the length L3 decreases due to removal of ice by ridging at the right-hand boundary. Based on these considerations one can construct a qualitative speed versus time of two arbitrary points, say p and p', where p' is located further left than p (Fig.2.)
Fig. 2. Qualitative plot of velocity versus time for two points in example of idealized build-up.
Obviously by varying strengths and/or the wind forcing the various slopes, magnitudes and spacing in time of these profiles can be modified. One of the more interesting features of the system is that due to the complexities of the thickness coupling, for appropriate strength differences, points near the right-hand coast will actually stop for a while and then speed up, even though external forcing is constant. The essential physics here is that, because of the discontinuous nature of the ridging front and the nonlinear rheology, points in the L3 region will not move at all until 1I3 becomes large enough to accumulate an adequate wind fetch to overcome the differential of plastic stresses at the boundaries.
4(c). Numerical investigation of response characteristics of a two-dimensional system
A series of two-dimensional numerical simulations yielded results that generally agree with the one-dimensional analysis. However, there are signify-cant differences associated with the fact that P does not change discontinuously but is instead a smooth function of A. For the standard case study, the coupled equations were integrated for 18 h at time steps of 15 min on a 9 × 9 grid. The initial conditions consisted of 10% open water together with a mean ice thickness of 0.5 m. To simplify analysis the ice strength is taken to depend only on the compactness, not on the ice thickness. As a consequence the ice strength in these particular idealized studies is given by
To make the test comparable to the one-dimensional analysis, the turning angles and the Coriolis parameter were set equal to zero. A constant wind speed of 9.23 m s”1 in the positive x direction was used. Other parameters are the same as in Table I. Tests using different values of C and P* (as well as a linear dependence of P upon A) are discussed in Hibler and others (in press).
The basic characteristics of this idealized numerical simulation are shown in Figures 3 and 4, which show x velocity components versus time for several grid points, together with velocity and compactness profiles for selected times. Both these plots were taken from grid points and grid cells centered in the y direction. The general behavior of the velocity time series is commensurate with the idealized one-dimensional analysis, with the points nearest the coast rapidly decreasing in speed with a later increase as the region of ridging moves further out. However, there are significant differences from the analytic case associated with the fact that the motion near the coast is balanced by a gradient in compactness (see Fig.4.(a)) rather than a discontinuous change. This gradient means that (i) the points do not ever totally stop (since some convergence must occur everywhere to allow the gradient to move outward) and (ii) kinematic waves (see Fig.3.(a)) are allowed to propagate upstream (or more precisely down the stress gradient).
Fig. 3. Time series of x component of ice velocity at grid points progressively further from right-hand boundary of build-up experiment. The grid points used were centered in the y direction and the distances from the right-hand boundary are labeled.
Fig. 4. (a) The profit Velocity and (b) compactness profiles at different times in the numerical experiments on build-up. Fîles were taken from grid cells centered in the y direction.
These waves arise from the fact that the velocity of ice is balanced in part by the stress gradient while the stress gradient is maintained by a convergence of the ice velocity field. As a consequence, a perturbation of either one of these quantities can cause a wave to propagate down the stress gradient slope. This wave can naturally develop in the evolution of the system since the initial build-up can be out of equilibrium with regard to kinematic waves (when the dependence of strength on compactness is nonlinear). Such a kinematic wave is apparent in Figure 4 mostly notably at hour 6 in the velocity time series of the point nearest the coast. Tests at smaller time steps verified that this wave was not a numerical artifact. However, while this wave is noticeable in the velocity time series, its effect on the compactness profiles is not major (see Fig.4.(b)). Closer examinations of this wave show it to slow down and diffuse as it progresses outward. While beyond the scope of this paper it should be noted that both these features can be explained using a one-dimensional analytical model.
An important ramification of compactness gradient is that there will also be a spatial velocity gradient (see Fig.4.(b)) with smaller velocities closer to the coast. This velocity gradient will, however, gradually decrease as the ice becomes more compact due to convergence. Observations in the Bay of Bothnia (see e.g. Omstedt and Sahlberg 1977, Leppäranta 1980) indicate that such velocity gradients are observed, and hence are a useful feature of this forecasting model. Specifically, observations from three different ships during a joint Swedish-Finnish field experiment in 1977 (Omstedt and Sahlberg 1977) showed that under onshore winds the drift of ships nearest the coast decreased more rapidly than did the drift of ships further out. Simulations with a modification of this model representing the Bay of Bothnia reproduced the main features of this observation with the ice build-up playing a significant role in the drift reduction (Hibler and others in press).
5. Concluding Remarks
The study reported here has yielded a number of insights into simulating ice build-up using nonlinear sea-ice forecasting models. One of the main results is the presence of fluctuating velocities during ice build-up due to the nonlinear ice interaction which allows the propagation of a ridging front- The essential feature here is that points nearest the coast will first slow down as the ice builds up and strengthens. However, as the extent of strengthened ice increases these points can speed up again if the cumulative wind force exceeds the difference in plastic yield between the strengthened and un-strengthened ice.
An additional interesting effect is the presence of kinematic waves in the coupled equations under suitable circumstances. Basically these waves arise from the coupling of the nonlinear rheology to the ice thickness equations and allow the divergence rate to fluctuate as small bulges in compactness propagate down the stress gradient. Such waves have not been previously demonstrated in equations of sea-ice dynamics, and they may well be relevant to a number of small-scale phenomena, both in the interior pack and near the ice margin. Further investigations focusing on these wave effects are needed and are currently in progress.
6. Acknowledgements
One of us (W D H) would like to thank Professor R Smith of Yale University for first suggesting that fluctuations in our simulations of ice build-up might be due to kinematic waves. This work was supported in the USA by the National Aeronautics and Space Administration and by the Office of Naval Research, and in Sweden by the Ice Forecasting Division of the Swedish Meteorological and Hydro!ogical Institute.
