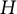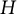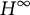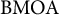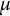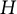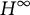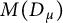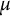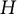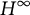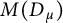1 Introduction
Let
![]() $\mathbb {D}$
be the unit disc in the complex plane
$\mathbb {D}$
be the unit disc in the complex plane
![]() $\mathbb {C}$
and let
$\mathbb {C}$
and let
![]() $\text {Hol}(\mathbb {D})$
be the space of analytic functions in
$\text {Hol}(\mathbb {D})$
be the space of analytic functions in
![]() $\mathbb {D}$
. With
$\mathbb {D}$
. With
![]() $\mathbb {T}$
we denote the unit circle, that is
$\mathbb {T}$
we denote the unit circle, that is
![]() $\mathbb {T}=\partial \mathbb {D}$
. The classical Hilbert matrix is
$\mathbb {T}=\partial \mathbb {D}$
. The classical Hilbert matrix is
 $$\begin{align*}H=\left( \begin{array}{ccccc} 1 & \frac{1}{2} & \frac{1}{3} & \dots \\[4pt] \frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \dots \\[4pt] \frac{1}{3} & \frac{1}{4} & \frac{1}{5} & \dots \\ \vdots & \vdots & \vdots & \ddots\\ \end{array} \right). \end{align*}$$
$$\begin{align*}H=\left( \begin{array}{ccccc} 1 & \frac{1}{2} & \frac{1}{3} & \dots \\[4pt] \frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \dots \\[4pt] \frac{1}{3} & \frac{1}{4} & \frac{1}{5} & \dots \\ \vdots & \vdots & \vdots & \ddots\\ \end{array} \right). \end{align*}$$
The matrix
![]() $H$
introduces an operator on spaces of analytic functions through its action on the sequence of Taylor coefficients. For
$H$
introduces an operator on spaces of analytic functions through its action on the sequence of Taylor coefficients. For
 $$ \begin{align*}f(z)=\sum_{m=0}^{\infty}a_{m}z^{m} \end{align*} $$
$$ \begin{align*}f(z)=\sum_{m=0}^{\infty}a_{m}z^{m} \end{align*} $$
in the Hardy space
![]() $H^1$
,
$H^1$
,
![]() $H(f)$
is defined as
$H(f)$
is defined as
 $$ \begin{align*}H(f)(z)=\sum_{n=0}^{\infty}\left(\sum_{k=0}^{\infty}\frac{a_{k}}{k+n+1}\right)z^{n}. \end{align*} $$
$$ \begin{align*}H(f)(z)=\sum_{n=0}^{\infty}\left(\sum_{k=0}^{\infty}\frac{a_{k}}{k+n+1}\right)z^{n}. \end{align*} $$
It is clear that
![]() $H(f)$
is an analytic function on the unit disk, since Hardy’s inequality [Reference Duren17, p. 48]
$H(f)$
is an analytic function on the unit disk, since Hardy’s inequality [Reference Duren17, p. 48]
 $$ \begin{align*}\sum_{m=0}^{\infty}\frac{|a_m|}{m+1}\leq \pi \|f\|_{H^{1}} \end{align*} $$
$$ \begin{align*}\sum_{m=0}^{\infty}\frac{|a_m|}{m+1}\leq \pi \|f\|_{H^{1}} \end{align*} $$
implies that the Taylor coefficients of
![]() $H(f)$
are bounded.
$H(f)$
are bounded.
In [Reference Diamantopoulos and Siskakis15], E. Diamantopoulos and A. Siskakis initiated the study of the Hilbert matrix as an operator on Hardy spaces by using the fact that for every
![]() $ z\in \mathbb {D}$
, the function
$ z\in \mathbb {D}$
, the function
![]() $H(f)$
has the equivalent integral representation
$H(f)$
has the equivalent integral representation
By considering
![]() $H$
as the average of weighted composition operators, they proved that
$H$
as the average of weighted composition operators, they proved that
![]() $H$
is a bounded operator on every Hardy space
$H$
is a bounded operator on every Hardy space
![]() $H^p$
with
$H^p$
with
![]() $p> 1$
and they estimated its norm. Their research was further extended by M. Dostanic, M. Jevtic, and D. Vukotic in [Reference Dostanic, Jevtić and Vukotić16]. Among other results, they showed that
$p> 1$
and they estimated its norm. Their research was further extended by M. Dostanic, M. Jevtic, and D. Vukotic in [Reference Dostanic, Jevtić and Vukotić16]. Among other results, they showed that
 $$ \begin{align*} \|H\|_{H^{p}\to H^p}=\frac{\pi}{\sin(\frac{\pi}{p})}, \end{align*} $$
$$ \begin{align*} \|H\|_{H^{p}\to H^p}=\frac{\pi}{\sin(\frac{\pi}{p})}, \end{align*} $$
for
![]() $1<p<\infty $
.
$1<p<\infty $
.
The study of the Hilbert matrix operator was subsequently extended to include the Bergman spaces of the unit disc. Diamantopoulos [Reference Diamantopoulos14], Dostanic et al. [Reference Dostanic, Jevtić and Vukotić16] and V. Bozin and B. Karapetrovic [Reference Božin and Karapetrović10] proved that
![]() $H$
is bounded on the Bergaman space
$H$
is bounded on the Bergaman space
![]() $A^p$
if and only if
$A^p$
if and only if
![]() $p>2$
. Moreover
$p>2$
. Moreover
 $$ \begin{align*}\|H\|_{A^p\to A^p}= \frac{\pi}{\sin\left(\frac{2\pi}{p}\right) }. \end{align*} $$
$$ \begin{align*}\|H\|_{A^p\to A^p}= \frac{\pi}{\sin\left(\frac{2\pi}{p}\right) }. \end{align*} $$
Following the classical case, a significant body of research has focused on generalizations of the Hilbert matrix operator, particularly regarding the characterization of their boundedness and compactness, see, for example, [Reference Bellavita, Daskalogiannis, Miihkinen, Norrbo, Stylogiannis and Virtanen9], and [Reference Bellavita, Daskalogiannis and Stylogiannis7] for a recent survey on the argument.
In this article, we study the action of
![]() $H$
from
$H$
from
![]() $H^\infty $
into conformally invariant Banach spaces. We recall that a Banach space X of analytic functions is conformally invariant if for every
$H^\infty $
into conformally invariant Banach spaces. We recall that a Banach space X of analytic functions is conformally invariant if for every
![]() $f \in X$
and
$f \in X$
and
![]() $\phi \in \text {Aut}(\mathbb {D})$
$\phi \in \text {Aut}(\mathbb {D})$
where the Mobius group
![]() $\text {Aut}(\mathbb {D})$
is the set made by all the one-to-one analytic functions mapping
$\text {Aut}(\mathbb {D})$
is the set made by all the one-to-one analytic functions mapping
![]() $\mathbb {D}$
onto itself, see [Reference Arazy, Fisher and Peetre2]. Main examples of conformally invariant spaces are the BMOA space, the
$\mathbb {D}$
onto itself, see [Reference Arazy, Fisher and Peetre2]. Main examples of conformally invariant spaces are the BMOA space, the
![]() $Q_p$
spaces and the classical Dirichlet space
$Q_p$
spaces and the classical Dirichlet space
![]() $D$
, while
$D$
, while
![]() $H^p$
with
$H^p$
with
![]() $1\leq p<\infty $
is not.
$1\leq p<\infty $
is not.
In this article, we consider the action of the Hilbert matrix operator from
![]() $H^\infty $
into the space of analytic bounded mean oscillation
$H^\infty $
into the space of analytic bounded mean oscillation
![]() $\text {BMOA}$
and the conformally invariant Dirichlet spaces
$\text {BMOA}$
and the conformally invariant Dirichlet spaces
![]() $M(D_\mu )$
.
$M(D_\mu )$
.
The
![]() $\text {BMOA}$
space consists of all the functions in the Hardy space
$\text {BMOA}$
space consists of all the functions in the Hardy space
![]() $H^2$
such that
$H^2$
such that
 $$ \begin{align*} \|f\|_{\text{BMOA}}=& |f(0)|+\left(\sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\left|f'(z)\right|^{2}\log\left|\frac{1-\overline{a}z}{a-z}\right|^{2}dA(z)\right)^{1/2}<\infty, \end{align*} $$
$$ \begin{align*} \|f\|_{\text{BMOA}}=& |f(0)|+\left(\sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\left|f'(z)\right|^{2}\log\left|\frac{1-\overline{a}z}{a-z}\right|^{2}dA(z)\right)^{1/2}<\infty, \end{align*} $$
where, if
![]() $z=x+iy$
,
$z=x+iy$
,
![]() $dA(z)=\pi ^{-1}dxdy$
. With the above norm
$dA(z)=\pi ^{-1}dxdy$
. With the above norm
![]() $\text {BMOA}$
is a conformally invariant Banach space and
$\text {BMOA}$
is a conformally invariant Banach space and
The norm
![]() $\|f\|_{\text {BMOA}}$
can be expressed by integration on
$\|f\|_{\text {BMOA}}$
can be expressed by integration on
![]() $\mathbb {T}$
,
$\mathbb {T}$
,
 $$ \begin{align} \|f\|_{\text{BMOA}}= |f(0)|+\left( \sup_{a\in\mathbb{D}}\int_{\mathbb{T}}|f(e^{i\theta})|^2\frac{1-|a|}{|e^{i\theta}-a|^2}\frac{d\theta}{2\pi}-|f(a)|^2\right)^{1/2}. \end{align} $$
$$ \begin{align} \|f\|_{\text{BMOA}}= |f(0)|+\left( \sup_{a\in\mathbb{D}}\int_{\mathbb{T}}|f(e^{i\theta})|^2\frac{1-|a|}{|e^{i\theta}-a|^2}\frac{d\theta}{2\pi}-|f(a)|^2\right)^{1/2}. \end{align} $$
For more information about
![]() $\text {BMOA}$
, we refer to [Reference Garnett19, Chapter VI] and [Reference Girela20].
$\text {BMOA}$
, we refer to [Reference Garnett19, Chapter VI] and [Reference Girela20].
Theorem 1.1 The Hilbert matrix operator maps
![]() $H^\infty $
into
$H^\infty $
into
![]() $\text {BMOA}$
and its norm is
$\text {BMOA}$
and its norm is
![]() $1+\dfrac {\pi }{\sqrt {2}}$
.
$1+\dfrac {\pi }{\sqrt {2}}$
.
The boundedness of
![]() $H$
from
$H$
from
![]() $H^\infty $
into
$H^\infty $
into
![]() $\text {BMOA}$
has been first observed by B. Lanucha, M. Nowak, and M. Pavlovic in [Reference Lanucha, Nowak and Pavlovic22]. Actually, it is also true that
$\text {BMOA}$
has been first observed by B. Lanucha, M. Nowak, and M. Pavlovic in [Reference Lanucha, Nowak and Pavlovic22]. Actually, it is also true that
 $$ \begin{align*}H\left( H^\infty\right)\subseteq \bigcap_{1<p<\infty}\Lambda\left(p,\frac{1}{p}\right)\subset \text{BMOA}, \end{align*} $$
$$ \begin{align*}H\left( H^\infty\right)\subseteq \bigcap_{1<p<\infty}\Lambda\left(p,\frac{1}{p}\right)\subset \text{BMOA}, \end{align*} $$
where
![]() $\Lambda (p,\frac {1}{p})$
are the mean Lipschitz spaces (see later for definition).
$\Lambda (p,\frac {1}{p})$
are the mean Lipschitz spaces (see later for definition).
Subsequently, we fix our attention on the conformally invariant Dirichlet space
![]() $M(D_\mu )$
. Let
$M(D_\mu )$
. Let
![]() $d\mu (z)$
be a positive, Borel measure in
$d\mu (z)$
be a positive, Borel measure in
![]() $\mathbb {D}$
. The spaces
$\mathbb {D}$
. The spaces
![]() $M(D_\mu )$
consists of all the functions
$M(D_\mu )$
consists of all the functions
![]() $f \in \text {Hol}(\mathbb {D})$
such that
$f \in \text {Hol}(\mathbb {D})$
such that
 $$ \begin{align} \|f\|_{M(D_{\mu})}=|f(0)|+\sup_{\phi \in \text{Aut}(\mathbb{D})}\left(\int_{\mathbb{D}} |f'(w)|^{2}U_{\mu}(\phi(w))dA(w)\right)^{1/2}, \end{align} $$
$$ \begin{align} \|f\|_{M(D_{\mu})}=|f(0)|+\sup_{\phi \in \text{Aut}(\mathbb{D})}\left(\int_{\mathbb{D}} |f'(w)|^{2}U_{\mu}(\phi(w))dA(w)\right)^{1/2}, \end{align} $$
where
 $$ \begin{align*}U_{\mu}(z) = \int_{\mathbb{D}}\log\left| \frac{1-\overline{w}z}{z-w}\right|^{2}d\mu(w) \end{align*} $$
$$ \begin{align*}U_{\mu}(z) = \int_{\mathbb{D}}\log\left| \frac{1-\overline{w}z}{z-w}\right|^{2}d\mu(w) \end{align*} $$
is a superharmonic function in
![]() $\mathbb {D}$
. The most famous examples of
$\mathbb {D}$
. The most famous examples of
![]() $M(D_\mu )$
spaces are the
$M(D_\mu )$
spaces are the
![]() $Q_p$
spaces, see (2.2) and [Reference Aulaskari, Xiao and Zhao3]. An equivalent expression for
$Q_p$
spaces, see (2.2) and [Reference Aulaskari, Xiao and Zhao3]. An equivalent expression for
![]() $\|f\|_{M(D_\mu )}$
is
$\|f\|_{M(D_\mu )}$
is
 $$ \begin{align} \|f\|_{M(D_\mu)} \sim |f(0)|+ \sup_{\phi \in \text{Aut}(\mathbb{D})}\left( \int_{\mathbb{D}} |f'(w)|^{2}V_{\mu}(\phi(w))dA(w)\right)^{1/2}, \end{align} $$
$$ \begin{align} \|f\|_{M(D_\mu)} \sim |f(0)|+ \sup_{\phi \in \text{Aut}(\mathbb{D})}\left( \int_{\mathbb{D}} |f'(w)|^{2}V_{\mu}(\phi(w))dA(w)\right)^{1/2}, \end{align} $$
where
We characterize the measures
![]() $d\mu (z)$
such that the Hilbert matrix operator
$d\mu (z)$
such that the Hilbert matrix operator
![]() $H$
is bounded from
$H$
is bounded from
![]() $H^\infty $
into
$H^\infty $
into
![]() $M(D_\mu )$
.
$M(D_\mu )$
.
Theorem 1.2 Let
![]() $d\mu (z)$
be a positive Borel measure on
$d\mu (z)$
be a positive Borel measure on
![]() $\mathbb {D}$
. The following conditions are equivalent:
$\mathbb {D}$
. The following conditions are equivalent:
-
(i) The Hilbert matrix operator
 $H$
sends
$H$
sends
 $H^\infty $
into
$H^\infty $
into
 $M(D_{\mu })$
.
$M(D_{\mu })$
. -
(ii)
 $\log (1-z) \in M(D_{\mu })$
.
$\log (1-z) \in M(D_{\mu })$
. -
(iii)
 $$ \begin{align*} \sup_{\lambda\in\mathbb{T}}\int_{\mathbb{D}}\frac{V_{\mu}(z)}{|1-\lambda z|^{2}}dA(z)<\infty. \end{align*} $$
$$ \begin{align*} \sup_{\lambda\in\mathbb{T}}\int_{\mathbb{D}}\frac{V_{\mu}(z)}{|1-\lambda z|^{2}}dA(z)<\infty. \end{align*} $$
-
(iv)
 $$ \begin{align*} \sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\frac{V_{\mu}(z)}{|1-az|^{2}}dA(z)<\infty. \end{align*} $$
$$ \begin{align*} \sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\frac{V_{\mu}(z)}{|1-az|^{2}}dA(z)<\infty. \end{align*} $$
We highlight that the proof of Theorem 1.2 is similar to the proof of the analogous result for the Cesáro operator, see [Reference Bao, Wulan and Ye6, Theorem 1.1]. In addition, for some measures
![]() $d\mu (z)$
, we also provide the norm of
$d\mu (z)$
, we also provide the norm of
![]() $H$
from
$H$
from
![]() $H^\infty $
into
$H^\infty $
into
![]() $M(D_\mu )$
.
$M(D_\mu )$
.
Theorem 1.3 Let
![]() $d\mu (z)$
be a positive, radial, Borel measure on
$d\mu (z)$
be a positive, radial, Borel measure on
![]() $\mathbb {D}$
. If
$\mathbb {D}$
. If
![]() $H:H^\infty \to M(\mathcal {D}_\mu )$
is bounded then
$H:H^\infty \to M(\mathcal {D}_\mu )$
is bounded then
 $$ \begin{align*} \|H\|_{H^\infty\to M(D_\mu)}=1+\left(\int_{\mathbb{D}}\frac{4}{|1-z^{2}|^{2}}U_{\mu}(z)dA(z)\right)^{1/2}. \end{align*} $$
$$ \begin{align*} \|H\|_{H^\infty\to M(D_\mu)}=1+\left(\int_{\mathbb{D}}\frac{4}{|1-z^{2}|^{2}}U_{\mu}(z)dA(z)\right)^{1/2}. \end{align*} $$
Significantly, the measure associated with the
![]() $Q_p$
spaces satisfies the hypothesis of the above theorem and we are able to compute the norm of the Hilbert matrix operator from
$Q_p$
spaces satisfies the hypothesis of the above theorem and we are able to compute the norm of the Hilbert matrix operator from
![]() $H^\infty $
into
$H^\infty $
into
![]() $Q_p$
.
$Q_p$
.
The methodology developed in this article also works for the Cesáro operator
 $$ \begin{align*}\mathcal{C}(f)(z) = \sum_{n=0}^{\infty} \frac{1}{n+1}\left(\sum_{k=0}^{n}a_{k}\right)z^{n}, \mathit{ with }\,f (z) = \sum_{n=0}^{\infty} a_{n}z^{n} \in \mathit{Hol}(\mathbb{D}). \end{align*} $$
$$ \begin{align*}\mathcal{C}(f)(z) = \sum_{n=0}^{\infty} \frac{1}{n+1}\left(\sum_{k=0}^{n}a_{k}\right)z^{n}, \mathit{ with }\,f (z) = \sum_{n=0}^{\infty} a_{n}z^{n} \in \mathit{Hol}(\mathbb{D}). \end{align*} $$
The analogy between the Hilbert matrix operator and the Cesáro operator comes from their matrix representations, that is
 $$\begin{align*}\mathcal{C}=\left( \begin{array}{ccccc} 1 & 0 & 0 & 0 & \dots \\[4pt] \frac{1}{2} & \frac{1}{2} & 0 & 0& \dots \\[4pt] \frac{1}{3} & \frac{1}{3} & \frac{1}{3} & 0 &\dots \\[4pt] \vdots & \vdots & \vdots & \vdots & \ddots\\ \end{array} \right). \end{align*}$$
$$\begin{align*}\mathcal{C}=\left( \begin{array}{ccccc} 1 & 0 & 0 & 0 & \dots \\[4pt] \frac{1}{2} & \frac{1}{2} & 0 & 0& \dots \\[4pt] \frac{1}{3} & \frac{1}{3} & \frac{1}{3} & 0 &\dots \\[4pt] \vdots & \vdots & \vdots & \vdots & \ddots\\ \end{array} \right). \end{align*}$$
We observe that
![]() $H$
is obtained from
$H$
is obtained from
![]() $C$
by the following formal manipulation: we erase the zeros in each column of
$C$
by the following formal manipulation: we erase the zeros in each column of
![]() $C$
and we shift up the columns to their first non-zero entry. In rigorous terms, this is equivalent to the following algebraic relation. Let
$C$
and we shift up the columns to their first non-zero entry. In rigorous terms, this is equivalent to the following algebraic relation. Let
![]() $e_n(z) = z^n, n = 0, 1, 2, ... $
be the monomials, which form an orthonormal basis of
$e_n(z) = z^n, n = 0, 1, 2, ... $
be the monomials, which form an orthonormal basis of
![]() $H^2$
. We have that
$H^2$
. We have that
where S is the shift operator, that is
![]() $Sf(z)=zf(z)$
.
$Sf(z)=zf(z)$
.
Theorem 1.4 Let
![]() $d\mu (z)$
be a positive, radial, Borel measure on
$d\mu (z)$
be a positive, radial, Borel measure on
![]() $\mathbb {D}$
. If
$\mathbb {D}$
. If
![]() $\mathcal {C}:H^\infty \to M(D_\mu )$
is bounded then
$\mathcal {C}:H^\infty \to M(D_\mu )$
is bounded then
 $$ \begin{align*} \|C\|_{H^\infty\to M(D_\mu)}=1+\left(\int_{\mathbb{D}}\frac{4}{|1-z^{2}|^{2}}U_{\mu}(z)dA(z)\right)^{1/2}. \end{align*} $$
$$ \begin{align*} \|C\|_{H^\infty\to M(D_\mu)}=1+\left(\int_{\mathbb{D}}\frac{4}{|1-z^{2}|^{2}}U_{\mu}(z)dA(z)\right)^{1/2}. \end{align*} $$
In light of the analogy between
![]() $C$
and
$C$
and
![]() $H$
, a comparative analysis of the Hilbert matrix operator results with their Cesáro operator counterparts is warranted.
$H$
, a comparative analysis of the Hilbert matrix operator results with their Cesáro operator counterparts is warranted.
The rest of the article is divided in six sections. Section 2 is devoted to preliminary material: we recall the definition of Hardy spaces and we describe the conformally invariant Dirichlet spaces
![]() $M(D_\mu )$
. In Section 3, we deal with
$M(D_\mu )$
. In Section 3, we deal with
![]() $\text {BMOA}$
and we prove Theorem 1.1. In Section 4, we briefly describe the action of the Hilbert matrix operator from
$\text {BMOA}$
and we prove Theorem 1.1. In Section 4, we briefly describe the action of the Hilbert matrix operator from
![]() $H^\infty $
into the mean Lipschitz spaces. In Section 5, we describe the action of the Hilbert matrix operator from
$H^\infty $
into the mean Lipschitz spaces. In Section 5, we describe the action of the Hilbert matrix operator from
![]() $H^\infty $
into
$H^\infty $
into
![]() $M(D_\mu )$
and we prove Theorem 1.2.
$M(D_\mu )$
and we prove Theorem 1.2.
We prove Theorem 1.4 in Section 7. Finally, in Section 6, we prove Theorem 1.3. We conclude the article with some open problems.
We use the following notation. By the expressions
![]() $f \lesssim g$
, we mean that there exists a positive constant C such that
$f \lesssim g$
, we mean that there exists a positive constant C such that
If both f ≲ g and f ≳ g hold, we write f ∼ g. The capital letter C, will denote constants whose values may change every time they appear. Finally with
![]() $\delta _{m,n}$
we denote the classical Kronecker symbol.
$\delta _{m,n}$
we denote the classical Kronecker symbol.
2 Preliminary
In this preliminary section, we recall some definitions that will be used throughout the whole article.
2.1 Hardy spaces
Let
![]() $1\leq p<\infty $
and
$1\leq p<\infty $
and
![]() $f\in \text {Hol}(\mathbb {D})$
. For
$f\in \text {Hol}(\mathbb {D})$
. For
![]() $0\leq r<1$
, let
$0\leq r<1$
, let
 $$\begin{align*}M_p(r,f)=\left(\dfrac{1}{2\pi}\int_{0}^{2\pi}\vert f(re^{i\theta})\vert^p\, d\theta\right)^{\frac{1}{p}}\ \end{align*}$$
$$\begin{align*}M_p(r,f)=\left(\dfrac{1}{2\pi}\int_{0}^{2\pi}\vert f(re^{i\theta})\vert^p\, d\theta\right)^{\frac{1}{p}}\ \end{align*}$$
be the usual integral means of f on the circle of radius r. The Hardy space
![]() $H^p =H^p(\mathbb {D})$
consists of all the functions
$H^p =H^p(\mathbb {D})$
consists of all the functions
![]() $f\in \text {Hol}(\mathbb D)$
such that
$f\in \text {Hol}(\mathbb D)$
such that
and, for
![]() $p=\infty $
,
$p=\infty $
,
![]() $\,H^\infty $
consists of the bounded analytic functions on
$\,H^\infty $
consists of the bounded analytic functions on
![]() $\mathbb {D}$
, i.e., all the functions in
$\mathbb {D}$
, i.e., all the functions in
![]() $\text {Hol}(\mathbb D)$
such that
$\text {Hol}(\mathbb D)$
such that
See [Reference Duren17] for the theory of Hardy spaces. Important examples of
![]() $H^\infty $
functions are the automorphisms,
$H^\infty $
functions are the automorphisms,
![]() $\phi \in \text {Aut}(\mathbb {D})$
. We recall that every
$\phi \in \text {Aut}(\mathbb {D})$
. We recall that every
![]() $\phi \in \text {Aut}(\mathbb {D})$
can be written as
$\phi \in \text {Aut}(\mathbb {D})$
can be written as
where
![]() $\theta $
is real and
$\theta $
is real and
![]() $a\in \mathbb {D}$
.
$a\in \mathbb {D}$
.
2.2 Conformally invariant Dirichlet spaces
The Möbius invariant spaces
![]() $M(D_\mu )$
generated by the Dirichlet space
$M(D_\mu )$
generated by the Dirichlet space
![]() $D_\mu $
are defined in (1.3)Footnote
1
. In order to avoid that,
$D_\mu $
are defined in (1.3)Footnote
1
. In order to avoid that,
![]() $M(D_\mu )$
contains only constant functions, we always assume that
$M(D_\mu )$
contains only constant functions, we always assume that
If (2.1) does not hold,
![]() $M(D_\mu )$
is called trivial. From [Reference Bao, Mashreghi, Pouliasis and Wulan5], it is known that if
$M(D_\mu )$
is called trivial. From [Reference Bao, Mashreghi, Pouliasis and Wulan5], it is known that if
![]() $M(D_\mu )$
is not trivial, then
$M(D_\mu )$
is not trivial, then
![]() $D \subseteq M(D_\mu ) \subseteq \mathit{BMOA}$
. Furthermore,
$D \subseteq M(D_\mu ) \subseteq \mathit{BMOA}$
. Furthermore,
![]() $M(D_\mu ) = \mathit{BMOA}$
if and only if
$M(D_\mu ) = \mathit{BMOA}$
if and only if
![]() $\mu (\mathbb {D}) < \infty $
.
$\mu (\mathbb {D}) < \infty $
.
For
![]() $0 < p < \infty $
, the
$0 < p < \infty $
, the
![]() $Q_p$
space consists of all the functions
$Q_p$
space consists of all the functions
![]() $f \in \text {Hol}(\mathbb {D})$
such that
$f \in \text {Hol}(\mathbb {D})$
such that
 $$ \begin{align} \|f\|_{Q_{p}}^{2} = |f(0)|+ \sup_{a\in\mathbb{D}}\left( \int_{\mathbb{D}} |f'(z)|^{2}(1 - |\sigma_{a}(z)|^{2})^{p} dA(z)\right)^{1/2} < \infty. \end{align} $$
$$ \begin{align} \|f\|_{Q_{p}}^{2} = |f(0)|+ \sup_{a\in\mathbb{D}}\left( \int_{\mathbb{D}} |f'(z)|^{2}(1 - |\sigma_{a}(z)|^{2})^{p} dA(z)\right)^{1/2} < \infty. \end{align} $$
Clearly,
![]() $Q_{p_{1}} \subseteq Q_{p_{2}}$
for
$Q_{p_{1}} \subseteq Q_{p_{2}}$
for
![]() $0 < p_1 < p_2 < \infty $
and for
$0 < p_1 < p_2 < \infty $
and for
![]() $0<p<1$
$0<p<1$
where
and
![]() $\Delta $
is the Laplacian [Reference Bao, Mashreghi, Pouliasis and Wulan5]. We have that
$\Delta $
is the Laplacian [Reference Bao, Mashreghi, Pouliasis and Wulan5]. We have that
![]() $Q_1 = \text {BMOA}$
and
$Q_1 = \text {BMOA}$
and
![]() $Q_p \subsetneq \text {BMOA}$
when
$Q_p \subsetneq \text {BMOA}$
when
![]() $0 < p < 1$
. We refer to J. Xiao’s monographs [Reference Xiao23] and [Reference Xiao24] for more results on
$0 < p < 1$
. We refer to J. Xiao’s monographs [Reference Xiao23] and [Reference Xiao24] for more results on
![]() $Q_p$
spaces.
$Q_p$
spaces.
3 Proof of Theorem 1.1
It is well known that
![]() $H$
does not map
$H$
does not map
![]() $H^\infty $
into its self. Indeed, by (1.1), we note that
$H^\infty $
into its self. Indeed, by (1.1), we note that
and this function does not belong to
![]() $H^\infty $
.
$H^\infty $
.
Proof of Theorem 1.1
In [Reference Lanucha, Nowak and Pavlovic22] Lanucha, Nowak, and Pavlovic proved that
![]() $H$
is bounded from
$H$
is bounded from
![]() $H^\infty $
into
$H^\infty $
into
![]() $\text {BMOA}$
. By using the same computations of Danikas and Siskakis [Reference Danikas and Siskakis13, Theorem 1] and the expression (1.2) for the
$\text {BMOA}$
. By using the same computations of Danikas and Siskakis [Reference Danikas and Siskakis13, Theorem 1] and the expression (1.2) for the
![]() $\text {BMOA}$
norm, we realize that
$\text {BMOA}$
norm, we realize that
from which it follows that
In order to prove the upper bound for the norm of
![]() $H$
, because of (1.1), we note that
$H$
, because of (1.1), we note that
The convergence of the integral and the analyticity of the function f guarantee that we can change the path of integration to
which describes circular arcs contained in
![]() $\mathbb {D}$
. Therefore, we obtain that
$\mathbb {D}$
. Therefore, we obtain that
 $$ \begin{align*} H(f)'(w)=\frac{1}{1-w}\int_{0}^{1}\frac{s}{(s-1)w+1}f\left(\frac{s}{(s-1)w+1}\right)ds. \end{align*} $$
$$ \begin{align*} H(f)'(w)=\frac{1}{1-w}\int_{0}^{1}\frac{s}{(s-1)w+1}f\left(\frac{s}{(s-1)w+1}\right)ds. \end{align*} $$
The quantity inside the integral is
![]() $\psi _{s}(w)f(\psi _{s}(w))$
, where
$\psi _{s}(w)f(\psi _{s}(w))$
, where
maps the unit disc into itself for each
![]() $0\leq s<1$
. Thus, in absolute value,
$0\leq s<1$
. Thus, in absolute value,
for each
![]() $w \in \mathbb {D}$
and
$w \in \mathbb {D}$
and
![]() $0\leq s\leq 1$
. Consequently,
$0\leq s\leq 1$
. Consequently,
 $$ \begin{align*} \begin{aligned} \|H(f)\|_{\mathit{BMOA}}&= |H(f)(0)|+\sup_{a\in\mathbb{D}}\left(\int_{\mathbb{D}}\left|H(f)'(z)\right|^{2}\log\left|\frac{1-\overline{a}z}{a-z}\right|^{2}dA(z)\right)^{1/2}\\ &\leq \left(1+\sup_{a\in\mathbb{D}}\left(\int_{\mathbb{D}}\left|\frac{1}{1-z}\right|^{2}\log\left|\frac{1-\overline{a}z}{a-z}\right|^{2}dA(z)\right)^{1/2}\right)\|f\|_{H^{\infty}}\\ &=\left(1+\frac{\pi}{\sqrt{2}}\right)\|f\|_{H^{\infty}}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|H(f)\|_{\mathit{BMOA}}&= |H(f)(0)|+\sup_{a\in\mathbb{D}}\left(\int_{\mathbb{D}}\left|H(f)'(z)\right|^{2}\log\left|\frac{1-\overline{a}z}{a-z}\right|^{2}dA(z)\right)^{1/2}\\ &\leq \left(1+\sup_{a\in\mathbb{D}}\left(\int_{\mathbb{D}}\left|\frac{1}{1-z}\right|^{2}\log\left|\frac{1-\overline{a}z}{a-z}\right|^{2}dA(z)\right)^{1/2}\right)\|f\|_{H^{\infty}}\\ &=\left(1+\frac{\pi}{\sqrt{2}}\right)\|f\|_{H^{\infty}}, \end{aligned} \end{align*} $$
where in the last equality we have used the fact that
![]() $\|\log (1-z)\|_{\text {BMOA}}=\frac {\pi }{\sqrt {2}}$
, see [Reference Danikas12]. Due to the above inequality and (3.2), we have the conclusion.
$\|\log (1-z)\|_{\text {BMOA}}=\frac {\pi }{\sqrt {2}}$
, see [Reference Danikas12]. Due to the above inequality and (3.2), we have the conclusion.
The proof of Theorem 1.1 provides a usefully identity for the derivative
![]() $H(f)'$
when
$H(f)'$
when
![]() $f\in H^\infty $
. Indeed
$f\in H^\infty $
. Indeed
with
![]() $b\in H^\infty $
and
$b\in H^\infty $
and
![]() $\|b\|_{H^{\infty }}\leq \|f\|_{H^{\infty }}$
.
$\|b\|_{H^{\infty }}\leq \|f\|_{H^{\infty }}$
.
4 Hilbert matrix operator into mean Lipschitz spaces
The inclusion
![]() $H\left ( H^\infty \right )\subset \mathit{BMOA}$
can be refined to
$H\left ( H^\infty \right )\subset \mathit{BMOA}$
can be refined to
 $$ \begin{align*}H\left( H^\infty\right)\subseteq \bigcap_{1<p<\infty}\Lambda\left(p,\frac{1}{p}\right). \end{align*} $$
$$ \begin{align*}H\left( H^\infty\right)\subseteq \bigcap_{1<p<\infty}\Lambda\left(p,\frac{1}{p}\right). \end{align*} $$
For
![]() $1 < p < \infty $
and
$1 < p < \infty $
and
![]() $0 < \alpha \leq 1,$
the mean Lipschitz space
$0 < \alpha \leq 1,$
the mean Lipschitz space
![]() $\Lambda (p,\alpha )$
consists all the analytic functions f on the unit disc for which
$\Lambda (p,\alpha )$
consists all the analytic functions f on the unit disc for which
The spaces
![]() $\Lambda (p,\frac {1}{p})$
with
$\Lambda (p,\frac {1}{p})$
with
![]() $ 1 < p < \infty $
grow in size with p, they are all subspaces of
$ 1 < p < \infty $
grow in size with p, they are all subspaces of
![]() $\text {BMOA}$
and they all contain unbounded functions such as
$\text {BMOA}$
and they all contain unbounded functions such as
![]() $\log (1-z)$
, see [Reference Bourdon, Shapiro and Sledd11].
$\log (1-z)$
, see [Reference Bourdon, Shapiro and Sledd11].
Theorem 4.1 The Hilbert matrix operator
![]() $H$
is bounded from
$H$
is bounded from
![]() $H^\infty $
into
$H^\infty $
into
![]() $\Lambda (p,1/p)$
and
$\Lambda (p,1/p)$
and
Proof The proof is similar to Theorem 1.1. By [Reference Hedenmalm, Korenblum and Zhu21, Theorem 1.7], we have that
![]() $\log (1-z) \in \Lambda (p,\frac {1}{p}) $
for
$\log (1-z) \in \Lambda (p,\frac {1}{p}) $
for
![]() $1<p<\infty $
with
$1<p<\infty $
with
 $$ \begin{align*}\|\log(1-z)\|_{\Lambda(p,\frac{1}{p})}=\sup_{0<r<1} (1-r)^{1-1/p}\left( \int_{\mathbb{T}} \left| \frac{1}{1-re^{-i\theta}}\right|^p d\theta\right)^{1/p}. \end{align*} $$
$$ \begin{align*}\|\log(1-z)\|_{\Lambda(p,\frac{1}{p})}=\sup_{0<r<1} (1-r)^{1-1/p}\left( \int_{\mathbb{T}} \left| \frac{1}{1-re^{-i\theta}}\right|^p d\theta\right)^{1/p}. \end{align*} $$
By (3.3), we have that
 $$ \begin{align*} (1-r^2)^{1-1/p}M_p(r,H(f)')&\leq (1-r^2)^{1-1/p}\left( \int_{\mathbb{T}} \left| \frac{1}{1-re^{-i\theta}}\right|^p d\theta\right)^{1/p}\|f\|_{H^\infty} \\ &\leq \|\log(1-z)\|_{\Lambda(p,\frac{1}{p})}\|f\|_{H^\infty}. \end{align*} $$
$$ \begin{align*} (1-r^2)^{1-1/p}M_p(r,H(f)')&\leq (1-r^2)^{1-1/p}\left( \int_{\mathbb{T}} \left| \frac{1}{1-re^{-i\theta}}\right|^p d\theta\right)^{1/p}\|f\|_{H^\infty} \\ &\leq \|\log(1-z)\|_{\Lambda(p,\frac{1}{p})}\|f\|_{H^\infty}. \end{align*} $$
Consequently
We point out that the exact value of the
![]() $\|H\|_{H^\infty \to \Lambda (p,\frac {1}{p})}$
is not provided by Theorem 4.1. However, we are able to compute it when
$\|H\|_{H^\infty \to \Lambda (p,\frac {1}{p})}$
is not provided by Theorem 4.1. However, we are able to compute it when
![]() $p=2$
.
$p=2$
.
Proposition 4.2 The Hilbert matrix operator
![]() $H$
is bounded from
$H$
is bounded from
![]() $H^\infty $
into
$H^\infty $
into
![]() $\Lambda (2,1/2)$
and
$\Lambda (2,1/2)$
and
Proof Since in Theorem 4.1 we have already shown the upper bound, we have to provide only the estimate from below. Since
![]() $H(1)(1)=1$
and
$H(1)(1)=1$
and
we have
 $$ \begin{align*} \|H\|_{H^\infty \to \Lambda(2,\frac{1}{2})}&\geq \|H(1)\|_{\Lambda(2,\frac{1}{2})}\\&=1+\sup_{0<r<1}M_2(r,H(1)')(1-r^{2})^{1/2}\\&\geq 1+ \lim_{r\to1}M_2(r,S\,H(1)')(1-r^{2})^{1/2}\\&\geq 1+\lim_{r\to1}|M_2(r,f_1)-M_2(r,f_2)|(1-r^{2})^{1/2}\\&=1+\lim_{r\to1}M_{2}(r, \left(\log(1-z)\right)')(1-r^{2})^{1/2}=1+\|\log(1-z)\|_{\Lambda(2,\frac{1}{2})}. \end{align*} $$
$$ \begin{align*} \|H\|_{H^\infty \to \Lambda(2,\frac{1}{2})}&\geq \|H(1)\|_{\Lambda(2,\frac{1}{2})}\\&=1+\sup_{0<r<1}M_2(r,H(1)')(1-r^{2})^{1/2}\\&\geq 1+ \lim_{r\to1}M_2(r,S\,H(1)')(1-r^{2})^{1/2}\\&\geq 1+\lim_{r\to1}|M_2(r,f_1)-M_2(r,f_2)|(1-r^{2})^{1/2}\\&=1+\lim_{r\to1}M_{2}(r, \left(\log(1-z)\right)')(1-r^{2})^{1/2}=1+\|\log(1-z)\|_{\Lambda(2,\frac{1}{2})}. \end{align*} $$
Since
![]() $\|\log (1-z)\|_{\Lambda (2,\frac {1}{2})}=1$
, conclusion follows.
$\|\log (1-z)\|_{\Lambda (2,\frac {1}{2})}=1$
, conclusion follows.
5 Hilbert matrix operator into conformally invariant Dirichlet spaces
We start by proving Theorem 1.2.
Proof of Theorem 1.2
The proof of Theorem 1.2 is similar to [Reference Bao, Wulan and Ye6, Theorem 1.2]. Nevertheless, for completeness, we include it here.
![]() $(i)\Rightarrow (ii)$
. Let
$(i)\Rightarrow (ii)$
. Let
![]() $H\left (H^\infty \right ) \subseteq M(D_{\mu })$
. Since
$H\left (H^\infty \right ) \subseteq M(D_{\mu })$
. Since
![]() $ H(1) \in H\left (H^\infty \right )$
, we have that
$ H(1) \in H\left (H^\infty \right )$
, we have that
![]() $M(D_{\mu })$
is not trivial and [Reference Bao, Mashreghi, Pouliasis and Wulan5, Theorem 3.3] implies that
$M(D_{\mu })$
is not trivial and [Reference Bao, Mashreghi, Pouliasis and Wulan5, Theorem 3.3] implies that
In order to prove that
![]() $\log (1-z)$
is in
$\log (1-z)$
is in
![]() $M(D_{\mu })$
, according to (1.4), it is enough to show that
$M(D_{\mu })$
, according to (1.4), it is enough to show that
 $$ \begin{align} \sup_{\phi \in \text{Aut}(\mathbb{D})}\int_{\mathbb{D}\setminus \frac{1}{2}\mathbb{D}}\left|\frac{1}{1-z}\right|^{2}V_{\mu}(\phi(z))dA(z)<\infty. \end{align} $$
$$ \begin{align} \sup_{\phi \in \text{Aut}(\mathbb{D})}\int_{\mathbb{D}\setminus \frac{1}{2}\mathbb{D}}\left|\frac{1}{1-z}\right|^{2}V_{\mu}(\phi(z))dA(z)<\infty. \end{align} $$
Indeed
 $$ \begin{align*} \infty&>\sup_{\phi \in \text{Aut}(\mathbb{D})}\int_{\mathbb{D}\setminus \frac{1}{2}\mathbb{D}}\left|H(1)'(z)\right|^{2}V_{\mu}(\phi(z))dA(z)\\ &=\sup_{\phi \in \text{Aut}(\mathbb{D})}\int_{\mathbb{D}\setminus \frac{1}{2}\mathbb{D}}\left|\frac{1}{z}\frac{1}{1-z}-\frac{1}{z^{2}}\log\frac{1}{1-z}\right|^{2}V_{\mu}(\phi(z))dA(z). \end{align*} $$
$$ \begin{align*} \infty&>\sup_{\phi \in \text{Aut}(\mathbb{D})}\int_{\mathbb{D}\setminus \frac{1}{2}\mathbb{D}}\left|H(1)'(z)\right|^{2}V_{\mu}(\phi(z))dA(z)\\ &=\sup_{\phi \in \text{Aut}(\mathbb{D})}\int_{\mathbb{D}\setminus \frac{1}{2}\mathbb{D}}\left|\frac{1}{z}\frac{1}{1-z}-\frac{1}{z^{2}}\log\frac{1}{1-z}\right|^{2}V_{\mu}(\phi(z))dA(z). \end{align*} $$
Since
 $$ \begin{align*} \sup_{\phi \in \text{Aut}(\mathbb{D})}\int_{\mathbb{D}\setminus \frac{1}{2}\mathbb{D}}\left|\frac{1}{z^{2}}\log\frac{1}{1-z}\right|^{2}&V_{\mu}(\phi(z))dA(z)\leq\\ &16\sup_{w\in\mathbb{D}} V_{\mu}(w)\int_{\mathbb{D}\setminus \frac{1}{2}\mathbb{D}}\left|\log\frac{1}{1-z}\right|^{2}dA(z)<\infty, \end{align*} $$
$$ \begin{align*} \sup_{\phi \in \text{Aut}(\mathbb{D})}\int_{\mathbb{D}\setminus \frac{1}{2}\mathbb{D}}\left|\frac{1}{z^{2}}\log\frac{1}{1-z}\right|^{2}&V_{\mu}(\phi(z))dA(z)\leq\\ &16\sup_{w\in\mathbb{D}} V_{\mu}(w)\int_{\mathbb{D}\setminus \frac{1}{2}\mathbb{D}}\left|\log\frac{1}{1-z}\right|^{2}dA(z)<\infty, \end{align*} $$
(5.1) holds.
![]() $(ii)\Rightarrow (iii)$
. Let
$(ii)\Rightarrow (iii)$
. Let
![]() $\log (1-z)\in M(D_{\mu })$
. By using (1.4) and a change of variables, we have that
$\log (1-z)\in M(D_{\mu })$
. By using (1.4) and a change of variables, we have that
 $$ \begin{align*}\sup_{a\in\mathbb{D},\lambda\in\mathbb{T}}\int_{\mathbb{D}}\left|\frac{1}{1-\lambda\sigma_{a}(z)}\right|^{2}\frac{(1-|a|^{2})^{2}}{|1-\overline{a}z|^{4}}V_{\mu}(z)dA(z)<\infty. \end{align*} $$
$$ \begin{align*}\sup_{a\in\mathbb{D},\lambda\in\mathbb{T}}\int_{\mathbb{D}}\left|\frac{1}{1-\lambda\sigma_{a}(z)}\right|^{2}\frac{(1-|a|^{2})^{2}}{|1-\overline{a}z|^{4}}V_{\mu}(z)dA(z)<\infty. \end{align*} $$
Taking
![]() $a=0$
in the above condition, we have
$a=0$
in the above condition, we have
 $$ \begin{align*}\sup_{\lambda\in\mathbb{T}}\int_{\mathbb{D}}\frac{V_{\mu}(z)}{\left|1-\lambda z\right|^{2}}dA(z)<\infty. \end{align*} $$
$$ \begin{align*}\sup_{\lambda\in\mathbb{T}}\int_{\mathbb{D}}\frac{V_{\mu}(z)}{\left|1-\lambda z\right|^{2}}dA(z)<\infty. \end{align*} $$
![]() $(iii)\Leftrightarrow (iv)$
. We set
$(iii)\Leftrightarrow (iv)$
. We set
![]() $(1-|z|^2)d\nu (z)=V_{\mu }(z)dA(z)$
and apply [Reference Bao, Göğüş and Pouliasis4, Lemma 2.2].
$(1-|z|^2)d\nu (z)=V_{\mu }(z)dA(z)$
and apply [Reference Bao, Göğüş and Pouliasis4, Lemma 2.2].
![]() $(iv)\Rightarrow (i)$
. Let
$(iv)\Rightarrow (i)$
. Let
![]() $f \in H^\infty $
. By using (3.3), we note that
$f \in H^\infty $
. By using (3.3), we note that
 $$ \begin{align*} &\int_{\mathbb{D}} \left|H(f)'(z)\right|^{2}V_{\mu}(\phi(z))dA(z)\\ &\qquad\leq \int_{\mathbb{D}} \left|\frac{1}{1-z}\right|^{2}V_{\mu}(\phi(z))dA(z)\,\|f\|_{\infty}^2\\ &\qquad =\int_{\mathbb{D}} \left|\frac{1}{1-\phi(z)}\right|^{2} \frac{\left(1-|a|^2\right)^2}{|1-\overline{a}z|^4}V_{\mu}(z)dA(z)\,\|f\|_{\infty}^2, \end{align*} $$
$$ \begin{align*} &\int_{\mathbb{D}} \left|H(f)'(z)\right|^{2}V_{\mu}(\phi(z))dA(z)\\ &\qquad\leq \int_{\mathbb{D}} \left|\frac{1}{1-z}\right|^{2}V_{\mu}(\phi(z))dA(z)\,\|f\|_{\infty}^2\\ &\qquad =\int_{\mathbb{D}} \left|\frac{1}{1-\phi(z)}\right|^{2} \frac{\left(1-|a|^2\right)^2}{|1-\overline{a}z|^4}V_{\mu}(z)dA(z)\,\|f\|_{\infty}^2, \end{align*} $$
where we have chosen
Consequently,
![]() $H$
is bounded from
$H$
is bounded from
![]() $H^\infty $
into
$H^\infty $
into
![]() $M(D_\mu )$
if
$M(D_\mu )$
if
 $$ \begin{align*} I=&\sup_{a\in\mathbb{D,\lambda\in\mathbb{T}}}\int_{\mathbb{D}}\left|\frac{1}{1-\lambda\sigma_{a}(z)}\right|^{2} \frac{(1-|a|^{2})^{2}}{|1- \overline{a}z|^{4}}V_{\mu}(z)dA(z)\\ =&\sup_{a\in\mathbb{D,\lambda\in\mathbb{T}}}\frac{(1-|a|^{2})^{2}}{|1- \lambda a|^{2}}\int_{\mathbb{D}}\left|\frac{1}{1+\frac{\lambda-\overline{a}}{1-\lambda a}z}\right|^{2} \frac{1}{|1- \overline{a}z|^{2}}V_{\mu}(z)dA(z)<\infty. \end{align*} $$
$$ \begin{align*} I=&\sup_{a\in\mathbb{D,\lambda\in\mathbb{T}}}\int_{\mathbb{D}}\left|\frac{1}{1-\lambda\sigma_{a}(z)}\right|^{2} \frac{(1-|a|^{2})^{2}}{|1- \overline{a}z|^{4}}V_{\mu}(z)dA(z)\\ =&\sup_{a\in\mathbb{D,\lambda\in\mathbb{T}}}\frac{(1-|a|^{2})^{2}}{|1- \lambda a|^{2}}\int_{\mathbb{D}}\left|\frac{1}{1+\frac{\lambda-\overline{a}}{1-\lambda a}z}\right|^{2} \frac{1}{|1- \overline{a}z|^{2}}V_{\mu}(z)dA(z)<\infty. \end{align*} $$
We set
![]() $\eta =\frac {\lambda -\overline {a}}{1-\lambda a}$
,
$\eta =\frac {\lambda -\overline {a}}{1-\lambda a}$
,
![]() $|\eta |=1$
. Through a change of variables, we get
$|\eta |=1$
. Through a change of variables, we get
 $$ \begin{align*} I&=\sup_{a\in\mathbb{D,\lambda\in\mathbb{T}}}\frac{(1-|a|^{2})^{2}}{|1- \lambda a|^{2}}\int_{\mathbb{D}}\left|\frac{1}{1+\zeta}\right|^{2} \frac{1}{|1- \overline{a\eta}\zeta|^{2}}V_{\mu}(\overline{\eta}\zeta)dA(\zeta)\\ &=\sup_{a\in\mathbb{D,\lambda\in\mathbb{T}}}\int_{\mathbb{D}}\left|\frac{1}{1+\zeta}+\frac{\overline{a\eta}\zeta}{1- \overline{a\eta}\zeta}\right|^{2}V_{\mu}(\overline{\eta}\zeta)dA(\zeta)\\ &\leq C\left(\sup_{\eta\in\mathbb{T}}\int_{\mathbb{D}}\left|\frac{1}{1+\zeta}\right|^{2}V_{\mu}(\overline{\eta}\zeta)dA(\zeta)+\sup_{a\in\mathbb{D,\lambda\in\mathbb{T}}}\int_{\mathbb{D}}\left|\frac{1}{1- \overline{a\eta}\zeta}\right|^{2}V_{\mu}(\overline{\eta}\zeta)dA(\zeta)\right) \\ &\leq C \sup_{\eta\in\mathbb{T}}\int_{\mathbb{D}}\left|\frac{1}{1+\eta z}\right|^{2}V_{\mu}(z)dA(z)+\sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\left|\frac{1}{1- \overline{a}z}\right|^{2}V_{\mu}(z)dA(z). \end{align*} $$
$$ \begin{align*} I&=\sup_{a\in\mathbb{D,\lambda\in\mathbb{T}}}\frac{(1-|a|^{2})^{2}}{|1- \lambda a|^{2}}\int_{\mathbb{D}}\left|\frac{1}{1+\zeta}\right|^{2} \frac{1}{|1- \overline{a\eta}\zeta|^{2}}V_{\mu}(\overline{\eta}\zeta)dA(\zeta)\\ &=\sup_{a\in\mathbb{D,\lambda\in\mathbb{T}}}\int_{\mathbb{D}}\left|\frac{1}{1+\zeta}+\frac{\overline{a\eta}\zeta}{1- \overline{a\eta}\zeta}\right|^{2}V_{\mu}(\overline{\eta}\zeta)dA(\zeta)\\ &\leq C\left(\sup_{\eta\in\mathbb{T}}\int_{\mathbb{D}}\left|\frac{1}{1+\zeta}\right|^{2}V_{\mu}(\overline{\eta}\zeta)dA(\zeta)+\sup_{a\in\mathbb{D,\lambda\in\mathbb{T}}}\int_{\mathbb{D}}\left|\frac{1}{1- \overline{a\eta}\zeta}\right|^{2}V_{\mu}(\overline{\eta}\zeta)dA(\zeta)\right) \\ &\leq C \sup_{\eta\in\mathbb{T}}\int_{\mathbb{D}}\left|\frac{1}{1+\eta z}\right|^{2}V_{\mu}(z)dA(z)+\sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\left|\frac{1}{1- \overline{a}z}\right|^{2}V_{\mu}(z)dA(z). \end{align*} $$
By using conditions
![]() $(iii)$
and
$(iii)$
and
![]() $(iv)$
, the proof is complete.
$(iv)$
, the proof is complete.
Remark 5.1 Let
 $$ \begin{align*}d\mu_{a}(z)=\Delta\left(\frac{1}{\left(\log\frac{e^{1+a}}{1-|z|^{2}}\right)^{a}}\right)dA(z) \end{align*} $$
$$ \begin{align*}d\mu_{a}(z)=\Delta\left(\frac{1}{\left(\log\frac{e^{1+a}}{1-|z|^{2}}\right)^{a}}\right)dA(z) \end{align*} $$
with
![]() $z \in \mathbb {D}$
,
$z \in \mathbb {D}$
,
![]() $a \in (0,\infty )$
and
$a \in (0,\infty )$
and
![]() $\Delta $
the classical Laplace operator. The proof [Reference Bao, Wulan and Ye6, Theorem 1.2] gives that
$\Delta $
the classical Laplace operator. The proof [Reference Bao, Wulan and Ye6, Theorem 1.2] gives that
-
(i) If
 $0 < a \leq 1$
, then
$0 < a \leq 1$
, then
 $M(D_{\mu _{a}} )$
is not trivial and
$M(D_{\mu _{a}} )$
is not trivial and
 $H(H^\infty ) \not \subseteq M(D_{\mu _{a}} )$
.
$H(H^\infty ) \not \subseteq M(D_{\mu _{a}} )$
. -
(ii) If
 $a>1$
, then
$a>1$
, then
 $H(H^\infty ) \not \subseteq M(D_{\mu _{a}} ) \not \subseteq \bigcap _{0<p<\infty } Q_p$
.
$H(H^\infty ) \not \subseteq M(D_{\mu _{a}} ) \not \subseteq \bigcap _{0<p<\infty } Q_p$
.
Consequently, there are measures
![]() $\mu $
for which
$\mu $
for which
![]() $H(H^\infty ) \not \subseteq M(D_\mu ).$
$H(H^\infty ) \not \subseteq M(D_\mu ).$
6 Norm of the Hilbert matrix operator into conformally invariant Dirichlet spaces
For particular measures
![]() $\mu $
, it is possible to compute
$\mu $
, it is possible to compute
![]() $\|H\|_{H^\infty \to M(D_\mu )}$
. We need two preliminary lemmas.
$\|H\|_{H^\infty \to M(D_\mu )}$
. We need two preliminary lemmas.
Lemma 6.1 Let
![]() $d\mu (z)$
be a radial measure. Then
$d\mu (z)$
be a radial measure. Then
![]() $U_\mu (z)dA(z)$
is also a radial measure.
$U_\mu (z)dA(z)$
is also a radial measure.
Proof Let
![]() $\lambda \in \mathbb {T}$
. We note that
$\lambda \in \mathbb {T}$
. We note that
 $$ \begin{align*} U_\mu(\lambda z)=&\int_{\mathbb{D}} \log \left\vert \frac{1-\overline{w}\lambda z}{\lambda z-w}\right\vert d\mu(w)=\int_{\mathbb{D}} \log \left\vert \frac{1-\overline{w\overline{\lambda}}z}{z-\overline{\lambda} w}\right\vert d\mu(w)\\ =&\int_{\mathbb{D}} \log \left\vert \frac{1-\overline{w\overline{\lambda}}z}{z-\overline{\lambda} w}\right\vert d\mu(\overline{\lambda}w)=U_\mu(z). \end{align*} $$
$$ \begin{align*} U_\mu(\lambda z)=&\int_{\mathbb{D}} \log \left\vert \frac{1-\overline{w}\lambda z}{\lambda z-w}\right\vert d\mu(w)=\int_{\mathbb{D}} \log \left\vert \frac{1-\overline{w\overline{\lambda}}z}{z-\overline{\lambda} w}\right\vert d\mu(w)\\ =&\int_{\mathbb{D}} \log \left\vert \frac{1-\overline{w\overline{\lambda}}z}{z-\overline{\lambda} w}\right\vert d\mu(\overline{\lambda}w)=U_\mu(z). \end{align*} $$
Therefore
from which the lemma follows.
Lemma 6.2 Let
![]() $d\mu (z)$
be a positive, radial measure such that
$d\mu (z)$
be a positive, radial measure such that
![]() $\log (1-z) \in M(D_\mu )$
. Then
$\log (1-z) \in M(D_\mu )$
. Then
 $$ \begin{align*}\sum_{n=1}^{\infty} \widehat{U_\mu}_{2n+1}<\infty , \end{align*} $$
$$ \begin{align*}\sum_{n=1}^{\infty} \widehat{U_\mu}_{2n+1}<\infty , \end{align*} $$
where
Proof We note that
 $$ \begin{align*} \sum_{n=1}^\infty \widehat{U_\mu}_{2n+1}=&\sum_{n=1}^\infty \int_{0}^1 r^{2n}U_\mu(r)rdr=\sum_{n=0}^\infty \int_{0}^1 r^{2n}U_\mu(r)rdr-\widehat{U_\mu}_{1}\\ \leq & \int_{0}^1 \frac{1}{1-r^2}U_\mu(r)rdr=\int_{0}^1 \int_{0}^{2\pi} \frac{1}{1-e^{i\theta}r}\frac{1}{1-e^{-i\theta}r} \frac{d\theta}{2\pi} U_\mu(r)rdr\\ =&\int_{\mathbb{D}} \left\vert \frac{1}{1-z}\right\vert^2 U_\mu(z)dA(z)\leq\|\log(1-z)\|_{M(D_\mu)}^2. \end{align*} $$
$$ \begin{align*} \sum_{n=1}^\infty \widehat{U_\mu}_{2n+1}=&\sum_{n=1}^\infty \int_{0}^1 r^{2n}U_\mu(r)rdr=\sum_{n=0}^\infty \int_{0}^1 r^{2n}U_\mu(r)rdr-\widehat{U_\mu}_{1}\\ \leq & \int_{0}^1 \frac{1}{1-r^2}U_\mu(r)rdr=\int_{0}^1 \int_{0}^{2\pi} \frac{1}{1-e^{i\theta}r}\frac{1}{1-e^{-i\theta}r} \frac{d\theta}{2\pi} U_\mu(r)rdr\\ =&\int_{\mathbb{D}} \left\vert \frac{1}{1-z}\right\vert^2 U_\mu(z)dA(z)\leq\|\log(1-z)\|_{M(D_\mu)}^2. \end{align*} $$
Since
![]() $\log (1-z) \in M(D_\mu )$
, the conclusion follows.
$\log (1-z) \in M(D_\mu )$
, the conclusion follows.
When
![]() $d\mu (z)$
is a radial measure, (1.3) becomes
$d\mu (z)$
is a radial measure, (1.3) becomes
 $$ \begin{align*} \|f\|_{M(D_{\mu})}& =|f(0)|+\sup_{a \in \mathbb{D}, \lambda \in \mathbb{T}}\left(\int_{\mathbb{D}} |f'(w)|^{2}U_{\mu}(\lambda\sigma_a(w))dA(w)\right)^{1/2}\\ &=|f(0)|+\sup_{a \in \mathbb{D}}\left(\int_{\mathbb{D}} |f'(w)|^{2}U_{\mu}(\sigma_a(w))dA(w)\right)^{1/2}. \end{align*} $$
$$ \begin{align*} \|f\|_{M(D_{\mu})}& =|f(0)|+\sup_{a \in \mathbb{D}, \lambda \in \mathbb{T}}\left(\int_{\mathbb{D}} |f'(w)|^{2}U_{\mu}(\lambda\sigma_a(w))dA(w)\right)^{1/2}\\ &=|f(0)|+\sup_{a \in \mathbb{D}}\left(\int_{\mathbb{D}} |f'(w)|^{2}U_{\mu}(\sigma_a(w))dA(w)\right)^{1/2}. \end{align*} $$
Proposition 6.3 Let
![]() $d\mu (z)$
be a positive, radial, Borel measure on
$d\mu (z)$
be a positive, radial, Borel measure on
![]() $\mathbb {D}$
. Then
$\mathbb {D}$
. Then
 $$ \begin{align*} \|\log(1-z)\|^2_{M(D_\mu)}= \int_{\mathbb{D}}\left|\frac{2}{1-z^2}\right|^{2}U_{\mu}(z)dA(z). \end{align*} $$
$$ \begin{align*} \|\log(1-z)\|^2_{M(D_\mu)}= \int_{\mathbb{D}}\left|\frac{2}{1-z^2}\right|^{2}U_{\mu}(z)dA(z). \end{align*} $$
Proof Since the measure
![]() $d\mu (z)$
is radial, we observe that
$d\mu (z)$
is radial, we observe that
 $$ \begin{align*} \|\log(1-z)\|_{M(D_\mu)}&=\sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\left|\frac{1}{1-z}\right|^{2}U_{\mu}(\sigma_{a}(z))dA(z)\\ &=\sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\left|\frac{1}{1-\sigma_{a}(z)}\right|^{2}|\sigma_{a}'(z)|^{2}U_{\mu}(z)dA(z)\\ &=\sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\frac{(1-|a|^{2})^{2}}{|1-a+(1-\overline{a})z|^{2}}\frac{1}{|1-\overline{a}z|^{2}}\,U_{\mu}(z)dA(z)\\ &=\sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\left|\frac{1-\overline{a}}{1-a+(1-\overline{a})z}+\frac{\overline{a}}{1-\overline{a}z}\right|^{2}U_{\mu}(z)dA(z). \end{align*} $$
$$ \begin{align*} \|\log(1-z)\|_{M(D_\mu)}&=\sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\left|\frac{1}{1-z}\right|^{2}U_{\mu}(\sigma_{a}(z))dA(z)\\ &=\sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\left|\frac{1}{1-\sigma_{a}(z)}\right|^{2}|\sigma_{a}'(z)|^{2}U_{\mu}(z)dA(z)\\ &=\sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\frac{(1-|a|^{2})^{2}}{|1-a+(1-\overline{a})z|^{2}}\frac{1}{|1-\overline{a}z|^{2}}\,U_{\mu}(z)dA(z)\\ &=\sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\left|\frac{1-\overline{a}}{1-a+(1-\overline{a})z}+\frac{\overline{a}}{1-\overline{a}z}\right|^{2}U_{\mu}(z)dA(z). \end{align*} $$
In particular, by using the power series expansion, we have that
 $$ \begin{align*} \|\log(1-z) \|_{M(D_\mu)} &=\sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\left|\sum_{n=0}^{\infty}\left((-1)^{n}\left(\frac{1-\overline{a}}{1-a}\right)^{n+1}+\overline{a}^{n+1}\right)z^{n}\right|^{2}U_{\mu}(z)dA(z)\\&=\sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\left|\sum_{n=0}^{\infty}\left(-\left(\frac{1-\overline{a}}{1-a}\right)^{n+1}+(\overline{-a})^{n+1}\right)(-z)^{n}\right|^{2}U_{\mu}(z)dA(z)\\&=\sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\left|\sum_{n=1}^{\infty}\left(-\left(\frac{1-\overline{a}}{1-a}\right)^{n}+(\overline{-a})^{n}\right)(-z)^{n-1}\right|^{2}U_{\mu}(z)dA(z). \end{align*} $$
$$ \begin{align*} \|\log(1-z) \|_{M(D_\mu)} &=\sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\left|\sum_{n=0}^{\infty}\left((-1)^{n}\left(\frac{1-\overline{a}}{1-a}\right)^{n+1}+\overline{a}^{n+1}\right)z^{n}\right|^{2}U_{\mu}(z)dA(z)\\&=\sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\left|\sum_{n=0}^{\infty}\left(-\left(\frac{1-\overline{a}}{1-a}\right)^{n+1}+(\overline{-a})^{n+1}\right)(-z)^{n}\right|^{2}U_{\mu}(z)dA(z)\\&=\sup_{a\in\mathbb{D}}\int_{\mathbb{D}}\left|\sum_{n=1}^{\infty}\left(-\left(\frac{1-\overline{a}}{1-a}\right)^{n}+(\overline{-a})^{n}\right)(-z)^{n-1}\right|^{2}U_{\mu}(z)dA(z). \end{align*} $$
Since
![]() $d\mu (z)$
is radial and
$d\mu (z)$
is radial and
we have that
 $$ \begin{align*} \|\log(1-z)\|_{M(D_\mu)}&=\sup_{a\in\mathbb{D}} \int_0^1 \sum_{n=1}^\infty\left\vert-\left(\frac{1-\overline{a}}{1-a}\right)^{n}-\overline{a}^{n}\right\vert^2 r^{2n+1}U_\mu(r)dr\\ &= \sup_{a\in\mathbb{D}} \sum_{n=1}^\infty\left\vert-\left(\frac{1-\overline{a}}{1-a}\right)^{n}-\overline{a}^{n}\right\vert^2 \widehat{U_\mu}_{2n+1}. \end{align*} $$
$$ \begin{align*} \|\log(1-z)\|_{M(D_\mu)}&=\sup_{a\in\mathbb{D}} \int_0^1 \sum_{n=1}^\infty\left\vert-\left(\frac{1-\overline{a}}{1-a}\right)^{n}-\overline{a}^{n}\right\vert^2 r^{2n+1}U_\mu(r)dr\\ &= \sup_{a\in\mathbb{D}} \sum_{n=1}^\infty\left\vert-\left(\frac{1-\overline{a}}{1-a}\right)^{n}-\overline{a}^{n}\right\vert^2 \widehat{U_\mu}_{2n+1}. \end{align*} $$
Hence,
 $$ \begin{align*} \|\log(1-z) \|_{M(D_\mu)}&=\sup_{a\in\mathbb{D}}\sum_{n=1}^\infty \widehat{U_\mu}_{2n+1}\left( 1+|a|^{2n}+2(-1)^{n+1}\Re\left(\frac{1-\overline{a}}{1-a} a\right)^{n}\right). \end{align*} $$
$$ \begin{align*} \|\log(1-z) \|_{M(D_\mu)}&=\sup_{a\in\mathbb{D}}\sum_{n=1}^\infty \widehat{U_\mu}_{2n+1}\left( 1+|a|^{2n}+2(-1)^{n+1}\Re\left(\frac{1-\overline{a}}{1-a} a\right)^{n}\right). \end{align*} $$
With the change of variable
where
![]() $|w|=|a|$
for
$|w|=|a|$
for
![]() $a \in \overline {\mathbb {D}}\setminus \{1\}$
and
$a \in \overline {\mathbb {D}}\setminus \{1\}$
and
![]() $|w|\to 1$
as
$|w|\to 1$
as
![]() $a\to 1$
, we note that the function
$a\to 1$
, we note that the function
 $$ \begin{align*}B(w)= \sum_{n=1}^\infty \widehat{U_\mu}_{2n+1} 2(-1)^{n+1}w^n \end{align*} $$
$$ \begin{align*}B(w)= \sum_{n=1}^\infty \widehat{U_\mu}_{2n+1} 2(-1)^{n+1}w^n \end{align*} $$
is analytic in the unit disc. Moreover, since
![]() $B(w)$
is continuous in
$B(w)$
is continuous in
![]() $\overline {\mathbb {D}}$
due to Lemma 6.2, the maximum principle for harmonic functions tells us that
$\overline {\mathbb {D}}$
due to Lemma 6.2, the maximum principle for harmonic functions tells us that
Consequently,
 $$ \begin{align*} \sup_{w \in \mathbb{T}}\Re B(w)&= -2\inf_{w \in \mathbb{T}}\Re\left( \sum_{n=1}^\infty \widehat{U_\mu}_{2n+1} (-1)^{n}w^n\right)\\ &=-2\inf_{w \in \mathbb{T}}\Re \int_{0}^1 \sum_{n=1}^\infty (-wr^2)^{n}U_\mu(r)rdr\\ &=2\widehat{U_\mu}_{1}-2\inf_{w \in \mathbb{T}}\Re \int_{0}^1 \frac{1}{1+wr^2}U_\mu(r)rdr\\ &=2\left( \widehat{U_\mu}_{1}-\int_{0}^1 \frac{1}{1+r^2}U_\mu(r)rdr\right)=\Re B(1). \end{align*} $$
$$ \begin{align*} \sup_{w \in \mathbb{T}}\Re B(w)&= -2\inf_{w \in \mathbb{T}}\Re\left( \sum_{n=1}^\infty \widehat{U_\mu}_{2n+1} (-1)^{n}w^n\right)\\ &=-2\inf_{w \in \mathbb{T}}\Re \int_{0}^1 \sum_{n=1}^\infty (-wr^2)^{n}U_\mu(r)rdr\\ &=2\widehat{U_\mu}_{1}-2\inf_{w \in \mathbb{T}}\Re \int_{0}^1 \frac{1}{1+wr^2}U_\mu(r)rdr\\ &=2\left( \widehat{U_\mu}_{1}-\int_{0}^1 \frac{1}{1+r^2}U_\mu(r)rdr\right)=\Re B(1). \end{align*} $$
In particular, due to Lemma 6.2, we know that
 $$ \begin{align*} \|\log(1-z) \|_{M(D_\mu)}=&\lim_{a\to 1} \int_{\mathbb{D}}\left|\frac{1}{1-z}\right|^{2}U_{\mu}(\sigma_{a}(z))dA(z)\\ =& \lim_{a\to 1, a\in \mathbb{R}} \int_{\mathbb{D}}\left|\frac{1}{1-z}\right|^{2}U_{\mu}(\sigma_{a}(z))dA(z)\,. \end{align*} $$
$$ \begin{align*} \|\log(1-z) \|_{M(D_\mu)}=&\lim_{a\to 1} \int_{\mathbb{D}}\left|\frac{1}{1-z}\right|^{2}U_{\mu}(\sigma_{a}(z))dA(z)\\ =& \lim_{a\to 1, a\in \mathbb{R}} \int_{\mathbb{D}}\left|\frac{1}{1-z}\right|^{2}U_{\mu}(\sigma_{a}(z))dA(z)\,. \end{align*} $$
Consequently
 $$ \begin{align*} \|\log(1-z) \|_{M(D_\mu)}&=\lim_{a\to 1, a\in \mathbb{R}} \int_{\mathbb{D}}\left|\frac{1}{1-z}\right|^{2}U_{\mu}(\sigma_{a}(z))dA(z)\\ &=\lim_{a\to 1, a\in \mathbb{R}} \int_{\mathbb{D}}\left|\frac{1}{1-\sigma_{a}(z)}\right|^{2}|\sigma_{a}'(z)|^{2}U_{\mu}(z)dA(z)\\ &=\lim_{a\to 1, a\in \mathbb{R}} \int_{\mathbb{D}} \left\vert \frac{1+a}{(1+z)(1-az)}\right\vert^2 U_{\mu}(z)dA(z)\\ &=\int_{\mathbb{D}} \left\vert \frac{2}{1-z^2}\right\vert^2 U_{\mu}(z)dA(z)\,.\\[-34pt] \end{align*} $$
$$ \begin{align*} \|\log(1-z) \|_{M(D_\mu)}&=\lim_{a\to 1, a\in \mathbb{R}} \int_{\mathbb{D}}\left|\frac{1}{1-z}\right|^{2}U_{\mu}(\sigma_{a}(z))dA(z)\\ &=\lim_{a\to 1, a\in \mathbb{R}} \int_{\mathbb{D}}\left|\frac{1}{1-\sigma_{a}(z)}\right|^{2}|\sigma_{a}'(z)|^{2}U_{\mu}(z)dA(z)\\ &=\lim_{a\to 1, a\in \mathbb{R}} \int_{\mathbb{D}} \left\vert \frac{1+a}{(1+z)(1-az)}\right\vert^2 U_{\mu}(z)dA(z)\\ &=\int_{\mathbb{D}} \left\vert \frac{2}{1-z^2}\right\vert^2 U_{\mu}(z)dA(z)\,.\\[-34pt] \end{align*} $$
By using Proposition 6.3, we are now able to prove Theorem 1.3.
Proof of Theorem 1.3
As we saw earlier (3.3), we have that
where
![]() $b\in H^\infty $
and
$b\in H^\infty $
and
![]() $\|b\|_{H^\infty }\leq \|f\|_{H^\infty }$
. Consequently,
$\|b\|_{H^\infty }\leq \|f\|_{H^\infty }$
. Consequently,
 $$ \begin{align*} \|H(f)\|_{M(D_{\mu})}&=|H(f)(0)|+\sup_{\phi \in \text{Aut}(\mathbb{D})}\left(\int_{\mathbb{D}} |H(f)'(w)|^{2}U_{\mu}(\phi(w))dA(w)\right)^{1/2}\\ &=\left\vert\int_{0}^{1}f(t)dt\right\vert+\sup_{\phi \in \text{Aut}(\mathbb{D})}\left(\int_{\mathbb{D}} \left|\frac{b(w)}{1-w}\right|^{2}U_{\mu}(\phi(w))dA(w)\right)^{1/2}\\ &\leq (1+\|\log(1-z) \|_{M(D_\mu)})\|f\|_{H^\infty}. \end{align*} $$
$$ \begin{align*} \|H(f)\|_{M(D_{\mu})}&=|H(f)(0)|+\sup_{\phi \in \text{Aut}(\mathbb{D})}\left(\int_{\mathbb{D}} |H(f)'(w)|^{2}U_{\mu}(\phi(w))dA(w)\right)^{1/2}\\ &=\left\vert\int_{0}^{1}f(t)dt\right\vert+\sup_{\phi \in \text{Aut}(\mathbb{D})}\left(\int_{\mathbb{D}} \left|\frac{b(w)}{1-w}\right|^{2}U_{\mu}(\phi(w))dA(w)\right)^{1/2}\\ &\leq (1+\|\log(1-z) \|_{M(D_\mu)})\|f\|_{H^\infty}. \end{align*} $$
By Proposition 6.3, we have that
 $$ \begin{align} \|H\|_{H^\infty\to M(D_\mu)}\leq 1+\left(\int_{\mathbb{D}}\frac{4}{|1-z^{2}|^{2}}U_{\mu}(z)dA(z)\right)^{1/2}. \end{align} $$
$$ \begin{align} \|H\|_{H^\infty\to M(D_\mu)}\leq 1+\left(\int_{\mathbb{D}}\frac{4}{|1-z^{2}|^{2}}U_{\mu}(z)dA(z)\right)^{1/2}. \end{align} $$
Once again, we recall that
We observe that the function
![]() $h(z)=(1-z)f_1(z)$
is in
$h(z)=(1-z)f_1(z)$
is in
![]() $H^\infty $
with
$H^\infty $
with
Let
![]() $0<a<1$
and set
$0<a<1$
and set
 $$ \begin{align*} I^a= \int_{\mathbb{D}} |f_1(z)|^{2}U_{\mu}(\sigma_{a}(z))dA(z)&=\int_{\mathbb{D}} \left|\frac{h(z)}{(1-z)}\right|^{2}U_{\mu}(\sigma_{a}(z))dA(z)\\ &=\int_{\mathbb{D}} \left|\frac{h(\sigma_{a}(z))}{1-\sigma_{a}(z)}\right|^{2}|\sigma_{a}'(z)|^{2}U_{\mu}(z)dA(z)\\ &=\int_{\mathbb{D}} g_{a}(z)dA(z), \end{align*} $$
$$ \begin{align*} I^a= \int_{\mathbb{D}} |f_1(z)|^{2}U_{\mu}(\sigma_{a}(z))dA(z)&=\int_{\mathbb{D}} \left|\frac{h(z)}{(1-z)}\right|^{2}U_{\mu}(\sigma_{a}(z))dA(z)\\ &=\int_{\mathbb{D}} \left|\frac{h(\sigma_{a}(z))}{1-\sigma_{a}(z)}\right|^{2}|\sigma_{a}'(z)|^{2}U_{\mu}(z)dA(z)\\ &=\int_{\mathbb{D}} g_{a}(z)dA(z), \end{align*} $$
where
 $$ \begin{align*}g_{a}(z)=\left|h(\sigma_{a}(z))\right|^{2}\frac{(1+a)^{2}}{|(1-az)(1+z)|^{2}}U_{\mu}(z). \end{align*} $$
$$ \begin{align*}g_{a}(z)=\left|h(\sigma_{a}(z))\right|^{2}\frac{(1+a)^{2}}{|(1-az)(1+z)|^{2}}U_{\mu}(z). \end{align*} $$
For
![]() $z\in \mathbb {D}$
fixed observe that
$z\in \mathbb {D}$
fixed observe that
![]() $\lim _{a\to 1}\sigma _{a}(z)=1$
. This implies that for each fixed
$\lim _{a\to 1}\sigma _{a}(z)=1$
. This implies that for each fixed
![]() $z\in \mathbb {D}$
,
$z\in \mathbb {D}$
,
![]() $g_a(z)\to 0$
as
$g_a(z)\to 0$
as
![]() $a\to 1$
. Since
$a\to 1$
. Since
![]() $h\in H^\infty $
with norm M, we have
$h\in H^\infty $
with norm M, we have
 $$ \begin{align*}g_{a}(z)\leq k_{a}(z)=M^2 \frac{(1+a)^{2}}{|(1-az)(1+z)|^{2}}U_{\mu}(z). \end{align*} $$
$$ \begin{align*}g_{a}(z)\leq k_{a}(z)=M^2 \frac{(1+a)^{2}}{|(1-az)(1+z)|^{2}}U_{\mu}(z). \end{align*} $$
Moreover
 $$ \begin{align*}k_a(z)\to \frac{4M^2}{|1-z^2|^{2}}U_{\mu}(z), \end{align*} $$
$$ \begin{align*}k_a(z)\to \frac{4M^2}{|1-z^2|^{2}}U_{\mu}(z), \end{align*} $$
as
![]() $a\to 1$
and, by repeating the proof of Proposition 6.3,
$a\to 1$
and, by repeating the proof of Proposition 6.3,
 $$ \begin{align*}\int_{\mathbb{D}}k_a (z)dA(z)\to \int_{\mathbb{D}}\frac{4M^2}{|1-z^2|^{2}}U_{\mu}(z)dA(z)<\infty. \end{align*} $$
$$ \begin{align*}\int_{\mathbb{D}}k_a (z)dA(z)\to \int_{\mathbb{D}}\frac{4M^2}{|1-z^2|^{2}}U_{\mu}(z)dA(z)<\infty. \end{align*} $$
Therefore by dominated convergence [Reference Folland18, p. 59; Example 20], we have that
According to Proposition 6.3, we have that
 $$ \begin{align*} \|H(1)\|_{M(D_{\mu})}&=|H(1)(0)|+\sup_{\phi \in \text{Aut}(\mathbb{D})}\left(\int_{\mathbb{D}} |H(1)'(w)|^{2}U_{\mu}(\phi(w))dA(w)\right)^{1/2}\\&\geq 1+\sup_{a\in\mathbb{D}}\left(\int_{\mathbb{D}} |z H(1)'(w)|^{2}U_{\mu}(\sigma_{a}(w))dA(w)\right)^{1/2}\\ &\geq 1+\lim_{\mathbb{R}\ni a\to1}\left(\int_{\mathbb{D}} |f_{1}(w)+f_{2}(w)|^{2}U_{\mu}(\sigma_{a}(w))dA(w)\right)^{1/2}. \end{align*} $$
$$ \begin{align*} \|H(1)\|_{M(D_{\mu})}&=|H(1)(0)|+\sup_{\phi \in \text{Aut}(\mathbb{D})}\left(\int_{\mathbb{D}} |H(1)'(w)|^{2}U_{\mu}(\phi(w))dA(w)\right)^{1/2}\\&\geq 1+\sup_{a\in\mathbb{D}}\left(\int_{\mathbb{D}} |z H(1)'(w)|^{2}U_{\mu}(\sigma_{a}(w))dA(w)\right)^{1/2}\\ &\geq 1+\lim_{\mathbb{R}\ni a\to1}\left(\int_{\mathbb{D}} |f_{1}(w)+f_{2}(w)|^{2}U_{\mu}(\sigma_{a}(w))dA(w)\right)^{1/2}. \end{align*} $$
By using (6.3), the last
![]() $\liminf $
becomes
$\liminf $
becomes
 $$ \begin{align*} \lim_{\mathbb{R}\ni a\to1}&\left(\int_{\mathbb{D}} |f_{1}(w)+f_{2}(w)|^{2}U_{\mu}(\sigma_{a}(w))dA(w)\right)^{1/2}\\ &\geq \lim_{\mathbb{R}\ni a\to1} \left|\,\left(\int_{\mathbb{D}} |f_{1}(w)|^{2}U_{\mu}(\sigma_{a}(w))dA(w)\right)^{1/2}-\left(\int_{\mathbb{D}} |f_{2}(w)|^{2}U_{\mu}(\sigma_{a}(w))dA(w)\right)^{1/2}\right|\\ &=\lim_{\mathbb{R}\ni a\to1}\left(\int_{\mathbb{D}} \left|\frac{1}{1-w}\right|^{2}U_{\mu}(\sigma_{a}(w))dA(w)\right)^{1/2}.\\ \end{align*} $$
$$ \begin{align*} \lim_{\mathbb{R}\ni a\to1}&\left(\int_{\mathbb{D}} |f_{1}(w)+f_{2}(w)|^{2}U_{\mu}(\sigma_{a}(w))dA(w)\right)^{1/2}\\ &\geq \lim_{\mathbb{R}\ni a\to1} \left|\,\left(\int_{\mathbb{D}} |f_{1}(w)|^{2}U_{\mu}(\sigma_{a}(w))dA(w)\right)^{1/2}-\left(\int_{\mathbb{D}} |f_{2}(w)|^{2}U_{\mu}(\sigma_{a}(w))dA(w)\right)^{1/2}\right|\\ &=\lim_{\mathbb{R}\ni a\to1}\left(\int_{\mathbb{D}} \left|\frac{1}{1-w}\right|^{2}U_{\mu}(\sigma_{a}(w))dA(w)\right)^{1/2}.\\ \end{align*} $$
This implies that
 $$ \begin{align*} \|H(1)\|_{M(D_{\mu})} &\geq 1+\lim_{\mathbb{R}\ni a\to1}\left(\int_{\mathbb{D}} \left|\frac{1}{1-w}\right|^{2}U_{\mu}(\sigma_{a}(w))dA(w)\right)^{1/2}.\\ &= 1+\lim_{\mathbb{R}\ni a\to1}\left(\int_{\mathbb{D}} \left|\frac{1}{1-\sigma_{a}(w)}\right|^{2}|\sigma_{a}'(w)|^{2}U_{\mu}((w))dA(w)\right)^{1/2}\\ &\geq 1+\left(\int_{\mathbb{D}} \frac{4}{|1-w^{2}|^{2}}U_{\mu}(w)dA(w)\right)^{1/2}. \end{align*} $$
$$ \begin{align*} \|H(1)\|_{M(D_{\mu})} &\geq 1+\lim_{\mathbb{R}\ni a\to1}\left(\int_{\mathbb{D}} \left|\frac{1}{1-w}\right|^{2}U_{\mu}(\sigma_{a}(w))dA(w)\right)^{1/2}.\\ &= 1+\lim_{\mathbb{R}\ni a\to1}\left(\int_{\mathbb{D}} \left|\frac{1}{1-\sigma_{a}(w)}\right|^{2}|\sigma_{a}'(w)|^{2}U_{\mu}((w))dA(w)\right)^{1/2}\\ &\geq 1+\left(\int_{\mathbb{D}} \frac{4}{|1-w^{2}|^{2}}U_{\mu}(w)dA(w)\right)^{1/2}. \end{align*} $$
A significant application of Theorem 1.3 to
![]() $Q_p$
spaces with
$Q_p$
spaces with
![]() $\|\cdot \|_{M(D_{\mu _p})}$
provides the norm of
$\|\cdot \|_{M(D_{\mu _p})}$
provides the norm of
![]() $H$
in this situation.
$H$
in this situation.
Corollary 6.4 The norm of
![]() $H:H^\infty \to Q_p$
is equal to
$H:H^\infty \to Q_p$
is equal to
7 The norm of he Cesaro operator
We use the following identity
where
![]() $\mu $
is a positive Borel measure such that
$\mu $
is a positive Borel measure such that
![]() $(1-|z|^{2})d\mu (z)$
is finite.
$(1-|z|^{2})d\mu (z)$
is finite.
Proof of Theorem 1.4
Firstly observe that
![]() $C(1)(z)=-\frac {1}{z}\log (1-z)$
. As for the Hilbert matrix operator, this implies that
$C(1)(z)=-\frac {1}{z}\log (1-z)$
. As for the Hilbert matrix operator, this implies that
 $$ \begin{align*}\|C\|_{H^\infty\to M(D_\mu)}\geq1+\left(\int_{\mathbb{D}}\frac{4}{|1-z^{2}|^{2}}U_{\mu}(z)dA(z)\right)^{1/2}. \end{align*} $$
$$ \begin{align*}\|C\|_{H^\infty\to M(D_\mu)}\geq1+\left(\int_{\mathbb{D}}\frac{4}{|1-z^{2}|^{2}}U_{\mu}(z)dA(z)\right)^{1/2}. \end{align*} $$
Let
![]() $f\in H^\infty $
. Set
$f\in H^\infty $
. Set
![]() $h(z)=z\,C(f)(z)$
, then
$h(z)=z\,C(f)(z)$
, then
![]() $(1-z)h'(z)=f(z)$
. We have that
$(1-z)h'(z)=f(z)$
. We have that
 $$ \begin{align*} ||Cf||_{M(D_\mu)}=|C(f)(0)|+ \sup_{a\in\mathbb{D}}\left(\int_{\mathbb{D}}|C(f)'(z)|^2 U_{\mu}(\sigma_{a}(z))dA(z)\right)^{1/2}, \end{align*} $$
$$ \begin{align*} ||Cf||_{M(D_\mu)}=|C(f)(0)|+ \sup_{a\in\mathbb{D}}\left(\int_{\mathbb{D}}|C(f)'(z)|^2 U_{\mu}(\sigma_{a}(z))dA(z)\right)^{1/2}, \end{align*} $$
and that
![]() $|C(f)(0)|\leq ||f||_{H^\infty }$
. For the integral we work as follows. Let
$|C(f)(0)|\leq ||f||_{H^\infty }$
. For the integral we work as follows. Let
![]() $Cf=g$
; then
$Cf=g$
; then
 $$ \begin{align*} &\int_{\mathbb{D}}|g'(z)|^2 U_{\mu}(\sigma_{a}(z))dA(z)=\int_{\mathbb{D}}|(g\circ\sigma_{a})'(z)|^2 U_{\mu}(z)dA(z)\\ &=\int_{\mathbb{D}}\left(\int_{0}^{2\pi}|g(\sigma_{a}(e^{i\theta}))|^{2}P_{\zeta}(e^{i\theta})\frac{d\theta}{2\pi}-|g(\sigma_{a}(\zeta))|^{2}\right) d\mu(\zeta)\\ &=\int_{\mathbb{D}}\left(\int_{0}^{2\pi}|h(\sigma_{a}(e^{i\theta}))|^{2}P_{\zeta}(e^{i\theta})\frac{d\theta}{2\pi}-|h(\sigma_{a}(\zeta))|^{2}+|h(\sigma_{a}(\zeta))|^2-|g(\sigma_{a}(\zeta))|^{2}\right) d\mu(\zeta)\\ &=\int_{\mathbb{D}}|h'(z)|^2 U_{\mu}(\sigma_{a}(z))dA(z)-\int_{\mathbb{D}}(1-|\sigma_{a}(\zeta)|^{2})|g(\sigma_{a}(\zeta))|^{2}d\mu(\zeta)\\ &\leq\int_{\mathbb{D}}|h'(z)|^2 U_{\mu}(\sigma_{a}(z))dA(z). \end{align*} $$
$$ \begin{align*} &\int_{\mathbb{D}}|g'(z)|^2 U_{\mu}(\sigma_{a}(z))dA(z)=\int_{\mathbb{D}}|(g\circ\sigma_{a})'(z)|^2 U_{\mu}(z)dA(z)\\ &=\int_{\mathbb{D}}\left(\int_{0}^{2\pi}|g(\sigma_{a}(e^{i\theta}))|^{2}P_{\zeta}(e^{i\theta})\frac{d\theta}{2\pi}-|g(\sigma_{a}(\zeta))|^{2}\right) d\mu(\zeta)\\ &=\int_{\mathbb{D}}\left(\int_{0}^{2\pi}|h(\sigma_{a}(e^{i\theta}))|^{2}P_{\zeta}(e^{i\theta})\frac{d\theta}{2\pi}-|h(\sigma_{a}(\zeta))|^{2}+|h(\sigma_{a}(\zeta))|^2-|g(\sigma_{a}(\zeta))|^{2}\right) d\mu(\zeta)\\ &=\int_{\mathbb{D}}|h'(z)|^2 U_{\mu}(\sigma_{a}(z))dA(z)-\int_{\mathbb{D}}(1-|\sigma_{a}(\zeta)|^{2})|g(\sigma_{a}(\zeta))|^{2}d\mu(\zeta)\\ &\leq\int_{\mathbb{D}}|h'(z)|^2 U_{\mu}(\sigma_{a}(z))dA(z). \end{align*} $$
Since
![]() $h'(z)(1-z)=f(z)$
and due to Proposition 6.3, we have
$h'(z)(1-z)=f(z)$
and due to Proposition 6.3, we have
 $$ \begin{align*} ||Cf||_{M(D_\mu)}&\leq ||f||_{H^\infty}+ \sup_{a\in\mathbb{D}}\left(\int_{\mathbb{D}}\left|\frac{f(z)}{1-z}\right|^2 U_{\mu}(\sigma_{a}(z))dA(z)\right)^{1/2} \\ &\leq \left(1+\left(\int_{\mathbb{D}}\frac{4}{|1-z^{2}|^{2}}U_{\mu}(z)dA(z)\right)^{1/2}\right)||f||_{H^\infty}. \end{align*} $$
$$ \begin{align*} ||Cf||_{M(D_\mu)}&\leq ||f||_{H^\infty}+ \sup_{a\in\mathbb{D}}\left(\int_{\mathbb{D}}\left|\frac{f(z)}{1-z}\right|^2 U_{\mu}(\sigma_{a}(z))dA(z)\right)^{1/2} \\ &\leq \left(1+\left(\int_{\mathbb{D}}\frac{4}{|1-z^{2}|^{2}}U_{\mu}(z)dA(z)\right)^{1/2}\right)||f||_{H^\infty}. \end{align*} $$
8 Open questions
We note that for every radial measure
![]() $\mu $
that satisfies (2.1),
$\mu $
that satisfies (2.1),
 $$ \begin{align*}\|H\|_{H^\infty \to M(D_\mu)} =1+\left(\int_{\mathbb{D}}\frac{4}{|1-z^{2}|^{2}}U_{\mu}(z)dA(z)\right)^{1/2}. \end{align*} $$
$$ \begin{align*}\|H\|_{H^\infty \to M(D_\mu)} =1+\left(\int_{\mathbb{D}}\frac{4}{|1-z^{2}|^{2}}U_{\mu}(z)dA(z)\right)^{1/2}. \end{align*} $$
However we are not able to compute the exact value of
![]() $\|H\|_{H^\infty \to M(D_\mu )}$
in general.
$\|H\|_{H^\infty \to M(D_\mu )}$
in general.
Question 8.1 What is the exact norm of
![]() $H$
from
$H$
from
![]() $H^\infty $
to
$H^\infty $
to
![]() $M(D_\mu )$
for non-radial
$M(D_\mu )$
for non-radial
![]() $\mu $
?
$\mu $
?
Acknowledgements
The authors would like to express their gratitude to professor Aristomenis Siskakis who point (3.3) out.
They would also like to thank the anonymous reviewer for her/his helpful suggestions which improve the article.