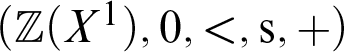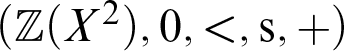1 Introduction
1.1 Background I: order types of models of Peano arithmetic and its extensions
It is well-known that non-standard models of Peano arithmetic have order type
![]() $\mathbb {N}+\mathbb {Z}\cdot D$
where D is a dense linear order without first or last element (cf. [Reference Kaye10, Theorem 6.4]). For countable models, this determines their order type up to isomorphism: it is necessarily
$\mathbb {N}+\mathbb {Z}\cdot D$
where D is a dense linear order without first or last element (cf. [Reference Kaye10, Theorem 6.4]). For countable models, this determines their order type up to isomorphism: it is necessarily
![]() $\mathbb {N}+\mathbb {Z}\cdot \mathbb {Q}$
. In general, not every order of the form
$\mathbb {N}+\mathbb {Z}\cdot \mathbb {Q}$
. In general, not every order of the form
![]() $\mathbb {N}+\mathbb {Z}\cdot D$
is the order type of a model of Peano arithmetic and it is not known how to characterise those dense orders D for which this is the case.
$\mathbb {N}+\mathbb {Z}\cdot D$
is the order type of a model of Peano arithmetic and it is not known how to characterise those dense orders D for which this is the case.
Question 1. For which dense orders D is there a model of Peano arithmetic with order type
![]() $\mathbb {N}+\mathbb {Z}\cdot D$
?
$\mathbb {N}+\mathbb {Z}\cdot D$
?
If T is any consistent extension of Peano arithmetic, we write
![]() $\mathcal {O}_T$
for the class of order types of models of T. Friedman asked the “especially vexing question” [Reference Kossak and Schmerl12, p. 281] whether this class depends on the choice of T:Footnote
1
$\mathcal {O}_T$
for the class of order types of models of T. Friedman asked the “especially vexing question” [Reference Kossak and Schmerl12, p. 281] whether this class depends on the choice of T:Footnote
1
Question 2 Friedman’s Question
Are there any consistent extensions T and
![]() $T'$
of Peano arithmetic such that
$T'$
of Peano arithmetic such that
![]() $\mathcal {O}_T \neq \mathcal {O}_{T'}$
?
$\mathcal {O}_T \neq \mathcal {O}_{T'}$
?
While Questions 1 and 2 are wide open, many results have been obtained that give us some information about the relationship between models of arithmetic and their order types. We refer the reader to the expertly written survey paper [Reference Bovykin and Kaye2] that outlines the state of knowledge.
Let
![]() $\lambda $
be a regular uncountable cardinal with
$\lambda $
be a regular uncountable cardinal with
![]() $2^{<\lambda } = \lambda $
. Then there is a unique dense saturated order
$2^{<\lambda } = \lambda $
. Then there is a unique dense saturated order
![]() $Q_\lambda $
of size
$Q_\lambda $
of size
![]() $\lambda $
[Reference Marker14, Corollary 4.3.14 and Theorem 4.3.20] and it follows from [Reference Kaye10, Theorem 6.4] that any saturated model of Peano arithmetic of cardinality
$\lambda $
[Reference Marker14, Corollary 4.3.14 and Theorem 4.3.20] and it follows from [Reference Kaye10, Theorem 6.4] that any saturated model of Peano arithmetic of cardinality
![]() $\lambda $
has order type
$\lambda $
has order type
![]() $\mathbb {N}+\mathbb {Z}\cdot Q_\lambda $
. However, Pabion’s Theorem shows that more is true:
$\mathbb {N}+\mathbb {Z}\cdot Q_\lambda $
. However, Pabion’s Theorem shows that more is true:
Theorem 3 Pabion; [Reference Pabion15, Proposition 2]
Let
![]() $\kappa $
be an uncountable cardinal. Then a model of Peano arithmetic is
$\kappa $
be an uncountable cardinal. Then a model of Peano arithmetic is
![]() $\kappa $
-saturated if and only if its order type is
$\kappa $
-saturated if and only if its order type is
![]() $\kappa $
-saturated.
$\kappa $
-saturated.
In his doctoral dissertation [Reference Bovykin1], Bovykin constructed many examples of additional order types of models of Peano arithmetic (under the appropriate assumptions that guarantee that the dense saturated orders exist), e.g.,
![]() $\mathbb {N}+\mathbb {Z}\cdot Q_{\aleph _1}\cdot \mathbb {N}$
,
$\mathbb {N}+\mathbb {Z}\cdot Q_{\aleph _1}\cdot \mathbb {N}$
,
![]() $\mathbb {N}+\mathbb {Z}\cdot Q_{\aleph _1}\cdot \mathbb {Z}$
,
$\mathbb {N}+\mathbb {Z}\cdot Q_{\aleph _1}\cdot \mathbb {Z}$
,
![]() $\mathbb {N}+\mathbb {Z}\cdot Q_{\aleph _1}\cdot (\omega _1^*+\omega _1)$
,
$\mathbb {N}+\mathbb {Z}\cdot Q_{\aleph _1}\cdot (\omega _1^*+\omega _1)$
,
![]() $\mathbb {N}+\mathbb {Z}\cdot Q_{\aleph _2}\cdot (\omega _2^*+\omega _2)$
,
$\mathbb {N}+\mathbb {Z}\cdot Q_{\aleph _2}\cdot (\omega _2^*+\omega _2)$
,
![]() $\mathbb {N}+\mathbb {Z}\cdot (Q_{\mathfrak {c}^+}+Q_{\mathfrak {c}^+}\cdot Q_{\mathfrak {c}^{++}})$
, and many others [Reference Bovykin and Kaye2, Section 5] (here, as usual,
$\mathbb {N}+\mathbb {Z}\cdot (Q_{\mathfrak {c}^+}+Q_{\mathfrak {c}^+}\cdot Q_{\mathfrak {c}^{++}})$
, and many others [Reference Bovykin and Kaye2, Section 5] (here, as usual,
![]() $\mathfrak {c} := 2^{\aleph _0}$
). He also gave examples of order types that have different non-isomorphic models of Peano arithmetic living on them, e.g.,
$\mathfrak {c} := 2^{\aleph _0}$
). He also gave examples of order types that have different non-isomorphic models of Peano arithmetic living on them, e.g.,
![]() $\mathbb {N}+\mathbb {Z}\cdot Q_{\aleph _1}\cdot \mathbb {N}$
[Reference Bovykin and Kaye2, Proposition 5.3]. However, for many similar orders, we do not know whether they are order types of models of Peano arithmetic, e.g.,
$\mathbb {N}+\mathbb {Z}\cdot Q_{\aleph _1}\cdot \mathbb {N}$
[Reference Bovykin and Kaye2, Proposition 5.3]. However, for many similar orders, we do not know whether they are order types of models of Peano arithmetic, e.g.,
![]() $\mathbb {N}+\mathbb {Z}\cdot (\mathbb {Q}+\mathbb {Q}\cdot Q_{\aleph _1})$
[Reference Bovykin and Kaye2, Question 3].
$\mathbb {N}+\mathbb {Z}\cdot (\mathbb {Q}+\mathbb {Q}\cdot Q_{\aleph _1})$
[Reference Bovykin and Kaye2, Question 3].
More is known if we restrict our attention to classes of particularly well-structured models of Peano arithmetic, e.g., order self-similar models [Reference Bovykin and Kaye2, Section 8] or resplendent models [Reference Bovykin and Kaye2, Sections 8 and 9] (cf. also [Reference Kossak11, Reference Schmerl22]). The most recent results in this direction are Shelah’s investigation of almost isomorphism of order rigid models in [Reference Shelah24]: we shall discuss these briefly in Section 8.
1.2 Background II: fragments of Peano arithmetic
All of the results mentioned in Section 1.1 are about models of Peano arithmetic or its extensions. In this paper, we shall go in the other direction and consider fragments of Peano arithmetic where the natural analogue of Friedman’s Question 2 would be:
Question 4. Given two fragments T and
![]() $T'$
of Peano arithmetic, when is
$T'$
of Peano arithmetic, when is
![]() $\mathcal {O}_T = \mathcal {O}_{T'}$
?
$\mathcal {O}_T = \mathcal {O}_{T'}$
?
The standard language of Peano arithmetic contains the symbols
![]() $<$
,
$<$
,
![]() $\mathrm {s}$
,
$\mathrm {s}$
,
![]() $+$
, and
$+$
, and
![]() $\cdot $
; the fragments we consider are those axiomatised in languages lacking some of these symbols, in particular, Successor arithmetic without
$\cdot $
; the fragments we consider are those axiomatised in languages lacking some of these symbols, in particular, Successor arithmetic without
![]() $+$
and
$+$
and
![]() $\cdot $
and Presburger arithmetic without
$\cdot $
and Presburger arithmetic without
![]() $\cdot $
(cf. [Reference Presburger17]). We shall not be considering the fragment containing only multiplication, known as Skolem arithmetic (cf. [Reference Skolem26]) for reasons discussed at the end of Section 2.1.Footnote
2
$\cdot $
(cf. [Reference Presburger17]). We shall not be considering the fragment containing only multiplication, known as Skolem arithmetic (cf. [Reference Skolem26]) for reasons discussed at the end of Section 2.1.Footnote
2
The axioms of our systems of arithmetic consist of a list of algebraic axioms governing the meaning of the symbols
![]() $<$
,
$<$
,
![]() $\mathrm {s}$
,
$\mathrm {s}$
,
![]() $+$
, and
$+$
, and
![]() $\cdot $
and the axiom scheme of induction. Almost all of the algebraic axioms are universal sentencesFootnote
3
and allow us to think of models as generated by the operations. Models of theories defined by the algebraic axioms alone therefore have an algebraic and constructive character. In contrast, theories with the full induction scheme (or sufficiently large fragments of the induction scheme) require model theoretic methods to analyse their models.Footnote
4
We shall discuss and illustrate this notable difference in Section 6 with some elementary examples.
$\cdot $
and the axiom scheme of induction. Almost all of the algebraic axioms are universal sentencesFootnote
3
and allow us to think of models as generated by the operations. Models of theories defined by the algebraic axioms alone therefore have an algebraic and constructive character. In contrast, theories with the full induction scheme (or sufficiently large fragments of the induction scheme) require model theoretic methods to analyse their models.Footnote
4
We shall discuss and illustrate this notable difference in Section 6 with some elementary examples.
1.3 Overview
We consider three operations, the unary successor operation and the binary operations of addition and multiplication, as well as their associated languages:
![]() $\mathcal {L}_{<,\mathrm {s}} := \{0,<,\mathrm {s}\}$
, the language with an order relation and the successor operation,
$\mathcal {L}_{<,\mathrm {s}} := \{0,<,\mathrm {s}\}$
, the language with an order relation and the successor operation,
![]() $\mathcal {L}_{<,\mathrm {s},+} := \{0,<,\mathrm {s},+\}$
, the language augmented with addition, and
$\mathcal {L}_{<,\mathrm {s},+} := \{0,<,\mathrm {s},+\}$
, the language augmented with addition, and
![]() $\mathcal {L}_{<,\mathrm {s},+,\cdot } := \{0,<,\mathrm {s},+,\cdot \}$
, the full language of arithmetic. For each of the languages, we shall define the appropriate arithmetical axiom systems and the corresponding axiom schemes of induction, resulting in a total of six theories,
$\mathcal {L}_{<,\mathrm {s},+,\cdot } := \{0,<,\mathrm {s},+,\cdot \}$
, the full language of arithmetic. For each of the languages, we shall define the appropriate arithmetical axiom systems and the corresponding axiom schemes of induction, resulting in a total of six theories,

where the theories in the left column are without induction and the theories in the right column are with the axiom scheme of induction (for definitions, cf. Section 2.1).
It is a folklore result that
![]() $\mathsf {SA}^-$
proves the axiom scheme of induction for
$\mathsf {SA}^-$
proves the axiom scheme of induction for
![]() $\mathcal {L}_{<,\mathrm {s}}$
(Theorem 11) and hence
$\mathcal {L}_{<,\mathrm {s}}$
(Theorem 11) and hence
![]() $\mathsf {SA}^-$
and
$\mathsf {SA}^-$
and
![]() $\mathsf {SA}$
are the same theory, reducing our diagram to five theories. We solve Question 4 for these theories by showing that for any two theories T and
$\mathsf {SA}$
are the same theory, reducing our diagram to five theories. We solve Question 4 for these theories by showing that for any two theories T and
![]() $T'$
from this list, we have
$T'$
from this list, we have
![]() $\mathcal {O}_T \neq \mathcal {O}_{T'}$
. In the following diagram, an arrow from a theory T to a theory S means “every order type that occurs in a model of T occurs in a model of S.” In Section 9, we shall show that the diagram is complete in the sense that if there is no arrow from T to S, then there is an order that is the order type of a model of T that cannot be the order type of a model of S.
$\mathcal {O}_T \neq \mathcal {O}_{T'}$
. In the following diagram, an arrow from a theory T to a theory S means “every order type that occurs in a model of T occurs in a model of S.” In Section 9, we shall show that the diagram is complete in the sense that if there is no arrow from T to S, then there is an order that is the order type of a model of T that cannot be the order type of a model of S.

2 Definitions and basic results
2.1 Definitions
In this section, we shall introduce the axiomatic systems studied in this paper. The axioms come in four groups corresponding to the order relation, the successor function, addition, and multiplication. As usual, we use the following syntactic abbreviations: for
![]() $n\in \mathbb {N}$
and a variable x, we write
$n\in \mathbb {N}$
and a variable x, we write
 $$ \begin{align*} \mathrm{s}^n(x) & := \underbrace{\mathrm{s}(\cdots(\mathrm{s}}_{n\ \text{times.}}(x))\cdots)\mbox{ and}\\ nx & :=\underbrace{x+\cdots+x}_{n\ \text{times.}}. \end{align*} $$
$$ \begin{align*} \mathrm{s}^n(x) & := \underbrace{\mathrm{s}(\cdots(\mathrm{s}}_{n\ \text{times.}}(x))\cdots)\mbox{ and}\\ nx & :=\underbrace{x+\cdots+x}_{n\ \text{times.}}. \end{align*} $$
The order axioms O1 to O4 express that
![]() $<$
describes a linear order with least element
$<$
describes a linear order with least element
![]() $0$
(O1 is trichotomy, O2 is transitivity, and O3 is irreflexivity):
$0$
(O1 is trichotomy, O2 is transitivity, and O3 is irreflexivity):
The successor axioms S1 to S4 express that
![]() $<$
is discrete and that
$<$
is discrete and that
![]() $\mathrm {s}$
is the successor operation with respect to
$\mathrm {s}$
is the successor operation with respect to
![]() $<$
:
$<$
:
Taken together, the axioms O1 to O4 and S1 to S4 (later called
![]() $\mathsf {SA}^-$
) constitute the theory of discrete linear orders with a minimum and a strictly increasing successor function. Note that all the order and successor axioms with the exception of S1 are universal sentences. The axiom S1 is a particular instance of the induction scheme and is in
$\mathsf {SA}^-$
) constitute the theory of discrete linear orders with a minimum and a strictly increasing successor function. Note that all the order and successor axioms with the exception of S1 are universal sentences. The axiom S1 is a particular instance of the induction scheme and is in
![]() $\forall \exists $
form.
$\forall \exists $
form.
The addition axioms P1 to P5 express the fact that
![]() $+$
and
$+$
and
![]() $<$
satisfy the axioms of ordered abelian monoids:
$<$
satisfy the axioms of ordered abelian monoids:
Axiom ⋇ expresses the fact that if
![]() $x<y$
, then the difference between them exists:
$x<y$
, then the difference between them exists:
Like S1, axiom ⋇ is an instance of the induction axiom scheme and not a universal sentence but in
![]() $\forall \exists $
form; we shall comment on S1 and ⋇ in Section 6.
$\forall \exists $
form; we shall comment on S1 and ⋇ in Section 6.
The multiplication axioms M1 to M6 express that
![]() $\cdot $
and
$\cdot $
and
![]() $+$
are commutative semiring operations respecting
$+$
are commutative semiring operations respecting
![]() $<$
:
$<$
:
Finally we have a schema of induction axioms.
When considering subsystems of these axioms, we denote the axiom schema of induction restricted to the formulas of a language
![]() $\mathcal {L}$
by
$\mathcal {L}$
by
![]() $\mathrm {Ind}(\mathcal {L})$
. We shall consider the following systems of axioms:
$\mathrm {Ind}(\mathcal {L})$
. We shall consider the following systems of axioms:
 $$ \begin{align*} \mathsf{SA}^- &= \text{O1}+\text{O2}+\text{O3}+\text{O4}+\text{S1}+\text{S2}+\text{S3}+\text{S4},\\ \mathsf{SA}\phantom{^-} &= \mathsf{SA}^-+\text{Ind}(\mathcal{L}_{<,\mathrm{s}}),\\ \mathsf{Pr}^- &= \mathsf{SA}^- +{\divideontimes}+\text{P1}+\text{P2}+\text{P3}+\text{P4}+\text{P5},\\ \mathsf{Pr}\phantom{^-} &= \mathsf{Pr}^- +\mathrm{Ind}(\mathcal{L}_{<,\mathrm{s},+}),\\ \mathsf{PA}^- &= \mathsf{Pr}^- +\text{M1}+\text{M2}+\text{M3}+\text{M4}+\text{M5}+\text{M6},\\ \mathsf{PA}\phantom{^-} &=\mathsf{PA}^- +\mathrm{Ind}(\mathcal{L}_{<,\mathrm{s},+,\cdot}); \end{align*} $$
$$ \begin{align*} \mathsf{SA}^- &= \text{O1}+\text{O2}+\text{O3}+\text{O4}+\text{S1}+\text{S2}+\text{S3}+\text{S4},\\ \mathsf{SA}\phantom{^-} &= \mathsf{SA}^-+\text{Ind}(\mathcal{L}_{<,\mathrm{s}}),\\ \mathsf{Pr}^- &= \mathsf{SA}^- +{\divideontimes}+\text{P1}+\text{P2}+\text{P3}+\text{P4}+\text{P5},\\ \mathsf{Pr}\phantom{^-} &= \mathsf{Pr}^- +\mathrm{Ind}(\mathcal{L}_{<,\mathrm{s},+}),\\ \mathsf{PA}^- &= \mathsf{Pr}^- +\text{M1}+\text{M2}+\text{M3}+\text{M4}+\text{M5}+\text{M6},\\ \mathsf{PA}\phantom{^-} &=\mathsf{PA}^- +\mathrm{Ind}(\mathcal{L}_{<,\mathrm{s},+,\cdot}); \end{align*} $$
standing for ‘Successor Arithmetic’, ‘Presburger Arithmetic’, and ‘Peano Arithmetic’, respectively.Footnote 5
In his original paper, Presburger uses a different axiomatisation of Presburger Arithmetic that we shall call
![]() $\mathsf {Pr^{D}}$
[Reference Presburger17]. The axioms of
$\mathsf {Pr^{D}}$
[Reference Presburger17]. The axioms of
![]() $\mathsf {Pr^{D}}$
are those of
$\mathsf {Pr^{D}}$
are those of
![]() $\mathsf {Pr}^-$
plus the following axiom schema:
$\mathsf {Pr}^-$
plus the following axiom schema:
for
![]() $0<n\in \mathbb {N}$
. Presburger’s famous theorem shows that
$0<n\in \mathbb {N}$
. Presburger’s famous theorem shows that
![]() $\mathsf {Pr^{D}}$
axiomatises the complete theory
$\mathsf {Pr^{D}}$
axiomatises the complete theory
![]() $\mathrm {Th}(\mathbb {N},+)$
. Since our
$\mathrm {Th}(\mathbb {N},+)$
. Since our
![]() $\mathsf {Pr}$
clearly implies
$\mathsf {Pr}$
clearly implies
![]() $\mathsf {Pr^{D}}$
, it also axiomatises
$\mathsf {Pr^{D}}$
, it also axiomatises
![]() $\mathrm {Th}(\mathbb {N},+)$
.
$\mathrm {Th}(\mathbb {N},+)$
.
In this paper we do not take into consideration Skolem arithmetic
![]() $\mathsf {Sk}$
, i.e., the multiplicative fragment of
$\mathsf {Sk}$
, i.e., the multiplicative fragment of
![]() $\mathsf {PA}$
. This is due to the fact that
$\mathsf {PA}$
. This is due to the fact that
![]() $\mathsf {Sk}$
, usually defined as
$\mathsf {Sk}$
, usually defined as
![]() $\mathrm {Th}(\mathbb {N},\cdot )$
, does not carry an order structure, i.e., the order is not definable in
$\mathrm {Th}(\mathbb {N},\cdot )$
, does not carry an order structure, i.e., the order is not definable in
![]() $\mathcal {L}_{\cdot }$
. Moreover, adding the order to Skolem arithmetic makes it much more expressive: Robinson showed that addition is definable in
$\mathcal {L}_{\cdot }$
. Moreover, adding the order to Skolem arithmetic makes it much more expressive: Robinson showed that addition is definable in
![]() $\mathrm {Th}(\mathbb {N},<,\cdot )$
, and thus
$\mathrm {Th}(\mathbb {N},<,\cdot )$
, and thus
![]() $\mathrm {Th}(\mathbb {N},<,\cdot )$
is essentially full arithmetic [Reference Robinson20, Theorem 1.1]. Therefore, an analysis of Skolem arithmetic in terms of order types is not fruitful.
$\mathrm {Th}(\mathbb {N},<,\cdot )$
is essentially full arithmetic [Reference Robinson20, Theorem 1.1]. Therefore, an analysis of Skolem arithmetic in terms of order types is not fruitful.
2.2 Order types
As usual, order types are the isomorphism classes of partial orders. If
![]() $\mathcal {L}$
is any language containing
$\mathcal {L}$
is any language containing
![]() $<$
and M is an
$<$
and M is an
![]() $\mathcal {L}$
-structure, by a slight abuse of language, we refer to the
$\mathcal {L}$
-structure, by a slight abuse of language, we refer to the
![]() $\{<\}$
-reduct of M as its order type. In situations where the order structure is clear from the context, we do not explicitly include it in the notation: e.g., the notation
$\{<\}$
-reduct of M as its order type. In situations where the order structure is clear from the context, we do not explicitly include it in the notation: e.g., the notation
![]() $\mathbb {Z}$
refers to both the set of integers and the ordered structure
$\mathbb {Z}$
refers to both the set of integers and the ordered structure
![]() $(\mathbb {Z},<)$
with the natural order
$(\mathbb {Z},<)$
with the natural order
![]() $<$
on
$<$
on
![]() $\mathbb {Z}$
.
$\mathbb {Z}$
.
If A and B are two linear orders, then
![]() $A^\ast $
is the inverse order of A,
$A^\ast $
is the inverse order of A,
![]() $A+B$
is the order sum, and
$A+B$
is the order sum, and
![]() $A\cdot B$
is the (anti-lexicographic) product order, i.e.,
$A\cdot B$
is the (anti-lexicographic) product order, i.e.,
![]() $(a,b) \leq (a',b')$
if and only if
$(a,b) \leq (a',b')$
if and only if
![]() $b<b'$
or
$b<b'$
or
![]() $b=b'$
and
$b=b'$
and
![]() $a\leq a'$
. If B has a least element
$a\leq a'$
. If B has a least element
![]() $0$
then
$0$
then
![]() $B^{A}$
is the set of functions f from A to B with finite support (i.e., the set
$B^{A}$
is the set of functions f from A to B with finite support (i.e., the set
![]() $\{a\in A\,;\,f(a)\neq 0\}$
is finite) ordered anti-lexicographically, i.e.,
$\{a\in A\,;\,f(a)\neq 0\}$
is finite) ordered anti-lexicographically, i.e.,
![]() $f<g$
if and only if
$f<g$
if and only if
![]() $f(a)<g(a)$
for the largest
$f(a)<g(a)$
for the largest
![]() $a\in A$
such that
$a\in A$
such that
![]() $f(a)\neq g(a)$
. Note that in the case that A and B are ordinal numbers, then the above operations of sum, product, and exponentiation correspond to the classical ordinal operations.
$f(a)\neq g(a)$
. Note that in the case that A and B are ordinal numbers, then the above operations of sum, product, and exponentiation correspond to the classical ordinal operations.
If
![]() $a\in A$
, we denote the initial segment defined by a as
$a\in A$
, we denote the initial segment defined by a as
![]() $\mathrm {IS}(a) := \{b\in A\,;\,b < a\}$
and the final segment defined by a as
$\mathrm {IS}(a) := \{b\in A\,;\,b < a\}$
and the final segment defined by a as
![]() $\mathrm {FS}(a) := \{b\in A\,;\,a < b\}$
.
$\mathrm {FS}(a) := \{b\in A\,;\,a < b\}$
.
If
![]() $(G,0,<,+)$
is an ordered abelian group (i.e., satisfies the axioms O1 to O4 and P1 to P4), then we define
$(G,0,<,+)$
is an ordered abelian group (i.e., satisfies the axioms O1 to O4 and P1 to P4), then we define
![]() $G^+ := \{g\in G\,;\,0<g\} = \mathrm {FS}(0)$
to be the positive part of G. We call linear orders groupable if and only if there is an ordered abelian group with the same order type.
$G^+ := \{g\in G\,;\,0<g\} = \mathrm {FS}(0)$
to be the positive part of G. We call linear orders groupable if and only if there is an ordered abelian group with the same order type.
Let
![]() $(G,<,+)$
be an ordered group. We define the standard monoid over G as the ordered monoid
$(G,<,+)$
be an ordered group. We define the standard monoid over G as the ordered monoid
![]() $(\mathbb {N}+\mathbb {Z}\cdot G^{+},<,+)$
where
$(\mathbb {N}+\mathbb {Z}\cdot G^{+},<,+)$
where
![]() $<$
is the order relation of
$<$
is the order relation of
![]() $\mathbb {N}+\mathbb {Z}\cdot G^{+}$
and
$\mathbb {N}+\mathbb {Z}\cdot G^{+}$
and
![]() $+$
is defined point-wise, i.e.,
$+$
is defined point-wise, i.e.,
 $$ \begin{align*}x+y=\begin{cases} n+m, &\text{ if}\ x=n, y=m\ \text{and}\ m,n \in \mathbb{N},\\ ( z+x,g ), &\text{ if}\ x\in \mathbb{N}\ \text{and}\ y=(z,g)\in \mathbb{Z}\cdot G^{+},\\ (z+y,g ), &\text{ if}\ y\in \mathbb{N}\ \text{and}\ x=(z,g)\in \mathbb{Z}\cdot G^{+},\\ (z_x+z_y,g_x+g_y ), &\text{ if}\ x=(z_x,g_x)\in \mathbb{Z}\cdot G^{+}\ \text{and}\\ &\quad y=( z_y,g_y ) \in \mathbb{Z}\cdot G^{+}. \end{cases}\end{align*} $$
$$ \begin{align*}x+y=\begin{cases} n+m, &\text{ if}\ x=n, y=m\ \text{and}\ m,n \in \mathbb{N},\\ ( z+x,g ), &\text{ if}\ x\in \mathbb{N}\ \text{and}\ y=(z,g)\in \mathbb{Z}\cdot G^{+},\\ (z+y,g ), &\text{ if}\ y\in \mathbb{N}\ \text{and}\ x=(z,g)\in \mathbb{Z}\cdot G^{+},\\ (z_x+z_y,g_x+g_y ), &\text{ if}\ x=(z_x,g_x)\in \mathbb{Z}\cdot G^{+}\ \text{and}\\ &\quad y=( z_y,g_y ) \in \mathbb{Z}\cdot G^{+}. \end{cases}\end{align*} $$
It is easy to see that for each ordered group G the standard monoid over G is indeed a monoid with least element
![]() $0$
.
$0$
.
If
![]() $(B,<,+)$
is any ordered group and X is a variable, we can consider the set
$(B,<,+)$
is any ordered group and X is a variable, we can consider the set
![]() $B[X]$
of polynomials in the variable X over B, consisting of terms
$B[X]$
of polynomials in the variable X over B, consisting of terms
with
![]() $b_n \neq 0$
(unless
$b_n \neq 0$
(unless
![]() $n=0)$
; the degree of a polynomial is the highest occurring exponent, i.e.,
$n=0)$
; the degree of a polynomial is the highest occurring exponent, i.e.,
![]() $\mathrm {deg}(f) = n$
in the term given above. If
$\mathrm {deg}(f) = n$
in the term given above. If
![]() $n= b_0 = 0$
(i.e.,
$n= b_0 = 0$
(i.e.,
![]() $f=0$
), we call f the zero polynomial. We order polynomials anti-lexicographically: if
$f=0$
), we call f the zero polynomial. We order polynomials anti-lexicographically: if
![]() $f = b_nX^n+\cdots +b_1X+b_0$
and
$f = b_nX^n+\cdots +b_1X+b_0$
and
![]() $g= c_mX^m+\cdots c_1X+c_0$
are different, find the largest natural number k such that
$g= c_mX^m+\cdots c_1X+c_0$
are different, find the largest natural number k such that
![]() $b_k\neq c_k$
; then
$b_k\neq c_k$
; then
This order respects addition and multiplication of polynomials in the sense of axioms P4 and M6, respectively. A polynomial is called positive if it is larger than the zero polynomial in this order. If we define
 $$ \begin{align*} O_0&=\varnothing,\\ O_{\gamma+1}&=O_\gamma+\mathbb{Z}^{\gamma} \cdot \mathbb{N},\\ O_\lambda&=\bigcup_{\gamma\in \lambda}O_\gamma \text{ for}\ \lambda\ \text{limit,} \end{align*} $$
$$ \begin{align*} O_0&=\varnothing,\\ O_{\gamma+1}&=O_\gamma+\mathbb{Z}^{\gamma} \cdot \mathbb{N},\\ O_\lambda&=\bigcup_{\gamma\in \lambda}O_\gamma \text{ for}\ \lambda\ \text{limit,} \end{align*} $$
then for every natural number
![]() $n>0$
, the linear order
$n>0$
, the linear order
![]() $O_n$
is the order type of non-negative polynomials with integer coefficients of degree at most
$O_n$
is the order type of non-negative polynomials with integer coefficients of degree at most
![]() $n-1$
and thus
$n-1$
and thus
![]() $O_\omega $
is the order type of all non-negative polynomials with integer coefficients.
$O_\omega $
is the order type of all non-negative polynomials with integer coefficients.
2.3 Basic properties
In this section, we shall remind the reader about basic tools of model theory of
![]() $\mathsf {PA}$
. We refer the reader to [Reference Kaye10] for a comprehensive introduction to the theory of non-standard models of
$\mathsf {PA}$
. We refer the reader to [Reference Kaye10] for a comprehensive introduction to the theory of non-standard models of
![]() $\mathsf {PA}$
. One of the main tools in studying the order types of models of
$\mathsf {PA}$
. One of the main tools in studying the order types of models of
![]() $\mathsf {PA}$
is the concept of Archimedean class.
$\mathsf {PA}$
is the concept of Archimedean class.
Definition 5. Let M be a model of
![]() $\mathsf {SA}^-$
. Given
$\mathsf {SA}^-$
. Given
![]() $x,y\in M$
we say that x and y are of the same magnitude, in symbols
$x,y\in M$
we say that x and y are of the same magnitude, in symbols
![]() $x\sim y$
, if there are
$x\sim y$
, if there are
![]() $m,n\in \mathbb {N}$
such that
$m,n\in \mathbb {N}$
such that
![]() $\mathrm {s}^{n}(y)\geq x$
and
$\mathrm {s}^{n}(y)\geq x$
and
![]() $y\leq \mathrm {s}^{m}(x)$
. The relation
$y\leq \mathrm {s}^{m}(x)$
. The relation
![]() $\sim $
is an equivalence relation. For every
$\sim $
is an equivalence relation. For every
![]() $x\in M$
, we shall denote by
$x\in M$
, we shall denote by
![]() $[x]$
the equivalence class of x with respect to
$[x]$
the equivalence class of x with respect to
![]() $\sim $
called the Archimedean class of x.
$\sim $
called the Archimedean class of x.
The Archimedean classes of a model of
![]() $\mathsf {SA}^-$
partition the model into convex blocks: if
$\mathsf {SA}^-$
partition the model into convex blocks: if
![]() $y,w\in [x]$
and
$y,w\in [x]$
and
![]() $y<z<w$
, then
$y<z<w$
, then
![]() $z\in [x]$
(the reader can check that only the axioms of
$z\in [x]$
(the reader can check that only the axioms of
![]() $\mathsf {SA}^-$
are needed for this). Therefore, the quotient structure
$\mathsf {SA}^-$
are needed for this). Therefore, the quotient structure
![]() $M/{\sim }$
of Archimedean classes is linearly ordered by the relation
$M/{\sim }$
of Archimedean classes is linearly ordered by the relation
![]() $<$
defined by
$<$
defined by
![]() $[x]<[y]$
if and only if
$[x]<[y]$
if and only if
![]() $x<y$
and
$x<y$
and
![]() $[x]\neq [y]$
. Furthermore,
$[x]\neq [y]$
. Furthermore,
![]() $[0]$
is the least element of the quotient structure. We refer to the classes that are different from
$[0]$
is the least element of the quotient structure. We refer to the classes that are different from
![]() $[0]$
as the non-zero Archimedean classes. In particular, if A is the order type of the non-zero Archimedean classes of M, then the order type of M is
$[0]$
as the non-zero Archimedean classes. In particular, if A is the order type of the non-zero Archimedean classes of M, then the order type of M is
![]() $\mathbb {N}+\mathbb {Z}\cdot A$
.
$\mathbb {N}+\mathbb {Z}\cdot A$
.
So far, we worked entirely in the language
![]() $\mathcal {L}_{<,\mathrm {s}}$
with just the axioms of
$\mathcal {L}_{<,\mathrm {s}}$
with just the axioms of
![]() $\mathsf {SA}^-$
. If we also have addition in our language, we observe:
$\mathsf {SA}^-$
. If we also have addition in our language, we observe:
Lemma 6. Let M be a non-standard model of
![]() $\mathsf {Pr}^-$
and
$\mathsf {Pr}^-$
and
![]() $a\in M$
be a non-standard element of M. Then for every
$a\in M$
be a non-standard element of M. Then for every
![]() $n,m\in \mathbb {N}$
such that
$n,m\in \mathbb {N}$
such that
![]() $n<m$
we have
$n<m$
we have
![]() $[na]<[ma]$
. In particular, if
$[na]<[ma]$
. In particular, if
![]() $\mathbb {N}+\mathbb {Z}\cdot A$
is the order type of M, then A does not have a largest element.
$\mathbb {N}+\mathbb {Z}\cdot A$
is the order type of M, then A does not have a largest element.
Proof Assume that
![]() $n<m$
. We want to prove that
$n<m$
. We want to prove that
![]() $[na]<[ma]$
. Let
$[na]<[ma]$
. Let
![]() $n'>0$
be such that
$n'>0$
be such that
![]() $m=n+n'$
. Let
$m=n+n'$
. Let
![]() $i\in \mathbb {N}$
we want to show that
$i\in \mathbb {N}$
we want to show that
![]() $na+\mathrm {s}^{i}(0)<ma$
. By definition,
$na+\mathrm {s}^{i}(0)<ma$
. By definition,
![]() $ma=(n+n')a=na+n'a$
. Now by P4 and by the fact that a is non-standard and
$ma=(n+n')a=na+n'a$
. Now by P4 and by the fact that a is non-standard and
![]() $n'>0$
we have
$n'>0$
we have
![]() $na+\mathrm {s}^{i}(0)<na+a=(n+1)a\leq (n+n')a=ma$
. Therefore
$na+\mathrm {s}^{i}(0)<na+a=(n+1)a\leq (n+n')a=ma$
. Therefore
![]() $[na]<[ma]$
as desired.
$[na]<[ma]$
as desired.
Another important tool in the classical study of order types of models of
![]() $\mathsf {PA}$
is the overspill property:
$\mathsf {PA}$
is the overspill property:
Definition 7. Let M be a model of
![]() $\mathsf {SA}^-$
. Then
$\mathsf {SA}^-$
. Then
![]() $I\subseteq M$
is a cut of M if it is an initial segment of M with respect to
$I\subseteq M$
is a cut of M if it is an initial segment of M with respect to
![]() $<$
and it is closed under
$<$
and it is closed under
![]() $\mathrm {s}$
, i.e., for every
$\mathrm {s}$
, i.e., for every
![]() $i\in I$
we have
$i\in I$
we have
![]() $\mathrm {s}(i)\in I$
. A cut of M is proper if it is neither empty nor M itself.
$\mathrm {s}(i)\in I$
. A cut of M is proper if it is neither empty nor M itself.
Definition 8. Let
![]() $\mathcal {L}\supseteq \mathcal {L}_{<,\mathrm {s}}$
be a language. A theory
$\mathcal {L}\supseteq \mathcal {L}_{<,\mathrm {s}}$
be a language. A theory
![]() $T\supseteq \mathsf {SA}^-$
has the
$T\supseteq \mathsf {SA}^-$
has the
![]() $\mathcal {L}$
-overspill property if for every model
$\mathcal {L}$
-overspill property if for every model
![]() $M\models T$
there are no
$M\models T$
there are no
![]() $\mathcal {L}$
-definable proper cuts of M.
$\mathcal {L}$
-definable proper cuts of M.
Overspill is essentially a notational variant of induction:
Theorem 9. Let
![]() $\mathcal {L}\supseteq \mathcal {L}_{<,\mathrm {s}}$
be a language and
$\mathcal {L}\supseteq \mathcal {L}_{<,\mathrm {s}}$
be a language and
![]() $T\supseteq \mathsf {SA}^-$
be any theory. Then the following are equivalent:
$T\supseteq \mathsf {SA}^-$
be any theory. Then the following are equivalent:
-
(i)
 $\mathrm {Ind}(\mathcal {L})\subseteq T$
and
$\mathrm {Ind}(\mathcal {L})\subseteq T$
and -
(ii) T has the
 $\mathcal {L}$
-overspill property.
$\mathcal {L}$
-overspill property.
Proof “(i)
![]() $\Rightarrow $
(ii).” Let
$\Rightarrow $
(ii).” Let
![]() $M\models T$
and I be a proper cut of M. Then
$M\models T$
and I be a proper cut of M. Then
![]() $0\in I$
. Suppose towards a contradiction that I is definable by an
$0\in I$
. Suppose towards a contradiction that I is definable by an
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $\varphi $
. Then
$\varphi $
. Then
![]() $\mathrm {Ind}_\varphi $
implies that
$\mathrm {Ind}_\varphi $
implies that
![]() $I=M$
, so I was not proper.
$I=M$
, so I was not proper.
“(ii)
![]() $\Rightarrow $
(i).” Assume that
$\Rightarrow $
(i).” Assume that
![]() $\mathrm {Ind}_\varphi \notin T$
for some
$\mathrm {Ind}_\varphi \notin T$
for some
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $\varphi $
and find
$\varphi $
and find
![]() $M\models T$
such that
$M\models T$
such that
![]() $M\models \neg \mathrm {Ind}_\varphi $
. Define the formula
$M\models \neg \mathrm {Ind}_\varphi $
. Define the formula
![]() $\varphi '(x):=\varphi (x)\land \forall y (y<x\rightarrow \varphi (y))$
. Then
$\varphi '(x):=\varphi (x)\land \forall y (y<x\rightarrow \varphi (y))$
. Then
![]() $\varphi '$
defines a proper cut in M, and thus, T does not have the
$\varphi '$
defines a proper cut in M, and thus, T does not have the
![]() $\mathcal {L}$
-overspill property.
$\mathcal {L}$
-overspill property.
In particular,
![]() $\mathsf {SA}$
,
$\mathsf {SA}$
,
![]() $\mathsf {Pr}$
, and
$\mathsf {Pr}$
, and
![]() $\mathsf {PA}$
have the overspill property for their respective languages
$\mathsf {PA}$
have the overspill property for their respective languages
![]() $\mathcal {L}_{<,\mathrm {s}}$
,
$\mathcal {L}_{<,\mathrm {s}}$
,
![]() $\mathcal {L}_{<,\mathrm {s},+}$
, and
$\mathcal {L}_{<,\mathrm {s},+}$
, and
![]() $\mathcal {L}_{<,\mathrm {s},+,\cdot }$
.
$\mathcal {L}_{<,\mathrm {s},+,\cdot }$
.
3 Successor arithmetic
We begin our study by considering the two subsystems obtained by restricting our language to
![]() $\mathcal {L}_{<,\mathrm {s}}$
, viz.
$\mathcal {L}_{<,\mathrm {s}}$
, viz.
![]() $\mathsf {SA}^-$
and
$\mathsf {SA}^-$
and
![]() $\mathsf {SA}$
. The theory
$\mathsf {SA}$
. The theory
![]() $\mathsf {SA}^-$
is the theory of discrete linear orders with a least element and a strictly increasing successor function. Model theoretic properties of
$\mathsf {SA}^-$
is the theory of discrete linear orders with a least element and a strictly increasing successor function. Model theoretic properties of
![]() $\mathsf {SA}^-$
are discussed in [Reference Chang and Keisler5, Example 3.4.4].
$\mathsf {SA}^-$
are discussed in [Reference Chang and Keisler5, Example 3.4.4].
It is a folklore result that the theory of the structure
![]() $(\mathbb {N},0,<,\mathrm {s})$
has quantifier elimination (cf., e.g., [Reference Marker14, Exercise 3.4.4]) and the argument works for the theory
$(\mathbb {N},0,<,\mathrm {s})$
has quantifier elimination (cf., e.g., [Reference Marker14, Exercise 3.4.4]) and the argument works for the theory
![]() $\mathsf {SA}^-$
. The standard reference for the axiomatic version is [Reference Enderton6, Theorem 32A] where Enderton shows quantifier elimination for a theory he calls
$\mathsf {SA}^-$
. The standard reference for the axiomatic version is [Reference Enderton6, Theorem 32A] where Enderton shows quantifier elimination for a theory he calls
![]() $A_L$
which is essentially the conjunction of our O1 to O4, S1, S3, and S4. Enderton claims that
$A_L$
which is essentially the conjunction of our O1 to O4, S1, S3, and S4. Enderton claims that
![]() $A_L = \mathrm {Th}(\mathbb {N},<,\mathrm {s},0)$
[Reference Enderton6, Corollary 32B(b)], but his theory cannot prove our axiom S2 (the discreteness of the order). For the sake of completeness, we give a proof of quantifier elimination in this paper.
$A_L = \mathrm {Th}(\mathbb {N},<,\mathrm {s},0)$
[Reference Enderton6, Corollary 32B(b)], but his theory cannot prove our axiom S2 (the discreteness of the order). For the sake of completeness, we give a proof of quantifier elimination in this paper.
Lemma 10. The theory
![]() $\mathsf {SA}^-$
satisfies quantifier elimination.
$\mathsf {SA}^-$
satisfies quantifier elimination.
Proof It is enough to prove that for every quantifier free formula
![]() $\chi (\overline {x},y)$
there is a quantifier free formula
$\chi (\overline {x},y)$
there is a quantifier free formula
![]() $\varphi $
such that
$\varphi $
such that
where y does not appear in
![]() $\varphi $
. We prove this claim by induction over
$\varphi $
. We prove this claim by induction over
![]() $\chi $
. The only interesting cases are the atomic formulas.
$\chi $
. The only interesting cases are the atomic formulas.
If
![]() $\chi (x,y)\equiv \mathrm {s}^{n}(x)<\mathrm {s}^{m}(y)$
: let
$\chi (x,y)\equiv \mathrm {s}^{n}(x)<\mathrm {s}^{m}(y)$
: let
![]() $\varphi \equiv x=x$
. Let
$\varphi \equiv x=x$
. Let
![]() $M\models \mathsf {SA}^-$
, we want to show
$M\models \mathsf {SA}^-$
, we want to show
![]() $M\models \exists y \chi (x,y)$
. First assume
$M\models \exists y \chi (x,y)$
. First assume
![]() $m\geq n$
. Since
$m\geq n$
. Since
![]() $\mathsf {SA}^-\vdash \forall x \mathrm {s}^n(x)<\mathrm {s}^{m+1}(x)$
we have
$\mathsf {SA}^-\vdash \forall x \mathrm {s}^n(x)<\mathrm {s}^{m+1}(x)$
we have
![]() $M\models \exists y \mathrm {s}^{n}(x)<\mathrm {s}^{m}(y)$
as desired. Otherwise if
$M\models \exists y \mathrm {s}^{n}(x)<\mathrm {s}^{m}(y)$
as desired. Otherwise if
![]() $n>m$
since
$n>m$
since
![]() $\mathsf {SA}^-\vdash \forall x x<\mathrm {s}^{(n-m)+1}(x)$
then
$\mathsf {SA}^-\vdash \forall x x<\mathrm {s}^{(n-m)+1}(x)$
then
![]() $M\models \exists y \chi (\overline {x},y)$
. Hence:
$M\models \exists y \chi (\overline {x},y)$
. Hence:
as desired.
If
![]() $\chi (x,y)\equiv \mathrm {s}^{n}(y)<\mathrm {s}^{m}(x)$
: first assume
$\chi (x,y)\equiv \mathrm {s}^{n}(y)<\mathrm {s}^{m}(x)$
: first assume
![]() $m>n$
then since
$m>n$
then since
![]() $\mathsf {SA}^-\vdash \forall x \mathrm {s}^n(x)<\mathrm {s}^{m}(x)$
we have
$\mathsf {SA}^-\vdash \forall x \mathrm {s}^n(x)<\mathrm {s}^{m}(x)$
we have
![]() $\mathsf {SA}^-\vdash \exists y \chi (x,y)\leftrightarrow x=x$
. If
$\mathsf {SA}^-\vdash \exists y \chi (x,y)\leftrightarrow x=x$
. If
![]() $m\leq n$
then
$m\leq n$
then
![]() $\mathsf {SA}^-\vdash \exists y \chi (x,y)\leftrightarrow \mathrm {s}^{n}(0)<\mathrm {s}^{m}(x)$
. Indeed, let
$\mathsf {SA}^-\vdash \exists y \chi (x,y)\leftrightarrow \mathrm {s}^{n}(0)<\mathrm {s}^{m}(x)$
. Indeed, let
![]() $M\models \mathsf {SA}^-$
be a model such that there is a
$M\models \mathsf {SA}^-$
be a model such that there is a
![]() $y\in M$
such that
$y\in M$
such that
![]() $M\models \mathrm {s}^{n}(y)<\mathrm {s}^{m}(x)$
and
$M\models \mathrm {s}^{n}(y)<\mathrm {s}^{m}(x)$
and
![]() $M\models \lnot \mathrm {s}^{n}(0)<\mathrm {s}^{m}(x)$
. We have two cases: if
$M\models \lnot \mathrm {s}^{n}(0)<\mathrm {s}^{m}(x)$
. We have two cases: if
![]() $M\models \mathrm {s}^{n}(0)=\mathrm {s}^{m}(x)$
then we would have
$M\models \mathrm {s}^{n}(0)=\mathrm {s}^{m}(x)$
then we would have
![]() $M\models \mathrm {s}^{n}(y)<\mathrm {s}^{m}(x)=\mathrm {s}^{n}(0)$
but since
$M\models \mathrm {s}^{n}(y)<\mathrm {s}^{m}(x)=\mathrm {s}^{n}(0)$
but since
![]() $M\models \forall x \mathrm {s}^n(x)<\mathrm {s}^{n}(y)\rightarrow x<y$
then we would have
$M\models \forall x \mathrm {s}^n(x)<\mathrm {s}^{n}(y)\rightarrow x<y$
then we would have
![]() $M\models y<0$
. If
$M\models y<0$
. If
![]() $M\models \mathrm {s}^{m}(x)<\mathrm {s}^{n}(0)$
again we would have
$M\models \mathrm {s}^{m}(x)<\mathrm {s}^{n}(0)$
again we would have
![]() $M\models \mathrm {s}^{n}(y)<\mathrm {s}^{m}(x)<\mathrm {s}^{n}(0)$
which implies
$M\models \mathrm {s}^{n}(y)<\mathrm {s}^{m}(x)<\mathrm {s}^{n}(0)$
which implies
![]() $M\models y<0$
. On the other hand if
$M\models y<0$
. On the other hand if
![]() $M\models \mathrm {s}^n(0)<\mathrm {s}^{m}(x)$
then trivially
$M\models \mathrm {s}^n(0)<\mathrm {s}^{m}(x)$
then trivially
![]() $M\models \exists y \chi (\overline {x},y)$
as desired.
$M\models \exists y \chi (\overline {x},y)$
as desired.
If
![]() $\chi (\overline {x},y)$
does not have occurrences of y: then
$\chi (\overline {x},y)$
does not have occurrences of y: then
![]() $\exists y \chi (\overline {x},y)$
is either equivalent to
$\exists y \chi (\overline {x},y)$
is either equivalent to
![]() $0=0$
or
$0=0$
or
![]() $\lnot (0=0)$
.
$\lnot (0=0)$
.
If
![]() $\chi (x,y)\equiv \mathrm {s}^{n}(x)=\mathrm {s}^{m}(y)$
: similar to the second case.
$\chi (x,y)\equiv \mathrm {s}^{n}(x)=\mathrm {s}^{m}(y)$
: similar to the second case.
By using quantifier elimination, it is not hard to see that
![]() $\mathsf {SA}^-$
proves the induction schema.Footnote
6
$\mathsf {SA}^-$
proves the induction schema.Footnote
6
Theorem 11. For every formula
![]() $\varphi $
in the language
$\varphi $
in the language
![]() $\mathcal {L}_{<,\mathrm {s}}$
we have
$\mathcal {L}_{<,\mathrm {s}}$
we have
Proof We shall prove that for every model M of
![]() $\mathsf {SA}^-$
, the only definable set which contains
$\mathsf {SA}^-$
, the only definable set which contains
![]() $0$
and is closed under
$0$
and is closed under
![]() $\mathrm {s}$
is M itself. This proves the claim by Theorem 9.
$\mathrm {s}$
is M itself. This proves the claim by Theorem 9.
We say that
![]() $I\subseteq M$
is an open interval if there are
$I\subseteq M$
is an open interval if there are
![]() $a,b\in M\cup \{\infty \}$
such that
$a,b\in M\cup \{\infty \}$
such that
![]() $I = \{x\in M\,;\,a < x < b\}$
and a set
$I = \{x\in M\,;\,a < x < b\}$
and a set
![]() $X\subseteq M$
is called basic if it is a finite union of open intervals and singletons. As usual, an
$X\subseteq M$
is called basic if it is a finite union of open intervals and singletons. As usual, an
![]() $\mathcal {L}$
-theory T is called o-minimal or order-minimal if every
$\mathcal {L}$
-theory T is called o-minimal or order-minimal if every
![]() $\mathcal {L}$
-definable subset is basic.
$\mathcal {L}$
-definable subset is basic.
We claim that
![]() $\mathsf {SA}^-$
is an o-minimal theory: Let
$\mathsf {SA}^-$
is an o-minimal theory: Let
![]() $(M,0,<,\mathrm {s})\models \mathsf {SA}^-$
and
$(M,0,<,\mathrm {s})\models \mathsf {SA}^-$
and
![]() $X\subseteq M$
be
$X\subseteq M$
be
![]() $\mathcal {L}_{<,\mathrm {s}}$
-definable; by Lemma 10,
$\mathcal {L}_{<,\mathrm {s}}$
-definable; by Lemma 10,
![]() $\mathsf {SA}^-$
has quantifier elimination and therefore, X is definable by a quantifier-free
$\mathsf {SA}^-$
has quantifier elimination and therefore, X is definable by a quantifier-free
![]() $\mathcal {L}_{<,\mathrm {s}}$
-formula. We observe that sets definable by atomic formulae are either open intervals or points, hence basic; we furthermore observe that the basic sets are closed under finite intersections and complements. Thus all sets definable by quantifier-free formulae are basic.
$\mathcal {L}_{<,\mathrm {s}}$
-formula. We observe that sets definable by atomic formulae are either open intervals or points, hence basic; we furthermore observe that the basic sets are closed under finite intersections and complements. Thus all sets definable by quantifier-free formulae are basic.
Now suppose X is an
![]() $\mathcal {L}_{<,\mathrm {s}}$
-definable cut in M. By o-minimality, we have that
$\mathcal {L}_{<,\mathrm {s}}$
-definable cut in M. By o-minimality, we have that
![]() $X=I_0\cup \cdots \cup I_n$
where for every
$X=I_0\cup \cdots \cup I_n$
where for every
![]() $0\leq j\leq n$
, the set
$0\leq j\leq n$
, the set
![]() $I_j$
is either a non-empty open interval
$I_j$
is either a non-empty open interval
![]() $(a_j,b_j)$
or a singleton
$(a_j,b_j)$
or a singleton
![]() $\{b_j\}$
. Towards a contradiction, let
$\{b_j\}$
. Towards a contradiction, let
![]() $y\in M$
be such that
$y\in M$
be such that
![]() $y\notin X$
. Let
$y\notin X$
. Let
![]() $m := \max \{b_j\,;\,0\leq j\leq n\}$
. Note that for all
$m := \max \{b_j\,;\,0\leq j\leq n\}$
. Note that for all
![]() $x\in X$
we have
$x\in X$
we have
![]() $x\leq m$
.
$x\leq m$
.
Case 1:
![]() $m\in X$
. Then, since X is closed under successors, and so
$m\in X$
. Then, since X is closed under successors, and so
![]() $\mathrm {s}(m)\in X$
. But then
$\mathrm {s}(m)\in X$
. But then
![]() $m<\mathrm {s}(m)$
which is a contradiction.
$m<\mathrm {s}(m)$
which is a contradiction.
Case 2:
![]() $m\notin X$
. Then there is some
$m\notin X$
. Then there is some
![]() $0\leq j\leq n$
with
$0\leq j\leq n$
with
![]() $I_j = (a_j,m)$
. By axiom S1, we find
$I_j = (a_j,m)$
. By axiom S1, we find
![]() $m'\in I_j\subseteq X$
such that
$m'\in I_j\subseteq X$
such that
![]() $\mathrm {s}(m')=m$
. Once more, since X is closed under successors,
$\mathrm {s}(m')=m$
. Once more, since X is closed under successors,
![]() $m\in X$
, but this yields a contradiction as we have seen before.
$m\in X$
, but this yields a contradiction as we have seen before.
In particular, this means that
![]() $\mathsf {SA}$
and
$\mathsf {SA}$
and
![]() $\mathsf {SA}^-$
axiomatize the same theory:
$\mathsf {SA}^-$
axiomatize the same theory:
Corollary 12. Let M be a structure in the language
![]() $\mathcal {L}_{<,\mathrm {s}}$
. Then
$\mathcal {L}_{<,\mathrm {s}}$
. Then
![]() $M\models \mathsf {SA}$
if and only if
$M\models \mathsf {SA}$
if and only if
![]() $M\models \mathsf {SA}^-$
.
$M\models \mathsf {SA}^-$
.
Visser asked whether there is a reasonable finitely axiomatised theory that satisfies full induction (preferably in the full language of arithmetic); it is known that such a theory cannot be sequential (cf. [Reference Pudlák18, Reference Visser28] for more on sequentiality). By Corollary 12,
![]() $\mathsf {SA}$
is a finitely axiomatised theory that satisfies full induction (and is not sequential).
$\mathsf {SA}$
is a finitely axiomatised theory that satisfies full induction (and is not sequential).
Corollary 13. A linear order L is the order type of a model of
![]() $\mathsf {SA}$
if and only if there is a linear order A such that
$\mathsf {SA}$
if and only if there is a linear order A such that
![]() $L \cong \mathbb {N}+\mathbb {Z}\cdot A$
.
$L \cong \mathbb {N}+\mathbb {Z}\cdot A$
.
Proof By Corollary 12, it is enough to show that a model satisfies
![]() $\mathsf {SA}^-$
in order to get full
$\mathsf {SA}^-$
in order to get full
![]() $\mathsf {SA}$
. We already observed that the forward direction holds in Section 2.3 (the linear order A is the quotient structure
$\mathsf {SA}$
. We already observed that the forward direction holds in Section 2.3 (the linear order A is the quotient structure
![]() $M/{\sim }$
with the least element removed). For the other direction, if A is a linear order then
$M/{\sim }$
with the least element removed). For the other direction, if A is a linear order then
![]() $\mathbb {N}+\mathbb {Z}\cdot A$
can be easily made into an
$\mathbb {N}+\mathbb {Z}\cdot A$
can be easily made into an
![]() $\mathsf {SA}^-$
model by defining
$\mathsf {SA}^-$
model by defining
![]() $\mathrm {s}(n) := n+1$
and
$\mathrm {s}(n) := n+1$
and
![]() $\mathrm {s}(z,a) := (z+1,a)$
.
$\mathrm {s}(z,a) := (z+1,a)$
.
4 Models based on generalised formal power series
4.1 Definitions
Generalised formal power series, introduced by Levi-Civita, are a generalisation of polynomials over a ring: while polynomials only have natural number exponents, generalised formal power series allow more general formal exponents.Footnote
7
In this section, we shall adapt the classical theory of generalised formal power series to our context. In particular, we shall show how generalised power series can be used as a tool in building non-standard models of
![]() $\mathsf {Pr}^-$
,
$\mathsf {Pr}^-$
,
![]() $\mathsf {PA}^-$
, and
$\mathsf {PA}^-$
, and
![]() $\mathsf {Pr}$
.
$\mathsf {Pr}$
.
A linear order
![]() $(\Gamma ,0,<)$
with a least element
$(\Gamma ,0,<)$
with a least element
![]() $0$
will be called an exponent order; an ordered abelian group
$0$
will be called an exponent order; an ordered abelian group
![]() $(B,0,<,+)$
with
$(B,0,<,+)$
with
![]() $\mathbb {Z}\subseteq B$
will be called the base group and its elements will be called coefficients. The generalised formal power series will generalise the idea of a polynomial with coefficients in B, using formal terms of the form
$\mathbb {Z}\subseteq B$
will be called the base group and its elements will be called coefficients. The generalised formal power series will generalise the idea of a polynomial with coefficients in B, using formal terms of the form
where a ranges over elements of
![]() $\Gamma $
.
$\Gamma $
.
If
![]() $f:\Gamma \to B$
, we shall call the set
$f:\Gamma \to B$
, we shall call the set
![]() $\mathrm {supp}(f)=\lbrace a\in \Gamma \,;\,f(a)\neq 0\rbrace \cup \lbrace 0 \rbrace $
the support of f. As usual, we say that a subset
$\mathrm {supp}(f)=\lbrace a\in \Gamma \,;\,f(a)\neq 0\rbrace \cup \lbrace 0 \rbrace $
the support of f. As usual, we say that a subset
![]() $S\subseteq \Gamma $
is reverse well-founded if it has no strictly increasing infinite sequences. A function
$S\subseteq \Gamma $
is reverse well-founded if it has no strictly increasing infinite sequences. A function
![]() $f:\Gamma \to B$
is called a formal power series with base B and exponent
$f:\Gamma \to B$
is called a formal power series with base B and exponent
![]() $\Gamma $
if
$\Gamma $
if
![]() $\mathrm {supp}(f)$
is reverse well-founded and
$\mathrm {supp}(f)$
is reverse well-founded and
![]() $f(0)\in \mathbb {Z}$
.Footnote
8
Since non-empty reverse well-founded sets have a maximal element, we can define the leading term of a formal power series f, denoted by
$f(0)\in \mathbb {Z}$
.Footnote
8
Since non-empty reverse well-founded sets have a maximal element, we can define the leading term of a formal power series f, denoted by
![]() ${\scriptstyle \mathrm {LT}}(f)$
, as the maximal element of
${\scriptstyle \mathrm {LT}}(f)$
, as the maximal element of
![]() $\mathrm {supp}(f)$
.
$\mathrm {supp}(f)$
.
We say that f is non-negative if
![]() $f({\scriptstyle \mathrm {LT}}(f))> 0$
or f is the function that is constant and equal to
$f({\scriptstyle \mathrm {LT}}(f))> 0$
or f is the function that is constant and equal to
![]() $0$
everywhere. The set of non-negative formal power series with base B and exponent
$0$
everywhere. The set of non-negative formal power series with base B and exponent
![]() $\Gamma $
is denoted by
$\Gamma $
is denoted by
![]() $B(X^\Gamma )$
.
$B(X^\Gamma )$
.
4.2 Addition of formal power series
We think of
![]() $f\in B(X^\Gamma )$
as the formal sum
$f\in B(X^\Gamma )$
as the formal sum
![]() $\sum _{a\in \mathrm {supp}(f)}f(a)X^a$
and define the order and additive structure on
$\sum _{a\in \mathrm {supp}(f)}f(a)X^a$
and define the order and additive structure on
![]() $B(X^\Gamma )$
according to this intuition:
$B(X^\Gamma )$
according to this intuition:
-
1. The order
 $<$
on
$<$
on
 $B(X^\Gamma )$
is the anti-lexicographic order: if
$B(X^\Gamma )$
is the anti-lexicographic order: if
 $f\neq g$
, then the reverse well-foundedness of
$f\neq g$
, then the reverse well-foundedness of
 $\mathrm {supp}(f)$
and
$\mathrm {supp}(f)$
and
 $\mathrm {supp}(g)$
implies that there is a largest
$\mathrm {supp}(g)$
implies that there is a largest
 $a\in \Gamma $
such that
$a\in \Gamma $
such that
 $f(a)\neq g(a)$
; we define
$f(a)\neq g(a)$
; we define
 $f<g$
if and only if
$f<g$
if and only if
 $f(a)< g(a)$
for that largest such a.
$f(a)< g(a)$
for that largest such a. -
2. The constant function that is equal to
 $0$
everywhere is clearly the minimal non-negative formal power series with respect to the order
$0$
everywhere is clearly the minimal non-negative formal power series with respect to the order
 $<$
and will be denoted by
$<$
and will be denoted by
 $0$
.
$0$
. -
3. If
 $f\in B(X^\Gamma )$
, we define its successor by
$f\in B(X^\Gamma )$
, we define its successor by  $$ \begin{align*}\mathrm{s}(f)(a) := \left\{ \begin{array}{cl} f(a), & \mbox{if}\ a\neq 0\ \mbox{and}\\ f(a)+1, & \mbox{if}\ a = 0. \end{array}\right.\end{align*} $$
$$ \begin{align*}\mathrm{s}(f)(a) := \left\{ \begin{array}{cl} f(a), & \mbox{if}\ a\neq 0\ \mbox{and}\\ f(a)+1, & \mbox{if}\ a = 0. \end{array}\right.\end{align*} $$
-
4. Given
 $f,g\in B(X^\Gamma )$
, we define
$f,g\in B(X^\Gamma )$
, we define
 $f+g$
pointwise by
$f+g$
pointwise by
 $(f+g)(a) := f(a) + g(a)$
. Note that
$(f+g)(a) := f(a) + g(a)$
. Note that
 $\mathrm {supp}(f+g)\subseteq \mathrm {supp}(f)\cup \mathrm {supp}(g)$
, so
$\mathrm {supp}(f+g)\subseteq \mathrm {supp}(f)\cup \mathrm {supp}(g)$
, so
 $\mathrm {supp}(f+g)$
is reverse well-founded. Furthermore, if f and g are both non-negative, then
$\mathrm {supp}(f+g)$
is reverse well-founded. Furthermore, if f and g are both non-negative, then
 $f+g$
is non-negative. Thus,
$f+g$
is non-negative. Thus,
 $+$
is a binary operation on
$+$
is a binary operation on
 $B(X^\Gamma )$
.
$B(X^\Gamma )$
.
Theorem 14. If
![]() $\Gamma $
is an exponent order and B is a base group, then
$\Gamma $
is an exponent order and B is a base group, then
![]() $(B(X^\Gamma ),0,<,\mathrm {s},+)$
is a model of
$(B(X^\Gamma ),0,<,\mathrm {s},+)$
is a model of
![]() $\mathsf {Pr}^-$
.
$\mathsf {Pr}^-$
.
Proof It is routine to check that the axioms of
![]() $\mathsf {Pr}^-$
are satisfied. Note that it is axiom S2 (the fact that
$\mathsf {Pr}^-$
are satisfied. Note that it is axiom S2 (the fact that
![]() $\mathrm {s}(x)$
is the order successor of x) that uses our additional requirement that
$\mathrm {s}(x)$
is the order successor of x) that uses our additional requirement that
![]() $f(0) \in \mathbb {Z}$
.
$f(0) \in \mathbb {Z}$
.
Let us consider a few instructive examples:
-
1. If
 $\Gamma =\lbrace 0\rbrace =1$
and
$\Gamma =\lbrace 0\rbrace =1$
and
 $B=\mathbb {Z}$
then
$B=\mathbb {Z}$
then
 $B(X^\Gamma ) = \mathbb {Z}(X^1)$
and
$B(X^\Gamma ) = \mathbb {Z}(X^1)$
and
 $(\mathbb {Z}(X^1),0,<, \mathrm {s},+)$
is isomorphic to the natural numbers.
$(\mathbb {Z}(X^1),0,<, \mathrm {s},+)$
is isomorphic to the natural numbers. -
2. If
 $\Gamma =\lbrace 0,1 \rbrace =2$
and
$\Gamma =\lbrace 0,1 \rbrace =2$
and
 $B=\mathbb {Z}$
, then
$B=\mathbb {Z}$
, then
 $B(X^\Gamma ) = \mathbb {Z}(X^2)$
and
$B(X^\Gamma ) = \mathbb {Z}(X^2)$
and
 $(\mathbb {Z}(X^2),0,<, \mathrm {s},+)$
is isomorphic to the non-negative polynomials of degree at most one on
$(\mathbb {Z}(X^2),0,<, \mathrm {s},+)$
is isomorphic to the non-negative polynomials of degree at most one on
 $\mathbb {Z}$
with the standard order and operations, and, more generally for every
$\mathbb {Z}$
with the standard order and operations, and, more generally for every
 $0<n\in \mathbb {N}$
, if
$0<n\in \mathbb {N}$
, if
 $\Gamma =n$
and
$\Gamma =n$
and
 $B=\mathbb {Z}$
, then
$B=\mathbb {Z}$
, then
 $(\mathbb {Z}(X^n),0,<,\mathrm {s},+)$
is isomorphic to the non-negative polynomials of degree at most
$(\mathbb {Z}(X^n),0,<,\mathrm {s},+)$
is isomorphic to the non-negative polynomials of degree at most
 $n-1$
over
$n-1$
over
 $\mathbb {Z}$
with the standard order and operations.
$\mathbb {Z}$
with the standard order and operations. -
3. Finally, by taking
 $\Gamma =\mathbb {N}$
and
$\Gamma =\mathbb {N}$
and
 $B=\mathbb {Z}$
we have that
$B=\mathbb {Z}$
we have that
 $(\mathbb {Z}(X^{\mathbb {N}}),0,<,\mathrm {s},+)$
is isomorphic to the non-negative polynomials over
$(\mathbb {Z}(X^{\mathbb {N}}),0,<,\mathrm {s},+)$
is isomorphic to the non-negative polynomials over
 $\mathbb {Z}$
with the standard order and operations. As mentioned in Section 2.2, this means that the order type of
$\mathbb {Z}$
with the standard order and operations. As mentioned in Section 2.2, this means that the order type of
 $\mathbb {Z}(X^n)$
is
$\mathbb {Z}(X^n)$
is
 $O_n$
and the order type of
$O_n$
and the order type of
 $\mathbb {Z}(X^{\mathbb {N}})$
is
$\mathbb {Z}(X^{\mathbb {N}})$
is
 $O_\omega $
.Footnote
9
$O_\omega $
.Footnote
9
If we require in addition that B is a divisible group, then Presburger’s theorem implies that the formal power series construction gives a model of
![]() $\mathsf {Pr}$
. This fits with Theorem 17(ii) (due to Llewellyn-Jones) discussed in the next section.
$\mathsf {Pr}$
. This fits with Theorem 17(ii) (due to Llewellyn-Jones) discussed in the next section.
Theorem 15. Let
![]() $(\Gamma ,0,<)$
be a linearly ordered set with least element
$(\Gamma ,0,<)$
be a linearly ordered set with least element
![]() $0$
and
$0$
and
![]() $(B,0,<,+)$
be a ordered divisible abelian group. Then
$(B,0,<,+)$
be a ordered divisible abelian group. Then
![]() $(B(X^\Gamma ), 0,<,\mathrm {s},+)$
is a model of
$(B(X^\Gamma ), 0,<,\mathrm {s},+)$
is a model of
![]() $\mathsf {Pr}$
.
$\mathsf {Pr}$
.
Proof By Theorem 14 and Presburger’s characterisation of
![]() $\mathsf {Pr}$
by
$\mathsf {Pr}$
by
![]() $\mathsf {Pr^{D}}$
, we only need to show that that for every natural number
$\mathsf {Pr^{D}}$
, we only need to show that that for every natural number
![]() $n>0$
, the axiom
$n>0$
, the axiom
![]() $\mathrm {D}_{n}$
holds.
$\mathrm {D}_{n}$
holds.
Let
![]() $f\in B(X^\Gamma )$
and
$f\in B(X^\Gamma )$
and
![]() $0<n\in \mathbb {N}$
; we shall define g such that
$0<n\in \mathbb {N}$
; we shall define g such that
![]() $f = \mathrm {s}^m(g\cdot n)$
. First find
$f = \mathrm {s}^m(g\cdot n)$
. First find
![]() $z\in \mathbb {Z}$
and
$z\in \mathbb {Z}$
and
![]() $0<m<n$
such that
$0<m<n$
such that
![]() $f(0)=zn+m$
. Use the divisibility of B to find for every
$f(0)=zn+m$
. Use the divisibility of B to find for every
![]() $a\in \Gamma $
an element
$a\in \Gamma $
an element
![]() $b_a\in B$
such that
$b_a\in B$
such that
![]() $f(a)=b_a\cdot n$
. Now, define
$f(a)=b_a\cdot n$
. Now, define
 $$ \begin{align*}g(a)=\begin{cases} z, &\text{if}\ a=0,\\ b_a, &\text{if}\ a>0. \end{cases}\end{align*} $$
$$ \begin{align*}g(a)=\begin{cases} z, &\text{if}\ a=0,\\ b_a, &\text{if}\ a>0. \end{cases}\end{align*} $$
Then
![]() $f=\mathrm {s}^m(g\cdot n)$
as desired.
$f=\mathrm {s}^m(g\cdot n)$
as desired.
4.3 Multiplication of formal power series
In order to define multiplication on formal power series, we need an additive structure on the exponents and a multiplicative structure on the coefficients. So, we now assume that we have an addition
![]() $+$
on our exponent order such that
$+$
on our exponent order such that
![]() $(\Gamma ,0,<,+)$
is an ordered abelian monoid with least element
$(\Gamma ,0,<,+)$
is an ordered abelian monoid with least element
![]() $0$
and a multiplication
$0$
and a multiplication
![]() $\cdot $
on the base group such that
$\cdot $
on the base group such that
![]() $(B,0,1,<,+,\cdot )$
is an ordered ring.
$(B,0,1,<,+,\cdot )$
is an ordered ring.
If
![]() $f,g\in B(X^\Gamma )$
, we define
$f,g\in B(X^\Gamma )$
, we define
![]() $f\cdot g$
by
$f\cdot g$
by
 $$ \begin{align*}(f\cdot g)(a):=\sum_{b+c=a}f(b)\cdot g(c).\end{align*} $$
$$ \begin{align*}(f\cdot g)(a):=\sum_{b+c=a}f(b)\cdot g(c).\end{align*} $$
In order to see that this defines a formal power series, we need to check that for every
![]() $a\in \Gamma $
, there are only finitely many pairs
$a\in \Gamma $
, there are only finitely many pairs
![]() $c,b\in \Gamma $
such that
$c,b\in \Gamma $
such that
![]() $c+b=a$
and
$c+b=a$
and
![]() $f(b)\neq 0$
and
$f(b)\neq 0$
and
![]() $g(c)\neq 0$
. Assume towards a contradiction that there are infinite sets
$g(c)\neq 0$
. Assume towards a contradiction that there are infinite sets
![]() $\{b_n\,;\,n\in \mathbb {N}\}$
and
$\{b_n\,;\,n\in \mathbb {N}\}$
and
![]() $\{c_n\,;\,n\in \mathbb {N}\}$
such that for all
$\{c_n\,;\,n\in \mathbb {N}\}$
such that for all
![]() $n\in \mathbb {N}$
, we have
$n\in \mathbb {N}$
, we have
![]() $b_n+c_n=a$
,
$b_n+c_n=a$
,
![]() $f(b_n)\neq 0$
, and
$f(b_n)\neq 0$
, and
![]() $g(c_n)\neq 0$
. From this, we now build either a strictly increasing sequence in
$g(c_n)\neq 0$
. From this, we now build either a strictly increasing sequence in
![]() $\mathrm {supp}(f)$
or in
$\mathrm {supp}(f)$
or in
![]() $\mathrm {supp}(g)$
, contradicting their reverse well-foundedness.
$\mathrm {supp}(g)$
, contradicting their reverse well-foundedness.
Given a sequence
![]() $s:\mathbb {N}\to \Gamma $
we call an element
$s:\mathbb {N}\to \Gamma $
we call an element
![]() $s(n)$
of the sequence a spike if for all
$s(n)$
of the sequence a spike if for all
![]() $m>n$
we have
$m>n$
we have
![]() $s(n)>s(m)$
. Consider
$s(n)>s(m)$
. Consider
![]() $b:\mathbb {N}\to \Gamma $
and
$b:\mathbb {N}\to \Gamma $
and
![]() $c:\mathbb {N}\to \Gamma $
as sequences defined by
$c:\mathbb {N}\to \Gamma $
as sequences defined by
![]() $b(n) := b_n$
and
$b(n) := b_n$
and
![]() $c(n) := c_n$
. Each of them either has infinitely many spikes or some n such that there are no spikes after n.
$c(n) := c_n$
. Each of them either has infinitely many spikes or some n such that there are no spikes after n.
If b has only finitely many spikes, then we can easily define a strictly increasing subsequence, contradicting the reverse well-foundedness of
![]() $\mathrm {supp}(f)$
. On the other hand, if b has infinitely many spikes, then the subsequence of spikes forms a strictly decreasing sequence, but since
$\mathrm {supp}(f)$
. On the other hand, if b has infinitely many spikes, then the subsequence of spikes forms a strictly decreasing sequence, but since
![]() $b_n+c_n = a$
, the corresponding subsequence of c must form a strictly increasing sequence, contradicting the reverse well-foundedness of g.
$b_n+c_n = a$
, the corresponding subsequence of c must form a strictly increasing sequence, contradicting the reverse well-foundedness of g.
A minor modification of that argument shows that if
![]() $f,g\in B(X^\Gamma )$
, then
$f,g\in B(X^\Gamma )$
, then
is reverse well-founded. Since
![]() $\mathrm {supp}(f\cdot g) \subseteq Z$
, we have that
$\mathrm {supp}(f\cdot g) \subseteq Z$
, we have that
![]() $\mathrm {supp}(f\cdot g)$
is reverse well-founded. Furthermore,
$\mathrm {supp}(f\cdot g)$
is reverse well-founded. Furthermore,
![]() ${\scriptstyle \mathrm {LT}}(f\cdot g)={\scriptstyle \mathrm {LT}}(f)+{\scriptstyle \mathrm {LT}}(g)$
and
${\scriptstyle \mathrm {LT}}(f\cdot g)={\scriptstyle \mathrm {LT}}(f)+{\scriptstyle \mathrm {LT}}(g)$
and
![]() $(f\cdot g)({\scriptstyle \mathrm {LT}}(f\cdot g)) = f({\scriptstyle \mathrm {LT}}(f))\cdot g({\scriptstyle \mathrm {LT}}(g))> 0$
, so
$(f\cdot g)({\scriptstyle \mathrm {LT}}(f\cdot g)) = f({\scriptstyle \mathrm {LT}}(f))\cdot g({\scriptstyle \mathrm {LT}}(g))> 0$
, so
![]() $f\cdot g$
is non-negative. Together,
$f\cdot g$
is non-negative. Together,
![]() $f\cdot g\in B(X^\Gamma )$
.
$f\cdot g\in B(X^\Gamma )$
.
Theorem 16. Let
![]() $(\Gamma ,0,<,+)$
be an ordered abelian monoid with least element
$(\Gamma ,0,<,+)$
be an ordered abelian monoid with least element
![]() $0$
and
$0$
and
![]() $(B,0,1,<,+,\cdot )$
be an ordered commutative ring. Then the structure
$(B,0,1,<,+,\cdot )$
be an ordered commutative ring. Then the structure
![]() $(B(X^\Gamma ), 0,<,\mathrm {s},+,\cdot )$
is a model of
$(B(X^\Gamma ), 0,<,\mathrm {s},+,\cdot )$
is a model of
![]() $\mathsf {PA}^-$
.
$\mathsf {PA}^-$
.
Proof It is routine to check the axioms M1 to M6.
Note that by Theorem 15, if
![]() $B=\mathbb {Q}$
and
$B=\mathbb {Q}$
and
![]() $\Gamma =2$
, then
$\Gamma =2$
, then
![]() $\mathbb {Q}(X^2)$
is a model of
$\mathbb {Q}(X^2)$
is a model of
![]() $\mathsf {Pr}$
of order type
$\mathsf {Pr}$
of order type
![]() $\mathbb {N}+\mathbb {Z}\cdot \mathbb {Q}$
, but it is not closed under multiplication and so cannot be a model of
$\mathbb {N}+\mathbb {Z}\cdot \mathbb {Q}$
, but it is not closed under multiplication and so cannot be a model of
![]() $\mathsf {PA}^-$
. This model is well-known in the literature; cf., e.g., [Reference Zoethout29].
$\mathsf {PA}^-$
. This model is well-known in the literature; cf., e.g., [Reference Zoethout29].
5 Presburger arithmetic
Presburger arithmetic, the additive fragment of arithmetic, is closely related to ordered abelian groups. Llewellyn-Jones considered an integer version of Presburger arithmetic, allowing for additive inverses and gives an axiomatisation for this theory that we shall call
![]() $\mathsf {Pr^{\mathbb {Z}}}$
[Reference Llewellyn-Jones13]. If
$\mathsf {Pr^{\mathbb {Z}}}$
[Reference Llewellyn-Jones13]. If
![]() $(M,0,<,\mathrm {s},+)\models \mathsf {Pr^{\mathbb {Z}}}$
, then
$(M,0,<,\mathrm {s},+)\models \mathsf {Pr^{\mathbb {Z}}}$
, then
![]() $(M,0,<,+)$
is an ordered abelian group; Llewellyn-Jones calls these groups Presburger groups and proves in his integer setting that G is a Presburger group if and only if G is isomorphic to
$(M,0,<,+)$
is an ordered abelian group; Llewellyn-Jones calls these groups Presburger groups and proves in his integer setting that G is a Presburger group if and only if G is isomorphic to
![]() $\mathbb {Z}\cdot H$
where H is an ordered divisible abelian group [Reference Llewellyn-Jones13, Sections 3.1 and 3.2]. In the following, we reformulate Llewellyn-Jones’s approach in the standard setting of arithmetic (i.e., without additive inverses).
$\mathbb {Z}\cdot H$
where H is an ordered divisible abelian group [Reference Llewellyn-Jones13, Sections 3.1 and 3.2]. In the following, we reformulate Llewellyn-Jones’s approach in the standard setting of arithmetic (i.e., without additive inverses).
Theorem 17. Let M be an
![]() $\mathcal {L}_{<,\mathrm {s},+}$
-structure.
$\mathcal {L}_{<,\mathrm {s},+}$
-structure.
-
(i) The structure M is a model of
 $\mathsf {Pr}^-$
if and only if there is an ordered abelian group G such that M is isomorphic to the standard monoid over G, and
$\mathsf {Pr}^-$
if and only if there is an ordered abelian group G such that M is isomorphic to the standard monoid over G, and -
(ii) the structure M is a model of
 $\mathsf {Pr}$
if and only if there is an ordered divisible abelian group G such that M is isomorphic to the standard monoid over G.
$\mathsf {Pr}$
if and only if there is an ordered divisible abelian group G such that M is isomorphic to the standard monoid over G.
Proof This proof is a reformulation of the characterisation of Presburger groups as in [Reference Llewellyn-Jones13] to the standard setting.
For the forward direction of (i), it is enough to see that in
![]() $\mathbb {N}+\mathbb {Z}\cdot G^+$
all the axioms of
$\mathbb {N}+\mathbb {Z}\cdot G^+$
all the axioms of
![]() $\mathsf {Pr}^-$
are trivially satisfied. For the other direction, if
$\mathsf {Pr}^-$
are trivially satisfied. For the other direction, if
![]() $M\models \mathsf {Pr}^-$
then by (the proof of) Corollary 13, the order type of M is
$M\models \mathsf {Pr}^-$
then by (the proof of) Corollary 13, the order type of M is
![]() $\mathbb {N}+\mathbb {Z}\cdot A$
for a linear order A consisting of the non-zero Archimedean classes of M. For each
$\mathbb {N}+\mathbb {Z}\cdot A$
for a linear order A consisting of the non-zero Archimedean classes of M. For each
![]() $a\in A$
, we define a formal negative element
$a\in A$
, we define a formal negative element
![]() $-a$
such that the negative elements are all distinct from the elements of A and pairwise distinct. Then we define
$-a$
such that the negative elements are all distinct from the elements of A and pairwise distinct. Then we define
![]() $-A := \{-a\,;\,a\in A\}$
and
$-A := \{-a\,;\,a\in A\}$
and
![]() $G := -A\cup \{[0]\}\cup A$
. For notational convenience, we define
$G := -A\cup \{[0]\}\cup A$
. For notational convenience, we define
![]() $-[0] := [0]$
. We define an abelian group structure on G as follows:
$-[0] := [0]$
. We define an abelian group structure on G as follows:
-
1. For any
 $g\in G$
,
$g\in G$
,
 $g+[0] := [0]+g := g$
.
$g+[0] := [0]+g := g$
. -
2. If
 $a,b\in A$
are non-zero Archimedean classes of M, then there is a unique
$a,b\in A$
are non-zero Archimedean classes of M, then there is a unique
 $c\in A$
such that for all
$c\in A$
such that for all
 $x\in a$
and
$x\in a$
and
 $y\in b$
, we have that
$y\in b$
, we have that
 $x+y \in c$
; define
$x+y \in c$
; define
 $a+b := b+a := c$
and
$a+b := b+a := c$
and
 $(-a)+(-b) := (-b)+(-a) := -c$
.
$(-a)+(-b) := (-b)+(-a) := -c$
. -
3. If
 $a,b\in A$
,
$a,b\in A$
,
 $x\in a$
, and
$x\in a$
, and
 $y\in b$
with
$y\in b$
with
 $x<y$
, then by ⋇, we find z such that
$x<y$
, then by ⋇, we find z such that
 $x+z = y$
. Let c be the Archimedean class of z, i.e.,
$x+z = y$
. Let c be the Archimedean class of z, i.e.,
 $c\in A\cup \{[0]\}$
. Then
$c\in A\cup \{[0]\}$
. Then
 $(-a)+b := b+(-a) := c$
and
$(-a)+b := b+(-a) := c$
and
 $a+(-b) := (-b)+a := -c$
.
$a+(-b) := (-b)+a := -c$
.
It is routine to check that
![]() $(G,0,<,+)$
is an ordered abelian group and that M isomorphic to
$(G,0,<,+)$
is an ordered abelian group and that M isomorphic to
![]() $\mathbb {N}+\mathbb {Z}\cdot G^+$
. For (ii), all that is left to show is that divisibility of the group corresponds to the additional axioms
$\mathbb {N}+\mathbb {Z}\cdot G^+$
. For (ii), all that is left to show is that divisibility of the group corresponds to the additional axioms
![]() $\mathrm {D}_n$
of
$\mathrm {D}_n$
of
![]() $\mathsf {Pr^{D}}$
.
$\mathsf {Pr^{D}}$
.
Corollary 18 Folklore
There is a model of
![]() $\mathsf {Pr}$
with order type
$\mathsf {Pr}$
with order type
![]() $\mathbb {N}+\mathbb {Z}\cdot \mathbb {R}$
.
$\mathbb {N}+\mathbb {Z}\cdot \mathbb {R}$
.
Proof The real numbers
![]() $\mathbb {R}$
are an ordered divisible abelian group, so by Theorem 17 (ii), there is a model of
$\mathbb {R}$
are an ordered divisible abelian group, so by Theorem 17 (ii), there is a model of
![]() $\mathsf {Pr}$
with order type
$\mathsf {Pr}$
with order type
![]() $\mathbb {N}+\mathbb {Z}\cdot \mathbb {R}^+$
. The claim follows from the fact that
$\mathbb {N}+\mathbb {Z}\cdot \mathbb {R}^+$
. The claim follows from the fact that
![]() $\mathbb {R}^+$
and
$\mathbb {R}^+$
and
![]() $\mathbb {R}$
have the same order type.
$\mathbb {R}$
have the same order type.
Corollary 19. Let M be a non-standard model of
![]() $\mathsf {Pr}$
. Then M has order type
$\mathsf {Pr}$
. Then M has order type
![]() $\mathbb {N}+\mathbb {Z}\cdot A$
where A is a dense linear order without endpoints.
$\mathbb {N}+\mathbb {Z}\cdot A$
where A is a dense linear order without endpoints.
Proof It is enough to observe that divisibility implies density and use Theorem 17.
We can use Theorem 17 and the general theory of groupable linear orders to get a characterisation theorem for the order types of models of
![]() $\mathsf {Pr}^-$
. First let us recall a classical result about groupable linear orders; cf., e.g., [Reference Rosenstein21, Theorem 8.14]:
$\mathsf {Pr}^-$
. First let us recall a classical result about groupable linear orders; cf., e.g., [Reference Rosenstein21, Theorem 8.14]:
Theorem 20. A linear order
![]() $(L,<)$
is groupable if and only if there is an ordinal
$(L,<)$
is groupable if and only if there is an ordinal
![]() $\alpha $
and a densely ordered abelian group
$\alpha $
and a densely ordered abelian group
![]() $(D,0,<,+)$
such that L has order type
$(D,0,<,+)$
such that L has order type
![]() $\mathbb {Z}^\alpha \cdot D$
.
$\mathbb {Z}^\alpha \cdot D$
.
Corollary 21. A structure M is a model of
![]() $\mathsf {Pr}^-$
if and only if there is an ordinal
$\mathsf {Pr}^-$
if and only if there is an ordinal
![]() $\alpha $
and a densely ordered abelian group
$\alpha $
and a densely ordered abelian group
![]() $(D,0,<,+)$
such that M has order type
$(D,0,<,+)$
such that M has order type
![]() $\mathbb {N}+\mathbb {Z}\cdot (\mathbb {Z}^\alpha \cdot D)^{+}$
.
$\mathbb {N}+\mathbb {Z}\cdot (\mathbb {Z}^\alpha \cdot D)^{+}$
.
As we have seen in Section 4, the non-negative formal power series on
![]() $\mathbb {Z}$
with exponent
$\mathbb {Z}$
with exponent
![]() $2$
are isomorphic to the ordered abelian monoid of polynomials of degree at most one with integer coefficients. Moreover, by Theorem 14 (or Theorem 17),
$2$
are isomorphic to the ordered abelian monoid of polynomials of degree at most one with integer coefficients. Moreover, by Theorem 14 (or Theorem 17),
![]() $(\mathbb {Z}(X^2),0,<,\mathrm {s},+)\models \mathsf {Pr}^-$
. The next theorem expresses that this is a lower bound for non-standard models of
$(\mathbb {Z}(X^2),0,<,\mathrm {s},+)\models \mathsf {Pr}^-$
. The next theorem expresses that this is a lower bound for non-standard models of
![]() $\mathsf {Pr}^-$
.
$\mathsf {Pr}^-$
.
Theorem 22. Let M be a non-standard model of
![]() $\mathsf {Pr}^-$
. Then M has a submodel isomorphic to
$\mathsf {Pr}^-$
. Then M has a submodel isomorphic to
![]() $(\mathbb {Z}(X^2),0,<,\mathrm {s},+)$
.
$(\mathbb {Z}(X^2),0,<,\mathrm {s},+)$
.
Proof Let M be a non-standard model of
![]() $\mathsf {Pr}^-$
and
$\mathsf {Pr}^-$
and
![]() $a\in M$
be a non-standard element of M. define the following mapping
$a\in M$
be a non-standard element of M. define the following mapping
![]() $\varphi :\mathbb {Z}(X^2)\rightarrow M$
:
$\varphi :\mathbb {Z}(X^2)\rightarrow M$
:
 $$ \begin{align*}\varphi(f)=\begin{cases} \mathrm{s}^{n}(0), &\text{if}\ {\scriptstyle \mathrm{LT}}(f)=0\ \text{and}\ f(0)=n,\\ \mathrm{s}^{m}(na), &\text{if}\ {\scriptstyle \mathrm{LT}}(f)=1\ \text{and}\ f(1)=n, f(0)=m\geq 0,\\ b, &\text{if}\ {\scriptstyle \mathrm{LT}}(f)=1\ \text{and}\ f(1)=n, f(0)=m<0\ \text{and}\\ &\quad \mathrm{s}^{-m}(b)=na. \end{cases} \end{align*} $$
$$ \begin{align*}\varphi(f)=\begin{cases} \mathrm{s}^{n}(0), &\text{if}\ {\scriptstyle \mathrm{LT}}(f)=0\ \text{and}\ f(0)=n,\\ \mathrm{s}^{m}(na), &\text{if}\ {\scriptstyle \mathrm{LT}}(f)=1\ \text{and}\ f(1)=n, f(0)=m\geq 0,\\ b, &\text{if}\ {\scriptstyle \mathrm{LT}}(f)=1\ \text{and}\ f(1)=n, f(0)=m<0\ \text{and}\\ &\quad \mathrm{s}^{-m}(b)=na. \end{cases} \end{align*} $$
It is easy to see that
![]() $\varphi $
is an order-preserving injection.
$\varphi $
is an order-preserving injection.
Corollary 23. Let M be a non-standard model of
![]() $\mathsf {Pr}^-$
then the order
$\mathsf {Pr}^-$
then the order
![]() $\mathbb {N}+\mathbb {Z}\cdot \mathbb {N}$
can be embedded in the order type of M.
$\mathbb {N}+\mathbb {Z}\cdot \mathbb {N}$
can be embedded in the order type of M.
Proof As mentioned,
![]() $\mathbb {Z}(X^2)$
is the set of non-negative polynomials of degree at most
$\mathbb {Z}(X^2)$
is the set of non-negative polynomials of degree at most
![]() $1$
over
$1$
over
![]() $\mathbb {Z}$
and clearly has order type
$\mathbb {Z}$
and clearly has order type
![]() $\mathbb {N}+\mathbb {Z}\cdot \mathbb {N}$
. The result then follows from Theorem 22.
$\mathbb {N}+\mathbb {Z}\cdot \mathbb {N}$
. The result then follows from Theorem 22.
Corollary 24. Every non-standard model of
![]() $\mathsf {Pr}^-$
has a proper non-standard submodel.
$\mathsf {Pr}^-$
has a proper non-standard submodel.
Proof By Theorem 22, it is enough to show that
![]() $\mathbb {Z}(X^2)$
has a non-standard submodel. Consider all polynomials with degree at most
$\mathbb {Z}(X^2)$
has a non-standard submodel. Consider all polynomials with degree at most
![]() $1$
and even leading terms, i.e.,
$1$
and even leading terms, i.e.,
Clearly, this set is closed under
![]() $\mathrm {s}$
and
$\mathrm {s}$
and
![]() $+$
, so it is a substructure of
$+$
, so it is a substructure of
![]() $\mathbb {Z}(X^2)$
. Moreover, every element of M except for
$\mathbb {Z}(X^2)$
. Moreover, every element of M except for
![]() $0$
has a predecessor. Therefore, M satisfies axiom
$0$
has a predecessor. Therefore, M satisfies axiom
![]() $\mathrm {S1}$
. The only existential axiom of
$\mathrm {S1}$
. The only existential axiom of
![]() $\mathsf {Pr}^-$
which still needs to be checked is ⋇. Let
$\mathsf {Pr}^-$
which still needs to be checked is ⋇. Let
![]() $f,g\in M$
such that
$f,g\in M$
such that
![]() $f<g$
. Define
$f<g$
. Define
![]() $h(a)=g(a)-f(a)$
. We want to show that
$h(a)=g(a)-f(a)$
. We want to show that
![]() $h\in M$
. If
$h\in M$
. If
![]() ${\scriptstyle \mathrm {LT}}(f)=0$
, this is trivially true since
${\scriptstyle \mathrm {LT}}(f)=0$
, this is trivially true since
![]() $h(1)=g(1)$
. If
$h(1)=g(1)$
. If
![]() ${\scriptstyle \mathrm {LT}}(f)=1$
, then
${\scriptstyle \mathrm {LT}}(f)=1$
, then
![]() $f(1)=2n$
and
$f(1)=2n$
and
![]() $g(1)=2n'$
for some
$g(1)=2n'$
for some
![]() $n,n'\in \mathbb {N}$
such that
$n,n'\in \mathbb {N}$
such that
![]() $n<n'$
. Then
$n<n'$
. Then
![]() $h(1)=2n'-2n=2(n'-n)$
; therefore
$h(1)=2n'-2n=2(n'-n)$
; therefore
![]() $h\in M$
. The fact that
$h\in M$
. The fact that
![]() $f+h=g$
follows trivially by the definition of
$f+h=g$
follows trivially by the definition of
![]() $+$
in
$+$
in
![]() $\mathbb {Z}(X^2)$
.
$\mathbb {Z}(X^2)$
.
6 The algebraic nature of models of theories without induction
In this section, we are going to discuss the difference between the theories without induction and those with induction: since almost all of the axioms in the former are universal sentence, they behave essentially like algebraic theories; this means that their models can be obtained as algebraic closures. In contrast, the latter require richer constructions.
We illustrate this by considering the simplest cases of non-standard models of
![]() $\mathsf {SA}$
and
$\mathsf {SA}$
and
![]() $\mathsf {Pr}^-$
as discussed in Sections 3 and 5. In the case of
$\mathsf {Pr}^-$
as discussed in Sections 3 and 5. In the case of
![]() $\mathsf {SA}^- = \mathsf {SA}$
, the axioms O1 to O4 and S2 to S4 are universal, so models of these axioms are just constructed by closing under the operation
$\mathsf {SA}^- = \mathsf {SA}$
, the axioms O1 to O4 and S2 to S4 are universal, so models of these axioms are just constructed by closing under the operation
![]() $\mathrm {s}$
. Axiom S1 requires the existence of a
$\mathrm {s}$
. Axiom S1 requires the existence of a
![]() $\mathrm {s}$
-predecessor for each element other than
$\mathrm {s}$
-predecessor for each element other than
![]() $0$
. The closure under
$0$
. The closure under
![]() $\mathrm {s}$
-successors and
$\mathrm {s}$
-successors and
![]() $\mathrm {s}$
-predecessors (i.e., the unique witnesses for all instances of the
$\mathrm {s}$
-predecessors (i.e., the unique witnesses for all instances of the
![]() $\forall \exists $
-axiom S1) of a given non-standard element is its Archimedean class and thus, if we take a set A of generators, it will generate the model of order type
$\forall \exists $
-axiom S1) of a given non-standard element is its Archimedean class and thus, if we take a set A of generators, it will generate the model of order type
![]() $\mathbb {N}+\mathbb {Z}\cdot A$
from Corollary 13.
$\mathbb {N}+\mathbb {Z}\cdot A$
from Corollary 13.
Concretely, if
![]() $A = \{a\}$
consists of just one generator, we get the standard part and a single additional Archimedean class, i.e., a model of order type
$A = \{a\}$
consists of just one generator, we get the standard part and a single additional Archimedean class, i.e., a model of order type
![]() $\mathbb {N}+\mathbb {Z}$
:
$\mathbb {N}+\mathbb {Z}$
:

Once we add the operation
![]() $+$
and want to extend our model to an
$+$
and want to extend our model to an
![]() $\mathcal {L}_{<,\mathrm {s},+}$
-structure, for each non-standard element a, we need to have the elements
$\mathcal {L}_{<,\mathrm {s},+}$
-structure, for each non-standard element a, we need to have the elements
![]() $a+a = 2a$
,
$a+a = 2a$
,
![]() $a+a+a = 3a$
, etc. By Lemma 6, their Archimedean classes must be separate, so we generate an
$a+a+a = 3a$
, etc. By Lemma 6, their Archimedean classes must be separate, so we generate an
![]() $\omega $
-sequence of Archimedean classes resulting in a model of order type
$\omega $
-sequence of Archimedean classes resulting in a model of order type
![]() $\mathbb {N}+\mathbb {Z}\cdot \mathbb {N}$
, the minimal order type of a non-standard model of
$\mathbb {N}+\mathbb {Z}\cdot \mathbb {N}$
, the minimal order type of a non-standard model of
![]() $\mathsf {Pr}^-$
. The following is a picture of the case where D is the one-element group and
$\mathsf {Pr}^-$
. The following is a picture of the case where D is the one-element group and
![]() $\alpha = 1$
in Corollary 21. It could be considered a picture proof of Corollary 23.
$\alpha = 1$
in Corollary 21. It could be considered a picture proof of Corollary 23.

Moving to the concrete case where
![]() $A = \{a,b\}$
with
$A = \{a,b\}$
with
![]() $a<b$
is a set of two generators, the models of
$a<b$
is a set of two generators, the models of
![]() $\mathsf {SA}$
remain purely generated: by Corollary 13, the generated model of
$\mathsf {SA}$
remain purely generated: by Corollary 13, the generated model of
![]() $\mathsf {SA}$
has order type
$\mathsf {SA}$
has order type
![]() $\mathbb {N}+\mathbb {Z}\cdot 2$
: each of the generators generates its own Archimedean class.
$\mathbb {N}+\mathbb {Z}\cdot 2$
: each of the generators generates its own Archimedean class.
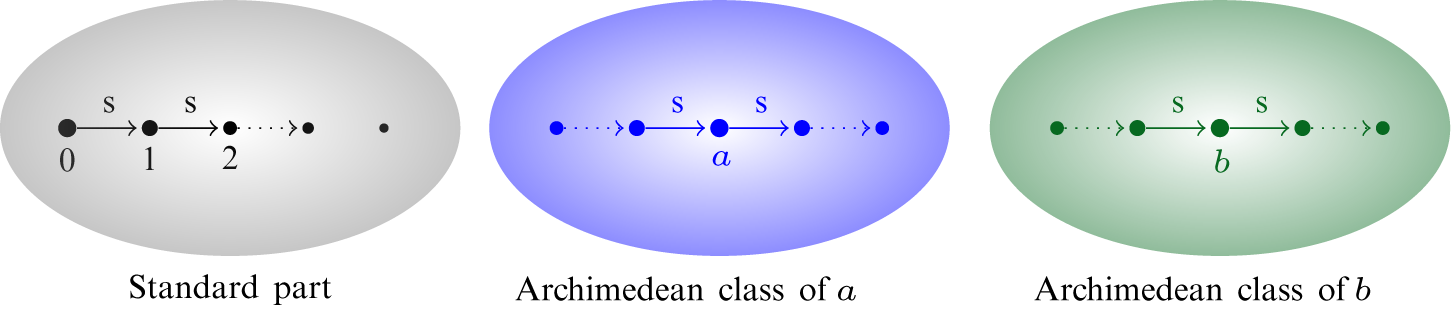
However, if we add the operation
![]() $+$
, a new phenomenon occurs. The closure of this model under
$+$
, a new phenomenon occurs. The closure of this model under
![]() $+$
(taking axiom P4 into account) will produce all of the terms of the form
$+$
(taking axiom P4 into account) will produce all of the terms of the form
![]() $na+mb$
for
$na+mb$
for
![]() $n,m\in \mathbb {N}$
with the order
$n,m\in \mathbb {N}$
with the order
These terms give us the generated Archimedean classes, and consequently, the generated non-standard elements of the model can be described as a pair
![]() $(z,na+mb)$
where
$(z,na+mb)$
where
![]() $na+mb$
is the term determining the Archimedean class and
$na+mb$
is the term determining the Archimedean class and
![]() $z\in \mathbb {Z}$
determines the position within the Archimedean class. The order type of this generated structure is
$z\in \mathbb {Z}$
determines the position within the Archimedean class. The order type of this generated structure is
![]() $\mathbb {N}+\mathbb {Z}\cdot \mathbb {N}\cdot \mathbb {N}$
with
$\mathbb {N}+\mathbb {Z}\cdot \mathbb {N}\cdot \mathbb {N}$
with
![]() $\omega $
many copies of the non-standard part of the model of
$\omega $
many copies of the non-standard part of the model of
![]() $\mathsf {Pr}^-$
with one generator.
$\mathsf {Pr}^-$
with one generator.

But this generated structure is not a model of
![]() $\mathsf {Pr}^-$
; this follows, e.g., from Theorem 17(i), since
$\mathsf {Pr}^-$
; this follows, e.g., from Theorem 17(i), since
![]() $\mathbb {N}\cdot \mathbb {N}$
is not the order type of the standard monoid of an ordered abelian group.
$\mathbb {N}\cdot \mathbb {N}$
is not the order type of the standard monoid of an ordered abelian group.
The reason for this failure is the is axiom ⋇ which –as mentioned before– is an instance of the induction scheme and the only axiom of
![]() $\mathsf {Pr}^-$
(other than S1 which we dealt with earlier) that is not in universal form. In this context, it guarantees the existence of an (additional) element c such that
$\mathsf {Pr}^-$
(other than S1 which we dealt with earlier) that is not in universal form. In this context, it guarantees the existence of an (additional) element c such that
![]() $a+c = b$
, i.e., the element
$a+c = b$
, i.e., the element
![]() $b-a$
. This element must be bigger than all finite products of a, i.e., above the part of the model
$b-a$
. This element must be bigger than all finite products of a, i.e., above the part of the model
![]() $+$
-generated from a, but smaller than b.
$+$
-generated from a, but smaller than b.
Yet ⋇ is of the syntactic form
![]() $\forall \exists $
, so we can form the closure of the above structure of order type
$\forall \exists $
, so we can form the closure of the above structure of order type
![]() $\mathbb {N}+\mathbb {Z}\cdot \mathbb {N}\cdot \mathbb {N}$
under adding (unique) witnesses for (⋇). This will produce the next case in Corollary 21 with D the one-element group and
$\mathbb {N}+\mathbb {Z}\cdot \mathbb {N}\cdot \mathbb {N}$
under adding (unique) witnesses for (⋇). This will produce the next case in Corollary 21 with D the one-element group and
![]() $\alpha =2$
with order type
$\alpha =2$
with order type
![]() $\mathbb {N}+\mathbb {Z}\cdot \mathbb {Z}\cdot \mathbb {N}$
.
$\mathbb {N}+\mathbb {Z}\cdot \mathbb {Z}\cdot \mathbb {N}$
.
Our discussion of models generated by one and two generators illustrates the main theme of this paper: theories without induction can be handled by simple closure techniques, but theories with induction require model theoretic arguments.
7 Peano arithmetic
Theorem 17 tells us that every model
![]() $M\models \mathsf {PA}^-$
(
$M\models \mathsf {PA}^-$
(
![]() $M\models \mathsf {PA}$
) must have the order type
$M\models \mathsf {PA}$
) must have the order type
![]() $\mathbb {N}+\mathbb {Z}\cdot G^+$
where G is an ordered (divisible) abelian group. However, in the case of Peano Arithmetic, this cannot be a sufficient condition since Potthoff proved that no model of
$\mathbb {N}+\mathbb {Z}\cdot G^+$
where G is an ordered (divisible) abelian group. However, in the case of Peano Arithmetic, this cannot be a sufficient condition since Potthoff proved that no model of
![]() $\mathsf {PA}$
can have the order type
$\mathsf {PA}$
can have the order type
![]() $\mathbb {N}+\mathbb {Z}\cdot \mathbb {R}$
[Reference Potthoff16]. It is easily checked that the proof of Potthoff’s theorem given in [Reference Bovykin and Kaye2, p. 5] works in
$\mathbb {N}+\mathbb {Z}\cdot \mathbb {R}$
[Reference Potthoff16]. It is easily checked that the proof of Potthoff’s theorem given in [Reference Bovykin and Kaye2, p. 5] works in
![]() $\mathsf {PA}^-$
:
$\mathsf {PA}^-$
:
Theorem 25. Let M be a non-standard model of
![]() $\mathsf {PA}^-$
with order type
$\mathsf {PA}^-$
with order type
![]() $\mathbb {N}+\mathbb {Z}\cdot A$
. If A is dense then there are
$\mathbb {N}+\mathbb {Z}\cdot A$
. If A is dense then there are
![]() $|M|$
many non empty disjoint intervals in A. In particular,
$|M|$
many non empty disjoint intervals in A. In particular,
![]() $A\neq \mathbb {R}$
.
$A\neq \mathbb {R}$
.
Proof Let
![]() $a\in M$
be non-standard. Consider the set
$a\in M$
be non-standard. Consider the set
![]() $\{a_m\,;\,m\in M\}$
where
$\{a_m\,;\,m\in M\}$
where
![]() $a_m=a\cdot m$
for every
$a_m=a\cdot m$
for every
![]() $m\in M$
. By M6, this set has cardinality
$m\in M$
. By M6, this set has cardinality
![]() $|M|$
. We shall now show that
$|M|$
. We shall now show that
![]() $\{([a_m],[a_{\mathrm {s}(m)}])\,;\,m\in M\}$
forms a collection of non-empty disjoint intervals of size
$\{([a_m],[a_{\mathrm {s}(m)}])\,;\,m\in M\}$
forms a collection of non-empty disjoint intervals of size
![]() $|M|$
in A:
$|M|$
in A:
By Lemma 6,
![]() $[a\cdot m]<[a\cdot \mathrm {s}(m)]$
for every
$[a\cdot m]<[a\cdot \mathrm {s}(m)]$
for every
![]() $m\in M$
. By density of A, the interval
$m\in M$
. By density of A, the interval
![]() $([a_m],[a_{\mathrm {s}(m)}])$
is not empty in A. Now if
$([a_m],[a_{\mathrm {s}(m)}])$
is not empty in A. Now if
![]() $m<m'$
, then by M6 we have
$m<m'$
, then by M6 we have
![]() $a\cdot \mathrm {s}(m)\leq a\cdot m'$
and
$a\cdot \mathrm {s}(m)\leq a\cdot m'$
and
![]() $[a\cdot \mathrm {s}(m)]\leq [a\cdot m']$
. Therefore
$[a\cdot \mathrm {s}(m)]\leq [a\cdot m']$
. Therefore
![]() $([a_m],[a_{\mathrm {s}(m)}])\cap ([a_{m'}],[a_{\mathrm {s}(m')}])=\varnothing $
as desired.
$([a_m],[a_{\mathrm {s}(m)}])\cap ([a_{m'}],[a_{\mathrm {s}(m')}])=\varnothing $
as desired.
If
![]() $A = \mathbb {R}$
, then the order type of M is
$A = \mathbb {R}$
, then the order type of M is
![]() $\mathbb {N}+\mathbb {Z}\cdot \mathbb {R}$
and hence
$\mathbb {N}+\mathbb {Z}\cdot \mathbb {R}$
and hence
![]() $|M| = 2^{\aleph _0}$
. Now the main claim of the theorem gives us an uncountable family of pairwise disjoint intervals in
$|M| = 2^{\aleph _0}$
. Now the main claim of the theorem gives us an uncountable family of pairwise disjoint intervals in
![]() $\mathbb {R}$
which contradicts the countable chain condition of the real line.
$\mathbb {R}$
which contradicts the countable chain condition of the real line.
Theorem 25 shows that the closure under multiplication adds more requirements on the order type of models of
![]() $\mathsf {PA}^-$
. The following is a natural requirement: we remind the reader of the definitions of initial and final segments and order exponentiation from Section 2.2. In particular, if L is a linear order and
$\mathsf {PA}^-$
. The following is a natural requirement: we remind the reader of the definitions of initial and final segments and order exponentiation from Section 2.2. In particular, if L is a linear order and
![]() $\ell \in L$
, then
$\ell \in L$
, then
![]() $\mathrm {IS}(\ell )$
is the initial segment given by
$\mathrm {IS}(\ell )$
is the initial segment given by
![]() $\ell $
and
$\ell $
and
![]() $\mathrm {IS}(\ell )^\omega $
is the set of functions from
$\mathrm {IS}(\ell )^\omega $
is the set of functions from
![]() $\omega $
to
$\omega $
to
![]() $\mathrm {IS}(\ell )$
with finite support, ordered anti-lexicographically.
$\mathrm {IS}(\ell )$
with finite support, ordered anti-lexicographically.
Definition 26. Let L be a linear order. We say that L is closed under finite products of initial segments if for every
![]() $\ell \in L$
the order
$\ell \in L$
the order
![]() $\mathrm {IS}(\ell )^\omega $
embeds into
$\mathrm {IS}(\ell )^\omega $
embeds into
![]() $\mathrm {FS}(\ell )$
.
$\mathrm {FS}(\ell )$
.
Theorem 27. Let M be a non-standard model of
![]() $\mathsf {PA}^-$
with order type
$\mathsf {PA}^-$
with order type
![]() $\mathbb {N}+\mathbb {Z}\cdot L$
. Then L is closed under finite products of initial segments.
$\mathbb {N}+\mathbb {Z}\cdot L$
. Then L is closed under finite products of initial segments.
Proof As before, we assume that L is the set of non-zero Archimedean classes of M. For every
![]() $\ell \in L$
choose a representative
$\ell \in L$
choose a representative
![]() $r_{\ell }\in M$
such that
$r_{\ell }\in M$
such that
![]() $r_\ell \in \ell $
and
$r_\ell \in \ell $
and
![]() $r_\ell>0$
. Let
$r_\ell>0$
. Let
![]() $\ell \in L$
be an element of the linear order L. We want to define an order embedding of
$\ell \in L$
be an element of the linear order L. We want to define an order embedding of
![]() $\mathrm {IS}(\ell )^\omega $
into
$\mathrm {IS}(\ell )^\omega $
into
![]() $\mathrm {FS}(\ell )$
. Fix some non-standard
$\mathrm {FS}(\ell )$
. Fix some non-standard
![]() $a\in M$
such that
$a\in M$
such that
![]() $\ell \leq [a]$
and consider the following function:
$\ell \leq [a]$
and consider the following function:
 $$ \begin{align*}\varphi(f)=\left[\sum_{i \leq {\scriptstyle \mathrm{LT}}(f)} r_{f(i)}\cdot a^{i+1}\right],\end{align*} $$
$$ \begin{align*}\varphi(f)=\left[\sum_{i \leq {\scriptstyle \mathrm{LT}}(f)} r_{f(i)}\cdot a^{i+1}\right],\end{align*} $$
for every
![]() $f\in \mathrm {IS}(\ell )^{\omega }$
. Note that since f has finite support, the function
$f\in \mathrm {IS}(\ell )^{\omega }$
. Note that since f has finite support, the function
![]() $\varphi $
is well defined. Now we want to prove that
$\varphi $
is well defined. Now we want to prove that
![]() $\varphi $
is order-preserving. First we prove the following claim:
$\varphi $
is order-preserving. First we prove the following claim:
Claim 28. For every
![]() $n>0$
and every finite sequence
$n>0$
and every finite sequence
![]() $(\ell _0,\ldots ,\ell _{n-1})$
of elements of
$(\ell _0,\ldots ,\ell _{n-1})$
of elements of
![]() $\mathrm {IS}(\ell )$
we have
$\mathrm {IS}(\ell )$
we have
 $$ \begin{align*}\sum_{i<n} r_{\ell_i} \cdot a^{i+1}< a^{n+1}.\\[-52pt]\end{align*} $$
$$ \begin{align*}\sum_{i<n} r_{\ell_i} \cdot a^{i+1}< a^{n+1}.\\[-52pt]\end{align*} $$
Proof By induction on n. For
![]() $n=1$
we have
$n=1$
we have
![]() $r_{\ell _0} \cdot a< a\cdot a$
. For
$r_{\ell _0} \cdot a< a\cdot a$
. For
![]() $n=n'+1>1$
we have
$n=n'+1>1$
we have
 $$ \begin{align*} \sum_{i<n'+1} r_{\ell_i} \cdot a^{i+1} &=\sum_{i<n'} r_{\ell_i} \cdot a^{i+1} + r_{\ell_{n'}}\cdot a^{n'+1}\\ &< a^{n'+1}+ r_{\ell_{n'}} \cdot a^{n'+1}\\ &= a^{n'+1} \cdot (\mathrm{s}(0)+ r_{\ell_{n'}})< a^{n'+2}. \\[-36pt]\end{align*} $$
$$ \begin{align*} \sum_{i<n'+1} r_{\ell_i} \cdot a^{i+1} &=\sum_{i<n'} r_{\ell_i} \cdot a^{i+1} + r_{\ell_{n'}}\cdot a^{n'+1}\\ &< a^{n'+1}+ r_{\ell_{n'}} \cdot a^{n'+1}\\ &= a^{n'+1} \cdot (\mathrm{s}(0)+ r_{\ell_{n'}})< a^{n'+2}. \\[-36pt]\end{align*} $$
We want to prove that if
![]() $f<f'$
are two elements of
$f<f'$
are two elements of
![]() $\mathrm {IS}(\ell )^{\omega }$
then
$\mathrm {IS}(\ell )^{\omega }$
then
![]() $\varphi (f)<\varphi (f')$
. Let
$\varphi (f)<\varphi (f')$
. Let
![]() $n\in \mathbb {N}$
be the biggest natural number such that
$n\in \mathbb {N}$
be the biggest natural number such that
![]() $f(n)\neq f'(n)$
. Since
$f(n)\neq f'(n)$
. Since
![]() $f<f'$
we have
$f<f'$
we have
![]() $f(n)<f'(n)$
, then
$f(n)<f'(n)$
, then
![]() $[r_{f(n)}]<[r_{f'(n)}]$
.
$[r_{f(n)}]<[r_{f'(n)}]$
.
Moreover since
![]() $n\leq {\scriptstyle \mathrm {LT}}(f')$
we have
$n\leq {\scriptstyle \mathrm {LT}}(f')$
we have
 $$ \begin{align*}\sum_{n<i\leq {\scriptstyle \mathrm{LT}}(f')} r_{f(i)} \cdot a^{i+1}=\sum_{n<i\leq {\scriptstyle \mathrm{LT}}(f')} r_{f'(i)}\cdot a^{i+1}.\end{align*} $$
$$ \begin{align*}\sum_{n<i\leq {\scriptstyle \mathrm{LT}}(f')} r_{f(i)} \cdot a^{i+1}=\sum_{n<i\leq {\scriptstyle \mathrm{LT}}(f')} r_{f'(i)}\cdot a^{i+1}.\end{align*} $$
Therefore, by monotonicity of
![]() $+$
it is enough to prove that for every
$+$
it is enough to prove that for every
![]() $n'\in \mathbb {N}$
we have
$n'\in \mathbb {N}$
we have
 $$ \begin{align*}\sum_{i\leq n} r_{f(i)}\cdot a^{i+1}+\mathrm{s}^{n'}(0)< r_{f'(n)}\cdot a^{n+1}.\end{align*} $$
$$ \begin{align*}\sum_{i\leq n} r_{f(i)}\cdot a^{i+1}+\mathrm{s}^{n'}(0)< r_{f'(n)}\cdot a^{n+1}.\end{align*} $$
For
![]() $n=0$
it is trivially true. For
$n=0$
it is trivially true. For
![]() $n>0$
, we have
$n>0$
, we have
 $$ \begin{align*} \sum_{i\leq n} r_{f(i)}\cdot a^{i+1}+\mathrm{s}^{n'}(0) &=\sum_{i< n} r_{f(i)}\cdot a^{i+1}+r_{f(n)}\cdot a^{n+1}+\mathrm{s}^{n'}(0)\\ &< a^{n+1}+ r_{f(n)}\cdot a^{n+1}+\mathrm{s}^{n'}(0)\\ &<a^{n+1} \cdot (r_{f(n)}+\mathrm{s}^{n'+1}(0))\\ &< a^{n+1} \cdot r_{f'(n)}, \end{align*} $$
$$ \begin{align*} \sum_{i\leq n} r_{f(i)}\cdot a^{i+1}+\mathrm{s}^{n'}(0) &=\sum_{i< n} r_{f(i)}\cdot a^{i+1}+r_{f(n)}\cdot a^{n+1}+\mathrm{s}^{n'}(0)\\ &< a^{n+1}+ r_{f(n)}\cdot a^{n+1}+\mathrm{s}^{n'}(0)\\ &<a^{n+1} \cdot (r_{f(n)}+\mathrm{s}^{n'+1}(0))\\ &< a^{n+1} \cdot r_{f'(n)}, \end{align*} $$
where we used Claim 28 in the first inequality. Therefore
![]() $\varphi $
is order-preserving as desired.⊣
$\varphi $
is order-preserving as desired.⊣
Theorem 16 showed that the non-negative polynomials with integer coefficients
![]() $\mathbb {Z}(X^{\mathbb {N}})$
are a model of
$\mathbb {Z}(X^{\mathbb {N}})$
are a model of
![]() $\mathsf {PA}^-$
. In analogy to Theorem 22, we show that this provides a lower bound for the order type of non-standard models of
$\mathsf {PA}^-$
. In analogy to Theorem 22, we show that this provides a lower bound for the order type of non-standard models of
![]() $\mathsf {PA}^-$
:
$\mathsf {PA}^-$
:
Theorem 29. Let M be a non-standard model of
![]() $\mathsf {PA}^-$
. Then there is a submodel of M isomorphic to
$\mathsf {PA}^-$
. Then there is a submodel of M isomorphic to
![]() $(\mathbb {Z}(X^{\mathbb {N}}), 0,<,\mathrm {s},+,\cdot )$
.
$(\mathbb {Z}(X^{\mathbb {N}}), 0,<,\mathrm {s},+,\cdot )$
.
Proof Let M be a non-standard model of
![]() $\mathsf {PA}^-$
and
$\mathsf {PA}^-$
and
![]() $a\in M$
be a non-standard element of M. Let
$a\in M$
be a non-standard element of M. Let
![]() $f\in \mathbb {Z}(X^{\mathbb {N}})$
; remember that if
$f\in \mathbb {Z}(X^{\mathbb {N}})$
; remember that if
![]() $\mathrm {supp}(f)\subseteq \{0,\ldots ,n\}$
and
$\mathrm {supp}(f)\subseteq \{0,\ldots ,n\}$
and
![]() ${\scriptstyle \mathrm {LT}}(f) = n$
, then f can be thought of as a polynomial
${\scriptstyle \mathrm {LT}}(f) = n$
, then f can be thought of as a polynomial
where
![]() $f(n)> 0$
and
$f(n)> 0$
and
![]() $f(i)\in \mathbb {Z}$
(for
$f(i)\in \mathbb {Z}$
(for
![]() $0\leq i<n$
). We define the function
$0\leq i<n$
). We define the function
where negative terms are uniquely interpreted by the fact that we have axiom ⋇. It is routine to check that
![]() $\varphi $
is an embedding of
$\varphi $
is an embedding of
![]() $(\mathbb {Z}(X^{\mathbb {N}}), 0,<,\mathrm {s},+,\cdot )$
into M.
$(\mathbb {Z}(X^{\mathbb {N}}), 0,<,\mathrm {s},+,\cdot )$
into M.
Corollary 30. Let M be a non-standard model of
![]() $\mathsf {PA}^-$
. Then the order type
$\mathsf {PA}^-$
. Then the order type
![]() $O_\omega $
can be embedded in the order type of M. In particular,
$O_\omega $
can be embedded in the order type of M. In particular,
![]() $\mathbb {Z}(X^2)$
is not a model of
$\mathbb {Z}(X^2)$
is not a model of
![]() $\mathsf {PA}^-$
.
$\mathsf {PA}^-$
.
Proof Since
![]() $O_\omega $
is the order type of the non-negative polynomials on
$O_\omega $
is the order type of the non-negative polynomials on
![]() $\mathbb {Z}$
, this follows directly from Theorem 29.
$\mathbb {Z}$
, this follows directly from Theorem 29.
Corollary 31. Every non-standard model of
![]() $\mathsf {PA}^-$
has a proper non-standard submodel.
$\mathsf {PA}^-$
has a proper non-standard submodel.
Proof As in the proof of Corollary 24, by Theorem 29, it is enough to check that
![]() $\mathbb {Z}(X^{\mathbb {N}})$
has a proper non-standard submodel. Consider the polynomials in which only terms with even exponent occur and observe that they are closed under addition and multiplication and that the structure satisfies ⋇.
$\mathbb {Z}(X^{\mathbb {N}})$
has a proper non-standard submodel. Consider the polynomials in which only terms with even exponent occur and observe that they are closed under addition and multiplication and that the structure satisfies ⋇.
The contrast between
![]() $\mathbb {Z}(X^2)\not \models \mathsf {PA}^-$
and
$\mathbb {Z}(X^2)\not \models \mathsf {PA}^-$
and
![]() $\mathbb {Z}(X^{\mathbb {N}})\models \mathsf {PA}^-$
derives from the fact that the exponential order
$\mathbb {Z}(X^{\mathbb {N}})\models \mathsf {PA}^-$
derives from the fact that the exponential order
![]() $\mathbb {N}$
is closed under addition and forms a monoid (allowing us to use Theorem 16) whereas the exponential order
$\mathbb {N}$
is closed under addition and forms a monoid (allowing us to use Theorem 16) whereas the exponential order
![]() $2$
is not.
$2$
is not.
This can be easily generalised: an ordinal
![]() $\alpha $
is called additively indecomposable (or a gamma number) if it cannot be written as
$\alpha $
is called additively indecomposable (or a gamma number) if it cannot be written as
![]() $\alpha = \xi +\eta $
for ordinals
$\alpha = \xi +\eta $
for ordinals
![]() $\xi ,\eta < \alpha $
; equivalently, it is closed under ordinal addition, i.e., for all
$\xi ,\eta < \alpha $
; equivalently, it is closed under ordinal addition, i.e., for all
![]() $\xi ,\eta \in \alpha $
, we have
$\xi ,\eta \in \alpha $
, we have
![]() $\xi +\eta \in \alpha $
. If
$\xi +\eta \in \alpha $
. If
![]() $\alpha $
is additively indecomposable, then it is also closed under the natural (Hessenberg) sum of ordinals, denoted by
$\alpha $
is additively indecomposable, then it is also closed under the natural (Hessenberg) sum of ordinals, denoted by
![]() $\oplus $
, which is a commutative operation (cf. [Reference Sierpiński25, XIV.28]).
$\oplus $
, which is a commutative operation (cf. [Reference Sierpiński25, XIV.28]).
Clearly, all ordinals of the form
![]() $\alpha = \omega ^\gamma $
are additively indecomposable, and if
$\alpha = \omega ^\gamma $
are additively indecomposable, and if
![]() $\alpha $
is additively indecomposable, then the structure
$\alpha $
is additively indecomposable, then the structure
![]() $(\alpha ,<,0,\oplus )$
is an ordered commutative positive monoid. Thus, by Theorem 16, the structure
$(\alpha ,<,0,\oplus )$
is an ordered commutative positive monoid. Thus, by Theorem 16, the structure
![]() $\mathbb {Z}(X^\alpha )$
is a model of
$\mathbb {Z}(X^\alpha )$
is a model of
![]() $\mathsf {PA}^-$
. Note that the order type of
$\mathsf {PA}^-$
. Note that the order type of
![]() $\mathbb {Z}(X^\alpha )$
is
$\mathbb {Z}(X^\alpha )$
is
![]() $O_\alpha $
(defined in Section 2.2).
$O_\alpha $
(defined in Section 2.2).
We end this section by showing that these order types give us many non-isomorphic order types of models of
![]() $\mathsf {PA}^-$
of a given cardinality. This yields a markedly different situation from the theories with induction,
$\mathsf {PA}^-$
of a given cardinality. This yields a markedly different situation from the theories with induction,
![]() $\mathsf {Pr}$
and
$\mathsf {Pr}$
and
![]() $\mathsf {PA}$
, in the countable case.
$\mathsf {PA}$
, in the countable case.
Lemma 32. Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be two ordinals. Then
$\beta $
be two ordinals. Then
![]() $O_\alpha $
and
$O_\alpha $
and
![]() $O_\beta $
are order isomorphic if and only if
$O_\beta $
are order isomorphic if and only if
![]() $\alpha = \beta $
.
$\alpha = \beta $
.
Proof We observe that for positive ordinals
![]() $\alpha $
,
$\alpha $
,
![]() $\omega ^\alpha $
embeds order-preservingly into
$\omega ^\alpha $
embeds order-preservingly into
![]() $O_\alpha $
. We shall show that
$O_\alpha $
. We shall show that
![]() $\omega ^{\alpha +1}$
does not embed into
$\omega ^{\alpha +1}$
does not embed into
![]() $O_\alpha $
. Once we have proved this, these two statements immediately imply the claim: if
$O_\alpha $
. Once we have proved this, these two statements immediately imply the claim: if
![]() $\alpha < \beta $
, then
$\alpha < \beta $
, then
![]() $O_\beta $
cannot embed order-preservingly into
$O_\beta $
cannot embed order-preservingly into
![]() $O_\alpha $
and so they cannot be isomorphic.
$O_\alpha $
and so they cannot be isomorphic.
In order to show our non-embedding results, we first prove the following claim by induction for positive ordinals
![]() $\alpha $
:
$\alpha $
:
The claim is obvious for
![]() $\alpha = 1$
and the limit case follows directly from the induction hypothesis. Let now
$\alpha = 1$
and the limit case follows directly from the induction hypothesis. Let now
![]() $\alpha =\beta +1$
and
$\alpha =\beta +1$
and
![]() $\varphi :\omega ^{\beta +1} \rightarrow \mathbb {Z}^{\beta +1}$
be an order-preserving embedding where we write elements of
$\varphi :\omega ^{\beta +1} \rightarrow \mathbb {Z}^{\beta +1}$
be an order-preserving embedding where we write elements of
![]() $\omega ^{\beta +1} = \omega ^\beta \cdot \omega $
as pairs
$\omega ^{\beta +1} = \omega ^\beta \cdot \omega $
as pairs
![]() $(\gamma ,n)$
with
$(\gamma ,n)$
with
![]() $\gamma \in \omega ^\beta $
and
$\gamma \in \omega ^\beta $
and
![]() $n\in \omega $
and elements of
$n\in \omega $
and elements of
![]() $\mathbb {Z}^{\beta +1} = \mathbb {Z}^\beta \cdot \mathbb {Z}$
as pairs
$\mathbb {Z}^{\beta +1} = \mathbb {Z}^\beta \cdot \mathbb {Z}$
as pairs
![]() $(g,z)$
with
$(g,z)$
with
![]() $g\in \mathbb {Z}^\beta $
and
$g\in \mathbb {Z}^\beta $
and
![]() $z\in \mathbb {Z}$
. If
$z\in \mathbb {Z}$
. If
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $z\in \mathbb {Z}$
, we write
$z\in \mathbb {Z}$
, we write
![]() $A_n := \{\varphi (\gamma ,n)\,;\,\gamma \in \omega ^\beta \}\subseteq \mathrm {ran}(\varphi )$
and
$A_n := \{\varphi (\gamma ,n)\,;\,\gamma \in \omega ^\beta \}\subseteq \mathrm {ran}(\varphi )$
and
![]() $B_z := \{(g,z)\,;\,g\in \mathbb {Z}^\beta \}$
; these sets have order type
$B_z := \{(g,z)\,;\,g\in \mathbb {Z}^\beta \}$
; these sets have order type
![]() $\omega ^\beta $
and
$\omega ^\beta $
and
![]() $\mathbb {Z}^\beta $
, respectively. Clearly,
$\mathbb {Z}^\beta $
, respectively. Clearly,
![]() $\mathrm {ran}(\varphi ) = \bigcup _{n\in \omega } A_n$
and
$\mathrm {ran}(\varphi ) = \bigcup _{n\in \omega } A_n$
and
![]() $\mathbb {Z}^{\beta +1} = \bigcup _{z\in \mathbb {Z}} B_z$
.
$\mathbb {Z}^{\beta +1} = \bigcup _{z\in \mathbb {Z}} B_z$
.
If we fix
![]() $n\in \omega $
, the set
$n\in \omega $
, the set
![]() $A_n$
is non-empty and bounded in
$A_n$
is non-empty and bounded in
![]() $\mathbb {Z}^{\beta +1}$
. Therefore there is a minimal integer
$\mathbb {Z}^{\beta +1}$
. Therefore there is a minimal integer
![]() $z_n$
such that for all
$z_n$
such that for all
![]() $z\geq z_n$
, we have
$z\geq z_n$
, we have
![]() $A_n\cap B_z = \varnothing $
. In particular,
$A_n\cap B_z = \varnothing $
. In particular,
![]() $A_n\cap B_{z_n-1} \neq \varnothing $
, and thus
$A_n\cap B_{z_n-1} \neq \varnothing $
, and thus
![]() $B_{z_n-1}$
contains a final segment of
$B_{z_n-1}$
contains a final segment of
![]() $A_n$
. The order type of
$A_n$
. The order type of
![]() $A_n$
is
$A_n$
is
![]() $\omega ^\beta $
, i.e., an additively indecomposable ordinal; therefore, final segments of
$\omega ^\beta $
, i.e., an additively indecomposable ordinal; therefore, final segments of
![]() $A_n$
still have order type
$A_n$
still have order type
![]() $\omega ^\beta $
. By the induction hypothesis, we know that
$\omega ^\beta $
. By the induction hypothesis, we know that
![]() $A_n\cap B_{z_n-1}$
must lie cofinal in
$A_n\cap B_{z_n-1}$
must lie cofinal in
![]() $B_{z_n-1}$
.
$B_{z_n-1}$
.
Now we consider elements of
![]() $A_{n+1}$
: these are strictly bigger than all of the elements of
$A_{n+1}$
: these are strictly bigger than all of the elements of
![]() $A_n$
, and therefore they must lie in some
$A_n$
, and therefore they must lie in some
![]() $B_z$
for
$B_z$
for
![]() $z> z_n$
. In particular,
$z> z_n$
. In particular,
![]() $z_{n+1}> z_n$
. This shows that the sequence
$z_{n+1}> z_n$
. This shows that the sequence
![]() $z_n$
is a strictly increasing sequence of integers indexed by natural numbers, hence cofinal in
$z_n$
is a strictly increasing sequence of integers indexed by natural numbers, hence cofinal in
![]() $\mathbb {Z}$
. This implies that
$\mathbb {Z}$
. This implies that
![]() $\mathrm {ran}(\varphi )$
is cofinal in
$\mathrm {ran}(\varphi )$
is cofinal in
![]() $\mathbb {Z}^\beta \cdot \mathbb {Z}$
, finishing the proof of (*).
$\mathbb {Z}^\beta \cdot \mathbb {Z}$
, finishing the proof of (*).
We now use (*) to prove that every order-preserving embedding from
![]() $\omega ^\alpha $
into
$\omega ^\alpha $
into
![]() $O_\alpha $
must be cofinal. This clearly implies our desired non-embedding claim for
$O_\alpha $
must be cofinal. This clearly implies our desired non-embedding claim for
![]() $\omega ^{\alpha +1}$
and therefore finishes the proof of the lemma.
$\omega ^{\alpha +1}$
and therefore finishes the proof of the lemma.
As in the proof of (*), the case
![]() $\alpha =1$
is obvious and the limit case follows directly from the induction hypothesis. Let
$\alpha =1$
is obvious and the limit case follows directly from the induction hypothesis. Let
![]() $\alpha = \beta +1$
and let
$\alpha = \beta +1$
and let
![]() $\varphi :\omega ^{\beta +1} \to O_{\beta +1} = O_\beta + \mathbb {Z}^\beta \cdot \mathbb {N}$
be an order-preserving embedding. We apply the induction hypothesis to
$\varphi :\omega ^{\beta +1} \to O_{\beta +1} = O_\beta + \mathbb {Z}^\beta \cdot \mathbb {N}$
be an order-preserving embedding. We apply the induction hypothesis to
![]() $\varphi {\upharpoonright }\omega ^\beta $
and obtain that its image cannot be bounded in
$\varphi {\upharpoonright }\omega ^\beta $
and obtain that its image cannot be bounded in
![]() $O_\beta $
; thus, a final segment of
$O_\beta $
; thus, a final segment of
![]() $\mathrm {ran}(\varphi )$
lies in the
$\mathrm {ran}(\varphi )$
lies in the
![]() $\mathbb {Z}^\beta \cdot \mathbb {N}$
part of
$\mathbb {Z}^\beta \cdot \mathbb {N}$
part of
![]() $O_{\beta +1}$
. By the fact that
$O_{\beta +1}$
. By the fact that
![]() $\omega ^{\beta +1}$
is additively indecomposable, this final segment has order type
$\omega ^{\beta +1}$
is additively indecomposable, this final segment has order type
![]() $\omega ^{\beta +1}$
, so we can partition it into a strictly increasing
$\omega ^{\beta +1}$
, so we can partition it into a strictly increasing
![]() $\omega $
-sequence of sets each of order type
$\omega $
-sequence of sets each of order type
![]() $\omega ^\beta $
. Applying (*) inductively to these fragments of the map
$\omega ^\beta $
. Applying (*) inductively to these fragments of the map
![]() $\varphi $
, we see that the nth of these sets has to lie cofinal in the nth copy of
$\varphi $
, we see that the nth of these sets has to lie cofinal in the nth copy of
![]() $\mathbb {Z}^\beta $
or reach beyond it. In total, the image of
$\mathbb {Z}^\beta $
or reach beyond it. In total, the image of
![]() $\varphi $
has to lie cofinal in the entire
$\varphi $
has to lie cofinal in the entire
![]() $\mathbb {Z}^\beta \cdot \mathbb {N}$
part of
$\mathbb {Z}^\beta \cdot \mathbb {N}$
part of
![]() $O_{\beta +1}$
and hence in
$O_{\beta +1}$
and hence in
![]() $O_{\beta +1}$
itself.
$O_{\beta +1}$
itself.
Theorem 33. There are at least
![]() $\lambda ^+$
non-isomorphic order types of models of
$\lambda ^+$
non-isomorphic order types of models of
![]() $\mathsf {PA}^-$
that are not models of
$\mathsf {PA}^-$
that are not models of
![]() $\mathsf {Pr}$
(or
$\mathsf {Pr}$
(or
![]() $\mathsf {PA}$
) of cardinality
$\mathsf {PA}$
) of cardinality
![]() $\lambda $
.
$\lambda $
.
Proof There are
![]() $\lambda ^+$
many additively indecomposable ordinals smaller than
$\lambda ^+$
many additively indecomposable ordinals smaller than
![]() $\lambda ^+$
. For each such
$\lambda ^+$
. For each such
![]() $\alpha $
, we have that
$\alpha $
, we have that
![]() $(\mathbb {Z}(X^{\alpha }),0,<,\mathrm {s},+,\cdot )$
is a model of
$(\mathbb {Z}(X^{\alpha }),0,<,\mathrm {s},+,\cdot )$
is a model of
![]() $\mathsf {PA}^-$
of cardinality
$\mathsf {PA}^-$
of cardinality
![]() $\lambda $
; by Lemma 32, they have pairwise non-isomorphic order types. It is easy to see that none of these models are models of
$\lambda $
; by Lemma 32, they have pairwise non-isomorphic order types. It is easy to see that none of these models are models of
![]() $\mathsf {Pr}$
using Corollary 19.
$\mathsf {Pr}$
using Corollary 19.
Note that for
![]() $\lambda =\omega $
, Theorem 33 gives us uncountably many non-isomorphic countable models of
$\lambda =\omega $
, Theorem 33 gives us uncountably many non-isomorphic countable models of
![]() $\mathsf {PA}^-$
in stark contrast with the two order types of countable models of
$\mathsf {PA}^-$
in stark contrast with the two order types of countable models of
![]() $\mathsf {PA}$
(by Cantor’s theorem,
$\mathsf {PA}$
(by Cantor’s theorem,
![]() $\mathbb {N}$
and
$\mathbb {N}$
and
![]() $\mathbb {N}+\mathbb {Z}\cdot \mathbb {Q}$
are the only possible order types).
$\mathbb {N}+\mathbb {Z}\cdot \mathbb {Q}$
are the only possible order types).
We note that for uncountable
![]() $\lambda $
, Theorem 33 is the consequence of a result related to Shelah’s famous Non-structure Theorem or Many-Models Theorem. As part of his proof of the Non-structure Theorem, Shelah considers the number of reducts in [Reference Shelah23, Chapter VIII]:
$\lambda $
, Theorem 33 is the consequence of a result related to Shelah’s famous Non-structure Theorem or Many-Models Theorem. As part of his proof of the Non-structure Theorem, Shelah considers the number of reducts in [Reference Shelah23, Chapter VIII]:
Theorem 34 Shelah; [Reference Shelah23, Theorem VIII.0.4]
Let
![]() $\lambda $
be an uncountable regular cardinal,
$\lambda $
be an uncountable regular cardinal,
![]() $\mathcal {L}\subseteq \mathcal {L}^*$
be two countable languages, T an
$\mathcal {L}\subseteq \mathcal {L}^*$
be two countable languages, T an
![]() $\mathcal {L}$
-theory, and
$\mathcal {L}$
-theory, and
![]() $T'\supseteq T$
an
$T'\supseteq T$
an
![]() $\mathcal {L}^*$
-theory. If
$\mathcal {L}^*$
-theory. If
![]() $T^*$
has infinite models and T is not stable, then there are
$T^*$
has infinite models and T is not stable, then there are
![]() $2^\lambda $
many pairwise non-isomorphic models of T that are
$2^\lambda $
many pairwise non-isomorphic models of T that are
![]() $\mathcal {L}$
-reducts of models of
$\mathcal {L}$
-reducts of models of
![]() $T^*$
.
$T^*$
.
Now let T be the complete theory of discrete linear orders with a least but no largest element (which is a standard example for an unstable theory) and
![]() $T'$
to be
$T'$
to be
![]() $\mathsf {PA}^-$
. Then Theorem 34 yields
$\mathsf {PA}^-$
. Then Theorem 34 yields
![]() $2^\lambda $
many non-isomorphic order types of models of
$2^\lambda $
many non-isomorphic order types of models of
![]() $\mathsf {PA}^-$
of regular size
$\mathsf {PA}^-$
of regular size
![]() $\lambda \geq \aleph _1$
.
$\lambda \geq \aleph _1$
.
Comparing Theorems 33 and 34, we see that our construction gets
![]() $\lambda ^+$
instead of
$\lambda ^+$
instead of
![]() $2^\lambda $
many models, but provides the additional information that they are not models of
$2^\lambda $
many models, but provides the additional information that they are not models of
![]() $\mathsf {Pr}$
and works for
$\mathsf {Pr}$
and works for
![]() $\lambda = \omega $
.
$\lambda = \omega $
.
8 Shelah on almost isomorphism of order rigid models
The most recent progress on Friedman’s Question 2 was made by Shelah in [Reference Shelah24]. Since this is one of the few other papers that discusses fragments of Peano arithmetic with no induction or only fragments of induction, we should like to present Shelah’s results here.
Let
![]() $(M,0,<,\mathrm {s},+,\cdot )$
be an
$(M,0,<,\mathrm {s},+,\cdot )$
be an
![]() $\mathcal {L}_{<,\mathrm {s},+,\cdot }$
-structure; as usual, without loss of generality, we assume that
$\mathcal {L}_{<,\mathrm {s},+,\cdot }$
-structure; as usual, without loss of generality, we assume that
![]() $\mathbb {N}\subseteq M$
. For
$\mathbb {N}\subseteq M$
. For
![]() $a,b\in M$
, we say that a is exponentially small relative to b if for all natural number n, we have that
$a,b\in M$
, we say that a is exponentially small relative to b if for all natural number n, we have that
![]() $a^n < b$
. We define two equivalence relations on M: we say that a is standardly close to b, in symbols
$a^n < b$
. We define two equivalence relations on M: we say that a is standardly close to b, in symbols
![]() $a\mathrel {E^2} b$
, if there is a natural number n such that
$a\mathrel {E^2} b$
, if there is a natural number n such that
![]() $a<b\cdot n$
and
$a<b\cdot n$
and
![]() $b<a\cdot n$
; we say that a is exponentially close to b, in symbols
$b<a\cdot n$
; we say that a is exponentially close to b, in symbols
![]() $a\mathrel {E^3} b$
, if there is a c which is exponentially small relative to both a and b such that
$a\mathrel {E^3} b$
, if there is a c which is exponentially small relative to both a and b such that
![]() $a<b\cdot c$
and
$a<b\cdot c$
and
![]() $b<a\cdot c$
.
$b<a\cdot c$
.
The structure
![]() $(M,0,<,\mathrm {s},+,\cdot )$
is called two-order rigid if any
$(M,0,<,\mathrm {s},+,\cdot )$
is called two-order rigid if any
![]() $a,b\in M$
that define order isomorphic initial segments are standardly close; it is called
$a,b\in M$
that define order isomorphic initial segments are standardly close; it is called
![]() $3$
-order rigid if any
$3$
-order rigid if any
![]() $a,b\in M$
that define order isomorphic initial segments are exponentially close.
$a,b\in M$
that define order isomorphic initial segments are exponentially close.
If
![]() $(M,0,<,\mathrm {s},+)$
and
$(M,0,<,\mathrm {s},+)$
and
![]() $(N,0,<,\mathrm {s},+)$
are any
$(N,0,<,\mathrm {s},+)$
are any
![]() $\mathcal {L}_{<,\mathrm {s},+}$
-structures, we call a map
$\mathcal {L}_{<,\mathrm {s},+}$
-structures, we call a map
![]() $f:M\to N$
an almost isomorphism if it is a
$f:M\to N$
an almost isomorphism if it is a
![]() $\mathcal {L}_{<,\mathrm {s}}$
-isomorphism and for any
$\mathcal {L}_{<,\mathrm {s}}$
-isomorphism and for any
![]() $a,b\in M$
, the elements
$a,b\in M$
, the elements
![]() $f(a)+f(b)$
and
$f(a)+f(b)$
and
![]() $f(a+b)$
are standardly close in N.
$f(a+b)$
are standardly close in N.
Theorem 35 Shelah; [Reference Shelah24, Theorems 2.6 and 3.5]
If
![]() $(M,0,<,\mathrm {s},+,\cdot )\models \mathsf {PA}$
is two-order rigid or three-order rigid and
$(M,0,<,\mathrm {s},+,\cdot )\models \mathsf {PA}$
is two-order rigid or three-order rigid and
![]() $(N,0,<,\mathrm {s},+,\cdot )\models \mathsf {PA}$
has the same order type as
$(N,0,<,\mathrm {s},+,\cdot )\models \mathsf {PA}$
has the same order type as
![]() $(M,<)$
, then the additive reducts
$(M,<)$
, then the additive reducts
![]() $(M,0,<,\mathrm {s},+)$
and
$(M,0,<,\mathrm {s},+)$
and
![]() $(N,0,<,\mathrm {s},+)$
are almost isomorphic.
$(N,0,<,\mathrm {s},+)$
are almost isomorphic.
Not much is known about how close the theorem is to being optimal: in particular, it is not known whether the additive reducts are isomorphic (rather than almost isomorphic) [Reference Shelah24, Question 2.7].
In our context, it is interesting to note that in [Reference Shelah24, Section 5], Shelah considers whether Theorem 35 holds for
![]() $\mathcal {L}_{<,\mathrm {s},+,\cdot }$
-structures that are models of fragments of
$\mathcal {L}_{<,\mathrm {s},+,\cdot }$
-structures that are models of fragments of
![]() $\mathsf {PA}$
without induction. He considers four weaker theories
$\mathsf {PA}$
without induction. He considers four weaker theories
![]() $\mathsf {PA}_{-4}$
,
$\mathsf {PA}_{-4}$
,
![]() $\mathsf {PA}_{-3}$
,
$\mathsf {PA}_{-3}$
,
![]() $\mathsf {PA}_{-2}$
, and
$\mathsf {PA}_{-2}$
, and
![]() $\mathsf {PA}_{-1}$
, of which
$\mathsf {PA}_{-1}$
, of which
![]() $\mathsf {PA}_{-4}$
is our
$\mathsf {PA}_{-4}$
is our
![]() $\mathsf {PA}^-$
and the others are
$\mathsf {PA}^-$
and the others are
![]() $\mathsf {PA}^-$
with an increasing amount of additional instances of induction. Shelah then observes that for Theorem 35 in the case of two-order rigidity, the theory
$\mathsf {PA}^-$
with an increasing amount of additional instances of induction. Shelah then observes that for Theorem 35 in the case of two-order rigidity, the theory
![]() $\mathsf {PA}_{-1}$
is sufficient [Reference Shelah24, Theorem 5.4].
$\mathsf {PA}_{-1}$
is sufficient [Reference Shelah24, Theorem 5.4].
9 Summary
We combine the various insights into possible order types of our five theories
![]() $\mathsf {SA}^- = \mathsf {SA}$
,
$\mathsf {SA}^- = \mathsf {SA}$
,
![]() $\mathsf {Pr}^-$
,
$\mathsf {Pr}^-$
,
![]() $\mathsf {Pr}$
,
$\mathsf {Pr}$
,
![]() $\mathsf {PA}^-$
, and
$\mathsf {PA}^-$
, and
![]() $\mathsf {PA}$
in order to provide the solution to Question 4 restricted to these five theories: they can all be separated by order types.
$\mathsf {PA}$
in order to provide the solution to Question 4 restricted to these five theories: they can all be separated by order types.
For the theories
![]() $\mathsf {SA}$
and
$\mathsf {SA}$
and
![]() $\mathsf {Pr}^-$
, we were able to give complete characterisations in Corollaries 13 and 21; for the theories
$\mathsf {Pr}^-$
, we were able to give complete characterisations in Corollaries 13 and 21; for the theories
![]() $\mathsf {Pr}$
and
$\mathsf {Pr}$
and
![]() $\mathsf {PA}^-$
, we were able to give necessary conditions in Corollary 19 and Theorems 25 and 27, respectively. In particular, the negative results from Sections 4 and 5 imply:
$\mathsf {PA}^-$
, we were able to give necessary conditions in Corollary 19 and Theorems 25 and 27, respectively. In particular, the negative results from Sections 4 and 5 imply:
Corollary 36. There is no model of
![]() $\mathsf {Pr}$
(and hence, no model of
$\mathsf {Pr}$
(and hence, no model of
![]() $\mathsf {PA}$
) with order type
$\mathsf {PA}$
) with order type
![]() $O_2$
or
$O_2$
or
![]() $O_\omega $
.
$O_\omega $
.
Proof We have that
![]() $O_2 = \mathbb {N}+\mathbb {Z}\cdot \mathbb {N}$
and
$O_2 = \mathbb {N}+\mathbb {Z}\cdot \mathbb {N}$
and
![]() $O_\omega = \mathbb {N}+\mathbb {Z}\cdot O_\omega $
. Clearly,
$O_\omega = \mathbb {N}+\mathbb {Z}\cdot O_\omega $
. Clearly,
![]() $\mathbb {N}$
and
$\mathbb {N}$
and
![]() $O_\omega $
are not the positive parts of a densely ordered abelian group, so by Corollary 19, no model of
$O_\omega $
are not the positive parts of a densely ordered abelian group, so by Corollary 19, no model of
![]() $\mathsf {Pr}$
can have these order types.
$\mathsf {Pr}$
can have these order types.
In the following diagram, an arrow from a theory T to a theory S means “every order type that occurs in a model of T occurs in a model of S”. The diagram is complete in the sense that the absence of an arrow means that no arrow can be drawn, i.e., “there is an order type of a model of T that cannot be an order type of a model of S.”

The non-implication
![]() $\mathsf {SA}\nrightarrow \mathsf {Pr}^-$
follows from Corollaries 13 and 23:
$\mathsf {SA}\nrightarrow \mathsf {Pr}^-$
follows from Corollaries 13 and 23:
![]() $\mathbb {N}+\mathbb {Z}$
is an order type witnessing the separation.
$\mathbb {N}+\mathbb {Z}$
is an order type witnessing the separation.
The non-implication
![]() $\mathsf {Pr}^-\nrightarrow \mathsf {Pr}$
follows from Theorem 14 and Corollary 36:
$\mathsf {Pr}^-\nrightarrow \mathsf {Pr}$
follows from Theorem 14 and Corollary 36:
![]() $\mathbb {N}+\mathbb {Z}\cdot \mathbb {N}$
is an order type witnessing the separation.
$\mathbb {N}+\mathbb {Z}\cdot \mathbb {N}$
is an order type witnessing the separation.
The non-implication
![]() $\mathsf {Pr}^-\nrightarrow \mathsf {PA}^-$
follows from Theorem 14 and Corollary 30:
$\mathsf {Pr}^-\nrightarrow \mathsf {PA}^-$
follows from Theorem 14 and Corollary 30:
![]() $\mathbb {N}+\mathbb {Z}\cdot \mathbb {N}$
is an order type witnessing the separation.
$\mathbb {N}+\mathbb {Z}\cdot \mathbb {N}$
is an order type witnessing the separation.
The non-implication
![]() $\mathsf {PA}^-\nrightarrow \mathsf {Pr}$
follows from Theorem 16 and Corollary 36:
$\mathsf {PA}^-\nrightarrow \mathsf {Pr}$
follows from Theorem 16 and Corollary 36:
![]() $O_\omega = \mathbb {N}+\mathbb {Z}\cdot O_\omega $
is an order type witnessing the separation.
$O_\omega = \mathbb {N}+\mathbb {Z}\cdot O_\omega $
is an order type witnessing the separation.
The non-implication
![]() $\mathsf {Pr}\nrightarrow \mathsf {PA}^-$
follows from Theorem 25 and Corollary 18:
$\mathsf {Pr}\nrightarrow \mathsf {PA}^-$
follows from Theorem 25 and Corollary 18:
![]() $\mathbb {N}+\mathbb {Z}\cdot \mathbb {R}$
is an order type witnessing the separation.
$\mathbb {N}+\mathbb {Z}\cdot \mathbb {R}$
is an order type witnessing the separation.
Acknowledgements
This work was initiated during the visit of Swaraj Dalmia in Amsterdam during the summer of 2016, funded by the Indo-European Research Training Network in Logic (IERTNiL); the authors would like to thank him for his involvement in the early phase of the project. Furthermore, the authors would like to thank Andrey Bovykin, Nathan Bowler, Chase Ford, Tim Henke, and Albert Visser for discussions about the material included in this paper, as well as the anonymous referee for a number of corrections and suggestions.