1. Introduction

In spite of recurring field activity and of a growing development of automatic devices, the coverage of in situ observation of the polar ice-sheets surface remains, for logistical reasons, spatially and temporally sparse. On the other hand, remote sensing by satellite-borne instruments has already provided decades of observation, with excellent spatial and temporal coverage. In particular, microwave radiometers are relatively independent of sunlight and most atmospheric conditions in the polar regions. On board polar-orbiting satellites, such instruments thus provide all-weather monitoring of the surface of the ice sheets. However, difficulties in interpreting satellite data in terms of surface climate and environment have been limiting. The emissivity of snow in the microwave bands is variable due to scattering by snow grains, the size, shape and arrangement of which can vary with age, temperature history, accumulation rates, surface winds and possibly other variables (Reference ZwallyZwally 1977). Reference Surdyk and FilySurdyk and Fily (1993) showed how passive microwave signatures of the surface of the Antarctic ice sheet can be related to the mean grain-size and stratigraphy of the upper snowpack. Reference Dang, Genthon and MartinDang and others (1997) showed that a temperate snow model (Crocus) reproduces, with limited adaptation to the polar environment, the basic characteristics of the upper snow at South Pole in Antarctica. A fully validated snow model would be a useful interface between atmospheric variables in input to the model, which characterize the surface climate, and satellite data which characterize snow structure and stratigraphy.

Here, we present selected aspects of the microwave emissivity of snow in central Greenland from the Scanning Multichannel Microwave Radiometer (SMMR) (section 2) and we show that these aspects correlate spatially with results of numerical simulations of snow (section 4). The Crocus model simulates the thermal and structural characteristics of surface snow in response to surface meteorology (section 3). Because large-scale observation of the surface meteorology of Greenland is not available, meteorological data extracted from the European Center for Medium-range Weather Forecasts (ECMWF) analysis and short-term forecast archives are used in input to the snow model. Two different meteorological datasets are extracted and used, which yield different reconstructions of the snowpack. The sensitivity of the simulated snowpack to typical uncertainties of analyzed and modeled surface meteorology can thus be studied (section 5). We argue (section 6) that our results confirm that combining satellite microwave data and a complex snow model can extend the search and validation of surface meteorology data beyond the limited set of available in situ observations. However, our approach, although innovative, is still very preliminary: snow modeling must be improved and further validated, and physically based translation of simulated snow parameters into microwave radiative properties should be used rather than empirical correlations.

2. Microwave Spectral Signatures from Smmr

Reference Surdyk and FilySurdyk and Fily (1993) exhibited correlations between observed grain-size and stratigraphy in Antarctica and the so-called gradient ratio (GR) and polarization ratio (PR) defined as follows:

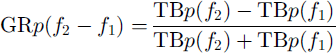
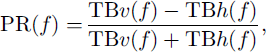
where TBp(f) is the surface brightness temperature (in K) at frequency f and polarization p. Polarization can be either vertical (p = v) or horizontal (p = h). Microwave emission and absorption in the snowpack result from the vertical distribution of snow temperature and of snow structure. TB is thus a complex integral with depth of temperature and absorption and scattering properties of snow (Reference Ulaby, Moore and FungUlaby and others, 1981). Temperature varies through time due to heat transfer between the surface and the deeper layers. The structure of snow evolves more slowly except maybe in the uppermost layers, and has limited time and depth correlation with temperature. As a consequence, the surface brightness temperature of a snowpack having the annual mean snow structure and temperature profile of an actual snowpack is close to the annual mean TB of this snowpack:

where T_s is the annual mean surface temperature and ep(f) is an annual mean snow emissivity at frequency f and polarization p (Reference ZwallyZwally, 1977; Reference Sherjal and FilySherjal and Fily, 1994). The annual mean ratios thus filter out T_s and are mainly normalized measures of snow emissivity at different frequencies and polarizations (Reference Cavalieri, Gloersen and CampbellCavaheri and others, 1984):

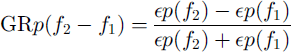
Over its almost 9 years of operation (October 1978-August 1987), the SMMR instrument measured microwave radiation from the Earth surface, and thus the brightness temperature TB, in both horizontal and vertical polarizations at five frequencies: 6.6, 10.7, 18, 21 and 37 GHz. Similar measurements have been subsequently made by other instruments (eg. the Special Sensor Microwave/Imager (SSM/I)), but not at the lowest frequency available from SMMR. Reference Surdyk and FilySurdyk and Fily (1993) report that the largest variability and correlation with snow-structure parameters in Antarctica occur for f = f1 = 6.6 GHz, f₂ = 18 GHz, and p = v.

Through principal-components analysis of the spatial distribution of TB over Antarctica, Reference Fily and BenoistFily and Benoist (1991) also point to particularities of the lowest frequencies. The authors find that, while the first loading of the analyses is highly correlated with surface snow temperature, the second and third loadings are not, yet they are very stable and they mainly reflect information from PR(6.6) and GR(6.6–18), respectively. If this information is not directly linearly temperature-related, then it characterizes the snow emissivity which is itself related to the structure of the snow. This structure results from the surface meteorology (temperature, precipitation, evaporation, wind, etc.), so it is in turn, but indirectly, related to temperature as well as to other surface climate variables.

SMMR, which flew on board the Nimbus-7 satellite, operated on alternate days due to energy limitations. Full coverage of the polar regions was insured every 3 days or less, except poleward of 84° N, an area which is not relevant for Greenland. Not all years in the period of activity are equally sampled. Here, we select years 1979, 1980, 1982, 1983 and 1985 which are particularly homogeneously sampled, and average all available data over all 5 years. The data we use were compiled on CD-ROMs by NASA and distributed by the U.S. National Snow and Ice Data Center (NSIDC, 1994). Figure 1 shows the spatial distribution of GRv(6.6–18) and PR(6.6) (henceforth simply referred to as GR and PR) over central Greenland. Figure 1 also presents the annual mean surface temperature of snow and the annual mean precipitation over the same region, from the ECMWF operational meteorological analyses and short-term forecasts over the period May 1985-April 1991 (see section 3 below for more on the ECMWF analyses and forecasts). This period does not coincide with the satellite data. As far as spatial distribution is concerned, however, there is little interannual variability in the satellite data, and the spatial resolution of the ECMWF operational meteorological analyses becomes reasonably high only after May 1985. Reference Genthon and BraunGenthon and Braun (1995) suggest that, although certainly not bias-free, these analyses provide a useful picture of the surface climate of Greenland and Antarctica.

Fig. 1. Spatial distribution over central Greenland of the annual mean (a) GR and (b) PR from SMMR (no unit; see text for details), and of (c) surface temperature (in °C) and (d) total precipitation (in mm cT₁) from the ECMWF meteorological analyses and short-term forecasts.

Figure 1 confirms that GR and PR are not simply linearly correlated with temperature, yet they are not unrelated. Precipitation also shows some relation with the satellite data. We assume (Equations (4) and (5)) that such relation has its origin in the structure of the snow and its dependence on surface meteorology. We now test this hypothesis with a snow model.

3. Snow Modeling and Meteorological Forging

Crocus (Reference Brun, David, Sudul and BrunotBrun and others, 1992) is a 50-layer unidimensional snow model initially developed for alpine snow studies and avalanche risk evaluation. The model was also shown to reasonably simulate some major features in the upper meters of snow at South Pole, Antarctica, with limited adaptation to the polar regions (Reference Dang, Genthon and MartinDang and others, 1997). One important change made to Crocus was in the parameterization of surface snow density with temperature and wind. The modified parameters result in surface densities of the order of 300 kg m⁻³, compared to < 100kg m⁻³ with the original formulation. Heat conduction, melting and refreezing, liquid-water percolation, metamorphism and packing in the snowpack are formulated and unchanged in the model, which is driven by hourly 2 m temperature and humidity, 10 m wind, precipitation (quantity and phase), downward infrared and visible, direct and diffuse radiation, and cloud cover. Crocus handles its own surface turbulent fluxes of heat and moisture.

For the present study, meteorological forcing is extracted from the archive of meteorological analyses and short-term forecasts at ECMWF. Meteorological analyses are the result of an assimilation of observations from the global meteorological network and from satellite data into a numerical meteorological model. They are operationally produced by major weather-prediction centers like ECMWF to initialize forecasting runs. At ECMWF, analysis is performed globally every 6 hours, thus providing a full spatial and temporal coverage picture of the global atmospheric dynamics and thermodynamics. Only a limited set of meteorological variables, those for which an extensive real-time observation set is available, are analyzed, including temperature, wind, atmospheric moisture and cloud cover. Other variables necessary for driving a snow model are obtained from the ECMWF short-term (6 h) forecasts.

Meteorological analyses may be considered as global physically based interpolations of observations. In largely observation-devoid areas, like the interior of the Greenland ice sheet, analyses fill huge gaps and thus provide unique and essential, yet somewhat questionable, climatological information. In addition to limited data constraint, assimilation and model flaws bias the analyses. The numerical tools used at forecasting centers to produce the operational analyses are continuously modified, and hopefully improved, over time. As a consequence, the quality of the analyses is not temporally consistent. To improve consistency, ECMWF and other forecasting centers have recently produced re-analyses over multi-year periods of the past using an up-to-date and stable numerical package (assimilation and numerical model). At ECMWF, both operational analyses and re-analyses (and associated forecasts) are available over the period 1979–93.

As a first analysis of the sensitivity of the snow model to uncertainty in the surface meteorology of central Greenland, two sets of meteorological forcing have been built, one from the operational analyses and one from the re-analyses. A common period has been selected, 1986–93, over which both analyses have a spectral resolution of T106 (or slightly more than 1° in spatial resolution) or better. This period does not coincide with the period of satellite-data analysis presented earlier (section 2), but negligible interannual variability of the spatial distribution of GR and PR has been observed in these data. In order to simulate 2 m of snow or more everywhere in the interior of Greenland, 32 years of snowpack are simulated by recycling meteorological forcing four times. Reference Surdyk and FilySurdyk and Fily (1993) suggest that PR and GR correlate with 2 m mean snow-structure parameters. Model results are thus averaged over the upper 2 m of simulated snow. Meteorological input, simulations and results will be referred to as EOA (European operational analyses) when obtained from operational analyses forcing, and otherwise as ERA (European re-analyses).

4. Model Results at 14 Test Sites

Figure 2 compares PR, GR and the 2 m mean simulated density, grain-size and number of layers at 14 test sites. Grain-size and layering directly affect the microwave emission of snow. Mean density in itself has a much weaker effect. However, Reference Surdyk and FilySurdyk and Fily (1993) report strong spatial correlation between mean density and PR in Antarctica. They suggest that mean density may be a proxy for other structural parameters. Mean density is less infrequently measured on the field than grain-size or stratigraphy because it is used to evaluate accumulation. We thus also retain density as a valid parameter here. The 14 test sites align along a northward (N), an eastward (E) and a southwestward (SW) transect as depicted in Figure 1. They are numbered as sites 1–5 (N), 6–8 (E) and 9–13 (SW), with a common origin of the three transects at site 0 which is at the summit of the Greenland ice sheet. Because the transects cut through strong gradients of GR and PR, we expect that the 14 test sites efficiently sample the spatial variability of microwave emissivity and snow structural characteristics in central Greenland.

Fig. 2. As a function of test site number (see Fig. 1 for localization of the test sites), the distribution of (a) the annual mean GR (no unit; +0.01 to make all values positive), (b) PR (no unit), (c) mean simulated density (kg m⁻³), (d) gram-size (diameter in mm) and (e) number of layers in the upper 2 m of ERA simulated snow, (f-h) Same as (c-e) but for the EOA simulated snow.

Linear correlation is obviously only a first-order characterization of the complex radiative physics behind the relations between snow structure and emissivity. However, it is probably meaningful to note that PR and GR contain common information (correlation r = 0.86, yet they differ largely along transect SW. The largest correlation between microwave signatures and snow structure parameters is obtained between GR and the ERA mean snow grain-size (Fig. 2d; r = 0.93). Correlation is somewhat lower (r =0.87) with stratigraphy (Fig. 2e) as quantified by the number of snow layers in the upper 2 m (leaving aside the uppermost thin layers of fresh and untransformed snow), and with density (Fig. 2c; r = –0.84). Reference Surdyk and FilySurdyk and Fily (1993) suggest that PR should be comparatively more sensitive to density and, to some extent, stratigraphy. Here again, however, the largest correlation is found with grain-size (r =0.85) and stratigraphy (r =0.83), then density (r =0.72). The comparison of the spatial distribution of the simulated structural parameters shows no evidence of the difference between GR and PR (Fig. 2a and b) along the SW transect.

Significantly different results are obtained with the EOA meteorology. Grain-size is similar to that obtained with ERA along the SW transect, but it is larger along the N and much larger along the E transects (Fig. 2g). As a consequence, the correlation of GR is lower with the EOA grain-size (r = 0.77) than with the ERA grain-size. For PR, the correlation coefficient is just the same (r =0.85) with the two meteorologies, although there is still no sign in the EOA grain-size of a characteristically different spatial distribution in PR and GR along the SW transect. There is a very slight and unconvincing hint of this difference in the EOA stratigraphy and density. The number of layers (Fig. 2h) actually also tends to increase with EOA, compared to ERA, particularly along the E transect, resulting in lower correlations with GR and PR (r=0.65 and 0.74, respectively). The same applies to density (Fig. 2f, r =0.71 and 0.76, respectively).

In conclusion, there is clearly some strong relation between the modeled snow grain structure and the observed microwave signatures. If such relation holds in the real world, then a snow model is the right tool to relate microwave data and climate. Further, finer statistical analysis (eg. principal-component analysis: Reference Fily and BenoistFily and Benoist, 1991) or even better, radiation transfer modeling (e.g. Reference Abdalati and SteffenAbdalati and Steffen, 1998; Reference Wiesmann and MatzlerWiesmann and Matzler, 1999) should provide a more extensive quantitative exploitation of the model results in relation to satellite data. However, work beyond a first-order study does not seem appropriate yet, because we still have limited control of the model results in central Greenland. In fact, visual estimates of grain-size have been made in the field at the 14 test sites, and these observations suggest that grains are larger than simulated (for more on possible model biases see section 6). Careful screening of these non-objective and possibly biased visual observations is in progress which, if conclusive, will make it possible to bring forward the above study. Meanwhile, the reasons why there is so much difference between model results forced by the two meteorologies can be investigated. Even if the snow model is not fully validated, this will yield basic aspects of the sensitivity of snow structure to surface climate.

5. Sensitivity of a Snow Model to Forging Meteorology

Figure 3 shows the ERA and EOA annual mean surface temperature and precipitation as a function of microwave signature. The differences between the two meteorologies are indicative of a range of results one may expect from up-to-date climate models over central Greenland. The EOA temperature is always warmer by a few °C, but the temperature difference is not the same at all test sites. In particular, the temperature distribution along the northernmost part of the N transect is very different in the two meteorologies. Precipitation is on average larger in EOA except at two sites. At three sites, precipitation is virtually the same in the two meteorologies but temperature is not. Incidentally, both temperature and precipitation show significant linear correlation with microwave signature. As discussed previously, there are regions where this correlation is poor (Fig. 1) and the ratios used here should essentially filter out temperature and retain mostly emissivity information (section 2). Much of the climate/microwave correlation shown in Figure 3 should therefore originate from structural characteristics, which in turn depend on surface climate. This dependence is examined now in the model.

Fig. 3. The ERA (circles) and EOA (squares) annual mean temperature (°C) as a function of (a) GR and (b) PR. (c, d) Sane as (a, b) butfor annual mean precipitation (mm d⁻¹).

Sensitivity simulations are carried out by swapping a selection of variables of the EOA meteorological forcing with the corresponding variables of the ERA meteorology, and running the snow model with the resulting modified EOA meteorology. Unmodified ERA and EOA simulations are used as controls. Figure 4 shows the sensitivity of the simulated mean grain-size to meteorology. Grain-size is plotted as a function of GR (results are qualitatively similar for PR) as in Figure 3, rather than as a function of test site number as in Figure 2, to illustrate changes in snow-structure/microwave-signature regressions. Figure 4 shows again that grains are systematically larger in EOA than in ERA. Grain-size sensitivity to temperature is high (Fig. 4a): only replacing EOA temperature by ERA temperature is sufficient to produce a result which is much closer to the ERA than to the EOA control simulation. Changing temperature alone may be rather inconsistent, though. For instance, infrared radiation is a direct function of temperature, and the two differ in a coherent way in the two meteorologies. Grain-size sensitivity to combined temperature and infrared downward radiation is larger than sensitivity to temperature alone (Fig. 4b). In fact, changing temperature and infrared radiation together and keeping all other forcing from EOA yields grains which are generally even smaller than in the ERA control. In addition, sensitivity to temperature and/or infrared radiation generally increases with mean grain-size, the smallest grains showing little sensitivity This is consistent with the fact that grain growth is largely a temperature- (Clapeyron-Clausius) dependent process. Largest grains in the ERA or EOA controls are those which have encountered the strongest metamorphism under the influence of warm temperatures and/or large temperature gradients. They are thus those which are most sensitive to a temperature change.

Fig. 4. Simulated gram-size (mm) as a function of GR from ERA (circles) and EOA (squares) simulations, and from sensitivity simulations (dots) made with the EOA meteorology except for the following variables which are replaced by corresponding ERA variables: (a) temperature, (b) temperature and downward infrared radiation, (c) precipitation and (d) temperature, infrared radiation and precipitation.

Sensitivity to precipitation (Fig. 4c) is also high but it is much less systematic and easy to understand than for temperature. At the two sites with the smallest GR, the change of precipitation in the sensitivity experiment is just about equal in amplitude but opposite in sign (Fig. 3c), yet the change in grain-size has the same sign. Also, precipitation change is just about the same (with same sign) at the site having the second smallest and at that having the largest GR, yet the grain-size change is very small at the former site and very large at the latter. Incidentally, at both sites and at a couple of others, the grain-size increases in the sensitivity experiment, compared to the EOA control, rather than decreases to converge towards the result of the ERA control. Then, comparing the two sites having the largest GR, sensitivity to precipitation is nil at the site with the larger mean precipitation change, while it is one of the largest of all at the other sites. Mean precipitation may not be the most relevant measure of the precipitation difference between ERA and EOA. The time typically spent by a layer of snow near the surface before it is covered by a new layer, which is controlled by the temporal distribution of precipitation, as well as the correlation between precipitation events and other meteorological variables such as temperature, may also be of importance. Such aspects can certainly be explored with a snow model, although additional model validation is awaited.

Together, temperature, infrared radiation and precipitation explain very well the differences in grain-size between the control ERA and EOA simulations (Fig. 4d). If the model is correct, then grain-size in the upper snow, obtained either directly from field investigations or indirectly from satellite data, can yield very valuable integrated information and control on essential surface meteorological variables.

Figure 5 is the same as Figure 4 but for the simulated number of layers in the upper 2 m of snow. Sensitivity to temperature alone is weak (Fig. 5a). It is surprisingly larger when temperature is combined with infrared radiation (Fig. 5b). Precipitation affects stratigraphy (Fig. 5c), but the effect is not consistent throughout the three transects. The number of layers tends to increase with decreasing precipitation along the N and SW transects and to decrease along the E transect. In Figure 5, the E transect corresponds to the three squares which stand out of the otherwise relatively aligned set of values for EOA (squares). For two of these outliers, the precipitation change from EOA to ERA is close to 0. This again demonstrates the importance of the frequency of precipitation events and associated internal snow processes, which affect snow stratigraphy beyond the simple mean accumulation effect. The three meteorological variables together largely explain, although significantly less than for grain-size, the differences between the control ERA and EOA. According to the model, layering does not seem as simple a recorder of surface meteorology as grain-size but it carries different and complementary information.

Fig. 5. Same as Figure 4, but for the simulated number of snow layers in the upper 2 m.

Figure 6 shows the sensitivity of the mean snow density to meteorology. Sensitivity to temperature and infrared radiation is relatively weak (Fig. 6a). Sensitivity to temperature alone is even weaker. Sensitivity to precipitation is higher (Fig. 6b), and, unlike the other structural parameters, using the ERA precipitation in the EOA meteorology makes density differ even more from the ERA control than the EOA control itself. Precipitation and density spatially correlate positively (cf Figs 3c and 6). In the sensitivity experiment, however, density increases in several instances with a decrease of precipitation. Again, the dependence on precipitation is complex, and more than annual means may have to be analyzed to understand it. Surface density is a parameterized function of surface wind and surface temperature (section 3), so that the mean density is much more sensitive to surface wind than the other snow parameters (Fig. 6c). Surface wind is systematically weaker in ERA, by 1–3 m s⁻¹. This results in a systematically lighter snow. Together, temperature, infrared radiation, precipitation and surface wind mostly explain the difference between ERA and EOA for density. Relatively complex methods (e.g. microphotography and image analysis) must be used to determine grain-size and stratigraphy objectively and reproducibly. On the other hand, relatively rustic methods (weighing a standard volume of snow) can be used to measure density. Therefore, density data may have a good potential for climate information. Again, this result is subject to the realism of the snow model used here, a point which is discussed next.

Fig. 6. Simulated density (kg m⁻³) as a function of GR from ERA (circles) and EOA (squares) simulations, and from sensitivity simulations (dots) made with the EOA meteorology except for the following variables which are replaced by corresponding ERA variables: (a) temperature and downward infrared radiation, (b) precipitation, (c) surface wind, and (d) temperature, infrared radiation, precipitation and wind.

6. Discussion and Conclusion

A comparison between microwave signatures of central Greenland snow and results of the Crocus snow model supports the well-known, yet still little exploited, potential of microwave remote sensing for meteorological reconstructions over the observation-sparse ice sheets. Annual mean temperature and, to a lesser extent, annual mean accumulation are accessible with glaciological means, yet this requires fieldwork which has so far been carried out at a limited number of sites in Greenland. Meteorological information (mean and variability of temperature, precipitation, wind, radiation, etc.) is available at only a few stations and in limited quantity and range. Model results presented here confirm that combining remote sensing and snow modeling can contribute to verification of interpolations between these sites, including physically based interpolations like the meteorological analyses and climate-model simulations. Such contribution is limited by difficulties at two levels: (1) relating integrated emissivity as observed from space to snow-thermal and -structure parameters; (2) relating snow parameters to surface climate. Both levels have been addressed here.

The first level is only crudely approached: it is seen that all the first-order snow-structure parameters (density grain-size, stratigraphy) in the simulated upper 2 m of snow correlate, albeit differently, with the 6.6 GHz PR and with the 6.6–18 GHz GR. GR and PR themselves are seen to carry partially different and hopefully complementary information, although correlation with snow parameters is systematically less for the latter. More complex approaches (eg. radiation transfer modeling in the snow) are necessary to further quantify these relations.

The second level of difficulty is also and more extensively addressed. Obviously, the spatial distribution of simulated snow-structure parameters reflects the spatial distribution of surface meteorology. In addition, very different results are obtained when the same snow model is forced by two different meteorological datasets. In particular, grain-size, stratigraphy or density show strong differential sensitivity to temperature, precipitation or wind: grain-size and stratigraphy are sensitive to both thermal and hydrological parameters; the thermal sensitivity of grain-size is more systematic and more exploitable in regions where grains are large on average (that is, the driest regions); the hydrological sensitivity is complex and clearly carries information on temporal variability; density is predictably sensitive to surface wind. The two meteorological datasets have a common origin, the ECMWF archive of analyses and forecasts, and their differences are qualitatively typical of uncertainties in the central Greenland surface meteorology. Satellite observation and a snow model used in direct mode thus have a potential for discrimination between different reconstructions of surface meteorology. Inverting snow structure in terms of surface climate is an even more attractive, yet probably remote perspective.

However, snow model validation over polar ice sheets is still limited. Although checked at South Pole (Reference Dang, Genthon and MartinDang and others, 1997), the Crocus model may have biases in other regions. Hoar layers have been more frequently reported in Greenland (e.g. Reference Abdalati and SteffenAbdalati and Steffen, 1998) than in Antarctic central snow. Central Greenland may thus be a more stringent test for snow grain metamorphism under strong temperature gradients. The formulae used in Crocus are the result of laboratory experiments which poorly cover the polar conditions. In addition, Crocus does not account for very slow metamorphism under weak or zero temperature gradient, a missing process which may have more consequences for Greenland because mean temperatures are warmer there than in central Antarctica. Also, an empirical parameterization of surface density is used, the possible deficiencies of which can have obvious consequences for the interpretation of density profiles, although grain-size and stratigraphy are probably weakly affected.

Finally, as is often the case when studying the environment of the ice sheets, lack of constraining observation is an important limiting factor. Series of coherent meteorological and snow observations at a few selected sites, or even at one representative site to start with, would be very welcome.