Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-17T00:39:23.934Z Has data issue: false hasContentIssue false
  • English
  • Français

Necessary condition for the L2 boundedness of the Riesz transform on Heisenberg groups

Part of: Classical measure theory Harmonic analysis in several variables

Published online by Cambridge University Press:  23 May 2023

DAMIAN DĄBROWSKI  and
MICHELE VILLA
DAMIAN DĄBROWSKI
Affiliation:
University of Jyväskylä, P.O. Box 35 (MaD), 40014, Finland e-mail: [email protected]
MICHELE VILLA
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, Edifici C Facultat de Ciències, 08193 Bellaterra, Barcelona, Catalonia, Spain and Mathematics Research Unit, University of Oulu. P.O.Box 8000 FI 90014, U.S.A. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 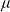$\mu$ be a Radon measure on the nth Heisenberg group 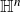${\mathbb{H}}^n$. In this note we prove that if the 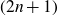$(2n+1)$-dimensional (Heisenberg) Riesz transform on 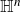${\mathbb{H}}^n$ is 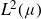$L^2(\mu)$-bounded, and if 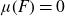$\mu(F)=0$ for all Borel sets with 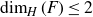${\text{dim}}_H(F)\leq 2$, then 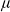$\mu$ must have 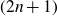$(2n+1)$-polynomial growth. This is the Heisenberg counterpart of a result of Guy David from [Dav91].

MSC classification

Primary: 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.)
Secondary: 28A75: Length, area, volume, other geometric measure theory
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 175 , Issue 2 , September 2023 , pp. 445 - 458
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported by Spanish Ministry of Economy and Competitiveness, through the María de Maeztu Programme for Units of Excellence in R&D (grant MDM-2014-0445). Partially supported by the Catalan Agency for Management of University and Research Grants (grant 2017-SGR-0395), and by the Spanish Ministry of Science, Innovation and Universities (grant MTM-2016-77635-P).

‡

Supported by The Maxwell Institute Graduate School in Analysis and its Applications, a Centre for Doctoral Training funded by the UK Engineering and Physical Sciences Research Council (grant EP/L016508/01), the Scottish Funding Council, Heriot-Watt University and the University of Edinburgh.

§

Partially supported by the grant 346300 for IMPAN from the Simons Foundation and the matching 2015-2019 Polish MNiSW fund.

References

Azzam, J., Hofmann, S., Martell, J. M., Mourgoglou, M. and Tolsa, X.. Harmonic measure and quantitative connectivity: geometric characterisation of the $L^p$ -solvability of the Dirichlet problem. Preprint arXiv:1907.07102 (2019).CrossRefGoogle Scholar
Azzam, J. and Schul, R.. An analyst’s traveling salesman theorem for sets of dimension larger than one. Math. Ann. 370(3-4) (2018), 1389–1476. doi: 10.1007/s00208-017-1609-0.CrossRefGoogle Scholar
Bonfiglioli, A., Lanconelli, E. and Uguzzoni, F.. Stratified Lie groups and potential theory for their sub-Laplacians. Springer Monogr. Math. (Springer, Berlin, Heidelberg, 2007). doi: 10.1007/978-3-540-71897-0.CrossRefGoogle Scholar
Badger, M. and Schul, R.. Multiscale analysis of 1-rectifiable measures: necessary conditions. Math. Ann. 361(3-4) (2015), 1055–1072. doi: 10.1007/s00208-014-1104-9.CrossRefGoogle Scholar
Capogna, L., Danielli, D., Pauls, S. D. and Tyson, J.. An introduction to the Heisenberg group and the sub-Riemannian isoperimetric problem Progr. Math. vol. 259 (Birkhäuser Basel, 2007). doi: 10.1007/978-3-7643-8133-2.CrossRefGoogle Scholar
Chousionis, V., Fässler, K. and Orponen, T.. Boundedness of singular integrals on $C^{1,\alpha}$ intrinsic graphs in the Heisenberg group. Adv. Math. 354 (2019), 106745. doi: 10.1016/j.aim.2019.106745.CrossRefGoogle Scholar
Christ, M.. A T(b) theorem with remarks on analytic capacity and the Cauchy integral. 2(60-61) (1990), 601–628. doi: 10.4064/cm-60-61-2-601-628.CrossRefGoogle Scholar
Chousionis, V. and Mattila, P.. Singular integrals on self-similar sets and removability for lipschitz harmonic functions in heisenberg groups. J. Reine Angew. Math. 2014(691) (2012),29–60. doi: 10.1515/crelle-2012-0078.CrossRefGoogle Scholar
David, G.. Morceaux de graphes lipschitziens et intégrales singulieres sur une surface. Rev. Mat. Iberoam. 4(1) (1988), 73–114. doi: 10.4171/RMI/64.CrossRefGoogle Scholar
David, G.. Wavelets and Singular Integrals on Curves and Surfaces. Lecture Notes in Math. vol. 1465. (Springer-Verlag, 1991). doi: 10.1007/BFb0091544.CrossRefGoogle Scholar
David, G.. Unrectifiable 1-sets have vanishing analytic capacity. Rev. Mat. Iberoam. 14(2) (1998), 369–479. doi: 10.4171/RMI/242.CrossRefGoogle Scholar
David, G. and Semmes, S.. Singular integrals and rectifiable sets in $\mathbb{R}^n$ : Au-delà des graphes lipschitziens. Astérisque, 193 (1991). doi: 10.24033/ast.68.CrossRefGoogle Scholar
David, G. and Semmes, S.. Analysis of and on Uniformly Rectifiable Sets Math. Surveys Monogr. vol. 38. (Amer. Math. Soc., 1993). doi: 10.1090/surv/038.CrossRefGoogle Scholar
Fässler, K.. Quantitative recitfiability in Heisenberg groups. Lecture notes for the Workshop in Geometry and Analysis, IMPAN (Warsaw, October 2019). URL https://seminarchive.wordpress.com/2019/07/01/quantitative-rectifiability-in-heisenberg-groups/.Google Scholar
Fässler, K. and Orponen, T.. Riesz transform and vertical oscillation in the Heisenberg group. Preprint arXiv:1810.13122 (2018).Google Scholar
Jones, P. W.. Rectifiable sets and the traveling salesman problem. Invent. Math. 102(1) (1990), 1–15. doi: 10.1007/BF01233418.CrossRefGoogle Scholar
Käenmäki, A., Rajala, T. and Suomala, V.. Existence of doubling measures via generalised nested cubes. Proc. Amer. Math. Soc., 140(9) (2012), 3275–3281. doi: 10.1090/S0002-9939-2012-11161-X.CrossRefGoogle Scholar
Mattila, P., Melnikov, M. S. and Verdera, J.. The Cauchy integral, analytic capacity, and uniform rectifiability. Ann. Math., 144(1) (1996), 127–136. doi: 10.2307/2118585.CrossRefGoogle Scholar
Nazarov, F., Tolsa, X. and Volberg, A.. On the uniform rectifiability of AD-regular measures with bounded Riesz transform operator: the case of codimension 1. Acta Math. 213(2) (2014), 237–321. doi: 10.1007/s11511-014-0120-7.CrossRefGoogle Scholar
Naor, A. and Young, R.. Vertical perimeter versus horizontal perimeter. Ann. Math., 188(1) (2018), 171–279. doi: 10.4007/annals.2018.188.1.4.CrossRefGoogle Scholar
Orponen, T.. Traveling salesman theorems and the Cauchy transfom. Lecture notes for the course “Geometric measure theory and singular integrals” at the University of Helsinki (Spring 2017). URL https://www.semanticscholar.org/paper/TRAVELING-SALESMAN-THEOREMS-AND-THE-CAUCHY-Orponen/e7af3955f36f7c663da965f140bc65b21257e37e.Google Scholar
Orponen, T.. The local symmetry condition in the Heisenberg group. Preprint arXiv:1807.05010 (2018).Google Scholar
Tolsa, X.. Painlevé’s problem and the semiadditivity of analytic capacity. Acta Math. 190(1) (2003), 105–149. doi: 10.1007/BF02393237.CrossRefGoogle Scholar
Tolsa, X.. Analytic capacity, the Cauchy transform, and non-homogeneous Calderón–Zygmund theory. Progr. Math. vol. 307 (Birkhäuser, 2014). doi: 10.1007/978-3-319-00596-6.CrossRefGoogle Scholar