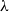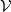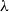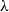1. Introduction
Motivated by probabilistic programming, Mardare et al. (Reference Mardare, Panangaden and Plotkin2016, Reference Mardare, Panangaden and Plotkin2017) introduced quantitative equations and developed universal algebra over metric spaces. In the recent paper Rosický (Reference Rosický2021), we have related their quantitative equational theories to the theories of Bourke and Garner (Reference Bourke and Garner2019). More papers were influenced by Mardare et al. (Reference Mardare, Panangaden and Plotkin2016, Reference Mardare, Panangaden and Plotkin2017), in particular Adámek (Reference Adámek2022) and Milius and Urbat (Reference Milius, Urbat, Boja ńczyk and Simpson2019). In the first one, Adámek showed that
![]() $\omega_1$
-basic quantitative equational theories correspond to
$\omega_1$
-basic quantitative equational theories correspond to
![]() $\aleph_1$
-ary enriched monads on metric spaces preserving surjections. In Milius and Urbat (Reference Milius, Urbat, Boja ńczyk and Simpson2019), Milius and Urbat clarified the Birkhoff-type theorems stated in Mardare et al. (Reference Mardare, Panangaden and Plotkin2017).
$\aleph_1$
-ary enriched monads on metric spaces preserving surjections. In Milius and Urbat (Reference Milius, Urbat, Boja ńczyk and Simpson2019), Milius and Urbat clarified the Birkhoff-type theorems stated in Mardare et al. (Reference Mardare, Panangaden and Plotkin2017).
In this paper, we work in a general symmetric monoidal closed category
![]() $\mathcal {V}$
which is locally
$\mathcal {V}$
which is locally
![]() $\lambda$
-presentable as a closed category. The leading examples are
$\lambda$
-presentable as a closed category. The leading examples are
![]() $\operatorname{\bf Pos}$
(posets) and
$\operatorname{\bf Pos}$
(posets) and
![]() $\operatorname{\bf Met}$
(metric spaces). Under discrete objects of
$\operatorname{\bf Met}$
(metric spaces). Under discrete objects of
![]() $\mathcal {V}$
, we mean copowers of the monoidal unit I. In
$\mathcal {V}$
, we mean copowers of the monoidal unit I. In
![]() $\operatorname{\bf Pos}$
, these are discrete posets and in
$\operatorname{\bf Pos}$
, these are discrete posets and in
![]() $\operatorname{\bf Met}$
discrete spaces (having all distances 0 or
$\operatorname{\bf Met}$
discrete spaces (having all distances 0 or
![]() $\infty$
). We introduce discrete theories whose operations are induced by those with a discrete arity. We show that discrete theories correspond to
$\infty$
). We introduce discrete theories whose operations are induced by those with a discrete arity. We show that discrete theories correspond to
![]() $\lambda$
-ary enriched monads on
$\lambda$
-ary enriched monads on
![]() $\mathcal {V}$
preserving surjections (i.e., morphisms for which is I projective). As a special case, we get the result of Reference AdámekAdámek (Reference Adámek2022). Under mild assumptions, surjections form a left part of a factorization system
$\mathcal {V}$
preserving surjections (i.e., morphisms for which is I projective). As a special case, we get the result of Reference AdámekAdámek (Reference Adámek2022). Under mild assumptions, surjections form a left part of a factorization system
![]() $(\!\operatorname{\it Surj},\operatorname{\it Inj})$
on the underlying category
$(\!\operatorname{\it Surj},\operatorname{\it Inj})$
on the underlying category
![]() $\mathcal {V}_0$
of
$\mathcal {V}_0$
of
![]() $\mathcal {V}$
. We assume that
$\mathcal {V}$
. We assume that
![]() $\mathcal {V}_0$
is
$\mathcal {V}_0$
is
![]() $\operatorname{\it Inj}$
-locally
$\operatorname{\it Inj}$
-locally
![]() $\mu$
-generated for
$\mu$
-generated for
![]() $\mu\leq\lambda$
in the sense of Di Liberti and Rosický (Reference Di Liberti and Rosický2022) and prove Birkhoff’s type theorems for categories of algebras of discrete theories. Metric spaces are locally
$\mu\leq\lambda$
in the sense of Di Liberti and Rosický (Reference Di Liberti and Rosický2022) and prove Birkhoff’s type theorems for categories of algebras of discrete theories. Metric spaces are locally
![]() $\aleph_1$
-presentable and also
$\aleph_1$
-presentable and also
![]() $\operatorname{\it Inj}$
-locally
$\operatorname{\it Inj}$
-locally
![]() $\aleph_0$
-generated and our Birkhoff-type theorems yield those of Mardare et al. (Reference Mardare, Panangaden and Plotkin2017).
$\aleph_0$
-generated and our Birkhoff-type theorems yield those of Mardare et al. (Reference Mardare, Panangaden and Plotkin2017).
The Appendix withdraws some claims of Rosický (Reference Rosický2021, Section 5).
2. Background on Algebraic Theories
Classical universal algebra starts with a signature
![]() $\Sigma$
giving a set of operations equipped with arities which are finite cardinals. A
$\Sigma$
giving a set of operations equipped with arities which are finite cardinals. A
![]() $\Sigma$
-algebra A assigns to every n-ary operation f a mapping
$\Sigma$
-algebra A assigns to every n-ary operation f a mapping
![]() $f_A:A^n\to A$
. Then one defines terms and equations, interprets terms on an algebra and says when an equation is satisfied by an algebra. An equational theory E is a set of equations and an algebra satisfies E if it satisfies all equations from E. The forgetful functor
$f_A:A^n\to A$
. Then one defines terms and equations, interprets terms on an algebra and says when an equation is satisfied by an algebra. An equational theory E is a set of equations and an algebra satisfies E if it satisfies all equations from E. The forgetful functor
![]() $U:\operatorname{\bf Alg}\!(E)\to\operatorname{\bf Set}$
from the category
$U:\operatorname{\bf Alg}\!(E)\to\operatorname{\bf Set}$
from the category
![]() $\operatorname{\bf Alg}\!(E)$
of algebras satisfying E has a left adjoint F and
$\operatorname{\bf Alg}\!(E)$
of algebras satisfying E has a left adjoint F and
![]() $\operatorname{\bf Alg}\!(E)$
is equivalent to the category
$\operatorname{\bf Alg}\!(E)$
is equivalent to the category
![]() $\operatorname{\bf Alg}\!(T)$
of algebras for the monad
$\operatorname{\bf Alg}\!(T)$
of algebras for the monad
![]() $T=UF$
. The algebra Fn consists of equivalence classes of n-ary terms and morphisms
$T=UF$
. The algebra Fn consists of equivalence classes of n-ary terms and morphisms
![]() $Fm\to Fn$
give m-tuples of n-ary terms. We can consider them as (n,m)-ary operations where the input arity n is the usual arity and the output arity m is the multiplicity. Then the superposition of terms is replaced by the composition of these operations. If
$Fm\to Fn$
give m-tuples of n-ary terms. We can consider them as (n,m)-ary operations where the input arity n is the usual arity and the output arity m is the multiplicity. Then the superposition of terms is replaced by the composition of these operations. If
![]() $\mathcal {N}$
is the full subcategory of
$\mathcal {N}$
is the full subcategory of
![]() $\operatorname{\bf Set}$
consisting of finite cardinals and
$\operatorname{\bf Set}$
consisting of finite cardinals and
![]() $\mathcal {T}$
the full subcategory of
$\mathcal {T}$
the full subcategory of
![]() $\operatorname{\bf Alg}\!(E)$
consisting of free algebras on finite cardinals, then the domain-codomain restriction of F gives an identity-on-objects functor
$\operatorname{\bf Alg}\!(E)$
consisting of free algebras on finite cardinals, then the domain-codomain restriction of F gives an identity-on-objects functor
![]() $J:\mathcal {N}\to\mathcal {T}$
. The dual
$J:\mathcal {N}\to\mathcal {T}$
. The dual
![]() $\mathcal {T}^{\operatorname{op}}$
of
$\mathcal {T}^{\operatorname{op}}$
of
![]() $\mathcal {T}$
is a Lawvere theory whose algebras A are functors
$\mathcal {T}$
is a Lawvere theory whose algebras A are functors
![]() $\hat{A}:\mathcal {T}^{\operatorname{op}}\to\operatorname{\bf Set}$
preserving finite products. This is the same as
$\hat{A}:\mathcal {T}^{\operatorname{op}}\to\operatorname{\bf Set}$
preserving finite products. This is the same as
![]() $\hat{A}J^{\operatorname{op}}=\operatorname{\bf Set}(K-, A)$
where
$\hat{A}J^{\operatorname{op}}=\operatorname{\bf Set}(K-, A)$
where
![]() $K:\mathcal {N}\to\operatorname{\bf Set}$
is the inclusion and
$K:\mathcal {N}\to\operatorname{\bf Set}$
is the inclusion and
![]() $A=\hat{A}(1)$
. Then
$A=\hat{A}(1)$
. Then
![]() $\operatorname{\bf Alg}\!(E)$
is equivalent to the category of algebras of
$\operatorname{\bf Alg}\!(E)$
is equivalent to the category of algebras of
![]() $\mathcal {T}^{\operatorname{op}}$
. Hence, classical universal algebra can be equivalently captured by equational theories, finitary monads (= monads preserving filtered colimits), or Lawvere theories. All this is well known due to Birkhoff, Lawvere and Linton (see Adámek et al. (Reference Adámek, Rosický and Vitale2011)).
$\mathcal {T}^{\operatorname{op}}$
. Hence, classical universal algebra can be equivalently captured by equational theories, finitary monads (= monads preserving filtered colimits), or Lawvere theories. All this is well known due to Birkhoff, Lawvere and Linton (see Adámek et al. (Reference Adámek, Rosický and Vitale2011)).
In ordered universal algebra, given a signature
![]() $\Sigma$
, a
$\Sigma$
, a
![]() $\Sigma$
-algebra is a poset A equipped with monotone mappings
$\Sigma$
-algebra is a poset A equipped with monotone mappings
![]() $f_A:A^n\to A$
for every n-ary operation f from
$f_A:A^n\to A$
for every n-ary operation f from
![]() $\Sigma$
. But, instead of equations, one takes inequations
$\Sigma$
. But, instead of equations, one takes inequations
![]() $p\leq q$
of terms (see Bloom (Reference Bloom1976)). An algebra satisfies this inequation if
$p\leq q$
of terms (see Bloom (Reference Bloom1976)). An algebra satisfies this inequation if
![]() $p_A\leq q_A$
in the poset of monotone mappings
$p_A\leq q_A$
in the poset of monotone mappings
![]() $A^n\to A$
. It is natural to take enriched signatures where arities are finite posets. Then the resulting enriched inequational theories correspond to finitary enriched monads on
$A^n\to A$
. It is natural to take enriched signatures where arities are finite posets. Then the resulting enriched inequational theories correspond to finitary enriched monads on
![]() $\operatorname{\bf Pos}$
(Adámek et al., Reference Adámek, Ford, Milius and Schröder2021). Recall that the category
$\operatorname{\bf Pos}$
(Adámek et al., Reference Adámek, Ford, Milius and Schröder2021). Recall that the category
![]() $\operatorname{\bf Pos}$
of posets and monotone mapping is locally finitely presentable as a cartesian closed category. The free algebra FX on a finite poset X consists of equivalence classes of X-ary terms and morphisms
$\operatorname{\bf Pos}$
of posets and monotone mapping is locally finitely presentable as a cartesian closed category. The free algebra FX on a finite poset X consists of equivalence classes of X-ary terms and morphisms
![]() $FY\to FX$
can be taken as (X,Y)-ary operations. The inequation
$FY\to FX$
can be taken as (X,Y)-ary operations. The inequation
![]() $p\leq q$
of X-ary terms, which is called an inequation in the context X, then means that the pair p,q of terms is an (X,2)-ary operation where 2 is a two-element chain. In this way, inequational theories can be replaced by equational theories in (X,Y)-ary operations (see Rosický (Reference Rosický2021, Example 4.11(1))). If
$p\leq q$
of X-ary terms, which is called an inequation in the context X, then means that the pair p,q of terms is an (X,2)-ary operation where 2 is a two-element chain. In this way, inequational theories can be replaced by equational theories in (X,Y)-ary operations (see Rosický (Reference Rosický2021, Example 4.11(1))). If
![]() $\mathcal {F}$
is the full subcategory of
$\mathcal {F}$
is the full subcategory of
![]() $\operatorname{\bf Pos}$
consisting of finite poset and
$\operatorname{\bf Pos}$
consisting of finite poset and
![]() $\mathcal {T}$
the full subcategory of
$\mathcal {T}$
the full subcategory of
![]() $\operatorname{\bf Alg}\!(E)$
consisting of free algebras on finite posets then the domain-codomain restriction of F gives an identity-on-objects enriched functor
$\operatorname{\bf Alg}\!(E)$
consisting of free algebras on finite posets then the domain-codomain restriction of F gives an identity-on-objects enriched functor
![]() $J:\mathcal {F}\to\mathcal {T}$
. The dual
$J:\mathcal {F}\to\mathcal {T}$
. The dual
![]() $\mathcal {T}^{\operatorname{op}}$
of
$\mathcal {T}^{\operatorname{op}}$
of
![]() $\mathcal {T}$
is an enriched Lawvere theory (Power, Reference Power2005). Hence, ordered universal algebra can be equivalently captured by inequational theories, enriched equational theories, finitary monads, or enriched Lawvere theories.
$\mathcal {T}$
is an enriched Lawvere theory (Power, Reference Power2005). Hence, ordered universal algebra can be equivalently captured by inequational theories, enriched equational theories, finitary monads, or enriched Lawvere theories.
In metric universal algebra, one has to take into account that the category
![]() $\operatorname{\bf Met}$
of metric spaces (distances
$\operatorname{\bf Met}$
of metric spaces (distances
![]() $\infty$
are allowed) and nonexpanding maps is only locally
$\infty$
are allowed) and nonexpanding maps is only locally
![]() $\aleph_1$
-presentable as a symmetric monoidal closed category. Thus, one has to take countable metric spaces as arities. Given such an enriched signature
$\aleph_1$
-presentable as a symmetric monoidal closed category. Thus, one has to take countable metric spaces as arities. Given such an enriched signature
![]() $\Sigma$
, a
$\Sigma$
, a
![]() $\Sigma$
-algebra is a metric space A equipped with nonexpanding mappings
$\Sigma$
-algebra is a metric space A equipped with nonexpanding mappings
![]() $f_A:A^X\to A$
for every X-ary operation f from
$f_A:A^X\to A$
for every X-ary operation f from
![]() $\Sigma$
. Now, instead of equations, one takes quantitative equations
$\Sigma$
. Now, instead of equations, one takes quantitative equations
![]() $p=_\varepsilon q$
of terms where
$p=_\varepsilon q$
of terms where
![]() $\varepsilon\geq 0$
is a real number (see Mardare et al. (Reference Mardare, Panangaden and Plotkin2016, Reference Mardare, Panangaden and Plotkin2017)). An algebra satisfies this quantitative equation if
$\varepsilon\geq 0$
is a real number (see Mardare et al. (Reference Mardare, Panangaden and Plotkin2016, Reference Mardare, Panangaden and Plotkin2017)). An algebra satisfies this quantitative equation if
![]() $d(p_A,q_A)\leq\varepsilon$
in the metric space of nonexpanding mappings
$d(p_A,q_A)\leq\varepsilon$
in the metric space of nonexpanding mappings
![]() $A^X\to A$
. These equations are called basic quantitative equations (in context X). This means that the pair p,q of terms is an
$A^X\to A$
. These equations are called basic quantitative equations (in context X). This means that the pair p,q of terms is an
![]() $(X,2_\varepsilon)$
-ary operation where
$(X,2_\varepsilon)$
-ary operation where
![]() $2_\varepsilon$
is a two-element metric space with the distance
$2_\varepsilon$
is a two-element metric space with the distance
![]() $\varepsilon$
between the two points. In this way, basic quantitative theories can be replaced by equational theories in (X,Y)-ary operations (see Rosický (Reference Rosický2021, Example 4.11(2))). If
$\varepsilon$
between the two points. In this way, basic quantitative theories can be replaced by equational theories in (X,Y)-ary operations (see Rosický (Reference Rosický2021, Example 4.11(2))). If
![]() $\mathcal {C}$
is the full subcategory of
$\mathcal {C}$
is the full subcategory of
![]() $\operatorname{\bf Met}$
consisting of countable metric spaces and
$\operatorname{\bf Met}$
consisting of countable metric spaces and
![]() $\mathcal {T}$
the full subcategory of
$\mathcal {T}$
the full subcategory of
![]() $\operatorname{\bf Alg}\!(E)$
consisting of free algebras on countable metric spaces then the domain-codomain restriction of F gives an identity-on-objects enriched functor
$\operatorname{\bf Alg}\!(E)$
consisting of free algebras on countable metric spaces then the domain-codomain restriction of F gives an identity-on-objects enriched functor
![]() $J:\mathcal {F}\to\mathcal {T}$
. The dual
$J:\mathcal {F}\to\mathcal {T}$
. The dual
![]() $\mathcal {T}^{\operatorname{op}}$
of
$\mathcal {T}^{\operatorname{op}}$
of
![]() $\mathcal {T}$
is an enriched
$\mathcal {T}$
is an enriched
![]() $\aleph_1$
-ary enriched Lawvere theory, and these theories correspond to enriched monads preserving
$\aleph_1$
-ary enriched Lawvere theory, and these theories correspond to enriched monads preserving
![]() $\aleph_1$
-filtered colimits (see Power (Reference Power2005)). Hence, metric universal algebra can be equivalently captured by basic quantitative theories, enriched equational theories,
$\aleph_1$
-filtered colimits (see Power (Reference Power2005)). Hence, metric universal algebra can be equivalently captured by basic quantitative theories, enriched equational theories,
![]() $\aleph_1$
-ary monads, or enriched
$\aleph_1$
-ary monads, or enriched
![]() $\aleph_1$
-ary Lawvere theories.
$\aleph_1$
-ary Lawvere theories.
In general, let
![]() $\mathcal {V}$
be a symmetric monoidal closed category with the unit object I and the underlying category
$\mathcal {V}$
be a symmetric monoidal closed category with the unit object I and the underlying category
![]() $\mathcal {V}_0$
. We assume that
$\mathcal {V}_0$
. We assume that
![]() $\mathcal {V}$
is locally
$\mathcal {V}$
is locally
![]() $\lambda$
-presentable as as a symmetric monoidal closed category which means that the underlying category
$\lambda$
-presentable as as a symmetric monoidal closed category which means that the underlying category
![]() $\mathcal {V}_0$
is locally
$\mathcal {V}_0$
is locally
![]() $\lambda$
-presentable, the tensor unit I is
$\lambda$
-presentable, the tensor unit I is
![]() $\lambda$
-presentable and
$\lambda$
-presentable and
![]() $X\otimes Y$
is
$X\otimes Y$
is
![]() $\lambda$
-presentable whenever X and Y are
$\lambda$
-presentable whenever X and Y are
![]() $\lambda$
-presentable. We will denote by
$\lambda$
-presentable. We will denote by
![]() $\mathcal {V}_\lambda$
the (representative) small, full subcategory consisting of
$\mathcal {V}_\lambda$
the (representative) small, full subcategory consisting of
![]() $\lambda$
-presentable objects.
$\lambda$
-presentable objects.
Following Reference Bourke and GarnerBourke and Garner (Reference Bourke and Garner2019), let
![]() $\mathcal {A}$
be a small, full, dense sub-
$\mathcal {A}$
be a small, full, dense sub-
![]() $\mathcal {V}$
-category of
$\mathcal {V}$
-category of
![]() $\mathcal {V}$
with the inclusion
$\mathcal {V}$
with the inclusion
![]() $K:\mathcal {A}\to\mathcal {V}$
. Objects of
$K:\mathcal {A}\to\mathcal {V}$
. Objects of
![]() $\mathcal {A}$
are called arities. Then an
$\mathcal {A}$
are called arities. Then an
![]() $\mathcal {A}$
-pretheory is an identity-on-objects
$\mathcal {A}$
-pretheory is an identity-on-objects
![]() $\mathcal {V}$
-functor
$\mathcal {V}$
-functor
![]() $J:\mathcal {A}\to\mathcal {T}$
. A
$J:\mathcal {A}\to\mathcal {T}$
. A
![]() $\mathcal {T}$
-algebra is an object A of
$\mathcal {T}$
-algebra is an object A of
![]() $\mathcal {V}$
together with a
$\mathcal {V}$
together with a
![]() $\mathcal {V}$
-functor
$\mathcal {V}$
-functor
![]() $\hat{A}:\mathcal {T}^{\operatorname{op}}\to\mathcal {V}$
whose composition with
$\hat{A}:\mathcal {T}^{\operatorname{op}}\to\mathcal {V}$
whose composition with
![]() $J^{\operatorname{op}}$
is
$J^{\operatorname{op}}$
is
![]() $\mathcal {V}(K-,A)$
(in Bourke and Garner (Reference Bourke and Garner2019),
$\mathcal {V}(K-,A)$
(in Bourke and Garner (Reference Bourke and Garner2019),
![]() $\mathcal {T}$
-algebras are called concrete
$\mathcal {T}$
-algebras are called concrete
![]() $\mathcal {T}$
-models). Every
$\mathcal {T}$
-models). Every
![]() $\mathcal {A}$
-pretheory induces a
$\mathcal {A}$
-pretheory induces a
![]() $\mathcal {V}$
-monad
$\mathcal {V}$
-monad
![]() $T:\mathcal {V}\to\mathcal {V}$
given by its
$T:\mathcal {V}\to\mathcal {V}$
given by its
![]() $\mathcal {V}$
-category
$\mathcal {V}$
-category
![]() $\operatorname{\bf Alg}\!(\mathcal {T})$
of algebras. Conversely, a
$\operatorname{\bf Alg}\!(\mathcal {T})$
of algebras. Conversely, a
![]() $\mathcal {V}$
-monad T induces an
$\mathcal {V}$
-monad T induces an
![]() $\mathcal {A}$
-pretheory
$\mathcal {A}$
-pretheory
![]() $J:\mathcal {A}\to\mathcal {T}$
where
$J:\mathcal {A}\to\mathcal {T}$
where
![]() $\mathcal {T}$
is the full subcategory of
$\mathcal {T}$
is the full subcategory of
![]() $\operatorname{\bf Alg}\!(T)$
consisting of free algebras on objects from
$\operatorname{\bf Alg}\!(T)$
consisting of free algebras on objects from
![]() $\mathcal {A}$
and J is the domain-codomain restriction of the free algebra functor. An
$\mathcal {A}$
and J is the domain-codomain restriction of the free algebra functor. An
![]() $\mathcal {A}$
-pretheory is an
$\mathcal {A}$
-pretheory is an
![]() $\mathcal {A}$
-theory if it is given by its monad. Then
$\mathcal {A}$
-theory if it is given by its monad. Then
![]() $\hat{A}$
is the hom-functor
$\hat{A}$
is the hom-functor
![]() $\operatorname{\bf Alg}\!(\mathcal {T})(-,A)$
restricted on free algebras over
$\operatorname{\bf Alg}\!(\mathcal {T})(-,A)$
restricted on free algebras over
![]() $\mathcal {A}$
. Conversely, a monad T is
$\mathcal {A}$
. Conversely, a monad T is
![]() $\mathcal {A}$
-nervous if it is given by its
$\mathcal {A}$
-nervous if it is given by its
![]() $\mathcal {A}$
-theory. In this way, we get a one-to-one correspondence between
$\mathcal {A}$
-theory. In this way, we get a one-to-one correspondence between
![]() $\mathcal {A}$
-theories and
$\mathcal {A}$
-theories and
![]() $\mathcal {A}$
-nervous monads (see Bourke and Garner (Reference Bourke and Garner2019, Corollary 21)).
$\mathcal {A}$
-nervous monads (see Bourke and Garner (Reference Bourke and Garner2019, Corollary 21)).
Under a
![]() $\lambda$
-ary
$\lambda$
-ary
![]() $\mathcal {V}$
-theory we will mean a
$\mathcal {V}$
-theory we will mean a
![]() $\mathcal {V}_\lambda$
-theory. Following Reference Bourke and GarnerBourke and Garner (Reference Bourke and Garner2019),
$\mathcal {V}_\lambda$
-theory. Following Reference Bourke and GarnerBourke and Garner (Reference Bourke and Garner2019),
![]() $\lambda$
-ary
$\lambda$
-ary
![]() $\mathcal {V}$
-theories correspond to
$\mathcal {V}$
-theories correspond to
![]() $\mathcal {V}$
-monads on
$\mathcal {V}$
-monads on
![]() $\mathcal {V}$
preserving
$\mathcal {V}$
preserving
![]() $\lambda$
-filtered colimits. They are called
$\lambda$
-filtered colimits. They are called
![]() $\lambda$
-ary
$\lambda$
-ary
![]() $\mathcal {V}$
-monads. Hence,
$\mathcal {V}$
-monads. Hence,
![]() $\lambda$
-ary monads are precisely
$\lambda$
-ary monads are precisely
![]() $\mathcal {V}_\lambda$
-nervous monads.
$\mathcal {V}_\lambda$
-nervous monads.
3. Surjections
The underlying functor
![]() $\mathcal {V}_0(I,-):\mathcal {V}_0\to\operatorname{\bf Set}$
has a left adjoint
$\mathcal {V}_0(I,-):\mathcal {V}_0\to\operatorname{\bf Set}$
has a left adjoint
![]() $-\cdot I$
sending a set X to the coproduct
$-\cdot I$
sending a set X to the coproduct
![]() $X\cdot I$
of X copies of I in
$X\cdot I$
of X copies of I in
![]() $\mathcal {V}_0$
. Objects
$\mathcal {V}_0$
. Objects
![]() $X\cdot I$
will be called discrete. Every object V of
$X\cdot I$
will be called discrete. Every object V of
![]() $\mathcal {V}$
determines a discrete object
$\mathcal {V}$
determines a discrete object
![]() $V_0=\mathcal {V}_0(I,V)\cdot I$
and morphism
$V_0=\mathcal {V}_0(I,V)\cdot I$
and morphism
![]() $\delta_V:V_0\to V$
given by the counit of the adjunction. Every morphism
$\delta_V:V_0\to V$
given by the counit of the adjunction. Every morphism
![]() $f:V\to W$
determines the morphism
$f:V\to W$
determines the morphism
![]() $f_0=\mathcal {V}_0(I,f)\cdot I$
between the underlying discrete objects.
$f_0=\mathcal {V}_0(I,f)\cdot I$
between the underlying discrete objects.
A morphism
![]() $f:A\to B$
will be called a surjection if
$f:A\to B$
will be called a surjection if
![]() $\mathcal {V}_0(I,f)$
is surjective. Let
$\mathcal {V}_0(I,f)$
is surjective. Let
![]() $\operatorname{\it Surj}$
denote the class of all surjections in
$\operatorname{\it Surj}$
denote the class of all surjections in
![]() $\mathcal {V}_0$
and let
$\mathcal {V}_0$
and let
![]() $\operatorname{\it Inj}$
be the class of morphisms of
$\operatorname{\it Inj}$
be the class of morphisms of
![]() $\mathcal {V}_0$
having the unique right lifting property with respect to every surjection. Morphisms from
$\mathcal {V}_0$
having the unique right lifting property with respect to every surjection. Morphisms from
![]() $\operatorname{\it Inj}$
will be called injections. Recall that g is an injection iff for every surjection f and every commutative square
$\operatorname{\it Inj}$
will be called injections. Recall that g is an injection iff for every surjection f and every commutative square

there is a unique
![]() $t:B\to C$
such that
$t:B\to C$
such that
![]() $tf=u$
and
$tf=u$
and
![]() $gt=v$
.
$gt=v$
.
Lemma 3.1.
![]() $\operatorname{\it Surj}$
is accessible and closed under
$\operatorname{\it Surj}$
is accessible and closed under
![]() $\lambda$
-directed colimits in
$\lambda$
-directed colimits in
![]() $\mathcal {V}_0^\to$
.
$\mathcal {V}_0^\to$
.
Proof.
f is a surjection iff it has the right lifting property with respect to
![]() $0\to I$
. Like in Rosický (Reference Rosický2009, Proposition 3.3), the result follows from Adámek and Rosický (Reference Adámek and Rosický1994, Proposition 4.7).
$0\to I$
. Like in Rosický (Reference Rosický2009, Proposition 3.3), the result follows from Adámek and Rosický (Reference Adámek and Rosický1994, Proposition 4.7).
Remark 3.2. (1) Surjections are right-cancellable, i.e., if gf is a surjection then g is a surjection.
(2) Surjections are closed under products and stable under pullbacks (because they are given by the right lifting property with respect to
![]() $0\to I$
).
$0\to I$
).
Lemma 3.3.
![]() $(\operatorname{\it Surj},\operatorname{\it Inj})$
is a factorization system in
$(\operatorname{\it Surj},\operatorname{\it Inj})$
is a factorization system in
![]() $\mathcal {V}_0$
if and only if
$\mathcal {V}_0$
if and only if
![]() $\operatorname{\it Surj}$
is closed under colimits in
$\operatorname{\it Surj}$
is closed under colimits in
![]() $\mathcal {V}_0^\to$
.
$\mathcal {V}_0^\to$
.
Proof. Necessity is evident. Conversely, following 3.1,
![]() $\operatorname{\it Surj}$
has a small dense subcategory
$\operatorname{\it Surj}$
has a small dense subcategory
![]() $\mathcal {S}$
. If
$\mathcal {S}$
. If
![]() $\operatorname{\it Surj}$
is closed under colimits in
$\operatorname{\it Surj}$
is closed under colimits in
![]() $\mathcal {V}_0^\to$
, then
$\mathcal {V}_0^\to$
, then
![]() $\operatorname{\it Surj}$
is the closure under
$\operatorname{\it Surj}$
is the closure under
![]() $\mathcal {S}$
under colimits in
$\mathcal {S}$
under colimits in
![]() $\mathcal {V}_0^\to$
. Following Fajstrup and Rosický (Reference Fajstrup and Rosický2008, Theorem 2.2),
$\mathcal {V}_0^\to$
. Following Fajstrup and Rosický (Reference Fajstrup and Rosický2008, Theorem 2.2),
![]() $(\operatorname{\it Surj},\operatorname{\it Inj})$
is a factorization system.
$(\operatorname{\it Surj},\operatorname{\it Inj})$
is a factorization system.
Lemma 3.4. Injections are monomorphisms.
Proof. Take an injection
![]() $g:C\to D$
and
$g:C\to D$
and
![]() $u,v:B\to C$
such that
$u,v:B\to C$
such that
![]() $gu=gv$
. Consider a commutative square
$gu=gv$
. Consider a commutative square
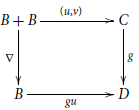
where
![]() $\nabla$
is the codiagonal. Since
$\nabla$
is the codiagonal. Since
![]() $\nabla$
is a split epimorphism, it is a surjection and thus there is a unique diagonal
$\nabla$
is a split epimorphism, it is a surjection and thus there is a unique diagonal
![]() $B\to C$
. Hence,
$B\to C$
. Hence,
![]() $u=v$
. We have proved that g is a monomorphism.
$u=v$
. We have proved that g is a monomorphism.
Lemma 3.5. Assume that
![]() $(\operatorname{\it Surj},\operatorname{\it Inj})$
is a factorization system. Then
$(\operatorname{\it Surj},\operatorname{\it Inj})$
is a factorization system. Then
(1)
 $\operatorname{\it Surj}$
contains all strong epimorphisms, and
$\operatorname{\it Surj}$
contains all strong epimorphisms, and(2) if I is a generator in
 $\mathcal {V}_0$
then
$\mathcal {V}_0$
then
 $\operatorname{\it Inj}$
contains all strong monomorphisms.
$\operatorname{\it Inj}$
contains all strong monomorphisms.
Proof. In every locally presentable category, (strong epi, mono) and (epi, strong mono) are factorization systems (see Adámek and Rosický (Reference Adámek and Rosický1994, Proposition 1.61)). Thus, (1) follows from 3.4. For (2), it suffices to show that every surjection is an epimorphism, which follows from I being a generator.
Recall that I is connected iff
![]() $\mathcal {V}_0(I,-)$
preserves coproducts.
$\mathcal {V}_0(I,-)$
preserves coproducts.
Lemma 3.6. If I is connected and every regular epimorphism is a surjection, then
![]() $(\operatorname{\it Surj},\operatorname{\it Inj})$
is a factorization system.
$(\operatorname{\it Surj},\operatorname{\it Inj})$
is a factorization system.
Proof. If I is connected, then
![]() $\operatorname{\it Surj}$
is closed under coproducts in
$\operatorname{\it Surj}$
is closed under coproducts in
![]() $\mathcal {V}_0^\to$
. If regular epimorphisms are surjections, then surjections are closed under coequalizers in
$\mathcal {V}_0^\to$
. If regular epimorphisms are surjections, then surjections are closed under coequalizers in
![]() $\mathcal {V}_0^\to$
. Indeed, let
$\mathcal {V}_0^\to$
. Indeed, let
![]() $f_0$
and
$f_0$
and
![]() $f_1$
be surjections and
$f_1$
be surjections and
be a coequalizer in
![]() $\mathcal {V}_0^\to$
. Then
$\mathcal {V}_0^\to$
. Then
is a coequalizer in
![]() $\mathcal {V}_0$
, hence v is a surjection. Following 3.2(1), f is a surjection.
$\mathcal {V}_0$
, hence v is a surjection. Following 3.2(1), f is a surjection.
The factorization system
![]() $(\operatorname{\it Surj},\operatorname{\it Inj})$
is
$(\operatorname{\it Surj},\operatorname{\it Inj})$
is
![]() $\lambda$
-convenient in the sense of Reference Di Liberti and RosickýDi Liberti and Rosický (Reference Di Liberti and Rosický2022) if
$\lambda$
-convenient in the sense of Reference Di Liberti and RosickýDi Liberti and Rosický (Reference Di Liberti and Rosický2022) if
(1)
 $\mathcal {V}$
is
$\mathcal {V}$
is
 $\operatorname{\it Surj}$
-cowellpowered, i.e., every object of
$\operatorname{\it Surj}$
-cowellpowered, i.e., every object of
 $\mathcal {V}$
has only a set of surjective quotients, and
$\mathcal {V}$
has only a set of surjective quotients, and(2)
 $\operatorname{\it Inj}$
is closed under
$\operatorname{\it Inj}$
is closed under
 $\lambda$
-directed colimits, i.e., every
$\lambda$
-directed colimits, i.e., every
 $\lambda$
-directed colimit of injections has the property that a colimit cocone
$\lambda$
-directed colimit of injections has the property that a colimit cocone(a) consists of injections, and
(b) for every cocone of injections, the factorizing morphism is an injection.
If I is a generator, then surjections are epimorphisms and (1) follows from the fact that every locally presentable category is co-wellpowered (see Adámek and Rosický (Reference Adámek and Rosický1994, Theorem 1.58)).
Examples 3.7.
(1) Let
 $\operatorname{\bf Pos}$
be the category of posets and monotone mappings.
$\operatorname{\bf Pos}$
be the category of posets and monotone mappings.
 $\operatorname{\bf Pos}$
is cartesian closed and I is the one-element poset 1. Surjections are surjective monotone mappings, i.e, epimorphisms. Injections are embeddings and
$\operatorname{\bf Pos}$
is cartesian closed and I is the one-element poset 1. Surjections are surjective monotone mappings, i.e, epimorphisms. Injections are embeddings and
 $(\operatorname{\it Surj},\operatorname{\it Inj})$
is an
$(\operatorname{\it Surj},\operatorname{\it Inj})$
is an
 $\omega$
-convenient factorization system.
$\omega$
-convenient factorization system.(2) Let
 $\operatorname{\bf Met}$
be the category of (generalized) metric spaces (i.e., with distances
$\operatorname{\bf Met}$
be the category of (generalized) metric spaces (i.e., with distances
 $\infty$
allowed) and nonexpanding maps.
$\infty$
allowed) and nonexpanding maps.
 $\operatorname{\bf Met}$
is a symmetric monoidal closed category where I is the one-element metric space 1 and
$\operatorname{\bf Met}$
is a symmetric monoidal closed category where I is the one-element metric space 1 and
 $A\otimes B$
has the underlying set
$A\otimes B$
has the underlying set
 $A\times B$
and the metric Surjections are surjective nonexpanding mappings, injections are isometries and
$A\times B$
and the metric Surjections are surjective nonexpanding mappings, injections are isometries and $$d((a,b),(a',b'))=d(a,a')+d(b,b').$$
is a factorization system (cf. Adámek and Rosický (Reference Adámek and Rosický2022, Example 3.16(1))). This factorization system is
$$d((a,b),(a',b'))=d(a,a')+d(b,b').$$
is a factorization system (cf. Adámek and Rosický (Reference Adámek and Rosický2022, Example 3.16(1))). This factorization system is $$(\!\operatorname{\it Surj},\operatorname{\it Inj})$$
$$(\!\operatorname{\it Surj},\operatorname{\it Inj})$$
 $\omega$
-convenient (see Adámek and Rosický (Reference Adámek and Rosický2022, Remark 2.5(2))).
$\omega$
-convenient (see Adámek and Rosický (Reference Adámek and Rosický2022, Remark 2.5(2))).
(3) Let
 $\operatorname{\bf Gra}$
be the cartesian closed category of graphs (i.e., sets with a symmetric binary relation) and graph homomorphisms. Then I is the one-element graph with a loop. Let V be a point (the one-element graph without a loop) and E an edge (the two-element graph without loops and with one edge). Then I is the coequalizer of two morphisms
$\operatorname{\bf Gra}$
be the cartesian closed category of graphs (i.e., sets with a symmetric binary relation) and graph homomorphisms. Then I is the one-element graph with a loop. Let V be a point (the one-element graph without a loop) and E an edge (the two-element graph without loops and with one edge). Then I is the coequalizer of two morphisms
 $V\to E$
. Since
$V\to E$
. Since
 $f:E\to I$
is not surjective, 3.5(1) implies that
$f:E\to I$
is not surjective, 3.5(1) implies that
 $(\operatorname{\it Surj},\operatorname{\it Inj})$
is not a factorization system on
$(\operatorname{\it Surj},\operatorname{\it Inj})$
is not a factorization system on
 $\mathcal {V}$
.
$\mathcal {V}$
.
4 Discrete Theories
Assumption 4.1 Throughout the rest of the paper, we assume that
![]() $\mathcal {V}$
is locally
$\mathcal {V}$
is locally
![]() $\lambda$
-presentable as a symmetric monoidal closed category and that the functor
$\lambda$
-presentable as a symmetric monoidal closed category and that the functor
![]() $\mathcal {V}_0(I,-):\mathcal {V}_0\to\operatorname{\bf Set}$
preserves
$\mathcal {V}_0(I,-):\mathcal {V}_0\to\operatorname{\bf Set}$
preserves
![]() $\lambda$
-presentable objects.
$\lambda$
-presentable objects.
Then the object
![]() $X_0$
of
$X_0$
of
![]() $\mathcal {V}$
is
$\mathcal {V}$
is
![]() $\lambda$
-presentable whenever X is
$\lambda$
-presentable whenever X is
![]() $\lambda$
-presentable.
$\lambda$
-presentable.
Definition 4.2 We say that a
![]() $\lambda$
-ary
$\lambda$
-ary
![]() $\mathcal {V}$
-theory
$\mathcal {V}$
-theory
![]() $\mathcal {T}$
is discrete if every morphism
$\mathcal {T}$
is discrete if every morphism
![]() $JI\to JX$
of
$JI\to JX$
of
![]() $\mathcal {T}$
is a composition
$\mathcal {T}$
is a composition
![]() $J(\delta_X)f$
for some morphism
$J(\delta_X)f$
for some morphism
![]() $f:JI\to JX_0$
.
$f:JI\to JX_0$
.
This means that operations of arity X are induced by those of arity
![]() $X_0$
.
$X_0$
.
Examples 4.3 (1)
![]() $\operatorname{\bf Pos}$
is locally finitely presentable as a cartesian closed category. Finitely presentable posets are finite posets; hence,
$\operatorname{\bf Pos}$
is locally finitely presentable as a cartesian closed category. Finitely presentable posets are finite posets; hence,
![]() $\operatorname{\bf Pos}(I,-):\operatorname{\bf Pos}\to\operatorname{\bf Set}$
preserves finitely presentable objects. Let
$\operatorname{\bf Pos}(I,-):\operatorname{\bf Pos}\to\operatorname{\bf Set}$
preserves finitely presentable objects. Let
![]() $\mathcal {T}$
be a discrete finitary theory. Let
$\mathcal {T}$
be a discrete finitary theory. Let
![]() $\Sigma$
be the finitary signature whose n-ary operation symbols are
$\Sigma$
be the finitary signature whose n-ary operation symbols are
![]() $\mathcal {T}$
-morphisms
$\mathcal {T}$
-morphisms
![]() $J1\to Jn$
where n denotes the discrete poset with n elements. Morphisms
$J1\to Jn$
where n denotes the discrete poset with n elements. Morphisms
![]() $J1\to JX$
are X-ary terms and, since
$J1\to JX$
are X-ary terms and, since
![]() $\mathcal {T}$
is discrete, they are the restrictions of usual
$\mathcal {T}$
is discrete, they are the restrictions of usual
![]() $X_0$
-ary operation symbols on X (in the sense of 4.2). Pairs
$X_0$
-ary operation symbols on X (in the sense of 4.2). Pairs
![]() $f\leq g$
, where
$f\leq g$
, where
![]() $f,g:J1\to JX$
yield inequations in context X in the sense of Adámek et al. (Reference Adámek, Ford, Milius and Schröder2021). Hence,
$f,g:J1\to JX$
yield inequations in context X in the sense of Adámek et al. (Reference Adámek, Ford, Milius and Schröder2021). Hence,
![]() $\mathcal {T}$
yields a set of inequations in context. The meaning of
$\mathcal {T}$
yields a set of inequations in context. The meaning of
![]() $f\leq g$
on a
$f\leq g$
on a
![]() $\mathcal {T}$
-algebra A is that
$\mathcal {T}$
-algebra A is that
![]() $f_A(a_1,\dots,a_n)\leq g_A(a_1,\dots,a_n)$
provided that
$f_A(a_1,\dots,a_n)\leq g_A(a_1,\dots,a_n)$
provided that
![]() $a:n\to A$
factorizes through
$a:n\to A$
factorizes through
![]() $X\to A$
; here,
$X\to A$
; here,
![]() $n=X_0$
. Hence,
$n=X_0$
. Hence,
![]() $\mathcal {T}$
-algebras coincide with algebras in the sense of Reference Adámek, Ford, Milius and SchröderAdámek et al. (Reference Adámek, Ford, Milius and Schröder2021). An example of a discrete finitary theory is the theory of ordered monoids which are commutative for comparable elements, i.e.,
$\mathcal {T}$
-algebras coincide with algebras in the sense of Reference Adámek, Ford, Milius and SchröderAdámek et al. (Reference Adámek, Ford, Milius and Schröder2021). An example of a discrete finitary theory is the theory of ordered monoids which are commutative for comparable elements, i.e.,
![]() $x\cdot y=y\cdot x$
for
$x\cdot y=y\cdot x$
for
![]() $x\leq y$
.
$x\leq y$
.
Conversely, given a finitary signature
![]() $\Sigma$
(with discrete arities), the free
$\Sigma$
(with discrete arities), the free
![]() $\Sigma$
-algebra FX on a poset X consists of
$\Sigma$
-algebra FX on a poset X consists of
![]() $X_0$
-ary terms where
$X_0$
-ary terms where
![]() $t\leq t'$
if
$t\leq t'$
if
![]() $t(x_1,\dots,x_n)$
and
$t(x_1,\dots,x_n)$
and
![]() $t'(x'_1,\dots,x'_n)$
have the same shape (i.e., we can get t’ from t by changing variables
$t'(x'_1,\dots,x'_n)$
have the same shape (i.e., we can get t’ from t by changing variables
![]() $x_1,\dots,x_n$
to
$x_1,\dots,x_n$
to
![]() $x'_1,\dots,x'_n$
) and
$x'_1,\dots,x'_n$
) and
![]() $x_i\leq x'_i$
in X for
$x_i\leq x'_i$
in X for
![]() $i=1,\dots,n$
. Let E be a set of inequations in context. Following Adámek et al. (Reference Adámek, Ford, Milius and Schröder2021, 3.22), free E-algebra JX on a poset X is a quotient
$i=1,\dots,n$
. Let E be a set of inequations in context. Following Adámek et al. (Reference Adámek, Ford, Milius and Schröder2021, 3.22), free E-algebra JX on a poset X is a quotient
![]() $q_X:FX\to JX$
of FX. If X is finite, every morphisms
$q_X:FX\to JX$
of FX. If X is finite, every morphisms
![]() $t:J1\to JX$
factorizes through
$t:J1\to JX$
factorizes through
![]() $q_X$
as
$q_X$
as
![]() $t=q_X\bar{t}$
. Hence,
$t=q_X\bar{t}$
. Hence,
![]() $\bar{t}$
is an
$\bar{t}$
is an
![]() $X_0$
-ary term and
$X_0$
-ary term and
![]() $q_{X_0}(\bar{t})$
yields a factorization of t through
$q_{X_0}(\bar{t})$
yields a factorization of t through
![]() $J(\delta_X)$
. Thus, J is a discrete
$J(\delta_X)$
. Thus, J is a discrete
![]() $\mathcal {V}$
-theory.
$\mathcal {V}$
-theory.
(2)
![]() $\operatorname{\bf Met}$
is locally
$\operatorname{\bf Met}$
is locally
![]() $\aleph_1$
-presentable as a symmetric monoidal closed category. Since
$\aleph_1$
-presentable as a symmetric monoidal closed category. Since
![]() $\aleph_1$
-presentable objects are the metric spaces having cardinality
$\aleph_1$
-presentable objects are the metric spaces having cardinality
![]() $<\aleph_1$
,
$<\aleph_1$
,
![]() $\operatorname{\bf Met}(I,-)$
preserves
$\operatorname{\bf Met}(I,-)$
preserves
![]() $\aleph_1$
-presentable objects. Let
$\aleph_1$
-presentable objects. Let
![]() $\mathcal {T}$
be a discrete
$\mathcal {T}$
be a discrete
![]() $\aleph_1$
-ary theory. Like in (1), let
$\aleph_1$
-ary theory. Like in (1), let
![]() $\Sigma$
be the signature whose n-ary operation symbols are
$\Sigma$
be the signature whose n-ary operation symbols are
![]() $\mathcal {T}$
-morphisms
$\mathcal {T}$
-morphisms
![]() $J1\to Jn$
where n denotes the discrete metric space with n elements where
$J1\to Jn$
where n denotes the discrete metric space with n elements where
![]() $n\leq\omega$
. Morphisms
$n\leq\omega$
. Morphisms
![]() $J1\to JX$
are X-ary terms and, since
$J1\to JX$
are X-ary terms and, since
![]() $\mathcal {T}$
is discrete, they are the restrictions of usual
$\mathcal {T}$
is discrete, they are the restrictions of usual
![]() $X_0$
-ary operation symbols on X. Pairs
$X_0$
-ary operation symbols on X. Pairs
![]() $f,g:J1\to JX$
where
$f,g:J1\to JX$
where
![]() $f,g:J1\to JX$
and
$f,g:J1\to JX$
and
![]() $d(f,g)\leq\varepsilon$
yield
$d(f,g)\leq\varepsilon$
yield
![]() $\omega_1$
-basic quantitative equations (Mardare et al., Reference Mardare, Panangaden and Plotkin2017). Hence,
$\omega_1$
-basic quantitative equations (Mardare et al., Reference Mardare, Panangaden and Plotkin2017). Hence,
![]() $\mathcal {T}$
yields an
$\mathcal {T}$
yields an
![]() $\omega_1$
-basic quantitative equational theory of Mardare et al. (Reference Mardare, Panangaden and Plotkin2017) (= a set of
$\omega_1$
-basic quantitative equational theory of Mardare et al. (Reference Mardare, Panangaden and Plotkin2017) (= a set of
![]() $\omega_1$
-basic quantitative equations). The meaning
$\omega_1$
-basic quantitative equations). The meaning
![]() $d(f,g)\leq\varepsilon$
on a
$d(f,g)\leq\varepsilon$
on a
![]() $\mathcal {T}$
-algebra A is that
$\mathcal {T}$
-algebra A is that
![]() $d(f_A(a_1,\dots,a_n),g_A(a_1,\dots,a_n))\leq\varepsilon$
provided that
$d(f_A(a_1,\dots,a_n),g_A(a_1,\dots,a_n))\leq\varepsilon$
provided that
![]() $a:n\to A$
factorizes through
$a:n\to A$
factorizes through
![]() $X\to A$
; here
$X\to A$
; here
![]() $n=X_0$
. Hence,
$n=X_0$
. Hence,
![]() $\mathcal {T}$
-algebras coincide with algebras in the sense of Mardare et al. (Reference Mardare, Panangaden and Plotkin2017).
$\mathcal {T}$
-algebras coincide with algebras in the sense of Mardare et al. (Reference Mardare, Panangaden and Plotkin2017).
Conversely, every
![]() $\omega_1$
-basic quantitative equational theory E (in a signature
$\omega_1$
-basic quantitative equational theory E (in a signature
![]() $\Sigma$
with discrete arities) yields a discrete
$\Sigma$
with discrete arities) yields a discrete
![]() $\aleph_1$
-ary enriched theory
$\aleph_1$
-ary enriched theory
![]() $\mathcal {T}$
. Analogously to (1), the free
$\mathcal {T}$
. Analogously to (1), the free
![]() $\Sigma$
-algebra on a countable metric space X consists
$\Sigma$
-algebra on a countable metric space X consists
![]() $X_0$
-ary terms and
$X_0$
-ary terms and
![]() $d(t,t')\leq\varepsilon$
if
$d(t,t')\leq\varepsilon$
if
![]() $t(x_1,\dots,x_n)$
and
$t(x_1,\dots,x_n)$
and
![]() $t'(x'_1,\dots,x'_n)$
have the same shape and
$t'(x'_1,\dots,x'_n)$
have the same shape and
![]() $d(x_i,x'_i)\leq\varepsilon$
in X for
$d(x_i,x'_i)\leq\varepsilon$
in X for
![]() $i=1,\dots,n$
(seeMardare et al. (Reference Mardare, Panangaden and Plotkin2016)). This means that
$i=1,\dots,n$
(seeMardare et al. (Reference Mardare, Panangaden and Plotkin2016)). This means that
![]() $d(t,t')=\infty$
if t and t’ do not have the same shape. Following Mardare et al. (Reference Mardare, Panangaden and Plotkin2016, 6.1), free E-algebra JX on a poset X is a quotient
$d(t,t')=\infty$
if t and t’ do not have the same shape. Following Mardare et al. (Reference Mardare, Panangaden and Plotkin2016, 6.1), free E-algebra JX on a poset X is a quotient
![]() $q_X:FX\to JX$
of FX. The rest is the same as in (1).
$q_X:FX\to JX$
of FX. The rest is the same as in (1).
Lemma 4.4. Let
![]() $\mathcal {T}$
be a
$\mathcal {T}$
be a
![]() $\lambda$
-ary
$\lambda$
-ary
![]() $\mathcal {V}$
-theory. The following conditions are equivalent:
$\mathcal {V}$
-theory. The following conditions are equivalent:
(1)
 $\mathcal {T}$
is discrete,
$\mathcal {T}$
is discrete,
(2) every morphism
 $JY\to JX$
of
$JY\to JX$
of
 $\mathcal {T}$
with Y discrete is a composition
$\mathcal {T}$
with Y discrete is a composition
 $J(\delta_X)f$
with
$J(\delta_X)f$
with
 $f:JY\to JX_0$
and
$f:JY\to JX_0$
and
(3) for every morphism
 $g:JY\to JX$
of
$g:JY\to JX$
of
 $\mathcal {T}$
, there is a morphism
$\mathcal {T}$
, there is a morphism
 $f:JY_0\to JX_0$
such that
$f:JY_0\to JX_0$
such that
 $gJ(\delta_Y)=J(\delta_X)f$
.
$gJ(\delta_Y)=J(\delta_X)f$
.
Proof. Clearly (3)
![]() $\to$
(2)
$\to$
(2)
![]() $\to$
(1).
$\to$
(1).
(1)
 $\to$
(2). Every discrete object is a coproduct of copies of I. Since
$\to$
(2). Every discrete object is a coproduct of copies of I. Since
 $\mathcal {T}$
is an
$\mathcal {T}$
is an
 $\mathcal {V}_\lambda$
-theory, J is given by free
$\mathcal {V}_\lambda$
-theory, J is given by free
 $\mathcal {T}$
-algebras and thus it preserves coproducts. Hence, (1) implies (2).
$\mathcal {T}$
-algebras and thus it preserves coproducts. Hence, (1) implies (2).(2)
 $\to$
(3). It suffices to apply (2) on the composition
$\to$
(3). It suffices to apply (2) on the composition
 $gJ(\delta_Y)$
.
$gJ(\delta_Y)$
.
Theorem 4.5. A
![]() $\lambda$
-ary
$\lambda$
-ary
![]() $\mathcal {V}$
-theory
$\mathcal {V}$
-theory
![]() $\mathcal {T}$
is discrete if and only if its induced monad preserves surjections.
$\mathcal {T}$
is discrete if and only if its induced monad preserves surjections.
Proof. I. Let
![]() $\mathcal {T}$
be discrete,
$\mathcal {T}$
be discrete,
![]() $U:\operatorname{\bf Alg}\!(\mathcal {T})\to\mathcal {V}$
be the forgetful
$U:\operatorname{\bf Alg}\!(\mathcal {T})\to\mathcal {V}$
be the forgetful
![]() $\mathcal {V}$
-functor and F its left
$\mathcal {V}$
-functor and F its left
![]() $\mathcal {V}$
-adjoint. Then the induced
$\mathcal {V}$
-adjoint. Then the induced
![]() $\mathcal {V}$
-monad is
$\mathcal {V}$
-monad is
![]() $T=UF$
. Consider a
$T=UF$
. Consider a
![]() $\lambda$
-presentable object X,
$\lambda$
-presentable object X,
![]() $\delta_X:X_0\to X$
and
$\delta_X:X_0\to X$
and
![]() $a:I\to UFX$
. Since
$a:I\to UFX$
. Since
![]() $\mathcal {T}$
is discrete, the adjoint transpose
$\mathcal {T}$
is discrete, the adjoint transpose
![]() $\tilde{a}:FI\to FX$
factorizes through
$\tilde{a}:FI\to FX$
factorizes through
![]() $F\delta_X$
, i.e.,
$F\delta_X$
, i.e.,
![]() $\tilde{a}=F(\delta_X)b$
where
$\tilde{a}=F(\delta_X)b$
where
![]() $b:FI\to FX_0$
. Hence,
$b:FI\to FX_0$
. Hence,
![]() $a=UF(\delta_X)\tilde{b}$
. We have proved that
$a=UF(\delta_X)\tilde{b}$
. We have proved that
![]() $UF(\delta_X)$
is surjective.
$UF(\delta_X)$
is surjective.
Consider an arbitrary X in
![]() $\mathcal {V}$
and express it as a
$\mathcal {V}$
and express it as a
![]() $\lambda$
-directed colimit of
$\lambda$
-directed colimit of
![]() $\lambda$
-presentable objects
$\lambda$
-presentable objects
![]() $X_m$
(
$X_m$
(
![]() $m\in M$
). Since I is
$m\in M$
). Since I is
![]() $\lambda$
-presentable,
$\lambda$
-presentable,
![]() $X_0=\operatorname{colim} X_{m0}$
and
$X_0=\operatorname{colim} X_{m0}$
and
![]() $\delta_X=\operatorname{colim}\delta_{X_m}$
. Hence,
$\delta_X=\operatorname{colim}\delta_{X_m}$
. Hence,
![]() $UF(\delta_X)=\operatorname{colim} UF(\delta_{X_m})$
and, since surjections are closed under
$UF(\delta_X)=\operatorname{colim} UF(\delta_{X_m})$
and, since surjections are closed under
![]() $\lambda$
-directed colimits (see 3.1),
$\lambda$
-directed colimits (see 3.1),
![]() $UF(\delta_X)$
is a surjection.
$UF(\delta_X)$
is a surjection.
Consider a surjective morphism
![]() $f:Y\to X$
in
$f:Y\to X$
in
![]() $\mathcal {V}$
and
$\mathcal {V}$
and
![]() $f_0:Y_0\to X_0$
be its underlying morphism. Then
$f_0:Y_0\to X_0$
be its underlying morphism. Then
![]() $f\delta_Y=\delta_Xf_0$
and thus
$f\delta_Y=\delta_Xf_0$
and thus
![]() $UF(f)UF(\delta_Y)=UF(\delta_X)UF(f_0)$
. Since epimorphisms in
$UF(f)UF(\delta_Y)=UF(\delta_X)UF(f_0)$
. Since epimorphisms in
![]() $\operatorname{\bf Set}$
split,
$\operatorname{\bf Set}$
split,
![]() $f_0$
is a split epimorphism and
$f_0$
is a split epimorphism and
![]() $UF(f_0)$
is surjective. Hence, UF(f) is surjective.
$UF(f_0)$
is surjective. Hence, UF(f) is surjective.
II. Let T be a
![]() $\lambda$
-ary
$\lambda$
-ary
![]() $\mathcal {V}$
-monad on
$\mathcal {V}$
-monad on
![]() $\mathcal {V}$
preserving surjections. Let
$\mathcal {V}$
preserving surjections. Let
![]() $\mathcal {T}$
be the corresponding
$\mathcal {T}$
be the corresponding
![]() $\lambda$
-ary
$\lambda$
-ary
![]() $\mathcal {V}$
-theory. We will show that
$\mathcal {V}$
-theory. We will show that
![]() $\mathcal {T}$
is discrete. Consider
$\mathcal {T}$
is discrete. Consider
![]() $f:FI\to FX$
and
$f:FI\to FX$
and
![]() $\tilde{f}:I\to UFX$
its adjoint transpose. Since
$\tilde{f}:I\to UFX$
its adjoint transpose. Since
![]() $\delta_X$
is surjective and T preserves surjections,
$\delta_X$
is surjective and T preserves surjections,
![]() $UF(\delta_X)$
is surjective. Thus, there is
$UF(\delta_X)$
is surjective. Thus, there is
![]() $g:I\to UFX_0$
such that
$g:I\to UFX_0$
such that
![]() $UF(\delta_X)g=\tilde{f}$
. Let
$UF(\delta_X)g=\tilde{f}$
. Let
![]() $\tilde{g}:FI\to FX_0$
be the adjoint transpose of g. Then
$\tilde{g}:FI\to FX_0$
be the adjoint transpose of g. Then
![]() $f=F(\delta_X)\tilde{g}$
and thus
$f=F(\delta_X)\tilde{g}$
and thus
![]() $\mathcal {T}$
is discrete.
$\mathcal {T}$
is discrete.
Examples 4.6. (1) 4.5 (together with 4.3) gives the result of J. Adámek that sets of inequations in context in finitary signatures correspond to enriched finitary monads preserving surjections (see his talk “Finitary monads on
![]() $\operatorname{\bf Pos}$
” at the conference Category theory CT20-21).
$\operatorname{\bf Pos}$
” at the conference Category theory CT20-21).
(2) Similarly, 4.5 gives the result of Adámek (Reference Adámek2022) that
![]() $\omega_1$
-basic quantitative equational theories (in signatures with discrete arities) correspond to enriched
$\omega_1$
-basic quantitative equational theories (in signatures with discrete arities) correspond to enriched
![]() $\omega_1$
-ary monads preserving surjections.
$\omega_1$
-ary monads preserving surjections.
Remark 4.7. Let
![]() $\mathcal {D}_\lambda$
consist of discrete
$\mathcal {D}_\lambda$
consist of discrete
![]() $\lambda$
-presentable objects. Then
$\lambda$
-presentable objects. Then
![]() $\mathcal {D}_\lambda$
-theories correspond to the
$\mathcal {D}_\lambda$
-theories correspond to the
![]() $\lambda$
-ary discrete Lawvere theories of Power (Reference Power2005). Over
$\lambda$
-ary discrete Lawvere theories of Power (Reference Power2005). Over
![]() $\operatorname{\bf Pos}$
these theories are discrete in the sense of 4.2 and inequations of terms are in discrete contexts. Following Adámek et al. (Reference Adámek, Dostál and Velebil2022)
$\operatorname{\bf Pos}$
these theories are discrete in the sense of 4.2 and inequations of terms are in discrete contexts. Following Adámek et al. (Reference Adámek, Dostál and Velebil2022)
![]() $\mathcal {D}_\omega$
-theories correspond to finitary enriched monads preserving reflexive coinserters. Over
$\mathcal {D}_\omega$
-theories correspond to finitary enriched monads preserving reflexive coinserters. Over
![]() $\operatorname{\bf Met}$
,
$\operatorname{\bf Met}$
,
![]() $\mathcal {D}_{\aleph_1}$
-theories correspond to unconditional quantitative theories of Mardare et al. (Reference Mardare, Panangaden and Plotkin2017) andMardare et al. (Reference Mardare, Panangaden and Plotkin2016) and are discrete in the sense of 4.2. In general, we do not know whether discrete Lawvere theories are discrete in the sense of 4.2.
$\mathcal {D}_{\aleph_1}$
-theories correspond to unconditional quantitative theories of Mardare et al. (Reference Mardare, Panangaden and Plotkin2017) andMardare et al. (Reference Mardare, Panangaden and Plotkin2016) and are discrete in the sense of 4.2. In general, we do not know whether discrete Lawvere theories are discrete in the sense of 4.2.
5. Birkhoff Subcategories
Assumption 5.1. Throughout this section, we assume, in addition to 4.1, that
![]() $\mathcal {T}$
is a discrete
$\mathcal {T}$
is a discrete
![]() $\lambda$
-ary
$\lambda$
-ary
![]() $\mathcal {V}$
-theory and
$\mathcal {V}$
-theory and
![]() $(\operatorname{\it Surj},\operatorname{\it Inj})$
is a proper
$(\operatorname{\it Surj},\operatorname{\it Inj})$
is a proper
![]() $\mu$
-convenient factorization system in
$\mu$
-convenient factorization system in
![]() $\mathcal {V}_0$
where
$\mathcal {V}_0$
where
![]() $\mu\leq\lambda$
.
$\mu\leq\lambda$
.
Observation 5.2.
Recall that
![]() $(\operatorname{\it Surj},\operatorname{\it Inj})$
is proper if surjections are epimorphisms and injections are monomorphisms. Let T be the
$(\operatorname{\it Surj},\operatorname{\it Inj})$
is proper if surjections are epimorphisms and injections are monomorphisms. Let T be the
![]() $\mathcal {V}$
-monad induced by
$\mathcal {V}$
-monad induced by
![]() $\mathcal {T}$
. The underlying category
$\mathcal {T}$
. The underlying category
![]() $\operatorname{\bf Alg}\!(\mathcal {T})_0$
is the category of algebras for the underlying monad
$\operatorname{\bf Alg}\!(\mathcal {T})_0$
is the category of algebras for the underlying monad
![]() $T_0$
. Let
$T_0$
. Let
![]() $U_0:\operatorname{\bf Alg}\!(\mathcal {T})_0\to\mathcal {V}_0$
be the forgetful functor. We will say that a morphism
$U_0:\operatorname{\bf Alg}\!(\mathcal {T})_0\to\mathcal {V}_0$
be the forgetful functor. We will say that a morphism
![]() $f:A\to B$
in
$f:A\to B$
in
![]() $\operatorname{\bf Alg}\!(\mathcal {T})_0$
is a surjection (injection) if U(f) is a surjection (injection). Following Manes (
Reference Manes1976
, Chapter 3, Proposition 4.17), (surjections, injections) form a proper factorization system on
$\operatorname{\bf Alg}\!(\mathcal {T})_0$
is a surjection (injection) if U(f) is a surjection (injection). Following Manes (
Reference Manes1976
, Chapter 3, Proposition 4.17), (surjections, injections) form a proper factorization system on
![]() $\operatorname{\bf Alg}\!(\mathcal {T})_0$
. Here we need that
$\operatorname{\bf Alg}\!(\mathcal {T})_0$
. Here we need that
![]() $\mathcal {T}$
is discrete because then, following 4.5,
$\mathcal {T}$
is discrete because then, following 4.5,
![]() $T_0$
preserves surjection. Given a morphism
$T_0$
preserves surjection. Given a morphism
![]() $f:A\to B$
of
$f:A\to B$
of
![]() $\mathcal {T}$
-algebras and
$\mathcal {T}$
-algebras and
![]() $(\operatorname{\it Surj},\operatorname{\it Inj})$
-factorization of
$(\operatorname{\it Surj},\operatorname{\it Inj})$
-factorization of
![]() $U_0(f)$
then f factorizes as
$U_0(f)$
then f factorizes as
where
![]() $U_0\overline{C}=C$
,
$U_0\overline{C}=C$
,
![]() $U_0(\overline{e})=e$
and
$U_0(\overline{e})=e$
and
![]() $U_0(\overline{m})=m$
.
$U_0(\overline{m})=m$
.
Since
![]() $\operatorname{\bf Alg}\!(\mathcal {T})_0$
is locally presentable (strong epimorphisms, monomorphisms) is a factorization system on
$\operatorname{\bf Alg}\!(\mathcal {T})_0$
is locally presentable (strong epimorphisms, monomorphisms) is a factorization system on
![]() $\operatorname{\bf Alg}\!(\mathcal {T})_0$
(see Reference Adámek and Rosický
Adámek and Rosický (1994
, 1.61)). Since injections are monomorphisms, strong epimorphisms in
$\operatorname{\bf Alg}\!(\mathcal {T})_0$
(see Reference Adámek and Rosický
Adámek and Rosický (1994
, 1.61)). Since injections are monomorphisms, strong epimorphisms in
![]() $\operatorname{\bf Alg}\!(\mathcal {T})_0$
are surjections.
$\operatorname{\bf Alg}\!(\mathcal {T})_0$
are surjections.
Following Manes (Reference Manes1976, Chapter 3, 3.1), a Birkhoff subcategory of
![]() $\operatorname{\bf Alg}\!(\mathcal {T})_0$
is a full replete subcategory of
$\operatorname{\bf Alg}\!(\mathcal {T})_0$
is a full replete subcategory of
![]() $\operatorname{\bf Alg}\!(\mathcal {T})_0$
closed under products, subalgebras and
$\operatorname{\bf Alg}\!(\mathcal {T})_0$
closed under products, subalgebras and
![]() $U_0$
-split quotients. Here, a morphism
$U_0$
-split quotients. Here, a morphism
![]() $g:K\to L$
in
$g:K\to L$
in
![]() $\operatorname{\bf Alg}\!(\mathcal {T})_0$
is
$\operatorname{\bf Alg}\!(\mathcal {T})_0$
is
![]() $U_0$
-split if
$U_0$
-split if
![]() $U_0(f)$
is a split epimorphism. Hence, for a Birkhoff subcategory
$U_0(f)$
is a split epimorphism. Hence, for a Birkhoff subcategory
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\operatorname{\bf Alg}\!(\mathcal {T})_0$
, the reflections
$\operatorname{\bf Alg}\!(\mathcal {T})_0$
, the reflections
![]() $\rho_K:K\to K^\ast$
are strong epimorphisms.
$\rho_K:K\to K^\ast$
are strong epimorphisms.
Lemma 5.3. A Birkhoff subcategory of
![]() $\operatorname{\bf Alg}\!(\mathcal {T})_0$
is
$\operatorname{\bf Alg}\!(\mathcal {T})_0$
is
![]() $\mathcal {V}$
-reflective in
$\mathcal {V}$
-reflective in
![]() $\operatorname{\bf Alg}\!(\mathcal {T})$
.
$\operatorname{\bf Alg}\!(\mathcal {T})$
.
Proof. Let
![]() $\mathcal {L}$
be a Birkhoff subcategory of
$\mathcal {L}$
be a Birkhoff subcategory of
![]() $\operatorname{\bf Alg}\!(\mathcal {T})$
. Since
$\operatorname{\bf Alg}\!(\mathcal {T})$
. Since
![]() $\mathcal {L}_0$
is reflective in
$\mathcal {L}_0$
is reflective in
![]() $\operatorname{\bf Alg}\!(\mathcal {T})_0$
, it suffices to show that
$\operatorname{\bf Alg}\!(\mathcal {T})_0$
, it suffices to show that
![]() $\mathcal {L}$
is closed in
$\mathcal {L}$
is closed in
![]() $\operatorname{\bf Alg}\!(\mathcal {T})$
under cotensors (see Borceux (Reference Borceux1994, 6.7.6). Consider V in
$\operatorname{\bf Alg}\!(\mathcal {T})$
under cotensors (see Borceux (Reference Borceux1994, 6.7.6). Consider V in
![]() $\mathcal {V}$
and A in
$\mathcal {V}$
and A in
![]() $\mathcal {L}$
. Since the cotensor functor
$\mathcal {L}$
. Since the cotensor functor
![]() $[V,-]:\operatorname{\bf Alg}\!(\mathcal {T})\to\operatorname{\bf Alg}\!(\mathcal {T})$
has a left
$[V,-]:\operatorname{\bf Alg}\!(\mathcal {T})\to\operatorname{\bf Alg}\!(\mathcal {T})$
has a left
![]() $\mathcal {V}$
-adjoint
$\mathcal {V}$
-adjoint
![]() $V\otimes -$
(see Borceux (Reference Borceux1994, 6.5.6)), and
$V\otimes -$
(see Borceux (Reference Borceux1994, 6.5.6)), and
![]() $\delta_V:V_0\to V$
is an epimorphism,
$\delta_V:V_0\to V$
is an epimorphism,
![]() $[\delta_V,A]:[V,A]\to [V_0,A]$
is a monomorphism. Since
$[\delta_V,A]:[V,A]\to [V_0,A]$
is a monomorphism. Since
![]() $[V_0,A]$
is a power of A, [V, A] is in
$[V_0,A]$
is a power of A, [V, A] is in
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
Hence, Birkhoff subcategories of
![]() $\operatorname{\bf Alg}\!(\mathcal {T})_0$
are
$\operatorname{\bf Alg}\!(\mathcal {T})_0$
are
![]() $\mathcal {V}$
-subcategories and, in what follows, we will take them as subcategories of
$\mathcal {V}$
-subcategories and, in what follows, we will take them as subcategories of
![]() $\operatorname{\bf Alg}\!(\mathcal {T})$
. The following definition goes back to Hatcher (Reference Hatcher1970), Herrlich and Ringel (Reference Herrlich and Ringel1972).
$\operatorname{\bf Alg}\!(\mathcal {T})$
. The following definition goes back to Hatcher (Reference Hatcher1970), Herrlich and Ringel (Reference Herrlich and Ringel1972).
Definition 5.4. An
![]() $\mathcal {T}$
-equation
$\mathcal {T}$
-equation
![]() $p=q$
is a pair of morphisms
$p=q$
is a pair of morphisms
![]() $p,q:FY\to FX$
in
$p,q:FY\to FX$
in
![]() $\operatorname{\bf Alg}\!(\mathcal {T})$
. A
$\operatorname{\bf Alg}\!(\mathcal {T})$
. A
![]() $\mathcal {T}$
-equational theory E is a set of
$\mathcal {T}$
-equational theory E is a set of
![]() $\mathcal {T}$
-equations.
$\mathcal {T}$
-equations.
A
![]() $\mathcal {T}$
-algebra A satisfies a
$\mathcal {T}$
-algebra A satisfies a
![]() $\mathcal {T}$
-equation
$\mathcal {T}$
-equation
![]() $p=q$
if
$p=q$
if
![]() $hp=hq$
for every morphism
$hp=hq$
for every morphism
![]() $h:FX\to A$
. It satisfies a
$h:FX\to A$
. It satisfies a
![]() $\mathcal {T}$
-equational theory E if it satisfies all equations of E.
$\mathcal {T}$
-equational theory E if it satisfies all equations of E.
![]() $\operatorname{\bf Alg}\!(E)$
will be the full subcategory of
$\operatorname{\bf Alg}\!(E)$
will be the full subcategory of
![]() $\operatorname{\bf Alg}\!(\mathcal {T})_0$
consisting of
$\operatorname{\bf Alg}\!(\mathcal {T})_0$
consisting of
![]() $\mathcal {T}$
-algebras satisfying all equations from E.
$\mathcal {T}$
-algebras satisfying all equations from E.
Proposition 5.5.
![]() $\operatorname{\bf Alg}\!(E)$
is a Birkhoff subcategory of
$\operatorname{\bf Alg}\!(E)$
is a Birkhoff subcategory of
![]() $\operatorname{\bf Alg}\!(\mathcal {T})$
for every
$\operatorname{\bf Alg}\!(\mathcal {T})$
for every
![]() $\mathcal {T}$
-equational theory E.
$\mathcal {T}$
-equational theory E.
Proof.
![]() $\operatorname{\bf Alg}\!(E)$
is clearly closed under products and subalgebras. Let
$\operatorname{\bf Alg}\!(E)$
is clearly closed under products and subalgebras. Let
![]() $f:A\to B$
be a
$f:A\to B$
be a
![]() $U_0$
-split quotient of an algebra A satisfying E, i.e., there is
$U_0$
-split quotient of an algebra A satisfying E, i.e., there is
![]() $s:UB\to UA$
such that
$s:UB\to UA$
such that
![]() $U(f)s=\operatorname{id}_{UB}$
. Let
$U(f)s=\operatorname{id}_{UB}$
. Let
![]() $p,q:FY\to FX$
give an equation
$p,q:FY\to FX$
give an equation
![]() $p=q$
from E. Consider
$p=q$
from E. Consider
![]() $h:FX\to B$
and
$h:FX\to B$
and
![]() $\tilde{h}:X\to UB$
be the adjoint transpose of h. Let
$\tilde{h}:X\to UB$
be the adjoint transpose of h. Let
![]() $g=s\tilde{h}$
and
$g=s\tilde{h}$
and
![]() $\tilde{g}:FX\to A$
be the adjoint transpose of g. Since
$\tilde{g}:FX\to A$
be the adjoint transpose of g. Since
![]() $U(f)g=U(f)s\tilde{h}=\tilde{h}$
, we have
$U(f)g=U(f)s\tilde{h}=\tilde{h}$
, we have
![]() $f\tilde{g}=h$
. Since
$f\tilde{g}=h$
. Since
![]() $\tilde{g}p=\tilde{g}q$
, we get
$\tilde{g}p=\tilde{g}q$
, we get
Thus B satisfies E.
Recall that an object V in
![]() $\mathcal {V}$
is
$\mathcal {V}$
is
![]() $\mu$
-generated with respect to
$\mu$
-generated with respect to
![]() $\operatorname{\it Inj}$
if
$\operatorname{\it Inj}$
if
![]() $\mathcal {V}_0(V,-):\mathcal {V}_0\to\operatorname{\bf Set}$
preserves
$\mathcal {V}_0(V,-):\mathcal {V}_0\to\operatorname{\bf Set}$
preserves
![]() $\mu$
-directed colimits of injections.
$\mu$
-directed colimits of injections.
Definition 5.6. We say that a morphism
![]() $f:A\to B$
in
$f:A\to B$
in
![]() $\mathcal {V}_0$
is a
$\mathcal {V}_0$
is a
![]() $\mu$
-pure epimorphism if it is projective with respect to
$\mu$
-pure epimorphism if it is projective with respect to
![]() $\mu$
-generated objects. Explicitly, for every
$\mu$
-generated objects. Explicitly, for every
![]() $\mu$
-generated object X, all morphisms
$\mu$
-generated object X, all morphisms
![]() $X\to B$
factor through f.
$X\to B$
factor through f.
Remark 5.7. (1) For
![]() $\mu=\lambda$
, this concept was introduced in Adámek and Rosický (Reference Adámek and Rosický2004).
$\mu=\lambda$
, this concept was introduced in Adámek and Rosický (Reference Adámek and Rosický2004).
(2) Every
![]() $\mu$
-pure epimorphism
$\mu$
-pure epimorphism
![]() $f:A\to B$
is an epimorphism. Indeed, assume that
$f:A\to B$
is an epimorphism. Indeed, assume that
![]() $uf=vf$
for
$uf=vf$
for
![]() $u,v:B\to C$
. Consider a
$u,v:B\to C$
. Consider a
![]() $\mu$
-generated object X and
$\mu$
-generated object X and
![]() $g:X\to B$
. Since g factors through f, we have
$g:X\to B$
. Since g factors through f, we have
![]() $ug=vg$
. Thus,
$ug=vg$
. Thus,
![]() $u=v$
.
$u=v$
.
(3) Every split epimorphism is
![]() $\mu$
-pure.
$\mu$
-pure.
(4) A morphism
![]() $f:A\to B$
$f:A\to B$
![]() $\omega$
-pure in
$\omega$
-pure in
![]() $\operatorname{\bf Met}$
iff it is
$\operatorname{\bf Met}$
iff it is
![]() $\omega$
-reflexive in the sense of Mardare et al. (Reference Mardare, Panangaden and Plotkin2017).
$\omega$
-reflexive in the sense of Mardare et al. (Reference Mardare, Panangaden and Plotkin2017).
Definition 5.8. We say that
![]() $\mathcal {L}$
is a
$\mathcal {L}$
is a
![]() $\mu$
-Birkhoff subcategory of
$\mu$
-Birkhoff subcategory of
![]() $\operatorname{\bf Alg}\!(\mathcal {T})$
if it is a Birkhoff subcategory closed under quotients
$\operatorname{\bf Alg}\!(\mathcal {T})$
if it is a Birkhoff subcategory closed under quotients
![]() $f:A\to B$
such that Uf is
$f:A\to B$
such that Uf is
![]() $\mu$
-pure.
$\mu$
-pure.
Thus
![]() $\mathcal {L}$
is a
$\mathcal {L}$
is a
![]() $\mu$
-Birkhoff subcategory of
$\mu$
-Birkhoff subcategory of
![]() $\operatorname{\bf Alg}\!(\mathcal {T})$
if and only if it is a full subcategory closed under products, subalgebras and
$\operatorname{\bf Alg}\!(\mathcal {T})$
if and only if it is a full subcategory closed under products, subalgebras and
![]() $\mu$
-pure quotients.
$\mu$
-pure quotients.
Recall that
![]() $\mathcal {V}_0$
is
$\mathcal {V}_0$
is
![]() $\operatorname{\it Inj}$
-locally
$\operatorname{\it Inj}$
-locally
![]() $\mu$
-generated if it has a set
$\mu$
-generated if it has a set
![]() $\mathcal {X}$
of
$\mathcal {X}$
of
![]() $\mu$
-generated objects with respect to
$\mu$
-generated objects with respect to
![]() $\operatorname{\it Inj}$
such that every object of
$\operatorname{\it Inj}$
such that every object of
![]() $\mathcal {V}_0$
is a
$\mathcal {V}_0$
is a
![]() $\mu$
-directed colimit of objects from
$\mu$
-directed colimit of objects from
![]() $\mathcal {X}$
and injections (see Di Liberti and Rosický (Reference Di Liberti and Rosický2022)).
$\mathcal {X}$
and injections (see Di Liberti and Rosický (Reference Di Liberti and Rosický2022)).
Remark 5.9. (1) Following Di Liberti and Rosický (Reference Di Liberti and Rosický2022, Remark 2.17),
![]() $\mathcal {V}_0$
is
$\mathcal {V}_0$
is
![]() $\operatorname{\it Inj}$
-locally
$\operatorname{\it Inj}$
-locally
![]() $\lambda$
-generated.
$\lambda$
-generated.
(2)
![]() $\operatorname{\bf Met}$
is
$\operatorname{\bf Met}$
is
![]() $\operatorname{\it Inj}$
-locally
$\operatorname{\it Inj}$
-locally
![]() $\omega$
-generated because finite metric spaces are
$\omega$
-generated because finite metric spaces are
![]() $\omega$
-generated with respect to
$\omega$
-generated with respect to
![]() $\operatorname{\it Inj}$
(following Adámek and Rosický (Reference Adámek and Rosický2022, Remark 2.5(2))).
$\operatorname{\it Inj}$
(following Adámek and Rosický (Reference Adámek and Rosický2022, Remark 2.5(2))).
The following definition and theorem were motivated by Milius and Urbat (Reference Milius, Urbat, Boja ńczyk and Simpson2019).
Definition 5.10. A
![]() $\mathcal {T}$
-equation
$\mathcal {T}$
-equation
![]() $p=q$
, where
$p=q$
, where
![]() $p,q:FY\to FX$
, will be called
$p,q:FY\to FX$
, will be called
![]() $\mu$
-clustered if X is a coproduct of
$\mu$
-clustered if X is a coproduct of
![]() $\mu$
-generated objects.
$\mu$
-generated objects.
Theorem 5.11. Assume 5.1 and, moreover, let
![]() $\mathcal {V}_0$
be
$\mathcal {V}_0$
be
![]() $\operatorname{\it Inj}$
-locally
$\operatorname{\it Inj}$
-locally
![]() $\mu$
-generated. Then
$\mu$
-generated. Then
![]() $\mathcal {L}$
is a
$\mathcal {L}$
is a
![]() $\mu$
-Birkhoff subcategory of
$\mu$
-Birkhoff subcategory of
![]() $\operatorname{\bf Alg}\!(\mathcal {T})$
if and only if
$\operatorname{\bf Alg}\!(\mathcal {T})$
if and only if
![]() $\mathcal {L}=\operatorname{\bf Alg}\!(E)$
where all equations from E are
$\mathcal {L}=\operatorname{\bf Alg}\!(E)$
where all equations from E are
![]() $\mu$
-clustered.
$\mu$
-clustered.
Proof. I. Necessity: Let E consist of
![]() $\mu$
-clustered equations. We have to show that
$\mu$
-clustered equations. We have to show that
![]() $\operatorname{\bf Alg}\!(E)$
is closed in
$\operatorname{\bf Alg}\!(E)$
is closed in
![]() $\operatorname{\bf Alg}\!(\mathcal {T})$
under quotients
$\operatorname{\bf Alg}\!(\mathcal {T})$
under quotients
![]() $f:A\to B$
such that Uf is
$f:A\to B$
such that Uf is
![]() $\mu$
-pure. So, let
$\mu$
-pure. So, let
![]() $f:A\to B$
be such a homomorphism. Consider an equation
$f:A\to B$
be such a homomorphism. Consider an equation
![]() $p=q$
from E where
$p=q$
from E where
![]() $p,q:FY\to FX$
and
$p,q:FY\to FX$
and
![]() $X=\coprod_i X_i$
with
$X=\coprod_i X_i$
with
![]() $X_i$
$X_i$
![]() $\mu$
-generated. Let
$\mu$
-generated. Let
![]() $h:FX\to B$
and
$h:FX\to B$
and
![]() $\tilde{h}:X\to UB$
be its adjoint transpose. If
$\tilde{h}:X\to UB$
be its adjoint transpose. If
![]() $u_i:X_i\to X$
are coproduct injections, then there are
$u_i:X_i\to X$
are coproduct injections, then there are
![]() $v_i:X_i\to UA$
such that
$v_i:X_i\to UA$
such that
![]() $U(f)v_i=\tilde{h}u_i$
for every i. We get
$U(f)v_i=\tilde{h}u_i$
for every i. We get
![]() $v:X\to UA$
such that
$v:X\to UA$
such that
![]() $U(f)v=\tilde{h}$
. Therefore,
$U(f)v=\tilde{h}$
. Therefore,
Hence, B satisfies E.
II. Sufficiency: Conversely, let
![]() $\mathcal {L}$
be a
$\mathcal {L}$
be a
![]() $\mu$
-Birkhoff subcategory of
$\mu$
-Birkhoff subcategory of
![]() $\operatorname{\bf Alg}\!(\mathcal {T})$
. Following 5.3,
$\operatorname{\bf Alg}\!(\mathcal {T})$
. Following 5.3,
![]() $\mathcal {L}$
is
$\mathcal {L}$
is
![]() $\mathcal {V}$
-reflective in
$\mathcal {V}$
-reflective in
![]() $\operatorname{\bf Alg}\!(\mathcal {T})$
. Moreover, following 5.2, the reflections
$\operatorname{\bf Alg}\!(\mathcal {T})$
. Moreover, following 5.2, the reflections
![]() $\rho_K:K\to K'$
are strong epimorphisms.
$\rho_K:K\to K'$
are strong epimorphisms.
Let
![]() $U':\mathcal {L}\to\mathcal {V}_0$
be the restriction of
$U':\mathcal {L}\to\mathcal {V}_0$
be the restriction of
![]() $U_0$
on
$U_0$
on
![]() $\mathcal {L}$
and F’ its left adjoint. Let E be given by pairs (p,q) where
$\mathcal {L}$
and F’ its left adjoint. Let E be given by pairs (p,q) where
![]() $p,q:FY\to FX$
with
$p,q:FY\to FX$
with
![]() $X=\coprod X_i$
, where
$X=\coprod X_i$
, where
![]() $X_i$
are
$X_i$
are
![]() $\mu$
-generated with respect to
$\mu$
-generated with respect to
![]() $\operatorname{\it Inj}$
$\operatorname{\it Inj}$
![]() $X_i$
, such that every
$X_i$
, such that every
![]() $A\in\mathcal {L}$
satisfies the equation
$A\in\mathcal {L}$
satisfies the equation
![]() $p=q$
. This is equivalent to
$p=q$
. This is equivalent to
![]() $\rho_{FX}p=\rho_{FX}q$
. Clearly,
$\rho_{FX}p=\rho_{FX}q$
. Clearly,
![]() $\mathcal {L}\subseteq\operatorname{\bf Alg}\!(E)$
. Following I.,
$\mathcal {L}\subseteq\operatorname{\bf Alg}\!(E)$
. Following I.,
![]() $\operatorname{\bf Alg}\!(E)$
is a
$\operatorname{\bf Alg}\!(E)$
is a
![]() $\mu$
-Birkhoff subcategory of
$\mu$
-Birkhoff subcategory of
![]() $\operatorname{\bf Alg}\!(\mathcal {T})$
. Hence,
$\operatorname{\bf Alg}\!(\mathcal {T})$
. Hence,
![]() $\operatorname{\bf Alg}\!(E)$
is
$\operatorname{\bf Alg}\!(E)$
is
![]() $\mathcal {V}$
-reflective in
$\mathcal {V}$
-reflective in
![]() $\operatorname{\bf Alg}\!(\mathcal {T})$
and the reflections
$\operatorname{\bf Alg}\!(\mathcal {T})$
and the reflections
![]() $\rho'_K:K\to K''$
are strong epimorphisms.
$\rho'_K:K\to K''$
are strong epimorphisms.
Let
![]() $U'':\operatorname{\bf Alg}\!(E)\to\mathcal {V}_0$
be the restriction of U on
$U'':\operatorname{\bf Alg}\!(E)\to\mathcal {V}_0$
be the restriction of U on
![]() $\operatorname{\bf Alg}\!(E)$
and F” its left adjoint. We get
$\operatorname{\bf Alg}\!(E)$
and F” its left adjoint. We get
![]() $\rho':F\to F''$
and
$\rho':F\to F''$
and
![]() $\tau:F''\to F'$
such that
$\tau:F''\to F'$
such that
![]() $\tau\rho'=\rho_F$
. Since both
$\tau\rho'=\rho_F$
. Since both
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\operatorname{\bf Alg}\!(E)$
are monadic, it suffices to prove that
$\operatorname{\bf Alg}\!(E)$
are monadic, it suffices to prove that
![]() $\tau$
is a natural isomorphism.
$\tau$
is a natural isomorphism.
Consider an arbitrary X in
![]() $\mathcal {V}$
and express UFX as a
$\mathcal {V}$
and express UFX as a
![]() $\mu$
-directed colimit
$\mu$
-directed colimit
of injections between objects
![]() $Z_m$
which are
$Z_m$
which are
![]() $\mu$
-generated with respect to
$\mu$
-generated with respect to
![]() $\operatorname{\it Inj}$
. Let
$\operatorname{\it Inj}$
. Let
![]() $\eta_Z:Z\to UFZ$
, Z in
$\eta_Z:Z\to UFZ$
, Z in
![]() $\mathcal {V}$
, be the adjunction units and
$\mathcal {V}$
, be the adjunction units and
![]() $\tilde{z}_m: FZ_m\to FX$
be given as
$\tilde{z}_m: FZ_m\to FX$
be given as
![]() $U(\tilde{z}_m)\eta_{Z_m}=z_m$
. Let
$U(\tilde{z}_m)\eta_{Z_m}=z_m$
. Let
be the induced morphism, i.e.,
![]() $t_XF(u_m)=\tilde{z}_m$
where
$t_XF(u_m)=\tilde{z}_m$
where
![]() $(u_m:Z_m\to \coprod Z_m)_{m\in M}$
is the coproduct. Then,
$(u_m:Z_m\to \coprod Z_m)_{m\in M}$
is the coproduct. Then,
![]() $U(t_X)$
is a
$U(t_X)$
is a
![]() $\mu$
-pure epimorphism. Indeed, every morphism
$\mu$
-pure epimorphism. Indeed, every morphism
![]() $f:Z\to UFX$
with Z
$f:Z\to UFX$
with Z
![]() $\mu$
-generated with respect to
$\mu$
-generated with respect to
![]() $\operatorname{\it Inj}$
factors through
$\operatorname{\it Inj}$
factors through
![]() $z_m$
for some
$z_m$
for some
![]() $m\in M$
as
$m\in M$
as
![]() $f=z_mg$
where
$f=z_mg$
where
![]() $g:Z\to Z_m$
. Hence,
$g:Z\to Z_m$
. Hence,
and thus
We have to prove that
![]() $\tau_X$
is an isomorphism for every X. Consider the commutative diagram
$\tau_X$
is an isomorphism for every X. Consider the commutative diagram
where
![]() $\varepsilon:FU\to\operatorname{Id}$
is the counit of the adjunction
$\varepsilon:FU\to\operatorname{Id}$
is the counit of the adjunction
![]() $F\dashv U$
. The arrow s is given by
$F\dashv U$
. The arrow s is given by
![]() $\rho'_{\coprod Z_m}$
being the reflection of
$\rho'_{\coprod Z_m}$
being the reflection of
![]() $F\coprod Z_m$
to
$F\coprod Z_m$
to
![]() $\operatorname{\bf Alg}\!(E)$
. Since
$\operatorname{\bf Alg}\!(E)$
. Since
![]() $U(\varepsilon_{F''X})$
is a split epimorphism and
$U(\varepsilon_{F''X})$
is a split epimorphism and
![]() $U(t_{UF''X})$
is a
$U(t_{UF''X})$
is a
![]() $\mu$
-pure epimorphism, the composition
$\mu$
-pure epimorphism, the composition
![]() $U(\varepsilon_{F''X}t_{UF''X})$
is a
$U(\varepsilon_{F''X}t_{UF''X})$
is a
![]() $\mu$
-pure epimorphism. Thus,U(s) is a
$\mu$
-pure epimorphism. Thus,U(s) is a
![]() $\mu$
-pure epimorphism. Thus, it suffices to show that
$\mu$
-pure epimorphism. Thus, it suffices to show that
![]() $F''\coprod Z_m$
belongs to
$F''\coprod Z_m$
belongs to
![]() $\mathcal {L}$
, i.e., that
$\mathcal {L}$
, i.e., that
![]() $\tau_Z$
is an isomorphism where
$\tau_Z$
is an isomorphism where
![]() $Z=\coprod Z_m$
.
$Z=\coprod Z_m$
.
Since
![]() $\rho_Z$
is a strong epimorphism,
$\rho_Z$
is a strong epimorphism,
![]() $\tau_Z$
is a strong epimorphism. Thus, it suffices to show that
$\tau_Z$
is a strong epimorphism. Thus, it suffices to show that
![]() $\tau_Z$
is a monomorphism. Consider
$\tau_Z$
is a monomorphism. Consider
![]() $p,q:FY\to F''Z$
such that
$p,q:FY\to F''Z$
such that
![]() $\tau_Zp=\tau_Zq$
. We have to show that
$\tau_Zp=\tau_Zq$
. We have to show that
![]() $p=q$
. Consider the pullback
$p=q$
. Consider the pullback
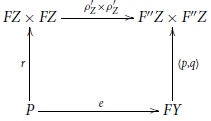
and take the compositions
![]() $p',q':P\to FZ$
of the product projections with r. Let
$p',q':P\to FZ$
of the product projections with r. Let
![]() $p'',q'':FUP\to FZ$
be the compositions of p’ and q’ with
$p'',q'':FUP\to FZ$
be the compositions of p’ and q’ with
![]() $\varepsilon_P:FUP\to P$
. Since
$\varepsilon_P:FUP\to P$
. Since
![]() $p''=q''$
belongs to E. Thus, we have
$p''=q''$
belongs to E. Thus, we have
![]() $\rho'_Zp''=\rho'_Zq''$
, i.e.,
$\rho'_Zp''=\rho'_Zq''$
, i.e.,
![]() $pe=qe$
. Since
$pe=qe$
. Since
![]() $\rho'_Z$
is a strong epimorphism, it is a surjection (see 5.2). Following 3.2, e is a surjection, hence an epimorphism. Thus,
$\rho'_Z$
is a strong epimorphism, it is a surjection (see 5.2). Following 3.2, e is a surjection, hence an epimorphism. Thus,
![]() $p=q$
and we have proved that
$p=q$
and we have proved that
![]() $\tau_Z$
is a monomorphism.
$\tau_Z$
is a monomorphism.
Definition 5.12. We will call a category
![]() $\mathcal {K}$
strongly connected if for every pair of objects K and K’ of
$\mathcal {K}$
strongly connected if for every pair of objects K and K’ of
![]() $\mathcal {K}$
, where K’ is not initial, there is a morphism
$\mathcal {K}$
, where K’ is not initial, there is a morphism
![]() $K\to K'$
.
$K\to K'$
.
Lemma 5.13. The following conditions are equivalent:
(1)
 $\mathcal {K}$
is strongly connected, and
$\mathcal {K}$
is strongly connected, and
(2) for a coproduct
 $\coprod_{m\in M} K_m$
of non-initial objects
$\coprod_{m\in M} K_m$
of non-initial objects
 $K_m$
, coproduct components
$K_m$
, coproduct components
 $u_m:K_m\to\coprod K_m$
are split monomorphisms.
$u_m:K_m\to\coprod K_m$
are split monomorphisms.
Proof. If
![]() $\mathcal {K}$
is strongly connected and
$\mathcal {K}$
is strongly connected and
![]() $u_m:K_m\to\coprod K_m$
a coproduct of non-initial objects, then there is a cocone
$u_m:K_m\to\coprod K_m$
a coproduct of non-initial objects, then there is a cocone
![]() $v_m:K_m\to K_n$
for every n with
$v_m:K_m\to K_n$
for every n with
![]() $v_n=\operatorname{id}_{K_n}$
. Hence
$v_n=\operatorname{id}_{K_n}$
. Hence
![]() $u_n$
is a split monomorphism.
$u_n$
is a split monomorphism.
Conversely, (2) applied to
![]() $K\coprod K'$
yields
$K\coprod K'$
yields
![]() $K\to K'$
.
$K\to K'$
.
Remark 5.14. In 5.13, all subcoproduct morphisms
![]() $\coprod_{m\in N} X_m\to\coprod_{m\in M} X_m$
,
$\coprod_{m\in N} X_m\to\coprod_{m\in M} X_m$
,
![]() $N\subseteq M$
, are split monomorphisms. In fact,
$N\subseteq M$
, are split monomorphisms. In fact,
![]() $\coprod_{m\in M} X_m=(\coprod_{m\in N} X_m)\coprod(\coprod_{m\notin N}X_m)$
.
$\coprod_{m\in M} X_m=(\coprod_{m\in N} X_m)\coprod(\coprod_{m\notin N}X_m)$
.
Theorem 5.15. Assume 5.1 and, moreover, let
![]() $\mathcal {V}_0$
be
$\mathcal {V}_0$
be
![]() $\operatorname{\it Inj}$
-locally
$\operatorname{\it Inj}$
-locally
![]() $\mu$
-generated, strongly connected and let U preserve
$\mu$
-generated, strongly connected and let U preserve
![]() $\mu$
-directed colimits of injections. Then
$\mu$
-directed colimits of injections. Then
![]() $\mathcal {L}$
is a
$\mathcal {L}$
is a
![]() $\mu$
-Birkhoff subcategory of
$\mu$
-Birkhoff subcategory of
![]() $\operatorname{\bf Alg}\!(\mathcal {T})$
if and only if
$\operatorname{\bf Alg}\!(\mathcal {T})$
if and only if
![]() $\mathcal {L}=\operatorname{\bf Alg}\!(E)$
where all equations
$\mathcal {L}=\operatorname{\bf Alg}\!(E)$
where all equations
![]() $p=q$
from E have
$p=q$
from E have
![]() $p,q:FY\to FX$
with X and Y being
$p,q:FY\to FX$
with X and Y being
![]() $\mu$
-generated with respect to
$\mu$
-generated with respect to
![]() $\operatorname{\it Inj}$
.
$\operatorname{\it Inj}$
.
Proof. Sufficiency is I. of the proof of 5.11. Conversely, let
![]() $\mathcal {L}$
be a
$\mathcal {L}$
be a
![]() $\mu$
-Birkhoff subcategory of
$\mu$
-Birkhoff subcategory of
![]() $\operatorname{\bf Alg}\!(\mathcal {T})$
. Following 5.11,
$\operatorname{\bf Alg}\!(\mathcal {T})$
. Following 5.11,
![]() $\mathcal {L}=\operatorname{\bf Alg}\!(E)$
where all equations
$\mathcal {L}=\operatorname{\bf Alg}\!(E)$
where all equations
![]() $p=q$
from E have
$p=q$
from E have
![]() $p,q:FY\to FX$
with X being a coproduct of objects
$p,q:FY\to FX$
with X being a coproduct of objects
![]() $\mu$
-generated with respect to
$\mu$
-generated with respect to
![]() $\operatorname{\it Inj}$
. Express Y as a
$\operatorname{\it Inj}$
. Express Y as a
![]() $\mu$
-directed colimit
$\mu$
-directed colimit
![]() $(y_m:Y_m\to Y)_{m\in M}$
of objects
$(y_m:Y_m\to Y)_{m\in M}$
of objects
![]() $Y_m$
$Y_m$
![]() $\mu$
-generated with respect to
$\mu$
-generated with respect to
![]() $\operatorname{\it Inj}$
. Then
$\operatorname{\it Inj}$
. Then
![]() $F(y_m):FY_m\to FY$
is a
$F(y_m):FY_m\to FY$
is a
![]() $\mu$
-directed colimit and
$\mu$
-directed colimit and
![]() $\rho_{FX}p=\rho_{FX}q$
if and only if
$\rho_{FX}p=\rho_{FX}q$
if and only if
![]() $\rho_{FX}pF(y_m)=\rho_{FX}qF(y_m)$
for every
$\rho_{FX}pF(y_m)=\rho_{FX}qF(y_m)$
for every
![]() $m\in M$
. Thus we have reduced our equations to
$m\in M$
. Thus we have reduced our equations to
![]() $p=q$
where
$p=q$
where
![]() $p,q:FY\to FX$
with X being a coproduct of objects
$p,q:FY\to FX$
with X being a coproduct of objects
![]() $\mu$
-generated with respect to
$\mu$
-generated with respect to
![]() $\operatorname{\it Inj}$
and Y being
$\operatorname{\it Inj}$
and Y being
![]() $\mu$
-generated with respect to
$\mu$
-generated with respect to
![]() $\operatorname{\it Inj}$
.
$\operatorname{\it Inj}$
.
Express
![]() $X=\coprod_{m\in M}X_m$
as a
$X=\coprod_{m\in M}X_m$
as a
![]() $\mu$
-directed colimit of subcoproducts
$\mu$
-directed colimit of subcoproducts
![]() $X_N=\coprod_{m\in N} X_m$
where
$X_N=\coprod_{m\in N} X_m$
where
![]() $|N|<\mu$
and
$|N|<\mu$
and
![]() $X_m$
are non-initial. Following 5.14, X is a
$X_m$
are non-initial. Following 5.14, X is a
![]() $\mu$
-directed colimit
$\mu$
-directed colimit
![]() $x_N:X_N\to X$
of split monomorphisms
$x_N:X_N\to X$
of split monomorphisms
![]() $x_{NN'}:X_N\to X_{N'}$
where
$x_{NN'}:X_N\to X_{N'}$
where
![]() $N\subseteq N'$
. Hence, UFX is a
$N\subseteq N'$
. Hence, UFX is a
![]() $\mu$
-directed colimit
$\mu$
-directed colimit
![]() $UF(x_N):UFX_N\to UFX$
of split monomorphisms
$UF(x_N):UFX_N\to UFX$
of split monomorphisms
![]() $UF(x_{NN'}):UFX_N\to UFX_{N'}$
. Following 3.5,
$UF(x_{NN'}):UFX_N\to UFX_{N'}$
. Following 3.5,
![]() $UF(x_{NN'})$
are injections. Let
$UF(x_{NN'})$
are injections. Let
![]() $\tilde{p},\tilde{q}:Y\to UFX$
be the adjoint transposes of
$\tilde{p},\tilde{q}:Y\to UFX$
be the adjoint transposes of
![]() $p,q:FY\to FX$
. Since Y is
$p,q:FY\to FX$
. Since Y is
![]() $\mu$
-generated with respect to
$\mu$
-generated with respect to
![]() $\operatorname{\it Inj}$
, there is
$\operatorname{\it Inj}$
, there is
![]() $N\subseteq M$
,
$N\subseteq M$
,
![]() $|N|<\mu$
and
$|N|<\mu$
and
![]() $p',q':Y\to UFX_N$
such that
$p',q':Y\to UFX_N$
such that
![]() $\tilde{p}=x_Np'$
and
$\tilde{p}=x_Np'$
and
![]() $\tilde{q}=x_Nq'$
.
$\tilde{q}=x_Nq'$
.
Now,
![]() $p=q$
is an equation from E, iff
$p=q$
is an equation from E, iff
![]() $U(\rho_{FX})\tilde{p}=U(\rho_{FX})\tilde{q}$
. Since
$U(\rho_{FX})\tilde{p}=U(\rho_{FX})\tilde{q}$
. Since
![]() $x_N$
is a split monomorphism, this is equivalent to
$x_N$
is a split monomorphism, this is equivalent to
![]() $U(\rho_{FX_N})p'=U(\rho_{X_N})q'$
, hence to
$U(\rho_{FX_N})p'=U(\rho_{X_N})q'$
, hence to
![]() $\rho_{X_N}p^\ast=\rho_{X_N}q^\ast$
where
$\rho_{X_N}p^\ast=\rho_{X_N}q^\ast$
where
![]() $p^\ast,q^\ast:FY\to FX_N$
are adjoint transposes of p’,q’. Since
$p^\ast,q^\ast:FY\to FX_N$
are adjoint transposes of p’,q’. Since
![]() $X_N$
is
$X_N$
is
![]() $\mu$
-generated with respect to
$\mu$
-generated with respect to
![]() $\operatorname{\it Inj}$
(see Di Liberti and Rosický (Reference Di Liberti and Rosický2022, Lemma 2.13)), the proof is finished.
$\operatorname{\it Inj}$
(see Di Liberti and Rosický (Reference Di Liberti and Rosický2022, Lemma 2.13)), the proof is finished.
Remark 5.16. Moreover,
![]() $\operatorname{\bf Alg}\!(E)$
is closed in
$\operatorname{\bf Alg}\!(E)$
is closed in
![]() $\operatorname{\bf Alg}\!(\mathcal {T})$
under
$\operatorname{\bf Alg}\!(\mathcal {T})$
under
![]() $\mu$
-directed colimits of injections.
$\mu$
-directed colimits of injections.
Indeed, let
![]() $k_m:K_m\to K$
be a
$k_m:K_m\to K$
be a
![]() $\mu$
-directed colimit of injections where
$\mu$
-directed colimit of injections where
![]() $K_m$
satisfy E. Consider an equation
$K_m$
satisfy E. Consider an equation
![]() $p=q$
from E where
$p=q$
from E where
![]() $p,q:FY\to FX$
. Since U preserves
$p,q:FY\to FX$
. Since U preserves
![]() $\mu$
-directed colimits of injections, F preserves
$\mu$
-directed colimits of injections, F preserves
![]() $\mu$
-generated objects (see Di Liberti and Rosický (Reference Di Liberti and Rosický2022, Lemma 3.11)). Hence, a morphism
$\mu$
-generated objects (see Di Liberti and Rosický (Reference Di Liberti and Rosický2022, Lemma 3.11)). Hence, a morphism
![]() $h:FX\to K$
factors through some
$h:FX\to K$
factors through some
![]() $k_m:K_m\to K$
,
$k_m:K_m\to K$
,
![]() $h=k_mh'$
. Since
$h=k_mh'$
. Since
![]() $K_m$
satisfies E,
$K_m$
satisfies E,
![]() $h'p=h'q$
. Thus,
$h'p=h'q$
. Thus,
![]() $hp=hq$
and K satisfies E.
$hp=hq$
and K satisfies E.
Remark 5.17. The assumption that
![]() $\mathcal {K}$
is strongly connected is needed in 5.15 because 5.16 is not valid for the category
$\mathcal {K}$
is strongly connected is needed in 5.15 because 5.16 is not valid for the category
![]() $\operatorname{\bf Set}^{\Bbb N}$
of
$\operatorname{\bf Set}^{\Bbb N}$
of
![]() $\Bbb N$
-sorted sets. Indeed, let T be a finitary monad in
$\Bbb N$
-sorted sets. Indeed, let T be a finitary monad in
![]() $\operatorname{\bf Set}^{\Bbb N}$
. Since epimorphisms in
$\operatorname{\bf Set}^{\Bbb N}$
. Since epimorphisms in
![]() $\operatorname{\bf Set}^{\Bbb N}$
split, every Birkhoff subcategory of
$\operatorname{\bf Set}^{\Bbb N}$
split, every Birkhoff subcategory of
![]() $(\operatorname{\bf Set}^{\Bbb N})^T$
is
$(\operatorname{\bf Set}^{\Bbb N})^T$
is
![]() $\omega$
-Birkhoff. Following Adámek et al. (Reference Adámek, Rosický and Vitale2012), it does not need to be closed under directed colimits. (Take the full subcategory of
$\omega$
-Birkhoff. Following Adámek et al. (Reference Adámek, Rosický and Vitale2012), it does not need to be closed under directed colimits. (Take the full subcategory of
![]() $\operatorname{\bf Set}^{\Bbb N}$
consisting of all
$\operatorname{\bf Set}^{\Bbb N}$
consisting of all
![]() $(X_n)_{n\in\Bbb N}$
such that either
$(X_n)_{n\in\Bbb N}$
such that either
![]() $X_n=\emptyset$
for some n or
$X_n=\emptyset$
for some n or
![]() $X_n=1$
for every n.)
$X_n=1$
for every n.)
As a consequence of 5.15, we get the Birkhoff theorems over
![]() $\operatorname{\bf Met}$
from Mardare et al. (Reference Mardare, Panangaden and Plotkin2017), see Adámek (Reference Adámek2022, Theorem 2.14). Here, under an
$\operatorname{\bf Met}$
from Mardare et al. (Reference Mardare, Panangaden and Plotkin2017), see Adámek (Reference Adámek2022, Theorem 2.14). Here, under an
![]() $\omega$
-ary theory over
$\omega$
-ary theory over
![]() $\operatorname{\bf Met}$
we mean an
$\operatorname{\bf Met}$
we mean an
![]() $\mathcal {F}$
-theory where
$\mathcal {F}$
-theory where
![]() $\mathcal {F}$
consists of finite metric spaces, i.e., of finitely generated metric spaces with respect to
$\mathcal {F}$
consists of finite metric spaces, i.e., of finitely generated metric spaces with respect to
![]() $\operatorname{\it Inj}$
.
$\operatorname{\it Inj}$
.
Manes (Reference Manes1976) defined a
![]() $\operatorname{\it Surj}$
-Birkhoff subcategory
$\operatorname{\it Surj}$
-Birkhoff subcategory
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\operatorname{\bf Alg}\!(\mathcal {T})_0$
as a full replete subcategory closed under products,
$\operatorname{\bf Alg}\!(\mathcal {T})_0$
as a full replete subcategory closed under products,
![]() $\operatorname{\it Inj}$
-subalgebras and
$\operatorname{\it Inj}$
-subalgebras and
![]() $U_0$
-split quotients. Here, a morphism
$U_0$
-split quotients. Here, a morphism
![]() $g:K\to L$
in
$g:K\to L$
in
![]() $\operatorname{\bf Alg}\!(\mathcal {T})_0$
is an
$\operatorname{\bf Alg}\!(\mathcal {T})_0$
is an
![]() $\operatorname{\it Inj}$
-subalgebra of L if g is an injection. Since the monad T preserves surjections, Manes (Reference Manes1976, Chapter 3, Theorem 4.23) shows that a full subcategory
$\operatorname{\it Inj}$
-subalgebra of L if g is an injection. Since the monad T preserves surjections, Manes (Reference Manes1976, Chapter 3, Theorem 4.23) shows that a full subcategory
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\operatorname{\bf Alg}\!(\mathcal {T})_0$
is a
$\operatorname{\bf Alg}\!(\mathcal {T})_0$
is a
![]() $\operatorname{\it Surj}$
-Birkhoff subcategory if and only if it is a reflective subcategory such that
$\operatorname{\it Surj}$
-Birkhoff subcategory if and only if it is a reflective subcategory such that
![]() $U_0(\rho_K)$
is a surjection for every reflection
$U_0(\rho_K)$
is a surjection for every reflection
![]() $\rho_K:K\to K^\ast$
. FollowingManes (Reference Manes1976, Chapter 3, Theorem 3.3)
$\rho_K:K\to K^\ast$
. FollowingManes (Reference Manes1976, Chapter 3, Theorem 3.3)
![]() $\mathcal {L}$
is monadic over
$\mathcal {L}$
is monadic over
![]() $\mathcal {V}_0$
. Hence, every Birkhoff subcategory of
$\mathcal {V}_0$
. Hence, every Birkhoff subcategory of
![]() $\operatorname{\bf Alg}\!(\mathcal {T})_0$
is a
$\operatorname{\bf Alg}\!(\mathcal {T})_0$
is a
![]() $\operatorname{\it Surj}$
-Birkhoff subcategory.
$\operatorname{\it Surj}$
-Birkhoff subcategory.
Corollary 5.18. Let
![]() $\Sigma$
be a
$\Sigma$
be a
![]() $\mu$
-ary (discrete) signature where
$\mu$
-ary (discrete) signature where
![]() $\mu=\omega$
or
$\mu=\omega$
or
![]() $\mu=\omega_1$
. Then a class of quantitative
$\mu=\omega_1$
. Then a class of quantitative
![]() $\Sigma$
-algebras is a
$\Sigma$
-algebras is a
![]() $\mu$
-Surj-Birkhoff subcategory of
$\mu$
-Surj-Birkhoff subcategory of
![]() $\operatorname{\bf Alg}\!(\Sigma)$
if and only it is given by an
$\operatorname{\bf Alg}\!(\Sigma)$
if and only it is given by an
![]() $\mu$
-basic quantitative equational theory.
$\mu$
-basic quantitative equational theory.
Proof. At first, we observe that, for a discrete
![]() $\mu$
-ary
$\mu$
-ary
![]() $\operatorname{\bf Met}$
-theory
$\operatorname{\bf Met}$
-theory
![]() $\mathcal {T}$
, the functor
$\mathcal {T}$
, the functor
![]() $U:\operatorname{\bf Alg}\!(\mathcal {T})\to\operatorname{\bf Met}$
preserves
$U:\operatorname{\bf Alg}\!(\mathcal {T})\to\operatorname{\bf Met}$
preserves
![]() $\mu$
-directed colimits of isometries. For
$\mu$
-directed colimits of isometries. For
![]() $\mu=\omega_1$
it is evident and, for
$\mu=\omega_1$
it is evident and, for
![]() $\mu=\omega$
, it follows from Rosický (Reference Rosický2021, Theorem 3.19).
$\mu=\omega$
, it follows from Rosický (Reference Rosický2021, Theorem 3.19).
Following 4.3(2),
![]() $\operatorname{\bf Alg}\!(\Sigma)\cong\operatorname{\bf Alg}\!(\mathcal {T})$
for a discrete
$\operatorname{\bf Alg}\!(\Sigma)\cong\operatorname{\bf Alg}\!(\mathcal {T})$
for a discrete
![]() $\mu$
-ary
$\mu$
-ary
![]() $\operatorname{\bf Met}$
-theory
$\operatorname{\bf Met}$
-theory
![]() $\mathcal {T}$
. Given a
$\mathcal {T}$
. Given a
![]() $\mu$
-basic quantitative equational theory E then, following 4.3(2) and I. of the proof of 5.11,
$\mu$
-basic quantitative equational theory E then, following 4.3(2) and I. of the proof of 5.11,
![]() $\operatorname{\bf Alg}\!(E)$
is a
$\operatorname{\bf Alg}\!(E)$
is a
![]() $\mu$
-
$\mu$
-
![]() $\operatorname{\it Surj}$
-Birkhoff subcategory of
$\operatorname{\it Surj}$
-Birkhoff subcategory of
![]() $\operatorname{\bf Alg}\!(\Sigma)$
.
$\operatorname{\bf Alg}\!(\Sigma)$
.
Conversely, let
![]() $\mathcal {L}$
be a
$\mathcal {L}$
be a
![]() $\mu$
-
$\mu$
-
![]() $\operatorname{\it Surj}$
-Birkhoff subcategory of
$\operatorname{\it Surj}$
-Birkhoff subcategory of
![]() $\operatorname{\bf Alg}\!(\Sigma)$
. We extend
$\operatorname{\bf Alg}\!(\Sigma)$
. We extend
![]() $\Sigma$
to a new signature
$\Sigma$
to a new signature
![]() $\Sigma^\ast$
by adding, for every
$\Sigma^\ast$
by adding, for every
![]() $\varepsilon>0$
, binary operations
$\varepsilon>0$
, binary operations
![]() $f_\varepsilon$
and
$f_\varepsilon$
and
![]() $g_\varepsilon$
satisfying the quantitative equations
$g_\varepsilon$
satisfying the quantitative equations
(1)
 $f_\varepsilon(x,y)=_\varepsilon g_\varepsilon(x,y)$
and
$f_\varepsilon(x,y)=_\varepsilon g_\varepsilon(x,y)$
and(2)
 $x=_\varepsilon y\vdash f_\varepsilon(x,y)=x,\quad x=_\varepsilon y\vdash g_\varepsilon(x,y)=y.$
$x=_\varepsilon y\vdash f_\varepsilon(x,y)=x,\quad x=_\varepsilon y\vdash g_\varepsilon(x,y)=y.$
Then subalgebras of
![]() $\Sigma^\ast$
-algebras satisfying (1) and (2) are
$\Sigma^\ast$
-algebras satisfying (1) and (2) are
![]() $\operatorname{\it Inj}$
-subalgebras. Indeed, let B be a subalgebra of a
$\operatorname{\it Inj}$
-subalgebras. Indeed, let B be a subalgebra of a
![]() $\Sigma^\ast$
-algebra A satisfying (1) and (2) and consider
$\Sigma^\ast$
-algebra A satisfying (1) and (2) and consider
![]() $a,b\in B$
such that
$a,b\in B$
such that
![]() $d_B(a,b)>d_A(a,b)$
. Following (2) for
$d_B(a,b)>d_A(a,b)$
. Following (2) for
![]() $\varepsilon=d_A(a,b)$
, we have
$\varepsilon=d_A(a,b)$
, we have
which contradicts (1).
Let
![]() $\mathcal {L}^\ast$
consist of all
$\mathcal {L}^\ast$
consist of all
![]() $\Sigma^\ast$
-algebras satisfying (1) and (2) whose
$\Sigma^\ast$
-algebras satisfying (1) and (2) whose
![]() $\Sigma$
-reduct is in
$\Sigma$
-reduct is in
![]() $\mathcal {L}$
. Then
$\mathcal {L}$
. Then
![]() $\mathcal {L}^\ast$
is a
$\mathcal {L}^\ast$
is a
![]() $\mu$
-Birkhoff subcategory of
$\mu$
-Birkhoff subcategory of
![]() $\operatorname{\bf Alg}\!(\Sigma^\ast)$
. Let
$\operatorname{\bf Alg}\!(\Sigma^\ast)$
. Let
![]() $\mathcal {T}^\ast$
be the discrete
$\mathcal {T}^\ast$
be the discrete
![]() $\mu$
-ary
$\mu$
-ary
![]() $\operatorname{\bf Met}$
-theory given by
$\operatorname{\bf Met}$
-theory given by
![]() $\Sigma^\ast$
, (1) and (2). Following 5.15,
$\Sigma^\ast$
, (1) and (2). Following 5.15,
![]() $\mathcal {L}^\ast=\operatorname{\bf Alg}\!(E^\ast)$
where equations
$\mathcal {L}^\ast=\operatorname{\bf Alg}\!(E^\ast)$
where equations
![]() $p=q$
from
$p=q$
from
![]() $E^\ast$
have
$E^\ast$
have
![]() $p,q:F^\ast Y \to F^\ast X$
with X and Y being
$p,q:F^\ast Y \to F^\ast X$
with X and Y being
![]() $\mu$
-generated with respect to
$\mu$
-generated with respect to
![]() $\operatorname{\it Inj}$
. Let E’ consist of those equations from
$\operatorname{\it Inj}$
. Let E’ consist of those equations from
![]() $E^\ast$
which do not contain the added operations
$E^\ast$
which do not contain the added operations
![]() $f_\varepsilon$
and
$f_\varepsilon$
and
![]() $g_\varepsilon$
. Clearly,
$g_\varepsilon$
. Clearly,
![]() $\operatorname{\bf Alg}\!(E')\subseteq\mathcal {L}$
. Consider
$\operatorname{\bf Alg}\!(E')\subseteq\mathcal {L}$
. Consider
![]() $A\in\mathcal {L}$
and interpret
$A\in\mathcal {L}$
and interpret
![]() $f_\varepsilon$
and
$f_\varepsilon$
and
![]() $g_\varepsilon$
on A as follows:
$g_\varepsilon$
on A as follows:
![]() $(f_\varepsilon)_A(x,y)=x$
and
$(f_\varepsilon)_A(x,y)=x$
and
![]() $(g_\varepsilon)_A(x,y)=y$
if
$(g_\varepsilon)_A(x,y)=y$
if
![]() $d(x,y)=\varepsilon$
and
$d(x,y)=\varepsilon$
and
![]() $(f_\varepsilon)_A=(g_\varepsilon)_A$
otherwise. Since we get an
$(f_\varepsilon)_A=(g_\varepsilon)_A$
otherwise. Since we get an
![]() $E^\ast$
-algebra,
$E^\ast$
-algebra,
![]() $\mathcal {L}\subseteq\operatorname{\bf Alg}\!(E')$
.
$\mathcal {L}\subseteq\operatorname{\bf Alg}\!(E')$
.
Acknowledgements
The author is grateful to Jiří Adámek for valuable discussions, to Jason Parker for pointing out that Rosický (Reference Rosický2021, Proposition 5.1) is false and to the anonymous referees for the careful examination of the paper and many valuable suggestions. In particular, they detected a gap in our original proof of Birkhoff type theorems.
Competing interests
The author declares none.
Appendix A. Appendix
Rosický (Reference Rosický2021, Proposition 5.1) claims that finite products commute with reflexive coequalizers in
![]() $\operatorname{\bf Met}$
. Equivalently, that the functor
$\operatorname{\bf Met}$
. Equivalently, that the functor
preserves reflexive coequalizers. Since this functor preserves coproducts, the preservation of reflexive coequalizers is equivalent to the preservation of all colimits, i.e., following the Special Adjoint Functor Theorem, to the cartesian closedness of
![]() $\operatorname{\bf Met}$
. Thus Rosický (Reference Rosický2021, Proposition 5.1) is not true and I am grateful to Jason Parker for pointing this out.
$\operatorname{\bf Met}$
. Thus Rosický (Reference Rosický2021, Proposition 5.1) is not true and I am grateful to Jason Parker for pointing this out.
In fact, Rosický (Reference Rosický2021, Proposition 5.1) proves that the functor
preserves reflexive coequalizers where
![]() $\operatorname{\bf Dist}$
is the category of distance spaces and nonexpanding mappings. Recall that a distance space is equipped with a metric
$\operatorname{\bf Dist}$
is the category of distance spaces and nonexpanding mappings. Recall that a distance space is equipped with a metric
![]() $d:X\to[0,\infty]$
satisfying
$d:X\to[0,\infty]$
satisfying
![]() $d(x,y)=d(y,x)$
and
$d(x,y)=d(y,x)$
and
![]() $d(x,x)=0$
. The category
$d(x,x)=0$
. The category
![]() $\operatorname{\bf Dist}$
is cartesian closed (Adámek and Reiterman, Reference Adámek and Reiterman1990).
$\operatorname{\bf Dist}$
is cartesian closed (Adámek and Reiterman, Reference Adámek and Reiterman1990).
The category
![]() $\operatorname{\bf PMet}$
of pseudometric spaces (i.e., with the triangle inequality added) is a reflective subcategory of
$\operatorname{\bf PMet}$
of pseudometric spaces (i.e., with the triangle inequality added) is a reflective subcategory of
![]() $\operatorname{\bf Dist}$
; the reflection of (X,d) is obtained by the pseudometric modification
$\operatorname{\bf Dist}$
; the reflection of (X,d) is obtained by the pseudometric modification
![]() $d^\ast$
of d:
$d^\ast$
of d:
 $$d^\ast(x,z)={\mathrm{inf}}\{\sum_{i=0}^{n-1}d(y_i,y_{i+1})\,|\, n\geq1, y_i\in X, y_0=x, y_n=z\}.$$
$$d^\ast(x,z)={\mathrm{inf}}\{\sum_{i=0}^{n-1}d(y_i,y_{i+1})\,|\, n\geq1, y_i\in X, y_0=x, y_n=z\}.$$
Hence,
![]() $\operatorname{\bf Met}$
is a reflective subcategory of
$\operatorname{\bf Met}$
is a reflective subcategory of
![]() $\operatorname{\bf Dist}$
. We have just explained that the reflector
$\operatorname{\bf Dist}$
. We have just explained that the reflector
![]() $F:\operatorname{\bf Dist}\to\operatorname{\bf Met}$
cannot preserve finite products. We will show that it does not even preserve finite powers.
$F:\operatorname{\bf Dist}\to\operatorname{\bf Met}$
cannot preserve finite products. We will show that it does not even preserve finite powers.
Example A.1. Consider the distance spaces
![]() $A_0=\{x,y,z\}$
and
$A_0=\{x,y,z\}$
and
![]() $A_1=\{u,v,w\}$
where
$A_1=\{u,v,w\}$
where
![]() $d(x,y)=d(v,w)=2$
,
$d(x,y)=d(v,w)=2$
,
![]() $d(y,z)=d(u,v)=1$
and
$d(y,z)=d(u,v)=1$
and
![]() $d(x,z)=d(u,w)=\infty$
. Let A be the coproduct
$d(x,z)=d(u,w)=\infty$
. Let A be the coproduct
![]() $A_0+A_1$
. Then the metric modification FA only changes d(x,z) and d(u,w) to 3. Hence, the distance of [x, u] and [z, w] in
$A_0+A_1$
. Then the metric modification FA only changes d(x,z) and d(u,w) to 3. Hence, the distance of [x, u] and [z, w] in
![]() $FA\times FA$
is 3.
$FA\times FA$
is 3.
In
![]() $A\times A$
, we have
$A\times A$
, we have
![]() $(d[x,u],[y,v])=d([y,v],[z,w])=2$
, hence
$(d[x,u],[y,v])=d([y,v],[z,w])=2$
, hence
![]() $[d[x,u],[z,w])=4$
in
$[d[x,u],[z,w])=4$
in
![]() $F(A\times A)$
.
$F(A\times A)$
.
The distance space
![]() $A_0$
above is the quotient in
$A_0$
above is the quotient in
![]() $\operatorname{\bf Dist}$
of the coproduct
$\operatorname{\bf Dist}$
of the coproduct
![]() $A_{00}+A_{01}+A_{02}$
of metric spaces
$A_{00}+A_{01}+A_{02}$
of metric spaces
![]() $A_{00}=\{x,y\}$
,
$A_{00}=\{x,y\}$
,
![]() $A_{01}=\{y',z\}$
and
$A_{01}=\{y',z\}$
and
![]() $A_{02}=\{x',z'\}$
where
$A_{02}=\{x',z'\}$
where
![]() $d(x,y)=2$
,
$d(x,y)=2$
,
![]() $d(y',z)=1$
and
$d(y',z)=1$
and
![]() $d(x',z')=\infty$
modulo the equivalence relation
$d(x',z')=\infty$
modulo the equivalence relation
![]() $x\sim x'$
,
$x\sim x'$
,
![]() $y\sim y'$
and
$y\sim y'$
and
![]() $z\sim z'$
. Thus,
$z\sim z'$
. Thus,
![]() $FA_0$
is the quotient of
$FA_0$
is the quotient of
![]() $A_{00}+A_{01}+A_{02}$
modulo this equivalence relation in
$A_{00}+A_{01}+A_{02}$
modulo this equivalence relation in
![]() $\operatorname{\bf Met}$
. Similarly,
$\operatorname{\bf Met}$
. Similarly,
![]() $A_1$
is the quotient in
$A_1$
is the quotient in
![]() $\operatorname{\bf Dist}$
of the coproduct
$\operatorname{\bf Dist}$
of the coproduct
![]() $A_{10}+A_{11}+A_{12}$
of metric spaces
$A_{10}+A_{11}+A_{12}$
of metric spaces
![]() $A_{10}=\{u,v\}$
,
$A_{10}=\{u,v\}$
,
![]() $A_{11}=\{v',w\}$
and
$A_{11}=\{v',w\}$
and
![]() $A_{12}=\{u',w'\}$
modulo the equivalence relation
$A_{12}=\{u',w'\}$
modulo the equivalence relation
![]() $u\sim u'$
,
$u\sim u'$
,
![]() $v\sim v'$
and
$v\sim v'$
and
![]() $w\sim w'$
. Hence,
$w\sim w'$
. Hence,
![]() $FA_1$
is the quotient of
$FA_1$
is the quotient of
![]() $A_{10}+A_{11}+A_{12}$
modulo this equivalence relation in
$A_{10}+A_{11}+A_{12}$
modulo this equivalence relation in
![]() $\operatorname{\bf Met}$
. Consequently, FA is the quotient of the equivalence relation
$\operatorname{\bf Met}$
. Consequently, FA is the quotient of the equivalence relation
![]() $\sim$
on
$\sim$
on
![]() $B=A_{00}+A_{01}+A_{02}+A_{10}+A_{11}+A_{12}$
in
$B=A_{00}+A_{01}+A_{02}+A_{10}+A_{11}+A_{12}$
in
![]() $\operatorname{\bf Met}$
. Similarly,
$\operatorname{\bf Met}$
. Similarly,
![]() $F(A\times A)$
is the quotient of
$F(A\times A)$
is the quotient of
![]() $\sim\times\sim$
on
$\sim\times\sim$
on
![]() $B\times B$
.
$B\times B$
.
Example A.1 thus shows that quotients of equivalence relations do not commute with finite powers in
![]() $\operatorname{\bf Met}$
. Hence, reflexive coequalizers do not commute with finite powers in
$\operatorname{\bf Met}$
. Hence, reflexive coequalizers do not commute with finite powers in
![]() $\operatorname{\bf Met}$
. Consequently, Rosický (Reference Rosický2021, Corollary 5.2, Corollary 5.3, Lemma 5.4 and Example 5.6) are false.
$\operatorname{\bf Met}$
. Consequently, Rosický (Reference Rosický2021, Corollary 5.2, Corollary 5.3, Lemma 5.4 and Example 5.6) are false.