Research Article
The Solution of the Biquadratic x4 + px3 + qx2 + rx + s = 0
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 239-241
-
- Article
-
- You have access
- Export citation
Direction-Cosines of the Axes of the Conicoid
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 242-243
-
- Article
-
- You have access
- Export citation
Proofs of some Inequalities and Limits
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 243-246
-
- Article
-
- You have access
- Export citation
Elementary Method of investigating the Centroid of a Uniform Circular Arc
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 247-248
-
- Article
-
- You have access
- Export citation
Nomogram for the Solution of the Equation z3 + pz + q = 0
-
- Published online by Cambridge University Press:
- 31 October 2008, p. 248
-
- Article
-
- You have access
- Export citation
Elementary Methods of interpreting the Equation of the first degree in two and three dimensions
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 250-253
-
- Article
-
- You have access
- Export citation
A simple form of Integrometer
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 253-254
-
- Article
-
- You have access
- Export citation
Front matter
MAN volume 21 Cover and Front matter
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation

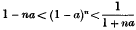 with certain restrictions as to the values of
with certain restrictions as to the values of 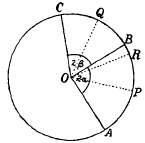
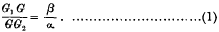
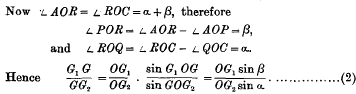
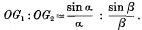
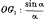 is independent of α, and therefore
is independent of α, and therefore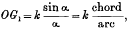
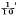 ″ vertically. It is graduated with the values of
″ vertically. It is graduated with the values of