Hostname: page-component-669899f699-rg895 Total loading time: 0 Render date: 2025-05-07T01:19:51.748Z Has data issue: false hasContentIssue false
  • English
  • Français

A characterization of alternating links in thickened surfaces

Published online by Cambridge University Press:  13 December 2021

Hans U. Boden Open the ORCID record for Hans U. Boden [Opens in a new window]  and
Homayun Karimi
Hans U. Boden
Affiliation:
Mathematics & Statistics, McMaster University, Hamilton, Ontario, ([email protected]; [email protected])
Homayun Karimi
Affiliation:
Mathematics & Statistics, McMaster University, Hamilton, Ontario, ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We use an extension of Gordon–Litherland pairing to thickened surfaces to give a topological characterization of alternating links in thickened surfaces. If $\Sigma$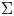 is a closed oriented surface and $F$ 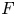is a compact unoriented surface in $\Sigma \times I$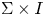, then the Gordon–Litherland pairing defines a symmetric bilinear pairing on the first homology of $F$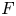. A compact surface in $\Sigma \times I$ 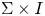is called definite if its Gordon–Litherland pairing is a definite form. We prove that a link $L$ 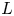in a thickened surface is non-split, alternating, and of minimal genus if and only if it bounds two definite surfaces of opposite sign.

Keywords

Links in thickened surfacesalternating linkspanning surfaceGordon–Litherland pairingdefinite surfacevirtual linkcheckerboard colouring
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 1 , February 2023 , pp. 177 - 195
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Boden, H. U., Chrisman, M. and Karimi, H., The Gordon-Litherland pairing for links in thickened surfaces, 2021 preprint. https://arxiv.org/pdf/2107.00426.pdfArXiv/2107.00426.Google Scholar
Boden, H. U., Gaudreau, R. I., Harper, E., Nicas, A. J. and White, L.. Virtual knot groups and almost classical knots. Fundam. Math. 138 (2017), 101–142.CrossRefGoogle Scholar
Boden, H. U. and Karimi, H., The Jones-Krushkal polynomial and minimal diagrams of surface links, 2019 preprint. https://arxiv.org/pdf/1908.06453.pdfArXiv/1908.06453, to appear in Ann. Inst. Fourier (Grenoble).Google Scholar
Boden, H. U., Karimi, H. and Sikora, A. S., Adequate links in thickened surfaces and the generalized Tait conjectures, 2020 preprint. https://arxiv.org/pdf/2008.09895.pdfArXiv/2008.09895.Google Scholar
Carter, J. S., Kamada, S. and Saito, M.. Stable equivalence of knots on surfaces and virtual knot cobordisms. J. Knot Theory Ramificat. 11 (2002), 311–322. Knots 2000 Korea, Vol. 1 (Yongpyong).CrossRefGoogle Scholar
Carter, J. S., Silver, D. S. and Williams, S. G.. Invariants of links in thickened surfaces. Algebr. Geom. Topol. 14 (2014), 1377–1394.CrossRefGoogle Scholar
McA. Gordon, C. and Litherland, R. A.. On the signature of a link. Invent. Math. 47 (1978), 53–69.CrossRefGoogle Scholar
Greene, J. E.. Alternating links and definite surfaces. Duke Math. J. 166 (2017), 2133–2151. With an appendix by András Juhász and Marc Lackenby.CrossRefGoogle Scholar
Hatcher, A., Notes on basic 3-manifold topology, 2007. (unpublished book) https://pi.math.cornell.edu/hatcher/3M/3Mfds.pdf.Google Scholar
Howie, J. A.. A characterisation of alternating knot exteriors. Geom. Topol. 21 (2017), 2353–2371.CrossRefGoogle Scholar
Ito, T.. A characterization of almost alternating knots. J. Knot Theory Ramificat. 27 (2018), 1850009.CrossRefGoogle Scholar
Kamada, N.. On the Jones polynomials of checkerboard colorable virtual links. Osaka J. Math. 39 (2002), 325–333.Google Scholar
Karimi, H., Alternating Virtual Knots. PhD thesis, McMaster University, September 2018. McMaster University.Google Scholar
Kauffman, L. H.. Virtual knot theory. European J. Combin. 20 (1999), 663–690.CrossRefGoogle Scholar
Kim, S.. A topological characterization of toroidally alternating knots. Comm. Anal. Geom. 27 (2019), 1825–1850.CrossRefGoogle Scholar
Kindred, T., A geometric proof of the Flyping Theorem, 2020 preprint. https://arxiv.org/pdf/2008.06490.pdfArXiv/2008.06490.Google Scholar
Krushkal, V.. Graphs, links, and duality on surfaces. Combin. Probab. Comput. 20 (2011), 267–287.CrossRefGoogle Scholar
Kuperberg, G.. What is a virtual link?. Algebr. Geom. Topol. 3 (2003), 587–591.CrossRefGoogle Scholar
Waldhausen, F.. On irreducible $3$-manifolds which are sufficiently large. Ann. Math. (2) 87 (1968), 56–88.CrossRefGoogle Scholar
Yasuhara, A.. An elementary proof for that all unoriented spanning surfaces of a link are related by attaching/deleting tubes and Möbius bands. J. Knot Theory Ramificat. 23 (2014), 1450004.CrossRefGoogle Scholar