Introduction
Recent work has suggested that as a glacier moves over a saturated, unconsolidated stratum, shear stresses exerted by the glacier can exceed the shear strength of the sediment, initiating deformation (Reference Boulton and JonesBoulton and Jones, 1979; Reference Alley, Blankenship, Bentley and RooneyAlley and others, 1987; Reference ClarkeClarke, 1987). This process is termed subglacial deformation and has been described in relation to Quaternary deposits (Reference ClarkClark, 1991; Reference Hart, Boulton, Ehlers, Gibbard and RoseHart and Boulton, 1991b; Reference Hicock and DreimanisHicock and Dreimanis, 1992; Reference HartHart, 1994; Reference HartHart and Roberts, 1994) and also beneath contemporary glaciers such as Breidamer- kurjokull in Iceland (Reference Boulton and JonesBoulton and Jones, 1979), Ice Stream B in western Antarctica (Reference Alley, Blankenship, Bentley and RooneyAlley and others, 1986; Englehardt and others, 1990) and Trapridge Glacier in Canada (Reference Blake and ClarkeBlake and Clarke, 1989). An extensive set of features has been associated with deforming-bed sediments including tectonic laminations, boudins and augens, folds, sharp basal décollement surfaces, predictable till fabrics, characteristic micromorphologies and boulder pavements (Reference Dowdeswell and SharpDowdeswell and Sharp, 1986; Reference HartHart and others, 1990; Reference ClarkClark, 1991; Reference Hart, Boulton, Ehlers, Gibbard and RoseHart and Boulton, 1991b; Reference HicockHicock, 1991; Reference Van der MeerVan der Meer, 1993; Reference HartHart and Roberts, 1994; Reference HartHart, 1998). Although it is possible to use such features to identify subglacial deposits, further criteria are needed to support interpretations. The need for unequivocal criteria to distinguish subglacial facies from other deposits has been highlighted by Reference HartHart and Roberts (1994) and Van der Meer (1993, 1997). In these cases, micromorphology has revealed new insights into the internal grain structure and behaviour of deforming bed tills.
Reference Hooke and IversonHooke and Iverson (1995) and Reference Iverson, Hooyer and HookeIverson and others (1996) propose a technique for facies analysis which uses fractal dimension of grain-size distributions to interpret styles and degrees of deformation in glacial sediments. Fractal dimension has been shown to be a useful interpretative tool in other areas of geology where highly deformed sediments exhibit self-similar grain-size distributions (Reference TurcotteTurcotte, 1986; Reference Biegel, Sammis and DieterichBiegel and others, 1989; Reference Brosch, Polsler and RiedMüllerBrosch and others, 1992). Reference Sammis, King and BiegelSammis and others (1987) carried out a detailed investigation of the grain-size distributions of fault breccia and concluded that the probability of fracture of any particle is independent of scale and after many fracture events a lognormal distribution of particle sizes results (Reference EpsteinEpstein, 1949). The theoretical fractal dimension of a fracture-dominated facies is 2.58 (Reference Sammis, King and BiegelSammis and others, 1987). The investigation of grain crushing has subsequently been applied in a variety of other environments, such as geotechnical shear planes (Reference Brosch, Polsler and RiedMüllerBrosch and others, 1992), granular sediments (Reference Mandl, dejong and MalthaMandl and others, 1977) and debris-rich basal ice (Reference Hubbard, Sharp and LawsonHubbard and others, 1996).
Reference Hooke and IversonHooke and Iverson (1995) suggest that high fractal dimensions in basal tills could be attributed to grain slippage and abrasion over grain fracture during deformation. Supplementary evidence to support this argument comes from scan- ning-electron-microscope photographs of rounded grains (from a basal till) exhibiting fracture surfaces. The workers suggest that with further studies, it may be possible to use grain-size distributions expressed as fractal dimensions to distinguish between tills that have undergone deformation and those that have not. In the double-log plots presented by Reference Hooke and IversonHooke and Iverson (1995), the basal tills exhibit a clearer linear relationship than the non-deformed sediments (outwash and dune facies). These two arguments imply that the fractal dimension can be used as a diagnostic criteria for interpreting deformed and non-deformed sediments.
In this paper, we will use the technique proposed by Reference Hooke and IversonHooke and Iverson (1995) to address two main objectives:
-
(1) To investigate whether the fractal dimension can distinguish between non-deformed and deformed facies, comparing supraglacial and subglacial facies explicitly; and
-
(2) To evaluate whether the fractal dimension can be used as a diagnostic criterion to discriminate between different styles and degrees of basal deformation. This is tested using a range of sediments from the deforming continuum suggested by Reference Hart, Boulton, Ehlers, Gibbard and RoseHart and Boulton (1991b).
Only one contemporary glacier (the Haut Glacier d’Arolla, Vallais, Switzerland) was used in our study to collect the supraglacial facies (due to logistical and time constraints). Collection of unequivocal subglacial sediments from contemporary glaciers is difficult and the techniques being developed to directly access this environment (Reference Blake, Clarke and GerinBlake and others, 1992; Reference Iverson, Jansson and HookeIverson and others, 1994) were not available during this study. For the purpose of this study, subglacial sediments interpreted to be deformed during the Quaternary were collected in England (Reference Hart, Boulton, Ehlers, Gibbard and RoseHart and Boulton, 1991a, b; Reference Rose and MitchellRose, 1991).
Application of Fractals to Deformed Sediments
The process of grain-crushing has been widely investigated in both cataclastic geology (Reference Mandl, dejong and MalthaMandl and others, 1977; Reference Sammis, King and BiegelSammis and others, 1987; Reference Biegel, Sammis and DieterichBiegel and others, 1989) and glacial sediments (Reference Boulton, Dent and MorrisBoulton and others, 1974; Reference HaldorsenHaldorsen, 1981; Reference Hooke and IversonHooke and Iverson, 1995; Reference Iverson, Hooyer and HookeIverson and others, 1996). Geological studies have focused on the process of structural faulting at shallow depths in the Earth’s crust, which causes rock to brecciate into a sediment termed fault breccia. The fault breccia is formed by the repeated fracture of grains, which eventually leads to a grain-size distribution in which the number of equal-sized particles is minimized over a wide range of scales. Reference Sammis, King and BiegelSammis and others (1987) argue that the highest inter- granular stresses occur when two grains of identical size are in contact with one another. In this case, one of the particles is likely to break allowing a grain-size distribution to evolve which separates similar-sized grains. This spatial organization of grains produces a uniform distribution of stresses which minimizes stress concentrations. As a consequence, the fault breccia exhibits a self-similar (or fractal) grain-size distribution (Reference Sammis, King and BiegelSammis and others, 1987). The fractal dimension for fault breccia calculated by these workers was 2.58.
Reference Hooke and IversonHooke and Iverson (1995) applied this theory to deformed glacial sediments. Within a subglacial environment, shear stresses are imposed on a basal layer of till. The granular material exhibits a resistance to shear through the formation of grain bridges which support a compressive stress. The failure of these grain bridges may take one of two forms, fracture or slippage. Reference Hooke and IversonHooke and Iverson (1995) suggest that because a subglacial till is vertically constrained beneath the ice mass, dilation is inhibited and grain fracture becomes an important mechanism for grain-bridge failure. Tests carried out on deforming granular sediments in a ring shear apparatus have demonstrated both of the mechanisms described above (Reference Mandl, dejong and MalthaMandl and others, 1977; Reference Biegel, Sammis and DieterichBiegel and others, 1989). Whether a bridge fails by slippage or fracture is dependent on the strength of the particles and the angle of interparticle slip. These factors in turn depend on the particle-size distribution and the packing geometry (Reference Biegel, Sammis and DieterichBiegel and others, 1989).
Reference Hooke and IversonHooke and Iverson (1995) studied the grain-size distributions of three basal tills (Storglaciaren, Sweden; Engabreen, Norway; Ice Stream B, Antarctica) and discovered that their fractal values yielded a mean value of ~2.9. This value is higher than the theoretical value (2.58) required to minimize stress concentrations, suggesting that the tills have a higher content of fines than can be explained by grain fracture alone. To explain this, Reference Hooke and IversonHooke and Iverson (1995) suggest that during failure by slippage, abrasion among grains produces finer particles. If fracture were the sole factor in the failure of bridges, two or more particles of roughly equal size would always result. Using evidence from photomicrographs of rounded grains (which do not display equally sized grain pairs), the workers suggest that slip failure is more important in deformation tills than in fault breccia.
Methodology
Sample collection
A range of sediment samples (Tables 1 and 2) were collected from contemporary and Quaternary glacial environments, including diamictons which have been interpreted as sub- glacially deformed sediments and also sediments of supra-glacial origin. These two facies groups are subject to varying degrees of deformation as they are transported through the glacial system and provide an excellent opportunity to test our two main objectives. Figure 1 illustrates the possible pathways of sediments through the glacier/sub-glacial system.

Fig. 1. Schematic diagram showing debris pathways through the glacier system.
Table 1. Range of supraglacial samples analysed from the Glacier d’Arolla.

Table 2. Range of subglacial samples analysed from Norfolk and Cumbria. The selection of these facies reflects the deforming continuum as suggested by Reference Hart, Boulton, Ehlers, Gibbard and RoseHart and Boulton (1991b).

Supraglacial samples
Bulk samples of supraglacial samples were collected from the Glacier d’Arolla. The samples were selected on the assumption they had not been subject to deformational processes during transportation through the glacial system (Fig. 1).
Subglacial samples
North Norfolk sites
Samples interpreted to be subglacially deformed diamictons were collected from a Quaternary site in Norfolk, England (Reference Hart, Boulton, Ehlers, Gibbard and RoseHart and Boulton, 1991a, b). This site was ideal for our analysis as we could sample a range of deformed facies.
The facies collected reflect the range of deformation within a subglacial environment. Facies groups grade from subglacial diamictons, through to boudins and tectonic laminae, and finally to a sample from an unconsolidated fault breccia. The diamictons at West Runton and Triming- ham display features characteristic of deformation such as sheath folds, boudins and augens (Reference Hart, Boulton, Ehlers, Gibbard and RoseHart and Boulton, 1991b; Reference HartHart and Roberts, 1994). These features are formed as a result of ductile deformation in the subglacial zone. Figure 1 illustrates how preglacial sediments are folded into the diamicton to form boudins, which become attenuated to form laminations, and then homogenized into a diamicton. This process can be conceptualized as a deformation continuum and is reflected in the sample selection.
The sediments of northeast Norfolk contain a number of distinct tills of the Anglian (Elsterian) glaciation. At West Runton (WR) a series of samples (WRP1, WRG3) were collected from the laminated diamicton (grid reference 187434) and at Trimingham (TGS6, grid reference 275394). These sediments have been interpreted as deforming bed tills (Reference Hart, Boulton, Ehlers, Gibbard and RoseHart and Boulton, 1991a) deposited during the Anglian (Elsterian) glaciation. Additionally, a fault breccia produced by a proglacial thrust fault within the Gromer Ridge push moraine (Reference HartHart, 1990) was sampled (Fig. 2). Figure 2b shows a cross-section of sedimentological features across the Trimingham fault zone (TFB). This area of intense brittle deformation was sampled (TFB1-5) but only TFB 4 was deemed suitable for analysis.
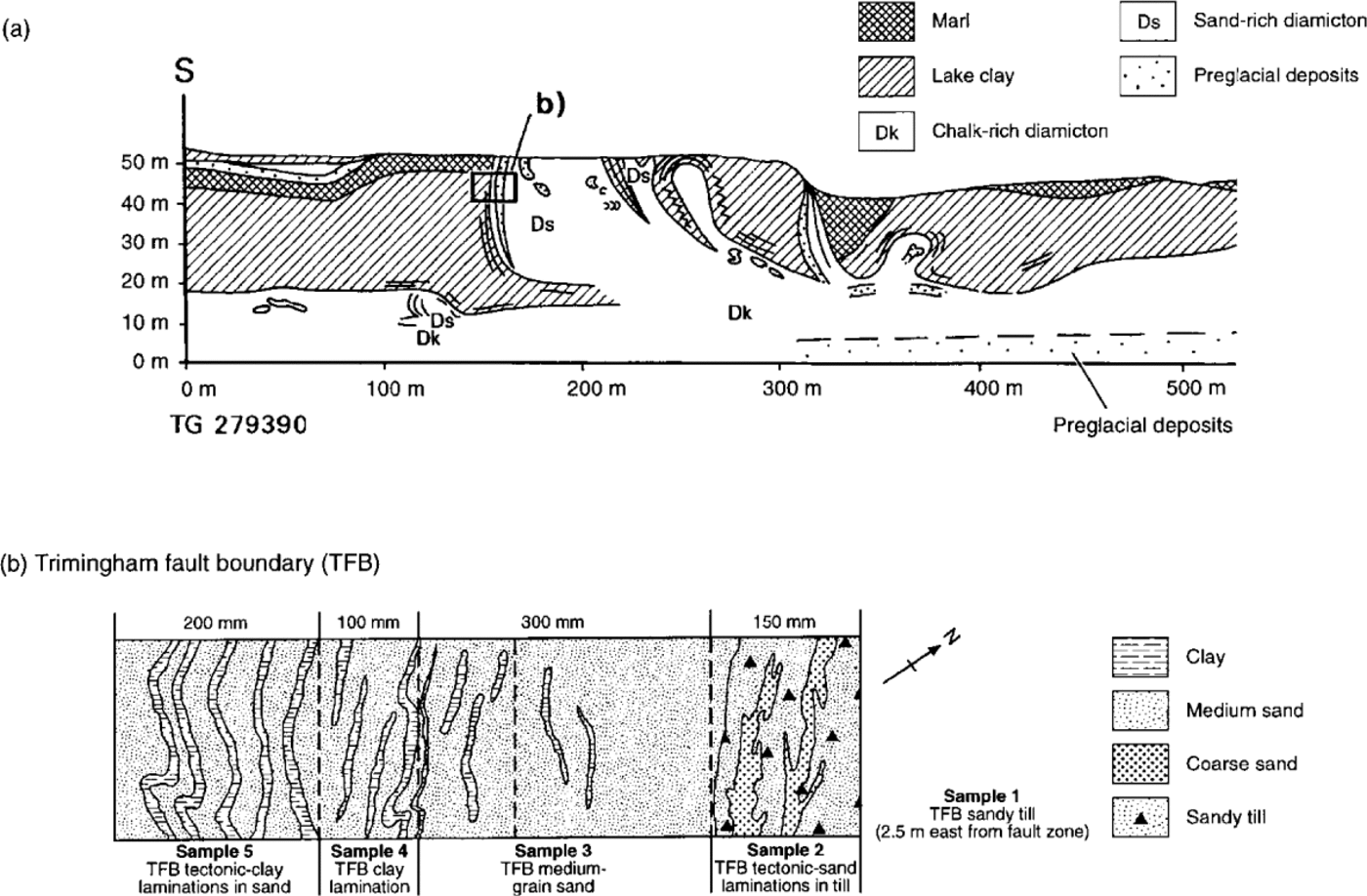
Fig. 2. Proglacial deformation at Trimingham: (a) large-scale section diagram of the listric thrustfault at the site (after Reference HartHart, 1990); (b) sedimentology along thefault breccia.
Drumlin sites
Many researchers consider drumlins to be associated with the deforming bed (e.g. Reference Boulton, Menzies and RoseBoulton, 1987). In addition, Reference HartHart (1997) has argued that the internal structures of drumlins can be depositional, deformational or erosional depending on the relative competencies of material within the core and the deforming layer. Depositional drumlins will be composed of till deposited during the drumlinization process; deformational drumlins will show brittle or ductile deformation; and erosional drumlins will contain sediment that was not deformed/deposited during the drumlinizing event. Samples were taken from two drumlin sites: Widdale Side, North Yorkshire (grid reference 834886) and Grisedale Beck, Gumbria (grid reference 778923).
At Widdale Side, three samples were collected from the stoss side (WSS1-3) and a further sample was obtained towards the lee side (WSL). According to an interpretation by Reference Rose and MitchellRose (1991), the lowest unit in the Widdale Side succession is a strongly over consolidated matrix-dominated diamicton. The matrix is composed of crushed mudstone with clasts exhibiting sub-angular to angular shapes. This particular unit has been interpreted as a subglacial till unit formed from local geology. The Grisedale Beck drumlin (grid reference 778923) was sampled in a similar fashion to Widdale Side; two samples were collected at the stoss side (GDS1-2) and a further one towards the lee (GDL).
Calculation of fractal dimension
The samples were mechanically sieved according to a method outlined by Reference McManus and TuckerMcManus (1988). Sediments sieved to under 125μm (3ϕ) were processed through a laser granulometer (LS Goulter counter). The combination of the two datasets assumed that particles were spherical, non-porous and of a constant density. Our grain-size classes ranged from 16.0 mm (~4ϕ) to 0.001 mm (10ϕ). In some cases data are absent from the coarse end of the grain-size spectrum.
The grain-size data allowed us to calculate the number of particles between the upper (d 1) and lower size class boundaries (d 2) of our grain-size range. These data yield N (the number of particles), which are plotted logarithmically against particle diameter (d). A linear relationship implies:

where N(d) is the number of particles of size d, N 0 is the number of particles of reference diameter d 0, and m is the fractal dimension. A well-constrained linear relationship on such a plot can then be used to calculate m (the fractal dimension or slope) using regression analysis, which reflects the ratio of smaller to larger particles over the size range analysed (Reference Hubbard, Sharp and LawsonHubbard and others, 1996). The calculation of N from d 1 and d 2 itself depends on the value of m. This means that the process must be iterated (Reference Hooke and IversonHooke and Iverson, 1995). Example plots are shown in Figures 3 and 4. Some plots display a slight displacement at the transition from Coulter counter data and sieve data. This transition does not affect our results significantly. Within our calculations, a bivariate slope-significance test was applied to the data (Reference WilliamsWilliams, 1984).

Fig. 3. Double-log plots of slope values for supraglacial facies comprising sieve and Coulter datasets (N is the number of particles and D is the particle diameter). The slope and correlation values are given on each graph.

Fig. 4. Double-log plots for: (a) subglacial diamicton-matrix facies; (b) boudin facies; (c) tectonic-lamination facies; and (d) fault-breccia facies. Plots comprise sieve and Coulter datasets (N is the number of particles and D is the particle diameter). The slope and correlation values are given on each graph.
Results
Supraglacial facies
The data on this facies are summarized in Table 3. The double-log plots for this facies can be seen in Figure 3. In summary, the three supraglacial samples collected from Haut Glacier d’Arolla have very similar values. The values display an average fractal dimension of 2.834 which is markedly higher than the value presented by Reference Hubbard, Sharp and LawsonHubbard and others (1996) for a medial moraine facies at 2.50.
Table 3. Fractal dimensions for the range of supraglacial samples analysed. The mean and standard deviation are presented. The values for these samples show little difference to the subglacial facies analysed.

Subglacial facies
The data for this facies are summarized in Table 4. The double-log plots of these facies can be seen in Figure 4a—d. The fractal values for the subglacial facies display little variation across the facies boundaries. The subglacial diamicton-matrix facies exhibit a mean value of 2.92, which is very similar to the values found by Reference Hooke and IversonHooke and Iverson (1995) in their basal-till analysis. Boudins and tectonic-lami- nation facies display a mean value which is only slightly lower (but not significantly) than the subglacial diamicton- matrix facies. The fault-breccia facies yields a value of 2.87, which is very similar to the other facies in the group. A Mann—Whitney U test showed there was no significant difference between the supraglacial and the subglacial diamic- ton-matrix fractal-dimension values. Also, that there was no significant difference between the fractal dimensions of the various tectonic facies within the subglacial group. The Mann—Whitney U test results can be seen inTable 5.
Table 4. Fractal dimensions for the range of subglacial samples analysed. The mean and standard deviations are presented. The values do not significantly vary across the deforming continuum nor are they significantly greater than the supraglacialfacies.

Table 5. Mann-Whitney U test for unmatched samples: Significance results.

Discussion
All the subglacial samples suggest a strong tendency towards self-similarity, where the mean value across facies ranges from 2.7–2.9. Although these data support the suggestion by Reference Hooke and IversonHooke and Iverson (1995) that basal tills exhibit fractal behaviour, the technique cannot differentiate between the specific glacial facies tested. In this context, it is interesting to note that the supraglacial facies also have high fractal dimensions. We will attempt to explain the high values associated with this facies in the first part of the discussion. Later, we will examine the various problems involved in this type of analysis.
Supraglacial facies: fractal or not?
The supraglacial facies exhibit high fractal dimensions with a mean value of 2.834. Supraglacial debris may be transported through complex subglacial or englacial pathways on its journey to the snout of the glacier (Reference BoultonBoulton, 1978). Therefore, facies collected in supraglacial locations on glaciers may have undergone deformation and abrasion on their passage through the glacier. This may account for the high fractal dimensions found for the supraglacial facies.
Evaluation of the fractal-analysis technique
Reference Hooke and IversonHooke and Iverson (1995) suggest that facies with fractal values yielding values of 2.9 have a higher content of fines, which can be attributed to grain slippage and abrasion rather than grain fracture. But are there other factors which may influence the amount of fines in a deforming sample just as strongly as grain behaviour?
Reference Hooke and IversonHooke and Iverson (1995) attribute the high fractal dimension of their basal tills to grain abrasion during slippage. However, fine-grained fractions may be inherited from parent lithology. An example of this is where Reference Tulaczyk, Kamb, Scherer and EngelhardtTulaczyk and others (1998) state that the clay-rich diamicton of Ice Stream B cores contained reworked diatoms and the fine-grained nature of the till inhibits glacial comminution because interparticle stress concentrations are cushioned. The origin of the sediment, therefore, not only contributes to the grain-size distribution, but it also affects grain behaviour. Additionally, erosive processes between the bedrock and the deforming bed may also generate fines, contributing to the grain-size distribution of the till.
This raises the question of whether the fractal value is a real indication of the significance of grain behaviour during deformation or just a method of evaluating the prominence of fines within the sediment. Further work is therefore needed to determine whether the fine-grained nature of deformed material is due to grain bridging or to lithological characteristics inherited from parent material. The potential importance of parent lithology brings into question the validity of comparing our data with samples tested by Reference Hooke and IversonHooke and Iverson (1995) and Reference Hubbard, Sharp and LawsonHubbard and others (1996).
Evidence of grain bridging within field samples has yet to be investigated in detail, but Van der Meer (1993, 1997) has discussed the existing evidence for the behaviour of grains during deformation at length. From the extensive analysis of the micromorphology of deformed subglacial sediments, he proposes that particle movements within the matrix are rotational and that grains move freely through the till mass. The particle movement becomes more complex where the areas of the till are dominated by shear zones. Rotational structures are characterized by a nucleus composed of a grain or stiff matrix, surrounded by finer grains. The finer grains have been observed to spiral around the nucleus, which has been termed a galaxy structure (Reference Van der MeerVan der Meer, 1997). Grain bridging in field samples has yet to be discovered and, until such evidence is found, grain rotation appears to be the dominant mechanism governing grain behaviour during deformation.
This process of grain rotation within deforming granular sediments could also be related to a feature observed in a deforming till at Cora Island, Spitsbergen (Reference BoultonBoulton and others, 1989; Reference HartHart, 1995). The presence of a bivalve shell was observed undisturbed within a deformed till where the upper half of the shell was displaced over the lower half. Although this till was interpreted as having been deformed under low shear strains (Reference HartHart, 1995), in a grain-bridging environment the shell would not have survived in this condition. The shell may have behaved as a competent material, being transported as a whole, while the smaller grains in the matrix flowed (or rotated) around it.
Conclusion
The subglacial diamicton-matrix sediments exhibited a mean fractal dimension of 2.92 which compares favourably with findings by Reference Hooke and IversonHooke and Iverson (1995), who calculated an average value of 2.90 for their basal-till samples. However, the technique was unable to distinguish facies across a subglacial continuum ranging from boudins to subglacial diamicton matrix. Although fractal dimension is useful in identifying the tendency of basal tills to self-similarity, it is inconclusive when used to identify deformation across a range of facies.
Acknowledgements
The authors would like to thank B. P. Hubbard for his assistance with calculating the fractal-dimension values. Also, many thanks to T. Aspden and his colleagues at the Cartographic Unit, Department of Geography for their diagram preparation. A. K. was in receipt of a British Federation of Women Graduates grant CF/1 and a University studentship during the field research for this paper.











