Published online by Cambridge University Press: 30 January 2020
We generalize current known distribution results on Shanks–Rényi prime number races to the case where arbitrarily many residue classes are involved. Our method handles both the classical case that goes back to Chebyshev and function field analogues developed in the recent years. More precisely, let 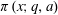 $\unicode[STIX]{x1D70B}(x;q,a)$ be the number of primes up to
$\unicode[STIX]{x1D70B}(x;q,a)$ be the number of primes up to  $x$ that are congruent to
$x$ that are congruent to  $a$ modulo
$a$ modulo 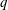 $q$. For a fixed integer
$q$. For a fixed integer 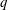 $q$ and distinct invertible congruence classes
$q$ and distinct invertible congruence classes  $a_{0},a_{1},\ldots ,a_{D}$, assuming the generalized Riemann Hypothesis and a weak version of the linear independence hypothesis, we show that the set of real
$a_{0},a_{1},\ldots ,a_{D}$, assuming the generalized Riemann Hypothesis and a weak version of the linear independence hypothesis, we show that the set of real  $x$ for which the inequalities
$x$ for which the inequalities 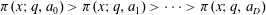 $\unicode[STIX]{x1D70B}(x;q,a_{0})>\unicode[STIX]{x1D70B}(x;q,a_{1})>\cdots >\unicode[STIX]{x1D70B}(x;q,a_{D})$ are simultaneously satisfied admits a logarithmic density.
$\unicode[STIX]{x1D70B}(x;q,a_{0})>\unicode[STIX]{x1D70B}(x;q,a_{1})>\cdots >\unicode[STIX]{x1D70B}(x;q,a_{D})$ are simultaneously satisfied admits a logarithmic density.
This work was partially supported by a Postdoctoral Fellowship at the University of Ottawa.
Please note a has been issued for this article.