Article contents
Asymptotic Nusselt numbers for internal flow in the Cassie state
Published online by Cambridge University Press: 12 December 2023
Abstract
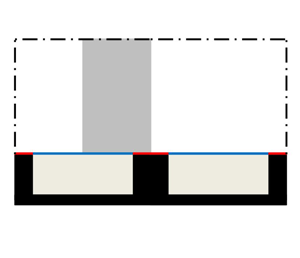
We consider laminar, fully developed, Poiseuille flows of liquid in the Cassie state through diabatic, parallel-plate microchannels symmetrically textured with isoflux ridges. Via matched asymptotic expansions, we develop expressions for (apparent hydrodynamic) slip lengths and Nusselt numbers. Our small parameter ( $\epsilon$) is the pitch of the ridges divided by the height of the microchannel. When the ridges are oriented parallel to the flow, we quantify the error in the Nusselt number expressions in the literature and provide a new closed-form result. It is accurate to
$\epsilon$) is the pitch of the ridges divided by the height of the microchannel. When the ridges are oriented parallel to the flow, we quantify the error in the Nusselt number expressions in the literature and provide a new closed-form result. It is accurate to  $O\left (\epsilon ^2\right )$ and valid for any solid (ridge) fraction, whereas previous ones are accurate to
$O\left (\epsilon ^2\right )$ and valid for any solid (ridge) fraction, whereas previous ones are accurate to  $O\left (\epsilon ^1\right )$ and breakdown in the important limit when the solid fraction approaches zero. When the ridges are oriented transverse to the (periodically fully developed) flow, the error associated with neglecting inertial effects in the slip length is shown to be
$O\left (\epsilon ^1\right )$ and breakdown in the important limit when the solid fraction approaches zero. When the ridges are oriented transverse to the (periodically fully developed) flow, the error associated with neglecting inertial effects in the slip length is shown to be  $O\left (\epsilon ^3{Re}\right )$, where
$O\left (\epsilon ^3{Re}\right )$, where  ${Re}$ is the channel-scale Reynolds number based on its hydraulic diameter. The corresponding Nusselt number expressions’ accuracies are shown to depend on the Reynolds number, Péclet number and Prandtl number in addition to
${Re}$ is the channel-scale Reynolds number based on its hydraulic diameter. The corresponding Nusselt number expressions’ accuracies are shown to depend on the Reynolds number, Péclet number and Prandtl number in addition to  $\epsilon$. Manipulating the solution to the inner temperature problem encountered in the vicinity of the ridges shows that classic results for the thermal spreading resistance are better expressed in terms of polylogarithm functions.
$\epsilon$. Manipulating the solution to the inner temperature problem encountered in the vicinity of the ridges shows that classic results for the thermal spreading resistance are better expressed in terms of polylogarithm functions.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 2
- Cited by



