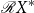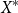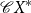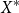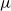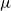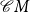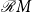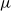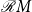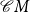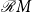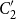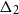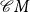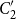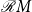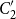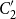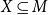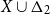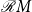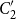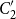1. Introduction
The classical Chomsky–Schützenberger theorem of Formal Language Theory relates the set
![]() ${\mathcal{C}} X^*$
of context-free languages of the free monoid
${\mathcal{C}} X^*$
of context-free languages of the free monoid
![]() $X^*$
over the finite set X to the set
$X^*$
over the finite set X to the set
![]() ${\mathcal{R}} (X\cup\Delta_2)^*$
of regular languages over an extension of X by a set
${\mathcal{R}} (X\cup\Delta_2)^*$
of regular languages over an extension of X by a set
![]() $\Delta_2 = \{b,d,p,q\}$
of two bracket pairs b,d and p,q. It says that every
$\Delta_2 = \{b,d,p,q\}$
of two bracket pairs b,d and p,q. It says that every
![]() $L\in {\mathcal{C}} X^*$
is the image of the intersection
$L\in {\mathcal{C}} X^*$
is the image of the intersection
![]() $R\cap D_2(X)$
of a regular language
$R\cap D_2(X)$
of a regular language
![]() $R\in{\mathcal{R}}(X\cup\Delta_2)^*$
with the Dyck language
$R\in{\mathcal{R}}(X\cup\Delta_2)^*$
with the Dyck language
![]() $D_2(X) \in{\mathcal{C}}(X\cup\Delta_2)^*$
of balanced bracketed strings under the homomorphism
$D_2(X) \in{\mathcal{C}}(X\cup\Delta_2)^*$
of balanced bracketed strings under the homomorphism
![]() $h_{X^*}:(X\cup\Delta_2)^*\to X^*$
that keeps elements of X fixed and maps those of
$h_{X^*}:(X\cup\Delta_2)^*\to X^*$
that keeps elements of X fixed and maps those of
![]() $\Delta_2$
to the unit of
$\Delta_2$
to the unit of
![]() $X^*$
. This result of Chomsky and Schützenberger (Reference Chomsky and Schützenberger1963) can be stated as
$X^*$
. This result of Chomsky and Schützenberger (Reference Chomsky and Schützenberger1963) can be stated as
Intuitively, for
![]() $L=h_{X^*}(R\cap D_2(X))$
, the set
$L=h_{X^*}(R\cap D_2(X))$
, the set
![]() $R\cap D_2(X)$
consists of the sentences of L enriched by begin- and end-markers of their phrases according to some context-free grammar for L, i.e. by their linearized parse trees; the two bracket pairs of
$R\cap D_2(X)$
consists of the sentences of L enriched by begin- and end-markers of their phrases according to some context-free grammar for L, i.e. by their linearized parse trees; the two bracket pairs of
![]() $\Delta_2$
are used to encode a begin- and end-marker for each phrase category of the grammar. The reverse inclusion
$\Delta_2$
are used to encode a begin- and end-marker for each phrase category of the grammar. The reverse inclusion
is trivial, since the intersection of a context-free set with a regular one and the homomorphic image of a context-free set are context-free. (It will no longer be trivial in the generalizations considered below.) Thus, balanced brackets are at the heart of the extension from regular to context-free sets.
To extend this relation
![]() ${\mathcal{C}} X^* = \left\{\,\!h_{X^*}(R\cap D_2(X))\,\mid\,R\in{\mathcal{R}}(X\cup\Delta_2)^*\!\,\right\}$
from finitely generated free monoids
${\mathcal{C}} X^* = \left\{\,\!h_{X^*}(R\cap D_2(X))\,\mid\,R\in{\mathcal{R}}(X\cup\Delta_2)^*\!\,\right\}$
from finitely generated free monoids
![]() $X^*$
to arbitrary monoids M, we define
$X^*$
to arbitrary monoids M, we define
![]() ${\mathcal{R}} M$
and
${\mathcal{R}} M$
and
![]() ${\mathcal{C}} M$
as suitable closures of the semiring
${\mathcal{C}} M$
as suitable closures of the semiring
![]() ${\mathcal{F}} M$
of finite subsets of M (with union as addition and elementwise product as multiplication) within the semiring
${\mathcal{F}} M$
of finite subsets of M (with union as addition and elementwise product as multiplication) within the semiring
![]() ${\mathcal{P}} M$
of all subsets of M. Namely, the family
${\mathcal{P}} M$
of all subsets of M. Namely, the family
![]() ${\mathcal{C}} M$
of context-free subsets of M is the closure of
${\mathcal{C}} M$
of context-free subsets of M is the closure of
![]() ${\mathcal{F}} M$
under components of least solutions of finite systems of inequations
${\mathcal{F}} M$
under components of least solutions of finite systems of inequations
between variables
![]() $y_i$
and polynomials
$y_i$
and polynomials
![]() $p_i\in {\mathcal{C}} M[y_1,\ldots,y_n]$
. Notice that each such inequation system does have a least solution in
$p_i\in {\mathcal{C}} M[y_1,\ldots,y_n]$
. Notice that each such inequation system does have a least solution in
![]() ${\mathcal{P}}M$
, so we can add the components of this solution to
${\mathcal{P}}M$
, so we can add the components of this solution to
![]() ${\mathcal{C}} M$
. By adding further unknowns and inequations for the coefficients from
${\mathcal{C}} M$
. By adding further unknowns and inequations for the coefficients from
![]() ${\mathcal{C}} M$
, we can ultimately do with polynomials
${\mathcal{C}} M$
, we can ultimately do with polynomials
![]() $p_i\in {\mathcal{F}} M[y_1,\ldots,y_n]$
in (1). The family
$p_i\in {\mathcal{F}} M[y_1,\ldots,y_n]$
in (1). The family
![]() ${\mathcal{R}} M$
of regular sets of M is the closure of
${\mathcal{R}} M$
of regular sets of M is the closure of
![]() ${\mathcal{F}} M$
under components of least solutions of finite systems of inequations
${\mathcal{F}} M$
under components of least solutions of finite systems of inequations
![]() $y_i\geq p_i(y_1,\ldots,y_n)$
with right-linear polynomials
$y_i\geq p_i(y_1,\ldots,y_n)$
with right-linear polynomials
![]() $p_i\in{\mathcal{R}} M[y_1,\ldots,y_n]$
, i.e. where
$p_i\in{\mathcal{R}} M[y_1,\ldots,y_n]$
, i.e. where
![]() $p_i$
is a sum of monomials A or Ay with
$p_i$
is a sum of monomials A or Ay with
![]() $A\in {\mathcal{R}} M$
and
$A\in {\mathcal{R}} M$
and
![]() $y\in\{y_1,\ldots,y_n\}$
. These definitions make
$y\in\{y_1,\ldots,y_n\}$
. These definitions make
![]() ${\mathcal{C}} M$
resp.
${\mathcal{C}} M$
resp.
![]() ${\mathcal{R}} M$
be closed under least fixed points of arbitrary resp. right-linear polynomials and do not assume that M be finitely generated.
${\mathcal{R}} M$
be closed under least fixed points of arbitrary resp. right-linear polynomials and do not assume that M be finitely generated.
In classical Formal Language Theory, regular and context-free languages are defined by regular and context-free grammars. A context-free grammar
![]() $G = (X,Y,P,S)$
over the set of terminal symbols X is a finite set
$G = (X,Y,P,S)$
over the set of terminal symbols X is a finite set
![]() $P\subseteq Y\times (X\cup Y)^*$
of grammar rules or productions
$P\subseteq Y\times (X\cup Y)^*$
of grammar rules or productions
![]() $(y,\alpha)$
, where Y is a set of variables or nonterminal symbols, disjoint from X, and a specific start symbol
$(y,\alpha)$
, where Y is a set of variables or nonterminal symbols, disjoint from X, and a specific start symbol
![]() $S\in Y$
. The productions give rise to a binary rewrite relation
$S\in Y$
. The productions give rise to a binary rewrite relation
![]() $\Rightarrow_G$
on
$\Rightarrow_G$
on
![]() $(X\cup Y)^*$
by
$(X\cup Y)^*$
by
![]() $w\Rightarrow_G w'$
iff for some
$w\Rightarrow_G w'$
iff for some
![]() $u,v\in (X\cup Y)^*$
and
$u,v\in (X\cup Y)^*$
and
![]() $(y,\alpha)\in P$
,
$(y,\alpha)\in P$
,
![]() $w=uyv$
and
$w=uyv$
and
![]() $w'=u\alpha v$
. Each
$w'=u\alpha v$
. Each
![]() $y\in Y$
leads to a language
$y\in Y$
leads to a language
![]() $L(G,y) = \left\{\,\!w\in X^*\,\mid\,y\Rightarrow^+_G w\!\,\right\}$
, where
$L(G,y) = \left\{\,\!w\in X^*\,\mid\,y\Rightarrow^+_G w\!\,\right\}$
, where
![]() $\Rightarrow_G^+$
is the transitive closure of
$\Rightarrow_G^+$
is the transitive closure of
![]() $\Rightarrow_G$
, and
$\Rightarrow_G$
, and
![]() $L(G) =L(G,S)$
is the language defined by G. A right-linear grammar is a context-free grammar where
$L(G) =L(G,S)$
is the language defined by G. A right-linear grammar is a context-free grammar where
![]() $P\subseteq Y\times (X^*\cup X^*Y)$
.
$P\subseteq Y\times (X^*\cup X^*Y)$
.
Notice that P gives rise to a system (1) with
![]() $Y=\{y_1,\ldots,y_n\}$
and
$Y=\{y_1,\ldots,y_n\}$
and
![]() $S=y_1$
where
$S=y_1$
where
![]() $p_i$
is the sum over all monomials
$p_i$
is the sum over all monomials
![]() $\alpha'\in {\mathcal{F}} X^*[y_1,\ldots,y_n]$
that arise from the right-hand side of a grammar rule
$\alpha'\in {\mathcal{F}} X^*[y_1,\ldots,y_n]$
that arise from the right-hand side of a grammar rule
![]() $(y_i,\alpha)$
by replacing each
$(y_i,\alpha)$
by replacing each
![]() $x\in X$
occurring in
$x\in X$
occurring in
![]() $\alpha$
by the singleton
$\alpha$
by the singleton
![]() $\{x\}\in {\mathcal{F}} X^*$
. The languages
$\{x\}\in {\mathcal{F}} X^*$
. The languages
![]() $(L(G,y_1),\ldots,L(G,y_n))$
are the least solution of the system (1) derived from G in this way. Conversely, a polynomial system (1) with parameters from
$(L(G,y_1),\ldots,L(G,y_n))$
are the least solution of the system (1) derived from G in this way. Conversely, a polynomial system (1) with parameters from
![]() ${\mathcal{F}} X^*$
gives rise to a context-free grammar
${\mathcal{F}} X^*$
gives rise to a context-free grammar
![]() $G=(X,Y,P,y_1)$
with
$G=(X,Y,P,y_1)$
with
![]() $Y=\{y_1,\ldots,y_n\}$
and P consisting of those
$Y=\{y_1,\ldots,y_n\}$
and P consisting of those
![]() $(y_i,\alpha)$
where
$(y_i,\alpha)$
where
![]() $\alpha$
arises from a monomial
$\alpha$
arises from a monomial
![]() $\alpha'$
of
$\alpha'$
of
![]() $p_i$
by replacing each parameter in
$p_i$
by replacing each parameter in
![]() $\alpha'$
by one of its members
$\alpha'$
by one of its members
![]() $w\in X^*$
. The least solution
$w\in X^*$
. The least solution
![]() $(L_1,\ldots,L_n)$
of the given polynomial system agrees with the languages
$(L_1,\ldots,L_n)$
of the given polynomial system agrees with the languages
![]() $(L(G,y_1),\ldots,L(G,y_n))$
of the grammar so derived from it.
$(L(G,y_1),\ldots,L(G,y_n))$
of the grammar so derived from it.
The grammatical way to define
![]() ${\mathcal{C}} X^*$
can be extended from free monoids
${\mathcal{C}} X^*$
can be extended from free monoids
![]() $X^*$
to arbitrary monoids M, following Hopkins (Reference Hopkins2008a). The free extension M[Y] of a monoid M by a set Y disjoint from M consists of the set of all finite sequences
$X^*$
to arbitrary monoids M, following Hopkins (Reference Hopkins2008a). The free extension M[Y] of a monoid M by a set Y disjoint from M consists of the set of all finite sequences
![]() $m_0y_1m_1\ldots y_km_k$
, where
$m_0y_1m_1\ldots y_km_k$
, where
![]() $m_0,\ldots,m_k\in M$
and
$m_0,\ldots,m_k\in M$
and
![]() $y_1,\ldots,y_k\in Y$
, with the sequence
$y_1,\ldots,y_k\in Y$
, with the sequence
![]() $m_0$
of length 1 with
$m_0$
of length 1 with
![]() $m_0=1$
as unit, and with the operation defined by
$m_0=1$
as unit, and with the operation defined by
for
![]() $k,k'\in{\mathbb{N}}, m_0,\ldots,m'_{k'}\in M, y_1,\ldots,y_{k'}'\in Y$
as product; for disjoint sets X and Y, there is an isomorphism
$k,k'\in{\mathbb{N}}, m_0,\ldots,m'_{k'}\in M, y_1,\ldots,y_{k'}'\in Y$
as product; for disjoint sets X and Y, there is an isomorphism
![]() $X^*[Y] \simeq (X\cup Y)^*$
, obtained by identifying
$X^*[Y] \simeq (X\cup Y)^*$
, obtained by identifying
![]() $y1y'\in X^*[Y]$
with
$y1y'\in X^*[Y]$
with
![]() $yy'\in Y^*$
. A context-free grammar
$yy'\in Y^*$
. A context-free grammar
![]() $G=(Y,P,S)$
over the monoid M then consists of a set Y of variables, disjoint from M, a finite set
$G=(Y,P,S)$
over the monoid M then consists of a set Y of variables, disjoint from M, a finite set
![]() $P\subseteq Y \times M[Y]$
of productions, and a main variable
$P\subseteq Y \times M[Y]$
of productions, and a main variable
![]() $S\in Y$
. As for free monoids, G gives rise to a binary relation
$S\in Y$
. As for free monoids, G gives rise to a binary relation
![]() $\Rightarrow_G$
on M[Y] such that
$\Rightarrow_G$
on M[Y] such that
![]() $w\Rightarrow_G w'$
iff for some
$w\Rightarrow_G w'$
iff for some
![]() $\alpha,\beta \in M[Y]$
and
$\alpha,\beta \in M[Y]$
and
![]() $(y,\gamma)\in P$
,
$(y,\gamma)\in P$
,
![]() $w=\alpha y \beta$
and
$w=\alpha y \beta$
and
![]() $w'=\alpha \gamma\beta$
. For each variable
$w'=\alpha \gamma\beta$
. For each variable
![]() $y \in Y$
, G defines a subset
$y \in Y$
, G defines a subset
![]() $L(G,y) = \left\{\,\!m\in M\,\mid\,y\Rightarrow_G^+ m\!\,\right\}$
of M, where
$L(G,y) = \left\{\,\!m\in M\,\mid\,y\Rightarrow_G^+ m\!\,\right\}$
of M, where
![]() $\Rightarrow^+_G$
is the transitive closure of
$\Rightarrow^+_G$
is the transitive closure of
![]() $\Rightarrow_G$
, and
$\Rightarrow_G$
, and
![]() $L(G) := L(G,S)$
. This gives us a grammatical definition of a set
$L(G) := L(G,S)$
. This gives us a grammatical definition of a set
The equivalence between the two definitions of
![]() ${\mathcal{C}} M$
can be shown by relating context-free grammars over M with finite systems of polynomial inequations with parameters from
${\mathcal{C}} M$
can be shown by relating context-free grammars over M with finite systems of polynomial inequations with parameters from
![]() ${\mathcal{F}} M$
, as in the case of free monoids. (For an equivalence proof, see also Remark 2 in Leiß and Hopkins Reference Leiß and Hopkins2018). The regular subsets
${\mathcal{F}} M$
, as in the case of free monoids. (For an equivalence proof, see also Remark 2 in Leiß and Hopkins Reference Leiß and Hopkins2018). The regular subsets
![]() ${\mathcal{R}} M$
can be defined analogously by context-free grammars with right-linear productions. Independently of the aims of the present article,
${\mathcal{R}} M$
can be defined analogously by context-free grammars with right-linear productions. Independently of the aims of the present article,
![]() ${\mathcal{R}} M$
and
${\mathcal{R}} M$
and
![]() ${\mathcal{C}} M$
with non-free monoid M are useful to study rational or context-free transductions T between a free input monoid
${\mathcal{C}} M$
with non-free monoid M are useful to study rational or context-free transductions T between a free input monoid
![]() $X^*$
and a free output monoid
$X^*$
and a free output monoid
![]() $Z^*$
as subsets of
$Z^*$
as subsets of
![]() $M=X^*\times Z^*$
.
$M=X^*\times Z^*$
.
The components of least solutions in
![]() ${\mathcal{P}} X^*$
of polynomial systems (1) with right-linear polynomials
${\mathcal{P}} X^*$
of polynomial systems (1) with right-linear polynomials
![]() $p_i\in {\mathcal{R}}X^*[y_1,\ldots, y_n]$
can be denoted by regular expressions in the elements of X. The regular expressions over X, defined by
$p_i\in {\mathcal{R}}X^*[y_1,\ldots, y_n]$
can be denoted by regular expressions in the elements of X. The regular expressions over X, defined by
are interpreted in the Kleene algebra
![]() ${\mathcal{R}} X^*$
by taking
${\mathcal{R}} X^*$
by taking
![]() $\emptyset$
for 0, the singleton containing the unit of
$\emptyset$
for 0, the singleton containing the unit of
![]() $X^*$
for 1,
$X^*$
for 1,
![]() $\{x\}$
for
$\{x\}$
for
![]() $x \in X$
, binary union for
$x \in X$
, binary union for
![]() $+$
, elementwise concatenation for
$+$
, elementwise concatenation for
![]() $\cdot$
, and iteration (aka monoid closure) for
$\cdot$
, and iteration (aka monoid closure) for
![]() ${}^*$
. If the right-linear polynomial
${}^*$
. If the right-linear polynomial
![]() $p_n$
of (1) is
$p_n$
of (1) is
![]() $q(y_1,\ldots,y_{n-1})+Ay_n$
and r denotes the parameter
$q(y_1,\ldots,y_{n-1})+Ay_n$
and r denotes the parameter
![]() $A\in {\mathcal{R}} X^*$
, then the least solution of
$A\in {\mathcal{R}} X^*$
, then the least solution of
![]() $y_n \geq p_n(y_1,\ldots,y_n)$
is denoted by
$y_n \geq p_n(y_1,\ldots,y_n)$
is denoted by
![]() $(r^* \cdot q)(y_1,\ldots,y_{n-1})$
. Substituting
$(r^* \cdot q)(y_1,\ldots,y_{n-1})$
. Substituting
![]() $y_n$
by
$y_n$
by
![]() $(r^*\cdot q)$
in the remaining inequations, and iterating this process, the first component of the least solution of (1) is named by a regular expression over X, free of unknowns
$(r^*\cdot q)$
in the remaining inequations, and iterating this process, the first component of the least solution of (1) is named by a regular expression over X, free of unknowns
![]() $y_1,\ldots,y_n$
.
$y_1,\ldots,y_n$
.
In a similar way, the components of least solutions of arbitrary polynomial inequations (1) with parameters from
![]() ${\mathcal{C}} X^*$
can be named by regular
${\mathcal{C}} X^*$
can be named by regular
![]() $\mu$
-terms over X,
$\mu$
-terms over X,
the extension of regular expressions over X by an infinite set of variables y and a unary least-fixed point operator
![]() $\mu$
binding a variable; then
$\mu$
binding a variable; then
![]() $(\mu y_n.p_n)(y_1,\ldots,y_{n-1})$
is a term denoting the least solution of
$(\mu y_n.p_n)(y_1,\ldots,y_{n-1})$
is a term denoting the least solution of
![]() $y_n\geq p_n(y_1,\ldots,y_n)$
of (1), relative to given values for
$y_n\geq p_n(y_1,\ldots,y_n)$
of (1), relative to given values for
![]() $y_1,\ldots,y_n$
in
$y_1,\ldots,y_n$
in
![]() ${\mathcal{C}} X^*$
. One of the results of this article is an algebraic notation for context-free languages that is close to the regular expressions and does not use a binding operator.
${\mathcal{C}} X^*$
. One of the results of this article is an algebraic notation for context-free languages that is close to the regular expressions and does not use a binding operator.
Now, the Chomsky–Schützenberger theorem and its reverse extend readily to the families
![]() ${\mathcal{R}} M$
of regular and
${\mathcal{R}} M$
of regular and
![]() ${\mathcal{C}} M$
of context-free subsets of an arbitrary finitely generated monoid M as
${\mathcal{C}} M$
of context-free subsets of an arbitrary finitely generated monoid M as
We here assume M to be finitely generated to have
![]() $D_2(M)\in {\mathcal{C}}(M[\Delta_2])$
, but this assumption can be avoided by a different formulation using the pure Dyck language
$D_2(M)\in {\mathcal{C}}(M[\Delta_2])$
, but this assumption can be avoided by a different formulation using the pure Dyck language
![]() $D_2\in {\mathcal{C}}\Delta_2^*$
of brackets only,
$D_2\in {\mathcal{C}}\Delta_2^*$
of brackets only,
where
![]() $\pi_1:M\times\Delta_2^*\to M$
is the first projection.
$\pi_1:M\times\Delta_2^*\to M$
is the first projection.
In a number of semi-published contributions, Hopkins (Reference Hopkins1993) has tried to turn this dependence of
![]() ${\mathcal{C}} M$
on
${\mathcal{C}} M$
on
![]() ${\mathcal{R}}(M[\Delta_2])$
into a dependence on
${\mathcal{R}}(M[\Delta_2])$
into a dependence on
![]() ${\mathcal{R}} M$
, express it in more algebraic terms, and generalize it to an algebraic construction of the fixed-point-closure of a
${\mathcal{R}} M$
, express it in more algebraic terms, and generalize it to an algebraic construction of the fixed-point-closure of a
![]() ${}^*$
-continuous Kleene algebra K. The idea is to let elements of M and
${}^*$
-continuous Kleene algebra K. The idea is to let elements of M and
![]() $\Delta_2$
commute with each other, i.e. replace
$\Delta_2$
commute with each other, i.e. replace
![]() $M[\Delta_2]$
by
$M[\Delta_2]$
by
![]() $M\times\Delta_2^*$
or
$M\times\Delta_2^*$
or
![]() ${\mathcal{R}}(M[\Delta_2])$
by a suitable product
${\mathcal{R}}(M[\Delta_2])$
by a suitable product
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2$
of
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2$
of
![]() ${\mathcal{R}} M$
with a “bra-ket algebra”
${\mathcal{R}} M$
with a “bra-ket algebra”
![]() $C_2$
, and perform the balance-check
$C_2$
, and perform the balance-check
![]() $\cap\,D_2(M)$
and the bracket-erasure
$\cap\,D_2(M)$
and the bracket-erasure
![]() $h_M$
of (2) by algebraic calculations in
$h_M$
of (2) by algebraic calculations in
![]() $C_2$
. The “bra-ket algebra”
$C_2$
. The “bra-ket algebra”
is the quotient of the regular sets
![]() ${\mathcal{R}} \Delta_2^*$
by a congruence that is generated by three conditions
Footnote 1
: by “match” conditions
${\mathcal{R}} \Delta_2^*$
by a congruence that is generated by three conditions
Footnote 1
: by “match” conditions
![]() $bd=1=pq$
that allow us to shorten strings by erasing all pairs bd or pq of matching adjacent brackets, by “mismatch” conditions
$bd=1=pq$
that allow us to shorten strings by erasing all pairs bd or pq of matching adjacent brackets, by “mismatch” conditions
![]() $bq=0=pd$
that allow us to throw away all strings containing a bracket mismatch bq or pd, and by a “completeness” condition
$bq=0=pd$
that allow us to throw away all strings containing a bracket mismatch bq or pd, and by a “completeness” condition
![]() $db+qp =1$
which ensures that corresponding bra-ket algebras
$db+qp =1$
which ensures that corresponding bra-ket algebras
![]() $C_n$
based on
$C_n$
based on
![]() $n>2$
bracket pairs can be embedded in
$n>2$
bracket pairs can be embedded in
![]() $C_2$
.
Footnote 2
The product
$C_2$
.
Footnote 2
The product
![]() ${\mathcal{R}} M \mathop{\otimes_{\mathcal{R}}} C_2$
is, intuitively, the smallest
${\mathcal{R}} M \mathop{\otimes_{\mathcal{R}}} C_2$
is, intuitively, the smallest
![]() ${}^*$
-continuous Kleene algebra extension of
${}^*$
-continuous Kleene algebra extension of
![]() ${\mathcal{R}} M$
and
${\mathcal{R}} M$
and
![]() $C_2$
in which elements of
$C_2$
in which elements of
![]() ${\mathcal{R}} M$
commute with those of
${\mathcal{R}} M$
commute with those of
![]() $C_2$
. The algebraic version of the Chomsky–Schützenberger theorem and its reverse then is that
$C_2$
. The algebraic version of the Chomsky–Schützenberger theorem and its reverse then is that
![]() ${\mathcal{C}} M$
is isomorphic to the centralizer of
${\mathcal{C}} M$
is isomorphic to the centralizer of
![]() $C_2$
in
$C_2$
in
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}}C_2$
,
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}}C_2$
,
i.e. to the set of elements that commute with every member of
![]() $C_2$
. All elements of
$C_2$
. All elements of
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2$
can be denoted by regular expressions in the generators of M and
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2$
can be denoted by regular expressions in the generators of M and
![]() $C_2$
, and it is easy to define a subset of expressions that denote the members of the centralizer of
$C_2$
, and it is easy to define a subset of expressions that denote the members of the centralizer of
![]() $C_2$
. This is the above-mentioned algebraic notation system for context-free sets that is much closer to the familiar one for regular sets than context-free grammars or regular
$C_2$
. This is the above-mentioned algebraic notation system for context-free sets that is much closer to the familiar one for regular sets than context-free grammars or regular
![]() $\mu$
-terms are.
$\mu$
-terms are.
The goal of the present work is to replace
![]() $C_2$
in (3) by a simpler algebra, the “polycyclic
$C_2$
in (3) by a simpler algebra, the “polycyclic
![]() ${}^*$
-continuous Kleene algebra on two generators,”
${}^*$
-continuous Kleene algebra on two generators,”
and instead of (3) prove
our first main result. The congruence used in
![]() $C_2'$
is generated by just the bracket match and mismatch conditions. These, but not the completeness condition, can be seen as monoid equations, provided we extend
$C_2'$
is generated by just the bracket match and mismatch conditions. These, but not the completeness condition, can be seen as monoid equations, provided we extend
![]() $\Delta_2^*$
by an annihilating monoid element 0. Doing so gives us the “polycyclic monoid on two generators,”
$\Delta_2^*$
by an annihilating monoid element 0. Doing so gives us the “polycyclic monoid on two generators,”
This allows us to treat
![]() $C_2'$
as
$C_2'$
as
![]() ${\mathcal{R}} P_2'$
modulo
${\mathcal{R}} P_2'$
modulo
![]() $\{0\}=\emptyset$
and
$\{0\}=\emptyset$
and
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
as
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
as
![]() ${\mathcal{R}} (M\times P_2')$
modulo
${\mathcal{R}} (M\times P_2')$
modulo
![]() $\{(1,0)\}=\emptyset$
. Moreover, it lets us understand the centralizer of
$\{(1,0)\}=\emptyset$
. Moreover, it lets us understand the centralizer of
![]() $C_2'$
in
$C_2'$
in
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}}C_2'$
: it contains (the equivalence classes of) those
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}}C_2'$
: it contains (the equivalence classes of) those
![]() $R\in {\mathcal{R}}(M\times P_2')$
where
$R\in {\mathcal{R}}(M\times P_2')$
where
![]() $R\subseteq M\times \{0,1\}$
.
$R\subseteq M\times \{0,1\}$
.
Intuitively, therefore, (4) says that the context-free sets
![]() $L\in {\mathcal{C}} M$
correspond to the regular sets
$L\in {\mathcal{C}} M$
correspond to the regular sets
![]() $R\in {\mathcal{R}}(M\times P_2')$
whose elements (m,t’) have
$R\in {\mathcal{R}}(M\times P_2')$
whose elements (m,t’) have
![]() $t'\in \{0,1\}$
: elements
$t'\in \{0,1\}$
: elements
![]() $(m,1)\in R$
come from an element
$(m,1)\in R$
come from an element
![]() $m\in M\cap L$
with a parse tree
$m\in M\cap L$
with a parse tree
![]() $t\in D_2\subseteq\Delta_2^*$
with respect to a context-free grammar for L, reduced to
$t\in D_2\subseteq\Delta_2^*$
with respect to a context-free grammar for L, reduced to
![]() $t'=1$
in
$t'=1$
in
![]() $P_2'$
; elements
$P_2'$
; elements
![]() $(m,0)\in R$
come from unparsable
$(m,0)\in R$
come from unparsable
![]() $m \in M \setminus L$
and are thrown away in the quotient of
$m \in M \setminus L$
and are thrown away in the quotient of
![]() ${\mathcal{R}}(M\times P_2')$
by
${\mathcal{R}}(M\times P_2')$
by
![]() $\{(1,0)\} =\emptyset$
.
$\{(1,0)\} =\emptyset$
.
However, the algebraic form (4) of the Chomsky–Schützenberger theorem and its reverse for monoids does not yet give an algebraic representation of the fixed-point closure of an arbitrary
![]() ${}^*$
-continuous Kleene algebra K, which need not be of the form
${}^*$
-continuous Kleene algebra K, which need not be of the form
![]() ${\mathcal{R}} M$
for some monoid M. Equipped with suitable notions of
${\mathcal{R}} M$
for some monoid M. Equipped with suitable notions of
![]() ${\mathcal{R}}$
- and
${\mathcal{R}}$
- and
![]() ${\mathcal{C}}$
-morphisms, the categories of
${\mathcal{C}}$
-morphisms, the categories of
![]() ${}^*$
-continuous Kleene algebras (Kozen Reference Kozen1981) and
${}^*$
-continuous Kleene algebras (Kozen Reference Kozen1981) and
![]() $\mu$
-continuous Chomsky algebras (Grathwohl et al. Reference Grathwohl, Henglein and Kozen2013), respectively, are subcategories
$\mu$
-continuous Chomsky algebras (Grathwohl et al. Reference Grathwohl, Henglein and Kozen2013), respectively, are subcategories
![]() ${\mathbb{D}}{\mathcal{R}}$
and
${\mathbb{D}}{\mathcal{R}}$
and
![]() ${\mathbb{D}}{\mathcal{C}}$
of the category
${\mathbb{D}}{\mathcal{C}}$
of the category
![]() ${\mathbb{D}}$
of dioids (i.e. idempotent semirings). In fact,
${\mathbb{D}}$
of dioids (i.e. idempotent semirings). In fact,
![]() ${\mathbb{D}}{\mathcal{R}}$
and
${\mathbb{D}}{\mathcal{R}}$
and
![]() ${\mathbb{D}}{\mathcal{C}}$
are the Eilenberg-Moore categories of certain monads on the category of monoids. The Kleene algebras
${\mathbb{D}}{\mathcal{C}}$
are the Eilenberg-Moore categories of certain monads on the category of monoids. The Kleene algebras
![]() ${\mathcal{R}} M$
and the Chomsky algebras
${\mathcal{R}} M$
and the Chomsky algebras
![]() ${\mathcal{C}} M$
, with monoid M, form the so-called Kleisli subcategories of
${\mathcal{C}} M$
, with monoid M, form the so-called Kleisli subcategories of
![]() ${\mathbb{D}}{\mathcal{R}}$
and
${\mathbb{D}}{\mathcal{R}}$
and
![]() ${\mathbb{D}}{\mathcal{C}}$
. We want to extend (4) from their Kleisli subcategories to the categories
${\mathbb{D}}{\mathcal{C}}$
. We want to extend (4) from their Kleisli subcategories to the categories
![]() ${\mathbb{D}}{\mathcal{R}}$
and
${\mathbb{D}}{\mathcal{R}}$
and
![]() ${\mathbb{D}}{\mathcal{C}}$
themselves. In an equivalent categorical formulation of Hopkins (Reference Hopkins2008a) and Leiß and Hopkins (Reference Leiß and Hopkins2018), the objects of
${\mathbb{D}}{\mathcal{C}}$
themselves. In an equivalent categorical formulation of Hopkins (Reference Hopkins2008a) and Leiß and Hopkins (Reference Leiß and Hopkins2018), the objects of
![]() ${\mathbb{D}}{\mathcal{R}}$
and
${\mathbb{D}}{\mathcal{R}}$
and
![]() ${\mathbb{D}}{\mathcal{C}}$
, called
${\mathbb{D}}{\mathcal{C}}$
, called
![]() ${\mathcal{R}}$
-dioids and
${\mathcal{R}}$
-dioids and
![]() ${\mathcal{C}}$
-dioids there, are dioids in which the regular resp. context-free subsets U of their multiplicative monoids have least upper bounds
${\mathcal{C}}$
-dioids there, are dioids in which the regular resp. context-free subsets U of their multiplicative monoids have least upper bounds
![]() $\sum U$
with respect to the partial order given by addition. As part of a broader program of algebraization of formal language theory, Hopkins (Reference Hopkins2008b) shows that there is an adjunction
$\sum U$
with respect to the partial order given by addition. As part of a broader program of algebraization of formal language theory, Hopkins (Reference Hopkins2008b) shows that there is an adjunction
between these categories, where
![]() ${Q_{\mathcal{C}}^{\mathcal{R}}}$
is the forgetful functor (restricting
${Q_{\mathcal{C}}^{\mathcal{R}}}$
is the forgetful functor (restricting
![]() $\sum$
to regular subsets) and
$\sum$
to regular subsets) and
![]() ${Q_{\mathcal{R}}^{\mathcal{C}}}$
maps an
${Q_{\mathcal{R}}^{\mathcal{C}}}$
maps an
![]() ${\mathcal{R}}$
-dioid K to its fixed-point- or
${\mathcal{R}}$
-dioid K to its fixed-point- or
![]() ${\mathcal{C}}$
-closure in
${\mathcal{C}}$
-closure in
![]() ${\mathbb{D}}{\mathcal{C}}$
, which extends K by a set of order-theoretic ideals of K. In yet unpublished work, Hopkins tries to show that the
${\mathbb{D}}{\mathcal{C}}$
, which extends K by a set of order-theoretic ideals of K. In yet unpublished work, Hopkins tries to show that the
![]() ${\mathcal{C}}$
-closure of an arbitrary
${\mathcal{C}}$
-closure of an arbitrary
![]() ${\mathcal{R}}$
-dioid K can also be algebraically described as
${\mathcal{R}}$
-dioid K can also be algebraically described as
Based on (4), our second main result is that, again,
![]() $C_2$
can be replaced by the simpler algebra
$C_2$
can be replaced by the simpler algebra
![]() $C_2'$
, yielding a “categorical” Chomsky–Schützenberger theorem
$C_2'$
, yielding a “categorical” Chomsky–Schützenberger theorem
In contrast to the case of the Kleisli subcategories, we here really need the categorical notion of product of
![]() ${\mathcal{R}}$
-dioids. A detailed presentation of the algebraic and categorical background used here is given in Hopkins and Leiß (Reference Hopkins and Leiß2018).
${\mathcal{R}}$
-dioids. A detailed presentation of the algebraic and categorical background used here is given in Hopkins and Leiß (Reference Hopkins and Leiß2018).
The rest of this paper is organized as follows. Section 2 gives the background of categories
![]() ${\mathbb{D}}{\mathcal{A}}$
of
${\mathbb{D}}{\mathcal{A}}$
of
![]() ${\mathcal{A}}$
-dioids for certain subfunctors
${\mathcal{A}}$
-dioids for certain subfunctors
![]() ${\mathcal{A}}$
of the powerset functor
${\mathcal{A}}$
of the powerset functor
![]() ${\mathcal{P}} : {\mathbb{M}}\to {\mathbb{M}}_\leq$
, where
${\mathcal{P}} : {\mathbb{M}}\to {\mathbb{M}}_\leq$
, where
![]() ${\mathbb{M}}$
(resp.
${\mathbb{M}}$
(resp.
![]() ${\mathbb{M}}_\leq$
) is the category of (partially ordered) monoids and (monotone) homomorphisms. Section 2 also collects definitions and known results on products and quotients of
${\mathbb{M}}_\leq$
) is the category of (partially ordered) monoids and (monotone) homomorphisms. Section 2 also collects definitions and known results on products and quotients of
![]() ${\mathcal{A}}$
-dioids and introduces polycyclic
${\mathcal{A}}$
-dioids and introduces polycyclic
![]() ${\mathcal{A}}$
-dioids
${\mathcal{A}}$
-dioids
![]() $C_{n,{\mathcal{A}}}'$
with n generators. Section 3 proves the algebraic version
$C_{n,{\mathcal{A}}}'$
with n generators. Section 3 proves the algebraic version
![]() ${\mathcal{C}} M \subseteq Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
of the Chomsky–Schützenberger theorem; Section 4 the algebraic version of the reverse Chomsky–Schützenberger theorem,
${\mathcal{C}} M \subseteq Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
of the Chomsky–Schützenberger theorem; Section 4 the algebraic version of the reverse Chomsky–Schützenberger theorem,
![]() ${\mathcal{C}} M \supseteq Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
. These are combined in Section 5 to a proof that
${\mathcal{C}} M \supseteq Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
. These are combined in Section 5 to a proof that
![]() $Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is the
$Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is the
![]() ${\mathcal{C}}$
-closure of
${\mathcal{C}}$
-closure of
![]() ${\mathcal{R}} M$
; for
${\mathcal{R}} M$
; for
![]() $M=X^*$
, this leads to a set of regular expressions over
$M=X^*$
, this leads to a set of regular expressions over
![]() $X\cup\Delta_2$
that evaluate to the context-free sets of
$X\cup\Delta_2$
that evaluate to the context-free sets of
![]() ${\mathcal{C}} M$
. Section 6 finally proves the general representation result: for an arbitrary
${\mathcal{C}} M$
. Section 6 finally proves the general representation result: for an arbitrary
![]() ${\mathcal{R}}$
-dioid K, the
${\mathcal{R}}$
-dioid K, the
![]() ${\mathcal{C}}$
-closure of K is isomorphic to
${\mathcal{C}}$
-closure of K is isomorphic to
![]() $Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
. In the Conclusion, we also sketch where Hopkins’ proof of (5) uses the completeness assumption and how it is avoided in our proof of (6).
$Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
. In the Conclusion, we also sketch where Hopkins’ proof of (5) uses the completeness assumption and how it is avoided in our proof of (6).
2. The Category of
 ${\mathcal{A}}$
-Dioids and
${\mathcal{A}}$
-Dioids and
 ${\mathcal{A}}$
-Morphisms
${\mathcal{A}}$
-Morphisms
Let
![]() ${\mathbb{M}}$
be the category of monoids
${\mathbb{M}}$
be the category of monoids
![]() $(M,\cdot,1)$
and homomorphisms between monoids, and
$(M,\cdot,1)$
and homomorphisms between monoids, and
![]() ${\mathbb{M}}_\leq$
the category of partially ordered monoids
${\mathbb{M}}_\leq$
the category of partially ordered monoids
![]() $(M,\cdot,1,\leq)$
and monotone homomorphisms between them. We consider subfunctors of the powerset functor
$(M,\cdot,1,\leq)$
and monotone homomorphisms between them. We consider subfunctors of the powerset functor
![]() ${\mathcal{P}}:{\mathbb{M}}\to{\mathbb{M}}_\leq$
and partially order them by
${\mathcal{P}}:{\mathbb{M}}\to{\mathbb{M}}_\leq$
and partially order them by
![]() ${\mathcal{A}}\leq{\mathcal{A}}'$
iff for all monoids M,
${\mathcal{A}}\leq{\mathcal{A}}'$
iff for all monoids M,
![]() ${\mathcal{A}} M\subseteq {\mathcal{A}}'M$
. A monadic operator
Footnote 3
is a functor
${\mathcal{A}} M\subseteq {\mathcal{A}}'M$
. A monadic operator
Footnote 3
is a functor
![]() ${\mathcal{A}}:{\mathbb{M}}\to {\mathbb{M}}_\leq$
such that for all monoids M, N,
${\mathcal{A}}:{\mathbb{M}}\to {\mathbb{M}}_\leq$
such that for all monoids M, N,
-
(
 $A_0$
)
$A_0$
)
 ${\mathcal{A}} M$
is a set of subsets of M,
${\mathcal{A}} M$
is a set of subsets of M, -
(
 $A_1$
)
$A_1$
)
 ${\mathcal{A}} M$
contains all singleton subsets of M,
${\mathcal{A}} M$
contains all singleton subsets of M, -
(
 $A_2$
)
$A_2$
)
 ${\mathcal{A}} M$
is closed under products; hence,
${\mathcal{A}} M$
is closed under products; hence,
 $({\mathcal{A}} M,\cdot,\{1\},\subseteq)$
is a partially ordered monoid, where
$({\mathcal{A}} M,\cdot,\{1\},\subseteq)$
is a partially ordered monoid, where  \begin{equation*} A\cdot B := \left\{\,a\cdot b\,\mid\,a\in A,b\in B\,\right\} \quad\textrm{for }A,B\in{\mathcal{A}} M,\end{equation*}
\begin{equation*} A\cdot B := \left\{\,a\cdot b\,\mid\,a\in A,b\in B\,\right\} \quad\textrm{for }A,B\in{\mathcal{A}} M,\end{equation*}
-
(
 $A_3$
)
$A_3$
)
 ${\mathcal{A}} M$
is closed under unions of sets from
${\mathcal{A}} M$
is closed under unions of sets from
 ${\mathcal{A}}(({\mathcal{A}} M,\cdot,\{1\}))$
, and
${\mathcal{A}}(({\mathcal{A}} M,\cdot,\{1\}))$
, and -
(
 $A_4$
) if
$A_4$
) if
 $f:M\to N$
is a homomorphism, so is
$f:M\to N$
is a homomorphism, so is
 ${\mathcal{A}} f:{\mathcal{A}} M \to {\mathcal{A}} N$
, where for
${\mathcal{A}} f:{\mathcal{A}} M \to {\mathcal{A}} N$
, where for
 $U\subseteq M$
,
$U\subseteq M$
,  \begin{equation*} ({\mathcal{A}} f)(U) := \left\{\,f(u)\,\mid\,u\in U\,\right\}. \end{equation*}
\begin{equation*} ({\mathcal{A}} f)(U) := \left\{\,f(u)\,\mid\,u\in U\,\right\}. \end{equation*}
We write
![]() ${\mathcal{A}} M$
for both the selected set of subsets of M and the partially ordered monoid
${\mathcal{A}} M$
for both the selected set of subsets of M and the partially ordered monoid
![]() $({\mathcal{A}} M,\cdot,\{1\},\subseteq)$
or just the monoid
$({\mathcal{A}} M,\cdot,\{1\},\subseteq)$
or just the monoid
![]() $({\mathcal{A}} M,\cdot,\{1\})$
. For the lifting
$({\mathcal{A}} M,\cdot,\{1\})$
. For the lifting
![]() ${\mathcal{A}} f$
of f, we often write
${\mathcal{A}} f$
of f, we often write
![]() $\widetilde f$
.
$\widetilde f$
.
An
![]() ${\mathcal{A}}$
-dioid
${\mathcal{A}}$
-dioid
![]() $(D,\cdot,1,\leq)$
is a partially ordered monoid which is
$(D,\cdot,1,\leq)$
is a partially ordered monoid which is
![]() ${\mathcal{A}}$
-complete, i.e. each
${\mathcal{A}}$
-complete, i.e. each
![]() $U\in {\mathcal{A}} D$
has a least upper bound,
$U\in {\mathcal{A}} D$
has a least upper bound,
![]() $\sum U \in D$
, and
$\sum U \in D$
, and
![]() ${\mathcal{A}}$
-distributive, i.e.
${\mathcal{A}}$
-distributive, i.e.
An
![]() ${\mathcal{A}}$
-morphism
${\mathcal{A}}$
-morphism
![]() $f:D \to D'$
between
$f:D \to D'$
between
![]() ${\mathcal{A}}$
-dioids D and D’ is a monotone homomorphism such that
${\mathcal{A}}$
-dioids D and D’ is a monotone homomorphism such that
![]() $f(\sum U)=\sum ({\mathcal{A}} f)(U)$
for all
$f(\sum U)=\sum ({\mathcal{A}} f)(U)$
for all
![]() $U\in {\mathcal{A}} D$
. Let
$U\in {\mathcal{A}} D$
. Let
![]() ${\mathbb{D}}{\mathcal{A}}$
be the category of
${\mathbb{D}}{\mathcal{A}}$
be the category of
![]() ${\mathcal{A}}$
-dioids and
${\mathcal{A}}$
-dioids and
![]() ${\mathcal{A}}$
-morphisms between
${\mathcal{A}}$
-morphisms between
![]() ${\mathcal{A}}$
-dioids.
${\mathcal{A}}$
-dioids.
Example 1 (Hopkins Reference Hopkins2008a) The following functors are monadic operators:
-
(1).
 ${\mathcal{I}}$
, where
${\mathcal{I}}$
, where
 ${\mathcal{I}} M$
is the set of all singleton subsets of M;
${\mathcal{I}} M$
is the set of all singleton subsets of M;
 ${\mathbb{D}}{\mathcal{I}}$
is the category
${\mathbb{D}}{\mathcal{I}}$
is the category
 ${\mathbb{M}}$
of monoids (with equality as partial order) and (monoid-) homomorphisms.
${\mathbb{M}}$
of monoids (with equality as partial order) and (monoid-) homomorphisms. -
(2).
 ${\mathcal{F}}$
, where
${\mathcal{F}}$
, where
 ${\mathcal{F}} M$
is the set of all finite subsets of M;
${\mathcal{F}} M$
is the set of all finite subsets of M;
 ${\mathbb{D}}{\mathcal{F}}$
is the category
${\mathbb{D}}{\mathcal{F}}$
is the category
 ${\mathbb{D}}$
of dioids and dioid homomorphisms.
${\mathbb{D}}$
of dioids and dioid homomorphisms. -
(3).
 ${\mathcal{R}}$
, where
${\mathcal{R}}$
, where
 ${\mathcal{R}} M$
is the set of all regular subsets of M;
${\mathcal{R}} M$
is the set of all regular subsets of M;
 ${\mathbb{D}}{\mathcal{R}}$
is the category of
${\mathbb{D}}{\mathcal{R}}$
is the category of
 ${}^*$
-continuous Kleene algebras and morphisms between them, see Kozen (Reference Kozen1981), Hopkins (Reference Hopkins2008a).
${}^*$
-continuous Kleene algebras and morphisms between them, see Kozen (Reference Kozen1981), Hopkins (Reference Hopkins2008a). -
(4).
 ${\mathcal{C}}$
, where
${\mathcal{C}}$
, where
 ${\mathcal{C}} M$
is the set of all context-free subsets of M;
${\mathcal{C}} M$
is the set of all context-free subsets of M;
 ${\mathbb{D}}{\mathcal{C}}$
is the category of
${\mathbb{D}}{\mathcal{C}}$
is the category of
 $\mu$
-continuous Chomsky algebras and morphisms between them, see Grathwohl et al. (Reference Grathwohl, Henglein and Kozen2013), Leiß and Hopkins (Reference Leiß and Hopkins2018).
$\mu$
-continuous Chomsky algebras and morphisms between them, see Grathwohl et al. (Reference Grathwohl, Henglein and Kozen2013), Leiß and Hopkins (Reference Leiß and Hopkins2018). -
(5).
 ${\mathcal{T}}$
, where
${\mathcal{T}}$
, where
 ${\mathcal{T}} M$
is the set of all Turing-subsets (r.e.) of M. Notice that (
${\mathcal{T}} M$
is the set of all Turing-subsets (r.e.) of M. Notice that (
 $A_3$
) generalizes the well-known fact that the union of an r.e. family of r.e. subsets of
$A_3$
) generalizes the well-known fact that the union of an r.e. family of r.e. subsets of
 ${\mathbb{N}}$
is an r.e. subset of
${\mathbb{N}}$
is an r.e. subset of
 ${\mathbb{N}}$
.
${\mathbb{N}}$
. -
(6).
 ${\mathcal{P}}_{\aleph_0}$
, where
${\mathcal{P}}_{\aleph_0}$
, where
 ${\mathcal{P}}_{\aleph_0} M$
is the set of countable subsets of M;
${\mathcal{P}}_{\aleph_0} M$
is the set of countable subsets of M;
 ${\mathbb{D}}{\mathcal{P}}_{\aleph_0}$
is the category of closed semirings, see Kozen (Reference Kozen1990).
${\mathbb{D}}{\mathcal{P}}_{\aleph_0}$
is the category of closed semirings, see Kozen (Reference Kozen1990). -
(7).
 ${\mathcal{P}}$
, the power set operator;
${\mathcal{P}}$
, the power set operator;
 ${\mathbb{D}}{\mathcal{P}}$
is the category of quantales with unit (Rosenthal Reference Rosenthal1990).
${\mathbb{D}}{\mathcal{P}}$
is the category of quantales with unit (Rosenthal Reference Rosenthal1990).
The sets
![]() ${\mathcal{R}} M$
,
${\mathcal{R}} M$
,
![]() ${\mathcal{C}} M$
,
${\mathcal{C}} M$
,
![]() ${\mathcal{T}} M$
can be defined by generalizing the grammatical approach of doing so for free monoids
${\mathcal{T}} M$
can be defined by generalizing the grammatical approach of doing so for free monoids
![]() $M=X^*$
(Hopkins Reference Hopkins2008a). We use the more algebraic, equivalent definitions for
$M=X^*$
(Hopkins Reference Hopkins2008a). We use the more algebraic, equivalent definitions for
![]() ${\mathcal{R}}$
and
${\mathcal{R}}$
and
![]() ${\mathcal{C}}$
given in Hopkins and Leiß (Reference Hopkins and Leiß2018).
${\mathcal{C}}$
given in Hopkins and Leiß (Reference Hopkins and Leiß2018).
![]() ${\mathcal{R}} M$
is the closure of
${\mathcal{R}} M$
is the closure of
![]() ${\mathcal{F}} M$
under (binary) union, elementwise product, and iteration
${\mathcal{F}} M$
under (binary) union, elementwise product, and iteration
![]() ${}^*$
, i.e. if
${}^*$
, i.e. if
![]() $A\in {\mathcal{R}} M$
, so is
$A\in {\mathcal{R}} M$
, so is
![]() $A^* := \bigcup\left\{\,A^n\,\mid\,n\in{\mathbb{N}}\,\right\}$
, where
$A^* := \bigcup\left\{\,A^n\,\mid\,n\in{\mathbb{N}}\,\right\}$
, where
![]() $A^0=\{1\}$
,
$A^0=\{1\}$
,
![]() $A^{n+1}= A^n\cdot A$
.
$A^{n+1}= A^n\cdot A$
.
![]() ${\mathcal{C}} M$
is the closure of
${\mathcal{C}} M$
is the closure of
![]() ${\mathcal{F}} M$
under components of least solutions of polynomial systems over
${\mathcal{F}} M$
under components of least solutions of polynomial systems over
![]() ${\mathcal{C}} M$
, i.e. the components
${\mathcal{C}} M$
, i.e. the components
![]() $A_1,\ldots,A_n$
of the least solution in
$A_1,\ldots,A_n$
of the least solution in
![]() ${\mathcal{P}} M$
of a system of inequations
${\mathcal{P}} M$
of a system of inequations
with polynomials
![]() $p_i$
in
$p_i$
in
![]() $x_1,\ldots,x_n$
with parameters from
$x_1,\ldots,x_n$
with parameters from
![]() ${\mathcal{C}} M$
all belong to
${\mathcal{C}} M$
all belong to
![]() ${\mathcal{C}} M$
.
${\mathcal{C}} M$
.
![]() $\diamond$
$\diamond$
A Kleene Algebra
![]() $(K,+,\cdot,{}^*,0,1)$
is an idempotent semiring with a unary operation
$(K,+,\cdot,{}^*,0,1)$
is an idempotent semiring with a unary operation
![]() ${}^*$
such that
${}^*$
such that
![]() $a^*b$
is the least solution x of
$a^*b$
is the least solution x of
![]() $ax+b\leq x$
and
$ax+b\leq x$
and
![]() $ba^*$
the least solution of
$ba^*$
the least solution of
![]() $xa+b\leq x$
, where
$xa+b\leq x$
, where
![]() $y \leq z$
is defined by
$y \leq z$
is defined by
![]() $y+z=z$
(Kozen Reference Kozen1994). The Kleene algebra K is
$y+z=z$
(Kozen Reference Kozen1994). The Kleene algebra K is
![]() ${}^*$
-continuous if
${}^*$
-continuous if
A Chomsky algebra (Grathwohl et al. Reference Grathwohl, Henglein and Kozen2013) is an idempotent semiring K that is algebraically closed, i.e. where every finite system of inequations
![]() $x_1\geq p_1(x_1,\ldots,x_n),\ldots,x_n\geq p_n(x_1,\ldots,x_n)$
with polynomials
$x_1\geq p_1(x_1,\ldots,x_n),\ldots,x_n\geq p_n(x_1,\ldots,x_n)$
with polynomials
![]() $p_i\in K[x_1,\ldots,x_n]$
has a least solution
$p_i\in K[x_1,\ldots,x_n]$
has a least solution
![]() $a_1,\ldots,a_n\in K$
. If semiring terms, i.e. terms in
$a_1,\ldots,a_n\in K$
. If semiring terms, i.e. terms in
![]() $0,1,+,\cdot$
, are extended to
$0,1,+,\cdot$
, are extended to
![]() $\mu$
-terms by adding a unary fixed-point operator
$\mu$
-terms by adding a unary fixed-point operator
![]() $\mu$
, the least solution of
$\mu$
, the least solution of
![]() $x\geq p(x,x_1,\ldots,x_k)$
can be named by the term
$x\geq p(x,x_1,\ldots,x_k)$
can be named by the term
![]() $(\mu x.p)(x_1,\ldots,x_k)$
. A Chomsky algebra is
$(\mu x.p)(x_1,\ldots,x_k)$
. A Chomsky algebra is
![]() $\mu$
-continuous, if for all
$\mu$
-continuous, if for all
![]() $\mu$
-terms
$\mu$
-terms
![]() $\mu x.p$
with parameters from K,
$\mu x.p$
with parameters from K,
In the
![]() ${}^*$
- and
${}^*$
- and
![]() $\mu$
-continuity conditions, the existence of the least upper bounds on the right is asserted, not assumed. Hence, these conditions are related to the
$\mu$
-continuity conditions, the existence of the least upper bounds on the right is asserted, not assumed. Hence, these conditions are related to the
![]() ${\mathcal{R}}$
- and
${\mathcal{R}}$
- and
![]() ${\mathcal{C}}$
-dioid axioms by the existence assertions
${\mathcal{C}}$
-dioid axioms by the existence assertions
![]() $U=\left\{\,c^m\,\mid\,m\in{\mathbb{N}}\,\right\}\in{\mathcal{R}} K$
resp.
$U=\left\{\,c^m\,\mid\,m\in{\mathbb{N}}\,\right\}\in{\mathcal{R}} K$
resp.
![]() $U=\left\{\,p^m(0)\,\mid\,m\in{\mathbb{N}}\,\right\} \in {\mathcal{C}}K$
and the
$U=\left\{\,p^m(0)\,\mid\,m\in{\mathbb{N}}\,\right\} \in {\mathcal{C}}K$
and the
![]() ${\mathcal{A}}$
-distributivity assertion, for
${\mathcal{A}}$
-distributivity assertion, for
![]() ${\mathcal{A}} = {\mathcal{R}}$
resp.
${\mathcal{A}} = {\mathcal{R}}$
resp.
![]() ${\mathcal{A}}={\mathcal{C}}$
,
${\mathcal{A}}={\mathcal{C}}$
,
which (assuming
![]() ${\mathcal{A}}$
-completeness) is equivalent to the
${\mathcal{A}}$
-completeness) is equivalent to the
![]() ${\mathcal{A}}$
-distributivity condition above. Of course, by
${\mathcal{A}}$
-distributivity condition above. Of course, by
![]() ${\mathcal{A}} K$
we mean
${\mathcal{A}} K$
we mean
![]() ${\mathcal{A}}$
applied to the multiplicative monoid of K. We refer to Hopkins (Reference Hopkins2008a) and Leiß and Hopkins (Reference Leiß and Hopkins2018) for the details of the equivalence between
${\mathcal{A}}$
applied to the multiplicative monoid of K. We refer to Hopkins (Reference Hopkins2008a) and Leiß and Hopkins (Reference Leiß and Hopkins2018) for the details of the equivalence between
![]() ${}^*$
-continuous Kleene algebras and
${}^*$
-continuous Kleene algebras and
![]() ${\mathcal{R}}$
-dioids and between
${\mathcal{R}}$
-dioids and between
![]() $\mu$
-continuous Chomsky algebras and
$\mu$
-continuous Chomsky algebras and
![]() ${\mathcal{C}}$
-dioids, respectively, and use the latter terminology in the following.
${\mathcal{C}}$
-dioids, respectively, and use the latter terminology in the following.
A dioid
![]() $(D,+,\cdot,0,1)$
is an idempotent semiring. Idempotency of
$(D,+,\cdot,0,1)$
is an idempotent semiring. Idempotency of
![]() $+$
provides a partial order
$+$
provides a partial order
![]() $\leq$
on D, via
$\leq$
on D, via
![]() $d\leq d'$
iff
$d\leq d'$
iff
![]() $d+d'=d'$
, with 0 as least element. Distributivity makes
$d+d'=d'$
, with 0 as least element. Distributivity makes
![]() $\cdot$
monotone with respect to
$\cdot$
monotone with respect to
![]() $\leq$
, and
$\leq$
, and
![]() $+$
guarantees a least upper bound
$+$
guarantees a least upper bound
![]() $\sum U =d_1+\ldots +d_n$
for each finite subset
$\sum U =d_1+\ldots +d_n$
for each finite subset
![]() $U=\{d_1,\ldots,d_n\}$
of D. Let
$U=\{d_1,\ldots,d_n\}$
of D. Let
![]() ${\mathbb{D}}$
be the category of dioids with dioid homomorphisms.
${\mathbb{D}}$
be the category of dioids with dioid homomorphisms.
For
![]() ${\mathcal{F}}\leq {\mathcal{A}}$
, (
${\mathcal{F}}\leq {\mathcal{A}}$
, (
![]() $A_3$
) implies that
$A_3$
) implies that
![]() ${\mathcal{A}} M$
is an idempotent semiring with
${\mathcal{A}} M$
is an idempotent semiring with
In this case, every
![]() ${\mathcal{A}}$
-dioid
${\mathcal{A}}$
-dioid
![]() $(D,\cdot,1,\leq)$
becomes a dioid
$(D,\cdot,1,\leq)$
becomes a dioid
![]() $(D,+,\cdot,0,1)$
, using
$(D,+,\cdot,0,1)$
, using
![]() $a+b := \sum\{a,b\}$
and
$a+b := \sum\{a,b\}$
and
![]() $0:=\sum\emptyset$
, and every
$0:=\sum\emptyset$
, and every
![]() ${\mathcal{A}}$
-morphism is a dioid homomorphism. Hence, we then view
${\mathcal{A}}$
-morphism is a dioid homomorphism. Hence, we then view
![]() ${\mathbb{D}}{\mathcal{A}}$
as a subcategory of
${\mathbb{D}}{\mathcal{A}}$
as a subcategory of
![]() ${\mathbb{D}}$
.
${\mathbb{D}}$
.
Let us collect a number of results of that will be frequently used below:
Theorem 1 (Hopkins Reference Hopkins2008a) Let
![]() ${\mathcal{A}}$
be a monadic operator with
${\mathcal{A}}$
be a monadic operator with
![]() ${\mathcal{F}}\leq{\mathcal{A}}$
. Let M,N be monoids and D be an
${\mathcal{F}}\leq{\mathcal{A}}$
. Let M,N be monoids and D be an
![]() ${\mathcal{A}}$
-dioid.
${\mathcal{A}}$
-dioid.
-
(1).
 ${\mathcal{A}} M$
is an
${\mathcal{A}} M$
is an
 ${\mathcal{A}}$
-dioid.
${\mathcal{A}}$
-dioid. -
(2).
 ${\mathcal{A}} M$
is the free
${\mathcal{A}} M$
is the free
 ${\mathcal{A}}$
-dioid extension of M. (i.e., any homomorphism
${\mathcal{A}}$
-dioid extension of M. (i.e., any homomorphism
 $f:M\to D$
to an
$f:M\to D$
to an
 ${\mathcal{A}}$
-dioid D extends uniquely to an
${\mathcal{A}}$
-dioid D extends uniquely to an
 ${\mathcal{A}}$
-morphism
${\mathcal{A}}$
-morphism
 $f^*:{\mathcal{A}} M\to D$
such that
$f^*:{\mathcal{A}} M\to D$
such that
 $f(m)=f^*(\{m\})$
.)
$f(m)=f^*(\{m\})$
.) -
(3). The least upper bound operator
 $\sum:{\mathcal{A}} D\to D$
is an
$\sum:{\mathcal{A}} D\to D$
is an
 ${\mathcal{A}}$
-morphism.
${\mathcal{A}}$
-morphism. -
(4). If
 $f:M\to N$
is a homomorphism, its lifting
$f:M\to N$
is a homomorphism, its lifting
 ${\mathcal{A}} f:{\mathcal{A}} M\to {\mathcal{A}} N$
is an
${\mathcal{A}} f:{\mathcal{A}} M\to {\mathcal{A}} N$
is an
 ${\mathcal{A}}$
-morphism.
${\mathcal{A}}$
-morphism. -
(5). If
 $f:M\to N$
is a surjective homomorphism, so is its lifting
$f:M\to N$
is a surjective homomorphism, so is its lifting
 ${\mathcal{A}} f:{\mathcal{A}} M\to {\mathcal{A}} N$
.
${\mathcal{A}} f:{\mathcal{A}} M\to {\mathcal{A}} N$
. -
(6). If M is a submonoid of N, then
 ${\mathcal{A}} M\subseteq {\mathcal{A}} N$
.
${\mathcal{A}} M\subseteq {\mathcal{A}} N$
.
In fact, by Theorem 16 of Hopkins (Reference Hopkins2008b),
![]() ${\mathcal{A}}:{\mathbb{M}}\to{\mathbb{D}}{\mathcal{A}}$
and the forgetful functor
${\mathcal{A}}:{\mathbb{M}}\to{\mathbb{D}}{\mathcal{A}}$
and the forgetful functor
![]() $\,\widehat{\!{\mathcal{A}}}:{\mathbb{D}}{\mathcal{A}}\to{\mathbb{M}}$
form an adjunction and combine to a monad
$\,\widehat{\!{\mathcal{A}}}:{\mathbb{D}}{\mathcal{A}}\to{\mathbb{M}}$
form an adjunction and combine to a monad
![]() $T_{\mathcal{A}}=(\widehat{\!{\mathcal{A}}}\circ{\mathcal{A}},\eta,\mu):{\mathbb{M}}\to{\mathbb{M}}$
with
$T_{\mathcal{A}}=(\widehat{\!{\mathcal{A}}}\circ{\mathcal{A}},\eta,\mu):{\mathbb{M}}\to{\mathbb{M}}$
with
![]() $m\in M \mapsto \{m\}\in{\mathcal{A}} M$
as unit
$m\in M \mapsto \{m\}\in{\mathcal{A}} M$
as unit
![]() $\eta$
and
$\eta$
and
![]() $U \in {\mathcal{A}}{\mathcal{A}} M\mapsto\bigcup U\in{\mathcal{A}} M$
as product
$U \in {\mathcal{A}}{\mathcal{A}} M\mapsto\bigcup U\in{\mathcal{A}} M$
as product
![]() $\mu$
. Therefore,
$\mu$
. Therefore,
![]() ${\mathcal{A}}$
-dioids are best viewed as Eilenberg-Moore T-algebras for this monad
${\mathcal{A}}$
-dioids are best viewed as Eilenberg-Moore T-algebras for this monad
![]() $T_{\mathcal{A}}$
, i.e. two-sorted structures
$T_{\mathcal{A}}$
, i.e. two-sorted structures
with
![]() $\sum$
as “structure map” (see Mac Lane Reference Mac Lane1971). The free
$\sum$
as “structure map” (see Mac Lane Reference Mac Lane1971). The free
![]() ${\mathcal{A}}$
-dioids
${\mathcal{A}}$
-dioids
![]() ${\mathcal{A}} M$
with monoid M are the objects of the Kleisli-category of this monad
${\mathcal{A}} M$
with monoid M are the objects of the Kleisli-category of this monad
![]() $T_{\mathcal{A}}$
.
$T_{\mathcal{A}}$
.
Besides the free
![]() ${\mathcal{A}}$
-dioid extensions
${\mathcal{A}}$
-dioid extensions
![]() ${\mathcal{A}} M$
of monoids M, further examples of
${\mathcal{A}} M$
of monoids M, further examples of
![]() ${\mathcal{A}}$
-dioids can be obtained from given ones by suitable quotient and tensor product constructions as defined later. Some categories
${\mathcal{A}}$
-dioids can be obtained from given ones by suitable quotient and tensor product constructions as defined later. Some categories
![]() ${\mathbb{D}}{\mathcal{A}}$
are closed under matrix semiring formation, in particular:
${\mathbb{D}}{\mathcal{A}}$
are closed under matrix semiring formation, in particular:
Example 2. Let J be a non-empty set and
![]() $D=(D,+^D,\cdot^D,0^D,1^D)$
a
$D=(D,+^D,\cdot^D,0^D,1^D)$
a
![]() ${\mathcal{P}}$
-dioid. Then,
${\mathcal{P}}$
-dioid. Then,
is a
![]() ${\mathcal{P}}$
-dioid, where
${\mathcal{P}}$
-dioid, where
![]() $D^{J\times J}$
is the set of functions from
$D^{J\times J}$
is the set of functions from
![]() $J\times J$
to D, 0 is the constant function with value
$J\times J$
to D, 0 is the constant function with value
![]() $0^D$
, 1 the function with
$0^D$
, 1 the function with
![]() $1(i,i) = 1^D$
and
$1(i,i) = 1^D$
and
![]() $1(i,j)=0^D$
for
$1(i,j)=0^D$
for
![]() $i\not=j$
, and
$i\not=j$
, and
![]() $+$
and
$+$
and
![]() $\cdot$
are given by
$\cdot$
are given by
![]() $(f+g)(i,j) =f(i,j)+^D g(i,j)$
and
$(f+g)(i,j) =f(i,j)+^D g(i,j)$
and
![]() $(f\cdot g)(i,j) = \sum\left\{\,f(i,k)\cdot^D g(k,j)\,\mid\,k\in J\,\right\}$
, for all
$(f\cdot g)(i,j) = \sum\left\{\,f(i,k)\cdot^D g(k,j)\,\mid\,k\in J\,\right\}$
, for all
![]() $i,j\in J$
.
$i,j\in J$
.
![]() ${{\textit Mat}_{J,J}(D)}$
is
${{\textit Mat}_{J,J}(D)}$
is
![]() ${\mathcal{P}}$
-complete, because any
${\mathcal{P}}$
-complete, because any
![]() $U\subseteq {{\textit Mat}_{J,J}(D)}$
has a least upper bound
$U\subseteq {{\textit Mat}_{J,J}(D)}$
has a least upper bound
![]() $\sum U$
defined componentwise by
$\sum U$
defined componentwise by
![]() $(\sum U)(i,j) =\sum\!\left\{\,f(i,j)\,\mid\,f\in U\,\right\}$
using
$(\sum U)(i,j) =\sum\!\left\{\,f(i,j)\,\mid\,f\in U\,\right\}$
using
![]() $\sum:{\mathcal{P}} D\to D$
; the
$\sum:{\mathcal{P}} D\to D$
; the
![]() ${\mathcal{P}}$
-distributivity of
${\mathcal{P}}$
-distributivity of
![]() ${{\textit Mat}_{J,J}(D)}$
follows from the definition of matrix product and the
${{\textit Mat}_{J,J}(D)}$
follows from the definition of matrix product and the
![]() ${\mathcal{P}}$
-distributivity of D:
${\mathcal{P}}$
-distributivity of D:
 \begin{eqnarray*} \left(g\cdot \left(\sum U\right)\cdot h\right)(i,j) &=& \sum\!\left\{\,\!g(i,k)\cdot^D \left(\sum\left\{\,f(k,l)\,\mid\,f\in U\,\right\}\right)\cdot^D h(l,j)\,\mid\,k,l\in J\!\,\right\} \\ &=& \sum\!\left\{\,\!g(i,k)\cdot^D f(k,l)\cdot^D h(l,j)\,\mid\,f\in U, k,l\in J\!\,\right\} \\ &=& \sum\!\left\{\,\!(g\cdot f\cdot h)(i,j)\,\mid\,f\in U\!\,\right\}.\end{eqnarray*}
\begin{eqnarray*} \left(g\cdot \left(\sum U\right)\cdot h\right)(i,j) &=& \sum\!\left\{\,\!g(i,k)\cdot^D \left(\sum\left\{\,f(k,l)\,\mid\,f\in U\,\right\}\right)\cdot^D h(l,j)\,\mid\,k,l\in J\!\,\right\} \\ &=& \sum\!\left\{\,\!g(i,k)\cdot^D f(k,l)\cdot^D h(l,j)\,\mid\,f\in U, k,l\in J\!\,\right\} \\ &=& \sum\!\left\{\,\!(g\cdot f\cdot h)(i,j)\,\mid\,f\in U\!\,\right\}.\end{eqnarray*}
Elements of
![]() ${{\textit Mat}_{J,J}(D)}$
will be called
${{\textit Mat}_{J,J}(D)}$
will be called
![]() $J\times J$
-matrices over D and often are denoted by A,B; as usual, we write
$J\times J$
-matrices over D and often are denoted by A,B; as usual, we write
![]() $A_{i,j}$
instead of A(i,j) etc. If M is a monoid,
$A_{i,j}$
instead of A(i,j) etc. If M is a monoid,
![]() ${{\textit Mat}_{J,J}({{\mathcal{P}} M})}$
is a
${{\textit Mat}_{J,J}({{\mathcal{P}} M})}$
is a
![]() ${\mathcal{P}}$
-dioid. In particular, since
${\mathcal{P}}$
-dioid. In particular, since
![]() ${\mathbb{B}} \simeq {{\mathcal{P}} M}$
for the trivial monoid M, the boolean matrices
${\mathbb{B}} \simeq {{\mathcal{P}} M}$
for the trivial monoid M, the boolean matrices
![]() ${{\textit Mat}_{J,J}({\mathbb{B}})}$
form a
${{\textit Mat}_{J,J}({\mathbb{B}})}$
form a
![]() ${\mathcal{P}}$
-dioid. We identify
${\mathcal{P}}$
-dioid. We identify
![]() ${{\textit Mat}_{J,J}({\mathbb{B}})}$
with the
${{\textit Mat}_{J,J}({\mathbb{B}})}$
with the
![]() ${\mathcal{P}}$
-dioid of binary relations on J and often write
${\mathcal{P}}$
-dioid of binary relations on J and often write
![]() $(i,j) \in A\subseteq J \times J$
instead of
$(i,j) \in A\subseteq J \times J$
instead of
![]() $A_{i,j}=1$
.
$A_{i,j}=1$
.
![]() $\diamond$
$\diamond$
Remark 2. Similarly,
![]() ${\mathbb{D}}{\mathcal{F}}$
is closed under
${\mathbb{D}}{\mathcal{F}}$
is closed under
![]() ${\textit Mat}_{n,n}(\cdot)$
for finite n and
${\textit Mat}_{n,n}(\cdot)$
for finite n and
![]() ${\mathbb{D}}{\mathcal{P}}_{\aleph_0}$
under
${\mathbb{D}}{\mathcal{P}}_{\aleph_0}$
under
![]() ${\textit Mat}_{J,J}(\cdot)$
for countable J. It is an open question whether
${\textit Mat}_{J,J}(\cdot)$
for countable J. It is an open question whether
![]() ${\textit Mat}_{n,n}(D)$
is an
${\textit Mat}_{n,n}(D)$
is an
![]() ${\mathcal{A}}$
-dioid for an arbitrary monadic operator
${\mathcal{A}}$
-dioid for an arbitrary monadic operator
![]() ${\mathcal{A}}$
and
${\mathcal{A}}$
and
![]() ${\mathcal{A}}$
-dioid D. The least upper bound
${\mathcal{A}}$
-dioid D. The least upper bound
![]() $\sum U$
of a set
$\sum U$
of a set
![]() $U\subseteq {\textit Mat}_{n,n}(D)$
has to satisfy
$U\subseteq {\textit Mat}_{n,n}(D)$
has to satisfy
![]() $(\sum U)_{i,j} =\sum\!\left\{\,\!A_{i,j}\,\mid\,A\in U\!\,\right\}$
, but
$(\sum U)_{i,j} =\sum\!\left\{\,\!A_{i,j}\,\mid\,A\in U\!\,\right\}$
, but
![]() $U\in{\mathcal{A}}({\textit Mat}_{n,n}(D))$
does not seem to imply
$U\in{\mathcal{A}}({\textit Mat}_{n,n}(D))$
does not seem to imply
![]() $\left\{\,\!A_{i,j}\,\mid\,A\in U\!\,\right\}\in{\mathcal{A}} D$
, so it is already unclear if the componentwise suprema exist and
$\left\{\,\!A_{i,j}\,\mid\,A\in U\!\,\right\}\in{\mathcal{A}} D$
, so it is already unclear if the componentwise suprema exist and
![]() ${\textit Mat}_{n,n}(D)$
is
${\textit Mat}_{n,n}(D)$
is
![]() ${\mathcal{A}}$
-complete. Defining the iteration
${\mathcal{A}}$
-complete. Defining the iteration
![]() $A^*$
of a matrix A of dimension
$A^*$
of a matrix A of dimension
![]() $n\times n$
by a formula of Conway (1971), Kozen (1994) shows that for a Kleene algebra K,
$n\times n$
by a formula of Conway (1971), Kozen (1994) shows that for a Kleene algebra K,
![]() ${\textit Mat}_{n,n}(K)$
is a Kleene algebra and extends this to
${\textit Mat}_{n,n}(K)$
is a Kleene algebra and extends this to
![]() ${}^*$
-continuous Kleene algebras in Kozen (1991), Chapter 7.1. So the category of
${}^*$
-continuous Kleene algebras in Kozen (1991), Chapter 7.1. So the category of
![]() ${\mathcal{R}}$
-dioids is closed under
${\mathcal{R}}$
-dioids is closed under
![]() ${\textit Mat}_{n,n}(\cdot)$
. Leiß (2016) shows that the category of
${\textit Mat}_{n,n}(\cdot)$
. Leiß (2016) shows that the category of
![]() ${\mathcal{C}}$
-dioids is closed under
${\mathcal{C}}$
-dioids is closed under
![]() ${\textit Mat}_{n,n}(\cdot)$
.
${\textit Mat}_{n,n}(\cdot)$
.
Lemma 3. Let
![]() $f:M\to D$
be a homomorphism from a monoid M to a dioid D. Suppose that for each
$f:M\to D$
be a homomorphism from a monoid M to a dioid D. Suppose that for each
![]() $L\in {\mathcal{A}} M$
, its image
$L\in {\mathcal{A}} M$
, its image
![]() $({\mathcal{A}} f)(L)\in{\mathcal{A}} D$
has a least upper bound in D,
$({\mathcal{A}} f)(L)\in{\mathcal{A}} D$
has a least upper bound in D,
![]() $\widehat{\,L\,} := \sum\left\{\,f(m)\,\mid\,m\in L\,\right\}$
and that
$\widehat{\,L\,} := \sum\left\{\,f(m)\,\mid\,m\in L\,\right\}$
and that
![]() $\,\widehat{\,\cdot\,} : {\mathcal{A}} M\to D$
is a surjective homomorphism. Then, D is an
$\,\widehat{\,\cdot\,} : {\mathcal{A}} M\to D$
is a surjective homomorphism. Then, D is an
![]() ${\mathcal{A}}$
-dioid.
${\mathcal{A}}$
-dioid.
Proof. By Theorem 1, the map
![]() ${\mathcal{A}}(\widehat{\,\cdot\,}):{\mathcal{A}}{\mathcal{A}} M\to {\mathcal{A}} D$
is a surjective homomorphism. Therefore, we can define a least upper bound operator
${\mathcal{A}}(\widehat{\,\cdot\,}):{\mathcal{A}}{\mathcal{A}} M\to {\mathcal{A}} D$
is a surjective homomorphism. Therefore, we can define a least upper bound operator
![]() $\sum$
that makes the following diagram commute:
$\sum$
that makes the following diagram commute:

For each
![]() $V\in{\mathcal{A}} D,$
there is
$V\in{\mathcal{A}} D,$
there is
![]() $U\in {\mathcal{A}}{\mathcal{A}} M$
such that
$U\in {\mathcal{A}}{\mathcal{A}} M$
such that
![]() $V=\left\{\,\widehat{\,L\,}\,\mid\,L\in U\,\right\}$
. Since
$V=\left\{\,\widehat{\,L\,}\,\mid\,L\in U\,\right\}$
. Since
![]() $\bigcup U\in {\mathcal{A}} M$
, its image under
$\bigcup U\in {\mathcal{A}} M$
, its image under
![]() $({\mathcal{A}} f)=\widetilde f$
has by assumption a least upper bound,
$({\mathcal{A}} f)=\widetilde f$
has by assumption a least upper bound,
![]() $\widehat{\bigcup U} = \sum\left\{\,f(m)\,\mid\,m\in\bigcup U\,\right\}\in D$
. Then,
$\widehat{\bigcup U} = \sum\left\{\,f(m)\,\mid\,m\in\bigcup U\,\right\}\in D$
. Then,
is an upper bound of V in D, since for each
![]() $L\in U$
,
$L\in U$
,
![]() $L\subseteq \bigcup U$
; hence,
$L\subseteq \bigcup U$
; hence,
![]() $\widetilde f(L)\subseteq \widetilde f(\bigcup U)$
and
$\widetilde f(L)\subseteq \widetilde f(\bigcup U)$
and
![]() $\widehat{\,L\,}\leq\widehat{\bigcup U}$
. If
$\widehat{\,L\,}\leq\widehat{\bigcup U}$
. If
![]() $e\in D$
is any upper bound of V, then for each
$e\in D$
is any upper bound of V, then for each
![]() $m\in\bigcup U$
there is
$m\in\bigcup U$
there is
![]() $L\in U$
with
$L\in U$
with
![]() $m\in L$
, so
$m\in L$
, so
Hence, e is an upper bound of
![]() $\left\{\,f(m)\,\mid\,m\in\bigcup U\,\right\}$
and so
$\left\{\,f(m)\,\mid\,m\in\bigcup U\,\right\}$
and so
![]() $\widehat{\bigcup U}\leq e$
. Therefore,
$\widehat{\bigcup U}\leq e$
. Therefore,
![]() $\sum V$
is the least upper bound of V in D, and D is
$\sum V$
is the least upper bound of V in D, and D is
![]() ${\mathcal{A}}$
-complete.
${\mathcal{A}}$
-complete.
To show that D is
![]() ${\mathcal{A}}$
-distributive, suppose
${\mathcal{A}}$
-distributive, suppose
![]() $V_1,V_2\in{\mathcal{A}} D$
. Since
$V_1,V_2\in{\mathcal{A}} D$
. Since
![]() ${\mathcal{A}}(\widehat{\,\cdot\,}) : {\mathcal{A}}{\mathcal{A}} M\to {\mathcal{A}} D$
is surjective, there are
${\mathcal{A}}(\widehat{\,\cdot\,}) : {\mathcal{A}}{\mathcal{A}} M\to {\mathcal{A}} D$
is surjective, there are
![]() $U_1,U_2\in {\mathcal{A}}{\mathcal{A}} M$
such that
$U_1,U_2\in {\mathcal{A}}{\mathcal{A}} M$
such that
![]() $V_i =\left\{\,\widehat{\,L\,}\,\mid\,L\in U_i\,\right\}$
and
$V_i =\left\{\,\widehat{\,L\,}\,\mid\,L\in U_i\,\right\}$
and
![]() $\sum V_i = \widehat{\bigcup U_i}$
for
$\sum V_i = \widehat{\bigcup U_i}$
for
![]() $i=1,2$
. Then,
$i=1,2$
. Then,
![]() $V_1V_2\in {\mathcal{A}} D$
has a least upper bound
$V_1V_2\in {\mathcal{A}} D$
has a least upper bound
![]() $\sum (V_1V_2)$
, and since
$\sum (V_1V_2)$
, and since
![]() $(\sum{V_1})(\sum{V_2})$
is an upper bound of
$(\sum{V_1})(\sum{V_2})$
is an upper bound of
![]() $V_1V_2$
, we have
$V_1V_2$
, we have
![]() $\sum(V_1V_2)\leq(\sum{V_1})(\sum{V_2})$
. For the reverse inequation, use that
$\sum(V_1V_2)\leq(\sum{V_1})(\sum{V_2})$
. For the reverse inequation, use that
![]() $\widehat{\,\cdot\,}$
and
$\widehat{\,\cdot\,}$
and
![]() $\bigcup$
are homomorphisms:
$\bigcup$
are homomorphisms:
 \begin{eqnarray*} \sum(V_1V_2) &=& \sum\left\{\,\widehat{L_1}\widehat{L_2}\,\mid\,L_1\in U_1, L_2\in U_2\,\right\}\\ &=& \sum\left\{\,\widehat{L_1L_2}\,\mid\,L_1\in U_1, L_2\in U_2\,\right\}\\ &=& \sum\left\{\,\widehat{\,L\,}\,\mid\,L \in U_1U_2\,\right\}\\ &=& \sum\left\{\,\sum\left\{\,f(m)\,\mid\,m\in L\,\right\}\,\mid\,L \in U_1U_2\,\right\}\\ &\geq& \sum\left\{\,f(m)\,\mid\,m\in \bigcup(U_1U_2)\,\right\}\\ &=& \widehat{\bigcup(U_1U_2)}\\ &=& \left(\bigcup U_1\cdot\bigcup U_2\right)^{\widehat{\quad}}\\ &=& \widehat{\bigcup U_1}\cdot \widehat{\bigcup U_2}\\ &=& \left(\sum V_1\right)\left(\sum V_2\right). \\[-28pt]\end{eqnarray*}
\begin{eqnarray*} \sum(V_1V_2) &=& \sum\left\{\,\widehat{L_1}\widehat{L_2}\,\mid\,L_1\in U_1, L_2\in U_2\,\right\}\\ &=& \sum\left\{\,\widehat{L_1L_2}\,\mid\,L_1\in U_1, L_2\in U_2\,\right\}\\ &=& \sum\left\{\,\widehat{\,L\,}\,\mid\,L \in U_1U_2\,\right\}\\ &=& \sum\left\{\,\sum\left\{\,f(m)\,\mid\,m\in L\,\right\}\,\mid\,L \in U_1U_2\,\right\}\\ &\geq& \sum\left\{\,f(m)\,\mid\,m\in \bigcup(U_1U_2)\,\right\}\\ &=& \widehat{\bigcup(U_1U_2)}\\ &=& \left(\bigcup U_1\cdot\bigcup U_2\right)^{\widehat{\quad}}\\ &=& \widehat{\bigcup U_1}\cdot \widehat{\bigcup U_2}\\ &=& \left(\sum V_1\right)\left(\sum V_2\right). \\[-28pt]\end{eqnarray*}
For monadic operators
![]() ${\mathcal{A}}\leq {\mathcal{B}}$
, the
${\mathcal{A}}\leq {\mathcal{B}}$
, the
![]() ${\mathcal{B}}$
-completion of an
${\mathcal{B}}$
-completion of an
![]() ${\mathcal{A}}$
-dioid D is a
${\mathcal{A}}$
-dioid D is a
![]() ${\mathcal{B}}$
-dioid
${\mathcal{B}}$
-dioid
![]() $\overline D$
together with an embedding
$\overline D$
together with an embedding
![]() ${\mathcal{A}}$
-morphism
${\mathcal{A}}$
-morphism
![]() $\eta_D:D\to \overline D$
such that the following “universal property” holds: any
$\eta_D:D\to \overline D$
such that the following “universal property” holds: any
![]() ${\mathcal{A}}$
-morphism f from D to a
${\mathcal{A}}$
-morphism f from D to a
![]() ${\mathcal{B}}$
-dioid D’ extends uniquely to a
${\mathcal{B}}$
-dioid D’ extends uniquely to a
![]() ${\mathcal{B}}$
-morphism
${\mathcal{B}}$
-morphism
![]() $\bar f : \overline D \to D'$
, in the sense that
$\bar f : \overline D \to D'$
, in the sense that
![]() $f=\bar f\circ \eta_D$
:
$f=\bar f\circ \eta_D$
:

By the universal property, the
![]() ${\mathcal{B}}$
-completion of D is unique up to a
${\mathcal{B}}$
-completion of D is unique up to a
![]() ${\mathcal{B}}$
-isomorphism.
${\mathcal{B}}$
-isomorphism.
The
![]() ${\mathcal{C}}$
-completion of a Kleene algebra or an
${\mathcal{C}}$
-completion of a Kleene algebra or an
![]() ${\mathcal{R}}$
-dioid is analogous to the algebraic closure of a field, but instead of adjoining roots to polynomials, we adjoin least fixed points. The
${\mathcal{R}}$
-dioid is analogous to the algebraic closure of a field, but instead of adjoining roots to polynomials, we adjoin least fixed points. The
![]() ${\mathcal{C}}$
-completion shall therefore also be called the
${\mathcal{C}}$
-completion shall therefore also be called the
![]() ${\mathcal{C}}$
-closure or fixed-point closure of the Kleene algebra.
${\mathcal{C}}$
-closure or fixed-point closure of the Kleene algebra.
Proposition 4. For monoids M, the
![]() ${\mathcal{C}}$
-completion of
${\mathcal{C}}$
-completion of
![]() ${\mathcal{R}} M$
is
${\mathcal{R}} M$
is
![]() ${\mathcal{C}} M$
with the inclusion as
${\mathcal{C}} M$
with the inclusion as
![]() $\eta_{{\mathcal{R}} M}$
.
$\eta_{{\mathcal{R}} M}$
.
Proof.
![]() ${\mathcal{C}} M$
is a
${\mathcal{C}} M$
is a
![]() ${\mathcal{C}}$
-dioid by Theorem 1 of Hopkins (Reference Hopkins2008a). If
${\mathcal{C}}$
-dioid by Theorem 1 of Hopkins (Reference Hopkins2008a). If
![]() $f:{\mathcal{R}} M\to C$
is an
$f:{\mathcal{R}} M\to C$
is an
![]() ${\mathcal{R}}$
-morphism to a
${\mathcal{R}}$
-morphism to a
![]() ${\mathcal{C}}$
-dioid C, we define
${\mathcal{C}}$
-dioid C, we define
![]() $\bar f:{\mathcal{C}} M\to C$
by
$\bar f:{\mathcal{C}} M\to C$
by
It is routine to check that
![]() $\bar f$
is the only
$\bar f$
is the only
![]() ${\mathcal{C}}$
-morphism
${\mathcal{C}}$
-morphism
![]() $h:{\mathcal{C}}M\to C$
with
$h:{\mathcal{C}}M\to C$
with
![]() $f=h\circ \eta_{{\mathcal{R}} M}$
.
$f=h\circ \eta_{{\mathcal{R}} M}$
. ![]()
In the rest of this paper, we give an algebraic construction of the
![]() ${\mathcal{C}}$
-closure
${\mathcal{C}}$
-closure
![]() ${\mathcal{C}} M$
of
${\mathcal{C}} M$
of
![]() ${\mathcal{R}} M$
for monoids M and generalize this to a construction of the
${\mathcal{R}} M$
for monoids M and generalize this to a construction of the
![]() ${\mathcal{C}}$
-closure of an arbitrary
${\mathcal{C}}$
-closure of an arbitrary
![]() ${\mathcal{R}}$
-dioid K.
${\mathcal{R}}$
-dioid K.
2.1 Quotients in
 ${\mathbb{D}}{\mathcal{A}}$
${\mathbb{D}}{\mathcal{A}}$
From now on, we assume
![]() ${\mathcal{F}}\leq {\mathcal{A}}$
, so that all
${\mathcal{F}}\leq {\mathcal{A}}$
, so that all
![]() ${\mathcal{A}}$
-dioids are dioids. For a partial order
${\mathcal{A}}$
-dioids are dioids. For a partial order
![]() $(D,\leq)$
, the down-closure of
$(D,\leq)$
, the down-closure of
![]() $U\subseteq D$
is
$U\subseteq D$
is
![]() $U^{\downarrow} := \left\{\,d\in D\,\mid\,d\leq u \textrm{ for some }u \in U\,\right\}$
.
$U^{\downarrow} := \left\{\,d\in D\,\mid\,d\leq u \textrm{ for some }u \in U\,\right\}$
.
If
![]() $D = (D,+^D,\cdot^D,0^D,1^D)$
is a dioid and
$D = (D,+^D,\cdot^D,0^D,1^D)$
is a dioid and
![]() $\rho$
a dioid-congruence on D, then
$\rho$
a dioid-congruence on D, then
![]() $D/\rho$
, the set of congruence classes of
$D/\rho$
, the set of congruence classes of
![]() $\rho$
, is a dioid under the operations
$\rho$
, is a dioid under the operations
The partial order
![]() $\leq$
on
$\leq$
on
![]() $D/\rho$
derived from
$D/\rho$
derived from
![]() $+$
is
$+$
is
An
![]() ${\mathcal{A}}$
-congruence on an
${\mathcal{A}}$
-congruence on an
![]() ${\mathcal{A}}$
-dioid D is a dioid-congruence
${\mathcal{A}}$
-dioid D is a dioid-congruence
![]() $\rho$
on D such that for all
$\rho$
on D such that for all
![]() $U,U'\in {\mathcal{A}} D$
, if
$U,U'\in {\mathcal{A}} D$
, if
![]() $(U/\rho)^{\downarrow} =(U'/\rho)^{\downarrow}$
, then
$(U/\rho)^{\downarrow} =(U'/\rho)^{\downarrow}$
, then
![]() $(\sum U)/\rho = (\sum U')/\rho$
.
$(\sum U)/\rho = (\sum U')/\rho$
.
Proposition 5
(Hopkins and Leiß Reference Hopkins and Leiß2018) If D is an
![]() ${\mathcal{A}}$
-dioid and
${\mathcal{A}}$
-dioid and
![]() $\rho$
an
$\rho$
an
![]() ${\mathcal{A}}$
-congruence on D, then
${\mathcal{A}}$
-congruence on D, then
![]() $D/\rho$
is an
$D/\rho$
is an
![]() ${\mathcal{A}}$
-dioid and the canonical map
${\mathcal{A}}$
-dioid and the canonical map
![]() $d \mapsto d/\rho$
is an
$d \mapsto d/\rho$
is an
![]() ${\mathcal{A}}$
-morphism.
${\mathcal{A}}$
-morphism.
Proof. For each
![]() $V\in {\mathcal{A}}(D/\rho)$
, there is
$V\in {\mathcal{A}}(D/\rho)$
, there is
![]() $U\in{\mathcal{A}} D$
such that
$U\in{\mathcal{A}} D$
such that
![]() $V=U/\rho = \left\{\,d/\rho\,\mid\,d\in U\,\right\}$
. Since
$V=U/\rho = \left\{\,d/\rho\,\mid\,d\in U\,\right\}$
. Since
![]() $\rho$
is an
$\rho$
is an
![]() ${\mathcal{A}}$
-congruence,
${\mathcal{A}}$
-congruence,
![]() $\sum (U/\rho) := (\sum U)/\rho$
is well-defined and a least upper bound of V. (This needs
$\sum (U/\rho) := (\sum U)/\rho$
is well-defined and a least upper bound of V. (This needs
![]() ${\mathcal{F}}\leq{\mathcal{A}}$
.)
${\mathcal{F}}\leq{\mathcal{A}}$
.) ![]()
If D is an
![]() ${\mathcal{A}}$
-dioid and
${\mathcal{A}}$
-dioid and
![]() $E\subseteq D\times D$
, there is a least
$E\subseteq D\times D$
, there is a least
![]() ${\mathcal{A}}$
-dioid-congruence
${\mathcal{A}}$
-dioid-congruence
![]() $\rho$
on D with
$\rho$
on D with
![]() $E\subseteq \rho$
, the intersection of all
$E\subseteq \rho$
, the intersection of all
![]() ${\mathcal{A}}$
-dioid-congruences on D above E.
${\mathcal{A}}$
-dioid-congruences on D above E.
The
![]() ${\mathcal{A}}$
-dioid
${\mathcal{A}}$
-dioid
![]() ${\mathcal{A}}(X^*/\rho)$
of the quotient monoid
${\mathcal{A}}(X^*/\rho)$
of the quotient monoid
![]() $X^*/\rho$
is isomorphic to the quotient
$X^*/\rho$
is isomorphic to the quotient
![]() ${\mathcal{A}} X^*/\tilde\rho$
of the free
${\mathcal{A}} X^*/\tilde\rho$
of the free
![]() ${\mathcal{A}}$
-dioid
${\mathcal{A}}$
-dioid
![]() ${\mathcal{A}} X^*$
by a suitable
${\mathcal{A}} X^*$
by a suitable
![]() ${\mathcal{A}}$
-congruence
${\mathcal{A}}$
-congruence
![]() $\tilde\rho$
. If
$\tilde\rho$
. If
![]() $\rho$
is determined by a set E of monoid equations,
$\rho$
is determined by a set E of monoid equations,
![]() $\tilde\rho$
is determined by the corresponding set of dioid equations between singleton sets:
$\tilde\rho$
is determined by the corresponding set of dioid equations between singleton sets:
Proposition 6 (Hopkins and Leiß Reference Hopkins and Leiß2018) Let
![]() $\rho$
be a congruence on the monoid M and
$\rho$
be a congruence on the monoid M and
![]() ${\mathcal{A}}\rho$
the least
${\mathcal{A}}\rho$
the least
![]() ${\mathcal{A}}$
-congruence on
${\mathcal{A}}$
-congruence on
![]() ${\mathcal{A}} M$
above
${\mathcal{A}} M$
above
![]() $\left\{\,(\{m\},\{m'\})\,\mid\,(m,m')\in \rho\,\right\}$
. Then
$\left\{\,(\{m\},\{m'\})\,\mid\,(m,m')\in \rho\,\right\}$
. Then
![]() ${\mathcal{A}}(M/\rho)\simeq {\mathcal{A}} M/{\mathcal{A}}\rho$
.
${\mathcal{A}}(M/\rho)\simeq {\mathcal{A}} M/{\mathcal{A}}\rho$
.
It is shown in Hopkins and Leiß (Reference Hopkins and Leiß2018) that
![]() ${\mathbb{D}}{\mathcal{A}}$
has coequalizers, and the quotient
${\mathbb{D}}{\mathcal{A}}$
has coequalizers, and the quotient
![]() $D/\rho$
of an
$D/\rho$
of an
![]() ${\mathcal{A}}$
-dioid D by an
${\mathcal{A}}$
-dioid D by an
![]() ${\mathcal{A}}$
-congruence
${\mathcal{A}}$
-congruence
![]() $\rho$
on D is the coequalizer of two suitable
$\rho$
on D is the coequalizer of two suitable
![]() ${\mathcal{A}}$
-morphisms
${\mathcal{A}}$
-morphisms
![]() $f,g:N\rightrightarrows D$
. The kernel
$f,g:N\rightrightarrows D$
. The kernel
![]() $\ker(f)$
of an
$\ker(f)$
of an
![]() ${\mathcal{A}}$
-morphism
${\mathcal{A}}$
-morphism
![]() $f:D\to D'$
between
$f:D\to D'$
between
![]() ${\mathcal{A}}$
-dioids is an
${\mathcal{A}}$
-dioids is an
![]() ${\mathcal{A}}$
-congruence on D.
${\mathcal{A}}$
-congruence on D.
2.2 The polycyclic
 ${\mathcal{A}}$
-dioids
${\mathcal{A}}$
-dioids
 $C_{n,{\mathcal{A}}}'$
$C_{n,{\mathcal{A}}}'$
Let
![]() $\Delta_n=\{p_0,\ldots,p_{n-1},q_0,\ldots,q_{n-1}\}$
be a set of n pairs of “brackets,”
$\Delta_n=\{p_0,\ldots,p_{n-1},q_0,\ldots,q_{n-1}\}$
be a set of n pairs of “brackets,”
![]() $p_0,q_0$
, …,
$p_0,q_0$
, …,
![]() $p_{n-1},q_{n-1}$
. We decompose
$p_{n-1},q_{n-1}$
. We decompose
![]() $\Delta_n = P_n\cup Q_n$
into the set
$\Delta_n = P_n\cup Q_n$
into the set
![]() $P_n=\left\{\,p_i\,\mid\,i<n\,\right\}$
of “opening” brackets and the set
$P_n=\left\{\,p_i\,\mid\,i<n\,\right\}$
of “opening” brackets and the set
![]() $Q_n=\left\{\,\!q_i\,\mid\,i<n\!\,\right\}$
of “closing” brackets. We also use
$Q_n=\left\{\,\!q_i\,\mid\,i<n\!\,\right\}$
of “closing” brackets. We also use
![]() ${\langle{i}\!\mid}$
for
${\langle{i}\!\mid}$
for
![]() $p_i$
and
$p_i$
and
![]() ${\mid\!{i}\rangle}$
for
${\mid\!{i}\rangle}$
for
![]() $q_i$
.
$q_i$
.
Let
![]() ${\mathcal{A}}$
be a monadic operator such that
${\mathcal{A}}$
be a monadic operator such that
![]() $\emptyset\in{\mathcal{A}} M$
for each monoid M. The polycyclic
$\emptyset\in{\mathcal{A}} M$
for each monoid M. The polycyclic
![]() ${\mathcal{A}}$
-dioid
${\mathcal{A}}$
-dioid
![]() $C_{n,{\mathcal{A}}}'$
is the quotient
$C_{n,{\mathcal{A}}}'$
is the quotient
![]() $C_{n,{\mathcal{A}}}' = {\mathcal{A}}\Delta_n^*/\rho_n$
of
$C_{n,{\mathcal{A}}}' = {\mathcal{A}}\Delta_n^*/\rho_n$
of
![]() ${\mathcal{A}}\Delta_n^*$
by the
${\mathcal{A}}\Delta_n^*$
by the
![]() ${\mathcal{A}}$
-congruence
${\mathcal{A}}$
-congruence
![]() $\rho_n$
generated by the relations
$\rho_n$
generated by the relations
where
![]() $\delta_{i,j}$
is the Kronecker
$\delta_{i,j}$
is the Kronecker
![]() $\delta$
. These equations allow us to algebraically distinguish matching brackets, where
$\delta$
. These equations allow us to algebraically distinguish matching brackets, where
![]() $p_iq_j=1$
, from non-matching ones, where
$p_iq_j=1$
, from non-matching ones, where
![]() $p_iq_j=0$
. Recall that in
$p_iq_j=0$
. Recall that in
![]() ${\mathcal{A}} \Delta^*_n$
, elements of
${\mathcal{A}} \Delta^*_n$
, elements of
![]() $\Delta_n^*$
are interpreted by their singleton sets, 0 by the empty set, so that
$\Delta_n^*$
are interpreted by their singleton sets, 0 by the empty set, so that
![]() $\rho_n$
is the least
$\rho_n$
is the least
![]() ${\mathcal{A}}$
-congruence containing
${\mathcal{A}}$
-congruence containing
![]() $(\{p_iq_i\},\{1\})$
and
$(\{p_iq_i\},\{1\})$
and
![]() $(\{p_iq_j\},\emptyset)$
for
$(\{p_iq_j\},\emptyset)$
for
![]() $i,j<n, i\not=j$
. The bra-ket algebra
$i,j<n, i\not=j$
. The bra-ket algebra
![]() $C_{n,{\mathcal{A}}}$
of Hopkins (Reference Hopkins2007) further assumes a “completeness” condition,
$C_{n,{\mathcal{A}}}$
of Hopkins (Reference Hopkins2007) further assumes a “completeness” condition,
![]() $1 =\sum\left\{\,q_ip_i\,\mid\,i<n\,\right\}$
, i.e.
$1 =\sum\left\{\,q_ip_i\,\mid\,i<n\,\right\}$
, i.e.
We will only use the case
![]() ${\mathcal{A}} ={\mathcal{R}}$
and abbreviate
${\mathcal{A}} ={\mathcal{R}}$
and abbreviate
![]() $C_{n,{\mathcal{R}}}$
and
$C_{n,{\mathcal{R}}}$
and
![]() $C_{n,{\mathcal{R}}}'$
by
$C_{n,{\mathcal{R}}}'$
by
![]() $C_n$
and
$C_n$
and
![]() $C_n'$
, respectively.
$C_n'$
, respectively.
Remark 7. The reason to call
![]() $1 = q_0p_0+\ldots + q_{n-1}p_{n-1}$
the completeness condition is as follows. A map
$1 = q_0p_0+\ldots + q_{n-1}p_{n-1}$
the completeness condition is as follows. A map
![]() $c:\{0,\ldots,n-1\}\to \{0,1\}^*$
is a prefix code if none of the code words
$c:\{0,\ldots,n-1\}\to \{0,1\}^*$
is a prefix code if none of the code words
![]() $c_0,\ldots,c_{n-1}$
is a prefix of another one. A prefix code c is complete if for each
$c_0,\ldots,c_{n-1}$
is a prefix of another one. A prefix code c is complete if for each
![]() $w\in \{0,1\}^*$
, either none or both successors w0, w1 of w are prefixes of code words. By induction on the word length, define
$w\in \{0,1\}^*$
, either none or both successors w0, w1 of w are prefixes of code words. By induction on the word length, define
![]() $p_w,q_w\in\Delta_2^*$
by
$p_w,q_w\in\Delta_2^*$
by
![]() $p_\varepsilon = \varepsilon =q_\varepsilon$
,
$p_\varepsilon = \varepsilon =q_\varepsilon$
,
![]() $p_{iw}= p_wp_i$
and
$p_{iw}= p_wp_i$
and
![]() $q_{iw} = q_iq_w$
for
$q_{iw} = q_iq_w$
for
![]() $i<2$
. Then, the map c is a prefix code iff in
$i<2$
. Then, the map c is a prefix code iff in
![]() $C_2$
,
$C_2$
,
![]() $p_{c_i}q_{c_j} = \delta_{i,j}$
for all
$p_{c_i}q_{c_j} = \delta_{i,j}$
for all
![]() $i,j<n$
, and a complete prefix code iff additionally
$i,j<n$
, and a complete prefix code iff additionally
![]() $\sum_{i<n}q_{c_i}p_{c_i} = 1$
. In the latter case,
$\sum_{i<n}q_{c_i}p_{c_i} = 1$
. In the latter case,
![]() $p_i\mapsto p_{c_i}$
,
$p_i\mapsto p_{c_i}$
,
![]() $q_i\mapsto q_{c_i}$
(
$q_i\mapsto q_{c_i}$
(
![]() $i<n$
) is an embedding of
$i<n$
) is an embedding of
![]() $C_n$
into
$C_n$
into
![]() $C_2$
, for
$C_2$
, for
![]() $n\geq 2$
. For example,
$n\geq 2$
. For example,
![]() $c_0 = 0$
,
$c_0 = 0$
,
![]() $c_1= 10$
,
$c_1= 10$
,
![]() $c_2=11$
is a complete prefix code
$c_2=11$
is a complete prefix code
![]() $c:\{0,1,2\} \to \{0,1\}^*$
, leading to an embedding of
$c:\{0,1,2\} \to \{0,1\}^*$
, leading to an embedding of
![]() $C_3$
into
$C_3$
into
![]() $C_2$
by mapping
$C_2$
by mapping
![]() $p_0,p_1,p_2$
to
$p_0,p_1,p_2$
to
![]() $p_0, p_0p_1, p_1p_1$
and
$p_0, p_0p_1, p_1p_1$
and
![]() $q_0,q_1,q_2$
to
$q_0,q_1,q_2$
to
![]() $q_0,q_1q_0,q_1q_1$
. The code words of different closing brackets are not prefixes of each other, those of different opening brackets are not suffixes of another.
$q_0,q_1q_0,q_1q_1$
. The code words of different closing brackets are not prefixes of each other, those of different opening brackets are not suffixes of another.
As we omit the completeness condition, we can view the semiring equations (7) as monoid equations, interpreted in monoids with an annihilating element 0, which leads to a different representation of
![]() $C_{n,{\mathcal{A}}}'$
that will be useful later.
$C_{n,{\mathcal{A}}}'$
that will be useful later.
The polycyclic monoid generated by
![]() $P_n$
is the quotient
$P_n$
is the quotient
![]() $P_n' := (\Delta_n\cup\{0\})^*/\rho_n$
, where
$P_n' := (\Delta_n\cup\{0\})^*/\rho_n$
, where
![]() $\rho_n$
now is the monoid congruence generated by
$\rho_n$
now is the monoid congruence generated by
Every string
![]() $w\in (\Delta_n\cup\{0\})^*$
can be reduced to a “normal form”
$w\in (\Delta_n\cup\{0\})^*$
can be reduced to a “normal form”
![]() $\textit{nf}_{n}(w)$
, using the equations generating
$\textit{nf}_{n}(w)$
, using the equations generating
![]() $\rho_n$
as rules to shorten a string. The reduction either runs into a bracket mismatch and returns 0, or finds matching brackets only and returns 1, or ends in a string with all closing brackets in front of all opening brackets. Hence, we can identify
$\rho_n$
as rules to shorten a string. The reduction either runs into a bracket mismatch and returns 0, or finds matching brackets only and returns 1, or ends in a string with all closing brackets in front of all opening brackets. Hence, we can identify
![]() $P_n'$
with
$P_n'$
with
![]() $(Q_n^*P_n^*\cup\{0\},\cdot,1)$
, where
$(Q_n^*P_n^*\cup\{0\},\cdot,1)$
, where
The Cayley graph of the polycyclic monoid
![]() $P_n'$
is the graph whose nodes are the elements
$P_n'$
is the graph whose nodes are the elements
![]() $x\in P_n'$
with edges
$x\in P_n'$
with edges
![]() $x{\,\stackrel{\delta}{\longrightarrow}\,} x\cdot\delta$
, for
$x{\,\stackrel{\delta}{\longrightarrow}\,} x\cdot\delta$
, for
![]() $\delta\in \Delta_n$
.
$\delta\in \Delta_n$
.
Example 3. A drawing of a part of the Cayley graph of
![]() $P_2'$
is given in Figure 1, not showing the sink node 0 and edges connected to it. For example, there is no edge
$P_2'$
is given in Figure 1, not showing the sink node 0 and edges connected to it. For example, there is no edge
![]() $q_0{\,\stackrel{{p_0}}{\longrightarrow}\,}1$
since
$q_0{\,\stackrel{{p_0}}{\longrightarrow}\,}1$
since
![]() $q_0p_0\not=1$
. As the picture indicates, the subgraph with nodes in
$q_0p_0\not=1$
. As the picture indicates, the subgraph with nodes in
![]() $P_2^*$
corresponds to a stack
$P_2^*$
corresponds to a stack
![]() $P_2^*\simeq \{0,1\}^*$
, with
$P_2^*\simeq \{0,1\}^*$
, with
![]() $p_i$
for
$p_i$
for
![]() $\textit{push}(i)$
and
$\textit{push}(i)$
and
![]() $q_i$
for
$q_i$
for
![]() $\textit{pop}(i)$
.
Footnote 4
For
$\textit{pop}(i)$
.
Footnote 4
For
![]() $u\in\Delta_2^*$
, an equation
$u\in\Delta_2^*$
, an equation
![]() $u=1$
holds in
$u=1$
holds in
![]() $P_2'$
iff u is the label of a path in the Cayley graph starting and ending in the node 1. The set of all those u is of course the pure Dyck language
$P_2'$
iff u is the label of a path in the Cayley graph starting and ending in the node 1. The set of all those u is of course the pure Dyck language
![]() $D_2\in {\mathcal{C}} \Delta_2^*$
of balanced strings over
$D_2\in {\mathcal{C}} \Delta_2^*$
of balanced strings over
![]() $\Delta_2$
, i.e. the least solution in
$\Delta_2$
, i.e. the least solution in
![]() ${\mathcal{P}}\Delta_2^*$
of
${\mathcal{P}}\Delta_2^*$
of
It is easy to define a pushdown automaton accepting
![]() $\left\{\,u\in\Delta_2^*\,\mid\,u=1 \textrm{ in }P_2'\,\right\}$
, keeping on its stack the
$\left\{\,u\in\Delta_2^*\,\mid\,u=1 \textrm{ in }P_2'\,\right\}$
, keeping on its stack the
![]() $\rho$
-normal form of the input sequence read.
$\rho$
-normal form of the input sequence read.
![]() $\diamond$
$\diamond$

Figure 1. Part of the Cayley graph of
![]() $P_2'$
.
$P_2'$
.
Nivat and Perrot (Reference Nivat and Perrot1970) initiated the study of the connection between polycyclic monoids and formal languages.
Remark 8. The polycyclic dioid
![]() $C_n'$
has an interpretation in the algebra of binary relations on the Cayley graph of
$C_n'$
has an interpretation in the algebra of binary relations on the Cayley graph of
![]() $P_n'$
, arising from the interpretation of
$P_n'$
, arising from the interpretation of
![]() $p_i$
and
$p_i$
and
![]() $q_i$
as the transition relations
$q_i$
as the transition relations
![]() ${\,\stackrel{{p_i}}{\longrightarrow}\,}$
and
${\,\stackrel{{p_i}}{\longrightarrow}\,}$
and
![]() ${\,\stackrel{{q_i}}{\longrightarrow}\,}$
shown in the graph. Under this interpretation, the completeness condition
${\,\stackrel{{q_i}}{\longrightarrow}\,}$
shown in the graph. Under this interpretation, the completeness condition
![]() $1= \sum_{i<n} q_ip_i$
is not valid, as node 1 is not related to itself by any of the relations
$1= \sum_{i<n} q_ip_i$
is not valid, as node 1 is not related to itself by any of the relations
![]() ${\,\stackrel{q_ip_i}{\longrightarrow}\,}$
. We will later use a restriction of this interpretation to the “stack part”
${\,\stackrel{q_ip_i}{\longrightarrow}\,}$
. We will later use a restriction of this interpretation to the “stack part”
![]() $P_n^*$
of
$P_n^*$
of
![]() $P_n'$
. It may seem that a constant
$P_n'$
. It may seem that a constant
![]() $\pi$
representing an “empty stack” test is needed to model a stack properly by
$\pi$
representing an “empty stack” test is needed to model a stack properly by
But in our case, this turns out to be unnecessary, since computations popping from the empty stack can be interpreted by the empty transition relation (cf. the proof of Theorem 17).
The map from
![]() $P_n'$
to
$P_n'$
to
![]() ${\mathcal{A}}\Delta_n^*$
given by
${\mathcal{A}}\Delta_n^*$
given by
![]() $0 \mapsto \emptyset$
,
$0 \mapsto \emptyset$
,
![]() $1\mapsto\{1\}$
, and
$1\mapsto\{1\}$
, and
![]() $p_i\mapsto\{p_i\}$
,
$p_i\mapsto\{p_i\}$
,
![]() $q_i \mapsto \{q_i\}$
for
$q_i \mapsto \{q_i\}$
for
![]() $i<n$
, extends to a homomorphism from
$i<n$
, extends to a homomorphism from
![]() $P_n'$
to the multiplicative monoid of
$P_n'$
to the multiplicative monoid of
![]() $C_{n,{\mathcal{A}}}'$
. Since
$C_{n,{\mathcal{A}}}'$
. Since
![]() $P_n'$
has no non-trivial congruences (by Nivat and Perrot Reference Nivat and Perrot1970), this is an embedding of
$P_n'$
has no non-trivial congruences (by Nivat and Perrot Reference Nivat and Perrot1970), this is an embedding of
![]() $P_n'$
into
$P_n'$
into
![]() $C_{n,{\mathcal{A}}}'$
, for
$C_{n,{\mathcal{A}}}'$
, for
![]() ${\mathcal{F}}\leq{\mathcal{A}}$
.
${\mathcal{F}}\leq{\mathcal{A}}$
.
In the original definition
![]() $C_n' = {\mathcal{R}} \Delta_n^*/\rho_n$
, we take the quotient of the regular sets
$C_n' = {\mathcal{R}} \Delta_n^*/\rho_n$
, we take the quotient of the regular sets
![]() ${\mathcal{R}}\Delta_n^*$
under the semiring congruence
${\mathcal{R}}\Delta_n^*$
under the semiring congruence
![]() $\rho_n$
, where 1 stands for
$\rho_n$
, where 1 stands for
![]() $\{1\}$
and 0 for
$\{1\}$
and 0 for
![]() $\emptyset$
. We now take the regular sets
$\emptyset$
. We now take the regular sets
![]() ${\mathcal{R}} P_n'$
of
${\mathcal{R}} P_n'$
of
![]() $P_n'$
and remove the annihilating element:
$P_n'$
and remove the annihilating element:
Proposition 9. If
![]() $\nu$
is the least
$\nu$
is the least
![]() ${\mathcal{R}}$
-congruence on
${\mathcal{R}}$
-congruence on
![]() ${\mathcal{R}} P_n'$
containing
${\mathcal{R}} P_n'$
containing
![]() $(\{0\},\emptyset)$
, then
$(\{0\},\emptyset)$
, then
![]() $ C_n' \simeq {\mathcal{R}} P_n'/\nu. $
Moreover, for
$ C_n' \simeq {\mathcal{R}} P_n'/\nu. $
Moreover, for
![]() $B,B'\in {\mathcal{R}} P_n'$
we have
$B,B'\in {\mathcal{R}} P_n'$
we have
![]() $B/\nu = B'/\nu$
iff
$B/\nu = B'/\nu$
iff
![]() $B\setminus\{0\} =B'\setminus\{0\}$
.
$B\setminus\{0\} =B'\setminus\{0\}$
.
Proof. We first prove the second statement.
![]() $\Leftarrow$
: Since
$\Leftarrow$
: Since
![]() $\{0\}/\nu=\emptyset/\nu$
is the least element of
$\{0\}/\nu=\emptyset/\nu$
is the least element of
![]() ${\mathcal{R}} P_n'/\nu$
, for
${\mathcal{R}} P_n'/\nu$
, for
![]() $B\in {\mathcal{R}} P_n'$
we have
$B\in {\mathcal{R}} P_n'$
we have
Hence, if
![]() $B,B'\in{\mathcal{R}} P_n'$
with
$B,B'\in{\mathcal{R}} P_n'$
with
![]() $B\setminus\{0\}=B'\setminus\{0\}$
, then
$B\setminus\{0\}=B'\setminus\{0\}$
, then
![]() $B/\nu=B'/\nu$
.
$B/\nu=B'/\nu$
.
![]() $\Rightarrow$
: One shows by induction on the regular operations that
$\Rightarrow$
: One shows by induction on the regular operations that
is an
![]() ${\mathcal{R}}$
-congruence containing
${\mathcal{R}}$
-congruence containing
![]() $(\{0\},\emptyset)$
, and obviously
$(\{0\},\emptyset)$
, and obviously
![]() $\nu\subseteq \nu_0$
.
$\nu\subseteq \nu_0$
.
For the first statement, notice that a congruence class
![]() $A/\rho_n$
of
$A/\rho_n$
of
![]() $C_n'= {\mathcal{R}}\Delta_n^*/\rho_n$
can be represented by a set of reduced strings,
$C_n'= {\mathcal{R}}\Delta_n^*/\rho_n$
can be represented by a set of reduced strings,
![]() $\left\{\,\textit{nf}_{n}(w)\,\mid\,w\in A\,\right\}\setminus\{0\}$
, and
$\left\{\,\textit{nf}_{n}(w)\,\mid\,w\in A\,\right\}\setminus\{0\}$
, and
![]() $A/\rho_n\mapsto\left\{\,\textit{nf}_{n}(w)\,\mid\,w\in A\,\right\}/\nu$
constitutes an isomorphism between
$A/\rho_n\mapsto\left\{\,\textit{nf}_{n}(w)\,\mid\,w\in A\,\right\}/\nu$
constitutes an isomorphism between
![]() $C_{n,{\mathcal{R}}}'$
and
$C_{n,{\mathcal{R}}}'$
and
![]() ${\mathcal{R}} P_n'/\nu$
.
${\mathcal{R}} P_n'/\nu$
. ![]()
The
![]() $n>2$
pairs of brackets
$n>2$
pairs of brackets
![]() $p_i,q_i$
,
$p_i,q_i$
,
![]() $i<n$
of
$i<n$
of
![]() $\Delta_n$
can be coded by two pairs, say b,d and p,q of
$\Delta_n$
can be coded by two pairs, say b,d and p,q of
![]() $\Delta_2$
, via
$\Delta_2$
, via
![]() $p_i:=bp^i$
and
$p_i:=bp^i$
and
![]() $q_i := q^id$
. This extends to an embedding of
$q_i := q^id$
. This extends to an embedding of
![]() $P_n'$
in
$P_n'$
in
![]() $P_2'$
.
$P_2'$
.
2.3 The tensor product of
 ${\mathcal{A}}$
-dioids
${\mathcal{A}}$
-dioids
In a category whose objects have a monoid structure, two morphisms
![]() $F_1:M_1\to M$
and
$F_1:M_1\to M$
and
![]() $F_2:M_2\to M$
are relatively commuting, if for all
$F_2:M_2\to M$
are relatively commuting, if for all
![]() $m_1\in M_1$
and
$m_1\in M_1$
and
![]() $m_2\in M_2$
,
$m_2\in M_2$
,
![]() $F_1(m_1)\cdot F_2(m_2) = F_2(m_2) \cdot F_1(m_1)$
.
$F_1(m_1)\cdot F_2(m_2) = F_2(m_2) \cdot F_1(m_1)$
.
The tensor product of
![]() $M_1$
and
$M_1$
and
![]() $M_2$
is an object
$M_2$
is an object
![]() $M_1\otimes M_2$
with two relatively commuting morphisms
$M_1\otimes M_2$
with two relatively commuting morphisms
![]() $\top_1 : M_1\to M_1\otimes M_2$
and
$\top_1 : M_1\to M_1\otimes M_2$
and
![]() $\top_2:M_2\to M_1\otimes M_2$
such that for any pair of relatively commuting morphisms
$\top_2:M_2\to M_1\otimes M_2$
such that for any pair of relatively commuting morphisms
![]() $f:M_1\to M$
and
$f:M_1\to M$
and
![]() $g:M_2\to M$
there is a unique morphism
$g:M_2\to M$
there is a unique morphism
![]() $h_{f,g}: M_1\otimes M_2\to M$
with
$h_{f,g}: M_1\otimes M_2\to M$
with
![]() $f=h_{f,g}\circ \top_1$
and
$f=h_{f,g}\circ \top_1$
and
![]() $g=h_{f,g}\circ \top_2$
:
$g=h_{f,g}\circ \top_2$
:

By the universal property, the tensor product of
![]() $M_1$
and
$M_1$
and
![]() $M_2$
is unique up to isomorphism.
$M_2$
is unique up to isomorphism.
Example 4. In the category
![]() ${\mathbb{M}}$
of monoids, the tensor product of
${\mathbb{M}}$
of monoids, the tensor product of
![]() $M_1$
and
$M_1$
and
![]() $M_2$
is the cartesian product
$M_2$
is the cartesian product
![]() $M_1\times M_2$
with componentwise multiplication, unit (1,1) and injections defined by
$M_1\times M_2$
with componentwise multiplication, unit (1,1) and injections defined by
![]() $\top_1(a)=(a,1)$
for
$\top_1(a)=(a,1)$
for
![]() $a\in M_1$
and
$a\in M_1$
and
![]() $\top_2(b)=(1,b)$
for
$\top_2(b)=(1,b)$
for
![]() $b\in M_2$
. The induced morphism
$b\in M_2$
. The induced morphism
![]() $h_{f,g}$
is the one given by
$h_{f,g}$
is the one given by
![]() $h_{f,g}(a,b) = f(a)\cdot g(b)$
.
$h_{f,g}(a,b) = f(a)\cdot g(b)$
.
![]() $\diamond$
$\diamond$
Theorem 10 (Hopkins and Leiß Reference Hopkins and Leiß2018) A tensor product of
![]() ${\mathcal{A}}$
-dioids
${\mathcal{A}}$
-dioids
![]() $D_1$
and
$D_1$
and
![]() $D_2$
exists,
$D_2$
exists,
consisting of
![]() $D_1\mathop{\otimes_{\mathcal{A}}} D_2 := {\mathcal{A}}(M_1\times M_2)/_\equiv$
, where
$D_1\mathop{\otimes_{\mathcal{A}}} D_2 := {\mathcal{A}}(M_1\times M_2)/_\equiv$
, where
![]() $M_i =\, \widehat{\!{\mathcal{A}}} D_i$
is the monoid underlying
$M_i =\, \widehat{\!{\mathcal{A}}} D_i$
is the monoid underlying
![]() $D_i$
and
$D_i$
and
![]() $\equiv$
is the
$\equiv$
is the
![]() ${\mathcal{A}}$
-congruence generated by the “tensor product relations”
${\mathcal{A}}$
-congruence generated by the “tensor product relations”
together with the embeddings
![]() $\top_1,\top_2$
defined by
$\top_1,\top_2$
defined by
The liftings of the embeddings of
![]() $M_i$
into
$M_i$
into
![]() $M_1\times M_2$
map
$M_1\times M_2$
map
![]() $A\in {\mathcal{A}}M_1$
to
$A\in {\mathcal{A}}M_1$
to
![]() $A\times\{1\}\in {\mathcal{A}}(M_1\times M_2)$
and
$A\times\{1\}\in {\mathcal{A}}(M_1\times M_2)$
and
![]() $B\in {\mathcal{A}} M_2$
to
$B\in {\mathcal{A}} M_2$
to
![]() $\{1\}\times B \in {\mathcal{A}}(M_1\times M_2);$
hence,
$\{1\}\times B \in {\mathcal{A}}(M_1\times M_2);$
hence,
![]() $A\times B =(A\times\{1\})(\{1\}\times B)\in {\mathcal{A}}(M_1\times M_2)$
. The tensor product relations are needed to make the
$A\times B =(A\times\{1\})(\{1\}\times B)\in {\mathcal{A}}(M_1\times M_2)$
. The tensor product relations are needed to make the
![]() $\top_i:D_i \to D_1\mathop{\otimes_{\mathcal{A}}} D_2$
be
$\top_i:D_i \to D_1\mathop{\otimes_{\mathcal{A}}} D_2$
be
![]() ${\mathcal{A}}$
-morphisms.
${\mathcal{A}}$
-morphisms.
For
![]() $U\in{\mathcal{A}}(M_1\times M_2)$
, we write [U] for
$U\in{\mathcal{A}}(M_1\times M_2)$
, we write [U] for
![]() $U/_\equiv$
. By the definition of
$U/_\equiv$
. By the definition of
![]() $\sum$
on
$\sum$
on
![]() $D_1\mathop{\otimes_{\mathcal{A}}} D_2$
,
$D_1\mathop{\otimes_{\mathcal{A}}} D_2$
,
using
![]() $a\otimes b$
for
$a\otimes b$
for
![]() $\top_1(a)\cdot \top_2(b)=[\{(a,b)\}]\in D_1\mathop{\otimes_{\mathcal{A}}} D_2$
. In particular, for
$\top_1(a)\cdot \top_2(b)=[\{(a,b)\}]\in D_1\mathop{\otimes_{\mathcal{A}}} D_2$
. In particular, for
![]() $A\in {\mathcal{A}} M_1, B\in {\mathcal{A}} M_2$
, via
$A\in {\mathcal{A}} M_1, B\in {\mathcal{A}} M_2$
, via
![]() $A \times B \in {\mathcal{A}}(M_1\times M_2)$
we have, by the tensor product relations,
$A \times B \in {\mathcal{A}}(M_1\times M_2)$
we have, by the tensor product relations,
Since
![]() $D_1\mathop{\otimes_{\mathcal{A}}} D_2 $
is the quotient of
$D_1\mathop{\otimes_{\mathcal{A}}} D_2 $
is the quotient of
![]() ${\mathcal{A}}(M_1\times M_2)$
by the
${\mathcal{A}}(M_1\times M_2)$
by the
![]() ${\mathcal{A}}$
-congruence
${\mathcal{A}}$
-congruence
![]() $\equiv$
, its partial order is the dioid-order on the quotient, i.e.
$\equiv$
, its partial order is the dioid-order on the quotient, i.e.
![]() $[U]\leq [V]$
iff
$[U]\leq [V]$
iff
![]() $[U\cup V] = [V]$
for
$[U\cup V] = [V]$
for
![]() $U,V\in{\mathcal{A}}(M_1\times M_2)$
, which is coarser than the order on
$U,V\in{\mathcal{A}}(M_1\times M_2)$
, which is coarser than the order on
![]() ${\mathcal{A}}(M_1\times M_2)$
among the representatives U,V.
${\mathcal{A}}(M_1\times M_2)$
among the representatives U,V.
Proposition 11 (Hopkins and Leiß Reference Hopkins and Leiß2018) For monoids
![]() $M_1$
and
$M_1$
and
![]() $M_2$
, the tensor product of the
$M_2$
, the tensor product of the
![]() ${\mathcal{A}}$
-dioids
${\mathcal{A}}$
-dioids
![]() ${\mathcal{A}} M_1$
and
${\mathcal{A}} M_1$
and
![]() ${\mathcal{A}} M_2$
is isomorphic to the
${\mathcal{A}} M_2$
is isomorphic to the
![]() ${\mathcal{A}}$
-dioid
${\mathcal{A}}$
-dioid
![]() ${\mathcal{A}}(M_1\times M_2)$
:
${\mathcal{A}}(M_1\times M_2)$
:
Proof. (Sketch) The isomorphism
![]() ${\mathcal{A}} M_1\mathop{\otimes_{\mathcal{A}}}{\mathcal{A}} M_2\to {\mathcal{A}}(M_1\times M_2)$
maps
${\mathcal{A}} M_1\mathop{\otimes_{\mathcal{A}}}{\mathcal{A}} M_2\to {\mathcal{A}}(M_1\times M_2)$
maps
![]() $[R]=\sum\left\{\,A\otimes B\,\mid\,(A,B)\in R\,\right\}\in {\mathcal{A}} M_1\mathop{\otimes_{\mathcal{A}}} {\mathcal{A}} M_2$
to
$[R]=\sum\left\{\,A\otimes B\,\mid\,(A,B)\in R\,\right\}\in {\mathcal{A}} M_1\mathop{\otimes_{\mathcal{A}}} {\mathcal{A}} M_2$
to
![]() $\bigcup\left\{\,A\times B\,\mid\,(A,B)\in R\,\right\}$
Footnote 5
, where
$\bigcup\left\{\,A\times B\,\mid\,(A,B)\in R\,\right\}$
Footnote 5
, where
![]() $R\in{\mathcal{A}}({\mathcal{A}} M_1 \times {\mathcal{A}} M_2)$
; the inverse maps
$R\in{\mathcal{A}}({\mathcal{A}} M_1 \times {\mathcal{A}} M_2)$
; the inverse maps
![]() $S\in{\mathcal{A}}(M_1\times M_2)$
to
$S\in{\mathcal{A}}(M_1\times M_2)$
to
![]() $\sum\left\{\,\{a\}\otimes \{b\}\,\mid\,(a,b)\in S\,\right\}$
.
$\sum\left\{\,\{a\}\otimes \{b\}\,\mid\,(a,b)\in S\,\right\}$
. ![]()
Since
![]() $(A,B)\mapsto A\times B$
is a homomorphism from
$(A,B)\mapsto A\times B$
is a homomorphism from
![]() ${\mathcal{A}} M\times {\mathcal{A}}N$
to
${\mathcal{A}} M\times {\mathcal{A}}N$
to
![]() ${\mathcal{A}}(M\times N)$
, its lifting is a homomorphism from
${\mathcal{A}}(M\times N)$
, its lifting is a homomorphism from
![]() ${\mathcal{A}}({\mathcal{A}}M\times{\mathcal{A}} N)$
to
${\mathcal{A}}({\mathcal{A}}M\times{\mathcal{A}} N)$
to
![]() ${\mathcal{A}}({\mathcal{A}}(M\times N))$
, so for
${\mathcal{A}}({\mathcal{A}}(M\times N))$
, so for
![]() $R\in{\mathcal{A}}({\mathcal{A}} M\times {\mathcal{A}} N)$
,
$R\in{\mathcal{A}}({\mathcal{A}} M\times {\mathcal{A}} N)$
,
By the isomorphism, we have
![]() $[R]=[R']$
iff
$[R]=[R']$
iff
![]() $S_R = S_{R'}$
. Conversely, for
$S_R = S_{R'}$
. Conversely, for
![]() $S\in{\mathcal{A}}(M\times N)$
,
$S\in{\mathcal{A}}(M\times N)$
,
hence,
![]() $[R_S] = \sum\left\{\,\{a\}\otimes\{b\}\,\mid\,(a,b)\in S\,\right\} \in {\mathcal{A}} M\mathop{\otimes_{\mathcal{A}}} {\mathcal{A}}N$
. Notice that
$[R_S] = \sum\left\{\,\{a\}\otimes\{b\}\,\mid\,(a,b)\in S\,\right\} \in {\mathcal{A}} M\mathop{\otimes_{\mathcal{A}}} {\mathcal{A}}N$
. Notice that
![]() $S_{(R_S)}=S$
and
$S_{(R_S)}=S$
and
![]() $[R_{(S_R)}]=[R]$
.
$[R_{(S_R)}]=[R]$
.
We can push this a bit further:
Theorem 12. Let M be a monoid and N a monoid with annihilating element 0. Then
where
![]() $\nu$
is the least
$\nu$
is the least
![]() ${\mathcal{A}}$
-congruence on
${\mathcal{A}}$
-congruence on
![]() ${\mathcal{A}} N$
containing
${\mathcal{A}} N$
containing
![]() $(\{0\},\emptyset)$
and
$(\{0\},\emptyset)$
and
![]() ${\tilde\nu}$
is the least
${\tilde\nu}$
is the least
![]() ${\mathcal{A}}$
-congruence on
${\mathcal{A}}$
-congruence on
![]() ${\mathcal{A}}(M\times N)$
containing
${\mathcal{A}}(M\times N)$
containing
![]() $(\{(1,0)\},\emptyset)$
.
$(\{(1,0)\},\emptyset)$
.
Putting
![]() $R_\nu := \left\{\,(A,B/\nu)\,\mid\,(A,B)\in R\,\right\}$
for
$R_\nu := \left\{\,(A,B/\nu)\,\mid\,(A,B)\in R\,\right\}$
for
![]() $R\in {\mathcal{A}}({\mathcal{A}}M\times {\mathcal{A}} N)$
, the isomorphism is given by
$R\in {\mathcal{A}}({\mathcal{A}}M\times {\mathcal{A}} N)$
, the isomorphism is given by
Proof. Since
![]() $B\mapsto B/\nu$
is a surjective
$B\mapsto B/\nu$
is a surjective
![]() ${\mathcal{A}}$
-morphism from
${\mathcal{A}}$
-morphism from
![]() ${\mathcal{A}} N$
to
${\mathcal{A}} N$
to
![]() ${\mathcal{A}} N/\nu$
, each element of
${\mathcal{A}} N/\nu$
, each element of
![]() ${\mathcal{A}}({\mathcal{A}} M\times ({\mathcal{A}} N/\nu))$
is of the form
${\mathcal{A}}({\mathcal{A}} M\times ({\mathcal{A}} N/\nu))$
is of the form
![]() $R_\nu$
for some
$R_\nu$
for some
![]() $R\in {\mathcal{A}}({\mathcal{A}} M\times{\mathcal{A}} N)$
.
$R\in {\mathcal{A}}({\mathcal{A}} M\times{\mathcal{A}} N)$
.
To prove
![]() ${\mathcal{A}} M\mathop{\otimes_{\mathcal{A}}} ({\mathcal{A}} N/\nu) \simeq {\mathcal{A}}(M\times N)/{\tilde\nu}$
, it is sufficient to show that
${\mathcal{A}} M\mathop{\otimes_{\mathcal{A}}} ({\mathcal{A}} N/\nu) \simeq {\mathcal{A}}(M\times N)/{\tilde\nu}$
, it is sufficient to show that
form a tensor product of
![]() ${\mathcal{A}} M$
and
${\mathcal{A}} M$
and
![]() ${\mathcal{A}} N/\nu$
in
${\mathcal{A}} N/\nu$
in
![]() ${\mathbb{D}}{\mathcal{A}}$
, where
${\mathbb{D}}{\mathcal{A}}$
, where
![]() $\top_1'$
and
$\top_1'$
and
![]() $\top_2'$
are defined by
$\top_2'$
are defined by
This will be done in the Appendix.
We here show that the isomorphism
![]() ${{\mathcal{A}} M\mathop{\otimes_{\mathcal{A}}} ({\mathcal{A}} N/\nu)}\simeq {{\mathcal{A}}(M\times N)/{\tilde\nu}}$
consisting of the
${{\mathcal{A}} M\mathop{\otimes_{\mathcal{A}}} ({\mathcal{A}} N/\nu)}\simeq {{\mathcal{A}}(M\times N)/{\tilde\nu}}$
consisting of the
![]() ${\mathcal{A}}$
-morphisms
${\mathcal{A}}$
-morphisms
![]() ${h_{\top_1',\top_2'}}$
and
${h_{\top_1',\top_2'}}$
and
![]() ${h'_{\top_1,\top_2}}$
induced by the universal properties of the two tensor product constructions
${h'_{\top_1,\top_2}}$
induced by the universal properties of the two tensor product constructions

is as claimed in the theorem. The induced
![]() ${\mathcal{A}}$
-morphisms are defined by
${\mathcal{A}}$
-morphisms are defined by
 \begin{eqnarray*} {h_{\top_1',\top_2'}}([R_\nu]) &:=& \sum\left\{\,\top_1'(A)\cdot\top_2'(B/\nu)\,\mid\,(A,B)\in R\,\right\}\\ &=& \sum\left\{\,(A\times\{1\})/{\tilde\nu}\cdot(\{1\}\times B)/{\tilde\nu}\,\mid\,(A,B)\in R\,\right\}\\ &=& \sum\left\{\,(A\times B)/{\tilde\nu}\,\mid\,(A,B)\in R\,\right\}\\ &=& \left(\bigcup\left\{\,A\times B\,\mid\,(A,B)\in R\,\right\}\right)/{\tilde\nu}= (S_R)/{\tilde\nu}\end{eqnarray*}
\begin{eqnarray*} {h_{\top_1',\top_2'}}([R_\nu]) &:=& \sum\left\{\,\top_1'(A)\cdot\top_2'(B/\nu)\,\mid\,(A,B)\in R\,\right\}\\ &=& \sum\left\{\,(A\times\{1\})/{\tilde\nu}\cdot(\{1\}\times B)/{\tilde\nu}\,\mid\,(A,B)\in R\,\right\}\\ &=& \sum\left\{\,(A\times B)/{\tilde\nu}\,\mid\,(A,B)\in R\,\right\}\\ &=& \left(\bigcup\left\{\,A\times B\,\mid\,(A,B)\in R\,\right\}\right)/{\tilde\nu}= (S_R)/{\tilde\nu}\end{eqnarray*}
and
 \begin{eqnarray*} {h'_{\top_1,\top_2}}(S/{\tilde\nu}) &:=& \sum\left\{\,\top_1(\{m\})\cdot\top_2(\{v\}/\nu)\,\mid\,(m,v)\in S\,\right\}\\ &=& \sum\left\{\,\{m\}\otimes \{v\}/\nu\,\mid\,(m,v)\in S\,\right\}\\ &=& [(R_S)_\nu].\end{eqnarray*}
\begin{eqnarray*} {h'_{\top_1,\top_2}}(S/{\tilde\nu}) &:=& \sum\left\{\,\top_1(\{m\})\cdot\top_2(\{v\}/\nu)\,\mid\,(m,v)\in S\,\right\}\\ &=& \sum\left\{\,\{m\}\otimes \{v\}/\nu\,\mid\,(m,v)\in S\,\right\}\\ &=& [(R_S)_\nu].\end{eqnarray*}
Since
![]() $S_{(R_S)} = S$
, we have
$S_{(R_S)} = S$
, we have
and since the tensor product embeddings
![]() $\top_1,\top_2$
are
$\top_1,\top_2$
are
![]() ${\mathcal{A}}$
-morphisms,
${\mathcal{A}}$
-morphisms,
 \begin{eqnarray*} ({h'_{\top_1,\top_2}}\circ{h_{\top_1',\top_2'}})([R_\nu]) &=& {h'_{\top_1,\top_2}}(S_R/{\tilde\nu}) = [(R_{(S_R)})_\nu]\\ &=& \sum\left\{\,A\otimes B/\nu\,\mid\,(A,B)\in R_{(S_R)}\,\right\}\\ &=& \sum\left\{\,\{m\}\otimes \{v\}/\nu\,\mid\,(m,v)\in S_R\,\right\}\\ &=& \sum\left\{\,\{m\}\otimes \{v\}/\nu\,\mid\,(m,v)\in A\times B, (A,B)\in R\,\right\}\\ &=& \sum\left\{\,A\otimes B/\nu\,\mid\,(A,B)\in R\,\right\} = [R_\nu]. \\[-28pt]\end{eqnarray*}
\begin{eqnarray*} ({h'_{\top_1,\top_2}}\circ{h_{\top_1',\top_2'}})([R_\nu]) &=& {h'_{\top_1,\top_2}}(S_R/{\tilde\nu}) = [(R_{(S_R)})_\nu]\\ &=& \sum\left\{\,A\otimes B/\nu\,\mid\,(A,B)\in R_{(S_R)}\,\right\}\\ &=& \sum\left\{\,\{m\}\otimes \{v\}/\nu\,\mid\,(m,v)\in S_R\,\right\}\\ &=& \sum\left\{\,\{m\}\otimes \{v\}/\nu\,\mid\,(m,v)\in A\times B, (A,B)\in R\,\right\}\\ &=& \sum\left\{\,A\otimes B/\nu\,\mid\,(A,B)\in R\,\right\} = [R_\nu]. \\[-28pt]\end{eqnarray*}
With Proposition 9, Theorem 12 provides us with a representation of
![]() ${\mathcal{R}} M \mathop{\otimes_{\mathcal{R}}} C_2'$
as a quotient of a free
${\mathcal{R}} M \mathop{\otimes_{\mathcal{R}}} C_2'$
as a quotient of a free
![]() ${\mathcal{R}}$
-dioid extension:
${\mathcal{R}}$
-dioid extension:
Corollary 13. Let
![]() $\nu$
be the least
$\nu$
be the least
![]() ${\mathcal{R}}$
-congruence on
${\mathcal{R}}$
-congruence on
![]() ${\mathcal{R}} P_2'$
containing
${\mathcal{R}} P_2'$
containing
![]() $(\{0\},\emptyset)$
and
$(\{0\},\emptyset)$
and
![]() ${\tilde\nu}$
the least
${\tilde\nu}$
the least
![]() ${\mathcal{R}}$
-congruence on
${\mathcal{R}}$
-congruence on
![]() ${\mathcal{R}}(M\times P_2')$
containing
${\mathcal{R}}(M\times P_2')$
containing
![]() $(\{(1,0)\},\emptyset)$
. Then
$(\{(1,0)\},\emptyset)$
. Then
The centralizer
![]() $Z_C(D)$
of a set C under an embedding
$Z_C(D)$
of a set C under an embedding
![]() $i:C\to D$
in an
$i:C\to D$
in an
![]() ${\mathcal{A}}$
-dioid D is the set
${\mathcal{A}}$
-dioid D is the set
of all elements of D that commute elementwise with the image of C in D under i.
In the following, we are concerned with
![]() $Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')$
, the centralizer of
$Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')$
, the centralizer of
![]() $C_2'$
in
$C_2'$
in
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
under the tensor product embedding
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
under the tensor product embedding
![]() $\top_2 : C_2'\to {\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
.
$\top_2 : C_2'\to {\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
.
Proposition 14. For each
![]() ${\mathcal{R}}$
-dioid K,
${\mathcal{R}}$
-dioid K,
![]() $Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is an
$Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is an
![]() ${\mathcal{R}}$
-dioid.
${\mathcal{R}}$
-dioid.
Proof. It is clear that
![]() $Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is closed under
$Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is closed under
![]() $0,1,+$
and
$0,1,+$
and
![]() $\cdot$
, so it is a sub-dioid of
$\cdot$
, so it is a sub-dioid of
![]() $K\mathop{\otimes_{\mathcal{R}}} C_2'$
. It is also closed under the restriction of
$K\mathop{\otimes_{\mathcal{R}}} C_2'$
. It is also closed under the restriction of
![]() $\sum:{\mathcal{R}}(K\mathop{\otimes_{\mathcal{R}}} C_2')\to K\mathop{\otimes_{\mathcal{R}}} C_2'$
to
$\sum:{\mathcal{R}}(K\mathop{\otimes_{\mathcal{R}}} C_2')\to K\mathop{\otimes_{\mathcal{R}}} C_2'$
to
![]() ${\mathcal{R}}(Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'}))$
: if
${\mathcal{R}}(Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'}))$
: if
![]() $c\in C_2'$
and
$c\in C_2'$
and
![]() $U\in {\mathcal{R}}(Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'}))\subseteq {\mathcal{R}}(K\mathop{\otimes_{\mathcal{R}}} C_2')$
, then since
$U\in {\mathcal{R}}(Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'}))\subseteq {\mathcal{R}}(K\mathop{\otimes_{\mathcal{R}}} C_2')$
, then since
![]() $K\mathop{\otimes_{\mathcal{R}}}{C_2'}$
is
$K\mathop{\otimes_{\mathcal{R}}}{C_2'}$
is
![]() ${\mathcal{R}}$
-distributive,
${\mathcal{R}}$
-distributive,
so
![]() $\sum U\in Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
.
$\sum U\in Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
. ![]()
We will later see that for monoids M,
![]() $Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is a
$Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is a
![]() ${\mathcal{C}}$
-dioid and isomorphic to
${\mathcal{C}}$
-dioid and isomorphic to
![]() ${\mathcal{C}} M$
. The reason to care about this is that it provides us with regular expressions as a notation system for context-free sets. Every
${\mathcal{C}} M$
. The reason to care about this is that it provides us with regular expressions as a notation system for context-free sets. Every
![]() $L\in {\mathcal{C}} M$
is, under
$L\in {\mathcal{C}} M$
is, under
![]() ${\mathcal{C}} M \simeq Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
, an element of the Kleene algebra
${\mathcal{C}} M \simeq Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
, an element of the Kleene algebra
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
and therefore denoted by a regular expression in the generators of
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
and therefore denoted by a regular expression in the generators of
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
.
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
.
Example 5. Let
![]() $\Delta_2=\{b,d,p,q\}$
and M be a monoid. For
$\Delta_2=\{b,d,p,q\}$
and M be a monoid. For
![]() $x,y\in M$
, consider
$x,y\in M$
, consider
![]() $L = \left\{\,x^ny^n\,\mid\,n\in{\mathbb{N}}\,\right\}\in{\mathcal{C}} M$
and the regular expression
$L = \left\{\,x^ny^n\,\mid\,n\in{\mathbb{N}}\,\right\}\in{\mathcal{C}} M$
and the regular expression
![]() $b(px)^*(yq)^*d$
. Interpreted in
$b(px)^*(yq)^*d$
. Interpreted in
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
, elements
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
, elements
![]() $m\in M$
mean
$m\in M$
mean
![]() $\top_1(\{m\}) = \{m\}\otimes \{1\}/\nu$
and elements
$\top_1(\{m\}) = \{m\}\otimes \{1\}/\nu$
and elements
![]() $\delta\in\Delta_2$
mean
$\delta\in\Delta_2$
mean
![]() $\top_2(\{\delta\})=\{1\}\otimes \{\delta\}/\nu$
. By
$\top_2(\{\delta\})=\{1\}\otimes \{\delta\}/\nu$
. By
![]() ${}^*$
-continuity and since m and
${}^*$
-continuity and since m and
![]() $\delta$
commute with each other in
$\delta$
commute with each other in
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
, we obtain
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
, we obtain
 \begin{eqnarray*} b(px)^*(yq)^*d &=& b\left(\sum\left\{\,(px)^k\,\mid\,k\in{\mathbb{N}}\,\right\}\right)\left(\sum\left\{\,(yq)^n\,\mid\,n\in{\mathbb{N}}\,\right\}\right)d\\ &=& \sum\left\{\,b(px)^k(yq)^nd\,\mid\,k\in{\mathbb{N}},n\in{\mathbb{N}}\,\right\}\\ &=& \sum\left\{\,x^ky^nbp^kq^nd\,\mid\,k\in{\mathbb{N}},n\in{\mathbb{N}}\,\right\}\\ &=& \sum\left\{\,x^ny^n\,\mid\,n\in{\mathbb{N}}\,\right\},\end{eqnarray*}
\begin{eqnarray*} b(px)^*(yq)^*d &=& b\left(\sum\left\{\,(px)^k\,\mid\,k\in{\mathbb{N}}\,\right\}\right)\left(\sum\left\{\,(yq)^n\,\mid\,n\in{\mathbb{N}}\,\right\}\right)d\\ &=& \sum\left\{\,b(px)^k(yq)^nd\,\mid\,k\in{\mathbb{N}},n\in{\mathbb{N}}\,\right\}\\ &=& \sum\left\{\,x^ky^nbp^kq^nd\,\mid\,k\in{\mathbb{N}},n\in{\mathbb{N}}\,\right\}\\ &=& \sum\left\{\,x^ny^n\,\mid\,n\in{\mathbb{N}}\,\right\},\end{eqnarray*}
where in the final step,
![]() $bp^kq^nd = \delta_{k,n}$
since
$bp^kq^nd = \delta_{k,n}$
since
![]() $pq=1=bd$
and
$pq=1=bd$
and
![]() $bq=0=pd$
. We will see that for any
$bq=0=pd$
. We will see that for any
![]() $L\in {\mathcal{C}} M$
, its image
$L\in {\mathcal{C}} M$
, its image
![]() $\widehat L := \sum\left\{\,\{m\}\otimes 1\,\mid\,m\in L\,\right\}$
in
$\widehat L := \sum\left\{\,\{m\}\otimes 1\,\mid\,m\in L\,\right\}$
in
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
belongs to
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
belongs to
![]() $Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
.
$Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
.
![]() $\diamond$
$\diamond$
To prove that
![]() $Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
, together with the embedding
$Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
, together with the embedding
![]() $\top_1$
, is the
$\top_1$
, is the
![]() ${\mathcal{C}}$
-closure of
${\mathcal{C}}$
-closure of
![]() ${\mathcal{R}} M$
, we want to show that any
${\mathcal{R}} M$
, we want to show that any
![]() ${\mathcal{R}}$
-morphism
${\mathcal{R}}$
-morphism
![]() $f:{\mathcal{R}} M\to C$
to a
$f:{\mathcal{R}} M\to C$
to a
![]() ${\mathcal{C}}$
-dioid C has a unique extension to a
${\mathcal{C}}$
-dioid C has a unique extension to a
![]() ${\mathcal{C}}$
-morphism
${\mathcal{C}}$
-morphism
![]() $\bar f: Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})\to C$
, which can be defined by
$\bar f: Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})\to C$
, which can be defined by
At least this works if for each element
![]() $e\in Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
there is a unique
$e\in Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
there is a unique
![]() $L\in {\mathcal{C}} M$
with
$L\in {\mathcal{C}} M$
with
![]() $e=\widehat L$
. This uniqueness condition will be established in the following two sections: by Theorem 17 of Section 3, there is at most one such
$e=\widehat L$
. This uniqueness condition will be established in the following two sections: by Theorem 17 of Section 3, there is at most one such
![]() $L\in {\mathcal{C}} M$
, by Theorem 26 of Section 4, there is at least one such L.
$L\in {\mathcal{C}} M$
, by Theorem 26 of Section 4, there is at least one such L.
We remark that the category
![]() ${\mathbb{D}}{\mathcal{A}}$
has coproducts and free extensions (Hopkins and Leiß Reference Hopkins and Leiß2018). In particular, the free
${\mathbb{D}}{\mathcal{A}}$
has coproducts and free extensions (Hopkins and Leiß Reference Hopkins and Leiß2018). In particular, the free
![]() ${\mathcal{A}}$
-dioid extension of
${\mathcal{A}}$
-dioid extension of
![]() ${\mathcal{A}} M$
by the set
${\mathcal{A}} M$
by the set
![]() $\Delta$
,
$\Delta$
,
![]() $({\mathcal{A}} M)[\Delta]$
, is isomorphic to
$({\mathcal{A}} M)[\Delta]$
, is isomorphic to
![]() ${\mathcal{A}}(M[\Delta])$
, whence we simply write
${\mathcal{A}}(M[\Delta])$
, whence we simply write
![]() ${\mathcal{A}} M[\Delta]$
below.
${\mathcal{A}} M[\Delta]$
below.
3. The CST for Monoids and its Algebraic Version
We now prove the Chomsky–Schützenberger theorem for arbitrary monoids M by reducing
![]() ${\mathcal{C}} M$
to
${\mathcal{C}} M$
to
![]() ${\mathcal{R}} M$
and the pure Dyck language
${\mathcal{R}} M$
and the pure Dyck language
![]() $D_2\in{\mathcal{C}} \Delta_2^*$
and then give an algebraic version that embeds
$D_2\in{\mathcal{C}} \Delta_2^*$
and then give an algebraic version that embeds
![]() ${\mathcal{C}} M$
into
${\mathcal{C}} M$
into
![]() $Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
. Recall that
$Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
. Recall that
![]() $\Delta_2$
is an alphabet of two pairs of brackets and
$\Delta_2$
is an alphabet of two pairs of brackets and
![]() $M[\Delta_2]$
the free extension of M by
$M[\Delta_2]$
the free extension of M by
![]() $\Delta_2$
, which is just
$\Delta_2$
, which is just
![]() $(X\cup\Delta_2)^*$
in case
$(X\cup\Delta_2)^*$
in case
![]() $M=X^*$
.
$M=X^*$
.
3.1 The CST for monoids
For a finite set X– and
![]() $\Delta_2=\{p_0,q_0,p_1,q_1\}$
–, Dyck’s language
$\Delta_2=\{p_0,q_0,p_1,q_1\}$
–, Dyck’s language
![]() $D_2(X)\in{\mathcal{C}} X^*[\Delta_2]$
of balanced strings over
$D_2(X)\in{\mathcal{C}} X^*[\Delta_2]$
of balanced strings over
![]() $X^*[\Delta_2]$
is the least solution of
$X^*[\Delta_2]$
is the least solution of
in
![]() ${\mathcal{P}}(X^*[\Delta_2])$
. By the classical theorem of Chomsky and Schützenberger (Reference Chomsky and Schützenberger1963),
${\mathcal{P}}(X^*[\Delta_2])$
. By the classical theorem of Chomsky and Schützenberger (Reference Chomsky and Schützenberger1963),
Since, for any monoid M,
![]() ${\mathcal{C}} M$
is defined inductively as an extension of
${\mathcal{C}} M$
is defined inductively as an extension of
![]() ${\mathcal{F}} M$
by least solutions (in
${\mathcal{F}} M$
by least solutions (in
![]() ${\mathcal{P}} M$
) of polynomial systems with parameters from
${\mathcal{P}} M$
) of polynomial systems with parameters from
![]() ${\mathcal{C}} M$
, one can reduce the parameters in the polynomial systems to the base case
${\mathcal{C}} M$
, one can reduce the parameters in the polynomial systems to the base case
![]() ${\mathcal{F}} M$
, so that all elements of M that occur in the parameters come from a finite set
${\mathcal{F}} M$
, so that all elements of M that occur in the parameters come from a finite set
![]() $X\subseteq M$
. Therefore,
$X\subseteq M$
. Therefore,
where
![]() ${\left\langle X\right\rangle}\subseteq M$
is the submonoid of M generated by X. We identify a system
${\left\langle X\right\rangle}\subseteq M$
is the submonoid of M generated by X. We identify a system
![]() $y_1\geq p_1,\ldots,y_n\geq p_k$
with polynomials
$y_1\geq p_1,\ldots,y_n\geq p_k$
with polynomials
![]() $p_i\in{\mathcal{C}} {\left\langle {X}\right\rangle}[y_1,\ldots,y_k]$
with a context-free grammar with nonterminal symbols
$p_i\in{\mathcal{C}} {\left\langle {X}\right\rangle}[y_1,\ldots,y_k]$
with a context-free grammar with nonterminal symbols
![]() $y_1,\ldots,y_k$
, start symbol
$y_1,\ldots,y_k$
, start symbol
![]() $y_1$
and terminal symbols from X. Since M resp.
$y_1$
and terminal symbols from X. Since M resp.
![]() $D_2(M)$
belong to
$D_2(M)$
belong to
![]() ${\mathcal{C}} M$
resp.
${\mathcal{C}} M$
resp.
![]() ${\mathcal{C}} M[\Delta_2]$
only if M is finitely generated, we first state the CST for finitely generated monoids:
${\mathcal{C}} M[\Delta_2]$
only if M is finitely generated, we first state the CST for finitely generated monoids:
Theorem 15 (CST for finitely generated monoids) For any finitely generated monoid M,
where
![]() $D_2(M)\in {\mathcal{C}} M[\Delta_2]$
is the set of elements of
$D_2(M)\in {\mathcal{C}} M[\Delta_2]$
is the set of elements of
![]() $M[\Delta_2]$
with balanced brackets.
$M[\Delta_2]$
with balanced brackets.
Our proof is essentially a proof of the classical Chomsky–Schützenberger theorem, with a perhaps more intuitive construction of R from L than can be found in textbooks; it may be helpful to first consider Example 6 below. We use the grammatical definitions of
![]() ${\mathcal{C}} M$
and
${\mathcal{C}} M$
and
![]() ${\mathcal{R}} M[\Delta_2]$
.
${\mathcal{R}} M[\Delta_2]$
.
Proof. Let
![]() $L_1,\ldots,L_k\in {\mathcal{C}} M$
be the least solution of the grammar
$L_1,\ldots,L_k\in {\mathcal{C}} M$
be the least solution of the grammar
![]() $G = {\left\langle {y_1\geq p_1,\ldots,y_k\geq p_k}\right\rangle}$
. We can assume that the parameters in
$G = {\left\langle {y_1\geq p_1,\ldots,y_k\geq p_k}\right\rangle}$
. We can assume that the parameters in
![]() $p_1,\ldots,p_k$
are singletons or empty. Suppose there are
$p_1,\ldots,p_k$
are singletons or empty. Suppose there are
![]() $n-1$
occurrences of the variables
$n-1$
occurrences of the variables
![]() $y_1,\ldots,y_k$
in
$y_1,\ldots,y_k$
in
![]() $p_1,\ldots,p_k$
. Let
$p_1,\ldots,p_k$
. Let
![]() $\Delta_n=\{{\langle{0}\!\mid},\ldots,{\langle{n-1}\!\mid},{\langle{0}\!\mid},\ldots,{\mid\!{n-1}\rangle}\}$
be a set of n of “opening brackets”
$\Delta_n=\{{\langle{0}\!\mid},\ldots,{\langle{n-1}\!\mid},{\langle{0}\!\mid},\ldots,{\mid\!{n-1}\rangle}\}$
be a set of n of “opening brackets”
![]() ${\langle{i}\!\mid}$
and n “closing brackets”
${\langle{i}\!\mid}$
and n “closing brackets”
![]() ${\mid\!{i}\rangle}$
,
${\mid\!{i}\rangle}$
,
![]() $i<n$
, and reserve the brackets
$i<n$
, and reserve the brackets
![]() ${\langle{0}\!\mid},{\langle{0}\!\mid}$
for later usage. Surrounding the i-th variable occurrence by the i-th bracket pair, for
${\langle{0}\!\mid},{\langle{0}\!\mid}$
for later usage. Surrounding the i-th variable occurrence by the i-th bracket pair, for
![]() $0< i< n$
, turns G into a grammar
$0< i< n$
, turns G into a grammar
![]() $G' = \langle y_1\geq p_1',\ldots,y_n\geq p_k'\rangle$
with least solution
$G' = \langle y_1\geq p_1',\ldots,y_n\geq p_k'\rangle$
with least solution
![]() $L_1',\ldots,L_k'\in {\mathcal{C}} M[\Delta_n]$
. For example, a monomial
$L_1',\ldots,L_k'\in {\mathcal{C}} M[\Delta_n]$
. For example, a monomial
![]() $m_1y_{j,1}\ldots m_sy_{j,s}m_{s+1}$
of
$m_1y_{j,1}\ldots m_sy_{j,s}m_{s+1}$
of
![]() $p_j$
is turned into a monomial
$p_j$
is turned into a monomial
![]() $m_1{\langle{i_1}\!\mid}y_{j,1}{\mid\!{i_1}\rangle}\ldots m_s{\langle{i_s}\!\mid}y_{j,s}{\mid\!{i_s}\rangle}m_{s+1}$
of
$m_1{\langle{i_1}\!\mid}y_{j,1}{\mid\!{i_1}\rangle}\ldots m_s{\langle{i_s}\!\mid}y_{j,s}{\mid\!{i_s}\rangle}m_{s+1}$
of
![]() $p_j'$
. By the choice of
$p_j'$
. By the choice of
![]() $p_1',\ldots,p_k'$
, clearly
$p_1',\ldots,p_k'$
, clearly
![]() $L_j'\subseteq D_n(M)$
and
$L_j'\subseteq D_n(M)$
and
![]() $L_j = h_M(L_j')$
for
$L_j = h_M(L_j')$
for
![]() $1\leq j\leq k$
.
$1\leq j\leq k$
.
Approximate
![]() $L_1'$
from above by a regular set
$L_1'$
from above by a regular set
![]() $R_1\in {\mathcal{R}} M[\Delta_n]$
as follows. To each monomial
$R_1\in {\mathcal{R}} M[\Delta_n]$
as follows. To each monomial
![]() $\alpha$
of
$\alpha$
of
![]() $p_j'$
(i.e. grammar rule
$p_j'$
(i.e. grammar rule
![]() $(y_j,\alpha)$
or
$(y_j,\alpha)$
or
![]() $y_j\to\alpha$
) attach a “follow”- or “continuation”-variable
$y_j\to\alpha$
) attach a “follow”- or “continuation”-variable
![]() $y_j^F$
and split
$y_j^F$
and split
![]() $\alpha y_j^F$
into right-linear factors m’y, where
$\alpha y_j^F$
into right-linear factors m’y, where
![]() $m'\in M[\Delta_n]$
and
$m'\in M[\Delta_n]$
and
![]() $y\in\{y_1,\ldots,y_k,y_j^F\}$
. Let
$y\in\{y_1,\ldots,y_k,y_j^F\}$
. Let
![]() $G^F$
be the right-linear polynomial system
$G^F$
be the right-linear polynomial system
where the monomials of
![]() $p_j''$
are the initial factors m’y of the monomials of
$p_j''$
are the initial factors m’y of the monomials of
![]() $p_j'y_j^F$
and those of
$p_j'y_j^F$
and those of
![]() $p_j^F$
are the factors m’y that follow the occurrences of
$p_j^F$
are the factors m’y that follow the occurrences of
![]() $y_j$
in
$y_j$
in
![]() $p_1'y_1^F,\ldots,p_k'y_k^F$
. Let
$p_1'y_1^F,\ldots,p_k'y_k^F$
. Let
![]() $R_1$
be the first component of the least solution of
$R_1$
be the first component of the least solution of
![]() $G^F$
in
$G^F$
in
![]() ${\mathcal{R}} M[\Delta_n]$
.
${\mathcal{R}} M[\Delta_n]$
.
Claim 1. For all
![]() $1\leq j\leq k$
and
$1\leq j\leq k$
and
![]() $w\in M[\Delta_n]$
, if
$w\in M[\Delta_n]$
, if
![]() $y_j\Rightarrow_{G'}^* w$
, then
$y_j\Rightarrow_{G'}^* w$
, then
![]() $y_j\Rightarrow^*_{G^F} wy_j^F$
.
$y_j\Rightarrow^*_{G^F} wy_j^F$
.
Proof of Claim 1. By induction on the derivation length
![]() $r\geq 1$
in
$r\geq 1$
in
![]() $y_j\Rightarrow^r_{G'} w$
. If
$y_j\Rightarrow^r_{G'} w$
. If
![]() $r=1$
, then
$r=1$
, then
![]() $y_j\to w$
is a rule of G’, hence
$y_j\to w$
is a rule of G’, hence
![]() $y_j\to wy_j^F$
is a rule of
$y_j\to wy_j^F$
is a rule of
![]() $G^F$
. If
$G^F$
. If
![]() $y_j \Rightarrow_{G'}^1 \alpha \Rightarrow_{G'}^r w$
, and the rule
$y_j \Rightarrow_{G'}^1 \alpha \Rightarrow_{G'}^r w$
, and the rule
![]() $y_j\to\alpha$
of G’ is
$y_j\to\alpha$
of G’ is
![]() $y_j\to m_1{\langle{i_1}\!\mid}y_{j,1}{\mid\!{i_1}\rangle}\ldots m_s{\langle{i_s}\!\mid}y_{j,s}{\mid\!{i_s}\rangle}m_{s+1}$
, then
$y_j\to m_1{\langle{i_1}\!\mid}y_{j,1}{\mid\!{i_1}\rangle}\ldots m_s{\langle{i_s}\!\mid}y_{j,s}{\mid\!{i_s}\rangle}m_{s+1}$
, then
![]() $G^F$
has the rules
$G^F$
has the rules
and so
![]() $y_j \Rightarrow^*_{G^F} \alpha$
. By the induction hypothesis, we get
$y_j \Rightarrow^*_{G^F} \alpha$
. By the induction hypothesis, we get
![]() $\alpha \Rightarrow^*_{G^F} wy_j^F$
; hence,
$\alpha \Rightarrow^*_{G^F} wy_j^F$
; hence,
![]() $y_j \Rightarrow^*_{G^F} wy_j^F$
.
$y_j \Rightarrow^*_{G^F} wy_j^F$
.
![]() $\triangleleft$
$\triangleleft$
Using
![]() $y_1^F \geq 1$
, Claim 1 implies
$y_1^F \geq 1$
, Claim 1 implies
![]() $L_1'\subseteq R_1$
; hence,
$L_1'\subseteq R_1$
; hence,
![]() $L_1'\subseteq R_1\cap D_n(M)$
.
$L_1'\subseteq R_1\cap D_n(M)$
.
Claim 2. For all
![]() $1\leq j\leq k$
and
$1\leq j\leq k$
and
![]() $w\in D_n(M)$
, if
$w\in D_n(M)$
, if
![]() $y_j\Rightarrow_{G^F}^* wy_j^F$
, then
$y_j\Rightarrow_{G^F}^* wy_j^F$
, then
![]() $y_j\Rightarrow_{G'}^* w$
.
$y_j\Rightarrow_{G'}^* w$
.
Proof of Claim 2. By induction on the derivation length
![]() $r\geq 1$
in
$r\geq 1$
in
![]() $y_j\Rightarrow_{G^F}^rwy_j^F$
. If
$y_j\Rightarrow_{G^F}^rwy_j^F$
. If
![]() $r=1$
, then
$r=1$
, then
![]() $y_j\to w$
is a rule of G’; hence,
$y_j\to w$
is a rule of G’; hence,
![]() $y_j\Rightarrow^*_{G'} w$
. For length
$y_j\Rightarrow^*_{G'} w$
. For length
![]() $r+1 > 1$
, suppose
$r+1 > 1$
, suppose
![]() $y_j\Rightarrow_{G^F}^1 \alpha \Rightarrow_{G^F}^r wy_j^F$
. By the choice of
$y_j\Rightarrow_{G^F}^1 \alpha \Rightarrow_{G^F}^r wy_j^F$
. By the choice of
![]() $y_j\geq p_j''$
of
$y_j\geq p_j''$
of
![]() $G^F$
, there is
$G^F$
, there is
![]() $m_1\in M$
such that
$m_1\in M$
such that
![]() $\alpha =m_1{\langle{i_1}\!\mid}y_{j,1}$
for some
$\alpha =m_1{\langle{i_1}\!\mid}y_{j,1}$
for some
![]() $i_1$
and
$i_1$
and
![]() $y_{j,1}\in \{y_1,\ldots,y_k\}$
, or
$y_{j,1}\in \{y_1,\ldots,y_k\}$
, or
![]() $\alpha = m_1 y_{j}^F$
. The second case cannot occur, since
$\alpha = m_1 y_{j}^F$
. The second case cannot occur, since
![]() $m_1y_j^F\Rightarrow_{G^F}^r wy_j^F$
with
$m_1y_j^F\Rightarrow_{G^F}^r wy_j^F$
with
![]() $r\geq 1$
is impossible: all monomials of
$r\geq 1$
is impossible: all monomials of
![]() $p_j^F$
either begin with a closing bracket
$p_j^F$
either begin with a closing bracket
![]() ${\mid\!{i}\rangle}$
for some i, or are 1. In the first case, we have
${\mid\!{i}\rangle}$
for some i, or are 1. In the first case, we have
![]() $m_1{\langle{i_1}\!\mid}y_{j,1} \Rightarrow_{G^F}^r wy_j^F$
. As
$m_1{\langle{i_1}\!\mid}y_{j,1} \Rightarrow_{G^F}^r wy_j^F$
. As
![]() $w\in D_n(M)$
, there are
$w\in D_n(M)$
, there are
![]() $u_1,w_1\in D_n(M)$
such that
$u_1,w_1\in D_n(M)$
such that
![]() $w =m_1{\langle{i_1}\!\mid}u_1{\mid\!{i_1}\rangle}w_1$
and
$w =m_1{\langle{i_1}\!\mid}u_1{\mid\!{i_1}\rangle}w_1$
and
![]() $y_{j,1} \Rightarrow_{G^F}^r u_1{\mid\!{i_1}\rangle}w_1y_j^F$
. By the construction of
$y_{j,1} \Rightarrow_{G^F}^r u_1{\mid\!{i_1}\rangle}w_1y_j^F$
. By the construction of
![]() $G^F$
,
$G^F$
,
![]() ${\mid\!{i_1}\rangle}$
occurs only in rules
${\mid\!{i_1}\rangle}$
occurs only in rules
![]() $y_{j,1}^F\to{\mid\!{i_1}\rangle}m_2y_{j}^F$
or
$y_{j,1}^F\to{\mid\!{i_1}\rangle}m_2y_{j}^F$
or
![]() $y_{j,1}^F\to {\mid\!{i_1}\rangle}m_2{\langle{i_2}\!\mid}y_{j,2}$
with
$y_{j,1}^F\to {\mid\!{i_1}\rangle}m_2{\langle{i_2}\!\mid}y_{j,2}$
with
![]() $m_2\in M$
and
$m_2\in M$
and
![]() $y_{j,2}\in \{y_1,\ldots,y_k\}$
. So we must have
$y_{j,2}\in \{y_1,\ldots,y_k\}$
. So we must have
Since
![]() $r_1\leq r$
, we get
$r_1\leq r$
, we get
![]() $y_{j,1} \Rightarrow_{G'}^* u_1$
by induction. If the part
$y_{j,1} \Rightarrow_{G'}^* u_1$
by induction. If the part
![]() $y_{j,1}^F \Rightarrow^{r_2}_{G^F} {\mid\!{i_1}\rangle}w_1y_j^F$
is
$y_{j,1}^F \Rightarrow^{r_2}_{G^F} {\mid\!{i_1}\rangle}w_1y_j^F$
is
we must have
![]() $r_2=1$
and
$r_2=1$
and
![]() $w_1=m_2$
, so
$w_1=m_2$
, so
![]() $y_j \to m_1{\langle{i_1}\!\mid}y_{j,1}{\mid\!{i_1}\rangle}m_2$
is a rule of G’, and since
$y_j \to m_1{\langle{i_1}\!\mid}y_{j,1}{\mid\!{i_1}\rangle}m_2$
is a rule of G’, and since
![]() $w=m_1{\langle{i_1}\!\mid}u_1{\mid\!{i_1}\rangle}m_2$
, the claim
$w=m_1{\langle{i_1}\!\mid}u_1{\mid\!{i_1}\rangle}m_2$
, the claim
![]() $y_j\Rightarrow_{G'}^* w$
is shown. If the part
$y_j\Rightarrow_{G'}^* w$
is shown. If the part
![]() $y_{j,1}^F \Rightarrow^{r_2}_{G^F} {\mid\!{i_1}\rangle}w_1y_j^F$
is
$y_{j,1}^F \Rightarrow^{r_2}_{G^F} {\mid\!{i_1}\rangle}w_1y_j^F$
is
there are
![]() $u_2,w_2\in D_n(M)$
such that
$u_2,w_2\in D_n(M)$
such that
![]() $w_1=m_2{\langle{i_2}\!\mid}u_2{\mid\!{i_2}\rangle}w_2$
and
$w_1=m_2{\langle{i_2}\!\mid}u_2{\mid\!{i_2}\rangle}w_2$
and
![]() $y_{j,2}\Rightarrow_{G^F}^{r_2-1}u_2{\mid\!{i_2}\rangle}w_2$
. As
$y_{j,2}\Rightarrow_{G^F}^{r_2-1}u_2{\mid\!{i_2}\rangle}w_2$
. As
![]() ${\mid\!{i_2}\rangle}$
occurs only in rules
${\mid\!{i_2}\rangle}$
occurs only in rules
![]() $y_{j,2}^F\to{\mid\!{i_2}\rangle}m_3y_j^F$
or
$y_{j,2}^F\to{\mid\!{i_2}\rangle}m_3y_j^F$
or
![]() $y_{j,2}^F\to{\mid\!{i_2}\rangle}m_3{\langle{i_3}\!\mid}y_{j,3}$
with
$y_{j,2}^F\to{\mid\!{i_2}\rangle}m_3{\langle{i_3}\!\mid}y_{j,3}$
with
![]() $m_3\in M$
and
$m_3\in M$
and
![]() $y_{j,3}\in\{y_1,\ldots,y_k\}$
, we can continue this way and get
$y_{j,3}\in\{y_1,\ldots,y_k\}$
, we can continue this way and get
![]() $1\leq i_1,\ldots,i_s\leq n$
,
$1\leq i_1,\ldots,i_s\leq n$
,
![]() $r_1,\ldots,r_s\leq r$
,
$r_1,\ldots,r_s\leq r$
,
![]() $m_1,\ldots,m_{s+1}\in M$
and
$m_1,\ldots,m_{s+1}\in M$
and
![]() $u_1,\ldots,u_s\in D_n(M)$
such that
$u_1,\ldots,u_s\in D_n(M)$
such that
![]() $w=m_1{\langle{i_1}\!\mid}u_1{\mid\!{i_1}\rangle}\ldots m_s{\langle{i_s}\!\mid}u_{s}{\mid\!{i_s}\rangle}m_{s+1}$
and
$w=m_1{\langle{i_1}\!\mid}u_1{\mid\!{i_1}\rangle}\ldots m_s{\langle{i_s}\!\mid}u_{s}{\mid\!{i_s}\rangle}m_{s+1}$
and
 \begin{eqnarray*}y_j\Rightarrow_{G^F} m_1{\langle{i_1}\!\mid}y_{j,1}, && \quad y_{j,1}\Rightarrow_{G^F}^{r_1} u_1 y_{j,1}^F,\quad y_{j,1}^F \Rightarrow_{G^F} {\mid\!{i_1}\rangle}m_2{\langle{i_2}\!\mid} y_{j,2}, \quad\ldots\\ & &{j,s}\Rightarrow_{G^F}^{r_s} u_s y_{j,s}^F,\quad y_{j,s}^F\Rightarrow_{G^F} {\mid\!{i_s}\rangle}m_{s+1} y_{j}^F.\end{eqnarray*}
\begin{eqnarray*}y_j\Rightarrow_{G^F} m_1{\langle{i_1}\!\mid}y_{j,1}, && \quad y_{j,1}\Rightarrow_{G^F}^{r_1} u_1 y_{j,1}^F,\quad y_{j,1}^F \Rightarrow_{G^F} {\mid\!{i_1}\rangle}m_2{\langle{i_2}\!\mid} y_{j,2}, \quad\ldots\\ & &{j,s}\Rightarrow_{G^F}^{r_s} u_s y_{j,s}^F,\quad y_{j,s}^F\Rightarrow_{G^F} {\mid\!{i_s}\rangle}m_{s+1} y_{j}^F.\end{eqnarray*}
By construction of
![]() $G^F,$
there is a rule
$G^F,$
there is a rule
![]() $y_j\to m_1{\langle{i_1}\!\mid}y_{j,1}{\mid\!{i_1}\rangle}\ldots{\langle{i_s}\!\mid}y_{j,s}{\mid\!{i_s}\rangle}m_{s+1}$
in G’, and by induction,
$y_j\to m_1{\langle{i_1}\!\mid}y_{j,1}{\mid\!{i_1}\rangle}\ldots{\langle{i_s}\!\mid}y_{j,s}{\mid\!{i_s}\rangle}m_{s+1}$
in G’, and by induction,
![]() $y_{j,1}\Rightarrow_{G'}^* u_1,\ \ldots,\ y_{j,s}\Rightarrow^*_{G'} u_s$
. The claim
$y_{j,1}\Rightarrow_{G'}^* u_1,\ \ldots,\ y_{j,s}\Rightarrow^*_{G'} u_s$
. The claim
![]() $y_j\Rightarrow^*_{G'} w$
follows.
$y_j\Rightarrow^*_{G'} w$
follows.
![]() $\triangleleft$
$\triangleleft$
Using
![]() $y_1^F\Rightarrow_{G^F} 1$
, Claim 2 implies
$y_1^F\Rightarrow_{G^F} 1$
, Claim 2 implies
![]() $R_1\cap D_n(M)\subseteq L_1'$
. So
$R_1\cap D_n(M)\subseteq L_1'$
. So
![]() $L_1'=R_1\cap D_n(M)$
, and
$L_1'=R_1\cap D_n(M)$
, and
![]() $L_1= h_M(L_1')=h_M(R_1\cap D_n(M))$
. Finally,
$L_1= h_M(L_1')=h_M(R_1\cap D_n(M))$
. Finally,
![]() $D_n(M)$
can be replaced by
$D_n(M)$
can be replaced by
![]() $D_2(M)$
, since two bracket pairs b,d and p,q can be used to code
$D_2(M)$
, since two bracket pairs b,d and p,q can be used to code
![]() ${\langle{i}\!\mid}$
by
${\langle{i}\!\mid}$
by
![]() $bp^i$
and
$bp^i$
and
![]() ${\mid\!{i}\rangle}$
by
${\mid\!{i}\rangle}$
by
![]() $q^id$
for
$q^id$
for
![]() $i< n$
.
$i< n$
. ![]()
Example 6. Let
![]() $a,b,c\in M$
and let
$a,b,c\in M$
and let
![]() $G = {\left\langle {y\geq p_y(y,z), z\geq p_z(y,z)}\right\rangle}$
be the following grammar
$G = {\left\langle {y\geq p_y(y,z), z\geq p_z(y,z)}\right\rangle}$
be the following grammar
which defines sets
![]() $L_y,L_z\in{\mathcal{C}} M$
. Adding brackets around the three variable occurrences on the right turns G into the grammar
$L_y,L_z\in{\mathcal{C}} M$
. Adding brackets around the three variable occurrences on the right turns G into the grammar
![]() $G' = {\left\langle {y\geq p_y', z\geq p_z'}\right\rangle}$
$G' = {\left\langle {y\geq p_y', z\geq p_z'}\right\rangle}$
defining
![]() $L_y',L_z'\in{\mathcal{C}} M[\Delta_3]$
. It is clear that
$L_y',L_z'\in{\mathcal{C}} M[\Delta_3]$
. It is clear that
![]() $L_y = h_M(L_y')$
and
$L_y = h_M(L_y')$
and
![]() $L_y'\subseteq D_4(M)$
. Now add follow- or continuation-variables to the summands of
$L_y'\subseteq D_4(M)$
. Now add follow- or continuation-variables to the summands of
![]() $p_y'$
resp.
$p_y'$
resp.
![]() $p_z'$
$p_z'$
now split the monomials of
![]() $p_y'y^F$
and
$p_y'y^F$
and
![]() $p_z'z^F$
into right-linear factors mx with
$p_z'z^F$
into right-linear factors mx with
![]() $m\in M[\Delta_3]$
and
$m\in M[\Delta_3]$
and
![]() $x\in \{y,z,y^F,z^F\}$
to build the right-linear grammar
$x\in \{y,z,y^F,z^F\}$
to build the right-linear grammar
![]() $G^F = {\left\langle {y\geq p_y'', z\geq p_z'', y^F\geq p_y^F + 1,z^F\geq p_z^F}\right\rangle}$
where
$G^F = {\left\langle {y\geq p_y'', z\geq p_z'', y^F\geq p_y^F + 1,z^F\geq p_z^F}\right\rangle}$
where
![]() $p_y''$
resp.
$p_y''$
resp.
![]() $p_z''$
are the sums of the initial factors from
$p_z''$
are the sums of the initial factors from
![]() $p_y'y^F$
resp.
$p_y'y^F$
resp.
![]() $p_z'z^F$
, and
$p_z'z^F$
, and
![]() $p_y^F$
resp.
$p_y^F$
resp.
![]() $p_z^F$
are the sums of factors following an occurrence of y resp. z in
$p_z^F$
are the sums of factors following an occurrence of y resp. z in
![]() $p_y'y^F$
and
$p_y'y^F$
and
![]() $p_z'z^F$
:
$p_z'z^F$
:
We need
![]() $y^F\geq 1$
, since y is the start symbol of G. Let
$y^F\geq 1$
, since y is the start symbol of G. Let
![]() $R_y\in {\mathcal{R}}M[\Delta_3]$
be the y-component of the least solution of
$R_y\in {\mathcal{R}}M[\Delta_3]$
be the y-component of the least solution of
![]() $G^F$
. Intuitively,
$G^F$
. Intuitively,
![]() $L_y'\subseteq R_y$
since
$L_y'\subseteq R_y$
since
![]() $y^F$
collects what follows any occurrence of y. A finite automaton accepting
$y^F$
collects what follows any occurrence of y. A finite automaton accepting
![]() $R_y$
is shown in Figure 1 (with initial node y and accepting node
$R_y$
is shown in Figure 1 (with initial node y and accepting node
![]() $y^F$
). A regular expression for
$y^F$
). A regular expression for
![]() $R_y$
can be obtained by solving the inequation system in Kleene algebra (i.e. replace
$R_y$
can be obtained by solving the inequation system in Kleene algebra (i.e. replace
![]() $x \geq Ax+B$
with constant A,B by
$x \geq Ax+B$
with constant A,B by
![]() $x=A^*B$
) with respect to y. This leads via
$x=A^*B$
) with respect to y. This leads via
![]() $z^F={\mid\!{1}\rangle} cy^F$
,
$z^F={\mid\!{1}\rangle} cy^F$
,
 \begin{eqnarray*} y^F &=& {\mid\!{2}\rangle}{\langle{3}\!\mid}y + {\mid\!{3}\rangle}{\mid\!{1}\rangle}c y^F +1\\ &=& ({\mid\!{3}\rangle}{\mid\!{1}\rangle}c)^*({\mid\!{2}\rangle}{\langle{3}\!\mid}y+1)\\ &=& ({\mid\!{3}\rangle}{\mid\!{1}\rangle}c)^*{\mid\!{2}\rangle}{\langle{3}\!\mid}y + ({\mid\!{3}\rangle}{\mid\!{1}\rangle}c)^*\end{eqnarray*}
\begin{eqnarray*} y^F &=& {\mid\!{2}\rangle}{\langle{3}\!\mid}y + {\mid\!{3}\rangle}{\mid\!{1}\rangle}c y^F +1\\ &=& ({\mid\!{3}\rangle}{\mid\!{1}\rangle}c)^*({\mid\!{2}\rangle}{\langle{3}\!\mid}y+1)\\ &=& ({\mid\!{3}\rangle}{\mid\!{1}\rangle}c)^*{\mid\!{2}\rangle}{\langle{3}\!\mid}y + ({\mid\!{3}\rangle}{\mid\!{1}\rangle}c)^*\end{eqnarray*}
and
![]() $z = {\langle{2}\!\mid} y$
to the least solution in y by
$z = {\langle{2}\!\mid} y$
to the least solution in y by
 \begin{eqnarray*} y &=& a y^F + b{\langle{l}\!\mid}{\langle{2}\!\mid}y\\ &=& a ({\mid\!{3}\rangle}{\mid\!{1}\rangle}c)^*{\mid\!{2}\rangle}{\langle{3}\!\mid}y + a ({\mid\!{3}\rangle}{\mid\!{1}\rangle}c)^* + b{\langle{l}\!\mid}{\langle{2}\!\mid}y\\ &=& (b{\langle{l}\!\mid}{\langle{2}\!\mid} + a ({\mid\!{3}\rangle}{\mid\!{1}\rangle}c)^*{\mid\!{2}\rangle}{\langle{3}\!\mid})y + a({\mid\!{3}\rangle}{\mid\!{1}\rangle}c)^*\\ &=& (b{\langle{l}\!\mid}{\langle{2}\!\mid}+ a ({\mid\!{3}\rangle}{\mid\!{1}\rangle}c)^*{\mid\!{2}\rangle}{\langle{3}\!\mid})^* a({\mid\!{3}\rangle}{\mid\!{1}\rangle}c)^*.\end{eqnarray*}
\begin{eqnarray*} y &=& a y^F + b{\langle{l}\!\mid}{\langle{2}\!\mid}y\\ &=& a ({\mid\!{3}\rangle}{\mid\!{1}\rangle}c)^*{\mid\!{2}\rangle}{\langle{3}\!\mid}y + a ({\mid\!{3}\rangle}{\mid\!{1}\rangle}c)^* + b{\langle{l}\!\mid}{\langle{2}\!\mid}y\\ &=& (b{\langle{l}\!\mid}{\langle{2}\!\mid} + a ({\mid\!{3}\rangle}{\mid\!{1}\rangle}c)^*{\mid\!{2}\rangle}{\langle{3}\!\mid})y + a({\mid\!{3}\rangle}{\mid\!{1}\rangle}c)^*\\ &=& (b{\langle{l}\!\mid}{\langle{2}\!\mid}+ a ({\mid\!{3}\rangle}{\mid\!{1}\rangle}c)^*{\mid\!{2}\rangle}{\langle{3}\!\mid})^* a({\mid\!{3}\rangle}{\mid\!{1}\rangle}c)^*.\end{eqnarray*}
For example,
![]() $R_y$
contains the description
$R_y$
contains the description
![]() $b{\langle{l}\!\mid}{\langle{2}\!\mid}a{\mid\!{2}\rangle}{\langle{3}\!\mid}a{\mid\!{3}\rangle}{\mid\!{1}\rangle}c$
of a parse tree of
$b{\langle{l}\!\mid}{\langle{2}\!\mid}a{\mid\!{2}\rangle}{\langle{3}\!\mid}a{\mid\!{3}\rangle}{\mid\!{1}\rangle}c$
of a parse tree of
![]() $baac\in L_y$
.
$baac\in L_y$
.
Let us add a preview to the algebraic version of the theorem and its reverse. Those elements of
![]() $R_y$
that are not descriptions of parse trees of words in
$R_y$
that are not descriptions of parse trees of words in
![]() $L_y$
contain (modulo commuting brackets with elements of M) bracket mismatches or have initial closing brackets or final opening brackets, like
$L_y$
contain (modulo commuting brackets with elements of M) bracket mismatches or have initial closing brackets or final opening brackets, like
![]() $w=a{\mid\!{3}\rangle} {\mid\!{1}\rangle} c{\mid\!{2}\rangle}{\langle{3}\!\mid}a\in R_y$
. With the reserved pair
$w=a{\mid\!{3}\rangle} {\mid\!{1}\rangle} c{\mid\!{2}\rangle}{\langle{3}\!\mid}a\in R_y$
. With the reserved pair
![]() ${\langle{0}\!\mid},{\langle{0}\!\mid}$
of brackets, we can go from
${\langle{0}\!\mid},{\langle{0}\!\mid}$
of brackets, we can go from
![]() $R_y$
to
$R_y$
to
![]() $\{{\langle{0}\!\mid}\}R_y\{{\langle{0}\!\mid}\}$
and thereby turn the latter kind of elements into further ones with bracket mismatches, like
$\{{\langle{0}\!\mid}\}R_y\{{\langle{0}\!\mid}\}$
and thereby turn the latter kind of elements into further ones with bracket mismatches, like
![]() ${\langle{0}\!\mid} w{\langle{0}\!\mid} = {\langle{0}\!\mid} a{\mid\!{3}\rangle}{\mid\!{1}\rangle} c{\mid\!{2}\rangle}{\langle{3}\!\mid} a{\langle{0}\!\mid}$
. The modified automaton shown in Figure 2 therefore is a description of
${\langle{0}\!\mid} w{\langle{0}\!\mid} = {\langle{0}\!\mid} a{\mid\!{3}\rangle}{\mid\!{1}\rangle} c{\mid\!{2}\rangle}{\langle{3}\!\mid} a{\langle{0}\!\mid}$
. The modified automaton shown in Figure 2 therefore is a description of
![]() $L_y$
: if we only extract sequences without bracket mismatches, we obtain all parse trees of words in
$L_y$
: if we only extract sequences without bracket mismatches, we obtain all parse trees of words in
![]() $L_y$
. An algorithm to extract only bracket mismatch-free strings from a similar automaton is given by Hulden (Reference Hulden2011) for a CFG-parser based on the Chomsky–Schützenberger theorem.
$L_y$
. An algorithm to extract only bracket mismatch-free strings from a similar automaton is given by Hulden (Reference Hulden2011) for a CFG-parser based on the Chomsky–Schützenberger theorem.

Figure 2. automaton for
![]() $R_y\in{\mathcal{R}} M[\Delta_3]$
.
$R_y\in{\mathcal{R}} M[\Delta_3]$
.

Figure 3. automaton for
![]() $L_y\in {\mathcal{C}} M \simeq Z_{C_4'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_4'})$
.
$L_y\in {\mathcal{C}} M \simeq Z_{C_4'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_4'})$
.
A version without the assumption that M be finitely generated follows:
Corollary 16 (CST for monoids). Let M be a monoid M and
![]() $D_2 \in {\mathcal{C}}\Delta_2^*$
the pure Dyck language over
$D_2 \in {\mathcal{C}}\Delta_2^*$
the pure Dyck language over
![]() $\Delta_2$
. For any
$\Delta_2$
. For any
![]() $L\in {\mathcal{C}} M,$
there is some
$L\in {\mathcal{C}} M,$
there is some
![]() $R\in {\mathcal{R}}(M\times\Delta_2^*)$
such that
$R\in {\mathcal{R}}(M\times\Delta_2^*)$
such that
Moreover, for
![]() $(m,d)\in R$
the normal form
$(m,d)\in R$
the normal form
![]() $\textit{nf}_{2}(d)$
in
$\textit{nf}_{2}(d)$
in
![]() $P_2'=Q_2^*P_2^*\cup\{0\}$
of d belongs to
$P_2'=Q_2^*P_2^*\cup\{0\}$
of d belongs to
![]() $\{0,1\}$
.
$\{0,1\}$
.
Proof. For each
![]() $L\in {\mathcal{C}} M,$
there is a finitely generated submonoid
$L\in {\mathcal{C}} M,$
there is a finitely generated submonoid
![]() $N\subseteq M$
with
$N\subseteq M$
with
![]() $L\in{\mathcal{C}} N$
, and by Theorem 15, there is
$L\in{\mathcal{C}} N$
, and by Theorem 15, there is
![]() $S\in{\mathcal{R}} N[\Delta_2]$
such that
$S\in{\mathcal{R}} N[\Delta_2]$
such that
![]() $L= h_N(S\cap D_2(N))$
. The homomorphism
$L= h_N(S\cap D_2(N))$
. The homomorphism
![]() ${\left\langle {h_N,h_{\Delta_2^*}}\right\rangle} : N[\Delta_2]\to N\times \Delta_2^*$
lifts to a homomorphism
${\left\langle {h_N,h_{\Delta_2^*}}\right\rangle} : N[\Delta_2]\to N\times \Delta_2^*$
lifts to a homomorphism
![]() $h:{\mathcal{R}} N[\Delta_2]\to {\mathcal{R}}(N\times\Delta_2^*)\subseteq {\mathcal{R}}(M\times \Delta_2^*)$
. Then,
$h:{\mathcal{R}} N[\Delta_2]\to {\mathcal{R}}(N\times\Delta_2^*)\subseteq {\mathcal{R}}(M\times \Delta_2^*)$
. Then,
![]() $R := h(S) \in{\mathcal{R}}(M\times \Delta_2^*)$
and
$R := h(S) \in{\mathcal{R}}(M\times \Delta_2^*)$
and
![]() $L = h_N(S\cap D_2(N)) = \pi_1(R\cap (M\times D_2))$
, where
$L = h_N(S\cap D_2(N)) = \pi_1(R\cap (M\times D_2))$
, where
![]() $\pi_1:M\times \Delta_2^*\to M$
is the first projection.
$\pi_1:M\times \Delta_2^*\to M$
is the first projection.
The normal form
![]() $\textit{nf}_{2}:(\Delta_2\cup\{0\})^*\to P_2'=Q_2^*P_2^*\cup\{0\}$
maps those
$\textit{nf}_{2}:(\Delta_2\cup\{0\})^*\to P_2'=Q_2^*P_2^*\cup\{0\}$
maps those
![]() $d\in\Delta_2^*$
with
$d\in\Delta_2^*$
with
![]() $d\in D_2$
to
$d\in D_2$
to
![]() $1\in Q_2^*P_2^*$
and those containing a bracket mismatch to 0. To obtain
$1\in Q_2^*P_2^*$
and those containing a bracket mismatch to 0. To obtain
![]() $\textit{nf}_{2}(d)\in \{0,1\}$
for all
$\textit{nf}_{2}(d)\in \{0,1\}$
for all
![]() $(m,d)\in R$
, the idea is to wrap all strings of
$(m,d)\in R$
, the idea is to wrap all strings of
![]() $\Delta_2^*$
with a third pair of brackets; this turns strings with normal form 0 or 1 into strings with the same normal form and those with normal form in
$\Delta_2^*$
with a third pair of brackets; this turns strings with normal form 0 or 1 into strings with the same normal form and those with normal form in
![]() $Q_2^*P_2^*\setminus\{1\}$
into strings with normal form 0, because of a mismatch with the new wrapping brackets; finally, the three bracket pairs are coded by two.
$Q_2^*P_2^*\setminus\{1\}$
into strings with normal form 0, because of a mismatch with the new wrapping brackets; finally, the three bracket pairs are coded by two.
To carry this out, suppose
![]() $\Delta_2=\{{\langle{0}\!\mid},{\langle{0}\!\mid},{\langle{1}\!\mid},{\mid\!{1}\rangle}\}$
. The embedding of
$\Delta_2=\{{\langle{0}\!\mid},{\langle{0}\!\mid},{\langle{1}\!\mid},{\mid\!{1}\rangle}\}$
. The embedding of
![]() $\Delta_2$
in
$\Delta_2$
in
![]() $\Delta_2^*$
given by
$\Delta_2^*$
given by
![]() ${\langle{i}\!\mid} \mapsto{\langle{0}\!\mid}{\langle{1}\!\mid}^{i+1}$
and
${\langle{i}\!\mid} \mapsto{\langle{0}\!\mid}{\langle{1}\!\mid}^{i+1}$
and
![]() ${\mid\!{i}\rangle} \mapsto {\mid\!{1}\rangle}^{i+1}{\langle{0}\!\mid}$
for
${\mid\!{i}\rangle} \mapsto {\mid\!{1}\rangle}^{i+1}{\langle{0}\!\mid}$
for
![]() $i<2$
extends to a homomorphism
$i<2$
extends to a homomorphism
![]() $':\Delta_2^*\to\Delta_2^*$
, such that
$':\Delta_2^*\to\Delta_2^*$
, such that
![]() $d \in D_2$
iff
$d \in D_2$
iff
![]() $d'\in D_2$
for each
$d'\in D_2$
for each
![]() $d\in \Delta_2^*$
. Then,
$d\in \Delta_2^*$
. Then,
![]() $(m,d) \mapsto(m,d')$
also is a homomorphism, which lifts to a homomorphism from
$(m,d) \mapsto(m,d')$
also is a homomorphism, which lifts to a homomorphism from
![]() ${\mathcal{R}}(M\times \Delta_2^*)$
to
${\mathcal{R}}(M\times \Delta_2^*)$
to
![]() ${\mathcal{R}}(M\times\Delta_2^*)$
. From
${\mathcal{R}}(M\times\Delta_2^*)$
. From
![]() $R\in{\mathcal{R}}(M\times \Delta_2^*),$
we therefore obtain
$R\in{\mathcal{R}}(M\times \Delta_2^*),$
we therefore obtain
![]() $R':= \left\{\,(m,d')\,\mid\,(m,d)\in R\,\right\}\in{\mathcal{R}}(M\times\Delta_2^*)$
; hence, also
$R':= \left\{\,(m,d')\,\mid\,(m,d)\in R\,\right\}\in{\mathcal{R}}(M\times\Delta_2^*)$
; hence, also
For
![]() $d\in\Delta_2^*,$
we have
$d\in\Delta_2^*,$
we have
![]() $d\in D_2$
iff
$d\in D_2$
iff
![]() $d'\in D_2$
iff
$d'\in D_2$
iff
![]() ${\langle{0}\!\mid} d'{\langle{0}\!\mid}\in D_2$
, so
${\langle{0}\!\mid} d'{\langle{0}\!\mid}\in D_2$
, so
![]() $\textit{nf}_{2}(d)=1$
iff
$\textit{nf}_{2}(d)=1$
iff
![]() $\textit{nf}_{2}{{\langle{0}\!\mid}d'{\langle{0}\!\mid}}=1$
, and
$\textit{nf}_{2}{{\langle{0}\!\mid}d'{\langle{0}\!\mid}}=1$
, and
Moreover, if
![]() $\textit{nf}_{2}(d)=0$
, then
$\textit{nf}_{2}(d)=0$
, then
![]() $\textit{nf}_{2}{{\langle{0}\!\mid} d'{\langle{0}\!\mid}}=0$
. Finally, if
$\textit{nf}_{2}{{\langle{0}\!\mid} d'{\langle{0}\!\mid}}=0$
. Finally, if
![]() $\textit{nf}_{2}(d)\in Q_2^*P_2^*\setminus\{1\}$
, then
$\textit{nf}_{2}(d)\in Q_2^*P_2^*\setminus\{1\}$
, then
![]() $\textit{nf}_{2}{d'}$
begins with
$\textit{nf}_{2}{d'}$
begins with
![]() ${\mid\!{1}\rangle}^{i+1}{\langle{0}\!\mid}$
or ends in
${\mid\!{1}\rangle}^{i+1}{\langle{0}\!\mid}$
or ends in
![]() ${\langle{0}\!\mid}{\langle{1}\!\mid}^{i+1}$
, for some
${\langle{0}\!\mid}{\langle{1}\!\mid}^{i+1}$
, for some
![]() $i<2$
, so that
$i<2$
, so that
![]() $\textit{nf}_{2}{{\langle{0}\!\mid}d'{\mid\!{0}\rangle}}=0$
. Hence, with
$\textit{nf}_{2}{{\langle{0}\!\mid}d'{\mid\!{0}\rangle}}=0$
. Hence, with
![]() $\widetilde R$
instead of R both claims in the statement of the corollary hold.
$\widetilde R$
instead of R both claims in the statement of the corollary hold. ![]()
3.2 Algebraic version of the CST for monoids
In the algebraic formulation, the Chomsky–Schützenberger theorem relates the objects
![]() ${\mathcal{R}} M$
and
${\mathcal{R}} M$
and
![]() ${\mathcal{C}} M$
of the Kleisli subcategories of
${\mathcal{C}} M$
of the Kleisli subcategories of
![]() ${\mathbb{D}}{\mathcal{R}}$
and
${\mathbb{D}}{\mathcal{R}}$
and
![]() ${\mathbb{D}}{\mathcal{C}}$
. While in the classical formulation, each
${\mathbb{D}}{\mathcal{C}}$
. While in the classical formulation, each
![]() $L\in{\mathcal{C}} M$
has a regular approximation
$L\in{\mathcal{C}} M$
has a regular approximation
![]() $R\in{\mathcal{R}} M[\Delta_2]$
such that
$R\in{\mathcal{R}} M[\Delta_2]$
such that
![]() $L=h_M(R\cap D_2(M))$
, one can now perform both the intersection with
$L=h_M(R\cap D_2(M))$
, one can now perform both the intersection with
![]() $D_2(M)$
and the removal of brackets by
$D_2(M)$
and the removal of brackets by
![]() $h_M$
algebraically in
$h_M$
algebraically in
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
, and the relation between L and R becomes one of representing the same tensor.
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
, and the relation between L and R becomes one of representing the same tensor.
Theorem 17 (Algebraic CST for monoids) For any monoid M and
![]() $L\in{\mathcal{C}} M$
, the elementwise
$L\in{\mathcal{C}} M$
, the elementwise
![]() $\top_1$
-image
$\top_1$
-image
![]() $\left\{\,\{m\}\otimes 1\,\mid\,m\in L\,\right\}\in {\mathcal{C}}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')$
of L has a least upper bound in
$\left\{\,\{m\}\otimes 1\,\mid\,m\in L\,\right\}\in {\mathcal{C}}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')$
of L has a least upper bound in
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
,
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
,
In fact, there is an injective map
![]() $\widehat{\,\cdot\,}: {\mathcal{C}} M \to Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')$
given by
$\widehat{\,\cdot\,}: {\mathcal{C}} M \to Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')$
given by
Proof. By Corollary 16, for
![]() $L\in{\mathcal{C}} M$
there is
$L\in{\mathcal{C}} M$
there is
![]() $S\in{\mathcal{R}}(M\times \Delta_2^*)$
with
$S\in{\mathcal{R}}(M\times \Delta_2^*)$
with
![]() $L = \left\{\,m\,\mid\,(m,d)\in S, d\in D_2\,\right\}$
, and the normal form
$L = \left\{\,m\,\mid\,(m,d)\in S, d\in D_2\,\right\}$
, and the normal form
![]() $\textit{nf}_{2}(d)$
of each
$\textit{nf}_{2}(d)$
of each
![]() $d\in\Delta_2^*$
with
$d\in\Delta_2^*$
with
![]() $(m,d)\in S$
belongs to
$(m,d)\in S$
belongs to
![]() $\{0,1\}\subset P_2'$
. There is an isomorphism
$\{0,1\}\subset P_2'$
. There is an isomorphism
![]() ${\mathcal{R}}(M\times\Delta_2^*) \simeq {\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}}{\mathcal{R}}\Delta_2^*$
which maps
${\mathcal{R}}(M\times\Delta_2^*) \simeq {\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}}{\mathcal{R}}\Delta_2^*$
which maps
![]() $S\in{\mathcal{R}}(M\times\Delta_2^*)$
to the congruence class of
$S\in{\mathcal{R}}(M\times\Delta_2^*)$
to the congruence class of
By definition, using
![]() $\{m\}\otimes \{d\} := [\{(\{m\},\{d\})\}]$
, this congruence class is
$\{m\}\otimes \{d\} := [\{(\{m\},\{d\})\}]$
, this congruence class is
where
![]() $\sum$
is the least upper bound in the tensor product. The canonical map
$\sum$
is the least upper bound in the tensor product. The canonical map
![]() $\cdot/\rho_2:{\mathcal{R}}\Delta_2^*\to C_2' = {\mathcal{R}}\Delta_2^*/\rho_2$
is an
$\cdot/\rho_2:{\mathcal{R}}\Delta_2^*\to C_2' = {\mathcal{R}}\Delta_2^*/\rho_2$
is an
![]() ${\mathcal{R}}$
-morphism mapping those
${\mathcal{R}}$
-morphism mapping those
![]() $\{d\}$
with
$\{d\}$
with
![]() $d\in D_2$
to
$d\in D_2$
to
![]() $1\in C_2'$
and those where d contains a bracket mismatch to
$1\in C_2'$
and those where d contains a bracket mismatch to
![]() $0\in C_2'$
. By the assumption on S, for all
$0\in C_2'$
. By the assumption on S, for all
![]() $(m,d)\in S$
either
$(m,d)\in S$
either
![]() $\textit{nf}_{2}(d)=1$
, i.e.
$\textit{nf}_{2}(d)=1$
, i.e.
![]() $d\in D_2$
, or
$d\in D_2$
, or
![]() $\textit{nf}_{2}(d)=0$
, i.e. d contains a bracket mismatch. Hence for all d with
$\textit{nf}_{2}(d)=0$
, i.e. d contains a bracket mismatch. Hence for all d with
![]() $(m,d)\in S$
,
$(m,d)\in S$
,
The image of
![]() $R_S$
under the homomorphism
$R_S$
under the homomorphism
![]() $h := {Id}\times \cdot/\rho_2:{\mathcal{R}} M\times{\mathcal{R}}\Delta_2^*\to{\mathcal{R}} M\times C_2'$
is
$h := {Id}\times \cdot/\rho_2:{\mathcal{R}} M\times{\mathcal{R}}\Delta_2^*\to{\mathcal{R}} M\times C_2'$
is
and therefore, since
![]() $\{m\}\otimes 0 = 0$
,
$\{m\}\otimes 0 = 0$
,
 \begin{eqnarray*} \sum\left\{\,\{m\}\otimes 1\,\mid\,m\in L\,\right\} &=& \sum\left\{\,\{m\}\otimes \{d\}/\rho_2\,\mid\,(m,d)\in S, d\in D_2\,\right\}\\ &=& \sum\left\{\,\{m\}\otimes \{d\}/\rho_2\,\mid\,(m,d)\in S\,\right\}\\ &=& \left[\left\{\,(\{m\},\{d\}/\rho_2)\,\mid\,(m,d)\in S\,\right\}\right] \in {\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'.\end{eqnarray*}
\begin{eqnarray*} \sum\left\{\,\{m\}\otimes 1\,\mid\,m\in L\,\right\} &=& \sum\left\{\,\{m\}\otimes \{d\}/\rho_2\,\mid\,(m,d)\in S, d\in D_2\,\right\}\\ &=& \sum\left\{\,\{m\}\otimes \{d\}/\rho_2\,\mid\,(m,d)\in S\,\right\}\\ &=& \left[\left\{\,(\{m\},\{d\}/\rho_2)\,\mid\,(m,d)\in S\,\right\}\right] \in {\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'.\end{eqnarray*}
Since each
![]() $\{m\}\otimes 1$
and
$\{m\}\otimes 1$
and
![]() $\{m\}\otimes 0$
commutes with each
$\{m\}\otimes 0$
commutes with each
![]() $1\otimes c$
for
$1\otimes c$
for
![]() $c\in C_2'$
, we have
$c\in C_2'$
, we have
by the
![]() ${\mathcal{R}}$
-distributivity of
${\mathcal{R}}$
-distributivity of
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
.
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
.
To show that the map
![]() $L\mapsto \widehat L$
is injective, we present two relatively commuting
$L\mapsto \widehat L$
is injective, we present two relatively commuting
![]() ${\mathcal{R}}$
-morphisms f,g such that the induced
${\mathcal{R}}$
-morphisms f,g such that the induced
![]() ${\mathcal{R}}$
-morphism
${\mathcal{R}}$
-morphism
![]() $h_{f,g}$
maps
$h_{f,g}$
maps
![]() $\widehat L$
back to a copy of L.
$\widehat L$
back to a copy of L.

Let f be defined by
![]() $f(A) = A \otimes I$
for
$f(A) = A \otimes I$
for
![]() $A\in{\mathcal{R}} M$
, where
$A\in{\mathcal{R}} M$
, where
![]() $I\in{\textit Mat}_{{P_2^*},{P_2^*}}({\mathbb{B}})$
is the unit matrix. By g we interpret
$I\in{\textit Mat}_{{P_2^*},{P_2^*}}({\mathbb{B}})$
is the unit matrix. By g we interpret
![]() $C_2'$
in
$C_2'$
in
![]() ${\textit Mat}_{{P_2^*},{P_2^*}}({\mathbb{B}})$
, which is isomorphic to the
${\textit Mat}_{{P_2^*},{P_2^*}}({\mathbb{B}})$
, which is isomorphic to the
![]() ${\mathcal{P}}$
-dioid of binary relations over
${\mathcal{P}}$
-dioid of binary relations over
![]() $P^*_2$
, the “stack part” of
$P^*_2$
, the “stack part” of
![]() $P_2' =(Q_2^*P_2^*\cup\{0\},\cdot,1)$
. To define g, let
$P_2' =(Q_2^*P_2^*\cup\{0\},\cdot,1)$
. To define g, let
![]() $\gamma: \Delta_2^*\to{\textit Mat}_{{P_2^*},{P_2^*}}({\mathbb{B}})$
be the homomorphism generated by the relations “push
$\gamma: \Delta_2^*\to{\textit Mat}_{{P_2^*},{P_2^*}}({\mathbb{B}})$
be the homomorphism generated by the relations “push
![]() $p_i$
” and “pop
$p_i$
” and “pop
![]() $p_i$
” on the stack part
$p_i$
” on the stack part
![]() $P_2^*$
of
$P_2^*$
of
![]() $P_2'$
,
$P_2'$
,
for
![]() $i<2$
. Clearly,
$i<2$
. Clearly,
![]() $\gamma$
extends to an
$\gamma$
extends to an
![]() ${\mathcal{R}}$
-morphism
${\mathcal{R}}$
-morphism
![]() $\gamma^*:{\mathcal{R}}\Delta_2^*\to {\textit Mat}_{{P_2^*},{P_2^*}}({\mathbb{B}})$
by
$\gamma^*:{\mathcal{R}}\Delta_2^*\to {\textit Mat}_{{P_2^*},{P_2^*}}({\mathbb{B}})$
by
The semiring equations
![]() $p_iq_j=\delta_{i,j}$
hold in
$p_iq_j=\delta_{i,j}$
hold in
![]() ${\textit Mat}_{{P_2^*},{P_2^*}}({\mathbb{B}})$
when 0 and 1 are interpreted by the matrices 0 and I, and
${\textit Mat}_{{P_2^*},{P_2^*}}({\mathbb{B}})$
when 0 and 1 are interpreted by the matrices 0 and I, and
![]() $p_i$
and
$p_i$
and
![]() $q_j$
by
$q_j$
by
![]() $\gamma^*(\{p_i\})$
and
$\gamma^*(\{p_i\})$
and
![]() $\gamma^*(\{q_j\})$
, for
$\gamma^*(\{q_j\})$
, for
![]() $i<2$
. Therefore,
$i<2$
. Therefore,
![]() $\gamma^*$
is constant on
$\gamma^*$
is constant on
![]() $\rho_2$
-congruence classes, and hence,
$\rho_2$
-congruence classes, and hence,
defines an
![]() ${\mathcal{R}}$
-morphism
${\mathcal{R}}$
-morphism
![]() $g:C_2'\to{\mathcal{P}} M\mathop{\otimes_{\mathcal{P}}} {\textit Mat}_{{P_2^*},{P_2^*}}({\mathbb{B}})$
. Obviously, f and g are relatively commuting.
$g:C_2'\to{\mathcal{P}} M\mathop{\otimes_{\mathcal{P}}} {\textit Mat}_{{P_2^*},{P_2^*}}({\mathbb{B}})$
. Obviously, f and g are relatively commuting.
By the choice of S for
![]() $L\in{\mathcal{C}} M,$
we have
$L\in{\mathcal{C}} M,$
we have
![]() $L=\left\{\,m\,\mid\,(m,d)\in S, d\in D_2\,\right\}$
and
$L=\left\{\,m\,\mid\,(m,d)\in S, d\in D_2\,\right\}$
and
 \begin{equation*} \{d\}/\rho_2 = \begin{cases} 1 & d \in \pi_2(S) \cap D_2, \\ 0 & d \in \pi_2(S) \setminus D_2.\end{cases}\end{equation*}
\begin{equation*} \{d\}/\rho_2 = \begin{cases} 1 & d \in \pi_2(S) \cap D_2, \\ 0 & d \in \pi_2(S) \setminus D_2.\end{cases}\end{equation*}
So
![]() $g(\{d\}/\rho_2)$
is the unit matrix for
$g(\{d\}/\rho_2)$
is the unit matrix for
![]() $d\in \pi_2(S)\cap D_2$
and the zero matrix for
$d\in \pi_2(S)\cap D_2$
and the zero matrix for
![]() $d\in\pi_2(S)\setminus D_2$
. As
$d\in\pi_2(S)\setminus D_2$
. As
![]() $h_{f,g}$
is an
$h_{f,g}$
is an
![]() ${\mathcal{R}}$
-morphism and
${\mathcal{R}}$
-morphism and
![]() $\left\{\,\{m\}\otimes \{d\}/\rho_2\,\mid\,(m,d)\in S\,\right\}\in{\mathcal{R}}({\mathcal{R}} M \mathop{\otimes_{\mathcal{R}}} C_2')$
, we obtain
$\left\{\,\{m\}\otimes \{d\}/\rho_2\,\mid\,(m,d)\in S\,\right\}\in{\mathcal{R}}({\mathcal{R}} M \mathop{\otimes_{\mathcal{R}}} C_2')$
, we obtain
 \begin{eqnarray*} h_{f,g}(\widehat L) &=& h_{f,g}\left(\sum\left\{\,\{m\}\otimes 1\,\mid\,m\in L\,\right\}\right)\\ &=& h_{f,g}\left(\sum\left\{\,\{m\}\otimes \{d\}/\rho_2\,\mid\,(m,d)\in S\,\right\}\right)\\ &=& \sum\left\{\,h_{f,g}(\{m\}\otimes \{d\}/\rho_2)\,\mid\,(m,d)\in S\,\right\}\\ &=& \sum\left\{\,f(\{m\})\cdot g(\{d\}/\rho_2)\,\mid\,(m,d)\in S\,\right\}\\ &=& \sum\left\{\,\{m\}\otimes I\,\mid\,m\in L\,\right\}\\ &=& L\otimes I,\end{eqnarray*}
\begin{eqnarray*} h_{f,g}(\widehat L) &=& h_{f,g}\left(\sum\left\{\,\{m\}\otimes 1\,\mid\,m\in L\,\right\}\right)\\ &=& h_{f,g}\left(\sum\left\{\,\{m\}\otimes \{d\}/\rho_2\,\mid\,(m,d)\in S\,\right\}\right)\\ &=& \sum\left\{\,h_{f,g}(\{m\}\otimes \{d\}/\rho_2)\,\mid\,(m,d)\in S\,\right\}\\ &=& \sum\left\{\,f(\{m\})\cdot g(\{d\}/\rho_2)\,\mid\,(m,d)\in S\,\right\}\\ &=& \sum\left\{\,\{m\}\otimes I\,\mid\,m\in L\,\right\}\\ &=& L\otimes I,\end{eqnarray*}
using the
![]() ${\mathcal{C}}$
-continuity of the embedding
${\mathcal{C}}$
-continuity of the embedding
![]() $\top_1':{\mathcal{P}} M \to {\mathcal{P}} M\mathop{\otimes_{\mathcal{P}}}{\textit Mat}_{{P_2'},{P_2'}}({\mathbb{B}})$
in the final step. Since
$\top_1':{\mathcal{P}} M \to {\mathcal{P}} M\mathop{\otimes_{\mathcal{P}}}{\textit Mat}_{{P_2'},{P_2'}}({\mathbb{B}})$
in the final step. Since
![]() $\top_1'$
is injective,
$\top_1'$
is injective,
![]() $h_{f,g}$
is essentially an inverse to
$h_{f,g}$
is essentially an inverse to
![]() $L \mapsto \widehat L$
.
Footnote 6
$L \mapsto \widehat L$
.
Footnote 6
![]()
4. The Reverse CST for Monoids and its Algebraic Version
The “reverse” Chomsky–Schützenberger theorem, i.e. that for finite X,
involves showing that
![]() $R\cap D_2(X)\in {\mathcal{C}}(X^*[\Delta_2])$
, which is usually done by coupling a finite-state acceptor with a pushdown automaton. This construction does not work for an arbitrary finitely generated monoid M, since there is no standard presentation of elements of M as a sequence of elements from a finite generating subset; we therefore give a grammatical proof of
$R\cap D_2(X)\in {\mathcal{C}}(X^*[\Delta_2])$
, which is usually done by coupling a finite-state acceptor with a pushdown automaton. This construction does not work for an arbitrary finitely generated monoid M, since there is no standard presentation of elements of M as a sequence of elements from a finite generating subset; we therefore give a grammatical proof of
![]() $h_M(R\cap D_2(M))\in{\mathcal{C}} M$
below. A version of a reverse CST for arbitrary monoids follows.
$h_M(R\cap D_2(M))\in{\mathcal{C}} M$
below. A version of a reverse CST for arbitrary monoids follows.
4.1 The reverse CST for monoids
If M is a finitely generated monoid, M belongs to
![]() ${\mathcal{C}} M$
and
${\mathcal{C}} M$
and
![]() $D_2(M)$
to
$D_2(M)$
to
![]() ${\mathcal{C}}(M[\Delta_2])$
. So we can formulate the reverse CST for such M as direct generalization from the classical case.
${\mathcal{C}}(M[\Delta_2])$
. So we can formulate the reverse CST for such M as direct generalization from the classical case.
Theorem 18 (Reverse CST for finitely generated monoids). For any finitely generated monoid M,
Proof. Since the erasing homomorphism
![]() $h_M:M[\Delta_2]\to M$
lifts to
$h_M:M[\Delta_2]\to M$
lifts to
![]() $h_M:{\mathcal{C}}(M[\Delta_2])\to {\mathcal{C}} M$
, it is sufficient to show
$h_M:{\mathcal{C}}(M[\Delta_2])\to {\mathcal{C}} M$
, it is sufficient to show
Suppose
![]() $R\in {\mathcal{R}}(M[\Delta_2])$
. Then, R is a component of the least solution
$R\in {\mathcal{R}}(M[\Delta_2])$
. Then, R is a component of the least solution
![]() $\vec R$
of a system
$\vec R$
of a system
with right-linear polynomials
![]() $p_1,\ldots,p_n\in {\mathcal{F}}(M[\Delta_2])[y_1,\ldots,y_n]$
. By means of additional variables and inequations, we can assume that all parameters from
$p_1,\ldots,p_n\in {\mathcal{F}}(M[\Delta_2])[y_1,\ldots,y_n]$
. By means of additional variables and inequations, we can assume that all parameters from
![]() ${\mathcal{F}}(M[\Delta_2])$
are singletons or the empty set, so that the system can be written as
${\mathcal{F}}(M[\Delta_2])$
are singletons or the empty set, so that the system can be written as
where the parameters
![]() $w_{i,j},w_i$
are from
$w_{i,j},w_i$
are from
![]() $M[\Delta_2]$
, standing for the singletons
$M[\Delta_2]$
, standing for the singletons
![]() $\{w_{i,j}\}$
resp.
$\{w_{i,j}\}$
resp.
![]() $\{w_i\}$
, or are 0 and stand for
$\{w_i\}$
, or are 0 and stand for
![]() $\emptyset$
. As any
$\emptyset$
. As any
![]() $w\in M[\Delta_2]$
is an interleaving sequence of products of generators of M and elements of
$w\in M[\Delta_2]$
is an interleaving sequence of products of generators of M and elements of
![]() $\Delta_2$
, we can further assume that
$\Delta_2$
, we can further assume that
![]() $w_{i,j}\in X\cup\Delta_2\cup\{0\}$
and
$w_{i,j}\in X\cup\Delta_2\cup\{0\}$
and
![]() $w_i \in \{0,1\}$
, where X is the finite set of generators of M. Then,
$w_i \in \{0,1\}$
, where X is the finite set of generators of M. Then,
![]() $\vec R$
can be obtained by first taking the least solution of (11) in
$\vec R$
can be obtained by first taking the least solution of (11) in
![]() ${\mathcal{R}}(X^*[\Delta_2])$
and then interpreting sequences
${\mathcal{R}}(X^*[\Delta_2])$
and then interpreting sequences
![]() $m_1\cdots m_k\in X^*$
by the product
$m_1\cdots m_k\in X^*$
by the product
![]() $m_1\cdot^M \cdots \cdot^M m_k\in M$
of their members. Let
$m_1\cdot^M \cdots \cdot^M m_k\in M$
of their members. Let
![]() $D_2(M)\in{\mathcal{C}}(M[\Delta_2])$
be the likewise interpretation of the Dyck language
$D_2(M)\in{\mathcal{C}}(M[\Delta_2])$
be the likewise interpretation of the Dyck language
![]() $D_2(X)\in{\mathcal{C}}(X^*[\Delta_2])$
. To show
$D_2(X)\in{\mathcal{C}}(X^*[\Delta_2])$
. To show
![]() $R\cap D_2(M)\in {\mathcal{C}}(M[\Delta_2])$
, we construct a context-free grammar G, the least solution of which assigns
$R\cap D_2(M)\in {\mathcal{C}}(M[\Delta_2])$
, we construct a context-free grammar G, the least solution of which assigns
![]() $R\cap D_2(M)$
to its main variable S. The variables Y of G are S and all [y,D,z], [y,d,z] and [y,D,1] with
$R\cap D_2(M)$
to its main variable S. The variables Y of G are S and all [y,D,z], [y,d,z] and [y,D,1] with
![]() $y,z\in\{y_1,\ldots,y_n\}, d\in\Delta_2$
and auxiliary symbol D. Its inequations
$y,z\in\{y_1,\ldots,y_n\}, d\in\Delta_2$
and auxiliary symbol D. Its inequations
![]() $Y \geq \alpha_1+\ldots+\alpha_k$
are obtained by combining all inequations
$Y \geq \alpha_1+\ldots+\alpha_k$
are obtained by combining all inequations
![]() $Y\geq \alpha_1,\ldots, Y\geq \alpha_k$
with the same left hand side Y from the following table:
$Y\geq \alpha_1,\ldots, Y\geq \alpha_k$
with the same left hand side Y from the following table:

Claim 1. For all
![]() $y\in\{y_1,\ldots,y_n\}$
and
$y\in\{y_1,\ldots,y_n\}$
and
![]() $z\in \{y_1,\ldots,y_n\}\cup\{1\}$
,
$z\in \{y_1,\ldots,y_n\}\cup\{1\}$
,
![]() $[y,D,z] \Rightarrow^*_G w$
and
$[y,D,z] \Rightarrow^*_G w$
and
![]() $w\in M[\Delta_2]$
iff
$w\in M[\Delta_2]$
iff
![]() $y\Rightarrow^*_R wz$
and
$y\Rightarrow^*_R wz$
and
![]() $w\in D_2(X)$
.
$w\in D_2(X)$
.
Proof of Claim 1.
![]() $\Rightarrow$
: This is easily shown by induction on k in
$\Rightarrow$
: This is easily shown by induction on k in
![]() $[y,D,z] \Rightarrow^k_G w$
.
$[y,D,z] \Rightarrow^k_G w$
.
![]() $\Leftarrow$
: Suppose
$\Leftarrow$
: Suppose
![]() $y\Rightarrow^k_R wz$
and
$y\Rightarrow^k_R wz$
and
![]() $w\in D_2(X)$
. There is a sequence
$w\in D_2(X)$
. There is a sequence
such that
![]() $y=y_{i_0}$
,
$y=y_{i_0}$
,
![]() $w=w_1\cdots w_k\in D_2(X)$
and
$w=w_1\cdots w_k\in D_2(X)$
and
![]() $y_{i_k}=z$
. We show by induction on k that
$y_{i_k}=z$
. We show by induction on k that
If
![]() $k=0$
, then
$k=0$
, then
![]() $w = 1$
, and
$w = 1$
, and
![]() $[y_{i_0},D,y_{i_0}]\Rightarrow_G 1$
. If
$[y_{i_0},D,y_{i_0}]\Rightarrow_G 1$
. If
![]() $k=1$
, then
$k=1$
, then
![]() $y_{i_0}\geq wy_{i_1}$
and
$y_{i_0}\geq wy_{i_1}$
and
![]() $w\in X\cup\Delta_2$
. From
$w\in X\cup\Delta_2$
. From
![]() $w\in D_2(X),$
we get
$w\in D_2(X),$
we get
![]() $w\in X$
, hence
$w\in X$
, hence
![]() $[y_{i_0},D,y_{i_1}]\Rightarrow_G w$
.
$[y_{i_0},D,y_{i_1}]\Rightarrow_G w$
.
Suppose
![]() $k>1$
. By the construction of
$k>1$
. By the construction of
![]() $D_2(X)$
, there either is
$D_2(X)$
, there either is
![]() $j<k$
with
$j<k$
with
![]() $u:=w_1\cdots w_j, v:=w_{j+1}\cdots w_k\in D_2(X)$
and
$u:=w_1\cdots w_j, v:=w_{j+1}\cdots w_k\in D_2(X)$
and
![]() $w=uv$
, or
$w=uv$
, or
![]() $w =p_0uq_0$
or
$w =p_0uq_0$
or
![]() $w=p_1uq_1$
with
$w=p_1uq_1$
with
![]() $u:=w_2\cdots w_{k-1}\in D_2(X)$
.
$u:=w_2\cdots w_{k-1}\in D_2(X)$
.
In the first case, we have
![]() $y_{i_0} \Rightarrow^*_R uy_{i_j}$
and
$y_{i_0} \Rightarrow^*_R uy_{i_j}$
and
![]() $y_{i_j}\Rightarrow^*_R vy_{i_k}$
in less than k steps; hence,
$y_{i_j}\Rightarrow^*_R vy_{i_k}$
in less than k steps; hence,
![]() $[y_{i_0},D,y_{i_j}]\Rightarrow^*_Gu$
and
$[y_{i_0},D,y_{i_j}]\Rightarrow^*_Gu$
and
![]() $[y_{i_j},D,y_{i_k}]\Rightarrow^*_G v$
by induction; hence,
$[y_{i_j},D,y_{i_k}]\Rightarrow^*_G v$
by induction; hence,
In the second case, we have
![]() $y_{i_1}\Rightarrow^*_R uy_{i_{k-1}}$
in less than k steps; hence,
$y_{i_1}\Rightarrow^*_R uy_{i_{k-1}}$
in less than k steps; hence,
![]() $[y_{i_1},D,y_{i_{k-1}}]\Rightarrow^*_G u$
by induction; hence for
$[y_{i_1},D,y_{i_{k-1}}]\Rightarrow^*_G u$
by induction; hence for
![]() $j\in\{0,1\}$
,
$j\in\{0,1\}$
,
It follows that G defines
![]() $R\cap D_2(X)$
: If
$R\cap D_2(X)$
: If
![]() $w\in L(G)$
, then
$w\in L(G)$
, then
![]() $S \Rightarrow^*_G w\in M[\Delta_2]$
, so by the claim,
$S \Rightarrow^*_G w\in M[\Delta_2]$
, so by the claim,
![]() $w\in R\cap D_2(X)$
. Conversely, if
$w\in R\cap D_2(X)$
. Conversely, if
![]() $y\Rightarrow^*_Rwz$
and y is the main variable of (11), then
$y\Rightarrow^*_Rwz$
and y is the main variable of (11), then
![]() $S\Rightarrow_G [y,D,z] \Rightarrow^*_G w$
, so
$S\Rightarrow_G [y,D,z] \Rightarrow^*_G w$
, so
![]() $w\in L(G)$
.
$w\in L(G)$
.
As with the CST, a version of the reverse CST for arbitrary monoids follows:
Corollary 19 (Reverse CST for monoids). For any monoid M and
![]() $R\in {\mathcal{R}}(M\times \Delta_2^*)$
,
$R\in {\mathcal{R}}(M\times \Delta_2^*)$
,
Proof. If
![]() $R\in {\mathcal{R}}(M\times \Delta_2^*)$
, there is a finitely generated submonoid
$R\in {\mathcal{R}}(M\times \Delta_2^*)$
, there is a finitely generated submonoid
![]() $N\subseteq M$
with
$N\subseteq M$
with
![]() $R\in{\mathcal{R}}(N\times \Delta_2^*)$
. The homomorphism
$R\in{\mathcal{R}}(N\times \Delta_2^*)$
. The homomorphism
![]() ${\left\langle {h_N,h_{\Delta_2^*}}\right\rangle} : N[\Delta_2]\to N\times \Delta_2^*$
is surjective and lifts to a surjective homomorphism
${\left\langle {h_N,h_{\Delta_2^*}}\right\rangle} : N[\Delta_2]\to N\times \Delta_2^*$
is surjective and lifts to a surjective homomorphism
![]() $h:{\mathcal{R}} N[\Delta_2]\to{\mathcal{R}}(N\times \Delta_2^*)$
, by Theorem 1. So there is
$h:{\mathcal{R}} N[\Delta_2]\to{\mathcal{R}}(N\times \Delta_2^*)$
, by Theorem 1. So there is
![]() $S\in{\mathcal{R}} N[\Delta_2]$
with
$S\in{\mathcal{R}} N[\Delta_2]$
with
![]() $R= h(S)$
. For any
$R= h(S)$
. For any
![]() $(m,d)\in R$
there is
$(m,d)\in R$
there is
![]() $w\in S$
with
$w\in S$
with
![]() $(m,d)={\left\langle {h_N,h_{\Delta_2^*}}\right\rangle}(w) = (h_N(w),h_{\Delta_2^*}(w))$
. Then,
$(m,d)={\left\langle {h_N,h_{\Delta_2^*}}\right\rangle}(w) = (h_N(w),h_{\Delta_2^*}(w))$
. Then,
![]() $d\in D_2$
iff
$d\in D_2$
iff
![]() $w\in D_2(N)$
iff
$w\in D_2(N)$
iff
![]() $w\in S\cap D_2(N)$
iff
$w\in S\cap D_2(N)$
iff
![]() $m\in h_N(S\cap D_2(N))$
. Hence,
$m\in h_N(S\cap D_2(N))$
. Hence,
using Theorem 18.
Using the first projection
![]() $\pi_1:M\times \Delta_2^*\to M$
, Corollaries 16 and 19 combine to:
$\pi_1:M\times \Delta_2^*\to M$
, Corollaries 16 and 19 combine to:
We can simplify this further by going from strings in
![]() $\Delta_2^*$
to their normal forms in the polycyclic monoid
$\Delta_2^*$
to their normal forms in the polycyclic monoid
![]() $P_2'\simeq (Q_2^*P_2^*\cup\{0\},\cdot,1)$
where
$P_2'\simeq (Q_2^*P_2^*\cup\{0\},\cdot,1)$
where
![]() $u\cdot v = \textit{nf}_{2}{uv}$
for
$u\cdot v = \textit{nf}_{2}{uv}$
for
![]() $u,v\in Q_2^*P_2^*\cup\{0\}$
Footnote 7
:
$u,v\in Q_2^*P_2^*\cup\{0\}$
Footnote 7
:
Proposition 20. For any monoid M,
Proof. Let
![]() $\eta:\Delta_2^*\to (\Delta_2\cup\{0\})^*$
be the inclusion homomorphism. Clearly,
$\eta:\Delta_2^*\to (\Delta_2\cup\{0\})^*$
be the inclusion homomorphism. Clearly,
![]() $\textit{nf}_{2}:(\Delta_2\cup\{0\})^*\to P_2'$
is a homomorphism and surjective since
$\textit{nf}_{2}:(\Delta_2\cup\{0\})^*\to P_2'$
is a homomorphism and surjective since
![]() $0=\textit{nf}_{2}({p_0q_1})$
. Therefore, the lifting of
$0=\textit{nf}_{2}({p_0q_1})$
. Therefore, the lifting of
![]() $\textit{Id}_M \times (\textit{nf}_{2}\circ\eta):M\times \Delta_2^*\to M\times P_2'$
to the set level is a surjective homomorphism — But the inclusion homomorphism
$\textit{Id}_M \times (\textit{nf}_{2}\circ\eta):M\times \Delta_2^*\to M\times P_2'$
to the set level is a surjective homomorphism — But the inclusion homomorphism
![]() ${\mathcal{R}}(M\times \Delta_2^*)\subseteq {\mathcal{R}}(M\times(\Delta_2\cup\{0\})^*)$
is not surjective!—
${\mathcal{R}}(M\times \Delta_2^*)\subseteq {\mathcal{R}}(M\times(\Delta_2\cup\{0\})^*)$
is not surjective!—
For
![]() $d\in \Delta_2^*$
,
$d\in \Delta_2^*$
,
![]() $\textit{nf}_{2}(d) = 1$
iff
$\textit{nf}_{2}(d) = 1$
iff
![]() $d\in D_2$
. So if
$d\in D_2$
. So if
![]() $S\in{\mathcal{R}}(M\times \Delta_2^*)$
and
$S\in{\mathcal{R}}(M\times \Delta_2^*)$
and
![]() $R\in {\mathcal{R}}(M\times P_2')$
with
$R\in {\mathcal{R}}(M\times P_2')$
with
![]() $R = h(S)$
, then
$R = h(S)$
, then
Since h is surjective, the claim follows from the above combination of Corollaries 16 and 19.
Intuitively, since each
![]() $w\in P_2'$
defines a binary transition relation
$w\in P_2'$
defines a binary transition relation
![]() $\left\{\,(u,v)\,\mid\,u\cdot w = v\,\right\}\subseteq P_2'\times P_2'$
, each
$\left\{\,(u,v)\,\mid\,u\cdot w = v\,\right\}\subseteq P_2'\times P_2'$
, each
![]() $(m,w)\in M \times P_2'$
gives a transition
$(m,w)\in M \times P_2'$
gives a transition
![]() ${\,\stackrel{m}{\Longrightarrow}_{w}\,}$
on
${\,\stackrel{m}{\Longrightarrow}_{w}\,}$
on
![]() $P_2'$
with output in M, via
$P_2'$
with output in M, via
If
![]() $(m,w) = (m,\textit{nf}_{2}(d))$
or
$(m,w) = (m,\textit{nf}_{2}(d))$
or
![]() $(m,w) = (h_M(\alpha),\textit{nf}_{2}({{h_{\Delta_2^*}}(\alpha)}))$
, the same relation is obtained from
$(m,w) = (h_M(\alpha),\textit{nf}_{2}({{h_{\Delta_2^*}}(\alpha)}))$
, the same relation is obtained from
![]() $(m,d)\in M\times \Delta_2^*$
or
$(m,d)\in M\times \Delta_2^*$
or
![]() $\alpha\in M[\Delta_2]$
. From
$\alpha\in M[\Delta_2]$
. From
![]() $R\in {\mathcal{R}}(M\times P_2'),$
an
$R\in {\mathcal{R}}(M\times P_2'),$
an
![]() $S\in{\mathcal{R}}(M\times\Delta_2^*)$
with
$S\in{\mathcal{R}}(M\times\Delta_2^*)$
with
![]() $R=h(S)$
as in the proof above can be obtained by induction on the construction of R, using
$R=h(S)$
as in the proof above can be obtained by induction on the construction of R, using
![]() $S=R$
for R of size 0 or 1, except
$S=R$
for R of size 0 or 1, except
![]() $S=\emptyset$
for
$S=\emptyset$
for
![]() $R=\{(m,0)\}$
. Similarly, when M is finitely generated we can obtain
$R=\{(m,0)\}$
. Similarly, when M is finitely generated we can obtain
![]() $S\in {\mathcal{R}} M[\Delta_2]$
with
$S\in {\mathcal{R}} M[\Delta_2]$
with
![]() $\left\{\,m\,\mid\,(m,1)\in R\,\right\} = h_M(S\cap D_2(M))$
by induction on the construction of R, using
$\left\{\,m\,\mid\,(m,1)\in R\,\right\} = h_M(S\cap D_2(M))$
by induction on the construction of R, using
![]() $S=\{mw\}$
for
$S=\{mw\}$
for
![]() $R=\{(m,w)\}$
in the singleton case, except again
$R=\{(m,w)\}$
in the singleton case, except again
![]() $S=\emptyset$
for
$S=\emptyset$
for
![]() $R=\{(m,0)\}$
.
$R=\{(m,0)\}$
.
Since, by Corollary 13,
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
is a quotient of
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
is a quotient of
![]() ${\mathcal{R}}(M\times P_2')$
, the above proposition can be used below to show
${\mathcal{R}}(M\times P_2')$
, the above proposition can be used below to show
![]() $Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'}) \mathrel{\stackrel{\subset}{{}_\sim}} {\mathcal{C}} M$
.
$Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'}) \mathrel{\stackrel{\subset}{{}_\sim}} {\mathcal{C}} M$
.
4.2 Algebraic version of the reverse CST for monoids
To prove an algebraic form of the reverse CST for monoids, i.e. that
![]() $Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')$
embeds into
$Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')$
embeds into
![]() ${\mathcal{C}} M$
, we need to know which elements of
${\mathcal{C}} M$
, we need to know which elements of
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}}{C_2'}$
belong to the centralizer of
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}}{C_2'}$
belong to the centralizer of
![]() $C_2'$
. For this, it is convenient to represent
$C_2'$
. For this, it is convenient to represent
![]() $C_2'$
by
$C_2'$
by
![]() $C_2' = {\mathcal{R}} P_2'/\nu$
as in Proposition 9 and to first characterize the elements of
$C_2' = {\mathcal{R}} P_2'/\nu$
as in Proposition 9 and to first characterize the elements of
![]() $C_2'$
that commute with all generators of
$C_2'$
that commute with all generators of
![]() $C_2'$
in
$C_2'$
in
![]() $C_2'$
, i.e.
$C_2'$
, i.e.
Let I be the set of idempotent elements of
![]() $P_2'$
, i.e. the set of those
$P_2'$
, i.e. the set of those
![]() $w\in P_2'$
such that
$w\in P_2'$
such that
![]() $ww = w$
.
$ww = w$
.
Proposition 21. The set of idempotent elements of
![]() $P_2'$
is
$P_2'$
is
Proof. Let
![]() $I' := \left\{\,{\vec{q}}{\vec{p}}\,\mid\,{\vec{q}}\in Q_2^*,{\vec{p}}\in P_2^*, {\vec{p}}{\vec{q}} =1\,\right\} \cup\{0\}$
. Clearly,
$I' := \left\{\,{\vec{q}}{\vec{p}}\,\mid\,{\vec{q}}\in Q_2^*,{\vec{p}}\in P_2^*, {\vec{p}}{\vec{q}} =1\,\right\} \cup\{0\}$
. Clearly,
![]() $0 \in I$
. Suppose
$0 \in I$
. Suppose
![]() ${\vec{q}}=q_{i_1}\cdots q_{i_k}\in Q_2^*$
,
${\vec{q}}=q_{i_1}\cdots q_{i_k}\in Q_2^*$
,
![]() ${\vec{p}} =p_{j_m}\cdots p_{j_1}\in P_2^*$
and
${\vec{p}} =p_{j_m}\cdots p_{j_1}\in P_2^*$
and
![]() ${\vec{q}}{\vec{p}}\in I'$
. Then,
${\vec{q}}{\vec{p}}\in I'$
. Then,
![]() ${\vec{p}}{\vec{q}}=1$
, so
${\vec{p}}{\vec{q}}=1$
, so
![]() ${\vec{q}}{\vec{p}}\cdot {\vec{q}}{\vec{p}} = {\vec{q}}({\vec{p}}{\vec{q}}){\vec{p}} = {\vec{q}}{\vec{p}}$
, so
${\vec{q}}{\vec{p}}\cdot {\vec{q}}{\vec{p}} = {\vec{q}}({\vec{p}}{\vec{q}}){\vec{p}} = {\vec{q}}{\vec{p}}$
, so
![]() ${\vec{q}}{\vec{p}}\in I$
.
${\vec{q}}{\vec{p}}\in I$
.
Suppose
![]() $w\in P_2' = Q_2^*P_2^*\cup\{0\}$
is idempotent. As
$w\in P_2' = Q_2^*P_2^*\cup\{0\}$
is idempotent. As
![]() $0\in I'$
, we may assume that
$0\in I'$
, we may assume that
![]() $w={\vec{q}}{\vec{p}}$
with
$w={\vec{q}}{\vec{p}}$
with
![]() ${\vec{q}} = q_{i_1}\cdots q_{i_k}\in Q_2^*$
and
${\vec{q}} = q_{i_1}\cdots q_{i_k}\in Q_2^*$
and
![]() ${\vec{p}}= p_{j_m}\cdots p_{j_1}\in P_2^*$
for some
${\vec{p}}= p_{j_m}\cdots p_{j_1}\in P_2^*$
for some
![]() $k,m\geq 0$
. Suppose
$k,m\geq 0$
. Suppose
![]() $k>m$
. Since
$k>m$
. Since
![]() $ww=w\not=0$
, we have
$ww=w\not=0$
, we have
![]() $p_{j_1}q_{i_1}=1,\ldots,p_{j_m}q_{i_m}=1$
and
$p_{j_1}q_{i_1}=1,\ldots,p_{j_m}q_{i_m}=1$
and
which is impossible. So
![]() $k\leq m$
, and by symmetry,
$k\leq m$
, and by symmetry,
![]() $k=m$
. It follows that
$k=m$
. It follows that
![]() ${\vec{p}}{\vec{q}} = 1$
; hence,
${\vec{p}}{\vec{q}} = 1$
; hence,
![]() ${\vec{q}}{\vec{p}}\in I'$
.
${\vec{q}}{\vec{p}}\in I'$
.
Proposition 22. If
![]() $R\subseteq P_2'$
satisfies
$R\subseteq P_2'$
satisfies
![]() $\{\delta\}R\setminus\{0\} =R\{\delta\}\setminus\{0\}$
, for all
$\{\delta\}R\setminus\{0\} =R\{\delta\}\setminus\{0\}$
, for all
![]() $\delta\in \Delta_2$
, then
$\delta\in \Delta_2$
, then
![]() $R\subseteq I$
. If additionally
$R\subseteq I$
. If additionally
![]() $R\not\subseteq \{0,1\}$
, then
$R\not\subseteq \{0,1\}$
, then
![]() $I_0\subseteq R$
or
$I_0\subseteq R$
or
![]() $I_1\subseteq R$
, where
$I_1\subseteq R$
, where
Proof. Clearly, if
![]() $R\subseteq\{0,1\}$
, then
$R\subseteq\{0,1\}$
, then
![]() $R\subseteq I$
. So suppose
$R\subseteq I$
. So suppose
![]() $w\in R\setminus\{0,1\}$
. By symmetry, we may assume
$w\in R\setminus\{0,1\}$
. By symmetry, we may assume
![]() $w\in Q_2^+P_2^*$
, say
$w\in Q_2^+P_2^*$
, say
![]() $w=q_0{\vec{q}}{\vec{p}}'$
for some
$w=q_0{\vec{q}}{\vec{p}}'$
for some
![]() ${\vec{q}}\in Q_2^*$
and
${\vec{q}}\in Q_2^*$
and
![]() ${\vec{p}}'\in P_2^*$
. Then
${\vec{p}}'\in P_2^*$
. Then
so there is
![]() $w'\in R$
such that
$w'\in R$
such that
![]() ${\vec{q}}{\vec{p}}'=w'p_0$
. It follows that
${\vec{q}}{\vec{p}}'=w'p_0$
. It follows that
![]() ${\vec{p}}' = {\vec{p}}p_0$
for some
${\vec{p}}' = {\vec{p}}p_0$
for some
![]() ${\vec{p}}\in P_2^*$
, so
${\vec{p}}\in P_2^*$
, so
![]() $w = q_0{\vec{q}}{\vec{p}} p_0$
. By induction on the length of
$w = q_0{\vec{q}}{\vec{p}} p_0$
. By induction on the length of
![]() $w'={\vec{q}}{\vec{p}}\in R\setminus\{0\}$
, it follows that
$w'={\vec{q}}{\vec{p}}\in R\setminus\{0\}$
, it follows that
![]() ${\vec{p}}$
is the inverse of
${\vec{p}}$
is the inverse of
![]() ${\vec{q}}$
, so
${\vec{q}}$
, so
![]() $w'\in I$
and
$w'\in I$
and
![]() $w\in I$
. Hence,
$w\in I$
. Hence,
![]() $R\subseteq I$
. We have also seen that when
$R\subseteq I$
. We have also seen that when
![]() $q_0wp_0\in R$
, then
$q_0wp_0\in R$
, then
![]() $w\in R$
; in particular, if
$w\in R$
; in particular, if
![]() $R\not\subseteq\{0\}$
, then
$R\not\subseteq\{0\}$
, then
![]() $1 \in R$
.
$1 \in R$
.
Finally, suppose
![]() $w\in R\setminus\{0,1\}$
. By the above argument, we may assume
$w\in R\setminus\{0,1\}$
. By the above argument, we may assume
![]() $w = q_jp_j$
with
$w = q_jp_j$
with
![]() $j\in \{0,1\}$
. For each
$j\in \{0,1\}$
. For each
![]() $i\in\{0,1\}$
,
$i\in\{0,1\}$
,
![]() $q_iw \in q_iR\setminus\{0\}\subseteq Rq_i\setminus\{0\}$
; hence, there is
$q_iw \in q_iR\setminus\{0\}\subseteq Rq_i\setminus\{0\}$
; hence, there is
![]() $w'\in R$
with
$w'\in R$
with
![]() $q_iw = w'q_i$
, and since
$q_iw = w'q_i$
, and since
![]() $w\in Q_2^+P_2^+$
, we must have
$w\in Q_2^+P_2^+$
, we must have
![]() $w'=q_iwp_i$
. By induction, it follows that
$w'=q_iwp_i$
. By induction, it follows that
![]() $\left\{\,{\vec{q}} w{\vec{p}}\,\mid\,{\vec{q}}\in Q_2^*,{\vec{p}}\in P_2^*,{\vec{p}}{\vec{q}} = 1\,\right\}\subseteq R$
, so
$\left\{\,{\vec{q}} w{\vec{p}}\,\mid\,{\vec{q}}\in Q_2^*,{\vec{p}}\in P_2^*,{\vec{p}}{\vec{q}} = 1\,\right\}\subseteq R$
, so
![]() $I_j\subseteq R$
.
$I_j\subseteq R$
.
We next want to see that the infinite sets R with
![]() $I_j\subseteq R\subseteq I = I_0\cup I_1\cup \{0\}$
of Proposition 22 are not regular, i.e. do not belong to
$I_j\subseteq R\subseteq I = I_0\cup I_1\cup \{0\}$
of Proposition 22 are not regular, i.e. do not belong to
![]() ${\mathcal{R}} P_2'$
. In order to show, say,
${\mathcal{R}} P_2'$
. In order to show, say,
![]() $I\notin{\mathcal{R}} P_2'$
, we want to apply a pumping lemma, representing I as the homomorphic image
$I\notin{\mathcal{R}} P_2'$
, we want to apply a pumping lemma, representing I as the homomorphic image
![]() $S/\rho_2$
of some regular set S of the free monoid
$S/\rho_2$
of some regular set S of the free monoid
![]() $(\Delta_2\cup\{0\})^*$
by the monoid congruence
$(\Delta_2\cup\{0\})^*$
by the monoid congruence
But if
![]() $w=uv\in S$
is a “long” word with a splitting
$w=uv\in S$
is a “long” word with a splitting
![]() $w=xyzv$
with
$w=xyzv$
with
![]() $xy^kzv\in S$
for all
$xy^kzv\in S$
for all
![]() $k\geq 0$
, the images
$k\geq 0$
, the images
![]() $\textit{nf}_{2}({xy^kzv})$
of the “pumped strings”
$\textit{nf}_{2}({xy^kzv})$
of the “pumped strings”
![]() $xy^kzv$
need not be outside of I: for example, if
$xy^kzv$
need not be outside of I: for example, if
![]() $w=u.v=qpqbdq.pp$
with
$w=u.v=qpqbdq.pp$
with
![]() $\textit{nf}_{2}({w})=qqpp \in I$
and
$\textit{nf}_{2}({w})=qqpp \in I$
and
![]() $u=x.y.z=qp.qb.dq$
, then for all
$u=x.y.z=qp.qb.dq$
, then for all
![]() $k\not=1$
,
$k\not=1$
,
![]() $\textit{nf}_{2}({xy^kzv}) = 0 \in I$
, since from
$\textit{nf}_{2}({xy^kzv}) = 0 \in I$
, since from
![]() $pd=0=bq$
we get
$pd=0=bq$
we get
![]() $\textit{nf}_{2}({xz})=\textit{nf}_{2}({qpdq})= 0$
and
$\textit{nf}_{2}({xz})=\textit{nf}_{2}({qpdq})= 0$
and
![]() $\textit{nf}_{2}({y^2}) = \textit{nf}_{2}({qbqb})=0$
. So a little care is needed to transfer the pumping of S to a pumping of
$\textit{nf}_{2}({y^2}) = \textit{nf}_{2}({qbqb})=0$
. So a little care is needed to transfer the pumping of S to a pumping of
![]() $\textit{nf}_{2}(S)=S/\rho_2$
.
$\textit{nf}_{2}(S)=S/\rho_2$
.
Proposition 23. If
![]() $R\in{\mathcal{R}} P_2'$
and
$R\in{\mathcal{R}} P_2'$
and
![]() $R\subseteq I$
, then R is finite.
$R\subseteq I$
, then R is finite.
Proof. Let
![]() $\Delta = \Delta_2\cup\{0\}$
. The polycyclic monoid
$\Delta = \Delta_2\cup\{0\}$
. The polycyclic monoid
![]() $P_2'$
is the quotient of the free monoid
$P_2'$
is the quotient of the free monoid
![]() $\Delta^*$
by the monoid congruence
$\Delta^*$
by the monoid congruence
![]() $\rho_2$
above. Since
$\rho_2$
above. Since
![]() $\cdot/\rho_2 : \Delta^*\to P_2'$
is a surjective homomorphism, every
$\cdot/\rho_2 : \Delta^*\to P_2'$
is a surjective homomorphism, every
![]() $R\in{\mathcal{R}} P_2'$
is the image under
$R\in{\mathcal{R}} P_2'$
is the image under
![]() $\cdot/\rho_2$
of some
$\cdot/\rho_2$
of some
![]() $S\in{\mathcal{R}} \Delta^*$
, i.e.
$S\in{\mathcal{R}} \Delta^*$
, i.e.
![]() $R=\textit{nf}_{2}(S)=\left\{\,\textit{nf}_{2}(w)\,\mid\,w\in S\,\right\}$
.
$R=\textit{nf}_{2}(S)=\left\{\,\textit{nf}_{2}(w)\,\mid\,w\in S\,\right\}$
.
We first show that we may assume
![]() $R\subseteq S$
. Let
$R\subseteq S$
. Let
be a finite automaton over
![]() $\Delta$
that recognizes S, with transition relations
$\Delta$
that recognizes S, with transition relations
![]() ${\,\stackrel{x}{\longrightarrow}\,}\subseteq A\times A$
for
${\,\stackrel{x}{\longrightarrow}\,}\subseteq A\times A$
for
![]() $x\in\Delta$
and identity relation
$x\in\Delta$
and identity relation
![]() ${\,\stackrel{1}{\longrightarrow}\,}\subseteq A\times A$
, and sets
${\,\stackrel{1}{\longrightarrow}\,}\subseteq A\times A$
, and sets
![]() $I^{\mathcal{A}}\subseteq A$
of initial and
$I^{\mathcal{A}}\subseteq A$
of initial and
![]() $F^{\mathcal{A}}\subseteq A$
of final states. Let
$F^{\mathcal{A}}\subseteq A$
of final states. Let
be the automaton obtained from
![]() ${\mathcal{A}}$
by “path-compression,” i.e. the relations
${\mathcal{A}}$
by “path-compression,” i.e. the relations
![]() ${\,\stackrel{x}{\longrightarrow}\,}'\supseteq {\,\stackrel{x}{\longrightarrow}\,}$
are obtained as follows: for edges
${\,\stackrel{x}{\longrightarrow}\,}'\supseteq {\,\stackrel{x}{\longrightarrow}\,}$
are obtained as follows: for edges
![]() $s{\,\stackrel{p_i}{\longrightarrow}\,}t{\,\stackrel{q_i}{\longrightarrow}\,}u$
,
$s{\,\stackrel{p_i}{\longrightarrow}\,}t{\,\stackrel{q_i}{\longrightarrow}\,}u$
,
![]() $i<2$
, add an edge
$i<2$
, add an edge
![]() $s{\,\stackrel{1}{\longrightarrow}\,}u$
, for edges
$s{\,\stackrel{1}{\longrightarrow}\,}u$
, for edges
![]() $s{\,\stackrel{x}{\longrightarrow}\,}t{\,\stackrel{1}{\longrightarrow}\,}u$
or
$s{\,\stackrel{x}{\longrightarrow}\,}t{\,\stackrel{1}{\longrightarrow}\,}u$
or
![]() $s{\,\stackrel{1}{\longrightarrow}\,}t{\,\stackrel{x}{\longrightarrow}\,}u$
, add an edge
$s{\,\stackrel{1}{\longrightarrow}\,}t{\,\stackrel{x}{\longrightarrow}\,}u$
, add an edge
![]() $s{\,\stackrel{x}{\longrightarrow}\,}u$
. Likewise, for edges
$s{\,\stackrel{x}{\longrightarrow}\,}u$
. Likewise, for edges
![]() $s{\,\stackrel{p_i}{\longrightarrow}\,}t{\,\stackrel{q_{1-i}}{\longrightarrow}\,}u$
,
$s{\,\stackrel{p_i}{\longrightarrow}\,}t{\,\stackrel{q_{1-i}}{\longrightarrow}\,}u$
,
![]() $i<2$
, add an edge
$i<2$
, add an edge
![]() $s{\,\stackrel{0}{\longrightarrow}\,}u$
, and for edges
$s{\,\stackrel{0}{\longrightarrow}\,}u$
, and for edges
![]() $s{\,\stackrel{x}{\longrightarrow}\,}t{\,\stackrel{0}{\longrightarrow}\,}u$
or
$s{\,\stackrel{x}{\longrightarrow}\,}t{\,\stackrel{0}{\longrightarrow}\,}u$
or
![]() $s{\,\stackrel{0}{\longrightarrow}\,}t{\,\stackrel{x}{\longrightarrow}\,}u$
add
$s{\,\stackrel{0}{\longrightarrow}\,}t{\,\stackrel{x}{\longrightarrow}\,}u$
add
![]() $s{\,\stackrel{0}{\longrightarrow}\,}u$
. Let
$s{\,\stackrel{0}{\longrightarrow}\,}u$
. Let
![]() $S'\in{\mathcal{R}}{\Delta^*}$
be the set recognized by
$S'\in{\mathcal{R}}{\Delta^*}$
be the set recognized by
![]() ${\mathcal{A}}'$
. As each accepting path of
${\mathcal{A}}'$
. As each accepting path of
![]() ${\mathcal{A}}'$
is the compression of an accepting path of
${\mathcal{A}}'$
is the compression of an accepting path of
![]() ${\mathcal{A}}$
, we have
${\mathcal{A}}$
, we have
![]() $S\subseteq S'$
, and as their labellings have the same normal form,
$S\subseteq S'$
, and as their labellings have the same normal form,
![]() $\textit{nf}_{2}(S')=\textit{nf}_{2}(S)=R$
. Since for each
$\textit{nf}_{2}(S')=\textit{nf}_{2}(S)=R$
. Since for each
![]() ${\vec{q}}{\vec{p}}\in R$
there is some
${\vec{q}}{\vec{p}}\in R$
there is some
![]() $w\in S$
with
$w\in S$
with
![]() $\textit{nf}_{2}(w)={\vec{q}}{\vec{p}}$
, there is an accepting path in
$\textit{nf}_{2}(w)={\vec{q}}{\vec{p}}$
, there is an accepting path in
![]() ${\mathcal{A}}'$
labeled by
${\mathcal{A}}'$
labeled by
![]() ${\vec{q}}{\vec{p}}$
, likewise for
${\vec{q}}{\vec{p}}$
, likewise for
![]() $0\in R$
, so
$0\in R$
, so
![]() $R\subseteq S'$
. Henceforth, we assume
$R\subseteq S'$
. Henceforth, we assume
![]() $S=S'$
and
$S=S'$
and
![]() ${\mathcal{A}}={\mathcal{A}}'$
.
${\mathcal{A}}={\mathcal{A}}'$
.
We can now show that R cannot be infinite, by applying the pumping lemma. Let m be the number of states of an automaton
![]() ${\mathcal{A}}$
recognizing a set
${\mathcal{A}}$
recognizing a set
![]() $S\in {\mathcal{R}} \Delta^*$
with
$S\in {\mathcal{R}} \Delta^*$
with
![]() $\textit{nf}_{2}(S) = R\subseteq S$
. Suppose
$\textit{nf}_{2}(S) = R\subseteq S$
. Suppose
![]() $R\subseteq I$
is infinite. Then there is
$R\subseteq I$
is infinite. Then there is
![]() ${\vec{q}}{\vec{p}} \in R\subseteq S$
with
${\vec{q}}{\vec{p}} \in R\subseteq S$
with
![]() $|{\vec{q}}| > m$
,
$|{\vec{q}}| > m$
,
![]() ${\vec{q}}\in Q_2^*$
,
${\vec{q}}\in Q_2^*$
,
![]() ${\vec{p}}\in P_2^*$
and
${\vec{p}}\in P_2^*$
and
![]() ${\vec{p}}{\vec{q}}=1$
. Since
${\vec{p}}{\vec{q}}=1$
. Since
![]() ${\mathcal{A}}$
has an accepting path labeled
${\mathcal{A}}$
has an accepting path labeled
![]() ${\vec{q}}{\vec{p}}$
and
${\vec{q}}{\vec{p}}$
and
![]() $m>|{\vec{q}}|$
, by the pumping lemma for S there is a splitting
$m>|{\vec{q}}|$
, by the pumping lemma for S there is a splitting
![]() ${\vec{q}}=xyz$
with
${\vec{q}}=xyz$
with
![]() $x,y,z\in Q_2^*$
with
$x,y,z\in Q_2^*$
with
![]() $0 < |y|\leq m$
such that
$0 < |y|\leq m$
such that
![]() $xy^kz{\vec{p}} \in S$
for all
$xy^kz{\vec{p}} \in S$
for all
![]() $k\geq 0$
. But since
$k\geq 0$
. But since
![]() $xz\in Q_2^*$
,
$xz\in Q_2^*$
,
![]() ${\vec{p}}\in P_2^*$
and
${\vec{p}}\in P_2^*$
and
![]() $xz{\vec{p}}\in S$
, we have
$xz{\vec{p}}\in S$
, we have
![]() $\textit{nf}_{2}({xz{\vec{p}}})=xz{\vec{p}}$
(and
$\textit{nf}_{2}({xz{\vec{p}}})=xz{\vec{p}}$
(and
![]() $\not=0$
), which is impossible since
$\not=0$
), which is impossible since
![]() $|xz|<|{\vec{q}}|=|{\vec{p}}|$
and
$|xz|<|{\vec{q}}|=|{\vec{p}}|$
and
![]() $\textit{nf}_{2}(S)=R\subseteq I$
. It follows that R cannot be infinite.
$\textit{nf}_{2}(S)=R\subseteq I$
. It follows that R cannot be infinite. ![]()
When using
![]() $C_2' \simeq {\mathcal{R}} P_2'/\nu$
according to Proposition 9, we write 0’ and l’ for the neutral elements of
$C_2' \simeq {\mathcal{R}} P_2'/\nu$
according to Proposition 9, we write 0’ and l’ for the neutral elements of
![]() $+$
and
$+$
and
![]() $\cdot$
in
$\cdot$
in
![]() $C_2'$
, respectively, to distinguish them from the elements 0 and 1 of
$C_2'$
, respectively, to distinguish them from the elements 0 and 1 of
![]() $P_2'$
. The following lemmata characterize the elements of the centralizer of
$P_2'$
. The following lemmata characterize the elements of the centralizer of
![]() $C_2'$
in
$C_2'$
in
![]() $C_2'$
and in
$C_2'$
and in
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
, respectively:
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
, respectively:
Lemma 24.
![]() $Z_{C_2'}(C_2')=\{{0'},{l'}\}=Z_{\Delta_2}(C_2')$
.
$Z_{C_2'}(C_2')=\{{0'},{l'}\}=Z_{\Delta_2}(C_2')$
.
Proof.
![]() $\{{0'},{l'}\}\subseteq Z_{C_2'}(C_2')\subseteq Z_{P_2'}(C_2')\subseteq Z_{\Delta_2}(C_2')$
: Clearly,
$\{{0'},{l'}\}\subseteq Z_{C_2'}(C_2')\subseteq Z_{P_2'}(C_2')\subseteq Z_{\Delta_2}(C_2')$
: Clearly,
![]() ${0'} = \emptyset/\nu=\{0\}/\nu$
and
${0'} = \emptyset/\nu=\{0\}/\nu$
and
![]() ${l'}= \{1\}/\nu=\{0,1\}/\nu$
commute with
${l'}= \{1\}/\nu=\{0,1\}/\nu$
commute with
![]() $R/\nu$
for every
$R/\nu$
for every
![]() $R\in {\mathcal{R}} P_2'$
. The other two inclusions follow from the representations of
$R\in {\mathcal{R}} P_2'$
. The other two inclusions follow from the representations of
![]() $w\in P_2'$
and
$w\in P_2'$
and
![]() $\delta\in\Delta_2$
in
$\delta\in\Delta_2$
in
![]() $C_2'$
by
$C_2'$
by
![]() $\{w\}/\nu$
and
$\{w\}/\nu$
and
![]() $\{\delta\}/\nu$
.
$\{\delta\}/\nu$
.
![]() $Z_{\Delta_2}(C_2') \subseteq \{{0'}, {l'}\}$
: Suppose
$Z_{\Delta_2}(C_2') \subseteq \{{0'}, {l'}\}$
: Suppose
![]() $R\in{\mathcal{R}} P_2'$
and
$R\in{\mathcal{R}} P_2'$
and
![]() $R/\nu$
commutes with
$R/\nu$
commutes with
![]() $\{\delta\}/\nu$
for every
$\{\delta\}/\nu$
for every
![]() $\delta\in\Delta_2$
. Then, by Proposition 9,
$\delta\in\Delta_2$
. Then, by Proposition 9,
![]() $\{\delta\}R\setminus\{0\}=R\{\delta\}\setminus\{0\}$
for every
$\{\delta\}R\setminus\{0\}=R\{\delta\}\setminus\{0\}$
for every
![]() $\delta\in\Delta_2$
, so
$\delta\in\Delta_2$
, so
![]() $R\subseteq I$
by Proposition 4.2, then R is finite by Proposition 23, and so by Proposition 22 again,
$R\subseteq I$
by Proposition 4.2, then R is finite by Proposition 23, and so by Proposition 22 again,
![]() $R\subseteq \{0,1\}$
. It follows that
$R\subseteq \{0,1\}$
. It follows that
![]() $R/\nu = \emptyset/\nu =\{0\}/\nu=0'$
or
$R/\nu = \emptyset/\nu =\{0\}/\nu=0'$
or
![]() $R/\nu = \{1\}/\nu = \{0,1\}/\nu=1'$
; hence,
$R/\nu = \{1\}/\nu = \{0,1\}/\nu=1'$
; hence,
![]() $Z_{\Delta_2}(C_2')\subseteq \{{0'},{l'}\}$
.
$Z_{\Delta_2}(C_2')\subseteq \{{0'},{l'}\}$
. ![]()
Lemma 25.
![]() $ Z_{C_2'}({\mathcal{R}} M \mathop{\otimes_{\mathcal{R}}} {C_2'}) = \left\{\,[R]\,\mid\,R\in {\mathcal{R}}({\mathcal{R}} M\times C_2'), R \subseteq {\mathcal{R}} M\times \{{0'},{l'}\}\,\right\}.$
$ Z_{C_2'}({\mathcal{R}} M \mathop{\otimes_{\mathcal{R}}} {C_2'}) = \left\{\,[R]\,\mid\,R\in {\mathcal{R}}({\mathcal{R}} M\times C_2'), R \subseteq {\mathcal{R}} M\times \{{0'},{l'}\}\,\right\}.$
Proof.
![]() $\supseteq$
: For each
$\supseteq$
: For each
![]() $c\in C_2'$
,
$c\in C_2'$
,
![]() $cb=bc$
for
$cb=bc$
for
![]() $b\in \{{0'},{l'}\}$
, so by
$b\in \{{0'},{l'}\}$
, so by
![]() ${\mathcal{R}}$
-distributivity,
${\mathcal{R}}$
-distributivity,
 \begin{eqnarray*} (\{1\}\otimes c)[R] &=& (\{1\}\otimes c)\sum\left\{\,A\otimes b\,\mid\,(A,b)\in R\,\right\}\\ &=& \left(\sum\left\{\,A\otimes b\,\mid\,(A,b)\in R\,\right\}\right)(\{1\}\otimes c)= [R](\{1\}\otimes c).\end{eqnarray*}
\begin{eqnarray*} (\{1\}\otimes c)[R] &=& (\{1\}\otimes c)\sum\left\{\,A\otimes b\,\mid\,(A,b)\in R\,\right\}\\ &=& \left(\sum\left\{\,A\otimes b\,\mid\,(A,b)\in R\,\right\}\right)(\{1\}\otimes c)= [R](\{1\}\otimes c).\end{eqnarray*}
![]() $\subseteq$
: Every element of
$\subseteq$
: Every element of
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} {C_2'}$
is of the form
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} {C_2'}$
is of the form
![]() $[R_\nu]$
with
$[R_\nu]$
with
![]() $R\in {\mathcal{R}}({\mathcal{R}} M\times {\mathcal{R}} P_2')$
and
$R\in {\mathcal{R}}({\mathcal{R}} M\times {\mathcal{R}} P_2')$
and
![]() $R_\nu =\left\{\,(A,B/\nu)\,\mid\,(A,B)\in R\,\right\}$
. The isomorphism
$R_\nu =\left\{\,(A,B/\nu)\,\mid\,(A,B)\in R\,\right\}$
. The isomorphism
of Corollary 13 maps
![]() $[R_\nu]$
to
$[R_\nu]$
to
![]() $(S_R)/{\tilde\nu}$
, where
$(S_R)/{\tilde\nu}$
, where
![]() $S_R = \bigcup\left\{\,A\times B\,\mid\,(A,B)\in R\,\right\}$
. Suppose
$S_R = \bigcup\left\{\,A\times B\,\mid\,(A,B)\in R\,\right\}$
. Suppose
![]() $[R_\nu]\in Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')$
. Then for every
$[R_\nu]\in Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')$
. Then for every
![]() $w\in P_2'\setminus\{0\}$
,
$w\in P_2'\setminus\{0\}$
,
![]() $[R_\nu]$
commutes with
$[R_\nu]$
commutes with
![]() $[T_\nu]$
for
$[T_\nu]$
for
![]() $T=\{(\{1\},\{w\})\}$
, so the image
$T=\{(\{1\},\{w\})\}$
, so the image
![]() $(S_R)/{\tilde\nu}$
of
$(S_R)/{\tilde\nu}$
of
![]() $[R_\nu]$
commutes with the image
$[R_\nu]$
commutes with the image
![]() $(S_T)/{\tilde\nu} = \{(1,w)\}/{\tilde\nu}$
of
$(S_T)/{\tilde\nu} = \{(1,w)\}/{\tilde\nu}$
of
![]() $[T_\nu]$
. Therefore,
$[T_\nu]$
. Therefore,
![]() $(S_R)/{\tilde\nu}\in Z_{P_2'}({\mathcal{R}}(M\times P_2')/{\tilde\nu})$
. In particular,
$(S_R)/{\tilde\nu}\in Z_{P_2'}({\mathcal{R}}(M\times P_2')/{\tilde\nu})$
. In particular,
![]() $(S_R)/{\tilde\nu} \in Z_{\Delta_2}({\mathcal{R}}(M\times P_2')/{\tilde\nu})$
, which is equivalent to
$(S_R)/{\tilde\nu} \in Z_{\Delta_2}({\mathcal{R}}(M\times P_2')/{\tilde\nu})$
, which is equivalent to
Let
![]() $X\in {\mathcal{R}} P_2'$
be the second projection of
$X\in {\mathcal{R}} P_2'$
be the second projection of
![]() $S_R\in {\mathcal{R}}(M\times P_2')$
. Then
$S_R\in {\mathcal{R}}(M\times P_2')$
. Then
i.e.
![]() $X/\nu\in Z_{\Delta_2}(C_2')$
, and by the proof of Lemma 24,
$X/\nu\in Z_{\Delta_2}(C_2')$
, and by the proof of Lemma 24,
![]() $X\subseteq \{0,1\}$
; hence,
$X\subseteq \{0,1\}$
; hence,
![]() $S_R\subseteq M\times\{0,1\}$
. So for
$S_R\subseteq M\times\{0,1\}$
. So for
![]() $(A,B)\in R$
,
$(A,B)\in R$
,
![]() $B\subseteq \{0,1\}$
, which implies
$B\subseteq \{0,1\}$
, which implies
![]() $R_\nu\subseteq {\mathcal{R}} M \times \{{0'},{l'}\}$
.
$R_\nu\subseteq {\mathcal{R}} M \times \{{0'},{l'}\}$
.
We can now prove the algebraic form of the reverse CST for monoids:
Theorem 26 (Algebraic reverse CST for monoids). For any monoid M and
![]() $R\in {\mathcal{R}}({\mathcal{R}} M\times C_2')$
,
$R\in {\mathcal{R}}({\mathcal{R}} M\times C_2')$
,
In fact, there is an injective, monotone map
![]() ${}^\vee:Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')\to{\mathcal{C}}M$
defined by
${}^\vee:Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')\to{\mathcal{C}}M$
defined by
Proof. We switch the notation and use
![]() $[R_\nu]$
for the [R] of the statement above, where
$[R_\nu]$
for the [R] of the statement above, where
for some
![]() $R\in {\mathcal{R}}({\mathcal{R}} M\times {\mathcal{R}} P_2')$
. For these R, put
$R\in {\mathcal{R}}({\mathcal{R}} M\times {\mathcal{R}} P_2')$
. For these R, put
By Lemma 25, if
![]() $[R_\nu]\in Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')$
, then
$[R_\nu]\in Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')$
, then
![]() $R_\nu\subseteq {\mathcal{R}} M\times\{{0'},{l'}\}$
and
$R_\nu\subseteq {\mathcal{R}} M\times\{{0'},{l'}\}$
and
![]() $R\subseteq {\mathcal{R}} M\times {\mathcal{P}}\{0,1\}$
.
$R\subseteq {\mathcal{R}} M\times {\mathcal{P}}\{0,1\}$
.
Claim 1. The map
![]() $\cdot^\vee : Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2') \to {\mathcal{P}} M$
, given by
$\cdot^\vee : Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2') \to {\mathcal{P}} M$
, given by
for
![]() $R\in {\mathcal{R}}({\mathcal{R}} M\times {\mathcal{R}} P_2')$
, is well-defined and has values in
$R\in {\mathcal{R}}({\mathcal{R}} M\times {\mathcal{R}} P_2')$
, is well-defined and has values in
![]() ${\mathcal{C}} M$
.
${\mathcal{C}} M$
.
Proof of Claim 1. Clearly,
![]() $\bigcup\left\{\,A\,\mid\,(A,1')\in R_\nu\,\right\} = L_R$
. Suppose there is
$\bigcup\left\{\,A\,\mid\,(A,1')\in R_\nu\,\right\} = L_R$
. Suppose there is
![]() $T\in{\mathcal{R}}({\mathcal{R}} M\times {\mathcal{R}} P_2')$
with
$T\in{\mathcal{R}}({\mathcal{R}} M\times {\mathcal{R}} P_2')$
with
![]() $[R_\nu] = [T_\nu]$
. By the isomorphism
$[R_\nu] = [T_\nu]$
. By the isomorphism
![]() $[R_\nu] \mapsto (S_R)/{\tilde\nu}$
of Corollary 13,
$[R_\nu] \mapsto (S_R)/{\tilde\nu}$
of Corollary 13,
![]() $(S_R)/{\tilde\nu} = (S_T)/{\tilde\nu}$
; hence,
$(S_R)/{\tilde\nu} = (S_T)/{\tilde\nu}$
; hence,
Therefore, using the fact that
![]() $S_R, T_R \subseteq M\times\{0,1\}$
,
$S_R, T_R \subseteq M\times\{0,1\}$
,
 \begin{eqnarray*} L_R &=& \bigcup\left\{\,A\,\mid\,(A,B)\in R, 1\in B\,\right\}\\ &=& \left\{\,m\,\mid\,(A,B)\in R, (m,1)\in A\times B\,\right\}\\ &=& \left\{\,m\,\mid\,(m,1)\in S_R\,\right\}\\ &=& \left\{\,m\,\mid\,(m,w)\in S_R\setminus (M\times\{0\}), w\in P_2'\,\right\}\\ &=& \left\{\,m\,\mid\,(m,w)\in S_T\setminus (M\times\{0\}), w\in P_2'\,\right\}\\ &=& L_T.\end{eqnarray*}
\begin{eqnarray*} L_R &=& \bigcup\left\{\,A\,\mid\,(A,B)\in R, 1\in B\,\right\}\\ &=& \left\{\,m\,\mid\,(A,B)\in R, (m,1)\in A\times B\,\right\}\\ &=& \left\{\,m\,\mid\,(m,1)\in S_R\,\right\}\\ &=& \left\{\,m\,\mid\,(m,w)\in S_R\setminus (M\times\{0\}), w\in P_2'\,\right\}\\ &=& \left\{\,m\,\mid\,(m,w)\in S_T\setminus (M\times\{0\}), w\in P_2'\,\right\}\\ &=& L_T.\end{eqnarray*}
It follows that
![]() $\bigcup\left\{\,A\,\mid\,(A,1')\in R_\nu\,\right\} = L_R = L_T =\bigcup\left\{\,A\,\mid\,(A,1')\in T_\nu\,\right\}$
, and
$\bigcup\left\{\,A\,\mid\,(A,1')\in R_\nu\,\right\} = L_R = L_T =\bigcup\left\{\,A\,\mid\,(A,1')\in T_\nu\,\right\}$
, and
![]() $\cdot^\vee$
is well-defined. Since
$\cdot^\vee$
is well-defined. Since
![]() $L_R = \left\{\,m\,\mid\,(m,1)\in S_R\,\right\}$
for
$L_R = \left\{\,m\,\mid\,(m,1)\in S_R\,\right\}$
for
![]() $S_R\in {\mathcal{R}}(M\times P_2')$
, we have
$S_R\in {\mathcal{R}}(M\times P_2')$
, we have
![]() $L_R\in {\mathcal{C}} M$
by Proposition 20.
$L_R\in {\mathcal{C}} M$
by Proposition 20.
![]() $\triangleleft$
$\triangleleft$
Claim 2. The map
![]() $\cdot^\vee : Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')\to {\mathcal{C}} M$
is injective.
$\cdot^\vee : Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')\to {\mathcal{C}} M$
is injective.
Proof of Claim 2. We show that the map
![]() $\widehat{\,\cdot\,}: {\mathcal{C}} M\to Z_{C_2'}({\mathcal{R}} M \mathop{\otimes_{\mathcal{R}}} {C_2'})$
of Theorem 17 is an inverse to
$\widehat{\,\cdot\,}: {\mathcal{C}} M\to Z_{C_2'}({\mathcal{R}} M \mathop{\otimes_{\mathcal{R}}} {C_2'})$
of Theorem 17 is an inverse to
![]() $\cdot^\vee$
. It maps
$\cdot^\vee$
. It maps
![]() $[R_\nu]^\vee=L_R \in{\mathcal{C}} M$
back to
$[R_\nu]^\vee=L_R \in{\mathcal{C}} M$
back to
![]() $[R_\nu]$
, because
$[R_\nu]$
, because
 \begin{eqnarray*} \widehat{[R_\nu]^\vee} &=& \widehat{L_R} = \sum\left\{\,\{m\}\otimes {l'}\,\mid\,m\in L_R\,\right\}\\ &=& \sum\left\{\,A\otimes {l'}\,\mid\,(A,B)\in R, 1\in B\,\right\}\\ &=& \sum\left\{\,A\otimes {l'}\,\mid\,(A,{l'})\in R_\nu\,\right\}\\ &=& [R_\nu]\end{eqnarray*}
\begin{eqnarray*} \widehat{[R_\nu]^\vee} &=& \widehat{L_R} = \sum\left\{\,\{m\}\otimes {l'}\,\mid\,m\in L_R\,\right\}\\ &=& \sum\left\{\,A\otimes {l'}\,\mid\,(A,B)\in R, 1\in B\,\right\}\\ &=& \sum\left\{\,A\otimes {l'}\,\mid\,(A,{l'})\in R_\nu\,\right\}\\ &=& [R_\nu]\end{eqnarray*}
since
![]() $R_\nu\subseteq {\mathcal{R}}({\mathcal{R}} M\times\{{0'},{l'}\})$
and
$R_\nu\subseteq {\mathcal{R}}({\mathcal{R}} M\times\{{0'},{l'}\})$
and
![]() $A\otimes {0'} = 0$
.
$A\otimes {0'} = 0$
.
![]() $\triangleleft$
$\triangleleft$
Claim 3. The map
![]() $\cdot^\vee : Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')\to {\mathcal{C}} M$
is monotone.
$\cdot^\vee : Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')\to {\mathcal{C}} M$
is monotone.
Proof of Claim 3. Suppose
![]() $R,S\in{\mathcal{R}}({\mathcal{R}} M \times {\mathcal{R}} P_2')$
such that
$R,S\in{\mathcal{R}}({\mathcal{R}} M \times {\mathcal{R}} P_2')$
such that
![]() $[R_\nu], [S_\nu] \in Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')$
and
$[R_\nu], [S_\nu] \in Z_{C_2'}({\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2')$
and
![]() $[R_\nu]\leq [S_\nu]$
. By the definition of
$[R_\nu]\leq [S_\nu]$
. By the definition of
![]() $\leq$
on
$\leq$
on
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
,
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
,
![]() $[R_\nu \cup S_\nu] = [S_\nu]$
; hence with Claim 1,
$[R_\nu \cup S_\nu] = [S_\nu]$
; hence with Claim 1,
so
![]() $\ \cdot^\vee$
is monotone.
$\ \cdot^\vee$
is monotone.
![]() $\triangleleft$
$\triangleleft$
![]()
5. Algebraic Representation of the
 ${\mathcal{C}}$
-Closure
${\mathcal{C}}$
-Closure
 ${\mathcal{C}} M$
of
${\mathcal{C}} M$
of
 ${\mathcal{R}} M$
${\mathcal{R}} M$
We can now prove our first main result, which combines the algebraic Chomsky–Schützenberger theorem for monoids M and its reverse, Theorems 17 and 26, to an algebraic representation of the
![]() $\mu$
-continuous Chomsky algebra
$\mu$
-continuous Chomsky algebra
![]() ${\mathcal{C}} M$
in the
${\mathcal{C}} M$
in the
![]() ${}^*$
-continuous Kleene algebra
${}^*$
-continuous Kleene algebra
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}}{C_2'}$
:
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}}{C_2'}$
:
Theorem 27. For any monoid M,
![]() $Z_{C_2'}({\mathcal{R}} M \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is a
$Z_{C_2'}({\mathcal{R}} M \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is a
![]() ${\mathcal{C}}$
-dioid, and the maps
${\mathcal{C}}$
-dioid, and the maps
form a
![]() ${\mathcal{C}}$
-isomorphism, where for
${\mathcal{C}}$
-isomorphism, where for
![]() $L\in{\mathcal{C}} M$
and
$L\in{\mathcal{C}} M$
and
![]() $R \in {\mathcal{R}}({\mathcal{R}} M\times C_2')$
with
$R \in {\mathcal{R}}({\mathcal{R}} M\times C_2')$
with
![]() $[R]\in Z_{C_2'}({\mathcal{R}} M \mathop{\otimes_{\mathcal{R}}} {C_2'})$
,
$[R]\in Z_{C_2'}({\mathcal{R}} M \mathop{\otimes_{\mathcal{R}}} {C_2'})$
,
Proof. We use
![]() $D := Z_{C_2'}({\mathcal{R}} M \mathop{\otimes_{\mathcal{R}}} {C_2'})$
to simplify the notation.
$D := Z_{C_2'}({\mathcal{R}} M \mathop{\otimes_{\mathcal{R}}} {C_2'})$
to simplify the notation.
Claim 1. The maps
![]() $\,\cdot^\vee:D\to{\mathcal{C}} M$
and
$\,\cdot^\vee:D\to{\mathcal{C}} M$
and
![]() $\widehat{\,\cdot\,}:{\mathcal{C}} M\to D$
are inverse to each other.
$\widehat{\,\cdot\,}:{\mathcal{C}} M\to D$
are inverse to each other.
Proof of Claim 1. In the proof of Theorem 17, we already showed that
![]() $\widehat{\,\cdot\,}$
is an inverse of
$\widehat{\,\cdot\,}$
is an inverse of
![]() ${\cdot}^\vee$
. For
${\cdot}^\vee$
. For
![]() $L\in {\mathcal{C}} M,$
there is
$L\in {\mathcal{C}} M,$
there is
![]() $R\in {\mathcal{R}}({\mathcal{R}} M\times {\mathcal{R}} P_2')$
with
$R\in {\mathcal{R}}({\mathcal{R}} M\times {\mathcal{R}} P_2')$
with
![]() $R_\nu\subseteq {\mathcal{R}}M\times\{{0'},{l'}\}$
and
$R_\nu\subseteq {\mathcal{R}}M\times\{{0'},{l'}\}$
and
![]() $\widehat L=[R_\nu]$
; hence,
$\widehat L=[R_\nu]$
; hence,
By applying
![]() $\widehat{\,\cdot\,}$
, we get
$\widehat{\,\cdot\,}$
, we get
![]() $\widehat L = \widehat{L_R}$
, and since
$\widehat L = \widehat{L_R}$
, and since
![]() $\widehat{\,\cdot\,}$
is injective by Theorem 17,
$\widehat{\,\cdot\,}$
is injective by Theorem 17,
![]() $(\widehat L)^\vee = L_R =L$
.
$(\widehat L)^\vee = L_R =L$
.
![]() $\triangleleft$
$\triangleleft$
It remains to be shown that the bijection between
![]() ${\mathcal{C}} M$
and D given by the maps
${\mathcal{C}} M$
and D given by the maps
![]() $\widehat{\,\cdot\,}$
and
$\widehat{\,\cdot\,}$
and
![]() $\cdot^\vee$
is a
$\cdot^\vee$
is a
![]() ${\mathcal{C}}$
-isomorphism.
${\mathcal{C}}$
-isomorphism.
Claim 2. The maps
![]() $\,{\widehat{\cdot}\,} : {{\mathcal{C}} M} \rightleftarrows {D} : {{\cdot\,}^\vee}$
are monotone homomorphisms.
$\,{\widehat{\cdot}\,} : {{\mathcal{C}} M} \rightleftarrows {D} : {{\cdot\,}^\vee}$
are monotone homomorphisms.
Proof of Claim 2. Obviously,
![]() $\widehat{\,\cdot\,}$
is monotone; the monotonicity of
$\widehat{\,\cdot\,}$
is monotone; the monotonicity of
![]() $\cdot^\vee$
is noted in Theorem 17.
$\cdot^\vee$
is noted in Theorem 17.
1. The map
![]() $\cdot^\vee: D\to {\mathcal{C}} M$
is a homomorphism: first,
$\cdot^\vee: D\to {\mathcal{C}} M$
is a homomorphism: first,
and, second, for
![]() $[R],[S] \in D$
represented by
$[R],[S] \in D$
represented by
![]() $R,S\in {\mathcal{R}}({\mathcal{R}}M\times C_2')$
with
$R,S\in {\mathcal{R}}({\mathcal{R}}M\times C_2')$
with
![]() $R,S\subseteq {\mathcal{R}} M\times \{{0'},{l'}\}$
,
$R,S\subseteq {\mathcal{R}} M\times \{{0'},{l'}\}$
,
 \begin{eqnarray*} ([R]\cdot [S])^\vee &=& [RS]^\vee\\ &=& \bigcup\left\{\,C\,\mid\,(C,{l'})\in RS\,\right\}\\ &=& \bigcup\left\{\,AB\,\mid\,(A,{l'})\in R, (B,{l'})\in S\,\right\}\\ &=& \bigcup\left\{\,A\,\mid\,(A,{l'})\in R\,\right\}\cdot \bigcup\left\{\,B\,\mid\,(B,{l'})\in S\,\right\}\\ &=& [R]^\vee\cdot [S]^\vee,\end{eqnarray*}
\begin{eqnarray*} ([R]\cdot [S])^\vee &=& [RS]^\vee\\ &=& \bigcup\left\{\,C\,\mid\,(C,{l'})\in RS\,\right\}\\ &=& \bigcup\left\{\,AB\,\mid\,(A,{l'})\in R, (B,{l'})\in S\,\right\}\\ &=& \bigcup\left\{\,A\,\mid\,(A,{l'})\in R\,\right\}\cdot \bigcup\left\{\,B\,\mid\,(B,{l'})\in S\,\right\}\\ &=& [R]^\vee\cdot [S]^\vee,\end{eqnarray*}
because
![]() $(C,{l'})=(A,a)(B,b)$
iff
$(C,{l'})=(A,a)(B,b)$
iff
![]() $AB=C$
and
$AB=C$
and
![]() $a={l'}=b$
, since
$a={l'}=b$
, since
![]() $a,b\in\{{0'},{l'}\}$
.
$a,b\in\{{0'},{l'}\}$
.
2. The map
![]() $\widehat{\,\cdot\,} : {\mathcal{C}} M\to D$
is a homomorphism: clearly
$\widehat{\,\cdot\,} : {\mathcal{C}} M\to D$
is a homomorphism: clearly
![]() $\widehat{\{1\}} = \{1\}\otimes {l'} = 1$
, and for
$\widehat{\{1\}} = \{1\}\otimes {l'} = 1$
, and for
![]() $L_1,L_2\in {\mathcal{C}} M$
, since
$L_1,L_2\in {\mathcal{C}} M$
, since
![]() $\cdot^\vee$
is a homomorphism and inverse to
$\cdot^\vee$
is a homomorphism and inverse to
![]() $\widehat{\,\cdot\,}$
by Claim 3.1, we have
$\widehat{\,\cdot\,}$
by Claim 3.1, we have
by the injectivity of
![]() ${\cdot}^\vee$
, we get
${\cdot}^\vee$
, we get
![]() $ \widehat L_1\cdot\widehat L_2 = \widehat{L_1\cdot L_2}.$
$ \widehat L_1\cdot\widehat L_2 = \widehat{L_1\cdot L_2}.$
![]() $\triangleleft$
$\triangleleft$
Claim 3.
D is a
![]() ${\mathcal{C}}$
-dioid.
${\mathcal{C}}$
-dioid.
Proof of Claim 3. By Theorem 17, for
![]() $L\in {\mathcal{C}} M$
,
$L\in {\mathcal{C}} M$
,
![]() $\widehat{L} = \sum\left\{\,\{m\}\otimes 1'\,\mid\,m\in L\,\right\}$
is the least upper bound of the image
$\widehat{L} = \sum\left\{\,\{m\}\otimes 1'\,\mid\,m\in L\,\right\}$
is the least upper bound of the image
![]() $\widetilde f(L)$
of L under the homomorphism
$\widetilde f(L)$
of L under the homomorphism
![]() $f:M\to D$
given by
$f:M\to D$
given by
![]() $f(m) = \{m\}\otimes 1'$
. By the previous claims,
$f(m) = \{m\}\otimes 1'$
. By the previous claims,
![]() $\widehat{\,\cdot\,}:{\mathcal{C}} M\to D$
is a surjective homomorphism. By Proposition 14, D is an
$\widehat{\,\cdot\,}:{\mathcal{C}} M\to D$
is a surjective homomorphism. By Proposition 14, D is an
![]() ${\mathcal{R}}$
-dioid; hence, a dioid, and so by Lemma 3, D is a
${\mathcal{R}}$
-dioid; hence, a dioid, and so by Lemma 3, D is a
![]() ${\mathcal{C}}$
-dioid.
${\mathcal{C}}$
-dioid.
![]() $\triangleleft$
$\triangleleft$
Claim 4.
![]() $\widehat{\,\cdot\,}:{\mathcal{C}} M\to D$
and
$\widehat{\,\cdot\,}:{\mathcal{C}} M\to D$
and
![]() $\,\cdot^\vee : D \to {\mathcal{C}} M$
are
$\,\cdot^\vee : D \to {\mathcal{C}} M$
are
![]() ${\mathcal{C}}$
-morphisms.
${\mathcal{C}}$
-morphisms.
Proof of Claim 4. Since
![]() $\widehat{\,\cdot\,}$
is a homomorphism, so is
$\widehat{\,\cdot\,}$
is a homomorphism, so is
![]() ${\mathcal{C}}(\widehat{\,\cdot\,}):{\mathcal{C}}{\mathcal{C}}M\to {\mathcal{C}} D$
. Hence for
${\mathcal{C}}(\widehat{\,\cdot\,}):{\mathcal{C}}{\mathcal{C}}M\to {\mathcal{C}} D$
. Hence for
![]() $U\in {\mathcal{C}}{\mathcal{C}} M$
,
$U\in {\mathcal{C}}{\mathcal{C}} M$
,
![]() $\left\{\,\widehat L\,\mid\,L\in U\,\right\}\in {\mathcal{C}}D$
, and by the proof of Lemma 3, its least upper bound is
$\left\{\,\widehat L\,\mid\,L\in U\,\right\}\in {\mathcal{C}}D$
, and by the proof of Lemma 3, its least upper bound is
![]() $\sum\left\{\,\widehat L\,\mid\,L\in U\,\right\} = \widehat{\bigcup U}$
. Since
$\sum\left\{\,\widehat L\,\mid\,L\in U\,\right\} = \widehat{\bigcup U}$
. Since
![]() $\widehat{\,\cdot\,}$
is a monotone homomorphism, this shows that
$\widehat{\,\cdot\,}$
is a monotone homomorphism, this shows that
![]() $\widehat{\,\cdot\,}$
is a
$\widehat{\,\cdot\,}$
is a
![]() ${\mathcal{C}}$
-morphism.
${\mathcal{C}}$
-morphism.
![]() $\triangleleft$
$\triangleleft$
For
![]() $\,\cdot^\vee$
, for each
$\,\cdot^\vee$
, for each
![]() $V\in {\mathcal{C}} D$
there is
$V\in {\mathcal{C}} D$
there is
![]() $U\in {\mathcal{C}}{\mathcal{C}} M$
such that
$U\in {\mathcal{C}}{\mathcal{C}} M$
such that
![]() $V=\left\{\,\widehat L\,\mid\,L\in U\,\right\}$
and
$V=\left\{\,\widehat L\,\mid\,L\in U\,\right\}$
and
![]() $\sum V = \widehat{\bigcup U}$
. Hence, since
$\sum V = \widehat{\bigcup U}$
. Hence, since
![]() $\,{\widehat{\,\cdot\,}} : {{\mathcal{C}} M} \rightleftarrows {D} : {\,\cdot^\vee}\,$
is a bijection,
$\,{\widehat{\,\cdot\,}} : {{\mathcal{C}} M} \rightleftarrows {D} : {\,\cdot^\vee}\,$
is a bijection,
![]() $(\widehat L)^\vee = L$
for each
$(\widehat L)^\vee = L$
for each
![]() $L\in {\mathcal{C}} M$
. With
$L\in {\mathcal{C}} M$
. With
![]() $\bigcup U\in {\mathcal{C}} M$
, it follows that
$\bigcup U\in {\mathcal{C}} M$
, it follows that
As
![]() $\cdot^\vee$
is a monotone homomorphism, this shows that it is a
$\cdot^\vee$
is a monotone homomorphism, this shows that it is a
![]() ${\mathcal{C}}$
-morphism.
${\mathcal{C}}$
-morphism.
![]() $\triangleleft$
$\triangleleft$
Before considering an algebraic representation of the fixed-point closure of an arbitrary
![]() ${\mathcal{R}}$
-dioid K, we remark that the case
${\mathcal{R}}$
-dioid K, we remark that the case
![]() $K={\mathcal{R}} M$
treated so far is sufficient to provide a semantics to regular expression tools for context-free languages, like the one proposed by Hopkins (Reference Hopkins2007).
$K={\mathcal{R}} M$
treated so far is sufficient to provide a semantics to regular expression tools for context-free languages, like the one proposed by Hopkins (Reference Hopkins2007).
The results proven for
![]() $n=2$
hold as well for
$n=2$
hold as well for
![]() $n>2$
, which is convenient to treat
$n>2$
, which is convenient to treat
![]() ${\langle{0}\!\mid}, {\langle{0}\!\mid}$
as a fresh, unused pair of brackets. If X is a finite set disjoint from
${\langle{0}\!\mid}, {\langle{0}\!\mid}$
as a fresh, unused pair of brackets. If X is a finite set disjoint from
![]() $\Delta_n$
, all regular expressions over
$\Delta_n$
, all regular expressions over
![]() $X\cup\Delta_n$
have an interpretation in
$X\cup\Delta_n$
have an interpretation in
![]() ${\mathcal{R}} X^*\mathop{\otimes_{\mathcal{R}}} C_n'$
. Using the tensor product embeddings, atoms
${\mathcal{R}} X^*\mathop{\otimes_{\mathcal{R}}} C_n'$
. Using the tensor product embeddings, atoms
![]() $x\in X$
are interpreted by
$x\in X$
are interpreted by
![]() $\{x\}\otimes1$
and atoms
$\{x\}\otimes1$
and atoms
![]() $\delta\in\Delta_n$
by
$\delta\in\Delta_n$
by
![]() $\{1\}\otimes \{\delta\}/\rho_n$
, as in Example 5. A subset of the regular expressions over
$\{1\}\otimes \{\delta\}/\rho_n$
, as in Example 5. A subset of the regular expressions over
![]() $X\cup\Delta_n$
that are sufficient to name all context-free sets of
$X\cup\Delta_n$
that are sufficient to name all context-free sets of
![]() ${\mathcal{C}}X^*\simeq Z_{C_n'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_n'})$
is easily selected as follows.
${\mathcal{C}}X^*\simeq Z_{C_n'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_n'})$
is easily selected as follows.
Corollary 28. For
![]() $n>2$
, an element
$n>2$
, an element
![]() $e\in {\mathcal{R}} X^*\mathop{\otimes_{\mathcal{R}}} {C_n'}$
belongs to
$e\in {\mathcal{R}} X^*\mathop{\otimes_{\mathcal{R}}} {C_n'}$
belongs to
![]() $Z_{C_n'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_n'})$
iff e is the value of a regular expression
$Z_{C_n'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_n'})$
iff e is the value of a regular expression
![]() ${\langle{0}\!\mid}r{\mid\!{0}\rangle}$
over
${\langle{0}\!\mid}r{\mid\!{0}\rangle}$
over
![]() $X\cup\Delta_n$
where
$X\cup\Delta_n$
where
![]() ${\langle{0}\!\mid}$
and
${\langle{0}\!\mid}$
and
![]() ${\langle{0}\!\mid}$
do not occur in r.
${\langle{0}\!\mid}$
do not occur in r.
Proof.
![]() $\Rightarrow$
: Suppose
$\Rightarrow$
: Suppose
![]() $e \in Z_{C_n'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_n'})$
. By Theorem 27, there is
$e \in Z_{C_n'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_n'})$
. By Theorem 27, there is
![]() $L \in {\mathcal{C}} X^*$
with
$L \in {\mathcal{C}} X^*$
with
![]() $L = e^\vee$
. Let
$L = e^\vee$
. Let
be a context-free grammar for L, i.e. L is the first component
![]() $L_1$
of its least solution
$L_1$
of its least solution
![]() $L_1,\ldots,L_k \in {\mathcal{C}} X^*$
. Construct the right-linear grammar
$L_1,\ldots,L_k \in {\mathcal{C}} X^*$
. Construct the right-linear grammar
as in the proof of Theorem 15. We can assume that
![]() ${\langle{1}\!\mid},\ldots,{\langle{n}\!\mid},{\mid\!{1}\rangle},\ldots, {\mid\!{n}\rangle}$
are sufficient to wrap each occurrence of a variable
${\langle{1}\!\mid},\ldots,{\langle{n}\!\mid},{\mid\!{1}\rangle},\ldots, {\mid\!{n}\rangle}$
are sufficient to wrap each occurrence of a variable
![]() $y_1,\ldots,y_k$
in
$y_1,\ldots,y_k$
in
![]() $p_1,\ldots, p_k$
by a different bracket pair
$p_1,\ldots, p_k$
by a different bracket pair
![]() ${\langle{i}\!\mid}, {\mid\!{i}\rangle}$
, otherwise use the two pairs
${\langle{i}\!\mid}, {\mid\!{i}\rangle}$
, otherwise use the two pairs
![]() ${\langle{1}\!\mid},{\mid\!{1}\rangle}$
and
${\langle{1}\!\mid},{\mid\!{1}\rangle}$
and
![]() ${\langle{2}\!\mid},{\mid\!{2}\rangle}$
to encode new bracket pairs. Let r be the regular expression over
${\langle{2}\!\mid},{\mid\!{2}\rangle}$
to encode new bracket pairs. Let r be the regular expression over
![]() $X\cup\Delta_n$
for the least solution in
$X\cup\Delta_n$
for the least solution in
![]() $y_1$
of the right-linear grammar; r does not contain
$y_1$
of the right-linear grammar; r does not contain
![]() ${\langle{0}\!\mid}$
and
${\langle{0}\!\mid}$
and
![]() ${\langle{0}\!\mid}$
. The corresponding regular set
${\langle{0}\!\mid}$
. The corresponding regular set
![]() $R\in {\mathcal{R}}(X^*[\Delta_n])$
satisfies
$R\in {\mathcal{R}}(X^*[\Delta_n])$
satisfies
![]() $L = h_{X^*}(R\cap D_n(X))$
, and the value of
$L = h_{X^*}(R\cap D_n(X))$
, and the value of
![]() ${\langle{0}\!\mid} r{\langle{0}\!\mid}$
in
${\langle{0}\!\mid} r{\langle{0}\!\mid}$
in
![]() ${\mathcal{R}} X^*\mathop{\otimes_{\mathcal{R}}} C_2'$
is
${\mathcal{R}} X^*\mathop{\otimes_{\mathcal{R}}} C_2'$
is
![]() $e=\widehat L \in Z_{C_n'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_n'})$
. We can see
$e=\widehat L \in Z_{C_n'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_n'})$
. We can see
![]() ${\langle{0}\!\mid} r{\langle{0}\!\mid}$
as the solution term for
${\langle{0}\!\mid} r{\langle{0}\!\mid}$
as the solution term for
![]() $\widehat y$
of the right-linear grammar
$\widehat y$
of the right-linear grammar
(Cf. the automata in Example 6.)
![]() $\Leftarrow$
: Let r be a regular expression over
$\Leftarrow$
: Let r be a regular expression over
![]() $X\cup\Delta_n$
not containing
$X\cup\Delta_n$
not containing
![]() ${\langle{0}\!\mid},{\langle{0}\!\mid}$
. By Corollary 13,
${\langle{0}\!\mid},{\langle{0}\!\mid}$
. By Corollary 13,
where
![]() $\tilde\nu$
is the
$\tilde\nu$
is the
![]() ${\mathcal{R}}$
-congruence generated by
${\mathcal{R}}$
-congruence generated by
![]() $\{(1,0)\}=\emptyset$
. So the value of r in
$\{(1,0)\}=\emptyset$
. So the value of r in
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
can be represented by
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
can be represented by
![]() $T/\tilde\nu$
with
$T/\tilde\nu$
with
![]() $T\in {\mathcal{R}}(X^*\times P_n')$
. By the choice of r, for no
$T\in {\mathcal{R}}(X^*\times P_n')$
. By the choice of r, for no
![]() $(m,w)\in T$
do
$(m,w)\in T$
do
![]() ${\langle{0}\!\mid}$
or
${\langle{0}\!\mid}$
or
![]() ${\langle{0}\!\mid}$
occur in its second component
${\langle{0}\!\mid}$
occur in its second component
![]() $w\in P_n'=Q_n^*P_n^*\cup\{0\}$
. So the value of
$w\in P_n'=Q_n^*P_n^*\cup\{0\}$
. So the value of
![]() ${\langle{0}\!\mid} r{\langle{0}\!\mid}$
is
${\langle{0}\!\mid} r{\langle{0}\!\mid}$
is
![]() $S/\tilde\nu$
for
$S/\tilde\nu$
for
![]() $S=\{(1,{\langle{0}\!\mid})\}T\{(1,{\langle{0}\!\mid})\}$
, and
$S=\{(1,{\langle{0}\!\mid})\}T\{(1,{\langle{0}\!\mid})\}$
, and
![]() $S\subseteq X^*\times \{0,1\}$
due to bracket mismatches in the second components. The isomorphisms of Theorem 12 and Proposition 9 map
$S\subseteq X^*\times \{0,1\}$
due to bracket mismatches in the second components. The isomorphisms of Theorem 12 and Proposition 9 map
![]() $S/\tilde\nu$
to some
$S/\tilde\nu$
to some
![]() $[R]\in {\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
with
$[R]\in {\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
with
![]() $R\subseteq {\mathcal{R}} X^*\times\{0',1'\}$
. By Lemma 25, the value [R] of
$R\subseteq {\mathcal{R}} X^*\times\{0',1'\}$
. By Lemma 25, the value [R] of
![]() ${\langle{0}\!\mid}r{\langle{0}\!\mid}$
belongs to the centralizer of
${\langle{0}\!\mid}r{\langle{0}\!\mid}$
belongs to the centralizer of
![]() $C_n'$
.
$C_n'$
.
Notice that regular combinations of expressions of the above form
![]() ${\langle{0}\!\mid} r{\langle{0}\!\mid}$
are no longer of this form, but of course also denote sets in
${\langle{0}\!\mid} r{\langle{0}\!\mid}$
are no longer of this form, but of course also denote sets in
![]() ${\mathcal{C}} X^*$
.
${\mathcal{C}} X^*$
.
There is another way to find, for
![]() $L\in {\mathcal{C}} X^*$
, a regular expression r such that
$L\in {\mathcal{C}} X^*$
, a regular expression r such that
![]() ${\langle{0}\!\mid} r{\langle{0}\!\mid}$
evaluates to
${\langle{0}\!\mid} r{\langle{0}\!\mid}$
evaluates to
![]() $\widehat L$
in
$\widehat L$
in
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}}{C_n'}$
, which is perhaps more appealing than the one in the proof above: a non-deterministic bottom-up, top-down or Earley parser (cf. Sikkel Reference Sikkel1998) for a context-free grammar
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}}{C_n'}$
, which is perhaps more appealing than the one in the proof above: a non-deterministic bottom-up, top-down or Earley parser (cf. Sikkel Reference Sikkel1998) for a context-free grammar
![]() $G=(X,Y,P,S)$
for L is an iterative program, i.e. a regular expression r over an alphabet of basic commands. Suppose that
$G=(X,Y,P,S)$
for L is an iterative program, i.e. a regular expression r over an alphabet of basic commands. Suppose that
![]() $\Delta_n$
contains, besides
$\Delta_n$
contains, besides
![]() ${\langle{0}\!\mid}$
and
${\langle{0}\!\mid}$
and
![]() ${\langle{0}\!\mid}$
, an opening bracket
${\langle{0}\!\mid}$
, an opening bracket
![]() ${\langle{z}\!\mid}$
and a closing bracket
${\langle{z}\!\mid}$
and a closing bracket
![]() ${\mid\!{z}\rangle}$
for each
${\mid\!{z}\rangle}$
for each
![]() $z\in X\cup Y$
. The bottom-up parser, for example, can then be expressed by
$z\in X\cup Y$
. The bottom-up parser, for example, can then be expressed by
with
![]() $\textit{shift}_x = x{\langle{x}\!\mid}$
and
$\textit{shift}_x = x{\langle{x}\!\mid}$
and
![]() $\textit{reduce}_{(A,\alpha)}={\mid\!{\alpha}\rangle}{\langle{A}\!\mid}$
, where
$\textit{reduce}_{(A,\alpha)}={\mid\!{\alpha}\rangle}{\langle{A}\!\mid}$
, where
![]() ${\mid\!{z_1\ldots z_k}\rangle}={\mid\!{z_k}\rangle}\ldots{\mid\!{z_1}\rangle}$
for
${\mid\!{z_1\ldots z_k}\rangle}={\mid\!{z_k}\rangle}\ldots{\mid\!{z_1}\rangle}$
for
![]() $z_i\in X\cup Y$
. Then,
$z_i\in X\cup Y$
. Then,
![]() $\widehat{L} = \sum\left\{\,\{m\}\otimes 1\,\mid\,m\in L\,\right\}= {\langle{0}\!\mid} r{\mid\!{S}\rangle}{\langle{0}\!\mid}$
. If G is the grammar of Example 6, the word baac is accepted by the shift-reduce sequence
$\widehat{L} = \sum\left\{\,\{m\}\otimes 1\,\mid\,m\in L\,\right\}= {\langle{0}\!\mid} r{\mid\!{S}\rangle}{\langle{0}\!\mid}$
. If G is the grammar of Example 6, the word baac is accepted by the shift-reduce sequence
its value in
![]() ${\mathcal{R}} X^*\mathop{\otimes_{\mathcal{R}}}{C_n'}$
is
${\mathcal{R}} X^*\mathop{\otimes_{\mathcal{R}}}{C_n'}$
is
![]() $\{baac\}\otimes\{{\langle{y}\!\mid}\}$
, and since y was the start symbol S,
$\{baac\}\otimes\{{\langle{y}\!\mid}\}$
, and since y was the start symbol S,
![]() $\{baac\}\otimes 1 \leq {\langle{0}\!\mid}r{\mid\!{S}\rangle}{\langle{0}\!\mid}= \widehat L$
. This indicates that
$\{baac\}\otimes 1 \leq {\langle{0}\!\mid}r{\mid\!{S}\rangle}{\langle{0}\!\mid}= \widehat L$
. This indicates that
![]() ${\mathcal{R}} X^*\mathop{\otimes_{\mathcal{R}}} C_2'$
may be useful to study parsing algebraically.
${\mathcal{R}} X^*\mathop{\otimes_{\mathcal{R}}} C_2'$
may be useful to study parsing algebraically.
6. Algebraic Representation of the
 $\mathbb{\mathcal{C}}$
-Closure of an Arbitrary
$\mathbb{\mathcal{C}}$
-Closure of an Arbitrary
 ${\mathcal{R}}$
-Dioid K
${\mathcal{R}}$
-Dioid K
We can now generalize Theorem 27, the algebraic representation of the
![]() ${\mathcal{C}}$
-closure of
${\mathcal{C}}$
-closure of
![]() ${\mathcal{R}}$
-dioids
${\mathcal{R}}$
-dioids
![]() ${\mathcal{R}} M$
with monoid M to an algebraic construction of the
${\mathcal{R}} M$
with monoid M to an algebraic construction of the
![]() ${\mathcal{C}}$
-closure
${\mathcal{C}}$
-closure
![]() ${Q_{\mathcal{R}}^{\mathcal{C}}} : {\mathbb{D}}{\mathcal{R}}\to {\mathbb{D}}{\mathcal{C}}$
on the Eilenberg-Moore category
${Q_{\mathcal{R}}^{\mathcal{C}}} : {\mathbb{D}}{\mathcal{R}}\to {\mathbb{D}}{\mathcal{C}}$
on the Eilenberg-Moore category
![]() ${\mathbb{D}}{\mathcal{R}}$
of all
${\mathbb{D}}{\mathcal{R}}$
of all
![]() ${\mathcal{R}}$
-dioids. We need a series of steps.
${\mathcal{R}}$
-dioids. We need a series of steps.
Lemma 29. For any
![]() ${\mathcal{R}}$
-dioid K,
${\mathcal{R}}$
-dioid K,
Proof.
![]() $\subseteq$
: For
$\subseteq$
: For
![]() $\Delta_2=\{p_0,q_0,p_1,q_1\}$
, let
$\Delta_2=\{p_0,q_0,p_1,q_1\}$
, let
![]() $\rho_2$
be the
$\rho_2$
be the
![]() ${\mathcal{R}}$
-congruence on
${\mathcal{R}}$
-congruence on
![]() ${\mathcal{R}}\Delta_2^*$
generated by the semiring equations
${\mathcal{R}}\Delta_2^*$
generated by the semiring equations
and
![]() $\cdot/\rho_2 : {\mathcal{R}}\Delta_2^*\to C_2' = {\mathcal{R}}\Delta_2^*/\rho_2$
the canonical
$\cdot/\rho_2 : {\mathcal{R}}\Delta_2^*\to C_2' = {\mathcal{R}}\Delta_2^*/\rho_2$
the canonical
![]() ${\mathcal{R}}$
-morphism. By Corollary 16 there is a set
${\mathcal{R}}$
-morphism. By Corollary 16 there is a set
![]() $S\in{\mathcal{R}}(M\times\Delta_2^*)$
such that
$S\in{\mathcal{R}}(M\times\Delta_2^*)$
such that
and for each
![]() $(m,d)\in S$
,
$(m,d)\in S$
,
 \begin{equation} \{d\}/\rho_2 = \begin{cases} 1 & d\in D_2,\\ 0, & d\notin D_2.\end{cases}\end{equation}
\begin{equation} \{d\}/\rho_2 = \begin{cases} 1 & d\in D_2,\\ 0, & d\notin D_2.\end{cases}\end{equation}
The isomorphism
![]() ${\mathcal{R}}(K\times\Delta_2^*)\simeq {\mathcal{R}} K\mathop{\otimes_{\mathcal{R}}} {\mathcal{R}}\Delta_2^*$
of Proposition 11 maps S to
${\mathcal{R}}(K\times\Delta_2^*)\simeq {\mathcal{R}} K\mathop{\otimes_{\mathcal{R}}} {\mathcal{R}}\Delta_2^*$
of Proposition 11 maps S to
![]() $[R_S]$
, where
$[R_S]$
, where
The lifting of the homomorphism
![]() $\sum\times(\cdot/\rho_2) : {\mathcal{R}} K\times {\mathcal{R}}\Delta_2^* \to K \times C_2'$
, maps
$\sum\times(\cdot/\rho_2) : {\mathcal{R}} K\times {\mathcal{R}}\Delta_2^* \to K \times C_2'$
, maps
![]() $R_S$
to
$R_S$
to
By (12), R is a subset of
![]() $K\times \{0,1\}$
such that
$K\times \{0,1\}$
such that
![]() $\supseteq$
: Suppose
$\supseteq$
: Suppose
![]() $R\in {\mathcal{R}}(K\times C_2')$
and
$R\in {\mathcal{R}}(K\times C_2')$
and
![]() $R\subseteq K\times\{0,1\}$
. Then for
$R\subseteq K\times\{0,1\}$
. Then for
![]() $R'=\left\{\,(\{m\},c)\,\mid\,(m,c)\in R\,\right\}$
, we have
$R'=\left\{\,(\{m\},c)\,\mid\,(m,c)\in R\,\right\}$
, we have
![]() $R'\in {\mathcal{R}}({\mathcal{R}} K\times C_2')$
and
$R'\in {\mathcal{R}}({\mathcal{R}} K\times C_2')$
and
![]() $R'\subseteq {\mathcal{R}} K\times \{0,1\}$
, so
$R'\subseteq {\mathcal{R}} K\times \{0,1\}$
, so
![]() $[R']\in Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
by Lemma 25; hence,
$[R']\in Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
by Lemma 25; hence,
by Theorem 26. ![]()
Since for
![]() $L\in{\mathcal{C}} K$
,
$L\in{\mathcal{C}} K$
,
![]() $\widetilde{\top_1}(L)=\left\{\,m\otimes 1\,\mid\,m\in L\,\right\}\in{\mathcal{C}}(Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'}))$
, the next lemma is a step towards the
$\widetilde{\top_1}(L)=\left\{\,m\otimes 1\,\mid\,m\in L\,\right\}\in{\mathcal{C}}(Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'}))$
, the next lemma is a step towards the
![]() ${\mathcal{C}}$
-completeness of
${\mathcal{C}}$
-completeness of
![]() $Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
.
$Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
.
Lemma 30. For each
![]() ${\mathcal{R}}$
-dioid K, there is a surjective homomorphism
${\mathcal{R}}$
-dioid K, there is a surjective homomorphism
that assigns to each
![]() $L\in {\mathcal{C}} K$
a least upper bound of
$L\in {\mathcal{C}} K$
a least upper bound of
![]() $\widetilde{\top_1}(L)$
in
$\widetilde{\top_1}(L)$
in
![]() $K\mathop{\otimes_{\mathcal{R}}} C_2'$
,
$K\mathop{\otimes_{\mathcal{R}}} C_2'$
,
Proof. For each
![]() $L\in{\mathcal{C}} K,$
there is, by Lemma 29, a set
$L\in{\mathcal{C}} K,$
there is, by Lemma 29, a set
![]() $R\in {\mathcal{R}}(K\times C_2')$
with
$R\in {\mathcal{R}}(K\times C_2')$
with
![]() $R\subseteq K\times\{0,1\}$
and
$R\subseteq K\times\{0,1\}$
and
![]() $L=\left\{\,m\,\mid\,(m,1)\in R\,\right\}$
. As
$L=\left\{\,m\,\mid\,(m,1)\in R\,\right\}$
. As
![]() $m\otimes 0 = 0$
for all
$m\otimes 0 = 0$
for all
![]() $m\in K$
, it follows that
$m\in K$
, it follows that
showing that
![]() $\widetilde{\top_1}(L)=\left\{\,m\otimes 1\,\mid\,m\in L\,\right\}$
has a least upper bound in
$\widetilde{\top_1}(L)=\left\{\,m\otimes 1\,\mid\,m\in L\,\right\}$
has a least upper bound in
![]() $K\mathop{\otimes_{\mathcal{R}}} C_2'$
, namely
$K\mathop{\otimes_{\mathcal{R}}} C_2'$
, namely
Since all
![]() $m\otimes d$
with
$m\otimes d$
with
![]() $(m,d)\in R$
belong to
$(m,d)\in R$
belong to
![]() $Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
, we have
$Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
, we have
![]() $[R]\in Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
by Proposition 14. This defines a map
$[R]\in Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
by Proposition 14. This defines a map
![]() $\widehat\cdot:{\mathcal{C}} K\to Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
.
$\widehat\cdot:{\mathcal{C}} K\to Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
.
The map
![]() $\widehat{\,\cdot\,}$
is a homomorphism:
$\widehat{\,\cdot\,}$
is a homomorphism:
![]() $\widehat{\{1\}} =\sum\{1\otimes 1\}=1\otimes 1 = 1$
and for
$\widehat{\{1\}} =\sum\{1\otimes 1\}=1\otimes 1 = 1$
and for
![]() $L_1,L_2\in{\mathcal{C}} K$
, by Lemma 29 there are
$L_1,L_2\in{\mathcal{C}} K$
, by Lemma 29 there are
![]() $R_1,R_2\in{\mathcal{R}}(K\times C_2')$
such that
$R_1,R_2\in{\mathcal{R}}(K\times C_2')$
such that
![]() $R_i\subseteq K\times\{0,1\}$
and
$R_i\subseteq K\times\{0,1\}$
and
![]() $L_i=\left\{\,m\,\mid\,(m,1)\in R_i\,\right\}$
for
$L_i=\left\{\,m\,\mid\,(m,1)\in R_i\,\right\}$
for
![]() $i=1,2$
. Therefore,
$i=1,2$
. Therefore,
 \begin{eqnarray*} \widehat{\,L_1}\cdot \widehat{\,L_2} &=& [R_1][R_2] = [R_1R_2]\\ &=& [\left\{\,(m_1m_2,1)\,\mid\,(m_1,1)\in R_1, (m_2,1)\in R_2\,\right\}]\\ &=& [\left\{\,(m_1m_2,1)\,\mid\,m_1\in L_1, m_2\in L_2\,\right\}]\\ &=& \sum\left\{\,m\otimes 1\,\mid\,m\in L_1L_2\,\right\}\\ &=& \widehat{\,L_1L_2},\end{eqnarray*}
\begin{eqnarray*} \widehat{\,L_1}\cdot \widehat{\,L_2} &=& [R_1][R_2] = [R_1R_2]\\ &=& [\left\{\,(m_1m_2,1)\,\mid\,(m_1,1)\in R_1, (m_2,1)\in R_2\,\right\}]\\ &=& [\left\{\,(m_1m_2,1)\,\mid\,m_1\in L_1, m_2\in L_2\,\right\}]\\ &=& \sum\left\{\,m\otimes 1\,\mid\,m\in L_1L_2\,\right\}\\ &=& \widehat{\,L_1L_2},\end{eqnarray*}
as summands
![]() $m_1m_2\otimes 0 = 0$
in
$m_1m_2\otimes 0 = 0$
in
![]() $[R_1R_2]$
can be ignored.
$[R_1R_2]$
can be ignored.
We still have to show that
![]() $\widehat{\,\cdot\,}$
is surjective. We use
$\widehat{\,\cdot\,}$
is surjective. We use
![]() $\sum$
and
$\sum$
and
![]() $\otimes$
for the given operations of
$\otimes$
for the given operations of
![]() $K\mathop{\otimes_{\mathcal{R}}} C_2'$
,
$K\mathop{\otimes_{\mathcal{R}}} C_2'$
,
![]() $\sum'$
and
$\sum'$
and
![]() $\otimes'$
for those of
$\otimes'$
for those of
![]() ${\mathcal{R}} K\mathop{\otimes_{\mathcal{R}}} C_2'$
. By the universal property of
${\mathcal{R}} K\mathop{\otimes_{\mathcal{R}}} C_2'$
. By the universal property of
![]() ${\mathcal{R}} K\mathop{\otimes_{\mathcal{R}}} C_2'$
, the given
${\mathcal{R}} K\mathop{\otimes_{\mathcal{R}}} C_2'$
, the given
![]() $\sum : {\mathcal{R}} K \to K$
induces an
$\sum : {\mathcal{R}} K \to K$
induces an
![]() ${\mathcal{R}}$
-morphism
${\mathcal{R}}$
-morphism
![]() $h=h_{f,g}$
for
$h=h_{f,g}$
for
![]() $f=\top_1\circ \sum$
and
$f=\top_1\circ \sum$
and
![]() $g=\top_2$
such that
$g=\top_2$
such that
![]() $f=h\circ \top_1'$
and
$f=h\circ \top_1'$
and
![]() $g=h\circ\top_2'$
:
$g=h\circ\top_2'$
:

Since h is a homomorphism and
![]() $h(\top_2'(c)) = \top_1(c)$
for
$h(\top_2'(c)) = \top_1(c)$
for
![]() $c\in C_2'$
, h preserves commutativity relations with
$c\in C_2'$
, h preserves commutativity relations with
![]() $C_2'$
, so its restriction is an
$C_2'$
, so its restriction is an
![]() ${\mathcal{R}}$
-morphism
${\mathcal{R}}$
-morphism
Clearly,
![]() $h:{\mathcal{R}} K\mathop{\otimes_{\mathcal{R}}} C_2'\to K\mathop{\otimes_{\mathcal{R}}} C_2'$
is surjective: if
$h:{\mathcal{R}} K\mathop{\otimes_{\mathcal{R}}} C_2'\to K\mathop{\otimes_{\mathcal{R}}} C_2'$
is surjective: if
![]() $R\in{\mathcal{R}}(K\times C_2')$
we have
$R\in{\mathcal{R}}(K\times C_2')$
we have
 \begin{eqnarray*} [R] &=& \sum\left\{\,m\otimes c\,\mid\,(m,c)\in R\,\right\} \\ &=& \sum\left\{\,\left(\sum\{m\}\right)\otimes c\,\mid\,(m,c)\in R\,\right\} \\ &=& h\left({\textstyle{\displaystyle\sum}'}\left\{\,\{m\}\otimes' c\,\mid\,(m,c)\in R\,\right\}\right)\\\ &=& h([R'])\end{eqnarray*}
\begin{eqnarray*} [R] &=& \sum\left\{\,m\otimes c\,\mid\,(m,c)\in R\,\right\} \\ &=& \sum\left\{\,\left(\sum\{m\}\right)\otimes c\,\mid\,(m,c)\in R\,\right\} \\ &=& h\left({\textstyle{\displaystyle\sum}'}\left\{\,\{m\}\otimes' c\,\mid\,(m,c)\in R\,\right\}\right)\\\ &=& h([R'])\end{eqnarray*}
for
![]() $ R'=\left\{\,(\{m\},c)\,\mid\,(m,c)\in R\,\right\} \in {\mathcal{R}}({\mathcal{R}} K\times C_2'). $
And if
$ R'=\left\{\,(\{m\},c)\,\mid\,(m,c)\in R\,\right\} \in {\mathcal{R}}({\mathcal{R}} K\times C_2'). $
And if
![]() $[R]\in Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
, then
$[R]\in Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
, then
![]() $[R']\in Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
, so the restriction
$[R']\in Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
, so the restriction
![]() $h:Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})\to Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
also is surjective.
$h:Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})\to Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
also is surjective.
Now take
![]() $[R]\in Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
with
$[R]\in Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
with
![]() $R\in{\mathcal{R}}(K\times C_2')$
, and let
$R\in{\mathcal{R}}(K\times C_2')$
, and let
![]() $R'=\left\{\,(\{m\},c)\,\mid\,(m,c)\in R\,\right\}$
. By Theorem 27, for
$R'=\left\{\,(\{m\},c)\,\mid\,(m,c)\in R\,\right\}$
. By Theorem 27, for
![]() $[R']\in Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
there is
$[R']\in Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
there is
![]() $L\in{\mathcal{C}} K$
such that
$L\in{\mathcal{C}} K$
such that
We claim that
![]() $[R] = \widehat L = \sum\left\{\,m\otimes 1\,\mid\,m\in L\,\right\}$
. By Lemma 29, there is
$[R] = \widehat L = \sum\left\{\,m\otimes 1\,\mid\,m\in L\,\right\}$
. By Lemma 29, there is
![]() $S\in {\mathcal{R}}(K\times C_2')$
with
$S\in {\mathcal{R}}(K\times C_2')$
with
![]() $S\subseteq K\times \{0,1\}$
and
$S\subseteq K\times \{0,1\}$
and
![]() $L = \left\{\,m\,\mid\,(m,1)\in S\,\right\}$
. Then
$L = \left\{\,m\,\mid\,(m,1)\in S\,\right\}$
. Then
![]() $S'=\left\{\,(\{m\},c)\,\mid\,(m,c)\in S\,\right\}\in{\mathcal{R}}({\mathcal{R}} K\times C_2')$
and
$S'=\left\{\,(\{m\},c)\,\mid\,(m,c)\in S\,\right\}\in{\mathcal{R}}({\mathcal{R}} K\times C_2')$
and
hence,
![]() $[R]=h([R'])=h([S'])=[S] = \sum\left\{\,m\otimes c\,\mid\,(m,c)\in S\,\right\} =\sum\widetilde{\top_1}(L) = \widehat L$
.
$[R]=h([R'])=h([S'])=[S] = \sum\left\{\,m\otimes c\,\mid\,(m,c)\in S\,\right\} =\sum\widetilde{\top_1}(L) = \widehat L$
. ![]()
In contrast to Theorem 17, the map
![]() $\widehat{\,\cdot\,}: {\mathcal{C}} K\to Z_{C_2}({K} \mathop{\otimes_{\mathcal{R}}} {C_2})$
need not be injective:
$\widehat{\,\cdot\,}: {\mathcal{C}} K\to Z_{C_2}({K} \mathop{\otimes_{\mathcal{R}}} {C_2})$
need not be injective:
Example 7. Take
![]() $K={\mathcal{R}} M$
for
$K={\mathcal{R}} M$
for
![]() $M= \{a,b\}^*$
. For
$M= \{a,b\}^*$
. For
![]() $L\in K$
,
$L\in K$
,
![]() $\left\{\,\{m\}\,\mid\,m\in L\,\right\}\in{\mathcal{R}}({\mathcal{R}}M)$
, and since
$\left\{\,\{m\}\,\mid\,m\in L\,\right\}\in{\mathcal{R}}({\mathcal{R}}M)$
, and since
![]() $L\mapsto L\otimes 1$
is the
$L\mapsto L\otimes 1$
is the
![]() ${\mathcal{R}}$
-morphism
${\mathcal{R}}$
-morphism
![]() $\top_1: K \to K\mathop{\otimes_{\mathcal{R}}} C_2'$
, we have
$\top_1: K \to K\mathop{\otimes_{\mathcal{R}}} C_2'$
, we have
It follows that for
![]() $U\in {\mathcal{C}} K$
,
$U\in {\mathcal{C}} K$
,
Consider the following two polynomial systems over K:
The least solutions
![]() $U_1, U_2\in {\mathcal{C}} K$
of these are, respectively,
$U_1, U_2\in {\mathcal{C}} K$
of these are, respectively,
But while
![]() $U_1\not=U_2$
, we have
$U_1\not=U_2$
, we have
![]() $\bigcup U_1 = \bigcup U_2=\left\{\,a^nb^n\,\mid\,n\in{\mathbb{N}}\,\right\}$
; hence,
$\bigcup U_1 = \bigcup U_2=\left\{\,a^nb^n\,\mid\,n\in{\mathbb{N}}\,\right\}$
; hence,
![]() $\widehat{U_1}=\widehat{U_2}$
.
$\widehat{U_1}=\widehat{U_2}$
.
![]() $\diamond$
$\diamond$
Lemma 31. For each
![]() ${\mathcal{R}}$
-dioid K,
${\mathcal{R}}$
-dioid K,
![]() $Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is a
$Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is a
![]() ${\mathcal{C}}$
-dioid. Moreover,
${\mathcal{C}}$
-dioid. Moreover,
Proof. By Lemma 30, the map
![]() $\widehat{\,\cdot\,}:{\mathcal{C}} K\to Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is a surjective homomorphism that assigns to
$\widehat{\,\cdot\,}:{\mathcal{C}} K\to Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is a surjective homomorphism that assigns to
![]() $L\in{\mathcal{C}} K$
the least upper bound of the image of L under the homomorphism
$L\in{\mathcal{C}} K$
the least upper bound of the image of L under the homomorphism
![]() $\top_1:K\to K\mathop{\otimes_{\mathcal{R}}} C_2'$
,
$\top_1:K\to K\mathop{\otimes_{\mathcal{R}}} C_2'$
,
![]() $\widehat{\,L\,}=\sum\widetilde{\top_1}(L)$
. By Lemma 3,
$\widehat{\,L\,}=\sum\widetilde{\top_1}(L)$
. By Lemma 3,
![]() $Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is a
$Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is a
![]() ${\mathcal{C}}$
-dioid, i.e. there is a
${\mathcal{C}}$
-dioid, i.e. there is a
![]() ${\mathcal{C}}$
-distributive least upper bound operator
${\mathcal{C}}$
-distributive least upper bound operator
where for
![]() $V\in {\mathcal{C}}(Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'}))$
,
$V\in {\mathcal{C}}(Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'}))$
,
![]() $\sum V = \widehat{\bigcup U}$
for any
$\sum V = \widehat{\bigcup U}$
for any
![]() $U\in {\mathcal{C}}{\mathcal{C}} K$
such that
$U\in {\mathcal{C}}{\mathcal{C}} K$
such that
![]() $V = \left\{\,\widehat L\,\mid\,L\in U\,\right\}$
.
$V = \left\{\,\widehat L\,\mid\,L\in U\,\right\}$
.
For
![]() $\supseteq$
of the equation, suppose
$\supseteq$
of the equation, suppose
![]() $R\in {\mathcal{R}}(K\times C_2')$
and
$R\in {\mathcal{R}}(K\times C_2')$
and
![]() $R\subseteq K\times\{0,1\}$
. By
$R\subseteq K\times\{0,1\}$
. By
![]() $\supseteq$
of Lemma 29,
$\supseteq$
of Lemma 29,
But then
![]() $[R] = \widehat{L} \in Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
by Lemma 30. The reverse inclusion
$[R] = \widehat{L} \in Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
by Lemma 30. The reverse inclusion
![]() $\subseteq$
follows from the surjectivity of
$\subseteq$
follows from the surjectivity of
![]() $\widehat{\,\cdot\,}$
and
$\widehat{\,\cdot\,}$
and
![]() $\subseteq$
of Lemma 29, as shown at the beginning of the proof of Lemma 30.
$\subseteq$
of Lemma 29, as shown at the beginning of the proof of Lemma 30. ![]()
Before we can present the second main result, that for any
![]() ${\mathcal{R}}$
-dioid K,
${\mathcal{R}}$
-dioid K,
![]() $Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is the
$Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is the
![]() ${\mathcal{C}}$
-closure of K, we have to consider a special case
Footnote 8
:
${\mathcal{C}}$
-closure of K, we have to consider a special case
Footnote 8
:
Theorem 32. Let C be a
![]() ${\mathcal{C}}$
-dioid and K its restriction to an
${\mathcal{C}}$
-dioid and K its restriction to an
![]() ${\mathcal{R}}$
-dioid. The
${\mathcal{R}}$
-dioid. The
![]() ${\mathcal{R}}$
-morphism
${\mathcal{R}}$
-morphism
![]() $\top_1: K\to K\mathop{\otimes_{\mathcal{R}}} C_2'$
is a
$\top_1: K\to K\mathop{\otimes_{\mathcal{R}}} C_2'$
is a
![]() ${\mathcal{C}}$
-isomorphism
${\mathcal{C}}$
-isomorphism
Proof. By Lemma 31,
![]() $D:=Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is a
$D:=Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is a
![]() ${\mathcal{C}}$
-dioid, so let
${\mathcal{C}}$
-dioid, so let
![]() $\sum:{\mathcal{C}}D\to D$
be its supremum operator. Since C and K have the same multiplicative monoid,
$\sum:{\mathcal{C}}D\to D$
be its supremum operator. Since C and K have the same multiplicative monoid,
![]() ${\mathcal{C}} C = {\mathcal{C}} K$
, so let
${\mathcal{C}} C = {\mathcal{C}} K$
, so let
![]() ${\textstyle{\sum'}}:{\mathcal{C}} K\to K$
be the supremum operator of the
${\textstyle{\sum'}}:{\mathcal{C}} K\to K$
be the supremum operator of the
![]() ${\mathcal{C}}$
-dioid C. We show that the
${\mathcal{C}}$
-dioid C. We show that the
![]() ${\mathcal{R}}$
-morphism
${\mathcal{R}}$
-morphism
![]() $\top_1$
of the tensor product
$\top_1$
of the tensor product
is a surjective
![]() ${\mathcal{C}}$
-morphism
${\mathcal{C}}$
-morphism
![]() $\top_1:C \to D$
, and its inverse
$\top_1:C \to D$
, and its inverse
![]() $m\otimes 1 \mapsto m$
is a
$m\otimes 1 \mapsto m$
is a
![]() ${\mathcal{C}}$
-morphism
${\mathcal{C}}$
-morphism
![]() $j:D\to C$
.
$j:D\to C$
.
With
![]() $\eta:K\to {\mathcal{C}} K$
,
$\eta:K\to {\mathcal{C}} K$
,
![]() $\eta(m)=\{m\}$
for
$\eta(m)=\{m\}$
for
![]() $m\in K$
, we have
$m\in K$
, we have
and consider the following diagram:

To show that
![]() $\top_1:K\to D$
is a
$\top_1:K\to D$
is a
![]() ${\mathcal{C}}$
-morphism, we must show that for every
${\mathcal{C}}$
-morphism, we must show that for every
![]() $L\in{\mathcal{C}} K$
,
$L\in{\mathcal{C}} K$
,
Clearly,
![]() $(\sum'L)\otimes 1$
is an upper bound of
$(\sum'L)\otimes 1$
is an upper bound of
![]() $\left\{\,m\otimes 1\,\mid\,m\in L\,\right\} = \widetilde{\top_1}(L)$
, so
$\left\{\,m\otimes 1\,\mid\,m\in L\,\right\} = \widetilde{\top_1}(L)$
, so
For the reverse inequation
![]() $\widehat L \geq (\sum'L)\otimes 1$
, recall that
$\widehat L \geq (\sum'L)\otimes 1$
, recall that
![]() $C_2' = {\mathcal{R}}\Delta_2^*/\rho_2$
embeds into the polycyclic
$C_2' = {\mathcal{R}}\Delta_2^*/\rho_2$
embeds into the polycyclic
![]() ${\mathcal{C}}$
-dioid
${\mathcal{C}}$
-dioid
![]() $C_{2,{\mathcal{C}}}' = {\mathcal{C}}\Delta_2^*/\rho_2$
of Section 2.2. Consider the tensor product
$C_{2,{\mathcal{C}}}' = {\mathcal{C}}\Delta_2^*/\rho_2$
of Section 2.2. Consider the tensor product
in the category of
![]() ${\mathcal{C}}$
-dioids. Since
${\mathcal{C}}$
-dioids. Since
![]() $\top_1'$
is a
$\top_1'$
is a
![]() ${\mathcal{C}}$
-morphism,
${\mathcal{C}}$
-morphism,
where we write 1’ for the unit in
![]() $C_{2,{\mathcal{C}}}'$
,
$C_{2,{\mathcal{C}}}'$
,
![]() $\top_1'(c)= c\otimes'1'$
for
$\top_1'(c)= c\otimes'1'$
for
![]() $c\in C$
, and on the right,
$c\in C$
, and on the right,
![]() $\sum'$
also for the supremum operator of
$\sum'$
also for the supremum operator of
![]() $C\mathop{\otimes_{\mathcal{C}}} C_{2,{\mathcal{C}}}'$
. Combined with the identity from K to C, the embedding of
$C\mathop{\otimes_{\mathcal{C}}} C_{2,{\mathcal{C}}}'$
. Combined with the identity from K to C, the embedding of
![]() $C_2'$
into
$C_2'$
into
![]() $C_{2,{\mathcal{C}}}'$
gives a monotone embedding
$C_{2,{\mathcal{C}}}'$
gives a monotone embedding
![]() ${\mathcal{R}}$
-morphism
${\mathcal{R}}$
-morphism
![]() $h:K\mathop{\otimes_{\mathcal{R}}} C_2' \to C\mathop{\otimes_{\mathcal{C}}}C_{2,{\mathcal{C}}}'$
. Therefore,
$h:K\mathop{\otimes_{\mathcal{R}}} C_2' \to C\mathop{\otimes_{\mathcal{C}}}C_{2,{\mathcal{C}}}'$
. Therefore,
 \begin{eqnarray*} h\left(\left({\textstyle{\sum'}} L\right)\otimes 1\right) &=& \left({\textstyle{\sum'}} L\right)\otimes' 1'\\ &=& {\textstyle{\displaystyle\sum}'}\left\{\,m\otimes' 1'\,\mid\,m\in L\,\right\}\\ &=& {\textstyle{\displaystyle\sum}'}\left\{\,h(m\otimes 1)\,\mid\,m\in L\,\right\}\\ &=& {\textstyle{\displaystyle\sum}'}\,\widetilde{h}(\widetilde{\top_1}(L))\\ &\leq& h(\widehat L),\end{eqnarray*}
\begin{eqnarray*} h\left(\left({\textstyle{\sum'}} L\right)\otimes 1\right) &=& \left({\textstyle{\sum'}} L\right)\otimes' 1'\\ &=& {\textstyle{\displaystyle\sum}'}\left\{\,m\otimes' 1'\,\mid\,m\in L\,\right\}\\ &=& {\textstyle{\displaystyle\sum}'}\left\{\,h(m\otimes 1)\,\mid\,m\in L\,\right\}\\ &=& {\textstyle{\displaystyle\sum}'}\,\widetilde{h}(\widetilde{\top_1}(L))\\ &\leq& h(\widehat L),\end{eqnarray*}
where the inequation holds since
![]() $\widehat L$
is an upper bound of
$\widehat L$
is an upper bound of
![]() $\widetilde{\top_1}(L)$
. Together with
$\widetilde{\top_1}(L)$
. Together with
![]() $\widehat L\leq (\sum' L)\otimes 1$
, this gives
$\widehat L\leq (\sum' L)\otimes 1$
, this gives
![]() $h((\sum' L)\otimes 1) = h(\widehat L)$
, and as h is injective, (13). So
$h((\sum' L)\otimes 1) = h(\widehat L)$
, and as h is injective, (13). So
![]() $\top_1:K \to D$
is a
$\top_1:K \to D$
is a
![]() ${\mathcal{C}}$
-morphism.
${\mathcal{C}}$
-morphism.
It follows that
![]() $\widehat{\,\cdot\,} = \top_1\circ \sum' : {\mathcal{C}} K \to D$
is a
$\widehat{\,\cdot\,} = \top_1\circ \sum' : {\mathcal{C}} K \to D$
is a
![]() ${\mathcal{C}}$
-morphism, because
${\mathcal{C}}$
-morphism, because
![]() ${\textstyle{\sum'}}:{\mathcal{C}} C\to C$
and
${\textstyle{\sum'}}:{\mathcal{C}} C\to C$
and
![]() $\top_1:C\to D$
are
$\top_1:C\to D$
are
![]() ${\mathcal{C}}$
-morphisms. Since
${\mathcal{C}}$
-morphisms. Since
![]() $\widehat{\,\cdot\,}:{\mathcal{C}} K\to D$
is surjective, so is
$\widehat{\,\cdot\,}:{\mathcal{C}} K\to D$
is surjective, so is
![]() $\top_1:K\to D$
, by (13); hence,
$\top_1:K\to D$
, by (13); hence,
It remains to be shown that its inverse
![]() $j:D\to K$
,
$j:D\to K$
,
![]() $m\otimes 1\mapsto m$
, is a
$m\otimes 1\mapsto m$
, is a
![]() ${\mathcal{C}}$
-morphism. The surjective homomorphism
${\mathcal{C}}$
-morphism. The surjective homomorphism
![]() $\widehat{\,\cdot\,}:{\mathcal{C}} K\to D$
lifts to a surjective homomorphism from
$\widehat{\,\cdot\,}:{\mathcal{C}} K\to D$
lifts to a surjective homomorphism from
![]() ${\mathcal{C}}{\mathcal{C}} K$
to
${\mathcal{C}}{\mathcal{C}} K$
to
![]() ${\mathcal{C}} D$
. Hence for
${\mathcal{C}} D$
. Hence for
![]() $V\in {\mathcal{C}} D,$
there is
$V\in {\mathcal{C}} D,$
there is
![]() $U\in {\mathcal{C}}{\mathcal{C}} K$
with
$U\in {\mathcal{C}}{\mathcal{C}} K$
with
![]() $V=\left\{\,\widehat L\,\mid\,L\in U\,\right\}$
, and since
$V=\left\{\,\widehat L\,\mid\,L\in U\,\right\}$
, and since
![]() $\bigcup U \in {\mathcal{C}} K$
and
$\bigcup U \in {\mathcal{C}} K$
and
![]() $\widehat{\,\cdot\,}$
is a
$\widehat{\,\cdot\,}$
is a
![]() ${\mathcal{C}}$
-morphism,
${\mathcal{C}}$
-morphism,
by (13). By applying j and using (13) for each
![]() $L\in U$
,
$L\in U$
,
 \begin{eqnarray*} j\left(\sum V\right) &=& {\textstyle{\displaystyle\sum}'}\bigcup U\\ &=&{\textstyle{\displaystyle\sum}'}\left\{\,{\textstyle{\displaystyle\sum}'} L\,\mid\,L\in U\,\right\}\\ &=& {\textstyle{\displaystyle\sum}'}\left\{\,j(({\textstyle{\displaystyle\sum}'} L)\otimes 1)\,\mid\,L\in U\,\right\}\\ &=& {\textstyle{\displaystyle\sum}'}\left\{\,j(\widehat L)\,\mid\,L\in U\,\right\}\\ &=& {\textstyle{\displaystyle\sum}'}\left\{\,j(v)\,\mid\,v\in V\,\right\}.\end{eqnarray*}
\begin{eqnarray*} j\left(\sum V\right) &=& {\textstyle{\displaystyle\sum}'}\bigcup U\\ &=&{\textstyle{\displaystyle\sum}'}\left\{\,{\textstyle{\displaystyle\sum}'} L\,\mid\,L\in U\,\right\}\\ &=& {\textstyle{\displaystyle\sum}'}\left\{\,j(({\textstyle{\displaystyle\sum}'} L)\otimes 1)\,\mid\,L\in U\,\right\}\\ &=& {\textstyle{\displaystyle\sum}'}\left\{\,j(\widehat L)\,\mid\,L\in U\,\right\}\\ &=& {\textstyle{\displaystyle\sum}'}\left\{\,j(v)\,\mid\,v\in V\,\right\}.\end{eqnarray*}
Therefore,
![]() $j:D\to K$
is
$j:D\to K$
is
![]() ${\mathcal{C}}$
-continuous, i.e. preserves suprema of
${\mathcal{C}}$
-continuous, i.e. preserves suprema of
![]() ${\mathcal{C}}$
-sets.
${\mathcal{C}}$
-sets. ![]()
Under the assumptions of Theorem 32,
![]() $\left\{\,(L,\{{\textstyle{\displaystyle\sum}'} L\})\,\mid\,L\in{\mathcal{C}} K\,\right\}\subseteq \ker(\widehat{\,\cdot\,})$
, because by (13)
$\left\{\,(L,\{{\textstyle{\displaystyle\sum}'} L\})\,\mid\,L\in{\mathcal{C}} K\,\right\}\subseteq \ker(\widehat{\,\cdot\,})$
, because by (13)
We can now prove our second main result, which will imply that
![]() ${\mathcal{C}}K/\ker(\widehat{\,\cdot\,}) \simeq {Q_{\mathcal{R}}^{\mathcal{C}}}(K)$
:
${\mathcal{C}}K/\ker(\widehat{\,\cdot\,}) \simeq {Q_{\mathcal{R}}^{\mathcal{C}}}(K)$
:
Theorem 33 (Algebraic representation of
![]() ${\mathcal{C}}$
-closure) For any
${\mathcal{C}}$
-closure) For any
![]() ${\mathcal{R}}$
-dioid K, there is a
${\mathcal{R}}$
-dioid K, there is a
![]() ${\mathcal{C}}$
-isomorphism
${\mathcal{C}}$
-isomorphism
Proof. It is sufficient to prove that
![]() $D:=Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is a
$D:=Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is a
![]() ${\mathcal{C}}$
-completion of K. Let
${\mathcal{C}}$
-completion of K. Let
![]() $\eta:K\to D$
be the embedding obtained from
$\eta:K\to D$
be the embedding obtained from
![]() $\top_1 :K\to K\mathop{\otimes_{\mathcal{R}}}{C_2'}$
,
$\top_1 :K\to K\mathop{\otimes_{\mathcal{R}}}{C_2'}$
,
and
![]() $f:K\to C$
an
$f:K\to C$
an
![]() ${\mathcal{R}}$
-morphism to a
${\mathcal{R}}$
-morphism to a
![]() ${\mathcal{C}}$
-dioid C. Define
${\mathcal{C}}$
-dioid C. Define
![]() $\bar f : D\to C$
by
$\bar f : D\to C$
by
We prove later that
![]() $\bar f$
is well-defined and first show the remaining properties.
$\bar f$
is well-defined and first show the remaining properties.
![]() $f = \bar f \circ \eta$
: for
$f = \bar f \circ \eta$
: for
![]() $m\in K$
,
$m\in K$
,
![]() $\bar f(\eta(m)) = \bar f(\sum\{m\otimes 1\}) = \bar f(\widehat{\{m\}}) = \sum\{f(m)\} = f(m)$
.
$\bar f(\eta(m)) = \bar f(\sum\{m\otimes 1\}) = \bar f(\widehat{\{m\}}) = \sum\{f(m)\} = f(m)$
.
![]() $\bar f$
is a monotone homomorphism:
$\bar f$
is a monotone homomorphism:
![]() $\bar f(1) = \bar f(\widehat{\{1\}}) =\sum\{f(1)\} = f(1) = 1$
, and since
$\bar f(1) = \bar f(\widehat{\{1\}}) =\sum\{f(1)\} = f(1) = 1$
, and since
![]() $\widehat{\,\cdot\,}:{\mathcal{C}} K\to D$
is a homomorphism and
$\widehat{\,\cdot\,}:{\mathcal{C}} K\to D$
is a homomorphism and
![]() $\sum\circ \widetilde f:{\mathcal{C}} K\to C$
is
$\sum\circ \widetilde f:{\mathcal{C}} K\to C$
is
![]() ${\mathcal{C}}$
-distributive,
${\mathcal{C}}$
-distributive,
![]() $\bar f$
is
$\bar f$
is
![]() ${\mathcal{C}}$
-continuous: Suppose
${\mathcal{C}}$
-continuous: Suppose
![]() $V\in{\mathcal{C}} D$
. Since
$V\in{\mathcal{C}} D$
. Since
![]() $\widehat{\,\cdot\,}:{\mathcal{C}} K\to D$
is a surjective homomorphism, so is its lifting to
$\widehat{\,\cdot\,}:{\mathcal{C}} K\to D$
is a surjective homomorphism, so is its lifting to
![]() ${\mathcal{C}}{\mathcal{C}} K\to {\mathcal{C}} D;$
hence, there is
${\mathcal{C}}{\mathcal{C}} K\to {\mathcal{C}} D;$
hence, there is
![]() $U\in {\mathcal{C}}{\mathcal{C}} K$
such that
$U\in {\mathcal{C}}{\mathcal{C}} K$
such that
![]() $V= \left\{\,\widehat L\,\mid\,L\in U\,\right\}\in {\mathcal{C}} D$
. Therefore,
$V= \left\{\,\widehat L\,\mid\,L\in U\,\right\}\in {\mathcal{C}} D$
. Therefore,
 \begin{eqnarray*} \bar f\left(\sum V\right) &=& \bar f\left(\sum\left\{\,m\otimes 1\,\mid\,m\in \bigcup U\,\right\}\right)\\ &=& \bar f\left(\widehat{\bigcup U}\right)\\ &=& \sum\widetilde f\left(\bigcup U\right)\\ &=& \sum\bigcup\left\{\,\widetilde f(L)\,\mid\,L\in U\,\right\}\\ &=& \sum\left\{\,\bar f(\widehat L)\,\mid\,L\in U\,\right\}.\\ &=& \sum\left\{\,\bar f(v)\,\mid\,v\in V\,\right\}.\end{eqnarray*}
\begin{eqnarray*} \bar f\left(\sum V\right) &=& \bar f\left(\sum\left\{\,m\otimes 1\,\mid\,m\in \bigcup U\,\right\}\right)\\ &=& \bar f\left(\widehat{\bigcup U}\right)\\ &=& \sum\widetilde f\left(\bigcup U\right)\\ &=& \sum\bigcup\left\{\,\widetilde f(L)\,\mid\,L\in U\,\right\}\\ &=& \sum\left\{\,\bar f(\widehat L)\,\mid\,L\in U\,\right\}.\\ &=& \sum\left\{\,\bar f(v)\,\mid\,v\in V\,\right\}.\end{eqnarray*}
![]() $\bar f$
is well-defined: Suppose
$\bar f$
is well-defined: Suppose
![]() $L,L'\in{\mathcal{C}} K$
and
$L,L'\in{\mathcal{C}} K$
and
![]() $\widehat{L}=\widehat{L'}$
. We must show
$\widehat{L}=\widehat{L'}$
. We must show
Let
![]() $K' = {Q_{\mathcal{C}}^{\mathcal{R}}}(C)$
be the restriction of C to an
$K' = {Q_{\mathcal{C}}^{\mathcal{R}}}(C)$
be the restriction of C to an
![]() ${\mathcal{R}}$
-dioid,
${\mathcal{R}}$
-dioid,
its tensor product with
![]() $C_2'$
in
$C_2'$
in
![]() ${\mathbb{D}}{\mathcal{R}}$
, and
${\mathbb{D}}{\mathcal{R}}$
, and
![]() $D' := Z_{C_2'}({K'} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
. By Theorem 32,
$D' := Z_{C_2'}({K'} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
. By Theorem 32,
![]() $\top_1' : C \to D'$
is a
$\top_1' : C \to D'$
is a
![]() ${\mathcal{C}}$
-isomorphism, with inverse
${\mathcal{C}}$
-isomorphism, with inverse
![]() $j:D'\to C$
. We write
$j:D'\to C$
. We write
![]() $\top_1'(c) =c\otimes' 1$
for
$\top_1'(c) =c\otimes' 1$
for
![]() $c\in K'$
and
$c\in K'$
and
![]() $\sum'$
for the least upper bound operator of D’ or
$\sum'$
for the least upper bound operator of D’ or
![]() $K'\mathop{\otimes_{\mathcal{R}}} C_2'$
.
$K'\mathop{\otimes_{\mathcal{R}}} C_2'$
.
Consider the commuting
![]() ${\mathcal{R}}$
-morphisms
${\mathcal{R}}$
-morphisms
![]() $f'=\top_1'\circ f$
and
$f'=\top_1'\circ f$
and
![]() $g'=\top_2'$
shown in
$g'=\top_2'$
shown in

Let
![]() $h_{f',g'}$
be the
$h_{f',g'}$
be the
![]() ${\mathcal{R}}$
-morphism with
${\mathcal{R}}$
-morphism with
![]() $f'=h_{f',g'}\circ \top_1$
and
$f'=h_{f',g'}\circ \top_1$
and
![]() $g'=h_{f',g'}\circ \top_2$
. For
$g'=h_{f',g'}\circ \top_2$
. For
![]() $R\in{\mathcal{R}}(K\times C_2')$
, put
$R\in{\mathcal{R}}(K\times C_2')$
, put
![]() $R_f = \left\{\,(f(m),c)\,\mid\,(m,c)\in R\,\right\}\in{\mathcal{R}}(K'\times C_2')$
. Then,
$R_f = \left\{\,(f(m),c)\,\mid\,(m,c)\in R\,\right\}\in{\mathcal{R}}(K'\times C_2')$
. Then,
 \begin{eqnarray*} h_{f',g'}([R]) &=& h_{f',g'}\left(\sum\left\{\,m\otimes c\,\mid\,(m,c)\in R\,\right\}\right)\\ &=& \sum\left\{\,f'(m)g'(c)\,\mid\,(m,c)\in R\,\right\}\\ &=& \sum\left\{\,(f(m)\otimes 1)(1'\otimes c)\,\mid\,(m,c)\in R\,\right\}\\ &=& \sum\left\{\,f(m)\otimes c\,\mid\,(m,c)\in R\,\right\}\\ &=& [R_f].\end{eqnarray*}
\begin{eqnarray*} h_{f',g'}([R]) &=& h_{f',g'}\left(\sum\left\{\,m\otimes c\,\mid\,(m,c)\in R\,\right\}\right)\\ &=& \sum\left\{\,f'(m)g'(c)\,\mid\,(m,c)\in R\,\right\}\\ &=& \sum\left\{\,(f(m)\otimes 1)(1'\otimes c)\,\mid\,(m,c)\in R\,\right\}\\ &=& \sum\left\{\,f(m)\otimes c\,\mid\,(m,c)\in R\,\right\}\\ &=& [R_f].\end{eqnarray*}
The restriction of
![]() $h_{f',g'}$
to
$h_{f',g'}$
to
![]() $D\subseteq K\mathop{\otimes_{\mathcal{R}}} C_2'$
clearly is an
$D\subseteq K\mathop{\otimes_{\mathcal{R}}} C_2'$
clearly is an
![]() ${\mathcal{R}}$
-morphism
${\mathcal{R}}$
-morphism
![]() $h':D\to D'$
. The situation is visualized by the following diagram:
$h':D\to D'$
. The situation is visualized by the following diagram:

By Lemma 29, there are
![]() $R,R'\in {\mathcal{R}}(K\times C_2')$
with
$R,R'\in {\mathcal{R}}(K\times C_2')$
with
![]() $R,R'\subseteq K\times\{0,1\}$
and
$R,R'\subseteq K\times\{0,1\}$
and
![]() $L=\left\{\,m\,\mid\,(m,1)\in R\,\right\}$
,
$L=\left\{\,m\,\mid\,(m,1)\in R\,\right\}$
,
![]() $L'=\left\{\,m\,\mid\,(m,1)\in R'\,\right\}$
, so
$L'=\left\{\,m\,\mid\,(m,1)\in R'\,\right\}$
, so
By an application of
![]() $h_{f',g'}$
,
$h_{f',g'}$
,
![]() $[R_f]=[R_f']$
. Using
$[R_f]=[R_f']$
. Using
![]() $\widetilde f(L)\in {\mathcal{C}} K'$
, we get
$\widetilde f(L)\in {\mathcal{C}} K'$
, we get
 \begin{equation*} \begin{array}{rcl@{\qquad}l} [R_f] &=& \widehat{\widetilde f(L)}'\\ &=& {\textstyle{\displaystyle\sum}'}\left\{\,f(m)\otimes' c\,\mid\,(m,c)\in R\,\right\} &\\ &=& {\textstyle{\displaystyle\sum}'}\left\{\,f(m)\otimes' 1\,\mid\,(m,1)\in R\,\right\} & (R\subseteq K\times \{0,1\})\\ &=&{\textstyle{\displaystyle\sum}'}\left\{\,f(m)\otimes' 1\,\mid\,m\in L\,\right\} & (L = \left\{\,m\,\mid\,(m,1)\in R\,\right\})\\ &=& \left({\textstyle{\displaystyle\sum}'}{\widetilde f}(L)\right)\otimes' 1 & (\textrm{by (13) on {D}'}).\end{array}\end{equation*}
\begin{equation*} \begin{array}{rcl@{\qquad}l} [R_f] &=& \widehat{\widetilde f(L)}'\\ &=& {\textstyle{\displaystyle\sum}'}\left\{\,f(m)\otimes' c\,\mid\,(m,c)\in R\,\right\} &\\ &=& {\textstyle{\displaystyle\sum}'}\left\{\,f(m)\otimes' 1\,\mid\,(m,1)\in R\,\right\} & (R\subseteq K\times \{0,1\})\\ &=&{\textstyle{\displaystyle\sum}'}\left\{\,f(m)\otimes' 1\,\mid\,m\in L\,\right\} & (L = \left\{\,m\,\mid\,(m,1)\in R\,\right\})\\ &=& \left({\textstyle{\displaystyle\sum}'}{\widetilde f}(L)\right)\otimes' 1 & (\textrm{by (13) on {D}'}).\end{array}\end{equation*}
Likewise,
![]() $[R_f'] = \widehat{\widetilde f(L')}'= (\sum\widetilde f (L')) \otimes' 1$
, and so
$[R_f'] = \widehat{\widetilde f(L')}'= (\sum\widetilde f (L')) \otimes' 1$
, and so
(Hence,
![]() $h'\circ \widehat{\,\cdot\,}\, =\, \widehat{\,\cdot\,}'\circ\widetilde f$
is a
$h'\circ \widehat{\,\cdot\,}\, =\, \widehat{\,\cdot\,}'\circ\widetilde f$
is a
![]() ${\mathcal{C}}$
-morphism.) An application of j gives (14).
${\mathcal{C}}$
-morphism.) An application of j gives (14).
![]() $\bar f$
is the unique
$\bar f$
is the unique
![]() ${\mathcal{C}}$
-morphism
${\mathcal{C}}$
-morphism
![]() $h:D\to C$
with
$h:D\to C$
with
![]() $f = h\circ \eta$
: Suppose h is such a
$f = h\circ \eta$
: Suppose h is such a
![]() ${\mathcal{C}}$
-morphism and e an element of D. By Lemma 30 there is
${\mathcal{C}}$
-morphism and e an element of D. By Lemma 30 there is
![]() $L\in{\mathcal{C}} K$
such that
$L\in{\mathcal{C}} K$
such that
![]() $e=\widehat L =\sum\!\left\{\,\!m\otimes 1\,\mid\,m\in L\!\,\right\}$
; hence,
$e=\widehat L =\sum\!\left\{\,\!m\otimes 1\,\mid\,m\in L\!\,\right\}$
; hence,
 \begin{eqnarray*} h(e) &=& h(\widehat L)\\ &=& h\left(\sum\left\{\,m\otimes 1\,\mid\,m\in L\,\right\}\right)\\ &=& \sum\left\{\,h(m\otimes 1)\,\mid\,m\in L\,\right\}\\ &=& \sum\left\{\,h(\eta(m))\,\mid\,m\in L\,\right\}\\ &=& \sum\left\{\,f(m)\,\mid\,m\in L\,\right\}\\ &=& \bar f(\widehat{L}) = \bar f(e).\end{eqnarray*}
\begin{eqnarray*} h(e) &=& h(\widehat L)\\ &=& h\left(\sum\left\{\,m\otimes 1\,\mid\,m\in L\,\right\}\right)\\ &=& \sum\left\{\,h(m\otimes 1)\,\mid\,m\in L\,\right\}\\ &=& \sum\left\{\,h(\eta(m))\,\mid\,m\in L\,\right\}\\ &=& \sum\left\{\,f(m)\,\mid\,m\in L\,\right\}\\ &=& \bar f(\widehat{L}) = \bar f(e).\end{eqnarray*}
Therefore,
![]() $h=\bar f$
.
$h=\bar f$
. ![]()
Corollary 34. For any
![]() ${\mathcal{R}}$
-dioid K, the
${\mathcal{R}}$
-dioid K, the
![]() ${\mathcal{C}}$
-closure of K is
${\mathcal{C}}$
-closure of K is
![]() ${\mathcal{C}} K/\ker({\widehat{\,\cdot\,}})$
.
${\mathcal{C}} K/\ker({\widehat{\,\cdot\,}})$
.
Proof. By Theorem 33,
![]() $D := Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is the
$D := Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is the
![]() ${\mathcal{C}}$
-closure of K, so we must show that
${\mathcal{C}}$
-closure of K, so we must show that
![]() ${\mathcal{C}} K/\ker(\widehat{\,\cdot\,})$
is a
${\mathcal{C}} K/\ker(\widehat{\,\cdot\,})$
is a
![]() ${\mathcal{C}}$
-dioid and there is a
${\mathcal{C}}$
-dioid and there is a
![]() ${\mathcal{C}}$
-isomorphism between D and
${\mathcal{C}}$
-isomorphism between D and
![]() ${\mathcal{C}}K/\ker(\widehat{\,\cdot\,})$
. By Lemma 30,
${\mathcal{C}}K/\ker(\widehat{\,\cdot\,})$
. By Lemma 30,
![]() $\widehat{\,\cdot\,}:{\mathcal{C}} K\to D$
is a monotone and surjective homomorphism between
$\widehat{\,\cdot\,}:{\mathcal{C}} K\to D$
is a monotone and surjective homomorphism between
![]() ${\mathcal{C}}$
-dioids. It is a
${\mathcal{C}}$
-dioids. It is a
![]() ${\mathcal{C}}$
-morphism, because
${\mathcal{C}}$
-morphism, because
![]() $\widehat{\bigcup U} = \sum\left\{\,\widehat L\,\mid\,L\in U\,\right\}$
for
$\widehat{\bigcup U} = \sum\left\{\,\widehat L\,\mid\,L\in U\,\right\}$
for
![]() $U\in{\mathcal{C}}{\mathcal{C}} K$
. Hence, its kernel
$U\in{\mathcal{C}}{\mathcal{C}} K$
. Hence, its kernel
![]() $\ker(\widehat{\,\cdot\,})$
is a
$\ker(\widehat{\,\cdot\,})$
is a
![]() ${\mathcal{C}}$
-congruence on
${\mathcal{C}}$
-congruence on
![]() ${\mathcal{C}} K$
, and so
${\mathcal{C}} K$
, and so
![]() ${\mathcal{C}} K/\ker(\widehat{\,\cdot\,})$
is a
${\mathcal{C}} K/\ker(\widehat{\,\cdot\,})$
is a
![]() ${\mathcal{C}}$
-dioid. Let us verify that the bijection between
${\mathcal{C}}$
-dioid. Let us verify that the bijection between
![]() ${\mathcal{C}}K/\ker(\widehat{\,\cdot\,})$
and D is a
${\mathcal{C}}K/\ker(\widehat{\,\cdot\,})$
and D is a
![]() ${\mathcal{C}}$
-isomorphism. In the one direction, the mapping
${\mathcal{C}}$
-isomorphism. In the one direction, the mapping
![]() $f:{\mathcal{C}} K/\ker(\widehat{\,\cdot\,})\to D$
, well-defined by
$f:{\mathcal{C}} K/\ker(\widehat{\,\cdot\,})\to D$
, well-defined by
![]() $f(L/\ker(\widehat{\,\cdot\,})) = \widehat{L}$
for
$f(L/\ker(\widehat{\,\cdot\,})) = \widehat{L}$
for
![]() $L\in{\mathcal{C}} K$
, is a
$L\in{\mathcal{C}} K$
, is a
![]() ${\mathcal{C}}$
-morphism, since for
${\mathcal{C}}$
-morphism, since for
![]() $V\in{\mathcal{C}}({\mathcal{C}} K/\ker(\widehat{\,\cdot\,}))$
there is
$V\in{\mathcal{C}}({\mathcal{C}} K/\ker(\widehat{\,\cdot\,}))$
there is
![]() $U\in {\mathcal{C}} {\mathcal{C}} K$
such that
$U\in {\mathcal{C}} {\mathcal{C}} K$
such that
![]() $V= \left\{\,L/\ker(\widehat{\,\cdot\,})\,\mid\,L\in U\,\right\}$
, and by the definition of
$V= \left\{\,L/\ker(\widehat{\,\cdot\,})\,\mid\,L\in U\,\right\}$
, and by the definition of
![]() $\sum$
on quotients,
$\sum$
on quotients,
![]() $\sum V= (\bigcup U)/\ker(\widehat{\,\cdot\,})$
, so
$\sum V= (\bigcup U)/\ker(\widehat{\,\cdot\,})$
, so
![]() $f(\sum V) = \widehat{\bigcup U} =\sum\left\{\,\widehat L\,\mid\,L\in U\,\right\}=\sum\widetilde f(V)$
. In the other direction, by Lemmas 31 and 29, elements of D are congruence classes [R] of sets
$f(\sum V) = \widehat{\bigcup U} =\sum\left\{\,\widehat L\,\mid\,L\in U\,\right\}=\sum\widetilde f(V)$
. In the other direction, by Lemmas 31 and 29, elements of D are congruence classes [R] of sets
![]() $R\in{\mathcal{R}}(K\times C_2')$
with
$R\in{\mathcal{R}}(K\times C_2')$
with
![]() $R\subseteq K\times\{0,1\}$
, such that
$R\subseteq K\times\{0,1\}$
, such that
![]() $[R]=\widehat{L_R}$
for
$[R]=\widehat{L_R}$
for
![]() $L_R :=\left\{\,m\,\mid\,(m,1)\in R\,\right\} \in {\mathcal{C}} K$
. Hence, a map
$L_R :=\left\{\,m\,\mid\,(m,1)\in R\,\right\} \in {\mathcal{C}} K$
. Hence, a map
![]() $g:D\to {\mathcal{C}}K/\ker(\widehat{\,\cdot\,})$
is well-defined by
$g:D\to {\mathcal{C}}K/\ker(\widehat{\,\cdot\,})$
is well-defined by
and obviously g and f are inverses of each other. To see that g is a
![]() ${\mathcal{C}}$
-morphism, suppose
${\mathcal{C}}$
-morphism, suppose
![]() $V\in {\mathcal{C}} D$
. There is
$V\in {\mathcal{C}} D$
. There is
![]() $U\in{\mathcal{C}}{\mathcal{C}} K$
such that
$U\in{\mathcal{C}}{\mathcal{C}} K$
such that
![]() $V= \left\{\,\widehat L\,\mid\,L\in U\,\right\}$
, and
$V= \left\{\,\widehat L\,\mid\,L\in U\,\right\}$
, and
![]() $\sum V = \widehat{\bigcup U}$
. There is
$\sum V = \widehat{\bigcup U}$
. There is
![]() $R\in{\mathcal{R}}(K\times C_2')$
with
$R\in{\mathcal{R}}(K\times C_2')$
with
![]() $R\subseteq K\times\{0,1\}$
and
$R\subseteq K\times\{0,1\}$
and
![]() $\widehat{\bigcup U} = [R]=\widehat{L_R}$
, and so
$\widehat{\bigcup U} = [R]=\widehat{L_R}$
, and so
using suitable
![]() $R_L\in {\mathcal{R}}(K\times C_2')$
with
$R_L\in {\mathcal{R}}(K\times C_2')$
with
![]() $R_L\subseteq K\times\{0,1\}$
and
$R_L\subseteq K\times\{0,1\}$
and
![]() $\widehat L = [R_L]$
for the last step.
$\widehat L = [R_L]$
for the last step. ![]()
7. Conclusion
The algebraic abstraction of the regular subsets
![]() ${\mathcal{R}} M$
and the context-free subsets
${\mathcal{R}} M$
and the context-free subsets
![]() ${\mathcal{C}} M$
of a monoid M are the categories of
${\mathcal{C}} M$
of a monoid M are the categories of
![]() ${\mathcal{R}}$
-dioids or
${\mathcal{R}}$
-dioids or
![]() ${}^*$
-continuous Kleene algebras and
${}^*$
-continuous Kleene algebras and
![]() ${\mathcal{C}}$
-dioids or
${\mathcal{C}}$
-dioids or
![]() $\mu$
-continuous Chomsky algebras. Just as
$\mu$
-continuous Chomsky algebras. Just as
![]() ${\mathcal{C}} M$
is the closure of
${\mathcal{C}} M$
is the closure of
![]() ${\mathcal{R}}M$
under a well-behaved least fixed-point operator
${\mathcal{R}}M$
under a well-behaved least fixed-point operator
![]() $\mu$
, each
$\mu$
, each
![]() ${\mathcal{R}}$
-dioid K has a closure
${\mathcal{R}}$
-dioid K has a closure
![]() $\overline K$
as
$\overline K$
as
![]() ${\mathcal{C}}$
-dioid, briefly called its fixed-point closure. We have shown that
${\mathcal{C}}$
-dioid, briefly called its fixed-point closure. We have shown that
![]() $\overline K$
can be represented in the product
$\overline K$
can be represented in the product
![]() $K\mathop{\otimes_{\mathcal{R}}} C_2'$
of K with
$K\mathop{\otimes_{\mathcal{R}}} C_2'$
of K with
![]() $C_2'$
in the category of
$C_2'$
in the category of
![]() ${\mathcal{R}}$
-dioids, where the polycyclic
${\mathcal{R}}$
-dioids, where the polycyclic
![]() ${\mathcal{R}}$
-dioid
${\mathcal{R}}$
-dioid
![]() $C_2'$
on two generators is a quotient of the regular sets
$C_2'$
on two generators is a quotient of the regular sets
![]() ${\mathcal{R}} \Delta_2^*$
over an alphabet
${\mathcal{R}} \Delta_2^*$
over an alphabet
![]() $\Delta_2=\{b,d,p,q\}$
of two pairs of brackets, b,d and p,q. Namely,
$\Delta_2=\{b,d,p,q\}$
of two pairs of brackets, b,d and p,q. Namely,
![]() $\overline K$
is isomorphic to the centralizer
$\overline K$
is isomorphic to the centralizer
![]() $Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
of
$Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
of
![]() $C_2'$
in
$C_2'$
in
![]() $K\mathop{\otimes_{\mathcal{R}}} C_2'$
, which, intuitively, consists of the sums over regular sets of elements
$K\mathop{\otimes_{\mathcal{R}}} C_2'$
, which, intuitively, consists of the sums over regular sets of elements
![]() $m\otimes c$
where
$m\otimes c$
where
![]() $m\in K$
and
$m\in K$
and
![]() $c\in C_2'$
is restricted to be 0 or 1.
$c\in C_2'$
is restricted to be 0 or 1.
This representation theorem is an algebraic form and categorical generalization of the classical Chomsky–Schützenberger theorem (and its reverse) of formal language theory. The latter reduces the set
![]() ${\mathcal{C}} X^*$
of context-free languages over a finite alphabet X to the set
${\mathcal{C}} X^*$
of context-free languages over a finite alphabet X to the set
![]() ${\mathcal{R}}(X\cup\Delta_2)^*$
of regular languages over
${\mathcal{R}}(X\cup\Delta_2)^*$
of regular languages over
![]() $X\cup\Delta_2$
, by means of intersection with the context-free Dyck language
$X\cup\Delta_2$
, by means of intersection with the context-free Dyck language
![]() $D_2(X)\in{\mathcal{C}}(X\cup\Delta_2)^*$
of balanced bracketed strings and the bracket-erasing homomorphism from
$D_2(X)\in{\mathcal{C}}(X\cup\Delta_2)^*$
of balanced bracketed strings and the bracket-erasing homomorphism from
![]() $(X\cup\Delta_2)^*$
to
$(X\cup\Delta_2)^*$
to
![]() $X^*$
. In the special case
$X^*$
. In the special case
![]() $K={\mathcal{R}} X^*$
with
$K={\mathcal{R}} X^*$
with
![]() $\overline K={\mathcal{C}} X^*$
, the representation theorem intuitively splits bracketed strings
$\overline K={\mathcal{C}} X^*$
, the representation theorem intuitively splits bracketed strings
![]() $u\in(X\cup\Delta_2)^*$
to pairs
$u\in(X\cup\Delta_2)^*$
to pairs
![]() $(w,t)\in X^*\times \Delta_2^*$
and performs the balance-checking and bracket-erasure within
$(w,t)\in X^*\times \Delta_2^*$
and performs the balance-checking and bracket-erasure within
![]() $C_2'$
by algebraically reducing the second component of
$C_2'$
by algebraically reducing the second component of
![]() $\{w\}\otimes \{t\} \in K\mathop{\otimes_{\mathcal{R}}} C_2'$
to 1 or 0, depending on whether t belongs to the pure Dyck language
$\{w\}\otimes \{t\} \in K\mathop{\otimes_{\mathcal{R}}} C_2'$
to 1 or 0, depending on whether t belongs to the pure Dyck language
![]() $D_2\in{\mathcal{C}}\Delta_2^*$
or not. The underlying part of deriving from
$D_2\in{\mathcal{C}}\Delta_2^*$
or not. The underlying part of deriving from
![]() $L\in {\mathcal{C}} X^*$
a suitable regular set R of strings
$L\in {\mathcal{C}} X^*$
a suitable regular set R of strings
![]() $u\in (X\cup\Delta_2)^*$
is as in the classical Chomsky–Schützenberger theorem (cf. Theorem 15). A finite automaton for
$u\in (X\cup\Delta_2)^*$
is as in the classical Chomsky–Schützenberger theorem (cf. Theorem 15). A finite automaton for
![]() $R\subseteq (X\cup\Delta_2)^*$
represents L in the sense that the words
$R\subseteq (X\cup\Delta_2)^*$
represents L in the sense that the words
![]() $u\in R$
evaluate in
$u\in R$
evaluate in
![]() ${\mathcal{R}} X^*\mathop{\otimes_{\mathcal{R}}} C_2'$
to 0 or to the elements
${\mathcal{R}} X^*\mathop{\otimes_{\mathcal{R}}} C_2'$
to 0 or to the elements
![]() $\{w\}\otimes 1$
with
$\{w\}\otimes 1$
with
![]() $w=h_{X^*}(u)\in L$
(cf. Figure 2).
$w=h_{X^*}(u)\in L$
(cf. Figure 2).
The algebra
![]() ${\mathcal{R}} X^*\mathop{\otimes_{\mathcal{R}}} C_2'$
is hoped to turn out useful to construct CFG-parsers for context-free languages over X, for example by simplifying the calculation of item-sets of LR-parsers.
${\mathcal{R}} X^*\mathop{\otimes_{\mathcal{R}}} C_2'$
is hoped to turn out useful to construct CFG-parsers for context-free languages over X, for example by simplifying the calculation of item-sets of LR-parsers.
Some remarks on the difference between using the bra-ket
![]() ${\mathcal{R}}$
-dioid
${\mathcal{R}}$
-dioid
![]() $C_2$
and the polycyclic
$C_2$
and the polycyclic
![]() ${\mathcal{R}}$
-dioid
${\mathcal{R}}$
-dioid
![]() $C_2'$
are in order. Theorem 5 of Hopkins and Leiß (Reference Hopkins and Leiß2018) announced that
$C_2'$
are in order. Theorem 5 of Hopkins and Leiß (Reference Hopkins and Leiß2018) announced that
![]() ${\mathcal{C}} M \simeq Z_{C_2}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2})$
for monoids M, indicating that “the equation
${\mathcal{C}} M \simeq Z_{C_2}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2})$
for monoids M, indicating that “the equation
![]() $db+qp=1$
not present in
$db+qp=1$
not present in
![]() $C_2'$
is needed to encode stack operations in
$C_2'$
is needed to encode stack operations in
![]() $C_2.$
” We here have shown that one can actually do without this equation and prove the stronger result
$C_2.$
” We here have shown that one can actually do without this equation and prove the stronger result
![]() ${\mathcal{C}} M\simeq Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
. One may obtain
${\mathcal{C}} M\simeq Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
. One may obtain
![]() $C_2$
as the quotient
$C_2$
as the quotient
![]() $C_2'/{\left\langle {db+qp=1}\right\rangle}$
of
$C_2'/{\left\langle {db+qp=1}\right\rangle}$
of
![]() $C_2'$
by the
$C_2'$
by the
![]() ${\mathcal{R}}$
-congruence generated by the completeness equation. The quotient map is not injective, but its extension to
${\mathcal{R}}$
-congruence generated by the completeness equation. The quotient map is not injective, but its extension to
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
apparently does not identify different members of
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
apparently does not identify different members of
![]() $Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
, so the announced claim with
$Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
, so the announced claim with
![]() $C_2$
should follow.
$C_2$
should follow.
The motivation for writing this article came from an effort to understand Hopkins’ unpublished proof that the fixed-point closure
![]() $\overline K$
of an
$\overline K$
of an
![]() ${\mathcal{R}}$
-dioid K can be algebraically represented by
${\mathcal{R}}$
-dioid K can be algebraically represented by
![]() $Z_{C_2}({K} \mathop{\otimes_{\mathcal{R}}} {C_2})$
. An inspection of the proof showed that the completeness assumption
$Z_{C_2}({K} \mathop{\otimes_{\mathcal{R}}} {C_2})$
. An inspection of the proof showed that the completeness assumption
![]() $db+qp=1$
of
$db+qp=1$
of
![]() $C_2$
was not used for the analog
$C_2$
was not used for the analog
![]() $\overline K \subseteq Z_{C_2}({K} \mathop{\otimes_{\mathcal{R}}} {C_2})$
of the Chomsky–Schützenberger theorem. For the reverse
$\overline K \subseteq Z_{C_2}({K} \mathop{\otimes_{\mathcal{R}}} {C_2})$
of the Chomsky–Schützenberger theorem. For the reverse
![]() $Z_{C_2}({K} \mathop{\otimes_{\mathcal{R}}} {C_2})\subseteq \overline K$
, the assumption is used to show that
$Z_{C_2}({K} \mathop{\otimes_{\mathcal{R}}} {C_2})\subseteq \overline K$
, the assumption is used to show that
![]() $\widehat{\,\cdot\,}:{\mathcal{C}} K\to Z_{C_2}({K} \mathop{\otimes_{\mathcal{R}}} {C_2})$
given by
$\widehat{\,\cdot\,}:{\mathcal{C}} K\to Z_{C_2}({K} \mathop{\otimes_{\mathcal{R}}} {C_2})$
given by
![]() $\widehat L = \sum\left\{\,m\otimes 1\,\mid\,m\in L\,\right\}$
is surjective. The surjectivity follows from an interesting automata-theoretic Normal Form Theorem for elements of
$\widehat L = \sum\left\{\,m\otimes 1\,\mid\,m\in L\,\right\}$
is surjective. The surjectivity follows from an interesting automata-theoretic Normal Form Theorem for elements of
![]() $K\mathop{\otimes_{\mathcal{R}}} C_2$
, which implicitly assumes that
$K\mathop{\otimes_{\mathcal{R}}} C_2$
, which implicitly assumes that
![]() ${\textit Mat}_{n,n}({K\mathop{\otimes_{\mathcal{R}}} C_2})$
is an
${\textit Mat}_{n,n}({K\mathop{\otimes_{\mathcal{R}}} C_2})$
is an
![]() ${\mathcal{R}}$
-dioid and shortly is as follows. For each element
${\mathcal{R}}$
-dioid and shortly is as follows. For each element
![]() $e=[R]\in K\mathop{\otimes_{\mathcal{R}}} C_2$
, by induction on the construction of
$e=[R]\in K\mathop{\otimes_{\mathcal{R}}} C_2$
, by induction on the construction of
![]() $R\in {\mathcal{R}}(K\times C_2),$
there is an automaton
$R\in {\mathcal{R}}(K\times C_2),$
there is an automaton
![]() ${\left\langle {S,A,F}\right\rangle}$
such that e is the language accepted by the automaton, i.e.
${\left\langle {S,A,F}\right\rangle}$
such that e is the language accepted by the automaton, i.e.
![]() $e=SA^*F =\sum\left\{\,SA^kF\,\mid\,k\in{\mathbb{N}}\,\right\}$
, where for some n,
$e=SA^*F =\sum\left\{\,SA^kF\,\mid\,k\in{\mathbb{N}}\,\right\}$
, where for some n,
![]() $S\in \{0,1\}^{1\times n}$
and
$S\in \{0,1\}^{1\times n}$
and
![]() $F\in \{0,1\}^{n\times 1}$
code the sets of initial and final states and A is a transition matrix
$F\in \{0,1\}^{n\times 1}$
code the sets of initial and final states and A is a transition matrix
![]() $U + X + V \in {\textit Mat}_{n,n}({K\mathop{\otimes_{\mathcal{R}}} C_2})$
with
$U + X + V \in {\textit Mat}_{n,n}({K\mathop{\otimes_{\mathcal{R}}} C_2})$
with
![]() $X\in K^{n\times n}$
,
$X\in K^{n\times n}$
,
![]() $U\in \{b,p,0\}^{n\times n}$
,
$U\in \{b,p,0\}^{n\times n}$
,
![]() $V\in\{d,q,0\}^{n\times n}$
. It is then shown that
$V\in\{d,q,0\}^{n\times n}$
. It is then shown that
![]() $N = b(Up+X+qV)d$
is a least solution of
$N = b(Up+X+qV)d$
is a least solution of
![]() $y\geq (UyV+X)^*$
in
$y\geq (UyV+X)^*$
in
![]() ${\textit Mat}_{n,n}({K\mathop{\otimes_{\mathcal{R}}} C_2})$
, a version of Dyck’s language, and
${\textit Mat}_{n,n}({K\mathop{\otimes_{\mathcal{R}}} C_2})$
, a version of Dyck’s language, and
![]() $N\in (Z_{C_2}({K} \mathop{\otimes_{\mathcal{R}}} {C_2}))^{n\times n}$
. Using the completeness assumption
$N\in (Z_{C_2}({K} \mathop{\otimes_{\mathcal{R}}} {C_2}))^{n\times n}$
. Using the completeness assumption
![]() $db+qp=1$
, Hopkins proves
$db+qp=1$
, Hopkins proves
which simplifies to
![]() $e=SNF$
for
$e=SNF$
for
![]() $e\in Z_{C_2}({K} \mathop{\otimes_{\mathcal{R}}} {C_2})$
. Notice that the Normal Form Theorem provides us with a description both of elements in the centralizer of
$e\in Z_{C_2}({K} \mathop{\otimes_{\mathcal{R}}} {C_2})$
. Notice that the Normal Form Theorem provides us with a description both of elements in the centralizer of
![]() $C_2$
and of arbitrary elements of
$C_2$
and of arbitrary elements of
![]() $K\mathop{\otimes_{\mathcal{R}}} C_2$
, while the proof of
$K\mathop{\otimes_{\mathcal{R}}} C_2$
, while the proof of
![]() $\overline K=Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
in Section 6 above only gives us a description of elements of the centralizer of
$\overline K=Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
in Section 6 above only gives us a description of elements of the centralizer of
![]() $C_2'$
as equivalence classes [R] of
$C_2'$
as equivalence classes [R] of
![]() $R\in{\mathcal{R}}(K\times C_2')$
with
$R\in{\mathcal{R}}(K\times C_2')$
with
![]() $R\subseteq K\times\{0,1\}$
. In Section 6, the surjectivity of
$R\subseteq K\times\{0,1\}$
. In Section 6, the surjectivity of
![]() $\widehat{\,\cdot\,}:{\mathcal{C}} K\to Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is reduced to that of
$\widehat{\,\cdot\,}:{\mathcal{C}} K\to Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is reduced to that of
![]() $\widehat{\,\cdot\,}:{\mathcal{C}} K\to Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
, which in turn is shown by giving an inverse. However, it is an interesting question whether the Normal Form Theorem also holds for
$\widehat{\,\cdot\,}:{\mathcal{C}} K\to Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
, which in turn is shown by giving an inverse. However, it is an interesting question whether the Normal Form Theorem also holds for
![]() $K\mathop{\otimes_{\mathcal{R}}} C_2'$
; Hopkins (personal communication, 2021) has found a partial positive answer. A least solution N of
$K\mathop{\otimes_{\mathcal{R}}} C_2'$
; Hopkins (personal communication, 2021) has found a partial positive answer. A least solution N of
![]() $y\geq(UyV+X)^*$
in
$y\geq(UyV+X)^*$
in
![]() ${\textit Mat}_{n,n}({Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})})$
exists, since
${\textit Mat}_{n,n}({Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})})$
exists, since
![]() $Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is a
$Z_{C_2'}({K} \mathop{\otimes_{\mathcal{R}}} {C_2'})$
is a
![]() ${\mathcal{C}}$
-dioid, and this category is closed under
${\mathcal{C}}$
-dioid, and this category is closed under
![]() $n\times n$
-matrix semirings.
$n\times n$
-matrix semirings.
Another difference of the proofs is that in the case
![]() ${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
we can replace the tensor product by a quotient (Corollary 13) and so, strictly speaking, need the tensor product only to represent the
${\mathcal{R}} M\mathop{\otimes_{\mathcal{R}}} C_2'$
we can replace the tensor product by a quotient (Corollary 13) and so, strictly speaking, need the tensor product only to represent the
![]() ${\mathcal{C}}$
-closure of arbitrary
${\mathcal{C}}$
-closure of arbitrary
![]() ${\mathcal{R}}$
-dioids K in
${\mathcal{R}}$
-dioids K in
![]() $K\mathop{\otimes_{\mathcal{R}}} C_2'$
.
$K\mathop{\otimes_{\mathcal{R}}} C_2'$
.
A minor question is whether our proof for the special case
![]() $K={\mathcal{R}} M$
can be simplified. Since it is well-known that
$K={\mathcal{R}} M$
can be simplified. Since it is well-known that
![]() ${\mathcal{C}} X^*$
is related to the polycyclic monoids
${\mathcal{C}} X^*$
is related to the polycyclic monoids
![]() $P_n'$
, Propositions 20–23 might be implicit in existing literature, such as the one referred to by Render and Kambites (Reference Render and Kambites2009). Moreover, it seems inelegant to first show that the maps
$P_n'$
, Propositions 20–23 might be implicit in existing literature, such as the one referred to by Render and Kambites (Reference Render and Kambites2009). Moreover, it seems inelegant to first show that the maps
![]() ${\widehat{\,\cdot\,}} : {{\mathcal{C}} M} \rightleftarrows {Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})} : {{\cdot}^\vee}$
form a bijection and then use this to show that they are
${\widehat{\,\cdot\,}} : {{\mathcal{C}} M} \rightleftarrows {Z_{C_2'}(\mathcal{R} \mathop{\otimes_{\mathcal{R}}} {C_2'})} : {{\cdot}^\vee}$
form a bijection and then use this to show that they are
![]() ${\mathcal{C}}$
-morphisms.
${\mathcal{C}}$
-morphisms.
Acknowledgements
I am glad to have had the opportunity to organize several joint seminars with Martin Hofmann and enjoy remembering our friendly and pleasant cooperation. I also had the pleasure to be welcome as a regular guest in his Oberseminar and thank all members of his group for interesting talks, questions, and conversations. Both Martin Hofmann’s Oberseminar in Computer Science and Helmut Schwichtenberg’s Oberseminar in Logic gave me the opportunity to present my current and previous work on formal language theory and to profit from comments and questions.
I am deeply indebted to Mark Hopkins for sharing his unpublished material with me and for giving numerous explanations of his ideas not only on the algebraization of formal language theory but also on the background in category theory and the relation to quantum physics. The essential idea of relating the fixed-point closure of a Kleene algebra to the centralizer of the bra-ket algebra in the tensor product is exclusively due to Hopkins.
Finally, I thank the library of the Deutsche Museum in Munich for offering a great opportunity to work in a quiet environment and the referees for careful reading and many comments that helped to improve the presentation considerably. The commutative diagrams are drawn with Paul Taylor’s package “diagrams.sty,” version 3.96.
Conflicts of interest
The author declares none.
A. Appendix A
The postponed part of the proof of Theorem 12 is as follows.
Proof. To prove
![]() ${\mathcal{A}} M\mathop{\otimes_{\mathcal{A}}} ({\mathcal{A}} N/\nu) \simeq {\mathcal{A}}(M\times N)/{\tilde\nu}$
, it is sufficient to show that
${\mathcal{A}} M\mathop{\otimes_{\mathcal{A}}} ({\mathcal{A}} N/\nu) \simeq {\mathcal{A}}(M\times N)/{\tilde\nu}$
, it is sufficient to show that
form a tensor product of
![]() ${\mathcal{A}} M$
and
${\mathcal{A}} M$
and
![]() ${\mathcal{A}} N/\nu$
in
${\mathcal{A}} N/\nu$
in
![]() ${\mathbb{D}}{\mathcal{A}}$
, where
${\mathbb{D}}{\mathcal{A}}$
, where
![]() $\top_1'$
and
$\top_1'$
and
![]() $\top_2'$
are defined by
$\top_2'$
are defined by
![]() $\top_1$
is an
$\top_1$
is an
![]() ${\mathcal{A}}$
-morphism, since
${\mathcal{A}}$
-morphism, since
![]() $A\mapsto A\times \{1\}$
and the quotient map
$A\mapsto A\times \{1\}$
and the quotient map
![]() $\cdot/{\tilde\nu}$
are. To see that
$\cdot/{\tilde\nu}$
are. To see that
![]() $\top_2'$
is well-defined, we first check that
$\top_2'$
is well-defined, we first check that
-
(1). For
 $B,B'\in {\mathcal{A}} N$
,
$B,B'\in {\mathcal{A}} N$
,
 $ B/\nu = B'/\nu \iff B\setminus\{0\} = B'\setminus\{0\},$
$ B/\nu = B'/\nu \iff B\setminus\{0\} = B'\setminus\{0\},$
-
(2). for
 $S,S'\in {\mathcal{A}}(M\times N)$
,
$S,S'\in {\mathcal{A}}(M\times N)$
,
 $S/{\tilde\nu} = S'/{\tilde\nu} \iff S\setminus(M\times\{0\}) = S'\setminus(M\times\{0\}).$
$S/{\tilde\nu} = S'/{\tilde\nu} \iff S\setminus(M\times\{0\}) = S'\setminus(M\times\{0\}).$
Concerning (1), since
![]() $\{0\}/\nu=\emptyset/\nu$
is the least element of
$\{0\}/\nu=\emptyset/\nu$
is the least element of
![]() ${\mathcal{A}} N/\nu$
, for
${\mathcal{A}} N/\nu$
, for
![]() $B\in {\mathcal{A}} N$
we have
$B\in {\mathcal{A}} N$
we have
Hence if
![]() $B,B'\in{\mathcal{A}} N$
with
$B,B'\in{\mathcal{A}} N$
with
![]() $B\setminus\{0\}=B'\setminus\{0\}$
, then
$B\setminus\{0\}=B'\setminus\{0\}$
, then
![]() $B/\nu=B'/\nu$
. For the converse, one shows that
$B/\nu=B'/\nu$
. For the converse, one shows that
is an
![]() ${\mathcal{A}}$
-congruence on
${\mathcal{A}}$
-congruence on
![]() ${\mathcal{A}} N$
containing
${\mathcal{A}} N$
containing
![]() $(\{0\},\emptyset)$
, and obviously
$(\{0\},\emptyset)$
, and obviously
![]() $\nu\subseteq \nu_0$
.
$\nu\subseteq \nu_0$
.
For (2), notice that for each
![]() $m\in M$
,
$m\in M$
,
Therefore, similar arguments as for (1) apply with
![]() $S\setminus(M\times\{0\})$
instead of
$S\setminus(M\times\{0\})$
instead of
![]() $B\setminus\{0\}$
.
$B\setminus\{0\}$
.
By (1) and (2), it follows that
![]() $\top_2$
is well-defined, since
$\top_2$
is well-defined, since
 \begin{eqnarray*} B/\nu = B'/\nu &\iff& B\setminus\{0\}=B'\setminus\{0\}\\ &\iff& (\{1\}\times B)\setminus(M\times\{0\}) = (\{1\}\times B')\setminus(M\times\{0\})\\ &\iff& (\{1\}\times B)/{\tilde\nu} = (\{1\}\times B')/{\tilde\nu}.\end{eqnarray*}
\begin{eqnarray*} B/\nu = B'/\nu &\iff& B\setminus\{0\}=B'\setminus\{0\}\\ &\iff& (\{1\}\times B)\setminus(M\times\{0\}) = (\{1\}\times B')\setminus(M\times\{0\})\\ &\iff& (\{1\}\times B)/{\tilde\nu} = (\{1\}\times B')/{\tilde\nu}.\end{eqnarray*}
![]() $\top_2'$
is an
$\top_2'$
is an
![]() ${\mathcal{A}}$
-morphism: it is clearly a monotone homomorphism, and if
${\mathcal{A}}$
-morphism: it is clearly a monotone homomorphism, and if
![]() $U\in {\mathcal{A}}({\mathcal{A}} N/\nu)$
, there is
$U\in {\mathcal{A}}({\mathcal{A}} N/\nu)$
, there is
![]() $U'\in {\mathcal{A}}{\mathcal{A}} N$
such that
$U'\in {\mathcal{A}}{\mathcal{A}} N$
such that
![]() $U =\left\{\,B/\nu\,\mid\,B\in U'\,\right\}$
; hence,
$U =\left\{\,B/\nu\,\mid\,B\in U'\,\right\}$
; hence,
 \begin{eqnarray*} \top_2'\left(\sum U\right) &=& \top_2'\left(\sum\left\{\,B/\nu\,\mid\,B\in U'\,\right\}\right) = \top_2\left(\left(\bigcup U'\right)/\nu\right)\\ &=& \left(\{1\}\times \left(\bigcup U'\right)\right)/{\tilde\nu} = \left(\bigcup\left\{\,\{1\}\times B\,\mid\,B\in U'\,\right\}\right)/{\tilde\nu}\\ &=& \sum \left\{\,(\{1\}\times B)/{\tilde\nu}\,\mid\,B\in U'\,\right\} = \sum\left\{\,\top_2'(B/\nu)\,\mid\,B/\nu\in U\,\right\}.\end{eqnarray*}
\begin{eqnarray*} \top_2'\left(\sum U\right) &=& \top_2'\left(\sum\left\{\,B/\nu\,\mid\,B\in U'\,\right\}\right) = \top_2\left(\left(\bigcup U'\right)/\nu\right)\\ &=& \left(\{1\}\times \left(\bigcup U'\right)\right)/{\tilde\nu} = \left(\bigcup\left\{\,\{1\}\times B\,\mid\,B\in U'\,\right\}\right)/{\tilde\nu}\\ &=& \sum \left\{\,(\{1\}\times B)/{\tilde\nu}\,\mid\,B\in U'\,\right\} = \sum\left\{\,\top_2'(B/\nu)\,\mid\,B/\nu\in U\,\right\}.\end{eqnarray*}
Clearly,
![]() $\top_1'$
and
$\top_1'$
and
![]() $\top_2'$
are relatively commuting.
$\top_2'$
are relatively commuting.
To show the universal property of a tensor product, let f,g be relatively commuting
![]() ${\mathcal{A}}$
-morphisms to an
${\mathcal{A}}$
-morphisms to an
![]() ${\mathcal{A}}$
-dioid D as shown:
${\mathcal{A}}$
-dioid D as shown:

We define an
![]() ${\mathcal{A}}$
-morphism
${\mathcal{A}}$
-morphism
![]() $h'_{f,g}:{\mathcal{A}}(M\times N)/{\tilde\nu}\to D$
by
$h'_{f,g}:{\mathcal{A}}(M\times N)/{\tilde\nu}\to D$
by
-
•
 $h'_{f,g}$
is well-defined: Since f and g are relatively commuting,
$h'_{f,g}$
is well-defined: Since f and g are relatively commuting,
 $(m,n)\mapsto f(\{m\})\cdot g(\{n\}/\nu)$
defines a homomorphism from
$(m,n)\mapsto f(\{m\})\cdot g(\{n\}/\nu)$
defines a homomorphism from
 $M\times N$
to D, so its lifting maps
$M\times N$
to D, so its lifting maps
 $S\in{\mathcal{A}}(M\times N)$
to an
$S\in{\mathcal{A}}(M\times N)$
to an
 ${\mathcal{A}}$
-set
${\mathcal{A}}$
-set
 $\left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in S\,\right\}\in {\mathcal{A}} D$
, and the
$\left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in S\,\right\}\in {\mathcal{A}} D$
, and the
 $\sum$
exists. Since g is a semiring-morphism, for
$\sum$
exists. Since g is a semiring-morphism, for
 $(m,0)\in S$
we have whence the value of
$(m,0)\in S$
we have whence the value of \begin{equation*} f(\{m\})\cdot g(\{0\}/\nu) = f(\{m\})\cdot g(0^{{\mathcal{A}} N/\nu}) = f(\{m\})\cdot 0^D = 0^D,\end{equation*}
\begin{equation*} f(\{m\})\cdot g(\{0\}/\nu) = f(\{m\})\cdot g(0^{{\mathcal{A}} N/\nu}) = f(\{m\})\cdot 0^D = 0^D,\end{equation*}
 $h'_{f,g}(S/{\tilde\nu})$
depends on
$h'_{f,g}(S/{\tilde\nu})$
depends on
 $S\setminus(M\times\{0\})$
only, i.e. on
$S\setminus(M\times\{0\})$
only, i.e. on
 $S/{\tilde\nu}$
by (2).
$S/{\tilde\nu}$
by (2).
-
•
 $h'_{f,g}$
is a homomorphism: clearly Since f and g are relatively commuting, for
$h'_{f,g}$
is a homomorphism: clearly Since f and g are relatively commuting, for \begin{eqnarray*} h'_{f,g}(\{(1,1\}/{\tilde\nu}) &=& \sum\{f(\{1\})\cdot g(\{1\}/\nu)\} = f(\{1\})\cdot g(\{1\}/\nu) = 1^D.\end{eqnarray*}
\begin{eqnarray*} h'_{f,g}(\{(1,1\}/{\tilde\nu}) &=& \sum\{f(\{1\})\cdot g(\{1\}/\nu)\} = f(\{1\})\cdot g(\{1\}/\nu) = 1^D.\end{eqnarray*}
 $S,S'\in {\mathcal{A}}(M\times N)$
the set
$S,S'\in {\mathcal{A}}(M\times N)$
the set
 $\left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in SS'\,\right\}$
is the product in
$\left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in SS'\,\right\}$
is the product in
 ${\mathcal{A}} D$
of and since
${\mathcal{A}} D$
of and since \begin{equation*} \left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in S\,\right\} \textrm{ and } \left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in S'\,\right\},\end{equation*}
\begin{equation*} \left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in S\,\right\} \textrm{ and } \left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in S'\,\right\},\end{equation*}
 $\sum:{\mathcal{A}} D\to D$
is
$\sum:{\mathcal{A}} D\to D$
is
 ${\mathcal{A}}$
-distributive, this gives
${\mathcal{A}}$
-distributive, this gives  \begin{eqnarray*} h'_{f,g}(S/{\tilde\nu}\cdot S'/{\tilde\nu}) &=& h'_{f,g}(SS'/{\tilde\nu})\\ &=& \sum\left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in SS'\,\right\},\\ &=& h'_{f,g}(S/{\tilde\nu})\cdot h'_{f,g}(S'/{\tilde\nu}).\end{eqnarray*}
\begin{eqnarray*} h'_{f,g}(S/{\tilde\nu}\cdot S'/{\tilde\nu}) &=& h'_{f,g}(SS'/{\tilde\nu})\\ &=& \sum\left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in SS'\,\right\},\\ &=& h'_{f,g}(S/{\tilde\nu})\cdot h'_{f,g}(S'/{\tilde\nu}).\end{eqnarray*}
-
•
 $h'_{f,g}$
is an
$h'_{f,g}$
is an
 ${\mathcal{A}}$
-morphism: If
${\mathcal{A}}$
-morphism: If
 $V\in {\mathcal{A}}({\mathcal{A}}(M\times N)/{\tilde\nu})$
, there is
$V\in {\mathcal{A}}({\mathcal{A}}(M\times N)/{\tilde\nu})$
, there is
 $U\in {\mathcal{A}}({\mathcal{A}}(M\times N))$
such that
$U\in {\mathcal{A}}({\mathcal{A}}(M\times N))$
such that
 $V = U/{\tilde\nu} := \left\{\,S/{\tilde\nu}\,\mid\,S\in U\,\right\}$
, and
$V = U/{\tilde\nu} := \left\{\,S/{\tilde\nu}\,\mid\,S\in U\,\right\}$
, and
 $\sum V = (\bigcup U)/{\tilde\nu}$
. So showing that
$\sum V = (\bigcup U)/{\tilde\nu}$
. So showing that \begin{eqnarray*} h'_{f,g}\left(\sum V\right) &=& h'_{f,g}\left(\left(\bigcup U\right)/{\tilde\nu}\right)\\ &=& \sum\left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in \bigcup U\,\right\},\\ &=& \sum\left\{\,\sum\left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in S\,\right\}\,\mid\,S\in U\,\right\},\\ &=& \sum\left\{\,h'_{f,g}(S/{\tilde\nu})\,\mid\,S\in U\,\right\} = \sum ({\mathcal{A}} {h'_{f,g}})(V),\end{eqnarray*}
\begin{eqnarray*} h'_{f,g}\left(\sum V\right) &=& h'_{f,g}\left(\left(\bigcup U\right)/{\tilde\nu}\right)\\ &=& \sum\left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in \bigcup U\,\right\},\\ &=& \sum\left\{\,\sum\left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in S\,\right\}\,\mid\,S\in U\,\right\},\\ &=& \sum\left\{\,h'_{f,g}(S/{\tilde\nu})\,\mid\,S\in U\,\right\} = \sum ({\mathcal{A}} {h'_{f,g}})(V),\end{eqnarray*}
 $h'_{f,g}$
is
$h'_{f,g}$
is
 ${\mathcal{A}}$
-continuous; this implies that it is monotone.
${\mathcal{A}}$
-continuous; this implies that it is monotone.
-
•
 $f = h'_{f,g}\circ \top_1'$
and
$f = h'_{f,g}\circ \top_1'$
and
 $g=h'_{f,g}\circ \top_2'$
: for
$g=h'_{f,g}\circ \top_2'$
: for
 $A\in {\mathcal{A}} M$
and
$A\in {\mathcal{A}} M$
and
 $B\in {\mathcal{A}} N$
,
$B\in {\mathcal{A}} N$
,  \begin{eqnarray*} h'_{f,g}(\top_1'(A)) &=& h'_{f,g}((A\times \{1\})/{\tilde\nu})\\ &=& \sum\left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in A\times\{1\}\,\right\}\\ &=& \sum\left\{\,f(\{m\})\cdot g(\{1\}/\nu)\,\mid\,m\in A\,\right\}\\ &=& \sum\left\{\,f(\{m\})\,\mid\,m\in A\,\right\}\\ &=& f\left(\bigcup\left\{\,\{m\}\,\mid\,m\in A\,\right\}\right)\\ &=& f(A),\end{eqnarray*}
\begin{eqnarray*} h'_{f,g}(\top_1'(A)) &=& h'_{f,g}((A\times \{1\})/{\tilde\nu})\\ &=& \sum\left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in A\times\{1\}\,\right\}\\ &=& \sum\left\{\,f(\{m\})\cdot g(\{1\}/\nu)\,\mid\,m\in A\,\right\}\\ &=& \sum\left\{\,f(\{m\})\,\mid\,m\in A\,\right\}\\ &=& f\left(\bigcup\left\{\,\{m\}\,\mid\,m\in A\,\right\}\right)\\ &=& f(A),\end{eqnarray*}
 \begin{eqnarray*} h'_{f,g}(\top_2'(B/\nu)) &=& h'_{f,g}((\{1\}\times B)/{\tilde\nu})\\ &=& \sum\left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in \{1\}\times B\,\right\}\\ &=& \sum\left\{\,f(\{1\})\cdot g(\{n\}/\nu)\,\mid\,n\in B\,\right\}\\ &=& \sum\left\{\,g(\{n\}/\nu)\,\mid\,n\in B\,\right\}\\ &=& g\left(\sum\left\{\,\{n\}/\nu\,\mid\,n\in B\,\right\}\right)\\ &=& g\left(\bigcup\left\{\,\{n\}\,\mid\,n\in B\,\right\}/\nu\right)\\ &=& g(B/\nu).\end{eqnarray*}
\begin{eqnarray*} h'_{f,g}(\top_2'(B/\nu)) &=& h'_{f,g}((\{1\}\times B)/{\tilde\nu})\\ &=& \sum\left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in \{1\}\times B\,\right\}\\ &=& \sum\left\{\,f(\{1\})\cdot g(\{n\}/\nu)\,\mid\,n\in B\,\right\}\\ &=& \sum\left\{\,g(\{n\}/\nu)\,\mid\,n\in B\,\right\}\\ &=& g\left(\sum\left\{\,\{n\}/\nu\,\mid\,n\in B\,\right\}\right)\\ &=& g\left(\bigcup\left\{\,\{n\}\,\mid\,n\in B\,\right\}/\nu\right)\\ &=& g(B/\nu).\end{eqnarray*}
-
•
 $h'_{f,g}$
is the only
$h'_{f,g}$
is the only
 ${\mathcal{A}}$
-morphism h’ with
${\mathcal{A}}$
-morphism h’ with
 $f=h'\circ \top_1'$
and
$f=h'\circ \top_1'$
and
 $g=h'\circ \top_2'$
: Suppose
$g=h'\circ \top_2'$
: Suppose
 $h':{\mathcal{A}}(M\times N)/{\tilde\nu}\to D$
is such an
$h':{\mathcal{A}}(M\times N)/{\tilde\nu}\to D$
is such an
 ${\mathcal{A}}$
-morphism. Then,
${\mathcal{A}}$
-morphism. Then, \begin{eqnarray*} h'_{f,g}(S/{\tilde\nu}) &=& \sum\left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in S\,\right\}\\ &=& \sum\left\{\,h'(\top_1'(\{m\}))\cdot h'(\top_2'(\{n\}/\nu))\,\mid\,(m,n)\in S\,\right\}\\ &=& \sum\left\{\,h'(\top_1'(\{m\})\cdot \top_2'(\{n\}/\nu))\,\mid\,(m,n)\in S\,\right\}\\ &=& h'\left(\sum\left\{\,\top_1'(\{m\})\cdot \top_2'(\{n\}/\nu)\,\mid\,(m,n)\in S\,\right\}\right)\\ &=& h'\left(\sum\left\{\,(\{m\}\times\{1\})/{\tilde\nu}\cdot (\{1\}\times \{n\})/{\tilde\nu}\,\mid\,(m,n)\in S\,\right\}\right)\\ &=& h'\left(\sum\left\{\,(\{m\}\times\{n\})/{\tilde\nu})\,\mid\,(m,n)\in S\,\right\}\right)\\ &=& h'\left(\sum\left\{\,\{(m,n)\}/{\tilde\nu}\,\mid\,(m,n)\in S\,\right\}\right)\\ &=& h'\left(\left(\bigcup\left\{\,\{(m,n)\}\,\mid\,(m,n)\in S\,\right\}\right)/{\tilde\nu}\right)\\ &=& h'(S/{\tilde\nu}). \\[-25pt]\end{eqnarray*}
\begin{eqnarray*} h'_{f,g}(S/{\tilde\nu}) &=& \sum\left\{\,f(\{m\})\cdot g(\{n\}/\nu)\,\mid\,(m,n)\in S\,\right\}\\ &=& \sum\left\{\,h'(\top_1'(\{m\}))\cdot h'(\top_2'(\{n\}/\nu))\,\mid\,(m,n)\in S\,\right\}\\ &=& \sum\left\{\,h'(\top_1'(\{m\})\cdot \top_2'(\{n\}/\nu))\,\mid\,(m,n)\in S\,\right\}\\ &=& h'\left(\sum\left\{\,\top_1'(\{m\})\cdot \top_2'(\{n\}/\nu)\,\mid\,(m,n)\in S\,\right\}\right)\\ &=& h'\left(\sum\left\{\,(\{m\}\times\{1\})/{\tilde\nu}\cdot (\{1\}\times \{n\})/{\tilde\nu}\,\mid\,(m,n)\in S\,\right\}\right)\\ &=& h'\left(\sum\left\{\,(\{m\}\times\{n\})/{\tilde\nu})\,\mid\,(m,n)\in S\,\right\}\right)\\ &=& h'\left(\sum\left\{\,\{(m,n)\}/{\tilde\nu}\,\mid\,(m,n)\in S\,\right\}\right)\\ &=& h'\left(\left(\bigcup\left\{\,\{(m,n)\}\,\mid\,(m,n)\in S\,\right\}\right)/{\tilde\nu}\right)\\ &=& h'(S/{\tilde\nu}). \\[-25pt]\end{eqnarray*}