Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-08T23:28:05.106Z Has data issue: false hasContentIssue false
  • English
  • Français

REGULARITY OF POWERS OF BIPARTITE GRAPHS

Part of: Commutative algebra: Homological methods Theory of modules and ideals Algebraic combinatorics

Published online by Cambridge University Press:  19 September 2022

AJAY KUMAR  and
RAJIV KUMAR
AJAY KUMAR*
Affiliation:
Department of Mathematics, Indian Institute of Technology Jammu, Jammu, India
RAJIV KUMAR
Affiliation:
Department of Mathematics, Indian Institute of Technology Jammu, Jammu, India e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a simple bipartite graph G, we give an upper bound for the regularity of powers of the edge ideal 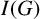$I(G)$ in terms of its vertex domination number. Consequently, we explicitly compute the regularity of powers of the edge ideal of a bipartite Kneser graph. Further, we compute the induced matching number of a bipartite Kneser graph.

Keywords

regularitybipartite Kneser graphedge idealvertex domination number

MSC classification

Primary: 05E40: Combinatorial aspects of commutative algebra
Secondary: 13C14: Cohen-Macaulay modules 13D02: Syzygies, resolutions, complexes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 107 , Issue 1 , February 2023 , pp. 1 - 9
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alilooee, A. and Banerjee, A., ‘Powers of edge ideals of regularity three bipartite graphs’, J. Commut. Algebra 9(4) (2017), 441–454.CrossRefGoogle Scholar
Banerjee, A., ‘The regularity of powers of edge ideals’, J. Algebraic Combin. 41(2) (2015), 303–321.CrossRefGoogle Scholar
Beyarslan, S., Hà, H. T. and Trung, T. N., ‘Regularity of powers of forests and cycles’, J. Algebraic Combin. 42(4) (2015), 1077–1095.CrossRefGoogle Scholar
Bıyıkoğlu, T. and Civan, Y., ‘Projective dimension of (hyper)graphs and the Castelnuovo–Mumford regularity of bipartite graphs’, Preprint, 2016, arXiv:1605.02956.Google Scholar
Cutkosky, S. D., Herzog, J. and Trung, N. V., ‘Asymptotic behaviour of the Castelnuovo–Mumford regularity, Compos. Math. 118(3) (1999), 243–261.CrossRefGoogle Scholar
Frankl, P., ‘An extremal problem for two families of sets’, European J. Combin. 3(2) (1982), 125–127.CrossRefGoogle Scholar
Herzog, J. and Hibi, T., ‘An upper bound for the regularity of powers of edge ideals’, Math. Scand. 126(2) (2020), 165–169.CrossRefGoogle Scholar
Jayanthan, A. V., Narayanan, N. and Selvaraja, S., ‘Regularity of powers of bipartite graphs’, J. Algebraic Combin. 47(1) (2018), 17–38.CrossRefGoogle Scholar
Jayanthan, A. V. and Selvaraja, S., ‘Asymptotic behavior of Castelnuovo–Mumford regularity of edge ideals of very well-covered graphs, Preprint, 2017.Google Scholar
Katzman, M., ‘Characteristic-independence of Betti numbers of graph ideals’, J. Combin. Theory Ser. A 113(3) (2006), 435–454.CrossRefGoogle Scholar
Kodiyalam, V., ‘Asymptotic behaviour of Castelnuovo–Mumford regularity’, Proc. Amer. Math. Soc. 128(2) (2000), 407–411.CrossRefGoogle Scholar
Kumar, A., Singh, P. and Verma, R., ‘Certain homological invariants of bipartite Kneser graphs’, J. Algebra Appl., to appear. Published online (2 July 2021).CrossRefGoogle Scholar
Mütze, T. and Su, P.. ‘Bipartite Kneser graphs are Hamiltonian’, Combinatorica 37(6) (2017), 1207–1219.CrossRefGoogle Scholar
Woodroofe, R., ‘Matchings, coverings, and Castelnuovo–Mumford regularity’, J. Commut. Algebra 6(2) (2014), 287–304.CrossRefGoogle Scholar