1. Introduction
Dislocations play an important role in ice flow for a large range of stress levels and grain-sizes. Although many studies emphasize the importance of dislocations, dislocation-based mechanisms have not been fully incorporated into constitutive models of ice because of the difficulty in quantifying the dislocation density. Some studies (Reference BakerBaker, 1997, Reference Baker2002) using X-ray topography provide a way to directly observe dislocations and semi-quantify the dislocation density. However, because of its low resolution, X-ray topography cannot give useful information when the dislocation density is higher than ~1 × 109m–2 (Reference BakerBaker, 2002), nor does it give any information on the mobile fraction of dislocations. However, a methodology (Reference ColeCole, 1995; Reference Cole and DurellCole and Durell, 2001) has been developed to calculate the effective mobile dislocation density from a specimen’s cyclic response and this, in turn, supports a quantitative assessment of dislocation processes during ice flow.
A dislocation-based model has been developed and successfully used to describe the mechanical response of sea ice (Reference ColeCole, 1995; Reference Cole and DurellCole and Durell, 2001). This model relates the dislocation density to the hysteresis loop area obtained from zero-mean-stress cyclic loading experiments, and can be used to quantify dislocation multiplication during creep. Previous studies (Reference Cole and DurellCole and Durell, 1995) indicated that both the responses of dislocations and grain boundaries during cyclic loading have effects on the hysteresis loop areas, but that they are separable because they have different magnitudes, central frequencies and activation energies. At –10°C, the central frequency of the dislocation relaxation peak is located at about 10–4Hz, while that of the grain boundary relaxation peak is located at about 5 Hz. Generally, with a dislocation density of ~1 × 109m–2, the strength of the dislocation relaxation is at least an order of magnitude higher than that of the grain boundary relaxation.
Although power-law creep with n = 3, referred to for ice as Glen’s law (Reference GlenGlen, 1958), is commonly observed at strain rates from 10–8 to 10–5s–1, experiments and field analysis frequently show a fall-off to lower-order stress dependence at low stresses, with n typically around 1 or 2 (Reference GlenGlen, 1955; Reference Jellinek and BrillJellinek and Brill, 1956; Reference Mellor and SmithMellor and Smith, 1966; Reference Bromer and KingeryBromer and Kingery, 1968; Reference Colbeck and EvansColbeck and Evans; 1973; Reference Pimienta and DuvalPimienta and Duval, 1987; Reference Duval and CastelnauDuval and Castelnau, 1995; Reference Durham, Stern and KirbyDurham and others, 2001; Reference Goldsby and KohlstedtGoldsby and Kohlstedt, 2001). The fall-off has been attributed to test techniques, or to mechanism shifts. However, Reference Pimienta and DuvalPimienta and Duval (1987) have shown quantitatively that it can be explained by dislocation glide with a constant dislocation density. Reference Jellinek and BrillJellinek and Brill (1956), Reference Mellor and SmithMellor and Smith (1966) and Reference Bromer and KingeryBromer and Kingery (1968) found that the exponent decreased to ~1; Reference Colbeck and EvansColbeck and Evans (1973) obtained an exponent of ~1.3; Reference GlenGlen (1955) and Reference Pimienta and DuvalPimienta and Duval (1987) obtained an exponent of ~1.5; while Reference Duval and CastelnauDuval and Castelnau (1995) obtained an exponent of ~1.8.
The fall-off of the stress exponent to the range of 1–2 has been observed at stresses lower than 0.2 MPa, and with the grain-size in the range 1–10mm. However, most low-stress exponents with values near to 1 are obtained from the data in the transition range, and the value of the exponent tends to approach 1 as the stress continues to decrease (see, e.g., data summarized by Reference Langdon, Whalley, Jones and GoldLangdon, 1973). Additionally, Reference Cole and DurellCole and Durell (2001) and Reference ColeCole (2003) demonstrated with experiments on sea ice and granular fresh-water ice, respectively, that the stress level associated with the fall-off from n = 3 behavior increases with the specimen’s mobile dislocation density.
Based on extensive creep studies of very small-grained (<0.2 mm) ice, Reference Goldsby and KohlstedtGoldsby and Kohlstedt (2001) suggested that the creep of ice occurs with three separate regimes with n values of 2.4, 1.8 and 4, which were identified, respectively, as basal slip–accommodated grain boundary sliding, grain boundary sliding–accommodated basal slip, and dislocation creep. Reference Durham, Stern and KirbyDurham and others (2001) also found an n = 4 flow law for dislocation creep at strain rates down to 2 × 10–8s–1 with differential stresses from 0.45 to 10 MPa, temperatures from 200 to 250 K, and under very high confining pressure (50 MPa). However, since the grain-size is <0.2 mm, which is much smaller than those of the studies cited in the previous paragraph, we believe that the stress dependencies observed in this work result from shifts in the balance of deformation mechanism brought about by very small grainsizes and high confining pressure, and may not necessarily apply to the larger-grained material and test conditions of the present work.
Since particles are frequently found in basal ice and the behavior of basal ice is very important to ice-sheet behavior, the effect of particles on ice flow is of continuing interest (Reference Holdsworth and BullHoldsworth and Bull, 1970; Reference Nayar, Lenel and AnsellNayar and others, 1971; Reference Baker and GerberichBaker and Gerberich, 1979; Reference Lange and AhrensLange and Ahrens, 1983; Reference Shoji and LangwayShoji and Langway, 1985; Reference Durham, Kirby and SternDurham and others, 1992). Prior studies have included a large range of particle sizes, from ultra-fine amorphous silica particles with an average size of 15 nm (Reference Nayar, Lenel and AnsellNayar and others, 1971; Reference Lange and AhrensLange and Ahrens, 1983) to sandsized particles (Reference Hooke, Dahlin and KauperHooke and others, 1972). Ice with ultra-fine amorphous silica particles shows similar mechanical behavior to particle-strengthened metals, in which, at low concentration, the strength increases as the particle content increases (Reference Nayar, Lenel and AnsellNayar and others, 1971). However, when the particle size increases to that of silt (tens and hundreds of microns) and sand, at relatively low concentrations the particle effect is contradictory, although most experimental data indicate that particles at low concentrations increase the creep rate. For example, Reference Baker and GerberichBaker and Gerberich (1979) found that at temperatures from –20°C to –5°C, solid inclusions in concentrations from 1.3 to 6.6 vol.% always increased the creep strain rate by up to 80%; Reference Shoji and LangwayShoji and Langway (1985) found an increased flow rate for dirty basal ice from Camp Century, Greenland, compared with clean basal ice;and Reference Holdsworth and BullHoldsworth and Bull (1970) also observed an enhanced flow rate in the basal amber-colored ice of the Meserve Glacier, Antarctica. However, Reference Hooke, Dahlin and KauperHooke and others (1972) found a high variability in strain rate for a range of sand concentrations up to 7 vol.%. More importantly, all these studies concentrated on a fixed stress level, which means that the effects of particles on creep as a function of stress level are still unclear.
In this paper, we report the results of staged creep and cyclic loading experiments that were conducted to quantify the dislocation processes that underlie the flow process on pure and debris-laden ice. The dislocation-based anelasticity model described in Reference ColeCole (1995) and the experimental methods described in Reference Cole and DurellCole and Durell (2001) provide the means to quantify changes in the dislocation density as a function of creep stress, thereby allowing us to examine the stress dependence of both the creep rate and the effective mobile dislocation density that develops during straining. Particular attention is paid to the fall-off of the stress exponent with decreasing stress, and the observation that linear flow is associated with a constant (e.g. stress-independent) dislocation density.
2. Experimental
Deionized, distilled and degassed water was used to grow thin plates of large-grained ice. These ice plates were then broken up, and a 3–5 mm sieve fraction was obtained. These grains were used to seed granular fresh-water ice specimens prepared by the method of Reference ColeCole (1979). The final specimen dimensions were 127 mm in length and 50.4 mm in diameter.
For ice specimens with particles, water with silt-sized soil particles (50 ± 10 μm) was frozen to a thickness of about 5 mm from bottom to top using a cooling plate. Another layer of ice with particles was then grown on top of the first layer. This procedure was repeated several times until the thickness of the ice plate was about 30 mm. Growing a multilayer ice plate was necessary to distribute the particles throughout the ice grains. The ice plate was subsequently broken up, and a 3–5 mm sieve fraction was obtained. These grains were then used to seed granular ice specimens as described above. The particle-free ice had an initial average grain-size of about 5.0 mm, while the ice with particles had an initial grain-size of 5.5 mm. Figure 1 shows photographs of a thin section with polarized light of fresh-water ice and ice with 1 wt.% particles.Figure 2 shows a thin section of ice with 4 wt.% particles. It can be seen that the particles tend to occur in clusters that are uniformly distributed (Fig. 2b).

Fig. 1. Photographs of thin sections of (a) particle-free ice and (b) ice with 1 wt.% particles. Specimen diameter is 50.4 mm and the average grain-size is 5 mm.

Fig. 2. (a) Photographs of an ice specimen with 4 wt.% particles and a thin section under incident light. (b) Enlarged view of the thin section showing the distribution of particles. The end caps are bonded to the specimen when it is formed and used to connect it to the creep jig.
Cyclic and creep tests were performed using the creep jig shown schematically in Figure 3. The creep jig was located in a cold room with a temperature 2°C lower than the test temperatures. Two insulated boxes were used to isolate the jig from the cold room, and a temperature-regulating system was located between the boxes. This method controls the temperature in the inner box to deviations of less than ±0.1 °C. For cyclic loading, the upper three collars were locked and a zero-mean-stress sinusoidal waveform was applied by the electrohydraulic actuator mounted on the bottom of the apparatus. The experiments employed the reversed direct-stress testing method developed by Reference Cole and DurellCole and Durell (1995), and the procedures described by Reference ColeCole (1993). Reference Cole and DurellCole and Durell (1995) indicated that for sea ice, the mobile dislocation density (as deduced from the hysteresis loop area) does not change as a consequence of the cyclic loading. This feature was verified in our studies on granular fresh-water ice. Since the hysteresis loop area is not influenced by immobile dislocations, the present analysis addresses only the effect of mobile dislocations. The total dislocation density will be studied in future work using X-ray topography.
For the constant compressive load creep tests, the bottom and top collars on the creep jig were locked and air pressure was applied to the pneumatic actuator. A set of load cycles was applied prior to creep deformation to assess the initial dislocation density of each specimen. Creep loading was applied until a specified total strain was reached, the creep load was then removed and the specimen was allowed to recover. Another set of load cycles was applied to assess the dislocation density at the end of each period of loading. Typically, frequencies of 10–3, 10–2, 10–1 and 1 Hz were applied to more fully understand the material response, and the 10–1 Hz frequency was used to assess the dislocation-based anelasticity. The 10–1 Hz frequency is low enough to avoid the contribution from grain boundary sliding to the loop area (because grain boundary sliding is in phase with the cyclic stress), and high enough to avoid the complicating effects of cyclic viscous strain (Reference Cole and DurellCole and Durell, 1995). Test temperatures were either –10°C or –12°C ±0.1 °C, selected for comparison with earlier work.
Two types of staged-creep tests were performed. One type was used to determine the effect of particles on the creep rate under constant stress;the other was used to determine the effect of particles on the stress dependence of the creep rate. In the first type of test, a given creep stress was applied in all stages and the strain for each stage of loading was kept small to closely track the dislocation density changes. Since the strain accumulated during each stage was small, no creep stage reached minimum strain rate. However, the minimum in the strain rate could be determined by examining the strain rates over all the stages of creep.

Fig. 3. Schematic of the creep jig. LVDT is linear variable displacement transducer; MTS is material testing system.
In the second type of test (used to determine the effects of particles on the stress dependence of granular ice), a series of staged-creep tests at increasing stress levels, alternating with cyclic loading, were performed. Unlike the previous type of test, each stage was performed for a sufficient time to ensure that the dislocation density reached equilibrium (constant creep rate). Figure 4 shows a stress–time record for a typical staged-creep test. First, cyclic loading was used to determine the initial dislocation density, and then a creep test with a low stress level was performed. After the specimen reached steady state (typically 0.5–1% strain) the stress was removed, allowing the elastic and anelastic strain to be recovered. The cyclic loading was then reapplied to determine the dislocation density at the end of the creep stage. Then another creep stage with a higher stress (∆σcreep = 0.05, 0.1 or 0.2 MPa) was performed. This procedure was repeated several times until the creep stress reached 1.4 MPa.

Fig. 4. Example stress–time history for a staged-creep test.
3. Results and Discussion
Figure 5 illustrates a typical set of hysteresis loops (ice with 1 wt.% particles at –12°C, cyclic stress = ± 0.6 MPa) for frequencies of 10–3, 10–2, 10–1 and 1 Hz before creep testing. Each set of hysteresis loops consists of three cycles of zero-mean-stress sinusoidal loading. The increased loop areas with decreasing frequency are due to the fact that the dislocation relaxation peak (located at about 10–4 Hz under these test conditions) is being approached, and because of the increasing contribution of viscous straining.

Fig. 5. Typical hysteresis loops at σ = ± 0.6 MPa and T = –12ºC for four test frequencies as indicated (prior to creep straining). The curves have been offset along the strain axis for clarity. This particular test is for ice with 0.1 wt.% particles.
Figure 6 shows the internal friction as a function of frequency for particle-free ice and ice with 1 wt.% particles, tested before creep at a temperature of –12ºC. The internal friction (the ratio of the hysteresis loop area to the peak strain energy during a load cycle) is a dimensionless measure of the energy dissipated per cycle. Typically, there is a grain boundary relaxation peak located at ~5 Hz at –12ºC. It can be seen that the internal friction at 1 Hz is much lower for ice with particles than for particle-free ice. This result is in accordance with a previous study (Reference Song, Cole and BakerSong and others, 2004), which focused on the effect of particles located only along the grain boundaries. When particles are uniformly distributed throughout the microstructure, some fraction of them will be located along the grain boundaries. The decrease in internal friction at 1 Hz for ice with particles indicates that there were a sufficient number of particles along the grain boundaries to block grain boundary sliding and thus eliminate the grain boundary relaxation peak. It can be seen that the error bars at 1 and 0.1 Hz are smaller than those at 10–2 and 10–3Hz. However, the coefficients of variation (standard deviation divided by the mean value) have similar values at all the test frequencies (10–3 to 1 Hz).

Fig. 6. Effect of particles on the internal friction vs frequency before creep straining. Data points are the average values of all tests, while the top and bottom of the error bars indicate the maximum and minimum values. Each point is an average of 3–5 tests.
Figure 7a shows a typical stage of a compressive creep test to study the effect of particles on the creep under a constant stress of 1.45 MPa and a temperature of –12ºC.

Fig. 7. Typical creep curves under a stress of 1.45 MPa and a temperature of –12ºC: (a) to study the effect of particles on creep under constant stress (b) to study the effect of particles on stress dependence.
Figure 7b shows a typical stage of a compressive creep test used to study the effect of particles on the stress dependence of the flow rate at a temperature of –12ºC. As indicated in section 2, strains sufficient to reach steady state were always used in this type of experiment. The curve of Figure 7b shows an initially decreasing creep rate with time (primary creep), followed by a period of approximately constant creep rate (secondary creep), followed by recovery after the stress was removed.
Figure 8 shows the relationship between strain rate, dislocation density and viscous strain for particle-free ice and ice with the particle concentrations indicated under a stress of 1.45 MPa. To obtain the relationship between the strain rate and viscous strain ε viscous, a series of staged-creep tests were performed on the specimens as described above. For each point on Figure 8a, the strain rate was measured during the creep stage, and the viscous strain values are the accumulated viscous strains from all previous creep stages. Thus, the creep curve in Figure 7a produces a single point on Figure 8a, and the creep strain, εn, is obtained from the total strain, minus the recovered strain (see Fig. 7a), i.e.


Fig. 8. Results from staged creep experiments under a constant stress level for several particle concentrations as indicated. (a) Viscous strain rate vs viscous strain. (b) Dislocation density vs viscous strain.
Both the creep rates and dislocation densities of ice with particles are always higher than those of particle-free ice. All the curves in Figure 8a show a common trend: the creep rate initially decreases (primary creep), reaches a minimum near 1% strain and subsequently increases. It can be seen that the dislocation density increases as the viscous strain increases. Typically, the total creep strain includes elastic, anelastic and viscous components. Elastic strain reaches a maximum when the peak stress is applied, while the anelastic strain is time-dependent and reaches its maximum (normally the total strain is <1% when anelastic strain reaches the maximum) as time increases. The total creep rate decreases during primary creep because the decrease in the anelastic strain rate is faster than the increase in the viscous strain rate (caused by the increase in dislocation density).
It is worth noting that the existence of particles in the ice specimens introduces a thin, liquid-like layer between the particle and the ice matrix (Reference Dash, Fu and WettlauferDash and others, 1995), which could play a role in the creep process. However, laboratory measurements indicate that the value of unfrozen water content per unit surface area of soil particles is relatively low (Reference Anderson, Tice, Hadas, Rijtema, Fuchs and YaronAnderson and Tice (1978) report <0.05 gm–2 for Wyoming bentonite frozen soil–water systems at T= –10°C), and Reference GilpinGilpin (1980) indicated that the thickness of water layer around wires imbedded in ice was <3 nm at –10°C. This small thickness, which has the same magnitude as the Burgers vector of ice, is not expected to significantly affect the shear processes that occur along the ice–particle interface during creep. However, this may not be the case at temperatures close to the melting point. It may be possible for the liquid-like layer to become sufficiently thick at high temperatures to decouple the particle from the ice matrix, thereby altering the microstructural stress field and enhancing diffusion.
Figure 6 indicates that the presence of the particles along grain boundaries inhibits grain boundary sliding (see internal friction decreasing at 1 Hz). At least at our test temperatures, this phenomenon produces higher strain energy along the grain boundaries and presumably generates more dislocations during creep, which in turn increases the creep rate compared with particle-free ice. We note that the generation of dislocations at grain boundary ledges in fresh-water ice has been well documented with synchrotron X-ray topography (Reference Liu, Baker and DudleyLiu and others, 1995).
Figure 9 illustrates the effect of particle concentration on the minimum (secondary) creep rate of granular ice under a stress level of 1.45 MPa at –12°C. The minimum creep rate increases above that of pure ice by approximately 100% for particle concentrations of 0.5–4wt.%, in agreement with some previous observations (Reference Holdsworth and BullHoldsworth and Bull, 1970; Reference Baker and GerberichBaker and Gerberich, 1979; Reference Shoji and LangwayShoji and Langway, 1985), which used either sand- or silt-sized particles. It can be seen that the minimum strain rates are roughly independent of particle concentrations between 0.5 and 4 wt.%. This is different from a previous study (Reference Song, Cole and BakerSong and others, 2004) on the creep of ice in which particles were located only along the grain boundaries. In that case, the minimum creep rate was at a maximum for a particle concentration of 1 wt.%.

Fig. 9. The effect of particle concentration on the minimum creep rate of granular ice at a stress level of 1.45 MPa and a temperature of –12°C. Data points are the average values of all tests, while the top and bottom of the error bars indicate the maximum and minimum values. Each point is an average of 3–5 tests.
Figure 10 shows the microstructures of particle-free ice and ice with 1 wt.% particles after straining under 1.45 MPa at T= –12°C to total strains of either 8% or 9%. It can be seen that grain-size decreases dramatically for both types of ice (compare Fig. 1a and b with Fig. 10a and b) but the ice with particles has a much smaller grain-size. This is presumably because of a greater dynamic recrystallization rate. Figure 10c shows slip bands in a particle-free zone of ice with particles after straining under 1.45 MPa at T – –12°C to a total strain of 9%. The presence of slip bands in the microstructure shows the importance of dislocation glide in creep under the stated experimental conditions.

Fig. 10. Thin sections of ice after creep. (a) Particle-free ice. (b) Ice with 1 wt.% particles. (c) Slip bands in a particle-free zone of ice with particles.
As indicated in section 2, the staged-creep tests for investigating the stress dependence of the creep rate reached steady state (see Fig. 7b). Figure 11 illustrates the stress dependence at –10°C for both particle-free granular ice and ice with 1 wt.% particles. To eliminate the elastic and anelastic contributions to stains, the strain-rate calculations use the viscous strain experienced during each creep stage divided by the time under load (see Fig. 7b), i.e.
where t is the time. Thus, the calculation of the stress exponent uses the average viscous strain rate for each stage of loading.

Fig. 11. Stress dependence of the strain rate for particle-free ice and ice with 1 wt.% particles.
At all stress levels from 0.1 to 1.4MPa, ice with 1 wt.% particles shows higher creep rates than particle-free ice. Power-law behavior with n – 2.98 for particle-free ice and 3.03 for ice with 1 wt.% particles is observed when the creep stress is above about 0.3 MPa. However, a transition to approximately linear behavior (n = 1.15 for particle-free ice and 1.06 for ice with 1 wt.% particles) is evident when the creep stress is below about 0.3 MPa. This is somewhat higher than the 0.1 MPa that has been observed for granular freshwater ice, but can be explained on the basis of the rather high initial dislocation density of our test material, as discussed below.
The effective dislocation density was determined from the dislocation-based model (Reference ColeCole, 1995; Reference Cole and DurellCole and Durell, 2001). The model gives the loss compliance due to dislocations as ![]()
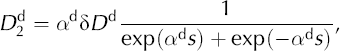
where
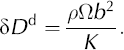
Since this model uses the anelasticity of ice (area of hysteresis loops) to calculate dislocation density, it will only include the mobile basal dislocations on the slip planes that experience a shear stress. In these equations, s = ln (τω) (τ is the temperature-dependent relaxation time for the dislocation relaxation mechanism and ω is the angular frequency of loading). The first equation contains a parameter α d, and is formulated such that the width of the relaxation peak is governed by α d, but the strength of the relaxation is constant. The value of α d is controlled by the distribution of dislocation relaxation times and can be determined from the experimental data;Ω is an orientation factor that converts the background normal stress to the average resolved shear stress on the basal planes (Ω – 0.32 for granular ice with randomly oriented grains); ρ is the dislocation density in reciprocal square meters; b is the magnitude of the Burgers vector (4.52 × 10–10 m) and K is the experimentally determined restoring stress constant (0.07 Pa). The K value was originally determined for sea ice and is assumed now to be suitable for fresh-water ice. However, the K value for fresh-water ice is the subject of ongoing work.
Figure 12 shows the dislocation density, calculated using the model developed by Reference ColeCole (1995) and Reference Cole and DurellCole and Durell (2001), as a function of creep stress. It can be seen that the initial dislocation density is about 1 × 109 m–2, which is close to that of unstrained sea ice (Reference Cole and DurellCole and Durell, 2001), and higher than most laboratory-grown fresh-water ice (Reference HigashiHigashi, 1974; Reference OguroOguro, 1988) and glacier ice (Reference Fukuda, Shoji and HigashiFukuda and Shoji, 1988). At each stress level, higher dislocation densities were noted in the ice with particles. Also, the power-law behavior observed at higher stress levels is associated with an increasing dislocation density with increasing stress, while the linear behavior observed for stress levels <0.3 MPa is associated with a dislocation density that is effectively independent of stress. This suggests that a process such as Harper–Dorn creep may operate below the threshold stress under the prevailing conditions. Note that although particles increase the creep rate, they do not affect the basic character of creep behavior: both power-law and linear behaviors are observed for particle-free ice and ice with 1 wt.% particles, and the stress exponents for both particle-free ice and ice with 1 wt.% particles have similar values.

Fig. 12. Calculated dislocation densities as a function of creep stress.
We note that the stress (~0.3 MPa) associated with the change from power-law behavior to linear behavior is rather high. Previous studies (Reference Mellor and TestaMellor and Testa, 1969; Reference Colbeck and EvansColbeck and Evans, 1973) indicated that this transition normally happens when the stress is <0.1 MPa. To explain this phenomenon the sample preparation methods need to be considered. We broke the ice plate using a hammer to produce the seed grains used in the specimens. This could easily increase the initial dislocation density of the specimens to the point where a stress above 0.3 MPa is required to generate new dislocations and thereby produce power-law behavior. In a previous study, Reference ColeCole (2003) using pre-strained (initial dislocation density of 4 × 109 m–2) fresh-water ice specimens showed that the transition could occur at ~1 MPa if the dislocation density is sufficiently high. Thus, the linear behavior with a rather high stress threshold of 0.3 MPa is due to the relatively high initial dislocation density, compared with most other studies. Actually, calculations using the dislocation-based model by Reference ColeCole (1995) and Reference Cole and DurellCole and Durell (2001) indicate that the transition stress is ~0.25 MPa for granular fresh-water ice if the dislocation density is 109m–2, which agrees well with the experimental data (transition stress is ~0.3 MPa with an initial dislocation density of 109 m–2).
The pioneering study of Reference Harper and DornHarper and Dorn (1957) on the creep of high-purity polycrystalline aluminum found that the secondary creep rate varied linearly with the stress when the stress was low and the temperature was high. Since the creep rates in the linear regime were a thousand times higher than those predicted by the Nabarro–Herring model, they developed a dislocation-climb mechanism to explain the high creep rates. Other studies (Reference Mohamed and GinterMohamed and Ginter, 1982; Reference Ruano, Wadsworth and SherbyRuano and others, 1988; Reference Ginter, Chaudhury and MohamedGinter and others, 2001) on metals (high-purity Al, β-Co, α-Fe, Ni, Mo, Cr, Cu and Ag) indicated that Harper–Dorn creep results in not only steady-state creep but also large strains of the order of 0.1–0.2 when the stress is low and the grain-size is large. Some studies (Reference Ruano, Wadsworth and SherbyRuano and others, 1988) showed that the creep rate in the Harper–Dorn regime is proportional to the square of the initial dislocation density. However, some recent studies (Reference Ginter, Chaudhury and MohamedGinter and others, 2001; Reference Blum, Eisenlohr and BreutingerBlum and others, 2002; Reference NabarroNabarro, 2002) question the Harper–Dorn creep mechanism. Reference NabarroNabarro (2002) indicated that Harper–Dorn creep is not a truly steady-state process, but a transient process of very long duration. Reference Blum, Eisenlohr and BreutingerBlum and others (2002) indicated that the inability to predict the low-stress, low-creep-rate phenomenon of Harper–Dorn creep suggests that it lacks generality. Reference Ginter, Chaudhury and MohamedGinter and others (2001) indicated that Harper–Dorn creep is not always observed unless the purity of materials is very high and the dislocation density in the annealed samples is low. However, regardless of the difficulties associated with establishing the existence of Harper–Dorn creep in ice, the key points from our observations are that we observed linear creep with a constant dislocation density when the stress was <0.3 MPa, and that this relatively high transition stress is due to a high initial dislocation density.
Reference Goldsby and KohlstedtGoldsby and Kohlstedt (2001) indicated that creep with an exponent of 1.8 was observed when the stress is low (under 0.1 MPa) which they associated with basal slip accommodated by grain boundary sliding. However, our initial grain-size (~5 mm) was much larger than that of Goldsby and Kohlstedt (<200 μm). So grain boundary sliding and the associated diffusion-based mechanisms are not ratecontrolling.
4. Conclusions
The effects of particles with an average size of 50 μm on the creep of granular ice have been studied. Based on the experimental results and model calculations, the following conclusions can be drawn:
Particles increase the creep rates of granular ice for concentrations up to at least 4 wt.%. The minimum strain rates of ice with particle concentrations from 0.5 to 4 wt.% increase by approximately 100%, compared with particle-free ice.
Ice with 1 wt.% particles shows a stress dependence that is similar to particle-free ice at –10°C. Power-law behavior with n ≈ 3 is observed for stress above 0.3 MPa for both particle-free ice and ice with 1 wt.% particles. A transition to linear behavior is observed when the stress drops below 0.3 MPa. We attribute this relatively high transition stress to a high initial dislocation density in our specimens.
Calculations show that linear creep behavior is associated with a dislocation density that is independent of stress, while power-law behavior is associated with increasing dislocation density with increasing stress.
Acknowledgements
This research was supported by US National Science Foundation Office of Polar Programs, Arctic Natural Sciences Program (OPP 011737). We thank G. Durell for his valuable assistance in developing the creep loading equipment.














