Published online by Cambridge University Press: 27 July 2023
This paper presents a robust adaptive controller based on the backstepping technique using an extended state observer (ESO), implemented on a 2PUS+RR parallel robot, to minimize the trajectory tracking error. The proposed backstepping-ESO controller scheme is designed to compensate for the robot’s structured (parametric) and unstructured (nonlinear friction, external disturbances, and dynamics) uncertainties. The overall stability of the controller is guaranteed by the Lyapunov theory. Cosimulation in MATLAB-Simulink and ADAMS View is presented to validate the results of the ESO and backstepping controller implemented in the virtual and physical prototype. For the virtual prototype, it was determined that the system is stable in 2 s and presents a maximum absolute error of 3.5 × 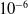 $10^{-6}$ m for the actuator position and 2.8 ×
$10^{-6}$ m for the actuator position and 2.8 × 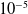 $10^{-5}$ rad for mobile platform orientation. Regarding the physical robot, a maximum absolute error of 5 ×
$10^{-5}$ rad for mobile platform orientation. Regarding the physical robot, a maximum absolute error of 5 × 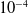 $10^{-4}$ m for the actuator position and 0.0575 rad for the orientation of the robot mobile platform values do not represent a problem for ankle rehabilitation movements. Experimental results were also presented and compared with ankle motion to demonstrate that the applied control system meets the motion requirements of the ankle rehabilitator.
$10^{-4}$ m for the actuator position and 0.0575 rad for the orientation of the robot mobile platform values do not represent a problem for ankle rehabilitation movements. Experimental results were also presented and compared with ankle motion to demonstrate that the applied control system meets the motion requirements of the ankle rehabilitator.