Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-05-04T18:03:19.948Z Has data issue: false hasContentIssue false
  • English
  • Français

On aerobreakup in the stagnation region of high-Mach-number flow over a bluff body

Published online by Cambridge University Press:  23 December 2024

A.R. Dworzanczyk Open the ORCID record for A.R. Dworzanczyk [Opens in a new window] ,
M. Viqueira-Moreira Open the ORCID record for M. Viqueira-Moreira [Opens in a new window] ,
J.D. Langhorn Open the ORCID record for J.D. Langhorn [Opens in a new window] ,
M.A. Libeau Open the ORCID record for M.A. Libeau [Opens in a new window] ,
C. Brehm Open the ORCID record for C. Brehm [Opens in a new window]  and
N.J. Parziale Open the ORCID record for N.J. Parziale [Opens in a new window]
A.R. Dworzanczyk
Affiliation:
Mechanical Engineering Department, Stevens Institute of Technology, Hoboken, NJ 07030, USA
M. Viqueira-Moreira
Affiliation:
Aerospace Engineering Department, University of Maryland, College Park, MD 20742, USA
J.D. Langhorn
Affiliation:
Mechanical Engineering Department, Stevens Institute of Technology, Hoboken, NJ 07030, USA
M.A. Libeau
Affiliation:
Integrated Engagement Systems Department, Naval Surface Warfare Center Dahlgren Division, Dahlgren, VA 22448, USA
C. Brehm
Affiliation:
Aerospace Engineering Department, University of Maryland, College Park, MD 20742, USA
N.J. Parziale*
Affiliation:
Mechanical Engineering Department, Stevens Institute of Technology, Hoboken, NJ 07030, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

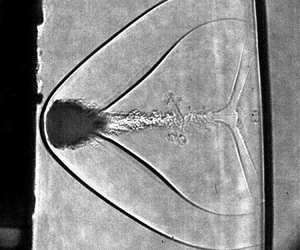
In this paper, aerobreakup in the stagnation region of high-Mach-number flow over a bluff body is studied with experiments and computations. Water drops of diameter 0.51–2.30 mm were acoustically levitated at sea level along the flight path of a rectangular $100\ {\rm mm} \times 150\ {\rm mm}$ rail-gun launched projectile. This enabled the study of aerobreakup at high Mach (3.03–5.12), post-shock Mach (1.5–1.9), Weber $(5 \times 10^4\unicode{x2013}4 \times 10^5)$ and Reynolds $(6 \times 10^4\unicode{x2013}3 \times 10^5)$ numbers. High-speed backlit shadowgraphy is used to record the flow structure. Computations are made for two cases, and it was found that the drop behaviour is not dominated by viscous or surface-tension effects and can be adequately captured by treating the gas as calorically perfect with the ratio of specific heats set to 1.3 to account for thermochemical effects. To assess drop surface stability at early breakup times, results from Newton's inclination method are used to determine the flow along the drop surface and input to a linear-stability analysis; from this, it was found that viscosity and surface tension can be neglected. Moreover, the acceleration term dominates the shear term at the stagnation point, a point accentuated as a drop flattens; this relation inverts closer to the drop equator. Linear-stability analysis was insufficient for modelling late-stage aerobreakup because the predicted wavelengths were too small and the expected aerobreakup times were non-physically short. To address this discrepancy, a nonlinear instability model with constant-rate growth is used that treats the accelerated drop surface as analogous to bubbles rising through a liquid; agreement with computations is good.

JFM classification

Compressible Flows: Gas dynamics Multiphase and Particle-laden Flows: Multiphase flow Drops and Bubbles: Breakup/coalescence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1002 , 10 January 2025 , A1
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abgrall, R. 1996 How to prevent pressure oscillations in multicomponent flow calculations: a quasi conservative approach. J. Comput. Phys. 125 (1), 150–160.CrossRefGoogle Scholar
Adler, W.F. 1975 Particulate erosion of glass surfaces at subsonic velocities. J. Non-Cryst. Solids 19, 335–353.CrossRefGoogle Scholar
Adler, W.F. 1982 Investigation of liquid drop impacts on ceramics. Tech. Rep. ETI-CR-82-1075. Office of Naval Research.Google Scholar
Adler, W.F. 1987 Development of design data for rain impact damage in infrared-transmitting windows and radomes. Opt. Engng 26 (2), 143–151.CrossRefGoogle Scholar
Adler, W.F. 1995 a Particulate impact damage predictions. Wear 186–187 (1), 35–44.CrossRefGoogle Scholar
Adler, W.F. 1995 b Waterdrop impact modeling. Wear 186–187 (2), 341–351.CrossRefGoogle Scholar
Adler, W.F. 1999 Rain impact retrospective and vision for the future. Wear 233-235, 25–38.CrossRefGoogle Scholar
Adler, W.F. & Hooker, S.V. 1978 Rain erosion mechanisms in brittle materials. Wear 50 (1), 11–38.CrossRefGoogle Scholar
Aguilera, C., Sosa, J., Hyde, E., Goodwin, G., Hess, A. & Kessler, D. 2023 Interaction of hypersonic vehicles with liquid hydrometeors. Tech. Rep. NRL/6043/MR—2023/1, AD1197391. Naval Research Laboratory.Google Scholar
Allaire, G., Clerc, S. & Kokh, S. 2002 A five-equation model for the simulation of interfaces between compressible fluids. J. Comput. Phys. 181 (2), 577–616.CrossRefGoogle Scholar
Anderson, J.D. 2011 Hypersonic and High Temperature Gas Dynamics, 2nd edn. AIAA.Google Scholar
Azouzi, M.E.M., Ramboz, C., Lenain, J.-F. & Caupin, F. 2012 A coherent picture of water at extreme negative pressure. Nat. Phys. 9 (1), 38–41.CrossRefGoogle Scholar
Barber, J.P. 1976 Water drop breakup/impact damage thresholds. Tech. Rep. AFML-TR-76-126. Air Force Materials Laboratory.Google Scholar
Barber, J.P., Taylor, H.R., Grood, E.S. & Hopkins, A.K. 1975 Water drop/bow shock interactions. Tech. Rep. AFML-TR-75-105. Air Force Materials Laboratory.CrossRefGoogle Scholar
Bass, H.E., Ezell, J. & Raspet, R. 1983 Effect of vibrational relaxation on rise times of shock waves in the atmosphere. J. Acoust. Soc. Am. 74 (5), 1514–1517.CrossRefGoogle Scholar
Bass, H.E. & Raspet, R. 1978 Vibrational relaxation effects on the atmospheric attenuation and rise times of explosion waves. J. Acoust. Soc. Am. 64 (4), 1208–1210.CrossRefGoogle Scholar
Beale, J.C. & Reitz, R.D. 1999 Modeling spray atomization with the Kelvin–Helmholtz/Rayleigh–Taylor hybrid model. Atomiz. Sprays 9 (6), 623–650.Google Scholar
Birkhoff, G. 1955 Taylor instability appendices to report LA-1862. Tech. Rep. LA-1927. Los Alamos National Laboratory.CrossRefGoogle Scholar
Boiko, V.M., Papyrin, A.N. & Poplavskii, S.V. 1987 Dynamics of droplet breakup in shock waves. J. Appl. Mech. Tech. Phys. 28, 263–269.CrossRefGoogle Scholar
Boustani, J., Barad, M.F., Kiris, C.C. & Brehm, C. 2021 An immersed boundary fluid–structure interaction method for thin, highly compliant shell structures. J. Comput. Phys. 438, 110369.CrossRefGoogle Scholar
Brehm, C., Barad, M.F. & Kiris, C.C. 2019 Development of immersed boundary computational aeroacoustic predication capabilities for open-rotor noise. J. Comput. Phys. 388, 690–716.CrossRefGoogle Scholar
Brehm, C., Hader, C. & Fasel, H.F. 2015 A locally stablilized immersed boundary method for the compressible Navier–Stokes equations. J. Comput. Phys. 295, 475–504.CrossRefGoogle Scholar
Browne, S.T., Ziegler, J.L., Bitter, N.P., Schmidt, B.E., Lawson, J. & Shepherd, J.E. 2018 Numerical solution methods for shock and detonation jump conditions. GALCIT - FM2018-001. Caltech.Google Scholar
Bryson, A.E. & Gross, R.W.F. 1961 Diffraction of strong shocks by cones, cylinders, and spheres. J. Fluid Mech. 10 (1), 1–16.CrossRefGoogle Scholar
Callens, E.E. Jr. & Lawrence, W.R. 1981 Study of impact frequency effects on hypervelocity erosion processes. Tech. Rep. AEDC-TR-81-15. Arnold Engineering Development Center.CrossRefGoogle Scholar
Caupin, F., Arvengas, A., Davitt, K., Azouzi, M.E.M., Shmulovich, K.I., Ramboz, C., Sessoms, D.A. & Stroock, A.D. 2012 Exploring water and other liquids at negative pressure. J. Phys.: Condens. Matter 24 (28), 284110.Google ScholarPubMed
Chou, W.-H., Hsiang, L.-P. & Faeth, G.M. 1997 Temporal properties of drop breakup in the shear breakup regime. Intl J. Multiphase Flow 23 (4), 651–669.CrossRefGoogle Scholar
Danehy, P.M., Weisberger, J., Johansen, C., Reese, D., Fahringer, T., Parziale, N.J., Dedic, C., Estevadeordal, J. & Cruden, B.A. 2018 Non-intrusive measurement techniques for flow characterization of hypersonic wind tunnels. In Flow Characterization and Modeling of Hypersonic Wind Tunnels, NATO Science and Technology Organization Lecture Series STO-AVT 325, NF1676L-31725. Von Kármán Institute.Google Scholar
Daniel, K.A., Guildenbecher, D.R., Delgado, P.M., White, G.E., Reardon, S.M., Stauffacher III, H.L. & Beresh, S.J. 2023 Drop interactions with the conical shock structure generated by a Mach 4.5 projectile. AIAA J. 61 (6), 2347–2355.CrossRefGoogle Scholar
Davies, R.M. & Taylor, G. 1950 The mechanics of large bubbles rising through extended liquids and through liquids in tubes. Proc. R. Soc. Lond. A Math. Phys. Sci. 200, 375–390.Google Scholar
Dorschner, B., Biasiori-Poulanges, L., Schmidmayer, K., El-Rabii, H. & Colonius, T. 2020 On the formation and recurrent shedding of ligaments in droplet aerobreakup. J. Fluid Mech. 904, A20.CrossRefGoogle Scholar
Drazin, P.G. & Reid, W.H. 2004 Hydrodynamic Stability. Cambridge University Press.CrossRefGoogle Scholar
Engel, O.G. 1955 Waterdrop collisions with solid surfaces. J. Res. Natl Bur. Stand. (1934) 54 (5), 281–298.CrossRefGoogle Scholar
Engel, O.G. 1958 Fragmentation of waterdrops in the zone behind an air shock. J. Res. Natl Bur. Stand. (1934) 60 (3), 245–280.CrossRefGoogle Scholar
Fishburn, B.D. 1974 Boundary layer stripping of liquid drops fragmented by Taylor instability. Acta Astronaut. 1 (9), 1267–1284.CrossRefGoogle Scholar
Funada, T. & Joseph, D.D. 2001 Viscous potential flow analysis of Kelvin–Helmholtz instability in a channel. J. Fluid Mech. 445, 263–283.CrossRefGoogle Scholar
Garabedian, P.R. 1957 On steady-state bubbles generated by Taylor instability. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 241 (1226), 423–431.Google Scholar
Gohardani, O. 2011 Impact of erosion testing aspects on current and future flight conditions. Prog. Aerosp. Sci. 47 (4), 280–303.CrossRefGoogle Scholar
Goodwin, D.G. 2003 An open-source, extensible software suite for CVD process simulation. In Proceedings of CVD XVI and EuroCVD Fourteen (ed. M. Allendorf, F. Maury & F. Teyssandier), pp. 155–162.Google Scholar
Goodwin, D.G., Moffat, H.K., Schoegl, I., Speth, R.L. & Weber, B.W. 2022 Cantera: an object-oriented software toolkit for chemical kinetics, thermodynamics, and transport processes. Available at: https://www.cantera.org.Google Scholar
Hanson, A.R., Domich, E.G. & Adams, H.S. 1963 Shock tube investigation of the breakup of drops by air blasts. Phys. Fluids 6 (8), 1070–1080.CrossRefGoogle Scholar
Hauser, E.A., Edgerton, H.E., Holt, B.M. & Cox, J.T. Jr. 1936 The application of the high-speed motion picture camera to research on the surface tension of liquids. J. Phys. Chem. 40 (8), 973–988.CrossRefGoogle Scholar
Hébert, D., Rullier, J.-L., Chevalier, J.-M., Bertron, I., Lescoute, E., Virot, F. & El-Rabii, H. 2020 Investigation of mechanisms leading to water drop breakup at Mach 4.4 and Weber numbers above $10^5$. SN Appl. Sci. 2, 1–23.CrossRefGoogle Scholar
Helmholtz, H.L.F. 1868 XLIII. On discontinuous movements of fluids. Lond. Edinb. Dublin Phil. Mag. J. Sci. 36 (244), 337–346.CrossRefGoogle Scholar
Hess, A., Kessler, D.A., Johnson, R.F., Goodwin, G.B., Aguilera, C. & Sosa, J. 2021 Evaluation of droplet aerodynamic breakup models in supersonic and hypersonic flows. In Proceedings of AIAA Scitech. Virtual Event: AIAA 2021-0751. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Hinze, J.O. 1949 a Critical speeds and sizes of liquid globules. Appl. Sci. Res. 1, 273–288.CrossRefGoogle Scholar
Hinze, J.O. 1949 b Forced deformations of viscous liquid globules. Appl. Sci. Res. 1, 263–272.CrossRefGoogle Scholar
Hinze, J.O. 1955 Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes. AIChE J. 1 (3), 289–295.CrossRefGoogle Scholar
Hong, Q., Wang, X., Hu, Y. & Sun, Q. 2020 Development of a stagnation streamline model for thermochemical nonequilibrium flow. Phys. Fluids 32 (4), 046102.CrossRefGoogle Scholar
Hornung, H.G. 1972 Non-equilibrium dissociating nitrogen flow over spheres and circular cylinders. J. Fluid Mech. 53 (1), 149–176.CrossRefGoogle Scholar
Hsiang, L.-P. & Faeth, G.M. 1995 Drop deformation and breakup due to shock wave and steady disturbances. Intl J. Multiphase Flow 21 (4), 545–560.CrossRefGoogle Scholar
Jaffe, N.A. 1975 Experimental investigation of the interaction between strong shock waves and water droplets. Tech. Rep. ADA035093. Aerotherm Division of Acurex Corporation.Google Scholar
Jain, S.S., Tyagi, N., Prakash, R.S., Ravikrishna, R.V. & Tomar, G. 2019 Secondary breakup of drops at moderate Weber numbers: effect of density ratio and Reynolds number. Intl J. Multiphase Flow 117, 25–41.CrossRefGoogle Scholar
Jalaal, M. & Mehravaran, K. 2014 Transient growth of droplet instabilities in a stream. Phys. Fluids 26 (1), 012101.CrossRefGoogle Scholar
Jenkins, D.C. 1966 Disintegration of raindrops by shockwaves ahead of conical bodies. Phil. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 260 (110), 153–160.Google Scholar
Joseph, D.D., Beavers, G.S. & Funada, T. 2002 Rayleigh–Taylor instability of viscoelastic drops at high Weber numbers. J. Fluid Mech. 453, 109–132.CrossRefGoogle Scholar
Joseph, D.D., Belanger, J. & Beavers, G.S. 1999 Breakup of a liquid drop suddenly exposed to a high-speed airstream. Intl J. Multiphase Flow 25 (6–7), 1263–1303.CrossRefGoogle Scholar
Kao, S., Ziegler, J.L., Bitter, N.P., Schmidt, B.E., Lawson, J. & Shepherd, J.E. 2023 Numerical solution methods for shock and detonation jump conditions. GALCIT - FM2018-001. Caltech.Google Scholar
Kelvin, W.T. 1871 XLVI. Hydrokinetic solutions and observations. Lond. Edinb. Dublin Phil. Mag. J. Sci. 42 (281), 362–377.Google Scholar
Krauss, W.E. 1970 Water drop deformation and fragmentation due to shock wave impact. PhD thesis, University of Florida.CrossRefGoogle Scholar
Kull, H.J. 1986 Nonlinear free-surface Rayleigh–Taylor instability. Phys. Rev. A 33 (3), 1957–1967.CrossRefGoogle ScholarPubMed
Kull, H.J. 1991 Theory of the Rayleigh–Taylor instability. Phys. Rep. 206 (5), 197–325.CrossRefGoogle Scholar
Lane, W.R. 1951 Shatter of drops in streams of air. Ind. Engng Chem. 43 (6), 1312–1317.CrossRefGoogle Scholar
Lapp, R.R., Stutzman, R.H. & Wahl, N.E. 1954 A study of rain erosion in plastics and metals. Tech. Rep. WADC 53-185. Wright Air Development Center.Google Scholar
Lee, M.W., Park, J.J., Farid, M.M. & Yoon, S.S. 2012 Comparison and correction of the drop breakup models for stochastic dilute spray flow. Appl. Math. Model. 36 (9), 4512–4520.CrossRefGoogle Scholar
Lees, L. 1956 Hypersonic flow. In Proceedings of 5th International Aeronautical Conference, pp. 241–276. Institute of Aeronautical Sciences.Google Scholar
Leibowitz, M.G. 2020 Hypervelocity shock tunnel studies of blunt body aerothermodynamics in carbon dioxide for Mars entry. PhD thesis, California Institute of Technology.Google Scholar
Leyva, I.A. 2017 The relentless pursuit of hypersonic flight. Phys. Today 70 (11), 30–36.CrossRefGoogle Scholar
Loth, E. 2008 Compressibility and rarefaction effects on drag of a spherical particle. AIAA J. 46 (9), 2219–2228.CrossRefGoogle Scholar
Marzo, A., Barnes, A. & Drinkwater, B.W. 2017 TinyLev: a multi-emitter single-axis acoustic levitator. Rev. Sci. Instrum. 88 (8), 085105.CrossRefGoogle ScholarPubMed
Meng, J.C. & Colonius, T. 2015 Numerical simulations of the early stages of high-speed droplet breakup. Shock Waves 25, 399–414.CrossRefGoogle Scholar
Meng, J.C. & Colonius, T. 2018 Numerical simulation of the aerobreakup of a water droplet. J. Fluid Mech. 835, 1108–1135.CrossRefGoogle Scholar
Moylan, B., Landrum, B. & Russell, G. 2013 Investigation of the physical phenomena associated with rain impacts on supersonic and hypersonic flight vehicles. Procedia Engng 58, 223–231.CrossRefGoogle Scholar
Nicholson, J.E. 1967 Drop breakup by airstream impact. Tech. Rep. AD0666525. Mithras.Google Scholar
O'Haver, T. 1997 A Pragmatic Introduction to Signal Processing. University of Maryland.Google Scholar
Olivier, H. 1993 An improved method to determine free stream conditions in hypersonic facilities. Shock Waves 3, 129–139.CrossRefGoogle Scholar
Olivier, H. 2000 A theoretical model for the shock stand-off distance in frozen and equilibrium flows. J. Fluid Mech. 413, 345–353.CrossRefGoogle Scholar
O'Rourke, P.J. & Amsden, A.A. 1987 The tab method for numerical calculation of spray droplet breakup. In Proceedings of International Fuels and Lubricants Meeting and Exposition. SAE 872089. Society of Automotive Engineers.CrossRefGoogle Scholar
O'Rourke, R. 2017 Navy lasers, railgun, and hypervelocity projectile: background and issues for congress. R44175. Congressional Research Service.Google Scholar
Perigaud, G. & Saurel, R. 2005 A compressible flow model with capillary effects. J. Comput. Phys. 209 (1), 139–178.CrossRefGoogle Scholar
Pilch, M. & Erdman, C.A. 1987 Use of breakup time data and velocity history data to predict the maximum size of stable fragments for acceleration-induced breakup of a liquid drop. Intl J. Multiphase Flow 13 (6), 741–757.CrossRefGoogle Scholar
Pilch, M., Erdman, C.A. & Reynolds, A.B. 1981 Acceleration induced fragmentation of liquid drops. Tech. Rep. Nureg/cr-2247. Department of Nuclear Engineering, University of Virginia.CrossRefGoogle Scholar
Ranger, A.A. & Nicholls, J.A. 1969 Aerodynamic shattering of liquid drops. AIAA J. 7 (2), 285–290.Google Scholar
Ranger, A.A. & Nicholls, J.A. 1972 Atomization of liquid droplets in a convective gas stream. Intl J. Heat Mass Transfer 15 (6), 1203–1211.CrossRefGoogle Scholar
Reinecke, W.G. 1974 Debris shielding during high-speed erosion. AIAA J. 12 (11), 1592–1594.CrossRefGoogle Scholar
Reinecke, W.G. & McKay, W.L. 1969 Experiments on water drop breakup behind Mach 3 to 12 shocks. Tech. Rep. SC-CR-70-6063. AVCO Government Products Group.CrossRefGoogle Scholar
Reinecke, W.G. & Waldman, G.D. 1975 Shock layer shattering of cloud drops in reentry flight. In Proceedings of 13th Aerospace Sciences Meeting. AIAA 1975-152. American Institute of Aeronautics and Astronautics.Google Scholar
Salauddin, S., Morales, A.J., Hytovick, R., Burke, R., Malik, V., Patten, J., Schroeder, S. & Ahmed, K.A. 2023 Detonation and shock-induced breakup characteristics of RP-2 liquid droplets. Shock Waves 33 (3), 191–203.CrossRefGoogle Scholar
Schmehl, R. 2002 Advanced modeling of droplet deformation and breakup for CFD analysis of mixture preparation. In Proceedings of the 18th Annual Conference on Liquid Atomization and Spray Systems. ILASS-Europe-012.Google Scholar
Schmitt, G.F. Jr. 1975 Influence of rainfall intensity on erosion of materials at supersonic velocities. J. Aircraft 12 (10), 761–762.CrossRefGoogle Scholar
Segall, B.A., Shekhtman, D., Hameed, A., Chen, J.H. & Parziale, N.J. 2023 Profiles of streamwise velocity and fluctuations in a hypersonic turbulent boundary layer using acetone tagging velocimetry. Exp. Fluids 64, 122.CrossRefGoogle Scholar
Settles, G.S. 2001 Schlieren and Shadowgraph Techniques, 1st edn. Springer.CrossRefGoogle Scholar
Sheldon, R. 2019 ParametricLev. GitHub.Google Scholar
Simpkins, P.G. & Bales, E.L. 1972 Water-drop response to sudden accelerations. J. Fluid Mech. 55, 629–639.CrossRefGoogle Scholar
Smith, D.H. 1976 Debris shielding in regions of high edge velocity. AIAA J. 14 (1), 94–96.CrossRefGoogle Scholar
Stefanitsis, D., Strotos, G., Nikolopoulos, N., Kakaras, E. & Gavaises, M. 2019 Improved droplet breakup models for spray applications. Intl J. Heat Fluid Flow 76, 274–286.CrossRefGoogle Scholar
Stine, H.A. & Wanlass, K. 1954 Theoretical and experimental investigation of aerodynamic-heating and isothermal heat-transfer parameters on a hemispherical nose with laminar boundary layer at supersonic Mach numbers. NACA Tech. Rep. TN 3344.Google Scholar
Stoffel, T.D., Viqueira-Moreira, M., Brehm, C. & Poovathingal, S.J. 2023 Application of a diffuse interface multiphase method for high temperature and hypersonic flows with phase change. In AIAA SCITECH 2023 Forum, p. 2305. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Stulov, V.P. 1969 Similarity law for supersonic flow past blunt bodies. Fluids Dyn. 4, 93–96.CrossRefGoogle Scholar
Su, T.F., Patterson, M.A., Reitz, R.D. & Farrell, P.V. 1996 Experimental and numerical studies of high pressure multiple injection sprays. SAE Trans. 105, 1281–1292.Google Scholar
Tadjdeh, Y. 2017 Navy's electromagnetic railgun project progressing. Natl Def. 102 (764), 33–34.Google Scholar
Theofanous, T.G. 2011 Aerobreakup of Newtonian and viscoelastic liquids. Annu. Rev. Fluid Mech. 43 (1), 661–690.CrossRefGoogle Scholar
Theofanous, T.G. & Li, G.J. 2008 On the physics of aerobreakup. Phys. Fluids 20 (5), 052103.CrossRefGoogle Scholar
Theofanous, T.G., Li, G.J. & Dinh, T.N. 2004 Aerobreakup in rarefied supersonic gas flows. Trans. ASME 126, 516–527.Google Scholar
Theofanous, T.G., Li, G.J., Dinh, T.N. & Chang, C.-H. 2007 Aerobreakup in disturbed subsonic and supersonic flow fields. J. Fluid Mech. 193, 131–170.CrossRefGoogle Scholar
Theofanous, T.G., Mitkin, V.V., Ng, C.L., Chang, C.H., Deng, X. & Sushchikh, S. 2012 The physics of aerobreakup. II. Viscous liquids. Phys. Fluids 24, 022104.CrossRefGoogle Scholar
Thompson, P.A. 1988 Compressible-Fluid Dynamics. McGraw-Hill.Google Scholar
Viqueira-Moreira, M., Dworzanczyk, A., Parziale, N.J. & Brehm, C. 2023 a Numerical investigation of droplet aerobreakup and impingement experiments at Mach 5. In Proceedings of AIAA Aviation 2023. Virtual Event: AIAA-2023-4251. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Viqueira-Moreira, M., Gonuleri, R.K., Leigh, J.R., Watson, K., Guven, I. & Brehm, C. 2023 b Higher-order simulations of droplet-shock interaction, aerobreakup and impingement at high Mach numbers. In AIAA SCITECH 2023 Forum, p. 2305. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Viqueira-Moreira, M., Stoffel, T.D., Poovathingal, S.J. & Brehm, C. 2022 Validation of a high-order diffuse interface multi-phase method for high-speed droplet shock interaction and impingement. In AIAA AVIATION 2022 Forum, p. 3922. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Virot, F., Tymen, G., Hébert, D., Rullier, J.-L. & Lescoute, E. 2023 Experimental investigation of the interaction between a water droplet and a shock wave above Mach 4. Shock Waves 33 (5), 369–383.CrossRefGoogle Scholar
Waldman, G.D. & Reinecke, W.G. 1971 Particle trajectories, heating, and breakup in hypersonic shock layers. AIAA J. 9 (6), 1040–1048.CrossRefGoogle Scholar
Waldman, G.D., Reinecke, W.G. & Glenn, D.C. 1972 Raindrop breakup in the shock layer of a high-speed vehicle. AIAA J. 10 (9), 1200–1204.CrossRefGoogle Scholar
Wang, Z., Hopfes, T., Giglmaier, M. & Adams, N.A. 2020 Effect of Mach number on droplet aerobreakup in shear stripping regime. Exp. Fluids 61 (193), 1–17.CrossRefGoogle ScholarPubMed
Wen, C.Y. & Hornung, H.G. 1995 Non-equilibrium dissociating flow over spheres. J. Fluid Mech. 299, 389–405.CrossRefGoogle Scholar
White, D.R. & Millikan, R.C. 1964 Vibrational relaxation in air. AIAA J. 2 (10), 1844–1846.CrossRefGoogle Scholar
Wierzba, A. & Takayama, K. 1988 Experimental investigation of the aerodynamic breakup of liquid drops. AIAA J. 26 (11), 1329–1335.CrossRefGoogle Scholar
Wong, M.L., Angel, J.B., Barad, M.F. & Kiris, C.C. 2021 A positivity-preserving high-order weighted compact nonlinear scheme for compressible gas-liquid flows. J. Comput. Phys. 444, 110569.CrossRefGoogle Scholar
Yanes, N.J. 2020 Ultraviolet radiation of hypervelocity stagnation flows and shock/boundary-layer interactions. PhD thesis, California Institute of Technology.Google Scholar
Zhou, Y., et al. 2021 Rayleigh–Taylor and Richtmyer–Meshkov instabilities: a journey through scales. Phys. D: Nonlinear Phenom. 423, 132838.CrossRefGoogle Scholar
Supplementary material: File

Dworzanczyk et al. supplementary movie 1

“First Successful Aerobreakup Experiment at railgun facility. A drop of diameter 1.89 mm is processed by a Mach 4.22 Projectile Bow Shock.”
Download Dworzanczyk et al. supplementary movie 1(File)
File 8.4 MB
Supplementary material: File

Dworzanczyk et al. supplementary movie 2

“Two drops (diameters 1.80 and 0.51 mm) are processed by a Mach 4.44 Projectile Bow Shock. The smaller drop reaches a much higher characteristic breakup time and totally breaks up before impact.”
Download Dworzanczyk et al. supplementary movie 2(File)
File 9.9 MB
Supplementary material: File

Dworzanczyk et al. supplementary movie 3

“Processing of Drop 3 (diameter 1.87 mm) by a Mach 5.12 Projectile Bow Shock.”
Download Dworzanczyk et al. supplementary movie 3(File)
File 8.7 MB
Supplementary material: File

Dworzanczyk et al. supplementary movie 4

“Processing of Drop 4 (diameter 1.99 mm) by a Mach 4.96 Projectile Bow Shock.”
Download Dworzanczyk et al. supplementary movie 4(File)
File 10.4 MB
Supplementary material: File

Dworzanczyk et al. supplementary movie 5

“Processing of Drops 5A (diameter 2.30 mm) and 5B (diameter 1.72 mm) by a Mach 4.92 Projectile Bow Shock.”
Download Dworzanczyk et al. supplementary movie 5(File)
File 7.9 MB
Supplementary material: File

Dworzanczyk et al. supplementary movie 6

“Processing of Drops 6A (diameter 2.18 mm) and 6B (diameter 1.27 mm) by a Mach 3.03 Projectile Bow Shock. Drop 6B appears to break up before impact.”
Download Dworzanczyk et al. supplementary movie 6(File)
File 7.1 MB
Supplementary material: File

Dworzanczyk et al. supplementary movie 7

“Railgun projectile flying through an acoustic levitator used in this experiment campaign.”
Download Dworzanczyk et al. supplementary movie 7(File)
File 6 MB