INTRODUCTION
Human salmonellosis is the second most common foodborne zoonosis in Europe, causing 160 649 confirmed cases in 2006 [1]. There are more than 2400 different serovars of Salmonella and the EU has designated Salmonella Enteritidis, S. Typhimurium, S. Hadar, S. Infantis and S. Virkow as Salmonella of public health significance as these are the most frequent serovars encountered in human disease. Of these, S. Typhimurium is the second most common serovar being isolated from 13% of human cases. An EU baseline survey of slaughter pigs was conducted between 2006 and 2007. Culture of lymph node samples showed that 10·3% of these pigs were infected with Salmonella spp. and the most common serovar was S. Typhimurium, which was isolated from the lymph nodes of 4·7% of slaughtered pigs [2]. There was a marked variation in the prevalence of S. Typhimurium in the lymph nodes of slaughtered pigs amongst member states. For example, the UK (13·8%) and Spain (10·6%) showed the highest prevalence of S. Typhimurium; Germany (6·1%), Denmark (4·5%) and The Netherlands (4·9%) showed a moderate prevalence and Poland (1·8%), Sweden (1·2%) and Finland (0%) showed a low prevalence. It is important to note that S. Typhimurium has also been isolated from a wide range of other domestic animals including poultry, cattle and sheep.
Regulation (EC) No. 2160/2003 of the European Commission provides for the setting of targets for the reduction of Salmonella in livestock in order to protect public health. In addition to the abattoir-based survey of fattening pigs that has been completed, the EU began a survey of breeding-pig holdings in January 2008 (EU Decision 2007/636/EC). In order for this survey to be conducted efficiently, a pooled sampling approach was adopted [3]. Pooled sampling offers advantages because fewer samples per farm need to be collected, which reduces technician time on farm. This also reduces disruption to normal farming business and thus, reduces the cost to industry. Since pooled faecal samples can be collected from a floor or paddock, no animal handling is required which greatly reduces impact on animal welfare and obviates animal handling costs. Finally, fewer samples reduce laboratory costs and the risk of over-stretching laboratory resources to the detriment of other routine work. However, it is important if the survey results are to be valid that the pooled sample sensitivity is known. This information is also necessary in order to estimate appropriate sample sizes to detect Salmonella infection at a pre-defined prevalence. Since the survey results will be used to inform the setting of targets to reduce the prevalence of infection with the ultimate aim of protecting public health, it is important for policy-makers and the producers who have to bear the costs of intervention that the results can be interpreted with confidence. It is also anticipated that further surveys might be conducted to monitor progress towards a set target by individual member states and that another baseline survey might be undertaken to confirm progress at an EU level. Thus, it is important that methodology is replicable and an estimation of pooled sample sensitivity is crucial for this purpose.
The objective of this study was to estimate sample sizes for pooled-pen faecal sampling to detect Salmonella in pig herds. Previous work [Reference Arnold, Cook and Davies4] has studied the sensitivity of pooled faecal samples, but there was uncertainty about how applicable these results were to pooled samples taken in the field due to the artificial nature of the creation of the pools. Therefore, the results of parallel sampling of pooled and individual samples from several pens of pigs from nine farms were analysed to obtain a comparison between pooling and individual sampling, where the pooling of samples was carried out as would usually be performed in surveillance. Analysis of these results provides an updated estimate of the sensitivity of pooled sampling, which is then used to estimate sample sizes. Furthermore, an important factor in detecting infection on a farm is the level of clustering of infection within pens. A large degree of clustering would mean that only a fraction of the infected pens would have sufficient infected pigs to be easily detected, and would influence the sample sizes required. Therefore, the data were also used to estimate the degree of clustering of Salmonella on pig farms, and this is incorporated into the estimation of sample sizes.
MATERIALS AND METHODS
Data collection
The nine farms were from 46 that had been selected at random from a national database and recruited to another study [5]. On each farm, a random selection of up to 40 pens were monitored from entry of pigs at about age 10 weeks through to despatch for slaughter at about age 24 weeks. Pooled faecal samples were collected from each pen at 4-weekly intervals. At the final, pre-slaughter visit, replicate pooled samples were collected and additional individual samples were obtained by rectal sampling. All samples were cultured for the isolation of Salmonella bacteria. Briefly, samples were pre-enriched in buffered peptone water and selectively enriched in Diassalm agar plates. Samples from this were inoculated onto a Rambach agar plate and suspected Salmonella colonies were subjected to a slide agglutination test using a range of typing sera and to the minimum phenotypic criteria for identification of Salmonella spp. [Reference Davies, Bedford and Shankster6]. A subculture of each confirmed Salmonella isolate was submitted for full serotyping and phage typing, where applicable.
Statistical methods
Model formulation
The data in the present study consist of a set of herds where both pooled faecal samples and individual rectal samples were taken from selected pens. This is a parallel situation to one considered in previous studies [Reference Branscum, Gardner and Johnson7, Reference Branscum, Johnson and Gardner8], where a Bayesian approach was developed to estimate both the region-level prevalence for a set of regions and the within-herd prevalence of each herd within each region. Therefore, we adopted a similar approach to that developed in [Reference Branscum, Gardner and Johnson7, Reference Branscum, Johnson and Gardner8], where in the present study herd was the equivalent of region and pen equivalent to herd in [Reference Branscum, Gardner and Johnson7, Reference Branscum, Johnson and Gardner8].
The resulting data for herd i and pen j are the number of rectal-test-positive individual pigs, y ij out of n ij tested and the number of positive pooled faecal samples x ij out of m ij tested. We assume that the data {y ij} and {x ij} follow binomial distributions:
where ηind, ηpool are the individual rectal sample and pooled pen faecal-sample sensitivity, respectively, and πij is the prevalence of infection in herd i and pen j.
The sensitivity of faecal sampling for Salmonella has been investigated previously [Reference Arnold, Cook and Davies4], where it was shown that the sensitivity of a pooled faecal sample of weight w consisting of a proportion π of positive faecal samples was given by:
where C and ρ were parameters estimated from experimental data. C represents the concentration of Salmonella clusters in pig faeces and ρ is a parameter that relates the probability of successful culture to the concentration of Salmonella clusters in the sample [Reference Arnold, Cook and Davies4]. Equation (1) describes the dilution effect of mixing positive and negative samples, since it was found in [Reference Arnold, Cook and Davies4] that the sensitivity of pooled sampling reduces as the proportion of positive samples in the pool reduces. This means that the value of ηpool will vary between pens according to πij.
We assume that the value of ηind varies according to the mass of faecal samples as determined by equation (1), and with π=1, i.e. an individual sample is equivalent to a pooled sample of equivalent weight but with all samples positive. Sample weight for individual samples, obtained via rectal palpation, was not known but it was estimated by those weighing the samples that 90% of samples weighed about 10 g, 3% weighed between 5 g and 9 g, 1·5% weighed between 1 g and 4 g, and from 5% of pigs no faecal samples were obtained. These pigs were sampled on farm immediately before despatch to slaughter, at around age 24 weeks and a bodyweight of around 90–120 kg. The amount of faecal material that could be collected was limited as many pigs had only scant rectal content. It is common practice not to feed pigs on the day before they are sent to the abattoir.
We expect that πij will depend on both the overall individual-level Salmonella prevalence in the herd and how that prevalence is distributed between pens. Since there is not homogenous mixing, i.e. pigs will have much closer contact with their pen mates than other pigs, we expect the prevalence to be clustered at the pen-level. This will influence πij because this will result in an excess of cases where the proportion of positive pigs in each pen is more extreme than would be expected from random sampling without any clustering of infection, in other words, the within-pen prevalence will be very high in some cases and very low in others. This will result in a higher variance for the distribution of positive pigs in each pen. Therefore πij was assumed to follow a beta distribution:
where a i=μiψ/τ, b=(1−μi/τ)ψ, and the parameter τ allows for the possibility that there are no infected pigs in the pen. This formulation, previously employed in [Reference Branscum, Gardner and Johnson7], allows for the mean animal-level prevalence in herd i to be fixed at μi (the mean prevalence in proportion τ infected pens equals μi/τ), but for the variance to vary according to ψ, with greater values of ψ resulting in lower values of variance (since the variance of the beta distribution is given by μi(1−μi)/(1+ψ)). It is possible that the prevalence of Salmonella-positive samples in the pool could differ from that of the pen, but since each pooled sample is made up of 10 environmental samples from different parts of the pen, each of which may contain contributions from several individual faecal samples, we expect there to be a close relationship between the distribution of prevalence in the pooled sample and the pen.
The parameter τ will depend upon the animal-level prevalence in the herd since if μi=1, then τ=1 (i.e. if all pigs in the herd are infected then all pens will be infected) and similarly if μi=0, then τ=0. We model this by assuming that
This satisfies the constraints that μi=1, then τ=1 and μi=0, then τ=0 and allows for a possible sublinear, linear and super-linear increase in the number of infected pens as the proportion of infected animals in the herd increases, according to the value of α. We also allow for the probability that the farm i is uninfected, with probability υi. The parameter α was constrained to be at most equal to 1 to ensure that τ was between 0 and 1.
Priors
The parameter μ was given a beta prior, the parameters of which were obtained by fitting a beta distribution to results from routine serological testing of pigs sent to abattoir in the UK in 2005. These data also provided a prior for the proportion of farms expected to be uninfected from the number of negative farms out of the number of farms tested. A prior for ψ was obtained by fitting a model of the form beta(μiψ(1−μi)ψ) to the output of a previously published stochastic simulation model of Salmonella transmission within and between pens on a UK finisher farm [Reference Hill9].
The sensitivity of individual samples (and its associated uncertainty) was assumed to follow the dependence on weight estimated in [Reference Arnold, Cook and Davies4]. The parameters C, ρ and their associated uncertainties were taken from the results in [Reference Arnold, Cook and Davies4].
The estimates for all the priors are given in Table 1. The estimation of the posterior densities of the unknown parameters was performed in WinBUGS 3.1.
Table 1. Summary of the priors used in the Bayesian model of pen-level prevalence of Salmonella on nine farms from the UK and their source

ZAP, Zoonoses Action Plan in the UK, under which routine serological testing of pigs sent to abattoir is carried out.
Estimation of sample sizes
From binomial probabilities, assuming that k pooled samples are tested from a farm, the probability of at least one positive sample is given by [Reference Cannon and Roe10]:
where ηpool(i) is the sensitivity of a pooled sample from the ith pen [given by equation (1)], and will depend upon the animal-level prevalence in the pen. The number of samples required for a detection probability of 95% for animal-level prevalence on farm of 30, 20, 10, 5, 2 and 1% was obtained by simulating the prevalence in each pen and calculating the resulting probability of detection for a range of sample sizes. The number of pens infected at each iteration was sampled from a binomial distribution with parameter p given by equation (2), and the animal-level prevalence in the pen sampled from the beta distribution as described above, with the overall animal-level prevalence constrained to equal 30, 20, 10, 5, 2 and 1% in turn. The number of samples required was taken to equal the least sample size for which the median probability of detection was >95%, sampled over 10 000 iterations. To explore the impact of the number of pens on the number of samples required, three scenarios were considered: 200 pens (representing the case where the number of pens sampled is much larger than the number of pens in the farm), 20 pens and 10 pens.
Where the number of samples required was larger than the number of pens then each pen was sampled once and then a second sample was taken from sufficient pens to achieve the estimated sample size. If more than two samples per pen were required then all pens would be sampled twice before third samples were taken, and so on. Sample size calculations were performed in Matlab 7.5.0.
RESULTS
Of the nine farms tested, six of them had positive faecal samples (Table 2). The results show highly variable prevalence of positive faecal samples, resulting in a range of estimates of the animal-level prevalence in the set of herds between 0% and 47% (Table 2). On all the positive farms, the proportion of pooled samples that were positive was higher than the proportion of individual samples that were positive, indicating that pooled sampling is more cost-effective on a per-sample basis than individual sampling. The proportion of positive pens was always higher than the proportion of positive pooled faecal samples (and the estimated animal-level prevalence), and this was reflected in an estimate of α close to 1 (Table 2), and this results in the relationship between the prevalence of infected pigs (in the herd) and the proportion of infected pens as given in Figure 1.
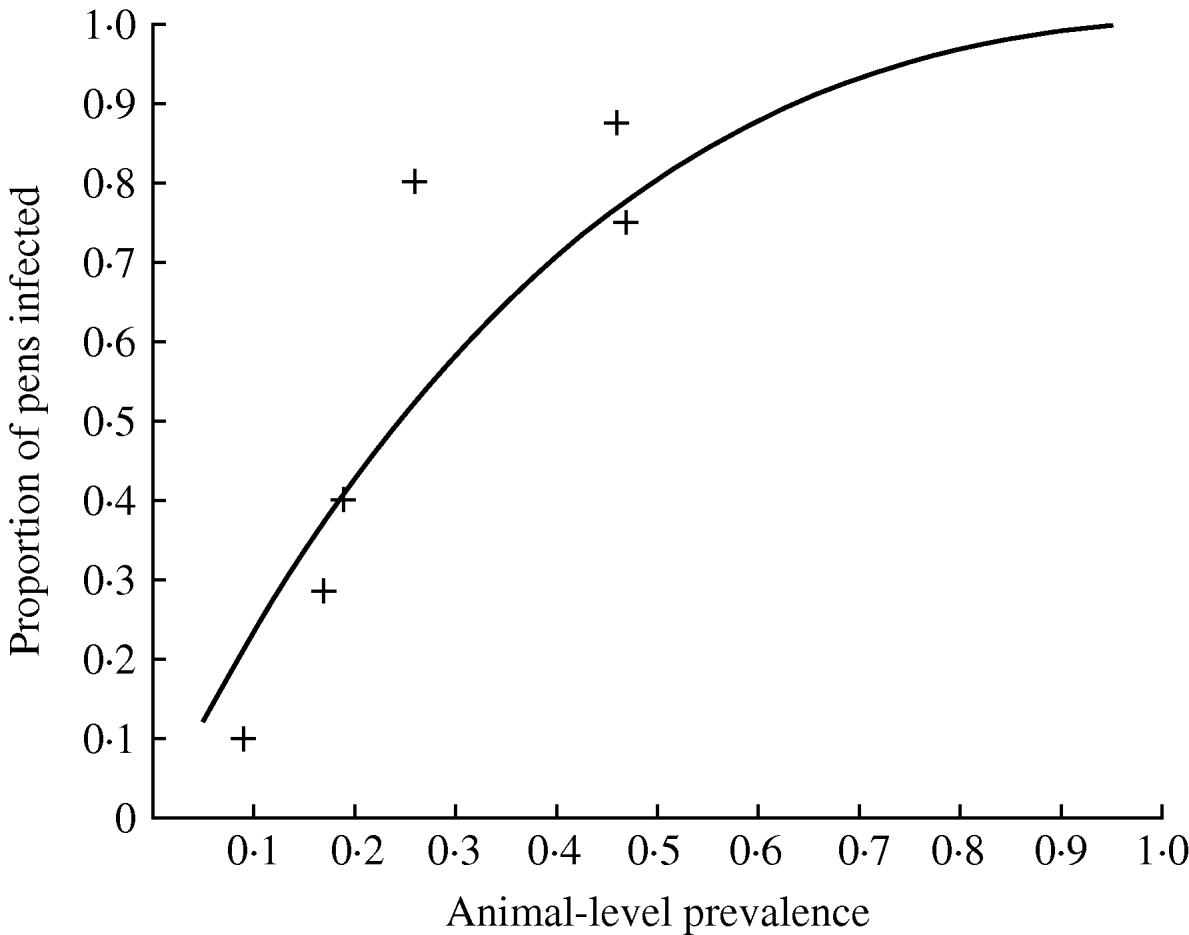
Fig. 1. How the proportion of pens infected varies according to the animal-level prevalence for Salmonella in pigs. The observed proportion of positive pens for the positive farms in a UK study are given by crosses (+) (the observed values are lower than the predicted proportion of positive pens at low prevalence since it is likely that some truly positive pens will be false negatives at low prevalence).
Table 2. Farm-level data for the results of the pooled and individual sample testing for Salmonella in pigs in the UK, and estimated mean prevalence of animal-level infection for each farm

The parameter ψ, determining the variance of the beta distribution describing pen-level prevalence, had a median value 2·69 (Table 3). The impact of this degree of clustering on the expected number of true positives in a pooled sample comprising 10 individual samples is shown in Figure 2, where it can be seen that clustering results in a much larger probability of having no infected samples in the pooled sample (since more pens will have no infected pigs) and also a larger probability of having a pooled sample containing all infected samples. The inclusion of the effect of clustering of infection within pens had the effect of reducing the mean pooled-pen sample sensitivity compared to the non-clustered case (Fig. 3). The reason for this loss of sensitivity when clustering of infection is taken into account is that there is a greater probability of having no positives in the pooled sample. While clustering also results in more samples with a large number of positives compared to no clustering, this only results in small increases in test sensitivity and does not compensate for the greater number of samples with no positives at all.
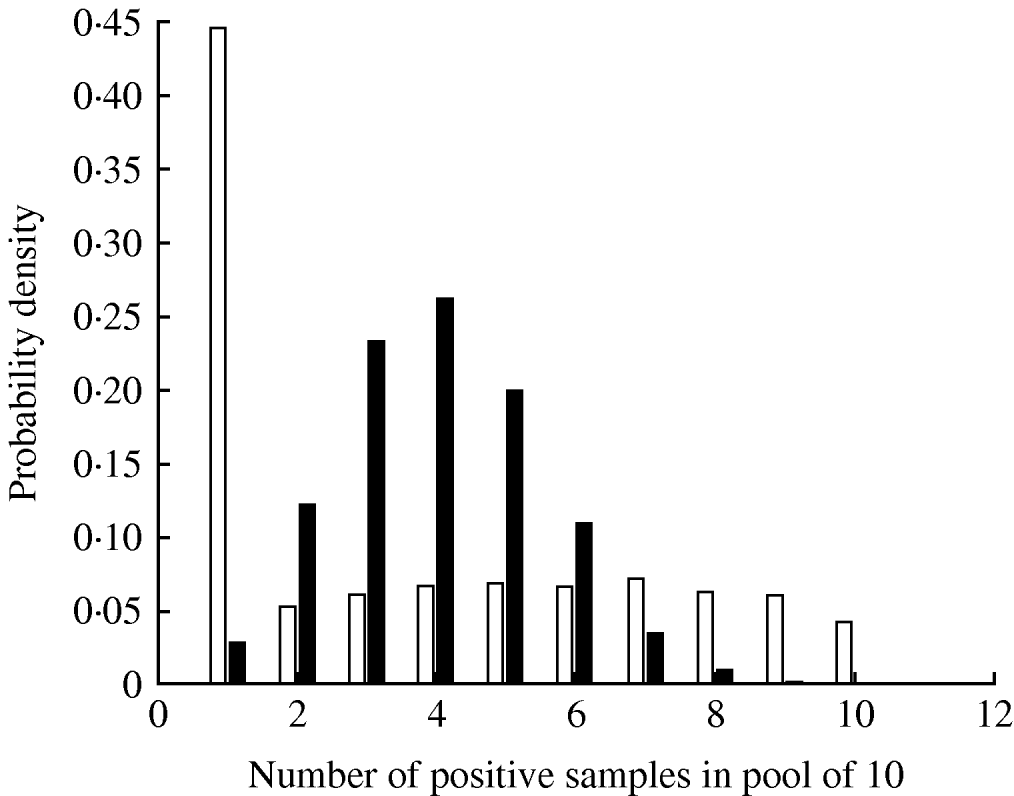
Fig. 2. Probability distribution of the number of positive samples in a pool of 10 given a herd-level prevalence of 30%, assuming clustering of infection in pens (□) and no clustering (▪).
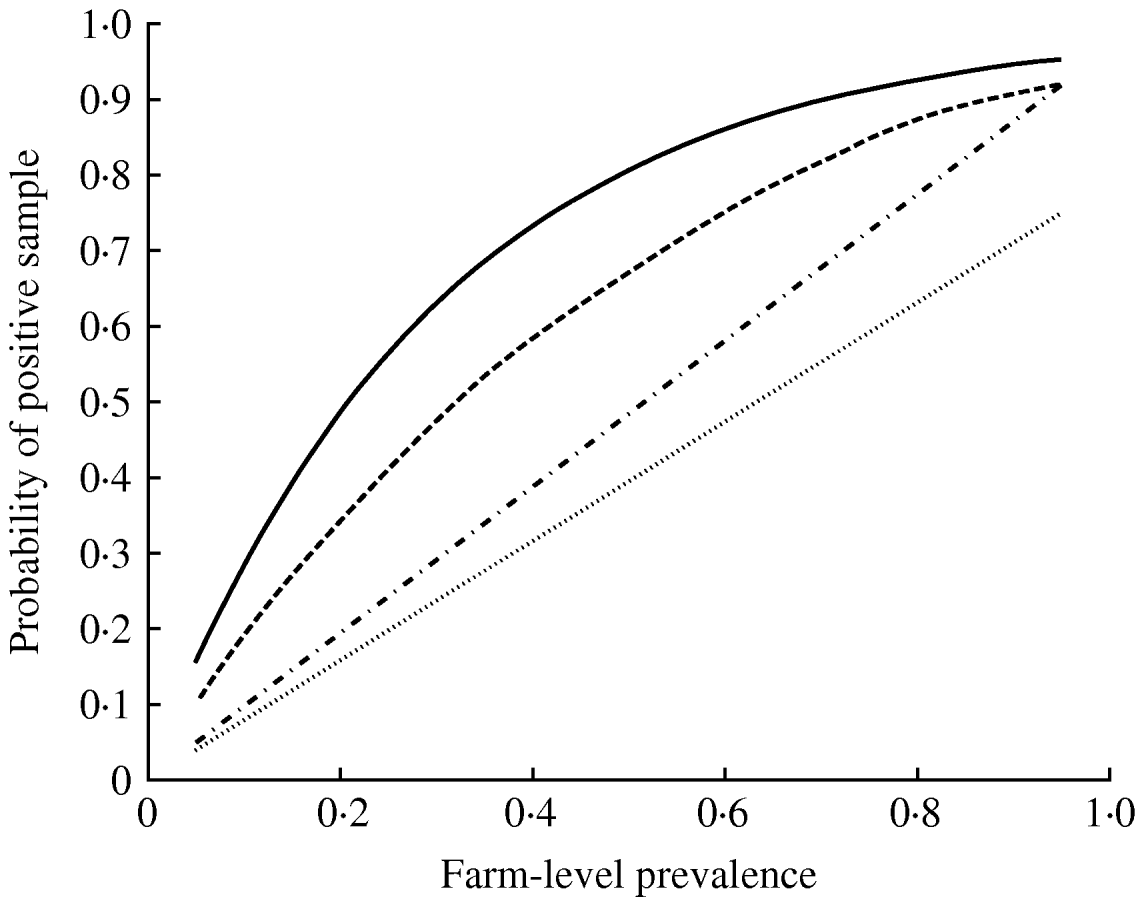
Fig. 3. Mean probability of a pooled-pen sample testing positive where (i) the pen prevalence follows a binomial distribution with P given by the farm-level prevalence (——), (ii) pen-prevalence is beta-distributed and is clustered at the pen-level (- - -), (iii) individual-level sampling, assuming 25 faeces and a population size much larger than the number of samples taken (- · - · -), and (iv) a rectal sample (……).
Table 3. Parameter estimates and 2·5 and 97·5 percentiles of C, ρ (the parameters that determine the sensitivity of pooled sampling) and rectal sample sensitivity to detect Salmonella estimated using a Bayesian approach applied to data for pooled faecal samples and rectal samples from pigs from nine herds

From the posterior estimates of C and ρ, and assuming that an individual sample has the same sensitivity as a pooled sample comprising entirely of positives, then equation (1) gives a median sensitivity of 25 g culture equal to 96% (2·5 and 97·5 percentiles, 91–99%). However, the lower mass of faeces included in the rectal samples results in much lower sensitivity of rectal sampling; the rectal samples were estimated to have a sensitivity of 79% (71–86%).
There was a clear benefit of testing pooled compared to individual-level samples (Fig. 3). In particular, pooled sampling is much more effective than rectal samples. As the number of pens reduces, so does the number of samples (Table 4), as also occurs in the case of individual samples [Reference Cannon and Roe10], although the effect is relatively small, especially at high prevalence.
Table 4. Estimated number of pooled faecal samples required to detect at least one positive sample in a pig herd with 95% certainty over a range of Salmonella prevalence

DISCUSSION
This study has provided estimates of the sensitivity of pooled and individual faecal samples for detection of Salmonella in pigs. However, the inference of the individual sample sensitivity is weakened by lack of knowledge of the exact sample weight of the rectal samples, which makes the prior uncertainty of the sensitivity of individual sampling much greater. The variation in weight of samples that can be obtained rectally reflects the varied quantity of faeces present, which may range from scant to copious even within one pen. Nevertheless, this study shows a clear benefit of pooling compared to individual sampling (Fig. 3), since on the positive farms a higher proportion of pooled samples were positive compared to individual samples, and this translates into fewer pooled samples required to detect infection compared to individual samples, thus confirming the conclusions in [Reference Arnold, Cook and Davies4].
The method of calculating the animal-level prevalence in a herd in our study differs from previous methods [Reference Abel, Schosser and Suss11, Reference Cowling, Gardner and Johnson12], since here we have had to take account of the dilution effect of mixing negative and positive samples; previous methods have assumed that the sensitivity of pooling is not affected by the ratio of negative to positive samples. For culture methods, taking into account the dilution effect is likely to be very important since the probability of successful culture is usually dependent on the number of target organisms in the sample. Such a dilution effect has also been found for VTEC O157 in cattle [Reference Arnold13, Reference Sanderson, Sargeant and Nagaraja14]. Previous studies of pooling of bacteriological samples for detection of Salmonella in pigs have also found a dilution effect. In a previous study [Reference Enøe15] 25-g samples of pen-floor faeces were collected, which comprised five samples each of 5 g. Twenty samples were collected per farm and these were then combined to create 10, four or one new combined pools. Relative sensitivity diminished to 73·1% in the final dilution. Another study [Reference Sørenson16] found that pooling of five carcass swabs provided only a threefold increase in the proportion of samples positive compared to individual sampling, whereas with no dilution effect a ratio closer to 5 would have been expected. However, while a dilution effect occurs, it is sufficiently small to mean that pooling is still more efficient than individual sampling if one is interested in determining whether a group of animals is infected with Salmonella.
One drawback of bacteriological culture methods for detection of Salmonella in pigs is that shedding from infected pigs may be intermittent, and thus such pigs might not be detected by individual faecal sampling. Sampling from the pen overcomes this to some extent, since faeces from a number of pigs over a period of time, determined by the frequency of cleaning and also by floor type (slatted vs. solid), is potentially included in the sample, thus increasing the likelihood that there is Salmonella in the sample. An alternative method of detection for Salmonella is serological testing, first adopted in Denmark [Reference Alban, Stege and Dahl17] for surveillance of pigs at the abattoir and the classification of premises into high, medium and low risk. However, serology is not ideal since it may represent a prior infection that has passed whereas faecal sampling is indicative of present infection, and thus a better representation of current risk in terms of potential human exposure in the food chain. Nevertheless, both serology and pen faecal sampling have been found to show a correlation [Reference Sørenson16, Reference Lo Fo Wong18], however, further studies showing how each of the tests correlate with infection, possibly using Bayesian methods for diagnostic test estimation in the absence of a gold standard [Reference Enøe, Georgiadis and Johnson19, Reference Branscum, Gardner and Johnson20] would be useful.
The degree of clustering is critically dependent on the ratio of the between-pen to within-pen transmission rates. This ratio may vary between farms, since it would predictably be influenced by farm-dependent factors such as the number of pigs per pen, the layout of the pens, etc. We were unable to explore such factors in detail due to the small number of farms from which data on both individual and pooled samples could be collected. Obtaining data on individual pig samples is very difficult in practice, since it is not often possible to identify individual pig faecal samples, and it is not practical to wait for pigs to defecate at a time when they are to be sent for slaughter. We tried to overcome this limitation by rectal sampling, but there are difficulties in obtaining sufficient faeces for a sensitive test. This leads to difficulties in obtaining large enough datasets to study farm-dependent factors that might influence clustering.
This model has demonstrated the important impact of clustering within pens and between pens upon the sensitivity of culture of pooled-pen samples for the detection of Salmonella. It is probable that clustering will be affected by floor type – solid-floored pens are more likely to be associated with a higher within-pen prevalence and a greater between-pen transmission rate than fully slatted floors. Dietary effects, including use of liquid fermented feeds or home-mixed meal rather than commercial pellets, may also impact within-herd prevalence whilst dung handling practices can also affect between-pen transmission rates. Such practices vary amongst European Community member states. It would be valuable to analyse data from several countries to determine whether this model is applicable beyond the UK and whether a single estimate of pooled faecal-sample culture sensitivity is appropriate for all member states or whether an estimate should be made for each individual member state. It is hoped that data from the current EU survey of breeding pigs may elucidate these queries.
In conclusion, this study has estimated sample sizes for the number of pooled samples for detection of Salmonella in pigs. It has also provided an estimate of the degree of clustering of infection at pen level, which influences the number of samples required for collection, and it would be helpful if more data could be collected on this. Pooled samples represent a simple, robust, replicable and cost-effective method for detection of Salmonella infection on pig farms, reducing animal-handling costs, handling stress to the animals, interruption to business and also reducing laboratory costs. For example, simple random sampling of individual pigs in a herd of 1000 individuals would require that 28 animals were restrained and subjected to rectal sampling to be 95% confident that at least one would be positive if the true prevalence of Salmonella infection were 10%, assuming 100% sensitivity and that every pig yielded a sample of adequate weight. If the estimated sensitivity of rectal sampling from this study (79%) was applied then the sample size required increases to more than 35. This compares with 18 pooled samples for the same probability of detection with no need to directly handle the animals. These results indicate that pooled faecal sampling can be used with confidence to monitor farm-level prevalence.
ACKNOWLEDGEMENTS
This work was funded through Defra project OZ0323. We are grateful to our colleagues in the Food & Environmental Safety Department at VLA for their laboratory work. Finally, we record our thanks to the farmers who kindly agreed to participate in this project and without whom our work could not have been completed.
DECLARATION OF INTEREST
None.









