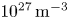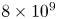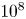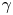2 Pair creation by ultra-intense laser pulse

Ultra-intense lasers can create pairs directly by inducing vacuum polarization with their strong electric fields. To estimate the intensity needed for this, we consider that for a good chance of pair creation, the energy of the pairs should be close to the potential energy felt by an electron over the Compton wavelength due to the laser's electric field. The electric field is

(2.1)\begin{equation} e E_0 \lambda_C = 2 m_e c^2, \end{equation}

where $E_0$ is the average electric field of the focused laser light and $\lambda _C$ is the Compton wavelength. From (2.1), we can calculate the threshold of the laser intensity,

(2.2)\begin{equation} I_{\text{Laser}} = \varepsilon_0 c E_0^2 = 5 \times 10^{28}\,\text{W}\,\text{cm}^{{-}2}, \end{equation}

where $\varepsilon _0$ is the dielectric constant. Achieving laser intensities as high as $10^{28}\,\text {W}\,\text {cm}^{-2}$ is currently beyond our capabilities. To create positrons, we explore alternative methods like using lasers to generate high-energy electrons, known as ‘hot electrons’, through interactions with matter. These electrons gain energy from the laser's electric field and electromagnetic waves. Estimating the average temperature ($T_{\text {hot}}$) of these hot electrons helps us to understand and control the process of positron creation using lasers (Wilks et al. Reference Wilks, Kruer, Tabak and Langdon1992), which can be done using

(2.3)\begin{equation} T_{\text{hot}} = m_e c^2 \sqrt{1 + \frac{I_{\text{Laser}} \lambda^2_\mu}{1.4 \times 10^{18}}} - 1. \end{equation}

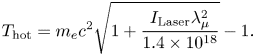
When irradiating a laser with a wavelength ($\lambda _\mu$) of $1\,\mathrm {\mu }$m and an intensity of $I_{\text {Laser}} = 10^{20}\,\text {W}\,\text {cm}^{-2}$, we can estimate the temperature of the resulting hot electrons using (2.3). In this scenario, the estimated hot electron temperature is approximately 4 MeV. This means that most of the hot electrons possess enough energy (above the 1.02 MeV threshold) to initiate pair creation.

Pair production near atomic nuclei is mostly driven by the BH process. Over the years, extensive calculations of the BH pair production cross-section have been carried out, and the findings are summarized in review papers by Motz, Olsen & Koch (Reference Motz, Olsen and Koch1969) and Hubbell, Gimm & O/verbo/ (Reference Hubbell, Gimm and O/verbo/1980) The BH process is strongly influenced by the atomic number ($Z$) of the target material. The cross-section for pair production through this process, disregarding screening effects, can be expressed by the following formula (Davies, Bethe & Maximon Reference Davies, Bethe and Maximon1954):

(2.4)\begin{equation} \sigma_{{\rm BH}} = \frac{28}{9}\alpha Z^2r_e^2 \left[\ln\left(\frac{2\epsilon_\gamma}{m_e c^2}\right) - \frac{109}{42} - f(Z)\right], \end{equation}

where $\epsilon _\gamma$ is the photon energy and

(2.5)\begin{equation} f(Z) = (\alpha Z)^2 \sum_{i=1}^\infty [i(i^2 + \alpha^2 Z^2)]^{{-}1}. \end{equation}

In experimental set-ups, substantial pair production has been attained by efficiently converting laser energy into relativistic electrons. These electrons then emit MeV high-energy photons via Bremsstrahlung, especially when interacting with dense targets featuring high $Z$.

Near solid target nuclei, pair production occurs via electron interactions with virtual photons, termed as the trident process. Studying the cross-section for this process at electron energies above MeV can be done using (Gryaznykh, Kandiev & Lykov Reference Gryaznykh, Kandiev and Lykov1998; Myatt et al. Reference Myatt, Delettrez, Maximov, Meyerhofer, Short, Stoeckl and Storm2009)

(2.6)\begin{equation} \sigma_T = \frac{28 {\rm \pi}(\alpha r_e Z)^2}{27}\log^3(\epsilon_e / m c^2). \end{equation}

In laser-driven pair production, the trident process is less dominant compared with the BH process when the target thickness exceeds $20\,\mathrm {\mu }$m. This is because thicker targets exhibit high electron conversion efficiency through Bremsstrahlung.

Pair production can arise from the interaction between high-energy photons and an intense laser field through the nonlinear Breit–Wheeler (NBW) process. This phenomenon was initially observed at SLAC during the collision of a 46.6 GeV electron beam with a terawatt (TW) laser pulse. In the SLAC experiment, the efficiency of pair production was found to be approximately 1 % with approximately 100 pairs created over 10 000 laser shots. The pair production rate for a nonlinear BW process is

(2.7)\begin{equation} \varGamma_{{\rm NBW}} \sim \alpha \frac{c}{\lambda_c} \frac{m_e c^2}{\epsilon_\gamma} \frac{K_{1/3}^2\left(\dfrac{2}{3 \chi}\right)}{\chi}, \end{equation}

where

(2.8)\begin{equation} \chi \simeq \epsilon_\gamma / (m_e c^2) E_L / E_c \end{equation}

is the quantum field strength experienced by a photon of energy $\epsilon _\gamma$ counter-propagating with a laser with electric field $E_L$, and $K_n$ is the modified Bessel function.

3 Target configurations and simulation results

The relativistic PIC code EPOCH, which incorporates the implemented QED module (Arber et al. Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz and Bell2015), is employed to examine the interaction between an ultra-intense laser pulse and an aluminium (Al) target. The laser pulse has a super-Gaussian spatial and temporal profile with a laser intensity of $4\times 10^{23}\,{\rm W}\,{\rm cm}^{-2}$ and the wavelength is $\lambda = 1\,\mathrm {\mu }$m with a pulse duration of FWHM 30 fs. The focal spot size is $2\,\mathrm {\mu }$m. The simulation box covers $10\,\mathrm {\mu }$m along the $x$ and $y$ directions with $1000 \times 1000$ grids in the $x$ and $y$ directions, respectively. The number of particles per cell is 500 electrons and 16 ions. The resolution of the simulation is 10 nm in both directions, sufficient to accurately calculate the laser–plasma interaction. The thickness of the target is $2\,\mathrm {\mu }$m with the electron density of $n_e = 711n_c$, where $n_c$ is the electron critical density $n_c=(\epsilon _0 m_e \omega _0^2)/(e^2 )$ with laser frequency $\omega _0 = 2{\rm \pi} c/\lambda _0$, where $\epsilon _0, m_e, e, \lambda _0$ are the permittivity of free space, the mass of an electron, electron charge, and laser wavelength, respectively. The critical density corresponding to the laser wavelength $\lambda _0 = 1\,\mathrm {\mu }$m is $n_c = 1.1\times 10^{21}\,{\rm cm}^{-3}$. The Al target, with a mass density of $2.7\,{\rm g}\,{\rm cm}^{-3}$, is fully ionized. The prepulse serves to ionize the target ahead of the arrival of the main pulse, considering the ultra-intense laser intensity employed in our study. The simulation interaction set-up is shown in figure 2.

Figure 2. Simulation interaction set-up.

A. Two laser pulses counter-incident on a thin solid target: Case (A)

Our study focuses on examining the impact of a simultaneous interaction between two counter-propagating laser beams and a target on the generation of positrons, to investigate how these dual laser beams influence positron production. These two lasers irradiated the target from the left and right sides of the simulation boundaries. It is worth noting that a similar type of study has been carried out by Luo et al. (Reference Luo, Zhu, Zhuo, Ma, Song, Zhu, Wang, Li, Turcu and Chen2015), although in our case, we investigate positron generation from the trident process also, and there are differences in the target thickness and simulation configuration as well.

Figure 3(a,b) displays the spatial density distributions of Al ions and gamma-ray photons. In the Al ion density distribution, the highly dense ions are compressed, forming a structure reminiscent of a standing wave. This compression facilitates a more symmetric irradiation and compression of the thin foil (Shen & Meyer-ter-Vehn Reference Shen and Meyer-ter-Vehn2001), resulting in a more stable structure with higher Al ion and gamma-ray density in the irradiation region. During the compression process, electrons within the target are propelled forward by the ponderomotive force exerted by the two incident lasers.

Figure 3. (a) Spatial density distribution of Al ions and (b) gamma-ray photons, and spatial energy distribution of (c) BW positrons and (d) trident positron. (e,f) Spatial density distribution of positrons for BW and trident processes in Case A configuration.

The corresponding spatial energy distributions of BW positrons and trident positrons are shown in figure 3(c,d). These spatial energy distributions for accelerated BW positrons and trident positrons exhibit a symmetrical pattern, with positrons reaching energies exceeding 1 GeV in the BW process. Conversely, the acceleration of positrons in the trident process appears to be suppressed. The positron density in the case of the BW process is observed to be one order of magnitude higher compared with the trident process. Figure 3(e,f) displays the spatial density distribution of positrons from both processes.

In a recent simulation conducted by Zi et al. (Reference Zi, Ma, Yang, Zhang, Liu, Yuan, Peng, Cui and Kawata2023), pair production using an Al target was explored by varying the transverse size of the target while employing two laser beams. In our single-beam case, the observed energy and density of both photons and positrons closely align. It is worth noting that in our study, we used a laser pulse intensity that was one order of magnitude lower than what was used in their research. Additionally, our approach involved irradiation from a single side.

B. Two laser pulses counter-incident on two thin solid targets: Case (B)

In the previous case, we observed a significant enhancement in photon and positron density, energy and yield by using two counter-propagating laser beams from both the BW and trident processes. Building upon these findings, we extended our study by implementing two targets, as depicted in figure 2 (Case B). The underlying idea for using these two targets is that the electric fields generated by both targets may converge in the vacuum. Additionally, there is a higher probability of retaining hot electrons in this case compared with Case A. The presence of these hot electrons in Case B plays a crucial role in enhancing both photon and positron energy. The density distributions of Al ions and photons for the dual-target configuration are displayed in figure 4(a,b). A closer examination of these panels reveals that the Al ion and photon density converge in the vacuum gap between the two targets.

Figure 4. Spatial density distribution of (a) Al ions and (b) gamma-ray photons, and spatial energy distribution of (c) BW positrons and (d) trident positron. (e,f) Spatial density distribution of positrons for BW and trident processes in Case B configuration.

The observation of the positron spatial energy distributions (figure 4c,d) for the BW and trident processes reveals that they exhibit a larger production area and higher energy, especially in the case of BW positrons (figure 4c), compared with the trident process. Moreover, the positrons generated in this dual-target configuration display both a high-energy production region and high density compared with Case A. For BW positrons, the energy exceeds 1.68 GeV, whereas in the trident case, it is reduced to 1 GeV. Notably, the dual-target configuration stands out by offering both a higher yield and higher energy for positron acceleration compared with the Case A configuration, underscoring the effectiveness of this set-up. Additionally, we also observed the distribution of positron density for both processes in figure 4(e,f). It is apparent that the density distribution of positrons follows a pattern similar to the energy distribution of positrons.

4 Comparison and discussions

The energy spectrum is illustrated in figure 5 for electrons, photons and positrons from both processes. The spectral distributions of electrons and photons are displayed in figure 5(a–d). It is evident from the electron energy spectrum that highly energetic electrons are generated in the dual-target set-up. In the dual-target configuration, the cutoff energy of the electrons reaches 1.4 GeV, while in Case A, it is approximately 1 GeV. The cutoff energy of the photons is depicted in figure 5(d). The maximum photon energy obtained was 28 MeV for Case A and 38 MeV for Case B, indicating an increase in energy with the dual-target set-up.

Figure 5. (a) Electron energy spectra, (b) positron energy spectra in BW process, (c) positron spectra for trident process and (d) gamma-ray energy spectra.

Figure 5(b) presents the positron spectra for BW process. Notably, the BW positron spectrum in the dual-target set-up displays a higher cutoff energy, approximately 1.68 GeV, compared with the single-target Case A of 1.15 GeV. The reason behind this enhancement in the dual-target configuration may be attributed to the initially accelerated potential well of the transverse electric field, which confines electrons and further enhances positron generation. However, in the trident positron energy spectra shown in figure 5(c), the maximum cutoff energy of 1.38 GeV is observed in the dual-target configuration. An energy of the trident positron of 810 MeV is obtained in Case A.

In two-sided laser irradiation (Case B), the positron count is two times higher compared with Case A, resulting in a maximum positron density exceeding $6 \times 10^{27}\,{\rm m}^3$. This increase is attributed to fast-moving electrons, accelerated by the laser, interacting strongly with both incoming and reflected waves from counter-propagating laser pulses.

In contrast, a significant number of electrons from one side of the target traverse through the dense plasma and effectively interact with the counter-incident laser pulse on the opposite side in Case B, contributing more high-energy photons and pairs. This phenomenon is absent in Case A.

The dual-target set-up provides a crucial advantage by generating a strong sheath electric field on the rear side of both targets. This field effectively accelerates high-energy electrons from both sides of the target. Furthermore, the annihilation of pairs can occur within this set-up, leading to a substantial increase in the production of high-energy gamma-rays.

To analyse how much laser energy is absorbed in each case, we calculated the conversion efficiency. The conversion efficiency ($\eta$) of the laser energy into electrons, gamma-rays and positrons is calculated from the simulation as

(4.1)\begin{equation} \eta = \frac{1}{E_{\text{laser}}} \sum_{j=1}^{N} w_j \times E_j, \end{equation}

where $\eta$ is the conversion efficiency, ${E_{\text {laser}}}$ is the total injected laser energy, $N$ is the number of macro-particles (electrons, gamma-rays or positrons), $w_j$ is the weight of the macro-particle and $E_j$ is the energy of the macro-particle. The calculated conversion efficiencies are presented in table 1, and it is evident that the absorption of laser energy into electrons, positrons and photons is notably improved in Case B.

Table 1. Numbers of photons ($N_\gamma$), positrons in BW process ($e^+_{{\rm BW}}$) and trident positrons ($e^+_{{\rm tri.}}$), the maximum positron energy ($E_{e^+_{{\rm BW}}}$), ($E_{e^+_{{\rm tri.}}}$) and electron energy ($E_{e^-}$). Energy conversion efficiencies from laser to $\gamma$-photons ($\eta _\gamma$), BW positrons ($\eta _{e^+_{{\rm BW}}}$) and electrons ($\eta _{e^-}$).

To strengthen our findings, we tracked the quantities of positrons generated via the BW process and the trident process, as well as photons, as depicted in figure 6. Our analysis revealed a trend: in Case B, the number of positrons doubled compared with Case A. Specifically, in figure 6(a) for BW positrons, we observed $8.2\times 10^{9}$ positrons in Case B, and $6\times 10^{9}$ in Case A. Similarly, in the trident process depicted in figure 6(b), Case B exhibited $3.9\times 10^{8}$ positrons, while Case A recorded $2\times 10^{8}$. From the photon number distribution depicted in figure 6(c), the number of photons generated in the Case B is higher compared with the Case A.

Figure 6. (a) Positron number in BW process, (b) trident positron number, (c) photon number and (d) angular distribution of BW positron.

Figure 6(d) provides a qualitative comparison of angular distribution of positron beams under two-target-type conditions. Case B exhibits a higher peak in positron angular distribution at $0^{\circ }$ and a significantly wider spread (FWHM) compared with Case A, attributed to the higher production of $\gamma$-photons covering a larger area. This indicates a larger positron yield, a slight divergence angle and effective restraint in Case B. In contrast, Case A shows a larger positron divergence angle and a lower yield due to deformations caused by the intense laser field deviating from plasma density, reducing the binding effect and increasing positron dispersion. These combined effects result in increased positron production and a smaller divergence angle in Case B, suggesting that Case B conditions are conducive to producing high-quality $\gamma$-photon and positron beams.

Here, we observed that using two counter-propagating laser beams can enhance the photon and pair energy and density. Following this, we extended our study to Case B, where two targets are irradiated by the two lasers. Upon interaction of the two counter-propagating lasers with the Case A and Case B target, the reflected wave overlaps with the incident wave, creating standing waves on both sides of the focused target and forming a potential well around it, as shown in the Al ion density distribution (figures 3a and 4a). This initially binds the hot electrons in the interaction region, leaving the incident wave as the main contributor to the intensity on the contact surface.

In the two scenarios, positrons are additionally accelerated by the electric sheath field formed at the rear surface of the laser-irradiated foil. This field reaches its maximum intensity around the peak of the laser pulse interaction and diminishes thereafter as the electrons and aluminium ions disperse away from the rear surface. In Case A, the rear side of the target encounters a weaker electric field, resulting in lower strengths of both the longitudinal and transverse electric fields compared with Case B. Figure 7 illustrates in detail how the strong electric field plays an important role in the dual-target set-up to enhance pair production and gamma-ray emission. This robust sheath field can effectively accelerate high-energy electrons, consequently leading to the emission of gamma-rays.

Figure 7. Interaction of the laser with the dual-target set-up, highlighting the formation of a robust sheath electric field on the rear surfaces of the targets. This electric field leads to the enhancement of pair production. Additionally, the strong sheath field facilitates the emission of gamma rays, contributing to the overall dynamics of the laser–target interaction.

Moreover, a confined electric field is observed at the target wall, as illustrated in figure 8. This field, along with the longitudinal electric field, amplifies the QED effect in both Case A and Case B. Particularly, the confined electric field from the inner wall of target B is higher than in Case A, which is effectively trapping the electrons within the interaction region leading to a substantial increase in QED emission, as evidenced by the density and energy of gamma-rays in figure 4(b).

Figure 8. Longitudinal electric field (ex) distributions for Case A and Case B.

Upon interaction of the opposite lasers with the single-target set-up, the reflected wave will overlap with the incident wave, resulting in the creation of standing waves on both sides of the focused target and forming a potential well around it, as shown in figures 3(a) and 4(a). This phenomenon initially binds the hot electrons within the interaction region. Additionally, the confined electric field produced by the dual-target set-up exerts a strong focusing and blocking effect on the electrons in the interaction region. These combined effects enhance the QED reaction rate.

As the laser energy is absorbed and the energy of the hot electrons increases in the dual-target set-up, more $\gamma$-photons are emitted by the hot electrons, which attenuates the original laser wave. Consequently, the conversion efficiency of the total laser energy into hot electrons and photons, and ultimately into positrons, is improved. Simulation results indicate that the energy conversion rate of $\gamma$-photons reaches in the dual-target set-up is higher, compared with in the single-target set-up. Table 1 summarizes observed parameters and the comparison between each configuration.

This confirms that the hot electron population generated in a single target set-up is smaller than in a dual-target set-up, where it is further reduced by photon emission in a manner similar to hot electrons in a laser field. The efficient conversion of the total laser energy in the dual-target set-up offers more advantages than the single-target set-up. Therefore, a dual-target set-up can generate high-density, high-energy $\gamma$-photon beams and a significant number of electron–positron pairs.

5 Possibility of investigating pair production by experiment in central laser facility

The current generation of high-repetition and high-intensity lasers has paved the way for experimental exploration of the QED regime. We propose conducting a potential experiment at facilities like CLF, such as Gemini and ELI, to investigate pair production. Our simulation studies confirm that positron production from thin foils is the primary option for the experiment. Our aim is to explore positron production in thin targets, where $e^+$ $e^-$ production by the BH process predominates over the trident process. This research could significantly impact the design of future linear colliders (Shuoquin et al. Reference Shuoquin, Clayton, Blue, Dodd, Marsh, Mori, Joshi, Lee, Muggli and Katsouleas2002; Johnson et al. Reference Johnson, Auerbach, Blumenfeld, Barnes, Clayton, Decker, Deng, Emma, Hogan and Huang2006). While the generation of positrons through this mechanism has been demonstrated (Gahn et al. Reference Gahn, Tsakiris, Pretzler, Witte, Delfin, Wahlström and Habs2000), the advantage of these laser facilities lies in their ability to confine positrons on both sides (Liang et al. Reference Liang, Wilks and Tabak1998), potentially leading to significantly enhanced positron numbers (Wilks et al. Reference Wilks, Chen, Liang, Patel, Price, Remington, Shepherd, Tabak and Kruer2005).

The basic experimental set-up, as shown in figure 9, involves using dual beams with two F/2 geometries to maximize intensity. Alternatively, a single beam split into two using a D-mirror (see Heinzl et al. Reference Heinzl, Liesfeld, Amthor, Schwoerer, Sauerbrey and Wipf2006) can also be employed. Even though the intensity will be reduced to a quarter of the maximum, this would prevent temporal and spatial jitter between the two beams.

Figure 9. Experimental layout.

Both parts of the experiment would share a similar geometry. The first part entails placing a thin foil at the focus of two temporally and spatially overlapped beams. Detecting $e^+$ $e^-$ pairs through the trident process and BH process (Heitler Reference Heitler1954) is relatively straightforward due to the substantial number of positron pairs generated in a single-shot event. An electron/positron spectrometer would be used for positron detection.

The experiment aims to explore the relative importance of $e^+$ $e^-$ production by charged particles versus Bremsstrahlung by varying the target thickness. Additionally, the impact of pair confinement in the signal will be examined by comparing the use of a single beam versus dual beams.