Introduction
Volume measurements of individual glaciers are crucial for projections of the contribution of glaciers and ice caps (henceforth termed ‘glacier’ sexcludes ice sheets) to future sea-level change because volume data are used to develop empirical volume–area scaling relationships (Reference Chen and OhmuraChen and Ohmura, 1990; Reference Van de Wal and WildVan de Wal and Wild, 2001; Reference Bahr, Dyurgerov and MeierBahr and others, 2009; Reference Radić and HockRadić and Hock, 2011; Reference Bahr and RadićBahr and Radić, 2012; Reference Huss and FarinottiHuss and Farinotti, 2012; Reference Marzeion, Jarosch and HoferMarzeion and others, 2012; Reference Slangen, Katsman, Van de Wal, Vermeersen and RivaSlangen and others, 2012; Reference Mernild, Yde, Malmros and KnudsenMernild and others, 2013a; Reference Radić, Bliss, Beedlow, Hock, Miles and CogleyRadić and others, 2014). While glacier area A is easily derived by remote sensing and is available in glacier inventories, direct measurements of glacier volumes V have only been performed on a very limited number of glaciers (e.g. Reference Cogley, Henderson-Sellers and GuffieCogley, 2012). This makes glacier volume the limiting variable in calibrating the power law exponent γ and coefficient c in volume-area scaling relationships (e.g. Reference ErasovErasov, 1968; Reference Zhuravlev and AvsyukZhuravlev, 1988; Reference Chen and OhmuraChen and Ohmura, 1990; Reference Bahr, Meier and PeckhamBahr and others, 1997):
For example, Reference GrinstedGrinsted (2013) applied an updated version of a glacier volume database compiled by Reference Cogley, Henderson-Sellers and GuffieCogley (2012) containing 220 glaciers and 34 ice caps to upscale the areas of ~ 170 000 glaciers, primarily compiled from the Randolph Glacier Inventory version 2.0 (RGI; Reference ArendtArendt and others, 2012), to estimate the global glacier volume to 0.35 ∓ 0.07 m sea-level equivalent (s.l.e.). Compared to previous estimates, Reference GrinstedGrinsted (2013) refined the scaling relationship by including continentality and glacier elevation range. Other scaling methods include volume–length (Reference Oerlemans, Dyurgerov and Van de WalOerlemans and others, 2007; Reference Leclercq, Weidick, Paul, Bolch, Citterio and OerlemansLeclercq and others, 2012) and volume–area–length relations (Radić and others, 2008; Reference Radić and HockRadić and Hock, 2011). Reference Radić, Bliss, Beedlow, Hock, Miles and CogleyRadić and others (2014) adopted RGI and a volume–area scaling law with c and γ derived from Reference Chen and OhmuraChen and Ohmura (1990) and Reference BahrBahr (1997) to estimate a global glacier volume of 0.52 m s.l.e. The discrepancy between the estimates of Reference Radić, Bliss, Beedlow, Hock, Miles and CogleyRadić and others (2014) and Reference GrinstedGrinsted (2013) is likely to be caused by differences in the values of the scaling parameters c and γ used. This is important because volume-area scaling is a nonlinear relation. For instance, Reference Slangen and Van de WalSlangen and Van de Wal (2011) found that even small variations in the scaling parameters cause significant variations in glacier volume estimations. These biases become even more pronounced when glaciers‘ dynamic disequilibrium with the current climate is considered (Reference Adhikary and MarshallAdhikary and Marshall, 2012). There is therefore a pressing need to better elucidate the variability of the scaling parameters by obtaining more field measurements of glacier volume (e.g. Reference NavarroNavarro and others, 2009; Martín-Espańol and others, 2013).
Global scaling between glacier volume and area is based on theoretical steady-state considerations (shallow-ice approximation) of typical glacier geometry, ice rheology and mass-balance gradient (Reference Bahr, Meier and PeckhamBahr and others, 1997) and empirical data (e.g. Reference Chen and OhmuraChen and Ohmura, 1990). However, the volume–area relationships for individual glaciers are likely to deviate significantly from a global average because glacier hypsometry, ice dynamics, climate and climatic sensitivity depend on local conditions. The range of deviation has not been quantified, but Reference MeierMeier and others (2007) are often referenced for suggesting that for individual glaciers the magnitude of uncertainty might be ~ 50%. As an example, advancing glaciers are likely to have a different volume–area relation than receding glaciers because increase in mass balance results in a proportionally higher increase in volume than in area (e.g. Reference Adhikary and MarshallAdhikary and Marshall, 2012), assuming that the advance is caused by climate change rather than dynamic instabilities (e.g. glacier surging). In the case of glacier surging, the area will increase significantly as the glacier advances, while volume is likely to decrease as part of the ice mass is relocated to lower and warmer elevations. Similarly, climate conditions and changes may cause biases as they vary widely on a global scale, but may affect glaciers in a similar way on local and regional scales. Taking these effects into consideration is important because almost all glaciers are in disequilibrium with their local climate (Stocker and others, 2013). Reference Adhikary and MarshallAdhikary and Marshall (2012) have addressed this issue of glacier transition in relation to volume-area scaling and found that the widely used exponent parameter γ = 1.375 (Reference Bahr, Meier and PeckhamBahr and others, 1997) is in agreement with the empirical parameter γ = 1.357 (Reference Chen and OhmuraChen and Ohmura, 1990) partly due to a coincidental offsetting of biases resulting from assuming climatic steady-state conditions (i.e. more volume) and systematic underestimation of modeled ice thicknesses (i.e. less volume). By constructing a synthetic dataset and running numerical Stokes model simulations, Reference Adhikary and MarshallAdhikary and Marshall (2012) estimate that glaciers exposed to 100 years of sustained recession have a mean γ of 1.38, which is close to γ = 1.375 (Reference Bahr, Meier and PeckhamBahr and others, 1997). For glaciers, most studies have used scaling laws with γ between 1.12 and 1.5 (summarized by Reference GrinstedGrinsted, 2013). For ice caps a lower γ value of 1.%#x2013;1.26 has been applied, as their geometry and ice dynamics may differ from those of valley and cirque glaciers (Reference GrinstedGrinsted, 2013; Reference Mernild, Lipscomb, Bahr, Radić and ZempMernild and others, 2013b).
By assuming that the scaling relationship is valid worldwide, regional volume estimates have been obtained from glacier inventories (Reference Radić and HockRadić and Hock, 2010; Reference Marzeion, Jarosch and HoferMarzeion and others, 2012; Reference GrinstedGrinsted, 2013). However, it is likely that local factors (e.g. the effects of climatic disequilibrium, glacier surge activity, differences in mass-balance gradient, and topography) may hamper the accuracy and precision of regional-scale volume estimates (Reference HarrisonHarrison, 2013). For instance, the updated Reference Cogley, Henderson-Sellers and GuffieCogley (2012) database contains no direct volume measurements from Greenlandic glaciers, despite the fact that the glaciers peripheral to the Greenland ice sheet cover ~ 130 000 ∓ 4000 km2 (Reference Rastner, Bolch, Mölg, Machguth, Le Bris and PaulRastner and others, 2012), or ~ 17% of the total area of glaciers (updated from RGI). If regional or local conditions are biased (e.g. in Greenland or parts of Greenland), then regional volume estimates might be inaccurate and in need of revision.
In this paper, we present a 2012 volume measurement of Mittivakkat Gletscher, southeast Greenland. Based on a previous volume measurement from 1994 (Reference Knudsen and HasholtKnudsen and Hasholt, 1999), we discuss the potential for applying the glacier‘s mass-balance record to validate volume change, its volume change in recent decades and its volume–area scaling parameter relationship. To our knowledge this is the first study that compares direct volume measurements on an individual glacier in order to analyze its volume–area scaling relation. The presented data also add to the limited number of glaciers with contemporary volume measurements and are valuable to better assess the contribution of Greenlandic glaciers to sea-level change, particularly when more direct volume measurements become available in the future.
Study Area
Mittivakkat Gletscher (65°42 ‘N, 37°48 ‘W) is located on Ammassalik Island (Fig. 1). The glacier is 5.5 km long and has an elevation range of 160-880 m a.s.l. (Reference Mernild, Pelto, Malmros, Yde, Knudsen and HannaMernild and others, 2013c). It has undergone continuous recession since the end of the Little Ice Age (Reference FristrupFristrup, 1970; Reference Knudsen, Yde, Hasholt and HeinemeierKnudsen and others, 2008; Reference MernildMernild and others, 2011). Another sign of regional warming temperature is that the equilibrium-line altitude (ELA) has moved from ~ 500 m a.s.l. (1996) to 730 m a.s.l. (average for 1996-2010) (Reference MernildMernild and others, 2011), emphasizing that the glacier dynamics of Mittivakkat Gletscher are in disequilibrium with the present climate (Reference MernildMernild and others, 2013d) in accordance with observations of glacier fluctuations in other regions in Greenland (Reference Yde and KnudsenYde and Knudsen, 2007; Reference BjørkBjørk and others, 2012; Reference KargelKargel and others, 2012; Reference Leclercq, Weidick, Paul, Bolch, Citterio and OerlemansLeclercq and others, 2012). At present, the observed mean annual air temperature at 515 m a.s.l. is ‒2.2°C (1993–2011; updated from Reference Mernild, Hansen, Jakobsen and HasholtMernild and others, 2008), and the mean annual precipitation ranges from 1400 to 1800 mm w.e. a‒1(1998-2006; Reference Mernild, Hansen, Jakobsen and HasholtMernild and others, 2008).
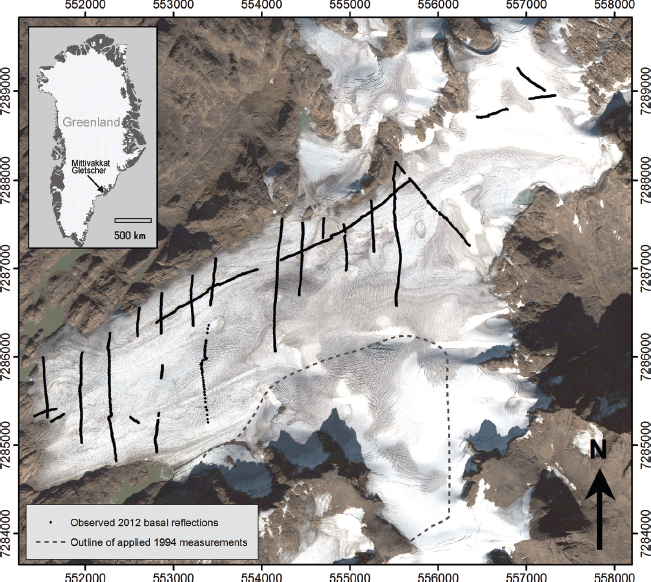
Fig. 1. Location map and QuickBird imagery (12 September 2005) of Mittivakkat Gletscher, southeast Greenland. The positions of interpretable basal reflections are marked by black dots, and the southeastern area, where the 1994 bed topography is applied, is outlined. Coordinates are given in UTM 24W (WGS 84).
Mittivakkat Gletscher is one of Greenland‘s most intensively studied glaciers, and is therefore an attractive site to conduct field-based studies with possibilities for independent validation of results. In relation to this study, two existing investigations are of interest: (1) annual net mass balance has been measured since 1995/96 (Reference Knudsen and HasholtKnudsen and Hasholt, 2008; Reference Mernild, Pelto, Malmros, Yde, Knudsen and HannaMernild and others, 2013c); and (2) a previous study of glacier volume was conducted in 1994 (Reference Knudsen and HasholtKnudsen and Hasholt, 1999). These studies provide a basis for examining recent volume change. Reference Knudsen and HasholtKnudsen and Hasholt (1999) also indicate that the glacier has a temperate basal regime, which is consistent with an observed lack of basal ice facies along the present glacier margin, indicating that basal melting is higher than basal refreezing of meltwater.
The geology consists of Precambrian metamorphic gneisses with sporadic Tertiary igneous intrusions. Areas exposed by glacier recession generally lack an unconsoli-dated subglacial sediment layer, although patches of preserved and dated vegetation and peat have been observed at several recently exposed locations (Reference Knudsen, Yde, Hasholt and HeinemeierKnudsen and others, 2008).
Methodology
Ground-penetrating radar (GPR) surveying is a well-established method for determining ice thicknesses along glacier surface profiles, which can subsequently be processed to give an estimation of glacier volume (e.g. Reference Binder, Brückl, Roch, Behm, Schöner and HynekBinder and others, 2009; Reference FischerFischer, 2009; Reference Bælum and BennBælum and Benn, 2011; Reference SaintenoySaintenoy and others, 2013). During the period 11–18 August 2012, one longitudinal and several transverse and marginal profiles were recorded on Mittivakkat Gletscher (Fig. 1). The separation between the transverse profiles was set to ~ 250 m, but areas with heavy crevassing and large supraglacial streams caused some deviation from this surveying strategy. In particular, the southern part of the study area had steepened and become more crevassed since the previous GPR survey in 1994, making it impossible to access in 2012 (Fig. 1).
The applied equipment was a MALÅ GeoScience 50 MHz Rough Terrain Antenna attached to a MALÅ ProEx GPR system carried in a backpack (MALÅ GeoScience, 2011). During measurements the antenna was dragged inline along the profile while recording at a 1 trace s−1 sampling interval. To keep a constant spacing of 4.0 m between the 50 MHz transmitter and receiver antennas, a person walked behind holding a rope attached to the end of the antenna. The radar propagation velocity was set to 0.168 m ns−1 in order to allow a direct comparison with the previous study by Reference Knudsen and HasholtKnudsen and Hasholt (1999). This assumed homogeneous velocity is similar to those applied in other studies (e.g. Reference Saetrang and WoldSaetrang and Wold, 1986 (0.169 m ns−1); Reference Melvold, Schuler, Hauck and KneiselMelvold and Schuler, 2008 (0.168 m ns−1)). However, considering that Mittivakkat Gletscher primarily consists of temperate ice with water present between ice crystals, it is likely that 0.168 m ns−1 is higher than actual propagation velocities (e.g. Reference Bradford and HarperBradford and Harper, 2005; Reference Bradford, Nichols, Mikesell and HarperBradford and others, 2009). No correction for propagation velocities in snow cover was needed as the ELA was above 880 m in 2012 (Reference Mernild, Pelto, Malmros, Yde, Knudsen and HannaMernild and others, 2013c). Also, the general lack of both debris-rich basal ice and unconsolidated subglacial sediments in areas recently exposed by glacier retreat indicates that a marked contrast in propagation velocities can be expected at the ice/bed interface.
A MALÅ single-frequency GPS was coupled to the GPR system to continuously record the positions of each GPR measurement. The uncertainty of the GPS was checked against a geodetic control point in front of the glacier and showed a vertical deviation less than 1 m, although the potential vertical uncertainty may be up to − 5-10 m according to the manufacturer. The glacier surface elevation was extracted from the Advanced Spaceborne Thermal Emission and Reflection Radiometer global digital elevation model version 2 (ASTER GDEM v2), a product of NASA and the Japan Ministry of Economy, Trade and Industry (METI). The elevation of the ASTER GDEM v2 is a stacked and averaged product of best observations obtained between 1999 and 2010 (Reference TachikawaTachikawa and others, 2011). The vertical error of the ASTER GDEM v2 was ± 5.8 m when compared with in situ GPS measurements. The horizontal error between ASTER GDEM v2 and Landsat 7 Enhanced Thematic Mapper Plus (ETM+) from measurements of 26 known points outside the glacier area in both datasets was found to be − 17 m root-mean-square error; a little more than half the pixel size. In order to provide the most accurate representation of the 2012 glacier surface topography, an interpolation of the difference between the ASTER GDEM v2 and the GPS measurements was used to correct the digital elevation model (DEM). The resulting surface topography was subsequently smoothed to remove remaining ASTER GDEM v2 artifacts.
A planimetric area of 15.9 km2 was produced in ArcGIS (Environmental Systems Research Institute (ESRI)) from a georeferenced Landsat 7 ETM+ image from 14 August 2011 (Reference Mernild, Pelto, Malmros, Yde, Knudsen and HannaMernild and others, 2013c). Between August 2011 and August 2012 a glacier terminus retreat of 9 m was measured in the field, indicating that the glacier area decreased and an adjustment is required to estimate the 2012 area. We therefore assume that the trend in area loss between 1994 (Reference Knudsen and HasholtKnudsen and Hasholt, 1999) and 2011 can be linearly projected to 2012, providing an estimated 2012 area of 15.8 km2. The error of area estimation is assessed to be within − 0.1 km2.
The processing software package RadExplorer 1.42 (MALÅ GeoScience) was used to apply direct current (d.c.) removal, time adjustment, automatic gain control, bandpass filtering and Stolt F-K (frequency-wavenumber) migration (cross-profiles only) to the raw data. Bottom reflectors were observed in 23 out of 32 profiles (profiles with bottom reflectors are shown in Fig. 1). As the southeastern part of the glacier was inaccessible in 2012 due to crevasses, ice thickness in this area was calculated by subtracting the 1994 bed topography (Reference Knudsen and HasholtKnudsen and Hasholt, 1999) from the 2012 DEM. The resulting ice thickness data were exported to the visualization tool ArcMap 10.1 (ESRI). Interpolation by radial basis functions was used to construct a contour map of the ice thickness, and the bed topography was calculated by subtracting the ice thickness interpolation from the DEM. The uncertainty in the measured ice thickness is often difficult to assess (e.g. Reference FischerFischer, 2009), but it seems reasonable to assume that it is ~ 5% (Knudsen and Hasholt, 1999; Reference FischerFischer, 2009; Reference Bælum and BennBælum and Benn, 2011) where a strong basal reflection is observed. Due to the use of a relatively high-frequency 50 MHz antenna combined with high water content within the glacier, the basal reflection was occasionally weak, so the uncertainty is likely to exceed 5% in the thickest parts of the glacier. At profile intersections, which are predominantly located in areas with relatively thick ice, the observed differences in ice thickness were generally <10 m (~10% of the total ice thickness). The uncertainty of the final ice thickness interpolation increases in areas where no measurements of ice thickness or bedrock topography exist. Finally, multiplying the mean ice thickness and the glacier area derived the glacier volume. The combined uncertainty in glacier volume arising from errors in ice thickness, propagation velocity, interpolation and glacier area is estimated to be on average 10%, which is similar to that observed in comparable studies (e.g. Reference SaintenoySaintenoy and others, 2013).
Results
Glacier surface and basal topography
The generated glacier surface contour map shows a surface topography that is consistent with glacier surface observations and the locations of crevasse patterns (Fig. 2) and has a mean surface slope of 5.9° (Reference MernildMernild and others, 2013d). Transverse crevasses are generally situated in areas with expansion below steeper compressed parts of the glacier (e.g. between 310 and 350 m and in the central part of the glacier between 570 and 630 m). Assuming a present mean ELA at 730 m (Reference MernildMernild and others, 2011), the mean accumulation area only constitutes 17% of the total study area. This is far less than glaciers in climatic equilibrium, which typically have accumulation areas comprising 50–60% (Reference Dyurgerov, Meier and BahrDyurgerov and others, 2009), suggesting that the glacier is severely out of equilibrium with the local climate (Reference MernildMernild and others, 2011, Reference Mernild, Pelto, Malmros, Yde, Knudsen and Hanna2013c).
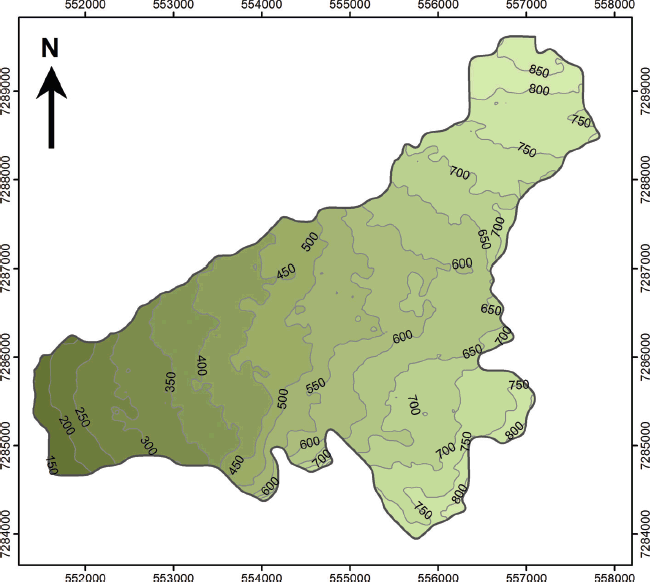
Fig. 2. Glacier surface contour map of Mittivakkat Gletscher derived from a digital elevation model based on ASTER GDEM v2 (2011). The contour interval is 50 m.
The glacier bed topography has an undulating appearance, with bedrock knobs and depressions (Fig. 3), similar to the topography surrounding the glacier to the north and west. A notable feature is a 3.5 km long subglacial ridge oriented parallel with the ice-flow direction between 300 and 600 m a.s.l. in the central and northern part of the glacier. This ridge was first revealed in the basal glacier topography by Reference Knudsen and HasholtKnudsen and Hasholt (1999) and is likely to cause the glacier to split into a northern and southern branch if the current trend in glacier recession and thinning continues. There is a good match between bedrock morphology shown in the new bed topography contour map and the map constructed by Reference Knudsen and HasholtKnudsen and Hasholt (1999). The observed correlation between the bed topography maps provides confidence in the accuracy of the 1994 GPR instrumentation and processing and implies that no significant biases will be introduced with its use in the present study to describe the now inaccessible southern part of the glacier.
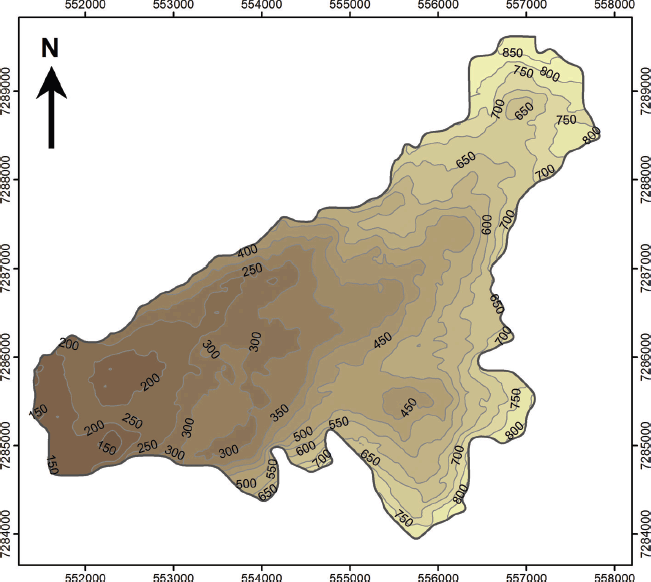
Fig. 3. Bed topography contour map of Mittivakkat Gletscher. The data for the southern part of the glacier are derived from Reference Knudsen and HasholtKnudsen and Hasholt (1999). The contour interval is 50 m.
Ice thickness and volume
The ice thickness rapidly increases away from the lateral glacier margins, but near the terminus and in the upper northeastern part of the glacier the marginal ice is thin and has thicknesses of <20 m (Fig. 4). This is consistent with measurements of low ice velocities in these areas (Reference MernildMernild and others, 2013d). A maximum ice thickness of 220 m was measured by the GPR at the deepest central valley, while an overall maximum interpolated ice thickness of 270 m was found in the southern cirque depression, where the 1994 bed topography was applied. This maximum ice thickness is actually higher than the maximum ice thickness of 245 m found at the same site in 1994, because of an increase in surface elevation. The computed interpolated mean ice thickness for 2012 was 90 m, and the glacier volume was calculated at 1.44 km3 Table 1.
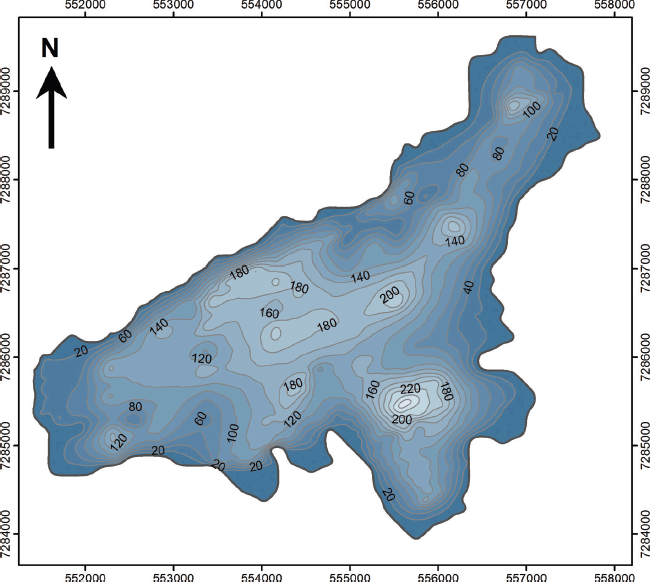
Fig. 4. Contour map of the 2012 ice thickness of Mittivakkat Gletscher. The contour interval is 20 m.
Table 1. Area, mean ice thickness and volume estimates of Mittivakkat Gletscher in 2012 and 1994. The area-corrected data are from Reference Knudsen and HasholtKnudsen and Hasholt (1999) and Reference Mernild, Pelto, Malmros, Yde, Knudsen and HannaMernild and others (2013c)

Discussion
Comparison with mass-balance record
The 2012 GPR survey allows a direct comparison with the findings from the 1994 GPR survey. Between 1994 and 2012 the glacier thinned by ~ 25 m on average, at a rate of 1.39 m a−1 (Table 1). When corrected to meters water equivalent using an ice density of 917 kg m−3, this thinning rate (1.27 m w.e. a−1) is slightly higher than the mean annual net mass-balance loss of 1.01 − 0.74 m w.e. a−1 between 1995/96 and 2011/12 (Reference Mernild, Pelto, Malmros, Yde, Knudsen and HannaMernild and others, 2013c). Given the uncertainties involved in both methods, the deviation in thinning rates is within an acceptable range. Reference MernildMernild and others (2013d) combined the 1994 ice volume measurement with modeled (1986−95) and observed (1996−2011) mass-balance estimates and adjusted the 1986−2011 area change using satellite images to calculate the annual volume changes of Mittivakkat Gletscher. Their study indicated a 15% reduction of the mean ice thickness between 1986 and 2011, comparable to the 22% ice thinning that we find by GPR between 1994 and 2012. There was a lack of significant change in mean ice thickness between 1986 and 1995 (Reference MernildMernild and others, 2013d). This may be explained by a stable local climate and a lack of extremes in air temperature (Reference Mernild, Hanna, Yde, Cappelen and MalmrosMernild and others, 2014a), combined with more winter precipitation during this period (Reference MernildMernild and others, 2014b). Since 1994 the local mean annual air temperature has increased by 0.07°C a−1 (r 2 = 0.22; p = 0.035; where r 2 is the square of the linear correlation coefficient and p is the level of significance), while the mean annual precipitation has changed by −26.5 mm a−1 (r 2 = 0.30; p = 0.013) (data from the synoptic station in the village of Tasiilaq located 10 km from the glacier; Reference CappelenCappelen, 2013). These recent local climatic changes are the likely explanation for the observed thinning and ice loss.
Volume and area change 1994–2012
Between 1994 and 2012 the area of Mittivakkat Gletscher decreased from 17.6 ± 0.1 km2 to 15.8 ± 0.1 km2, and its ice volume decreased by 0.58 km3, equal to 29% of its 1994 volume, or 1.6% a−1 (Table 1). This has resulted in recession of the glacier front by >100 m between 1999 and 2010 (calculated from satellite images; Mernild and others, 2011), affecting the proglacial groundwater (Reference Kristiansen, Yde, Jakobsen, Olsen and KnudsenKristiansen and others, 2013) and the rate of microbial-mediated methane fluxes in exposed areas (Reference Bárcena, Yde and FinsterBárcena and others, 2010, Reference Bárcena, Finster and Yde2011). Also, model simulations of runoff indicate that, on average, ~ 35% of the current runoff is explained by net mass loss (Reference Liston and MernildListon and Mernild, 2012).
Volume–area scaling for Mittivakkat Gletscher
Based on the two datasets of measured volume and area from 1994 and 2012, it is possible to quantify the power law coefficient c and exponent γ for Mittivakkat Gletscher using Eqn (1). This calculation shows that γ = 3.14 and c = 0.00025 km3−2γ. While γ is higher than has been shown even for synthetic individual glaciers in transient states (Reference Radić, Hock and OerlemansRadić and others, 2007; Reference Adhikary and MarshallAdhikary and Marshall, 2012), c is far lower than previous estimates. This association between a high and a low parameter is characteristic when using free parameters in power laws and partly compensates for extreme values (Reference Adhikary and MarshallAdhikary and Marshall, 2012). These values of γ and c are expected to be unrealistic when projected to large changes in area and volume, but may give a better representation of the volume−area scaling of local systems far from climatic equilibrium on short timescales. It is clear that the power law parameters γ and c are sensitive to uncertainties in volume and area measurements. One way to assess this sensitivity is to determine the end-member uncertainty range by calculating minimum and maximum power law coefficients c and exponents γ from end-member uncertainties of volume and area changes. In the case of Mittivakkat Gletscher we assume volume and area change uncertainties of 10% and − 0.1 km2, respectively. This sensitivity test shows that the uncertainty range of γ is 2.05−4.34, whereas c ranges between 0.0051 km3−2γ and 0.0000080 km3−2γ. Here it is interesting to note that the widely used γ = 1.375 (Reference Bahr, Meier and PeckhamBahr and others, 1997) falls below the uncertainty range for Mittivakkat Gletscher. This may indicate that the results for Mittivakkat Gletscher have at least two wider implications: (1) the ranges of γ and c for individual glaciers are likely to be even larger than previously expected; and (2) the consequences of glacier-specific conditions and significant climatic disequilibrium have to be understood in more detail in order to more accurately assess glacier volumes from volume−area relations on local and regional scales. However, it must be emphasized that the scaling parameters obtained serve to illustrate that there are large local deviations from the global behavior and should not be used for extrapolation in space and time.
The coefficient c is considered to be poorly constrained as its unit depends on γ (Reference Slangen and Van de WalSlangen and Van de Wal, 2011).
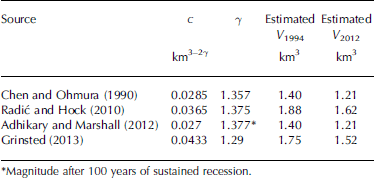
Therefore, it is also problematic to compare c between studies if different γ have been applied. As the geometry of Mittivakkat Gletscher resembles that of a valley glacier, it seems appropriate to compare the degree of scaling γ at Mittivakkat Gletscher with other studies by constraining c to 0.0433, the empirical value determined by Reference GrinstedGrinsted (2013) on a set of 220 glaciers updated from Reference Cogley, Henderson-Sellers and GuffieCogley (2012). This shows that the associated γ changes from 1.34 to 1.27 between 1994 and 2012. This decrease in γ provides empirical support for the finding of Reference Adhikary and MarshallAdhikary and Marshall (2012), based on synthetic data, that sustained glacier recession causes a decreasing trend in γ. It should also be noted that the values of γ are close to γ = 1.29 as used by Reference GrinstedGrinsted (2013). This proximity is reflected in the fact that the scaling regression used by Reference GrinstedGrinsted (2013) only underestimates the 1994 volume of Mittivakkat Gletscher by 13% and overestimates the 2012 volume by 6% (Table 2). Other global scaling regressions fit Mittivakkat Gletscher less accurately. For example, the scaling regressions used by Reference Chen and OhmuraChen and Ohmura (1990) and Reference Adhikary and MarshallAdhikary and Marshall (2012) underestimate the 1994 and 2012 volumes by 31% and 15%, respectively, whereas the Reference Radić and HockRadić and Hock (2010) scaling regression underestimates the 1994 volume by 7% and overestimates the volume in 2012 by 14% (Table 2). Based on volume residuals, the scaling regression by Reference Radić and HockRadić and Hock (2010) provides the best fit of the four scaling regressions (Table 2). These deviations highlight the considerable range of volume estimates and potential biases for an individual glacier, although it has to be remembered that uncertainties are involved in both the applied volume−area scaling equations and the underlying volume and area measurements.
Table 2. The performance of global-scale power law relations in estimating the volume of Mittivakkat Gletscher in 1994 (V 1994) and 2012 (V 2012)
Conclusions
We have provided a new volume measurement of Mittivakkat Gletscher to analyze its volume−area scaling parameter relation. The glacier is severely out of equilibrium with the local climate, and a comparison between a previous direct volume survey in 1994 and the new survey in 2012 shows that the volume of the glacier has changed from 2.02 km3 to 1.44 km3, a decrease equal to 29% of its 1994 volume. Meanwhile, the glacier area has decreased from 17.6 km2 to 15.8 km2. In 2012, the mean ice thickness was 90 m, with a maximum ice thickness of 270 m. The mean thinning rate between 1994 and 2012 was 1.27 m w.e. a−1. This change in ice volume provides independent validation of the mean mass change of −1.01 − 0.74 m w.e. a−1 observed by mass-balance measurements (1995/96−2011/12). The contemporary volume−area scaling exponent γ = 3.14 and coefficient c = 0.00025 km3−2γ of Mittivakkat Gletscher are outside the range of global scaling parameters, which is likely due to climate disequilibrium and local glaciological conditions (e.g. glacier hypsometry and ice dynamics).
Although Mittivakkat Gletscher has been in disequilibrium with the local climate since the mid-1990s, the volume−area scaling relationships by Reference Radić and HockRadić and Hock (2010) and Reference GrinstedGrinsted (2013) estimate the volume to be within 14% of the measured volume, whereas volume estimates based on the scaling relationships by Reference Chen and OhmuraChen and Ohmura (1990) and Reference Adhikary and MarshallAdhikary and Marshall (2012) are within 31%. Considering the uncertainties involved in both GPR measurements and applied volume−area scaling relationships, the volume−area scaling relationships are accurate to within the range of 50% suggested for individual glaciers by Reference MeierMeier and others (2007).
Acknowledgements
This study was funded by an EC FP7 (European Commission seventh framework program) Interact grant agreement No. 262693 (project GLAMOSEG II). R.L. was supported by funding from Sogn og Fjordane University College.








