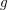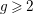0 Introduction
Throughout this paper, we work over
$\mathbb{C}$
, the complex number field.
0.1 Results
The purpose of this paper is to show the following result:
Theorem 0.1.1. The moduli space
${\mathcal{S}}_{g,1}^{0,\text{hyp}}$
of one-pointed genus
$g$
hyperelliptic ineffective spin curves is an irreducible rational variety.
We have the following immediate corollary:
Corollary 0.1.2. The moduli space
${\mathcal{S}}_{g}^{0,\text{hyp}}$
of genus
$g$
hyperelliptic ineffective spin curves is an irreducible unirational variety.
Now we give necessary definitions and notions to understand the statements of the above results. We recall that a couple
$(C,\unicode[STIX]{x1D703})$
is called a genus
$g$
spin curve if
$C$
is a genus
$g$
curve and
$\unicode[STIX]{x1D703}$
is a theta characteristic on
$C$
, namely, a half canonical divisor of
$C$
. If the linear system
$|\unicode[STIX]{x1D703}|$
is empty, then
$\unicode[STIX]{x1D703}$
is called an ineffective theta characteristic, and we also say that such a spin curve is ineffective. A hyperelliptic spin curve
$(C,\unicode[STIX]{x1D703})$
means that
$C$
is hyperelliptic. A pair of a spin curve
$(C,\unicode[STIX]{x1D703})$
and a point
$p\in C$
is called a one-pointed spin curve. One-pointed spin curves
$(C,\unicode[STIX]{x1D703},p)$
and
$(C^{\prime },\unicode[STIX]{x1D703}^{\prime },p^{\prime })$
are said to be isomorphic to each other if there exists an isomorphism
$\unicode[STIX]{x1D709}:C\rightarrow C^{\prime }$
such that
$\unicode[STIX]{x1D709}^{\ast }\unicode[STIX]{x1D703}^{\prime }\simeq \unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D709}^{\ast }p^{\prime }=p$
. Finally, we denote by
${\mathcal{S}}_{g,1}^{0,\text{hyp}}$
(resp.
${\mathcal{S}}_{g}^{0,\text{hyp}}$
) the coarse moduli space of isomorphism classes of one-pointed genus
$g$
hyperelliptic ineffective spin curves (resp. genus
$g$
hyperelliptic ineffective spin curves).
0.2 Background
Main motivations of our study are the rationalities of the moduli spaces of hyperelliptic curves [Reference Bogomolov2], [Reference Katsylo7] and of pointed hyperelliptic curves [Reference Casnati3].
One feature of the paper is that the above rationality is proved via the geometry of a certain smooth projective threefold. We developed such a method in our previous works [Reference Takagi and Zucconi11–Reference Takagi and Zucconi13]. In these works, we established the interplay between
∙ even spin trigonal curves, where even spin curve means that the considered theta characteristics have even-dimensional spaces of global sections; and
∙ the quintic del Pezzo threefold
$B$
, which is known to be unique up to isomorphisms and is isomorphic to a codimension three linear section of
$\text{G}(2,5)$
.
The relationship between curves and
$3$
-folds are a kind of mystery but many such relationships have been known to nowadays. A common philosophy of such works is that a parameter space of certain objects in a certain threefold is an algebraic curve with some extra data. In [Reference Takagi and Zucconi11, Cor. 4.1.1], we showed that a genus
$d-2$
trigonal curve appears as the family of lines on
$B$
which intersect a fixed another rational curve of degree
$d\geqslant 2$
, and, in [Reference Takagi and Zucconi12, Prop. 3.1.2], we constructed a theta characteristic on the trigonal curve from the incidence correspondence of intersecting lines on
$B$
. The mathematician who first met such an interplay is S. Mukai, who discovered that lines on a genus twelve prime Fano threefold
$V$
is parameterized by a genus three curve, and constructed a theta characteristic on the genus three curve from the incidence correspondence of intersecting lines on
$V$
[Reference Mukai9, Reference Mukai10]. In our previous works [Reference Takagi and Zucconi11–Reference Takagi and Zucconi13], we interpreted Mukai’s work from the view point of the quintic del Pezzo threefold
$B$
and generalized it.
The study of this paper is directly related to our paper [Reference Takagi and Zucconi13], in which we showed that the moduli of even spin genus four curves is rational by using the above mentioned interplay.
0.3 Methods
We are going to show our main result also by using such an interplay, but we replace the quintic del Pezzo threefold by a certain degeneration of it. This is a new feature of this paper. The degeneration is a quintic del Pezzo threefold with one node, which is also known to be unique up to isomorphisms and is isomorphic to a codimension three linear section of
$\text{G}(2,5)$
by [Reference Fujita4]. Moreover, it is not factorial at the node, and hence it admits two small resolutions, which we call
$B_{a}$
and
$B_{b}$
in this paper. Actually, we do not work on this singular threefold directly but work on small resolutions, mainly on
$B_{a}$
. Along the above mentioned philosophy, we consider a family of “lowest degree” rational curves on
$B_{a}$
, which we call
$B_{a}$
-lines, intersecting a fixed another “higher degree” rational curve
$R$
. Then we show such
$B_{a}$
-lines are parameterized by a hyperelliptic curve
$C_{R}$
, and we construct an ineffective theta characteristic
$\unicode[STIX]{x1D703}_{R}$
on it from the incidence correspondence of intersecting
$B_{a}$
-lines. Then we may reduce the rationality problem of the moduli to that of a certain quotient of family of rational curves on
$B_{a}$
by the group acting on
$B_{a}$
, and solve the latter by computing invariants.
0.4 Structure of the paper
Finally, we sketch the structure of the paper. In Section 1, we define a projective threefold
$B_{a}$
, which is the key variety for our investigation of one-pointed ineffective spin hyperelliptic curves. In this section, we also review several properties of
$B_{a}$
. In Section 2, we construct the above mentioned families of rational curves
$R$
on
$B_{a}$
, and the family of
$B_{a}$
-lines. Then, in Section 3, we construct hyperelliptic curves
$C_{R}$
as the parameter space of one-pointed
$B_{a}$
-lines intersecting each fixed
$R$
. In Section 4, we construct an ineffective theta characteristic
$\unicode[STIX]{x1D703}_{R}$
on
$C_{R}$
from the incidence correspondence of intersecting
$B_{a}$
-lines parameterized by
$C_{R}$
. We also remark that
$C_{R}$
comes with a marked point from its construction. Finally in this section, we interpret the moduli
${\mathcal{S}}_{g,1}^{0,\text{hyp}}$
by a certain group quotient of the family of
$R$
. One crucial point for this is to show that a general one-pointed ineffective spin hyperelliptic curve conversely comes from a smooth rational curve
$R$
on
$B_{a}$
(Theorem 4.2.1). Then, in Section 5, we show the rationality of the latter by computing invariants.
1 The key projective threefold
$B_{a}$
1.1 Definition of
$B_{a}$
The key variety to show the rationality of
${\mathcal{S}}_{g,1}^{0,\text{hyp}}$
is the threefold, which we denote by
$B_{a}$
in this paper, with the following properties:
(1)
$B_{a}$
is a smooth almost del Pezzo threefold, which is, by definition, a smooth projective threefold with nef and big but nonample anticanonical divisor divisible by
$2$
in the Picard group.(2) If we write
$-K_{B_{a}}=2M_{B_{a}}$
, then
$M_{B_{a}}^{3}=5$
.(3)
$\unicode[STIX]{x1D70C}(B_{a})=2$
.(4)
$B_{a}$
has two elementary contractions, one of which is the anticanonical model
$B_{a}\rightarrow B$
and it is a small contraction, and another is a
$\mathbb{P}^{1}$
-bundle
$\unicode[STIX]{x1D70B}_{a}:B_{a}\rightarrow \mathbb{P}^{2}$
.
1.2 Descriptions of
$B_{a}$
(1.2.a) Fujita’s description
Many people met the threefold
$B_{a}$
in several contexts. The first one is probably Fujita. In his classification of singular del Pezzo threefolds [Reference Fujita4],
$B_{a}$
appears as a small resolution of a quintic del Pezzo threefold
$B$
. Here we do not review Fujita’s construction of
$B_{a}$
in detail except that we sum up his results as follows:
Proposition 1.2.1. The projective variety
$B_{a}$
is unique up to isomorphism. In other words,
$B_{a}$
is characterized by the properties
$(1)$
–
$(4)$
as above. Moreover, the anticanonical model
$B_{a}\rightarrow B$
contracts a single smooth rational curve, say,
$\unicode[STIX]{x1D6FE}_{a}$
to a node of
$B$
. In particular the normal bundle of
$\unicode[STIX]{x1D6FE}_{a}$
is
${\mathcal{O}}_{\mathbb{P}^{1}}(-1)^{\oplus 2}$
.
(1.2.b) Associated rank two bundle
Fujita treats
$B_{a}$
less directly, so descriptions of
$B_{a}$
by [Reference Langer8], [Reference Jahnke and Peternell6], [Reference Takeuchi14] and [Reference Hulek5], which we review below, are more convenient for our purpose.
By [Reference Langer8, §3] and [Reference Jahnke and Peternell6, Thm. 3.6], we may write
$B_{a}\simeq \mathbb{P}({\mathcal{E}})$
with a stable rank two bundle
${\mathcal{E}}$
on
$\mathbb{P}^{2}$
with
$c_{1}({\mathcal{E}})=-1$
and
$c_{2}({\mathcal{E}})=2$
fitting in the following exact sequence:
$$\begin{eqnarray}0\rightarrow {\mathcal{O}}(-3)\rightarrow {\mathcal{O}}(-1)^{\oplus 2}\oplus {\mathcal{O}}(-2)\rightarrow {\mathcal{E}}\rightarrow 0.\end{eqnarray}$$
Let
$H_{{\mathcal{E}}}$
be the tautological divisor for
${\mathcal{E}}$
and
$L$
the
$\unicode[STIX]{x1D70B}_{a}$
-pullback of a line in
$\mathbb{P}^{2}$
. By the canonical bundle formula for projective bundle, we may write
$$\begin{eqnarray}-K_{B_{a}}=2H_{{\mathcal{E}}}+4L.\end{eqnarray}$$
Therefore, by the definition of
$M_{B_{a}}$
as in Section 1.1, we see that
$M_{B_{a}}$
is the tautological line bundle associated to
${\mathcal{E}}(2)$
.
Generally, let
${\mathcal{F}}$
be a stable bundle on
$\mathbb{P}^{2}$
with
$c_{1}({\mathcal{F}})=-1$
. In [Reference Hulek5], Hulek studies jumping lines for such an
${\mathcal{F}}$
, where a line
$\mathsf{j}$
on
$\mathbb{P}^{2}$
is called a jumping line for
${\mathcal{F}}$
if
${\mathcal{F}}_{|\mathsf{j}}\not \simeq {\mathcal{O}}_{\mathbb{P}^{1}}\oplus {\mathcal{O}}_{\mathbb{P}^{1}}(-1)$
. We also recall that a line
$\mathsf{l}$
on
$\mathbb{P}^{2}$
is called a jumping line of the second kind for
${\mathcal{F}}$
if
$h^{0}({\mathcal{F}}_{|2\mathsf{l}})\not =0$
, where
$2\mathsf{l}$
is the double line supported on the line
$\mathsf{l}$
. In [Reference Hulek5, Thm. 3.2.2], it is shown that the locus
$C({\mathcal{F}})$
in the dual projective plane
$(\mathbb{P}^{2})^{\ast }$
parameterizing jumping lines of the second kind is a curve of degree
$2(c_{2}({\mathcal{F}})-1)$
.
Therefore, in our case,
$C({\mathcal{E}})$
is a conic. The following properties of
${\mathcal{E}}$
are crucial in this paper:
Proposition 1.2.2.
(1)
${\mathcal{E}}$
is unique up to an automorphism of
$\mathbb{P}^{2}$
;(2)
$C({\mathcal{E}})\subset (\mathbb{P}^{2})^{\ast }$
is a line pair, which we denote by
$\ell _{1}\cup \ell _{2}$
;(3)
${\mathcal{E}}$
has a unique jumping line
$\subset \mathbb{P}^{2}$
, which we denote by
$\mathsf{j}$
, and the point
$[\mathsf{j}]$
in the dual projective plane
$(\mathbb{P}^{2})^{\ast }$
is equal to
$\ell _{1}\cap \ell _{2}$
; and(4)
${\mathcal{E}}_{|\mathsf{j}}\simeq {\mathcal{O}}_{\mathbb{P}^{1}}(-2)\oplus {\mathcal{O}}_{\mathbb{P}^{1}}(1)$
.
Proof. The claims (1)–(3) follow from [Reference Hulek5, Prop. 8.2], and the claim (4) follows from [Reference Hulek5, Prop. 9.1]. ◻
Notation 1.2.1. For a line
$\mathsf{m}\subset \mathbb{P}^{2}$
, we set
$L_{\mathsf{m}}:=\unicode[STIX]{x1D70B}_{a}^{-1}(\mathsf{m})\subset B_{a}$
. We denote by
$C_{0}(\mathsf{m})$
the negative section of
$L_{\mathsf{m}}$
.
Here we can interpret the jumping line of
${\mathcal{E}}$
by the birational geometry of
$B_{a}$
as follows:
Corollary 1.2.3. It holds that
(1) the
$\unicode[STIX]{x1D70B}_{a}$
-image on
$\mathbb{P}^{2}$
of the exceptional curve
$\unicode[STIX]{x1D6FE}_{a}$
of
$B_{a}\rightarrow B$
is the jumping line
$\mathsf{j}$
; and(2) the curve
$\unicode[STIX]{x1D6FE}_{a}$
is the negative section of
$L_{\mathsf{j}}$
.
Proof. (1) By the uniqueness of
$\unicode[STIX]{x1D6FE}_{a}$
as in Proposition 1.2.1, we have only to show that the negative section
$C_{0}(\mathsf{j})$
of
$L_{\mathsf{j}}$
is numerically trivial for
$-K_{B_{a}}$
. By Proposition 1.2.2(4), we have
$H_{{\mathcal{E}}}\cdot C_{0}(\mathsf{j})=-2$
. Therefore, since
$-K_{B_{a}}=2H_{{\mathcal{E}}}+4L_{\mathsf{j}}$
, we have
$-K_{B_{a}}\cdot C_{0}(\mathsf{j})=2\times (-2)+4=0$
.
The assertion (2) follows from the proof of (1). ◻
1.3 Two-ray link
By [Reference Jahnke and Peternell6, Thm. 3.5 and 3.6] and [Reference Takeuchi14, Thm. 2.3], a part of the birational geometry of
$B_{a}$
is described by the following two-ray link:
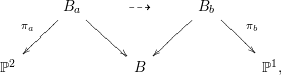
where
(i)
$B_{a}{\dashrightarrow}B_{b}$
is the flop of a single smooth rational curve
$\unicode[STIX]{x1D6FE}_{a}$
.(ii)
$\unicode[STIX]{x1D70B}_{b}$
is a quadric bundle.(iii) Let
$L$
be the pullback of a line by
$\unicode[STIX]{x1D70B}_{a}$
, and
$H$
a fiber of
$\unicode[STIX]{x1D70B}_{b}$
. Then it holds that (1.4)where we consider this equality both on$$\begin{eqnarray}-K=2(H+L),\end{eqnarray}$$
$B_{a}$
and
$B_{b}$
, and
$-K$
denotes both of the anticanonical divisors.
Notation 1.3.1.
(1) We denote by
$\unicode[STIX]{x1D6FE}_{a}$
and
$\unicode[STIX]{x1D6FE}_{b}$
the flopping curves on
$B_{a}$
and
$B_{b}$
, respectively.(2) It is important to notice that there exist exactly two singular
$\unicode[STIX]{x1D70B}_{b}$
-fibers, which are isomorphic to the quadric cone (this follows from the calculation of the topological Euler number of
$B_{a}$
and invariance of Euler number under flop). We denote them by
$F_{1}$
and
$F_{2}$
.
Though we mainly work on
$B_{a}$
, the threefold
$B_{b}$
is also useful to understand the properties of
$B_{a}$
related to the jumping lines of the second kind since the definition of such jumping lines is less geometric (see Section 2.4).
1.4 Group action on
$B_{a}$
In this subsection, we show that
$B_{a}$
has a natural action by the subgroup of
$\operatorname{Aut}(\mathbb{P}^{2})^{\ast }$
preserving
$\ell _{1}\cup \ell _{2}$
. This fact should be known for experts but we do not know appropriate literatures.
Our way to see this is based on the elementary transformation of the
$\mathbb{P}^{1}$
-bundle
$\unicode[STIX]{x1D70B}_{a}:B_{a}\rightarrow \mathbb{P}^{2}$
centered at the flopping curve
$\unicode[STIX]{x1D6FE}_{a}$
. This make it possible to describe the group action quite explicitly.
Proposition 1.4.1. Let
$\unicode[STIX]{x1D707}:\widetilde{B}_{a}\rightarrow B_{a}$
be the blow-up along the flopping curve
$\unicode[STIX]{x1D6FE}_{a}$
. Let
$\unicode[STIX]{x1D708}:\widetilde{B}_{a}\rightarrow B_{c}$
be the blow down over
$\mathbb{P}^{2}$
contracting the strict transform of
$L_{\mathsf{j}}=\unicode[STIX]{x1D70B}_{a}^{-1}(\mathsf{j})$
to a smooth rational curve
$\unicode[STIX]{x1D6FE}_{c}$
(the existence of the blow down follows from Mori theory in a standard way). Then
$B_{c}\simeq \mathbb{P}^{1}\times \mathbb{P}^{2}$
. Moreover,
$\unicode[STIX]{x1D6FE}_{c}$
is a divisor of type
$(1,2)$
in
$\mathbb{P}^{1}\times \mathsf{j}$
.
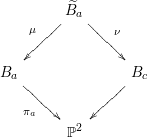
Proof. This follows from [Reference Fujita4, p.166, (si111o) Case (a)]. ◻
To describe
$B_{c}$
, let
$(x_{1}:x_{2})$
be a coordinate of
$\mathbb{P}^{1}$
and
$(y_{1}:y_{2}:y_{3})$
be a coordinate of
$\mathbb{P}^{2}$
. By a coordinate change, we may assume that
$\mathsf{j}=\{y_{3}=0\}\subset \mathbb{P}^{2}$
and the two ramification points of
$\unicode[STIX]{x1D6FE}_{c}{\hookrightarrow}\mathbb{P}^{1}\times \mathbb{P}^{2}\overset{p_{1}}{\rightarrow }\mathbb{P}^{1}$
are
$(0:1)\times (1:0:0)$
and
$(1:0)\times (0:1:0)$
. Then
$\unicode[STIX]{x1D6FE}_{c}=\{\unicode[STIX]{x1D6FC}x_{1}y_{1}^{2}+\unicode[STIX]{x1D6FD}x_{2}y_{2}^{2}=y_{3}=0\}$
with
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\not =0$
. By a further coordinate change, we may assume that
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{c}=\{x_{1}y_{1}^{2}+x_{2}y_{2}^{2}=y_{3}=0\}.\end{eqnarray}$$
Let us denote by
$G$
the automorphism group of
$B_{a}$
. We can obtain the following description of
$G$
from Proposition 1.4.1. For this, we denote by
$G_{m}\simeq \mathbb{C}^{\ast }$
the multiplicative group and by
$G_{a}\simeq \mathbb{C}$
the additive group.
Corollary 1.4.2. The automorphism group
$G$
of
$B_{a}$
is isomorphic to the subgroup of the automorphism group of
$B_{c}$
which preserves
$\unicode[STIX]{x1D6FE}_{c}$
. Explicitly, let an element
$(A,B)\in \operatorname{PGL}_{2}\times \operatorname{PGL}_{3}$
acts on
$B_{c}\simeq \mathbb{P}^{1}\times \mathbb{P}^{2}$
as
$(\mathbf{x},\mathbf{y})\mapsto (A\mathbf{x},B\mathbf{y})$
by matrix multiplication. If
$(A,B)$
preserve
$\unicode[STIX]{x1D6FE}_{c}$
with the equation (1.6) as above, then
$(A,B)$
is of the form
(i)
$A=\Bigl(\!\begin{smallmatrix}a_{1}^{2} & 0\\ 0 & 1\end{smallmatrix}\!\Bigr),B=\Bigl(\!\begin{smallmatrix}1 & 0 & b_{1}\\ 0 & a_{1} & b_{2}\\ 0 & 0 & a_{2}\end{smallmatrix}\!\Bigr)$
, or(ii)
$A=\Bigl(\!\begin{smallmatrix}0 & a_{1}^{2}\\ 1 & 0\end{smallmatrix}\!\Bigr),B=\Bigl(\!\begin{smallmatrix}0 & 1 & b_{1}\\ a_{1} & 0 & b_{2}\\ 0 & 0 & a_{2}\end{smallmatrix}\!\Bigr)$
,
where
$a_{1},a_{2}\in G_{m}$
and
$b_{1},b_{2}\in G_{a}$
in both cases.
In particular, the
$G$
-orbit of
$(1:1)\times (0:0:1)$
in
$\mathbb{P}^{1}\times \mathbb{P}^{2}$
is open. Therefore, the action of
$G$
on
$B_{c}$
is, and hence the one on
$B_{a}$
is quasi-homogeneous.
Proof. Note that
$G=\operatorname{Aut}B_{a}=\operatorname{Aut}(B_{a},\unicode[STIX]{x1D6FE}_{a},L_{\mathsf{j}})$
since
$\unicode[STIX]{x1D6FE}_{a}$
and
$L_{\mathsf{j}}$
are preserved by
$G$
. By universality of blow-ups, a
$G$
-action on
$\widetilde{B}_{a}$
is naturally induced and then the map
$\unicode[STIX]{x1D707}$
is
$G$
-equivariant. Thus we have
$\operatorname{Aut}(B_{a},\unicode[STIX]{x1D6FE}_{a},L_{\mathsf{j}})=\operatorname{Aut}(\widetilde{B}_{a},E_{a},\widetilde{L}_{\mathsf{j}})$
, where
$E_{a}$
is the
$\unicode[STIX]{x1D707}$
-exceptional divisor and
$\widetilde{L}_{\mathsf{j}}$
is the strict transform of
$L_{\mathsf{j}}$
. By a similar reason to the above, a
$G$
-action on
$B_{c}$
is naturally induced and then the map
$\unicode[STIX]{x1D708}$
is
$G$
-equivariant. Thus we have
$\operatorname{Aut}(\widetilde{B}_{a},E_{a},\widetilde{L}_{\mathsf{j}})=\operatorname{Aut}(B_{c},\mathbb{P}^{1}\times \mathsf{j},\unicode[STIX]{x1D6FE}_{c})$
since the images of
$E_{a}$
and
$\widetilde{L}_{\mathsf{j}}$
on
$B_{c}$
are
$\mathbb{P}^{1}\times \mathsf{j}$
and
$\unicode[STIX]{x1D6FE}_{c}$
respectively by Proposition 1.4.1. Moreover, since
$\mathbb{P}^{1}\times \mathsf{j}$
is uniquely determined from
$\unicode[STIX]{x1D6FE}_{c}$
, we have
$\operatorname{Aut}(\mathbb{P}^{1}\times \mathbb{P}^{2},\mathbb{P}^{1}\times \mathsf{j},\unicode[STIX]{x1D6FE}_{c})=\operatorname{Aut}(\mathbb{P}^{1}\times \mathbb{P}^{2},\unicode[STIX]{x1D6FE}_{c}).$
Therefore, we have
$G=\operatorname{Aut}(\mathbb{P}^{1}\times \mathbb{P}^{2},\unicode[STIX]{x1D6FE}_{c})$
and the first assertion follows. Explicit descriptions of
$G$
as a subgroup of
$\operatorname{Aut}B_{b}$
can be obtained by elementary calculations.◻
It is also easy and is convenient to write down the
$G$
-action on the base
$\mathbb{P}^{2}$
.
Corollary 1.4.3.
(1) The projective plane
$\mathbb{P}^{2}$
consists of the following three orbits of
$G$
: where$$\begin{eqnarray}\mathbb{P}^{2}=G\cdot (0:0:1)\sqcup G\cdot (1:1:0)\sqcup \{(1:0:0)\sqcup (0:1:0)\},\end{eqnarray}$$
$G\cdot (0:0:1)$
is the open orbit,
$G\cdot (1:1:0)$
is an open subset of the jumping line
$\mathsf{j}:=\{y_{3}=0\}$
, and the two points
$(1:0:0),(0:1:0)\in \mathsf{j}$
form one orbit and correspond to the lines
$\ell _{1}$
and
$\ell _{2}$
by projective duality.(2) The dual projective plane
$(\mathbb{P}^{2})^{\ast }$
has the following three orbits of
$G$
by the contragradient action of
$G:$
where$$\begin{eqnarray}(\mathbb{P}^{2})^{\ast }=G\cdot (1:1:0)\sqcup \{G\cdot (1:0:0)\sqcup G\cdot (0:1:0)\}\sqcup (0:0:1),\end{eqnarray}$$
$G\cdot (1:1:0)$
is the open orbit, the closures of
$G\cdot (1:0:0)$
and
$G\cdot (0:1:0)$
are the two lines
$\ell _{1}$
and
$\ell _{2}$
.
Proof. We only show that the two points
$(1:0:0),(0:1:0)\in \mathsf{j}$
correspond to the lines
$\ell _{1}$
and
$\ell _{2}$
by projective duality. This follows from the orbit decomposition of
$\mathbb{P}^{2}$
by the identity component
$G_{0}$
of
$G$
since the two points
$\in \mathbb{P}^{2}$
corresponding to the lines
$\ell _{1}$
and
$\ell _{2}$
are fixed by
$G_{0}$
, and
$G_{0}$
has only two fixed points.◻
In Section 5, a central role is played by the following explicit description of the action of
$G$
on
$B_{a}$
preserving
$L_{\mathsf{m}}$
for a line
$\mathsf{m}$
such that
$[\mathsf{m}]\not \in \ell _{1}\cup \ell _{2}$
. By quasi-homogeneity of the action on
$B_{a}$
as in Corollary 1.4.2, we may assume that
$\mathsf{m}=\{y_{1}=y_{2}\}$
.
Lemma 1.4.4. An element
$(A,B)\in \operatorname{PGL}_{2}\times \operatorname{PGL}_{3}$
of
$G$
preserves
$L_{\mathsf{m}}$
, equivalently, preserves
$\mathsf{m}$
if and only if
$(A,B)$
is of the form
$$\begin{eqnarray}(a)~A=\left(\begin{array}{@{}cc@{}}1 & 0\\ 0 & 1\end{array}\right),\qquad B=\left(\begin{array}{@{}ccc@{}}1 & 0 & b_{1}\\ 0 & 1 & b_{1}\\ 0 & 0 & a_{2}\end{array}\right),\end{eqnarray}$$
or
$$\begin{eqnarray}(b)~A=\left(\begin{array}{@{}cc@{}}0 & 1\\ 1 & 0\end{array}\right),\qquad B=\left(\begin{array}{@{}ccc@{}}0 & 1 & b_{1}\\ 1 & 0 & b_{1}\\ 0 & 0 & a_{2}\end{array}\right),\end{eqnarray}$$
where
$a_{2}\in G_{m}$
and
$b_{1}\in G_{a}$
in both cases.
In particular, such elements form a subgroup
$\unicode[STIX]{x1D6E4}\simeq (\mathbb{Z}_{2}\times G_{a})\rtimes G_{m}$
of
$G$
and
$\unicode[STIX]{x1D6E4}$
is generated by the following three type elements:
∙
$G_{m}:$
$(\!\begin{smallmatrix}1 & 0\\ 0 & 1\end{smallmatrix}\!)\times \Bigl(\!\begin{smallmatrix}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & a\end{smallmatrix}\!\Bigr)$
with
$a\in G_{m}$
;∙
$G_{a}:$
$(\!\begin{smallmatrix}1 & 0\\ 0 & 1\end{smallmatrix}\!)\times \Bigl(\!\begin{smallmatrix}1 & 0 & b\\ 0 & 1 & b\\ 0 & 0 & 1\end{smallmatrix}\!\Bigr)$
with
$b\in G_{a}$
; and∙
$\mathbb{Z}_{2}:$
$(\!\begin{smallmatrix}0 & 1\\ 1 & 0\end{smallmatrix}\!)\times \Bigl(\!\begin{smallmatrix}0 & 1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 1\end{smallmatrix}\!\Bigr)$
.
2 Families of rational curves on
$B_{a}$
In this section, we construct families of rational curves on
$B_{a}$
, which will ties the geometries of
$B_{a}$
and one-pointed ineffective spin hyperelliptic curves.
2.1 Preliminaries
Lemma 2.1.1. If a line
$\mathsf{m}$
is not equal to the jumping line
$\mathsf{j}$
, then
$(H-L)_{|L_{\mathsf{m}}}$
is linearly equivalent to the negative section
$C_{0}(\mathsf{m})$
of
$L_{\mathsf{m}}\simeq \mathbb{F}_{1}$
. If
$\mathsf{m}=\mathsf{j}$
, then
$(H-L)_{|L_{\mathsf{m}}}$
is linearly equivalent to the negative section
$\unicode[STIX]{x1D6FE}_{a}$
plus a ruling of
$L_{\mathsf{j}}\simeq \mathbb{F}_{3}$
.
Proof. As we mention in Section (1.2.b),
$M_{B_{a}}$
is the tautological line bundle on
$B_{a}$
associated to the bundle
${\mathcal{E}}(2)$
. Therefore, comparing (1.2) and (1.4), we see that
$H-L=M_{B_{a}}-2L$
is the tautological line bundle associated to the bundle
${\mathcal{E}}$
. If
$\mathsf{m}$
is not equal to the jumping line
$\mathsf{j}$
, then
${\mathcal{E}}_{|\mathsf{m}}\simeq {\mathcal{O}}_{\mathbb{P}^{1}}\oplus {\mathcal{O}}_{\mathbb{P}^{1}}(-1)$
and hence
$(H-L)_{|L_{\mathsf{m}}}$
is linearly equivalent to the negative section
$C_{0}(\mathsf{m})$
of
$L_{\mathsf{m}}\simeq \mathbb{F}_{1}$
. If
$\mathsf{m}=\mathsf{j}$
, then
${\mathcal{E}}_{|\mathsf{m}}\simeq {\mathcal{O}}_{\mathbb{P}^{1}}(-2)\oplus {\mathcal{O}}_{\mathbb{P}^{1}}(1)$
by Proposition 1.2.2(4) and hence
$(H-L)_{|L_{\mathsf{m}}}$
is linearly equivalent to the negative section
$\unicode[STIX]{x1D6FE}_{a}$
plus a ruling of
$L_{\mathsf{j}}\simeq \mathbb{F}_{3}$
.◻
By this lemma, it is easy to show the following proposition:
Proposition 2.1.2. Let
$\mathsf{m}\subset \mathbb{P}^{2}$
be a line and
$g\geqslant -1$
an integer. If
$\mathsf{m}\not =\mathsf{j}$
(resp.
$\mathsf{m}=\mathsf{j}$
and
$g\geqslant 1$
), then a general element
$R$
of the linear system
$|(H+gL)_{|L_{\mathsf{m}}}|$
is a smooth rational curve with
$H\cdot R=g+1$
and
$L\cdot R=1$
. Moreover, if
$\mathsf{m}\not =\mathsf{j}$
and
$g\geqslant 0$
(resp.
$\mathsf{m}=\mathsf{j}$
and
$g\geqslant 1$
), then
$|(H+gL)_{|L_{\mathsf{m}}}|$
has no base point.
Definition 2.1.1. We define
${\mathcal{L}}$
to be the following subscheme of
$B_{a}\times (\mathbb{P}^{2})^{\ast }$
:
$$\begin{eqnarray}{\mathcal{L}}:=\{(x,[\mathsf{m}])\mid x\in L_{\mathsf{m}}=\unicode[STIX]{x1D70B}_{a}^{-1}(\mathsf{m})\}.\end{eqnarray}$$
Let
$p_{1}:{\mathcal{L}}\rightarrow B_{a}$
and
$p_{2}:{\mathcal{L}}\rightarrow (\mathbb{P}^{2})^{\ast }$
be the first and the second projections, respectively. Note that the
$p_{2}$
-fiber over a point
$[\mathsf{m}]$
is nothing but
$L_{\mathsf{m}}$
. In particular,
${\mathcal{L}}$
is smooth.
Remark 2.1.2. To follow the sequel easily, it is useful to notice that
${\mathcal{L}}$
is the pullback by the composite
$B_{a}\times (\mathbb{P}^{2})^{\ast }\overset{\unicode[STIX]{x1D70B}_{a}\times \text{id}}{\longrightarrow }\mathbb{P}^{2}\times (\mathbb{P}^{2})^{\ast }$
of the point-line incidence variety
$\{(x,[\mathsf{m}])\mid x\in \mathsf{m}\}\subset \mathbb{P}^{2}\times (\mathbb{P}^{2})^{\ast }$
. Therefore, we also see that
${\mathcal{L}}$
is
$G$
-invariant, where the
$G$
-action is induced on
$B_{a}\times (\mathbb{P}^{2})^{\ast }$
by the
$G$
-action on
$B_{a}$
defined as above and the contragradient
$G$
-action on
$(\mathbb{P}^{2})^{\ast }$
.
2.2 Families of rational curves of higher degrees
Definition 2.2.1.
(1) For an integer
$g\geqslant 0$
, we set We see that$$\begin{eqnarray}{\mathcal{R}}_{g}:=p_{2\ast }p_{1}^{\ast }{\mathcal{O}}_{B_{a}}(H+gL).\end{eqnarray}$$
$\dim H^{0}({\mathcal{O}}_{L_{\mathsf{m}}}(H\,+\,gL))$
is constant since
$H^{1}({\mathcal{O}}_{L_{\mathsf{m}}}(H\,+\,gL))=\{0\}$
for any
$\mathsf{m}$
and
$g\geqslant 0$
. Therefore, by Grauert’s theorem, the coherent sheaf
${\mathcal{R}}_{g}$
is a locally free sheaf on
$(\mathbb{P}^{2})^{\ast }$
. Set which is nothing but the projective bundle over$$\begin{eqnarray}\unicode[STIX]{x1D6F4}_{g}:=\mathbb{P}({\mathcal{R}}_{g}^{\ast }),\end{eqnarray}$$
$(\mathbb{P}^{2})^{\ast }$
whose fiber over a point
$[\mathsf{m}]$
is the projective space
$\mathbb{P}(H^{0}({\mathcal{O}}_{L_{\mathsf{m}}}(H+gL)))$
.(2) We denote by
${\mathcal{H}}_{g}\subset \unicode[STIX]{x1D6F4}_{g}$
the sublocus parameterizing smooth rational curves. Note that
${\mathcal{H}}_{g}$
is a nonempty open subset of
$\unicode[STIX]{x1D6F4}_{g}$
by Proposition 2.1.2.
2.3 Family of
$B_{a}$
-Lines
Now we construct a family of curves parameterizing the negative section of
$L_{\mathsf{m}}$
for a line
$\mathsf{m}\not =\mathsf{j}$
, and the negative section
$\unicode[STIX]{x1D6FE}_{a}$
plus a ruling of
$L_{\mathsf{j}}$
. Intuitively, it is easy to imagine such a family exists by Lemma 2.1.1 but a rigorous construction needs some works.
Lemma 2.3.1. The following hold:
(1)
$H^{0}({\mathcal{O}}_{B_{a}}(H-L))=\{0\}$
and
$H^{1}({\mathcal{O}}_{B_{a}}(H-L))=\mathbb{C}$
.(2)
$H^{0}({\mathcal{O}}_{B_{a}}(H-2L))=\{0\}$
,
$H^{1}({\mathcal{O}}_{B_{a}}(H-2L))=\mathbb{C}^{2}$
, and
$H^{2}({\mathcal{O}}_{B_{a}}(H-2L))=\{0\}$
.
Proof. The claims follow easily from the exact sequence (1.1) noting that
$H-L$
is the tautological line bundle associated to
${\mathcal{E}}$
. Here we only show that
$H^{2}({\mathcal{O}}_{B_{a}}(H-2L))\simeq H^{2}(\mathbb{P}^{2},{\mathcal{E}}(-1))=\{0\}$
. By the Serre duality, we have
$H^{2}(\mathbb{P}^{2},{\mathcal{E}}(-1))\simeq H^{0}(\mathbb{P}^{2},{\mathcal{E}}^{\ast }(-2))^{\ast }\simeq H^{0}(\mathbb{P}^{2},{\mathcal{E}}(-1))^{\ast }$
, which is zero by (1.1).◻
Notation 2.3.1. Let
$b:\widetilde{(\mathbb{P}^{2})^{\ast }}\rightarrow (\mathbb{P}^{2})^{\ast }$
be the blow-up at the point
$[\mathsf{j}]$
. Let
$E_{0}$
be the
$b$
-exceptional curve, and
$r$
be a ruling of
$\widetilde{(\mathbb{P}^{2})^{\ast }}\simeq \mathbb{F}_{1}$
. The surface
$\widetilde{(\mathbb{P}^{2})^{\ast }}$
will be the parameter space of the family of
$B_{a}$
-lines which we are going to construct.
For a point
$[\mathsf{m}]\in (\mathbb{P}^{2})^{\ast }\setminus [\mathsf{j}]$
, we use the same character
$[\mathsf{m}]$
for the corresponding point on
$\widetilde{(\mathbb{P}^{2})^{\ast }}$
.
Let
$b_{{\mathcal{L}}}:\widetilde{{\mathcal{L}}}\rightarrow {\mathcal{L}}$
be the blow-up along the fiber of
$p_{2}:{\mathcal{L}}\rightarrow (\mathbb{P}^{2})^{\ast }$
over
$[\mathsf{j}]$
. By universality of blow-up, the variety
$\widetilde{{\mathcal{L}}}$
is contained in
$B_{a}\times \widetilde{(\mathbb{P}^{2})^{\ast }}$
and a unique map
$\tilde{p}_{2}:\widetilde{{\mathcal{L}}}\rightarrow \widetilde{(\mathbb{P}^{2})^{\ast }}$
is induced. We denote by
$\tilde{p}_{1}:\widetilde{{\mathcal{L}}}\rightarrow B_{a}$
the map obtained by composing
$b_{{\mathcal{L}}}:\widetilde{{\mathcal{L}}}\rightarrow {\mathcal{L}}$
with
$p_{1}:{\mathcal{L}}\rightarrow B_{a}$
.
Lemma 2.3.2. It holds that
$H^{0}(\tilde{p}_{1}^{\ast }{\mathcal{O}}_{B_{a}}(H-L)\otimes \tilde{p}_{2}^{\ast }{\mathcal{O}}(E_{0}+2r))\simeq \mathbb{C}$
.
Proof. By noting the natural isomorphism
$$\begin{eqnarray}\displaystyle & & \displaystyle H^{0}(\widetilde{p}_{1}^{\ast }{\mathcal{O}}_{B_{a}}(H-L)\otimes \widetilde{p}_{2}^{\ast }{\mathcal{O}}(E_{0}+2r))\nonumber\\ \displaystyle & & \displaystyle \quad \simeq H^{0}(\widetilde{p}_{2\ast }\widetilde{p}_{1}^{\ast }{\mathcal{O}}_{B_{a}}(H-L)\otimes {\mathcal{O}}(E_{0}+2r)),\nonumber\end{eqnarray}$$
the assertion follows once we show that
$$\begin{eqnarray}\tilde{p}_{2\ast }\tilde{p}_{1}^{\ast }{\mathcal{O}}_{B_{a}}(H-L)\simeq {\mathcal{O}}(-E_{0}-2r).\end{eqnarray}$$
Let
$\tilde{\unicode[STIX]{x1D70C}}_{1}:B_{a}\times \widetilde{(\mathbb{P}^{2})^{\ast }}\rightarrow B_{a}$
and
$\unicode[STIX]{x1D70C}_{1}:B_{a}\times (\mathbb{P}^{2})^{\ast }\rightarrow B_{a}$
be the first projections, and
$\tilde{\unicode[STIX]{x1D70C}}_{2}:B_{a}\times \widetilde{(\mathbb{P}^{2})^{\ast }}\rightarrow \widetilde{(\mathbb{P}^{2})^{\ast }}$
and
$\unicode[STIX]{x1D70C}_{2}:B_{a}\times (\mathbb{P}^{2})^{\ast }\rightarrow (\mathbb{P}^{2})^{\ast }$
the second projections. By Remark 2.1.2, when we consider the variety
${\mathcal{L}}$
as a divisor on
$B_{a}\times (\mathbb{P}^{2})^{\ast }$
, it is a member of
$|\unicode[STIX]{x1D70C}_{1}^{\ast }L+\unicode[STIX]{x1D70C}_{2}^{\ast }{\mathcal{O}}_{(\mathbb{P}^{2})^{\ast }}(1)|$
. Since
${\mathcal{L}}$
does not contain the fiber of
$B_{a}\times (\mathbb{P}^{2})^{\ast }\rightarrow (\mathbb{P}^{2})^{\ast }$
over
$[\mathsf{j}]$
, the variety
$\widetilde{{\mathcal{L}}}$
is the total pullback of
${\mathcal{L}}$
by
$B_{a}\times \widetilde{(\mathbb{P}^{2})^{\ast }}\rightarrow B_{a}\times (\mathbb{P}^{2})^{\ast }$
. Hence
$\widetilde{{\mathcal{L}}}$
belongs to the linear system
$|\tilde{\unicode[STIX]{x1D70C}}_{1}^{\ast }L+\tilde{\unicode[STIX]{x1D70C}}_{2}^{\ast }(E_{0}+r)|$
since
${\mathcal{O}}(E_{0}+r)=b^{\ast }{\mathcal{O}}_{(\mathbb{P}^{2})^{\ast }}(1)$
.
To compute
$\tilde{p}_{2\ast }\tilde{p}_{1}^{\ast }{\mathcal{O}}_{B_{a}}(H-L)$
, let us consider the following exact sequence:
$$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle \widetilde{\unicode[STIX]{x1D70C}}_{1}^{\ast }{\mathcal{O}}_{B_{a}}(H-2L)\otimes \widetilde{\unicode[STIX]{x1D70C}}_{2}^{\ast }{\mathcal{O}}(-E_{0}-r)\nonumber\\ \displaystyle & \rightarrow & \displaystyle \widetilde{\unicode[STIX]{x1D70C}}_{1}^{\ast }{\mathcal{O}}_{B_{a}}(H-L)\rightarrow \widetilde{p}_{1}^{\ast }{\mathcal{O}}_{B_{a}}(H-L)\rightarrow 0,\nonumber\end{eqnarray}$$
which is obtained from the natural exact sequence
$$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{B_{a}\times \widetilde{(\mathbb{P}^{2})^{\ast }}}(-\widetilde{{\mathcal{L}}})\rightarrow {\mathcal{O}}_{B_{a}\times \widetilde{(\mathbb{P}^{2})^{\ast }}}\rightarrow {\mathcal{O}}_{\widetilde{{\mathcal{L}}}}\rightarrow 0\end{eqnarray}$$
by tensoring
$\widetilde{\unicode[STIX]{x1D70C}}_{1}^{\ast }{\mathcal{O}}_{B_{a}}(H-L)$
. By Lemma 2.3.1, the pushforward of the exact sequence by
$\widetilde{\unicode[STIX]{x1D70C}}_{2}$
is
$$\begin{eqnarray}\displaystyle 0\rightarrow \tilde{p}_{2\ast }\tilde{p}_{1}^{\ast }{\mathcal{O}}_{B_{a}}(H-L)\rightarrow {\mathcal{O}}(-E_{0}-r)^{\oplus 2}\rightarrow {\mathcal{O}}\rightarrow R^{1}\tilde{p}_{2\ast }\tilde{p}_{1}^{\ast }{\mathcal{O}}_{B_{a}}(H-L)\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$
Note that, for a point
$[\mathsf{m}]\not =[\mathsf{j}]$
, it holds that
$H^{0}({\mathcal{O}}_{L_{\mathsf{m}}}(H-L))\simeq \mathbb{C}$
and
$H^{1}({\mathcal{O}}_{L_{\mathsf{m}}}(H-L))=\{0\}$
by Lemma 2.1.1. Therefore, by Grauert’s theorem,
$\tilde{p}_{2\ast }\tilde{p}_{1}^{\ast }{\mathcal{O}}_{B_{a}}(H-L)$
is an invertible sheaf possibly outside
$E_{0}$
, and the support of
$R^{1}:=R^{1}\tilde{p}_{2\ast }\tilde{p}_{1}^{\ast }{\mathcal{O}}_{B_{a}}(H-L)$
is contained in
$E_{0}$
.
Let
${\mathcal{I}}$
be the image of the map
${\mathcal{O}}(-E_{0}-r)^{\oplus 2}\rightarrow {\mathcal{O}}$
in the above exact sequence, which is an ideal sheaf. Note that
$R^{1}={\mathcal{O}}_{\unicode[STIX]{x1D6E5}}$
, where
$\unicode[STIX]{x1D6E5}$
is the closed subscheme defined by
${\mathcal{I}}$
. We show that
$\unicode[STIX]{x1D6E5}=E_{0}$
as a closed subscheme. Indeed,
$\unicode[STIX]{x1D6E5}$
is a member of
$|E_{0}+r|$
, or the intersection of two members of
$|E_{0}+r|$
. In particular,
$\unicode[STIX]{x1D6E5}$
is nonempty. Noting the support of
${\mathcal{O}}_{\unicode[STIX]{x1D6E5}}=R^{1}$
is contained in
$E_{0}$
, the subscheme
$\unicode[STIX]{x1D6E5}$
must be equal to
$E_{0}$
.
Therefore, the map
${\mathcal{O}}(-E_{0}-r)^{\oplus 2}\rightarrow {\mathcal{O}}$
is decomposed as
${\mathcal{O}}(-E_{0}-r)^{\oplus 2}\rightarrow {\mathcal{O}}(-E_{0}){\hookrightarrow}{\mathcal{O}}$
and
${\mathcal{O}}(-E_{0}-r)^{\oplus 2}\rightarrow {\mathcal{O}}(-E_{0})$
is surjective. Hence the kernel
$\tilde{p}_{2\ast }\tilde{p}_{1}^{\ast }{\mathcal{O}}_{B_{a}}(H-L)$
of the map
${\mathcal{O}}(-E_{0}-r)^{\oplus 2}\rightarrow {\mathcal{O}}(-E_{0})$
is isomorphic to
${\mathcal{O}}(-E_{0}-2r)$
. Now we have shown (2.2) and finished the proof of this lemma.◻
In the next proposition, we obtain the desired family of curves.
Proposition 2.3.3. Let
${\mathcal{U}}_{1}$
be the unique member of
$|\tilde{p}_{1}^{\ast }{\mathcal{O}}_{B_{a}}(H-L)\otimes \tilde{p}_{2}^{\ast }{\mathcal{O}}(E_{0}+2r)|$
. Then
${\mathcal{U}}_{1}$
is irreducible and the natural map
${\mathcal{U}}_{1}\rightarrow \widetilde{(\mathbb{P}^{2})^{\ast }}$
is flat. Moreover, the fibers are described as follows:
(1) the fiber over a point
$[\mathsf{m}]\not =[\mathsf{j}]$
is the negative section of
$L_{\mathsf{m}}$
; and(2) the fiber over a point
$x$
of
$E_{0}$
is the negative section
$\unicode[STIX]{x1D6FE}_{a}$
plus a ruling of
$L_{\mathsf{j}}$
.
Proof. Note that
${\mathcal{U}}_{1}$
is Cohen–Macaulay since it is a divisor on the smooth variety
$\widetilde{{\mathcal{L}}}$
. Therefore, the flatness follows from the smoothness of
$\widetilde{(\mathbb{P}^{2})^{\ast }}$
and the descriptions of fibers as in (1) and (2). Besides, the irreducibility of
${\mathcal{U}}_{1}$
also follows from the descriptions of fibers, which now we are going to give below.
Note that, by the uniqueness of
${\mathcal{U}}_{1}$
, the group
$G$
acts on
${\mathcal{U}}_{1}$
, where
$G$
acts on
${\mathcal{L}}$
and hence on
$\widetilde{{\mathcal{L}}}$
by Remark 2.1.2. Let
$x$
be a point of
$\widetilde{(\mathbb{P}^{2})^{\ast }}$
. Set
$[\mathsf{m}]:=b(x)\in (\mathbb{P}^{2})^{\ast }$
. Note that the fiber of
$\widetilde{{\mathcal{L}}}\rightarrow \widetilde{(\mathbb{P}^{2})^{\ast }}$
over
$x$
is
$L_{\mathsf{m}}$
.
Proof of (1). If
$x\not \in E_{0}$
, then
$L_{\mathsf{m}}\subset {\mathcal{U}}_{1}$
or
${{\mathcal{U}}_{1}}_{|L_{\mathsf{m}}}$
is the negative section of
$L_{\mathsf{m}}\simeq \mathbb{F}_{1}$
by Lemma 2.1.1 since
${\mathcal{U}}_{1}\in |\tilde{p}_{1}^{\ast }{\mathcal{O}}_{B_{a}}(H-L)\otimes \tilde{p}_{2}^{\ast }{\mathcal{O}}(E_{0}+2r)|$
. We show that the latter occurs for any
$x\not \in E_{0}$
, which implies the assertion (1). If
$L_{\mathsf{m}}\subset {\mathcal{U}}_{1}$
for an
$x\not \in E_{0}$
such that
$[\mathsf{m}]\not \in \ell _{1}\cup \ell _{2}$
, then, by the description of the group action of
$G$
(Corollary 1.4.3),
$L_{\mathsf{m}}\subset {\mathcal{U}}_{1}$
hold for all such
$x$
’s, which implies that
${\mathcal{U}}_{1}=\widetilde{{\mathcal{L}}}$
, a contradiction. If
$L_{\mathsf{m}}\subset {\mathcal{U}}_{1}$
for an
$x\not \in E_{0}$
such that
$[\mathsf{m}]\in \ell _{i}$
for
$i=1~\text{or}~2$
, then, again by the group action of
$G$
, we have
$L_{\mathsf{m}}\subset {\mathcal{U}}_{1}$
for all such
$x$
’s, which implies that
${\mathcal{U}}_{1}$
contains the pullback of the strict transform
$\ell _{i}^{\prime }\subset \widetilde{(\mathbb{P}^{2})^{\ast }}$
of
$\ell _{i}$
. Since
$\ell _{i}^{\prime }$
is a ruling of
$\widetilde{(\mathbb{P}^{2})^{\ast }}$
, this implies that
$H^{0}(\tilde{p}_{1}^{\ast }{\mathcal{O}}_{B_{a}}(H-L)\otimes \tilde{p}_{2}^{\ast }{\mathcal{O}}(E_{0}+r))\not =0$
, which is impossible by the proof of Lemma 2.3.2.
Proof of (2). Now assume that
$x\in E_{0}$
. By a similar argument to the above one using the group action, we see that
${{\mathcal{U}}_{1}}_{|L_{\mathsf{j}}\times \{x\}}$
is the negative section
$\unicode[STIX]{x1D6FE}_{a}$
plus a ruling if
$x$
is not contained in the strict transforms
$\ell _{i}^{\prime }$
of
$\ell _{i}$
(
$i=1,2$
). Therefore,
${{\mathcal{U}}_{1}}_{|L_{\mathsf{j}}\times E_{0}}$
is a member of the linear system
$|{\mathcal{O}}_{L_{\mathsf{j}}}(H-L)\boxtimes {\mathcal{O}}_{E_{0}}(1)|$
on
$L_{\mathsf{j}}\times E_{0}$
. Suppose by contradiction that
${{\mathcal{U}}_{1}}_{|L_{\mathsf{j}}\times \{x\}}=L_{\mathsf{j}}\times \{x\}$
for
$x=\ell _{1}^{\prime }\cap E_{0}$
or
$\ell _{2}^{\prime }\cap E_{0}$
. Then, since the group action interchanges
$\ell _{1}^{\prime }\cap E_{0}$
and
$\ell _{2}^{\prime }\cap E_{0}$
,
${{\mathcal{U}}_{1}}_{|L_{\mathsf{j}}\times \{x\}}=L_{\mathsf{j}}\times \{x\}$
for both
$x=\ell _{1}^{\prime }\cap E_{0}$
and
$\ell _{2}^{\prime }\cap E_{0}$
. This would imply that
$|{\mathcal{O}}_{L_{\mathsf{j}}}(H-L)\boxtimes {\mathcal{O}}_{E_{0}}(-1)|$
is nonempty, which is absurd. Therefore, the assertion (2) follows.◻
Definition 2.3.2. We call a fiber of
${\mathcal{U}}_{1}\rightarrow \widetilde{(\mathbb{P}^{2})^{\ast }}$
a
$B_{a}$
-line. Explicitly, by Proposition 2.3.3, a
$B_{a}$
-line is the negative section
$C_{0}(\mathsf{m})$
of
$L_{\mathsf{m}}$
for
$[\mathsf{m}]\not =[\mathsf{j}]$
, or the negative section
$\unicode[STIX]{x1D6FE}_{a}$
plus a ruling of
$L_{\mathsf{j}}$
.
The name comes from the fact that the image of a
$B_{a}$
-line on the anticanonical model
$B$
is a line in the usual sense when
$B$
is embedded by
$|M_{B}|$
, where
$M_{B}$
is the ample generator of
$\operatorname{Pic}B$
.
2.4
$B_{a}$
-Lines interpreted on
$B_{b}$
In section 3, we construct hyperelliptic curves using the map
$\tilde{p}_{1|{\mathcal{U}}_{1}}:{\mathcal{U}}_{1}\rightarrow B_{a}$
. To understand the map
$\tilde{p}_{1|{\mathcal{U}}_{1}}$
, it is convenient to interpret
$B_{a}$
-lines by the geometry of
$B_{b}$
.
Notation 2.4.1.
(1) We recall that the two singular
$\unicode[STIX]{x1D70B}_{b}$
-fibers are denoted by
$F_{1}$
and
$F_{2}$
, which are singular quadrics. We denote by
$v_{i}$
the vertex of
$F_{i}$
(
$i=1,2$
).(2) We denote by
$F_{i}^{\prime }$
the strict transform on
$B_{a}$
of
$F_{i}$
(
$i=1,2$
).(3) By Corollary 1.2.3, we have
$L\cdot \unicode[STIX]{x1D6FE}_{a}=1$
, and, by a standard property of flop, we have
$L\cdot \unicode[STIX]{x1D6FE}_{b}=-1$
. This and the equality (1.4) imply that
$\unicode[STIX]{x1D6FE}_{b}$
is a
$\unicode[STIX]{x1D70B}_{b}$
-section. Therefore,
$\unicode[STIX]{x1D6FE}_{b}$
does not pass through
$v_{1}$
nor
$v_{2}$
and so
$B_{b}{\dashrightarrow}B_{a}$
is isomorphic near
$v_{1}$
and
$v_{2}$
. We denote by
$v_{i}^{\prime }$
the point on
$B_{a}$
corresponding to
$v_{i}$
$(i=1,2)$
.
Lemma 2.4.1. The following hold:
(1) The
$\unicode[STIX]{x1D70B}_{a}$
-images of
$v_{1}^{\prime }$
and
$v_{2}^{\prime }$
in
$\mathbb{P}^{2}$
correspond to the lines
$\ell _{1}$
and
$\ell _{2}$
in
$(\mathbb{P}^{2})^{\ast }$
by projective duality. In other words,
$\ell _{i}$
$(i=1,2)$
parameterizes lines through the point
$\unicode[STIX]{x1D70B}_{a}(v_{i}^{\prime })\in \mathbb{P}^{2}$
.(2) For a line
$\mathsf{m}\not =\mathsf{j}$
on
$\mathbb{P}^{2}$
, the negative section
$C_{0}(\mathsf{m})$
of
$L_{\mathsf{m}}$
is disjoint from
$\unicode[STIX]{x1D6FE}_{a}$
.
Proof. (1) We use the group actions of
$G$
on
$B_{a}$
and
$B_{b}$
. The action of
$G$
on
$B_{b}$
fixes or interchanges
$F_{1}$
and
$F_{2}$
, and hence
$v_{1}$
and
$v_{2}$
. Since
$B_{b}{\dashrightarrow}B_{a}$
is isomorphic near
$v_{1}$
and
$v_{2}$
as we noted in Notation 2.4.1(3), the group action on
$B_{a}$
fixes or interchanges
$v_{1}^{\prime }$
and
$v_{2}^{\prime }$
. By Corollary 1.4.3, this implies that the images of
$v_{1}^{\prime }$
and
$v_{2}^{\prime }$
correspond to the lines
$\ell _{1}$
and
$\ell _{2}$
by projective duality.
(2) Let
$C_{0}^{\prime }(\mathsf{m})$
be the strict transform of
$C_{0}(\mathsf{m})$
on
$B_{b}$
. Note that
$H\cdot C_{0}(\mathsf{m})=0$
by Lemma 2.1.1. If
$C_{0}(\mathsf{m})\cap \unicode[STIX]{x1D6FE}_{a}\not =\emptyset$
, then
$H\cdot C_{0}^{\prime }(\mathsf{m})<H\cdot C_{0}(\mathsf{m})=0$
by a standard property of flop, which is a contradiction since
$H$
is nef on
$B_{b}$
.◻
Proposition 2.4.2. The following hold:
(1) For a line
$\mathsf{m}\not =\mathsf{j}$
on
$\mathbb{P}^{2}$
, the curve
$C_{0}(\mathsf{m})$
is the strict transform of a ruling of a
$\unicode[STIX]{x1D70B}_{b}$
-fiber disjoint from
$\unicode[STIX]{x1D6FE}_{b}$
, and vice versa. Moreover, under this condition,
$C_{0}(\mathsf{m})$
is the strict transform of a ruling of
$F_{1}$
or
$F_{2}$
if and only if
$[\mathsf{m}]\in \ell _{1}\cup \ell _{2}$
.(2) A ruling
$f$
of
$L_{\mathsf{j}}$
is the strict transform of a ruling of a
$\unicode[STIX]{x1D70B}_{b}$
-fiber intersecting
$\unicode[STIX]{x1D6FE}_{b}$
, and vice versa (note that
$f\cap \unicode[STIX]{x1D6FE}_{a}\not =\emptyset$
, and
$\unicode[STIX]{x1D6FE}_{a}\cup f$
is a
$B_{a}$
-line as in Proposition 2.3.3(2)). Moreover, under this condition,
$f$
is the strict transform of a ruling of
$F_{1}$
or
$F_{2}$
if and only if the point
$\unicode[STIX]{x1D70B}_{a}(f)\in \mathbb{P}^{2}$
corresponds to the line
$\ell _{1}$
or
$\ell _{2}$
in
$(\mathbb{P}^{2})^{\ast }$
by projective duality.
Proof. We show the first assertions of (1) and (2). Since the proofs are similar, we only show (2), which is more difficult. We also only prove the only if part since the if part follows by reversing the argument. Recall that
$\unicode[STIX]{x1D6FE}_{a}+f\sim (H-L)_{|L_{\mathsf{j}}}$
by Lemma 2.1.1. Thus
$H\cdot f=1$
. Since
$f$
intersects
$\unicode[STIX]{x1D6FE}_{a}$
transversely at one point, and
$H\cdot \unicode[STIX]{x1D6FE}_{a}=-1$
, we have
$H\cdot f^{\prime }=0$
, where
$f^{\prime }$
is the strict transform of
$f$
on
$B_{b}$
. Hence
$f^{\prime }$
is contained in a
$\unicode[STIX]{x1D70B}_{b}$
-fiber
$F$
. By the equality (1.4), we have
$-K_{F}=-K_{B_{b}}|_{F}=2L|_{F}$
. Therefore,
$f^{\prime }$
is a ruling of
$F$
since
$L\cdot f^{\prime }=L\cdot f+1=1$
.
The latter assertions of (1) and (2) follows from Lemma 2.4.1(1). ◻
Corollary 2.4.3. Let
$x$
be a point of
$B_{a}\setminus (\unicode[STIX]{x1D6FE}_{a}\cup v_{1}^{\prime }\cup v_{2}^{\prime })$
. If
$x$
is not in
$F_{1}^{\prime }$
nor
$F_{2}^{\prime }$
, then
$x$
is contained in exactly two
$B_{a}$
-lines. If
$x$
is in
$F_{1}^{\prime }$
or
$F_{2}^{\prime }$
, then
$x$
is contained in exactly one
$B_{a}$
-line.
In particular, outside
$\unicode[STIX]{x1D6FE}_{a}\cup v_{1}^{\prime }\cup v_{2}^{\prime }$
, the map
$\tilde{p}_{1|{\mathcal{U}}_{1}}:{\mathcal{U}}_{1}\rightarrow B_{a}$
is flat, finite of degree two and is branched along
$F_{1}^{\prime }$
and
$F_{2}^{\prime }$
.
Proof. The assertions follow from Proposition 2.4.2(1) and (2), and the description of rulings on quadric surfaces. ◻
3 Hyperelliptic curves parameterizing
$B_{a}$
-lines
3.1 Basic constructions
Definition 3.1.1. Let
$\unicode[STIX]{x1D6FE}$
be a curve contained in
$B_{a}\setminus (\unicode[STIX]{x1D6FE}_{a}\cup v_{1}^{\prime }\cup v_{2}^{\prime })$
. Then note that
$\tilde{p}_{1|{\mathcal{U}}_{1}}:{\mathcal{U}}_{1}\rightarrow B_{a}$
is flat and finite of degree two near
$\unicode[STIX]{x1D6FE}$
by Corollary 2.4.3.
(1) We define
$C_{\unicode[STIX]{x1D6FE}}\rightarrow \unicode[STIX]{x1D6FE}$
to be the flat base change of
$\tilde{p}_{1|{\mathcal{U}}_{1}}$
. Note that
$C_{\unicode[STIX]{x1D6FE}}$
is contained in
${\mathcal{U}}_{1}$
, and parameterizes pairs
$(l,x)$
with
$B_{a}$
-lines
$l$
intersecting
$\unicode[STIX]{x1D6FE}$
and points
$x\in \unicode[STIX]{x1D6FE}\cap l$
. In other words,
$C_{\unicode[STIX]{x1D6FE}}$
parameterizes one-pointed
$B_{a}$
-lines intersecting
$\unicode[STIX]{x1D6FE}$
.(2) We define
$\widetilde{M}_{\unicode[STIX]{x1D6FE}}\subset \widetilde{(\mathbb{P}^{2})^{\ast }}$
and
$M_{\unicode[STIX]{x1D6FE}}\subset (\mathbb{P}^{2})^{\ast }$
to be the cycle-theoretic pushforwards of
$C_{\unicode[STIX]{x1D6FE}}$
to
$\widetilde{(\mathbb{P}^{2})^{\ast }}$
and
$(\mathbb{P}^{2})^{\ast }$
respectively (cf. the diagram (2.1)). Note that the support of
$\widetilde{M}_{\unicode[STIX]{x1D6FE}}$
parameterizes
$B_{a}$
-lines intersecting
$\unicode[STIX]{x1D6FE}$
.
3.2 Generality conditions
Let
$\mathsf{m}\subset \mathbb{P}^{2}$
be a line and
$R\subset L_{\mathsf{m}}$
a member of the linear system
$|(H+gL)_{|L_{\mathsf{m}}}|$
(
$R$
belongs to the family
$\unicode[STIX]{x1D6F4}_{g}$
constructed as in Section 2.2). In Proposition 3.3.1 below, we are going to show that
$C_{R}$
is a hyperelliptic curve of genus
$g$
under the following generality conditions for
$\mathsf{m}$
and
$R$
:
Condition 3.2.1. Let
$\mathsf{m}\subset \mathbb{P}^{2}$
be a line and
$R\subset L_{\mathsf{m}}$
a member of the linear system
$|(H+gL)_{|L_{\mathsf{m}}}|$
. We consider the following conditions for
$\mathsf{m}$
and
$R$
:
(a)
$[\mathsf{m}]\not \in \ell _{1}\cup \ell _{2}$
. In particular,
$v_{1}^{\prime },v_{2}^{\prime }\not \in R$
by Lemma 2.4.1(1).(b)
$R$
is smooth.(c)
$R\cap \unicode[STIX]{x1D6FE}_{a}=\emptyset$
.(d)
$R$
intersects
$F_{1}^{\prime }$
and
$F_{2}^{\prime }$
transversely at
$g+1$
points, respectively (note that, by
$R\sim (H+gL)_{|L_{\mathsf{m}}}$
, we have
$F_{i}^{\prime }\cdot R=H\cdot R=g+1$
).Note that the condition (c) implies that
$R\cap F_{1}^{\prime }\cap F_{2}^{\prime }=R\cap \unicode[STIX]{x1D6FE}_{a}=\emptyset$
.
It is easy to see that, if
$g\geqslant 0$
, then general
$\mathsf{m}$
and
$R$
satisfy these conditions by Proposition 2.1.2.
Lemma 3.2.1. If
$[\mathsf{m}]\not \in \ell _{1}\cup \ell _{2}$
, then
${F_{i}^{\prime }}_{|L_{\mathsf{m}}}$
is linearly equivalent to
$C_{0}(\mathsf{m})+L_{|L_{\mathsf{m}}}$
, and is irreducible
$(i=1,2)$
. In particular,
$C_{0}(\mathsf{m})$
is disjoint from
$F_{i}^{\prime }$
.
Proof. Under the assumption that
$[\mathsf{m}]\not \in \ell _{1}\cup \ell _{2}$
, the strict transform
$C_{0}^{\prime }(\mathsf{m})$
of
$C_{0}(\mathsf{m})$
on
$B_{b}$
is a ruling of a
$\unicode[STIX]{x1D70B}_{b}$
-fiber which is different from
$F_{1}$
and
$F_{2}$
by Proposition 2.4.2(1). In particular,
$C_{0}(\mathsf{m})$
is not contained in
$F_{i}^{\prime }$
. We see that
${F_{i}^{\prime }}_{|L_{\mathsf{m}}}$
is linearly equivalent to
$C_{0}(\mathsf{m})+L_{|L_{\mathsf{m}}}$
by (1.4) since
$F_{i}^{\prime }\sim H$
. Therefore, if
${F_{i}^{\prime }}_{|L_{\mathsf{m}}}$
were reducible, then
$C_{0}(\mathsf{m})\subset {F_{i}^{\prime }}_{|L_{\mathsf{m}}}\,\!$
, a contradiction.◻
Lemma 3.2.2. Assume that a
$\unicode[STIX]{x1D70B}_{a}$
-fiber
$f$
is disjoint from
$\unicode[STIX]{x1D6FE}_{a}$
. Then the following hold:
(1)
$v_{1}^{\prime },v_{2}^{\prime }\not \in f$
. In particular, such an
$f$
satisfies the conditions of Definition 3.1.1.(2)
$f$
intersects
$F_{1}^{\prime }$
and
$F_{2}^{\prime }$
at one point, respectively, and
$f\cap F_{1}^{\prime }\cap F_{2}^{\prime }=\emptyset$
.
Proof. (1) The assumption
$f\cap \unicode[STIX]{x1D6FE}_{a}=\emptyset$
is equivalent to that
$\unicode[STIX]{x1D70B}_{a}(f)\in \mathbb{P}^{2}$
belongs to the open orbit of
$G$
. Therefore, the assertion (1) follows from Corollary 1.4.3 and Lemma 2.4.1(1).
(2) We show that
$f$
intersects
$F_{i}^{\prime }$
$(i=1,2)$
at one point. By (1.4), we have
$F_{i}^{\prime }\cdot f=H\cdot f=1$
since
$-K_{B_{a}}\cdot f=2$
and
$L\cdot f=0$
. Therefore, we have only to show that
$f$
is not contained in
$F_{i}^{\prime }$
. If
$f\subset F_{i}^{\prime }$
, then the strict transform
$f^{\prime }$
of
$f$
is contained in
$F_{i}$
. Then, however,
$-K_{F_{i}}\cdot f^{\prime }=2L_{|F_{i}}\cdot f^{\prime }=0$
, a contradiction.
The assumption implies that
$f\cap F_{1}^{\prime }\cap F_{2}^{\prime }=f\cap \unicode[STIX]{x1D6FE}_{a}=\emptyset$
. Therefore, we have the assertion (2).◻
3.3
$C_{R}$
is hyperelliptic
Proposition 3.3.1. Assume that
$g\geqslant 2$
, and
$\mathsf{m}$
and
$R$
satisfy Condition 3.2.1(a)–(d). Then the following hold:
(1) The scheme
$C_{R}$
is a smooth hyperelliptic curve of genus
$g$
. The hyperelliptic structure is given by the map
$\tilde{p}_{1|C_{R}}:C_{R}\rightarrow R\simeq \mathbb{P}^{1}$
and the map is branched at
$R\cap (F_{1}^{\prime }\cup F_{2}^{\prime })$
.(2) Assume that a
$\unicode[STIX]{x1D70B}_{a}$
-fiber
$f$
is disjoint from
$\unicode[STIX]{x1D6FE}_{a}$
. Then
$C_{f}$
is a smooth rational curve and
$C_{f}\rightarrow f$
is a double cover branched at the two points
$f\cap (F_{1}^{\prime }\cup F_{2}^{\prime })$
(cf. Lemma 3.2.2(2)). Moreover,
$M_{f}$
is the line of
$(\mathbb{P}^{2})^{\ast }$
corresponding to the point
$\unicode[STIX]{x1D70B}_{a}(f)\in \mathbb{P}^{2}$
by projective duality.(3) The curve
$M_{R}$
is a degree
$g+2$
plane curve, smooth outside
$[\mathsf{m}]$
, and has a
$g$
-ple point at
$[\mathsf{m}]$
.(4) The natural map
$C_{R}\rightarrow M_{R}$
is the normalization, and the unique
$g_{2}^{1}$
on
$C_{R}$
is given by the pullback of the pencil of lines through
$[\mathsf{m}]$
.
Proof. We use the notation in Section 2 freely.
(1) By definition,
$C_{R}\rightarrow R$
is flat and finite of degree two (note that
$R$
satisfies the conditions of Definition 3.1.1 by Condition 3.2.1(a) and (c)). Moreover, by Condition 3.2.1(d), the branch locus of
$C_{R}\rightarrow R$
is smooth and of degree
$2g+2$
. Therefore, by Condition 3.2.1(b), the scheme
$C_{R}$
is a smooth hyperelliptic curve of genus
$g$
.
(2) The assertions for
$C_{f}$
can be proved similarly to (1) by Lemma 3.2.2. We show the assertion for
$M_{f}$
. Since
$f\cap \unicode[STIX]{x1D6FE}_{a}=\emptyset$
, a
$B_{a}$
-line intersecting
$f$
satisfies Proposition 2.3.3(1), namely, such a
$B_{a}$
-line is the negative section of
$L_{\mathsf{m}}$
with a line
$\mathsf{m}\not =\mathsf{j}$
containing
$\unicode[STIX]{x1D70B}_{a}(f)$
. Therefore, the support of
$M_{f}$
is the line of
$(\mathbb{P}^{2})^{\ast }$
corresponding to the point
$\unicode[STIX]{x1D70B}_{a}(f)$
by projective duality. Moreover,
$C_{f}\rightarrow \operatorname{Supp}M_{f}$
is one to one since
$f$
intersects a
$B_{a}$
-line at most at one point. Thus
$M_{f}$
is actually the line.
To show the remaining assertions (3) and (4), we investigate fibers of
$\tilde{p}_{1}^{-1}(L_{\mathsf{m}})\cap {\mathcal{U}}_{1}\rightarrow \widetilde{(\mathbb{P}^{2})^{\ast }}$
induced by
$\tilde{p}_{2}$
. For this, we note that the fiber over a point
$s\in \widetilde{(\mathbb{P}^{2})^{\ast }}$
is the intersection between
$L_{\mathsf{m}}$
and the
$B_{a}$
-line corresponding to
$s$
. Therefore, the fiber over
$[\mathsf{m}]\in \widetilde{(\mathbb{P}^{2})^{\ast }}$
can be identified with the negative section
$C_{0}(\mathsf{m})$
of
$L_{\mathsf{m}}$
. Recall that
$E_{0}$
is as in Notation 2.3.1. Let
$t$
be the point of
$E_{0}$
over which the fiber of
${\mathcal{U}}_{1}\rightarrow \widetilde{(\mathbb{P}^{2})^{\ast }}$
is the union
$\unicode[STIX]{x1D6FE}_{a}\cup \unicode[STIX]{x1D70B}_{a}^{-1}(\mathsf{j}\cap \mathsf{m})$
. Then the fiber of
$\tilde{p}_{1}^{-1}(L_{\mathsf{m}})\cap {\mathcal{U}}_{1}\rightarrow \widetilde{(\mathbb{P}^{2})^{\ast }}$
over
$t$
is
$\unicode[STIX]{x1D70B}_{a}^{-1}(\mathsf{j}\cap \mathsf{m})$
. Besides, over
$\widetilde{(\mathbb{P}^{2})^{\ast }}\setminus ([\mathsf{m}]\cup t)$
, the map
$\tilde{p}_{1}^{-1}(L_{\mathsf{m}})\cap {\mathcal{U}}_{1}\rightarrow \widetilde{(\mathbb{P}^{2})^{\ast }}$
is one to one, hence is an isomorphism by the Zariski main theorem.
We denote by
$E_{\mathsf{m}}$
and
$E_{t}$
the exceptional curves of
$\tilde{p}_{1}^{-1}(L_{\mathsf{m}})\cap {\mathcal{U}}_{1}\rightarrow \widetilde{(\mathbb{P}^{2})^{\ast }}$
over
$[\mathsf{m}]$
and
$t$
, respectively. By Lemmas 2.4.1(2), 3.2.1 and Corollary 2.4.3, the map
$\tilde{p}_{1}^{-1}(L_{\mathsf{m}})\cap {\mathcal{U}}_{1}\rightarrow \widetilde{(\mathbb{P}^{2})^{\ast }}$
is an étale double cover near
$C_{0}(\mathsf{m})$
. Hence
$\tilde{p}_{1}^{-1}(C_{0}(\mathsf{m}))\cap {\mathcal{U}}_{1}$
consists of two disjoint smooth rational curves, and
$\tilde{p}_{1}^{-1}(L_{\mathsf{m}})\cap {\mathcal{U}}_{1}$
is smooth near
$\tilde{p}_{1}^{-1}(C_{0}(\mathsf{m}))\cap {\mathcal{U}}_{1}$
. Since
$E_{\mathsf{m}}\subset \tilde{p}_{1}^{-1}(C_{0}(\mathsf{m}))\cap {\mathcal{U}}_{1}$
, we see that
$E_{\mathsf{m}}$
is one of its components. Therefore,
$\tilde{p}_{1}^{-1}(L_{\mathsf{m}})\cap {\mathcal{U}}_{1}\rightarrow \widetilde{(\mathbb{P}^{2})^{\ast }}$
is the blow-up at
$[\mathsf{m}]$
around
$[\mathsf{m}]$
.
(3) We show that
$M_{R}$
is reduced. Indeed, since
$R\cap \unicode[STIX]{x1D6FE}_{a}=\emptyset$
, a
$B_{a}$
-line intersecting
$R$
satisfies Proposition 2.3.3(1) or is the
$B_{a}$
-line
$\unicode[STIX]{x1D6FE}_{a}$
plus the
$\unicode[STIX]{x1D70B}_{a}$
-fiber
$\unicode[STIX]{x1D70B}_{a}^{-1}(\mathsf{j}\cap \mathsf{m})$
. Therefore, such a
$B_{a}$
-line intersects
$R$
at one point except the negative section
$C_{0}(\mathsf{m})$
which intersects
$R$
at
$g$
points counted with multiplicity. Thus
$C_{R}\rightarrow \operatorname{Supp}M_{R}$
is one to one outside the point
$[\mathsf{m}]$
, which in particular shows that
$M_{R}$
is reduced.
We show that
$M_{R}$
has a
$g$
-ple point at
$[\mathsf{m}]$
. Note that
$\widetilde{M}_{R}\rightarrow M_{R}$
is isomorphic outside
$[\mathsf{j}]\in M_{R}$
since
$b:\widetilde{(\mathbb{P}^{2})^{\ast }}\rightarrow (\mathbb{P}^{2})^{\ast }$
is the blow-up at
$[\mathsf{j}]$
. Therefore, to show
$M_{R}$
has a
$g$
-ple point at
$[\mathsf{m}]$
, it suffices to show that
$\widetilde{M}_{R}$
has a
$g$
-ple point at
$[\mathsf{m}]$
, where we denote by the same letter the point of
$\widetilde{M}_{R}$
corresponding to
$[\mathsf{m}]$
. Note that
$R\cdot C_{0}(\mathsf{m})=g$
in
$L_{\mathsf{m}}$
. Therefore, by the results of the paragraph before the proof of (3), we have
$C_{R}\cdot E_{\mathsf{m}}=g$
in
$\tilde{p}_{1}^{-1}(L_{\mathsf{m}})\cap {\mathcal{U}}_{1}$
. Hence we see that
$\widetilde{M}_{R}$
has a
$g$
-ple point at
$[\mathsf{m}]$
by blowing down
$E_{\mathsf{m}}$
.
Now we compute
$\deg M_{R}$
. Let us take a general fiber
$f$
of
$L_{\mathsf{m}}\rightarrow \mathsf{m}$
such that
$f\cap \unicode[STIX]{x1D6FE}_{a}=\emptyset$
and
$R\cap f\not \in F_{1}^{\prime }\cup F_{2}^{\prime }\cup C_{0}(\mathsf{m})$
. Then, since
$R\cap f\not \in F_{1}^{\prime }\cup F_{2}^{\prime }$
, we see that
$C_{R}$
and
$C_{f}$
intersect transversely at two points, which is the inverse image of one point
$R\cap f$
. Since
$R\cap f\not \in C_{0}(\mathsf{m})$
, we see that
$C_{R}$
and
$C_{f}$
does not intersect on
$E_{\mathsf{m}}$
. Therefore, the intersection multiplicity of
$M_{R}$
and
$M_{f}$
at
$[\mathsf{m}]$
is
$g$
. Thus we conclude that
$\deg M_{R}=M_{R}\cdot M_{f}=g+2$
since
$M_{f}$
is a line by generality of
$f$
and the assertion (2).
It remains to show that
$M_{R}$
is smooth outside
$[\mathsf{m}]$
. Let
$M_{R}^{\prime }$
be the strict transform of
$M_{R}$
by the blow-up of
$\mathbb{P}^{2}$
at
$[\mathsf{m}]$
. Since
$\deg M_{R}=g+2$
and
$M_{R}$
has a
$g$
-ple point at
$[\mathsf{m}]$
, the arithmetic genus of
$M_{R}^{\prime }$
is
$g$
. Since we have shown that
$C_{R}\rightarrow M_{R}$
is birational above,
$C_{R}$
is the normalization of
$M_{R}^{\prime }$
. Since
$p_{a}(M_{R}^{\prime })=g(C_{R})=g$
, we see that
$M_{R}^{\prime }$
is smooth, hence
$M_{R}$
is smooth outside
$[\mathsf{m}]$
.
(4) We have already shown that
$C_{R}\rightarrow M_{R}$
is the normalization. A general line in
$(\mathbb{P}^{2})^{\ast }$
through
$[\mathsf{m}]$
intersects
$M_{R}$
at two points outside
$[\mathsf{m}]$
since
$M_{R}$
has a
$g$
-ple point at
$[\mathsf{m}]$
. Therefore, we obtain the description of the unique
$g_{2}^{1}$
of the hyperelliptic curve
$C_{R}$
.◻
Notation 3.3.1. (The marked point
$[\mathsf{j}]_{R}$
on
$C_{R}$
) Assume that
$R$
satisfies Condition 3.2.1(a)–(d). Then, since
$R\cap \unicode[STIX]{x1D6FE}_{a}=\emptyset$
, the
$\unicode[STIX]{x1D70B}_{a}$
-fiber
$\unicode[STIX]{x1D70B}_{a}^{-1}(\mathsf{m}\cap \mathsf{j})$
is the only one which intersects both
$R$
and
$\unicode[STIX]{x1D6FE}_{a}$
. Therefore,
$\unicode[STIX]{x1D6FE}_{a}\cup \unicode[STIX]{x1D70B}_{a}^{-1}(\mathsf{m}\cap \mathsf{j})$
is the unique
$B_{a}$
-line intersecting
$R$
of the form
$\unicode[STIX]{x1D6FE}_{a}$
plus a
$\unicode[STIX]{x1D70B}_{a}$
-fiber. Since
$C_{R}\rightarrow M_{R}$
is an isomorphism outside
$[\mathsf{m}]$
by Proposition 3.3.1(1) and (4), we denote by
$[\mathsf{j}]_{R}$
the point of the hyperelliptic curve
$C_{R}$
corresponding to this
$B_{a}$
-line (note that this point
$[\mathsf{j}]_{R}$
is mapped to
$[\mathsf{j}]\in M_{R}\subset (\mathbb{P}^{2})^{\ast }$
).
4 Theta characteristics on the hyperelliptic curves
4.1 Constructing theta characteristics
By the above understanding of the hyperelliptic double cover
$C_{R}\rightarrow R$
, we may construct an ineffective theta characteristic on
$C_{R}$
as follows:
Proposition 4.1.1. For a curve
$R$
satisfying Condition 3.2.1(a)–(d) and
$g\geqslant 2$
, we denote by
$h_{R}$
the unique
$g_{2}^{1}$
on the hyperelliptic curve
$C_{R}$
. Let
$\unicode[STIX]{x1D708}:C_{R}\rightarrow M_{R}$
be the morphism constructed in Proposition 3.3.1(4), which is the normalization. Then
$$\begin{eqnarray}{\mathcal{O}}_{C_{R}}(\unicode[STIX]{x1D703}_{R}):=\unicode[STIX]{x1D708}^{\ast }{\mathcal{O}}_{M_{R}}(1)\otimes _{{\mathcal{O}}_{C_{R}}}{\mathcal{O}}_{C_{R}}(-h_{R}-[\mathsf{j}]_{R})\end{eqnarray}$$
is an ineffective theta characteristic on
$C_{R}$
.
Proof. Let
$F$
be one of the two singular
$\unicode[STIX]{x1D70B}_{b}$
-fibers and
$F^{\prime }$
its strict transform on
$B_{a}$
. By Condition 3.2.1(d),
$R$
intersects
$F^{\prime }$
transversely at
$g+1$
points, which we denote by
$s_{1},\ldots ,s_{g+1}$
. By Proposition 3.3.1(1), these points are contained in the branched locus of the hyperelliptic double cover
$C_{R}\rightarrow R$
. We denote by
$t_{1},\ldots ,t_{g+1}$
the inverse images on
$C_{R}$
of
$s_{1},\ldots ,s_{g+1}$
, and by
$u_{1},\ldots ,u_{g+1}$
the images on
$M_{R}$
of
$t_{1},\ldots ,t_{g+1}$
. By Proposition 3.3.1(1),
$C_{0}(\mathsf{m})$
is not the strict transform of a ruling of
$F$
since
$[\mathsf{m}]\not \in \ell _{1}\cup \ell _{2}$
. Therefore,
$u_{1},\ldots ,u_{g+1}\not =[\mathsf{m}]$
. By Proposition 3.3.1(2),
$\unicode[STIX]{x1D70B}_{a}^{-1}(\mathsf{m}\cap \mathsf{j})$
is not the strict transform of a ruling of
$F$
since
$[\mathsf{m}]\not \in \ell _{1}\cup \ell _{2}$
. Therefore,
$u_{1},\ldots ,u_{g+1}\not =[\mathsf{j}]$
. By Proposition 2.4.2(1),
$u_{1},\ldots ,u_{g+1}$
are contained in
$\ell :=\ell _{1}$
or
$\ell _{2}$
. Therefore, since
$\ell$
and
$M_{R}$
contain
$[\mathsf{j}]$
, and
$\deg M_{R}=g+2$
, we have
$\ell _{|M_{R}}=u_{1}+\cdots +u_{g+1}+[\mathsf{j}]$
. Then, by the definition of
$\unicode[STIX]{x1D703}_{R}$
, we have
$\unicode[STIX]{x1D703}_{R}=t_{1}+\cdots +t_{g+1}-h_{R}$
. Now the assertion follows from [Reference Arbarello, Cornalba, Griffiths and Harris1, p. 288, Exercise 32].◻
Remark 4.1.1.
(1) In the proof of Proposition 4.1.1, we obtain the presentation
$\unicode[STIX]{x1D703}_{R}=t_{1}+\cdots +t_{g+1}-h_{R}$
. So there are two such presentations according to choosing
$\ell _{1}$
or
$\ell _{2}$
. This is compatible with [Reference Arbarello, Cornalba, Griffiths and Harris1, p. 288, Exercise 32(ii)].(2) In Section 0.3, we say that we construct the theta characteristic from the incidence correspondence of intersecting
$B_{a}$
-lines. We add explanations about this since this is not obvious from the above construction.The flow of the consideration below is quite similar to the proof of Proposition 4.1.1. Instead of a singular
$\unicode[STIX]{x1D70B}_{b}$
-fiber, we consider a smooth general
$\unicode[STIX]{x1D70B}_{b}$
-fiber
$H\simeq \mathbb{P}^{1}\times \mathbb{P}^{1}$
. By generality of
$H$
, we may assume that any ruling of
$H$
intersecting the strict transform
$R^{\prime }\subset B_{b}$
of
$R$
is disjoint from
$\unicode[STIX]{x1D6FE}_{b}$
, and is not equal to the strict transform of
$C_{0}(\mathsf{m})$
. Moreover, we may also assume that
$R^{\prime }$
intersects
$H$
transversely at
$g+1$
points.Let
$\unicode[STIX]{x1D6FF}_{1}$
be one connected family of rulings of
$H$
. Then the strict transforms of rulings in
$\unicode[STIX]{x1D6FF}_{1}$
intersecting
$R$
satisfies Proposition 2.3.3(1), and each of them intersects
$R$
at one point. Therefore, there exist
$g+1$
$B_{a}$
-lines
$l_{1},\ldots ,l_{g+1}$
intersecting
$R$
which are the strict transforms of rulings in
$\unicode[STIX]{x1D6FF}_{1}$
. By the above choice of
$H$
, the point
$[\mathsf{j}]$
is different from
$[l_{1}],\ldots ,[l_{g+1}]$
.Let
$\unicode[STIX]{x1D6FF}_{2}$
be the other family of rulings in
$H$
and
$s_{2}$
a ruling in
$\unicode[STIX]{x1D6FF}_{2}$
not intersecting
$\unicode[STIX]{x1D6FE}_{b}$
. We denote by
$s_{2}^{\prime }$
the strict transform on
$B_{a}$
of
$s_{2}$
. Then, by Definition 3.1.1, we may define
$M_{s_{2}^{\prime }}$
. In a similar way to the proof of Proposition 3.3.1(3), we can show that
$M_{s_{2}^{\prime }}$
is a line. By construction,
$[l_{1}],\ldots ,[l_{g+1}]\in \widetilde{M}_{s_{2}^{\prime }}$
. For simplicity of notation, we denote by the same letters the images on
$M_{s_{2}^{\prime }}$
of the points
$[l_{i}]$
. Let
$r_{1}$
be the ruling in
$\unicode[STIX]{x1D6FF}_{1}$
intersecting
$\unicode[STIX]{x1D6FE}_{b}$
, and
$r_{1}^{\prime }$
the strict transform on
$B_{a}$
of
$r_{1}$
. Note that the
$B_{a}$
-line
$r_{1}^{\prime }\cup \unicode[STIX]{x1D6FE}_{a}$
belongs to
$\widetilde{M}_{s_{2}^{\prime }}$
and corresponds to the point
$[\mathsf{j}]\in (\mathbb{P}^{2})^{\ast }$
. Therefore,
$[\mathsf{j}],[l_{1}],\ldots ,[l_{g+1}]\in M_{R}\cap M_{s_{2}^{\prime }}$
. Hence we have
$M_{s_{2}^{\prime }}\cap M_{R}=[l_{1}]+\ldots +[l_{g+1}]+[\mathsf{j}]$
.Considering
$\unicode[STIX]{x1D6FF}_{2}$
, we may take
$g+1$
$B_{a}$
-lines
$m_{1},\ldots ,m_{g+1}$
intersecting
$R$
which are the strict transforms of rulings in
$\unicode[STIX]{x1D6FF}_{2}$
. By relabeling if necessary, we may assume that
$h_{R}\sim [l_{i}]+[m_{i}]$
by Corollary 2.4.3. Choose one of
$m_{i}$
’s, say,
$m_{1}$
. Then, by the definition of
$\unicode[STIX]{x1D703}_{R}$
, we have
$\unicode[STIX]{x1D703}_{R}+[m_{1}]=[l_{2}]+\cdots +[l_{g+1}]$
. The
$B_{a}$
-lines
$l_{2},\ldots ,l_{g+1}$
are nothing but those intersecting both
$m_{1}$
and
$R$
(
$l_{1}$
is excluded since it will be disjoint from
$m_{1}$
after the blow-up along
$R$
. See [Reference Takagi and Zucconi11, §4] and [Reference Takagi and Zucconi12, §3.1] for this consideration).
4.2 Reconstructing rational curves from spin curves
Let
$g\geqslant 2$
. By Propositions 3.3.1, and 4.1.1 (see also Notation 3.3.1), we obtain a rational map
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{g,1}:{\mathcal{H}}_{g+2}{\dashrightarrow}{\mathcal{S}}_{g,1}^{0,\text{hyp}},\,\,[R]\mapsto [C_{R},[\mathsf{j}]_{R},\unicode[STIX]{x1D703}_{R}],\end{eqnarray}$$
which is fundamental for our purpose.
The next theorem shows how to construct the rational curve
$R$
such that
$\unicode[STIX]{x1D70B}_{g,1}([R])=[(C,p,\unicode[STIX]{x1D703})]$
for a general element
$[(C,p,\unicode[STIX]{x1D703})]$
in
${\mathcal{S}}_{g,1}^{0,\text{hyp}}$
.
This is one of our key result to show the rationality of
${\mathcal{S}}_{g,1}^{0,\text{hyp}}$
.
Theorem 4.2.1. (Reconstruction theorem)
The map
$\unicode[STIX]{x1D70B}_{g,1}$
is dominant. More precisely, let
$[(C,p,\unicode[STIX]{x1D703})]\in {\mathcal{S}}_{g,1}^{0,\text{hyp}}$
be any element such that
$p$
is not a Weierstrass point, then there exists a point
$[R]\in {\mathcal{H}}_{g+2}$
such that
$R$
and
$\mathsf{m}$
satisfy Condition 3.2.1(a)–(d) and
$\unicode[STIX]{x1D70B}_{g,1}([R])=[(C,p,\unicode[STIX]{x1D703})]$
.
For our proof of the theorem, we need the following general results for an element of
${\mathcal{S}}_{g,1}^{0,\text{hyp}}$
. The proof given below is slightly long but it is elementary and only uses standard techniques from algebraic curve theory.
Lemma 4.2.2. Let
$[(C,p,\unicode[STIX]{x1D703})]$
be any element of
${\mathcal{S}}_{g,1}^{0,\text{hyp}}$
. Let
$\{p_{1},\ldots ,p_{g+1}\}\cup \{p_{1}^{\prime },\ldots ,p_{g+1}^{\prime }\}$
be the partition of the set of the Weierstrass points of
$C$
such that
$\unicode[STIX]{x1D703}$
has the following two presentations:
$$\begin{eqnarray}\unicode[STIX]{x1D703}\sim p_{1}+\cdots +p_{g+1}-g_{2}^{1}\sim p_{1}^{\prime }+\cdots +p_{g+1}^{\prime }-g_{2}^{1}\end{eqnarray}$$
(cf. [Reference Arbarello, Cornalba, Griffiths and Harris1, p. 288, Exercise 32]). The following assertions hold:
(1) The linear system
$|\unicode[STIX]{x1D703}+g_{2}^{1}+p|$
defines a birational morphism from
$C$
to a plane curve of degree
$g+2$
.(2)
$|\unicode[STIX]{x1D703}+p|$
has a unique member
$D$
and it is mapped to a single point
$t$
by the map
$\unicode[STIX]{x1D711}_{|\unicode[STIX]{x1D703}+g_{2}^{1}+p|}$
.(3) The unique
$g_{2}^{1}$
of
$C$
is defined by the pullback of the pencil of lines through
$t$
.For the assertions
$(4)$
and
$(5)$
, we set $$\begin{eqnarray}S:=\{p,p_{1},\ldots ,p_{g+1},p_{1}^{\prime },\ldots ,p_{g+1}^{\prime }\}.\end{eqnarray}$$
(4) The support of
$D$
contains no point of
$S$
.(5) The point
$t$
as in
$(2)$
is different from the
$\unicode[STIX]{x1D711}_{|\unicode[STIX]{x1D703}+g_{2}^{1}+p|}$
-images of points of
$S$
. Besides, by the map
$\unicode[STIX]{x1D711}_{|\unicode[STIX]{x1D703}+g_{2}^{1}+p|}$
, no two points of
$S$
are mapped to the same point.
Proof. (1) We show that the linear system
$|\unicode[STIX]{x1D703}+g_{2}^{1}+p|$
has no base points. By (4.2), we see that
$\operatorname{Bs}|\unicode[STIX]{x1D703}+g_{2}^{1}+p|\subset \{p\}$
. By the Serre duality, we have
$$\begin{eqnarray}H^{1}(\unicode[STIX]{x1D703}+g_{2}^{1}+p)\simeq H^{0}(K_{C}-\unicode[STIX]{x1D703}-g_{2}^{1}-p)^{\ast }=H^{0}(\unicode[STIX]{x1D703}-g_{2}^{1}-p)=0\end{eqnarray}$$
since
$\unicode[STIX]{x1D703}$
is ineffective. Similarly, we have
$H^{1}(\unicode[STIX]{x1D703}+g_{2}^{1})=\{0\}$
. Therefore, by the Riemann–Roch theorem,
$$\begin{eqnarray}h^{0}(\unicode[STIX]{x1D703}+g_{2}^{1}+p)-h^{0}(\unicode[STIX]{x1D703}+g_{2}^{1})=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D703}+g_{2}^{1}+p)-\unicode[STIX]{x1D712}(\unicode[STIX]{x1D703}+g_{2}^{1})=1,\end{eqnarray}$$
which implies that
$p\not \in \operatorname{Bs}|\unicode[STIX]{x1D703}+g_{2}^{1}+p|$
.
By the above argument, we see that
$h^{0}(\unicode[STIX]{x1D703}+g_{2}^{1}+p)=\deg (\unicode[STIX]{x1D703}+g_{2}^{1}+p)+1-g=3$
. Therefore,
$|\unicode[STIX]{x1D703}+g_{2}^{1}+p|$
gives a morphism
$\unicode[STIX]{x1D711}_{|\unicode[STIX]{x1D703}+g_{2}^{1}+p|}:C\rightarrow \mathbb{P}(V)\simeq \mathbb{P}^{2}$
with
$V=H^{0}(C,{\mathcal{O}}_{C}(\unicode[STIX]{x1D703}+g_{2}^{1}+p))^{\ast }$
. Let
$M:=\unicode[STIX]{x1D711}_{|\unicode[STIX]{x1D703}+g_{2}^{1}+p|}(C)$
be the image of
$C$
. We show that
$C\rightarrow M$
is birational. Note that by the Riemann–Roch theorem and
$h^{1}(\unicode[STIX]{x1D703}+p)=h^{0}(K-\unicode[STIX]{x1D703}-p)=0$
, we have
$h^{0}(\unicode[STIX]{x1D703}+p)=1$
. Therefore, the hyperelliptic double cover
$\unicode[STIX]{x1D711}_{|g_{2}^{1}|}:C\rightarrow \mathbb{P}^{1}$
factors through the map
$\unicode[STIX]{x1D711}_{|g_{2}^{1}+\unicode[STIX]{x1D703}+p|}$
. So we have only to show that
$|\unicode[STIX]{x1D703}+g_{2}^{1}+p|$
separates the two points in a member of
$|g_{2}^{1}|$
. This is equivalent to
$h^{0}(\unicode[STIX]{x1D703}+g_{2}^{1}+p-g_{2}^{1})=h^{0}(\unicode[STIX]{x1D703}+g_{2}^{1}+p)-2$
, which follows from the above computations. Therefore, we have shown that
$C\rightarrow M$
is birational. This implies that the degree of
$M$
is
$g+2$
.
(2) Since
$h^{0}(\unicode[STIX]{x1D703}+p)=1$
as in the proof of (1), the linear system
$|\unicode[STIX]{x1D703}+p|$
has a unique member
$D$
. We see that
$D$
is mapped to a point since
$\unicode[STIX]{x1D703}+g_{2}^{1}+p$
is the pullback of
${\mathcal{O}}_{\mathbb{P}^{2}}(1)|_{M}$
and
$h^{0}(\unicode[STIX]{x1D703}+g_{2}^{1}+p-(\unicode[STIX]{x1D703}+p))=h^{0}(g_{2}^{1})=2$
.
(3) The assertion clearly follows from (2).
(4) The point
$p$
is not contained in the support of
$D$
since
$h^{0}(\unicode[STIX]{x1D703}+p-p)=h^{0}(\unicode[STIX]{x1D703})=0$
. Let us consider points of
$S\setminus \{p\}$
. Without loss of generality, we have only to show that
$h^{0}(\unicode[STIX]{x1D703}+p-p_{1})=0$
. By the Riemann–Roch theorem, the assertion is equivalent to
$h^{1}(\unicode[STIX]{x1D703}+p-p_{1})=0$
. By (4.2),
$\unicode[STIX]{x1D703}+p-p_{1}=p_{2}+\cdots +p_{g+1}+p-g_{2}^{1}$
. Therefore, by the Serre duality, we have
$$\begin{eqnarray}h^{1}(\unicode[STIX]{x1D703}+p-p_{1})=h^{0}(g\times g_{2}^{1}-(p_{2}+\cdots +p_{g+1}+p))\end{eqnarray}$$
since
$K_{C}=(g-1)g_{2}^{1}$
. Now it is easy to verify this is zero by using the hyperelliptic morphism
$C\rightarrow \mathbb{P}^{1}$
.
(5) First we show that
$t$
is different from the image of any point
$x$
of
$C\setminus D$
. Indeed, we have
$$\begin{eqnarray}h^{0}(\unicode[STIX]{x1D703}+g_{2}^{1}+p-(\unicode[STIX]{x1D703}+p)-x)=h^{0}(g_{2}^{1}-x)=1,\end{eqnarray}$$
which means that
$|\unicode[STIX]{x1D703}+g_{2}^{1}+p|$
separates
$D$
and
$x$
. In particular, we have the former assertion of (5) by (4).
We show that
$|\unicode[STIX]{x1D703}+g_{2}^{1}+p|$
separates any two of
$p_{1},\ldots ,p_{g+1}$
. Without loss of generality, we have only to consider the case of
$p_{1}$
and
$p_{2}$
. It suffices to show that
$h^{0}(\unicode[STIX]{x1D703}+g_{2}^{1}+p-p_{1}-p_{2})=h^{0}(\unicode[STIX]{x1D703}+g_{2}^{1}+p)-2=1$
, which is equivalent to
$h^{1}(\unicode[STIX]{x1D703}+g_{2}^{1}+p-p_{1}-p_{2})=0$
by the Riemann–Roch theorem. By the presentation (4.2), we have
$h^{1}(\unicode[STIX]{x1D703}+g_{2}^{1}+p-p_{1}-p_{2})=h^{1}(p_{3}+\cdots +p_{g+1}+p)$
. By the Serre duality, we have
$$\begin{eqnarray}h^{1}(p_{3}+\cdots +p_{g+1}+p)=h^{0}((g-1)g_{2}^{1}-p_{3}-\cdots -p_{g+1}-p)\end{eqnarray}$$
since
$K_{C}=(g-1)g_{2}^{1}$
. Now it is easy to verify the r.h.s. is zero by using the hyperelliptic morphism
$C\rightarrow \mathbb{P}^{1}$
.
The same argument shows that
$|\unicode[STIX]{x1D703}+g_{2}^{1}+p|$
separates any two of
$p_{1}^{\prime },\ldots ,p_{g+1}^{\prime }$
. Moreover, if
$p$
is distinct from a
$p_{i}$
or
$p_{j}^{\prime }$
, the same proof works for the separation of
$p$
and
$p_{i}$
or
$p_{j}^{\prime }$
.
It remains to show that
$|\unicode[STIX]{x1D703}+g_{2}^{1}+p|$
separates one of
$p_{1},\ldots ,p_{g+1}$
and one of
$p_{1}^{\prime },\ldots ,p_{g+1}^{\prime }$
. Without loss of generality, we have only to consider the case of
$p_{1}$
and
$p_{1}^{\prime }$
. If
$p=p_{1}$
, then
$p\not =p_{1}^{\prime }$
, and hence we have already shown that the images of
$p=p_{1}$
and
$p_{1}^{\prime }$
are different. Thus we may assume that
$p\not =p_{1},p_{1}^{\prime }$
. By (4.2),
$D_{1}:=p+p_{1}+\cdots +p_{g+1}$
and
$D_{2}:=p+p_{1}^{\prime }+\cdots +p_{g+1}^{\prime }$
are two distinct members of
$|\unicode[STIX]{x1D703}+g_{2}^{1}+p|$
. If the images of
$p_{1}$
and
$p_{1}^{\prime }$
by the map
$\unicode[STIX]{x1D711}_{|\unicode[STIX]{x1D703}+g_{2}^{1}+p|}$
coincides, then the images of
$D_{1}$
and
$D_{2}$
coincides since they are the line through the images of
$p$
and
$p_{1}$
, and the line through the images of
$p$
and
$p_{1}^{\prime }$
. This is a contradiction to a property of the map defined by
$|\unicode[STIX]{x1D703}+g_{2}^{1}+p|$
.◻
Proof of Theorem 4.2.1.
We set
$V\,=\,H^{0}(C,{\mathcal{O}}_{C}(\unicode[STIX]{x1D703}\,+\,g_{2}^{1}\,+\,p))^{\ast }$
. Let
$M\,\subset \,\mathbb{P}(V)$
be the
$\unicode[STIX]{x1D711}_{|\unicode[STIX]{x1D703}+g_{2}^{1}+p|}$
-image of
$C$
. Let
$r_{1},\ldots ,r_{g+1}$
and
$r_{1}^{\prime },\ldots ,r_{g+1}^{\prime }\in M$
be the
$\unicode[STIX]{x1D711}_{|\unicode[STIX]{x1D703}+g_{2}^{1}+p|}$
-images of the Weierstrass points
$p_{1},\ldots ,p_{g+1}$
and
$p_{1}^{\prime },\ldots ,p_{g+1}^{\prime }$
of
$C$
as in (4.2), respectively. Let
$r\in M$
be the image of
$p$
and
$t\in M$
the image of the unique member of
$|\unicode[STIX]{x1D703}+p|$
. By Lemma 4.2.2(4) and (5),
$r$
,
$t$
,
$r_{1},\ldots ,r_{g+1}$
,
$r_{1}^{\prime },\ldots ,r_{g+1}^{\prime }$
are distinct points (recall that now we are assuming
$p$
is not a Weierstrass point). By (4.2), there are two lines
$\ell ,\ell ^{\prime }\subset \mathbb{P}(V)$
such that
$\ell _{|M}=r_{1}+\cdots +r_{g+1}+r$
and
$\ell _{|M}^{\prime }=r_{1}^{\prime }+\cdots +r_{g+1}^{\prime }+r$
(note also that
$\deg M=g+2$
by Lemma 4.2.2(1)).
We then identify the polarized space
$(\mathbb{P}(V),\ell \cup \ell ^{\prime })$
with
$((\mathbb{P}^{2})^{\ast },\ell _{1}\cup \ell _{2})$
(recall the notation as in Proposition 1.2.2). By this identification, the point
$r$
corresponds to
$[\mathsf{j}]$
. Let
$\mathsf{m}$
be the line of
$\mathbb{P}^{2}$
such that
$[\mathsf{m}]$
corresponds to the point
$t$
.
Condition 3.2.1(a). Since
$r\not =t$
, the line
$\mathsf{m}$
is not the jumping line
$\mathsf{j}$
of the bundle
${\mathcal{E}}$
such that
$B_{a}\simeq \mathbb{P}({\mathcal{E}})$
. Moreover,
$\mathsf{m}$
is not a jumping line of the second kind of
${\mathcal{E}}$
, equivalently,
$[\mathsf{m}]\not \in \ell _{1}\cup \ell _{2}$
since
$t$
is distinct from
$r$
,
$r_{1},\ldots ,r_{g+1}$
,
$r_{1}^{\prime },\ldots ,r_{g+1}^{\prime }$
. This shows that
$[\mathsf{m}]$
satisfies Condition 3.2.1(a).
We look for a member
$R$
of the linear system
$|C_{0}(\mathsf{m})+(g+1)L_{|L_{\mathsf{m}}}|$
on
$L_{\mathsf{m}}\subset B_{a}$
with Condition 3.2.1(b)–(d) such that
$C=C_{R}$
. Let
$\mathsf{m}_{i}$
and
$\mathsf{m}_{j}^{\prime }$
be the lines of
$\mathbb{P}^{2}$
such that
$[\mathsf{m}_{i}]=r_{i}$
and
$[\mathsf{m}_{j}^{\prime }]=r_{j}^{\prime }$
(
$1\leqslant i,j\leqslant g+1$
). As we have seen above,
$\mathsf{m}_{i}$
and
$\mathsf{m}_{j}^{\prime }$
are different from
$\mathsf{j}$
. Therefore, the negative sections
$C_{0}(\mathsf{m}_{i})$
and
$C_{0}(\mathsf{m}_{j}^{\prime })$
are
$B_{a}$
-lines disjoint from
$\unicode[STIX]{x1D6FE}_{a}$
by Lemma 2.4.1(2). Note that the condition for an
$R\in |C_{0}(\mathsf{m})+(g+1)L_{|L_{\mathsf{m}}}|$
to intersect one fixed
$B_{a}$
-line is at most of codimension
$1$
. Hence there exists at least one
$R\in |C_{0}(\mathsf{m})+(g+1)L_{|L_{\mathsf{m}}}|$
intersecting the
$2g+2$
$B_{a}$
-lines
$C_{0}(\mathsf{m}_{i})$
and
$C_{0}(\mathsf{m}_{j}^{\prime })$
(
$1\leqslant i,j\leqslant g+1$
) since
$\dim H^{0}(C_{0}(\mathsf{m})+(g+1)L_{|L_{\mathsf{m}}})=2g+3$
.
Condition 3.2.1(d). Since
$\mathsf{m}_{i}$
and
$\mathsf{m}_{j}^{\prime }$
are different from
$\mathsf{m}$
, the curve
$R$
intersects each one of
$C_{0}(\mathsf{m}_{i})$
and
$C_{0}(\mathsf{m}_{j}^{\prime })$
at one point. Since
$[\mathsf{m}]$
satisfies Condition 3.2.1(a), the points
$v_{1}^{\prime }$
,
$v_{2}^{\prime }$
are not contained in
$R$
. Therefore,
$R\cap C_{0}(\mathsf{m}_{i})$
(
$1\leqslant i\leqslant g+1$
) are different and so are
$R\cap C_{0}(\mathsf{m}_{j}^{\prime })$
(
$1\leqslant j\leqslant g+1$
). Then, by Proposition 2.4.2(1),
$R$
intersects
$F_{1}^{\prime }$
and
$F_{2}^{\prime }$
at least at
$g+1$
points
$R\cap C_{0}(\mathsf{m}_{i})$
(
$1\leqslant i\leqslant g+1$
) and
$R\cap C_{0}(\mathsf{m}_{j}^{\prime })$
(
$1\leqslant j\leqslant g+1$
), respectively. Therefore,
$R$
intersects
$F_{1}^{\prime }$
and
$F_{2}^{\prime }$
at
$g+1$
points respectively transversely since
$F_{1}^{\prime }\cdot R=F_{2}^{\prime }\cdot R=g+1$
. This shows that
$R$
satisfies Condition 3.2.1(d).
Condition 3.2.1(c). Assume by contradiction that
$R$
intersects
$\unicode[STIX]{x1D6FE}_{a}$
. Then
$R$
would intersect
$F_{1}^{\prime }$
and
$F_{2}^{\prime }$
at some points outside
$C_{0}(\mathsf{m}_{i})$
and
$C_{0}(\mathsf{m}_{j}^{\prime })$
(
$1\leqslant i,j\leqslant g+1$
) since
$\unicode[STIX]{x1D6FE}_{a}\subset F_{1}^{\prime }\cap F_{2}^{\prime }$
and
$\unicode[STIX]{x1D6FE}_{a}$
is disjoint from
$C_{0}(\mathsf{m}_{i})$
and
$C_{0}(\mathsf{m}_{j}^{\prime })$
. This contradicts the argument to show Condition 3.2.1(d). Therefore,
$R$
satisfies Condition 3.2.1(c).
Condition 3.2.1(b). It suffices to show that
$R$
is irreducible. Assume by contradiction that
$R$
is reducible. Then
$R$
contains a ruling of
$L_{\mathsf{m}}$
, say,
$f$
. We have
$f\cap \unicode[STIX]{x1D6FE}_{a}=\emptyset$
since
$R\cap \unicode[STIX]{x1D6FE}_{a}=\emptyset$
. Thus we can define the curve
$M_{f}$
, which is a line in
$(\mathbb{P}^{2})^{\ast }$
by Proposition 3.3.1(2). Besides the line
$M_{f}$
contains
$t=[\mathsf{m}]$
, and one of
$r_{1},\ldots ,r_{g+1}$
and one of
$r_{1}^{\prime },\ldots ,r_{g+1}^{\prime }$
corresponding to
$F_{1}^{\prime }\cap f$
and
$F_{2}^{\prime }\cap f$
, respectively. By reordering the points, we may assume that
$r_{1},r_{1}^{\prime }\in M_{f}$
. Therefore,
$t,r_{1},r_{1}^{\prime }$
are collinear. This is, however, a contradiction since the line through
$t$
and
$r_{1}$
touches
$M$
only at
$t$
and
$r_{1}$
by Lemma 4.2.2(3) (recall that
$r_{1}$
is the image of a Weierstrass point of
$C$
).
Finally we show
$M=M_{R}$
(note that we can define
$M_{R}$
since we have checked that
$\mathsf{m}$
and
$R$
satisfy Condition 3.2.1(a)–(d)). Note that, by the constructions of
$M$
and
$M_{R}$
as the images of the map
$\unicode[STIX]{x1D711}_{|\unicode[STIX]{x1D703}+g_{2}^{1}+p|}$
and
$\unicode[STIX]{x1D711}_{|\unicode[STIX]{x1D703}_{R}+h_{R}+[\mathsf{j}]_{R}|}$
respectively, there exists a line through
$t$
and touches both
$M$
and
$M_{R}$
at
$r_{i}$
with multiplicity two
$(i=1,\ldots ,g+1)$
, and the same is true for
$r_{j}^{\prime }$
$(j=1,\ldots ,g+1)$
. Hence the intersection multiplicities of
$M_{R}$
and
$M$
at
$r_{i}$
and
$r_{j}^{\prime }$
are at least two. Therefore, the scheme theoretic intersection
$M\cap M_{R}$
contains
$r$
, the
$2(g+1)$
points
$r_{i},r_{j}^{\prime }$
,
$i,j=1,...,g+1$
with multiplicity
${\geqslant}2$
and we also have a fat point of multiplicity
$g^{2}$
at
$t$
. This implies that, if
$M\not =M_{R}$
, then
$M\cdot M_{R}\geqslant 1+4(g+1)+g^{2}=(g+2)^{2}+1$
, which is a contradiction since
$\deg M=\deg M_{R}=g+2$
. Now we conclude that
$M_{R}=M$
.◻
Theorem 4.2.1 has a nice corollary, which seems to be unknown.
Corollary 4.2.3. The moduli space
${\mathcal{S}}_{g,1}^{0,\text{hyp}}$
and the moduli space
${\mathcal{S}}_{g}^{0,\text{hyp}}$
of ineffective spin hyperelliptic curves are irreducible.
Proof. By Definition 2.2.1,
${\mathcal{H}}_{g+2}$
is an open subset of the projective bundle
$\unicode[STIX]{x1D6F4}_{g+2}$
over the projective plane. Therefore,
${\mathcal{H}}_{g+2}$
is irreducible. By Theorem 4.2.1 we know that the map
$\unicode[STIX]{x1D70B}_{g,1}:{\mathcal{H}}_{g+2}{\dashrightarrow}{\mathcal{S}}_{g,1}^{0,\text{hyp}}$
is dominant to each irreducible component of
${\mathcal{S}}_{g,1}^{0,\text{hyp}}$
. The forgetful morphism
${\mathcal{S}}_{g,1}^{0,\text{hyp}}\rightarrow {\mathcal{S}}_{g}^{0,\text{hyp}}$
is dominant too. Hence the claim follows.◻
4.3 Birational model of
${\mathcal{S}}_{g,1}^{0,\text{hyp}}$
Let
$\mathsf{m}$
be a general line in
$\mathbb{P}^{2}$
. By Theorem 4.2.1 and the group action of
$G$
on
${\mathcal{H}}_{g+2}$
, the map
$\unicode[STIX]{x1D70B}_{g,1}:{\mathcal{H}}_{g+2}{\dashrightarrow}{\mathcal{S}}_{g,1}^{0,\text{hyp}}$
induces a dominant rational map
$\unicode[STIX]{x1D70C}_{g,1}:|(H+gL)_{|L_{\mathsf{m}}}|{\dashrightarrow}{\mathcal{S}}_{g,1}^{0,\text{hyp}}$
. Recall the definition of the subgroup
$\unicode[STIX]{x1D6E4}$
of
$G$
as in Lemma 1.4.4. By the classical Rosenlicht theorem, we can find an
$\unicode[STIX]{x1D6E4}$
-invariant open set
$U$
of
$|(H+gL)_{|L_{\mathsf{m}}}|$
such that the quotient
$U/\unicode[STIX]{x1D6E4}$
exists. Since a general
$\unicode[STIX]{x1D6E4}$
-orbit in
$|(H+gL)_{|L_{\mathsf{m}}}|$
is mapped to a point by
$\unicode[STIX]{x1D70C}_{g,1}$
, we obtain a dominant map
$\overline{\unicode[STIX]{x1D70C}}_{g,1}:U/\unicode[STIX]{x1D6E4}\rightarrow {\mathcal{S}}_{g,1}^{0,\text{hyp}}$
.
Proposition 4.3.1. The dominant map
$\overline{\unicode[STIX]{x1D70C}}_{g,1}:U/\unicode[STIX]{x1D6E4}\rightarrow {\mathcal{S}}_{g,1}^{0,\text{hyp}}$
is birational.
Proof. We show that
$\overline{\unicode[STIX]{x1D70C}}_{g,1}$
is generically injective. We consider two general elements
$R,R^{\prime }\in U$
and the two corresponding
$\unicode[STIX]{x1D6E4}$
-orbits
$\unicode[STIX]{x1D6E4}\cdot R$
,
$\unicode[STIX]{x1D6E4}\cdot R^{\prime }$
. Note that
$M_{R}$
and
$M_{R^{\prime }}$
both pass through the points
$[\mathsf{j}]$
and
$[\mathsf{m}]$
, and they both have Weierstrass points distributed on the two lines
$\ell _{1}$
and
$\ell _{2}$
. Now assume that
$[C_{R},p,\unicode[STIX]{x1D703}_{R}]=[C_{R^{\prime }},p^{\prime },\unicode[STIX]{x1D703}_{R^{\prime }}]\in {\mathcal{S}}_{g,1}^{0,\text{hyp}}$
, equivalently, there exists an isomorphism
$\unicode[STIX]{x1D709}:C_{R}\rightarrow C_{R^{\prime }}$
such that
$\unicode[STIX]{x1D709}^{\ast }\unicode[STIX]{x1D703}_{R^{\prime }}=\unicode[STIX]{x1D703}_{R}$
and
$\unicode[STIX]{x1D709}(p)=p^{\prime }$
. We consider the following diagram:
Note that
$(b\circ \tilde{p}_{2})|_{C_{R}}(p)=(b\circ \tilde{p}_{2})|_{C_{R}}(p^{\prime })=[\mathsf{j}]$
by Notation 3.3.1. Since the
$g_{2}^{1}$
is unique on an hyperelliptic curve, we have
$\unicode[STIX]{x1D709}^{\ast }h_{R^{\prime }}=h_{R}$
where
$h_{R}$
and
$h_{R^{\prime }}$
are respectively the
$g_{2}^{1}$
’s of
$C_{R}$
and
$C_{R^{\prime }}$
. Therefore, there exists a projective isomorphism
$\unicode[STIX]{x1D709}_{M}$
from
$M_{R}$
to
$M_{R^{\prime }}$
such that
$(b\circ \tilde{p}_{2})|_{C_{R^{\prime }}}\circ \unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{M}\circ (b\circ \tilde{p}_{2})|_{C_{R}}$
and hence
$\unicode[STIX]{x1D709}_{M}([\mathsf{j}])=[\mathsf{j}]$
since the morphisms
$(b\circ \tilde{p}_{2})|_{C_{R}}:C_{R}\rightarrow M_{R}\subset (\mathbb{P}^{2})^{\ast }$
and
$(b\circ \tilde{p}_{2})|_{C_{R^{\prime }}}:C_{R^{\prime }}\rightarrow M_{R^{\prime }}\subset (\mathbb{P}^{2})^{\ast }$
are given respectively by
$|\unicode[STIX]{x1D703}_{R}+p+h_{R}|$
and
$|\unicode[STIX]{x1D703}_{R^{\prime }}+p^{\prime }+h_{R^{\prime }}|$
. We also have
$\unicode[STIX]{x1D709}_{M}([\mathsf{m}])=[\mathsf{m}]$
since
$[\mathsf{m}]$
is a unique
$g$
-ple point of
$M_{R}$
and
$M_{R^{\prime }}$
respectively by Proposition 3.3.1(3). Let
$g$
be an element of
$\operatorname{Aut}(\mathbb{P}^{2})^{\ast }$
inducing the projective isomorphism
$\unicode[STIX]{x1D709}_{M}$
. Since
$\unicode[STIX]{x1D709}$
sends the Weierstrass points of
$C_{R}$
to those of
$C_{R^{\prime }}$
, the line pair
$\ell _{1}\cup \ell _{2}$
must be sent into itself by
$g$
. Hence
$g\in G$
. Moreover, since
$g$
fixes
$[\mathsf{m}]$
as we noted above, we have
$g\in \unicode[STIX]{x1D6E4}$
. In summary, we have shown
$gM_{R}=M_{R^{\prime }}$
with
$g\in \unicode[STIX]{x1D6E4}$
. It remains to show that
$gR=R^{\prime }$
. For this, we have only to show that
$R$
is recovered from
$M_{R}$
. Take a general line
$\ell$
through
$[\mathsf{m}]$
and set
$\ell _{|M_{R}}=[\mathsf{m}]+[\mathsf{m}_{1}]+[\mathsf{m}_{2}]$
set-theoretically. By generality, it holds that
$\mathsf{m}_{1}\not =\mathsf{m}_{2}$
, and the negative sections
$C_{0}(\mathsf{m}_{1})$
and
$C_{0}(\mathsf{m}_{2})$
of
$L_{\mathsf{m}_{1}}$
and
$L_{\mathsf{m}_{2}}$
respectively are
$B_{a}$
-lines. By Proposition 3.3.1(4),
$[C_{0}(\mathsf{m}_{1})]+[C_{0}(\mathsf{m}_{2})]\sim h_{R}$
, and hence
$C_{0}(\mathsf{m}_{1})\cap C_{0}(\mathsf{m}_{2})$
is one point of
$R$
by the definition of
$C_{R}$
. Then
$R$
is recovered as the closure of the locus of
$C_{0}(\mathsf{m}_{1})\cap C_{0}(\mathsf{m}_{2})$
when
$\ell$
varies.◻
5 Proof of rationality
In this section, we show the main result of this paper.
Proof of Theorem 0.1.1.
As in Section 4.3, we fix a general line
$\mathsf{m}$
in
$\mathbb{P}^{2}$
. By Proposition 4.3.1, we have only to show that
$U/\unicode[STIX]{x1D6E4}$
is a rational variety.
Using the elementary transformation of
$B_{a}=\mathbb{P}({\mathcal{E}})$
as in Proposition 1.4.1, we are going to reduce the problem to that on
$\mathbb{P}^{1}\times \mathsf{m}$
. We use the notation as in Section 1.4. In particular,
$(x_{1}:x_{2})$
and
$(y_{1}:y_{2}:y_{3})$
are homogeneous coordinates of
$\mathbb{P}^{1}$
and
$\mathbb{P}^{2}$
respectively such that
$\mathsf{m}=\{y_{1}=y_{2}\}$
. Let
$r_{v}$
and
$r_{h}$
are rulings of the projections
$\mathbb{P}^{1}\times \mathsf{m}\rightarrow \mathsf{m}$
and
$\mathbb{P}^{1}\times \mathsf{m}\rightarrow \mathbb{P}^{1}$
, respectively. From now on, we identify
$\mathbb{P}^{1}\times \mathsf{m}$
with
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
having the bi-homogeneous coordinate
$(x_{1}^{\prime }:x_{2}^{\prime })\times (y_{2}:y_{3})$
with
$x_{1}^{\prime }:=(x_{1}-x_{2})/2$
and
$x_{2}^{\prime }:=(x_{1}+x_{2})/2$
. To clarify the difference of the two factors of
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
, we keep denoting it by
$\mathbb{P}^{1}\times \mathsf{m}$
. With this coordinate of
$\mathbb{P}^{1}\times \mathsf{m}$
, the action of
$\unicode[STIX]{x1D6E4}\simeq (\mathbb{Z}_{2}\times G_{a})\rtimes G_{m}$
on
$\mathbb{P}^{1}\times \mathsf{m}$
is described by multiplications of the following matrices by Lemma 1.4.4:
∙
$G_{m}:$
$(\!\begin{smallmatrix}1 & 0\\ 0 & 1\end{smallmatrix}\!)\times (\!\begin{smallmatrix}1 & 0\\ 0 & a\end{smallmatrix}\!)$
with
$a\in G_{m}$
;∙
$G_{a}:$
$(\!\begin{smallmatrix}1 & 0\\ 0 & 1\end{smallmatrix}\!)\times (\!\begin{smallmatrix}1 & b\\ 0 & 1\end{smallmatrix}\!)$
with
$b\in G_{a}$
; and∙
$\mathbb{Z}_{2}:$
$(\!\begin{smallmatrix}-1 & 0\\ 0 & 1\end{smallmatrix}\!)\times (\!\begin{smallmatrix}1 & 0\\ 0 & 1\end{smallmatrix}\!)$
.
By Proposition 1.4.1, we see that members of
$|(H+gL)_{|L_{\mathsf{m}}}|$
corresponds to those of the linear system
$|r_{h}+(g+1)r_{v}|$
through the point
$c:=\unicode[STIX]{x1D6FE}_{c}\cap (\mathbb{P}^{1}\times \mathsf{m})=(1:0)\times (1:0)$
. We denote by
$\unicode[STIX]{x1D6EC}$
the sublinear system consisting of such members. A member of
$\unicode[STIX]{x1D6EC}$
is the zero set of a bi-homogeneous polynomial of bidegree
$(1,g+1)$
of the form
$x_{1}^{\prime }f_{g+1}(y_{2},y_{3})+x_{2}^{\prime }g_{g+1}(y_{2},y_{3})$
, where
$f_{g+1}(y_{2},y_{3})$
and
$g_{g+1}(y_{2},y_{3})$
are binary
$(g+1)$
-forms
$$\begin{eqnarray}\displaystyle f_{g+1}(y_{2},y_{3}) & = & \displaystyle p_{g}y_{2}^{g}y_{3}+\cdots +p_{i}y_{2}^{i}y_{3}^{g+1-i}+\cdots +p_{0}y_{3}^{g+1},\nonumber\\ \displaystyle g_{g+1}(y_{2},y_{3}) & = & \displaystyle q_{g+1}y_{2}^{g+1}+\cdots +q_{i}y_{2}^{i}y_{3}^{g+1-i}+\cdots +q_{0}y_{3}^{g+1}.\nonumber\end{eqnarray}$$
Then the linear system
$\unicode[STIX]{x1D6EC}$
can be identified with the projective space
$\mathbb{P}^{2g+2}$
with the homogeneous coordinate
$(p_{0}:\cdots :p_{g}:q_{0}:\cdots :q_{g+1})$
. A point
$(p_{0}:\cdots :p_{i}:\cdots :p_{g}:q_{0}:\cdots :q_{j}:\cdots :q_{g+1})$
is mapped by elements of the subgroups
$G_{m}$
,
$G_{a}$
, and
$\mathbb{Z}_{2}\subset \unicode[STIX]{x1D6E4}$
as above to the following points:
(a)
$G_{m}:(a^{g+1}p_{0}:\cdots :a^{g+1-i}p_{i}:\cdots :ap_{g}:a^{g+1}q_{0}:\cdots :a^{g+1-j}q_{j}:\cdots :q_{g+1})$
;(b)
$G_{a}:$
the point
$(p_{0}^{\prime }:\cdots :p_{i}^{\prime }:\cdots :p_{g}^{\prime }:q_{0}^{\prime }:\cdots :q_{j}^{\prime }:\cdots :q_{g+1}^{\prime })$
with (5.1)$$\begin{eqnarray}\displaystyle p_{i}^{\prime } & = & \displaystyle \mathop{\sum }_{k=i}^{g}\binom{k}{i}b^{k-i}p_{k},\nonumber\\ \displaystyle q_{j}^{\prime } & = & \displaystyle \mathop{\sum }_{l=j}^{g+1}\binom{l}{j}b^{l-j}q_{l},\end{eqnarray}$$
(c)
$\mathbb{Z}_{2}:(-p_{0}:\cdots :-p_{i}:\cdots :-p_{g}:q_{0}:\cdots :q_{j}:\cdots :q_{g+1})$
.
Step 1. The quotient
$\unicode[STIX]{x1D6EC}_{1}:=\unicode[STIX]{x1D6EC}/\mathbb{Z}_{2}$
is rational.
The rationality is well known by the description of
$\mathbb{Z}_{2}$
-action as in (c). In the following steps, it is convenient to show this more explicitly. On the open set
$\{q_{g+1}\not =0\}\subset \unicode[STIX]{x1D6EC}$
, which is
$\unicode[STIX]{x1D6E4}$
-invariant, we may consider
$q_{g+1}=1$
. Then the action is
$$\begin{eqnarray}(p_{0},\ldots ,p_{g},q_{0},\ldots ,q_{g})\mapsto (-p_{0},\ldots ,-p_{g},q_{0},\ldots ,q_{g}).\end{eqnarray}$$
Therefore, the quotient map can be written on the
$\unicode[STIX]{x1D6E4}$
-invariant open subset
$\{p_{g}\not =0\}$
as follows:
$$\begin{eqnarray}(p_{0},\ldots ,p_{i},\ldots ,p_{g},q_{0},\ldots ,q_{g})\mapsto (p_{0}p_{g},\ldots ,p_{i}p_{g},\ldots ,p_{g}^{2},q_{0},\ldots ,q_{g}).\end{eqnarray}$$
We denote by
${^{\unicode[STIX]{x1D70F}}\mathbb{C}}^{2g+2}$
the target
$\mathbb{C}^{2g+2}$
of this map and by
$(\tilde{p}_{0},\ldots ,\tilde{p}_{g},\tilde{q}_{0},\ldots ,\tilde{q}_{g})$
its coordinate. Using this presentation, we compute the quotient by the additive group
$G_{a}$
in the next step.
Step 2. The quotient
$\unicode[STIX]{x1D6EC}_{2}:=\unicode[STIX]{x1D6EC}_{1}/G_{a}$
is rational.
Let
$(\tilde{p}_{0}^{\prime },\ldots ,\tilde{p}_{g}^{\prime },\tilde{q}_{0}^{\prime },\ldots ,\tilde{q}_{g}^{\prime })$
be the image of the point
$(\tilde{p}_{0},\ldots ,\tilde{p}_{g},\tilde{q}_{0},\ldots ,\tilde{q}_{g})$
by the action of an element of
$G_{a}$
as in (b). By the choice of coordinate, it is easy to check
$\tilde{p}_{i}^{\prime }$
and
$\tilde{q}_{j}^{\prime }$
can be written by
$\tilde{p}_{0},\ldots ,\tilde{p}_{g}$
and
$\tilde{q}_{0},\ldots ,\tilde{q}_{g}$
respectively by the formulas obtained from (5.1) by setting
$q_{g+1}=1$
and replacing
$p_{i}^{\prime }$
,
$p_{k}$
,
$q_{j}^{\prime }$
and
$q_{l}$
with
$\tilde{p}_{i}^{\prime }$
,
$\tilde{p}_{k}$
,
$\tilde{q}_{j}^{\prime }$
and
$\tilde{q}_{l}$
. Then note that we have
$\tilde{q}_{g}^{\prime }=\tilde{q}_{g}+(g+1)b$
. Therefore, the stabilizer group of every point is trivial and every
$G_{a}$
-orbit intersects the closed set
$\{\tilde{q}_{g}=0\}$
at a single point. Hence we may identified birationally the quotient
${^{\unicode[STIX]{x1D70F}}\mathbb{C}}^{2g+2}/G_{a}$
with the closed set
$\{\tilde{q}_{g}=0\}{\subset ^{\unicode[STIX]{x1D70F}}\mathbb{C}}^{2g+2}$
. In particular, the quotient is rational.
Step 3. The quotient
$\unicode[STIX]{x1D6EC}_{3}:=\unicode[STIX]{x1D6EC}_{2}/G_{m}$
is rational.
We may consider the closed set
$\{\tilde{q}_{g}=0\}$
as the affine space
$\mathbb{C}^{2g+1}$
with the coordinate
$(\tilde{p}_{0},\ldots ,\tilde{p}_{g},\tilde{q}_{0},\ldots ,\tilde{q}_{g-1})$
. Note that this closed set has the naturally induced
$G_{m}$
-action such that, by the element of
$G_{m}$
as in (a), a point
$(\tilde{p}_{0},\ldots ,\tilde{p}_{g},\tilde{q}_{0},\ldots ,\tilde{q}_{g-1})$
is mapped to
$(a^{g+2}\tilde{p}_{0},\ldots ,a^{2}\tilde{p}_{g},a^{g+1}\tilde{q}_{0},\ldots ,a^{2}\tilde{q}_{g-1})$
. Therefore, the quotient
$\mathbb{C}^{2g+1}/G_{m}$
is a weighted projective space, hence is rational.◻
Acknowledgments
The authors thank Professor Yuri Prokhorov for very useful conversations about the topic. They also thank the anonymous referee for valuable comments. This research is supported by MIUR funds, PRIN project Geometria delle varietà algebriche (2010), coordinator A. Verra (F.Z.), and, by Grant-in-Aid for Young Scientists (B 20740005, H.T.) and by Grant-in-Aid for Scientific Research (C 16K05090, H.T.).
