Ice-core DEP data

The complex relative dielectrical constant can be written as

(1)

where the real part 4 is the ordinary relative permittivity of the medium. The imaginary part ε" is the dielectric loss factor and can be expressed as a function of conductivity a , angular frequency OJ , and the permittivity of vacuum ε₀. The last expression defines the loss tangent, tan δ = ε"/ε' .

Along an ice core, ε can be determined by means of DEP (Reference MooreMoore and Paren, 1987). An improved DEP device developed by Reference WilhelmsWilhelms and others (1998), and further refined by Reference Wahr, Wingham and BentleyWilhelms (2000), essentially a calibrated guarded scanning capacitor, allows the simultaneous measurement of both components of e . This device was used at a frequency of 250 kHz to determine ε along the ice core B32 in Δz = 5 mm increments with a systematic accuracy of about 1% and a statistical error of ∼0.1% for each component, and an accuracy of 1 cm in depth (Fig. 2). The depth error results from the positioning of the 1m long core sections in the measuring bench.

Fig. 2. Depth distribution of the measured ordinary relative permittivity">; dielectric loss factor ε", scaled to 200 MHz; density variation δp; the real part R of the complex reflection coefficient; and name and date of identified volcanic events of the ice core B32. The density variation is calculated from γ-absorption measurements, corrected for core breaks, in respect to the boxcar filtered mean density of a 5 m window. The wide grey horizontal bars labeled A–H on the right indicate the depth and vertical extent of the most prominent reflection horizons in the GPR profile (Fig 1) near B32, corrected to the 1998 surface. The narrow grey horizontal bars indicate gaps in the DEP data record.

Several schemes to reject sections with poor core quality, and thus false DEP data, were investigated. The best compromise between least rejection and least disturbed convolution signals is obtained by calculating running mean and standard deviation within a 2.5 m window along the core. DEP values that show a permittivity which is more than one standard deviation below the window mean are rejected, as the lower permittivity values are most likely caused by cracks in the ice.

Following this procedure, about 3.5% of the DEP data with an average section length of 2 cm had to be removed in the upper 100 m of the core. I ntotal, 4.5% of the DEP data are missing.

The complex reflection coefficient

The complex reflection coefficient at an interface of two media with different dielectrical properties is determined by their complex impedance contrast. The reflection coefficient of two adjacent layers with complex dielectric constants ε_k and ε_k+1 measured at depths kΔz and (k + 1)Δz, respectively, is given by

(2)

which can be separated and rearrange d to obtain and _k as a function of and δk+1. The indexs that the corresponding depth value for R is the meandepth of both data points, i.e.

Several tests show that gaps larger than _{k +} .The several Δz produce too low reflection coefficients when using a linear interpolation, and too large reflection coefficients when applying different spline interpolation schemes. To avoid artificial values, the DEP data are linearly interpolated in gaps that are ~3Δz in length or smaller, and R is calculated from Equation (2). If the gap length exceeds this limit, R is set to 0 (Fig. 2). We consider this to be a more accurate way of treating

missing DEP data than to interpolate ε on an equidistant grid before calculating the reflection coefficient, as the change in ε is more important than the actual value. Support for this procedure comes from test runs with downsampled DEP data, as, with a new sample interval of ~5Δz, significant changes in the reflection characteristics are already evident.

Analogous to the TWT of a reflected radar pulse in ice, a propagation time for each data point of the R(Δz) series can be calculated from the in situ EM wave speed, with c₀ being the wave speed in vacuum. The resulting non-equidistant series is then projected onto an equidistant grid by means of a linear interpolation and a time increment Δt = Δz/c_ice = 29.7 ps, yielding the series R(Δt) (Δt is the time necessary for an EM wave to propagate the DEP sampling distance of 5 mm in ice with c_ice = 1.68 6 10₈ ms–₁ (Reference Bogorodsky, Bentley and GudmandsenBogorodsky and others, 1985)).

Radar wavelets

Numerous authors emphasize the crucial role of the transmitted radar wavelet for forward modeling of radargrams and GPR processing (Reference Miners, Hildebrand, Gerland, Blindow, Steinhage and WolffMoore, 1988; Reference Arcone, Lawson and DelaneyArcone and others, 1995; Reference HildebrandHildebrand, 1996). We investigate several wavelets from raw GPR data, among which are the direct airwave, reflections from the ice-shelf–water boundary, and several internal reflections. Although the EM reflections from the ice-shelf–sea-water boundary represent a close image of the original reflected pulse, this wavelet only partly reproduces reflections in the upper 30 m of the ice using DEP data. The most likely reason for this is the different physical in situ properties in the upper layers of the ice shelf in comparison to site DML05 on the polar plateau. The wavelet was recorded near Neumayer station, with refrozen melt-water at the surface and solid ice underneath. Thus, absorption, dispersion, phase shifts, etc. lead to a different wavelet shape, and thus to different reflections. Best results are obtained with a wavelet determined from a strong internal reflection recorded during a CMP survey near DML05, which is resampled using an Akima spline interpolation at 2048 equidistant points and a time increment Δt as above (Fig. 3). This results in the wavelet series W(Δt) we use for further calculations.

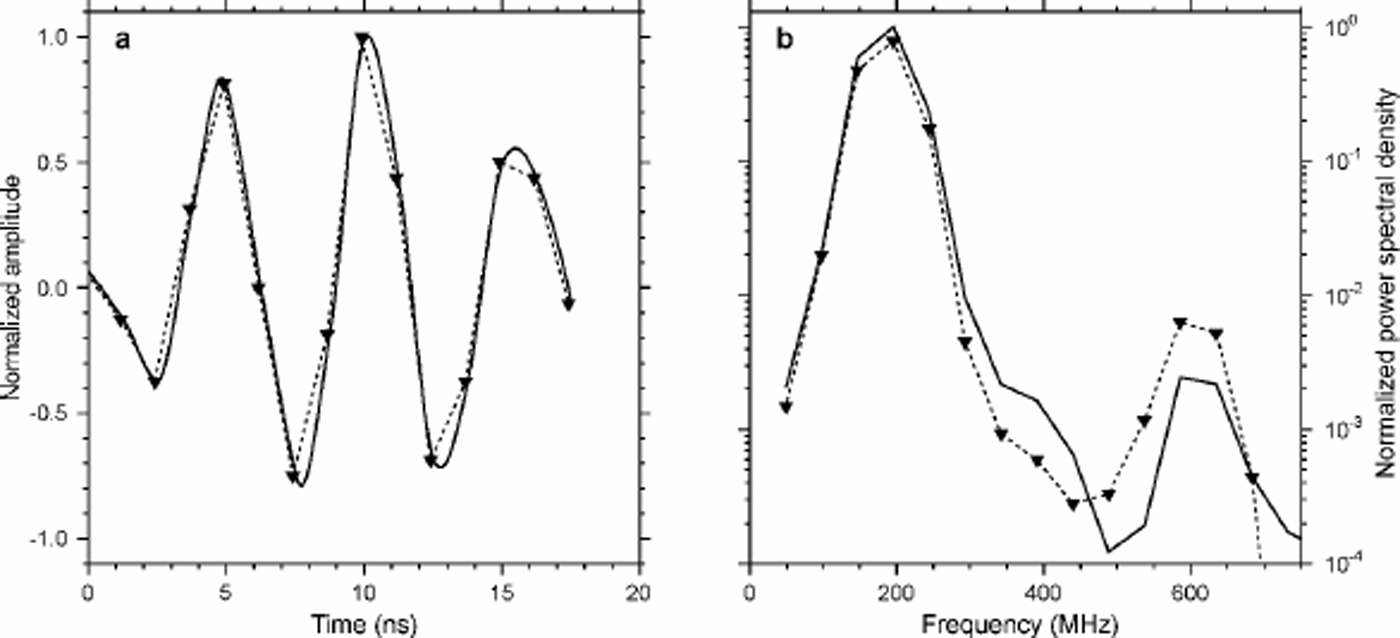
Fig. 3. Time-domain signals (a) and power spectrum (b) of the raw-data wavelet (thin dashed determined line with triangles) from an internal reflection, and the interpolated resampled wavelet used for the convolution (thick line).

Frequency domain convolution

The convolution of the wavelet series W(Δt) with the reflection coefficient series R(Δt), S_DEP = W*Ris carried out in the frequency domain by multiplying their fast Fourier transforms. The resulting synthetic DEP radargram S_DEP(Δt) is transformed to depth by applying the inverse TWT–depth conversion introduced above.

DEP vs GPR radargram

For the direct comparison of both radargrams we use their squared envelopes, which are proportional to energy, calcuated from the single trace radargrams. Due to the influence of the direct air and ground wave as well as antenna ringing, signals with a TWT 550ns (∼10m) are neglected in the following comparison.

Most prominent IRHs in the GPR profile (events A–H, Fig. 1) are visible in SGPR as strong peaks (Fig. 4). Some, however, have rather small amplitudes (e.g. event E), but can nevertheless be clearly identified as continuous signals in the GPR profile.

Fig. 4. Variable-amplitude wiggle plot of the synthetic DEP radargram SDEP (left) and the measured gain-corrected GPR radargram SGPR (right). In the middle, the squared envelopes of each radargram are shown, with the power of SDEP increasing to the left and SGPR increasing to the right. The GPR signal is corrected to the1998 surface; the first 3 m have been muted because of the influence of the direct and ground wave. A 10 cm wide mean boxcar filter has been applied to the envelopes to increase clarity. Wide grey bars the right half labeled A–H indicate prominent reflection horizons in the GPR profile (Fig. 1); narrow grey bars in the left half indicate gaps in the DEP data (Fig. 2).

In general, the power envelope of the synthetic trace SDEP shows a good agreement in numerous incidents with the power envelope of SGPR, enabling the identification of distinct reflections. However, some outliers are also present on either side. Matching partners of comparable size to the GPR envelope are visible in the DEP envelope for events A, B, C, Fand G. A very good agreement, even in phase structure, exists for events A, Fand G. Events B and E have SDEP envelope peaks of only about half the width of the SGPR signal, and their maxima are shifted by 0.5 and –1.0 m, respectively. For events C and F, the directly matching envelope peak is of the same size, but while event C is preceded by a stronger signal which is not visible in SGPR, event F is followed by one. A direct partner in SDEP is missing for event D, andthe peak in SDEP is smaller in size and with a slightly shifted maximum for event H, but still comparable in phase. The most obvious outliers in SDEP occur at 16.5, 49 and 64 m. We now discuss probable reasons for these differences.

Qualitative error analysis

Numerous factors affect the shape of the synthetic and the recorded radargrams. Themost obvious problems are missing DEP data, strongly altering interference patterns of reflected wave trains, and the presence of noise in the GPR profiles.

Comparison studies with single GPR traces or small ensembles of stacked traces were only partly successful. The GPR processing sequence described above makes use of coherent positions of reflecting horizons with depth within a radius of 50 m around B32, i.e. time shifts during the recording due to surface of reflector roughness are smaller than half a wavelength (0.5m for c = 2.06108 ms–1).

Although stacking of more than 500 traces significantly increases the SNR and emphasizes dominant horizons, weaker signals might be destroyed.

The original DEP data, on the other hand, represent a point measurement, which therefore has a low SNR but a high vertical resolution. Lateral inhomogeneities are present, especially in the upper part of the firn, where sastrugi are still distinguishable and might lead to a reflectivity over one Fresnel zone different than that calculated from the DEP data. Moreover, parts of the data are missing, and cannot be interpolated easily without introducing artificial reflection properties. Gaps of a few centimeters in length might already result in the loss of considerable information on reflectivity. For example, four gaps with a total length of 8 cm occur within event D. Three of these gaps occur at points where ε seems to change significantly, suggesting that the strong peak of SGPR at 45.5 m lacks a matching peak in SDEP because of wrong values for R. Likewise, event H is interrupted in the DEP data by five gaps.

Additional causes for differences of both radargrams come along with the convolution scheme. In general, the propagating wave changes shape due to dispersion effects, and a complex reflection coefficient causes phase shifts at each layer boundary. The use of a constant wavelet neglects both processes. Sensitivity runs with different wavelets indicate that the reflection characteristics for longer travel times depend on the wavelet choice (e.g. with a different signal the single DEP reflection at 86 m is strongly reduced in magnitude and becomes a multi-peak signal). Moreover, interferences due to multiple reflections are not accounted for by a simple convolution. This could be the reason for the sharp peaks in SDEP at 49 and 64 m, which do not have any peak in SGPR. The broad peak between 16.0 and 17.5 m, on the other hand, is matched by two much smaller and sharper GPR peaks, and might be the result of constructive interference caused by missing reflectivity and multiple reflections, or negative interference in the GPR because of pronounced lateral inhomogeneities at this depth.

The AGC applied to the GPR trace basically compensates for energy losses due to geometric spreading. As pointed out by Reference HildebrandHildebrand (1996), absorption and reflection losses as well as focusing are of minor importance in the upper part of the considered depth range, and are therefore not major factors for discrepancies. At larger travel times, however, the reflected GPR signal is close to the noise level, unavoidably decreasing the SNR, and thus resulting in larger differences in magnitude of matching peaks.

Physical origin of reflections

To reveal the physical origin of the observed matching synthetic reflections, we perform two sensitivity studies. For the calculation of the synthetic radargram SDI EP of the first study, "00 is smoothed with a 20 m boxcar mean filter and "0 is left unchanged. For the second study, resulting in SDIIEP, selected individual peaks in "0, that show a correlation with conductivity signals at same depths, are smoothed and "00 is left unchanged.

The synthetic radargram SDI EP is quasi-identical to the original SDEP. The second study demonstrates that amplitudes of reflections in SDIIEP are 1–2 orders of magnitude smaller than prominent peaks in SDEP at the same depth. Moreover, because of the increased variability of the conductivity record, the positions of reflections in SDIIEP show a less clear agreement with SGPR, i.e. they cannot explain the observed matching IRHs of SDEP and SGPR. These results confirm earlier findings (Reference MooreMoore, 1988; Reference HildebrandHildebrand, 1996; Reference Miners, Hildebrand, Gerland, Blindow, Steinhage and WolffMiners and others, 1997) that the reflection coefficient is dominated by changes in permittivity and that conductivity changes are negligible. As we relate the origin of reflections to changes in permittivity coinciding with acidic layers, two questions arise: what is the cause of the correlation between chemical impurities and permittivity? and do acidic layers affect the permittivity of the firn?

We rule out measurement artifacts related to the relaxation frequency of ice, as the DEP processing scheme has been extensively tested in this respect (Reference WilhelmsWilhelms, 2000). In some cases (e.g. the Coseguina (1835; 21.7 m) (Nicaragua) and Tambora (1815; 23.8 m) (Indonesia) events), the γ-absorption density record shows distinct peaks in density as well. In the case of the adjacent unknown eruption (1809; 24.5m), a comparable peak in density is missing (Fig. 2). The DEP-based density at the same depth, calculated with the complex mixing model (Reference WilhelmsWilhelms, 2000), i.e. corrected for dielectrical mixing of density and conductivity of the complex ε of firn, shows the same pattern. This indicates that the correlations between acidic peaks in conductivity, permittivity and density are not systematic, but that different mechanisms are present, as pointed out by Reference Fujita, Matsuoka, Ishida, Matsuoka, Mae and HondohFujita and others (2000).

The simplest explicative process is of meteorological origin (e.g. accumulation coming along with unusual circulation patterns, increasing chemical impurities and changing snow properties simultaneously). Nevertheless, complex dielectrical mixing between the air and snow phase, changes in the firn lattice, or protonic defects, related to chemical impurities, might play a role at different frequencies, requiring further investigations on the microphysical level.

Identifying isochrones

The ice core B32 has been dated by counting annual layers in various chemical records (Reference Siegert and HodgkinsSommer and others, 2000), and volcanic events have been identified by Reference GoktasGoktas (2002) by a combination of annual-layer counting, nss-sulphate concentrations and identified H2SO4 depositions (Fig. 2).

Having related the physical origin of matching peaks of SGPR and SDEP to permittivity peaks in the "–depth distributions (Fig. 2) enables us to connect certain chemical events with dominant signals in the DEP radargram.Because of the comparable structure of several permittivity and conductivity peaks, we have to assume that these permittivity peaks are related to volcanic eruptions or other chemical events, with the consequence that the corresponding IRHs are isochrones. The ice-core dating can then be transferred via several matching peaks to the GPR radargram and further to the GPR profile. It has to be kept in mind that the strongest peak of an IRH observed in the radargram is slightly shifted to larger travel times, or depths, as the wavelet maximum is delayed from the first arrival by ∼10 ns, correspondingto about 2 m.

Of the set of prominent IRHs we selected for our analysis, the double peak of event A is coincident with the Tambora and one unknown eruption in 1815 and 1809, respectively. Events C and F coincide with strong peaks in "00, which result from above-normal values in several chemical species (dated to 1620 and 1375, respectively), but which make it difficult to attribute these signals solely to volcanic eruptions (personal communication from H. Reference Oerter, Graf, Wilhelms, Minikin and MillerOerter, 2002). Although for event H the matching peak is of less good quality than at shallower depths, it is striking that two eruptions, Tarawera, New Zealand, in 1180 and one unknown in 1170, are dominant at the same depth. Event D is coincident with the Ruiz (Colombia) eruption (1593), but as a corresponding peak in SDEP is missing, the origin of the IRH is unclear.

To summarize, six out of the eight strongest IRHs evident from the GPR profile show matching peaks in GPR- and DEP-based radargrams, all of which are caused by peaks in permittivity. Four of these coincide with signals in the conductivity of chemical origin, with a very good correlation to permittivity, two of which are attributed to volcanic events. This evidence strongly suggests that these four events are isochrones. As all dominant observed continuous IRHs in the considered depth range are parallel to adjacent identified isochrones, they must be of isochronous origin as well.