2 Small-scale experiments

The experimental set-up consists of a 1.8 m long smooth Perspex chute, inclined at an angle $\unicode[STIX]{x1D703}$ to the horizontal, with rigid side walls 5 cm apart. The base of the chute incorporates a smooth bump extending across the width of the channel, described by a hyperbolic secant profile with a maximum height of 4.75 cm and with its centre located 43 cm downstream of the inflow. The bump has a characteristic length scale of 4 cm, which implies that ${\sim}90\,\%$ of its amplitude change occurs over a downstream distance of 12 cm and its wavelength is therefore approximately 24 cm. The experiments are performed with spherical glass beads of diameter 600– $800~\unicode[STIX]{x03BC}$ m, which are coloured blue and white to aid visualisation. Grains are loaded into a hopper at the top of the channel and released from rest using a double gate system consisting of a fixed gate to control the initial flow thickness $h_{0}$ and another movable barrier to control the release time. For all of the experiments presented here the gate height remains constant at $h_{0}=1.5$  cm; qualitatively similar behaviour has been observed when different values are used.

Two different types of initial condition are implemented in experiments. In the first, the chute is cleared of all downstream particles before the gate is opened, so that the granular material flows down a smooth, empty channel. In the second, static particles (of the same type) are placed slightly upstream of the bump, and the oncoming flow from the hopper then travels over a partially erodible bed. These different initial conditions evolve to two dramatically different stable steady-state regimes, which shall be referred to as the ‘jet’ and the ‘shock’, respectively. Figures 1 and 2 show the time evolution of these two types of flows, and figure 3 shows the final steady-state behaviour. Supplementary movies of these flows are available online at https://doi.org/10.1017/jfm.2017.41.

Figure 3. Experimental results showing the two different steady states possible for the same slope angle and different initial conditions. Both experiments have been performed at $\unicode[STIX]{x1D703}=40^{\circ }$ with the same inflow conditions. Note that the images have been slightly rotated to maximise space. The bump height of 4.75 cm acts as a scale.

An initially empty chute usually leads to the formation of a jet. As soon as the gate is opened, the grains flow out of the hopper and accelerate downstream. For slope angles $\unicode[STIX]{x1D703}\geqslant 35^{\circ }$ , they reach a sufficiently high velocity to detach from the base and become airborne as they flow over the bump. Once they have passed this take-off point, the grains approximately follow ballistic trajectories, before landing at a point downstream of the bump (see figure 1 and movie 1).

A jet may still form when only a small mass of particles is placed in front of the obstacle. In this case, the oncoming material has enough momentum to entrain the erodible bed into the bulk flow, which then takes off as before. However, adding more static particles can lead to the formation of a steady shock upstream of the bump (see figure 2 and movie 2). When sufficient mass is added, the erodible layer provides enough resistance to drastically decrease the bulk velocity of the accelerating flow from the inlet, without itself being pushed over the top of the bump. To conserve mass, the flow thickness must consequently increase, and this sharp transition in flow height and velocity is referred to as a granular shock. Some material may also be scattered into the air during initial impact with the stationary material, as seen in figure 2. The shock propagates upstream until it reaches a steady-state position. It is also possible to generate shocks using alternative dissipative mechanisms. One such approach is demonstrated in supplementary movie 3, where an initially empty chute leads to the formation of a jet, and a rigid obstacle is temporarily placed into the path of the flow. This again leads to a shock that eventually settles down to an equilibrium position. Movie 3 also shows that the shock position remains stable to perturbations in the flow. After reaching steady state, the flow is again obstructed downstream of the shock. This momentarily causes the shock to migrate upstream, but as soon as the obstacle is removed the shock relaxes back to its steady-state position. Similarly, sweeping away small amounts of the slower moving material in the shock causes it to temporarily move downstream before returning to its original position. However, sweeping away a larger proportion of the slowly moving grains can lead to complete remobilisation and transition back to the jet regime.

Figure 4. Phase diagram showing the formation of a steady jet (○) or a shock (●) depending on the slope angle $\unicode[STIX]{x1D703}$ and mass of stationary material upstream of the bump. Also shown are the extreme slope angle regions, where it is not possible to keep any particles at rest (high slope angles) or a spontaneous shock forms and propagates upstream to the gate (low angles).

When an initial deposit of static particles is used to generate a steady shock, a critical mass of stationary material is required to sufficiently reduce the momentum of the flowing grains. This critical mass depends on the inclination angle of the chute. Several experiments have been performed with varying slope angles and masses of erodible particles to determine the necessary conditions for the formation of a steady shock. The results are summarised in figure 4, which shows a phase diagram indicating whether a shock or a jet is formed, depending on the slope angle and mass of static grains. As expected, more particles are needed to generate a shock when the slope angle is higher. For slope angles of $34^{\circ }$ or lower, the flow never becomes fast enough to pass over the bump, and a shock is spontaneously generated even when there are no static particles. However, the shock does not reach a steady state and keeps propagating upwards until it reaches the gate and the flow stops completely. Contrastingly, for steep slopes $\unicode[STIX]{x1D703}\geqslant 41^{\circ }$ , the friction on the smooth base is not sufficient to keep any particles placed in front of the obstacle at rest. They roll over the bump and a jet always forms. Assuming there are enough particles in front of the bump to create a shock in the first place, the position of the shock does not depend on the initial mass. Note that the phase diagram of figure 4 is specific to this precise experimental set-up. In general, the critical mass and maximum and minimum slope angles for steady-shock formation will depend on the geometry and position of the bump, the inflow gate height and the frictional properties of the chute and specific granular material used. However, it is expected that qualitatively similar behaviour will be found for all configurations.

3 Depth-averaged terrain-following avalanche theory

The flow is modelled using a depth-averaged avalanche theory that is based on the work of Savage & Hutter (Reference Savage and Hutter1991) and Gray et al. (Reference Gray, Wieland and Hutter1999), and which uses a curvilinear coordinate system to follow the basal topography. This is referred to throughout this paper as the terrain-following avalanche model. In order to construct the curvilinear coordinates, an inclined Cartesian coordinate system $OXZ$ is first defined, with the unit vector $\boldsymbol{i}$ aligned with the downslope direction of the chute, which lies at a constant angle $\unicode[STIX]{x1D703}$ to the horizontal. The unit vector $\boldsymbol{k}$ is perpendicular to the chute and points upwards. The shape of the rigid topography on which the avalanche flows is then described by

(3.1) $$\begin{eqnarray}Z=b(X)=0.0475\,\text{sech}\left(\frac{X-0.43}{0.04}\right),\end{eqnarray}$$

where the coefficients are all in metres. This is illustrated in figure 5(a) and forms a reference surface for the terrain-following curvilinear coordinate system $Oxz$ , where the position vector of a point is given by the distance $x$ along this reference surface and the height $z$ in the direction normal to the base (see Gray et al. Reference Gray, Wieland and Hutter1999, and figure 6 for details). For a small increment in the down chute coordinate $\text{d}X$ , there is a small increment in the topography height $\text{d}b$ and by Pythagoras’ theorem the associated increment in the curvilinear coordinate $\text{d}x$ satisfies $\text{d}x^{2}=\text{d}X^{2}+\text{d}b^{2}$ . In differential form this implies

(3.2) $$\begin{eqnarray}\frac{\text{d}x}{\text{d}X}=\sqrt{1+\left(\frac{\text{d}b}{\text{d}X}\right)^{2}},\end{eqnarray}$$

which can be integrated to give a mapping between the downstream distance in curvilinear and Cartesian coordinates, i.e.

(3.3) $$\begin{eqnarray}x=\int _{0}^{X}\sqrt{1+\left(\frac{\text{d}b}{\text{d}X}\right)^{2}}\,\text{d}X^{\prime }.\end{eqnarray}$$

Figure 5. Plots of (a) the topography, (b) the curvilinear coordinate $x$ (dashed line) and $X$ (solid line) (c) the local slope inclination angle $\unicode[STIX]{x1D701}$ for a chute angle $\unicode[STIX]{x1D703}=39^{\circ }$ and (d) the curvature $\unicode[STIX]{x1D705}$ (solid line) and second derivative of the topography $\text{d}^{2}b/\text{d}X^{2}$ (dashed line), as functions of the Cartesian downslope coordinate $X$ .

The curvilinear coordinate is therefore just the arc length of the basal topography. As a result, the curvilinear distance is slightly longer than the Cartesian distance as shown in figure 5(b). A key advantage of the terrain-following model (Savage & Hutter Reference Savage and Hutter1991; Gray et al. Reference Gray, Wieland and Hutter1999) is that, as the avalanche flows over the topography, it experiences changes in the local slope inclination $\unicode[STIX]{x1D701}$ with the downstream coordinate $x$ . The angle is computed from the definition of the topography (3.1) by

(3.4) $$\begin{eqnarray}\unicode[STIX]{x1D701}=\unicode[STIX]{x1D703}-\tan ^{-1}\left(\frac{\text{d}b}{\text{d}X}\right),\end{eqnarray}$$

where $\unicode[STIX]{x1D703}$ is the angle of the Cartesian coordinates to the horizontal. If the chute is inclined at an angle of $\unicode[STIX]{x1D703}=39^{\circ }$ then the local slope inclination $\unicode[STIX]{x1D701}$ ranges between approximately $8^{\circ }$ and $70^{\circ }$ as shown in figure 5(c). The local variation of the inclination angle $\unicode[STIX]{x1D701}$ has a very important influence on the net balance between the downslope acceleration and the resistance due to basal friction in the terrain-following model. The final element of the curvilinear coordinate system is that it also takes account of changes in curvature $\unicode[STIX]{x1D705}$ , which is defined as

(3.5) $$\begin{eqnarray}\unicode[STIX]{x1D705}=-\frac{\text{d}\unicode[STIX]{x1D701}}{\text{d}x}=-\frac{1}{\unicode[STIX]{x1D6E5}_{b}}\frac{\text{d}\unicode[STIX]{x1D701}}{\text{d}X}=\frac{1}{\unicode[STIX]{x1D6E5}_{b}^{3}}\frac{\text{d}^{2}b}{\text{d}X^{2}},\end{eqnarray}$$

where the factor

(3.6) $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{b}=\sqrt{1+\left(\frac{\text{d}b}{\text{d}X}\right)^{2}}.\end{eqnarray}$$

Note that the final result in (3.5) follows from differentiating arctan. Once the local inclination $\unicode[STIX]{x1D701}$ and the curvature $\unicode[STIX]{x1D705}$ have been computed from the prescribed topography (3.1), the mapping (3.3) is used to convert them to functions of $x$ . It should be noted that the curvilinear coordinates introduce a singularity corresponding to where adjacent $z$ -axes intersect (Gray et al. Reference Gray, Wieland and Hutter1999), which occurs at a height $z=1/\unicode[STIX]{x1D705}$ . For the flow over a smooth bump considered here, $\unicode[STIX]{x1D705}$ is never large enough that the thickness of the avalanche is greater than the local radius of curvature $1/\unicode[STIX]{x1D705}$ of the topography, so there is no overlap of coordinates.

Figure 6. Sketch of the different coordinate systems used in this paper. The Cartesian $OXZ$ axes are aligned at a constant angle $\unicode[STIX]{x1D703}$ to the horizontal. The topography on which the avalanche flows is then defined in terms of a surface $Z=b(X)$ . This forms a reference surface for the slope-fitted curvilinear coordinate system $Oxz$ , with the $x$ -axis following the reference surface and being locally inclined at an angle $\unicode[STIX]{x1D701}(x)$ to the horizontal. The $z$ -axis is in the direction of the local normal, which is at an angle $\unicode[STIX]{x1D701}$ to the gravity acceleration vector.

Following Gray et al. (Reference Gray, Wieland and Hutter1999) the depth-averaged mass and momentum balance equations for the terrain-following avalanche model in curvilinear coordinates are

(3.7) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(h\bar{u})=0, & \displaystyle\end{eqnarray}$$

(3.8) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}(h\bar{u})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(\unicode[STIX]{x1D712}h\bar{u}^{2})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\frac{1}{2}gh^{2}\cos \unicode[STIX]{x1D701}\right)=h\left(g\sin \unicode[STIX]{x1D701}-\frac{\bar{u}}{|\bar{u}|}\unicode[STIX]{x1D707}(g\cos \unicode[STIX]{x1D701}+\unicode[STIX]{x1D712}\unicode[STIX]{x1D705}\bar{u}^{2})\right), & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

respectively, where $g$ represents the gravitational acceleration, $h$ is the flow thickness measured normal to the base, $\bar{u}$ is the depth-averaged velocity in the direction of the reference surface and $\unicode[STIX]{x1D707}$ is the effective friction coefficient, which may, in general, depend on the flow variables. Note that the system (3.7)–(3.8) implicitly assumes that the density is constant and uniform, i.e. the flow is incompressible. In addition, the earth pressure coefficient (Savage & Hutter Reference Savage and Hutter1989) is assumed to be unity, based on the scaling analysis of Gray & Edwards (Reference Gray and Edwards2014).

The shape factor

(3.9) $$\begin{eqnarray}\unicode[STIX]{x1D712}=\frac{\overline{u^{2}}}{\bar{u}^{2}},\end{eqnarray}$$

arises in the depth integration of the momentum transport equation to account for the fact that the product of the depth-averaged velocity is not, in general, equal to the average of the velocity product. Particle image velocimetry (PIV) measurements of the accelerating region through the side walls suggest that the vertical velocity may be approximated by a linear profile of the form $u=\bar{u}(\unicode[STIX]{x1D6FC}+2(1-\unicode[STIX]{x1D6FC})z/h)$ , with a shear parameter $\unicode[STIX]{x1D6FC}\approx 0.87$ representing a large degree of basal slip. This gives a corresponding shape factor $\unicode[STIX]{x1D712}=1.006$ . Although the presence of side wall friction may influence these measurements (Baker, Barker & Gray Reference Baker, Barker and Gray2016) they are consistent with surface and basal velocity measurements performed by Faug et al. (Reference Faug, Childs, Wyburn and Einav2015) in the centre of their channel, which suggest $\unicode[STIX]{x1D712}=1.009$ if a Bagnold profile with basal slip is used to calculate $\unicode[STIX]{x1D712}$ . Similarly small deviations of $\unicode[STIX]{x1D712}$ away from unity are also obtained in the discrete element simulations of Brodu, Richard & Delannay (Reference Brodu, Richard and Delannay2013). For this reason the velocity profile is approximated here by plug flow, which corresponds to a value $\unicode[STIX]{x1D712}=1$ . The curvature term $\unicode[STIX]{x1D705}\unicode[STIX]{x1D712}h\bar{u}^{2}$ on the right-hand side of (3.8) is a key feature of the depth-averaged terrain-following model, and describes the enhancement or reduction of the basal pressure due to centrifugal forces as the avalanche flows over topography, in the same way as one is pushed down harder or thrown up into the air on a roller coaster.

With the assumption that $\unicode[STIX]{x1D712}=1$ , the characteristics of the governing equations (3.7) and (3.8) are given in $(x,t)$ space by

(3.10) $$\begin{eqnarray}\frac{\text{d}x}{\text{d}t}=\unicode[STIX]{x1D706}^{\pm },\end{eqnarray}$$

where the characteristic wave speeds are

(3.11) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}^{\pm }=\bar{u}\pm \sqrt{gh\cos \unicode[STIX]{x1D701}}. & & \displaystyle\end{eqnarray}$$

This motivates the definition of the granular Froude number

(3.12) $$\begin{eqnarray}Fr=\frac{|\bar{u}|}{\sqrt{gh\cos \unicode[STIX]{x1D701}}},\end{eqnarray}$$

as the ratio of the flow speed to the speed of surface gravity waves, and it can be seen that for supercritical flow ( $Fr>1$ ) both characteristics move in the same direction, whereas in the subcritical regime ( $Fr<1$ ) they travel in opposite directions.

3.1 Steady solution

As observed during the experiments, the flow can evolve into a steady state, and in this steady state the depth-averaged mass and momentum balance equations, (3.7) and (3.8), reduce to

(3.13) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}x}(h\bar{u})=0, & \displaystyle\end{eqnarray}$$

(3.14) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}x}(h\bar{u}^{2})+\frac{\text{d}}{\text{d}x}\left(\frac{1}{2}gh^{2}\cos \unicode[STIX]{x1D701}\right)=h\left(g\sin \unicode[STIX]{x1D701}-\frac{\bar{u}}{|\bar{u}|}\unicode[STIX]{x1D707}(g\cos \unicode[STIX]{x1D701}+\unicode[STIX]{x1D705}\bar{u}^{2})\right). & \displaystyle\end{eqnarray}$$

The mass balance equation (3.13) can be integrated directly, subject to the boundary condition that the avalanche velocity and thickness at the inflow are $\bar{u}_{0}$ and $h_{0}$ , respectively, to give a relation between the flow thickness and the velocity

(3.15) $$\begin{eqnarray}h\bar{u}=h_{0}\bar{u}_{0}.\end{eqnarray}$$

By expanding out the derivatives, noting that the slope angle $\unicode[STIX]{x1D701}$ is $x$ -dependent in this curvilinear system, and dividing equation (3.14) by $h$ , the depth-averaged momentum balance becomes

(3.16) $$\begin{eqnarray}\bar{u}\frac{\text{d}\bar{u}}{\text{d}x}+g\cos \unicode[STIX]{x1D701}\frac{\text{d}h}{\text{d}x}-\frac{1}{2}gh\sin \unicode[STIX]{x1D701}\frac{\text{d}\unicode[STIX]{x1D701}}{\text{d}x}=g\cos \unicode[STIX]{x1D701}(\tan \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707})-\unicode[STIX]{x1D707}\unicode[STIX]{x1D705}\bar{u}^{2},\end{eqnarray}$$

where (3.13) has been used to simplify (3.16) and it has been assumed that $\bar{u}>0$ . Substituting $\unicode[STIX]{x1D705}=-\unicode[STIX]{x2202}\unicode[STIX]{x1D701}/\unicode[STIX]{x2202}x$ for the curvature and using (3.15) to replace the depth-averaged velocity allows (3.16) to be written as a single ordinary differential equation (ODE) governing the evolution of the flow thickness,

(3.17) $$\begin{eqnarray}\frac{\text{d}h}{\text{d}x}=\displaystyle \frac{h^{3}g\cos \unicode[STIX]{x1D701}(\tan \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707})-h\unicode[STIX]{x1D707}\unicode[STIX]{x1D705}(h_{0}\bar{u}_{0})^{2}-\frac{1}{2}gh^{4}\unicode[STIX]{x1D705}\sin \unicode[STIX]{x1D701}}{h^{3}g\cos \unicode[STIX]{x1D701}-(h_{0}\bar{u}_{0})^{2}}.\end{eqnarray}$$

For a given basal friction coefficient $\unicode[STIX]{x1D707}$ and inflow conditions $(h_{0},\bar{u}_{0})$ , equation (3.17) can be integrated numerically subject to $h=h_{0}$ at $x=0$ . This gives the thickness profile $h(x)$ as material leaves the hopper, which is identical for both the jet and shock regimes. The depth-averaged velocity profile can then be recovered from the mass balance equation (3.15). In the experiments material accelerates and thins as it comes out of the inflow gate, and this behaviour is recovered in the numerical solutions if $\text{d}h/\text{d}x\leqslant 0$ at $x=0$ . The curvature terms in (3.17) are negligible at the inflow, and since $\tan \unicode[STIX]{x1D701}>\unicode[STIX]{x1D707}$ for accelerating flows the numerator is always positive at $x=0$ . Examining the denominator, it can be seen that (3.17) only admits accelerating solutions if $Fr_{0}\geqslant 1$ , where

(3.18) $$\begin{eqnarray}Fr_{0}=\frac{\bar{u}_{0}}{\sqrt{gh_{0}\cos \unicode[STIX]{x1D701}_{0}}},\end{eqnarray}$$

is the inflow Froude number and $\unicode[STIX]{x1D701}_{0}$ is the inclination angle at $x=0$ . For the rest of this paper it will be assumed that the Froude number at the inflow equals unity, i.e. $Fr_{0}=1$ , which corresponds to an infinite gradient at the inflow. This is consistent with the notion that particles are fully mobilised along the inside wall of the hopper and are free to move downwards, i.e. there is no dead zone adjacent to the hopper wall. As these particles exit the hopper they are therefore moving down normal to the chute, before they are accelerated downstream. Note that it is possible to choose other values $Fr_{0}>1$ with less steep thickness profiles (see e.g. Cui & Gray Reference Cui and Gray2013), but further justification for setting $Fr_{0}=1$ will be given in § 3.2. With this choice there is a singularity in (3.17) at the origin. A power series expansion can be used to integrate directly from the inflow position. To achieve this, the curvature terms are neglected and the ODE is written in the alternative form

(3.19) $$\begin{eqnarray}\frac{\text{d}x}{\text{d}h}=f(h),\end{eqnarray}$$

where the function

(3.20) $$\begin{eqnarray}f(h)=\frac{h^{3}g\cos \unicode[STIX]{x1D701}_{0}-(h_{0}\bar{u}_{0})^{2}}{h^{3}g\cos \unicode[STIX]{x1D701}_{0}(\tan \unicode[STIX]{x1D701}_{0}-\unicode[STIX]{x1D707})},\end{eqnarray}$$

satisfies $f(h_{0})=0$ . Expanding about this point by assuming

(3.21) $$\begin{eqnarray}h(x)=h_{0}+h_{\unicode[STIX]{x1D716}}(x),\qquad |h_{\unicode[STIX]{x1D716}}|\ll |h_{0}|,\end{eqnarray}$$

allows the leading-order behaviour of the ODE (3.19) near the inflow to be written as

(3.22) $$\begin{eqnarray}\frac{\text{d}x}{\text{d}h_{\unicode[STIX]{x1D716}}}=h_{\unicode[STIX]{x1D716}}f^{\prime }(h_{0}),\quad \text{where }f^{\prime }(h_{0})=\frac{3}{h_{0}(\tan \unicode[STIX]{x1D701}_{0}-\unicode[STIX]{x1D707}(h_{0}))}.\end{eqnarray}$$

Here, the relationship $\bar{u}_{0}=\sqrt{gh_{0}\cos \unicode[STIX]{x1D701}_{0}}$ has been used to simplify the derivative $f^{\prime }(h_{0})$ , which is a positive constant. Equation (3.22) can be solved, subject to $h_{\unicode[STIX]{x1D716}}=0$ at $x=0$ , to give

(3.23) $$\begin{eqnarray}h_{\unicode[STIX]{x1D716}}(x)=\pm \sqrt{\frac{2x}{f^{\prime }(h_{0})}}.\end{eqnarray}$$

Choosing the negative root to ensure a thinning, accelerating flow, the thickness is calculated near the hopper by the algebraic expression

(3.24) $$\begin{eqnarray}h(x)=h_{0}-\sqrt{\frac{2x}{f^{\prime }(h_{0})}},\end{eqnarray}$$

and for positions further downstream it is computed numerically using the full ODE (3.17). In the complete absence of curvature terms, and a constant basal friction coefficient $\unicode[STIX]{x1D707}$ , it is also possible to construct an exact solution by integrating (3.17) directly and solving a cubic equation for $\bar{u}$ (see Cui & Gray Reference Cui and Gray2013, p. 320).

3.2 Basal and wall friction

For a given basal topography, the only parameter left in (3.7), (3.8) is the effective friction $\unicode[STIX]{x1D707}$ . An efficient way to determine this coefficient on a smooth slope is to measure the surface velocity of the accelerating flow and match it to the one-dimensional theory (see Cui & Gray Reference Cui and Gray2013). A similar approach is adopted here by using a high-speed camera (Teledyne DALSA Falcon2 with macro lens) to capture images of the top of the flow at a frame rate of 2000 frames per second (fps). The resolution is sufficient to capture details of circa 100  $\unicode[STIX]{x03BC}$ m, and individual grains are seen to travel approximately one grain diameter between frames for the highest slope angles. These images are processed with the PIV software PIVlab for MATLAB (Thielicke & Stamhuis Reference Thielicke and Stamhuis2014) to calculate the surface velocity profiles $u_{s}(y)$ (where $y$ is the transverse coordinate across the chute) at different downstream locations $X$ . The camera is always aligned perpendicular to the local slope, so the measured velocity corresponds to the curvilinear value, and the velocities are averaged over the time window that the images cover.

Figure 7. Time-averaged surface velocity profiles $u_{s}(y)$ at different downslope locations $X$ , calculated using high-speed camera images and PIV from the top of the flow.

The results of this PIV are shown in figure 7 for slope angles $\unicode[STIX]{x1D703}=38^{\circ }$ and $\unicode[STIX]{x1D703}=40^{\circ }$ . All of the profiles show clear curvature across the chute, with wall friction effects leading to noticeably smaller velocities towards the lateral boundaries (Brodu et al. Reference Brodu, Richard and Delannay2013; Faug et al. Reference Faug, Childs, Wyburn and Einav2015; Baker et al. Reference Baker, Barker and Gray2016). This confirms that any measurements made from the side may not be representative of the overall flow, and also suggests that the effective friction coefficient should account for friction at the wall as well as the base. Following Taberlet et al. (Reference Taberlet, Richard, Valance, Losert, Jenkins and Delannay2003), an effective friction coefficient that models both the basal and side wall contributions can be expressed as

(3.25) $$\begin{eqnarray}\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{b}+\frac{h}{W}\unicode[STIX]{x1D707}_{w},\end{eqnarray}$$

where $\unicode[STIX]{x1D707}_{b}$ and $\unicode[STIX]{x1D707}_{w}$ are constant coefficients for the basal and wall friction, respectively, and $W$ is the chute width. This is a friction law designed for smooth frictional beds, as opposed to a rough bed friction law, such as those of Pouliquen (Reference Pouliquen1999) and Pouliquen & Forterre (Reference Pouliquen and Forterre2002), where a layer of particles is glued to the bed. The thickness-dependent wall friction term will be negligible for a thin accelerating flow, but might become significant after the shock where the flow thickness is comparable to the channel width. Note that expression (3.25) only has empirical support for $h/W<1.5$ (Taberlet et al. Reference Taberlet, Richard, Valance, Losert, Jenkins and Delannay2003), but the flows studied in this paper remain in this regime. Substituting (3.25) into the ODE (3.17) allows the thickness profile, and subsequently the depth-averaged velocity, to be calculated for material leaving the gate. Figure 8 shows the resulting velocity profiles, which have been converted to Cartesian downslope distances $X$ , for ease of comparison, by inverting the integral mapping (3.3). Material accelerates downslope as it leaves the hopper, is slowed down by the topography and then accelerates once more after passing the bump. All of the experimental measurements are taken upstream of the take-off point for the formation of the jet, which implies that the equations for dense granular flows still apply. For calibration, the PIV results are averaged in the cross-slope direction (since the model is one-dimensional). Assuming plug flow, the surface velocities correspond to the depth-averaged $\bar{u}$ , and choosing $\unicode[STIX]{x1D707}_{b}=\tan (23^{\circ })$ and $\unicode[STIX]{x1D707}_{w}=\tan (7.5^{\circ })$ gives a good fit for both slope angles, as shown in figure 8 (solid lines). Note that this agreement provides justification for the choice $Fr_{0}=1$ at the inflow, since trying to model the experimental results using larger values $Fr_{0}>1$ give unphysical values for the friction parameters and/or less satisfactory fits to the data points. Also shown in figure 8 are the theoretical profiles in the absence of wall friction (dashed lines). In this thin accelerating regime this additional friction term is almost negligible, but it is expected to play a more significant role in the thicker flows near the shock and hence is included in the effective friction coefficient $\unicode[STIX]{x1D707}$ . As a final point, the corresponding basal topography is also represented in figure 8, with shaded regions corresponding to where the basal friction is greater than the downslope component of the gravitational acceleration ( $\unicode[STIX]{x1D707}_{b}>\tan \unicode[STIX]{x1D701}$ ). The evolution of the flow velocity with this topography strongly resembles the results obtained from numerical simulations of rock falls in Montserrat (Levy et al. Reference Levy, Mangeney, Bonilla, Hibert, Calder and Smith2015).

Figure 8. Surface velocities, averaged in both time and transverse position, measured at different downslope locations $X$ using PIV ( $\circ$ ). Solid and dashed lines represent the solution to (3.17) with $\unicode[STIX]{x1D707}=\tan (23^{\circ })+(h/W)\tan (7.5^{\circ })$ and $\unicode[STIX]{x1D707}=\text{tan}(23^{\circ })$ respectively, both with $h_{0}=0.015$  m and $Fr_{0}=1$ at the inflow. A not-to-scale schematic of the basal topography is included for both slope angles, with shaded areas representing where $\unicode[STIX]{x1D707}_{b}>\tan \unicode[STIX]{x1D701}$ .

4 Formation of a jet downstream of the obstacle

When there are no (or too few) grains initially upstream of the bump, a jet usually appears downstream of the obstacle (see figures 1, 3(a) and 4, as well as movie 1). When the flow is released from the hopper it accelerates downslope before being directed upwards (relative to the chute base) and detaching from the topography at a take-off point, where all the particles lose contact with the base and proceed to follow a parabolic trajectory. The take-off point corresponds to where the normal traction at the base of the avalanche vanishes. Following Gray et al. (Reference Gray, Wieland and Hutter1999), this normal traction in curvilinear coordinates is expressed by

(4.1) $$\begin{eqnarray}\boldsymbol{n}^{b}\boldsymbol{\cdot }(\unicode[STIX]{x1D748}^{b}\boldsymbol{n}^{b})=-\unicode[STIX]{x1D70C}gh\cos \unicode[STIX]{x1D701}-\unicode[STIX]{x1D70C}\unicode[STIX]{x1D705}h\bar{u}^{2},\end{eqnarray}$$

where $\unicode[STIX]{x1D748}^{b}$ is the Cauchy stress at the base, $\unicode[STIX]{x1D70C}$ is the flow density (assumed constant) and $h,\unicode[STIX]{x1D701},\unicode[STIX]{x1D705}$ and $\bar{u}$ are all $x$ -dependent. Setting (4.1) to zero, the normal traction vanishes when

(4.2) $$\begin{eqnarray}\bar{u}^{2}=-\frac{g\cos \unicode[STIX]{x1D701}}{\unicode[STIX]{x1D705}}.\end{eqnarray}$$

The depth-averaged velocity along the chute can be calculated by integrating the ODE (3.17) to determine $h(x)$ and then using the mass balance equation (3.15) to determine $\bar{u}$ , as shown in § 3.2 and figure 8. The computed velocity can then be used to determine the take-off point $x=x_{J}$ , where condition (4.2) is satisfied. The corresponding flow thickness $h_{J}=h(x_{J})$ and depth-averaged velocity $\bar{u}_{J}=\bar{u}(x_{J})$ can then be extracted and used as initial conditions for the jet, whose motion is computed by using Newton’s second law (assuming the only body forces are due to gravity) to determine the trajectory of airborne particles. Note that it is much easier to compute the jet dynamics in the aligned Cartesian coordinate system than in the curvilinear system. In Cartesian variables the initial take-off point at the free surface of the flow $(X_{JS},Z_{JS})$ is found from the curvilinear coordinates by the projections

(4.3) $$\begin{eqnarray}\displaystyle & \displaystyle X_{JS}=X(x_{J})-h_{J}\sin \unicode[STIX]{x1D6FD}_{J}, & \displaystyle\end{eqnarray}$$

(4.4) $$\begin{eqnarray}\displaystyle & \displaystyle Z_{JS}=b(X(x_{J}))+h_{J}\cos \unicode[STIX]{x1D6FD}_{J}, & \displaystyle\end{eqnarray}$$

where $X(x_{J})$ represents the Cartesian abscissa of the take-off point $x_{J}$ , $\unicode[STIX]{x1D701}_{J}=\unicode[STIX]{x1D701}(x_{J})$ is the inclination of the $x$ -axis at the take-off point and $\unicode[STIX]{x1D6FD}_{J}=\unicode[STIX]{x1D703}-\unicode[STIX]{x1D701}_{J}$ is the angle between the $z$ and $Z$ axes at this same position. Throughout this paper the free surface of the non-airborne avalanche is reconstructed with a similar projection method to (4.3)–(4.4) at a general point $(x,h)$ . Assuming the dominant velocity is purely downslope at $x=x_{J}$ (i.e. the flow is tangential to the topography at the take-off point), the initial take-off velocity has components $(U_{J},W_{J})$ in the downslope and normal directions, respectively, where

(4.5) $$\begin{eqnarray}\displaystyle & \displaystyle U_{J}=\bar{u}_{J}\cos \unicode[STIX]{x1D6FD}_{J}, & \displaystyle\end{eqnarray}$$

(4.6) $$\begin{eqnarray}\displaystyle & \displaystyle W_{J}=\bar{u}_{J}\sin \unicode[STIX]{x1D6FD}_{J}. & \displaystyle\end{eqnarray}$$

The trajectories $(X(t),Z(t))$ are then governed by the second-order ODEs

(4.7) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}^{2}X}{\text{d}t^{2}}=g\sin \unicode[STIX]{x1D703}, & \displaystyle\end{eqnarray}$$

(4.8) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}^{2}Z}{\text{d}t^{2}}=-g\cos \unicode[STIX]{x1D703}, & \displaystyle\end{eqnarray}$$

which may be integrated subject to the initial conditions (4.3)–(4.6) to give

(4.9) $$\begin{eqnarray}\displaystyle & \displaystyle X(t)={\textstyle \frac{1}{2}}gt^{2}\sin \unicode[STIX]{x1D703}+U_{J}t+X_{JS}, & \displaystyle\end{eqnarray}$$

(4.10) $$\begin{eqnarray}\displaystyle & \displaystyle Z(t)=-{\textstyle \frac{1}{2}}gt^{2}\cos \unicode[STIX]{x1D703}+W_{J}t+Z_{JS}. & \displaystyle\end{eqnarray}$$

Solving (4.9) for time $t$ and substituting into (4.10) implies that

(4.11) $$\begin{eqnarray}Z(X)=-{\textstyle \frac{1}{2}}gT(X)^{2}\cos \unicode[STIX]{x1D703}+W_{J}T(X)+Z_{JS},\end{eqnarray}$$

where

(4.12) $$\begin{eqnarray}T(X)=-\frac{U_{J}}{g\sin \unicode[STIX]{x1D703}}+\sqrt{\left(\frac{U_{J}}{g\sin \unicode[STIX]{x1D703}}\right)^{2}+\frac{2(X-X_{JS})}{g\sin \unicode[STIX]{x1D703}}},\end{eqnarray}$$

and the positive root is chosen in (4.12) to ensure that $X>X_{JS}$ for positive times. Equations (4.11), (4.12) determine the trajectory of the top surface of the jet once the initial positions (4.3) and (4.4) are determined. Trajectories for particles starting at heights between zero and $h_{J}$ may also be constructed in a similar manner, but lie close to the surface jet trajectory, due to the shallowness of the flow and the assumption of plug flow prior to take-off.

Figure 9. Comparison of the surface jet trajectories for the depth-averaged theory (4.11), (4.12) (dashed lines) and experimental results for a slope angle (a) $\unicode[STIX]{x1D703}=38^{\circ }$ and (b) $\unicode[STIX]{x1D703}=40^{\circ }$ . The solid lines are calculated using the measured surface velocities at the centre of the channel for the top of the jet, and the dash-dotted lines are using the wall velocity for the lower trajectory (see figure 7). The red dots represent the surface take-off points $(x_{J},h_{J})$ . Note that the images have been slightly rotated to maximise space. The bump height of 4.75 cm acts as a scale.

Figure 9 shows a comparison between the theoretical and experimental surface jet trajectories, at two different slope angles $\unicode[STIX]{x1D703}=38^{\circ }$ and $\unicode[STIX]{x1D703}=40^{\circ }$ . In both cases, the (dashed) paths given by (4.11) and (4.12) show fairly good agreement with experiments for the centre of the jet. There is, however, significant vertical spreading of the airborne material, with the effective flow thickness becoming much greater compared to the upstream region. One possible explanation for this is that there is vertical shear through the depth of the avalanche prior to take-off, since this would imply that the upper particles have greater take-off velocities and follow higher trajectories. However, as already noted, the amount of shear is low, and a more probable reason for the vertical spreading is the effect of wall friction. The theory is quasi-one-dimensional, with a single mean value of velocity used at each cross-slope position in the flow. However, as shown in figure 7, particles at the walls are slower than the mean and those in the centre are faster. The images in figure 9 are taken from the side of the chute through clear walls, so that the upper trajectories in figure 9 actually correspond to the fastest particles in the centre. Similarly, the lower paths are the slower moving wall particles. By keeping the take-off position $x_{J}$ predicted by (4.2) and instead imposing the surface velocity measured at the middle of the flow for $X=0.40~\text{m}$ (near the take-off point), much better agreement is found for the surface trajectories at both slope angles (see solid lines in figure 9). In the same way, using the surface velocity measured near the walls gives a significantly improved fit for the lower paths (see dash-dotted lines in figure 9). Hence, much of the apparent spreading of the jet can be accounted for by including wall friction effects. The underestimation of the top surface of the jet may also be explained by the fact that the surface velocities are slightly underestimated by the theory near the take-off point (especially for $\unicode[STIX]{x1D703}=40^{\circ }$ ), as seen in figure 8.

5 Formation of a steady shock upstream of the obstacle

As observed during the experiments, introducing a static deposit of particles in front of the obstacle can cause a steady shock to form before the bump instead of a jet behind it (figure 3 and movie 2). This shock separates a thin fast moving (supercritical) upstream region from a slower (subcritical) regime with an associated increase in thickness on the downstream side. Experimentally, there is a rapid, but smooth, transition across the shock, with a width that is controlled by the viscosity of the system (Whitham Reference Whitham1974). The mean shock position (referred to as simply shock position from this point onwards) is defined to be the point of maximal free-surface gradient $\text{d}h/\text{d}x$ in this zone. Conversely, in the hyperbolic inviscid depth-averaged theory (3.7)–(3.8) the shock represents a mathematical discontinuity and therefore has an infinitesimally small width and unique downslope position. Despite this important difference, the model is able to predict the key features of the position of the shock and corresponding thickness profile.

The jump conditions govern the conservation of mass and momentum when the thickness and velocity are discontinuous. They are derived from the integral form of the conservation laws using a limiting argument (see e.g. Chadwick Reference Chadwick1976). For the case of a one-dimensional stationary shock at $x=x_{s}$ , the general form (e.g. Gray et al. Reference Gray, Tai and Noelle2003; Gray & Cui Reference Gray and Cui2007) reduces to

(5.1) $$\begin{eqnarray}\displaystyle & \displaystyle \left.\unicode[STIX]{x27E6}h\bar{u}\right.\unicode[STIX]{x27E7}=0, & \displaystyle\end{eqnarray}$$

(5.2) $$\begin{eqnarray}\displaystyle & \displaystyle \left.\unicode[STIX]{x27E6}h\bar{u}^{2}+{\textstyle \frac{1}{2}}gh^{2}\cos \unicode[STIX]{x1D701}_{s}\right.\unicode[STIX]{x27E7}=0, & \displaystyle\end{eqnarray}$$

where the local chute inclination angle $\unicode[STIX]{x1D701}_{s}=\unicode[STIX]{x1D701}(x_{s})$ and the jump brackets $\unicode[STIX]{x27E6}f\unicode[STIX]{x27E7}=f_{+}-f_{-}$ denote the difference between the enclosed function on the forward $(+)$ and rearward $(-)$ sides of the shock. Note that the source terms do not enter into the momentum jump (5.2), since their integral vanishes as the control volume is shrunk down onto the shock (Chadwick Reference Chadwick1976). Written out explicitly, equations (5.1) and (5.2) are

(5.3) $$\begin{eqnarray}\displaystyle & \displaystyle h_{-}\bar{u}_{-}=h_{+}\bar{u}_{+}, & \displaystyle\end{eqnarray}$$

(5.4) $$\begin{eqnarray}\displaystyle & \displaystyle h_{-}(\bar{u}_{-})^{2}+{\textstyle \frac{1}{2}}gh_{-}^{2}\cos \unicode[STIX]{x1D701}_{s}=h_{+}(\bar{u}_{+})^{2}+{\textstyle \frac{1}{2}}gh_{+}^{2}\cos \unicode[STIX]{x1D701}_{s}, & \displaystyle\end{eqnarray}$$

giving two expressions relating the unknown quantities $h_{\pm },\bar{u}_{\pm }$ . The shock position $x_{s}$ is also unknown at this stage.

The mass jump condition (5.1) implies that $h\bar{u}$ is the same on either side of the shock and, using (3.15), it follows that the volume flux is equal to $h_{0}\bar{u}_{0}$ everywhere on the chute, i.e.

(5.5) $$\begin{eqnarray}h_{0}\bar{u}_{0}=h_{-}\bar{u}_{-}=h_{+}\bar{u}_{+}=h\bar{u}.\end{eqnarray}$$

This can be used to eliminate the velocities $\bar{u}_{\pm }$ in the momentum jump condition (5.4) and it also follows that the ODE (3.17) governs the thickness on both the upstream and downstream sides of the shock.

Figure 10. Diagram showing a sketch of the solution structure of the shock. There is a supercritical flow ( $Fr>1$ ) out of the hopper, which transitions to a subcritical flow ( $Fr<1$ ) across a shock located at $x_{s}$ in curvilinear and $X_{s}$ in Cartesian coordinates, respectively. At $x_{1}$ and $X_{1}$ the flow transitions smoothly back from a subcritical to a supercritical flow of height $h_{1}$ . The inflow height is denoted $h_{0}$ .

To ensure that sufficient information is propagated into the shock in order to determine its position, the causality condition (see e.g. Ockendon et al. Reference Ockendon, Howison, Lacey and Movchan2004) states that three families of characteristics must travel into the discontinuity. Note this is also equivalent to the Lax entropy condition (Lax Reference Lax1957), which ensures that the vanishing viscosity solution of the equations is selected. Assuming that $\bar{u}$ is positive, it follows from the definition of the characteristics (3.10)–(3.11) that this occurs if and only if the upstream side is supercritical $(Fr>1)$ and the downstream side is subcritical $(Fr<1)$ , giving a range of permissible shock positions. The ODE (3.17) can then be integrated forward in space from $x=0$ up to $x=x_{s}$ , giving $h_{-}$ and $\bar{u}_{-}$ , before applying the jump conditions (5.3) and (5.4) to calculate $h_{+}$ and $\bar{u}_{+}$ . The downstream region of the flow is found by integrating (3.17) with initial condition $h=h_{+}$ at $x=x_{s}$ .

Even after enforcing the causality condition, there is a non-unique way of choosing the shock position $x_{s}$ . This is in direct contrast to the experimental set-up, which selects a specific shock position for a given slope angle. There is a very simple mathematical resolution of this issue. Immediately after the shock the flow is subcritical, so the solution can either continue to decelerate and thicken, which is not what is observed, or it can accelerate. If it accelerates, then the Froude number will increase, and when it reaches unity the denominator of the ODE (3.17) will be zero and hence the thickness gradient becomes infinite ( $\text{d}h/\text{d}x\rightarrow \infty$ ), which is again unphysical. The only exception to this is when the numerator of (3.17) is also zero, which implies that the gradient is undefined, or at least must still be determined by L’Hôpital’s rule. In this latter case it is possible to produce a smooth transition from subcritical to supercritical flow as the avalanche accelerates down the chute, as sketched in figure 10 and shown in figure 11. There is therefore a critical point, $x=x_{1}$ (say), where the Froude number is equal to one and hence the flow speed is equal to the gravity wave speed.

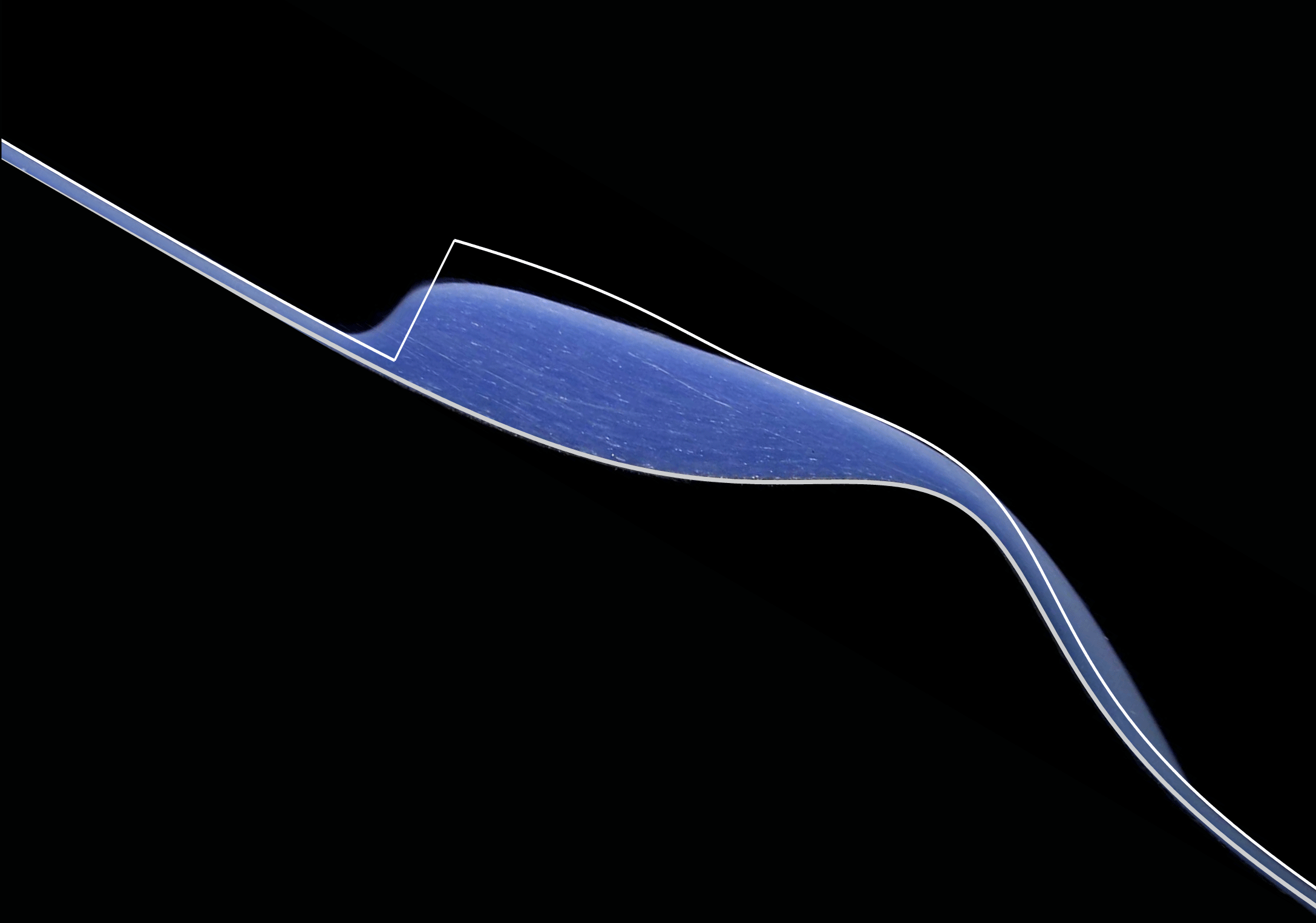
Figure 11. Comparison of the experimental and theoretical (white line) free-surface profile for the steady shock at a slope angle $\unicode[STIX]{x1D703}=39^{\circ }$ . Note that the image has been slightly rotated to maximise space. The bump height of 4.75 cm acts as a scale.

The critical point is analogous to the sonic point in gas dynamics (e.g. Laney Reference Laney1998) and plays a vital role in selecting the correct shock position, in a parallel way to flows in collapsible tubes (Shapiro Reference Shapiro1977). Denoting the flow thickness and velocity at $x_{1}$ by $h_{1}$ and $\bar{u}_{1}$ , respectively, and recalling that $Fr_{0}=1$ at the inflow as well as at the critical point, it follows that

(5.6) $$\begin{eqnarray}\displaystyle & \displaystyle h_{0}\bar{u}_{0}=h_{1}\bar{u}_{1}, & \displaystyle\end{eqnarray}$$

(5.7) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\bar{u}_{0}}{\sqrt{gh_{0}\cos \unicode[STIX]{x1D701}_{0}}}=\frac{\bar{u}_{1}}{\sqrt{gh_{1}\cos \unicode[STIX]{x1D701}_{1}}}=1, & \displaystyle\end{eqnarray}$$

where (5.6) represents the conservation of mass (3.15), and the slope angles at the inflow and the critical point are $\unicode[STIX]{x1D701}_{0}=\unicode[STIX]{x1D701}(0)$ and $\unicode[STIX]{x1D701}_{1}=\unicode[STIX]{x1D701}(x_{1})$ , respectively. Using (5.6) and (5.7) the thickness at the critical point is

(5.8) $$\begin{eqnarray}h_{1}=h_{0}\left(\frac{\cos \unicode[STIX]{x1D701}_{0}}{\cos \unicode[STIX]{x1D701}_{1}}\right)^{1/3},\end{eqnarray}$$

which can be substituted into the numerator of (3.17) to give

(5.9) $$\begin{eqnarray}h_{1}^{3}g\cos \unicode[STIX]{x1D701}_{1}(\tan \unicode[STIX]{x1D701}_{1}-\unicode[STIX]{x1D707}(h_{1}))-h_{1}\unicode[STIX]{x1D707}(h_{1})\unicode[STIX]{x1D705}_{1}(h_{0}\bar{u}_{0})^{2}-{\textstyle \frac{1}{2}}gh_{1}^{4}\unicode[STIX]{x1D705}_{1}\sin \unicode[STIX]{x1D701}_{1}=0.\end{eqnarray}$$

This can then be solved for the location $x=x_{1}$ of the critical point using a standard numerical root finding technique. At the critical point the Froude number is equal to unity and both the numerator and the denominator of the ODE (3.17) are equal to zero. The gradient of the solution at the critical point therefore has to be determined either by a Taylor series expansion or by L’Hôpital’s rule (see appendix A for details). However, once the position and gradient of the critical point have been determined, the ODE (3.17) can be integrated both upstream and downstream of $x=x_{1}$ , to construct a solution that transitions smoothly from subcritical flow (for $x<x_{1}$ ) to supercritical flow (for $x>x_{1}$ ) as sketched in figure 10. The final part of the problem is to connect the smoothly varying solution through the critical point to the supercritical solution that emerges from the hopper described in § 3. By construction the mass jump condition (5.1) is satisfied everywhere, so it only remains to find the shock position $x=x_{s}$ where the momentum jump condition (5.2) is satisfied, which can again be solved for using a standard numerical root finding method. There are in fact two solutions; however, only the one that lies furthest upstream is stable to small perturbations and this is the one that is observed in experiments.

Figure 11 shows a comparison of the thickness profile for the experiment and theory, at a slope angle $\unicode[STIX]{x1D703}=39^{\circ }$ . The shock position is in relatively good agreement with the experiment. There are, however, some discrepancies in the flow thickness, especially in the shock region, where, as already noted, the flow is non-shallow and has a rapid (but smooth) transition in thickness. This is in contrast with the discontinuity predicted by the shallow-water model. It is possible to construct smooth shocks by including a depth-averaged version of the $\unicode[STIX]{x1D707}(I)$ -rheology (Gray & Edwards Reference Gray and Edwards2014) into the theory as in Edwards & Gray (Reference Edwards and Gray2015). However, this is based on the rough-bed friction law (Pouliquen Reference Pouliquen1999), which is inconsistent with the Coulomb-type law (3.25) and thus not included here. Another important effect that is missing is the dilatation of the flow. Faug et al. (Reference Faug, Childs, Wyburn and Einav2015) recently observed that, for avalanches on steep slopes on a smooth base, the supercritical flow becomes more dilute as it leaves the gate and accelerates downstream, whereas after the shock the solids volume fraction is increased in the slower moving regime. This would potentially lead to an under prediction of the flow thickness in the accelerating region and an over prediction of the thickness after the shock.

In addition, a much greater degree of shear is observed in the thick region, immediately behind the shock, compared to the accelerating regions, with particles at the bottom becoming close to static, especially at lower angles of inclination. Long exposure photographs indicate that all the grains are in fact in motion, but there is certainly much greater shear through the flow, than in the region upstream of the shock. This shear is not accounted for by the theory, since plug flow is assumed everywhere. In the thick region the velocity profile at the side wall is better approximated by an exponential function (see e.g. Wiederseiner et al. Reference Wiederseiner, Andreini, Epely-Chauvin, Moser, Monnereau, Gray and Ancey2011) of the form

(5.10) $$\begin{eqnarray}u=\frac{\unicode[STIX]{x1D6EC}\bar{u}}{\exp (\unicode[STIX]{x1D6EC})-1}\exp \left(\unicode[STIX]{x1D6EC}\frac{z}{h}\right),\end{eqnarray}$$

which has a corresponding shape factor

(5.11) $$\begin{eqnarray}\unicode[STIX]{x1D712}=\frac{\overline{u^{2}}}{\bar{u}^{2}}=\frac{\unicode[STIX]{x1D6EC}}{2}\left(\frac{\exp (\unicode[STIX]{x1D6EC})+1}{\exp (\unicode[STIX]{x1D6EC})-1}\right).\end{eqnarray}$$

For the value of $\unicode[STIX]{x1D6EC}=3.24$ found by Wiederseiner et al. (Reference Wiederseiner, Andreini, Epely-Chauvin, Moser, Monnereau, Gray and Ancey2011) this gives a shape factor $\unicode[STIX]{x1D712}=1.75$ , which is no longer close to unity. It is therefore surprising that the theory is able to accurately describe such regions. There are two places in (3.8) where $\unicode[STIX]{x1D712}$ appears. The first is in the momentum transport term and the second is in the centrifugal correction to the basal pressure. It is useful to define two non-dimensional parameters

(5.12a,b ) $$\begin{eqnarray}P_{1}=\frac{\unicode[STIX]{x1D712}h\bar{u}^{2}}{\frac{1}{2}gh^{2}\cos \unicode[STIX]{x1D701}}=2\unicode[STIX]{x1D712}Fr^{2},\quad \text{and}\quad P_{2}=\frac{\unicode[STIX]{x1D705}\unicode[STIX]{x1D712}h\bar{u}^{2}}{gh\cos \unicode[STIX]{x1D701}}=\unicode[STIX]{x1D712}\unicode[STIX]{x1D705}hFr^{2}.\end{eqnarray}$$

The first is the ratio of the momentum transport terms to the depth-averaged pressure gradient in the momentum balance (3.8), whilst the second is the ratio of the centrifugal pressure correction to the basal pressure in the source terms. The product $\unicode[STIX]{x1D705}h$ is always less than unity, otherwise the avalanche is thicker than the intersection point of the curvilinear coordinates. Moreover the Froude number typically lies between $0.19<Fr<0.25$ in the thick slowly moving region of the flow, as shown in figure 13. Hence the Froude number squared lies in the range 0.03 to 0.06, and the ratios $P_{1}$ and $P_{2}$ are very small unless $\unicode[STIX]{x1D712}$ is very large. It follows that even if there was a fairly large deviation of $\unicode[STIX]{x1D712}$ away from unity, its effect in the thick, slowly moving region would be small. The simple depth-averaged model therefore provides a good approximation in the slowly moving region despite the shape factor being unrepresentative of the shear profile. Conversely, in the thin fast moving regions, where momentum transport terms and centrifugal effects can dominate, there is considerable slip at the base of the avalanche, so that $\unicode[STIX]{x1D712}=1$ (as assumed) is a good approximation. Remarkably, then, despite the simplicity of the model there is an excellent agreement between the experimental and theoretical shock position for a wide range of slope angles, using the same friction coefficients obtained in § 3.2, as shown in figure 12.

Figure 12. Variation of the mean shock position $X_{s}$ with slope angle $\unicode[STIX]{x1D703}$ for experiments (symbols) and the depth-averaged terrain-following model (solid line). The horizontal error bars of $\pm 0.1^{\circ }$ are determined by the precision of our digital inclinometer, while the vertical error bars indicate the relative uncertainties associated with the measurement of the shock position.

Figure 13. The Froude number $Fr$ as a function of the curvilinear coordinate $x$ for a steady-shock solution at an inclination $\unicode[STIX]{x1D703}=39^{\circ }$ . The shock lies at $x=x_{s}$ and the Froude number equals unity at $x=x_{1}$ . The thick slowly moving region lies approximately between $x_{s}\leqslant x\leqslant 0.37$ m.

6 Time and spatially dependent numerical simulations

The full governing equations (3.7)–(3.8) are now solved numerically to show the transient evolution to the equilibrium shock state described in the previous section, as well as the formation of a static deposit on the bump when the inflow ceases. The hyperbolic system is solved using the shock-capturing non-oscillatory central scheme of Kurganov & Tadmor (Reference Kurganov and Tadmor2000), whose semi-discrete formulation is combined with a second-order Runge–Kutta time integrator.

Figure 14. Temporal evolution of the free-surface height towards steady state for a shock at slope angle $\unicode[STIX]{x1D703}=39^{\circ }$ . Note that the images have been slightly rotated to maximise space, the aspect ratio is 1:1 and the bump height of 4.75 cm acts as a scale. The final image corresponds to $t_{steady}=8$  s. A supplementary movie is available online.

Figure 15. Temporal evolution of the free-surface height once the inflow ceases at slope angle $\unicode[STIX]{x1D703}=39^{\circ }$ . Note that the images have been slightly rotated to maximise space, the aspect ratio is 1:1 and the bump height of 4.75 cm acts as a scale. The final image corresponds to $t_{steady}=15$  s. A supplementary movie is available online.

In order to solve the system, the depth-averaged equations (3.7), (3.8) together with the friction law (3.25) are written in terms of conserved variables in vector form as

(6.1) $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\boldsymbol{w}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}\boldsymbol{f}(\boldsymbol{w})}{\unicode[STIX]{x2202}x}=\boldsymbol{S}(\boldsymbol{w}),\end{eqnarray}$$

where $\boldsymbol{w}=(h,m)^{\text{T}}$ is the vector of conserved variables $h$ and $m=h\bar{u}$ . The resulting convection flux function $\boldsymbol{f}$ and source term vector $\boldsymbol{S}=(0,S)^{\text{T}}$ are given by

(6.2) $$\begin{eqnarray}\boldsymbol{f}=\left(\begin{array}{@{}c@{}}m\\ \displaystyle \frac{m^{2}}{h}+\frac{h^{2}}{2}g\cos \unicode[STIX]{x1D701}\end{array}\right),\quad \boldsymbol{S}=\left(\begin{array}{@{}c@{}}0\\ \displaystyle hg\sin \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707}\frac{\bar{u}}{|\bar{u}|}\left(hg\cos \unicode[STIX]{x1D701}+\unicode[STIX]{x1D705}\unicode[STIX]{x1D712}m^{2}/h\right)\end{array}\right).\end{eqnarray}$$

The critical inflow $Fr=1$ at $x=0$ means that two inflow conditions must be specified (e.g. Weiyan Reference Weiyan1992), which are the same as those for the steady ODE, i.e.

(6.3) $$\begin{eqnarray}\displaystyle & \displaystyle h(0,t)=h_{0}, & \displaystyle\end{eqnarray}$$

(6.4) $$\begin{eqnarray}\displaystyle & \displaystyle m(0,t)=h_{0}\bar{u}_{0}. & \displaystyle\end{eqnarray}$$

Computations are carried out in a domain $0\leqslant x\leqslant 0.8$  m, which is discretised over 16 000 grid cells. The initial static distribution of mass that is placed in front of the bump in order to trigger the shock is parameterised by the initial conditions

(6.5a,b ) $$\begin{eqnarray}h(x,0)=h_{init}(x),\qquad m(x,0)=0,\end{eqnarray}$$

where the function $h_{init}(x)$ is prescribed. Figure 14 shows a simulation of an avalanche as it flows down a plane inclined at $\unicode[STIX]{x1D703}=39^{\circ }$ and hits a static deposit that has been left by a previously computed avalanche. In fact, the final deposit that is computed at the end of this simulation, which is shown in figure 15, is indistinguishable from the initially assumed deposit, so the solution is quasi-periodic in nature.

As the avalanche first impinges on the deposit, at approximately 0.22 s, it generates an erosion shock that accelerates the thin static deposit on the bump into a slowly moving thick layer of material. This shock, which is similar to those observed by Edwards & Gray (Reference Edwards and Gray2015), propagates rapidly downslope and reaches the end of the static deposit at approximately 0.52 s, and dissipates. At the same time as the static material is being mobilised, the fast moving upstream avalanche produces a shock at the rear of the thick slowly moving layer, which also moves downslope, but at a much slower rate than the erosive shock at the front. At approximately 0.68 s this shock reverses direction and slowly starts to propagate upstream, reaching the steady-state equilibrium position at approximately $t=5$  s, with no further propagation of the shock occurring before the final image in figure 14 at $t=8$  s.

It is very important to note that if the static layer of grains were replaced by a rigid smooth topography with the same shape, the flow would automatically develop into the jet solution, which would be even stronger due to the slightly steeper slope. In the absence of the dissipation mechanism, provided by the erodible grains, the oncoming avalanche tip would simply propagate smoothly across the new topography in the same way as it does upstream and downstream of the erodible layer. The erodible material is therefore vital for the brief formation of the downslope-facing erosive shock shown at $t=0.3$ and $t=0.4$ s in figure 14. This dissipates a lot of energy by mobilising the static grains, and, crucially, thickens and slows the oncoming flow allowing the upslope-facing shock to be triggered. This very fine balancing of different physical effects is what makes this experiment such a sensitive and interesting one.

Figure 16. Temporal evolution of the theoretical free-surface profile (red solid lines) to the exact steady-state solution (green dashed line) for a shock at slope angle $\unicode[STIX]{x1D703}=39^{\circ }$ . Note that the images have been slightly rotated to maximise space, the aspect ratio is 1:1 and the bump height of 4.75 cm acts as a scale.

Figure 15 shows another sequence of simulation images, which start from the steady-shock solution shown in figure 14. At $t=10$  s the inflow is instantaneously closed off, with the fast moving tail of the avalanche reaching the shock at $t=10.24$  s. At this point the steep shock collapses, with some material being pushed upslope until 10.50 s and the avalanche then slowly thinning as the residual material, that is able to creep over the bump, slowly flows downslope. By $t=14$  s a static deposit is formed on the upstream side of the bump. This material is sufficient to trigger any subsequent oncoming avalanche into the steady-shock regime. As previously mentioned it is essentially this deposit that provided the initial condition (6.5a,b ) for the beginning of the simulations shown in figure 14. A supplementary movie showing the full time-dependent development of the solution from the impingement of the avalanche onto the static deposit to the formation of the static deposit at the end is available online.

The numerical computations are compared to experiments in figure 16, where the free-surface profiles are overlaid on the experimental photos. The slope angle is again $\unicode[STIX]{x1D703}=39^{\circ }$ , but this time the initial condition is set by the actual free-surface profile of the static grains in the experiment. As the avalanche impinges on the static deposit some of the particles are thrown into the air during the mobilisation process, rather than generating the simulated erosive shock on the downstream side of the slowly moving material. However, this anomaly rapidly propagates through the deposit and dissipates. The rearward shock between the slowly moving, recently mobilised, grains and the rapid upstream avalanche has already started to move upslope by $t=0.8$  s in both the experiments and the computation. The experimental shock wave is diffuse and probably somewhat upstream of the computed shock, but it is in reasonable agreement. As the experimental shock attains its equilibrium position, described in § 5, the numerical shock catches up with it, so that at steady state, the mean position of the diffuse shock and the jump are remarkably close. This is a particularly strong vindication of the theory given how sensitively dependent the shock position is on the basal friction and the chute inclination. It should be noted, however, that when the grains flow over the bump, the avalanche is on the verge of detaching from the base at $t=0.8$  s, and the flow is quite dilute on the downstream side. As the backward-propagating shock establishes itself, it becomes more efficient at slowing the grains, and the dilute region on the lee side of the bump is reduced in size, although there is some dilation even at steady state, which occurs at times greater than 4 s.

7 Comparison between standard and terrain-following approaches

It is also possible to derive a simpler depth-averaged theory in aligned Cartesian coordinates $OXZ$ for modelling the shock evolution and steady-state position (see e.g. Savage & Hutter Reference Savage and Hutter1989; Gray et al. Reference Gray, Tai and Noelle2003; Gray & Edwards Reference Gray and Edwards2014). This is referred to as the standard depth-averaged avalanche model throughout this paper. This theory assumes that the slope is inclined at a fixed mean angle and the effects of terrain only enter the equations via a topography height gradient in the source term, i.e. there is no local variation in the slope angle and there are no centrifugal effects. For this rather sensitive experiment, the terrain-following model (see e.g. Savage & Hutter Reference Savage and Hutter1991; Gray et al. Reference Gray, Wieland and Hutter1999) described in §§ 3–6 is much more successful at predicting the steady-state shock position than the standard model. In addition, the standard approach is also unable to predict the take-off point of the jet. These results therefore provide compelling evidence of the advantages of the terrain-following approach.

7.1 The standard depth-averaged avalanche model

Using a Cartesian coordinate system $OXZ$ aligned at a constant angle $\unicode[STIX]{x1D703}$ to the horizontal (as shown in figure 6), the flow thickness $H(X,T)$ and depth-averaged velocity $\bar{U}(X,T)$ are now measured perpendicular and parallel, respectively, to the $X$ -axis. The depth-integrated mass and momentum balance equations (see e.g. Savage & Hutter Reference Savage and Hutter1989; Gray et al. Reference Gray, Tai and Noelle2003; Gray & Edwards Reference Gray and Edwards2014) are then

(7.1) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}H}{\unicode[STIX]{x2202}T}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}X}(H\bar{U})=0, & \displaystyle\end{eqnarray}$$

(7.2) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}T}(H\bar{U})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}X}(H\bar{U}^{2})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}X}\left(\frac{1}{2}gH^{2}\cos \unicode[STIX]{x1D703}\right)=HS, & \displaystyle\end{eqnarray}$$

where the shape factor $\unicode[STIX]{x1D712}$ has been assumed to equal unity. The source term $S$ is composed of the downslope component of gravity, Coulomb basal friction, wall friction and topography gradients, and is equal to

(7.3) $$\begin{eqnarray}S=g\cos \unicode[STIX]{x1D703}\left(\tan \unicode[STIX]{x1D703}-\frac{\bar{U}}{|\bar{U}|}\left(\unicode[STIX]{x1D707}_{b}+\unicode[STIX]{x1D707}_{w}\frac{H}{W}\right)-\frac{\text{d}b}{\text{d}X}\right).\end{eqnarray}$$

Note that in the standard approach, the effect of topography arises purely from the downslope component of the basal pressure acting on the bump in the basal shear stress (see e.g. Gray et al. Reference Gray, Tai and Noelle2003; Gray & Edwards Reference Gray and Edwards2014). This is, therefore, a much less sophisticated treatment of the topography than the terrain-following approach, where both the local inclination angle varies as a function of $x$ and the basal pressure accounts for centrifugal forces. It has, nevertheless, proved to be very useful for simulating complicated flows past obstacles, where shock waves are generated (see e.g. Gray et al. Reference Gray, Tai and Noelle2003; Gray & Cui Reference Gray and Cui2007; Aker & Bokhove Reference Aker and Bokhove2008; Cui & Gray Reference Cui and Gray2013).

Following the same approach as in § 3.1, it follows that integrating the steady-state depth-integrated mass balance equation (7.1) in $X$ implies that

(7.4) $$\begin{eqnarray}H\bar{U}=H_{0}\bar{U}_{0},\end{eqnarray}$$

where the thickness and depth-averaged velocity at the inflow are $H_{0}$ and $\bar{U}_{0}$ , respectively. Moreover, the mass jump condition, $\unicode[STIX]{x27E6}H\bar{U}\unicode[STIX]{x27E7}=0$ , implies that the volume flux per unit width is equal to $H_{0}\bar{U}_{0}$ everywhere. The steady-state depth-integrated momentum balance (7.2) then implies that the ODE governing the thickness upstream and downstream of the shock is

(7.5) $$\begin{eqnarray}\frac{\text{d}H}{\text{d}X}=\displaystyle \frac{H^{3}g\cos \unicode[STIX]{x1D703}\left(\tan \unicode[STIX]{x1D703}-\unicode[STIX]{x1D707}_{b}-\displaystyle \unicode[STIX]{x1D707}_{w}\frac{H}{W}-\displaystyle \frac{\text{d}b}{\text{d}X}\right)}{H^{3}g\cos \unicode[STIX]{x1D703}-(H_{0}\bar{U}_{0})^{2}},\end{eqnarray}$$

where it has implicitly been assumed that $\bar{U}>0$ . Note that the denominator in (7.5) takes the same form as in the terrain-following system (3.17), and the numerator is similar except with a topography gradient replacing the curvature term. In the standard model, the Froude number is defined as

(7.6) $$\begin{eqnarray}Fr=\frac{|\bar{U}|}{\sqrt{gH\cos \unicode[STIX]{x1D703}}},\end{eqnarray}$$

and this is again assumed to be equal to unity at the inflow. Hence, the inflow velocity $\bar{U}_{0}=\sqrt{gH_{0}\cos \unicode[STIX]{x1D703}}$ . At the critical point, which lies at $X=X_{1}$ , the Froude number is also equal to unity and the denominator in the ODE (7.5) is equal to zero. It follows that the thickness at the critical point, $H_{1}$ , is the same as the thickness at the inflow, i.e.

(7.7) $$\begin{eqnarray}H_{1}=H_{0}.\end{eqnarray}$$

In order to ensure the thickness gradients in the ODE (7.5) remain bounded at $X=X_{1}$ the numerator must also be zero, which implies that

(7.8) $$\begin{eqnarray}\tan \unicode[STIX]{x1D703}-\unicode[STIX]{x1D707}_{b}-\unicode[STIX]{x1D707}_{w}\frac{H_{1}}{W}-\left.\frac{\text{d}b}{\text{d}X}\right|_{X_{1}}=0.\end{eqnarray}$$

Since the topography $b=b(X)$ is given by (3.1) and $H_{1}=H_{0}$ , equation (7.8) can be solved numerically to find the position of the critical point $X=X_{1}$ .

Figure 17. Shock position $X_{s}$ as a function of the slope angle $\unicode[STIX]{x1D703}$ . The symbols are experimental data, and the solid red line shows the terrain-following theory, computed in curvilinear coordinates with the measured $\unicode[STIX]{x1D707}_{b}=\tan (23^{\circ })$ and $\unicode[STIX]{x1D707}_{w}=\tan (7.5^{\circ })$ from PIV. The different black dashed lines denote the standard Cartesian theory, calculated with fixed wall friction $\unicode[STIX]{x1D707}_{w}=\tan (7.5^{\circ })$ and varying basal friction $\unicode[STIX]{x1D707}_{b}$ , with the value $\unicode[STIX]{x1D707}_{b}=\tan (27.5^{\circ })$ chosen as the best fit to the shock position at $\unicode[STIX]{x1D703}=39^{\circ }$ (dash-dotted line). The green dashed line shows the terrain-following avalanche model computed independently in Cartesian coordinates, which, as expected, exactly reproduce the curvilinear results.

Figure 18. Comparison of the experimental steady-state free-surface position with the solution of the terrain-following avalanche model (solid white line) and the standard theory (red dashed line) for (a) a slope angle $\unicode[STIX]{x1D703}=37^{\circ }$ and (b) a slope angle $\unicode[STIX]{x1D703}=39^{\circ }$ . Note that the images have been slightly rotated to maximise space. The bump height of 4.75 cm acts as a scale.

In the same way as in the terrain-following solution, the ODE (7.5) is integrated backwards, and forwards, away from the critical point to construct a solution for $H$ that varies smoothly between subcritical ( $X<X_{1}$ ) and supercritical flow ( $X>X_{1}$ ). A smoothly varying supercritical solution can also be constructed from the inflow and the two portions are pieced together by applying the momentum jump condition

(7.9) $$\begin{eqnarray}\left.\unicode[STIX]{x27E6}H\bar{U}^{2}+{\textstyle \frac{1}{2}}gH^{2}\cos \unicode[STIX]{x1D703}\right.\unicode[STIX]{x27E7}=0,\end{eqnarray}$$

to find the position of the shock $X=X_{s}$ . Figure 17 shows the computed shock position as a function of the slope angle $\unicode[STIX]{x1D703}$ . The inflow conditions and wall friction $\unicode[STIX]{x1D707}_{w}=\tan (7.5^{\circ })$ are kept at the same constant values as in § 3, but different basal friction coefficients $\unicode[STIX]{x1D707}_{b}$ are plotted (black dashed lines). For each angle, it is possible to choose $\unicode[STIX]{x1D707}_{b}$ so that the shock position is predicted by the Cartesian theory, for example the value $\unicode[STIX]{x1D707}_{b}=\tan (27.5^{\circ })$ gives good agreement at $\unicode[STIX]{x1D703}=39^{\circ }$ (dash-dotted line in figure 17). However, the same parameters are unable to reproduce the results at other slope angles, whereas the terrain-following approach matches the shock position across the whole range for the same friction coefficients (solid line). This is highlighted in figure 18, which shows a comparison between the thickness profiles obtained with both theories and the experiments. At 39 $^{\circ }$ there is little difference between the two theories and both fit the experimental data equally well. However, at 37 $^{\circ }$ the terrain-following system gives a significantly improved fit, with the standard model predicting a shock position far upstream of the actual location. Note that the basal friction value $\unicode[STIX]{x1D707}_{b}=\tan (27.5^{\circ })$ required for fitting the standard theory at $\unicode[STIX]{x1D703}=39^{\circ }$ is unphysically high and not representative of that calculated using PIV ( $\unicode[STIX]{x1D707}_{b}=\tan (23^{\circ })$ ). When using the experimentally measured value ( $\unicode[STIX]{x1D707}_{b}=\tan (23^{\circ })$ ), the prediction of the shock position is far away from the actual values at low slope angles. At higher angles ( $\unicode[STIX]{x1D703}=36^{\circ }$ ) for $\unicode[STIX]{x1D707}_{b}=\tan (23^{\circ })$ , the standard theory is unable to predict any shock solutions at all. The measured friction values are not high enough to be able to satisfy the momentum shock condition in the standard system. This is another advantage of the terrain-following model since shocks are observed experimentally for a wider range of angles than the standard theory predicts.

7.2 Coordinate transformation of the terrain-following model

For practical applications the topography is often defined by a geographical information system (GIS) model in Cartesian coordinates with a vertical axis aligned with gravity. In order to benefit from the improved predictive power of the terrain-following model it would therefore be useful to express it in a Cartesian coordinate system. As a specific example of this, it is now shown how the terrain-following model can be transformed from the curvilinear $Oxz$ coordinates to the aligned Cartesian coordinates $OXZ$ used by the standard model. This can be achieved by making the simple transformation of variables

(7.10a,b ) $$\begin{eqnarray}t=T,\quad \quad x=\int _{0}^{X}\sqrt{1+\left(\frac{\text{d}b}{\text{d}X}\right)^{2}}\,\text{d}X^{\prime },\end{eqnarray}$$

which implies that the derivatives

(7.11a,b ) $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}T},\quad \quad \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}=\frac{1}{\unicode[STIX]{x1D6E5}_{b}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}X},\end{eqnarray}$$

where the normalisation factor $\unicode[STIX]{x1D6E5}_{b}$ , defined in (3.6), is repeated here for completeness

(7.12) $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{b}=\sqrt{1+\left(\frac{\text{d}b}{\text{d}X}\right)^{2}}.\end{eqnarray}$$

Since $\unicode[STIX]{x1D6E5}_{b}$ is a function of $X$ only, it can be incorporated inside the time derivative to write the terrain-following mass and momentum balances (3.7)–(3.8) in conservative form and in Cartesian coordinates as

(7.13) $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}T}(\unicode[STIX]{x1D6E5}_{b}h)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}X}(h\bar{u})=0,\end{eqnarray}$$

(7.14) $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}T}(\unicode[STIX]{x1D6E5}_{b}h\bar{u})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}X}(\unicode[STIX]{x1D712}h\bar{u}^{2})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}X}\left(\frac{1}{2}gh^{2}\cos \unicode[STIX]{x1D701}\right)=\unicode[STIX]{x1D6E5}_{b}hS_{\mathit{terrain}\text{-}\mathit{following}},\end{eqnarray}$$

where the terrain-following source term is

(7.15) $$\begin{eqnarray}S_{\mathit{terrain}\text{-}\mathit{following}}=\left(g\sin \unicode[STIX]{x1D701}-\frac{\bar{u}}{|\bar{u}|}\unicode[STIX]{x1D707}(g\cos \unicode[STIX]{x1D701}+\unicode[STIX]{x1D712}\unicode[STIX]{x1D705}\bar{u}^{2})\right).\end{eqnarray}$$

It is important to recognise that the transformation (7.10a,b ) does not change the model, i.e. it is still the terrain-following theory of Savage & Hutter (Reference Savage and Hutter1991) and Gray et al. (Reference Gray, Wieland and Hutter1999). It is just expressed in a Cartesian coordinate system. For GIS applications, the same transformation will also work, except that now the topography height (3.1) must be given relative to Cartesian coordinates aligned with gravity, rather than the inclined coordinates used by the standard model. This idea is not new. Bouchut et al. (Reference Bouchut, Mangeney-Castelnau, Perthame and Vilotte2003) and Bouchut & Westdickenberg (Reference Bouchut and Westdickenberg2004) have investigated various general transformations of the Savage & Hutter (Reference Savage and Hutter1991) model, including into an arbitrary system of final coordinates. A simplified treatment is provided in § 3.1 and appendix A of Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007), but the new features of the transformed model are not really exploited fully, since the paper is focused on levee formation on an inclined plane, where the standard and terrain-following models are identical.

7.3 The steady-shock solution for the terrain-following model in Cartesian coordinates

The steady-shock problem of § 5 is now considered again to explicitly demonstrate that the transformation of variables (7.10a,b ) does not change the resultant predictions of the terrain-following model. In general, the unsteady jump conditions for the depth-averaged mass and momentum balances, (7.13) and (7.14), are

(7.16) $$\begin{eqnarray}\displaystyle & \displaystyle \left.\unicode[STIX]{x27E6}h\bar{u}-\unicode[STIX]{x1D6E5}_{b}hV_{n}\right.\unicode[STIX]{x27E7}=0, & \displaystyle\end{eqnarray}$$

(7.17) $$\begin{eqnarray}\displaystyle & \displaystyle \left.\unicode[STIX]{x27E6}h\bar{u}^{2}-\unicode[STIX]{x1D6E5}_{b}h\bar{u}V_{n}+{\textstyle \frac{1}{2}}gh^{2}\cos \unicode[STIX]{x1D701}\right.\unicode[STIX]{x27E7}=0, & \displaystyle\end{eqnarray}$$

where $V_{n}=\text{d}X/\text{d}T$ is the shock speed expressed in Cartesian variables. Since the curvilinear shock velocity $v_{n}=\unicode[STIX]{x1D6E5}_{b}V_{n}$ , it follows that the Cartesian curvilinear jump conditions (7.16) and (7.17) are precisely the same as the general unsteady curvilinear jump conditions. In particular, when the shock speed is equal to zero, these also reduce to the steady curvilinear jump conditions (5.1) and (5.2) used in the shock solution in § 5.

Assuming steady fully developed flow, the mass balance (7.13) can be integrated subject to the condition that $h=h_{0}$ and $\bar{u}=\bar{u}_{0}$ at the inflow to show that

(7.18) $$\begin{eqnarray}h\bar{u}=h_{0}\bar{u}_{0},\end{eqnarray}$$

which, by virtue of the steady mass jump condition, is valid everywhere. Similarly, assuming that the shape factor $\unicode[STIX]{x1D712}$ is equal to unity, the steady-state depth-averaged momentum balance (7.14) can be expanded using (7.18) and (3.5) to show that the ODE governing the flow thickness is

(7.19) $$\begin{eqnarray}\frac{1}{\unicode[STIX]{x1D6E5}_{b}}\frac{\text{d}h}{\text{d}X}=\displaystyle \frac{h^{3}g\cos \unicode[STIX]{x1D701}(\tan \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707})-h\unicode[STIX]{x1D707}\unicode[STIX]{x1D705}(h_{0}\bar{u}_{0})^{2}-\frac{1}{2}gh^{4}\unicode[STIX]{x1D705}\sin \unicode[STIX]{x1D701}}{h^{3}g\cos \unicode[STIX]{x1D701}-(h_{0}\bar{u}_{0})^{2}}.\end{eqnarray}$$

Since

(7.20) $$\begin{eqnarray}\frac{\text{d}h}{\text{d}x}=\frac{1}{\unicode[STIX]{x1D6E5}_{b}}\frac{\text{d}h}{\text{d}X},\end{eqnarray}$$

equation (7.19) is precisely the same as the curvilinear formulation of the ODE (3.17) except that it is expressed in Cartesian coordinates. It follows that both the jump conditions and the ODE are exactly equivalent and, hence, that the terrain-following model gives the same results in both the Cartesian and the curvilinear formulations.

To confirm this, the steady-state shock solution has been computed independently, using the terrain-following model in Cartesian coordinates. In figure 17 the shock position as a function of inclination angle, computed using Cartesian coordinates, is shown by the green dashed line. It lies precisely on top of the red solid line, which shows the solution of the terrain-following model computed in curvilinear coordinates. The results of the terrain-following model are, as one would expect, therefore completely independent of the coordinate system that the equations are solved in.

Using the terrain-following model in Cartesian coordinates does, however, have the advantage that if the topography is defined in Cartesian coordinates, it does not have to be converted into curvilinear variables before the model can be used. Moreover, the results no longer have to be mapped back from curvilinear coordinates in order to plot them. It should be noted, however, that both the thickness and the velocity are the curvilinear ones, which are implicitly assumed to lie normal and tangential to the local topography. As a result, in order to reconstruct the free-surface position it is still important to project the thickness using the equations

(7.21) $$\begin{eqnarray}\displaystyle & \displaystyle X_{surface}=X-h\sin (\unicode[STIX]{x1D703}-\unicode[STIX]{x1D701}(X)), & \displaystyle\end{eqnarray}$$

(7.22) $$\begin{eqnarray}\displaystyle & \displaystyle Z_{surface}=b(X)+h\cos (\unicode[STIX]{x1D703}-\unicode[STIX]{x1D701}(X)). & \displaystyle\end{eqnarray}$$

These are in fact the same formulae as (4.3) and (4.4), which were used in § 4 to project the free surface at the take-off point back into Cartesian coordinates. It is therefore possible to have the improved accuracy of the terrain-following model, (7.13)–(7.15), while still using a simple Cartesian coordinate system.