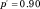Peer review “makes the publishing world go around” (Djupe Reference Djupe2015, 350), improves the quality of manuscripts that proceed through the process (Goodman et al. Reference Goodman, Berlin, Fletcher and Fletcher1994), and identifies the most impactful contributions to science (Li and Agha Reference Li and Agha2015). However, peer review also frequently misses major errors in submitted papers (Nylenna, Riis, and Karlsson Reference Nylenna, Riis and Karlsson1994; Schroter et al. Reference Schroter, Black, Evans, Carpenter, Godlee and Smith2004; Reference Schroter, Black, Evans, Godlee, Osorio and Smith2008), allows chance to strongly influence whether a paper will be published (Baxt et al. Reference Baxt, Waeckerle, Berlin and Callaham1998; Cole, Cole, and Simon Reference Cole, Cole and Simon1981; Mayo et al. Reference Mayo, Brophy, Goldberg, Klein, Miller, Platt and Ritchie2006), and is subject to confirmatory biases by peer reviewers (Mahoney Reference Mahoney1977). Given the mixed blessings of peer review and researchers’ equally mixed feelings about it (Mulligan, Hall, and Raphael Reference Mulligan, Hall and Raphael2013; Smith Reference Smith2006; Sweitzer and Cullen 1994; Weber et al. Reference Weber, Katz, Waeckerle and Callaham2002), it is natural to inquire whether the structure of the process influences its outcomes. Journal editors using peer review can determine the number of reviews they solicit, which reviewers they choose, how they convert reviews into decisions, and many other aspects of the process. Do these choices matter and, if so, how?
The question is of interest to political scientists because there is considerable variance in how journals in our discipline implement peer review. Most obviously, some journals accept a greater proportion of submissions than others. However, a difference in acceptance rates can obscure subtler differences in journal peer review practices. For example, International Studies Quarterly (ISQ) conducts a relatively thorough editorial review of papers on a substantive and scientific basis, desk-rejecting any papers found wanting, before soliciting anonymous peer reviewers (Nexon Reference Nexon2014a; Reference Nexon2014b). Consequently, ISQ desk-rejects a high proportion of papers received: 46.2% of submissions in 2014 (Nexon 2014c). Other journals desk-reject far fewer papers; for example, the American Journal of Political Science (AJPS) desk-rejected only 20.7% of its submissions in 2014 (Jacoby et al. Reference Jacoby, Lupton, Armaly and Carabellese2015). Thus, although the AJPS overall 9.6% acceptance rate is comparable to the ISQ 8.9% rate, the manner in which these rates are achieved is quite different—with potentially substantial implications for which papers are published.
Desk-rejection practices comprise only one of the many “degrees of freedom” available to an editor; for example, editors almost certainly do not identically convert the anonymous reviews they solicit into a final decision. Unfortunately, these procedures are rarely documented (and are probably not totally formulaic). It would be helpful for editors and authors in political science to know which practices—if any—improve a journal’s quality. For the purposes of my analysis, I define the “quality” of a single publication as an average reader’s holistic ranking relative to the distribution of other papers (and the quality of a journal as the average quality of the papers it publishes).
In my study, I computationally simulate several idealized archetypes of the peer review process to investigate how they influence the character of papers accepted by a journal. The goal is not to precisely mirror the editorial process of any extant journals but rather to explore the implications of pure forms of the systems an editor might choose to use. Simulation already has proven to be a valuable method of studying the peer review process. For example, a previous simulation study revealed that subjectivity in the review process is a helpful antidote to premature scientific convergence on a false conclusion via “herding” behavior (Park, Peacey, and Munafo Reference Park, Peacey and Munafo2014). Simulation also allows me to expand on analytical studies that use considerably simplified models of peer review (Somerville Reference Somerville2016), tempering earlier conclusions and drawing new ones.
In my simulations, I find that the preference heterogeneity of a journal’s readership (and reviewer pool) is the most important influence on the character of its published work, regardless of the structure of the peer review system. When reviewers and readers have heterogeneous ideas about scientific importance and quality (as expected for general-interest journals including American Political Science Review [APSR], Perspectives on Politics, and AJPS), a majority of papers accepted via peer review will be evaluated by an average reader as not meeting the standards of the journal under any of the review systems that I study. Relatedly, all of these systems allow luck to exert a strong influence on which papers are published. Although a paper’s merit is associated with receiving sufficiently favorable reviews for publication, reviewer heterogeneity creates a “luck of the draw” that no system I studied can counteract effectively. Previous empirical studies showed low levels of agreement among reviewers in their evaluations of a paper (Bornmann, Mutz, and Daniel Reference Bornmann, Mutz and Daniel2010; Goodman et al. Reference Goodman, Berlin, Fletcher and Fletcher1994; Mahoney Reference Mahoney1977; Mayo et al. Reference Mayo, Brophy, Goldberg, Klein, Miller, Platt and Ritchie2006; Nylenna, Riis, and Karlsson Reference Nylenna, Riis and Karlsson1994; Schroter et al. Reference Schroter, Black, Evans, Godlee, Osorio and Smith2008). This fact may explain why empirical studies (Cole, Cole, and Simon Reference Cole, Cole and Simon1981) and the reports of editors themselves (Smith Reference Smith2006) have often observed that peer review decisions are subject to the whims of chance. The upshot is that readers and authors in political science may want to rethink how specialized and general-interest journals compare as outlets for high-quality research and how these journals rank in the prestige hierarchy of publications (Garand and Giles Reference Garand and Giles2003; Giles and Garand Reference Giles and Garand2007). I explore some possible implications in this article’s conclusion.
Although a paper’s merit is associated with receiving sufficiently favorable reviews for publication, reviewer heterogeneity creates a “luck of the draw” that no system I studied can counteract effectively.
Although the influences of the peer review process are dominated by the effect of reviewer heterogeneity, two important lessons for editors and reviewers about its structure emerge from the simulations. First, systems with active editorial control over decision making tend to result in more consistently high-quality publications compared to systems that rely primarily on reviewer voting. For example, using the reviewers’ written commentary (which presumably contains a direct assessment of the paper’s quality) to inform an editor’s unilateral decision results in fewer low-quality publications compared to reviewer approval voting; desk rejection by editors prior to review also has a salutary effect. Concordantly, the simulations indicate that reviewers should focus on maximizing the informational content of their written review rather than on voting, which is consistent with the advice of Miller et al. (Reference Miller, Pevehouse, Rogowski, Tingley and Wilson2013). Second, when asked to submit up or down votes, reviewers and editors must apply a comparatively lenient standard for choosing to approve papers in order to avoid undershooting a rigorous acceptance target. If reviewers recommend acceptance Footnote 1 at a rate matching the journal’s overall acceptance target, as encouraged by some editors (Coronel and Opthof Reference Coronel and Opthof1999), then far too few papers will be accepted because the reviewers too often disagree. The structure of the peer review process can reduce the severity of this problem, but it is ultimately a product of reviewer heterogeneity.
THEORETICAL ASSUMPTIONS
I begin by describing the framework of assumptions about the review process on which I base my analysis. I assume that there exists a population of potentially publishable papers, some of which will be submitted to a journal; I also assume that submitted papers are representative of the overall population.
Footnote 2
The journal’s editor seeks to publish papers that are in the top
![]() ${p^ \star }$
percentile of papers in the population in terms of quality. When editors receive a paper, I assume that they solicit three blind reviews; I later relax this assumption to allow editors to desk-reject papers before review. I further assume that editors assign papers to reviewers at random, conditional on expertise, and that any refusals to review are unrelated to paper quality. This assumption rules out the possibility that editors selectively choose reviewers in anticipation of the review that they believe they will receive or that reviewers self-select out of bad (or good) reviews.
Footnote 3
${p^ \star }$
percentile of papers in the population in terms of quality. When editors receive a paper, I assume that they solicit three blind reviews; I later relax this assumption to allow editors to desk-reject papers before review. I further assume that editors assign papers to reviewers at random, conditional on expertise, and that any refusals to review are unrelated to paper quality. This assumption rules out the possibility that editors selectively choose reviewers in anticipation of the review that they believe they will receive or that reviewers self-select out of bad (or good) reviews.
Footnote 3
Each reviewer
![]() $i \in \{ 1,2,3\}$
and the editor i = 4 forms an opinion about paper j’s overall quality,
$i \in \{ 1,2,3\}$
and the editor i = 4 forms an opinion about paper j’s overall quality,
![]() ${p_{ij}} \in [0,1]$
, where p
ij
corresponds to the proportional rank of the paper’s holistic quality relative to the population of papers. For example,
${p_{ij}} \in [0,1]$
, where p
ij
corresponds to the proportional rank of the paper’s holistic quality relative to the population of papers. For example,
![]() ${p_{ij}} = 0.8$
means that reviewer i believes that paper j is better than 80% of the other papers in the population. If papers are randomly assigned to reviewers (conditional on expertise), then approximately p proportion of the papers assigned to a reviewer will have quality less than or equal to p for every value of
${p_{ij}} = 0.8$
means that reviewer i believes that paper j is better than 80% of the other papers in the population. If papers are randomly assigned to reviewers (conditional on expertise), then approximately p proportion of the papers assigned to a reviewer will have quality less than or equal to p for every value of
![]() $p \in [0,1]$
. As a result, every reviewer’s marginal distribution of reviews
$p \in [0,1]$
. As a result, every reviewer’s marginal distribution of reviews
![]() ${f_i}(p)$
should be uniform. Reviewers have partially dissimilar preferences, limited time to review a paper, and the possibility of making errors; they also cannot influence one another’s opinion before forming their judgment. For all of these reasons, I assume that reviewers’ judgments of a paper are imperfectly associated with one another, which is consistent with the findings of a long empirical literature (Bornmann, Mutz, and Daniel Reference Bornmann, Mutz and Daniel2010; Goodman et al. Reference Goodman, Berlin, Fletcher and Fletcher1994; Mahoney Reference Mahoney1977; Mayo et al. Reference Mayo, Brophy, Goldberg, Klein, Miller, Platt and Ritchie2006; Nylenna, Riis, and Karlsson Reference Nylenna, Riis and Karlsson1994; Schroter et al. Reference Schroter, Black, Evans, Godlee, Osorio and Smith2008). Functionally, I presume that the three reviewers’ opinions and the editor’s are drawn from a normal copula with correlation
${f_i}(p)$
should be uniform. Reviewers have partially dissimilar preferences, limited time to review a paper, and the possibility of making errors; they also cannot influence one another’s opinion before forming their judgment. For all of these reasons, I assume that reviewers’ judgments of a paper are imperfectly associated with one another, which is consistent with the findings of a long empirical literature (Bornmann, Mutz, and Daniel Reference Bornmann, Mutz and Daniel2010; Goodman et al. Reference Goodman, Berlin, Fletcher and Fletcher1994; Mahoney Reference Mahoney1977; Mayo et al. Reference Mayo, Brophy, Goldberg, Klein, Miller, Platt and Ritchie2006; Nylenna, Riis, and Karlsson Reference Nylenna, Riis and Karlsson1994; Schroter et al. Reference Schroter, Black, Evans, Godlee, Osorio and Smith2008). Functionally, I presume that the three reviewers’ opinions and the editor’s are drawn from a normal copula with correlation
![]() $\rho \in [0,1]$
. I intend that higher values of
$\rho \in [0,1]$
. I intend that higher values of
![]() $\rho$
model the behavior of reviewers for journals with narrower topical and methodological coverage (e.g., Legislative Studies Quarterly and Political Analysis), whereas lower values of
$\rho$
model the behavior of reviewers for journals with narrower topical and methodological coverage (e.g., Legislative Studies Quarterly and Political Analysis), whereas lower values of
![]() $\rho$
model the behavior of reviewers for general-interest journals (e.g., American Political Science Review [APSR]). In practice, editors could exert some control over
$\rho$
model the behavior of reviewers for general-interest journals (e.g., American Political Science Review [APSR]). In practice, editors could exert some control over
![]() $\rho$
by choosing more or less like-minded reviewers, but (consistent with previous assumptions)
$\rho$
by choosing more or less like-minded reviewers, but (consistent with previous assumptions)
![]() $\rho$
is fixed and not chosen by the editor in this model.
$\rho$
is fixed and not chosen by the editor in this model.
Each reviewer i submits a vote about paper j to the editor,
![]() ${v_{ij}} \in \{ A,R\}$
, based on paper j’s quality. I assume that reviewers recommend the best papers to the editors for publication; thus, the reviewers compare
${v_{ij}} \in \{ A,R\}$
, based on paper j’s quality. I assume that reviewers recommend the best papers to the editors for publication; thus, the reviewers compare
![]() ${p_{ij}}$
to an internal threshold for quality
${p_{ij}}$
to an internal threshold for quality
![]() ${p^'}$
and submit a vote of A if
${p^'}$
and submit a vote of A if
![]() ${p_{ij}} \ge {p^'}$
and a vote of R otherwise. Given the uniform distribution of quality, this implies that the probability that a reviewer returns a positive review (of
${p_{ij}} \ge {p^'}$
and a vote of R otherwise. Given the uniform distribution of quality, this implies that the probability that a reviewer returns a positive review (of
![]() ${v_{ij}} = A$
) is equal to
${v_{ij}} = A$
) is equal to
![]() $(1 - {p^'})$
. One particularly interesting threshold to investigate is
$(1 - {p^'})$
. One particularly interesting threshold to investigate is
![]() ${p^'} = {p^ \star }$
, where the reviewers set their probability of recommending that a paper be accepted equal to the journal’s target acceptance rate.
Footnote 4
Reviewers also submit a qualitative written report to the editor that contains
${p^'} = {p^ \star }$
, where the reviewers set their probability of recommending that a paper be accepted equal to the journal’s target acceptance rate.
Footnote 4
Reviewers also submit a qualitative written report to the editor that contains
![]() ${p_{ij}}$
, which allows a more finely grained evaluation of papers.
Footnote 5
${p_{ij}}$
, which allows a more finely grained evaluation of papers.
Footnote 5
I assume that reviewers sincerely report their
![]() ${v_{ij}}$
to editors. Editors then use their own opinion about paper j’s quality (
${v_{ij}}$
to editors. Editors then use their own opinion about paper j’s quality (
![]() ${p_{4j}}$
), their holistic judgment about the paper (
${p_{4j}}$
), their holistic judgment about the paper (
![]() ${v_{4j}} = A$
if
${v_{4j}} = A$
if
![]() ${p_{4j}} \ge {p^'}$
, and = R otherwise), the reviewers’ qualitative reports (
${p_{4j}} \ge {p^'}$
, and = R otherwise), the reviewers’ qualitative reports (
![]() ${p_{ij}}$
), and the reviewers’ votes to decide whether to accept or reject the paper. I consider four possible editorial regimes for converting reviews into decisions, as follows:
${p_{ij}}$
), and the reviewers’ votes to decide whether to accept or reject the paper. I consider four possible editorial regimes for converting reviews into decisions, as follows:
-
• unanimity approval voting by the reviewers, excluding the editor
-
• simple majority voting by the reviewers, excluding the editor
-
• majority voting with the editor’s vote included (i.e., to be accepted, a paper must achieve support from all three reviewers or two reviewers and the editor)
-
• unilateral editor decision making based on the average report
 ${\bar p_j} = {1 \over 4}\mathop \sum \limits_{i = 1}^4 {p_{ij}}$
, with the paper accepted if
${\bar p_j} = {1 \over 4}\mathop \sum \limits_{i = 1}^4 {p_{ij}}$
, with the paper accepted if
 ${\bar p_j} \ge {p^'}$
and reviewers’ votes ignored
${\bar p_j} \ge {p^'}$
and reviewers’ votes ignored
The final regime acknowledges that editors try to follow the advice of the reviewers whose participation they solicit but may choose not to follow the reviewers’ up or down recommendation. This regime is analogous to a system under which an editor reads reviewers’ written reports to collect information about the paper’s quality that will influence his/her decision but either does not request or simply ignores the reviewers’ actual vote to accept or reject.
The model I propose is substantially more complex than another model recently proposed by Somerville (Reference Somerville2016). In Somerville’s model, the quality of a journal article is binary—good (G) or bad (B)—and the review process is abstracted into a single probability of accepting an article based on its quality (
![]() $\Pr (A|G)$
and
$\Pr (A|G)$
and
![]() $\Pr (A|B)$
). The goal of Somerville’s study was to use Bayes’s rule to calculate the probability of an article being good conditional on its being accepted (
$\Pr (A|B)$
). The goal of Somerville’s study was to use Bayes’s rule to calculate the probability of an article being good conditional on its being accepted (
![]() $\Pr (G|A)$
). By comparison, my model explicitly includes multiple reviewers with competing (but correlated) opinions of continuous paper quality, editors with decision-making authority, and institutional rules that can be systematically changed and studied. I compare our results in the summary of my findings below.
$\Pr (G|A)$
). By comparison, my model explicitly includes multiple reviewers with competing (but correlated) opinions of continuous paper quality, editors with decision-making authority, and institutional rules that can be systematically changed and studied. I compare our results in the summary of my findings below.
ACCEPTANCE TARGETS AND REVIEWER STANDARDS
I begin by investigating the simple relationship between each editorial system (i.e., unanimity approval voting, majority approval voting, majority approval voting with editor participation, and unilateral editor decision making based on reviewer reports) and the journal’s final acceptance rate. For every value of the degree of correlation in reviewer reports
![]() $\rho \in [0.02,0.98]$
in increments of 0.02, I simulate 2,000 papers from the population distribution and three reviews for each paper, as well as the editor’s personal opinion (for a total of four reviews). I then apply the specified decision rule for acceptance to each paper and determine the acceptance rate. I plot the overall journal acceptance rate as a function of
$\rho \in [0.02,0.98]$
in increments of 0.02, I simulate 2,000 papers from the population distribution and three reviews for each paper, as well as the editor’s personal opinion (for a total of four reviews). I then apply the specified decision rule for acceptance to each paper and determine the acceptance rate. I plot the overall journal acceptance rate as a function of
![]() $\rho$
and examine the relationship for
$\rho$
and examine the relationship for
![]() ${p^'} = 0.90$
, a reviewer/editor acceptance rate of 10%. All simulations are conducted using R 3.2.5 (R Core Team 2015) with the copula package (Kojadinovic and Yan Reference Kojadinovic and Yan2010).
${p^'} = 0.90$
, a reviewer/editor acceptance rate of 10%. All simulations are conducted using R 3.2.5 (R Core Team 2015) with the copula package (Kojadinovic and Yan Reference Kojadinovic and Yan2010).
The simulation results are shown in figure 1. As the figure indicates, the probability of a manuscript being accepted is always considerably less than any individual reviewer’s probability of submitting a positive review unless
![]() $\rho \approx 1$
. The systems vary in the disparity between the individual acceptance threshold
$\rho \approx 1$
. The systems vary in the disparity between the individual acceptance threshold
![]() ${p^'}$
and the journal’s overall acceptance rate, but all of them undershoot the target. For a journal to accept 10% of its submissions, reviewers and editors must recommend papers that they perceive to be considerably below the top 10%.
${p^'}$
and the journal’s overall acceptance rate, but all of them undershoot the target. For a journal to accept 10% of its submissions, reviewers and editors must recommend papers that they perceive to be considerably below the top 10%.

Figure 1 Simulated Outcomes of Peer Review under Various Peer Review Systems
Notes: Points indicate the proportion of 2,000 simulated manuscripts under the peer review system indicated; lines are predictions from a local linear regression of the data using loess in R. Reviewer acceptance thresholds
![]() ${p^'} = 0.90$
(i.e., a reviewer recommends the top 10% of papers for acceptance) for all systems.
${p^'} = 0.90$
(i.e., a reviewer recommends the top 10% of papers for acceptance) for all systems.
THE EFFECT OF THE PEER REVIEW SYSTEM ON THE QUALITY OF THE PUBLISHED LITERATURE
Will peer review accept the papers that the discipline views as the best despite heterogeneity in reviewer opinions? To what extent will quality and chance determine the outcomes of peer review? To answer these questions, I conduct another simulation similar to the previous one but with a much larger population of 50,000 papers and 500 readers. I assume that readers’ opinions are correlated at
![]() $\rho = 0.5$
, consistent with a flagship journal; this is a greater degree of reviewer correlation than empirical studies typically find (Bornmann, Mutz, and Daniel Reference Bornmann, Mutz and Daniel2010). The first three simulated readers are selected as reviewers and the fourth as the editor; their opinions serve as the basis for editorial decisions in each of the four systems examined. I choose an acceptance threshold
$\rho = 0.5$
, consistent with a flagship journal; this is a greater degree of reviewer correlation than empirical studies typically find (Bornmann, Mutz, and Daniel Reference Bornmann, Mutz and Daniel2010). The first three simulated readers are selected as reviewers and the fourth as the editor; their opinions serve as the basis for editorial decisions in each of the four systems examined. I choose an acceptance threshold
![]() ${p^'}$
based on initial simulations to produce an overall journal acceptance rate of
${p^'}$
based on initial simulations to produce an overall journal acceptance rate of
![]() $\approx 10\%$
.
Footnote 6
I then compute the average reader value of
$\approx 10\%$
.
Footnote 6
I then compute the average reader value of
![]() $p$
for all 500 readers for the papers that are accepted for publication according to the system and plot the distribution of these average values for all 50,000 papers.
$p$
for all 500 readers for the papers that are accepted for publication according to the system and plot the distribution of these average values for all 50,000 papers.
An average reader believes that such a paper is worse than 35% of other papers in the population of papers, many of which are not published by the journal.
I ran this simulation twice: once for every review system as previously described and again under a system in which the editor desk-rejects a certain proportion of papers before submitting them for review. I simulate the process of desk rejection by having the editor refuse to publish any paper for which
![]() ${p_{4j}} < 0.5$
; that is, the editor desk-rejects any paper that he or she believes is worse than the median paper in the population. Figure 2 presents kernel density estimates for the results with and without desk rejection.
${p_{4j}} < 0.5$
; that is, the editor desk-rejects any paper that he or she believes is worse than the median paper in the population. Figure 2 presents kernel density estimates for the results with and without desk rejection.

Figure 2 Discipline-Wide Evaluation of Papers Published under Various Peer Review Systems, Reader and Reviewer Opinion Correlation ρ = 0.5
Notes: Plots indicate kernel density estimates (using density in R) of 500 simulated readers’ average evaluation (p) for the subset of 50,000 simulated papers that were accepted under the peer review system indicated in the legend. Reviewer acceptance thresholds
![]() ${p^'}$
were chosen to set acceptance rates
${p^'}$
were chosen to set acceptance rates
![]() $\approx 10\%$
. The acceptance rate without desk rejection was 10.58% for the unilateral-editor system, 10.01% under unanimity voting, 10.05% under majority rule including the editor, and 11.1% under majority rule excluding the editor. The acceptance rate with desk rejection was 9.64% for the unilateral-editor system, 9.96% under unanimity voting, 12.5% under majority rule including the editor, and 10.5% under majority rule excluding the editor.
$\approx 10\%$
. The acceptance rate without desk rejection was 10.58% for the unilateral-editor system, 10.01% under unanimity voting, 10.05% under majority rule including the editor, and 11.1% under majority rule excluding the editor. The acceptance rate with desk rejection was 9.64% for the unilateral-editor system, 9.96% under unanimity voting, 12.5% under majority rule including the editor, and 10.5% under majority rule excluding the editor.
Figure 2 indicates that all of the systems produce distributions of published papers that are centered on a mean reader evaluation near 0.8. In every peer review system, a majority of papers are perceived by readers as not being in the top 10% of quality despite the journal’s acceptance rate of 10%. Furthermore, a substantial proportion of the published papers have surprisingly low mean reader evaluations under every system. For example, 11.7% of papers published under the majority-voting system without desk rejection have reader evaluations of less than 0.65. An average reader believes that such a paper is worse than 35% of other papers in the population of papers, many of which are not published by the journal. This result is surprisingly consistent with what political scientists actually report about the APSR, a highly selective journal with a heterogeneous readership: although it is the best-known journal among political scientists by a considerable margin, it is ranked only 17th in quality (Garand and Giles Reference Garand and Giles2003). This result also complements the earlier findings of Somerville (2016, 35), who concluded that “if the rate of accepting bad papers is 10%, then a journal that has space for 10% of submissions may not gain much additional quality from the review process.” The peer review systems that I study all improve on the baseline expectation of quality without review (i.e., a mean evaluation near 0.5), but they do not serve as a perfect filter.
There are meaningful differences among the reviewing systems: only 5.6% of papers published under the unilateral editor decision system without desk rejection have reader evaluations of less than 0.65. If editors desk-reject 50% of papers under this system, then the proportion decreases to 1.4%; this is the best-performing system in the simulation on this criterion. Footnote 7 These better-performing systems are analogous to those in which reviewers provide a qualitative written evaluation of the paper’s quality to the editor but no up or down vote to accept the paper (or when that vote is ignored by the editor).
It is important that the simulated peer review systems tend to accept papers that are better (on average) than the rejected papers, which is consistent with the empirical evidence of Lee et al. (Reference Lee, Schotland, Bacchetti and Bero2002) that journal selectivity is associated with higher average methodological quality of publications. However, luck still plays a strong role in determining which papers are published under any system. Both of these findings are shown in figure 3, which plots an average reader’s evaluation of a simulated paper against its loess-predicted probability of acceptance. In all systems, the highest-quality papers are the most likely to be published; however, a paper that an average reader evaluates as near the 80th percentile of quality (or 85th percentile when desk rejection is used) has a chance of being accepted similar to a coin flip.

Figure 3 The Role of Chance in Publication under Various Peer Review Systems, Reader and Reviewer Opinion Correlation ρ = 0.5
Notes: Plots indicate zeroth-degree local regression estimates (using loess in R) of the empirical probability of acceptance for 50,000 simulated papers under the peer review system indicated in the legend as a function of 500 simulated readers’ average evaluation (
![]() $p$
). Reviewer acceptance thresholds
$p$
). Reviewer acceptance thresholds
![]() ${p^'}$
were chosen to set acceptance rates
${p^'}$
were chosen to set acceptance rates
![]() $\approx 10\%$
. The acceptance rate without desk rejection was 10.58% for the unilateral-editor system, 10.01% under unanimity voting, 10.05% under majority rule including the editor, and 11.1% under majority rule excluding the editor. The acceptance rate with desk rejection was 9.64% for the unilateral-editor system, 9.96% under unanimity voting, 12.5% under majority rule including the editor, and 10.5% under majority rule excluding the editor.
$\approx 10\%$
. The acceptance rate without desk rejection was 10.58% for the unilateral-editor system, 10.01% under unanimity voting, 10.05% under majority rule including the editor, and 11.1% under majority rule excluding the editor. The acceptance rate with desk rejection was 9.64% for the unilateral-editor system, 9.96% under unanimity voting, 12.5% under majority rule including the editor, and 10.5% under majority rule excluding the editor.
THE STRUCTURE OF PREFERENCES AND ITS EFFECT ON PEER-REVIEWED PUBLICATION QUALITY
The structure of preferences in the underlying population of a journal’s readership (and reviewer pool) is powerfully associated with how the quality of publications that survive the peer review system is perceived in the simulations. This structure incorporates the overall degree to which opinion is correlated in the population of a journal’s readers and reviewers; however, it also includes the degree to which scientists in a discipline are organized into subfields within which opinions about scientific importance and merit are comparatively more homogeneous. I find that journals with a more homogeneous readership—or with disparate but internally homogeneous subfields—tend to publish more consistently high-quality papers (as defined by the judgment of its readers) than journals with a heterogeneous readership.
I find that journals with a more homogeneous readership—or with disparate but internally homogeneous subfields—tend to publish more consistently high-quality papers (as defined by the judgment of its readers) than journals with a heterogeneous readership.
To demonstrate this point, I repeat the simulation of 50,000 papers (using unilateral editor decision making) under three conditions: (1) reader and reviewer opinions correlated at 0.5 to represent a flagship journal in a heterogeneous field (e.g., APSR); (2) reader and reviewer opinions correlated at 0.75 to represent a journal in a more homogeneous field (e.g., Political Analysis) Footnote 8 ; and (3) readers and reviewers organized into two equally sized subfields of 250 people each, within which opinions correlated at 0.9 but between which opinions correlated at 0.1 (for an average correlation of 0.5). Footnote 9 When subfields exist, reviewers are chosen so that two reviewers are from one subfield and the final reviewer and editor are from the other. These subfields may represent different topical specialties or different methodological approaches within a discipline, such as qualitative area specialists and quantitative large-N comparativists who both read a comparative politics journal.
As the results in figure 4 demonstrate, the organization of scientists by subfield has a dramatic impact on the perceived quality of publications in the journal. Specifically, the simulation with two highly correlated but disparate subfields produces few papers with an overall quality of less than 0.8; the average quality is 0.85 (without desk rejection) or 0.90 (with desk rejection). By comparison, the subfield-free simulation with low correlation (0.5) indicates that many more low-quality papers are published under this condition. The subfield-free simulation with high correlation (0.75) produced papers with high average quality (0.88 without desk rejection, 0.92 with desk rejection) but still allows a substantial number of lower-quality papers to be published.

Figure 4 Average Discipline-Wide Evaluation of Papers Published under a Unilateral-Editor Approval System Informed by Submitted Reviewer Reports with Varying Structure of Opinion
Notes: Plots indicate kernel density estimates (using density in R) of 500 simulated readers’ average evaluation (
![]() $p$
) for the subset of 50,000 simulated papers that were accepted under the unilateral-editor review system for the structure of reader and reviewer opinion correlation indicated in the legend. Reviewer acceptance thresholds
$p$
) for the subset of 50,000 simulated papers that were accepted under the unilateral-editor review system for the structure of reader and reviewer opinion correlation indicated in the legend. Reviewer acceptance thresholds
![]() ${p^'}$
were chosen to set acceptance rates
${p^'}$
were chosen to set acceptance rates
![]() $\approx 10\%$
. The acceptance rate for all readers correlated at 0.5 was 10.58% without desk rejection and 9.65% with desk rejection. The acceptance rate for all readers correlated at 0.75 was 10.50% without desk rejection and 10.23% with desk rejection. The acceptance rate for the two-subfield discipline was 10.16% without desk rejection and 9.46% with desk rejection.
$\approx 10\%$
. The acceptance rate for all readers correlated at 0.5 was 10.58% without desk rejection and 9.65% with desk rejection. The acceptance rate for all readers correlated at 0.75 was 10.50% without desk rejection and 10.23% with desk rejection. The acceptance rate for the two-subfield discipline was 10.16% without desk rejection and 9.46% with desk rejection.
CONCLUSION
This simulation study indicates that heterogeneity of reviewer opinion is a key influence on journal outcomes. When readers and reviewers have heterogeneous standards for scientific importance and quality—as might be expected for a general-interest journal serving an entire discipline such as the APSR or AJPS—chance will strongly determine publication outcomes. Even highly selective general-interest journals will not necessarily publish the work that its readership perceives to be the best in the field. However, a system with greater editorial involvement and discretion will publish papers that are better regarded and more consistent compared to other peer review systems. In particular, I find that a system in which editors accept papers based on the quality reports of reviewers—but not their up or down judgment to accept the paper—after an initial round of desk rejection tends to produce fewer low-quality published papers compared to other systems I examined. This finding suggests that reviewers should focus on providing informative, high-quality reports to editors that they can use to make a judgment about final publication; they should not focus on their vote to accept or reject the paper. When a journal does solicit up or down recommendations, a reviewer should recommend revise and resubmit or acceptance for a substantially greater proportion of papers than the journal’s overall acceptance target to enable the journal to actually meet that target.
The strong relationship between reader/reviewer heterogeneity and journal quality suggests that political scientists may want to reconsider their attitude about the prestige and importance of general-interest journal publications relative to those in topically and/or methodologically specialized journals. As mentioned previously, the APSR was ranked 17th in quality by political scientists in a survey—yet those same survey respondents also ranked the APSR as the journal to which they would most prefer to submit a high-quality manuscript! Moreover, APSR was the only journal ranked in the top three most-preferred submission targets by all four subfields of political science studied (Garand and Giles Reference Garand and Giles2003).
The reason for this apparent contradiction is easy to explain:
The American Political Science Review, American Journal of Political Science, and Journal of Politics continue to rank among the top three journals in terms of their impact on the political science discipline, as measured to take into account both scholars’ evaluation of the quality of work reported in these journals and their familiarity with these journals. …Ultimately, publication in these journals represents a feather in one’s proverbial hat or, in this case, in one’s vitae. (Garand and Giles Reference Garand and Giles2003, 306–7)
There are immense rewards for publishing in any of these journals precisely because they are selective and are viewed by a huge and heterogeneous audience. Unfortunately, the simulation evidence presented in this article suggests that any career benefit is at odds with the proffered justification for that benefit:
Articles published in the most highly regarded journals presumably go through a rigorous process of peer review and a competition for scarce space that results in high rejection rates and a high likelihood of quality. Articles published in these journals pass a difficult test on the road to publication and are likely to be seen by broad audiences of interested readers. Other journals publish research findings that are of interest to political scientists, to be sure, but articles published in these journals either pass a less rigorous test or are targeted to narrower audiences. (Garand and Giles Reference Garand and Giles2003, 293)
It would be premature to radically reconsider our judgments about journal prestige (and the tenure and promotion decisions that are based on them) because of one simulation study. Perhaps one study is enough, however, to begin asking whether our judgments are truly consistent with our scholarly and scientific standards, particularly when evidence suggests that underrepresented groups in the discipline are systematically disadvantaged by how we think about the journal hierarchy (Breuning and Sanders Reference Breuning and Sanders2007).
ACKNOWLEDGMENT
I thank Cliff Morgan, Jane Lawrence Sumner, Rick Wilson, Samuel Esarey, Andrew Gelman, and Jeffrey Lax for helpful comments and suggestions on previous drafts. This article includes ideas first articulated (in a much simpler form) in “How Tough Should Reviewers Be?” in The Political Methodologist, available at http://thepoliticalmethodologist.com/2014/12/18/how-tough-should-reviewers-be. Replication files are available at http://dx.doi.org/10.7910/DVN/TT17NY.