Introduction

Two important properties of snow are surface grain-size and liquid-water fraction. The albedo of snow, which affects the energy balance, is a function of grain-size. The distribution of liquid water released from snow, which impacts the hydrology, is a function of the amount of melting. Measuring the distribution of grain-size and snowmelt from an Earth remote-sensing perspective would contribute to current and future Earth energy-balance and hydrological modeling and prediction. Previous snow-modeling and measurement work has shown that snow spectral reflectance is a strong function of grain-size and may be modeled from the optical properties of ice (Reference Bohren and BarkstromBohren and Barkstrom, 1974; Reference WiscombeWiscombe and Warren, 1980; Reference WarrenWarren 1982; Reference DozierDozier, 1989; Reference Nolin and J. DozierNolin and Dozier 1993; Reference Painter, Roberts, Green and DozierPainter and others, 1998; Reference Nolin and DozierNolin and Dozier 2000). The research presented here describes, evaluates and tests two new snow-reflectance models that account for both grain-size and liquid-water fraction.

Snow Models

The snow models developed here are based upon the inherent optical properties of pure ice and liquid water. These properties are reported in the form of the complex refractive index of ice and liquid water (Reference WarrenWarren, 1982; Reference Kou, Labrie and ChýlekKou and others, 1993) shown in Figure 1. For both ice and liquid water the real component of the refractive index varies slightly across the spectral range 400–2500nm. In contrast, the imaginary component varies by seven orders of magnitude and contains several local minima. Of interest for this research is the displacement of the minima at 1030 nm for ice to 980nm for liquid water. This displacement provides a basis for a difference in the spectrum of frozen vs melting snow that contains liquid water.

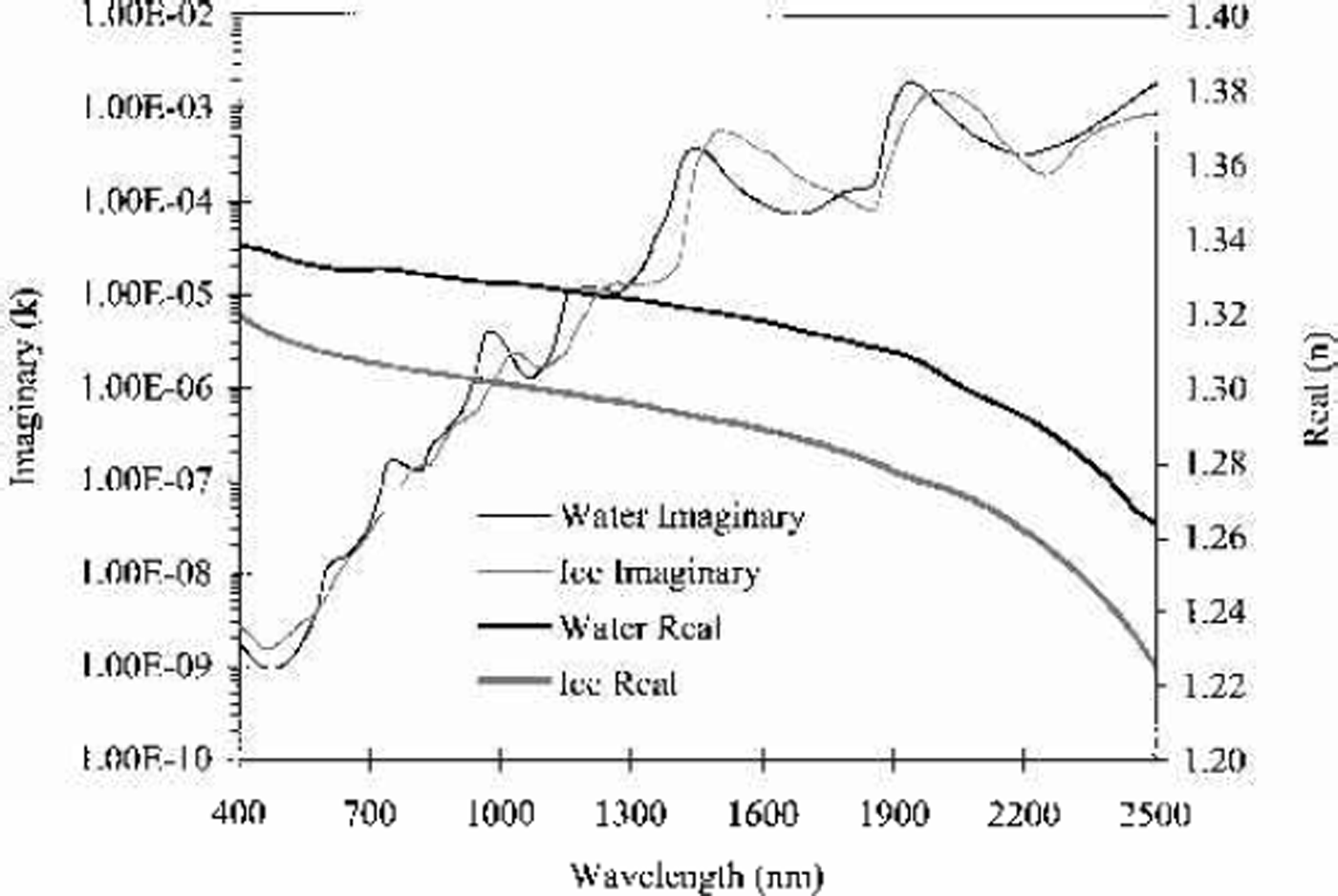
Fig. 1. Real and imaginary component of the refractive index of ice and liquid water.

To develop the snow models, the refractive indices were used to calculate the required extinction, scattering and asymmetry properties of snow grains modeled as spheres with Mie computations (Reference Wiscombe and WarrenWiscombe, 1980). The Mie-calculated optical properties were then used to constrain a discrete-ordinate radiative transfer code (DISORT) (Reference Stamnes, Tsay, Wiscombe and JayaweeraStamnes and others, 1988) and model the spectral reflectance of snow. Figure 2 shows the calculated spectral reflectance of frozen snow for grain-sizes of 100, 500 and 1000 mm. The modeled spectra show the expected high reflectance from 400 to 800 nm, the strongly grain-size-dependent reflectance from 800 to 1400 nm, and the comparatively low reflectance from 1400 to 2500nm. The local snow-reflectance minimum at 1030 nm is well expressed at all grain-sizes.

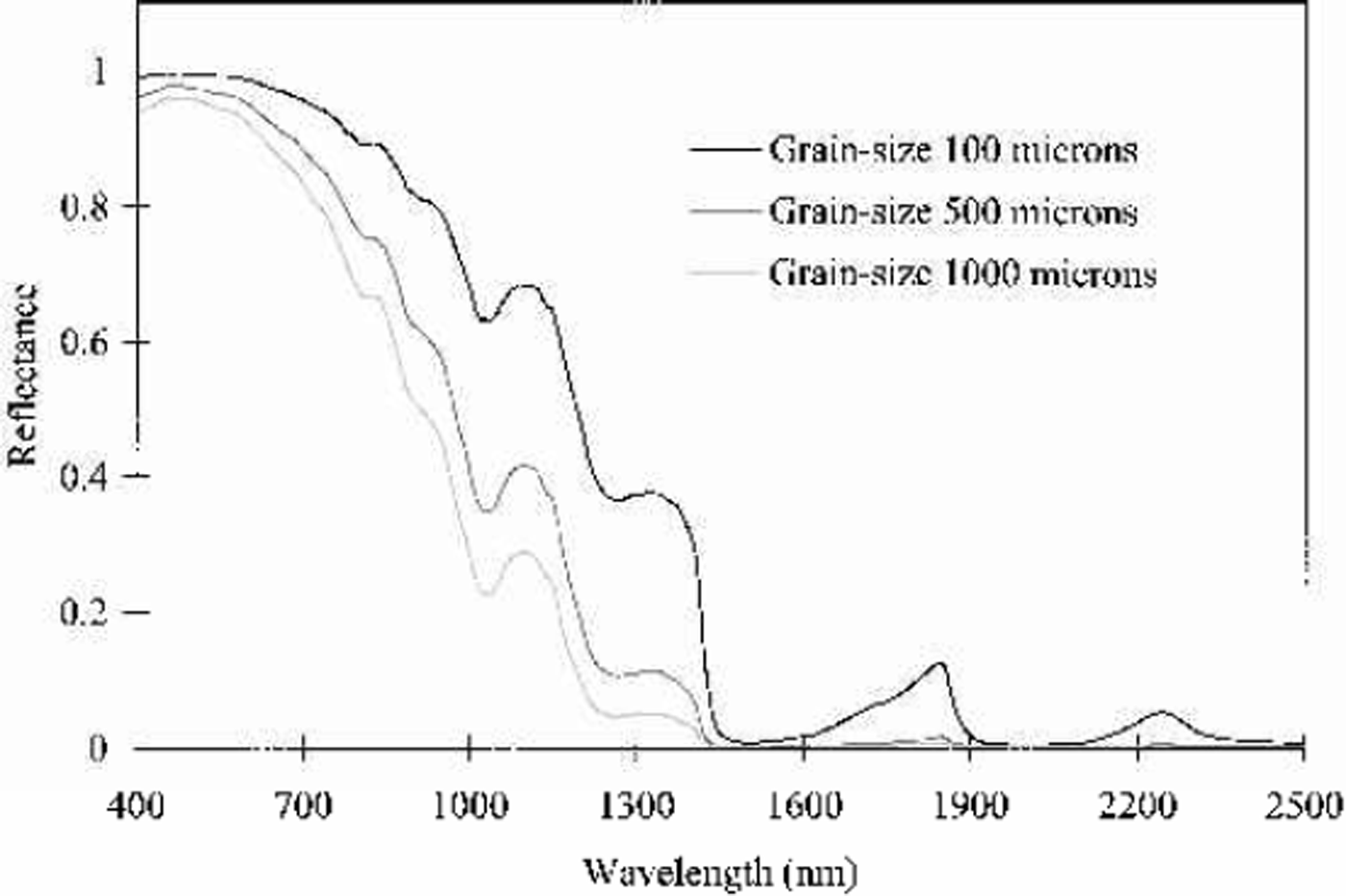
Fig. 2. Modeled frozen-snow reflectance for grain-sizes of 100, 500 and 1000 mm.

To include the effect of liquid water, two approaches were explored. The first approach models the effect of liquid water as interspersed ice and water spheres. This approximates the case where water is filling some portion of the interstitial spaces of the snow. Mie calculations were performed for ice grains and liquid-water spheres. These calculated parameters were combined in area-weighted averages (Reference Warren and WiscombeWarren and Wiscombe, 1980) to provide the extinction, scattering and asymmetry properties of the snow. DISORT was used to model the spectral reflectance of frozen and melting snow shown in Figure 3a. As the fraction of liquid water increases, the 1030 nm snow-absorption feature in the modeled spectra shifts to shorter wavelengths. The second approach to model the effect of liquid water uses a layered-sphere model. Layered-sphere Mie calculations (Reference Toon and AckermanToon and Ackerman, 1981) were used to calculate the extinction, scattering and asymmetry properties of snow grains with liquid-water shells. These Mie parameters were then used to constrain DISORT to model the reflectance of snow. The DISORT model is directional, allowing specification of illumination and observation angles. Figure 3b shows the modeled spectral reflectance for the layered-sphere approach. As with the interspersed-sphere model, the 1030 nm absorption feature shifts to shorter wavelengths with increasing liquid-water content. As expected based on the different melting-snow model assumptions, the form of the spectral shift is different between the interspersed-and layered-spheremodels.

Fig. 3. Modeled melting-snow reflectance for a grain-size of 500 μm with liquid-water mass fraction of 0%, 5% and 25%. (a) The snow is modeled as interspersed spheres of ice and liquid water. (b) The liquid water is modeled as coated spheres with ice cores and liquid-water shells.

Initialvalidation

As an initial test of the models, spectral reflectance measurements of a frozen and melting snow sample were acquired. A 30 by 30 by 30 cm block of snow with an estimated grain-size of 500 μm was collected and placed in a freezer at –20°C.To measure the snow a portable field spectrometer (ASDFR, ASD Inc., Boulder, CO 80301) with a wavelength range of 350–2500nm with nominally 10 nm spectral resolution was used. A spectralon reference target (Labsphere Inc., North Suton, NH 03620) was used as a reflectance calibration standard. The spectrometer was configured to measure spectra every 30 s. The frozen-snow sample was removed from the freezer and placed in the field of view of the spectrometer under clear-sky solar illumination. The solar zenith angle was 36° and air temperature was 23°C. A time series of measurements was acquired as the snow warmed to 0°C and began to melt. Figure 4 shows the first spectrum of the frozen snow and 15 min spectrum after surface melting is well advanced. As predicted by the models, this measurement shows a shift of the 1030 nm absorption feature towards shorter wavelengths. Inspection of the measured frozen- and melting-snow spectra shows the shift in the 1030 nm feature to have a form more closely represented by the coated-sphere model.

Fig. 4. Spectra from a single snow sample in a frozen and melting state.

To explore derivation of grain-size and liquid-water fraction from spectral snow-reflectance measurements, a spectral fitting algorithm was developed. A library of snow-reflectance spectra was calculated with the coated-sphere model for a grain-size range of 50–1500 μm and a water-fraction range of 0–25%. The library was then searched for the minimum residual difference between the frozen and melting measured spectra and every spectrum in the library. Figure 5a shows the best fit between the measured frozen-snow spectrum and the library. This fit was achieved with a value of 550 μm grain-size and 0% liquid water. Figure 5b shows the best fit for the melting-snow spectrum. A value of 550 μm grain-size and 10% liquid water was derived. This initial validation shows simultaneous derivation of grain-size and liquid-water content from measured snow-reflectance spectra using a spectral snow-reflectance model inversion.

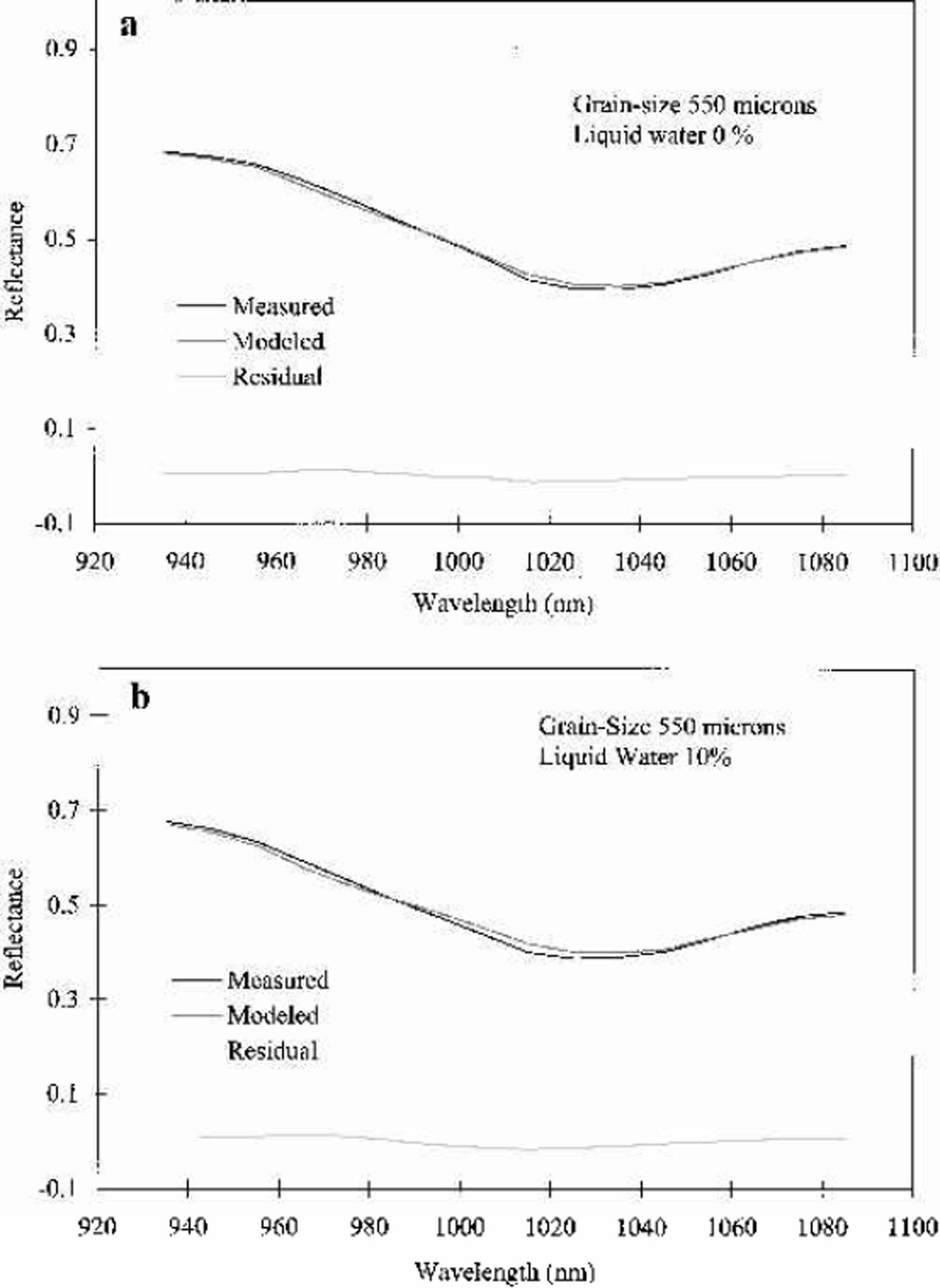
Fig. 5. Spectral fit of the coated-grain melting-snow model to the measured spectrum of (a) frozen snow and (b) melting snow.

Conclusion

Two models of the spectral reflectance of melting snow are described with initial validation results reported. Themodels are based on the complex refractive index of ice and liquid water. These fundamental optical properties were used with Mie-theory codes to calculate the extinction, scattering and asymmetry parameters for two models of melting snow. In the first, the melting snow is modeled as interspersed spheres of ice and liquid water. In the second, the melting snow is modeled as coated ice spheres with liquid-water shells. These Mie-calculated optical properties were used to constrain DISORT to generate the spectral reflectance of snow with varying contents of liquid water. Both the coated- and interspersed-sphere models showed a shift of the absorption features centered at 1030 nm towards shorter wavelengths. This is consistent with the location of minima in the complex refractive index of ice vs liquid water.

Initial validation was performed by comparing the modeled snow spectra with measured spectra of frozen and melting snow. As with the model, the measured spectra showed a shift of the 1030 nm absorption features towards shorter wavelength. A spectral fitting algorithm was developed to invert for grain-size and liquid-water fraction using the coated-sphere model. This inversion algorithm produced grain-size and liquid-water fraction consistent with the expected snow properties.

This research shows that both the grain-size and melting status of snow can be derived with measurements from the solar-reflected portion of the spectrum. With the inclusion of atmospheric correction, terrain and bidirectional reflectance distribution function factors, this approach may be extended to airborne and spaceborne imaging spectrometer datasets at regional scales with global sampling. Theresulting snowgrain-size and melt-status maps would then contribute to energy balance and hydrological modeling and prediction efforts.