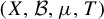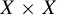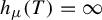1 Introduction
Many dynamical properties of a continuous or measure-preserving transformation T can be discerned from the behavior of the self-product map
![]() $T\times T$
. For example, in the category of probability-preserving transformations, continuous spectrum is equivalent to ergodicity of the self-product (this is weak mixing), and in the topological category of homeomorphisms of compact metric spaces, distality is equivalent to the self-product decomposing into disjoint minimal systems. This note concerns two relatively recent additions to this list, which relate the behavior of self-products to entropy. (Other recent work in this direction can be found in [Reference Downarowicz and Lacroix3, Reference Lesigne, Rittaud and de la Rue4], among others.) In what follows, we assume that T is invertible.
$T\times T$
. For example, in the category of probability-preserving transformations, continuous spectrum is equivalent to ergodicity of the self-product (this is weak mixing), and in the topological category of homeomorphisms of compact metric spaces, distality is equivalent to the self-product decomposing into disjoint minimal systems. This note concerns two relatively recent additions to this list, which relate the behavior of self-products to entropy. (Other recent work in this direction can be found in [Reference Downarowicz and Lacroix3, Reference Lesigne, Rittaud and de la Rue4], among others.) In what follows, we assume that T is invertible.
-
• A topological system
 $(X,T)$
is called doubly minimal if, for every
$(X,T)$
is called doubly minimal if, for every
 $x,y\in X$
that do not lie on the same orbit,
$x,y\in X$
that do not lie on the same orbit,
 $(x,y)$
has a dense two-sided orbit under
$(x,y)$
has a dense two-sided orbit under
 $T\times T$
. Benjamin Weiss [Reference Weiss7] showed that this property implies
$T\times T$
. Benjamin Weiss [Reference Weiss7] showed that this property implies
 $h_{\mathrm {top}}(T)=0$
, and conversely, if an ergodic measure-preserving system has zero entropy, then it can be realized as an invariant measure on a doubly minimal system.
$h_{\mathrm {top}}(T)=0$
, and conversely, if an ergodic measure-preserving system has zero entropy, then it can be realized as an invariant measure on a doubly minimal system. -
• A topological system
 $(X,T)$
is mean distal if for every
$(X,T)$
is mean distal if for every
 $x\neq y$
in X, the Besicovitch pseudo-metric is positive, and an invariant measure
$x\neq y$
in X, the Besicovitch pseudo-metric is positive, and an invariant measure $$ \begin{align*} \overline{d}(x,y)=\limsup_{n\rightarrow\infty}\frac{1}{2n+1}\sum_{i=-n}^{n}d(T^{i}x,T^{i}y) \end{align*} $$
$$ \begin{align*} \overline{d}(x,y)=\limsup_{n\rightarrow\infty}\frac{1}{2n+1}\sum_{i=-n}^{n}d(T^{i}x,T^{i}y) \end{align*} $$
 $\mu $
on X is called tight if, after removing a nullset,
$\mu $
on X is called tight if, after removing a nullset,
 $\overline {d}(x,y)>0$
for every
$\overline {d}(x,y)>0$
for every
 $x,y$
. Thus, every invariant measure on a mean distal system is tight (we note that tightness is a property of the measure-preserving system
$x,y$
. Thus, every invariant measure on a mean distal system is tight (we note that tightness is a property of the measure-preserving system
 $(X,T,\mu )$
, rather than of the topological product system
$(X,T,\mu )$
, rather than of the topological product system
 $X\times X$
). In [Reference Ornstein and Weiss5], Ornstein and Weiss showed that positive, finite entropy precludes tightness, whereas every zero-entropy measure-preserving system has an extension that is realized on a mean distal system.
$X\times X$
). In [Reference Ornstein and Weiss5], Ornstein and Weiss showed that positive, finite entropy precludes tightness, whereas every zero-entropy measure-preserving system has an extension that is realized on a mean distal system.
Let us say that
![]() $x\in X$
is two-sided (respectively forward) recurrent if there exists an unbounded sequence
$x\in X$
is two-sided (respectively forward) recurrent if there exists an unbounded sequence
![]() $n_{k}\in \mathbb {Z}$
(respectively
$n_{k}\in \mathbb {Z}$
(respectively
![]() $n_{k}\in \mathbb {N}$
) such that
$n_{k}\in \mathbb {N}$
) such that
![]() $T^{n_{k}}x\rightarrow x$
. In his study of doubly minimal systems, Weiss observed that double minimality implies that every point in
$T^{n_{k}}x\rightarrow x$
. In his study of doubly minimal systems, Weiss observed that double minimality implies that every point in
![]() $X\times X$
is two-sided recurrent, a property that we shall call double recurrence, and asked whether double recurrence by itself implies entropy zero.
$X\times X$
is two-sided recurrent, a property that we shall call double recurrence, and asked whether double recurrence by itself implies entropy zero.
If one asks for forward (instead of two-sided) recurrence of every pair, then the answer is affirmative, because every positive entropy system possesses an off-diagonal positively asymptotic pair [Reference Blanchard, Host and Ruette2]. From this, it follows that a positive-entropy system X cannot have all points two-sided recurrent in
![]() $X^{4}$
, since one can take
$X^{4}$
, since one can take
![]() $(x_{1},x_{2})$
forward asymptotic and
$(x_{1},x_{2})$
forward asymptotic and
![]() $(x_{3},x_{4})$
backward asymptotic, with
$(x_{3},x_{4})$
backward asymptotic, with
![]() $x_{1}\neq x_{2}$
and
$x_{1}\neq x_{2}$
and
![]() $x_{3}\neq x_{4}$
, and then
$x_{3}\neq x_{4}$
, and then
![]() $(x_{1},x_{2},x_{3},x_{4})\in X^{4}$
is not recurrent. In unpublished work, Weiss extended this conclusion to
$(x_{1},x_{2},x_{3},x_{4})\in X^{4}$
is not recurrent. In unpublished work, Weiss extended this conclusion to
![]() $X^{3}$
, but the original question for
$X^{3}$
, but the original question for
![]() $X\times X$
was not resolved. The following is our main result.
$X\times X$
was not resolved. The following is our main result.
Theorem 1.1. Let
![]() $(X,\mathcal {B},\mu ,T)$
be an invertible ergodic measure-preserving system on a compact metric space. If
$(X,\mathcal {B},\mu ,T)$
be an invertible ergodic measure-preserving system on a compact metric space. If
![]() $h_{\mu }(T)>0$
, then there exists
$h_{\mu }(T)>0$
, then there exists
![]() $(x,x')\in X\times X$
that is not two-sided recurrent under
$(x,x')\in X\times X$
that is not two-sided recurrent under
![]() $T\times T$
.
$T\times T$
.
In view of this and of Weiss’s realization result on doubly minimal systems, it follows that a measure-preserving system has positive entropy if and only if it can be realized on a doubly recurrent system.
Our second result concerns the notion of tightness, defined above. Ornstein and Weiss showed that if
![]() $0<h_{\mu }(T)<\infty $
, then T is not tight. Their proof, however, did not apply when
$0<h_{\mu }(T)<\infty $
, then T is not tight. Their proof, however, did not apply when
![]() $h_{\mu }(T)=\infty $
[Reference Ornstein and Weiss5, Problem 1], and no proof for it has yet appeared. We provide a proof via a slight modification of Ornstein and Weiss’s original argument.
$h_{\mu }(T)=\infty $
[Reference Ornstein and Weiss5, Problem 1], and no proof for it has yet appeared. We provide a proof via a slight modification of Ornstein and Weiss’s original argument.
Theorem 1.2. Infinite entropy systems are never tight.
Together with the results in [Reference Ornstein and Weiss5], this provides yet another characterization of zero/positive entropy: a system has entropy zero if and only if it is a factor of a mean distal system.
The remainder of the paper consists of two sections, one for each theorem. By convention, all our measure spaces are Borel spaces endowed with a compatible compact metric, and all sets and measures are Borel. The transformations
![]() $T,S$
defining our dynamical are always homeomorphisms. Intervals
$T,S$
defining our dynamical are always homeomorphisms. Intervals
![]() $[a,b]$
are often identified with their integer counterparts,
$[a,b]$
are often identified with their integer counterparts,
![]() $[a,b]\cap \mathbb {Z}$
. If
$[a,b]\cap \mathbb {Z}$
. If
![]() $(\xi _{i})$
is a sequence, then we write
$(\xi _{i})$
is a sequence, then we write
![]() $\xi _{k}^{\ell }=\xi _{k}\xi _{k+1}\cdots \xi _{\ell }$
and sometimes
$\xi _{k}^{\ell }=\xi _{k}\xi _{k+1}\cdots \xi _{\ell }$
and sometimes
![]() $\xi _{[k,\ell ]}=\xi _{k}\xi _{k+1}\cdots \xi _{\ell }$
.
$\xi _{[k,\ell ]}=\xi _{k}\xi _{k+1}\cdots \xi _{\ell }$
.
2 Double recurrence
In this section, we prove Theorem 1.1, first for symbolic systems and then in general. For brevity, from here, two-sided recurrent points will simply be called recurrent points.
The heuristic of the proof is that a positive-entropy system
![]() $(X,T)$
should decompose, approximately, as a product; and if there were an exact product structure
$(X,T)$
should decompose, approximately, as a product; and if there were an exact product structure
![]() $X=X_{1}\times X_{2}$
for systems
$X=X_{1}\times X_{2}$
for systems
![]() $X_{1},X_{2}$
of positive entropy, then we could find a forward asymptotic pair
$X_{1},X_{2}$
of positive entropy, then we could find a forward asymptotic pair
![]() $(u_{1},u_{2})\in X_{1}\times X_{1}$
and a backward asymptotic pair
$(u_{1},u_{2})\in X_{1}\times X_{1}$
and a backward asymptotic pair
![]() $(v_{1},v_{2})\in X_{2}\times X_{2}$
. Then, the point
$(v_{1},v_{2})\in X_{2}\times X_{2}$
. Then, the point
![]() $((u_{1},v_{1}),(u_{2},v_{2}))\in X\times X$
would not be recurrent.
$((u_{1},v_{1}),(u_{2},v_{2}))\in X\times X$
would not be recurrent.
Such an exact product structure is available in the measure-theoretic framework, by the weak Pinsker property [Reference Austin1], but not in the topological one. Nevertheless, positive entropy still gives some semblance of independence, in that we can partition time into complementary periodic sets
![]() $E_{1},E_{2}\subseteq \mathbb {Z}$
, such that the behavior of orbits on the two sets is approximately independent. Using this, we will be able to find
$E_{1},E_{2}\subseteq \mathbb {Z}$
, such that the behavior of orbits on the two sets is approximately independent. Using this, we will be able to find
![]() $u,v\in X$
which are (‘forward’) asymptotic along
$u,v\in X$
which are (‘forward’) asymptotic along
![]() $E_{1}^{+}=E_{1}\cap \mathbb {N}$
and (‘backward’) asymptotic along
$E_{1}^{+}=E_{1}\cap \mathbb {N}$
and (‘backward’) asymptotic along
![]() $E_{2}^{-}=E_{2}\cap (-\mathbb {N})$
, and
$E_{2}^{-}=E_{2}\cap (-\mathbb {N})$
, and
![]() $u,v$
differ on a set all of whose translates intersect both
$u,v$
differ on a set all of whose translates intersect both
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
. This will be enough to establish non-recurrence of
$E_{2}$
. This will be enough to establish non-recurrence of
![]() $(u,v)$
.
$(u,v)$
.
2.1 A combinatorial lemma
Let A be a finite alphabet and
![]() $L\subseteq A^{m}$
. We say that L admits a full binary treeif there are sets
$L\subseteq A^{m}$
. We say that L admits a full binary treeif there are sets
![]() $L_{i}\subseteq A^{i}$
for
$L_{i}\subseteq A^{i}$
for
![]() $0\leq i\leq m$
, such that
$0\leq i\leq m$
, such that
![]() $L_{0}$
consists of the empty word,
$L_{0}$
consists of the empty word,
![]() $L_{m}=L$
, and each
$L_{m}=L$
, and each
![]() $a\in L_{i}$
extends in exactly two ways to
$a\in L_{i}$
extends in exactly two ways to
![]() $a',a"\in L_{i+1}$
. Functions or random variables
$a',a"\in L_{i+1}$
. Functions or random variables
![]() $W_{1},\ldots ,W_{m}:\Omega \rightarrow A$
admit a full binary tree if the image of
$W_{1},\ldots ,W_{m}:\Omega \rightarrow A$
admit a full binary tree if the image of
![]() $(W_{1},\ldots ,W_{m})$
does.
$(W_{1},\ldots ,W_{m})$
does.
Lemma 2.1. For every
![]() $0<\eta <1$
and
$0<\eta <1$
and
![]() $m\in \mathbb {N}$
, there is an
$m\in \mathbb {N}$
, there is an
![]() $\varepsilon>0$
so that the following holds.
$\varepsilon>0$
so that the following holds.
Let B be a finite set and
![]() $B_{1},\ldots ,B_{m}\subseteq B$
. Let
$B_{1},\ldots ,B_{m}\subseteq B$
. Let
![]() $W=(W_{1},\ldots ,W_{m})$
be B-valued random variables and
$W=(W_{1},\ldots ,W_{m})$
be B-valued random variables and
![]() $\mathcal {F}$
a
$\mathcal {F}$
a
![]() $\sigma $
-algebra in the underlying sample space. Assume:
$\sigma $
-algebra in the underlying sample space. Assume:
-
(1)
 $|B_{i}|>|B|^{\eta }$
;
$|B_{i}|>|B|^{\eta }$
; -
(2)
 $\mathbb {P}(W_{i}\in B_{i})>1-\varepsilon $
;
$\mathbb {P}(W_{i}\in B_{i})>1-\varepsilon $
; -
(3)
 $|H(W|\mathcal {F})-\sum _{i=1}^{m}\log |B_{i}||<\varepsilon \log |B|$
.
$|H(W|\mathcal {F})-\sum _{i=1}^{m}\log |B_{i}||<\varepsilon \log |B|$
.
Then, with probability
![]() $1-\eta $
over atoms
$1-\eta $
over atoms
![]() $F\in \mathcal {F}$
, the restriction of
$F\in \mathcal {F}$
, the restriction of
![]() $W_{1},\ldots ,W_{m}$
to F admits a full binary tree.
$W_{1},\ldots ,W_{m}$
to F admits a full binary tree.
If we assume in addition that
![]() $|B|$
is bounded, then the conditional distribution of
$|B|$
is bounded, then the conditional distribution of
![]() $W_{1}^{m}$
on the atoms of
$W_{1}^{m}$
on the atoms of
![]() $\mathcal {F}$
will tend to independence as
$\mathcal {F}$
will tend to independence as
![]() $\varepsilon \rightarrow 0$
, and the conclusion is trivial. However, in general, there is no such implication. The example to have in mind is when
$\varepsilon \rightarrow 0$
, and the conclusion is trivial. However, in general, there is no such implication. The example to have in mind is when
![]() $(X_{n})_{n=-\infty }^{\infty }$
is an ergodic process of positive entropy and
$(X_{n})_{n=-\infty }^{\infty }$
is an ergodic process of positive entropy and
![]() $W_{i}$
are consecutive blocks of n variables,
$W_{i}$
are consecutive blocks of n variables,
![]() $W_{i}=X_{in}\cdots X_{(i+1)n-1}$
. If
$W_{i}=X_{in}\cdots X_{(i+1)n-1}$
. If
![]() $\mathcal {F}$
is trivial, or a factor algebra that does not exhaust the entropy, then for small
$\mathcal {F}$
is trivial, or a factor algebra that does not exhaust the entropy, then for small
![]() $\eta>0$
and every
$\eta>0$
and every
![]() $m\in \mathbb {N}$
and
$m\in \mathbb {N}$
and
![]() $\varepsilon>0$
, the random variables
$\varepsilon>0$
, the random variables
![]() $W_{1},\ldots ,W_{m}$
will satisfy the hypotheses of the lemma if n is large enough.
$W_{1},\ldots ,W_{m}$
will satisfy the hypotheses of the lemma if n is large enough.
Proof. Let E denote the event
![]() $W_{i}\in B_{i}$
for all i. We claim that we can assume that
$W_{i}\in B_{i}$
for all i. We claim that we can assume that
![]() $\mathbb {P}(E)=1$
. By condition (1), the entropy of each
$\mathbb {P}(E)=1$
. By condition (1), the entropy of each
![]() $W_{i}$
on
$W_{i}$
on
![]() $E^{c}$
is bounded by
$E^{c}$
is bounded by
![]() $\log |B|<(1/\eta )\log |B_{i}|$
, and by condition (2),
$\log |B|<(1/\eta )\log |B_{i}|$
, and by condition (2),
![]() $\mu (E^{c})\leq m\varepsilon $
. Thus, restricting W and
$\mu (E^{c})\leq m\varepsilon $
. Thus, restricting W and
![]() $\mathcal {F}$
to E changes
$\mathcal {F}$
to E changes
![]() $H(W|\mathcal {F})$
by no more than
$H(W|\mathcal {F})$
by no more than
![]() $\varepsilon '\sum \log |B_{i}|$
for an
$\varepsilon '\sum \log |B_{i}|$
for an
![]() $\varepsilon '$
that can be made arbitrarily small by decreasing
$\varepsilon '$
that can be made arbitrarily small by decreasing
![]() $\varepsilon $
, so after restricting, condition (3) still holds for a slightly larger
$\varepsilon $
, so after restricting, condition (3) still holds for a slightly larger
![]() $\varepsilon $
.
$\varepsilon $
.
Now proceed by induction on m. When
![]() $m=1$
, we must show that, for a
$m=1$
, we must show that, for a
![]() $1-\eta $
fraction of
$1-\eta $
fraction of
![]() $F\in \mathcal {F}$
, the variable
$F\in \mathcal {F}$
, the variable
![]() $W_{1}$
is not almost surely (a.s.) constant on F, or equivalently that the conditional entropy of
$W_{1}$
is not almost surely (a.s.) constant on F, or equivalently that the conditional entropy of
![]() $W_{1}$
on F is positive. Since
$W_{1}$
on F is positive. Since
![]() $W_{1}\in B_{1}$
, we have a pointwise upper bound
$W_{1}\in B_{1}$
, we have a pointwise upper bound
![]() $\log |B_{1}|$
on the entropy of
$\log |B_{1}|$
on the entropy of
![]() $W_{1}$
on each atom of
$W_{1}$
on each atom of
![]() $\mathcal {F}$
, and these conditional entropies average to
$\mathcal {F}$
, and these conditional entropies average to
![]() $H(W_{1}|\mathcal {F})$
, which by conditions (3) and (1) is at least
$H(W_{1}|\mathcal {F})$
, which by conditions (3) and (1) is at least
![]() $\log |B_{1}|-\varepsilon \log |B|>(1-\varepsilon /\eta )\log |B_{1}|$
. As
$\log |B_{1}|-\varepsilon \log |B|>(1-\varepsilon /\eta )\log |B_{1}|$
. As
![]() $\varepsilon $
decreases, these upper (pointwise) and lower (average) bounds approach each other, so, for small enough
$\varepsilon $
decreases, these upper (pointwise) and lower (average) bounds approach each other, so, for small enough
![]() $\varepsilon $
, on a fraction of atoms approaching full measure, we get a lower pointwise bound of the same magnitude.
$\varepsilon $
, on a fraction of atoms approaching full measure, we get a lower pointwise bound of the same magnitude.
For
![]() $m>1$
, our assumption
$m>1$
, our assumption
![]() $W_{i}\in B_{i}$
implies the trivial bounds
$W_{i}\in B_{i}$
implies the trivial bounds
![]() $H(W_{1}|\mathcal {F})\leq \log |B_{1}|$
and
$H(W_{1}|\mathcal {F})\leq \log |B_{1}|$
and
![]() $H(W_{2}^{m}|\mathcal {F}\lor \sigma (W_{1}))\leq \sum _{i=2}^{m}\log |B_{i}|$
. Using the chain rule for entropy, condition (3) becomes
$H(W_{2}^{m}|\mathcal {F}\lor \sigma (W_{1}))\leq \sum _{i=2}^{m}\log |B_{i}|$
. Using the chain rule for entropy, condition (3) becomes
 $$ \begin{align*} \bigg|(\log|B_{1}|-H(W_{1}|\mathcal{F}))+\bigg(\sum_{i=2}^{m}\log|B_{i}|-H(W_{2}^{m}|\mathcal{F}\lor\sigma(W_{1}))\bigg)\bigg|<\varepsilon\log|B|. \end{align*} $$
$$ \begin{align*} \bigg|(\log|B_{1}|-H(W_{1}|\mathcal{F}))+\bigg(\sum_{i=2}^{m}\log|B_{i}|-H(W_{2}^{m}|\mathcal{F}\lor\sigma(W_{1}))\bigg)\bigg|<\varepsilon\log|B|. \end{align*} $$
Since both summands on the left are non-negative, the bound
![]() $\varepsilon \log |B|$
applies to both, and this is condition (3) for the sequence
$\varepsilon \log |B|$
applies to both, and this is condition (3) for the sequence
![]() $W_{2}^{m}$
and algebra
$W_{2}^{m}$
and algebra
![]() $\mathcal {F}\lor \sigma (W_{1})$
. Thus, for
$\mathcal {F}\lor \sigma (W_{1})$
. Thus, for
![]() $\varepsilon $
small, we can apply the induction hypothesis to
$\varepsilon $
small, we can apply the induction hypothesis to
![]() $W_{2}^{m}$
and
$W_{2}^{m}$
and
![]() $\mathcal {F}\lor \sigma (W_{1})$
with parameters
$\mathcal {F}\lor \sigma (W_{1})$
with parameters
![]() $\eta ^{2}/4$
instead of
$\eta ^{2}/4$
instead of
![]() $\eta $
(the decreasing
$\eta $
(the decreasing
![]() $\eta $
does not invalidate condition (1)).
$\eta $
does not invalidate condition (1)).
We conclude that on
![]() $1-\eta ^{2}/4$
of the atoms of
$1-\eta ^{2}/4$
of the atoms of
![]() $\mathcal {F}\lor \sigma (W_{1})$
, the restriction of
$\mathcal {F}\lor \sigma (W_{1})$
, the restriction of
![]() $W_{2}^{m}$
admits a full binary tree. Thus, on
$W_{2}^{m}$
admits a full binary tree. Thus, on
![]() $1-\eta /2$
of the atoms
$1-\eta /2$
of the atoms
![]() $F\in \mathcal {F}$
, at least
$F\in \mathcal {F}$
, at least
![]() $1-\eta /2$
of the atoms
$1-\eta /2$
of the atoms
![]() $G\in \sigma (W_{1})$
(with respect to the conditional measure on F) are such that
$G\in \sigma (W_{1})$
(with respect to the conditional measure on F) are such that
![]() $W_{2}^{m}$
admits a full binary tree on
$W_{2}^{m}$
admits a full binary tree on
![]() $F\cap G$
. Also, arguing as in the case for
$F\cap G$
. Also, arguing as in the case for
![]() $m=1$
, on a
$m=1$
, on a
![]() $1-\eta /2$
fraction of atoms
$1-\eta /2$
fraction of atoms
![]() $F\in \mathcal {F}$
, the conditional distribution of
$F\in \mathcal {F}$
, the conditional distribution of
![]() $W_{1}$
has large entropy, and in particular does not take any single value with probability higher than
$W_{1}$
has large entropy, and in particular does not take any single value with probability higher than
![]() $1-\eta /2$
. It follows that, with probability
$1-\eta /2$
. It follows that, with probability
![]() $1-\eta $
over
$1-\eta $
over
![]() $F\in \mathcal {F}$
, there are two atoms
$F\in \mathcal {F}$
, there are two atoms
![]() $G_{1},G_{2}\in \sigma (W_{1})$
such that
$G_{1},G_{2}\in \sigma (W_{1})$
such that
![]() $W_{2}^{m}$
admit a full binary tree on
$W_{2}^{m}$
admit a full binary tree on
![]() $F\cap G_{1}$
,
$F\cap G_{1}$
,
![]() $F\cap G_{2}$
, and therefore
$F\cap G_{2}$
, and therefore
![]() $W_{1}^{m}$
admits a full binary tree on F.
$W_{1}^{m}$
admits a full binary tree on F.
Corollary 2.2. If
![]() $L\subseteq A^{m}$
admits a binary tree, then there are
$L\subseteq A^{m}$
admits a binary tree, then there are
![]() $u,v\in L$
such that
$u,v\in L$
such that
![]() $u_{i}\neq v_{i}$
for
$u_{i}\neq v_{i}$
for
![]() $i=1,\ldots ,m$
. In particular, in the setting of Lemma 2.1, there exist realizations
$i=1,\ldots ,m$
. In particular, in the setting of Lemma 2.1, there exist realizations
![]() $u,v$
of
$u,v$
of
![]() $W_{1}^{m}$
satisfying the above and coming from the same atom of
$W_{1}^{m}$
satisfying the above and coming from the same atom of
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
Proof. If
![]() $L\subseteq A^{m}$
admits a full binary tree, let
$L\subseteq A^{m}$
admits a full binary tree, let
![]() $L_{i}\subseteq A^{i}$
be as in the definition. Choose any
$L_{i}\subseteq A^{i}$
be as in the definition. Choose any
![]() $u\in L_{m}$
and construct
$u\in L_{m}$
and construct
![]() $v\in L_{m}$
inductively: start with the empty word and, having constructed a word
$v\in L_{m}$
inductively: start with the empty word and, having constructed a word
![]() $v^{(i)}\in L_{i}$
, let
$v^{(i)}\in L_{i}$
, let
![]() $v^{(i+1)}\in L_{i+1}$
be an extension whose last symbol is different from
$v^{(i+1)}\in L_{i+1}$
be an extension whose last symbol is different from
![]() $u_{i}$
; one exists since there are two ways to distinct extensions in
$u_{i}$
; one exists since there are two ways to distinct extensions in
![]() $L_{i+1}$
. Set
$L_{i+1}$
. Set
![]() $v=v^{(m)}.$
$v=v^{(m)}.$
2.2 Proof of the theorem in the symbolic case
In this section, we prove that if
![]() $\Omega \subseteq A^{\mathbb {Z}}$
is a subshift of positive entropy, then it is not doubly recurrent. By the variational principle, we may fix an ergodic shift invariant measure on
$\Omega \subseteq A^{\mathbb {Z}}$
is a subshift of positive entropy, then it is not doubly recurrent. By the variational principle, we may fix an ergodic shift invariant measure on
![]() $\Omega $
with positive entropy. Taking
$\Omega $
with positive entropy. Taking
![]() $X_{n}:\Omega \rightarrow A$
to be the coordinate projections,
$X_{n}:\Omega \rightarrow A$
to be the coordinate projections,
![]() $(X_{n})_{n=-\infty }^{\infty }$
becomes an A-valued stationary ergodic process of positive entropy, and our goal is to find two realizations
$(X_{n})_{n=-\infty }^{\infty }$
becomes an A-valued stationary ergodic process of positive entropy, and our goal is to find two realizations
![]() $u,v$
of
$u,v$
of
![]() $(X_{n})$
such that
$(X_{n})$
such that
![]() $(u,v)$
is not recurrent in
$(u,v)$
is not recurrent in
![]() $A^{\mathbb {Z}}\times A^{\mathbb {Z}}$
.
$A^{\mathbb {Z}}\times A^{\mathbb {Z}}$
.
For
![]() $n\in \mathbb {N}$
, define an n-interval to be a set of the form
$n\in \mathbb {N}$
, define an n-interval to be a set of the form
![]() $I=[kn,(k+1)n)$
with
$I=[kn,(k+1)n)$
with
![]() $k\in \mathbb {Z}$
, and say that I is odd or even according to the parity of k. Suppressing the parameter n from the notation, let
$k\in \mathbb {Z}$
, and say that I is odd or even according to the parity of k. Suppressing the parameter n from the notation, let
be the blocks of variables in even and in odd n-intervals, respectively. Then,
![]() $\mathbb {Z}$
decomposes into disjoint n-intervals which are alternately odd and even, and similarly
$\mathbb {Z}$
decomposes into disjoint n-intervals which are alternately odd and even, and similarly
Let
![]() $h>0$
denote the entropy of the process
$h>0$
denote the entropy of the process
![]() $(X_{n})$
, so that
$(X_{n})$
, so that
(all error terms are asymptotic as
![]() $n\rightarrow \infty $
). It is not hard to see that for large n, the processes
$n\rightarrow \infty $
). It is not hard to see that for large n, the processes
![]() $(Y_{i})$
and
$(Y_{i})$
and
![]() $(Z_{i})$
are roughly independent, in the sense that the entropy of each is
$(Z_{i})$
are roughly independent, in the sense that the entropy of each is
![]() $\tfrac 12(h+o(1))$
, and their joint entropy is h. We will not use this property directly, although it is implicit in the proof below. Set
$\tfrac 12(h+o(1))$
, and their joint entropy is h. We will not use this property directly, although it is implicit in the proof below. Set
 $$ \begin{align*} E^{-} & =\bigcup\{\mathrm{even}\ {n}\text{-}\mathrm{intervals\ to\ the\ left\ of}\ {0}\},\\E^{+} & =\bigcup\{\mathrm{odd}\ {n}\text{-}\mathrm{intervals\ to\ the\ right\ of}\ {0}\}. \end{align*} $$
$$ \begin{align*} E^{-} & =\bigcup\{\mathrm{even}\ {n}\text{-}\mathrm{intervals\ to\ the\ left\ of}\ {0}\},\\E^{+} & =\bigcup\{\mathrm{odd}\ {n}\text{-}\mathrm{intervals\ to\ the\ right\ of}\ {0}\}. \end{align*} $$
Lemma 2.3. As
![]() $n\to\infty$
, we have
$n\to\infty$
, we have
In the lemma, we have conditioned on both past and future times, and it is important to note that, in general, this can lead to a sharp decrease in entropy, even when the density of the times is small. For example, if one takes the even blocks in both directions, it can happen that
![]() $H(Y_{0}|Y_{-\infty }^{\infty })=0$
for all n, as can be shown using a construction similar to that in [Reference Ornstein and Weiss6]. The validity of the lemma relies crucially on the asymmetry between the blocks that we condition on in the past and in the future.
$H(Y_{0}|Y_{-\infty }^{\infty })=0$
for all n, as can be shown using a construction similar to that in [Reference Ornstein and Weiss6]. The validity of the lemma relies crucially on the asymmetry between the blocks that we condition on in the past and in the future.
Proof of the lemma
The inequality
![]() $\leq $
is trivial since
$\leq $
is trivial since
Thus, we need only prove
![]() $\geq $
. Note that
$\geq $
. Note that
![]() $X_{-n}^{n-1}=(Z_{-1},Y_{0})$
and
$X_{-n}^{n-1}=(Z_{-1},Y_{0})$
and
 $$ \begin{align*} H(Z_{-1},Y_{0}|Y_{-\infty}^{-1},Z_{0}^{\infty}) & =H(Y_{0}|Y_{-\infty}^{-1},Z_{0}^{\infty})+H(Z_{-1}|Y_{-\infty}^{0},Z_{0}^{\infty})\\ & \geq H(Y_{0}|Y_{-\infty}^{-1},Z_{-\infty}^{\infty})+H(Z_{-1}|Y_{-\infty}^{\infty},Z_{0}^{\infty}). \end{align*} $$
$$ \begin{align*} H(Z_{-1},Y_{0}|Y_{-\infty}^{-1},Z_{0}^{\infty}) & =H(Y_{0}|Y_{-\infty}^{-1},Z_{0}^{\infty})+H(Z_{-1}|Y_{-\infty}^{0},Z_{0}^{\infty})\\ & \geq H(Y_{0}|Y_{-\infty}^{-1},Z_{-\infty}^{\infty})+H(Z_{-1}|Y_{-\infty}^{\infty},Z_{0}^{\infty}). \end{align*} $$
It suffices to show that each of the summands on the right-hand side is
![]() $n(h+o(1))$
. We prove this for the first summand, the second is similar.
$n(h+o(1))$
. We prove this for the first summand, the second is similar.
Fix a large integer
![]() $\ell $
and note that
$\ell $
and note that
 $$ \begin{align*} 4\ell n(h+o(1)) & =H(X_{-2\ell n},X_{-\ell n+1},\ldots,X_{2\ell n-1})\\ & =H(Y_{-\ell},Z_{-\ell},Y_{-\ell+1},Z_{-\ell+1},\ldots,Y_{\ell-1},Z_{\ell-1})\\ & =H(Z_{-\ell}^{\ell-1})+H(Y_{-\ell}^{\ell-1}|Z_{-\ell}^{\ell-1})\\ & =H(Z_{-\ell}^{\ell-1})+\sum_{i=-\ell}^{\ell-1}H(Y_{i}|Y_{-\ell}^{i-1},Z_{-\ell}^{\ell-1})\\ & =2\ell n(h+o(1))+\sum_{i=-\ell}^{\ell-1}H(Y_{0}|Y_{-\ell-i}^{-1},Z_{-\ell-i}^{\ell-i-1}). \end{align*} $$
$$ \begin{align*} 4\ell n(h+o(1)) & =H(X_{-2\ell n},X_{-\ell n+1},\ldots,X_{2\ell n-1})\\ & =H(Y_{-\ell},Z_{-\ell},Y_{-\ell+1},Z_{-\ell+1},\ldots,Y_{\ell-1},Z_{\ell-1})\\ & =H(Z_{-\ell}^{\ell-1})+H(Y_{-\ell}^{\ell-1}|Z_{-\ell}^{\ell-1})\\ & =H(Z_{-\ell}^{\ell-1})+\sum_{i=-\ell}^{\ell-1}H(Y_{i}|Y_{-\ell}^{i-1},Z_{-\ell}^{\ell-1})\\ & =2\ell n(h+o(1))+\sum_{i=-\ell}^{\ell-1}H(Y_{0}|Y_{-\ell-i}^{-1},Z_{-\ell-i}^{\ell-i-1}). \end{align*} $$
Rearranging and dividing by
![]() $2\ell $
, we have
$2\ell $
, we have
 $$ \begin{align*} \frac{1}{2\ell}\sum_{i=-\ell}^{\ell-1}H(Y_{0}|Y_{-\ell-i}^{-1},Z_{-\ell-i}^{\ell-i-1})=n(h+o(1)). \end{align*} $$
$$ \begin{align*} \frac{1}{2\ell}\sum_{i=-\ell}^{\ell-1}H(Y_{0}|Y_{-\ell-i}^{-1},Z_{-\ell-i}^{\ell-i-1})=n(h+o(1)). \end{align*} $$
However, by Martingale convergence and monotonicity of entropy under conditioning,
Inserting this in the previous equation and letting
![]() $\ell \rightarrow \infty $
gives
$\ell \rightarrow \infty $
gives
as required.
Returning to the proof of the theorem, split
![]() $[-n,n)$
into disjoint intervals
$[-n,n)$
into disjoint intervals
![]() $I_{1},\ldots ,I_{8}$
of length
$I_{1},\ldots ,I_{8}$
of length
![]() $n/4$
(we can assume
$n/4$
(we can assume
![]() $n/4\in \mathbb {N}$
) and note that every sub-interval
$n/4\in \mathbb {N}$
) and note that every sub-interval
![]() $J\subseteq [-n,n)$
of length
$J\subseteq [-n,n)$
of length
![]() $n/2$
contains one of the
$n/2$
contains one of the
![]() $I_{i}$
. Let
$I_{i}$
. Let
We would like to apply Corollary 2.2 to
![]() $W_{1},\ldots ,W_{8}$
and the
$W_{1},\ldots ,W_{8}$
and the
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {F}=\sigma (Y_{-\infty }^{-1},Z_{0}^{\infty })$
, with suitable sets
$\mathcal {F}=\sigma (Y_{-\infty }^{-1},Z_{0}^{\infty })$
, with suitable sets
![]() $B,B_{1},\ldots ,B_{8}$
. To set things up, apply the Shannon–MacMillan theorem to find a set
$B,B_{1},\ldots ,B_{8}$
. To set things up, apply the Shannon–MacMillan theorem to find a set
![]() $A'\subseteq A^{n/4}$
of size
$A'\subseteq A^{n/4}$
of size
for
![]() $c=\log 2/(4\log |A|)>0$
and satisfying
$c=\log 2/(4\log |A|)>0$
and satisfying
Set
![]() $\eta =c/2$
,
$\eta =c/2$
,
![]() $B=A^{n/4}$
, and
$B=A^{n/4}$
, and
![]() $B_{1},\ldots ,B_{8}=A'$
in the hypothesis of Corollary 2.2. Also, by Lemma 2.3,
$B_{1},\ldots ,B_{8}=A'$
in the hypothesis of Corollary 2.2. Also, by Lemma 2.3,
but we also have
![]() $H(W_{i})=(h-o(1))\cdot n/2$
, so
$H(W_{i})=(h-o(1))\cdot n/2$
, so
 $$ \begin{align*} H(W_{1}^{8}|Y_{-\infty}^{-1},Z_{0}^{\infty})\leq\sum_{i=1}^{8}H(W_{i})\leq2(h+o(1))n. \end{align*} $$
$$ \begin{align*} H(W_{1}^{8}|Y_{-\infty}^{-1},Z_{0}^{\infty})\leq\sum_{i=1}^{8}H(W_{i})\leq2(h+o(1))n. \end{align*} $$
Combining these bounds,
 $$ \begin{align*} \bigg|H(W_{1}^{8})-\sum_{i=1}^{8}H(W_{i})\bigg|=o(n), \end{align*} $$
$$ \begin{align*} \bigg|H(W_{1}^{8})-\sum_{i=1}^{8}H(W_{i})\bigg|=o(n), \end{align*} $$
which, assuming n is large, completes the hypotheses of Corollary 2.2.
The corollary now provides us with samples
![]() $u,v$
for the process satisfying:
$u,v$
for the process satisfying:
-
•
 $u,v$
are realized on the same atom of
$u,v$
are realized on the same atom of
 $\mathcal {F}=\sigma (Y_{-\infty }^{-1},Z_{0}^{\infty })$
, and hence
$\mathcal {F}=\sigma (Y_{-\infty }^{-1},Z_{0}^{\infty })$
, and hence
 $u,v$
agree on every n-interval in
$u,v$
agree on every n-interval in
 $E^{-}\cup E^{+}$
;
$E^{-}\cup E^{+}$
; -
•
 $u|_{I_{i}}\neq v|_{I_{i}}$
for
$u|_{I_{i}}\neq v|_{I_{i}}$
for
 $i=1,\ldots ,8$
, that is, for each i, there is
$i=1,\ldots ,8$
, that is, for each i, there is
 $j\in I_{i}$
with
$j\in I_{i}$
with
 $u_{j}\neq v_{j}$
.
$u_{j}\neq v_{j}$
.
To conclude the proof, we must show that
![]() $(u,v)$
is not recurrent. Indeed, let
$(u,v)$
is not recurrent. Indeed, let
![]() $(u',v')$
be a shift of
$(u',v')$
be a shift of
![]() $(u,v)$
by k, with
$(u,v)$
by k, with
![]() $|k|>2n$
.
$|k|>2n$
.
-
• Since
 $E^{-},E^{+}$
consist of n-intervals separated by gaps of length n, after shifting
$E^{-},E^{+}$
consist of n-intervals separated by gaps of length n, after shifting
 $E^{-}\cup E^{+}$
by k, some n-interval
$E^{-}\cup E^{+}$
by k, some n-interval
 $J\subseteq (E^{-}\cup E^{+})+k$
will intersect
$J\subseteq (E^{-}\cup E^{+})+k$
will intersect
 $[-n,n)$
in a set of size at least
$[-n,n)$
in a set of size at least
 $n/2$
, implying that
$n/2$
, implying that
 $u^{\prime }_{j}=v^{\prime }_{j}$
for all
$u^{\prime }_{j}=v^{\prime }_{j}$
for all
 $j\in J\cap [-n,n)$
.
$j\in J\cap [-n,n)$
. -
• Every interval of length
 $n/2$
in
$n/2$
in
 $[-n,n]$
and, in particular, the interval
$[-n,n]$
and, in particular, the interval
 $J\cap [-n,n)$
contains one of the
$J\cap [-n,n)$
contains one of the
 $I_{i}$
. Thus, there is then a
$I_{i}$
. Thus, there is then a
 $j\in I_{i}\subseteq J$
such that
$j\in I_{i}\subseteq J$
such that
 $u_{j}\neq v_{j}$
.
$u_{j}\neq v_{j}$
.
It follows that
![]() $(u,v)$
and
$(u,v)$
and
![]() $(u',v')$
differ on at least one coordinate
$(u',v')$
differ on at least one coordinate
![]() $j\in [-n,n)$
. This holds for all shifts
$j\in [-n,n)$
. This holds for all shifts
![]() $(u',v')$
of
$(u',v')$
of
![]() $(u,v)$
by
$(u,v)$
by
![]() $2n$
or more, so
$2n$
or more, so
![]() $(u,v)$
is not recurrent.
$(u,v)$
is not recurrent.
2.3 The general case
Let
![]() $(X,T)$
be a topological system and
$(X,T)$
be a topological system and
![]() $\mu $
a T-invariant Borel probability measure of positive entropy. Our plan is as follows.
$\mu $
a T-invariant Borel probability measure of positive entropy. Our plan is as follows.
First, we pass to a measure-theoretic factor
![]() $(X,\mu )\rightarrow (Y,\nu )$
, where Y is a subshift over a countable alphabet (for concreteness,
$(X,\mu )\rightarrow (Y,\nu )$
, where Y is a subshift over a countable alphabet (for concreteness,
![]() $Y\subseteq \mathbb {N}^{\mathbb {Z}}$
) and the entropy of Y is positive and finite. This factor will be defined using a partition
$Y\subseteq \mathbb {N}^{\mathbb {Z}}$
) and the entropy of Y is positive and finite. This factor will be defined using a partition
![]() $\mathcal {C}=\{C_{1},C_{2},\ldots \}$
of X (modulo
$\mathcal {C}=\{C_{1},C_{2},\ldots \}$
of X (modulo
![]() $\mu $
) into closed sets that are separated from each other in the sense that, for every n, no pair of atoms
$\mu $
) into closed sets that are separated from each other in the sense that, for every n, no pair of atoms
![]() $C_{i},C_{j}$
with
$C_{i},C_{j}$
with
![]() $i,j<n$
can be simultaneously
$i,j<n$
can be simultaneously
![]() $\delta _{n}$
-close to a third atom.
$\delta _{n}$
-close to a third atom.
Next, pass to a further factor
![]() $(Y,\nu )\rightarrow (Z,\theta )$
, chosen so that Y has a finite generator relative to Z and, conditioned on Z, the relative entropy is positive. This factor is obtained by merging a large finite number of symbols
$(Y,\nu )\rightarrow (Z,\theta )$
, chosen so that Y has a finite generator relative to Z and, conditioned on Z, the relative entropy is positive. This factor is obtained by merging a large finite number of symbols
![]() $1,\ldots ,r$
in the alphabet of Y.
$1,\ldots ,r$
in the alphabet of Y.
We can now run a relative version of the argument from the symbolic case on Y, conditioned on Z. This yields a pair of points
![]() $u,v\in Y$
that lie above the same point in Z and such that
$u,v\in Y$
that lie above the same point in Z and such that
![]() $(u,v)$
is not recurrent in
$(u,v)$
is not recurrent in
![]() $Y\times Y$
. More precisely, the lack of recurrence arises because every large enough shift
$Y\times Y$
. More precisely, the lack of recurrence arises because every large enough shift
![]() $(u',v')$
of
$(u',v')$
of
![]() $(u,v)$
admits an index
$(u,v)$
admits an index
![]() $j\in [-n,n)$
at which
$j\in [-n,n)$
at which
![]() $u',v'$
display a common symbol k, while
$u',v'$
display a common symbol k, while
![]() $u,v$
display distinct symbols from among
$u,v$
display distinct symbols from among
![]() $1,\ldots ,r$
.
$1,\ldots ,r$
.
Finally, taking preimages
![]() $x,y\in X$
of
$x,y\in X$
of
![]() $u,v\in Y$
, respectively, we find that any large enough shift
$u,v\in Y$
, respectively, we find that any large enough shift
![]() $(x',y')$
of
$(x',y')$
of
![]() $(x,y)$
can be brought, after another bounded shift, into an atom
$(x,y)$
can be brought, after another bounded shift, into an atom
![]() $C_{k}$
, whereas the corresponding shifts of
$C_{k}$
, whereas the corresponding shifts of
![]() $x,y$
lie in distinct atoms from among
$x,y$
lie in distinct atoms from among
![]() $C_{1},\ldots ,C_{r}$
. The separation properties of
$C_{1},\ldots ,C_{r}$
. The separation properties of
![]() $\mathcal {C}$
now ensure that
$\mathcal {C}$
now ensure that
![]() $(x',y')$
is at least
$(x',y')$
is at least
![]() $\delta _{r}$
-far from
$\delta _{r}$
-far from
![]() $(x,y)$
, which is non-recurrence.
$(x,y)$
, which is non-recurrence.
We now give this argument in detail.
2.3.1 Step 1: constructing the factor
 $X\rightarrow Y$
$X\rightarrow Y$
We inductively construct a sequence of disjoint closed sets
![]() $C_{1},C_{2},\ldots \subseteq X$
that exhaust the measure
$C_{1},C_{2},\ldots \subseteq X$
that exhaust the measure
![]() $\mu $
.
$\mu $
.
Begin with a finite measurable partition
![]() $\mathcal {A}=\{A_{1},\ldots ,A_{n_{1}}\}$
of positive entropy and
$\mathcal {A}=\{A_{1},\ldots ,A_{n_{1}}\}$
of positive entropy and
![]() $\varepsilon>0$
, and choose closed sets
$\varepsilon>0$
, and choose closed sets
![]() $C_{i}\subseteq A_{i}$
such that
$C_{i}\subseteq A_{i}$
such that
![]() $\mu (\bigcup _{i=1}^{n_{1}}C_{i})>1-\varepsilon _{1}$
.
$\mu (\bigcup _{i=1}^{n_{1}}C_{i})>1-\varepsilon _{1}$
.
Set
![]() $n_{k}=2^{k-1}n_{1}$
and suppose that after k steps, we have defined disjoint closed sets
$n_{k}=2^{k-1}n_{1}$
and suppose that after k steps, we have defined disjoint closed sets
![]() $C_{1},\ldots ,C_{n_{k}}$
. Let
$C_{1},\ldots ,C_{n_{k}}$
. Let
![]() $\varepsilon _{k+1}$
be given. For
$\varepsilon _{k+1}$
be given. For
![]() $i=1,\ldots ,n_{k}$
, let
$i=1,\ldots ,n_{k}$
, let
![]() $A_{i}^{k},\subseteq X$
denote the measurable sets that form the ‘Voronoi anuli’ of the sets
$A_{i}^{k},\subseteq X$
denote the measurable sets that form the ‘Voronoi anuli’ of the sets
![]() $C_{1},\ldots ,C_{n_{k}}$
:
$C_{1},\ldots ,C_{n_{k}}$
:
 $$ \begin{align*} A_{i}^{k}=\left\{ x\in X\left|\begin{array}{@{}c@{}} d(x,C_{i})<d(x,C_{j})\text{ for }j<i\text{ and }\\ d(x,C_{i})\leq d(x,C_{j})\text{ for }j>i \end{array}\right.\!\right\} \setminus C_{i}. \end{align*} $$
$$ \begin{align*} A_{i}^{k}=\left\{ x\in X\left|\begin{array}{@{}c@{}} d(x,C_{i})<d(x,C_{j})\text{ for }j<i\text{ and }\\ d(x,C_{i})\leq d(x,C_{j})\text{ for }j>i \end{array}\right.\!\right\} \setminus C_{i}. \end{align*} $$
The sets
![]() $A_{1}^{k},\ldots ,A_{n_{k}}^{k}$
are measurable, pairwise disjoint, and, together with
$A_{1}^{k},\ldots ,A_{n_{k}}^{k}$
are measurable, pairwise disjoint, and, together with
![]() $C_{1},\ldots ,C_{n_{k}}$
, they form a partition of X. Now choose closed sets
$C_{1},\ldots ,C_{n_{k}}$
, they form a partition of X. Now choose closed sets
![]() $C_{n_{k}+i}\subseteq A_{i}^{k}$
,
$C_{n_{k}+i}\subseteq A_{i}^{k}$
,
![]() $i=1,\ldots ,n_{k}$
, satisfying
$i=1,\ldots ,n_{k}$
, satisfying
![]() $\mu (\bigcup _{i=1}^{n_{k+1}}C_{i})>1-\varepsilon _{k+1}$
. We have defined
$\mu (\bigcup _{i=1}^{n_{k+1}}C_{i})>1-\varepsilon _{k+1}$
. We have defined
![]() $C_{1},\ldots ,C_{n_{k+1}}$
.
$C_{1},\ldots ,C_{n_{k+1}}$
.
Let
![]() $\mathcal {C}=\{C_{1},C_{2},\ldots \}$
denote the resulting family of sets. Observe the following.
$\mathcal {C}=\{C_{1},C_{2},\ldots \}$
denote the resulting family of sets. Observe the following.
-
(1) If
 $\varepsilon _{k}\rightarrow 0$
, then
$\varepsilon _{k}\rightarrow 0$
, then
 $\mathcal {C}$
is a partition of X up to
$\mathcal {C}$
is a partition of X up to
 $\mu $
-null sets.
$\mu $
-null sets. -
(2) If
 $\varepsilon _{k}\rightarrow 0$
quickly enough,
$\varepsilon _{k}\rightarrow 0$
quickly enough,
 $H_{\mu }(\mathcal {C})<\infty $
. In particular,
$H_{\mu }(\mathcal {C})<\infty $
. In particular,
 $h_{\mu }(T,\mathcal {C})<\infty $
. This is true because
$h_{\mu }(T,\mathcal {C})<\infty $
. This is true because
 $n_{k}=2^{n}n_{1}$
partition elements added at stage k of the construction contribute at most
$n_{k}=2^{n}n_{1}$
partition elements added at stage k of the construction contribute at most
 $\varepsilon _{k}\cdot k\log n_{1}$
to the total entropy, so taking
$\varepsilon _{k}\cdot k\log n_{1}$
to the total entropy, so taking
 $\varepsilon _{k}=1/k^{3}$
, for example, gives
$\varepsilon _{k}=1/k^{3}$
, for example, gives
 $H_{\mu }(\mathcal {C})\leq \sum _{k}({1}/{k^{2}})\log n_{1}<\infty $
.
$H_{\mu }(\mathcal {C})\leq \sum _{k}({1}/{k^{2}})\log n_{1}<\infty $
. -
(3) If
 $\varepsilon _{k}\rightarrow 0$
quickly enough and
$\varepsilon _{k}\rightarrow 0$
quickly enough and
 $\varepsilon _{1}$
is small enough, then
$\varepsilon _{1}$
is small enough, then
 $h_{\mu }(T,\mathcal {C})>0$
. This is because for any
$h_{\mu }(T,\mathcal {C})>0$
. This is because for any
 $\varepsilon _{2},\varepsilon _{3},\ldots $
such that
$\varepsilon _{2},\varepsilon _{3},\ldots $
such that
 $H_{\mu }(\mathcal {C})<\infty $
, the Rohlin distance
$H_{\mu }(\mathcal {C})<\infty $
, the Rohlin distance
 $H_{\mu }(\mathcal {A}|\mathcal {C})+H_{\mu }(\mathcal {C}|\mathcal {A})$
tends to zero as
$H_{\mu }(\mathcal {A}|\mathcal {C})+H_{\mu }(\mathcal {C}|\mathcal {A})$
tends to zero as
 $\varepsilon _{1}\rightarrow 0$
, and hence
$\varepsilon _{1}\rightarrow 0$
, and hence
 $h_{\mu }(T,\mathcal {C})\rightarrow h_{\mu }(T,\mathcal {A})>0$
.
$h_{\mu }(T,\mathcal {C})\rightarrow h_{\mu }(T,\mathcal {A})>0$
. -
(4) For every
 $\ell \neq m$
, Indeed, suppose
$\ell \neq m$
, Indeed, suppose $$ \begin{align*} \delta_{m,\ell}=\inf_{i\in\mathbb{N}}\{ \max\{d(C_{\ell},C_{i}),d(C_{m},C_{i})\}\}>0. \end{align*} $$
$$ \begin{align*} \delta_{m,\ell}=\inf_{i\in\mathbb{N}}\{ \max\{d(C_{\ell},C_{i}),d(C_{m},C_{i})\}\}>0. \end{align*} $$
 $1\leq \ell ,m<n_{k}$
. Because the sets
$1\leq \ell ,m<n_{k}$
. Because the sets
 $C_{1},\ldots ,C_{n_{k}}$
are closed and disjoint, the infimum above is positive as i ranges over
$C_{1},\ldots ,C_{n_{k}}$
are closed and disjoint, the infimum above is positive as i ranges over
 $\{1,\ldots ,n_{k}\}$
. For
$\{1,\ldots ,n_{k}\}$
. For
 $i>n_{k}$
, each
$i>n_{k}$
, each
 $C_{i}$
is contained in the Voronoi cell of exactly one of the previously defined sets and, in particular, either
$C_{i}$
is contained in the Voronoi cell of exactly one of the previously defined sets and, in particular, either
 $d(C_{i},C_{\ell })\geq \tfrac 12d(C_{\ell },C_{m})$
or
$d(C_{i},C_{\ell })\geq \tfrac 12d(C_{\ell },C_{m})$
or
 $d(C_{i},C_{m})\geq \tfrac 12d(C_{\ell },C_{m})$
. Thus, the infimum is positive over all i.
$d(C_{i},C_{m})\geq \tfrac 12d(C_{\ell },C_{m})$
. Thus, the infimum is positive over all i.
Assume that
![]() $\varepsilon _{k}$
have been chosen so that properties (1)–(3) above are satisfied and let
$\varepsilon _{k}$
have been chosen so that properties (1)–(3) above are satisfied and let
![]() $\pi :X\rightarrow \mathbb {N}^{\mathbb {Z}}$
be the associated measurable map,
$\pi :X\rightarrow \mathbb {N}^{\mathbb {Z}}$
be the associated measurable map,
Let
![]() $\nu =\pi \mu $
be the push-forward measure, which is invariant under the shift S on
$\nu =\pi \mu $
be the push-forward measure, which is invariant under the shift S on
![]() $\mathbb {N}^{\mathbb {Z}}$
. Then,
$\mathbb {N}^{\mathbb {Z}}$
. Then,
2.3.2 Step 2: constructing the factor
 $Y\rightarrow Z$
$Y\rightarrow Z$
Let
![]() $\mathcal {D}$
denote the cylinder partition of
$\mathcal {D}$
denote the cylinder partition of
![]() $\mathbb {N}^{\mathbb {Z}}$
and let
$\mathbb {N}^{\mathbb {Z}}$
and let
![]() $\mathcal {D}^{(r)}$
denote the partition of Y obtained by merging the first r symbols into a single atom. Since
$\mathcal {D}^{(r)}$
denote the partition of Y obtained by merging the first r symbols into a single atom. Since
![]() $H_{\nu }(\mathcal {D})<\infty $
,
$H_{\nu }(\mathcal {D})<\infty $
,
and since
![]() $h_{\nu }(S)>0$
, we can choose r large enough that
$h_{\nu }(S)>0$
, we can choose r large enough that
![]() $H_{\nu }(D^{(r)})<h_{\nu }(S)$
, and hence
$H_{\nu }(D^{(r)})<h_{\nu }(S)$
, and hence
Consider the factor algebra
![]() $\mathcal {E}=\bigvee _{i\in \mathbb {Z}}S^{-i}\mathcal {D}^{(r)}$
. Evidently,
$\mathcal {E}=\bigvee _{i\in \mathbb {Z}}S^{-i}\mathcal {D}^{(r)}$
. Evidently,
Let
![]() $\mathcal {B}$
denote the partition of
$\mathcal {B}$
denote the partition of
![]() $\mathbb {N}^{\mathbb {Z}}$
obtained by identifying all symbols
$\mathbb {N}^{\mathbb {Z}}$
obtained by identifying all symbols
![]() $r+1,r+2,\ldots $
, and observe that
$r+1,r+2,\ldots $
, and observe that
![]() $\mathcal {D}=\mathcal {B}\lor \mathcal {D}^{(r)}$
, so
$\mathcal {D}=\mathcal {B}\lor \mathcal {D}^{(r)}$
, so
![]() $\mathcal {B}$
generates relative to
$\mathcal {B}$
generates relative to
![]() $\mathcal {E}$
, and hence
$\mathcal {E}$
, and hence
2.3.3 Step 3: applying the symbolic argument
We can now run the entire argument from the finite-alphabet case for the process
![]() $(X_{i})$
determined by
$(X_{i})$
determined by
![]() $\mathcal {B}$
, but conditioning the whole while on
$\mathcal {B}$
, but conditioning the whole while on
![]() $\mathcal {E}$
. We will then find an n and samples
$\mathcal {E}$
. We will then find an n and samples
![]() $u,v\in \mathbb {N}^{\mathbb {Z}}$
of the process which lie in the same atom of
$u,v\in \mathbb {N}^{\mathbb {Z}}$
of the process which lie in the same atom of
![]() $\sigma (Y_{-\infty }^{-1},Z_{1}^{\infty })\lor \mathcal {E}$
, and with the property that if
$\sigma (Y_{-\infty }^{-1},Z_{1}^{\infty })\lor \mathcal {E}$
, and with the property that if
![]() $(u',v')$
is a shift of
$(u',v')$
is a shift of
![]() $(u,v)$
by more than n in either direction, there exists
$(u,v)$
by more than n in either direction, there exists
![]() $-n\leq j\leq n$
such that
$-n\leq j\leq n$
such that
![]() $u_{j}\neq v_{j}$
and
$u_{j}\neq v_{j}$
and
![]() $u^{\prime }_{j}=v^{\prime }_{j}$
. Importantly,
$u^{\prime }_{j}=v^{\prime }_{j}$
. Importantly,
![]() $u_{j}\neq v_{j}$
implies
$u_{j}\neq v_{j}$
implies
![]() $u_{j},v_{j}\in \{1,\ldots ,n\}$
, because otherwise, they would not lie in the same atom of
$u_{j},v_{j}\in \{1,\ldots ,n\}$
, because otherwise, they would not lie in the same atom of
![]() $\mathcal {E}$
.
$\mathcal {E}$
.
We must adjust one minor point in this argument: we should work with the process defined by the partition
![]() $\pi ^{-1}\mathcal {B}$
on
$\pi ^{-1}\mathcal {B}$
on
![]() $(X,\mu ,T)$
instead of by
$(X,\mu ,T)$
instead of by
![]() $\mathcal {B}$
on
$\mathcal {B}$
on
![]() $(\mathbb {N}^{\mathbb {Z}},\nu ,S)$
, and the algebra
$(\mathbb {N}^{\mathbb {Z}},\nu ,S)$
, and the algebra
![]() $\pi ^{-1}\mathcal {E}$
. The two processes have the same distribution, but this change ensures that the resulting samples
$\pi ^{-1}\mathcal {E}$
. The two processes have the same distribution, but this change ensures that the resulting samples
![]() $u,v$
lie in the image of
$u,v$
lie in the image of
![]() $\pi $
. We remark that the fact that the process is not defined on a subshift is not a problem: in the proof of the symbolic case in §2.2, we did not rely on the underlying subshift, only on the process.
$\pi $
. We remark that the fact that the process is not defined on a subshift is not a problem: in the proof of the symbolic case in §2.2, we did not rely on the underlying subshift, only on the process.
2.3.4 Step 4: lifting
 $u,v$
to X
$u,v$
to X
Let
![]() $x\in \pi ^{-1}(u)$
and
$x\in \pi ^{-1}(u)$
and
![]() $y\in \pi ^{-1}(v)$
. To conclude the argument, we shall show that
$y\in \pi ^{-1}(v)$
. To conclude the argument, we shall show that
![]() $(x,y)$
is non-recurrent for
$(x,y)$
is non-recurrent for
![]() $T\times T$
. Indeed, let
$T\times T$
. Indeed, let
Fix
![]() $i\in \mathbb {Z}$
with
$i\in \mathbb {Z}$
with
![]() $|i|>n$
, and write
$|i|>n$
, and write
![]() $x'=T^{i}x$
and
$x'=T^{i}x$
and
![]() $y'=T^{i}y$
, so
$y'=T^{i}y$
, so
![]() $\pi x'=u'$
and
$\pi x'=u'$
and
![]() $\pi y'=v'$
. By assumption, there exists
$\pi y'=v'$
. By assumption, there exists
![]() $j\in \{-n,\ldots ,n\}$
such that
$j\in \{-n,\ldots ,n\}$
such that
![]() $\ell =u_{j}$
,
$\ell =u_{j}$
,
![]() $m=v_{j}$
satisfy
$m=v_{j}$
satisfy
![]() $1{\kern-1pt}\leq{\kern-1pt} \ell {\kern-1pt}\neq{\kern-1pt} m{\kern-1pt}\leq{\kern-1pt} n$
, and there is a
$1{\kern-1pt}\leq{\kern-1pt} \ell {\kern-1pt}\neq{\kern-1pt} m{\kern-1pt}\leq{\kern-1pt} n$
, and there is a
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
![]() $u^{\prime }_{j}=v^{\prime }_{j}=k$
. In other words,
$u^{\prime }_{j}=v^{\prime }_{j}=k$
. In other words,
![]() $T^{j}x\in C_{\ell }$
,
$T^{j}x\in C_{\ell }$
,
![]() $T^{j}y\in C_{m}$
, and
$T^{j}y\in C_{m}$
, and
![]() $T^{j}x',T^{j}y'\in C_{k}$
. Thus, using the max-metric
$T^{j}x',T^{j}y'\in C_{k}$
. Thus, using the max-metric
![]() $d_{\infty }$
on
$d_{\infty }$
on
![]() $X\times X$
,
$X\times X$
,
 $$ \begin{align*} \delta & \leq\delta_{\ell,m}\\ & \leq\max\{d(C_{\ell},C_{k}),d(C_{k},C_{m})\}\\ & \leq\max\{d(T^{j}x,T^{j}x'),d(T^{j}y',T^{j}y)\}\\ & =d_{\infty}(T^{j}(x,y),T^{j}(x',y')), \end{align*} $$
$$ \begin{align*} \delta & \leq\delta_{\ell,m}\\ & \leq\max\{d(C_{\ell},C_{k}),d(C_{k},C_{m})\}\\ & \leq\max\{d(T^{j}x,T^{j}x'),d(T^{j}y',T^{j}y)\}\\ & =d_{\infty}(T^{j}(x,y),T^{j}(x',y')), \end{align*} $$
where, for brevity, in the last line, we wrote T for
![]() $T\times T$
. Since
$T\times T$
. Since
![]() $-n\leq j\leq n$
and T is a homeomorphism, this implies
$-n\leq j\leq n$
and T is a homeomorphism, this implies
for some
![]() $\delta '>0$
depending only on
$\delta '>0$
depending only on
![]() $\delta ,n$
. Since i was arbitrary and
$\delta ,n$
. Since i was arbitrary and
![]() $(x',y')=T^{i}(x,y)$
, this proves non-recurrence of
$(x',y')=T^{i}(x,y)$
, this proves non-recurrence of
![]() $(x,y)$
.
$(x,y)$
.
3 Infinite entropy systems are not tight
In this section, we discuss Theorem 1.2, which says that a measure-preserving system of infinite entropy is not tight. Our contribution to this topic is a small adaptation of the the argument appearing in the original paper of Ornstein and Weiss for the finite-entropy case [Reference Ornstein and Weiss5]. We do not reproduce the full proof, but briefly outline the argument and the necessary changes.
3.1 The original argument
In the original proof, one begins with a measure-preserving system
![]() $(X,\mathcal {B},\mu ,T)$
with
$(X,\mathcal {B},\mu ,T)$
with
![]() $X=\{1,\ldots ,a\}^{\mathbb {Z}}$
, T the shift, and
$X=\{1,\ldots ,a\}^{\mathbb {Z}}$
, T the shift, and
![]() $h_{\mu }(T)\in (0,\infty )$
. Let
$h_{\mu }(T)\in (0,\infty )$
. Let
![]() $\mathcal {P}=\{P_{1},\ldots ,P_{a}\}$
be the partition according to the symbol at time zero. Let
$\mathcal {P}=\{P_{1},\ldots ,P_{a}\}$
be the partition according to the symbol at time zero. Let
![]() $E\subseteq X$
be a null set; we wish to find
$E\subseteq X$
be a null set; we wish to find
![]() $x,y\in X\setminus E$
with
$x,y\in X\setminus E$
with
![]() $\overline {d}(x,y)=0$
.
$\overline {d}(x,y)=0$
.
Choose an open set
![]() $U\supseteq E$
of measure small enough that the partition
$U\supseteq E$
of measure small enough that the partition
generates a factor
![]() $X_{0}$
of X of entropy less than
$X_{0}$
of X of entropy less than
![]() $h_{\mu }(T)$
. Now one constructs a tower of measure-theoretic factors
$h_{\mu }(T)$
. Now one constructs a tower of measure-theoretic factors
![]() $X_{n}$
between X and
$X_{n}$
between X and
![]() $X_{0}$
,
$X_{0}$
,
such that
![]() $X_{n}$
is generated by a finite partition
$X_{n}$
is generated by a finite partition
![]() $\mathcal {Q}_{n}$
that refines
$\mathcal {Q}_{n}$
that refines
![]() $\mathcal {Q}_{n-1}$
, all the factors have entropy strictly less than
$\mathcal {Q}_{n-1}$
, all the factors have entropy strictly less than
![]() $h_{\mu }(X)$
, and there are numbers
$h_{\mu }(X)$
, and there are numbers
![]() $N_{1},N_{2}\cdots \in \mathbb {N}$
, such that:
$N_{1},N_{2}\cdots \in \mathbb {N}$
, such that:
If
![]() $x,y\in X$
map to the same point in
$x,y\in X$
map to the same point in
![]() $X_{n}$
, then the finite sequences
$X_{n}$
, then the finite sequences
![]() $x|_{[-N_{n},N_{n}]},y|_{[-N_{n},N_{n}]}$
agree on at least a
$x|_{[-N_{n},N_{n}]},y|_{[-N_{n},N_{n}]}$
agree on at least a
![]() $1-({1}/{n})$
faction of their coordinates.
$1-({1}/{n})$
faction of their coordinates.
Assuming this, for each n, use the fact that
![]() $X\rightarrow X_{n}$
has positive relative entropy to choose a pair
$X\rightarrow X_{n}$
has positive relative entropy to choose a pair
![]() $x^{(n)}\neq y^{(n)}$
that lie above the same point in
$x^{(n)}\neq y^{(n)}$
that lie above the same point in
![]() $X_{n}$
. This means that
$X_{n}$
. This means that
![]() $x^{(n)},y^{(n)}$
project to the same point in
$x^{(n)},y^{(n)}$
project to the same point in
![]() $X_{0}$
as well. By shifting the points if necessary, we can assume
$X_{0}$
as well. By shifting the points if necessary, we can assume
![]() $x_{0}^{(n)}\neq y_{0}^{(n)}$
, and hence
$x_{0}^{(n)}\neq y_{0}^{(n)}$
, and hence
![]() $x^{(n)},y^{(n)}\in X\setminus U$
, for otherwise, they would lie in different atoms of
$x^{(n)},y^{(n)}\in X\setminus U$
, for otherwise, they would lie in different atoms of
![]() $\mathcal {Q}_{0}$
and hence project to different points in
$\mathcal {Q}_{0}$
and hence project to different points in
![]() $X_{0}$
.
$X_{0}$
.
Now pass to a subsequence so that
![]() $x^{(n)}\rightarrow x$
and
$x^{(n)}\rightarrow x$
and
![]() $y^{(n)}\rightarrow y$
. We still have
$y^{(n)}\rightarrow y$
. We still have
![]() $x_{0}\neq y_{0}$
so
$x_{0}\neq y_{0}$
so
![]() $x\neq y$
, and since
$x\neq y$
, and since
![]() $x^{(n)},y^{(n)}\in X\setminus U$
and U is open, also
$x^{(n)},y^{(n)}\in X\setminus U$
and U is open, also
![]() $x,y\in X\setminus U$
. However, every common shift
$x,y\in X\setminus U$
. However, every common shift
![]() $\widehat {x},\widehat {y}$
of
$\widehat {x},\widehat {y}$
of
![]() $x,y$
are limits of corresponding shifts
$x,y$
are limits of corresponding shifts
![]() $\widehat {x}^{(n)},\widehat {y}^{(n)}$
of
$\widehat {x}^{(n)},\widehat {y}^{(n)}$
of
![]() $x^{(n)},y^{(n)}$
, and
$x^{(n)},y^{(n)}$
, and
![]() $\widehat {x}^{(n)},\widehat {y}^{(n)}$
still project to the same point in
$\widehat {x}^{(n)},\widehat {y}^{(n)}$
still project to the same point in
![]() $X_{n}$
, so they agree on the central block
$X_{n}$
, so they agree on the central block
![]() $[-N_{n},N_{n}]$
except for a
$[-N_{n},N_{n}]$
except for a
![]() $1/n$
-fraction of the coordinates. This means that the same is true for
$1/n$
-fraction of the coordinates. This means that the same is true for
![]() $\widehat {x},\widehat {y}$
. What this argument shows is that on every block of length
$\widehat {x},\widehat {y}$
. What this argument shows is that on every block of length
![]() $2N_{n}$
, the points
$2N_{n}$
, the points
![]() $x,y$
agree on a
$x,y$
agree on a
![]() $1-({1}/{n})$
fraction of the coordinates. Thus,
$1-({1}/{n})$
fraction of the coordinates. Thus,
![]() $\overline {d}(x,y)<1/n$
for every n, and hence
$\overline {d}(x,y)<1/n$
for every n, and hence
![]() ${\overline {d}(x,y)=0}$
.
${\overline {d}(x,y)=0}$
.
To construct the factor
![]() $X_{n}$
(the partition
$X_{n}$
(the partition
![]() $\mathcal {Q}_{n}$
), for a large
$\mathcal {Q}_{n}$
), for a large
![]() $L_{n}\in \mathbb {N}$
, one wants to encode enough information about the
$L_{n}\in \mathbb {N}$
, one wants to encode enough information about the
![]() $(\mathcal {P},L_{n})$
-names so as to reveal a
$(\mathcal {P},L_{n})$
-names so as to reveal a
![]() $1-1/n$
fraction of the coordinates, but omit enough information that the entropy remains below
$1-1/n$
fraction of the coordinates, but omit enough information that the entropy remains below
![]() $h_{\mu }(T)$
. To achieve this, one partitions the typical
$h_{\mu }(T)$
. To achieve this, one partitions the typical
![]() $(\mathcal {P},L_{n})$
-names into families of names that are close in the hamming distance (that is, differ in a small fraction of their coordinates), and combinatorial estimates show that one can do so in a way that replacing
$(\mathcal {P},L_{n})$
-names into families of names that are close in the hamming distance (that is, differ in a small fraction of their coordinates), and combinatorial estimates show that one can do so in a way that replacing
![]() $(\mathcal {P},L_{n})$
-names by the name of the corresponding family gives the desired result.
$(\mathcal {P},L_{n})$
-names by the name of the corresponding family gives the desired result.
3.2 The infinite-entropy case
The reason this proof fails when
![]() $h_{\mu }(T)=\infty $
is that the system does not have a finite generator (indexed by a finite alphabet); and if we use an infinite alphabet, we lose compactness and cannot pass to the limit
$h_{\mu }(T)=\infty $
is that the system does not have a finite generator (indexed by a finite alphabet); and if we use an infinite alphabet, we lose compactness and cannot pass to the limit
![]() $x,y$
of
$x,y$
of
![]() $x^{(n)},y^{(n)}$
.
$x^{(n)},y^{(n)}$
.
Our observation is that the entire argument can be carried out relative to a factor Z of X, provided that the relative entropy is positive and finite. Indeed, a measure-theoretic factor Z of finite relative entropy can be obtained using standard techniques or, in a more heavy-handed manner, by appealing to the weak Pinsker property [Reference Austin1]. One can then realize the factor
![]() $X\rightarrow Z$
topologically with
$X\rightarrow Z$
topologically with
![]() $X=Z\times \{1,a\}^{\mathbb {Z}}$
and the factor being a projection to the first coordinate. From this point, the entire argument proceeds as before. One should note that the construction of the extension
$X=Z\times \{1,a\}^{\mathbb {Z}}$
and the factor being a projection to the first coordinate. From this point, the entire argument proceeds as before. One should note that the construction of the extension
![]() $X_{n}$
of
$X_{n}$
of
![]() $X_{n-1}$
in Ornstein and Weiss’s original paper already involves a relative argument, considering typical names in X relative to
$X_{n-1}$
in Ornstein and Weiss’s original paper already involves a relative argument, considering typical names in X relative to
![]() $X_{n-1}$
, and this can be carried out just as well when
$X_{n-1}$
, and this can be carried out just as well when
![]() $X_{n-1}$
contains the factor Z. We leave the details to the interested reader.
$X_{n-1}$
contains the factor Z. We leave the details to the interested reader.
Acknowledgement
This research was supported by ISF research grant 3056/21.