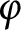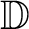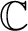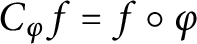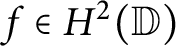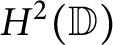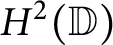1 Preliminaries
Let
![]() $\mathbb {D}$
denote the open unit disk of the complex plane
$\mathbb {D}$
denote the open unit disk of the complex plane
![]() $\mathbb {C}$
, and let
$\mathbb {C}$
, and let
![]() $H^2(\mathbb {D})$
denote the Hardy space over
$H^2(\mathbb {D})$
denote the Hardy space over
![]() $\mathbb {D}$
. For
$\mathbb {D}$
. For
![]() $\varphi $
a holomorphic self-map of
$\varphi $
a holomorphic self-map of
![]() $\mathbb {D}$
, define the composition operator
$\mathbb {D}$
, define the composition operator
![]() $C_\varphi $
on
$C_\varphi $
on
![]() $H^2(\mathbb {D})$
by
$H^2(\mathbb {D})$
by
 $$ \begin{align*} C_\varphi f = f \circ \varphi \qquad (f \in H^2(\mathbb{D})). \end{align*} $$
$$ \begin{align*} C_\varphi f = f \circ \varphi \qquad (f \in H^2(\mathbb{D})). \end{align*} $$
It follows from the Littlewood subordination principle that
![]() $C_\varphi \in \mathcal {B}(H^2(\mathbb {D}))$
[Reference Shapiro22]. Here
$C_\varphi \in \mathcal {B}(H^2(\mathbb {D}))$
[Reference Shapiro22]. Here
![]() $\mathcal {B}(H^2(\mathbb {D}))$
denotes the set of all bounded linear operators on
$\mathcal {B}(H^2(\mathbb {D}))$
denotes the set of all bounded linear operators on
![]() $H^2(\mathbb {D})$
.
$H^2(\mathbb {D})$
.
The theory of composition operators is highly interdisciplinary with its natural connections to complex analysis, linear dynamics, complex geometry, and functional analysis. For instance, the question of the existence of nontrivial invariant subspaces of bounded linear operators on Hilbert spaces can be formulated in terms of minimal invariant subspaces of composition operators induced by hyperbolic automorphisms of
![]() $\mathbb {D}$
[Reference Montes-Rodríguez, Ponce-Escudero and Shkarin18–Reference Nordgren, Rosenthal and Wintrobe20].
$\mathbb {D}$
[Reference Montes-Rodríguez, Ponce-Escudero and Shkarin18–Reference Nordgren, Rosenthal and Wintrobe20].
The theme of this paper is also in line with the invariant subspaces of composition operators, but restricted to model (or inner function based quotient) spaces of
![]() $H^2(\mathbb {D})$
. Recall that a function
$H^2(\mathbb {D})$
. Recall that a function
![]() $\theta \in H^\infty (\mathbb {D})$
is said to be inner if
$\theta \in H^\infty (\mathbb {D})$
is said to be inner if
![]() $|\theta | = 1$
a.e. on
$|\theta | = 1$
a.e. on
![]() $\partial \mathbb {D}$
in the sense of nontangential boundary values, where
$\partial \mathbb {D}$
in the sense of nontangential boundary values, where
![]() $H^\infty (\mathbb {D})$
denotes the commutative Banach algebra of all bounded holomorphic functions on
$H^\infty (\mathbb {D})$
denotes the commutative Banach algebra of all bounded holomorphic functions on
![]() $\mathbb {D}$
. Given an inner function
$\mathbb {D}$
. Given an inner function
![]() $\theta $
, the model space
$\theta $
, the model space
![]() $\mathcal {Q}_\theta $
is the quotient space
$\mathcal {Q}_\theta $
is the quotient space
The aim of this paper is to describe some results and methods of the calculation of model spaces that are invariant under composition operators. On the other hand, a celebrated result of Beurling [Reference Beurling1] states that a closed subspace
![]() $\mathcal {Q} \subseteq H^2(\mathbb {D})$
is invariant under
$\mathcal {Q} \subseteq H^2(\mathbb {D})$
is invariant under
![]() $M_z^*$
if and only if
$M_z^*$
if and only if
![]() $\mathcal {Q}$
is a model space. Here
$\mathcal {Q}$
is a model space. Here
![]() $M_zf = z f$
,
$M_zf = z f$
,
![]() $f \in H^2(\mathbb {D})$
, and
$f \in H^2(\mathbb {D})$
, and
![]() $M_z^*$
is the backward shift
$M_z^*$
is the backward shift
 $$ \begin{align*} M_z^* f= \frac{f(z) - f(0)}{z} \qquad (f \in H^2(\mathbb{D})). \end{align*} $$
$$ \begin{align*} M_z^* f= \frac{f(z) - f(0)}{z} \qquad (f \in H^2(\mathbb{D})). \end{align*} $$
In other words, we are interested in joint invariant subspaces of the (noncommuting) pair
![]() $(M_z^*, C_\varphi )$
on
$(M_z^*, C_\varphi )$
on
![]() $H^2(\mathbb {D})$
. Yet another motivation comes from the recent classification [Reference Bose, Muthukumar and Sarkar2] of joint invariant subspaces of the noncommuting pair
$H^2(\mathbb {D})$
. Yet another motivation comes from the recent classification [Reference Bose, Muthukumar and Sarkar2] of joint invariant subspaces of the noncommuting pair
![]() $(M_z, C_\varphi )$
on
$(M_z, C_\varphi )$
on
![]() $H^2(\mathbb {D})$
. In this context, we further remark that the concept of joint invariant subspaces of
$H^2(\mathbb {D})$
. In this context, we further remark that the concept of joint invariant subspaces of
![]() $(M_z, C_\varphi )$
was independently introduced by Chalendar and Partington [Reference Chalendar and Partington4] and Mahvidi [Reference Mahvidi16]. For recent results related to the subject we refer to [Reference Bose, Muthukumar and Sarkar2, Reference Jones14, Reference Matache17] and the references therein.
$(M_z, C_\varphi )$
was independently introduced by Chalendar and Partington [Reference Chalendar and Partington4] and Mahvidi [Reference Mahvidi16]. For recent results related to the subject we refer to [Reference Bose, Muthukumar and Sarkar2, Reference Jones14, Reference Matache17] and the references therein.
Often, results on composition operators are case-based. For instance, the theory of
![]() $C_{\varphi }$
corresponding to the holomorphic self-map of
$C_{\varphi }$
corresponding to the holomorphic self-map of
![]() $\mathbb {D}$
as
$\mathbb {D}$
as
 $$ \begin{align*} \varphi(z) = az+b \text{ or } \frac{az+b}{cz+d} \end{align*} $$
$$ \begin{align*} \varphi(z) = az+b \text{ or } \frac{az+b}{cz+d} \end{align*} $$
is extremely demanding and complete answers to many basic questions are not known (cf. [Reference Deddens7, Reference Cowen6], and also see [Reference Gallardo-Gutiérrez and Schroderus11, Reference Lefèvre, Li, Queffélec and Rodríguez-Piazza15] for more recent accounts). Even norm computations and invariant subspaces of
![]() $C_\varphi $
for linear fractional transformations are known to be case-based (cf. [Reference Bourdon, Fry, Hammond and Spofford3, Reference Montes-Rodríguez, Ponce-Escudero and Shkarin18]). In fact, the results of this paper are also no exception. For example, Theorem 3.1 states: Let
$C_\varphi $
for linear fractional transformations are known to be case-based (cf. [Reference Bourdon, Fry, Hammond and Spofford3, Reference Montes-Rodríguez, Ponce-Escudero and Shkarin18]). In fact, the results of this paper are also no exception. For example, Theorem 3.1 states: Let
![]() $\varphi $
be a holomorphic self-map of
$\varphi $
be a holomorphic self-map of
![]() $\mathbb {D}$
. Fix
$\mathbb {D}$
. Fix
![]() $\alpha \in \mathbb {D}$
and
$\alpha \in \mathbb {D}$
and
![]() $n \in \mathbb {N}$
, and consider the inner function
$n \in \mathbb {N}$
, and consider the inner function
 $$ \begin{align*} \theta(z)=\left(\frac{z- \alpha}{1-\bar{\alpha}z}\right)^n \qquad (z \in \mathbb{D}). \end{align*} $$
$$ \begin{align*} \theta(z)=\left(\frac{z- \alpha}{1-\bar{\alpha}z}\right)^n \qquad (z \in \mathbb{D}). \end{align*} $$
Then
![]() $\mathcal {Q}_\theta $
is invariant under
$\mathcal {Q}_\theta $
is invariant under
![]() $C_\varphi $
if and only if there exist scalars
$C_\varphi $
if and only if there exist scalars
![]() $a,b$
, and
$a,b$
, and
![]() $c (\neq 0)$
such that
$c (\neq 0)$
such that
 $$ \begin{align} \varphi(z)= \begin{cases} a + bz, & \mbox{if } \alpha = 0 \text{ and } n> 1, \\ \frac{1-c}{\bar{\alpha}} + cz, & \mbox{if } \alpha \neq 0, \end{cases} \end{align} $$
$$ \begin{align} \varphi(z)= \begin{cases} a + bz, & \mbox{if } \alpha = 0 \text{ and } n> 1, \\ \frac{1-c}{\bar{\alpha}} + cz, & \mbox{if } \alpha \neq 0, \end{cases} \end{align} $$
where,
![]() $|a| + |b| \leq 1$
and
$|a| + |b| \leq 1$
and
 $|\frac {1-c}{\bar {\alpha }}| + |c| \leq 1$
.
$|\frac {1-c}{\bar {\alpha }}| + |c| \leq 1$
.
Note that the above model space
![]() $\mathcal {Q}_\theta $
is an n-dimensional Hilbert space. Even though we all know the structure of finite-dimensional model spaces (they are essentially parameterized by n-Blaschke products), but we do not know a general method to classify holomorphic self-maps
$\mathcal {Q}_\theta $
is an n-dimensional Hilbert space. Even though we all know the structure of finite-dimensional model spaces (they are essentially parameterized by n-Blaschke products), but we do not know a general method to classify holomorphic self-maps
![]() $\varphi $
of
$\varphi $
of
![]() $\mathbb {D}$
for which a given finite-dimensional model space remains invariant under
$\mathbb {D}$
for which a given finite-dimensional model space remains invariant under
![]() $C_\varphi $
(see Question 3.3). In order to make this problem more convincing, in Proposition 3.4, we consider the two-dimensional model space
$C_\varphi $
(see Question 3.3). In order to make this problem more convincing, in Proposition 3.4, we consider the two-dimensional model space
![]() $\mathcal {Q}_\theta $
corresponding to the (special) Blaschke product
$\mathcal {Q}_\theta $
corresponding to the (special) Blaschke product
![]() $\theta (z) = z \frac {z- \alpha }{1 - \bar {\alpha } z}$
,
$\theta (z) = z \frac {z- \alpha }{1 - \bar {\alpha } z}$
,
![]() $z \in \mathbb {D}$
, and prove that
$z \in \mathbb {D}$
, and prove that
![]() $C_{\varphi } \mathcal {Q}_\theta \subseteq \mathcal {Q}_\theta $
if and only if
$C_{\varphi } \mathcal {Q}_\theta \subseteq \mathcal {Q}_\theta $
if and only if
![]() $\varphi $
is the special Möbius map
$\varphi $
is the special Möbius map
 $$ \begin{align*} \varphi(z) = \frac{(c_1 - 1) + (\bar{\alpha} + c_2) z}{\bar{\alpha}(c_1 + c_2z)} \qquad (z \in \mathbb{D}), \end{align*} $$
$$ \begin{align*} \varphi(z) = \frac{(c_1 - 1) + (\bar{\alpha} + c_2) z}{\bar{\alpha}(c_1 + c_2z)} \qquad (z \in \mathbb{D}), \end{align*} $$
for some scalars
![]() $c_1$
and
$c_1$
and
![]() $c_2$
such that at least one of them is nonzero (see (3.2)). The above answers do not seem to tell us much about a possible answer to our general question.
$c_2$
such that at least one of them is nonzero (see (3.2)). The above answers do not seem to tell us much about a possible answer to our general question.
We also put special emphasis on composition operators induced by linear fractional symbols (cf. Theorem 4.5): Let
![]() $\theta $
be an inner function, and let
$\theta $
be an inner function, and let
 $\varphi (z)= \frac {az+b}{cz+d}$
be a nonconstant holomorphic self-map of
$\varphi (z)= \frac {az+b}{cz+d}$
be a nonconstant holomorphic self-map of
![]() $\mathbb {D}$
, where
$\mathbb {D}$
, where
![]() $ad - bc = 1$
. Suppose
$ad - bc = 1$
. Suppose
 $\sigma (z)= \frac {\bar {a}z-\bar {c}}{-\bar {b}z+\bar {d}}$
and
$\sigma (z)= \frac {\bar {a}z-\bar {c}}{-\bar {b}z+\bar {d}}$
and
![]() $\theta (0) = 0$
. If we denote
$\theta (0) = 0$
. If we denote
 $\psi = (\frac {\theta }{z}\circ \sigma )(\frac {\theta }{z})^{-1}$
, then the following are equivalent:
$\psi = (\frac {\theta }{z}\circ \sigma )(\frac {\theta }{z})^{-1}$
, then the following are equivalent:
-
(1)
 $\mathcal {Q}_\theta $
is invariant under
$\mathcal {Q}_\theta $
is invariant under
 $C_\varphi $
.
$C_\varphi $
. -
(2)
 $\psi \in H^2(\mathbb {D})$
or
$\psi \in H^2(\mathbb {D})$
or
 $\psi \in H^\infty (\mathbb {D})$
.
$\psi \in H^\infty (\mathbb {D})$
. -
(3)
 $\frac {\theta }{z}H^2(\mathbb {D})$
is invariant under
$\frac {\theta }{z}H^2(\mathbb {D})$
is invariant under
 $C_\sigma $
.
$C_\sigma $
.
A similar (but not same as above) consideration also holds for composition operators induced by affine transformations (see Theorem 4.3).
In the application part, we consider direct interpretations of our results to simple model spaces and reducing subspaces of composition operators. For instance, Theorem 5.3 states that:
-
(1)
 $\mathcal {Q}_\theta $
is invariant under
$\mathcal {Q}_\theta $
is invariant under
 $C_\varphi $
for all inner function
$C_\varphi $
for all inner function
 $\theta $
if and only if
$\theta $
if and only if
 $\varphi $
is the identity map.
$\varphi $
is the identity map. -
(2)
 $\mathcal {Q}_\theta $
is invariant under
$\mathcal {Q}_\theta $
is invariant under
 $C_\varphi $
for all holomorphic self-map
$C_\varphi $
for all holomorphic self-map
 $\varphi $
if and only if
$\varphi $
if and only if
 $\theta (z)=\alpha z$
or
$\theta (z)=\alpha z$
or
 $\theta \equiv \alpha $
, where
$\theta \equiv \alpha $
, where
 $\alpha $
is an unimodular constant.
$\alpha $
is an unimodular constant.
We now discuss the issue of reducing subspaces of composition operators from our perspective. Let T be a bounded linear operator on a Hilbert space
![]() $\mathcal {H}$
. A closed subspace
$\mathcal {H}$
. A closed subspace
![]() $\mathcal {M} \subseteq \mathcal {H}$
is called reducing subspace for T (or
$\mathcal {M} \subseteq \mathcal {H}$
is called reducing subspace for T (or
![]() $\mathcal {M}$
reduces T) if both
$\mathcal {M}$
reduces T) if both
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {M}^{\bot }$
are invariant under T. It is known that
$\mathcal {M}^{\bot }$
are invariant under T. It is known that
![]() $M_z$
on
$M_z$
on
![]() $H^2(\mathbb {D})$
is irreducible, that is,
$H^2(\mathbb {D})$
is irreducible, that is,
![]() $M_z$
has no nontrivial reducing subspaces. In the setting of composition operators, if
$M_z$
has no nontrivial reducing subspaces. In the setting of composition operators, if
![]() $\alpha \in \mathbb {C}$
with
$\alpha \in \mathbb {C}$
with
![]() $\text {Re}(\alpha )> 0$
, then
$\text {Re}(\alpha )> 0$
, then
![]() $C_{\varphi _{\alpha }}$
is also irreducible [Reference Montes-Rodríguez, Ponce-Escudero and Shkarin18, Theorem 1.3], where
$C_{\varphi _{\alpha }}$
is also irreducible [Reference Montes-Rodríguez, Ponce-Escudero and Shkarin18, Theorem 1.3], where
 $$ \begin{align*} \varphi_{\alpha}(z)=\frac{(2- \alpha )z+ \alpha}{-\alpha z+(2+ \alpha)} \qquad (z \in \mathbb{D}). \end{align*} $$
$$ \begin{align*} \varphi_{\alpha}(z)=\frac{(2- \alpha )z+ \alpha}{-\alpha z+(2+ \alpha)} \qquad (z \in \mathbb{D}). \end{align*} $$
Another example is the composition operator corresponding to univalent loxodromic type self-map with nonzero Denjoy–Wolff point [Reference Guyker13, Theorem 1]. At the other extreme, we discuss reducibility of compositor operators restricted to model spaces. In Theorem 5.5, we prove the following: Let
![]() $\varphi $
be a holomorphic self-map of
$\varphi $
be a holomorphic self-map of
![]() $\mathbb {D}$
,
$\mathbb {D}$
,
![]() $\alpha \in \mathbb {D}$
,
$\alpha \in \mathbb {D}$
,
![]() $n \geq 1$
, and suppose
$n \geq 1$
, and suppose
 $\theta (z)=\left (\frac {z- \alpha }{1-\bar {\alpha }z}\right )^n$
. Then
$\theta (z)=\left (\frac {z- \alpha }{1-\bar {\alpha }z}\right )^n$
. Then
![]() $\mathcal {Q}_\theta $
reduces
$\mathcal {Q}_\theta $
reduces
![]() $C_\varphi $
if and only if there exist a scalar c,
$C_\varphi $
if and only if there exist a scalar c,
![]() $|c| \leq 1$
, and
$|c| \leq 1$
, and
![]() $\psi \in H^\infty (\mathbb {D})$
,
$\psi \in H^\infty (\mathbb {D})$
,
![]() $\|\psi \|_{\infty } \leq 1$
, such that
$\|\psi \|_{\infty } \leq 1$
, such that
 $$ \begin{align*} \varphi(z)= \begin{cases} z \psi, & \mbox{if } \alpha = 0 \text{ and } n = 1, \\ c z, & \mbox{if } \alpha = 0 \text{ and } n \geq 2,\\ z, & \mbox{if } \alpha \neq 0. \end{cases} \end{align*} $$
$$ \begin{align*} \varphi(z)= \begin{cases} z \psi, & \mbox{if } \alpha = 0 \text{ and } n = 1, \\ c z, & \mbox{if } \alpha = 0 \text{ and } n \geq 2,\\ z, & \mbox{if } \alpha \neq 0. \end{cases} \end{align*} $$
Finally, we make a general remark. Recall that a linear fractional transformation
 $\varphi (z) = \frac {az+b}{cz+d}$
is a self-map of
$\varphi (z) = \frac {az+b}{cz+d}$
is a self-map of
![]() $\mathbb {D}$
if and only if
$\mathbb {D}$
if and only if
In particular, since
![]() $\varphi $
is a holomorphic self-map, the inequalities following (1.1) are automatically true. In this paper, whenever no confusion can arise, we will not explicitly mention the above inequality for linear fractional transformations that are self-maps of
$\varphi $
is a holomorphic self-map, the inequalities following (1.1) are automatically true. In this paper, whenever no confusion can arise, we will not explicitly mention the above inequality for linear fractional transformations that are self-maps of
![]() $\mathbb {D}$
. In particular, the above inequality is applicable to Theorem 3.1, Example 3.4, and Theorem 4.3.
$\mathbb {D}$
. In particular, the above inequality is applicable to Theorem 3.1, Example 3.4, and Theorem 4.3.
The rest of the paper is organized as follows. Section 2 recalls (rather a modified version of) the classification of Beurling type invariant subspaces from [Reference Bose, Muthukumar and Sarkar2]. Section 3 relates affine transformations and certain finite-dimensional model spaces. Section 4 deals with model subspaces invariant under composition operators corresponding to fractional linear transformations. The final section, Section 5, deals with some of the direct applications of our main results. We also discuss reducible composition operators at the level of model spaces.
2 Beurling type invariant subspaces
The purpose of this short section is to recall the classification of Beurling type invariant subspaces of composition operators from [Reference Bose, Muthukumar and Sarkar2].
We begin with the formal definition of Hardy space
![]() $H^2(\mathbb {D})$
. Recall that the Hardy space is the function Hilbert space of all holomorphic functions on
$H^2(\mathbb {D})$
. Recall that the Hardy space is the function Hilbert space of all holomorphic functions on
![]() $\mathbb {D}$
whose power series have square-summable coefficients. The following equivalent description of
$\mathbb {D}$
whose power series have square-summable coefficients. The following equivalent description of
![]() $H^2(\mathbb {D})$
is also well known:
$H^2(\mathbb {D})$
is also well known:
 $$ \begin{align*} H^2(\mathbb{D}) = \Big\{f \in \text{Hol}(\mathbb{D}): \|f\|:= \Big[\sup_{0 \leq r < 1} \frac{1}{2 \pi} \int_{0}^{2\pi} |f(r e^{it})|^2 dt\Big]^{\frac{1}{2}} < \infty\Big\}. \end{align*} $$
$$ \begin{align*} H^2(\mathbb{D}) = \Big\{f \in \text{Hol}(\mathbb{D}): \|f\|:= \Big[\sup_{0 \leq r < 1} \frac{1}{2 \pi} \int_{0}^{2\pi} |f(r e^{it})|^2 dt\Big]^{\frac{1}{2}} < \infty\Big\}. \end{align*} $$
Also, we denote the closed unit ball of
![]() $H^\infty (\mathbb {D})$
(which is popularly known as Schur class) by
$H^\infty (\mathbb {D})$
(which is popularly known as Schur class) by
 $$ \begin{align*} {\mathcal S}(\mathbb{D}) = \{\psi \in H^\infty(\mathbb{D}): \|\psi\|_\infty: = \sup_{z \in \mathbb{D}} |\psi(z)| \leq 1\}. \end{align*} $$
$$ \begin{align*} {\mathcal S}(\mathbb{D}) = \{\psi \in H^\infty(\mathbb{D}): \|\psi\|_\infty: = \sup_{z \in \mathbb{D}} |\psi(z)| \leq 1\}. \end{align*} $$
We will follow the standard notation: Given a bounded linear operator T on some Hilbert space
![]() $\mathcal {H}$
, the lattice of all closed T-invariant subspaces is denoted by
$\mathcal {H}$
, the lattice of all closed T-invariant subspaces is denoted by
![]() $\mathrm{Lat} T$
, that is
$\mathrm{Lat} T$
, that is
By Beurling’s Theorem, we know that
and
A closed subspace
![]() $\mathcal {S} \subseteq H^2(\mathbb {D})$
is said to be a Beurling type invariant subspace if
$\mathcal {S} \subseteq H^2(\mathbb {D})$
is said to be a Beurling type invariant subspace if
![]() $\mathcal {S} = \theta H^2(\mathbb {D})$
for some inner function
$\mathcal {S} = \theta H^2(\mathbb {D})$
for some inner function
![]() $\theta $
, or equivalently (in view of Beurling),
$\theta $
, or equivalently (in view of Beurling),
![]() $\mathcal {S}$
is invariant under
$\mathcal {S}$
is invariant under
![]() $M_z$
. The following theorem is a simple refinement of [Reference Bose, Muthukumar and Sarkar2, Theorem 2.3]. We only prove the new component of the result.
$M_z$
. The following theorem is a simple refinement of [Reference Bose, Muthukumar and Sarkar2, Theorem 2.3]. We only prove the new component of the result.
Theorem 2.1 Let
![]() $\theta $
be an inner function and
$\theta $
be an inner function and
![]() $\varphi $
be a holomorphic self-map of
$\varphi $
be a holomorphic self-map of
![]() $\mathbb {D}$
. The following are equivalent:
$\mathbb {D}$
. The following are equivalent:
-
(1)
 $\theta H^2(\mathbb {D}) \in \mathrm{Lat} C_\varphi $
.
$\theta H^2(\mathbb {D}) \in \mathrm{Lat} C_\varphi $
. -
(2)
 $\frac {\theta \circ \varphi }{\theta }\in {\mathcal S}(\mathbb {D})$
.
$\frac {\theta \circ \varphi }{\theta }\in {\mathcal S}(\mathbb {D})$
. -
(3)
 $\frac {\theta \circ \varphi }{\theta }\in H^\infty (\mathbb {D})$
.
$\frac {\theta \circ \varphi }{\theta }\in H^\infty (\mathbb {D})$
. -
(4)
 $\frac {\theta \circ \varphi }{\theta }\in H^2(\mathbb {D})$
.
$\frac {\theta \circ \varphi }{\theta }\in H^2(\mathbb {D})$
.
Proof The equivalence
![]() $(1) \Leftrightarrow (2)$
follows from [Reference Bose, Muthukumar and Sarkar2, Theorem 2.3]. Since
$(1) \Leftrightarrow (2)$
follows from [Reference Bose, Muthukumar and Sarkar2, Theorem 2.3]. Since
it follows that
![]() $(2) \Rightarrow (3) \Rightarrow (4)$
. Therefore, it suffices to verify that
$(2) \Rightarrow (3) \Rightarrow (4)$
. Therefore, it suffices to verify that
![]() $(4) \Rightarrow (2)$
. Suppose that
$(4) \Rightarrow (2)$
. Suppose that
 $\frac {\theta \circ \varphi }{\theta }\in H^2(\mathbb {D})$
. Since
$\frac {\theta \circ \varphi }{\theta }\in H^2(\mathbb {D})$
. Since
![]() $\theta $
is inner, we have
$\theta $
is inner, we have
 $$ \begin{align*} \left|\frac{\theta\circ\varphi}{\theta}(e^{it})\right|= |(\theta\circ\varphi)(e^{it})|\leq 1 \mbox{~for all~} t\in [0,2 \pi] \mbox{~a.e.} \end{align*} $$
$$ \begin{align*} \left|\frac{\theta\circ\varphi}{\theta}(e^{it})\right|= |(\theta\circ\varphi)(e^{it})|\leq 1 \mbox{~for all~} t\in [0,2 \pi] \mbox{~a.e.} \end{align*} $$
Therefore,
 $\frac {\theta \circ \sigma }{\theta } \in H^\infty (\mathbb {D})$
with
$\frac {\theta \circ \sigma }{\theta } \in H^\infty (\mathbb {D})$
with
 $\left \|\frac {\theta \circ \varphi }{\theta }\right \|_\infty \leq 1$
[Reference Duren9, Theorem 2.11], that is,
$\left \|\frac {\theta \circ \varphi }{\theta }\right \|_\infty \leq 1$
[Reference Duren9, Theorem 2.11], that is,
 $\frac {\theta \circ \varphi }{\theta }\in {\mathcal S}(\mathbb {D})$
, which completes the proof of the theorem.▪
$\frac {\theta \circ \varphi }{\theta }\in {\mathcal S}(\mathbb {D})$
, which completes the proof of the theorem.▪
This result will play a key role in what follows.
3 Finite-dimensional model spaces
Recall that the Hardy space
![]() $H^2(\mathbb {D})$
is a reproducing kernel Hilbert space corresponding to the Szegö kernel
$H^2(\mathbb {D})$
is a reproducing kernel Hilbert space corresponding to the Szegö kernel
![]() $k: \mathbb {D} \times \mathbb {D} \rightarrow \mathbb {C}$
, where
$k: \mathbb {D} \times \mathbb {D} \rightarrow \mathbb {C}$
, where
Therefore, the linear span of
![]() $\{k(\cdot , w): w \in \mathbb {D}\}$
is dense in
$\{k(\cdot , w): w \in \mathbb {D}\}$
is dense in
![]() $H^2(\mathbb {D})$
, and
$H^2(\mathbb {D})$
, and
![]() $f(w) = \langle f, k(\cdot , w) \rangle _{H^2(\mathbb {D})}$
for all
$f(w) = \langle f, k(\cdot , w) \rangle _{H^2(\mathbb {D})}$
for all
![]() $f \in H^2(\mathbb {D})$
and
$f \in H^2(\mathbb {D})$
and
![]() $w \in \mathbb {D}$
. For each
$w \in \mathbb {D}$
. For each
![]() $\alpha \in \mathbb {D}$
, define the Blaschke factor
$\alpha \in \mathbb {D}$
, define the Blaschke factor
![]() $b_{\alpha }$
by
$b_{\alpha }$
by
 $$ \begin{align*} b_{\alpha}(z) = \frac{z - \alpha}{1 - \bar{\alpha} z} \qquad (z \in \mathbb{D}). \end{align*} $$
$$ \begin{align*} b_{\alpha}(z) = \frac{z - \alpha}{1 - \bar{\alpha} z} \qquad (z \in \mathbb{D}). \end{align*} $$
It is known that a model space
![]() $\mathcal {Q}_{\theta }$
is finite dimensional if and only if
$\mathcal {Q}_{\theta }$
is finite dimensional if and only if
![]() $\theta $
is a finite Blaschke product (cf. [Reference Radjavi and Rosenthal21, Theorem 3.8]). More specifically, if
$\theta $
is a finite Blaschke product (cf. [Reference Radjavi and Rosenthal21, Theorem 3.8]). More specifically, if
![]() $\text {dim}\mathcal {Q}_{\theta } = n < \infty $
, then there exists
$\text {dim}\mathcal {Q}_{\theta } = n < \infty $
, then there exists
![]() $\alpha _1, \ldots , \alpha _m \in \mathbb {D}$
, and
$\alpha _1, \ldots , \alpha _m \in \mathbb {D}$
, and
![]() $n_1, \ldots , n_m \in \mathbb {N}$
such that
$n_1, \ldots , n_m \in \mathbb {N}$
such that
![]() $\sum _{i=1}^m n_i = n$
and
$\sum _{i=1}^m n_i = n$
and
 $$ \begin{align*} \theta =\prod_{i=1}^{m} b_{\alpha_i}^{n_i}. \end{align*} $$
$$ \begin{align*} \theta =\prod_{i=1}^{m} b_{\alpha_i}^{n_i}. \end{align*} $$
Moreover,
 $\{c_{\alpha _i}^{(l_i)}: 0 \leq l_i \leq n_i-1, 1 \leq i \leq m\} $
is a basis for
$\{c_{\alpha _i}^{(l_i)}: 0 \leq l_i \leq n_i-1, 1 \leq i \leq m\} $
is a basis for
![]() $\mathcal {Q}_{\theta }$
(see [Reference Garcia, Mashreghi and Ross12, Proposition 5.16]), where
$\mathcal {Q}_{\theta }$
(see [Reference Garcia, Mashreghi and Ross12, Proposition 5.16]), where
 $$ \begin{align*} c_{\alpha}^{(t)} := \frac{z^{t}}{(1 - \bar{\alpha} z)^{t+1}} \qquad (t \in \mathbb{Z}_+). \end{align*} $$
$$ \begin{align*} c_{\alpha}^{(t)} := \frac{z^{t}}{(1 - \bar{\alpha} z)^{t+1}} \qquad (t \in \mathbb{Z}_+). \end{align*} $$
In the following, we prove that a “simple” finite dimensional model space is invariant under
![]() $C_\varphi $
if and only if
$C_\varphi $
if and only if
![]() $\varphi $
is a special affine map.
$\varphi $
is a special affine map.
Theorem 3.1 Let
![]() $\varphi $
be a holomorphic self-map of
$\varphi $
be a holomorphic self-map of
![]() $\mathbb {D}$
,
$\mathbb {D}$
,
![]() $\alpha \in \mathbb {D}$
,
$\alpha \in \mathbb {D}$
,
![]() $n \in \mathbb {N}$
, and suppose
$n \in \mathbb {N}$
, and suppose
 $\theta (z)=\left (\frac {z- \alpha }{1-\bar {\alpha }z}\right )^n$
. Then
$\theta (z)=\left (\frac {z- \alpha }{1-\bar {\alpha }z}\right )^n$
. Then
![]() $\mathcal {Q}_\theta \in \mathrm{Lat} C_\varphi $
if and only if there exist scalars
$\mathcal {Q}_\theta \in \mathrm{Lat} C_\varphi $
if and only if there exist scalars
![]() $a,b$
, and
$a,b$
, and
![]() $c (\neq 0)$
such that
$c (\neq 0)$
such that
 $$ \begin{align*} \varphi(z)= \begin{cases} a + bz, & \mbox{if } \alpha = 0 \text{ and } n> 1, \\ \frac{1-c}{\bar{\alpha}} + cz, & \mbox{if } \alpha \neq 0. \end{cases} \end{align*} $$
$$ \begin{align*} \varphi(z)= \begin{cases} a + bz, & \mbox{if } \alpha = 0 \text{ and } n> 1, \\ \frac{1-c}{\bar{\alpha}} + cz, & \mbox{if } \alpha \neq 0. \end{cases} \end{align*} $$
Proof In view of the preceding discussion, we have
 $$ \begin{align*} \mathcal{Q}_\theta = \left\{ \frac{p(z)}{(1- \bar{\alpha} z)^n}: p \in \mathbb{C}[z], \text{deg } p \leq n-1 \right\}\!. \end{align*} $$
$$ \begin{align*} \mathcal{Q}_\theta = \left\{ \frac{p(z)}{(1- \bar{\alpha} z)^n}: p \in \mathbb{C}[z], \text{deg } p \leq n-1 \right\}\!. \end{align*} $$
Suppose
![]() $\alpha = 0$
. Then
$\alpha = 0$
. Then
![]() $\theta (z)=z^n$
and
$\theta (z)=z^n$
and
Let
![]() $\varphi = a + bz$
. Clearly, if
$\varphi = a + bz$
. Clearly, if
 $f = \sum _{j=0}^{n-1} a_{j} z^{j} \in \mathcal {Q}_\theta $
, then
$f = \sum _{j=0}^{n-1} a_{j} z^{j} \in \mathcal {Q}_\theta $
, then
 $$ \begin{align*} f\circ \varphi = \sum_{j=0}^{n-1} a_{j} \varphi^{j} = \sum_{j=0}^{n-1} a_{j} (a + bz)^{j}, \end{align*} $$
$$ \begin{align*} f\circ \varphi = \sum_{j=0}^{n-1} a_{j} \varphi^{j} = \sum_{j=0}^{n-1} a_{j} (a + bz)^{j}, \end{align*} $$
and hence
![]() $C_\varphi f = f\circ \varphi \in \mathcal {Q}_\theta $
. For the converse part, suppose
$C_\varphi f = f\circ \varphi \in \mathcal {Q}_\theta $
. For the converse part, suppose
![]() $C_{\varphi } \mathcal {Q}_\theta \subseteq \mathcal {Q}_{\theta }$
. Since the identity map
$C_{\varphi } \mathcal {Q}_\theta \subseteq \mathcal {Q}_{\theta }$
. Since the identity map
![]() $f(z)=z$
,
$f(z)=z$
,
![]() $z \in \mathbb {D}$
, is in
$z \in \mathbb {D}$
, is in
![]() $\mathcal {Q}_\theta $
, if follows that
$\mathcal {Q}_\theta $
, if follows that
which implies that
![]() $\varphi $
is a polynomial. Also note that
$\varphi $
is a polynomial. Also note that
![]() $g \in \mathcal {Q}_\theta $
, where
$g \in \mathcal {Q}_\theta $
, where
![]() $g(z)=z^{n-1}$
,
$g(z)=z^{n-1}$
,
![]() $z \in \mathbb {D}$
. Then
$z \in \mathbb {D}$
. Then
which implies that
Since
![]() $n-1\neq 0$
, it follows that
$n-1\neq 0$
, it follows that
![]() $\mbox {deg}(\varphi )\leq 1$
, and hence
$\mbox {deg}(\varphi )\leq 1$
, and hence
![]() $\varphi $
is an affine map.
$\varphi $
is an affine map.
Now suppose that
![]() $\alpha \neq 0$
, and let
$\alpha \neq 0$
, and let
![]() $C_{\varphi } \mathcal {Q}_\theta \subseteq \mathcal {Q}_\theta $
. Since
$C_{\varphi } \mathcal {Q}_\theta \subseteq \mathcal {Q}_\theta $
. Since
![]() $k(\cdot , \alpha ) \in \mathcal {Q}_\theta $
, it follows that
$k(\cdot , \alpha ) \in \mathcal {Q}_\theta $
, it follows that
 $$ \begin{align*} k(\cdot, \alpha) \circ \varphi=\displaystyle\frac{1}{1-\bar{\alpha}\varphi} \in \mathcal{Q}_\theta, \end{align*} $$
$$ \begin{align*} k(\cdot, \alpha) \circ \varphi=\displaystyle\frac{1}{1-\bar{\alpha}\varphi} \in \mathcal{Q}_\theta, \end{align*} $$
and hence, there exists a polynomial p of degree
![]() $\leq n-1$
such that
$\leq n-1$
such that
 $$ \begin{align*} \frac{1}{1- \bar{\alpha} \varphi}=\frac{p(z)}{(1-\bar{\alpha}z)^n}. \end{align*} $$
$$ \begin{align*} \frac{1}{1- \bar{\alpha} \varphi}=\frac{p(z)}{(1-\bar{\alpha}z)^n}. \end{align*} $$
In particular,
![]() $\varphi $
is a nonconstant polynomial. Suppose
$\varphi $
is a nonconstant polynomial. Suppose
![]() $\mbox {deg}(\varphi )=m>0$
. Since
$\mbox {deg}(\varphi )=m>0$
. Since
 $$ \begin{align*} g = \frac{1}{(1-\bar{\alpha}z)^n} \in \mathcal{Q}_\theta, \end{align*} $$
$$ \begin{align*} g = \frac{1}{(1-\bar{\alpha}z)^n} \in \mathcal{Q}_\theta, \end{align*} $$
we have
 $$ \begin{align*} g\circ \varphi = \frac{1}{(1-\bar{\alpha}\varphi)^n}\in \mathcal{Q}_\theta. \end{align*} $$
$$ \begin{align*} g\circ \varphi = \frac{1}{(1-\bar{\alpha}\varphi)^n}\in \mathcal{Q}_\theta. \end{align*} $$
Thus, there exists
![]() $q \in \mathbb {C}[z]$
such that
$q \in \mathbb {C}[z]$
such that
Comparing the degrees of both sides, we have
![]() $mn\leq n$
, which implies
$mn\leq n$
, which implies
![]() $\mbox {deg}(\varphi )=1$
. Then
$\mbox {deg}(\varphi )=1$
. Then
![]() $\mbox {deg}(q)=0$
, and hence q is a nonzero constant. Therefore, there exists a nonzero scalar c such that
$\mbox {deg}(q)=0$
, and hence q is a nonzero constant. Therefore, there exists a nonzero scalar c such that
![]() $1-\bar {\alpha }\varphi =c (1-\bar {\alpha }z)$
, that is
$1-\bar {\alpha }\varphi =c (1-\bar {\alpha }z)$
, that is
 $$ \begin{align*} \varphi(z)= \frac{1-c}{\bar{\alpha}} + cz. \end{align*} $$
$$ \begin{align*} \varphi(z)= \frac{1-c}{\bar{\alpha}} + cz. \end{align*} $$
We now turn to the converse direction. Let
![]() $c \neq 0$
and
$c \neq 0$
and
 $\varphi (z)= \frac {1-c}{\bar {\alpha }}+cz$
. Then
$\varphi (z)= \frac {1-c}{\bar {\alpha }}+cz$
. Then
![]() $1 - \bar {\alpha } \varphi = c (1 - \bar {\alpha } z)$
, and hence
$1 - \bar {\alpha } \varphi = c (1 - \bar {\alpha } z)$
, and hence
 $$ \begin{align*} \left(\frac{1}{1- \bar{\alpha} \varphi} \right)^l\in \mbox{span}\left\{\frac{1}{(1- \bar{\alpha} z)^j}: j =1, \ldots, n \right\} = \mathcal{Q}_\theta \end{align*} $$
$$ \begin{align*} \left(\frac{1}{1- \bar{\alpha} \varphi} \right)^l\in \mbox{span}\left\{\frac{1}{(1- \bar{\alpha} z)^j}: j =1, \ldots, n \right\} = \mathcal{Q}_\theta \end{align*} $$
for all
![]() $l=1,2,\ldots , n$
. It follows that
$l=1,2,\ldots , n$
. It follows that
![]() $f\circ \varphi \in \mathcal {Q}_\theta $
for all
$f\circ \varphi \in \mathcal {Q}_\theta $
for all
![]() $f\in \mathcal {Q}_\theta $
. This completes the proof of the theorem.▪
$f\in \mathcal {Q}_\theta $
. This completes the proof of the theorem.▪
We would like to point out that even affine transformations (as symbols) play a prominent role in the complexity of composition operators (cf. Deddens [Reference Deddens7]).
Remark 3.2 In the context of Theorem 3.1, we note that if
![]() $\alpha = 0$
and
$\alpha = 0$
and
![]() $n = 1$
, then
$n = 1$
, then
![]() $\mathcal {Q}_z=(z H^2(\mathbb {D}))^{\bot }$
, which is the one dimensional subspace of all constant functions in
$\mathcal {Q}_z=(z H^2(\mathbb {D}))^{\bot }$
, which is the one dimensional subspace of all constant functions in
![]() $H^2(\mathbb {D})$
. Clearly,
$H^2(\mathbb {D})$
. Clearly,
![]() $\mathcal {Q}_z$
is invariant under every composition operator.
$\mathcal {Q}_z$
is invariant under every composition operator.
We do not know the answer to the following compelling question.
Question 3.3 Consider the finite Blaschke product
![]() $\prod _{i=1}^{m} b_{\alpha _i}$
corresponding to
$\prod _{i=1}^{m} b_{\alpha _i}$
corresponding to
![]() $\alpha _1, \ldots , \alpha _n \in \mathbb {D}$
. Characterize holomorphic self-maps
$\alpha _1, \ldots , \alpha _n \in \mathbb {D}$
. Characterize holomorphic self-maps
![]() $\varphi $
of
$\varphi $
of
![]() $\mathbb {D}$
such that
$\mathbb {D}$
such that
We also put forward the following simpler (two-dimensional) version: Suppose
![]() $\alpha \neq \beta $
in
$\alpha \neq \beta $
in
![]() $\mathbb {D}$
, and suppose
$\mathbb {D}$
, and suppose
![]() $\theta = b_{\alpha } b_{\beta }$
. Classify holomorphic self-maps
$\theta = b_{\alpha } b_{\beta }$
. Classify holomorphic self-maps
![]() $\varphi $
of
$\varphi $
of
![]() $\mathbb {D}$
such that
$\mathbb {D}$
such that
![]() $C_\varphi \mathcal {Q}_\theta \subseteq \mathcal {Q}_\theta $
.
$C_\varphi \mathcal {Q}_\theta \subseteq \mathcal {Q}_\theta $
.
We do not know the complete answer to this question but the following special case (
![]() $\alpha \neq 0$
and
$\alpha \neq 0$
and
![]() $\beta = 0$
):
$\beta = 0$
):
Proposition 3.4 Let
![]() $\alpha \in \mathbb {D}$
be a nonzero scalar, and suppose
$\alpha \in \mathbb {D}$
be a nonzero scalar, and suppose
![]() $\theta = z b_{\alpha }$
. Let
$\theta = z b_{\alpha }$
. Let
![]() $\varphi $
be a holomorphic self-map of
$\varphi $
be a holomorphic self-map of
![]() $\mathbb {D}$
. Then
$\mathbb {D}$
. Then
![]() $C_{\varphi } \mathcal {Q}_\theta \subseteq \mathcal {Q}_\theta $
if and only if
$C_{\varphi } \mathcal {Q}_\theta \subseteq \mathcal {Q}_\theta $
if and only if
![]() $\varphi $
is the special Möbius map
$\varphi $
is the special Möbius map
 $$ \begin{align} \varphi(z) = \frac{(c_1 - 1) + (\bar{\alpha} + c_2) z}{\bar{\alpha}(c_1 + c_2z)} \qquad (z \in \mathbb{D}), \end{align} $$
$$ \begin{align} \varphi(z) = \frac{(c_1 - 1) + (\bar{\alpha} + c_2) z}{\bar{\alpha}(c_1 + c_2z)} \qquad (z \in \mathbb{D}), \end{align} $$
for some scalars
![]() $c_1$
and
$c_1$
and
![]() $c_2$
such that at least one of them is nonzero.
$c_2$
such that at least one of them is nonzero.
Proof Here the two-dimensional model space
![]() $\mathcal {Q}_\theta $
is given by
$\mathcal {Q}_\theta $
is given by
![]() $\mathcal {Q}_\theta = \text {span} \{1, k(\cdot , \alpha )\}$
. As the space of all constant functions is invariant under every composition operators (see Remark 3.2),
$\mathcal {Q}_\theta = \text {span} \{1, k(\cdot , \alpha )\}$
. As the space of all constant functions is invariant under every composition operators (see Remark 3.2),
![]() $\mathcal {Q}_\theta $
is invariant under
$\mathcal {Q}_\theta $
is invariant under
![]() $C_\varphi $
if and only if
$C_\varphi $
if and only if
 $$ \begin{align*} k(\cdot, \alpha) \circ \varphi = \frac{1}{1 - \bar{\alpha} \varphi} \in \mathcal{Q}_\theta. \end{align*} $$
$$ \begin{align*} k(\cdot, \alpha) \circ \varphi = \frac{1}{1 - \bar{\alpha} \varphi} \in \mathcal{Q}_\theta. \end{align*} $$
This is equivalent to the fact that
 $$ \begin{align*} \frac{1}{1 - \bar{\alpha} \varphi} = \frac{c_1 + c_2 z}{1 - \bar{\alpha} z} \qquad (z \in \mathbb{D}), \end{align*} $$
$$ \begin{align*} \frac{1}{1 - \bar{\alpha} \varphi} = \frac{c_1 + c_2 z}{1 - \bar{\alpha} z} \qquad (z \in \mathbb{D}), \end{align*} $$
for some scalars
![]() $c_1$
and
$c_1$
and
![]() $c_2$
such that at least one of them is nonzero, which is equivalent to (3.2). This completes the proof of the proposition.▪
$c_2$
such that at least one of them is nonzero, which is equivalent to (3.2). This completes the proof of the proposition.▪
Putting together the representations of linear fractional transformations from (3.2) and Theorem 3.1, it is perhaps evident that the answer to Question 3.3 will be also case-based.
4 Linear fractional symbols
Our aim in this section is to describe the structure of model invariant subspaces of composition operators whose symbols are linear fractional transformations mapping
![]() $\mathbb {D}$
into itself. We are also motivated by the intricate analysis presented in Cowen [Reference Cowen6] and Deddens [Reference Deddens7].
$\mathbb {D}$
into itself. We are also motivated by the intricate analysis presented in Cowen [Reference Cowen6] and Deddens [Reference Deddens7].
Before we begin with a general observation, we introduce the following (standard) notation: For each
![]() $\varphi \in H^\infty (\mathbb {D})$
, we denote by
$\varphi \in H^\infty (\mathbb {D})$
, we denote by
![]() $M_\varphi $
the multiplication operator
$M_\varphi $
the multiplication operator
![]() ${M_\varphi f = \varphi f}$
,
${M_\varphi f = \varphi f}$
,
![]() $f \in H^2(\mathbb {D})$
. It is well known that
$f \in H^2(\mathbb {D})$
. It is well known that
![]() $M_\varphi \in \mathcal {B}(H^2(\mathbb {D}))$
with
$M_\varphi \in \mathcal {B}(H^2(\mathbb {D}))$
with
![]() $\|M_\varphi \| = \|\varphi \|_{\infty }$
for all
$\|M_\varphi \| = \|\varphi \|_{\infty }$
for all
![]() $\varphi \in H^\infty (\mathbb {D})$
, and
$\varphi \in H^\infty (\mathbb {D})$
, and
![]() $\{M_z\}' = \{M_{\varphi }: \varphi \in H^\infty (\mathbb {D})\}$
, where
$\{M_z\}' = \{M_{\varphi }: \varphi \in H^\infty (\mathbb {D})\}$
, where
![]() $\{M_z\}'$
denotes the commutator of
$\{M_z\}'$
denotes the commutator of
![]() $M_z$
.
$M_z$
.
Let
![]() $\varphi $
be a holomorphic self-map of
$\varphi $
be a holomorphic self-map of
![]() $\mathbb {D}$
and let
$\mathbb {D}$
and let
![]() $\theta $
be an inner function. Clearly,
$\theta $
be an inner function. Clearly,
![]() $C_\varphi \mathcal {Q}_\theta \subseteq \mathcal {Q}_\theta $
if and only if
$C_\varphi \mathcal {Q}_\theta \subseteq \mathcal {Q}_\theta $
if and only if
 $C_\varphi ^*(\theta H^2(\mathbb {D})) \subseteq \theta H^2(\mathbb {D})$
, which is, by the Douglas range inclusion theorem [Reference Douglas8, Theorem 1] (as
$C_\varphi ^*(\theta H^2(\mathbb {D})) \subseteq \theta H^2(\mathbb {D})$
, which is, by the Douglas range inclusion theorem [Reference Douglas8, Theorem 1] (as
 $\mbox {ran} (C_{\varphi }^* M_{\theta }) \subseteq \mbox {ran} M_{\theta }$
), equivalent to the existence of some
$\mbox {ran} (C_{\varphi }^* M_{\theta }) \subseteq \mbox {ran} M_{\theta }$
), equivalent to the existence of some
![]() $X \in \mathcal {B}(H^2(\mathbb {D}))$
such that
$X \in \mathcal {B}(H^2(\mathbb {D}))$
such that
 $$ \begin{align*} C_\varphi^* M_\theta= M_\theta X. \end{align*} $$
$$ \begin{align*} C_\varphi^* M_\theta= M_\theta X. \end{align*} $$
Now if the above equality holds, then
 $\theta X(f) = C_{\varphi }^*(\theta f)$
for all
$\theta X(f) = C_{\varphi }^*(\theta f)$
for all
![]() $f \in H^2(\mathbb {D})$
, and hence zeros of
$f \in H^2(\mathbb {D})$
, and hence zeros of
![]() $\theta $
are also zeros of
$\theta $
are also zeros of
 $C_{\varphi }^*(\theta f)$
and
$C_{\varphi }^*(\theta f)$
and
 $$ \begin{align*} \text{multiplicity}_{w} \theta \leq \text{multiplicity}_{w} C_{\varphi}^*(\theta f), \end{align*} $$
$$ \begin{align*} \text{multiplicity}_{w} \theta \leq \text{multiplicity}_{w} C_{\varphi}^*(\theta f), \end{align*} $$
for all
![]() $w \in \mathcal {Z}(\theta )$
(the zero set of
$w \in \mathcal {Z}(\theta )$
(the zero set of
![]() $\theta $
). This implies that
$\theta $
). This implies that
 $\frac {1}{\theta } C_\varphi ^*(\theta f)$
is a well defined holomorphic function on
$\frac {1}{\theta } C_\varphi ^*(\theta f)$
is a well defined holomorphic function on
![]() $\mathbb {D}$
. Therefore, we have proved the following general (but perhaps less practical) characterization.
$\mathbb {D}$
. Therefore, we have proved the following general (but perhaps less practical) characterization.
Lemma 4.1
![]() $Q_{\theta }$
is invariant under
$Q_{\theta }$
is invariant under
![]() $C_\varphi $
if and only if
$C_\varphi $
if and only if
 $f \in H^2(\mathbb {D}) \mapsto \frac {1}{\theta } C_\varphi ^* M_\theta f$
defines a bounded linear operator on
$f \in H^2(\mathbb {D}) \mapsto \frac {1}{\theta } C_\varphi ^* M_\theta f$
defines a bounded linear operator on
![]() $H^2(\mathbb {D})$
.
$H^2(\mathbb {D})$
.
Now we turn to linear fractional transformations. The following adjoint formula is due to Cowen [Reference Cowen6, Theorem 2]. There is a wide range of applications of Cowen’s adjoint formula (cf. [Reference Clifford and Zheng5, Reference Gallardo-Gutiérrez and Montes-Rodríguez10, Reference Gallardo-Gutiérrez and Schroderus11]).
Theorem 4.2 Let
 $\varphi (z)=\frac {az+b}{cz+d}$
be a nonconstant holomorphic self-map of
$\varphi (z)=\frac {az+b}{cz+d}$
be a nonconstant holomorphic self-map of
![]() $\mathbb {D}$
, where
$\mathbb {D}$
, where
![]() $ad - bc = 1$
. Then
$ad - bc = 1$
. Then
 $\sigma (z) = \frac {\bar {a}z-\bar {c}} {-\bar {b}z+\bar {d}}$
is a holomorphic self-map of
$\sigma (z) = \frac {\bar {a}z-\bar {c}} {-\bar {b}z+\bar {d}}$
is a holomorphic self-map of
![]() $\mathbb {D}$
,
$\mathbb {D}$
,
 $g(z)= \frac {1}{-\bar {b}z+\bar {d}}$
and
$g(z)= \frac {1}{-\bar {b}z+\bar {d}}$
and
![]() $h(z)=cz+d$
are in
$h(z)=cz+d$
are in
![]() $H^\infty (\mathbb {D})$
, and
$H^\infty (\mathbb {D})$
, and
![]() $C_\varphi ^*=M_g C_\sigma M_h^*$
.
$C_\varphi ^*=M_g C_\sigma M_h^*$
.
Note that if
![]() $\varphi $
is a constant map, then
$\varphi $
is a constant map, then
![]() $\mathcal {Q}_\theta $
is invariant for
$\mathcal {Q}_\theta $
is invariant for
![]() $C_\varphi $
if and only if
$C_\varphi $
if and only if
![]() $\theta (0)=0$
. Indeed, the constant function
$\theta (0)=0$
. Indeed, the constant function
![]() $1 \in \mathcal {Q}_\theta $
if and only if
$1 \in \mathcal {Q}_\theta $
if and only if
![]() $\theta (0) = \langle 1, \theta \rangle _{H^2(\mathbb {D})} = 0$
. Now we turn to nonconstant affine self-maps.
$\theta (0) = \langle 1, \theta \rangle _{H^2(\mathbb {D})} = 0$
. Now we turn to nonconstant affine self-maps.
In what follows, we denote by
![]() $\mathcal {H}(\mathbb {D})$
either
$\mathcal {H}(\mathbb {D})$
either
![]() $H^2(\mathbb {D})$
or
$H^2(\mathbb {D})$
or
![]() $H^\infty (\mathbb {D})$
.
$H^\infty (\mathbb {D})$
.
Theorem 4.3 Let
![]() $\theta $
be an inner function, and let
$\theta $
be an inner function, and let
![]() $\varphi (z)=az+b, a\neq 0$
. Suppose
$\varphi (z)=az+b, a\neq 0$
. Suppose
 $\sigma (z)= \frac {\bar {a}z}{1-\bar {b}z}$
,
$\sigma (z)= \frac {\bar {a}z}{1-\bar {b}z}$
,
![]() $z \in \mathbb {D}$
. The following are equivalent.
$z \in \mathbb {D}$
. The following are equivalent.
-
(1)
 $\mathcal {Q}_\theta \in \mathrm{Lat} C_\varphi $
.
$\mathcal {Q}_\theta \in \mathrm{Lat} C_\varphi $
. -
(2)
 $\frac {\theta \circ \sigma }{\theta } \in \mathcal {H}(\mathbb {D})$
.
$\frac {\theta \circ \sigma }{\theta } \in \mathcal {H}(\mathbb {D})$
. -
(3)
 $\theta H^2(\mathbb {D}) \in \mathrm{Lat} C_\sigma $
.
$\theta H^2(\mathbb {D}) \in \mathrm{Lat} C_\sigma $
.
Proof If we apply Theorem 4.2 to the case when
![]() $c=0$
and
$c=0$
and
![]() $d = 1$
, we get
$d = 1$
, we get
 $$ \begin{align*} C_\varphi^*=M_\psi C_\sigma, \end{align*} $$
$$ \begin{align*} C_\varphi^*=M_\psi C_\sigma, \end{align*} $$
where
 $\psi (z)= \frac {1}{1-\bar {b}z}$
. Now suppose that
$\psi (z)= \frac {1}{1-\bar {b}z}$
. Now suppose that
![]() $\mathcal {Q}_\theta $
is invariant under
$\mathcal {Q}_\theta $
is invariant under
![]() $C_\varphi $
. By Lemma 4.1, we know that the map
$C_\varphi $
. By Lemma 4.1, we know that the map
 $$ \begin{align*} Xf= \frac{1}{\theta} C_\varphi^*M_\theta f \qquad (f \in H^2(\mathbb{D})), \end{align*} $$
$$ \begin{align*} Xf= \frac{1}{\theta} C_\varphi^*M_\theta f \qquad (f \in H^2(\mathbb{D})), \end{align*} $$
defines a bounded linear operator X on
![]() $H^2(\mathbb {D})$
, and hence, using
$H^2(\mathbb {D})$
, and hence, using
![]() $C_\varphi ^*=M_\psi C_\sigma $
, we have
$C_\varphi ^*=M_\psi C_\sigma $
, we have
 $$ \begin{align*} Xf = \frac{1}{\theta} C_\varphi^*M_\theta f = \frac{1}{\theta} \psi (\theta\circ\sigma) (f\circ\sigma) \in H^2(\mathbb{D}), \end{align*} $$
$$ \begin{align*} Xf = \frac{1}{\theta} C_\varphi^*M_\theta f = \frac{1}{\theta} \psi (\theta\circ\sigma) (f\circ\sigma) \in H^2(\mathbb{D}), \end{align*} $$
for all
![]() $f\in H^2(\mathbb {D})$
. Applying this with
$f\in H^2(\mathbb {D})$
. Applying this with
![]() $f = 1$
yields
$f = 1$
yields
 $$ \begin{align*} \psi\frac{\theta\circ\sigma}{\theta} \in H^2(\mathbb{D}). \end{align*} $$
$$ \begin{align*} \psi\frac{\theta\circ\sigma}{\theta} \in H^2(\mathbb{D}). \end{align*} $$
But since
 $\frac {1}{\psi }= 1 - \bar {b}z \in H^\infty (\mathbb {D})$
, it follows that
$\frac {1}{\psi }= 1 - \bar {b}z \in H^\infty (\mathbb {D})$
, it follows that
 $\frac {\theta \circ \sigma }{\theta } \in H^2(\mathbb {D})$
. Theorem 2.1 then implies that
$\frac {\theta \circ \sigma }{\theta } \in H^2(\mathbb {D})$
. Theorem 2.1 then implies that
![]() $\theta H^2(\mathbb {D})$
is invariant under
$\theta H^2(\mathbb {D})$
is invariant under
![]() $C_\sigma $
. This proves
$C_\sigma $
. This proves
![]() $(1) \Rightarrow (2) \Rightarrow (3)$
.
$(1) \Rightarrow (2) \Rightarrow (3)$
.
Now we assume that
![]() $C_\sigma (\theta H^2(\mathbb {D})) \subseteq \theta H^2(\mathbb {D})$
. Again, Theorem 2.1 implies that
$C_\sigma (\theta H^2(\mathbb {D})) \subseteq \theta H^2(\mathbb {D})$
. Again, Theorem 2.1 implies that
 $\frac {\theta \circ \sigma }{\theta } \in {\mathcal S}(\mathbb {D})$
, and therefore
$\frac {\theta \circ \sigma }{\theta } \in {\mathcal S}(\mathbb {D})$
, and therefore
 $\psi \frac {\theta \circ \sigma }{\theta } \in H^\infty (\mathbb {D})$
. Then
$\psi \frac {\theta \circ \sigma }{\theta } \in H^\infty (\mathbb {D})$
. Then
 $\frac {1}{\theta } C_{\varphi }^* M_\theta $
defines a bounded linear operator on
$\frac {1}{\theta } C_{\varphi }^* M_\theta $
defines a bounded linear operator on
![]() $H^2(\mathbb {D})$
, and hence,
$H^2(\mathbb {D})$
, and hence,
![]() $\mathcal {Q}_\theta $
is invariant under
$\mathcal {Q}_\theta $
is invariant under
![]() $C_\varphi $
. This proves that
$C_\varphi $
. This proves that
![]() $(3) \Rightarrow (2) \Rightarrow (1)$
and completes the proof of the theorem.▪
$(3) \Rightarrow (2) \Rightarrow (1)$
and completes the proof of the theorem.▪
Now we consider model spaces that are invariant under composition operators induced by linear fractional transformations. However, we will be restricted to inner functions that vanish at the origin. In fact, our main tool is the following adjoint formula [Reference Shapiro23, Equation (3.6)], which concerns functions vanishing at the origin:
Lemma 4.4 Let
 $\varphi (z)=\frac {az+b}{cz+d}$
be a nonconstant holomorphic self-map of
$\varphi (z)=\frac {az+b}{cz+d}$
be a nonconstant holomorphic self-map of
![]() $\mathbb {D}$
, where
$\mathbb {D}$
, where
![]() $ad - bc = 1$
. If
$ad - bc = 1$
. If
 $\sigma (z) = \frac {\bar {a}z-\bar {c}} {-\bar {b}z+\bar {d}}$
, then
$\sigma (z) = \frac {\bar {a}z-\bar {c}} {-\bar {b}z+\bar {d}}$
, then
 $$ \begin{align*} C_\varphi^*f(z)=z\sigma'(z) \frac{f(\sigma(z))}{\sigma(z)} \qquad (f\in H^2(\mathbb{D}), f(0)=0). \end{align*} $$
$$ \begin{align*} C_\varphi^*f(z)=z\sigma'(z) \frac{f(\sigma(z))}{\sigma(z)} \qquad (f\in H^2(\mathbb{D}), f(0)=0). \end{align*} $$
As pointed our earlier, if
![]() $\theta $
is an inner function, then the constant function
$\theta $
is an inner function, then the constant function
![]() $1 \in \mathcal {Q}_\theta $
if and only if
$1 \in \mathcal {Q}_\theta $
if and only if
![]() $\theta (0) = 0$
. In the following, under the assumption that the inner functions vanish at the origin, we present a classification of model spaces that are invariant under composition operators induced by linear fractional transformations. Recall that
$\theta (0) = 0$
. In the following, under the assumption that the inner functions vanish at the origin, we present a classification of model spaces that are invariant under composition operators induced by linear fractional transformations. Recall that
![]() $\mathcal {H}(\mathbb {D})$
is either
$\mathcal {H}(\mathbb {D})$
is either
![]() $H^2(\mathbb {D})$
or
$H^2(\mathbb {D})$
or
![]() $H^\infty (\mathbb {D})$
.
$H^\infty (\mathbb {D})$
.
Theorem 4.5 Let
![]() $\theta $
be an inner function,
$\theta $
be an inner function,
![]() $\theta (0) = 0$
, and let
$\theta (0) = 0$
, and let
 $\varphi (z)= \frac {az+b}{cz+d}$
be a nonconstant holomorphic self-map of
$\varphi (z)= \frac {az+b}{cz+d}$
be a nonconstant holomorphic self-map of
![]() $\mathbb {D}$
, where
$\mathbb {D}$
, where
![]() $ad - bc = 1$
. Suppose
$ad - bc = 1$
. Suppose
 $\sigma (z)= \frac {\bar {a}z-\bar {c}}{-\bar {b}z+\bar {d}}$
and
$\sigma (z)= \frac {\bar {a}z-\bar {c}}{-\bar {b}z+\bar {d}}$
and
 $$ \begin{align*} \psi = \frac{\frac{\theta}{z}\circ\sigma}{\frac{\theta}{z}}. \end{align*} $$
$$ \begin{align*} \psi = \frac{\frac{\theta}{z}\circ\sigma}{\frac{\theta}{z}}. \end{align*} $$
The following are equivalent:
-
(1)
 $\mathcal {Q}_\theta \in \mathrm{Lat} C_\varphi $
.
$\mathcal {Q}_\theta \in \mathrm{Lat} C_\varphi $
. -
(2)
 $\psi \in \mathcal {H}(\mathbb {D})$
.
$\psi \in \mathcal {H}(\mathbb {D})$
. -
(3)
 $\frac {\theta }{z}H^2(\mathbb {D}) \in \mathrm{Lat} C_\sigma $
.
$\frac {\theta }{z}H^2(\mathbb {D}) \in \mathrm{Lat} C_\sigma $
.
Proof Since
![]() $\theta (0)=0$
, we see that
$\theta (0)=0$
, we see that
![]() $\frac {\theta }{z}$
is an inner function. Suppose that
$\frac {\theta }{z}$
is an inner function. Suppose that
![]() $\mathcal {Q}_\theta $
is invariant under
$\mathcal {Q}_\theta $
is invariant under
![]() $C_\varphi $
. Lemma 4.1 implies that
$C_\varphi $
. Lemma 4.1 implies that
 $$ \begin{align*} Xf = \frac{1}{\theta}C_\varphi^*(\theta f) \qquad (f \in H^2(\mathbb{D})), \end{align*} $$
$$ \begin{align*} Xf = \frac{1}{\theta}C_\varphi^*(\theta f) \qquad (f \in H^2(\mathbb{D})), \end{align*} $$
defines a bounded linear operator X on
![]() $H^2(\mathbb {D})$
and
$H^2(\mathbb {D})$
and
![]() $C_{\varphi }^* M_\theta = M_\theta X$
. In view of Lemma 4.4, it then follows that
$C_{\varphi }^* M_\theta = M_\theta X$
. In view of Lemma 4.4, it then follows that
 $$ \begin{align*} Xf = \sigma' \frac{z (\theta\circ\sigma)}{\theta\sigma} (f\circ\sigma) = \sigma' \psi (f\circ\sigma), \end{align*} $$
$$ \begin{align*} Xf = \sigma' \frac{z (\theta\circ\sigma)}{\theta\sigma} (f\circ\sigma) = \sigma' \psi (f\circ\sigma), \end{align*} $$
where
![]() $\sigma '$
is the derivative of
$\sigma '$
is the derivative of
![]() $\sigma $
. In particular
$\sigma $
. In particular
from which, using the fact that
 $\frac {1}{\sigma '} \in H^\infty (\mathbb {D})$
, it follows that
$\frac {1}{\sigma '} \in H^\infty (\mathbb {D})$
, it follows that
![]() $\psi \in H^2(\mathbb {D})$
. And finally, by Theorem 2.1,
$\psi \in H^2(\mathbb {D})$
. And finally, by Theorem 2.1,
 $\displaystyle \frac {\theta }{z}H^2(\mathbb {D})$
is invariant under
$\displaystyle \frac {\theta }{z}H^2(\mathbb {D})$
is invariant under
![]() $C_\sigma $
, which proves
$C_\sigma $
, which proves
![]() $(1) \Rightarrow (2) \Rightarrow (3)$
.
$(1) \Rightarrow (2) \Rightarrow (3)$
.
Now if
![]() $(3)$
is true, then Theorem 2.1 implies that
$(3)$
is true, then Theorem 2.1 implies that
![]() $(2)$
is true, that is,
$(2)$
is true, that is,
![]() $\psi \in H^\infty (\mathbb {D})$
. In particular, since
$\psi \in H^\infty (\mathbb {D})$
. In particular, since
![]() $\sigma ' \in H^\infty (\mathbb {D})$
, X (defined as above) defines a bounded linear operator on
$\sigma ' \in H^\infty (\mathbb {D})$
, X (defined as above) defines a bounded linear operator on
![]() $H^2(\mathbb {D})$
and satisfy the equality
$H^2(\mathbb {D})$
and satisfy the equality
![]() $C_{\varphi }^* M_\theta = M_\theta X$
. By Lemma 4.1,
$C_{\varphi }^* M_\theta = M_\theta X$
. By Lemma 4.1,
![]() $\mathcal {Q}_\theta $
is invariant under
$\mathcal {Q}_\theta $
is invariant under
![]() $C_\varphi $
, which complete the proof of
$C_\varphi $
, which complete the proof of
![]() $(2) \Rightarrow (1)$
.▪
$(2) \Rightarrow (1)$
.▪
We do not know, in general, how to classify an inner function
![]() $\theta $
for which
$\theta $
for which
![]() $\mathcal {Q}_\theta $
is invariant under a composition operator induced by a linear fractional transformation.
$\mathcal {Q}_\theta $
is invariant under a composition operator induced by a linear fractional transformation.
5 Applications
The main goal of this section is to discuss some direct applications of our main results to some elementary invariant subspaces of composition operators.
First, we prove that the identity map is the only self-map of
![]() $\mathbb {D}$
, which leaves all model spaces invariant.
$\mathbb {D}$
, which leaves all model spaces invariant.
Theorem 5.1 Let
![]() $\varphi $
be a holomorphic self-map of
$\varphi $
be a holomorphic self-map of
![]() $\mathbb {D}$
. Then
$\mathbb {D}$
. Then
![]() $\theta H^2(\mathbb {D})$
is invariant under
$\theta H^2(\mathbb {D})$
is invariant under
![]() $C_\varphi $
for all inner function
$C_\varphi $
for all inner function
![]() $\theta $
if and only if
$\theta $
if and only if
![]() $\varphi $
is the identity map.
$\varphi $
is the identity map.
Proof If
![]() $\varphi (z) = z$
,
$\varphi (z) = z$
,
![]() $z \in \mathbb {D}$
, then
$z \in \mathbb {D}$
, then
![]() $C_\varphi = I_{H^2(\mathbb {D})}$
(the identity operator). In particular,
$C_\varphi = I_{H^2(\mathbb {D})}$
(the identity operator). In particular,
![]() $\theta H^2(\mathbb {D})$
is invariant under
$\theta H^2(\mathbb {D})$
is invariant under
![]() $C_\varphi $
. Conversely, suppose
$C_\varphi $
. Conversely, suppose
![]() $\theta H^2(\mathbb {D})\in \mbox {Lat}C_\varphi $
for all inner function
$\theta H^2(\mathbb {D})\in \mbox {Lat}C_\varphi $
for all inner function
![]() $\theta $
. Fix
$\theta $
. Fix
![]() $\alpha \in \mathbb {D}$
. Then
$\alpha \in \mathbb {D}$
. Then
![]() $\alpha $
is the only zero of the Blaschke factor (which is also an inner function)
$\alpha $
is the only zero of the Blaschke factor (which is also an inner function)
![]() $b_\alpha (z) = \frac {\alpha - z}{1-\bar {\alpha } z}$
,
$b_\alpha (z) = \frac {\alpha - z}{1-\bar {\alpha } z}$
,
![]() $z \in \mathbb {D}$
. Since
$z \in \mathbb {D}$
. Since
![]() $b_\alpha H^2(\mathbb {D})\in \mbox {Lat}C_\varphi $
, by assumption, Theorem 2.1 implies that
$b_\alpha H^2(\mathbb {D})\in \mbox {Lat}C_\varphi $
, by assumption, Theorem 2.1 implies that
 $$ \begin{align*} \frac{b_\alpha\circ\varphi}{b_\alpha}\in {\mathcal S}(\mathbb{D}). \end{align*} $$
$$ \begin{align*} \frac{b_\alpha\circ\varphi}{b_\alpha}\in {\mathcal S}(\mathbb{D}). \end{align*} $$
This forces
![]() $b_\alpha (\varphi (\alpha ))=0$
, and hence
$b_\alpha (\varphi (\alpha ))=0$
, and hence
![]() $\varphi (\alpha )=\alpha $
. Since
$\varphi (\alpha )=\alpha $
. Since
![]() $\alpha \in \mathbb {D}$
is arbitrary, we have that
$\alpha \in \mathbb {D}$
is arbitrary, we have that
![]() $\varphi (z)=z$
,
$\varphi (z)=z$
,
![]() $z\in \mathbb {D}$
, which completes the proof.▪
$z\in \mathbb {D}$
, which completes the proof.▪
Before examining the other extreme property of the invariant subspaces of composition operators, we need to recall the following fact which concerns fixed points of holomorphic self-maps [Reference Bose, Muthukumar and Sarkar2, Corollary 3.4]: Let
![]() $\varphi $
be a holomorphic self-map of
$\varphi $
be a holomorphic self-map of
![]() $\mathbb {D}$
and let
$\mathbb {D}$
and let
![]() $w \in \mathbb {D}$
be the fixed point of
$w \in \mathbb {D}$
be the fixed point of
![]() $\varphi $
. If
$\varphi $
. If
![]() $\theta $
is an inner function and
$\theta $
is an inner function and
![]() $\theta (w)\neq 0$
, then
$\theta (w)\neq 0$
, then
![]() $\theta H^2(\mathbb {D})$
is invariant under
$\theta H^2(\mathbb {D})$
is invariant under
![]() $C_\varphi $
if and only if
$C_\varphi $
if and only if
![]() $\theta \circ \varphi =\theta $
.
$\theta \circ \varphi =\theta $
.
Recall that a point
![]() $w \in \mathbb {D}$
is said to be a fixed point of a holomorphic self-map
$w \in \mathbb {D}$
is said to be a fixed point of a holomorphic self-map
![]() $\varphi $
of
$\varphi $
of
![]() $\mathbb {D}$
if
$\mathbb {D}$
if
![]() $\varphi (w) = w.$
$\varphi (w) = w.$
Theorem 5.2 Let
![]() $\theta $
be an inner function. Then
$\theta $
be an inner function. Then
![]() $\theta H^2(\mathbb {D}) \in \mathrm{Lat} C_{\varphi }$
for all self-maps
$\theta H^2(\mathbb {D}) \in \mathrm{Lat} C_{\varphi }$
for all self-maps
![]() $\varphi $
of
$\varphi $
of
![]() $\mathbb {D}$
if and only if
$\mathbb {D}$
if and only if
![]() $\theta $
is an unimodular constant.
$\theta $
is an unimodular constant.
Proof If
![]() $\theta $
is an unimodular constant, then
$\theta $
is an unimodular constant, then
 $\frac {\theta \circ \varphi }{\theta }$
is also unimodular constant. Theorem 2.1 then implies that
$\frac {\theta \circ \varphi }{\theta }$
is also unimodular constant. Theorem 2.1 then implies that
![]() $\theta H^2(\mathbb {D})\in \mbox {Lat} C_\varphi $
.
$\theta H^2(\mathbb {D})\in \mbox {Lat} C_\varphi $
.
Conversely, assume that
![]() $\theta H^2(\mathbb {D}) \in \mathrm{Lat} C_\varphi $
for all holomorphic self-map
$\theta H^2(\mathbb {D}) \in \mathrm{Lat} C_\varphi $
for all holomorphic self-map
![]() $\varphi $
of
$\varphi $
of
![]() $\mathbb {D}$
. First, we claim that
$\mathbb {D}$
. First, we claim that
![]() $\theta $
has no zeros in
$\theta $
has no zeros in
![]() $\mathbb {D}$
. Suppose toward a contradiction that
$\mathbb {D}$
. Suppose toward a contradiction that
![]() $\theta (\alpha )=0$
for some
$\theta (\alpha )=0$
for some
![]() $\alpha \in \mathbb {D}$
. Since
$\alpha \in \mathbb {D}$
. Since
![]() $\theta $
is an inner function, there exists
$\theta $
is an inner function, there exists
![]() $\beta \in \mathbb {D}$
such that
$\beta \in \mathbb {D}$
such that
![]() $\theta (\beta ) \neq 0$
. Set
$\theta (\beta ) \neq 0$
. Set
Note that
![]() $\varphi $
is an inner function and
$\varphi $
is an inner function and
![]() $\varphi (\alpha ) = \beta $
. Therefore,
$\varphi (\alpha ) = \beta $
. Therefore,
 $\frac {\theta \circ \varphi }{\theta } \notin H^\infty (\mathbb {D})$
, and hence, by Theorem 2.1,
$\frac {\theta \circ \varphi }{\theta } \notin H^\infty (\mathbb {D})$
, and hence, by Theorem 2.1,
![]() $\theta H^2(\mathbb {D})$
is not invariant under
$\theta H^2(\mathbb {D})$
is not invariant under
![]() $C_\varphi $
. This contradiction completes the proof of the claim that
$C_\varphi $
. This contradiction completes the proof of the claim that
![]() $\theta (z)\neq 0$
for all
$\theta (z)\neq 0$
for all
![]() $z\in \mathbb {D}$
. If we consider a constant function
$z\in \mathbb {D}$
. If we consider a constant function
![]() $\varphi \equiv c$
, then in view of the discussion preceding the statement of this theorem,
$\varphi \equiv c$
, then in view of the discussion preceding the statement of this theorem,
![]() $C_\varphi (\theta H^2(\mathbb {D})) \subseteq \theta H^2(\mathbb {D})$
implies that
$C_\varphi (\theta H^2(\mathbb {D})) \subseteq \theta H^2(\mathbb {D})$
implies that
Since
![]() $\theta $
is an inner function,
$\theta $
is an inner function,
![]() $\theta (c)$
must be unimodular, and hence
$\theta (c)$
must be unimodular, and hence
![]() $\theta $
is an unimodular constant. This completes the proof of the theorem.▪
$\theta $
is an unimodular constant. This completes the proof of the theorem.▪
Now we turn to special model invariant subspaces of composition operators. In the following, we will let
![]() $\theta $
and
$\theta $
and
![]() $\varphi $
denote inner function and holomorphic self-map of
$\varphi $
denote inner function and holomorphic self-map of
![]() $\mathbb {D}$
, respectively.
$\mathbb {D}$
, respectively.
Theorem 5.3 The following holds true:
-
(1)
 $\mathcal {Q}_\theta \in \mathrm{Lat} C_\varphi $
for all inner function
$\mathcal {Q}_\theta \in \mathrm{Lat} C_\varphi $
for all inner function
 $\theta $
if and only if
$\theta $
if and only if
 $\varphi $
is the identity map.
$\varphi $
is the identity map. -
(2)
 $\mathcal {Q}_\theta \in \mathrm{Lat} C_\varphi $
for all self-map
$\mathcal {Q}_\theta \in \mathrm{Lat} C_\varphi $
for all self-map
 $\varphi $
if and only if
$\varphi $
if and only if
 $\theta (z)=\alpha z$
or
$\theta (z)=\alpha z$
or
 $\theta \equiv \alpha $
, where
$\theta \equiv \alpha $
, where
 $\alpha $
is an unimodular constant.
$\alpha $
is an unimodular constant.
Proof If
![]() $\mathcal {Q}_\theta \in \mathrm{Lat} C_\varphi $
for all inner function
$\mathcal {Q}_\theta \in \mathrm{Lat} C_\varphi $
for all inner function
![]() $\theta $
, then, in particular,
$\theta $
, then, in particular,
![]() $\mathcal {Q}_{b_{\alpha }}, \mathcal {Q}_{b_{\beta }} \in \mathrm{Lat} C_\varphi $
, where
$\mathcal {Q}_{b_{\alpha }}, \mathcal {Q}_{b_{\beta }} \in \mathrm{Lat} C_\varphi $
, where
![]() $\alpha \neq \beta $
are in
$\alpha \neq \beta $
are in
![]() $\mathbb {D} \setminus \{0\}$
. By Theorem 3.1, there exist nonzero scalars a and b such that
$\mathbb {D} \setminus \{0\}$
. By Theorem 3.1, there exist nonzero scalars a and b such that
 $$ \begin{align*} \varphi(z)= \frac{1-a}{\bar{\alpha}}+ a z = \frac{1-b}{\bar{\beta}} + b z \qquad (z \in \mathbb{D}). \end{align*} $$
$$ \begin{align*} \varphi(z)= \frac{1-a}{\bar{\alpha}}+ a z = \frac{1-b}{\bar{\beta}} + b z \qquad (z \in \mathbb{D}). \end{align*} $$
Thus, comparing both sides of the above and noting the fact that
![]() $\alpha \neq \beta $
, we have
$\alpha \neq \beta $
, we have
![]() $a = b =1$
, which implies that
$a = b =1$
, which implies that
![]() $\varphi (z)=z$
,
$\varphi (z)=z$
,
![]() $z\in \mathbb {D}$
. The converse part of
$z\in \mathbb {D}$
. The converse part of
![]() $(1)$
is trivial.
$(1)$
is trivial.
Now we turn to prove
![]() $(2)$
. If
$(2)$
. If
![]() $\theta (z)=\alpha z$
for some unimodular
$\theta (z)=\alpha z$
for some unimodular
![]() $\alpha $
, then
$\alpha $
, then
![]() $\mathcal {Q}_\theta = k(\cdot , 0) \mathbb {C}$
is the space of all constant functions, which is clearly invariant under all composition operators (cf. Remark 3.2). In the case of
$\mathcal {Q}_\theta = k(\cdot , 0) \mathbb {C}$
is the space of all constant functions, which is clearly invariant under all composition operators (cf. Remark 3.2). In the case of
![]() $\theta \equiv \alpha $
, we have
$\theta \equiv \alpha $
, we have
![]() $\mathcal {Q}_\theta =\{0\}$
, which is also invariant under all composition operators.
$\mathcal {Q}_\theta =\{0\}$
, which is also invariant under all composition operators.
For the converse part, we first note that if
![]() $\mathcal {Q}_\theta =\{0\}$
, then
$\mathcal {Q}_\theta =\{0\}$
, then
![]() $\theta H^2(\mathbb {D})=H^2(\mathbb {D})$
, and hence
$\theta H^2(\mathbb {D})=H^2(\mathbb {D})$
, and hence
![]() $\theta $
is an unimodular constant. So suppose,
$\theta $
is an unimodular constant. So suppose,
![]() $\mathcal {Q}_\theta \neq \{0\}$
. Then there exist
$\mathcal {Q}_\theta \neq \{0\}$
. Then there exist
![]() $\alpha \in \mathbb {D}$
and
$\alpha \in \mathbb {D}$
and
![]() $f\in \mathcal {Q}_\theta $
such that
$f\in \mathcal {Q}_\theta $
such that
![]() $f(\alpha )\neq 0$
. By taking
$f(\alpha )\neq 0$
. By taking
![]() $\varphi \equiv \alpha $
, we see that
$\varphi \equiv \alpha $
, we see that
![]() $1 \in \mathcal {Q}_\theta $
, which implies
$1 \in \mathcal {Q}_\theta $
, which implies
Then
 $\omega = \frac {\theta }{z}$
is an inner function. By Theorem 4.5,
$\omega = \frac {\theta }{z}$
is an inner function. By Theorem 4.5,
![]() $\omega H^2(\mathbb {D})$
invariant under
$\omega H^2(\mathbb {D})$
invariant under
![]() $C_\sigma $
for every linear fractional self-map
$C_\sigma $
for every linear fractional self-map
![]() $\sigma $
of
$\sigma $
of
![]() $\mathbb {D}$
.
$\mathbb {D}$
.
Now we claim that
![]() $\omega $
has no zeros in
$\omega $
has no zeros in
![]() $\mathbb {D}$
. Suppose toward a contradiction that
$\mathbb {D}$
. Suppose toward a contradiction that
![]() $\omega (\alpha )=0$
for some
$\omega (\alpha )=0$
for some
![]() $\alpha \in \mathbb {D}$
. Since
$\alpha \in \mathbb {D}$
. Since
![]() $\omega $
is an inner function,
$\omega $
is an inner function,
![]() $\omega (\beta ) \neq 0$
for some
$\omega (\beta ) \neq 0$
for some
![]() $\beta \in \mathbb {D}$
. Set
$\beta \in \mathbb {D}$
. Set
![]() $\sigma = b_\beta \circ b_\alpha $
so that
$\sigma = b_\beta \circ b_\alpha $
so that
![]() $\sigma (\alpha ) = \beta $
. Then
$\sigma (\alpha ) = \beta $
. Then
 $$ \begin{align*} \frac{\omega\circ\sigma}{\omega} \notin H^\infty(\mathbb{D}), \end{align*} $$
$$ \begin{align*} \frac{\omega\circ\sigma}{\omega} \notin H^\infty(\mathbb{D}), \end{align*} $$
and hence
![]() $\omega H^2(\mathbb {D})$
is not invariant under
$\omega H^2(\mathbb {D})$
is not invariant under
![]() $C_\sigma $
. This is a contradiction, and hence
$C_\sigma $
. This is a contradiction, and hence
![]() $\omega (z)\neq 0$
,
$\omega (z)\neq 0$
,
![]() $z\in \mathbb {D}$
.
$z\in \mathbb {D}$
.
Finally, consider a nonautomorphic and holomorphic self-map
![]() $\sigma $
of
$\sigma $
of
![]() $\mathbb {D}$
with a fixed point in
$\mathbb {D}$
with a fixed point in
![]() $\mathbb {D}$
(for instance, consider
$\mathbb {D}$
(for instance, consider
 $\sigma (z)= \frac {1}{2}z$
). As
$\sigma (z)= \frac {1}{2}z$
). As
![]() $\omega H^2(\mathbb {D})$
invariant under
$\omega H^2(\mathbb {D})$
invariant under
![]() $C_\sigma $
, by [Reference Bose, Muthukumar and Sarkar2, Corollary 3.5], it follows that
$C_\sigma $
, by [Reference Bose, Muthukumar and Sarkar2, Corollary 3.5], it follows that
![]() $\omega $
is an unimodular constant. This implies that
$\omega $
is an unimodular constant. This implies that
![]() $\theta (z)=\alpha z$
for some unimodular constant
$\theta (z)=\alpha z$
for some unimodular constant
![]() $\alpha $
.▪
$\alpha $
.▪
We conclude this section by proving a reducing property of composition operators. Here we will be restricted to finite-dimensional model spaces, as in Theorem 3.1. Before we begin this discussion, we recall the following result [Reference Bose, Muthukumar and Sarkar2, Corollary 2.4]:
Theorem 5.4 Let B be a Blaschke product and let
![]() $\varphi $
be a holomorphic self-map of
$\varphi $
be a holomorphic self-map of
![]() $\mathbb {D}$
. Then
$\mathbb {D}$
. Then
![]() $BH^2(\mathbb {D}) \in \mathrm{Lat}C_\varphi $
if and only if
$BH^2(\mathbb {D}) \in \mathrm{Lat}C_\varphi $
if and only if
![]() $\text {multiplicity}\ {}_w B \leq \text {multiplicity}\ {}_w {B\circ \varphi }$
for all
$\text {multiplicity}\ {}_w B \leq \text {multiplicity}\ {}_w {B\circ \varphi }$
for all
![]() $w \in \mathbb {D}$
such that
$w \in \mathbb {D}$
such that
![]() $B(w)=0$
.
$B(w)=0$
.
We are now ready for the reducing subspace property of elementary composition operators.
Theorem 5.5 Let
![]() $\varphi $
be a holomorphic self-map of
$\varphi $
be a holomorphic self-map of
![]() $\mathbb {D}$
,
$\mathbb {D}$
,
![]() $\alpha \in \mathbb {D}$
,
$\alpha \in \mathbb {D}$
,
![]() $n \geq 1$
, and suppose
$n \geq 1$
, and suppose
 $\theta (z)=\left (\frac {z- \alpha }{1-\bar {\alpha }z}\right )^n$
. Then
$\theta (z)=\left (\frac {z- \alpha }{1-\bar {\alpha }z}\right )^n$
. Then
![]() $\mathcal {Q}_\theta $
reduces
$\mathcal {Q}_\theta $
reduces
![]() $C_\varphi $
if and only if there exist a scalar c,
$C_\varphi $
if and only if there exist a scalar c,
![]() $|c| \leq 1$
, and
$|c| \leq 1$
, and
![]() $\psi \in \mathcal {S}(\mathbb {D})$
such that
$\psi \in \mathcal {S}(\mathbb {D})$
such that
 $$ \begin{align*} \varphi(z)= \begin{cases} z \psi, & \mbox{if } \alpha = 0 \text{ and } n = 1 \\ c z, & \mbox{if } \alpha = 0 \text{ and } n \geq 2\\ z, & \mbox{if } \alpha \neq 0. \end{cases} \end{align*} $$
$$ \begin{align*} \varphi(z)= \begin{cases} z \psi, & \mbox{if } \alpha = 0 \text{ and } n = 1 \\ c z, & \mbox{if } \alpha = 0 \text{ and } n \geq 2\\ z, & \mbox{if } \alpha \neq 0. \end{cases} \end{align*} $$
Proof Suppose
![]() $\alpha = 0$
. If
$\alpha = 0$
. If
![]() $n=1$
, then the one-dimensional subspace
$n=1$
, then the one-dimensional subspace
![]() $(z H^2(\mathbb {D}))^{\bot } = \mathcal {Q}_z$
is invariant under every composition operator (see Remark 3.2), where
$(z H^2(\mathbb {D}))^{\bot } = \mathcal {Q}_z$
is invariant under every composition operator (see Remark 3.2), where
![]() $z H^2(\mathbb {D})$
is invariant under
$z H^2(\mathbb {D})$
is invariant under
![]() $C_\varphi $
if and only if
$C_\varphi $
if and only if
![]() $\varphi = z \psi $
for some
$\varphi = z \psi $
for some
![]() $\psi \in {\mathcal S}(\mathbb {D})$
(see Theorem 5.4). If
$\psi \in {\mathcal S}(\mathbb {D})$
(see Theorem 5.4). If
![]() $n \geq 2$
, then, by Theorem 3.1,
$n \geq 2$
, then, by Theorem 3.1,
![]() $\mathcal {Q}_\theta $
is invariant under
$\mathcal {Q}_\theta $
is invariant under
![]() $C_\varphi $
if and only if
$C_\varphi $
if and only if
![]() $\varphi $
is an affine map. By Theorem 5.4,
$\varphi $
is an affine map. By Theorem 5.4,
![]() $\theta H^2(\mathbb {D})$
is invariant under
$\theta H^2(\mathbb {D})$
is invariant under
![]() $C_\varphi $
if and only if
$C_\varphi $
if and only if
![]() $\varphi = z \psi $
for some
$\varphi = z \psi $
for some
![]() $\psi \in {\mathcal S}(\mathbb {D})$
. In particular,
$\psi \in {\mathcal S}(\mathbb {D})$
. In particular,
![]() $\varphi (0)=0$
, and hence
$\varphi (0)=0$
, and hence
![]() $\theta H^2(\mathbb {D})$
reduces
$\theta H^2(\mathbb {D})$
reduces
![]() $C_\varphi $
if and only if
$C_\varphi $
if and only if
![]() $\varphi (z)= cz$
for some
$\varphi (z)= cz$
for some
![]() $|c|\leq 1$
.
$|c|\leq 1$
.
Finally, assume that
![]() $\alpha \neq 0$
. If
$\alpha \neq 0$
. If
![]() $\varphi $
is the identity map, then
$\varphi $
is the identity map, then
![]() $C_\varphi = I_{H^2(\mathbb {D})}$
, and hence
$C_\varphi = I_{H^2(\mathbb {D})}$
, and hence
![]() $\mathcal {Q}_\theta $
reduces
$\mathcal {Q}_\theta $
reduces
![]() $C_\varphi $
. Next, we assume that
$C_\varphi $
. Next, we assume that
![]() $\mathcal {Q}_\theta $
reduces
$\mathcal {Q}_\theta $
reduces
![]() $C_\varphi $
. By Theorem 3.1, there exists a scalar
$C_\varphi $
. By Theorem 3.1, there exists a scalar
![]() $c (\neq 0)$
such that
$c (\neq 0)$
such that
 $\varphi (z)= \frac {1-c}{\bar {\alpha }} + cz$
. Again, by Theorem 5.4,
$\varphi (z)= \frac {1-c}{\bar {\alpha }} + cz$
. Again, by Theorem 5.4,
![]() $(\theta \circ \varphi )(\alpha )=0$
, and hence
$(\theta \circ \varphi )(\alpha )=0$
, and hence
![]() $\varphi (\alpha )= \alpha $
. Now
$\varphi (\alpha )= \alpha $
. Now
 $$ \begin{align*} \frac{1-c}{\bar{\alpha}} + c \alpha = \alpha \end{align*} $$
$$ \begin{align*} \frac{1-c}{\bar{\alpha}} + c \alpha = \alpha \end{align*} $$
is equivalent to
As
![]() $|\alpha | < 1$
, we must have
$|\alpha | < 1$
, we must have
![]() $c=1$
, that is,
$c=1$
, that is,
![]() $\varphi (z)=z$
,
$\varphi (z)=z$
,
![]() $z\in \mathbb {D}$
, which completes the proof.▪
$z\in \mathbb {D}$
, which completes the proof.▪
Finally, we would like to point out that the present theory of model spaces and composition operators complement the recent paper [Reference Bose, Muthukumar and Sarkar2]. The classification of Beurling type invariant subspaces of composition operators ([Reference Bose, Muthukumar and Sarkar2, Theorem 2.3] or Theorem 2.1) also plays an important role in our consideration, and evidently, some of our results are in duality (cf. Theorem 4.3 and 4.5). On the other hand, model spaces are fairly complex objects in operator theory and function theory, which also represent a large class of bounded linear operators. The present analysis clearly shows a challenging role of model spaces to the theory of composition operators (and vice versa).
Acknowledgment
The authors thank the referee for corrections and suggestions which helped to improve the presentation. The second author is supported in part by NBHM (National Board of Higher Mathematics, India) grant NBHM/R.P.64/2014, and the Mathematical Research Impact Centric Support (MATRICS) grant, File No: MTR/2017/000522, by the Science and Engineering Research Board (SERB), Department of Science & Technology (DST), Government of India.