Introduction
The temperature distribution in the Earth’s crust is a result of (a) heat generation, thermal characteristics of rocks, and tectonic movements in the Earth’s interior, (b) the complex history of topography, sedimentation, and erosion at the Earth’s surface, and (c) temperature variations at the air/ground interface of various frequencies and amplitudes. Among the temperature variations during palaeoclimatic evolution, the most prominent thermal effects in the uppermost kilometres of the crust were caused by two events: the pronounced depression of surface temperatures during the last ice age and the sharp rise in temperature between the time of maximum glaciation (around 18 ka BP) and the beginning of the thermally more stable post-glacial period (about 10 ka BP). It is in the uppermost kilometres that the studies on potential geothermal energy in the Swiss plateau are concentrated (Reference Rybach and JafféRybach and Jaffé 1976, Reference Rybach, Bodmer, Pavoni and MuellerRybach and others 1978). In addition, geothermal information from deep drillings in connection with prospecting for salt, oil and gas, or studies concerning possible places for radioactive waste disposal may possibly help to verify palaeoclimatic reconstructions (Reference HaeberliHaeberli 1982). The purpose of this paper is to introduce briefly three important aspects of geothermal ice-age effects in the Swiss plateau: ice conditions (permafrost and glaciers at 18 ka BP) discussed by Haeberli, heat diffusion effects in bedrock discussed by Rellstab, and combined heat diffusion and latent heat exchange effects in unconsolidated sediments which have undergone phase changes during the formation and thawing of permafrost, discussed by Harrison.
Ice Conditions at 18 ka BP
Around 18 ka BP, Switzerland was situated entirely within the zone of continuous permafrost distribution (Reference WashburnWashburn 1979). Periglacial ice wedges not only formed in loess deposits, but even in coarse gravels (e.g. Reference Van der MeerVan der Meer 1980); perennially frozen sediments were deformed by glaciers in many places (“push moraines” in the strict sense, i.e. deformed frozen sediments, e.g. Reference Schindler, Röthlisberger and GygerSchindler and others 1978, Reference Van der MeerVan der Meer unpublished, cf. Reference HaeberliHaeberli 1981) and the karst drainage in the limestone region of the Jura mountains was blocked by perennial frost (e.g. Reference BarschBarsch 1968, Reference Haeberli, Schneider and ZollerHaeberli and others 1976). These examples provide morphological evidence of permafrost with a high ice content and indicate that, during this time, extensive underground 1ce accumulated in unconsolidated sediments of periglacial valleys and perhaps also in the limestone sediments of the Jura mountains (Fig.1). The depression of the permafrost boundary by more than 3 000 m with respect to today’s conditions (Reference HaeberliHaeberli in press) corresponds to a lowering of the mean annual air temperature by at least 15°C compared to the present. Surface temperatures in the periglacial areas of the Swiss plateau were around −3°C and lower.

Fig. 1 Sketch map of ice conditions in the Swiss plateau around 18 ka BP.
The equilibrium line on glaciers was depressed with respect to present conditions by about 1 200 to 1 300 m. At the corresponding altitudes of about 1 000 to 1 500 m a.s.l. the mean annual air temperature can be estimated at −10°C or colder. Surface ice temperatures were well below zero and a temperate firn zone probably did not exist. From the well-documented geometry of the piedmont glaciers in the Swiss plateau (e.g. Reference JäckliJäckli 1970, Reference Keller and KrayssKeller and Krayss 1980), it can be inferred that the basal shear stresses were extremely low, as were mass balance gradients and flow velocities (cf. Reference Blatter and HaeberliBlatter and Haeberli 1984). The low glacier activity (cg. Reference MeierMeier 1961, Reference HaeberliHaeberli in press) makes it difficult to assume that these glaciers ever came close to steady-state conditions during the time available (cf. Fig.2), and the build-up mechanism of the large ice lobes within a limited time remains an unsolved problem. It can nevertheless be assumed that the glacier beds were temperate in a zone of 1imited extent near the ice fronts only, and that large glaciers may have transported very cold ice from high altitudes to those parts of their beds situated at the Alpine border of the plateau, thus greatly enhancing depressions of ground temperatures at 18 ka BP (Reference Blatter and HaeberliBlatter and Haeberli 1984).

Fig. 2 Palaeoclimatic evolution during the last 100 ka as assumed for the model calculations in the Swiss plateau. ΔT-values are deviations of the mean annual surface temperature from the present, time is in a BP. p represents periglacial conditions and g subglacial conditions where glacier beds were temperate. Present time is at right end of graph.
In good agreement with palynological reconstructions, ice conditions during 18 ka BP in the Swiss plateau and relative displacements of permafrost and glacier boundaries reflect a very cold, dry climate during this time of maximum glaciation. Permafrost and glaciers of this time should not be compared to conditions in maritime regions today (such as, for example, southern Alaska), since they most closely resembled features of arid mountains (e.g. in Asia, cf. Reference Shih, Hsieh, Cheng and LiShih and others 1980). The reduction in precipitation by a factor of three or even more compared to values today (Reference HaeberliHaeberli 1982, Reference Haeberliin press) may be attributed to large-scale subsidence (Reference Manabe and BroccoliManabe and Broccoli 1984).
Geothermal Effects Due to Heat Diffusion in Bedrock
Palaeoclimatic corrections are applied to profiles drawn from bore-hole temperature observations (Reference BodmerBodmer unpublished), in connection with heat flow studies and research into the possibilities of exploiting geothermal energy in the Swiss plateau. In principle, thermal effects (ΔT* in Figs.3 and 4) due to palaeoclimatic changes of surface temperatures (ΔT in Fig.2) have to be computed as deviations of actual thermal conditions from steady-state conditions. Details of calculation and input data were described by Reference RellstabRellstab (1981 (revised 1982)). Following theoretical considerations by Reference BirchBirch (1948) and Reference Carslaw and JaegerCarslaw and Jaeger (1959), a superposition of error functions is used to calculate temperature T as a function of depth z and time t:

Fig. 3 Thermal effects Δ?* of the palaeoclimatic evolution during different time periods on present-day temperature profiles. Z is depth below surface; time is indicated in a BP for the time periods considered.

Fig. 4 Thermal effects Δ?* of the palaeoclimatic evolution on present-day temperature profiles for different ice-age surface temperatures. −1°C may represent conditions of temperate glacier beds, whereas −2 to −5°C is typical for periglacial conditions and non-temperate glacier beds during the same time period. Z is depth below surface.

where t1 is the youngest of n intervals of time tj during which the deviation of the mean annual surface temperature Tj from today’s is assumed to be constant, and κ is thermal diffusivity. In the corresponding computer program, the number and length of the time intervals, surface temperatures during these intervals, the length of the total time period under consideration, the heat diffusion coefficient, and the depth below the surface have to be selected. Present-day surface temperatures are estimated from air temperature data at or close to the considered site. The past glacial conditions have to be selected for each bore hole because subglacial temperatures may be different from periglacial temperatures. In connection with test runs using different models, extensive literature searches were carried out to determine the best step function representing the palaeoclimatic evolution as reconstructed by geologists and palaeontologists. For the last ice age, for example, the palaeotemperature curve is mainly based on a compilation by Reference Rudloff, Oeschger, Messerli and SvilarRudloff (1980), Figure 2 shows the section of the palaeoclimatic curve used in this paper. Figure 3 illustrates the relative Importance of different time periods for present-day borehole temperatures, calculated with a very detailed step function of palaeotemperatures (n = 36). The calculation shows that the time period between 10 and 100 ka BP, roughly corresponding to the “last ice age”, has by far the most Important effect for depths around 500 to 2 000 m. It is followed in importance by the time period between 100 and 1 000 ka BP, an order of magnitude which suggests an expression like “Quaternary before the last ice age” for this period. These two most important time periods probably experienced comparable temperature conditions. Older time periods are of minor importance only and need not be considered, since input data are extremely uncertain for several (geological) reasons. The test runs also showed that n = 15 was a minimum to give reasonable results, but that high numbers of considered intervals did not markedly change the results of the calculations. Figure 4 gives the calculated influence of (spatially) varying surface temperatures during full glacial development: −1°C may be considered as a typical value for formerly temperate glacier beds (phase equilibrium temperature, cf. Reference HarrisonHarrison 1975), whereas −2 to −5°C is more likely to represent periglacial conditions and conditions in regions of non-temperate glacier beds. It can be seen that, in the Swiss plateau, past cold periods during the Quaternary, and especially the last ice age, have lowered ground temperatures at a depth of about 1 000 to 1 500 m by 5°C or more. This corresponds to a heat flow correction of 0.25 to 0.5 heat flow units (HFU), or 20 to 30% of the observed values. The palaeoclimatic effect in regions of formerly temperate glacier beds is 1 to 3°C smaller than in formerly periglacial regions. In practice, it is probably impossible to observe this temperature difference, because of the limited accuracy of geothermal measurements (temperature in deep bore holes, thermal characteristics of rock samples). Moreover, the effect can easily be offset by heat convection due to circulating groundwater. The effect may, however, be enhanced by the temporary formation of ice rich permafrost in unconsolidated sediments.
Buffering of the Temperature Response of Deeper Rocks by Ice-Rich Permafrost
Porous sediments at the surface can have an important effect on the response of deeper rocks to surface temperature change. The source of the effect is the high latent heat exchange required for the formation and thawing of ice-rich permafrost in porous sediments. In the Swiss plateau, with postglacial surface temperatures around +8 to +10°C, formation of ice-rich permafrost in periglacial areas must have occurred for the last time about 20 ka BP, as indicated by the palaeotemperature curve (Fig.2) used for calculating ice-age effects on temperature distribution in the crust.
The warming-up of the surface to positive temperatures causes ice-age permafrost to become thinner from above and below until it vanishes. (The thinning effect from below is due to deep-seated geothermal heat.) The approximate time for complete thaw, and the effect on temperatures in deeper layers, can be assessed by a simple approach. The main approximation is that sensible heat is neglected in the thaw time calculation. In this limit the calculation becomes very simple: the temperature varies linearly above, in, and below the ice-rich permafrost, and at its base the heat flux has its geothermal value. The time t for permafrost of initial thickness Yo to thaw completely after the surface has warmed up to a positive temperature Tp can then be shown to be given by:

where C1 and C2 are defined by:
and
Here h is the latent heat per unit volume, q is the geothermal heat flux and k is the thermal conductivity of the thawed sediments. (More details are given in the appendix.) Given the approximations leading to Equation (2), it 1s probably valid to adopt for these parameters the values recently determined for Prudhoe Bay, Alaska, where the lithology is rather similar and the heat flux has a fairly typical value (Reference Lachenbruch, Sass, Marshall and MosesLachenbruch and others 1982). Then C1 ≈ 2.2 ka °C−1 and C2 ≈ 0.028°C m−1.
Figure 5 shows the resulting dependence of thaw time on initial permafrost thickness, assuming different post-glacial ground surface temperature values. To assess the effect of relict permafrost on the evolution of temperatures in deeper layers during the post-glacial period, it is reasonable to assume that the presence or absence of permafrost determines the surface boundary condition to which these temperatures respond. While permafrost is present, this temperature is 0°C; after thawing it is the actual post-glacial surface temperature (e.g. +8 to +10°C in the Swiss plateau). Only if the permafrost persists for an appreciable fraction of the post-glacial period will the permafrost buffering effect be significant. From Figure 5 it can be seen that negligible effects only should occur when, for example, Y0 < 100 m and Tp > 2°C, but that significant effects may occur when Yo = 400 m and Tp = 8°C.

Fig. 5 Thaw time t for ice-rich permafrost as a function of initial thickness Y0 and post-glacial surface temperature. During the disappearance of of ice-rich permafrost, the surface temperature of the Earth can be considered to remain at 0°C. Thus the palaeoclimatic curve represented in Figure 2 may have to be changed in cases of long thaw times.
Discussions and Conclusions
Thermal effects of quaternary temperature and ice conditions in the Swiss plateau produced by heat diffusion in low-porosity bedrock have lowered today’s rock temperatures by the order of 5 to 6°C at about 1 to 2 km depth in regions of former temperate glacier beds; in former periglacial regions, the temperature reduction is somewhat greater. Effects of latent heat exchange during the formation and thawing of ice-rich permafrost in high-porosity sediments are superimposed on the effects of heat diffusion. With periglacial surface temperatures of −3°C and less, ice-rich permafrost in unconsolidated sediments of unlimited thickness could have reached a thickness of ZOO m or more at 18 ka BP in the Swiss plateau; in most places, however, the thickness of unconsolidated sediments is much less than 200 m. For typical values of 50 m the thaw time of ice-rich permafrost is of the order of 200 to 300 a, which is too short to be important.. Effects due to the former existence and buffering influence of ice-rich permafrost in the Swiss plateau need therefore be considered only in situations which have exceptionally thick (>100 m), high-porosity sediments. The fact that the limit to the thickness of ice-rich permafrost is given by the lithology of the plateau rather than by the palaeotemperature, makes it difficult to check palaeoclimatic reconstructions by observations of corresponding temperature anomalies. On the other hand, this also means that geocryologieal evidence of the formation of cold, ice-rich permafrost is not necessarily contradicted by the lack of pronounced temperature anomalies in deep bore holes within the Swiss plateau.
The situation is obviously different in somewhat colder regions with thicker deposits of unconsolidated, porous sediments. There, even relict permafrost may be found which must have survived many thousands of years (Reference Balobaev, Devyatkin and KutasovBalobaev and others 1978, Reference Baulin, Dubikov and UvarkinBaulin and others 1978). In Switzerland, the largest thermal effects may be expected in deep Alpine valleys where the basal temperature of ice-age glaciers was well below 0°C (Reference Blatter and HaeberliBlatter and Haeberli 1984), and sediment thickness can be considerable (cf. Reference Aric and SteinhauserAric and Steinhauser 1976).
The authors are grateful to Dr H Röthlisberger, Dr A Iken and Jürg Alean (VAW/AG/ETHZ) for reading the manuscript critically. Pamela Alean assisted in preparing the manuscript and Werner Nobs completed the drawings.
Appendix
A rigorous calculation of the effect of ice-rich permafrost on deep temperature response would require a complete, simultaneous calculation of the temperature fields above, in, and below the permafrost, using appropriate Stefan boundary conditions at the ice interfaces. However, a simple approach for dealing with the permafrost separately is possible if sensible heat is neglected. This is equivalent to assuming an infinitely rapid temperature response, and in this limit temperature varies linearly above, in, and below the permafrost, as shown in Figure 1A. Y0 is the initial permafrost thickness at time t = 0, and Y1 and Y2 the thicknesses that have thawed from top and bottom, respectively, at time t. Products of the thaw rates and the latent heat per unit volume h are given by heat fluxes

Fig. 1A Thawing ice-rich permafrost. For explanation see text.
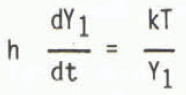
and

where k is the thermal conductivity of thawed permafrost, T is the surface temperature, and q is the heat flux into the base of the permafrost. Integration gives
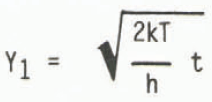
and

Thawing is complete when
with Y1 and Y2 given by Equations (A3) and (A4). Solution of Equation (A5) for the time when this occurs gives Equation (2) in the main text.
The validity of the key approximation, the neglect of all sensible heat, needs to be considered. This heat above and in the permafrost can be neglected as long as (ρc) ΔT << h, where (ρC) is volumetric heat capacity and ΔT the difference between surface temperature T and initial permafrost temperature. This tends to hold in the-saturated sediments of high porosity. However, the neglect of the sensible heat below the permafrost is a more delicate matter, because the heat flux q will not be the steady-state geothermal value implied by the approximation, but a transient value that should be calculated in the course of a complete solution of the problem. Nevertheless it is clear that the exact value of q will not be important as long as most of the thawing occurs from the top:

From Equations (A1) and (A2) this is true if

which is not violated seriously enough to affect the conclusions in the main text.








