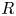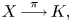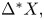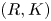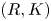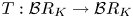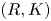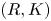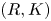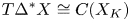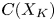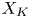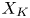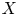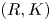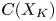1. Introduction; description of results
This article is an addition to a theory of blocked surgery, pioneered by Ranicki, augmented by others in [Reference Adams-Florou and Macko1, Reference Connolly, Davis and Khan4, Reference Connolly, Davis and Khan5, Reference Connolly6, Reference Davis and Rovi8, Reference Farrell and Jones9, Reference Ranicki16, Reference Ranicki and Weiss17], and still in a developing state.
Let $R$![]() be a commutative ring; let $K$
be a commutative ring; let $K$![]() be a finite simplicial complex. In [Reference Ranicki16] Ranicki introduced the category of $(R,K)$
be a finite simplicial complex. In [Reference Ranicki16] Ranicki introduced the category of $(R,K)$![]() chain complexes and chain maps denoted $\mathcal {B} R_K$
chain complexes and chain maps denoted $\mathcal {B} R_K$![]() here. He also defined algebraically, a contravariant functor $T:\mathcal {B} R_K\to \mathcal {B} R_K$
here. He also defined algebraically, a contravariant functor $T:\mathcal {B} R_K\to \mathcal {B} R_K$![]() .Footnote 1
.Footnote 1
The simplest geometric example of an $(R,K)$![]() chain complex arises from a
chain complex arises from a
$K$![]() -space $(X,\pi )$
-space $(X,\pi )$![]() . This is a finite simplicial complex $X$
. This is a finite simplicial complex $X$![]() and a simplicial map,
and a simplicial map,
$\pi :X\to K$![]() . In that case, the simplicial cochains on $X$
. In that case, the simplicial cochains on $X$![]() (with $R$
(with $R$![]() coefficients) form an $(R,K)$
coefficients) form an $(R,K)$![]() chain complex denoted $\Delta ^*X$
chain complex denoted $\Delta ^*X$![]() .
.
At the same time, $(X,\pi )$![]() specifies a regular CW complex $X_K$
specifies a regular CW complex $X_K$![]() , which is a (non-simplicial) subdivision of $X$
, which is a (non-simplicial) subdivision of $X$![]() . We show that the cellular chain complex (with $R$
. We show that the cellular chain complex (with $R$![]() coefficients) of $X_K$
coefficients) of $X_K$![]() forms a second $(R,K)$
forms a second $(R,K)$![]() chain complex $C(X_K)$
chain complex $C(X_K)$![]() .
.
Our main theorem, theorem 8.1, exhibits a geometrically defined chain isomorphism between $C(X_K)$![]() and $T\Delta ^*X$
and $T\Delta ^*X$![]() . Roughly put:
. Roughly put:
It is also our aim to give a transparent definition of this duality functor $T$![]() , a clear treatment of Ranicki's natural transformation $e:T^2\to id$
, a clear treatment of Ranicki's natural transformation $e:T^2\to id$![]() . and a simple proof that $e_C:T^2C\to C$
. and a simple proof that $e_C:T^2C\to C$![]() is an $(R,K)$
is an $(R,K)$![]() chain equivalence for all $C$
chain equivalence for all $C$![]() .
.
Our larger goal is to facilitate applications of Ranicki's theory to geometric questions such as the topological rigidity of non-positively curved groups as in [Reference Connolly, Davis and Khan4, Reference Connolly, Davis and Khan5, Reference Farrell and Jones9, Reference Farrell and Jones10] when those groups have elements of finite order.
The vehicle for such applications would be a full blown $K$![]() -blocked surgery theory of which there are only hints in [Reference Ranicki16]. This would start with a degree-one normal map between closed manifolds, $(f, b): (M,\nu (M))\to (X,\xi )$
-blocked surgery theory of which there are only hints in [Reference Ranicki16]. This would start with a degree-one normal map between closed manifolds, $(f, b): (M,\nu (M))\to (X,\xi )$![]() (as in [Reference Browder2]) together with a reference map, $\pi :X\to K$
(as in [Reference Browder2]) together with a reference map, $\pi :X\to K$![]() as above. It would seek an $L$
as above. It would seek an $L$![]() -theoretic obstruction to finding a normal cobordism of $(f,b)$
-theoretic obstruction to finding a normal cobordism of $(f,b)$![]() to a ‘K-blocked homotopy equivalence,’ $M'\to X$
to a ‘K-blocked homotopy equivalence,’ $M'\to X$![]() . But we will not pursue this here or even define the terms precisely.
. But we will not pursue this here or even define the terms precisely.
In the classical case ($K=$![]() point; [Reference Browder2, Reference Kervaire and Milnor12, Reference Ranicki18, Reference Wall19, Reference Wall20]) one has the ‘surgery obstruction’ $\sigma _*(f,b)\in L_n(\mathbb {Z}[\pi _1(X)])$
point; [Reference Browder2, Reference Kervaire and Milnor12, Reference Ranicki18, Reference Wall19, Reference Wall20]) one has the ‘surgery obstruction’ $\sigma _*(f,b)\in L_n(\mathbb {Z}[\pi _1(X)])$![]() to such a normal cobordism. But this functor $L_n()$
to such a normal cobordism. But this functor $L_n()$![]() , was generalized in [Reference Ranicki16] to yield obstruction groups $L_n(\mathcal {A})$
, was generalized in [Reference Ranicki16] to yield obstruction groups $L_n(\mathcal {A})$![]() for any ‘category-with-chain-involution’ $(A, *, \epsilon )$
for any ‘category-with-chain-involution’ $(A, *, \epsilon )$![]() . Here $A$
. Here $A$![]() is an additive category, $\mathcal {B} A\mathop {\to }\limits ^{*} \mathcal {B} A$
is an additive category, $\mathcal {B} A\mathop {\to }\limits ^{*} \mathcal {B} A$![]() is a contravariant functor satisfying certain conditions, on the category $\mathcal {B} A$
is a contravariant functor satisfying certain conditions, on the category $\mathcal {B} A$![]() , of finite chain complexes in $A$
, of finite chain complexes in $A$![]() , and $\epsilon :(*)^2\to id$
, and $\epsilon :(*)^2\to id$![]() , is an equivalence in the homotopy category of $\mathcal {B} A$
, is an equivalence in the homotopy category of $\mathcal {B} A$![]() .
.
Ranicki, in [Reference Ranicki16], then starts with a finite complex $K$![]() and a category with chain involution, $\mathcal {A}= (A, *, \varepsilon )$
and a category with chain involution, $\mathcal {A}= (A, *, \varepsilon )$![]() as above. He then constructs the additive category $A_K$
as above. He then constructs the additive category $A_K$![]() of $K$
of $K$![]() -blocked objects from $A$
-blocked objects from $A$![]() , and $K$
, and $K$![]() -blocked $A$
-blocked $A$![]() -maps. From $*$
-maps. From $*$![]() , and $\varepsilon$
, and $\varepsilon$![]() , he defines the Ranicki Duality Functor $T:\mathcal {B}(A_K)\to \mathcal {B}(A_K)$
, he defines the Ranicki Duality Functor $T:\mathcal {B}(A_K)\to \mathcal {B}(A_K)$![]() , and the natural transformation $e: T^2\to id_{\mathcal {B}(A_K)}$
, and the natural transformation $e: T^2\to id_{\mathcal {B}(A_K)}$![]() . This construction allows one to define the surgery obstruction groups, $L_n(\mathcal {A}_K)$
. This construction allows one to define the surgery obstruction groups, $L_n(\mathcal {A}_K)$![]() where $\mathcal {A}_K =(A_K, T, e)$
where $\mathcal {A}_K =(A_K, T, e)$![]() .
.
This seems to apply directly to a $K$![]() -blocked normal map, $M^n\mathop {\longrightarrow }\limits ^{(f,b)} X^n\mathop {\to }\limits ^{\pi } K$
-blocked normal map, $M^n\mathop {\longrightarrow }\limits ^{(f,b)} X^n\mathop {\to }\limits ^{\pi } K$![]() . Here the relevant category seems to be $A=A(R)$
. Here the relevant category seems to be $A=A(R)$![]() , the category of finitely generated free modules over a fixed commutative ring $R$
, the category of finitely generated free modules over a fixed commutative ring $R$![]() . We write $A R_K$
. We write $A R_K$![]() for $(A R)_K$
for $(A R)_K$![]() and $\mathcal {B} R_K$
and $\mathcal {B} R_K$![]() for $\mathcal {B}(A R_K)$
for $\mathcal {B}(A R_K)$![]() . Its objects are $(R,K)$
. Its objects are $(R,K)$![]() -chain complexes. So the simplicial cochain complexes of $X$
-chain complexes. So the simplicial cochain complexes of $X$![]() and $M$
and $M$![]() denoted $\Delta ^*X$
denoted $\Delta ^*X$![]() and $\Delta ^*M$
and $\Delta ^*M$![]() , and the simplicial chain complexes, $\Delta X'$
, and the simplicial chain complexes, $\Delta X'$![]() and $\Delta M'$
and $\Delta M'$![]() , are $(R,K)$
, are $(R,K)$![]() -chain complexes. (See § 3). Thus the $L$
-chain complexes. (See § 3). Thus the $L$![]() -groups of $(\mathcal {A} R_K, T, e)$
-groups of $(\mathcal {A} R_K, T, e)$![]() seem likely to be useful.
seem likely to be useful.
However, Ranicki's definition of $\mathcal {B} R_K \mathop {\longrightarrow }\limits ^{T}\mathcal {B} R_K$![]() was only a starting point. Indeed his assertion in [Reference Ranicki16] of the crucial theorem that $(\mathcal {A} R_K, T, e)$
was only a starting point. Indeed his assertion in [Reference Ranicki16] of the crucial theorem that $(\mathcal {A} R_K, T, e)$![]() is a category with chain involution was only proved in 2018 (by Adams-Florou and Macko, [Reference Adams-Florou and Macko1]).
is a category with chain involution was only proved in 2018 (by Adams-Florou and Macko, [Reference Adams-Florou and Macko1]).
This paper interprets Ranicki's notions geometrically. Section 2 fixes chain-complex conventions. Section 3 reviews Ranicki's concepts concerning $(R,K)$![]() complexes while attempting to simplify notation. In § 5 we introduce the $(R,K)$
complexes while attempting to simplify notation. In § 5 we introduce the $(R,K)$![]() chain complex $C\otimes _KD$
chain complex $C\otimes _KD$![]() , defined if $D$
, defined if $D$![]() is an $(R,K)$
is an $(R,K)$![]() complex and $C$
complex and $C$![]() is an $(R,K^{op})$
is an $(R,K^{op})$![]() complex. This complex $C\otimes _KD$
complex. This complex $C\otimes _KD$![]() is a certain quotient of $C\otimes _RD$
is a certain quotient of $C\otimes _RD$![]() .
.
Our definition (see 6.1) of the Ranicki dual $TC$![]() , of an $(R,K)$
, of an $(R,K)$![]() complex $C$
complex $C$![]() , is:
, is:
In § 7 we show, using work of M. Cohen [Reference Cohen3], that each $K$![]() -space $(X,\pi )$
-space $(X,\pi )$![]() defines a certain regular CW-complex $X_K$
defines a certain regular CW-complex $X_K$![]() , whose cellular chain complex has a natural $(R, K)$
, whose cellular chain complex has a natural $(R, K)$![]() structure. Therefore from each $K$
structure. Therefore from each $K$![]() -space $(X,\pi )$
-space $(X,\pi )$![]() we obtain three $(R,K)$
we obtain three $(R,K)$![]() chain complexes:
chain complexes:
(1) $\Delta ^*X$
 , the simplicial cochain complex of $X$
, the simplicial cochain complex of $X$ (definition 4.1).
(definition 4.1).(2) $C(X_K)$
 , the cellular chain complex of the CW complex $X_K$
, the cellular chain complex of the CW complex $X_K$ (§ 8).
(§ 8).(3) $\Delta X'$
 , the simplicial chain complex of $X'$
, the simplicial chain complex of $X'$ , the barycentric subdivision of $X$
, the barycentric subdivision of $X$ (definition 7.2).
(definition 7.2).
This paper shows that these three are closely related by $T$![]() . Our main result, theorem 8.1, exhibits an isomorphism of $(R,K)$
. Our main result, theorem 8.1, exhibits an isomorphism of $(R,K)$![]() chain complexes:
chain complexes:
Then, using [Reference McCrory13], we prove there are $(R,K)$![]() chain homotopy equivalences:
chain homotopy equivalences:
When $X$![]() is a pl-manifold, and $C=C(X_K)$
is a pl-manifold, and $C=C(X_K)$![]() , Poincare duality then becomes an $n$
, Poincare duality then becomes an $n$![]() -cycle in the $(R,K^{\mathrm {op}})$
-cycle in the $(R,K^{\mathrm {op}})$![]() complex, $Hom_{(R,K)}(TC, C)$
complex, $Hom_{(R,K)}(TC, C)$![]() .
.
This CW complex $X_K$![]() is a subdivision of $X$
is a subdivision of $X$![]() , and $X'$
, and $X'$![]() is a simplicial subdivision of $X_K$
is a simplicial subdivision of $X_K$![]() . In fact, for each simplex $S$
. In fact, for each simplex $S$![]() of $X$
of $X$![]() and each face $\sigma$
and each face $\sigma$![]() of $\pi (S)\in K$
of $\pi (S)\in K$![]() , there is a single cell $S_\sigma$
, there is a single cell $S_\sigma$![]() of $X_K$
of $X_K$![]() . Specifically, if $D(\sigma,\pi (S))$
. Specifically, if $D(\sigma,\pi (S))$![]() is the dual cell of $\sigma$
is the dual cell of $\sigma$![]() in $\pi (S)$
in $\pi (S)$![]() :
:
The author is indebted to Jim Davis for his helpful comments. He also wants to acknowledge, with thanks, the referee's suggestions for improving the text.
2. Chain complex conventions
Throughout this paper, $R$![]() denotes a fixed commutative ring; $AR$
denotes a fixed commutative ring; $AR$![]() is the additive category of finitely generated free $R$
is the additive category of finitely generated free $R$![]() modules.
modules.
For any additive category $A$![]() we will write $\mathcal {B} A$
we will write $\mathcal {B} A$![]() for the additive category of finite chain complexes, $C=\{C_q, \partial _q\}_{q\in \mathbb {Z}}$
for the additive category of finite chain complexes, $C=\{C_q, \partial _q\}_{q\in \mathbb {Z}}$![]() and chain maps $f=\{f_q:C_q\to D_q\}_{q\in \mathbb {Z}}$
and chain maps $f=\{f_q:C_q\to D_q\}_{q\in \mathbb {Z}}$![]() from $A$
from $A$![]() . (Finite means: $C_q=0$
. (Finite means: $C_q=0$![]() for all but finitely many $q$
for all but finitely many $q$![]() ). We abbreviate $\mathcal {B} (AR)$
). We abbreviate $\mathcal {B} (AR)$![]() to $\mathcal {B} R$
to $\mathcal {B} R$![]() .
.
As usual two chain maps $f,g: C\to D$![]() are chain homotopic if there is a sequence of $A$
are chain homotopic if there is a sequence of $A$![]() maps, $h=\{h_q:C_q\to D_{q+1}\}$
maps, $h=\{h_q:C_q\to D_{q+1}\}$![]() , for which $d^D_{q+1}h_q + h_{q-1}d^C_q = g_q-f_q \ \forall q$
, for which $d^D_{q+1}h_q + h_{q-1}d^C_q = g_q-f_q \ \forall q$![]() .
.
We regard $A$![]() as the full subcategory of $\mathcal {B} A$
as the full subcategory of $\mathcal {B} A$![]() consisting of chain complexes concentrated in degree zero.
consisting of chain complexes concentrated in degree zero.
Let $C,D\in Ob(\mathcal {B} R)$![]() . The complexes $C\otimes _R D$
. The complexes $C\otimes _R D$![]() , and $Hom_R(C,D)$
, and $Hom_R(C,D)$![]() in $Ob(\mathcal {B} R)$
in $Ob(\mathcal {B} R)$![]() , are:
, are:

The evaluation map, $eval_{C,D}:Hom_R(C,D)\otimes _R C\longrightarrow D$![]() is the R-chain map:
is the R-chain map:
Note that $eval_{R,D}:Hom_R(R,D)\otimes _R R\cong D$![]() .
.
Write $ev_C:C^*\otimes C\to R$![]() for $eval_{C,R}$
for $eval_{C,R}$![]() .
.
The contravariant functor $\mathcal {B} R\mathop {\to }\limits ^{*} \mathcal {B} R$![]() is : $C^*= Hom(C,R); \; f^* = Hom(f, 1_R)$
is : $C^*= Hom(C,R); \; f^* = Hom(f, 1_R)$![]() .
.
Therefore we have:
The functor $*$![]() comes with a natural equivalence, $\varepsilon : (*)^2\to 1_{\mathcal {B} R}$
comes with a natural equivalence, $\varepsilon : (*)^2\to 1_{\mathcal {B} R}$![]() . Specifically, the chain isomorphism $\epsilon _C: C^{**}\to C$
. Specifically, the chain isomorphism $\epsilon _C: C^{**}\to C$![]() is characterized by the identity:
is characterized by the identity:
3. Basic definitions for $(R,K)$ chain complexes
chain complexes
Definition 3.1 Let $K$![]() be a finite poset with partial order $\leq$
be a finite poset with partial order $\leq$![]() .
.
$K^{op}$![]() denotes the same set with the opposite partial order.
denotes the same set with the opposite partial order.
(Later we will specialize to the case when $K$![]() is a finite simplicial complex).
is a finite simplicial complex).
(1) An (R,K) module is an ordered pair $M= (M(K), \{M(\sigma )\}_{\sigma \in K})$
 such that:
such that:
(a) $M(K)$
 and each $M(\sigma )$
and each $M(\sigma )$ are $R$
are $R$ -modules in $Ob(A R)$
-modules in $Ob(A R)$ ;
;(b) $M(K) = \oplus _{\sigma \in K} M(\sigma )$
 .
.
More generally, for any $S\subset K$
 we write: $M(S)= \oplus _{\sigma \in S} M(\sigma ).$
we write: $M(S)= \oplus _{\sigma \in S} M(\sigma ).$
(2) An $(R,K)$
 map $M\mathop {\to }\limits ^{f}N$
map $M\mathop {\to }\limits ^{f}N$ of $(R,K)$
of $(R,K)$ modules is a map $M(K)\mathop {\to }\limits ^{f} N(K)$
modules is a map $M(K)\mathop {\to }\limits ^{f} N(K)$ of $R$
of $R$ modules, whose components, $f(\tau,\sigma ):M(\sigma )\to N(\tau ),$
modules, whose components, $f(\tau,\sigma ):M(\sigma )\to N(\tau ),$ satisfy:
\[ f(\tau,\sigma)=\,0\text{ unless }\tau\geq\sigma. \]
satisfy:
\[ f(\tau,\sigma)=\,0\text{ unless }\tau\geq\sigma. \]
(3) The additive category of $(R,K)$
 maps and modules is written $AR_K$
maps and modules is written $AR_K$ .
.We abbreviate the category of chain complexes, $\mathcal {B}(AR_K)$
 , to $\mathcal {B} R_K$
, to $\mathcal {B} R_K$ .
.(4) An object $C =\{ C_q, \partial _q \}_{q\in \mathbb {Z}}$
 of $\mathcal {B} R_K$
of $\mathcal {B} R_K$ is an ( $R,K)$
is an ( $R,K)$ chain complex. We then write $C(K)$
chain complex. We then write $C(K)$ for $\{C_q(K), \partial _q\}_{q\in \mathbb {Z}}$
for $\{C_q(K), \partial _q\}_{q\in \mathbb {Z}}$ , an $R$
, an $R$ -chain complex in $ob(\mathcal {B} R)$
-chain complex in $ob(\mathcal {B} R)$ .
.Note: $C\in ob(\mathcal {B} R_K)$
 is specified by specifying the $R$
is specified by specifying the $R$ complex $C(K)$
complex $C(K)$ and the required collection $\{C_q(\sigma )\}_{\sigma \in K, q\in \mathbb {Z}}$
and the required collection $\{C_q(\sigma )\}_{\sigma \in K, q\in \mathbb {Z}}$ of $R$
of $R$ submodules.
submodules.(5) Let $C,D\in ob(\mathcal {B} R_K).$
 $Hom_{(R,K)}(C,D)$
$Hom_{(R,K)}(C,D)$ is the $(R,K^{op})$
is the $(R,K^{op})$ complex such that:
complex such that:
(a) $Hom_{(R,K)}(C,D)(K)$
 is the subcomplex of $Hom_R(C(K), D(K))$
is the subcomplex of $Hom_R(C(K), D(K))$ given by those $f =\{f_q : C_q\to D_{q+|f|}\}_{q \in \mathbb {Z} }$
given by those $f =\{f_q : C_q\to D_{q+|f|}\}_{q \in \mathbb {Z} }$ for which each $f_q$
for which each $f_q$ is an $(R,K)$
is an $(R,K)$ map.
map.(b) $Hom_{(R,K)}(C, D)_p(\sigma )$
 is the set of $f\in Hom_{(R,K)}(C, D)(K)_p$
is the set of $f\in Hom_{(R,K)}(C, D)(K)_p$ satisfying:
\[ f_q \mid_{C_q(\tau) } =0\text{ if }\tau \neq \sigma,\; \forall\; q. \]
satisfying:
\[ f_q \mid_{C_q(\tau) } =0\text{ if }\tau \neq \sigma,\; \forall\; q. \]
(6) We say a sequence of chain maps $0\to C'\mathop {\to }\limits ^{i} C\mathop {\to }\limits ^{j} C''\to 0$
 in $\mathcal {B} R_K$
in $\mathcal {B} R_K$ is exact if for each $\sigma \neq \tau$
is exact if for each $\sigma \neq \tau$ , $i(\sigma, \tau )=0,\; j(\sigma,\tau )=0,$
, $i(\sigma, \tau )=0,\; j(\sigma,\tau )=0,$ and, for all $q$
and, for all $q$ , the corresponding sequence, $0\to C'_q(\sigma )\to C_q(\sigma )\to C''_q(\sigma )\to 0$
, the corresponding sequence, $0\to C'_q(\sigma )\to C_q(\sigma )\to C''_q(\sigma )\to 0$ . is an exact sequence in $\mathcal {A} R$
. is an exact sequence in $\mathcal {A} R$ . We then say $i$
. We then say $i$ is an $(R,K)$
is an $(R,K)$ monomorphism and $j$
monomorphism and $j$ is an $(R,K)$
is an $(R,K)$ epimorphism.
epimorphism.(7) Note that $*$
 specifies a contravariant functor, $\mathcal {B} R_K\mathop {\longrightarrow }\limits ^{*}\mathcal {B} R_{K^{op}}$
specifies a contravariant functor, $\mathcal {B} R_K\mathop {\longrightarrow }\limits ^{*}\mathcal {B} R_{K^{op}}$ , provided that we define $(C^*)_q (\sigma )$
, provided that we define $(C^*)_q (\sigma )$ as $(C_{-q}(\sigma ))^*$
as $(C_{-q}(\sigma ))^*$ and $d^{C^*}$
and $d^{C^*}$ as $d^{C(K)^*}$
as $d^{C(K)^*}$ for $C\in ob(\mathcal {B} R_K)$
for $C\in ob(\mathcal {B} R_K)$ . $\mathcal {B} R_K\mathop {\longrightarrow }\limits ^{*}\mathcal {B} R_{K^{op}}$
. $\mathcal {B} R_K\mathop {\longrightarrow }\limits ^{*}\mathcal {B} R_{K^{op}}$ preserves exactness and homotopy. The transformation $\varepsilon _C: C^{**}\to C$
preserves exactness and homotopy. The transformation $\varepsilon _C: C^{**}\to C$ of § 2 is an $(R,K)$
of § 2 is an $(R,K)$ isomorphism, for all $C\in ob(\mathcal {B} R_K).$
isomorphism, for all $C\in ob(\mathcal {B} R_K).$
(8) We say $S\subset K$
 is full in K if, whenever $\rho, \tau \in S$
is full in K if, whenever $\rho, \tau \in S$ , then:
\[ \{\sigma\in K \mid \rho\leq \sigma\leq \tau\} \subset S. \]Let $C$
, then:
\[ \{\sigma\in K \mid \rho\leq \sigma\leq \tau\} \subset S. \]Let $C$
 be an $(R,K)$
be an $(R,K)$ complex. Let $S$
complex. Let $S$ be a full subset of $K$
be a full subset of $K$ . We define $\partial _q^{C(S)}:C_q(S) \to C_{q-1}(S)$
. We define $\partial _q^{C(S)}:C_q(S) \to C_{q-1}(S)$ by:
\[ \partial_q^{C(S)} x = \sum_{\tau\in S}\partial^C(\tau, \sigma)x, \quad \forall x\in C_q(\sigma), \forall \tau, \sigma \in S. \]Then $C(S):=\{ C_q(S), \partial _q^{C(S)}\}_{q \in \mathbb {Z}}$
by:
\[ \partial_q^{C(S)} x = \sum_{\tau\in S}\partial^C(\tau, \sigma)x, \quad \forall x\in C_q(\sigma), \forall \tau, \sigma \in S. \]Then $C(S):=\{ C_q(S), \partial _q^{C(S)}\}_{q \in \mathbb {Z}}$
 is an $R$
is an $R$ chain complex. But in many cases, it is neither a subcomplex nor a quotient complex of $C(K)$
chain complex. But in many cases, it is neither a subcomplex nor a quotient complex of $C(K)$ .
.
4. $K$ spaces and their chain complexes
spaces and their chain complexes
For the rest of this paper, $K$![]() denotes a finite simplicial complex.
denotes a finite simplicial complex.
A simplicial complex $K$![]() is a poset so the above definitions apply. In this case $\sigma \leq \tau$
is a poset so the above definitions apply. In this case $\sigma \leq \tau$![]() means that the simplex $\sigma$
means that the simplex $\sigma$![]() is a face (not necessarily proper) of the simplex $\tau$
is a face (not necessarily proper) of the simplex $\tau$![]() .
.
$\Delta _*(K;R)=\{ \Delta _q(K;R),\partial _q\}_{q\in \mathbb {Z}}$![]() denotes the simplicial chain complex of $K$
denotes the simplicial chain complex of $K$![]() .
.
$\Delta ^*(K;R)=Hom_R(\Delta _*(X;R), R)$![]() denotes the simplicial cochain complex of $K$
denotes the simplicial cochain complex of $K$![]() .
.
One can choose a basis, $bK$![]() for $\Delta _*(K;R)$
for $\Delta _*(K;R)$![]() consisting of one oriented $q$
consisting of one oriented $q$![]() -simplex, $\sigma =\langle v_0\dots, v_q\rangle \in \Delta _q(K;R)$
-simplex, $\sigma =\langle v_0\dots, v_q\rangle \in \Delta _q(K;R)$![]() for each $q$
for each $q$![]() -simplex with vertices $v_0,\dots v_q$
-simplex with vertices $v_0,\dots v_q$![]() , of $K$
, of $K$![]() . Recall: $\langle v_0,\dots,v_q\rangle = sgn(\pi )\langle v_{\pi (0)},\dots,v_{\pi (q)}\rangle$
. Recall: $\langle v_0,\dots,v_q\rangle = sgn(\pi )\langle v_{\pi (0)},\dots,v_{\pi (q)}\rangle$![]() for each $\pi \in S_{q+1}$
for each $\pi \in S_{q+1}$![]() . The oriented $q$
. The oriented $q$![]() -simplex $\sigma \in \Delta _q(K;R)$
-simplex $\sigma \in \Delta _q(K;R)$![]() defines a dual cochain $\sigma ^*\in \Delta ^*(K;R)_{-q}$
defines a dual cochain $\sigma ^*\in \Delta ^*(K;R)_{-q}$![]() such that $\sigma ^*(\tau ) =0$
such that $\sigma ^*(\tau ) =0$![]() for all $\tau \neq \pm \sigma$
for all $\tau \neq \pm \sigma$![]() , and $\sigma ^*(\sigma )=1$
, and $\sigma ^*(\sigma )=1$![]() .
.
One then defines $\sigma ^{**}\in \Delta _q(K;R)^{**}$![]() by: $\varepsilon (\sigma ^{**}) = \sigma$
by: $\varepsilon (\sigma ^{**}) = \sigma$![]() .
.
Each simplex $\sigma \in K$![]() defines subcomplexes, $\overline {\sigma }$
defines subcomplexes, $\overline {\sigma }$![]() and $\partial \sigma$
and $\partial \sigma$![]() , and a subset $st(\sigma )$
, and a subset $st(\sigma )$![]() :
:
The incidence number $[\tau, \sigma ]\in \{1,-1, 0\}$![]() is defined for any oriented simplices $\sigma, \tau$
is defined for any oriented simplices $\sigma, \tau$![]() of $K$
of $K$![]() . It satisfies: $\partial _q(\sigma )= \sum _{\tau \in bK} [\sigma, \tau ] \tau$
. It satisfies: $\partial _q(\sigma )= \sum _{\tau \in bK} [\sigma, \tau ] \tau$![]() for any basis, $bK$
for any basis, $bK$![]() of oriented simplices of $K$
of oriented simplices of $K$![]() . $[\sigma,\tau ]\neq 0$
. $[\sigma,\tau ]\neq 0$![]() iff $\tau$
iff $\tau$![]() is a codimension-one face of $\sigma$
is a codimension-one face of $\sigma$![]() .
.
Definition 4.1 ($K$![]() -spaces, $\Delta ^*X$
-spaces, $\Delta ^*X$![]() and $\Delta X$
and $\Delta X$![]() )
)
Let $K$![]() be a finite simplicial complex. A $K$
be a finite simplicial complex. A $K$![]() -space is a pair $(X, \pi )$
-space is a pair $(X, \pi )$![]() where $X$
where $X$![]() is a finite simplicial complex and $|X|\mathop {\to }\limits ^{\pi } |K|$
is a finite simplicial complex and $|X|\mathop {\to }\limits ^{\pi } |K|$![]() is a simplicial map, $X\to K$
is a simplicial map, $X\to K$![]() . A map of $K$
. A map of $K$![]() -spaces, $(X,\pi _X)\to (Y, \pi _Y)$
-spaces, $(X,\pi _X)\to (Y, \pi _Y)$![]() is a simplicial map $f:|X|\to |Y|$
is a simplicial map $f:|X|\to |Y|$![]() satisfying: $\pi _Y f=\pi _X$
satisfying: $\pi _Y f=\pi _X$![]() .
.
Let $(X,\pi )$![]() be a $K$
be a $K$![]() -space.
-space.
$\Delta X$![]() denotes the $(R,K^{op})$
denotes the $(R,K^{op})$![]() complex for which $\Delta X(K)= \Delta _*(X;R)$
complex for which $\Delta X(K)= \Delta _*(X;R)$![]() . For each $\sigma \in K$
. For each $\sigma \in K$![]() , $(\Delta X)_p(\sigma )$
, $(\Delta X)_p(\sigma )$![]() is the submodule generated by oriented $p$
is the submodule generated by oriented $p$![]() -simplices in $\Delta _p(X;R)$
-simplices in $\Delta _p(X;R)$![]() whose underlying p-simplex, $S\in X$
whose underlying p-simplex, $S\in X$![]() , satisfies $\sigma = \pi (S)\in K$
, satisfies $\sigma = \pi (S)\in K$![]() .
.
By definition, $\Delta ^*X= (\Delta X)^*$![]() . Therefore $\Delta ^*X(K) = Hom_R(\Delta _*(X;R), R)=\Delta ^*(X; R)$
. Therefore $\Delta ^*X(K) = Hom_R(\Delta _*(X;R), R)=\Delta ^*(X; R)$![]() , the simplicial cochain complex of $X$
, the simplicial cochain complex of $X$![]() . For each $\sigma \in K$
. For each $\sigma \in K$![]() , $(\Delta ^*X)_{-p}(\sigma )$
, $(\Delta ^*X)_{-p}(\sigma )$![]() is therefore the submodule spanned by all $S^*$
is therefore the submodule spanned by all $S^*$![]() for which $S\in \Delta _p(X;R)$
for which $S\in \Delta _p(X;R)$![]() is an oriented simplex and $\sigma =\pi (S)\in K$
is an oriented simplex and $\sigma =\pi (S)\in K$![]() .
.
A map $f:X \to Y$![]() of $K$
of $K$![]() -spaces induces an $(R,K)$
-spaces induces an $(R,K)$![]() chain map $f^*:\Delta ^*Y\to \Delta ^*X$
chain map $f^*:\Delta ^*Y\to \Delta ^*X$![]() and an $(R,K^{op})$
and an $(R,K^{op})$![]() chain map $f_*:\Delta Y\to \Delta X$
chain map $f_*:\Delta Y\to \Delta X$![]() .
.
The next lemma will be used in § 6.
Lemma 4.2 Suppose $S\in K$![]() and there is no $\tau \in K$
and there is no $\tau \in K$![]() for which $S<\tau$
for which $S<\tau$![]() . The $K$
. The $K$![]() -space $(\overline {S},inclusion)$
-space $(\overline {S},inclusion)$![]() specifies the $(R,K)$
specifies the $(R,K)$![]() complex $\Delta ^*\overline {S}$
complex $\Delta ^*\overline {S}$![]() . Then $\Delta ^*\overline {S}(st(\sigma ))$
. Then $\Delta ^*\overline {S}(st(\sigma ))$![]() is a contractible $R$
is a contractible $R$![]() -complex for all $\sigma \in K$
-complex for all $\sigma \in K$![]() such that $\sigma \neq S$
such that $\sigma \neq S$![]() . Also $\Delta ^*\overline {S}(st(S)) = R S^*.$
. Also $\Delta ^*\overline {S}(st(S)) = R S^*.$![]()
Proof. It is obvious that $\Delta ^*\overline {S}(st(S)) = R S^*$![]() (after orienting $S$
(after orienting $S$![]() ) and that $\Delta ^*\overline {S}(st(\sigma )) =0$
) and that $\Delta ^*\overline {S}(st(\sigma )) =0$![]() if $\sigma$
if $\sigma$![]() is not a face of $S$
is not a face of $S$![]() . So we assume $\sigma < S$
. So we assume $\sigma < S$![]() . Let $\tau$
. Let $\tau$![]() be the complementary face of $\sigma$
be the complementary face of $\sigma$![]() in $S$
in $S$![]() . Then the joins, $\overline {S} = \sigma * \tau$
. Then the joins, $\overline {S} = \sigma * \tau$![]() and $\partial \sigma *\tau$
and $\partial \sigma *\tau$![]() are contractible simplicial complexes. Note $st(\sigma )= \overline {S} -\partial \sigma *\tau$
are contractible simplicial complexes. Note $st(\sigma )= \overline {S} -\partial \sigma *\tau$![]() . Consequently, $\Delta ^*\overline {S}(st(\sigma )) = \Delta ^*(\sigma * \tau, \partial \sigma * \tau ;R)$
. Consequently, $\Delta ^*\overline {S}(st(\sigma )) = \Delta ^*(\sigma * \tau, \partial \sigma * \tau ;R)$![]() is a contractible chain complex.
is a contractible chain complex.
5. $C\otimes _K D$ and the isomorphism $Hom_{(R,K)}(D, C^*) \cong (C\otimes _K D)^*$
and the isomorphism $Hom_{(R,K)}(D, C^*) \cong (C\otimes _K D)^*$
Throughout this section, $C$![]() denotes an $(R,K^{op})$
denotes an $(R,K^{op})$![]() complex and $D$
complex and $D$![]() denotes an $(R,K)$
denotes an $(R,K)$![]() complex.
complex.
We will first define two $(R,K)$![]() complexes: $C\otimes _R D$
complexes: $C\otimes _R D$![]() and a quotient of this, ${C\otimes _K D}$
and a quotient of this, ${C\otimes _K D}$![]() .
.
In $K$![]() , the star of any simplex , $st(\sigma )$
, the star of any simplex , $st(\sigma )$![]() , as well as $K-st(\sigma )$
, as well as $K-st(\sigma )$![]() are full in $K$
are full in $K$![]() . Moreover the chain complex $C(K-st(\sigma ))$
. Moreover the chain complex $C(K-st(\sigma ))$![]() is a subcomplex of $C(K)$
is a subcomplex of $C(K)$![]() and $C(st(\sigma ))$
and $C(st(\sigma ))$![]() is a quotient complex. These fit into a short exact sequence of chain maps in $\mathcal {B} R$
is a quotient complex. These fit into a short exact sequence of chain maps in $\mathcal {B} R$![]() :
:
Here $C(K)\mathop {\longrightarrow }\limits ^{p_{st(\sigma )}}C(st(\sigma ))$![]() is defined by: $p_{st(\sigma )}|_{C_q(st(\sigma ))}= 1_ {C_q(st(\sigma ))}$
is defined by: $p_{st(\sigma )}|_{C_q(st(\sigma ))}= 1_ {C_q(st(\sigma ))}$![]() ; and $p_{st(\sigma )}|_{C(K-st(\sigma ))}=0$
; and $p_{st(\sigma )}|_{C(K-st(\sigma ))}=0$![]() .
.
(For the $(R,K)$![]() complex $D$
complex $D$![]() , we get $0\to D(st(\sigma ))\to D(K)\to D(K- st(\sigma )){\to 0}$
, we get $0\to D(st(\sigma ))\to D(K)\to D(K- st(\sigma )){\to 0}$![]() ).
).
Definition 5.1 ($C\otimes _KD$![]() , $C\otimes _RD$
, $C\otimes _RD$![]() , and $C\otimes _RD \mathop {\longrightarrow }\limits ^{\pi _{C,D}}C\otimes _K D$
, and $C\otimes _RD \mathop {\longrightarrow }\limits ^{\pi _{C,D}}C\otimes _K D$![]() ).
).
Let $C$![]() be an $(R,K^{op})$
be an $(R,K^{op})$![]() complex and $D$
complex and $D$![]() be an $(R,K)$
be an $(R,K)$![]() complex.
complex.
(1) Let $C\otimes _RD$
 be the $(R,K)$
be the $(R,K)$ complex for which:
\begin{align*} & (C\otimes_RD)(K)= C(K)\otimes_R D(K); \\ & (C\otimes_R D)_q(\rho)= (C(K)\otimes_R D(\rho))_q \quad \forall \rho\in K, q\in \mathbb{Z} \end{align*}
complex for which:
\begin{align*} & (C\otimes_RD)(K)= C(K)\otimes_R D(K); \\ & (C\otimes_R D)_q(\rho)= (C(K)\otimes_R D(\rho))_q \quad \forall \rho\in K, q\in \mathbb{Z} \end{align*}
(2) Let $C\otimes _KD$
 be the $(R,K)$
be the $(R,K)$ complex for which:
complex for which:
(a) $(C\otimes _K D)_q(K)= \sum _{\rho \in K} (C(st(\rho ))\otimes _R D(\rho ))_q \ \forall q\in \mathbb {Z}$

(b) $(C\otimes _K D)(\rho )= C(st(\rho ))\otimes _R D(\rho ) \ \forall \;\rho \in K$

(c) The map $C\otimes _RD\mathop {\longrightarrow }\limits ^{\pi _{C,D}} C\otimes _KD$
 is an $(R,K)$
is an $(R,K)$ chain epimorphism, if we define $\pi _{C,D}$
chain epimorphism, if we define $\pi _{C,D}$ by requiring that $\pi _{C,D}(\sigma,\rho )=0$
by requiring that $\pi _{C,D}(\sigma,\rho )=0$ for $\sigma \neq \rho$
for $\sigma \neq \rho$ and:
\[ \pi_{C,D}(\rho, \rho)= p_{st(\rho)}\otimes_R 1_{D(\rho) }:C(K)\otimes_R D(\rho) \longrightarrow C(st(\tau))\otimes _R D(\rho). \]
and:
\[ \pi_{C,D}(\rho, \rho)= p_{st(\rho)}\otimes_R 1_{D(\rho) }:C(K)\otimes_R D(\rho) \longrightarrow C(st(\tau))\otimes _R D(\rho). \]
Expicitly, for any $\rho \leq \tau$![]() and $x\otimes _Ry\in C_r(\tau )\otimes _RD_{q-r}(\rho )\subset (C\otimes _KD)_q(\rho )$
and $x\otimes _Ry\in C_r(\tau )\otimes _RD_{q-r}(\rho )\subset (C\otimes _KD)_q(\rho )$![]() , we have
, we have

We now show that $(C\otimes _KD)^*$![]() is a convenient expression for $Hom_{(R,K)}(D, C^*)$
is a convenient expression for $Hom_{(R,K)}(D, C^*)$![]() :
:
Lemma 5.2 There is a natural isomorphism $\Psi$![]() of functors, denoted,
of functors, denoted,
for any $(C,D)\in Ob(\mathcal {B} R_{K^{op}}\times \mathcal {B} R_{K})$![]() .
.
Proof. Suppose $f$![]() is in $Hom_{(R,K)}(D, C^*)_q(\sigma )$
is in $Hom_{(R,K)}(D, C^*)_q(\sigma )$![]() for some $\sigma \in K$
for some $\sigma \in K$![]() and $q\in \mathbb {Z}$
and $q\in \mathbb {Z}$![]() . Define an $R$
. Define an $R$![]() -map, $\Psi (f): C(st(\sigma ))\otimes D(\sigma )_{-q}\to R$
-map, $\Psi (f): C(st(\sigma ))\otimes D(\sigma )_{-q}\to R$![]() , by the formula:
, by the formula:
The same formula yields $0$![]() , if $x\otimes y$
, if $x\otimes y$![]() is in $(C\otimes _KD)(\tau )_{-q}$
is in $(C\otimes _KD)(\tau )_{-q}$![]() for $\tau \neq \sigma$
for $\tau \neq \sigma$![]() . One easily sees that this rule (i.e. $f\mapsto \Psi (f)$
. One easily sees that this rule (i.e. $f\mapsto \Psi (f)$![]() gives an isomorphism,
gives an isomorphism,
of $(R,K^{op})$![]() complexes for all $(C,D) \in Ob(\mathcal {B} R_{K^{op}}\times \mathcal {B} R_{K})$
complexes for all $(C,D) \in Ob(\mathcal {B} R_{K^{op}}\times \mathcal {B} R_{K})$![]() . Naturality is obvious.
. Naturality is obvious.
6. Ranicki Duality and the $(R,K)$ chain equivalence $e:T^2\to 1_{\mathcal {B} R_K}$
chain equivalence $e:T^2\to 1_{\mathcal {B} R_K}$
Definition 6.1 Ranicki Duality is the contravariant functor $\mathcal {B} R_K\mathop {\longrightarrow }\limits ^{T}\mathcal {B} R_K$![]() defined for a chain complex $C\in Ob(\mathcal {B} R_K)$
defined for a chain complex $C\in Ob(\mathcal {B} R_K)$![]() and a $(R,K)$
and a $(R,K)$![]() chain map, $f:C\to D$
chain map, $f:C\to D$![]() by:
by:
$\Delta ^*K$![]() comes from the $K$
comes from the $K$![]() -space, $(K,1_K)$
-space, $(K,1_K)$![]() . After examining [Reference Ranicki16], p. 75 and p. 26, lines -6 to -4 one can see that this is in agreement with the definition indicated there, up to isomorphism and differences in sign conventions. In particular compare our formula for $d^{C\otimes _KD}$
. After examining [Reference Ranicki16], p. 75 and p. 26, lines -6 to -4 one can see that this is in agreement with the definition indicated there, up to isomorphism and differences in sign conventions. In particular compare our formula for $d^{C\otimes _KD}$![]() with that on p.26, line -5 of [Reference Ranicki16].
with that on p.26, line -5 of [Reference Ranicki16].
Corollary 6.2 $T$![]() is an exact homotopy functor.
is an exact homotopy functor.
Proof. By lemma 5.2, $TC= C^*\otimes _K \Delta ^* K$![]() is isomorphic to $Hom_{(R,K)}(\Delta ^*K, C)^*$
is isomorphic to $Hom_{(R,K)}(\Delta ^*K, C)^*$![]() (since $\varepsilon _C:C^{**}\cong C$
(since $\varepsilon _C:C^{**}\cong C$![]() for all $C$
for all $C$![]() ). But $C\mapsto C^*$
). But $C\mapsto C^*$![]() and $C\mapsto Hom(\Delta ^*K, C)$
and $C\mapsto Hom(\Delta ^*K, C)$![]() are both exact homotopy functors. The result follows.
are both exact homotopy functors. The result follows.
We now want to show that $T^2C$![]() and $C$
and $C$![]() are $(R,K)$
are $(R,K)$![]() -chain equivalent. See 6.5.
-chain equivalent. See 6.5.
Definition 6.3 (of $E_C:Hom_{(R,K)}(\Delta ^*K, C)\otimes _K \Delta ^*K\to C$![]() ).
).
Let $C$![]() be an $(R,K)$
be an $(R,K)$![]() complex.
complex.
Consider the evaluation chain map, $eval_{A,B}:Hom_R(A,B)\otimes _R A\to B$![]() , when $A=\Delta ^*K(K)$
, when $A=\Delta ^*K(K)$![]() and $B=C(K)$
and $B=C(K)$![]() . Its restriction to $(Hom_{(R,K)}(\Delta ^*K, C)\otimes _R\Delta ^*K)(K),$
. Its restriction to $(Hom_{(R,K)}(\Delta ^*K, C)\otimes _R\Delta ^*K)(K),$![]() denoted $E'_C,$
denoted $E'_C,$![]() is an $(R,K)$
is an $(R,K)$![]() chain map,
chain map,
(by definition of an $(R,K)$![]() map). Moreover, for each $\sigma \in K$
map). Moreover, for each $\sigma \in K$![]() , $E'_C$
, $E'_C$![]() annihilates $Hom_{(R,K)}(\Delta ^*K, C)(K-st(\sigma ))\otimes _R\Delta ^*K(\sigma )$
annihilates $Hom_{(R,K)}(\Delta ^*K, C)(K-st(\sigma ))\otimes _R\Delta ^*K(\sigma )$![]() . Therefore $E'_C$
. Therefore $E'_C$![]() descends uniquely to an $(R,K)$
descends uniquely to an $(R,K)$![]() chain map,
chain map,
satisfying: $E'_C= E_C\circ \pi _{H, \,\Delta ^*K}$![]() . Here $H= Hom_{(R,K)}(\Delta ^*K, C)$
. Here $H= Hom_{(R,K)}(\Delta ^*K, C)$![]() (see 5.1).
(see 5.1).
$E$![]() is obviously natural in $C$
is obviously natural in $C$![]() .
.
For each $(R,K)$![]() complex $C$
complex $C$![]() , define
, define
In view of lemma 5.2. we have an $(R, K)$![]() chain isomorphism:
chain isomorphism:
Definition 6.4 For each $(R,K)$![]() complex $C$
complex $C$![]() define $e_C:T^2C\to C$
define $e_C:T^2C\to C$![]() by
by

Note $e_C$![]() is an $(R,K)$
is an $(R,K)$![]() chain epimorphism and $e$
chain epimorphism and $e$![]() is a natural transformation.
is a natural transformation.
Theorem 6.5 $e_C: T^2C\longrightarrow C$![]() is an $(R,K)$
is an $(R,K)$![]() chain equivalence, for each $(R,K)$
chain equivalence, for each $(R,K)$![]() complex $C$
complex $C$![]() .
.
Proof. By [Reference Ranicki16] (proposition 4.7), we need only prove that $e_C(\sigma,\sigma ): T^2C(\sigma ) \to C(\sigma )$![]() is an $R$
is an $R$![]() -chain equivalence, for all $\sigma \in K$
-chain equivalence, for all $\sigma \in K$![]() . (No proof of this proposition appears in [Reference Ranicki16]. A brief proof appears in Appendix 2).
. (No proof of this proposition appears in [Reference Ranicki16]. A brief proof appears in Appendix 2).
Case I: Assume there is a simplex $S\in K$![]() for which: $C(\sigma )=0 \ \forall \;\sigma \neq S$
for which: $C(\sigma )=0 \ \forall \;\sigma \neq S$![]() .
.
We need only show $e_C(S,S)$![]() is a chain isomorphism, and $T^2C(\sigma )$
is a chain isomorphism, and $T^2C(\sigma )$![]() is contractible for $\sigma \neq S$
is contractible for $\sigma \neq S$![]() . We compute, for all $\sigma \in K$
. We compute, for all $\sigma \in K$![]() , in view of the restriction on $C$
, in view of the restriction on $C$![]() :
:

So for $\sigma \neq S, \; T^2C(\sigma )$![]() is contractible because $\Delta ^{**}\overline {S} (st(\sigma ))$
is contractible because $\Delta ^{**}\overline {S} (st(\sigma ))$![]() is contractible by 4.2.
is contractible by 4.2.
Next we prove that the map
is an isomorphism, or equivalently that $E_C(S,S)$![]() is an isomorphism.
is an isomorphism.
Assume $S$![]() has been oriented. Because $C(\sigma )=0$
has been oriented. Because $C(\sigma )=0$![]() for $\sigma \neq S$
for $\sigma \neq S$![]() ,
,
is simply: $eval_{RS^*, C(S)}:Hom_R(RS^*, C(S))\otimes _R RS^*\to C(S)$![]() .
.
This is a chain isomorphism as observed in § 2. So $e_C(\sigma,\sigma )$![]() is a chain isomorphism for $\sigma = S$
is a chain isomorphism for $\sigma = S$![]() and a chain equivalence for $\sigma \neq S$
and a chain equivalence for $\sigma \neq S$![]() . This completes the proof in Case I.
. This completes the proof in Case I.
Case II (the general case): For any $C\neq 0$![]() in $\mathcal {B} R_K$
in $\mathcal {B} R_K$![]() one can choose some $S\in K$
one can choose some $S\in K$![]() for which $C(S)\neq 0$
for which $C(S)\neq 0$![]() , and an exact sequence $0\to C'\mathop {\longrightarrow }\limits ^{i} C\mathop {\longrightarrow }\limits ^{j} C''\to 0$
, and an exact sequence $0\to C'\mathop {\longrightarrow }\limits ^{i} C\mathop {\longrightarrow }\limits ^{j} C''\to 0$![]() for which $i(S,S):C'(S)\to C(S)$
for which $i(S,S):C'(S)\to C(S)$![]() is an isomorphism, and $C'(\sigma )= 0$
is an isomorphism, and $C'(\sigma )= 0$![]() for $\sigma \neq S$
for $\sigma \neq S$![]() . For example, choose $S$
. For example, choose $S$![]() to be of maximum dimension among $\{\sigma \in K \mid \; C(\sigma )\neq 0\}$
to be of maximum dimension among $\{\sigma \in K \mid \; C(\sigma )\neq 0\}$![]() ).
).
The argument is by induction on the number $n$![]() , of $\sigma \in K$
, of $\sigma \in K$![]() , for which $C(\sigma )\neq 0$
, for which $C(\sigma )\neq 0$![]() .
.
If $n=1$![]() , Case I applies. If $n>1$
, Case I applies. If $n>1$![]() , by induction, $e_{C''}(\sigma,\sigma )$
, by induction, $e_{C''}(\sigma,\sigma )$![]() and $e_{C'}(\sigma,\sigma )$
and $e_{C'}(\sigma,\sigma )$![]() are $R$
are $R$![]() chain equivalences. Also the commuting diagram below has exact rows.
chain equivalences. Also the commuting diagram below has exact rows.

Therefore $e_C(\sigma,\sigma )$![]() is an $R$
is an $R$![]() -chain equivalence for all $\sigma$
-chain equivalence for all $\sigma$![]() . This completes the proof.
. This completes the proof.
Note: The first proof of the above theorem appeared in [Reference Adams-Florou and Macko1].
7. Construction of the ball complex $X_K$
The purpose of this section is to construct the complex $X_K$![]() advertised in the introduction and establish its properties.
advertised in the introduction and establish its properties.
Definition 7.1 (of $X'$![]() ): Let $X$
): Let $X$![]() be a finite simplicial complex in a euclidean space, with vertex set $V_X$
be a finite simplicial complex in a euclidean space, with vertex set $V_X$![]() . Its underlying polyhedron is: $|X|=\cup \{\sigma \;| \;\sigma \in X\}$
. Its underlying polyhedron is: $|X|=\cup \{\sigma \;| \;\sigma \in X\}$![]() . For each $p\geq 0$
. For each $p\geq 0$![]() , $X_p$
, $X_p$![]() denotes the set of $p$
denotes the set of $p$![]() -simplices of $X$
-simplices of $X$![]() .
.
If $|X|$![]() is pl-homeomorphic to $I^n$
is pl-homeomorphic to $I^n$![]() we say $|X|$
we say $|X|$![]() or $X$
or $X$![]() is a pl $n$
is a pl $n$![]() -ball and write $\partial X$
-ball and write $\partial X$![]() for the subcomplex for which $|\partial X|= \partial |X|$
for the subcomplex for which $|\partial X|= \partial |X|$![]() .
.
Each p-simplex $\sigma \in X$![]() is the convex hull, $[v_0, v_1,\dots, v_p]$
is the convex hull, $[v_0, v_1,\dots, v_p]$![]() , of its vertices in $V_X$
, of its vertices in $V_X$![]() . Its barycenter is $\hat {\sigma }:= \frac {1}{p+1} \sum _{i=0}^p v_i \in \sigma ^\circ$
. Its barycenter is $\hat {\sigma }:= \frac {1}{p+1} \sum _{i=0}^p v_i \in \sigma ^\circ$![]() .
.
Choose a point $b\sigma \in \sigma ^\circ$![]() , the interior of $\sigma$
, the interior of $\sigma$![]() , for each $\sigma \in X$
, for each $\sigma \in X$![]() .
.
The derived complex $X'$![]() is defined as the unique simplicial subdivision of $X$
is defined as the unique simplicial subdivision of $X$![]() for which $V_{X'} = \{b\sigma \mid \; \sigma \in X\}$
for which $V_{X'} = \{b\sigma \mid \; \sigma \in X\}$![]() . $X'$
. $X'$![]() has one $p$
has one $p$![]() -simplex, $[b\sigma _0, b\sigma _{1} \dots b\sigma _p]$
-simplex, $[b\sigma _0, b\sigma _{1} \dots b\sigma _p]$![]() , for each decreasing sequence of simplices $\sigma _0>\dots >\sigma _p$
, for each decreasing sequence of simplices $\sigma _0>\dots >\sigma _p$![]() of $X$
of $X$![]() .
.
If $\sigma _0>\dots >\sigma _p$![]() , the ordered $p+1$
, the ordered $p+1$![]() tuple $(b\sigma _0, b\sigma _{1}, \dots, b\sigma _p)$
tuple $(b\sigma _0, b\sigma _{1}, \dots, b\sigma _p)$![]() then specifies an oriented $p$
then specifies an oriented $p$![]() -simplex in $\Delta _p(X';R)$
-simplex in $\Delta _p(X';R)$![]() which we denote $\langle \sigma _0, \sigma _{1} \dots, \sigma _p\rangle$
which we denote $\langle \sigma _0, \sigma _{1} \dots, \sigma _p\rangle$![]() (suppressing the barycenters for concision).
(suppressing the barycenters for concision).
These form a canonical basis for $\Delta _p(X';R)$![]() (in contrast to $\Delta _p(X;R)$
(in contrast to $\Delta _p(X;R)$![]() ).
).
Because we want to use the McCrory cap product, we follow the orderings of [Reference McCrory13] regarding simplices of $X'$![]() .
.
Definition 7.2 (of $\Delta X'$![]() ): Let $(X,\pi )$
): Let $(X,\pi )$![]() be a $K$
be a $K$![]() -space. The derived complexes of $(X,\pi )$
-space. The derived complexes of $(X,\pi )$![]() are the simplicial subdivisions $X'$
are the simplicial subdivisions $X'$![]() of $X$
of $X$![]() , and $K'$
, and $K'$![]() of $K$
of $K$![]() whose vertex sets $\{b\sigma \mid \sigma \in K\}$
whose vertex sets $\{b\sigma \mid \sigma \in K\}$![]() and $\{bS\mid S\in X\}$
and $\{bS\mid S\in X\}$![]() are chosen as follows:
are chosen as follows:
By construction, $\pi (V_{X'})\subset V_{K'}$![]() . So $\pi$
. So $\pi$![]() is also a simplicial map from $X'$
is also a simplicial map from $X'$![]() to $K'$
to $K'$![]() , because $\pi$
, because $\pi$![]() is linear on each simplex of $X'$
is linear on each simplex of $X'$![]() .
.
$X'$![]() provides a second geometric example, $\Delta X'$
provides a second geometric example, $\Delta X'$![]() , of an $(R,K)$
, of an $(R,K)$![]() complex:
complex:
We define $\Delta X'$![]() by,
by,
(1) $\Delta X'(K)= \Delta _*(X';R)$
 .
.(2) For each $\sigma \in K, p\in \mathbb {Z},\;\; (\Delta X')_p(\sigma )$
 is the submodule of $\Delta _p(X';R)$
is the submodule of $\Delta _p(X';R)$ spanned by all $\langle Q^0,\dots Q^p\rangle$
spanned by all $\langle Q^0,\dots Q^p\rangle$ in $X'$
in $X'$ for which $\sigma = \pi (Q^p)$
for which $\sigma = \pi (Q^p)$ .
.
It is straightforward to see that $\Delta X'$![]() is an $(R,K)$
is an $(R,K)$![]() complex.
complex.
The dual cone of a simplex $\sigma \in K$![]() , denoted $D(\sigma, K)$
, denoted $D(\sigma, K)$![]() , is a subcomplex of $K'$
, is a subcomplex of $K'$![]() first defined in [Reference Poincare15], § 7. It is a pl ball if $K$
first defined in [Reference Poincare15], § 7. It is a pl ball if $K$![]() is a pl-manifold). It gives rise to several ‘dual’ subcomplexes in $K'$
is a pl-manifold). It gives rise to several ‘dual’ subcomplexes in $K'$![]() and $X'$
and $X'$![]() which we define now.
which we define now.
Definition 7.3 Let $(X,\pi )$![]() be a $K$
be a $K$![]() -space. Suppose $\sigma, \tau \in K$
-space. Suppose $\sigma, \tau \in K$![]() , $T\in X$
, $T\in X$![]() .
.
(1) $D(\sigma, K):=\{\langle \sigma _0, \sigma _1,\dots, \sigma _p\rangle \in K' \mid \sigma _p\geq \sigma \}$

(2) $D(\sigma, \tau ):=\{\langle \sigma _0, \sigma _1,\dots, \sigma _p\rangle \in K' \mid \sigma _p\geq \sigma, \; \tau \geq \sigma _0 \}$
 , the dual cell of $\sigma$
, the dual cell of $\sigma$ in $\tau$
in $\tau$ .
.(3) $D_\sigma T:=\{\langle S_0, S_1,\dots, S_p\rangle \in X' \mid \sigma \leq \pi (S_p),\; S_0\leq T\}$

(4) $T_\sigma := |D_\sigma T|$
 . (Therefore, $T_\sigma =(\pi \mid T)^{-1}|D(\sigma,\pi (T))|$
. (Therefore, $T_\sigma =(\pi \mid T)^{-1}|D(\sigma,\pi (T))|$ ).
).
Of course, $D(\sigma, \tau )=\emptyset$![]() unless $\sigma \leq \tau$
unless $\sigma \leq \tau$![]() , and $D_\sigma T=\emptyset$
, and $D_\sigma T=\emptyset$![]() unless $\sigma \leq \pi (T)$
unless $\sigma \leq \pi (T)$![]() .
.
$D_\sigma T$![]() is a subcomplex of $X'$
is a subcomplex of $X'$![]() . $D(\sigma, K)$
. $D(\sigma, K)$![]() and $D(\sigma, \tau )$
and $D(\sigma, \tau )$![]() are subcomplexes of $K'$
are subcomplexes of $K'$![]() .
.
Lemma 7.4 Let $(X,\pi )$![]() be a $K$
be a $K$![]() -space. Suppose $\sigma \in K$
-space. Suppose $\sigma \in K$![]() , $T\in X$
, $T\in X$![]() , and $\sigma \leq \pi (T)$
, and $\sigma \leq \pi (T)$![]() .
.
(1) $T_\sigma =|D_\sigma T|$
 is a pl ball. $dim(T_\sigma ) = dim(T)-dim(\sigma )$
is a pl ball. $dim(T_\sigma ) = dim(T)-dim(\sigma )$ .
.(2) $\partial D_\sigma T=\partial ^i D_\sigma T \cup \partial ^o D_\sigma T$
 , (the inner and outer boundaries) where:
\[ \partial^i D_\sigma T={\cup} \{D_\rho T\;\mid \sigma< \rho \};\quad \partial^oD_\sigma T={\cup} \{D_\sigma S\;\mid S< T\} \]
, (the inner and outer boundaries) where:
\[ \partial^i D_\sigma T={\cup} \{D_\rho T\;\mid \sigma< \rho \};\quad \partial^oD_\sigma T={\cup} \{D_\sigma S\;\mid S< T\} \]
(3) Suppose $\sigma <\pi (T)$
 . Then $|\partial ^iD_\sigma T|$
. Then $|\partial ^iD_\sigma T|$ and $|\partial ^o D_\sigma T|$
and $|\partial ^o D_\sigma T|$ are pl balls of dimension $dim(D_\sigma T)-1$
are pl balls of dimension $dim(D_\sigma T)-1$ , and
\[ \partial (\partial^iD_\sigma T)=\partial(\partial^oD_\sigma T)=\partial^iD_\sigma T\cap \partial^oD_\sigma T\;. \]
, and
\[ \partial (\partial^iD_\sigma T)=\partial(\partial^oD_\sigma T)=\partial^iD_\sigma T\cap \partial^oD_\sigma T\;. \]
Proof. of (1): For each vertex $v$![]() of $\tau$
of $\tau$![]() note that,
note that,
where $a_v: |K|\to [0,1]$![]() denotes the barycentric coordinate function defined by the vertex $v$
denotes the barycentric coordinate function defined by the vertex $v$![]() . This is a convex subset of $\tau$
. This is a convex subset of $\tau$![]() . So
. So
is also convex. Therefore $T_\sigma =(\pi _{|T})^{-1} (|D(\sigma, \tau )|)$![]() is also convex since $\pi _{|T}: T\to \tau$
is also convex since $\pi _{|T}: T\to \tau$![]() is simplicial. So $T_\sigma$
is simplicial. So $T_\sigma$![]() is a compact convex polyhedron and therefore a pl ball.
is a compact convex polyhedron and therefore a pl ball.
Since $|D(\sigma, \tau )|\cap \tau ^\circ \neq \emptyset$![]() , this operator $(\pi _{|T})^{-1}$
, this operator $(\pi _{|T})^{-1}$![]() preserves codimension:
preserves codimension:
Since $dim(D(\sigma, \tau )) = dim(\tau )- dim(\sigma )$![]() , we get: $dim(D_\sigma T)= dim(T)-dim(\sigma )$
, we get: $dim(D_\sigma T)= dim(T)-dim(\sigma )$![]() .
.
Proof. of (2): See [Reference Cohen3], proposition 5.6(2), applied to $\pi _{|\overline {T}} :\overline {T}\to \pi (\overline {T})$![]() .
.
Proof. of (3): The equation in (3), and the fact that $|\partial ^iD_\sigma T|$![]() and $|\partial ^o D_\sigma T|$
and $|\partial ^o D_\sigma T|$![]() are both pl manifolds, are proved in [Reference Cohen3] [proposition 5.6 (3),(4)]. To show $|\partial ^iD_\sigma T|$
are both pl manifolds, are proved in [Reference Cohen3] [proposition 5.6 (3),(4)]. To show $|\partial ^iD_\sigma T|$![]() is a pl ball, it suffices to note that it collapses to the vertex $bT$
is a pl ball, it suffices to note that it collapses to the vertex $bT$![]() , and so $|\partial ^iD_\sigma T|$
, and so $|\partial ^iD_\sigma T|$![]() is a regular neighbourhood of $bT$
is a regular neighbourhood of $bT$![]() in $|\partial D_\sigma T|$
in $|\partial D_\sigma T|$![]() (by 3.30 of [Reference Rourke and Sanderson14]). Then by 3.13 of [Reference Rourke and Sanderson14], $\partial ^oD_\sigma T$
(by 3.30 of [Reference Rourke and Sanderson14]). Then by 3.13 of [Reference Rourke and Sanderson14], $\partial ^oD_\sigma T$![]() is also a pl ball.
is also a pl ball.
Definition 7.5 ([Reference Rourke and Sanderson14] p.27) A ball complex is a finite collection $Z=\{B_i\}_{i\in I}$![]() of pl balls in a euclidean space, such that each point of $|Z|:=\cup \{ B\;\mid \; B\in Z\}$
of pl balls in a euclidean space, such that each point of $|Z|:=\cup \{ B\;\mid \; B\in Z\}$![]() lies in the interior of precisely one ball of $Z$
lies in the interior of precisely one ball of $Z$![]() , and the boundary of each $B\in Z$
, and the boundary of each $B\in Z$![]() is a union of balls of lesser dimension of $Z$
is a union of balls of lesser dimension of $Z$![]() . Therefore $(|Z|, Z)$
. Therefore $(|Z|, Z)$![]() is a regular CW-complex.
is a regular CW-complex.
Let $Z$![]() and $Y$
and $Y$![]() be ball complexes A pl map $f:|Z|\to |Y|$
be ball complexes A pl map $f:|Z|\to |Y|$![]() is a map of ball complexes if for each ball $B$
is a map of ball complexes if for each ball $B$![]() of $Z$
of $Z$![]() , $f(B)$
, $f(B)$![]() is a ball of $Y$
is a ball of $Y$![]() .
.
Definition 7.6 Let $(X,\pi )$![]() be a $K$
be a $K$![]() -space. We define
-space. We define
Theorem 7.7 Let $(X,\pi )$![]() be a $K$
be a $K$![]() -space. Then $X_K$
-space. Then $X_K$![]() is a ball complex. Moreover $X'$
is a ball complex. Moreover $X'$![]() is a simplicial subdivision of $X_K$
is a simplicial subdivision of $X_K$![]() . Also, $X_K$
. Also, $X_K$![]() is a subdivision of $X$
is a subdivision of $X$![]() .
.
Let $f:(X,\pi _X)\to (Y,\pi _Y)$![]() is a map of $K$
is a map of $K$![]() -spaces. The induced map $f':X'\to Y'$
-spaces. The induced map $f':X'\to Y'$![]() of derived complexes is then a map of ball complexes, $f_K: X_K\to Y_K$
of derived complexes is then a map of ball complexes, $f_K: X_K\to Y_K$![]() .
.
Proof. (The induced map $f'$![]() means the simplicial map $f':X'\to Y'$
means the simplicial map $f':X'\to Y'$![]() for which $f'(bS)= b(f(S))$
for which $f'(bS)= b(f(S))$![]() for each $S\in X.$
for each $S\in X.$![]() ) By lemma 7.4 the boundary of each $T_\sigma$
) By lemma 7.4 the boundary of each $T_\sigma$![]() is a union of balls of $X_K$
is a union of balls of $X_K$![]() with smaller dimension and
with smaller dimension and
This can be rewritten as:
By equation (7.1), for each $A\in X'$![]() there is a unique $T_\sigma \in X_K$
there is a unique $T_\sigma \in X_K$![]() for which $A^\circ \subset T_\sigma ^\circ$
for which $A^\circ \subset T_\sigma ^\circ$![]() . Therefore : $|X'|= \coprod \{T_\sigma ^\circ \; \mid \; \; T_\sigma \in X_K \}=|X_K|$
. Therefore : $|X'|= \coprod \{T_\sigma ^\circ \; \mid \; \; T_\sigma \in X_K \}=|X_K|$![]() .
.
This proves that $X_K$![]() is a ball complex and that $X'$
is a ball complex and that $X'$![]() is a subdivision of $X_K$
is a subdivision of $X_K$![]() . Because $T_\sigma \subset T$
. Because $T_\sigma \subset T$![]() , we see $X_K$
, we see $X_K$![]() is a subdivision of $X$
is a subdivision of $X$![]() .
.
Now let $f:(X,\pi _X)\to (Y, \pi _Y)$![]() be a map of $K$
be a map of $K$![]() -spaces. For each simplex $S\in X$
-spaces. For each simplex $S\in X$![]() we see $f(S)\in Y$
we see $f(S)\in Y$![]() because $f$
because $f$![]() is simplicial. For each face $\sigma$
is simplicial. For each face $\sigma$![]() of $\pi _X(S)$
of $\pi _X(S)$![]() in $K$
in $K$![]() , we see from the definitions that $f'(D_\sigma S)= D_\sigma f(S)$
, we see from the definitions that $f'(D_\sigma S)= D_\sigma f(S)$![]() . So $f'$
. So $f'$![]() is a map of ball complexes, $f_K: X_K \to Y_K$
is a map of ball complexes, $f_K: X_K \to Y_K$![]() .
.
8. The isomorphism $\Phi _X:T\Delta ^*X\cong C(X_K)$
Our main theorem is:
Theorem 8.1 For each $K$![]() -space $(X, \pi )$
-space $(X, \pi )$![]() the cellular chain complex of $X_K$
the cellular chain complex of $X_K$![]() with $R$
with $R$![]() coefficients, denoted $C(X_K)$
coefficients, denoted $C(X_K)$![]() , comes with a natural $(R,K)$
, comes with a natural $(R,K)$![]() complex structure. There is defined (below) an isomorphism of $(R,K)$
complex structure. There is defined (below) an isomorphism of $(R,K)$![]() chain complexes:
chain complexes:
For each map $f:(X, \pi _X)\to (Y,\pi _Y)$![]() of $K$
of $K$![]() -spaces, the square below commutes.
-spaces, the square below commutes.

Proof. Choose a basis $bK$![]() of oriented cells for $\Delta _*(K;R)$
of oriented cells for $\Delta _*(K;R)$![]() . Choose next, a basis $b_*X$
. Choose next, a basis $b_*X$![]() of oriented cells for $\Delta _*(X;R)$
of oriented cells for $\Delta _*(X;R)$![]() . But choose the orientations in $b_*X$
. But choose the orientations in $b_*X$![]() so that if $T\in b_*X$
so that if $T\in b_*X$![]() and $\sigma \in bK$
and $\sigma \in bK$![]() are both $q$
are both $q$![]() -cells, and if $\pi _*(T)=\pm \sigma \in \Delta _q(K;R)$
-cells, and if $\pi _*(T)=\pm \sigma \in \Delta _q(K;R)$![]() , then:
, then:
We call such a pair, $(bK, b_*X)$![]() an orientation for $(X,\pi )$
an orientation for $(X,\pi )$![]() .
.
Our first task is to construct the cellular chain complex $C_*(X_K;R)$![]() as the underlying $R$
as the underlying $R$![]() -complex of an $(R,K)$
-complex of an $(R,K)$![]() complex $C(X_K)$
complex $C(X_K)$![]() . Define
. Define
For each oriented simplex $\rho \in bK$![]() and oriented simplex $T\in b_*X$
and oriented simplex $T\in b_*X$![]() , define
, define
(The geometric intuition for this definition is the fact that, the map $C_X$![]() , of corollary 9.3, takes $T\otimes _K \rho ^*$
, of corollary 9.3, takes $T\otimes _K \rho ^*$![]() to a fundamental cycle, in $\Delta X'$
to a fundamental cycle, in $\Delta X'$![]() , for the cell $D_\rho T$
, for the cell $D_\rho T$![]() , whose underlying space is $T_\rho$
, whose underlying space is $T_\rho$![]() ).
).
Define $bX_K= \{ [T_\rho ]\mid T\in b_*X,\; \rho \in bK, \;T_\rho \leq \pi (T)\}$![]() . Then $bX_K$
. Then $bX_K$![]() is an $R$
is an $R$![]() -basis for $C_*(X_K;R)$
-basis for $C_*(X_K;R)$![]() in bicorrespondence with the cells of $X_K$
in bicorrespondence with the cells of $X_K$![]() . Write $\partial _q$
. Write $\partial _q$![]() for the boundary map in $C_*(X_K;R)$
for the boundary map in $C_*(X_K;R)$![]() , namely: $\partial _q=(d^{\Delta X\otimes _K\Delta ^*K})_q$
, namely: $\partial _q=(d^{\Delta X\otimes _K\Delta ^*K})_q$![]() .
.
But to justify these definitions, we must check that $C_*(X_K;R)$![]() does compute the cellular homology of $X_K$
does compute the cellular homology of $X_K$![]() . It suffices to check, for any $[T_\rho ]\in bX_K,$
. It suffices to check, for any $[T_\rho ]\in bX_K,$![]() that $\partial _q([T_\rho ])$
that $\partial _q([T_\rho ])$![]() is a sum with $\pm 1$
is a sum with $\pm 1$![]() coefficients of those $[S_\sigma ]\in bX_K$
coefficients of those $[S_\sigma ]\in bX_K$![]() which are $(q-1)$
which are $(q-1)$![]() -faces of $T_\rho$
-faces of $T_\rho$![]() . (See [Reference Cooke and Finney7], for example.)
. (See [Reference Cooke and Finney7], for example.)
All proper faces of $T_\rho$![]() have the form $T_\sigma,$
have the form $T_\sigma,$![]() for $\rho <\sigma$
for $\rho <\sigma$![]() , or $S_\rho$
, or $S_\rho$![]() , for $S< T$
, for $S< T$![]() .
.
Suppose $[T_\rho ]\in bX_K$![]() . So $T\in b_*X$
. So $T\in b_*X$![]() , $\rho \in bK$
, $\rho \in bK$![]() . Set $\tau = \pi (T)\in K$
. Set $\tau = \pi (T)\in K$![]() . By (5.1):
. By (5.1):

which is as required.
This completes the construction of the cellular chain complex of $X_K$![]() , as an $(R,K)$
, as an $(R,K)$![]() complex, $C(X_K)$
complex, $C(X_K)$![]() .
.
The $(R,K)$![]() isomorphism, $\Phi _X: T\Delta ^* X\cong C(X_K)$
isomorphism, $\Phi _X: T\Delta ^* X\cong C(X_K)$![]() is simply:
is simply:
Naturality of $\Phi$![]() is obvious from the naturality of $\varepsilon$
is obvious from the naturality of $\varepsilon$![]() .
.
9. The McCrory cap product, $\Delta ^*X$ and $\Delta X'$
and $\Delta X'$
We now use the work of McCrory [Reference McCrory13] to construct, for any $K$![]() -space, $(X, \pi )$
-space, $(X, \pi )$![]() , an $(R,K)$
, an $(R,K)$![]() chain monomorphism $C(X_K)\mathop {\longrightarrow }\limits ^{C_X} \Delta X'.$
chain monomorphism $C(X_K)\mathop {\longrightarrow }\limits ^{C_X} \Delta X'.$![]() serving two purposes.
serving two purposes.
First, it defines an $(R,K)$![]() chain homotopy equivalence, $T\Delta ^*X\simeq \Delta X'$
chain homotopy equivalence, $T\Delta ^*X\simeq \Delta X'$![]() .
.
Second, $C_X$![]() identifies $C(X_K)$
identifies $C(X_K)$![]() with that $(R, K)$
with that $(R, K)$![]() subcomplex of $\Delta X'$
subcomplex of $\Delta X'$![]() which admits a basis consisting of one fundamental $q$
which admits a basis consisting of one fundamental $q$![]() -cycle, in $\Delta _q (D_\sigma T,\partial D_\sigma T)\subset \Delta _q(X')$
-cycle, in $\Delta _q (D_\sigma T,\partial D_\sigma T)\subset \Delta _q(X')$![]() , for each $q$
, for each $q$![]() -cell $T_\sigma$
-cell $T_\sigma$![]() of $X_K$
of $X_K$![]() . (This will complete our geometric interpretation of $T$
. (This will complete our geometric interpretation of $T$![]() ).
).
Let $K$![]() be a finite simplicial complex. McCrory (see [Reference McCrory13], and also [Reference Flexner11]) defines a map, $c': \Delta _*(K;R)\otimes _R\Delta ^*(K;R)\to \Delta _*(K';R)$
be a finite simplicial complex. McCrory (see [Reference McCrory13], and also [Reference Flexner11]) defines a map, $c': \Delta _*(K;R)\otimes _R\Delta ^*(K;R)\to \Delta _*(K';R)$![]() which he shows is chain homotopic to the composite,
which he shows is chain homotopic to the composite,
where $\cap$![]() denotes the Whitney-Cech cap product. We will write $c_K$
denotes the Whitney-Cech cap product. We will write $c_K$![]() for $c'$
for $c'$![]() . We repeat his definition here with appropriate sign changes because McCrory's sign conventions differ slightly from ours.
. We repeat his definition here with appropriate sign changes because McCrory's sign conventions differ slightly from ours.
For any $q$![]() -simplex, $Q=\langle Q^0, Q^1, \ldots Q^q\rangle \text { of } K'$
-simplex, $Q=\langle Q^0, Q^1, \ldots Q^q\rangle \text { of } K'$![]() in which each $Q_i$
in which each $Q_i$![]() is oriented, McCrory then defines
is oriented, McCrory then defines
This is independent of the orientations on $Q_1, Q_2,\ldots Q_{q-1}$![]() . If $q=0$
. If $q=0$![]() , set $\varepsilon (Q)=0$
, set $\varepsilon (Q)=0$![]() .
.
For any $n$![]() -simplex $\tau$
-simplex $\tau$![]() and $(n-q)$
and $(n-q)$![]() -simplex $\sigma$
-simplex $\sigma$![]() of $K$
of $K$![]() , each simplex $Q=\langle Q^0, Q^1, \ldots Q^q\rangle$
, each simplex $Q=\langle Q^0, Q^1, \ldots Q^q\rangle$![]() of $D(\sigma, \tau )_q$
of $D(\sigma, \tau )_q$![]() satisfies: $Q^0= \tau ; \;Q^q=\sigma$
satisfies: $Q^0= \tau ; \;Q^q=\sigma$![]() . Therefore, $\varepsilon (Q)$
. Therefore, $\varepsilon (Q)$![]() makes sense if $\tau$
makes sense if $\tau$![]() and $\sigma$
and $\sigma$![]() are oriented simplices chosen from some basis $bK$
are oriented simplices chosen from some basis $bK$![]() of oriented simplices for $\Delta _*(K;R)$
of oriented simplices for $\Delta _*(K;R)$![]() (but not if $\sigma =-\tau ).$
(but not if $\sigma =-\tau ).$![]()
The McCrory Cap Product, $\Delta _*(K;R)\otimes _R\Delta ^*(K;R)\mathop {\longrightarrow }\limits ^{c_K} \Delta _*(K';R)$![]() is the map defined by:
is the map defined by:

for any oriented simplices $\sigma, \tau$![]() in some basis $bK$
in some basis $bK$![]() . Here $q= dim(\tau )-dim(\sigma )$
. Here $q= dim(\tau )-dim(\sigma )$![]() . Note this is zero unless $\sigma \leq \tau$
. Note this is zero unless $\sigma \leq \tau$![]() . Note that $c_K$
. Note that $c_K$![]() does not change if we change the basis.
does not change if we change the basis.
$c_K$![]() is a chain map. We reprove this in Appendix I, § A, because of the sign changes and because McCrory's proof, [Reference McCrory13] p.155 lines 7-8, is only a sketch.
is a chain map. We reprove this in Appendix I, § A, because of the sign changes and because McCrory's proof, [Reference McCrory13] p.155 lines 7-8, is only a sketch.
Now suppose $(X,\pi )$![]() is a $K$
is a $K$![]() -space.
-space.
Note that if $T$![]() and $\sigma$
and $\sigma$![]() are oriented simplices of $X$
are oriented simplices of $X$![]() and $K$
and $K$![]() and $q=dim(T)-dim(\sigma )\neq 0$
and $q=dim(T)-dim(\sigma )\neq 0$![]() :
:
(because $D_\sigma T=\cup \{D(S,T)\; |\; S\in X, dim(S)=dim(\sigma ), \pi (S)= \sigma \}$![]() ). This formula still makes sense and is true if $q=0$
). This formula still makes sense and is true if $q=0$![]() and $\pi _*(T)\neq -\sigma$
and $\pi _*(T)\neq -\sigma$![]() ).
).
In this way, $c_X\circ (1\otimes \pi ^*)$![]() defines an $(R,K)$
defines an $(R,K)$![]() chain map,
chain map,
Proposition 9.1 There is a unique $(R,K)$![]() chain map
chain map
satisfying:
$C_X$![]() is an $(R,K)$
is an $(R,K)$![]() monomorphism. For all $q$
monomorphism. For all $q$![]() -cells $T_\sigma$
-cells $T_\sigma$![]() of $X_K$
of $X_K$![]() , with $q\neq 0$
, with $q\neq 0$![]() ,
,
For a $0$![]() -cell $T_\sigma$
-cell $T_\sigma$![]() , of $X_K$
, of $X_K$![]() , with $T\in \Delta _n(X;R), \sigma \in \Delta _n(K;R)$
, with $T\in \Delta _n(X;R), \sigma \in \Delta _n(K;R)$![]() oriented so that $\pi _*(T)=\sigma$
oriented so that $\pi _*(T)=\sigma$![]() , then
, then
Proof. Note that $c_X(T\otimes _R \pi ^*\sigma ^*)=0$![]() unless $\pi (T)\geq \sigma$
unless $\pi (T)\geq \sigma$![]() . Also $c_X(T\otimes _R \pi ^*\sigma ^*)\in \Delta X'(\sigma )$
. Also $c_X(T\otimes _R \pi ^*\sigma ^*)\in \Delta X'(\sigma )$![]() for all $\sigma \in K$
for all $\sigma \in K$![]() and $T\in X$
and $T\in X$![]() because each $q$
because each $q$![]() -cell $Q\in D_\sigma T$
-cell $Q\in D_\sigma T$![]() is in $\Delta _qX'(\sigma )$
is in $\Delta _qX'(\sigma )$![]() if $q= dim(T_\sigma )$
if $q= dim(T_\sigma )$![]() .
.
So $c_X\,\circ (1\otimes \pi ^*):\Delta X\otimes _R \Delta ^*K\to \Delta X'$![]() is an $(R,K)$
is an $(R,K)$![]() chain map annihilating each $\Delta X(K-st(\sigma ))\otimes _R \Delta ^*K(\sigma )$
chain map annihilating each $\Delta X(K-st(\sigma ))\otimes _R \Delta ^*K(\sigma )$![]() . Hence there is a unique $(R,K)$
. Hence there is a unique $(R,K)$![]() chain map monomorphism, $\Delta X\otimes _K \Delta ^*K\mathop {\longrightarrow }\limits ^{C_X} \Delta X'$
chain map monomorphism, $\Delta X\otimes _K \Delta ^*K\mathop {\longrightarrow }\limits ^{C_X} \Delta X'$![]() such that $c_X\circ (1\otimes \pi ^*) = C_X\circ \pi _{\Delta X, \Delta ^*K}$
such that $c_X\circ (1\otimes \pi ^*) = C_X\circ \pi _{\Delta X, \Delta ^*K}$![]() . The calculation follows if $q\neq 0$
. The calculation follows if $q\neq 0$![]() . If $q=0$
. If $q=0$![]() , then $(\pi _{\mid T})^* \sigma ^*=T^*$
, then $(\pi _{\mid T})^* \sigma ^*=T^*$![]() , so
, so
Clearly $C_X$![]() is natural in $(X,\pi )$
is natural in $(X,\pi )$![]() .
.
Remark 9.2 If we choose an orientation $(bK, b_*X)$![]() for $X_K$
for $X_K$![]() , then for each $0$
, then for each $0$![]() -cell $T_\sigma = T_{\pi (T)}$
-cell $T_\sigma = T_{\pi (T)}$![]() of $X_K$
of $X_K$![]() , with $[T_\sigma ]\in bX_K$
, with $[T_\sigma ]\in bX_K$![]() , we have $C_X([T_\sigma ])= \langle T\rangle \in \Delta _0(X';R)$
, we have $C_X([T_\sigma ])= \langle T\rangle \in \Delta _0(X';R)$![]() .
.
Corollary 9.3 For each $q$![]() -cell $T_\sigma$
-cell $T_\sigma$![]() of $X_K$
of $X_K$![]() , $C_X(T\otimes \sigma ^*)$
, $C_X(T\otimes \sigma ^*)$![]() is a fundamental cycle, in $\Delta _q(D_\sigma T, \partial D_\sigma T; R)$
is a fundamental cycle, in $\Delta _q(D_\sigma T, \partial D_\sigma T; R)$![]() for the $q$
for the $q$![]() -manifold $D_\sigma T$
-manifold $D_\sigma T$![]() .
.
Proof. $C_X(T\otimes _K \sigma ^*)$![]() is a fundamental cycle in $\Delta _q(D_\sigma T, \partial D_\sigma T; R)$
is a fundamental cycle in $\Delta _q(D_\sigma T, \partial D_\sigma T; R)$![]() since $C_X$
since $C_X$![]() is a chain map and since each $Q\in (D_\sigma T)_q$
is a chain map and since each $Q\in (D_\sigma T)_q$![]() appears with coefficient $\pm 1$
appears with coefficient $\pm 1$![]() in $C_X(T\otimes _K \sigma ^*)$
in $C_X(T\otimes _K \sigma ^*)$![]() .
.
Theorem 9.4 For each $K$![]() -space $(X,\pi )$
-space $(X,\pi )$![]() , the map $C(X_K)\mathop {\longrightarrow }\limits ^{C_X} \Delta X'$
, the map $C(X_K)\mathop {\longrightarrow }\limits ^{C_X} \Delta X'$![]() is an $(R,K)$
is an $(R,K)$![]() chain homotopy equivalence.
chain homotopy equivalence.
Proof. By 9.3, for all $T_\sigma$![]() , $C_X$
, $C_X$![]() restricts to a homotopy equivalence,
restricts to a homotopy equivalence,
and it takes chains on any subcomplex of $X_K$![]() to chains on its subdivision. By an induction-excision argument on the number of cells in the subcomplex one sees $C_X$
to chains on its subdivision. By an induction-excision argument on the number of cells in the subcomplex one sees $C_X$![]() yields a homology equivalence and then a chain homotopy equivalence on each such subcomplex. So $C_X(\sigma,\sigma )$
yields a homology equivalence and then a chain homotopy equivalence on each such subcomplex. So $C_X(\sigma,\sigma )$![]() is an $R$
is an $R$![]() -chain equivalence for each $\sigma$
-chain equivalence for each $\sigma$![]() . Therefore $C_X$
. Therefore $C_X$![]() is an $(R,K)$
is an $(R,K)$![]() chain equivalence.
chain equivalence.
Together, 9.4 and 8.1 clearly prove:
Corollary 9.5 $T\Delta ^*X\mathop {\longrightarrow }\limits ^{ C_X \Phi _X} \Delta X'$![]() is an $(R,K)$
is an $(R,K)$![]() chain homotopy equivalence. Consequently $e_{\Delta ^*X}\circ T(C_X\Phi _X)$
chain homotopy equivalence. Consequently $e_{\Delta ^*X}\circ T(C_X\Phi _X)$![]() is an explicit $(R,K)$
is an explicit $(R,K)$![]() chain homotopy equivalence,
chain homotopy equivalence,
Appendix A.
We must prove:
Proposition A.1 $\Delta _*(K;R)\otimes _R\Delta ^*(K;R)\mathop {\longrightarrow }\limits ^{c_K} \Delta _*(K';R)$![]() is a chain map. That is to say, for any oriented simplices $\sigma, \tau$
is a chain map. That is to say, for any oriented simplices $\sigma, \tau$![]() in some basis $bK$
in some basis $bK$![]() for $\Delta K$
for $\Delta K$![]() , with $p= dim(\tau )-dim(\sigma )$
, with $p= dim(\tau )-dim(\sigma )$![]() ,
,
where, by the definitions,
and for any $p$![]() -simplex $Q=\langle Q^0, Q^1,\dots Q^p\rangle$
-simplex $Q=\langle Q^0, Q^1,\dots Q^p\rangle$![]() of $K'$
of $K'$![]() ,
,

Proof. We first prove: $d^oc(\tau \otimes \sigma ^*) = c(d^K\tau \otimes \sigma ^*)$![]() , where $c=c_K$
, where $c=c_K$![]() .
.

Next we show: $(-1)^pd^p c(\tau \otimes \sigma ^*)=(-1)^{dim(\tau )}c( \tau \otimes d^{\Delta ^*(K)}\sigma ^*)$![]() :
:

Finally we prove $d^ic(\tau \otimes \sigma ^*)=0$![]() for $0< i< p$
for $0< i< p$![]() .
.
For such $i$![]() and for $Q\in D(\sigma, \tau )$
and for $Q\in D(\sigma, \tau )$![]() note $d^iQ=\langle \tau,\dots \sigma \rangle \in D(\sigma,\tau )- \partial D(\sigma,\tau )$
note $d^iQ=\langle \tau,\dots \sigma \rangle \in D(\sigma,\tau )- \partial D(\sigma,\tau )$![]() . So suppose $P$
. So suppose $P$![]() is a $p-1$
is a $p-1$![]() simplex of the form $d^iQ$
simplex of the form $d^iQ$![]() in the $p$
in the $p$![]() manifold $D(\sigma,\tau )$
manifold $D(\sigma,\tau )$![]() . Then there is exactly one other $S\in D(\sigma,\tau )_p$
. Then there is exactly one other $S\in D(\sigma,\tau )_p$![]() having $Q$
having $Q$![]() as a face. We can identify $S$
as a face. We can identify $S$![]() by listing the vertices of $\tau$
by listing the vertices of $\tau$![]() as $v_0, \ldots v_n$
as $v_0, \ldots v_n$![]() so that $Q^j =[ v_j, \ldots v_n]$
so that $Q^j =[ v_j, \ldots v_n]$![]() for all $j$
for all $j$![]() . Define $S^i=[v_0\ldots v_{i-1}, v_{i+1}\ldots v_n]$
. Define $S^i=[v_0\ldots v_{i-1}, v_{i+1}\ldots v_n]$![]() and define $S^j=Q^j$
and define $S^j=Q^j$![]() for $j\neq i$
for $j\neq i$![]() . Then $S:= \langle S^0, S^1, \ldots S^p\rangle$
. Then $S:= \langle S^0, S^1, \ldots S^p\rangle$![]() in $D(\sigma,\tau )_p$
in $D(\sigma,\tau )_p$![]() satisfies $d^iS=P;\; \varepsilon (S)=-\varepsilon (Q)$
satisfies $d^iS=P;\; \varepsilon (S)=-\varepsilon (Q)$![]() so $P$
so $P$![]() must appear with zero coefficient in $d^i c(\tau \otimes \sigma ^*)$
must appear with zero coefficient in $d^i c(\tau \otimes \sigma ^*)$![]() for all $p-1$
for all $p-1$![]() simplices $P$
simplices $P$![]() . So $d^ic(\tau \otimes \sigma ^*)=0$
. So $d^ic(\tau \otimes \sigma ^*)=0$![]() .
.
Appendix B.
We must prove the following result of Ranicki and Weiss:
Proposition B.1 Let $i:A\to B$![]() be an $(R,K)$
be an $(R,K)$![]() chain map in $\mathcal {B} R_K$
chain map in $\mathcal {B} R_K$![]() for some finite poset $K$
for some finite poset $K$![]() . Then $i$
. Then $i$![]() is a chain equivalence in $\mathcal {B} R_K$
is a chain equivalence in $\mathcal {B} R_K$![]() if and only if $i(\sigma,\sigma )$
if and only if $i(\sigma,\sigma )$![]() is a chain equivalence in $\mathcal {B} R$
is a chain equivalence in $\mathcal {B} R$![]() for all $\sigma \in K$
for all $\sigma \in K$![]() .
.
Lemma B.2 [(The Contraction Principle)]: For any additive category $A$![]() , with the split exact structure, and any exact sequence of chain complexes in $\mathcal {B} A$
, with the split exact structure, and any exact sequence of chain complexes in $\mathcal {B} A$![]() ,
,
$C''$![]() is contractible if and only if $f$
is contractible if and only if $f$![]() has a left inverse $r:C\to C'$
has a left inverse $r:C\to C'$![]() which is a chain homotopy inverse of f.
which is a chain homotopy inverse of f.
Proof. For any $h''\in Hom_A(C'',C'')_1$![]() there is an $h\in Hom_A(C,C)_1$
there is an $h\in Hom_A(C,C)_1$![]() such that $gh= h''g$
such that $gh= h''g$![]() and $hf=0$
and $hf=0$![]() . Then $h''$
. Then $h''$![]() is a contraction of $C''$
is a contraction of $C''$![]() iff $h$
iff $h$![]() is a chain homotopy from $1_C$
is a chain homotopy from $1_C$![]() to a chain map $\rho :C\to C$
to a chain map $\rho :C\to C$![]() for which $\rho =fr$
for which $\rho =fr$![]() for some chain map $r:C\to C'$
for some chain map $r:C\to C'$![]() . $r$
. $r$![]() satisfies $rf=1_{C'}$
satisfies $rf=1_{C'}$![]() . So $r$
. So $r$![]() is a left inverse of $f$
is a left inverse of $f$![]() and $fr$
and $fr$![]() is chain homotopic to $1_C$
is chain homotopic to $1_C$![]() .
.
Proof. of B.1: First assume $i$![]() is a chain equivalence. Note, for each $\sigma \in K$
is a chain equivalence. Note, for each $\sigma \in K$![]() , the functor $B\to B(\sigma )$
, the functor $B\to B(\sigma )$![]() is an additive functor $AR_K\to A_R$
is an additive functor $AR_K\to A_R$![]() . So it induces a homotopy functor $\mathcal {B} R_K\to \mathcal {B} R$
. So it induces a homotopy functor $\mathcal {B} R_K\to \mathcal {B} R$![]() . Therefore $i(\sigma,\sigma )$
. Therefore $i(\sigma,\sigma )$![]() is a chain equivalence for each $\sigma \in K$
is a chain equivalence for each $\sigma \in K$![]() .
.
Conversely suppose $i(\sigma,\sigma )$![]() is a chain equivalence in $\mathcal {B} R$
is a chain equivalence in $\mathcal {B} R$![]() for all $\sigma \in K$
for all $\sigma \in K$![]() . We prove that $i$
. We prove that $i$![]() is a chain equivalence in $\mathcal {B} R_K$
is a chain equivalence in $\mathcal {B} R_K$![]() . Replacing $B$
. Replacing $B$![]() by the mapping cylinder of $i$
by the mapping cylinder of $i$![]() if necessary, we can assume $i$
if necessary, we can assume $i$![]() fits into an exact sequence, $0\to A\mathop {\to }\limits ^{i} B\mathop {\to }\limits ^{j} C\to 0$
fits into an exact sequence, $0\to A\mathop {\to }\limits ^{i} B\mathop {\to }\limits ^{j} C\to 0$![]() .
.
By B.2 then, each $C(\sigma )$![]() is contractible, and we have only to prove the claim that $C$
is contractible, and we have only to prove the claim that $C$![]() is contractible. The proof is by induction on the number, $n(C)$
is contractible. The proof is by induction on the number, $n(C)$![]() , of $\sigma \in K$
, of $\sigma \in K$![]() for which $C(\sigma )\neq 0$
for which $C(\sigma )\neq 0$![]() . If $n=0$
. If $n=0$![]() we are done. We can assume this claim is proved for complexes $C'$
we are done. We can assume this claim is proved for complexes $C'$![]() for which $0\leq n(C')< n(C)$
for which $0\leq n(C')< n(C)$![]() .
.
There is some $\rho \in K$![]() for which $C(\rho )\neq 0$
for which $C(\rho )\neq 0$![]() , and an exact sequence of the form:
, and an exact sequence of the form:
for which $f(\rho,\rho )$![]() is an isomorphism, and $g(\sigma,\sigma )$
is an isomorphism, and $g(\sigma,\sigma )$![]() is an isomorphism for all $\sigma \neq \rho$
is an isomorphism for all $\sigma \neq \rho$![]() . (For example pick $\rho$
. (For example pick $\rho$![]() to be maximal in $\{\sigma \in K\mid C(\sigma )\neq 0\}$
to be maximal in $\{\sigma \in K\mid C(\sigma )\neq 0\}$![]() ). $C'$
). $C'$![]() is contractible because $C(\rho )$
is contractible because $C(\rho )$![]() is contractible. But $C''$
is contractible. But $C''$![]() is contractible by induction, so that $f$
is contractible by induction, so that $f$![]() is a chain equivalence, by B.2. So $C$
is a chain equivalence, by B.2. So $C$![]() is contractible as claimed.
is contractible as claimed.