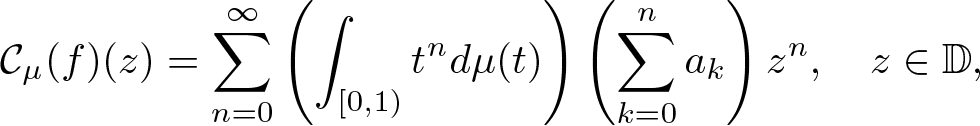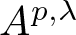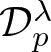1. Introduction
Denote by ![]() $\mathbb{D}$ the open unit disc in the complex plane and by
$\mathbb{D}$ the open unit disc in the complex plane and by ![]() $\partial\mathbb{D}=\{z:|z|=1\}$ the unit circle.
$\partial\mathbb{D}=\{z:|z|=1\}$ the unit circle.
Let ![]() $(a)=\{a_k\}_{k=0}^{\infty}$ be a sequence of complex numbers, and the classical Cesàro operator acting on (a) is defined by
$(a)=\{a_k\}_{k=0}^{\infty}$ be a sequence of complex numbers, and the classical Cesàro operator acting on (a) is defined by
 \begin{equation*}\mathcal{C}((a)):=\left\lbrace \frac{1}{n+1}\sum^{n}_{k=0}a_k\right\rbrace ^{\infty}_{n=0} .\end{equation*}
\begin{equation*}\mathcal{C}((a)):=\left\lbrace \frac{1}{n+1}\sum^{n}_{k=0}a_k\right\rbrace ^{\infty}_{n=0} .\end{equation*} In the 1920s, the conditions for the boundedness of this Cesàro operator on ![]() $\ell^p$ were given by Hardy [Reference Hardy21] and Landau [Reference Landau28].
$\ell^p$ were given by Hardy [Reference Hardy21] and Landau [Reference Landau28].
Cesàro operators can also be regarded as operators acting on functions defined on ![]() $\mathbb{D}$. In fact, for any
$\mathbb{D}$. In fact, for any ![]() $f\in H(\mathbb{D})$, the space of all analytic functions defined on
$f\in H(\mathbb{D})$, the space of all analytic functions defined on ![]() $\mathbb{D}$ , if
$\mathbb{D}$ , if ![]() $f(z)=\sum^{\infty}_{k=0}a_kz^k$,
$f(z)=\sum^{\infty}_{k=0}a_kz^k$, ![]() $z\in \mathbb{D}$, then the Cesàro operator
$z\in \mathbb{D}$, then the Cesàro operator ![]() $\mathcal{C}:H(\mathbb{D})\rightarrow H(\mathbb{D})$ is given by
$\mathcal{C}:H(\mathbb{D})\rightarrow H(\mathbb{D})$ is given by
 \begin{equation*}\mathcal{C}(f)(z):=\sum^{\infty}_{n=0}\left(\frac{1}{n+1}\sum^{n}_{k=0}a_k \right)z^n=\int^{1}_0\frac{f(tz)}{1-tz}\text{d}t. \end{equation*}
\begin{equation*}\mathcal{C}(f)(z):=\sum^{\infty}_{n=0}\left(\frac{1}{n+1}\sum^{n}_{k=0}a_k \right)z^n=\int^{1}_0\frac{f(tz)}{1-tz}\text{d}t. \end{equation*} The boundedness and compactness of Cesàro operators have been of interest to many complex and functional analysts. One early exploration involving the characterizations of boundedness of the Cesàro operators on Hardy spaces Hp for ![]() $1 \lt p \lt \infty$ was achieved via Hardy’s work on Fourier series [Reference Hardy22] and the boundedness of Riesz transforms. Recall that for
$1 \lt p \lt \infty$ was achieved via Hardy’s work on Fourier series [Reference Hardy22] and the boundedness of Riesz transforms. Recall that for ![]() $0 \lt p \lt \infty$, the Hardy space Hp is the space consisting of all analytic functions
$0 \lt p \lt \infty$, the Hardy space Hp is the space consisting of all analytic functions ![]() $f\in H( \mathbb{D})$ such that
$f\in H( \mathbb{D})$ such that
 \begin{equation*}\|f\|^p_{H^p}:=\sup_{0 \lt r \lt 1}\frac{1}{2\pi}\int^{2\pi}_{0}|f(re^{i\theta})|^p\text{d}\theta \lt \infty.\end{equation*}
\begin{equation*}\|f\|^p_{H^p}:=\sup_{0 \lt r \lt 1}\frac{1}{2\pi}\int^{2\pi}_{0}|f(re^{i\theta})|^p\text{d}\theta \lt \infty.\end{equation*} By using semigroup theory of composition operators, Siskakis provided an alternative proof in [Reference Siskakis42]. After that, the case p = 1 was also investigated by Siskakis [Reference Siskakis43]. Following his work, Miao [Reference Miao34] demonstrated that the Cesàro operator is bounded on Hp for ![]() $0 \lt p \lt 1$. On the other hand, Stempak [Reference Stempak46] obtained the case
$0 \lt p \lt 1$. On the other hand, Stempak [Reference Stempak46] obtained the case ![]() $1 \lt p\leq 2$ in terms of interpolation theorem, while for all
$1 \lt p\leq 2$ in terms of interpolation theorem, while for all ![]() $p\in(0,\infty)$, Andersen [Reference Andersen5] presented a new proof. For more studies for Cesàro operators on some other function spaces, we refer the interested readers to [Reference Andersen6, Reference Galanopoulos15, Reference Siskakis44, Reference Stević47] and the references therein.
$p\in(0,\infty)$, Andersen [Reference Andersen5] presented a new proof. For more studies for Cesàro operators on some other function spaces, we refer the interested readers to [Reference Andersen6, Reference Galanopoulos15, Reference Siskakis44, Reference Stević47] and the references therein.
Over the last two decades, some generalized forms of the above Cesàro operator have been introduced and studied one after another. The interested readers are referred to [Reference Abadias and Miana1, Reference Agrawal, Howlett, Lucas, Naik and Ponnusamy4, Reference Borgohain and Naik10, Reference Naik36, Reference Stević48]. Recently, Galanopoulos, Girela and Merchán [Reference Galanopoulos, Girela and Merchán17] proposed a generalized form of the Cesàro operator, defined as follows: given a positive finite Borel measure µ on ![]() $[0,1)$ and
$[0,1)$ and ![]() $f(z)=\sum^{\infty}_{n=0}a_nz^n\in H(\mathbb{D})$,
$f(z)=\sum^{\infty}_{n=0}a_nz^n\in H(\mathbb{D})$,
 \begin{equation*}\mathcal{C}_{\mu}(f)(z):=\sum^{\infty}_{n=0}\mu_n\left(\sum^{n}_{k=0}a_k \right)z^n=\int_{[0,1)}\frac{f(tz)}{1-tz}\text{d}\mu(t), ~z\in \mathbb{D},\end{equation*}
\begin{equation*}\mathcal{C}_{\mu}(f)(z):=\sum^{\infty}_{n=0}\mu_n\left(\sum^{n}_{k=0}a_k \right)z^n=\int_{[0,1)}\frac{f(tz)}{1-tz}\text{d}\mu(t), ~z\in \mathbb{D},\end{equation*} where µn denotes the moment of order n of µ for any ![]() $n=0,1,2,\cdots,$ i.e.,
$n=0,1,2,\cdots,$ i.e.,
 \begin{equation*}\mu_n=\int_{[0,1)}t^n\text{d}\mu(t).\end{equation*}
\begin{equation*}\mu_n=\int_{[0,1)}t^n\text{d}\mu(t).\end{equation*} Such operator ![]() $\mathcal{C}_{\mu}$ is called the Cesàro-type operator and will be the object of our study in this paper.
$\mathcal{C}_{\mu}$ is called the Cesàro-type operator and will be the object of our study in this paper.
The characterizations of boundedness and compactness of the Cesàro-type operator ![]() $\mathcal{C}_{\mu}$ on Hardy spaces Hp, weighted Bergman spaces
$\mathcal{C}_{\mu}$ on Hardy spaces Hp, weighted Bergman spaces ![]() $A^{p}_{\alpha}$, BMOA and Bloch space
$A^{p}_{\alpha}$, BMOA and Bloch space ![]() $\mathcal{B}$ in terms of Carleson measures were obtained by Galanopoulos–Girela–Merchán [Reference Galanopoulos, Girela and Merchán17]. Some of their conclusions are exhibited as follows: let µ be a positive finite Borel measure supported on
$\mathcal{B}$ in terms of Carleson measures were obtained by Galanopoulos–Girela–Merchán [Reference Galanopoulos, Girela and Merchán17]. Some of their conclusions are exhibited as follows: let µ be a positive finite Borel measure supported on ![]() $[0,1)$, then
$[0,1)$, then
(1)
 $1\leq p \lt \infty$,
$1\leq p \lt \infty$,  $\mathcal{C}_{\mu}:H^p\rightarrow H^p$ is bounded
$\mathcal{C}_{\mu}:H^p\rightarrow H^p$ is bounded  $\Leftrightarrow$ µ is a Carleson measure;
$\Leftrightarrow$ µ is a Carleson measure;(2)
 $1\leq p \lt \infty$,
$1\leq p \lt \infty$,  $\mathcal{C}_{\mu}:H^p\rightarrow H^p$ is compact
$\mathcal{C}_{\mu}:H^p\rightarrow H^p$ is compact  $\Leftrightarrow$ µ is a vanishing Carleson measure;
$\Leftrightarrow$ µ is a vanishing Carleson measure;(3)
 $1 \lt p \lt \infty$,
$1 \lt p \lt \infty$,  $\alpha \gt -1$,
$\alpha \gt -1$,  $\mathcal{C}_{\mu}:A^p_{\alpha}\rightarrow A^p_{\alpha}$ is bounded
$\mathcal{C}_{\mu}:A^p_{\alpha}\rightarrow A^p_{\alpha}$ is bounded  $\Leftrightarrow$ µ is a Carleson measure;
$\Leftrightarrow$ µ is a Carleson measure;(4)
 $\mathcal{C}_{\mu}:\text{BMOA}\rightarrow \text{BMOA}$ is bounded
$\mathcal{C}_{\mu}:\text{BMOA}\rightarrow \text{BMOA}$ is bounded  $\Leftrightarrow$ µ is a 1-logarithmic 1-Carleson measure;
$\Leftrightarrow$ µ is a 1-logarithmic 1-Carleson measure;(5)
 $\mathcal{C}_{\mu}:\text{BMOA}\rightarrow \text{BMOA}$ is compact
$\mathcal{C}_{\mu}:\text{BMOA}\rightarrow \text{BMOA}$ is compact  $\Leftrightarrow$ µ is a vanishing 1-logarithmic 1-Carleson measure;
$\Leftrightarrow$ µ is a vanishing 1-logarithmic 1-Carleson measure;(6)
 $\mathcal{C}_{\mu}:\mathcal{B}\rightarrow \mathcal{B}$ is bounded
$\mathcal{C}_{\mu}:\mathcal{B}\rightarrow \mathcal{B}$ is bounded  $\Leftrightarrow$ µ is a 1-logarithmic 1-Carleson measure;
$\Leftrightarrow$ µ is a 1-logarithmic 1-Carleson measure;(7)
 $\mathcal{C}_{\mu}:\mathcal{B}\rightarrow \mathcal{B}$ is compact
$\mathcal{C}_{\mu}:\mathcal{B}\rightarrow \mathcal{B}$ is compact  $\Leftrightarrow$ µ is a vanishing 1-logarithmic 1-Carleson measure.
$\Leftrightarrow$ µ is a vanishing 1-logarithmic 1-Carleson measure.
Meanwhile, they posed the problem: does the fact that µ is a Carleson measure imply that ![]() $\mathcal{C}_{\mu}(H^{\infty})\subset BMOA$? Recall that
$\mathcal{C}_{\mu}(H^{\infty})\subset BMOA$? Recall that ![]() $H^{\infty}$ is the space of all bounded analytic functions f in
$H^{\infty}$ is the space of all bounded analytic functions f in ![]() $H(\mathbb{D})$ with the norm
$H(\mathbb{D})$ with the norm
The above question was solved by Bao–Sun–Wulan [Reference Bao, Sun and Wulan7]. They showed that the operator ![]() $\mathcal{C}_{\mu}$ can map the elements of the space
$\mathcal{C}_{\mu}$ can map the elements of the space ![]() $H^{\infty}$ into a smaller space Qp which is strictly contained in BMOA. By considering complex Borel measures on the open unit disc, Blasco [Reference Blasco9] dealt with boundedness of Cesàro-type operators on Hardy spaces, BMOA and Bloch spaces, which generalizes the works of [Reference Galanopoulos, Girela and Merchán17]. Moreover, he gave another approach to prove that
$H^{\infty}$ into a smaller space Qp which is strictly contained in BMOA. By considering complex Borel measures on the open unit disc, Blasco [Reference Blasco9] dealt with boundedness of Cesàro-type operators on Hardy spaces, BMOA and Bloch spaces, which generalizes the works of [Reference Galanopoulos, Girela and Merchán17]. Moreover, he gave another approach to prove that ![]() $\mathcal{C}_{\mu}(H^{\infty})\subset \text{BMOA}$ . Continuing Blasco’s work, Galanopoulos et al. [Reference Galanopoulos, Girela and Merchán18] further considered the boundedness of Cesàro-type operators, associated with complex Borel measures, acting on H 2 and
$\mathcal{C}_{\mu}(H^{\infty})\subset \text{BMOA}$ . Continuing Blasco’s work, Galanopoulos et al. [Reference Galanopoulos, Girela and Merchán18] further considered the boundedness of Cesàro-type operators, associated with complex Borel measures, acting on H 2 and ![]() $A^2_{\alpha}$. For more studies of Cesàro-type operators acting on some other function spaces, we refer the interested readers to [Reference Galanopoulos, Girela, Mas and Merchán16, Reference Jin and Tang25, Reference Sun, Ye and Zhou49, Reference Tang50].
$A^2_{\alpha}$. For more studies of Cesàro-type operators acting on some other function spaces, we refer the interested readers to [Reference Galanopoulos, Girela, Mas and Merchán16, Reference Jin and Tang25, Reference Sun, Ye and Zhou49, Reference Tang50].
The notion of Morrey spaces was first introduced in the work of Morrey [Reference Morrey35]. This space has received a lot of attention from researchers due to the fact that it can be applied in harmonic analysis and partial differential equations. For instance, the characterization of the potential theory on Morrey spaces was derived by Adams–Xiao [Reference Adams and Xiao2]. They also investigated the boundedness of the classical operators of harmonic analysis on Morrey spaces in [Reference Adams and Xiao3]. For the study of Morrey spaces with heat kernel, bounds can be seen from the work of Duong–Xiao–Yan [Reference Duong, Xiao and Yan14]. In [Reference Lemarié-Rieusset30], Lemarié-Rieusset discussed the set of pointwise multipliers between different Morrey spaces. In addition, Morrey spaces have been studied extensively on partial differential equations. We refer the reader to [Reference Kozono and Yamazaki26, Reference Kukavica27, Reference Lemarié-Rieusset29, Reference Olsen38, Reference Palagachev and Softova40, Reference Pinchover and Psaradakis41, Reference Souplet45, Reference Taylor51, Reference Wakabayashi52] for more results. In [Reference Wu and Xie54], Wu and Xie introduced the notion of analytic Morrey spaces, which is a real case of Morrey space. Analytic Morrey spaces plays a crucial role in the study of function space and operator theory. Wu and Xie also showed the characterization of analytic Morrey spaces in terms of the Carleson measure. Some properties of this space were obtained by Liu et al. [Reference Liu and Lou31, Reference Liu and Lou32]. More research on analytic Morrey spaces can be found in the works of Wulan–Zhou [Reference Wulan and Zhou53] and Galanopoulos–Merchán–Siskakis [Reference Galanopoulos, Merchán and Siskakis20].
In this paper, motivated by the above works, we are interested in studing the boundedness and compactness of Cesàro-type operators acting on two new Morrey-type spaces of analytic functions (i.e., Bergman–Morrey spaces and Dirichlet–Morrey spaces). So, let us recall their definitions.
Definition 1.1. Given ![]() $0\leq\lambda\leq 2$ and p > 0, a function f in
$0\leq\lambda\leq 2$ and p > 0, a function f in ![]() $H(\mathbb{D})$ is said to belong to Bergman–Morrey space
$H(\mathbb{D})$ is said to belong to Bergman–Morrey space ![]() $A^{p,\lambda}$ if
$A^{p,\lambda}$ if
 \begin{equation*}\|f\|_{A^{p,\lambda}}:=\left(|f(0)|^p+ \sup\limits_{a\in\mathbb{D}} (1-|a|^{2})^{2-\lambda}\int_{\mathbb{D}}|f'(z)|^{p}(1-|z|^{2})^{p}|\sigma'_{a}(z)|^{2}\text{d}A(z)\right)^{1/p} \lt \infty,\end{equation*}
\begin{equation*}\|f\|_{A^{p,\lambda}}:=\left(|f(0)|^p+ \sup\limits_{a\in\mathbb{D}} (1-|a|^{2})^{2-\lambda}\int_{\mathbb{D}}|f'(z)|^{p}(1-|z|^{2})^{p}|\sigma'_{a}(z)|^{2}\text{d}A(z)\right)^{1/p} \lt \infty,\end{equation*} where ![]() $\sigma_{a}(z)=\frac{a-z}{1-\overline{a}z}$.
$\sigma_{a}(z)=\frac{a-z}{1-\overline{a}z}$.
In particular, when λ = 0, ![]() $A^{p,0}=A^{p}$. If
$A^{p,0}=A^{p}$. If ![]() $0 \lt \lambda\leq2+p \lt \infty$ and
$0 \lt \lambda\leq2+p \lt \infty$ and ![]() $\alpha=(p+2-\lambda)/p$, then
$\alpha=(p+2-\lambda)/p$, then ![]() $A^{p,\lambda}$ is contained in the Bloch-type spaces
$A^{p,\lambda}$ is contained in the Bloch-type spaces ![]() $\mathcal{B}^{\alpha}$. Very recently, the notion of Bergman–Morrey spaces was introduced by Yang and Liu [Reference Yang and Liu55]. They investigated several problems concerning two integral operators on Bergman–Morrey spaces
$\mathcal{B}^{\alpha}$. Very recently, the notion of Bergman–Morrey spaces was introduced by Yang and Liu [Reference Yang and Liu55]. They investigated several problems concerning two integral operators on Bergman–Morrey spaces ![]() $A^{p,\lambda}$, including boundedness, norm and essential norm. In addition, they showed the Carleson embedding theorem for Bergman–Morrey spaces.
$A^{p,\lambda}$, including boundedness, norm and essential norm. In addition, they showed the Carleson embedding theorem for Bergman–Morrey spaces.
Definition 1.2. Let ![]() $0\leq \lambda,p\leq1$, and the Dirichlet–Morrey space
$0\leq \lambda,p\leq1$, and the Dirichlet–Morrey space  $\mathcal{D}^{\lambda}_{p}$ consists of
$\mathcal{D}^{\lambda}_{p}$ consists of ![]() $f\in H(\mathbb{D})$ such that
$f\in H(\mathbb{D})$ such that
 \begin{equation*}\|f\|_{\mathcal{D}^{\lambda}_{p}}=|f(0)|+\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p(1-\lambda)}{2}}\left( \int_{\mathbb{D}}|f'(z)|^2(1-|\sigma_{a}(z)|^2)^p\text{d}A(z)\right) ^{1/2}.\end{equation*}
\begin{equation*}\|f\|_{\mathcal{D}^{\lambda}_{p}}=|f(0)|+\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p(1-\lambda)}{2}}\left( \int_{\mathbb{D}}|f'(z)|^2(1-|\sigma_{a}(z)|^2)^p\text{d}A(z)\right) ^{1/2}.\end{equation*} In fact, when λ = 1, the Dirichlet–Morrey space ![]() $\mathcal{D}^{1}_{p}$ coincides with the space Qp with equivalence of norms. If
$\mathcal{D}^{1}_{p}$ coincides with the space Qp with equivalence of norms. If ![]() $0 \lt \lambda \lt 1$, then the space Qp is contained in the Dirichlet–Morrey space
$0 \lt \lambda \lt 1$, then the space Qp is contained in the Dirichlet–Morrey space  $\mathcal{D}^{\lambda}_{p}$. (see [Reference Wulan and Zhou53, p. 1690]).
$\mathcal{D}^{\lambda}_{p}$. (see [Reference Wulan and Zhou53, p. 1690]).
The Dirichlet–Morrey spaces is first introduced by Galanopoulos–Merchán–Siskakis [Reference Galanopoulos, Merchán and Siskakis19]. They characterized the boundedness of integration and multiplication operators acting on Dirichlet–Morrey spaces and obtained some properties of such spaces. In [Reference Zhu, Qian and Hu59], Zhu et al. obtained the Carleson embedding theorem for Dirichlet–Morrey spaces in terms of Carlesom measure. Later on, Corona and Wolff theorems for the multiplier algebra of Dirichlet–Morrey spaces were demonstrated by Hu–Li–Yang [Reference Hu, Li and Yang24].
Now let us highlight our main results briefly. We completely characterize the boundedness and compactness of Cesàro-type operators from ![]() $A^{p_1,\lambda_1}$ into
$A^{p_1,\lambda_1}$ into ![]() $A^{p_2,\lambda_2}$ by means of Carleson type measure (see Theorems 3.1 and 3.4). Meanwhile, we present that Cesàro-type operators are bounded from
$A^{p_2,\lambda_2}$ by means of Carleson type measure (see Theorems 3.1 and 3.4). Meanwhile, we present that Cesàro-type operators are bounded from ![]() $\mathcal{B}^{\alpha}$ into
$\mathcal{B}^{\alpha}$ into ![]() $\mathcal{B}^{\alpha}$ when µ is a Carleson measure for all α > 1 (see Corollary 3.3). Interestingly, we discover that in the problem of Galanopoulos et al., the fact that µ is a Carlesom measure is no longer sufficient to derive that the operators
$\mathcal{B}^{\alpha}$ when µ is a Carleson measure for all α > 1 (see Corollary 3.3). Interestingly, we discover that in the problem of Galanopoulos et al., the fact that µ is a Carlesom measure is no longer sufficient to derive that the operators ![]() $\mathcal{C}_{\mu}$ are bounded if the spaces
$\mathcal{C}_{\mu}$ are bounded if the spaces ![]() $H^{\infty}$ are replaced by a larger space
$H^{\infty}$ are replaced by a larger space ![]() $\mathcal{B}^{\alpha}$, as shown in our Theorem 3.7. Furthermore, we give the boundeness and compactness of Cesàro-type operators from the Bloch space
$\mathcal{B}^{\alpha}$, as shown in our Theorem 3.7. Furthermore, we give the boundeness and compactness of Cesàro-type operators from the Bloch space ![]() $\mathcal{B}$ into the space Qp, which generalizes the result of Bao et al. (see Theorems 4.9 and 4.11).
$\mathcal{B}$ into the space Qp, which generalizes the result of Bao et al. (see Theorems 4.9 and 4.11).
The structure of this paper is organized as follows.
In Section 2, we provide some preliminary lemmas that will be used throughout the paper.
In Section 3, we consider the Cesàro-type operators on Bergman-Morrey spaces. The boundedness and compactness of ![]() $\mathcal{C}_{\mu}$ from Bergman–Morrey spaces
$\mathcal{C}_{\mu}$ from Bergman–Morrey spaces ![]() $A^{p_1,\lambda_1}$ into the mean Lipschitz spaces
$A^{p_1,\lambda_1}$ into the mean Lipschitz spaces  $\Lambda^{p_2}_{1/p_2}$ are shown in Theorems 3.7 and 3.10 , respectively. The boundedness and compactness of
$\Lambda^{p_2}_{1/p_2}$ are shown in Theorems 3.7 and 3.10 , respectively. The boundedness and compactness of ![]() $\mathcal{C}_{\mu}$ from the mean Lipschitz spaces
$\mathcal{C}_{\mu}$ from the mean Lipschitz spaces  $\Lambda^{p_1}_{1/p_1}$ into Bergman–Morrey spaces
$\Lambda^{p_1}_{1/p_1}$ into Bergman–Morrey spaces ![]() $A^{p_2,\lambda_2}$ will also be obtained (see Theorems 3.13 and 3.15).
$A^{p_2,\lambda_2}$ will also be obtained (see Theorems 3.13 and 3.15).
In Section 4, we deal with the Cesàro-type operators on Dirichlet–Morrey spaces. Theorem 4.1 gives the boundedness of ![]() $\mathcal{C}_{\mu}$ between different Dirichlet–Morrey spaces, and Theorem 4.3 gives the compactness of
$\mathcal{C}_{\mu}$ between different Dirichlet–Morrey spaces, and Theorem 4.3 gives the compactness of ![]() $\mathcal{C}_{\mu}$ between different Dirichlet–Morrey spaces. Next, we show boundedness and compactness between Dirichlet–Morrey spaces and the mean Lipschitz spaces, respectively (see Theorems 4.5, 4.6, 4.7 and 4.8).
$\mathcal{C}_{\mu}$ between different Dirichlet–Morrey spaces. Next, we show boundedness and compactness between Dirichlet–Morrey spaces and the mean Lipschitz spaces, respectively (see Theorems 4.5, 4.6, 4.7 and 4.8).
Throughout the paper, the letter ‘C’ will denote (possibly different) constants that are independent of the essential variables.
2. Preliminaries
For ![]() $0 \lt p \lt \infty$ and
$0 \lt p \lt \infty$ and ![]() $-1 \lt \alpha \lt \infty$, the weighted Bergman space
$-1 \lt \alpha \lt \infty$, the weighted Bergman space ![]() $A^p_{\alpha}$ consists of
$A^p_{\alpha}$ consists of ![]() $f\in H(\mathbb{D})$ such that
$f\in H(\mathbb{D})$ such that
 \begin{equation*}\|f\|^p_{A^p_{\alpha}}:=\int_{\mathbb{D}}|f(w)|^p\text{d}A_{\alpha}(w) \lt \infty,\end{equation*}
\begin{equation*}\|f\|^p_{A^p_{\alpha}}:=\int_{\mathbb{D}}|f(w)|^p\text{d}A_{\alpha}(w) \lt \infty,\end{equation*} where ![]() $\text{d}A(w)=(1/\pi)\text{d}x\text{d}y$ is the normalized Lebesgue area measure on
$\text{d}A(w)=(1/\pi)\text{d}x\text{d}y$ is the normalized Lebesgue area measure on ![]() $\mathbb{D}$ and
$\mathbb{D}$ and ![]() $dA_{\alpha}(w)=(1+\alpha)(1-|w|^2)^{\alpha}d\text{d}(w)$ is the weighted Lebesgue measure. (See [Reference Zhu58] for more information about Bergman spaces.)
$dA_{\alpha}(w)=(1+\alpha)(1-|w|^2)^{\alpha}d\text{d}(w)$ is the weighted Lebesgue measure. (See [Reference Zhu58] for more information about Bergman spaces.)
For α > 0, the Bloch type space ![]() $\mathcal{B}^{\alpha}$ is defined to be the space of
$\mathcal{B}^{\alpha}$ is defined to be the space of ![]() $f\in H(\mathbb{D})$ such that
$f\in H(\mathbb{D})$ such that
When α = 1, ![]() $\mathcal{B}:=\mathcal{B}^1$ is the classical Bloch space. Readers interested in the Bloch type spaces are referred to [Reference Zhu57].
$\mathcal{B}:=\mathcal{B}^1$ is the classical Bloch space. Readers interested in the Bloch type spaces are referred to [Reference Zhu57].
Let ![]() $1\leq p\leq\infty$ and
$1\leq p\leq\infty$ and ![]() $0 \lt \alpha\leq1$, and the mean Lipschitz space
$0 \lt \alpha\leq1$, and the mean Lipschitz space ![]() $\Lambda^{p}_{\alpha}$ consists of
$\Lambda^{p}_{\alpha}$ consists of ![]() $f\in H(\mathbb{D})$ such that
$f\in H(\mathbb{D})$ such that
 \begin{equation*}\|f\|_{\Lambda^{p}_{\alpha}}:=|f(0)|+\sup_{0 \lt r \lt 1}(1-r)^{1-\alpha}\left( \frac{1}{2\pi}\int^{2\pi}_{0}|f'(r\text{e}^{i\theta})|^p\text{d}\theta\right) ^{1/p} \lt \infty.\end{equation*}
\begin{equation*}\|f\|_{\Lambda^{p}_{\alpha}}:=|f(0)|+\sup_{0 \lt r \lt 1}(1-r)^{1-\alpha}\left( \frac{1}{2\pi}\int^{2\pi}_{0}|f'(r\text{e}^{i\theta})|^p\text{d}\theta\right) ^{1/p} \lt \infty.\end{equation*} As is well known, ![]() $\Lambda^{p}_{\alpha}$ is a subset of Hp. One of the interesting spaces is the space
$\Lambda^{p}_{\alpha}$ is a subset of Hp. One of the interesting spaces is the space  $\Lambda^{p}_{1/p}$ with p > 1 contained in BMOA (cf. [Reference Bourdon, Shapiro and Sledd11]).
$\Lambda^{p}_{1/p}$ with p > 1 contained in BMOA (cf. [Reference Bourdon, Shapiro and Sledd11]).
Let ![]() $I\subset\partial\mathbb{D}$ be an interval, and the length of I is denoted by
$I\subset\partial\mathbb{D}$ be an interval, and the length of I is denoted by ![]() $|I|$. The Carleson square is defined as
$|I|$. The Carleson square is defined as
 \begin{equation*}S(I)=\left\lbrace re^{it}\in \mathbb{D}:\text{e}^{it}\in I, 1-\frac{|I|}{2\pi}\leq r \lt 1\right\rbrace. \end{equation*}
\begin{equation*}S(I)=\left\lbrace re^{it}\in \mathbb{D}:\text{e}^{it}\in I, 1-\frac{|I|}{2\pi}\leq r \lt 1\right\rbrace. \end{equation*} Let s > 0. Given a positive Borel measure µ on ![]() $\mathbb{D}$, we say that µ is an s-Carleson measure if
$\mathbb{D}$, we say that µ is an s-Carleson measure if
 \begin{equation*}\|\mu\|=\sup\left\lbrace \frac{\mu(S(I))}{|I|^s}:I\in\partial\mathbb{D},|I| \gt 0\right\rbrace \lt \infty.\end{equation*}
\begin{equation*}\|\mu\|=\sup\left\lbrace \frac{\mu(S(I))}{|I|^s}:I\in\partial\mathbb{D},|I| \gt 0\right\rbrace \lt \infty.\end{equation*}A positive Borel measure µ is called a vanishing s-Carleson measure if
 \begin{equation*}\lim_{\substack{|I|\rightarrow0\\I\subset\partial\mathbb{D}}}\frac{\mu(S(I))}{|I|^s}=0.\end{equation*}
\begin{equation*}\lim_{\substack{|I|\rightarrow0\\I\subset\partial\mathbb{D}}}\frac{\mu(S(I))}{|I|^s}=0.\end{equation*}When s = 1, 1-Carleson measures are called Carleson measures and vanishing 1-Carleson measures are called vanishing Carleson measures.
Carleson measures play important roles in complex function theory and operator theory. It was originally presented by Carleson [Reference Carleson12, Reference Carleson13] to investigate interpolating sequences and the famous corona problem for bounded analytic functions. Indeed, the boundedness of the inclusion maps from Hardy spaces into Lebesgue spaces with positive Borel measures can be described in terms of Carleson measures. This investigation was extended to the case of Bergman spaces [Reference Hastings23]. We refer the readers to [Reference Zhu58] for more detailed studies on Carleson measures.
Following Zhao [Reference Zhao56], we recall the notion of logarithmic Carleson measures. Given ![]() $0 \lt s \lt \infty$ and
$0 \lt s \lt \infty$ and ![]() $0\leq \alpha \lt \infty$, a positive Borel measure µ on
$0\leq \alpha \lt \infty$, a positive Borel measure µ on ![]() $\mathbb{D}$ is called an α-logarithmic s-Carleson measure if there is a positive constant C > 0 such that
$\mathbb{D}$ is called an α-logarithmic s-Carleson measure if there is a positive constant C > 0 such that
 \begin{equation*}\frac{\left(\log\frac{2}{|I|} \right)^{\alpha} \mu(S(I))}{|I|^s}\leq C\end{equation*}
\begin{equation*}\frac{\left(\log\frac{2}{|I|} \right)^{\alpha} \mu(S(I))}{|I|^s}\leq C\end{equation*} for any ![]() $I\subset\partial \mathbb{D}$ with
$I\subset\partial \mathbb{D}$ with ![]() $|I| \gt 0$. If in addition,
$|I| \gt 0$. If in addition,  $\left(\log\frac{2}{|I|} \right)^{\alpha} \mu(S(I))=o(|I|^s)$, as
$\left(\log\frac{2}{|I|} \right)^{\alpha} \mu(S(I))=o(|I|^s)$, as ![]() $|I|\rightarrow0$, then µ is called a vanishing α-logarithmic s-Carleson measure.
$|I|\rightarrow0$, then µ is called a vanishing α-logarithmic s-Carleson measure.
A positive Borel measure µ on ![]() $[0,1)$ can be regarded as a Borel measure on
$[0,1)$ can be regarded as a Borel measure on ![]() $\mathbb{D}$ with support contained in the radius
$\mathbb{D}$ with support contained in the radius ![]() $[0,1)$. So a positive Borel measure µ on
$[0,1)$. So a positive Borel measure µ on ![]() $[0,1)$ is an α-logarithmic s-Carleson measure if and only if there is a positive constant C > 0 such that
$[0,1)$ is an α-logarithmic s-Carleson measure if and only if there is a positive constant C > 0 such that
 \begin{equation*}\left(\log\frac{2}{1-t} \right)^{\alpha}\mu([t,1))\leq C(1-t)^s\end{equation*}
\begin{equation*}\left(\log\frac{2}{1-t} \right)^{\alpha}\mu([t,1))\leq C(1-t)^s\end{equation*} for each ![]() $t\in[0,1)$.
$t\in[0,1)$.
The following lemma shows an equivalent characterization of logarithmic Carleson measure.
Lemma 2.1. See [Reference Blasco8, Reference MacCluer and Zhao33]
Suppose ![]() $0 \lt \alpha \lt \infty$,
$0 \lt \alpha \lt \infty$, ![]() $0\leq k \lt \infty$,
$0\leq k \lt \infty$, ![]() $0 \lt s \lt \infty$ and µ is a finite positive Borel measure on
$0 \lt s \lt \infty$ and µ is a finite positive Borel measure on ![]() $\mathbb{D}$.
$\mathbb{D}$.
(i) µ is a k-logarithmic s-Carleson measure if and only if
 \begin{equation*}\sup_{w\in\mathbb{D}}\left( \log\frac{e}{1-|w|^2}\right)^{k} \int_{\mathbb{D}}\frac{(1-|w|^2)^{\alpha}}{|1-\overline{w}z|^{s+\alpha}}d\mu(z) \lt \infty.\end{equation*}
\begin{equation*}\sup_{w\in\mathbb{D}}\left( \log\frac{e}{1-|w|^2}\right)^{k} \int_{\mathbb{D}}\frac{(1-|w|^2)^{\alpha}}{|1-\overline{w}z|^{s+\alpha}}d\mu(z) \lt \infty.\end{equation*}(ii) µ is a vanishing k-logarithmic s-Carleson measure if and only if
 \begin{align*}
\lim_{\substack{|w|\rightarrow1\\
w\in\mathbb{D}}}\left( \log\frac{e}{1-|w|^2}\right)^{k} \int_{\mathbb{D}}\frac{(1-|w|^2)^{\alpha}}{|1-\overline{w}z|^{s+\alpha}}d\mu(z)=0.
\end{align*}
\begin{align*}
\lim_{\substack{|w|\rightarrow1\\
w\in\mathbb{D}}}\left( \log\frac{e}{1-|w|^2}\right)^{k} \int_{\mathbb{D}}\frac{(1-|w|^2)^{\alpha}}{|1-\overline{w}z|^{s+\alpha}}d\mu(z)=0.
\end{align*}
There is also an equivalent characterization of logarithmic Carleson measure on ![]() $[0,1)$.
$[0,1)$.
Lemma 2.2. See [Reference Bao, Sun and Wulan7]
Suppose ![]() $0 \lt \alpha \lt \infty$,
$0 \lt \alpha \lt \infty$, ![]() $0\leq k \lt \infty$,
$0\leq k \lt \infty$, ![]() $0\leq\beta \lt s \lt \infty$ and µ is a finite positive Borel measure on
$0\leq\beta \lt s \lt \infty$ and µ is a finite positive Borel measure on ![]() $[0,1)$. Then, the following three conditions are equivalent:
$[0,1)$. Then, the following three conditions are equivalent:
(i) µ is a k-logarithmic s-Carleson measure;
(ii)
 \begin{equation*}\sup_{w\in\mathbb{D}}\int_{[0,1)}\left( \log\frac{e}{1-|w|}\right) ^{k}\frac{(1-|w|)^\alpha}{(1-t)^{\beta}(1-|w|t)^{s+\alpha-\beta}}\text{d}\mu(t) \lt \infty;\end{equation*}
\begin{equation*}\sup_{w\in\mathbb{D}}\int_{[0,1)}\left( \log\frac{e}{1-|w|}\right) ^{k}\frac{(1-|w|)^\alpha}{(1-t)^{\beta}(1-|w|t)^{s+\alpha-\beta}}\text{d}\mu(t) \lt \infty;\end{equation*}(iii)
 \begin{equation*}\sup_{w\in\mathbb{D}}\int_{[0,1)}\left( \log\frac{e}{1-|w|}\right) ^{k}\frac{(1-|w|)^\alpha}{(1-t)^{\beta}|1-wt|^{s+\alpha-\beta}}\text{d}\mu(t) \lt \infty.\end{equation*}
\begin{equation*}\sup_{w\in\mathbb{D}}\int_{[0,1)}\left( \log\frac{e}{1-|w|}\right) ^{k}\frac{(1-|w|)^\alpha}{(1-t)^{\beta}|1-wt|^{s+\alpha-\beta}}\text{d}\mu(t) \lt \infty.\end{equation*}
Lemma 2.3. See [Reference Bao, Sun and Wulan7]
Suppose ![]() $0 \lt \alpha \lt \infty$,
$0 \lt \alpha \lt \infty$, ![]() $0\leq\beta \lt s \lt \infty$ and µ is a finite positive Borel measure on
$0\leq\beta \lt s \lt \infty$ and µ is a finite positive Borel measure on ![]() $[0,1)$. Then, the following three conditions are equivalent:
$[0,1)$. Then, the following three conditions are equivalent:
(i) µ is a vanishing k-logarithmic s-Carleson measure;
(ii)
 \begin{equation*}\lim_{|w|\rightarrow1}\int_{[0,1)}\left( \log\frac{e}{1-|w|}\right)^{k}\frac{(1-|w|)^\alpha}{(1-t)^{\beta}(1-|w|t)^{s+\alpha-\beta}}\text{d}\mu(t)=0 \end{equation*}
\begin{equation*}\lim_{|w|\rightarrow1}\int_{[0,1)}\left( \log\frac{e}{1-|w|}\right)^{k}\frac{(1-|w|)^\alpha}{(1-t)^{\beta}(1-|w|t)^{s+\alpha-\beta}}\text{d}\mu(t)=0 \end{equation*}(iii)
 \begin{equation*}\lim_{|w|\rightarrow1}\int_{[0,1)}\left( \log\frac{e}{1-|w|}\right) ^{k}\frac{(1-|w|)^\alpha}{(1-t)^{\beta}|1-wt|^{s+\alpha-\beta}}\text{d}\mu(t)=0.\end{equation*}
\begin{equation*}\lim_{|w|\rightarrow1}\int_{[0,1)}\left( \log\frac{e}{1-|w|}\right) ^{k}\frac{(1-|w|)^\alpha}{(1-t)^{\beta}|1-wt|^{s+\alpha-\beta}}\text{d}\mu(t)=0.\end{equation*}
Next, we need the following two estimates, which will be used frequently later.
Lemma 2.4. See Lemma 2.5 in [Reference Ortega and Fábrega39]
Let ![]() $s \gt -1$,
$s \gt -1$, ![]() $r,t\geq0$ and
$r,t\geq0$ and ![]() $r+t-s \gt 2$.
$r+t-s \gt 2$.
(1) For all ![]() $a,b\in\mathbb{D}$, if
$a,b\in\mathbb{D}$, if ![]() $r,t \lt 2+s$ , then
$r,t \lt 2+s$ , then
 \begin{equation*}\int_{\mathbb{D}}\frac{(1-|z|^2)^s}{|1-az|^r|1-bz|^t}dA(z)\lesssim\frac{1}{|1-a\overline{b}|^{r+t-s-2}}.\end{equation*}
\begin{equation*}\int_{\mathbb{D}}\frac{(1-|z|^2)^s}{|1-az|^r|1-bz|^t}dA(z)\lesssim\frac{1}{|1-a\overline{b}|^{r+t-s-2}}.\end{equation*} (2) For all ![]() $a,b\in\mathbb{D}$, if
$a,b\in\mathbb{D}$, if ![]() $t \lt 2+s \lt r$, then
$t \lt 2+s \lt r$, then
 \begin{equation*}\int_{\mathbb{D}}\frac{(1-|z|^2)^s}{|1-az|^r|1-bz|^t}dA(z)\lesssim\frac{1}{|1-a\overline{b}|^{t}(1-|a|^2)^{r-2-s}}.\end{equation*}
\begin{equation*}\int_{\mathbb{D}}\frac{(1-|z|^2)^s}{|1-az|^r|1-bz|^t}dA(z)\lesssim\frac{1}{|1-a\overline{b}|^{t}(1-|a|^2)^{r-2-s}}.\end{equation*}Lemma 2.5. See Lemma 3.10 in [Reference Zhu58]
Suppose ![]() $z\in\mathbb{D}$ and α is real, then
$z\in\mathbb{D}$ and α is real, then
 \begin{align*}
\begin{split}
\int^{2\pi}_{0}\frac{1}{|1-z\text{e}^{-i\theta}|^{1+\alpha}}\text{d}\theta\approx \left \{
\begin{array}{ll}
1, & if~\alpha \lt 0\,;\\
\log\frac{2}{1-|z|^2}, & if~\alpha=0\,;\\
\frac{1}{(1-|z|^2)^{\alpha}} & if~\alpha \gt 0\,.
\end{array}
\right.
\end{split}
\end{align*}
\begin{align*}
\begin{split}
\int^{2\pi}_{0}\frac{1}{|1-z\text{e}^{-i\theta}|^{1+\alpha}}\text{d}\theta\approx \left \{
\begin{array}{ll}
1, & if~\alpha \lt 0\,;\\
\log\frac{2}{1-|z|^2}, & if~\alpha=0\,;\\
\frac{1}{(1-|z|^2)^{\alpha}} & if~\alpha \gt 0\,.
\end{array}
\right.
\end{split}
\end{align*} Moreover, the growth estimates of elements in ![]() $\mathcal{B}^{\alpha}$ are given in the following lemma.
$\mathcal{B}^{\alpha}$ are given in the following lemma.
Lemma 2.6. See [Reference Ohno, Stroethoff and Zhao37]
Let ![]() $0 \lt \alpha \lt \infty$. If
$0 \lt \alpha \lt \infty$. If ![]() $f\in \mathcal{B}^{\alpha}$, then for any
$f\in \mathcal{B}^{\alpha}$, then for any ![]() $z\in \mathbb D$,
$z\in \mathbb D$,
(1) if
 $0 \lt \alpha \lt 1$,
$0 \lt \alpha \lt 1$,  $|f(z)|\lesssim\|f\|_{\mathcal{B}^{\alpha}}$ ;
$|f(z)|\lesssim\|f\|_{\mathcal{B}^{\alpha}}$ ;(2) if α = 1,
 $|f(z)|\lesssim\|f\|_{\mathcal{B}^{\alpha}} \log\frac{2}{1-|z|^2} $ ;
$|f(z)|\lesssim\|f\|_{\mathcal{B}^{\alpha}} \log\frac{2}{1-|z|^2} $ ;(3) if α > 1,
 $|f(z)|\lesssim \frac{\|f\|_{\mathcal{B}^{\alpha}}}{(1-|z|^2)^{\alpha-1}}$ .
$|f(z)|\lesssim \frac{\|f\|_{\mathcal{B}^{\alpha}}}{(1-|z|^2)^{\alpha-1}}$ .
3. The Cesàro-type operator  $\mathcal{C}_{\mu}$ on
$\mathcal{C}_{\mu}$ on  $A^{p,\lambda}$
$A^{p,\lambda}$
This section is devoted to the study of boundedness and compactness of Cesàro-type operators on Bergman–Morrey spaces. In the next theorem, we establish a necessary and sufficient condition for the boundedness of ![]() $\mathcal{C}_{\mu}$ between different Bergman–Morrey spaces.
$\mathcal{C}_{\mu}$ between different Bergman–Morrey spaces.
Theorem 3.1 Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $0 \lt p_1 \lt \infty$,
$0 \lt p_1 \lt \infty$, ![]() $1\leq p_2 \lt \infty$ and
$1\leq p_2 \lt \infty$ and ![]() $0 \lt \lambda_1,\lambda_2 \lt 2$ such that
$0 \lt \lambda_1,\lambda_2 \lt 2$ such that  $1+\frac{2-\lambda_1}{p_1} \gt \frac{2-\lambda_2}{p_2}$. Suppose that X and Y are two Banach spaces contained in
$1+\frac{2-\lambda_1}{p_1} \gt \frac{2-\lambda_2}{p_2}$. Suppose that X and Y are two Banach spaces contained in ![]() $H(\mathbb{D})$ such that
$H(\mathbb{D})$ such that  $A^{p_1,\lambda_1}\subset X\subset \mathcal{B}^{\frac{p_{1}+2-\lambda_1}{p_1}}$ and
$A^{p_1,\lambda_1}\subset X\subset \mathcal{B}^{\frac{p_{1}+2-\lambda_1}{p_1}}$ and  $A^{p_2,\lambda_2}\subset Y\subset \mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}$. Then, the following two statements are equivalent:
$A^{p_2,\lambda_2}\subset Y\subset \mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}$. Then, the following two statements are equivalent:
(1) the operator
 $\mathcal{C}_{\mu}:X\rightarrow Y$ is bounded;
$\mathcal{C}_{\mu}:X\rightarrow Y$ is bounded;(2) the measure µ is a
 $\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure.
$\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure.
Proof. If the measure µ is a  $\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure, for any
$\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure, for any  $f\in X\subset\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}$, by the definition of Bergman–Morrey spaces, we have
$f\in X\subset\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}$, by the definition of Bergman–Morrey spaces, we have
 \begin{align*}
\|\mathcal{C}_{\mu}(f)\|^{p_2}_{A^{p_2,\lambda_2}}\approx&\sup_{a\in \mathbb{D}}(1-|a|^2)^{2-\lambda_2}\int_{\mathbb{D}}\left|\int_{[0,1)}\frac{tf'(tz)}{1-tz}\text{d}\mu(t)+\int_{[0,1)}\frac{tf(tz)}{(1-tz)^2}\text{d}\mu(t) \right|^{p_2}\\ & \quad(1-|z|^2)^{p_2}|\sigma_a'(z)|^2dA(z)\\
\leq&\sup_{a\in \mathbb{D}}(1-|a|^2)^{4-\lambda_2}\int_{\mathbb{D}}\left(\int_{[0,1)}\frac{|tf'(tz)|}{|1-tz|}\text{d}\mu(t)+\int_{[0,1)}\frac{|tf(tz)|}{|1-tz|^2}\text{d}\mu(t) \right)^{p_2}\\ & \quad\frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z).
\end{align*}
\begin{align*}
\|\mathcal{C}_{\mu}(f)\|^{p_2}_{A^{p_2,\lambda_2}}\approx&\sup_{a\in \mathbb{D}}(1-|a|^2)^{2-\lambda_2}\int_{\mathbb{D}}\left|\int_{[0,1)}\frac{tf'(tz)}{1-tz}\text{d}\mu(t)+\int_{[0,1)}\frac{tf(tz)}{(1-tz)^2}\text{d}\mu(t) \right|^{p_2}\\ & \quad(1-|z|^2)^{p_2}|\sigma_a'(z)|^2dA(z)\\
\leq&\sup_{a\in \mathbb{D}}(1-|a|^2)^{4-\lambda_2}\int_{\mathbb{D}}\left(\int_{[0,1)}\frac{|tf'(tz)|}{|1-tz|}\text{d}\mu(t)+\int_{[0,1)}\frac{|tf(tz)|}{|1-tz|^2}\text{d}\mu(t) \right)^{p_2}\\ & \quad\frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z).
\end{align*} Since ![]() $p_2\geq1$, we can apply Minkowski’s inequality to obtain
$p_2\geq1$, we can apply Minkowski’s inequality to obtain
 \begin{align*}
\|\mathcal{C}_{\mu}(f)\|_{A^{p_2,\lambda_2}}&\lesssim\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{|f'(tz)|^{p_2}}{|1-tz|^{p_2}}\frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}dA(z)\right)^{1/p_2} \text{d}\mu(t)\\
&\quad +\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)} \left(\int_{\mathbb{D}} \frac{|f(tz)|^{p_2}}{|1-tz|^{2p_2}} \frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2}\text{d}\mu(t)\\
& =:I_1+I_2.
\end{align*}
\begin{align*}
\|\mathcal{C}_{\mu}(f)\|_{A^{p_2,\lambda_2}}&\lesssim\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{|f'(tz)|^{p_2}}{|1-tz|^{p_2}}\frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}dA(z)\right)^{1/p_2} \text{d}\mu(t)\\
&\quad +\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)} \left(\int_{\mathbb{D}} \frac{|f(tz)|^{p_2}}{|1-tz|^{2p_2}} \frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2}\text{d}\mu(t)\\
& =:I_1+I_2.
\end{align*}To prove that I 1 is finite, we consider the following two cases:
Case 1: ![]() $1\leq p_2\leq2$.
$1\leq p_2\leq2$.
Choose the positive constant c such that
 \begin{equation*}\frac{(2-\lambda_2)p_1}{p_2(p_1+2-\lambda_1)} \lt c \lt \min\left\{1,\frac{2p_1}{p_2(p_1+2-\lambda_1)},\frac{(p_2+2-\lambda_2)p_1}{p_2(p_1+2-\lambda_1)}\right\}.\end{equation*}
\begin{equation*}\frac{(2-\lambda_2)p_1}{p_2(p_1+2-\lambda_1)} \lt c \lt \min\left\{1,\frac{2p_1}{p_2(p_1+2-\lambda_1)},\frac{(p_2+2-\lambda_2)p_1}{p_2(p_1+2-\lambda_1)}\right\}.\end{equation*}Since
for any ![]() $z\in\mathbb{D}$ and
$z\in\mathbb{D}$ and ![]() $t\in[0,1)$, then we have
$t\in[0,1)$, then we have
 \begin{equation*}|f'(tz)|\lesssim\frac{\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}}{(1-|tz|^2)^{\frac{p_1+2-\lambda_1}{p_1}}}\lesssim\frac{\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}}{(1-|z|^2)^{\frac{c(p_1+2-\lambda_1)}{p_1}}(1-t^2)^{\frac{(1-c)(p_1+2-\lambda_1)}{p_1}}}.\end{equation*}
\begin{equation*}|f'(tz)|\lesssim\frac{\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}}{(1-|tz|^2)^{\frac{p_1+2-\lambda_1}{p_1}}}\lesssim\frac{\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}}{(1-|z|^2)^{\frac{c(p_1+2-\lambda_1)}{p_1}}(1-t^2)^{\frac{(1-c)(p_1+2-\lambda_1)}{p_1}}}.\end{equation*}Combining this with Lemma 2.4, we obtain
 \begin{align*}
I_1&\lesssim\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{(1-|z|^2)^{p_2\left( 1-\frac{c(p_1+2-\lambda_1)}{p_1}\right) }}{|1-tz|^{p_2}|1-\overline{a}z|^{4}}\text{d}A(z)\right)^{1/p_2}\\
& \quad \frac{1}{(1-t)^{\frac{(1-c)(p_1+2-\lambda_1)}{p_1}}}d\mu(t)\\
&\lesssim\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{a\in \mathbb{D}}\int_{[0,1)} \frac{(1-|a|^2)^{\frac{2-\lambda_2}{p_2}+ 1-\frac{c(p_1+2-\lambda_1)}{p_1}}}{|1-ta|(1-t)^{\frac{(1-c)(p_1+2-\lambda_1)}{p_1}}}\text{d}\mu(t).
\end{align*}
\begin{align*}
I_1&\lesssim\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{(1-|z|^2)^{p_2\left( 1-\frac{c(p_1+2-\lambda_1)}{p_1}\right) }}{|1-tz|^{p_2}|1-\overline{a}z|^{4}}\text{d}A(z)\right)^{1/p_2}\\
& \quad \frac{1}{(1-t)^{\frac{(1-c)(p_1+2-\lambda_1)}{p_1}}}d\mu(t)\\
&\lesssim\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{a\in \mathbb{D}}\int_{[0,1)} \frac{(1-|a|^2)^{\frac{2-\lambda_2}{p_2}+ 1-\frac{c(p_1+2-\lambda_1)}{p_1}}}{|1-ta|(1-t)^{\frac{(1-c)(p_1+2-\lambda_1)}{p_1}}}\text{d}\mu(t).
\end{align*}That I 1 is finite follows from Lemma 2.2.
Case 2: ![]() $2 \lt p_2$.
$2 \lt p_2$.
When ![]() $p_2+\lambda_2 \gt 4$, fix the constant d such that
$p_2+\lambda_2 \gt 4$, fix the constant d such that
 \begin{equation*}\frac{(2-\lambda_2)p_1}{p_2(p_1+2-\lambda_1)} \lt d \lt \min\left\{\frac{2p_1}{p_2(p_1+2-\lambda_1) },\frac{(p_2-2)p_1}{p_2(p_1+2-\lambda_1)}\right\}.\end{equation*}
\begin{equation*}\frac{(2-\lambda_2)p_1}{p_2(p_1+2-\lambda_1)} \lt d \lt \min\left\{\frac{2p_1}{p_2(p_1+2-\lambda_1) },\frac{(p_2-2)p_1}{p_2(p_1+2-\lambda_1)}\right\}.\end{equation*}From Lemmas 2.2 and 2.4 (1), we get
 \begin{align*}
I_1&\lesssim\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{(1-|z|^2)^{p_2\left( 1-\frac{d(p_1+2-\lambda_1)}{p_1}\right) }}{|1-tz|^{p_2}|1-\overline{a}z|^{4}}\text{d}A(z)\right)^{1/p_2}\\
& \quad \frac{1}{(1-t)^{\frac{(1-d)(p_1+2-\lambda_1)}{p_1}}}d\mu(t)\\
&\lesssim\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{a\in \mathbb{D}}\int_{[0,1)} \frac{(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}}{|1-ta|^{\frac{2}{p_2}+\frac{d(p_1+2-\lambda_1)}{p_1}}(1-t)^{\frac{(1-d)(p_1+2-\lambda_1)}{p_1}}}\text{d}\mu(t)\\
&\lesssim\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}.
\end{align*}
\begin{align*}
I_1&\lesssim\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{(1-|z|^2)^{p_2\left( 1-\frac{d(p_1+2-\lambda_1)}{p_1}\right) }}{|1-tz|^{p_2}|1-\overline{a}z|^{4}}\text{d}A(z)\right)^{1/p_2}\\
& \quad \frac{1}{(1-t)^{\frac{(1-d)(p_1+2-\lambda_1)}{p_1}}}d\mu(t)\\
&\lesssim\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{a\in \mathbb{D}}\int_{[0,1)} \frac{(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}}{|1-ta|^{\frac{2}{p_2}+\frac{d(p_1+2-\lambda_1)}{p_1}}(1-t)^{\frac{(1-d)(p_1+2-\lambda_1)}{p_1}}}\text{d}\mu(t)\\
&\lesssim\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}.
\end{align*} If ![]() $p_2+\lambda_2\leq4$, let the constant d be
$p_2+\lambda_2\leq4$, let the constant d be
 \begin{equation*}\frac{(2-\lambda_2)p_1}{p_2(p_1+2-\lambda_1)} \lt d \lt \frac{2p_1}{p_2(p_1+2-\lambda_1) }.\end{equation*}
\begin{equation*}\frac{(2-\lambda_2)p_1}{p_2(p_1+2-\lambda_1)} \lt d \lt \frac{2p_1}{p_2(p_1+2-\lambda_1) }.\end{equation*}By Lemmas 2.2 and 2.4 (2), we have
 \begin{align*}
I_1 \lesssim\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{a\in \mathbb{D}}\int_{[0,1)} \frac{(1-|a|^2)^{\frac{2-\lambda_2}{p_2}+1-\frac{d(p_1+2-\lambda_1)}{p_1}}}{|1-ta|(1-t)^{\frac{(1-d)(p_1+2-\lambda_1)}{p_1}}}\text{d}\mu(t)\lesssim\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}.
\end{align*}
\begin{align*}
I_1 \lesssim\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{a\in \mathbb{D}}\int_{[0,1)} \frac{(1-|a|^2)^{\frac{2-\lambda_2}{p_2}+1-\frac{d(p_1+2-\lambda_1)}{p_1}}}{|1-ta|(1-t)^{\frac{(1-d)(p_1+2-\lambda_1)}{p_1}}}\text{d}\mu(t)\lesssim\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}.
\end{align*}Hence, we conclude that I 1 is finite.
Now, let us consider I 2. By Lemma 2.6, we have
 \begin{equation*}|f(tz)|\lesssim\frac{\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}}{(1-|tz|^2)^{\frac{2-\lambda_1}{p_1}}}\lesssim\frac{\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}}{(1-t)^{\frac{2-\lambda_1}{p_1}}}\end{equation*}
\begin{equation*}|f(tz)|\lesssim\frac{\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}}{(1-|tz|^2)^{\frac{2-\lambda_1}{p_1}}}\lesssim\frac{\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}}{(1-t)^{\frac{2-\lambda_1}{p_1}}}\end{equation*} for any ![]() $z\in \mathbb{D}$ and
$z\in \mathbb{D}$ and ![]() $t\in[0,1)$. Accordingly, we have
$t\in[0,1)$. Accordingly, we have
 \begin{align*}
I_2& \lesssim \|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)} \left(\int_{\mathbb{D}} \frac{(1-|z|^2)^{p_2}}{|1-tz|^{2p_2}|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \\ & \quad \frac{1}{(1-t)^{\frac{2-\lambda_1}{p_1}}}\text{d}\mu(t).
\end{align*}
\begin{align*}
I_2& \lesssim \|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)} \left(\int_{\mathbb{D}} \frac{(1-|z|^2)^{p_2}}{|1-tz|^{2p_2}|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \\ & \quad \frac{1}{(1-t)^{\frac{2-\lambda_1}{p_1}}}\text{d}\mu(t).
\end{align*}Note that
for any ![]() $t\in[0,1)$ and
$t\in[0,1)$ and ![]() $z\in\mathbb{D}$. It follows that
$z\in\mathbb{D}$. It follows that
 \begin{align*}
I_2&
\lesssim \|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)} \left(\int_{\mathbb{D}} \frac{(1-|z|^2)^{p_2\left(1-\frac{k(p_1+2-\lambda_1)}{p_1} \right) }}{|1-tz|^{p_2}|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \\ & \quad \frac{1}{(1-t)^{\frac{(1-k)(p_1+2-\lambda_1)}{p_1}}}d\mu(t),
\end{align*}
\begin{align*}
I_2&
\lesssim \|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)} \left(\int_{\mathbb{D}} \frac{(1-|z|^2)^{p_2\left(1-\frac{k(p_1+2-\lambda_1)}{p_1} \right) }}{|1-tz|^{p_2}|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \\ & \quad \frac{1}{(1-t)^{\frac{(1-k)(p_1+2-\lambda_1)}{p_1}}}d\mu(t),
\end{align*} where ![]() $k=\{c,d\}$. Processing similar to I 1, we have
$k=\{c,d\}$. Processing similar to I 1, we have
 \begin{align*}
I_2\lesssim\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}.
\end{align*}
\begin{align*}
I_2\lesssim\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}.
\end{align*} Therefore, we deduce that ![]() $\mathcal{C}_{\mu}:X\rightarrow Y$ is bounded.
$\mathcal{C}_{\mu}:X\rightarrow Y$ is bounded.
Conversely, let  $\frac{1}{2} \lt b \lt 1$, fix the test function
$\frac{1}{2} \lt b \lt 1$, fix the test function
 \begin{equation*}f_b(z)=\frac{1-b}{(1-bz)^{\frac{p_1+2-\lambda_1}{p_1}}},~z\in \mathbb{D}.\end{equation*}
\begin{equation*}f_b(z)=\frac{1-b}{(1-bz)^{\frac{p_1+2-\lambda_1}{p_1}}},~z\in \mathbb{D}.\end{equation*} It is easy to check that ![]() $f_b\in A^{p_1,\lambda_1}$ and
$f_b\in A^{p_1,\lambda_1}$ and ![]() $\|f_b\|_{A^{p_1,\lambda_1}}\lesssim1$ (see for instance [Reference Yang and Liu55, Lemma 4.2]). Since
$\|f_b\|_{A^{p_1,\lambda_1}}\lesssim1$ (see for instance [Reference Yang and Liu55, Lemma 4.2]). Since ![]() $\mathcal{C}_{\mu}$ is bounded from X into Y, we arrive
$\mathcal{C}_{\mu}$ is bounded from X into Y, we arrive
 \begin{align*}
1 \gt rsim\|f_b\|_{A^{p_1,\lambda_1}} \gt rsim&\|\mathcal{C}_{\mu}(f_b)\|_{\mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}}\\ \gt rsim&(1-b)^{\frac{p_{2}+2-\lambda_2}{p_2}}|\mathcal{C}_{\mu}(f_b)'(b)|\\
=&(1-b)^{\frac{p_{2}+2-\lambda_2}{p_2}}\left(\int_{[0,1)}\frac{tf'(tb)}{1-tb}\text{d}\mu(t)+\int_{[0,1)}\frac{tf(tb)}{(1-tb)^2}\text{d}\mu(t) \right)\\ \gt rsim& (1-b)^{\frac{p_{2}+2-\lambda_2}{p_2}}\left(\int_{[0,1)}\frac{t(1-b)b}{(1-tb)(1-tb^2)^{\frac{2p_1+2-\lambda_1}{p_1}}}d\mu(t)\right. \\ & \left. \quad +\int_{[0,1)}\frac{t(1-b)}{(1-tb)^2(1-tb^2)^{\frac{p_1+2-\lambda_1}{p_1}}}\text{d}\mu(t) \right) \\ \gt rsim& (1-b)^{\frac{p_{2}+2-\lambda_2}{p_2}}\left(\int_{[b,1)}\frac{t(1-b)b}{(1-tb)(1-tb^2)^{\frac{2p_1+2-\lambda_1}{p_1}}}\text{d}\mu(t)\right. \\ & \left. \quad +\int_{[b,1)}\frac{t(1-b)}{(1-tb)^2(1-tb^2)^{\frac{p_1+2-\lambda_1}{p_1}}}\text{d}\mu(t) \right)\\ \gt rsim& (1-b)^{\frac{p_{2}+2-\lambda_2}{p_2}}\left(\frac{\mu([b,1))(1-b)b^2}{(1-b^2)(1-b^3)^{\frac{2p_1+2-\lambda_1}{p_1}}}\right. \\ & \left. \quad +\frac{\mu([b,1))(1-b)b}{(1-b^2)^2(1-b^3)^{\frac{p_1+2-\lambda_1}{p_1}}} \right),
\end{align*}
\begin{align*}
1 \gt rsim\|f_b\|_{A^{p_1,\lambda_1}} \gt rsim&\|\mathcal{C}_{\mu}(f_b)\|_{\mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}}\\ \gt rsim&(1-b)^{\frac{p_{2}+2-\lambda_2}{p_2}}|\mathcal{C}_{\mu}(f_b)'(b)|\\
=&(1-b)^{\frac{p_{2}+2-\lambda_2}{p_2}}\left(\int_{[0,1)}\frac{tf'(tb)}{1-tb}\text{d}\mu(t)+\int_{[0,1)}\frac{tf(tb)}{(1-tb)^2}\text{d}\mu(t) \right)\\ \gt rsim& (1-b)^{\frac{p_{2}+2-\lambda_2}{p_2}}\left(\int_{[0,1)}\frac{t(1-b)b}{(1-tb)(1-tb^2)^{\frac{2p_1+2-\lambda_1}{p_1}}}d\mu(t)\right. \\ & \left. \quad +\int_{[0,1)}\frac{t(1-b)}{(1-tb)^2(1-tb^2)^{\frac{p_1+2-\lambda_1}{p_1}}}\text{d}\mu(t) \right) \\ \gt rsim& (1-b)^{\frac{p_{2}+2-\lambda_2}{p_2}}\left(\int_{[b,1)}\frac{t(1-b)b}{(1-tb)(1-tb^2)^{\frac{2p_1+2-\lambda_1}{p_1}}}\text{d}\mu(t)\right. \\ & \left. \quad +\int_{[b,1)}\frac{t(1-b)}{(1-tb)^2(1-tb^2)^{\frac{p_1+2-\lambda_1}{p_1}}}\text{d}\mu(t) \right)\\ \gt rsim& (1-b)^{\frac{p_{2}+2-\lambda_2}{p_2}}\left(\frac{\mu([b,1))(1-b)b^2}{(1-b^2)(1-b^3)^{\frac{2p_1+2-\lambda_1}{p_1}}}\right. \\ & \left. \quad +\frac{\mu([b,1))(1-b)b}{(1-b^2)^2(1-b^3)^{\frac{p_1+2-\lambda_1}{p_1}}} \right),
\end{align*}which implies
 \begin{equation*}\mu([b,1))\lesssim(1-b)^{1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}}.\end{equation*}
\begin{equation*}\mu([b,1))\lesssim(1-b)^{1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}}.\end{equation*} Therefore, µ is a  $\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right)$-Carleson measure. This completes the proof.
$\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right)$-Carleson measure. This completes the proof.
It is obvious that Theorem 3.1 leads to the following results:
Corollary 3.2. Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $0 \lt p_1 \lt \infty$,
$0 \lt p_1 \lt \infty$, ![]() $1\leq p_2 \lt \infty$ and
$1\leq p_2 \lt \infty$ and ![]() $0 \lt \lambda_1,\lambda_2 \lt 2$ such that
$0 \lt \lambda_1,\lambda_2 \lt 2$ such that  $1+\frac{2-\lambda_1}{p_1} \gt \frac{2-\lambda_2}{p_2}$. Then, the operator
$1+\frac{2-\lambda_1}{p_1} \gt \frac{2-\lambda_2}{p_2}$. Then, the operator ![]() $\mathcal{C}_{\mu}:A^{p_1,\lambda_1}\rightarrow A^{p_2,\lambda_2}$ is bounded if and only if the measure µ is a
$\mathcal{C}_{\mu}:A^{p_1,\lambda_1}\rightarrow A^{p_2,\lambda_2}$ is bounded if and only if the measure µ is a  $\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure.
$\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure.
Corollary 3.3. Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $\alpha_1,\alpha_2\in(1,\infty)$ such that
$\alpha_1,\alpha_2\in(1,\infty)$ such that ![]() $1+\alpha_1 \gt \alpha_2$. Then, the operator
$1+\alpha_1 \gt \alpha_2$. Then, the operator ![]() $\mathcal{C}_{\mu}:\mathcal{B}^{\alpha_1}\rightarrow \mathcal{B}^{\alpha_2}$ is bounded if and only if the measure µ is a
$\mathcal{C}_{\mu}:\mathcal{B}^{\alpha_1}\rightarrow \mathcal{B}^{\alpha_2}$ is bounded if and only if the measure µ is a ![]() $\left( 1+\alpha_1-\alpha_2\right) $-Carleson measure.
$\left( 1+\alpha_1-\alpha_2\right) $-Carleson measure.
Next, we consider the compactness of Cesàro-type operators between different Bergman–Morrey spaces.
Theorem 3.4 Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $0 \lt p_1 \lt \infty$,
$0 \lt p_1 \lt \infty$, ![]() $1\leq p_2 \lt \infty$ and
$1\leq p_2 \lt \infty$ and ![]() $0 \lt \lambda_1,\lambda_2 \lt 2$ such that
$0 \lt \lambda_1,\lambda_2 \lt 2$ such that  $1+\frac{2-\lambda_1}{p_1} \gt \frac{2-\lambda_2}{p_2}$. Suppose that X and Y are two Banach spaces contained in
$1+\frac{2-\lambda_1}{p_1} \gt \frac{2-\lambda_2}{p_2}$. Suppose that X and Y are two Banach spaces contained in ![]() $H(\mathbb{D})$ such that
$H(\mathbb{D})$ such that  $A^{p_1,\lambda_1}\subset X\subset \mathcal{B}^{\frac{p_{1}+2-\lambda_1}{p_1}}$ and
$A^{p_1,\lambda_1}\subset X\subset \mathcal{B}^{\frac{p_{1}+2-\lambda_1}{p_1}}$ and  $A^{p_2,\lambda_2}\subset Y\subset \mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}$. Then, the following two statements are equivalent:
$A^{p_2,\lambda_2}\subset Y\subset \mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}$. Then, the following two statements are equivalent:
(1) the operator
 $\mathcal{C}_{\mu}:X\rightarrow Y$ is compact;
$\mathcal{C}_{\mu}:X\rightarrow Y$ is compact;(2) the measure µ is a vanishing
 $\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure.
$\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure.
Proof. If µ is a vanishing  $\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right)$-Carleson measure. By choosing the sequence
$\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right)$-Carleson measure. By choosing the sequence ![]() $\{f_i\}_{i=1}^{\infty}\subset X$,
$\{f_i\}_{i=1}^{\infty}\subset X$, ![]() $\|f_i\|_{X}\leq1$ for all i.
$\|f_i\|_{X}\leq1$ for all i. ![]() $f_i\rightarrow0$ uniformly on compact subsets of
$f_i\rightarrow0$ uniformly on compact subsets of ![]() $\mathbb{D}$ as
$\mathbb{D}$ as ![]() $i\rightarrow\infty$. Next, we need to prove that
$i\rightarrow\infty$. Next, we need to prove that ![]() $\|\mathcal{C}_{\mu}(f_i)\|_{A^{p_2,\lambda_2}}\rightarrow0$ as
$\|\mathcal{C}_{\mu}(f_i)\|_{A^{p_2,\lambda_2}}\rightarrow0$ as ![]() $i\rightarrow\infty$.
$i\rightarrow\infty$.
Since µ is a vanishing  $\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right)$-Carleson measure, in other words, for any ɛ > 0, there exist
$\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right)$-Carleson measure, in other words, for any ɛ > 0, there exist ![]() $t_0\in(0,1)$ such that for every
$t_0\in(0,1)$ such that for every ![]() $t_0\leq t \lt 1$,
$t_0\leq t \lt 1$,
 \begin{equation}
\mu([t,1)) \lt \varepsilon(1-t)^{1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}}.
\end{equation}
\begin{equation}
\mu([t,1)) \lt \varepsilon(1-t)^{1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}}.
\end{equation}Note that
 \begin{align*}
\|\mathcal{C}_{\mu}(f_i)\|_{A^{p_2,\lambda_2}}\lesssim& |\mathcal{C}_{\mu}(f_i)(0)|+\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\\
& \int_{[0,1)}\left(\int_{\mathbb{D}}\frac{|tf'_{i}(tz)|^{p_2}}{|1-tz|^{p_2}}\frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \text{d}\mu(t)\\
&+\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)} \left(\int_{\mathbb{D}} \frac{|tf_i(tz)|^{p_2}}{|1-tz|^{2p_2}} \frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2}\text{d}\mu(t).
\end{align*}
\begin{align*}
\|\mathcal{C}_{\mu}(f_i)\|_{A^{p_2,\lambda_2}}\lesssim& |\mathcal{C}_{\mu}(f_i)(0)|+\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\\
& \int_{[0,1)}\left(\int_{\mathbb{D}}\frac{|tf'_{i}(tz)|^{p_2}}{|1-tz|^{p_2}}\frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \text{d}\mu(t)\\
&+\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)} \left(\int_{\mathbb{D}} \frac{|tf_i(tz)|^{p_2}}{|1-tz|^{2p_2}} \frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2}\text{d}\mu(t).
\end{align*}Writing
 \begin{align*}
\sup_{a\in \mathbb{D}}&(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{|tf'_i(tz)|^{p_2}}{|1-tz|^{p_2}}\frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \text{d}\mu(t)\\
=& \sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,t_0)}\left(\int_{\mathbb{D}}\frac{|tf'_i(tz)|^{p_2}}{|1-tz|^{p_2}}\frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \text{d}\mu(t)\\
&+\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[t_0,1)}\left(\int_{\mathbb{D}}\frac{|tf'_i(tz)|^{p_2}}{|1-tz|^{p_2}}\frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \text{d}\mu(t)\\
=:&A_1^{i}+A_2.
\end{align*}
\begin{align*}
\sup_{a\in \mathbb{D}}&(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{|tf'_i(tz)|^{p_2}}{|1-tz|^{p_2}}\frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \text{d}\mu(t)\\
=& \sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,t_0)}\left(\int_{\mathbb{D}}\frac{|tf'_i(tz)|^{p_2}}{|1-tz|^{p_2}}\frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \text{d}\mu(t)\\
&+\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[t_0,1)}\left(\int_{\mathbb{D}}\frac{|tf'_i(tz)|^{p_2}}{|1-tz|^{p_2}}\frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \text{d}\mu(t)\\
=:&A_1^{i}+A_2.
\end{align*} For ![]() $A_1^{i}$,
$A_1^{i}$, ![]() $f_i\rightarrow0$ implies
$f_i\rightarrow0$ implies ![]() $f_i(0)\rightarrow0$ and
$f_i(0)\rightarrow0$ and ![]() $f'_i\rightarrow0$ uniformly on compact subsets of
$f'_i\rightarrow0$ uniformly on compact subsets of ![]() $\mathbb{D}$ as
$\mathbb{D}$ as ![]() $i\rightarrow\infty$. So we have
$i\rightarrow\infty$. So we have
Since µ is finite, we have
 \begin{align*}\lim_{i\rightarrow\infty}A_1^{i}& \lesssim\lim_{i\rightarrow\infty} \sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,t_0)}\left(\int_{\mathbb{D}}\frac{(1-|z|^2)^{p_2}}{|1-tz|^{p_2}|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \\& \quad \text{d}\mu(t)\cdot\sup_{|x|\leq t_0}|f'_i(x)|=0.\end{align*}
\begin{align*}\lim_{i\rightarrow\infty}A_1^{i}& \lesssim\lim_{i\rightarrow\infty} \sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,t_0)}\left(\int_{\mathbb{D}}\frac{(1-|z|^2)^{p_2}}{|1-tz|^{p_2}|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \\& \quad \text{d}\mu(t)\cdot\sup_{|x|\leq t_0}|f'_i(x)|=0.\end{align*}For A 2, we discuss it in two cases.
Case 1: ![]() $1\leq p_2 \lt 4$.
$1\leq p_2 \lt 4$.
Taking the constant c is satisfying
 \begin{equation*}\max\left\lbrace 1-\frac{2}{p_2},\frac{2-\lambda_2}{p_2}\right\rbrace \lt c \lt \min\left\lbrace \frac{2}{p_2},1+\frac{2-\lambda_1}{p_1},1+\frac{2-\lambda_2}{p_2}\right\rbrace .\end{equation*}
\begin{equation*}\max\left\lbrace 1-\frac{2}{p_2},\frac{2-\lambda_2}{p_2}\right\rbrace \lt c \lt \min\left\lbrace \frac{2}{p_2},1+\frac{2-\lambda_1}{p_1},1+\frac{2-\lambda_2}{p_2}\right\rbrace .\end{equation*} Then, for any ![]() $z\in\mathbb{D}$ and all
$z\in\mathbb{D}$ and all ![]() $t\in(0,1)$,
$t\in(0,1)$,
 \begin{equation*}(1-|tz|)^{\frac{p_1+2-\lambda_1}{p_1}} \gt rsim(1-|z|)^{c}(1-t)^{\frac{p_1+2-\lambda_1}{p_1}-c}.\end{equation*}
\begin{equation*}(1-|tz|)^{\frac{p_1+2-\lambda_1}{p_1}} \gt rsim(1-|z|)^{c}(1-t)^{\frac{p_1+2-\lambda_1}{p_1}-c}.\end{equation*}By Lemmas 2.4 and 2.6, we arrive at
 \begin{align*}
A_2\lesssim&\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[t_0,1)}\left(\int_{\mathbb{D}}\frac{(1-|z|^2)^{p_2-p_2c}}{|1-tz|^{p_2}|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \frac{1}{(1-t)^{\frac{p_1+2-\lambda_1}{p_1}-c}}\text{d}\mu(t)\\
\lesssim&\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[t_0,1)}\frac{1}{(1-t|a|)(1-|a|)^{\frac{2}{p_2}+c-1}}\cdot\frac{1}{(1-t)^{\frac{p_1+2-\lambda_1}{p_1}-c}} \text{d}\mu(t)\\
\lesssim&\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{2-\lambda_2}{p_2}+1-c}\int_{[t_0,1)}\frac{1}{(1-t|a|)(1-t)^{\frac{p_1+2-\lambda_1}{p_1}-c}} \text{d}\mu(t).
\end{align*}
\begin{align*}
A_2\lesssim&\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[t_0,1)}\left(\int_{\mathbb{D}}\frac{(1-|z|^2)^{p_2-p_2c}}{|1-tz|^{p_2}|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \frac{1}{(1-t)^{\frac{p_1+2-\lambda_1}{p_1}-c}}\text{d}\mu(t)\\
\lesssim&\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[t_0,1)}\frac{1}{(1-t|a|)(1-|a|)^{\frac{2}{p_2}+c-1}}\cdot\frac{1}{(1-t)^{\frac{p_1+2-\lambda_1}{p_1}-c}} \text{d}\mu(t)\\
\lesssim&\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{2-\lambda_2}{p_2}+1-c}\int_{[t_0,1)}\frac{1}{(1-t|a|)(1-t)^{\frac{p_1+2-\lambda_1}{p_1}-c}} \text{d}\mu(t).
\end{align*}Integrating by part and using (3.1), we obtain
 \begin{align*}
A_2\lesssim&\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{2-\lambda_2}{p_2}+1-c}\frac{\mu([t_0,1))}{(1-t_0|a|)(1-t_0)^{\frac{p_1+2-\lambda_1}{p_1}-c}}\\
& +\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{2-\lambda_2}{p_2}+1-c} \int_{t_0}^{1}\frac{|a|\mu([t,1))}{(1-t|a|)^2(1-t)^{\frac{p_1+2-\lambda_1}{p_1}-c}} \text{d}t\\
&+\left(\frac{2-\lambda_1}{p_2}+1-c \right)\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{2-\lambda_2}{p_2}+1-c} \int_{t_0}^1\frac{\mu([t,1))}{(1-t|a|)(1-t)^{\frac{2-\lambda_1}{p_1}+2-c}} \text{d}t\\
\lesssim&\varepsilon+\varepsilon
\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{2-\lambda_2}{p_2}+1-c} \left( \int_{0}^{1}\frac{(1-t)^{c-\frac{2-\lambda_2}{p_2}}}{(1-t|a|)^2}\text{d}t
+\int_{0}^{1}\frac{(1-t)^{c-1-\frac{2-\lambda_2}{p_2}}}{(1-t|a|)}\text{d}t\right)\\
\lesssim&\varepsilon.
\end{align*}
\begin{align*}
A_2\lesssim&\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{2-\lambda_2}{p_2}+1-c}\frac{\mu([t_0,1))}{(1-t_0|a|)(1-t_0)^{\frac{p_1+2-\lambda_1}{p_1}-c}}\\
& +\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{2-\lambda_2}{p_2}+1-c} \int_{t_0}^{1}\frac{|a|\mu([t,1))}{(1-t|a|)^2(1-t)^{\frac{p_1+2-\lambda_1}{p_1}-c}} \text{d}t\\
&+\left(\frac{2-\lambda_1}{p_2}+1-c \right)\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{2-\lambda_2}{p_2}+1-c} \int_{t_0}^1\frac{\mu([t,1))}{(1-t|a|)(1-t)^{\frac{2-\lambda_1}{p_1}+2-c}} \text{d}t\\
\lesssim&\varepsilon+\varepsilon
\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{2-\lambda_2}{p_2}+1-c} \left( \int_{0}^{1}\frac{(1-t)^{c-\frac{2-\lambda_2}{p_2}}}{(1-t|a|)^2}\text{d}t
+\int_{0}^{1}\frac{(1-t)^{c-1-\frac{2-\lambda_2}{p_2}}}{(1-t|a|)}\text{d}t\right)\\
\lesssim&\varepsilon.
\end{align*} Case 2: ![]() $p_2\geq4$.
$p_2\geq4$.
Let d be a constant such that  $\frac{2-\lambda_2}{p_2} \lt d \lt \frac{2}{p_2}$. Lemma 2.6 now leads to
$\frac{2-\lambda_2}{p_2} \lt d \lt \frac{2}{p_2}$. Lemma 2.6 now leads to
 \begin{align*}
A_2\lesssim&\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[t_0,1)}\left(\int_{\mathbb{D}}\frac{(1-|z|^2)^{p_2-p_2d}}{|1-tz|^{p_2}|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \frac{1}{(1-t)^{\frac{p_1+2-\lambda_1}{p_1}-d}}\text{d}\mu(t)\\
\lesssim&\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[t_0,1)}\frac{1}{(1-t|a|)^{\frac{2}{p_2}+d}(1-t)^{\frac{p_1+2-\lambda_1}{p_1}-d}} \text{d}\mu(t).
\end{align*}
\begin{align*}
A_2\lesssim&\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[t_0,1)}\left(\int_{\mathbb{D}}\frac{(1-|z|^2)^{p_2-p_2d}}{|1-tz|^{p_2}|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \frac{1}{(1-t)^{\frac{p_1+2-\lambda_1}{p_1}-d}}\text{d}\mu(t)\\
\lesssim&\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[t_0,1)}\frac{1}{(1-t|a|)^{\frac{2}{p_2}+d}(1-t)^{\frac{p_1+2-\lambda_1}{p_1}-d}} \text{d}\mu(t).
\end{align*}Here, we used Lemma 2.4 to obtain the last inequality. Integrating by part and (3.1) yields
 \begin{align*}
A_2\lesssim&\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\frac{\mu([t_0,1))}{(1-t_0|a|)^{\frac{2}{p_2}+d}(1-t_0)^{\frac{p_1+2-\lambda_1}{p_1}-d}}\\
&+\left(\frac{2}{p_2}+d \right)\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}} \int_{t_0}^{1}\frac{|a|\mu([t,1))}{(1-t|a|)^{\frac{2}{p_2}+d+1}(1-t)^{\frac{p_1+2-\lambda_1}{p_1}-d}} \text{d}t\\
&+\left(\frac{2-\lambda_1}{p_1}+1-d \right)\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}} \int_{[t_0,1)}\frac{\mu([t,1))}{(1-t|a|)^{\frac{2}{p_2}+d}(1-t)^{\frac{2-\lambda_1}{p_1}+2-d}} \text{d}t\\
& \lesssim\varepsilon+\varepsilon
\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}} \left( \int_{0}^{1}\frac{(1-t)^{d-\frac{2-\lambda_2}{p_2}}}{(1-t|a|)^{\frac{2}{p_2}+d+1}}\text{d}t
+\int_{0}^{1}\frac{(1-t)^{d-1-\frac{2-\lambda_2}{p_2}}}{(1-t|a|)^{\frac{2}{p_2}+d}}\text{d}t\right)\\
&\lesssim \varepsilon.
\end{align*}
\begin{align*}
A_2\lesssim&\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\frac{\mu([t_0,1))}{(1-t_0|a|)^{\frac{2}{p_2}+d}(1-t_0)^{\frac{p_1+2-\lambda_1}{p_1}-d}}\\
&+\left(\frac{2}{p_2}+d \right)\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}} \int_{t_0}^{1}\frac{|a|\mu([t,1))}{(1-t|a|)^{\frac{2}{p_2}+d+1}(1-t)^{\frac{p_1+2-\lambda_1}{p_1}-d}} \text{d}t\\
&+\left(\frac{2-\lambda_1}{p_1}+1-d \right)\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}} \int_{[t_0,1)}\frac{\mu([t,1))}{(1-t|a|)^{\frac{2}{p_2}+d}(1-t)^{\frac{2-\lambda_1}{p_1}+2-d}} \text{d}t\\
& \lesssim\varepsilon+\varepsilon
\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}} \left( \int_{0}^{1}\frac{(1-t)^{d-\frac{2-\lambda_2}{p_2}}}{(1-t|a|)^{\frac{2}{p_2}+d+1}}\text{d}t
+\int_{0}^{1}\frac{(1-t)^{d-1-\frac{2-\lambda_2}{p_2}}}{(1-t|a|)^{\frac{2}{p_2}+d}}\text{d}t\right)\\
&\lesssim \varepsilon.
\end{align*}According to ɛ is arbitrary, we arrive at
 \begin{equation*}\lim_{i\rightarrow\infty}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{|tf'_i(tz)|^{p_2}}{|1-tz|^{p_2}}\frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \text{d}\mu(t)=0.\end{equation*}
\begin{equation*}\lim_{i\rightarrow\infty}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{|tf'_i(tz)|^{p_2}}{|1-tz|^{p_2}}\frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \text{d}\mu(t)=0.\end{equation*}A similar analysis leads to
 \begin{equation*}\lim_{i\rightarrow\infty}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)} \left(\int_{\mathbb{D}} \frac{|tf_i(tz)|^{p_2}}{|1-tz|^{2p_2}} \frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2}\text{d}\mu(t)=0.\end{equation*}
\begin{equation*}\lim_{i\rightarrow\infty}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)} \left(\int_{\mathbb{D}} \frac{|tf_i(tz)|^{p_2}}{|1-tz|^{2p_2}} \frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2}\text{d}\mu(t)=0.\end{equation*} Therefore, we conclude that ![]() $\mathcal{C}_{\mu}$ is compact from X into Y.
$\mathcal{C}_{\mu}$ is compact from X into Y.
Conversely, for  $\frac{1}{2} \lt b \lt 1$, let us first consider the function
$\frac{1}{2} \lt b \lt 1$, let us first consider the function
 \begin{equation*}f_b(z)=\frac{1-b}{(1-bz)^{\frac{p_1+2-\lambda_1}{p_1}}},\end{equation*}
\begin{equation*}f_b(z)=\frac{1-b}{(1-bz)^{\frac{p_1+2-\lambda_1}{p_1}}},\end{equation*} where ![]() $z\in \mathbb{D}$. By Theorem 3.1, we know that
$z\in \mathbb{D}$. By Theorem 3.1, we know that ![]() $\|f_b\|_{A^{p_1,\lambda_1}}\lesssim1$ for any b and, also,
$\|f_b\|_{A^{p_1,\lambda_1}}\lesssim1$ for any b and, also, ![]() $f_b\rightarrow0$ uniformly on compact subsets of
$f_b\rightarrow0$ uniformly on compact subsets of ![]() $\mathbb{D}$ as
$\mathbb{D}$ as ![]() $b\rightarrow1$. The compactness of
$b\rightarrow1$. The compactness of ![]() $\mathcal{C}_{\mu}$ implies that
$\mathcal{C}_{\mu}$ implies that
Since Y is continuously embedded in  $\mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}$, then
$\mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}$, then
 \begin{equation*}\|\mathcal{C}_{\mu}(f_b)\|_{\mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}}\rightarrow0,~\text{as}~ b\rightarrow1.\end{equation*}
\begin{equation*}\|\mathcal{C}_{\mu}(f_b)\|_{\mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}}\rightarrow0,~\text{as}~ b\rightarrow1.\end{equation*}In the proof of Theorem 3.1, we see
 \begin{equation*}\lim_{b\rightarrow1^-}\frac{\mu([b,1))}{(1-b)^{\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right)} }\lesssim\lim_{b\rightarrow1^-}\|\mathcal{C}_{\mu}(f_b)\|_{\mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}}=0.\end{equation*}
\begin{equation*}\lim_{b\rightarrow1^-}\frac{\mu([b,1))}{(1-b)^{\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right)} }\lesssim\lim_{b\rightarrow1^-}\|\mathcal{C}_{\mu}(f_b)\|_{\mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}}=0.\end{equation*} This proves that µ is a vanishing  $\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure. The proof is completed.
$\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure. The proof is completed.
Corollary 3.5. Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $0 \lt p_1 \lt \infty$,
$0 \lt p_1 \lt \infty$, ![]() $1\leq p_2 \lt \infty$ and
$1\leq p_2 \lt \infty$ and ![]() $0 \lt \lambda_1,\lambda_2 \lt 2$ such that
$0 \lt \lambda_1,\lambda_2 \lt 2$ such that  $1+\frac{2-\lambda_1}{p_1} \gt \frac{2-\lambda_2}{p_2}$. Then, the operator
$1+\frac{2-\lambda_1}{p_1} \gt \frac{2-\lambda_2}{p_2}$. Then, the operator ![]() $\mathcal{C}_{\mu}:A^{p_1,\lambda_1}\rightarrow A^{p_2,\lambda_2}$ is compact if and only if the measure µ is a vanishing
$\mathcal{C}_{\mu}:A^{p_1,\lambda_1}\rightarrow A^{p_2,\lambda_2}$ is compact if and only if the measure µ is a vanishing  $\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure.
$\left( 1+\frac{2-\lambda_1}{p_1}-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure.
Corollary 3.6. Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $\alpha_1,\alpha_2\in(1,\infty)$ such that
$\alpha_1,\alpha_2\in(1,\infty)$ such that ![]() $1+\alpha_1 \gt \alpha_2$. Then, the operator
$1+\alpha_1 \gt \alpha_2$. Then, the operator ![]() $\mathcal{C}_{\mu}:\mathcal{B}^{\alpha_1}\rightarrow \mathcal{B}^{\alpha_2}$ is compact if and only if the measure µ is a vanishing
$\mathcal{C}_{\mu}:\mathcal{B}^{\alpha_1}\rightarrow \mathcal{B}^{\alpha_2}$ is compact if and only if the measure µ is a vanishing ![]() $\left( 1+\alpha_1-\alpha_2\right) $-Carleson measure.
$\left( 1+\alpha_1-\alpha_2\right) $-Carleson measure.
Inspired by [Reference Galanopoulos, Girela, Mas and Merchán16, Theorem 7], we investigate the boundedness of ![]() $\mathcal{C}_{\mu}$ from the Bergman–Morrey spaces into the mean Lipschitz spaces in the following theorem.
$\mathcal{C}_{\mu}$ from the Bergman–Morrey spaces into the mean Lipschitz spaces in the following theorem.
Theorem 3.7 Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $0 \lt p_1 \lt \infty$,
$0 \lt p_1 \lt \infty$, ![]() $1 \lt p_2 \lt \infty$ and
$1 \lt p_2 \lt \infty$ and ![]() $0 \lt \lambda_1 \lt 2$. Suppose that X and Y are two Banach spaces contained in
$0 \lt \lambda_1 \lt 2$. Suppose that X and Y are two Banach spaces contained in ![]() $H(\mathbb{D})$ such that
$H(\mathbb{D})$ such that  $A^{p_1,\lambda_1}\subset X\subset \mathcal{B}^{\frac{p_{1}+2-\lambda_1}{p_1}}$ and
$A^{p_1,\lambda_1}\subset X\subset \mathcal{B}^{\frac{p_{1}+2-\lambda_1}{p_1}}$ and  $\Lambda^{p_2}_{\frac{1}{p_2}}\subset Y\subset \mathcal{B}$. Then, the following two statements are equivalent:
$\Lambda^{p_2}_{\frac{1}{p_2}}\subset Y\subset \mathcal{B}$. Then, the following two statements are equivalent:
(1) the operator
 $\mathcal{C}_{\mu}:X\rightarrow Y$ is bounded;
$\mathcal{C}_{\mu}:X\rightarrow Y$ is bounded;(2) the measure µ is a
 $\frac{p_1+2-\lambda_1}{p_1}$-Carleson measure.
$\frac{p_1+2-\lambda_1}{p_1}$-Carleson measure.
Proof. Assume that the measure µ is a  $\frac{p_1+2-\lambda_1}{p_1}$-Carleson measure, then for any
$\frac{p_1+2-\lambda_1}{p_1}$-Carleson measure, then for any ![]() $f\in X$, we want to show that
$f\in X$, we want to show that  $\mathcal{C}_{\mu}(f)\subset\Lambda^{p_2}_{\frac{1}{p_2}}$. Applying Minkowski inequality yields
$\mathcal{C}_{\mu}(f)\subset\Lambda^{p_2}_{\frac{1}{p_2}}$. Applying Minkowski inequality yields
 \begin{align*}
\sup_{0 \lt r \lt 1}(1-r)^{1-\frac{1}{p_2}}&\left(\frac{1}{2\pi} \int^{2\pi}_{0}|\mathcal{C}_{\mu}(f)'(re^{i\theta})|^{p_2}\text{d}\theta\right)^{\frac{1}{p_2}} \\
\lesssim&\sup_{0 \lt r \lt 1}(1-r)^{1-\frac{1}{p_2}}\int_{[0,1)}\left(\frac{1}{2\pi} \int_{0}^{2\pi}\frac{|tf'(tre^{i\theta})|^{p_2}}{|1-tre^{i\theta}|^{p_2}}\text{d}\theta\right)^{1/p_2}\text{d}\mu(t)\\
&+
\sup_{0 \lt r \lt 1}(1-r)^{1-\frac{1}{p_2}}\int_{[0,1)}\left(\frac{1}{2\pi} \int_{0}^{2\pi}\frac{|tf(tre^{i\theta})|^{p_2}}{|1-tre^{i\theta}|^{2p_2}} \text{d}\theta\right)^{1/p_{2}}\text{d}\mu(t)\\
=&:A_1+A_2.
\end{align*}
\begin{align*}
\sup_{0 \lt r \lt 1}(1-r)^{1-\frac{1}{p_2}}&\left(\frac{1}{2\pi} \int^{2\pi}_{0}|\mathcal{C}_{\mu}(f)'(re^{i\theta})|^{p_2}\text{d}\theta\right)^{\frac{1}{p_2}} \\
\lesssim&\sup_{0 \lt r \lt 1}(1-r)^{1-\frac{1}{p_2}}\int_{[0,1)}\left(\frac{1}{2\pi} \int_{0}^{2\pi}\frac{|tf'(tre^{i\theta})|^{p_2}}{|1-tre^{i\theta}|^{p_2}}\text{d}\theta\right)^{1/p_2}\text{d}\mu(t)\\
&+
\sup_{0 \lt r \lt 1}(1-r)^{1-\frac{1}{p_2}}\int_{[0,1)}\left(\frac{1}{2\pi} \int_{0}^{2\pi}\frac{|tf(tre^{i\theta})|^{p_2}}{|1-tre^{i\theta}|^{2p_2}} \text{d}\theta\right)^{1/p_{2}}\text{d}\mu(t)\\
=&:A_1+A_2.
\end{align*} Since  $f\in \mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}$, it holds that
$f\in \mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}$, it holds that
 \begin{align*}
A_1\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{0 \lt r \lt 1}(1-r)^{1-\frac{1}{p_2}}\int_{[0,1)}\left(\frac{1}{2\pi} \int_{0}^{2\pi}\frac{1}{|1-tre^{i\theta}|^{p_2}}\text{d}\theta\right)^{1/p_2}\\ & \frac{1}{(1-tr)^{\frac{p_1+2-\lambda_1}{p_1}}}\text{d}\mu(t)\\
\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{0 \lt r \lt 1}\int_{[0,1)} \frac{(1-r)^{1-\frac{1}{p_2}}}{(1-tr)^{1-\frac{1}{p_2}+\frac{p_1+2-\lambda_1}{p_1}}}\text{d}\mu(t)\,,
\end{align*}
\begin{align*}
A_1\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{0 \lt r \lt 1}(1-r)^{1-\frac{1}{p_2}}\int_{[0,1)}\left(\frac{1}{2\pi} \int_{0}^{2\pi}\frac{1}{|1-tre^{i\theta}|^{p_2}}\text{d}\theta\right)^{1/p_2}\\ & \frac{1}{(1-tr)^{\frac{p_1+2-\lambda_1}{p_1}}}\text{d}\mu(t)\\
\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{0 \lt r \lt 1}\int_{[0,1)} \frac{(1-r)^{1-\frac{1}{p_2}}}{(1-tr)^{1-\frac{1}{p_2}+\frac{p_1+2-\lambda_1}{p_1}}}\text{d}\mu(t)\,,
\end{align*}where we use Lemma 2.5 to obtain the last inequality. It follows from Lemma 2.2 that
 \begin{equation*}A_1\lesssim\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}.\end{equation*}
\begin{equation*}A_1\lesssim\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}.\end{equation*}For A 2, by applying Lemma 2.5 and then Lemma 2.2 again, we arrive at
 \begin{align*}
A_2\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{0 \lt r \lt 1}(1-r)^{1-\frac{1}{p_2}}\int_{[0,1)}\left(\frac{1}{2\pi} \int_{0}^{2\pi}\frac{1}{|1-tre^{i\theta}|^{2p_2}} \text{d}\theta\right)^{1/p_{2}}\\ & \frac{1}{(1-tr)^{\frac{2-\lambda_1}{p_1}}}\text{d}\mu(t)\\
\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{0 \lt r \lt 1}\int_{[0,1)} \frac{(1-r)^{1-\frac{1}{p_2}}}{(1-tr)^{1-\frac{1}{p_2}+\frac{p_1+2-\lambda_1}{p_1}}}\text{d}\mu(t)\\
\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}.
\end{align*}
\begin{align*}
A_2\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{0 \lt r \lt 1}(1-r)^{1-\frac{1}{p_2}}\int_{[0,1)}\left(\frac{1}{2\pi} \int_{0}^{2\pi}\frac{1}{|1-tre^{i\theta}|^{2p_2}} \text{d}\theta\right)^{1/p_{2}}\\ & \frac{1}{(1-tr)^{\frac{2-\lambda_1}{p_1}}}\text{d}\mu(t)\\
\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{0 \lt r \lt 1}\int_{[0,1)} \frac{(1-r)^{1-\frac{1}{p_2}}}{(1-tr)^{1-\frac{1}{p_2}+\frac{p_1+2-\lambda_1}{p_1}}}\text{d}\mu(t)\\
\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}.
\end{align*} Therefore, the boundedness of ![]() $\mathcal{C}_{\mu}$ from X into Y is proved.
$\mathcal{C}_{\mu}$ from X into Y is proved.
Conversely, since ![]() $\mathcal{C}_{\mu}$ is bounded from X into Y, similar to the process of proving Theorem 3.1, we have
$\mathcal{C}_{\mu}$ is bounded from X into Y, similar to the process of proving Theorem 3.1, we have
 \begin{align*}
1 \gt rsim\|f_b\|_{A^{p_1,\lambda_1}} \gt rsim&\|\mathcal{C}_{\mu}(f_b)\|_{\mathcal{B}}\\ \gt rsim&(1-b)|\mathcal{C}_{\mu}(f_b)'(b)|\\ \gt rsim& (1-b)\left(\frac{\mu([b,1))(1-b)b^2}{(1-b^2)(1-b^3)^{\frac{2p_1+2-\lambda_1}{p_1}}}+\frac{\mu([b,1))(1-b)b}{(1-b^2)^2(1-b^3)^{\frac{p_1+2-\lambda_1}{p_1}}} \right).
\end{align*}
\begin{align*}
1 \gt rsim\|f_b\|_{A^{p_1,\lambda_1}} \gt rsim&\|\mathcal{C}_{\mu}(f_b)\|_{\mathcal{B}}\\ \gt rsim&(1-b)|\mathcal{C}_{\mu}(f_b)'(b)|\\ \gt rsim& (1-b)\left(\frac{\mu([b,1))(1-b)b^2}{(1-b^2)(1-b^3)^{\frac{2p_1+2-\lambda_1}{p_1}}}+\frac{\mu([b,1))(1-b)b}{(1-b^2)^2(1-b^3)^{\frac{p_1+2-\lambda_1}{p_1}}} \right).
\end{align*}This gives
 \begin{equation*}\mu([b,1))\lesssim(1-b)^{\frac{p_1+2-\lambda_1}{p_1}}.\end{equation*}
\begin{equation*}\mu([b,1))\lesssim(1-b)^{\frac{p_1+2-\lambda_1}{p_1}}.\end{equation*} It follows that µ is a  $ \frac{p_1+2-\lambda_1}{p_1}$-Carleson measure. This completes the proof.
$ \frac{p_1+2-\lambda_1}{p_1}$-Carleson measure. This completes the proof.
Corollary 3.8. Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $0 \lt p_1 \lt \infty$,
$0 \lt p_1 \lt \infty$, ![]() $1 \lt p_2 \lt \infty$ and
$1 \lt p_2 \lt \infty$ and ![]() $0 \lt \lambda_1 \lt 2$. Then, the operator
$0 \lt \lambda_1 \lt 2$. Then, the operator  $\mathcal{C}_{\mu}:A^{p_1,\lambda_1}\rightarrow \Lambda^{p_2}_{\frac{1}{p_2}}$ is bounded if and only if the measure µ is a
$\mathcal{C}_{\mu}:A^{p_1,\lambda_1}\rightarrow \Lambda^{p_2}_{\frac{1}{p_2}}$ is bounded if and only if the measure µ is a  $\frac{p_1+2-\lambda_1}{p_1}$-Carleson measure.
$\frac{p_1+2-\lambda_1}{p_1}$-Carleson measure.
Corollary 3.9. Let µ be a positive finite Borel measure on ![]() $[0,1)$ and α > 1. Then, the operator
$[0,1)$ and α > 1. Then, the operator ![]() $\mathcal{C}_{\mu}:\mathcal{B}^{\alpha}\rightarrow \mathcal{B}$ is bounded if and only if the measure µ is an α-Carleson measure.
$\mathcal{C}_{\mu}:\mathcal{B}^{\alpha}\rightarrow \mathcal{B}$ is bounded if and only if the measure µ is an α-Carleson measure.
It is also worth considering the compactness of Cesàro-type operators from the Bergman–Morrey spaces into the mean Lipschitz spaces.
Theorem 3.10 Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $0 \lt p_1 \lt \infty$,
$0 \lt p_1 \lt \infty$, ![]() $1 \lt p_2 \lt \infty$ and
$1 \lt p_2 \lt \infty$ and ![]() $0 \lt \lambda_1 \lt 2$. Suppose that X and Y are two Banach spaces contained in
$0 \lt \lambda_1 \lt 2$. Suppose that X and Y are two Banach spaces contained in ![]() $H(\mathbb{D})$ such that
$H(\mathbb{D})$ such that  $A^{p_1,\lambda_1}\subset X\subset \mathcal{B}^{\frac{p_{1}+2-\lambda_1}{p_1}}$ and
$A^{p_1,\lambda_1}\subset X\subset \mathcal{B}^{\frac{p_{1}+2-\lambda_1}{p_1}}$ and  $\Lambda^{p_2}_{\frac{1}{p_2}}\subset Y\subset \mathcal{B}$. Then, the following two statements are equivalent:
$\Lambda^{p_2}_{\frac{1}{p_2}}\subset Y\subset \mathcal{B}$. Then, the following two statements are equivalent:
(1) the operator
 $\mathcal{C}_{\mu}:X\rightarrow Y$ is compact;
$\mathcal{C}_{\mu}:X\rightarrow Y$ is compact;(2) the measure µ is a vanishing
 $\frac{p_1+2-\lambda_1}{p_1}$-Carleson measure.
$\frac{p_1+2-\lambda_1}{p_1}$-Carleson measure.
Proof. Assume that µ is a vanishing  $\frac{p_1+2-\lambda_1}{p_1}$-Carleson measure. To show that
$\frac{p_1+2-\lambda_1}{p_1}$-Carleson measure. To show that ![]() $\mathcal{C}_{\mu}$ is compact from X into Y, let us first choose the sequence
$\mathcal{C}_{\mu}$ is compact from X into Y, let us first choose the sequence ![]() $\{f_n\}^{\infty}_{n=1}\subset X$ such that
$\{f_n\}^{\infty}_{n=1}\subset X$ such that ![]() $\|f_n\|_{X}\leq 1$ for any n, and
$\|f_n\|_{X}\leq 1$ for any n, and ![]() $f_n\rightarrow0$ uniformly on compact subsets of
$f_n\rightarrow0$ uniformly on compact subsets of ![]() $\mathbb{D}$ when
$\mathbb{D}$ when ![]() $n\rightarrow\infty$.
$n\rightarrow\infty$.
By Lemma 2.3, we know that for any ɛ > 0, there exists a constant ![]() $\delta\in(0,1)$ such that
$\delta\in(0,1)$ such that
 \begin{equation*}\int_{[0,1)} \frac{(1-r)^{1-\frac{1}{p_2}}}{(1-tr)^{1-\frac{1}{p_2}+\frac{p_1+2-\lambda_1}{p_1}}}\text{d}\mu(t) \lt \varepsilon\end{equation*}
\begin{equation*}\int_{[0,1)} \frac{(1-r)^{1-\frac{1}{p_2}}}{(1-tr)^{1-\frac{1}{p_2}+\frac{p_1+2-\lambda_1}{p_1}}}\text{d}\mu(t) \lt \varepsilon\end{equation*} for any ![]() $r\in(\delta,1)$. Since X is continuously embedded in
$r\in(\delta,1)$. Since X is continuously embedded in  $\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}$, it follows that
$\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}$, it follows that  $f_n\in\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}$ and
$f_n\in\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}$ and  $\|f_n\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\lesssim1$ for every n. From the proof of Theorem 3.7, we get
$\|f_n\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\lesssim1$ for every n. From the proof of Theorem 3.7, we get
 \begin{align*}
& \sup_{\delta \lt r \lt 1}(1-r)^{1-\frac{1}{p_2}}\left(\frac{1}{2\pi} \int^{2\pi}_{0}|\mathcal{C}_{\mu}(f_n)'(r\text{e}^{i\theta})|^{p_2}\text{d}\theta\right)^{\frac{1}{p_2}}\\& \quad
\lesssim
\|f_n\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{\delta \lt r \lt 1}\int_{[0,1)} \frac{(1-r)^{1-\frac{1}{p_2}}}{(1-tr)^{1-\frac{1}{p_2}+\frac{p_1+2-\lambda_1}{p_1}}}d\mu(t)\lesssim\varepsilon.
\end{align*}
\begin{align*}
& \sup_{\delta \lt r \lt 1}(1-r)^{1-\frac{1}{p_2}}\left(\frac{1}{2\pi} \int^{2\pi}_{0}|\mathcal{C}_{\mu}(f_n)'(r\text{e}^{i\theta})|^{p_2}\text{d}\theta\right)^{\frac{1}{p_2}}\\& \quad
\lesssim
\|f_n\|_{\mathcal{B}^{\frac{p_1+2-\lambda_1}{p_1}}}\sup_{\delta \lt r \lt 1}\int_{[0,1)} \frac{(1-r)^{1-\frac{1}{p_2}}}{(1-tr)^{1-\frac{1}{p_2}+\frac{p_1+2-\lambda_1}{p_1}}}d\mu(t)\lesssim\varepsilon.
\end{align*} On the other hand, let ![]() $S:=\{z\in \mathbb{D}:|z|\leq\delta\}$, then
$S:=\{z\in \mathbb{D}:|z|\leq\delta\}$, then ![]() $f_n\rightarrow0$ and
$f_n\rightarrow0$ and ![]() $f'_n\rightarrow0$ uniformly on S as
$f'_n\rightarrow0$ uniformly on S as ![]() $n\rightarrow\infty$. This means that for each ɛ > 0, there is an
$n\rightarrow\infty$. This means that for each ɛ > 0, there is an ![]() $n_0\in \mathbb{N}$ such that
$n_0\in \mathbb{N}$ such that ![]() $\sup_{z\in S}|f_n(z)| \lt \varepsilon$ and
$\sup_{z\in S}|f_n(z)| \lt \varepsilon$ and ![]() $\sup_{z\in S}|f'_n(z)| \lt \varepsilon$ for any
$\sup_{z\in S}|f'_n(z)| \lt \varepsilon$ for any ![]() $n \gt n_0$. From the fact that µ is a finite positive measure, we have
$n \gt n_0$. From the fact that µ is a finite positive measure, we have
 \begin{equation*}\sup_{0 \lt r\leq\delta}\int_{[0,1)}\frac{(1-r)^{1-\frac{1}{p_2}}}{(1-tr)^{1-\frac{1}{p_2}}}\text{d}\mu(t)+\sup_{0 \lt r\leq\delta}\int_{[0,1)}\frac{(1-r)^{1-\frac{1}{p_2}}}{(1-tr)^{2-\frac{1}{p_2}}}\text{d}\mu(t) \lt \infty.\end{equation*}
\begin{equation*}\sup_{0 \lt r\leq\delta}\int_{[0,1)}\frac{(1-r)^{1-\frac{1}{p_2}}}{(1-tr)^{1-\frac{1}{p_2}}}\text{d}\mu(t)+\sup_{0 \lt r\leq\delta}\int_{[0,1)}\frac{(1-r)^{1-\frac{1}{p_2}}}{(1-tr)^{2-\frac{1}{p_2}}}\text{d}\mu(t) \lt \infty.\end{equation*} It follows from Lemma 2.5 that for any ![]() $n \gt n_0$,
$n \gt n_0$,
 \begin{align*}
\sup_{0 \lt r\leq\delta}(1-r)^{1-\frac{1}{p_2}}&\left(\frac{1}{2\pi} \int^{2\pi}_{0}|\mathcal{C}_{\mu}(f_n)'(re^{i\theta})|^{p_2}\text{d}\theta\right)^{\frac{1}{p_2}}\\ \lt &\varepsilon\sup_{0 \lt r\leq\delta}(1-r)^{1-\frac{1}{p_2}}\int_{[0,1)}\left(\frac{1}{2\pi} \int_{0}^{2\pi}\frac{1}{|1-tre^{i\theta}|^{p_2}}d\theta\right)^{1/p_2}\text{d}\mu(t)\\
&+
\varepsilon\sup_{0 \lt r\leq\delta}(1-r)^{1-\frac{1}{p_2}}\int_{[0,1)}\left(\frac{1}{2\pi} \int_{0}^{2\pi}\frac{1}{|1-tre^{i\theta}|^{2p_2}} d\theta\right)^{1/p_{2}}\text{d}\mu(t)\\
\lesssim&\varepsilon\sup_{0 \lt r\leq\delta}\int_{[0,1)}\frac{(1-r)^{1-\frac{1}{p_2}}}{(1-tr)^{1-\frac{1}{p_2}}}\text{d}\mu(t)+\varepsilon\sup_{0 \lt r\leq\delta}\int_{[0,1)}\frac{(1-r)^{1-\frac{1}{p_2}}}{(1-tr)^{2-\frac{1}{p_2}}}\text{d}\mu(t)\\
\lesssim&\varepsilon.
\end{align*}
\begin{align*}
\sup_{0 \lt r\leq\delta}(1-r)^{1-\frac{1}{p_2}}&\left(\frac{1}{2\pi} \int^{2\pi}_{0}|\mathcal{C}_{\mu}(f_n)'(re^{i\theta})|^{p_2}\text{d}\theta\right)^{\frac{1}{p_2}}\\ \lt &\varepsilon\sup_{0 \lt r\leq\delta}(1-r)^{1-\frac{1}{p_2}}\int_{[0,1)}\left(\frac{1}{2\pi} \int_{0}^{2\pi}\frac{1}{|1-tre^{i\theta}|^{p_2}}d\theta\right)^{1/p_2}\text{d}\mu(t)\\
&+
\varepsilon\sup_{0 \lt r\leq\delta}(1-r)^{1-\frac{1}{p_2}}\int_{[0,1)}\left(\frac{1}{2\pi} \int_{0}^{2\pi}\frac{1}{|1-tre^{i\theta}|^{2p_2}} d\theta\right)^{1/p_{2}}\text{d}\mu(t)\\
\lesssim&\varepsilon\sup_{0 \lt r\leq\delta}\int_{[0,1)}\frac{(1-r)^{1-\frac{1}{p_2}}}{(1-tr)^{1-\frac{1}{p_2}}}\text{d}\mu(t)+\varepsilon\sup_{0 \lt r\leq\delta}\int_{[0,1)}\frac{(1-r)^{1-\frac{1}{p_2}}}{(1-tr)^{2-\frac{1}{p_2}}}\text{d}\mu(t)\\
\lesssim&\varepsilon.
\end{align*}Thus, we obtain that
 \begin{equation*}\lim_{n\rightarrow\infty}\|\mathcal{C}_{\mu}(f_n)\|_{\Lambda^{p_2}_{\frac{1}{p_2}}}=0.\end{equation*}
\begin{equation*}\lim_{n\rightarrow\infty}\|\mathcal{C}_{\mu}(f_n)\|_{\Lambda^{p_2}_{\frac{1}{p_2}}}=0.\end{equation*} Since  $\Lambda^{p_2}_{\frac{1}{p_2}}\subset Y$, we conclude that
$\Lambda^{p_2}_{\frac{1}{p_2}}\subset Y$, we conclude that ![]() $\mathcal{C}_{\mu}$ is compact from X into Y.
$\mathcal{C}_{\mu}$ is compact from X into Y.
The proof of the converse is quite similar to Theorem 3.4 and is omitted.
Corollary 3.11. Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $0 \lt p_1 \lt \infty$,
$0 \lt p_1 \lt \infty$, ![]() $1 \lt p_2 \lt \infty$ and
$1 \lt p_2 \lt \infty$ and ![]() $0 \lt \lambda_1 \lt 2$. Then, the operator
$0 \lt \lambda_1 \lt 2$. Then, the operator  $\mathcal{C}_{\mu}:A^{p_1,\lambda_1}\rightarrow \Lambda^{p_2}_{\frac{1}{p_2}}$ is compact if and only if the measure µ is a vanishing
$\mathcal{C}_{\mu}:A^{p_1,\lambda_1}\rightarrow \Lambda^{p_2}_{\frac{1}{p_2}}$ is compact if and only if the measure µ is a vanishing  $\frac{p_1+2-\lambda_1}{p_1}$-Carleson measure.
$\frac{p_1+2-\lambda_1}{p_1}$-Carleson measure.
Corollary 3.12. Let µ be a positive finite Borel measure on ![]() $[0,1)$ and α > 1. Then, the operator
$[0,1)$ and α > 1. Then, the operator ![]() $\mathcal{C}_{\mu}:\mathcal{B}^{\alpha}\rightarrow \mathcal{B}$ is compact if and only if the measure µ is a vanishing α-Carleson measure.
$\mathcal{C}_{\mu}:\mathcal{B}^{\alpha}\rightarrow \mathcal{B}$ is compact if and only if the measure µ is a vanishing α-Carleson measure.
The following result shows the boundedness of Cesáro-type operators from the mean Lipschitz spaces into the Bergman-Morrey spaces.
Theorem 3.13 Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $1 \lt p_1 \lt \infty$,
$1 \lt p_1 \lt \infty$, ![]() $1\leq p_2 \lt \infty$ and
$1\leq p_2 \lt \infty$ and ![]() $0 \lt \lambda_2 \lt 2$ such that
$0 \lt \lambda_2 \lt 2$ such that ![]() $p_2+\lambda_2 \gt 2$. Suppose that X and Y are two Banach spaces contained in
$p_2+\lambda_2 \gt 2$. Suppose that X and Y are two Banach spaces contained in ![]() $H(\mathbb{D})$ such that
$H(\mathbb{D})$ such that  $\Lambda^{p_1}_{\frac{1}{p_1}}\subset X\subset \mathcal{B}$ and
$\Lambda^{p_1}_{\frac{1}{p_1}}\subset X\subset \mathcal{B}$ and  $A^{p_2,\lambda_2}\subset Y\subset \mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}$. Then, the following two statements are equivalent:
$A^{p_2,\lambda_2}\subset Y\subset \mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}$. Then, the following two statements are equivalent:
(1) the operator
 $\mathcal{C}_{\mu}:X\rightarrow Y$ is bounded;
$\mathcal{C}_{\mu}:X\rightarrow Y$ is bounded;(2) the measure µ is a 1-logarithmic
 $\left( 1-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure.
$\left( 1-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure.
Proof. For any ![]() $f\in X$, following from the argument in the proof of Theorem 3.1, we see that
$f\in X$, following from the argument in the proof of Theorem 3.1, we see that
 \begin{align*}
\|\mathcal{C}_{\mu}(f)\|_{A^{p_2,\lambda_2}}
&\lesssim\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{|tf'(tz)|^{p_2}}{|1-tz|^{p_2}}\frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \text{d}\mu(t)\\
&\quad +\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)} \left(\int_{\mathbb{D}} \frac{|tf(tz)|^{p_2}}{|1-tz|^{2p_2}} \frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2}\text{d}\mu(t)\\
& =: I_1+I_2.
\end{align*}
\begin{align*}
\|\mathcal{C}_{\mu}(f)\|_{A^{p_2,\lambda_2}}
&\lesssim\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{|tf'(tz)|^{p_2}}{|1-tz|^{p_2}}\frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2} \text{d}\mu(t)\\
&\quad +\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)} \left(\int_{\mathbb{D}} \frac{|tf(tz)|^{p_2}}{|1-tz|^{2p_2}} \frac{(1-|z|^2)^{p_2}}{|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2}\text{d}\mu(t)\\
& =: I_1+I_2.
\end{align*}First, we discuss I 1 from the following two cases:
Case 1: ![]() $1\leq p_2\leq2$.
$1\leq p_2\leq2$.
Take a positive constant c satisfying  $\frac{2-\lambda_2}{p_2} \lt c \lt 1$. By Lemmas 2.6 and 2.4, we get that
$\frac{2-\lambda_2}{p_2} \lt c \lt 1$. By Lemmas 2.6 and 2.4, we get that
 \begin{align*}
I_1&\lesssim\|f\|_{\mathcal{B}}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{(1-|z|^2)^{p_2 }}{|1-tz|^{p_2}|1-\overline{a}z|^{4}(1-t|z|)^{p_2}} \text{d}A(z)\right)^{1/p_2} \text{d}\mu(t)\\
&\lesssim\|f\|_{\mathcal{B}}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{(1-|z|^2)^{p_2\left( 1-c\right) }}{|1-tz|^{p_2}|1-\overline{a}z|^{4}}\text{d}A(z)\right)^{1/p_2} \frac{1}{(1-t)^{1-c}}\text{d}\mu(t)\\
&\lesssim\|f\|_{\mathcal{B}}\sup_{a\in \mathbb{D}}\int_{[0,1)} \frac{(1-|a|^2)^{\frac{2-\lambda_2}{p_2}+ 1-c}}{|1-ta|(1-t)^{(1-c)}}\text{d}\mu(t).
\end{align*}
\begin{align*}
I_1&\lesssim\|f\|_{\mathcal{B}}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{(1-|z|^2)^{p_2 }}{|1-tz|^{p_2}|1-\overline{a}z|^{4}(1-t|z|)^{p_2}} \text{d}A(z)\right)^{1/p_2} \text{d}\mu(t)\\
&\lesssim\|f\|_{\mathcal{B}}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{(1-|z|^2)^{p_2\left( 1-c\right) }}{|1-tz|^{p_2}|1-\overline{a}z|^{4}}\text{d}A(z)\right)^{1/p_2} \frac{1}{(1-t)^{1-c}}\text{d}\mu(t)\\
&\lesssim\|f\|_{\mathcal{B}}\sup_{a\in \mathbb{D}}\int_{[0,1)} \frac{(1-|a|^2)^{\frac{2-\lambda_2}{p_2}+ 1-c}}{|1-ta|(1-t)^{(1-c)}}\text{d}\mu(t).
\end{align*} Since µ is a 1-logarithmic  $\left( 1-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure, then µ is also a
$\left( 1-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure, then µ is also a  $\left( 1-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure. Lemma 2.2 then implies that
$\left( 1-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure. Lemma 2.2 then implies that ![]() $I_1\lesssim \|f\|_{\mathcal{B}}$.
$I_1\lesssim \|f\|_{\mathcal{B}}$.
Case 2: ![]() $2 \lt p_2$.
$2 \lt p_2$.
If ![]() $p_2+\lambda_2 \gt 4$, choose a positive constant d so that
$p_2+\lambda_2 \gt 4$, choose a positive constant d so that
 \begin{equation*}\frac{2-\lambda_2}{p_2} \lt d \lt \min\left\{\frac{2}{p_2},1-\frac{2}{p_2}\right\}.\end{equation*}
\begin{equation*}\frac{2-\lambda_2}{p_2} \lt d \lt \min\left\{\frac{2}{p_2},1-\frac{2}{p_2}\right\}.\end{equation*}According to Lemmas 2.2 and 2.4 (1), we have
 \begin{align*}
I_1&\lesssim\|f\|_{\mathcal{B}}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{(1-|z|^2)^{p_2\left(1-d\right) }}{|1-tz|^{p_2}|1-\overline{a}z|^{4}}\text{d}A(z)\right)^{1/p_2} \frac{1}{(1-t)^{(1-d)}}\text{d}\mu(t)\\
&\lesssim\|f\|_{\mathcal{B}}\sup_{a\in \mathbb{D}}\int_{[0,1)} \frac{(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}}{|1-ta|^{\frac{2}{p_2}+d}(1-t)^{(1-d)}}\text{d}\mu(t)\\
&\lesssim\|f\|_{\mathcal{B}}.
\end{align*}
\begin{align*}
I_1&\lesssim\|f\|_{\mathcal{B}}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{(1-|z|^2)^{p_2\left(1-d\right) }}{|1-tz|^{p_2}|1-\overline{a}z|^{4}}\text{d}A(z)\right)^{1/p_2} \frac{1}{(1-t)^{(1-d)}}\text{d}\mu(t)\\
&\lesssim\|f\|_{\mathcal{B}}\sup_{a\in \mathbb{D}}\int_{[0,1)} \frac{(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}}{|1-ta|^{\frac{2}{p_2}+d}(1-t)^{(1-d)}}\text{d}\mu(t)\\
&\lesssim\|f\|_{\mathcal{B}}.
\end{align*} If ![]() $p_2+\lambda_2\leq4$, then let the constant d be
$p_2+\lambda_2\leq4$, then let the constant d be
 \begin{equation*}\frac{2-\lambda_2}{p_2} \lt d \lt \frac{2}{p_2}.\end{equation*}
\begin{equation*}\frac{2-\lambda_2}{p_2} \lt d \lt \frac{2}{p_2}.\end{equation*}By Lemmas 2.2 and 2.4 (2), we obtain
 \begin{equation*}I_1\lesssim\|f\|_{\mathcal{B}}\sup_{a\in \mathbb{D}}\int_{[0,1)} \frac{(1-|a|^2)^{\frac{2-\lambda_2}{p_2}+1-d}}{|1-ta|(1-t)^{(1-d)}}\text{d}\mu(t)\lesssim\|f\|_{\mathcal{B}}.\end{equation*}
\begin{equation*}I_1\lesssim\|f\|_{\mathcal{B}}\sup_{a\in \mathbb{D}}\int_{[0,1)} \frac{(1-|a|^2)^{\frac{2-\lambda_2}{p_2}+1-d}}{|1-ta|(1-t)^{(1-d)}}\text{d}\mu(t)\lesssim\|f\|_{\mathcal{B}}.\end{equation*} On the other hand, for any ![]() $z\in \mathbb{D}$ and
$z\in \mathbb{D}$ and ![]() $t\in[0,1)$, by Lemma 2.6, we have
$t\in[0,1)$, by Lemma 2.6, we have
 \begin{equation*}|f(tz)|\lesssim\|f\|_{\mathcal{B}}\log\frac{2}{1-|tz|^2}\lesssim\|f\|_{\mathcal{B}}\log\frac{2}{1-t^2}.\end{equation*}
\begin{equation*}|f(tz)|\lesssim\|f\|_{\mathcal{B}}\log\frac{2}{1-|tz|^2}\lesssim\|f\|_{\mathcal{B}}\log\frac{2}{1-t^2}.\end{equation*}Consequently,
 \begin{align*}
I_2\lesssim \|f\|_{\mathcal{B}}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)} \left(\int_{\mathbb{D}} \frac{(1-|z|^2)^{p_2}}{|1-tz|^{2p_2}|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2}\log\frac{2}{1-t^2}\text{d}\mu(t).
\end{align*}
\begin{align*}
I_2\lesssim \|f\|_{\mathcal{B}}\sup_{a\in \mathbb{D}}(1-|a|^2)^{\frac{4-\lambda_2}{p_2}}\int_{[0,1)} \left(\int_{\mathbb{D}} \frac{(1-|z|^2)^{p_2}}{|1-tz|^{2p_2}|1-\overline{a}z|^4}\text{d}A(z)\right)^{1/p_2}\log\frac{2}{1-t^2}\text{d}\mu(t).
\end{align*}Borrowing the idea of the proof in Theorem 3.1, we obtain
because µ is a 1-logarithmic  $\left( 1-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure. Hence, we can deduce that
$\left( 1-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure. Hence, we can deduce that ![]() $\mathcal{C}_{\mu}(f)\in A^{p_2,\lambda_2}$ by Lemma 2.2.
$\mathcal{C}_{\mu}(f)\in A^{p_2,\lambda_2}$ by Lemma 2.2.
Conversely, for any ![]() $z\in \mathbb{D}$, we choose the test function
$z\in \mathbb{D}$, we choose the test function
 \begin{equation*}f(z)=\log\frac{1}{1-z}=\sum^{\infty}_{n=1}\frac{z^n}{n}.\end{equation*}
\begin{equation*}f(z)=\log\frac{1}{1-z}=\sum^{\infty}_{n=1}\frac{z^n}{n}.\end{equation*} Simple calculations give that  $f\in \Lambda^{p_1}_{\frac{1}{p_1}}$ and
$f\in \Lambda^{p_1}_{\frac{1}{p_1}}$ and  $\|f\|_{\Lambda^{p_1}_{\frac{1}{p_1}}}\lesssim1$. Since
$\|f\|_{\Lambda^{p_1}_{\frac{1}{p_1}}}\lesssim1$. Since  $\Lambda^{p_1}_{\frac{1}{p_1}}\subset X$ and
$\Lambda^{p_1}_{\frac{1}{p_1}}\subset X$ and  $Y\subset \mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}$, the boundedness of
$Y\subset \mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}$, the boundedness of ![]() $\mathcal{C}_{\mu}$ from X into Y implies that
$\mathcal{C}_{\mu}$ from X into Y implies that  $\|\mathcal{C}_{\mu}(f)\|_{\mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}}\lesssim\|f\|_{\Lambda^{p_1}_{\frac{1}{p_1}}}\lesssim1$. As
$\|\mathcal{C}_{\mu}(f)\|_{\mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}}\lesssim\|f\|_{\Lambda^{p_1}_{\frac{1}{p_1}}}\lesssim1$. As
 \begin{equation*}\mathcal{C}_{\mu}(f)(z)=\sum_{n=1}^{\infty}\mu_n\left( \sum^{n}_{k=1}\frac{1}{k}\right)z^n,\end{equation*}
\begin{equation*}\mathcal{C}_{\mu}(f)(z)=\sum_{n=1}^{\infty}\mu_n\left( \sum^{n}_{k=1}\frac{1}{k}\right)z^n,\end{equation*} then for any ![]() $0 \lt b \lt 1$,
$0 \lt b \lt 1$,  $|\mathcal{C}_{\mu}(f)'(b)|(1-b)^{\frac{p_{2}+2-\lambda_2}{p_2}}\lesssim1.$ This means that
$|\mathcal{C}_{\mu}(f)'(b)|(1-b)^{\frac{p_{2}+2-\lambda_2}{p_2}}\lesssim1.$ This means that
 \begin{equation*}\sum_{n=1}^{\infty}
n\mu_n\left( \sum^{n}_{k=1}\frac{1}{k}\right)b^n\lesssim\frac{1}{(1-b)^{\frac{p_{2}+2-\lambda_2}{p_2}}}.\end{equation*}
\begin{equation*}\sum_{n=1}^{\infty}
n\mu_n\left( \sum^{n}_{k=1}\frac{1}{k}\right)b^n\lesssim\frac{1}{(1-b)^{\frac{p_{2}+2-\lambda_2}{p_2}}}.\end{equation*} For any positive integer ![]() $N\geq2$, let
$N\geq2$, let  $b_N=1-\frac{1}{N}$, using the fact that the sequence
$b_N=1-\frac{1}{N}$, using the fact that the sequence ![]() $\{\mu_n\}$ is decreasing, we have that
$\{\mu_n\}$ is decreasing, we have that
 \begin{align*}
\mu_{N}N^2\log N& \approx\mu_{N}\sum^{N}_{n=1}n\log n\lesssim\sum^{N}_{n=1}n\mu_n(\log n)b_{N}^n\lesssim\sum^{N}_{n=1}n\mu_n\left( \sum^{n}_{k=1}\frac{1}{k}\right)b_{N}^n\\ & \lesssim\sum^{\infty}_{n=1}n\mu_n\left( \sum^{n}_{k=1}\frac{1}{k}\right)b_{N}^n\lesssim N^{\frac{p_{2}+2-\lambda_2}{p_2}}.
\end{align*}
\begin{align*}
\mu_{N}N^2\log N& \approx\mu_{N}\sum^{N}_{n=1}n\log n\lesssim\sum^{N}_{n=1}n\mu_n(\log n)b_{N}^n\lesssim\sum^{N}_{n=1}n\mu_n\left( \sum^{n}_{k=1}\frac{1}{k}\right)b_{N}^n\\ & \lesssim\sum^{\infty}_{n=1}n\mu_n\left( \sum^{n}_{k=1}\frac{1}{k}\right)b_{N}^n\lesssim N^{\frac{p_{2}+2-\lambda_2}{p_2}}.
\end{align*}This shows that
 \begin{equation*}\mu_N\lesssim\frac{1}{N^{1-\frac{2-\lambda_2}{p_2}}\log N},\end{equation*}
\begin{equation*}\mu_N\lesssim\frac{1}{N^{1-\frac{2-\lambda_2}{p_2}}\log N},\end{equation*} and so µ is a 1-logarithmic  $\left( 1-\frac{2-\lambda_2}{p_2}\right)$-Carleson measure. This completes the proof.
$\left( 1-\frac{2-\lambda_2}{p_2}\right)$-Carleson measure. This completes the proof.
Corollary 3.14. Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $1\leq p_2 \lt \infty$ and
$1\leq p_2 \lt \infty$ and ![]() $0 \lt \lambda_2 \lt 2$ such that
$0 \lt \lambda_2 \lt 2$ such that ![]() $p_2+\lambda_2 \gt 2$. The operator
$p_2+\lambda_2 \gt 2$. The operator ![]() $\mathcal{C}_{\mu}:\mathcal{B}\rightarrow A^{p_2,\lambda_2}$ is bounded if and only if the measure µ is a 1-logarithmic
$\mathcal{C}_{\mu}:\mathcal{B}\rightarrow A^{p_2,\lambda_2}$ is bounded if and only if the measure µ is a 1-logarithmic  $\left( 1-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure.
$\left( 1-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure.
The theorem states the compactness of Cesáro-type operators from the mean Lipschitz spaces into the Bergman-Morrey spaces.
Theorem 3.15 Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $1 \lt p_1 \lt \infty$,
$1 \lt p_1 \lt \infty$, ![]() $1\leq p_2 \lt \infty$ and
$1\leq p_2 \lt \infty$ and ![]() $0 \lt \lambda_2 \lt 2$ such that
$0 \lt \lambda_2 \lt 2$ such that ![]() $p_2+\lambda_2 \gt 2$. Suppose that X and Y are two Banach spaces contained in
$p_2+\lambda_2 \gt 2$. Suppose that X and Y are two Banach spaces contained in ![]() $H(\mathbb{D})$ such that
$H(\mathbb{D})$ such that  $\Lambda^{p_1}_{\frac{1}{p_1}}\subset X\subset \mathcal{B}$ and
$\Lambda^{p_1}_{\frac{1}{p_1}}\subset X\subset \mathcal{B}$ and  $A^{p_2,\lambda_2}\subset Y\subset \mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}$. Then, the following two statements are equivalent:
$A^{p_2,\lambda_2}\subset Y\subset \mathcal{B}^{\frac{p_{2}+2-\lambda_2}{p_2}}$. Then, the following two statements are equivalent:
(1) the operator
 $\mathcal{C}_{\mu}:X\rightarrow Y$ is compact;
$\mathcal{C}_{\mu}:X\rightarrow Y$ is compact;(2) the measure µ is a vanishing 1-logarithmic
 $\left( 1-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure.
$\left( 1-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure.
Proof. The proof is similar to the proof of Theorem 3.10 and so is omitted.
Corollary 3.16. Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $1\leq p_2 \lt \infty$ and
$1\leq p_2 \lt \infty$ and ![]() $0 \lt \lambda_2 \lt 2$ such that
$0 \lt \lambda_2 \lt 2$ such that ![]() $p_2+\lambda_2 \gt 2$. The operator
$p_2+\lambda_2 \gt 2$. The operator ![]() $\mathcal{C}_{\mu}:\mathcal{B}\rightarrow A^{p_2,\lambda_2}$ is compact if and only if the measure µ is a vanishing 1-logarithmic
$\mathcal{C}_{\mu}:\mathcal{B}\rightarrow A^{p_2,\lambda_2}$ is compact if and only if the measure µ is a vanishing 1-logarithmic  $\left( 1-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure.
$\left( 1-\frac{2-\lambda_2}{p_2}\right) $-Carleson measure.
4. The Cesàro-type operator  $\mathcal{C}_{\mu}$ on
$\mathcal{C}_{\mu}$ on  $\mathcal{D}^{\lambda}_{p}$
$\mathcal{D}^{\lambda}_{p}$
In this section, we aim to examine the boundedness and compactness of Cesàro-type operators on Dirichlet–Morrey spaces.
4.1. The case of λ ≠ 1
Theorem 4.1 Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $0 \lt p_1,p_2,\lambda_1,\lambda_2 \lt 1$. Suppose that X and Y are two Banach spaces contained in
$0 \lt p_1,p_2,\lambda_1,\lambda_2 \lt 1$. Suppose that X and Y are two Banach spaces contained in ![]() $H(\mathbb{D})$ such that
$H(\mathbb{D})$ such that  $\mathcal{D}^{\lambda_1}_{p_1}\subset X\subset \mathcal{B}^{\frac{p_1(1-\lambda_1)}{2}+1}$ and
$\mathcal{D}^{\lambda_1}_{p_1}\subset X\subset \mathcal{B}^{\frac{p_1(1-\lambda_1)}{2}+1}$ and  $\mathcal{D}^{\lambda_2}_{p_2}\subset Y\subset \mathcal{B}^{\frac{p_2(1-\lambda_2)}{2}+1}$. Then, the following two statements are equivalent:
$\mathcal{D}^{\lambda_2}_{p_2}\subset Y\subset \mathcal{B}^{\frac{p_2(1-\lambda_2)}{2}+1}$. Then, the following two statements are equivalent:
(1) the operator
 $\mathcal{C}_{\mu}:X\rightarrow Y$ is bounded;
$\mathcal{C}_{\mu}:X\rightarrow Y$ is bounded;(2) the measure µ is a
 $\left( 1+\frac{p_1(1-\lambda_1)}{2}-\frac{p_2(1-\lambda_2)}{2}\right) $-Carleson measure.
$\left( 1+\frac{p_1(1-\lambda_1)}{2}-\frac{p_2(1-\lambda_2)}{2}\right) $-Carleson measure.
Proof. If the measure µ is a  $\left( 1+\frac{p_1(1-\lambda_1)}{2}-\frac{p_2(1-\lambda_2)}{2}\right) $-Carleson measure, for any
$\left( 1+\frac{p_1(1-\lambda_1)}{2}-\frac{p_2(1-\lambda_2)}{2}\right) $-Carleson measure, for any  $f\in \mathcal{B}^{\frac{p_1(1-\lambda_1)}{2}+1}$, by Minkowski’s inequality, we get
$f\in \mathcal{B}^{\frac{p_1(1-\lambda_1)}{2}+1}$, by Minkowski’s inequality, we get
 \begin{align*}
\|\mathcal{C}_{\mu}(f)\|_{\mathcal{D}^{\lambda_2}_{p_2}}\approx&\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p_2(1-\lambda_2)}{2}}\left(\int_{\mathbb{D}}\left|\int_{[0,1)}\frac{tf'(tz)}{|1-tz|}\text{d}\mu(t)+\int_{[0,1)}\frac{tf(tz)}{(1-tz)^2}\text{d}\mu(t) \right|^2 \right. \\ & \left. (1-|\sigma_a(z)|^2)^{p_2}\text{d}A(z) \right)^{1/2}\\[6pt]
\leq&\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p_2(1-\lambda_2)}{2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{|tf'(tz)|^2}{|1-tz|^2} \frac{(1-|a|^2)^{p_2}(1-|z|^2)^{p_2}}{|1-\overline{a}z|^{2p_2}}\text{d}A(z)\right)^{1/2} \\[6pt]
& \text{d}\mu(t)\\[6pt]
&+\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p_2(1-\lambda_2)}{2}}\int_{[0,1)}\left( \int_{\mathbb{D}}\frac{|tf(tz)|^2}{|1-tz|^4}\right. \\[6pt]
& \left.\cdot \frac{(1-|a|^2)^{p_2}(1-|z|^2)^{p_2}}{|1-\overline{a}z|^{2p_2}} \text{d}A(z) \right)^{1/2} \text{d}\mu(t)\\[6pt]
=:&I_1+I_2.
\end{align*}
\begin{align*}
\|\mathcal{C}_{\mu}(f)\|_{\mathcal{D}^{\lambda_2}_{p_2}}\approx&\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p_2(1-\lambda_2)}{2}}\left(\int_{\mathbb{D}}\left|\int_{[0,1)}\frac{tf'(tz)}{|1-tz|}\text{d}\mu(t)+\int_{[0,1)}\frac{tf(tz)}{(1-tz)^2}\text{d}\mu(t) \right|^2 \right. \\ & \left. (1-|\sigma_a(z)|^2)^{p_2}\text{d}A(z) \right)^{1/2}\\[6pt]
\leq&\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p_2(1-\lambda_2)}{2}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{|tf'(tz)|^2}{|1-tz|^2} \frac{(1-|a|^2)^{p_2}(1-|z|^2)^{p_2}}{|1-\overline{a}z|^{2p_2}}\text{d}A(z)\right)^{1/2} \\[6pt]
& \text{d}\mu(t)\\[6pt]
&+\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p_2(1-\lambda_2)}{2}}\int_{[0,1)}\left( \int_{\mathbb{D}}\frac{|tf(tz)|^2}{|1-tz|^4}\right. \\[6pt]
& \left.\cdot \frac{(1-|a|^2)^{p_2}(1-|z|^2)^{p_2}}{|1-\overline{a}z|^{2p_2}} \text{d}A(z) \right)^{1/2} \text{d}\mu(t)\\[6pt]
=:&I_1+I_2.
\end{align*}Now, fix a positive constant c such that
 \begin{equation*}\frac{p_2(1-\lambda_2)}{p_1(1-\lambda_1)+2} \lt c \lt \frac{p_2}{p_1(1-\lambda_1)+2}.\end{equation*}
\begin{equation*}\frac{p_2(1-\lambda_2)}{p_1(1-\lambda_1)+2} \lt c \lt \frac{p_2}{p_1(1-\lambda_1)+2}.\end{equation*}By Lemma 2.4, we see
 \begin{align*}
I_1\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1(1-\lambda_1)+2}{2}}}\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p_2(2-\lambda_2)}{2}}\int_{[0,1)}\\ & \left(\int_{\mathbb{D}} \frac{(1-|z|^2)^{p_2}}{|1-tz|^2|1-\overline{a}z|^{2p_2}(1-|tz|^2)^{(p_1(1-\lambda_1)+2)}}\text{d}A(z)\right)^{1/2} \text{d}\mu(t)\\
\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1(1-\lambda_1)+2}{2}}}\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p_2(2-\lambda_2)}{2}}\int_{[0,1)}\\ & \left(\int_{\mathbb{D}} \frac{(1-|z|^2)^{p_2-[p_1(1-\lambda_1)+2]c}}{|1-tz|^2|1-\overline{a}z|^{2p_2}}\text{d}A(z)\right)^{1/2}\frac{1}{(1-t^2)^{\frac{[p_1(1-\lambda_1)+2](1-c)}{2}}} \text{d}\mu(t)\\
\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1(1-\lambda_1)+2}{2}}}\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p_2(2-\lambda_2)}{2}}\int_{[0,1)}\\ & \frac{1}{|1-ta|^{\frac{p_2+[p_1(1-\lambda_1)+2]c}{2}}(1-t^2)^{\frac{[p_1(1-\lambda_1)+2](1-c)}{2}}} \text{d}\mu(t).
\end{align*}
\begin{align*}
I_1\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1(1-\lambda_1)+2}{2}}}\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p_2(2-\lambda_2)}{2}}\int_{[0,1)}\\ & \left(\int_{\mathbb{D}} \frac{(1-|z|^2)^{p_2}}{|1-tz|^2|1-\overline{a}z|^{2p_2}(1-|tz|^2)^{(p_1(1-\lambda_1)+2)}}\text{d}A(z)\right)^{1/2} \text{d}\mu(t)\\
\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1(1-\lambda_1)+2}{2}}}\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p_2(2-\lambda_2)}{2}}\int_{[0,1)}\\ & \left(\int_{\mathbb{D}} \frac{(1-|z|^2)^{p_2-[p_1(1-\lambda_1)+2]c}}{|1-tz|^2|1-\overline{a}z|^{2p_2}}\text{d}A(z)\right)^{1/2}\frac{1}{(1-t^2)^{\frac{[p_1(1-\lambda_1)+2](1-c)}{2}}} \text{d}\mu(t)\\
\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1(1-\lambda_1)+2}{2}}}\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p_2(2-\lambda_2)}{2}}\int_{[0,1)}\\ & \frac{1}{|1-ta|^{\frac{p_2+[p_1(1-\lambda_1)+2]c}{2}}(1-t^2)^{\frac{[p_1(1-\lambda_1)+2](1-c)}{2}}} \text{d}\mu(t).
\end{align*} Using Lemma 2.2 and the fact that µ is a  $\left( 1+\frac{p_1(1-\lambda_1)}{2}-\frac{p_2(1-\lambda_2)}{2}\right) $-Carleson measure, we have
$\left( 1+\frac{p_1(1-\lambda_1)}{2}-\frac{p_2(1-\lambda_2)}{2}\right) $-Carleson measure, we have
 \begin{equation*}I_1\lesssim\|f\|_{\mathcal{B}^{\frac{p_1(1-\lambda_1)+2}{2}}}.\end{equation*}
\begin{equation*}I_1\lesssim\|f\|_{\mathcal{B}^{\frac{p_1(1-\lambda_1)+2}{2}}}.\end{equation*}On the other hand, from Lemmas 2.2, 2.4 and 2.6, we get
 \begin{align*}
I_2\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1(1-\lambda_1)+2}{2}}}\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p_2(2-\lambda_2)}{2}}\int_{[0,1)}\left( \int_{\mathbb{D}}\frac{(1-|z|^2)^{p_2}}{|1-tz|^4|1-\overline{a}z|^{2p_2}} \text{d}A(z) \right)^{1/2}\\ & \frac{1}{(1-t^2)^{\frac{p_1(1-\lambda_1)}{2}}}\text{d}\mu(t)\\
\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1(1-\lambda_1)+2}{2}}}\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p_2(2-\lambda_2)}{2}}\int_{[0,1)}\frac{1}{(1-t^2)^{1-\frac{p_2}{2}}|1-ta|^{p_2}} \\ &\cdot\frac{1}{(1-t^2)^{\frac{p_1(1-\lambda_1)}{2}}}\text{d}\mu(t)\\
=&\|f\|_{\mathcal{B}^{\frac{p_1(1-\lambda_1)+2}{2}}}\sup_{a\in\mathbb{D}}\int_{[0,1)}\frac{(1-|a|^2)^{\frac{p_2(2-\lambda_2)}{2}}}{(1-t^2)^{1+\frac{p_1(1-\lambda_1)}{2}-\frac{p_2}{2}}|1-ta|^{p_2}} \text{d}\mu(t)\\
\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1(1-\lambda_1)+2}{2}}}.
\end{align*}
\begin{align*}
I_2\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1(1-\lambda_1)+2}{2}}}\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p_2(2-\lambda_2)}{2}}\int_{[0,1)}\left( \int_{\mathbb{D}}\frac{(1-|z|^2)^{p_2}}{|1-tz|^4|1-\overline{a}z|^{2p_2}} \text{d}A(z) \right)^{1/2}\\ & \frac{1}{(1-t^2)^{\frac{p_1(1-\lambda_1)}{2}}}\text{d}\mu(t)\\
\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1(1-\lambda_1)+2}{2}}}\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p_2(2-\lambda_2)}{2}}\int_{[0,1)}\frac{1}{(1-t^2)^{1-\frac{p_2}{2}}|1-ta|^{p_2}} \\ &\cdot\frac{1}{(1-t^2)^{\frac{p_1(1-\lambda_1)}{2}}}\text{d}\mu(t)\\
=&\|f\|_{\mathcal{B}^{\frac{p_1(1-\lambda_1)+2}{2}}}\sup_{a\in\mathbb{D}}\int_{[0,1)}\frac{(1-|a|^2)^{\frac{p_2(2-\lambda_2)}{2}}}{(1-t^2)^{1+\frac{p_1(1-\lambda_1)}{2}-\frac{p_2}{2}}|1-ta|^{p_2}} \text{d}\mu(t)\\
\lesssim&\|f\|_{\mathcal{B}^{\frac{p_1(1-\lambda_1)+2}{2}}}.
\end{align*} This means that  $\mathcal{C}_{\mu}f\subset\mathcal{D}^{\lambda_2}_{p_2}$.
$\mathcal{C}_{\mu}f\subset\mathcal{D}^{\lambda_2}_{p_2}$.
Conversely, if ![]() $\mathcal{C}_{\mu}X\subset Y$. For
$\mathcal{C}_{\mu}X\subset Y$. For  $\frac{1}{2} \lt b \lt 1$, let us consider the test function
$\frac{1}{2} \lt b \lt 1$, let us consider the test function
 \begin{equation*}f_b(z)=\frac{1}{(1-bz)^{\frac{p_1(1-\lambda_1)}{2}}}\end{equation*}
\begin{equation*}f_b(z)=\frac{1}{(1-bz)^{\frac{p_1(1-\lambda_1)}{2}}}\end{equation*} for any ![]() $z\in \mathbb{D}$. By [Reference Galanopoulos, Merchán and Siskakis19, Lemma 1], we know that
$z\in \mathbb{D}$. By [Reference Galanopoulos, Merchán and Siskakis19, Lemma 1], we know that  $f_b\in\mathcal{D}^{\lambda_1}_{p_1}$ and
$f_b\in\mathcal{D}^{\lambda_1}_{p_1}$ and  $\|f_b\|_{\mathcal{D}^{\lambda_1}_{p_1}}\lesssim1$. Then,
$\|f_b\|_{\mathcal{D}^{\lambda_1}_{p_1}}\lesssim1$. Then, ![]() $f_b\in X$ and hence
$f_b\in X$ and hence  $\mathcal{C}_{\mu}(f_b)\in Y\subset \mathcal{B}^{\frac{p_2(1-\lambda_2)}{2}+1}$. Consequently, we have
$\mathcal{C}_{\mu}(f_b)\in Y\subset \mathcal{B}^{\frac{p_2(1-\lambda_2)}{2}+1}$. Consequently, we have
 \begin{align*}
1 \gt rsim\|f_b\|_{\mathcal{D}^{\lambda_1}_{p_1}} \gt rsim&\|\mathcal{C}_{\mu}(f_b)\|_{\mathcal{B}^{\frac{p_2(1-\lambda_2)}{2}+1}}\\ \gt rsim&(1-b)^{\frac{p_2(1-\lambda_2)}{2}+1}\int_{[0,1)}\frac{bt}{(1-tb)(1-b^2t)^{\frac{p_1}{2}(1-\lambda_1)+1}}\text{d}\mu(t)\\
&+(1-b)^{\frac{p_2(1-\lambda_2)}{2}+1}\int_{[0,1)}\frac{t}{(1-tb)^2(1-b^2t)^{\frac{p_1}{2}(1-\lambda_1)}}\text{d}\mu(t)\\ \gt rsim&(1-b)^{\frac{p_2(1-\lambda_2)}{2}+1}\int_{[b,1)}\frac{bt}{(1-tb)(1-b^2t)^{\frac{p_1}{2}(1-\lambda_1)+1}}\text{d}\mu(t)\\
&+(1-b)^{\frac{p_2(1-\lambda_2)}{2}+1}\int_{[b,1)}\frac{t}{(1-tb)^2(1-b^2t)^{\frac{p_1}{2}(1-\lambda_1)}}\text{d}\mu(t)\\ \gt rsim&(1-b)^{\frac{p_2(1-\lambda_2)}{2}+1}\left(\frac{b^2\mu([b,1))}{(1-b^2)(1-b^3)^{\frac{p_1}{2}(1-\lambda_1)+1}}\right .\\ & \left. +\frac{b\mu([b,1))}{(1-b^2)^2(1-b^3)^{\frac{p_1}{2}(1-\lambda_1)}} \right),
\end{align*}
\begin{align*}
1 \gt rsim\|f_b\|_{\mathcal{D}^{\lambda_1}_{p_1}} \gt rsim&\|\mathcal{C}_{\mu}(f_b)\|_{\mathcal{B}^{\frac{p_2(1-\lambda_2)}{2}+1}}\\ \gt rsim&(1-b)^{\frac{p_2(1-\lambda_2)}{2}+1}\int_{[0,1)}\frac{bt}{(1-tb)(1-b^2t)^{\frac{p_1}{2}(1-\lambda_1)+1}}\text{d}\mu(t)\\
&+(1-b)^{\frac{p_2(1-\lambda_2)}{2}+1}\int_{[0,1)}\frac{t}{(1-tb)^2(1-b^2t)^{\frac{p_1}{2}(1-\lambda_1)}}\text{d}\mu(t)\\ \gt rsim&(1-b)^{\frac{p_2(1-\lambda_2)}{2}+1}\int_{[b,1)}\frac{bt}{(1-tb)(1-b^2t)^{\frac{p_1}{2}(1-\lambda_1)+1}}\text{d}\mu(t)\\
&+(1-b)^{\frac{p_2(1-\lambda_2)}{2}+1}\int_{[b,1)}\frac{t}{(1-tb)^2(1-b^2t)^{\frac{p_1}{2}(1-\lambda_1)}}\text{d}\mu(t)\\ \gt rsim&(1-b)^{\frac{p_2(1-\lambda_2)}{2}+1}\left(\frac{b^2\mu([b,1))}{(1-b^2)(1-b^3)^{\frac{p_1}{2}(1-\lambda_1)+1}}\right .\\ & \left. +\frac{b\mu([b,1))}{(1-b^2)^2(1-b^3)^{\frac{p_1}{2}(1-\lambda_1)}} \right),
\end{align*}which leads to
 \begin{equation*}\mu([b,1))\lesssim(1-b)^{1+\frac{p_1(1-\lambda_1)}{2}-\frac{p_2(1-\lambda_2)}{2}}.\end{equation*}
\begin{equation*}\mu([b,1))\lesssim(1-b)^{1+\frac{p_1(1-\lambda_1)}{2}-\frac{p_2(1-\lambda_2)}{2}}.\end{equation*} This shows that µ is a  $\left( 1+\frac{p_1(1-\lambda_1)}{2}-\frac{p_2(1-\lambda_2)}{2}\right) $-Carleson measure. The proof is completed.
$\left( 1+\frac{p_1(1-\lambda_1)}{2}-\frac{p_2(1-\lambda_2)}{2}\right) $-Carleson measure. The proof is completed.
Corollary 4.2. Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $0 \lt p_1,p_2,\lambda_1,\lambda_2 \lt 1$. The operator
$0 \lt p_1,p_2,\lambda_1,\lambda_2 \lt 1$. The operator  $\mathcal{C}_{\mu}:\mathcal{D}^{\lambda_1}_{p_1}\rightarrow\mathcal{D}^{\lambda_2}_{p_2}$ is bounded if and only if the measure µ is a
$\mathcal{C}_{\mu}:\mathcal{D}^{\lambda_1}_{p_1}\rightarrow\mathcal{D}^{\lambda_2}_{p_2}$ is bounded if and only if the measure µ is a  $\left( 1+\frac{p_1(1-\lambda_1)}{2}-\frac{p_2(1-\lambda_2)}{2}\right) $-Carleson measure.
$\left( 1+\frac{p_1(1-\lambda_1)}{2}-\frac{p_2(1-\lambda_2)}{2}\right) $-Carleson measure.
The following theorem shows the compactness of ![]() $\mathcal{C}_{\mu}$ between different Dirichlet–Morrey spaces.
$\mathcal{C}_{\mu}$ between different Dirichlet–Morrey spaces.
Theorem 4.3 Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $0 \lt p_1,p_2,\lambda_1,\lambda_2 \lt 1$. Suppose that X and Y are two Banach spaces contained in
$0 \lt p_1,p_2,\lambda_1,\lambda_2 \lt 1$. Suppose that X and Y are two Banach spaces contained in ![]() $H(\mathbb{D})$ such that
$H(\mathbb{D})$ such that  $\mathcal{D}^{\lambda_1}_{p_1}\subset X\subset \mathcal{B}^{\frac{p_1(1-\lambda_1)}{2}+1}$ and
$\mathcal{D}^{\lambda_1}_{p_1}\subset X\subset \mathcal{B}^{\frac{p_1(1-\lambda_1)}{2}+1}$ and  $\mathcal{D}^{\lambda_2}_{p_2}\subset Y\subset \mathcal{B}^{\frac{p_2(1-\lambda_2)}{2}+1}$. Then, the following two statements are equivalent:
$\mathcal{D}^{\lambda_2}_{p_2}\subset Y\subset \mathcal{B}^{\frac{p_2(1-\lambda_2)}{2}+1}$. Then, the following two statements are equivalent:
(1) the operator
 $\mathcal{C}_{\mu}:X\rightarrow Y$ is compact;
$\mathcal{C}_{\mu}:X\rightarrow Y$ is compact;(2) the measure µ is a vanishing
 $\left( 1+\frac{p_1(1-\lambda_1)}{2}-\frac{p_2(1-\lambda_2)}{2}\right) $-Carleson measure.
$\left( 1+\frac{p_1(1-\lambda_1)}{2}-\frac{p_2(1-\lambda_2)}{2}\right) $-Carleson measure.
Proof. The idea of the proof is similar to Theorem 3.4, and so we omit it.
Corollary 4.4. Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $0 \lt p_1,p_2,\lambda_1,\lambda_2 \lt 1$. The operator
$0 \lt p_1,p_2,\lambda_1,\lambda_2 \lt 1$. The operator  $\mathcal{C}_{\mu}:\mathcal{D}^{\lambda_1}_{p_1}\rightarrow\mathcal{D}^{\lambda_2}_{p_2}$ is compact if and only if the measure µ is a vanishing
$\mathcal{C}_{\mu}:\mathcal{D}^{\lambda_1}_{p_1}\rightarrow\mathcal{D}^{\lambda_2}_{p_2}$ is compact if and only if the measure µ is a vanishing  $\left( 1+\frac{p_1(1-\lambda_1)}{2}-\frac{p_2(1-\lambda_2)}{2}\right) $-Carleson measure.
$\left( 1+\frac{p_1(1-\lambda_1)}{2}-\frac{p_2(1-\lambda_2)}{2}\right) $-Carleson measure.
Similar to the previous section, we state the boundedness and compactness of the operator ![]() $\mathcal{C}_{\mu}$ between the Dirichlet–Morrey spaces and the mean Lipschitz spaces directly in the following theorem. Since the proof is analogous to the previous theorem, we leave it to the interested readers.
$\mathcal{C}_{\mu}$ between the Dirichlet–Morrey spaces and the mean Lipschitz spaces directly in the following theorem. Since the proof is analogous to the previous theorem, we leave it to the interested readers.
Theorem 4.5 Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $0 \lt p_1,\lambda_1 \lt 1$ and
$0 \lt p_1,\lambda_1 \lt 1$ and ![]() $1 \lt p_2 \lt \infty$. Suppose that X and Y are two Banach spaces contained in
$1 \lt p_2 \lt \infty$. Suppose that X and Y are two Banach spaces contained in ![]() $H(\mathbb{D})$ such that
$H(\mathbb{D})$ such that  $\mathcal{D}^{\lambda_1}_{p_1}\subset X\subset \mathcal{B}^{\frac{p_1(1-\lambda_1)}{2}+1}$ and
$\mathcal{D}^{\lambda_1}_{p_1}\subset X\subset \mathcal{B}^{\frac{p_1(1-\lambda_1)}{2}+1}$ and  $\Lambda^{p_2}_{\frac{1}{p_2}}\subset Y\subset \mathcal{B}$. Then, the following two statements are equivalent:
$\Lambda^{p_2}_{\frac{1}{p_2}}\subset Y\subset \mathcal{B}$. Then, the following two statements are equivalent:
(1) the operator
 $\mathcal{C}_{\mu}:X\rightarrow Y$ is bounded;
$\mathcal{C}_{\mu}:X\rightarrow Y$ is bounded;(2) the measure µ is a
 $1+\frac{p_1(1-\lambda_1)}{2}$-Carleson measure.
$1+\frac{p_1(1-\lambda_1)}{2}$-Carleson measure.
Theorem 4.6 Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $0 \lt p_1,\lambda_1 \lt 1$ and
$0 \lt p_1,\lambda_1 \lt 1$ and ![]() $1 \lt p_2 \lt \infty$. Suppose that X and Y are two Banach spaces contained in
$1 \lt p_2 \lt \infty$. Suppose that X and Y are two Banach spaces contained in ![]() $H(\mathbb{D})$ such that
$H(\mathbb{D})$ such that  $\mathcal{D}^{\lambda_1}_{p_1}\subset X\subset \mathcal{B}^{\frac{p_1(1-\lambda_1)}{2}+1}$ and
$\mathcal{D}^{\lambda_1}_{p_1}\subset X\subset \mathcal{B}^{\frac{p_1(1-\lambda_1)}{2}+1}$ and  $\Lambda^{p_2}_{\frac{1}{p_2}}\subset Y\subset \mathcal{B}$. Then, the following two statements are equivalent:
$\Lambda^{p_2}_{\frac{1}{p_2}}\subset Y\subset \mathcal{B}$. Then, the following two statements are equivalent:
(1) the operator
 $\mathcal{C}_{\mu}:X\rightarrow Y$ is compact;
$\mathcal{C}_{\mu}:X\rightarrow Y$ is compact;(2) the measure µ is a vanishing
 $1+\frac{p_1(1-\lambda_1)}{2}$-Carleson measure.
$1+\frac{p_1(1-\lambda_1)}{2}$-Carleson measure.
Theorem 4.7 Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $1 \lt p_1 \lt \infty$ and
$1 \lt p_1 \lt \infty$ and ![]() $0 \lt p_2,\lambda_2 \lt 1$. Suppose that X and Y are two Banach spaces contained in
$0 \lt p_2,\lambda_2 \lt 1$. Suppose that X and Y are two Banach spaces contained in ![]() $H(\mathbb{D})$ such that
$H(\mathbb{D})$ such that  $\Lambda^{p_1}_{\frac{1}{p_1}}\subset Y\subset \mathcal{B}$ and
$\Lambda^{p_1}_{\frac{1}{p_1}}\subset Y\subset \mathcal{B}$ and  $\mathcal{D}^{\lambda_2}_{p_2}\subset X\subset \mathcal{B}^{\frac{p_2(1-\lambda_2)}{2}+1}$. Then, the following two statements are equivalent:
$\mathcal{D}^{\lambda_2}_{p_2}\subset X\subset \mathcal{B}^{\frac{p_2(1-\lambda_2)}{2}+1}$. Then, the following two statements are equivalent:
(1) the operator
 $\mathcal{C}_{\mu}:X\rightarrow Y$ is bounded;
$\mathcal{C}_{\mu}:X\rightarrow Y$ is bounded;(2) the measure µ is a 1-logarithmic
 $1-\frac{p_2(1-\lambda_2)}{2}$-Carleson measure.
$1-\frac{p_2(1-\lambda_2)}{2}$-Carleson measure.
Theorem 4.8 Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $1 \lt p_1 \lt \infty$ and
$1 \lt p_1 \lt \infty$ and ![]() $0 \lt p_2,\lambda_2 \lt 1$. Suppose that X and Y are two Banach spaces contained in
$0 \lt p_2,\lambda_2 \lt 1$. Suppose that X and Y are two Banach spaces contained in ![]() $H(\mathbb{D})$ such that
$H(\mathbb{D})$ such that  $\Lambda^{p_1}_{\frac{1}{p_1}}\subset Y\subset \mathcal{B}$ and
$\Lambda^{p_1}_{\frac{1}{p_1}}\subset Y\subset \mathcal{B}$ and  $\mathcal{D}^{\lambda_2}_{p_2}\subset X\subset \mathcal{B}^{\frac{p_2(1-\lambda_2)}{2}+1}$. Then, the following two statements are equivalent:
$\mathcal{D}^{\lambda_2}_{p_2}\subset X\subset \mathcal{B}^{\frac{p_2(1-\lambda_2)}{2}+1}$. Then, the following two statements are equivalent:
(1) the operator
 $\mathcal{C}_{\mu}:X\rightarrow Y$ is compact;
$\mathcal{C}_{\mu}:X\rightarrow Y$ is compact;(2) the measure µ is a vanishing 1-logarithmic
 $1-\frac{p_2(1-\lambda_2)}{2}$-Carleson measure.
$1-\frac{p_2(1-\lambda_2)}{2}$-Carleson measure.
4.2. The case of λ = 1
In this subsection, the following two theorems assert boundedness and compactness, respectively, of the operator ![]() $\mathcal{C}_{\mu}$ from the space
$\mathcal{C}_{\mu}$ from the space ![]() $Q_{p_1}$ into the space
$Q_{p_1}$ into the space ![]() $Q_{p_2}$.
$Q_{p_2}$.
Theorem 4.9 Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $0 \lt p_1,p_2 \lt 1$. Suppose that X and Y are two Banach spaces contained in
$0 \lt p_1,p_2 \lt 1$. Suppose that X and Y are two Banach spaces contained in ![]() $H(\mathbb{D})$ such that
$H(\mathbb{D})$ such that  $\mathcal{D}^{1}_{p_1}\subset X\subset \mathcal{B}$ and
$\mathcal{D}^{1}_{p_1}\subset X\subset \mathcal{B}$ and  $\mathcal{D}^{1}_{p_2}\subset Y\subset \mathcal{B}$. Then, the following two statements are equivalent:
$\mathcal{D}^{1}_{p_2}\subset Y\subset \mathcal{B}$. Then, the following two statements are equivalent:
(1) the operator
 $\mathcal{C}_{\mu}:X\rightarrow Y$ is bounded;
$\mathcal{C}_{\mu}:X\rightarrow Y$ is bounded;(2) the measure µ is a 1-logarithmic 1-Carleson measure.
Proof. First assume that the measure µ is a 1-logarithmic 1-Carleson measure. From the proof of Theorem 4.1, we have
 \begin{align*}
\|\mathcal{C}_{\mu}(f)\|_{\mathcal{D}^{1}_{p_2}}
\leq&\sup_{a\in\mathbb{D}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{|tf'(tz)|^2}{|1-tz|^2} \frac{(1-|a|^2)^{p_2}(1-|z|^2)^{p_2}}{|1-\overline{a}z|^{2p_2}}\text{d}A(z)\right)^{1/2} \text{d}\mu(t)\\
&+\sup_{a\in\mathbb{D}}\int_{[0,1)}\left( \int_{\mathbb{D}}\frac{|tf(tz)|^2}{|1-tz|^4}\cdot \frac{(1-|a|^2)^{p_2}(1-|z|^2)^{p_2}}{|1-\overline{a}z|^{2p_2}} \text{d}A(z) \right)^{1/2}\text{d}\mu(t)\\
=:&I_1+I_2,
\end{align*}
\begin{align*}
\|\mathcal{C}_{\mu}(f)\|_{\mathcal{D}^{1}_{p_2}}
\leq&\sup_{a\in\mathbb{D}}\int_{[0,1)}\left(\int_{\mathbb{D}}\frac{|tf'(tz)|^2}{|1-tz|^2} \frac{(1-|a|^2)^{p_2}(1-|z|^2)^{p_2}}{|1-\overline{a}z|^{2p_2}}\text{d}A(z)\right)^{1/2} \text{d}\mu(t)\\
&+\sup_{a\in\mathbb{D}}\int_{[0,1)}\left( \int_{\mathbb{D}}\frac{|tf(tz)|^2}{|1-tz|^4}\cdot \frac{(1-|a|^2)^{p_2}(1-|z|^2)^{p_2}}{|1-\overline{a}z|^{2p_2}} \text{d}A(z) \right)^{1/2}\text{d}\mu(t)\\
=:&I_1+I_2,
\end{align*} for any ![]() $f\in \mathcal{B}$. By [Reference Bao, Sun and Wulan7, Theorem 3.1],
$f\in \mathcal{B}$. By [Reference Bao, Sun and Wulan7, Theorem 3.1], ![]() $I_1\lesssim\|f\|_{\mathcal{B}}$.
$I_1\lesssim\|f\|_{\mathcal{B}}$.
By Lemma 2.6, we obtain
 \begin{equation*}|f(tz)|\lesssim\|f\|_{\mathcal{B}}\log\frac{2}{1-|tz|^2}\lesssim\|f\|_{\mathcal{B}}\log\frac{2}{1-t^2},\end{equation*}
\begin{equation*}|f(tz)|\lesssim\|f\|_{\mathcal{B}}\log\frac{2}{1-|tz|^2}\lesssim\|f\|_{\mathcal{B}}\log\frac{2}{1-t^2},\end{equation*} where ![]() $t\in[0,1)$ and
$t\in[0,1)$ and ![]() $z\in\mathbb{D}$. It follows from Lemmas 2.2 and 2.4 that
$z\in\mathbb{D}$. It follows from Lemmas 2.2 and 2.4 that
 \begin{align*}
I_2\lesssim&\|f\|_{\mathcal{B}}\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p_2}{2}}\int_{[0,1)}\left( \int_{\mathbb{D}} \frac{(1-|z|^2)^{p_2}}{|1-tz|^4|1-\overline{a}z|^{2p_2}} \text{d}A(z) \right)^{1/2}\log\frac{2}{1-t^2}\text{d}\mu(t)\\
\lesssim&\|f\|_{\mathcal{B}}\sup_{a\in\mathbb{D}}\int_{[0,1)}\frac{(1-|a|^2)^{\frac{p_2}{2}}}{(1-t^2)^{1-\frac{p_2}{2}}|1-ta|^{p_2}} \cdot\left( \log\frac{2}{1-t^2}\right) \text{d}\mu(t)\\
\lesssim&\|f\|_{\mathcal{B}}.
\end{align*}
\begin{align*}
I_2\lesssim&\|f\|_{\mathcal{B}}\sup_{a\in\mathbb{D}}(1-|a|^2)^{\frac{p_2}{2}}\int_{[0,1)}\left( \int_{\mathbb{D}} \frac{(1-|z|^2)^{p_2}}{|1-tz|^4|1-\overline{a}z|^{2p_2}} \text{d}A(z) \right)^{1/2}\log\frac{2}{1-t^2}\text{d}\mu(t)\\
\lesssim&\|f\|_{\mathcal{B}}\sup_{a\in\mathbb{D}}\int_{[0,1)}\frac{(1-|a|^2)^{\frac{p_2}{2}}}{(1-t^2)^{1-\frac{p_2}{2}}|1-ta|^{p_2}} \cdot\left( \log\frac{2}{1-t^2}\right) \text{d}\mu(t)\\
\lesssim&\|f\|_{\mathcal{B}}.
\end{align*} This proves the boundedness of ![]() $\mathcal{C}_{\mu}$ from X into Y.
$\mathcal{C}_{\mu}$ from X into Y.
Conversely, let  $\frac{1}{2} \lt b \lt 1$, consider the function
$\frac{1}{2} \lt b \lt 1$, consider the function
 \begin{equation*}f_b(z)=\log\frac{2}{1-bz},~z\in \mathbb{D}.\end{equation*}
\begin{equation*}f_b(z)=\log\frac{2}{1-bz},~z\in \mathbb{D}.\end{equation*} It can easily be verified that  $f_b\in\mathcal{D}^{1}_{p_1}$ and
$f_b\in\mathcal{D}^{1}_{p_1}$ and  $\|f_b\|_{\mathcal{D}^{1}_{p_1}}\lesssim1$. Since
$\|f_b\|_{\mathcal{D}^{1}_{p_1}}\lesssim1$. Since  $\mathcal{D}^{1}_{p_1}\subset X$ and
$\mathcal{D}^{1}_{p_1}\subset X$ and ![]() $Y\subset \mathcal{B}$, then the boundedness of
$Y\subset \mathcal{B}$, then the boundedness of ![]() $\mathcal{C}_{\mu}:X\rightarrow Y$ gives
$\mathcal{C}_{\mu}:X\rightarrow Y$ gives
 \begin{align*}
1 \gt rsim\|f_b\|_{\mathcal{D}^{1}_{p_1}} \gt rsim&(1-b)|\mathcal{C}_{\mu}(f_b)'(b)|\\ \gt rsim&(1-b)\int_{[0,1)}\frac{bt}{(1-tb)(1-b^2t)}\text{d}\mu(t)+(1-b)\\ & \int_{[0,1)}\frac{t}{(1-tb)^2}\log\frac{2}{1-b^2t}\text{d}\mu(t)\\ \gt rsim&(1-b)\left(\frac{b^2\mu([b,1))}{(1-b^2)(1-b^3)}+\frac{b\mu([b,1))}{(1-b^2)^2}\log\frac{2}{1-b^3} \right).
\end{align*}
\begin{align*}
1 \gt rsim\|f_b\|_{\mathcal{D}^{1}_{p_1}} \gt rsim&(1-b)|\mathcal{C}_{\mu}(f_b)'(b)|\\ \gt rsim&(1-b)\int_{[0,1)}\frac{bt}{(1-tb)(1-b^2t)}\text{d}\mu(t)+(1-b)\\ & \int_{[0,1)}\frac{t}{(1-tb)^2}\log\frac{2}{1-b^2t}\text{d}\mu(t)\\ \gt rsim&(1-b)\left(\frac{b^2\mu([b,1))}{(1-b^2)(1-b^3)}+\frac{b\mu([b,1))}{(1-b^2)^2}\log\frac{2}{1-b^3} \right).
\end{align*}This implies that
 \begin{equation*}\mu([b,1))\lesssim(1-b)\left( \log\frac{2}{1-b}\right)^{-1} .\end{equation*}
\begin{equation*}\mu([b,1))\lesssim(1-b)\left( \log\frac{2}{1-b}\right)^{-1} .\end{equation*}Hence, µ is a 1-logarithmic 1-Carleson measure. The proof is completed.
Corollary 4.10. [Reference Galanopoulos, Girela and Merchán17, Theorem 7]
Let µ be a positive finite Borel measure on ![]() $[0,1)$. The operator
$[0,1)$. The operator ![]() $\mathcal{C}_{\mu}:\mathcal{B}\rightarrow\mathcal{B}$ is bounded if and only if the measure µ is a 1-logarithmic 1-Carleson measure.
$\mathcal{C}_{\mu}:\mathcal{B}\rightarrow\mathcal{B}$ is bounded if and only if the measure µ is a 1-logarithmic 1-Carleson measure.
Theorem 4.11 Let µ be a positive finite Borel measure on ![]() $[0,1)$. Let
$[0,1)$. Let ![]() $0 \lt p_1,p_2 \lt 1$. Suppose that X and Y are two Banach spaces contained in
$0 \lt p_1,p_2 \lt 1$. Suppose that X and Y are two Banach spaces contained in ![]() $H(\mathbb{D})$ such that
$H(\mathbb{D})$ such that  $\mathcal{D}^{1}_{p_1}\subset X\subset \mathcal{B}$ and
$\mathcal{D}^{1}_{p_1}\subset X\subset \mathcal{B}$ and  $\mathcal{D}^{1}_{p_2}\subset Y\subset \mathcal{B}$. Then, the following two statements are equivalent:
$\mathcal{D}^{1}_{p_2}\subset Y\subset \mathcal{B}$. Then, the following two statements are equivalent:
(1) the operator
 $\mathcal{C}_{\mu}:X\rightarrow Y$ is compact;
$\mathcal{C}_{\mu}:X\rightarrow Y$ is compact;(2) the measure µ is a vanishing 1-logarithmic 1-Carleson measure.
Corollary 4.12. [Reference Galanopoulos, Girela and Merchán17, Theorem 8]
Let µ be a positive finite Borel measure on ![]() $[0,1)$. The operator
$[0,1)$. The operator ![]() $\mathcal{C}_{\mu}:\mathcal{B}\rightarrow\mathcal{B}$ is compact if and only if the measure µ is a vanishing 1-logarithmic 1-Carleson measure.
$\mathcal{C}_{\mu}:\mathcal{B}\rightarrow\mathcal{B}$ is compact if and only if the measure µ is a vanishing 1-logarithmic 1-Carleson measure.
By studying boundedness and compactness of Cesàro-type operators between different Dirichlet–Morrey spaces (this space is also known as the space Qp), we can obtain Corollaries 4.10 and 4.12, even though these two results have been proved by Galanopoulos–Girela–Merchán [Reference Galanopoulos, Girela and Merchán17].
Acknowledgements
The authors express their heartfelt thanks to the reviewer for his (or her) responsible and professional comments.
Funding Statement
This work was supported by National Natural Science Foundation of China (Grant Nos. 11801094 and 62072119) and NNSF of Guangdong Province (Grant No. 2023A1515010001).