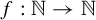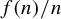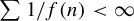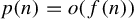1 Introduction
It is well known that there exist dynamical systems in which two seemingly opposite properties can coexist: zero entropy, which implies that a system is in a sense ‘simple’ or ‘deterministic’, and (measure-theoretic) strong mixing, which implies that sets become ‘asymptotically independent’ under repeated application (the first construction of such a system is due to Girsanov, see §15 of [Reference RohlinRoh67]; see also [Reference PinskerPin60]). For the symbolically defined dynamical systems known as subshifts, the concept of word complexity provides further quantification within zero entropy; zero entropy means that word complexity function
![]() $p(n)$
grows subexponentially, but of course one can study slower growth rates as well. Many recent results treat subshifts with very low complexity (see, among others, [Reference Cyr and KraCK15, Reference Cyr and KraCK19, Reference Cyr and KraCK20, Reference Donoso, Durand, Maass and PetiteDDMP16, Reference Dykstra, Ormes and PavlovDOP21, Reference Pavlov and SchmeidingPS22]), showing that they must be ‘simple’ in various ways. In contrast, our results show that such subshifts can still be ‘complex’ in the sense of having a strong mixing measure.
$p(n)$
grows subexponentially, but of course one can study slower growth rates as well. Many recent results treat subshifts with very low complexity (see, among others, [Reference Cyr and KraCK15, Reference Cyr and KraCK19, Reference Cyr and KraCK20, Reference Donoso, Durand, Maass and PetiteDDMP16, Reference Dykstra, Ormes and PavlovDOP21, Reference Pavlov and SchmeidingPS22]), showing that they must be ‘simple’ in various ways. In contrast, our results show that such subshifts can still be ‘complex’ in the sense of having a strong mixing measure.
Using this framework, in [Reference FerencziFer96] Ferenczi described a subshift example supporting a strongly mixing invariant measure whose word complexity satisfies
![]() ${p(q)}/{q^2} \rightarrow 0.5$
. He somewhat glibly conjectured that this was the minimal possible word complexity for such a shift, but also said that he would ‘wait confidently for the next counterexample’. Ferenczi also showed that such a subshift must have
${p(q)}/{q^2} \rightarrow 0.5$
. He somewhat glibly conjectured that this was the minimal possible word complexity for such a shift, but also said that he would ‘wait confidently for the next counterexample’. Ferenczi also showed that such a subshift must have
![]() $\limsup\!{p(q)}/{q} = \infty $
, that is, its word complexity function cannot be bounded from above by any linear function.
$\limsup\!{p(q)}/{q} = \infty $
, that is, its word complexity function cannot be bounded from above by any linear function.
Ferenczi’s example was the symbolic model of a so-called rank-one system. Rank-one systems are traditionally defined by a cutting and stacking procedure on an interval with Lebesgue measure, but they are measure-theoretically isomorphic to the empirical measure on a recursively defined subshift (see [Reference Adams, Ferenczi and PetersenAFP17, Reference DanilenkoDan16]). The rank-one examples from [Reference FerencziFer96] are well-studied examples called staircase transformations, originally defined by Smorodinsky and Adams, and which were proved to be measure-theoretically mixing in [Reference AdamsAda98, Reference Creutz and SilvaCS04, Reference Creutz and SilvaCS10].
Somewhat surprisingly, we show that a fairly simple alteration of the traditional staircase yields rank-one systems, which we call extremely elevated staircase transformations, which have word complexity much lower than quadratic (though unavoidably superlinear) and whose symbolic models are measure-theoretically mixing. We prove several results about how slowly complexity can grow for such examples.
We first show that the complexity
![]() $p(q)$
can grow more slowly than any sequence whose sum of reciprocals converges.
$p(q)$
can grow more slowly than any sequence whose sum of reciprocals converges.
Theorem 4.1. Let
![]() $f : \mathbb {N} \to \mathbb {N}$
be a function such that
$f : \mathbb {N} \to \mathbb {N}$
be a function such that
![]() ${f(q)}/{q}$
is non-decreasing and
${f(q)}/{q}$
is non-decreasing and
![]() $\sum {1}/{f(q)} < \infty $
. Then there exists a (mixing) extremely elevated staircase transformation where
$\sum {1}/{f(q)} < \infty $
. Then there exists a (mixing) extremely elevated staircase transformation where
![]() $\lim ( {p(q)}/{f(q)}) = 0$
.
$\lim ( {p(q)}/{f(q)}) = 0$
.
This is not, however, a necessary restriction on word complexity, as we can construct some examples with even slower growth.
Theorem 4.2. There exists a (mixing) extremely elevated staircase transformation where
![]() $\sum {1}/{p(q)} = \infty $
.
$\sum {1}/{p(q)} = \infty $
.
We also prove that there exist such mixing subshifts with even lower complexity along sequences.
Theorem 4.3. For every
![]() $\epsilon> 0$
, there exists a (mixing) extremely elevated staircase transformation where
$\epsilon> 0$
, there exists a (mixing) extremely elevated staircase transformation where
![]() $\liminf\!{p(q)}/{q (\log q)^\epsilon }= 0$
.
$\liminf\!{p(q)}/{q (\log q)^\epsilon }= 0$
.
However, we then show that there is a superlinear lower bound of
![]() $q\log (q)$
for the complexity function.
$q\log (q)$
for the complexity function.
Theorem 4.4. For every extremely elevated staircase transformation,
![]() $\limsup\!{p(q)}/ {q \log q} = \infty $
.
$\limsup\!{p(q)}/ {q \log q} = \infty $
.
Finally, we show that an extremely elevated staircase cannot achieve linear complexity even along a sequence.
Theorem 4.5. For every extremely elevated staircase transformation,
![]() ${\lim\!{p(q)}/{q} = \infty }$
.
${\lim\!{p(q)}/{q} = \infty }$
.
In the spirit of Ferenczi’s ‘waiting confidently for the next counterexample’, we also wonder whether there are other classes of subshifts supporting mixing measures which can achieve even lower complexity.
Question 1.1. Is there any non-trivial lower bound on complexity growth for all subshifts with a mixing measure, that is, does there exist
![]() $f> 1$
so that
$f> 1$
so that
![]() $\liminf\!{p(q)}/({qf(q)})> 1$
for all such subshifts?
$\liminf\!{p(q)}/({qf(q)})> 1$
for all such subshifts?
Question 1.2. Is there a superlinear lower bound on complexity growth along a sequence for all subshifts with a mixing measure, that is, does there exist unbounded g so that
![]() $\limsup\!{p(q)}/{qg(q)} = \infty $
for all such subshifts?
$\limsup\!{p(q)}/{qg(q)} = \infty $
for all such subshifts?
We note that in Question 1.1, we chose phrasing to admit the possibility that there exist such examples which have linear complexity along a subsequence, as this was not ruled out by Ferenczi’s results and we do not know whether it is possible.
2 Definitions and preliminaries
2.1 General symbolic dynamics and ergodic theory
We begin with some general definitions in ergodic theory.
Definition 2.1. A measure-theoretic dynamical system (MDS) is a quadruple
![]() $(X, \mathcal {B}, \mu , T)$
, where
$(X, \mathcal {B}, \mu , T)$
, where
![]() $(X, \mathcal {B}, \mu )$
is a standard Borel or Lebesgue measure space and
$(X, \mathcal {B}, \mu )$
is a standard Borel or Lebesgue measure space and
![]() $T: X \rightarrow X$
is an invertible measure-preserving map, that is,
$T: X \rightarrow X$
is an invertible measure-preserving map, that is,
![]() $\mu (T^{-1} A) = \mu (A)$
for all
$\mu (T^{-1} A) = \mu (A)$
for all
![]() $A \in \mathcal {B}$
.
$A \in \mathcal {B}$
.
Definition 2.2. An MDS
![]() $(X, \mathcal {B}, \mu , T)$
is ergodic if
$(X, \mathcal {B}, \mu , T)$
is ergodic if
![]() $A = T^{-1} A$
implies that
$A = T^{-1} A$
implies that
![]() $\mu (A) = 0$
or
$\mu (A) = 0$
or
![]() $\mu (A^c) = 0$
.
$\mu (A^c) = 0$
.
A crucial usage of ergodicity is the mean ergodic theorem.
Theorem 2.1. If
![]() $(X, \mathcal {B}, \mu , T)$
is ergodic, then for any
$(X, \mathcal {B}, \mu , T)$
is ergodic, then for any
![]() $f \in L^2(X)$
with
$f \in L^2(X)$
with
![]() $\int f\, d\mu = 0$
,
$\int f\, d\mu = 0$
,
 $$ \begin{align*} \lim_{n \rightarrow \infty} \int \bigg{|} \frac{1}{n} \sum_{i = 0}^{n-1} f \circ T^{-i} \bigg{|}^{2} \, d\mu = 0. \end{align*} $$
$$ \begin{align*} \lim_{n \rightarrow \infty} \int \bigg{|} \frac{1}{n} \sum_{i = 0}^{n-1} f \circ T^{-i} \bigg{|}^{2} \, d\mu = 0. \end{align*} $$
Definition 2.3. An MDS
![]() $(X, \mathcal {B}, \mu , T)$
is strongly mixing if for all
$(X, \mathcal {B}, \mu , T)$
is strongly mixing if for all
![]() $A, B \in \mathcal {B}$
,
$A, B \in \mathcal {B}$
,
![]() $\mu (A \cap T^{-n} B) \rightarrow \mu (A) \mu (B)$
.
$\mu (A \cap T^{-n} B) \rightarrow \mu (A) \mu (B)$
.
Definition 2.4. An MDS
![]() $(X, \mathcal {B}, \mu , T)$
and an MDS
$(X, \mathcal {B}, \mu , T)$
and an MDS
![]() $(X', \mathcal {B}', \mu ', T')$
are measure-theoretically isomorphic if there exists a bijective map
$(X', \mathcal {B}', \mu ', T')$
are measure-theoretically isomorphic if there exists a bijective map
![]() $\phi $
between full measure subsets
$\phi $
between full measure subsets
![]() $X_0 \subset X$
and
$X_0 \subset X$
and
![]() $X^{\prime }_0 \subset X'$
where
$X^{\prime }_0 \subset X'$
where
![]() $\mu (\phi ^{-1} A) = \mu '(A)$
for all measurable
$\mu (\phi ^{-1} A) = \mu '(A)$
for all measurable
![]() $A \subset X^{\prime }_0$
and
$A \subset X^{\prime }_0$
and
![]() $(\phi \circ T)x = (T' \circ \phi )x$
for all
$(\phi \circ T)x = (T' \circ \phi )x$
for all
![]() $x \in X_0$
.
$x \in X_0$
.
Most of the systems we study in this work will be symbolically defined systems called subshifts.
Definition 2.5. A subshift on the finite set
![]() $\mathcal {A}$
is any subset
$\mathcal {A}$
is any subset
![]() $X \subset \mathcal {A}^{\mathbb {Z}}$
which is closed in the product topology and shift-invariant, that is, for all
$X \subset \mathcal {A}^{\mathbb {Z}}$
which is closed in the product topology and shift-invariant, that is, for all
![]() $x = (x(n))_{n \in \mathbb {Z}} \in X$
and
$x = (x(n))_{n \in \mathbb {Z}} \in X$
and
![]() $k \in \mathbb {Z}$
, the translation
$k \in \mathbb {Z}$
, the translation
![]() $(x(n+k))_{n \in \mathbb {Z}}$
of x by k is also in X.
$(x(n+k))_{n \in \mathbb {Z}}$
of x by k is also in X.
Definition 2.6. A word on the finite set
![]() $\mathcal {A}$
is any element of
$\mathcal {A}$
is any element of
![]() $\mathcal {A}^n$
for some n, which is called the length of w and which we denote by
$\mathcal {A}^n$
for some n, which is called the length of w and which we denote by
![]() $\|{w}\|$
. A word w of length
$\|{w}\|$
. A word w of length
![]() $\ell $
is said to be a subword of a word or bi-infinite sequence x if there exists k so that
$\ell $
is said to be a subword of a word or bi-infinite sequence x if there exists k so that
![]() $w(i) = x(i+k)$
for all
$w(i) = x(i+k)$
for all
![]() $1 \leq i \leq \ell $
. When x is a word, say with length m, we say that w is a prefix of x if it occurs at the beginning of x (that is,
$1 \leq i \leq \ell $
. When x is a word, say with length m, we say that w is a prefix of x if it occurs at the beginning of x (that is,
![]() $k = 0$
in the above) and a suffix of x if it occurs at the end of x (that is,
$k = 0$
in the above) and a suffix of x if it occurs at the end of x (that is,
![]() $k = m - \ell $
in the above).
$k = m - \ell $
in the above).
For words
![]() $v,w$
, we denote by
$v,w$
, we denote by
![]() $vw$
their concatenation, that is, the word obtained by following v immediately by w. We use similar notation for concatenations of multiple words, for example,
$vw$
their concatenation, that is, the word obtained by following v immediately by w. We use similar notation for concatenations of multiple words, for example,
![]() $w_1 w_2 \ldots w_n$
. When it is notationally convenient, we may sometimes refer to such a concatenation with product or exponential notation, for example,
$w_1 w_2 \ldots w_n$
. When it is notationally convenient, we may sometimes refer to such a concatenation with product or exponential notation, for example,
![]() $\prod _i w_i$
or
$\prod _i w_i$
or
![]() $0^n$
.
$0^n$
.
Definition 2.7. The language of a subshift X, denoted
![]() $\mathcal {L}(X)$
, is the set of all words w which are subwords of some
$\mathcal {L}(X)$
, is the set of all words w which are subwords of some
![]() $x \in X$
.
$x \in X$
.
Definition 2.8. The word complexity function of a subshift X over
![]() $\mathcal {A}$
is the function
$\mathcal {A}$
is the function
![]() $p_X: \mathbb {N} \rightarrow \mathbb {N}$
defined by
$p_X: \mathbb {N} \rightarrow \mathbb {N}$
defined by
![]() $p_X(n) = |\mathcal {L}(X) \cap \mathcal {A}^n|$
, the number of words of length n in the language of X.
$p_X(n) = |\mathcal {L}(X) \cap \mathcal {A}^n|$
, the number of words of length n in the language of X.
When X is clear from context, we suppress the subscript and just write
![]() $p(n)$
.
$p(n)$
.
Definition 2.9. A word w is right special in a subshift X over
![]() $\{0,1\}$
if
$\{0,1\}$
if
![]() $w0, w1 \in \mathcal {L}(X)$
.
$w0, w1 \in \mathcal {L}(X)$
.
We note that this property is often called right special in the literature. All subshifts we examine are on the alphabet
![]() $\{0,1\}$
, and in this setting we will repeatedly make use of the following basic lemma due to Cassaigne [Reference CassaigneCas97].
$\{0,1\}$
, and in this setting we will repeatedly make use of the following basic lemma due to Cassaigne [Reference CassaigneCas97].
Lemma 2.2. For any subshift X over
![]() $\{0,1\}$
, if we denote by
$\{0,1\}$
, if we denote by
![]() $\mathcal {L}^{\mathrm {RS}}_\ell (X)$
the set of right-special words in X of length
$\mathcal {L}^{\mathrm {RS}}_\ell (X)$
the set of right-special words in X of length
![]() $\ell $
, then for all positive
$\ell $
, then for all positive
![]() $m < n$
,
$m < n$
,
 $$ \begin{align*} p(n) = p(m) + \sum_{\ell = m}^{n-1} |\mathcal{L}^{\mathrm{RS}}_\ell(X)|. \end{align*} $$
$$ \begin{align*} p(n) = p(m) + \sum_{\ell = m}^{n-1} |\mathcal{L}^{\mathrm{RS}}_\ell(X)|. \end{align*} $$
The classical Hedlund–Morse theorem [Reference Morse and HedlundMH38] states that every infinite subshift X has at least one right-special word for each length, and so every such subshift satisfies
![]() ${p(n)> n}$
for all n.
${p(n)> n}$
for all n.
2.2 Rank-one transformations and their symbolic models
A rank-one transformation is an MDS
![]() $(X, \mathcal {B}(X), m, T)$
(from now on referred to just as
$(X, \mathcal {B}(X), m, T)$
(from now on referred to just as
![]() $(X,T)$
) constructed by a so-called cutting and stacking construction; here X represents a (possibly infinite) interval,
$(X,T)$
) constructed by a so-called cutting and stacking construction; here X represents a (possibly infinite) interval,
![]() $\mathcal {B}(X)$
is the induced Borel
$\mathcal {B}(X)$
is the induced Borel
![]() $\sigma $
-algebra from
$\sigma $
-algebra from
![]() $\mathbb {R}$
, and m is Lebesgue measure. We give only a brief introduction here, and refer the reader to [Reference Foreman, Gao, Hill, Silva and WeissFGH+21] or [Reference SilvaSil08] for a more detailed presentation.
$\mathbb {R}$
, and m is Lebesgue measure. We give only a brief introduction here, and refer the reader to [Reference Foreman, Gao, Hill, Silva and WeissFGH+21] or [Reference SilvaSil08] for a more detailed presentation.
The transformation T is defined inductively on larger and larger portions of the space by the use of Rokhlin towers or columns, denoted
![]() $C_n$
. Each column
$C_n$
. Each column
![]() $C_n$
consists of levels
$C_n$
consists of levels
![]() $I_{n,a}$
where
$I_{n,a}$
where
![]() $0 \leq a < h_{n}$
is the height of the level within the column. All levels
$0 \leq a < h_{n}$
is the height of the level within the column. All levels
![]() $I_{n,a}$
in
$I_{n,a}$
in
![]() $C_n$
are intervals with the same length, and the total number of levels in a column is the height of the column, denoted by
$C_n$
are intervals with the same length, and the total number of levels in a column is the height of the column, denoted by
![]() $h_n$
. The transformation T is defined on all levels
$h_n$
. The transformation T is defined on all levels
![]() $I_{n,a}$
except the top one
$I_{n,a}$
except the top one
![]() $I_{n, h_n - 1}$
by sending each
$I_{n, h_n - 1}$
by sending each
![]() $I_{n,a}$
to
$I_{n,a}$
to
![]() $I_{n,a+1}$
using the unique affine map between them.
$I_{n,a+1}$
using the unique affine map between them.
We start with
![]() $C_1=[0,1)$
with height
$C_1=[0,1)$
with height
![]() $h_1=1$
. To obtain
$h_1=1$
. To obtain
![]() $C_{n+1}$
from
$C_{n+1}$
from
![]() $C_n$
, we require a cut sequence
$C_n$
, we require a cut sequence
![]() $\{r_n\}$
such that
$\{r_n\}$
such that
![]() $r_n \geq 1 \: \text { for all } n$
. For each n, we make
$r_n \geq 1 \: \text { for all } n$
. For each n, we make
![]() $r_n$
vertical cuts of
$r_n$
vertical cuts of
![]() $C_n$
to create
$C_n$
to create
![]() $r_n+1$
subcolumns of equal width. We denote a sublevel of
$r_n+1$
subcolumns of equal width. We denote a sublevel of
![]() $C_n$
by
$C_n$
by
![]() $I_{n,a}^{[i]}$
where
$I_{n,a}^{[i]}$
where
![]() $0 \leq a < h_{n}$
is the height of the level within that column, and i represents the position of the subcolumn, where
$0 \leq a < h_{n}$
is the height of the level within that column, and i represents the position of the subcolumn, where
![]() $i=0$
represents the leftmost subcolumn and
$i=0$
represents the leftmost subcolumn and
![]() $i=r_n$
is the rightmost subcolumn. After cutting
$i=r_n$
is the rightmost subcolumn. After cutting
![]() $C_n$
into subcolumns, we add extra intervals called spacers on top of each subcolumn to function as levels of the next column. The spacer sequence
$C_n$
into subcolumns, we add extra intervals called spacers on top of each subcolumn to function as levels of the next column. The spacer sequence
![]() $\{s_{n,i}\}$
specifies how many sublevels to add above each subcolumn, where n represents the column we are working with, i represents the subcolumn that spacers are added above, and
$\{s_{n,i}\}$
specifies how many sublevels to add above each subcolumn, where n represents the column we are working with, i represents the subcolumn that spacers are added above, and
![]() $s_{n,i} \geq 0$
for
$s_{n,i} \geq 0$
for
![]() $0 \leq i\leq r_n$
. Spacers are the same width as the sublevels, act as new levels in the column
$0 \leq i\leq r_n$
. Spacers are the same width as the sublevels, act as new levels in the column
![]() $C_{n+1}$
, and are always taken to be the leftmost intervals in
$C_{n+1}$
, and are always taken to be the leftmost intervals in
![]() $\mathbb {R}$
not currently part of a level. Once the spacers are added on top of the subcolumns, we stack the subcolumns with their spacers right on top of left. This gives us the next column,
$\mathbb {R}$
not currently part of a level. Once the spacers are added on top of the subcolumns, we stack the subcolumns with their spacers right on top of left. This gives us the next column,
![]() $C_{n+1}$
.
$C_{n+1}$
.
Each column
![]() $C_n$
yields a definition of T on
$C_n$
yields a definition of T on
![]() $\bigcup _{a = 0}^{h_n - 2} I_{n,a}$
; it is routine to check that the partially defined map T on
$\bigcup _{a = 0}^{h_n - 2} I_{n,a}$
; it is routine to check that the partially defined map T on
![]() $C_{n+1}$
agrees with that of
$C_{n+1}$
agrees with that of
![]() $C_n$
, extending the definition of T to a portion of the top level of
$C_n$
, extending the definition of T to a portion of the top level of
![]() $C_n$
, where it was previously undefined. Continuing this process gives the sequence of columns
$C_n$
, where it was previously undefined. Continuing this process gives the sequence of columns
![]() $\{C_1, \ldots , C_n, C_{n+1}, \ldots \}$
and T is then the limit of the partially defined maps.
$\{C_1, \ldots , C_n, C_{n+1}, \ldots \}$
and T is then the limit of the partially defined maps.
Though in theory this construction could result in X being an infinite interval with infinite Lebesgue measure, it is known that X has finite measure if and only if
![]() $\sum _{n} ({1}/{r_{n}h_{n}})\sum _{i=0}^{r_{n}} s_{n,i} < \infty $
(see, for example, [Reference Creutz and SilvaCS10]). All rank-one transformations we define will satisfy this condition, and for convenience we always renormalize so that
$\sum _{n} ({1}/{r_{n}h_{n}})\sum _{i=0}^{r_{n}} s_{n,i} < \infty $
(see, for example, [Reference Creutz and SilvaCS10]). All rank-one transformations we define will satisfy this condition, and for convenience we always renormalize so that
![]() $X = [0,1)$
. Since X is always
$X = [0,1)$
. Since X is always
![]() $[0,1)$
equipped with the Lebesgue measure, we hereafter refer to the MDS by just the map T. Every rank-one transformation T is an invertible and ergodic MDS.
$[0,1)$
equipped with the Lebesgue measure, we hereafter refer to the MDS by just the map T. Every rank-one transformation T is an invertible and ergodic MDS.
Remark 2.3. The reader should be aware that we are making
![]() $r_{n}$
cuts and obtaining
$r_{n}$
cuts and obtaining
![]() $r_{n}+1$
subcolumns (following Ferenczi [Reference FerencziFer96]), while other papers (for example, [Reference CreutzCre21]) use
$r_{n}+1$
subcolumns (following Ferenczi [Reference FerencziFer96]), while other papers (for example, [Reference CreutzCre21]) use
![]() $r_{n}$
as the number of subcolumns.
$r_{n}$
as the number of subcolumns.
We will later need the following general bounds for rank-one transformations.
Proposition 2.4. Let
![]() $\{ r_{n} \}$
and
$\{ r_{n} \}$
and
![]() $\{ h_{n} \}$
be the cut and height sequences for a rank-one transformation on a probability space with initial base level
$\{ h_{n} \}$
be the cut and height sequences for a rank-one transformation on a probability space with initial base level
![]() $C_{1}$
. Then
$C_{1}$
. Then
 $$ \begin{align*} \prod_{j=1}^{n-1} (r_{j}+1) \leq h_{n} \leq \frac{1}{\mu(C_{1})}\prod_{j=1}^{n-1} (r_{j}+1) \quad\text{and}\quad \frac{1}{h_{n}}\prod \limits_{j=1}^{n-1} (r_{j}+1) \to \mu(C_{1}). \end{align*} $$
$$ \begin{align*} \prod_{j=1}^{n-1} (r_{j}+1) \leq h_{n} \leq \frac{1}{\mu(C_{1})}\prod_{j=1}^{n-1} (r_{j}+1) \quad\text{and}\quad \frac{1}{h_{n}}\prod \limits_{j=1}^{n-1} (r_{j}+1) \to \mu(C_{1}). \end{align*} $$
Proof. Define
![]() $s_{n} = ({1}/({r_{n}+1})) \sum _{i=0}^{r_{n}} s_{n,i}$
, where
$s_{n} = ({1}/({r_{n}+1})) \sum _{i=0}^{r_{n}} s_{n,i}$
, where
![]() $\{ s_{n,i} \}_{\{r_{n}\}}$
is the spacer sequence so that
$\{ s_{n,i} \}_{\{r_{n}\}}$
is the spacer sequence so that
![]() $\mu (C_{n+1}) = \mu (C_{n}) + s_{n}\mu (I_{n}) = \mu (C_{n})(1 + {s_{n}}/{h_{n}})$
, meaning that
$\mu (C_{n+1}) = \mu (C_{n}) + s_{n}\mu (I_{n}) = \mu (C_{n})(1 + {s_{n}}/{h_{n}})$
, meaning that
![]() $\mu (C_{n}) = \mu (C_{1})\prod _{j=1}^{n-1}(1 + {s_{j}}/{h_{j}} )$
. Since
$\mu (C_{n}) = \mu (C_{1})\prod _{j=1}^{n-1}(1 + {s_{j}}/{h_{j}} )$
. Since
![]() $h_{n+1} = (r_{n}+1)h_{n} + \sum _{i=0}^{r_{n}}s_{n,i} = (r_{n}+1)h_{n} ( 1 + {s_{n}}/{h_{n}})$
and
$h_{n+1} = (r_{n}+1)h_{n} + \sum _{i=0}^{r_{n}}s_{n,i} = (r_{n}+1)h_{n} ( 1 + {s_{n}}/{h_{n}})$
and
![]() $h_{0} = 1$
, we have
$h_{0} = 1$
, we have
![]() $h_{n} = \prod _{j=1}^{n-1} (r_{j}+1)(1 + {s_{j}}/{h_{j}}) = (\prod _{j=1}^{n-1}(r_{j}+1)) ({\mu (C_{n})}/ {\mu (C_{1})})$
and
$h_{n} = \prod _{j=1}^{n-1} (r_{j}+1)(1 + {s_{j}}/{h_{j}}) = (\prod _{j=1}^{n-1}(r_{j}+1)) ({\mu (C_{n})}/ {\mu (C_{1})})$
and
![]() $\mu (C_{n}) \to 1$
.
$\mu (C_{n}) \to 1$
.
In order to discuss word complexity for rank-one transformations, we need to deal with symbolic models. Suppose that T is a rank-one system as defined above, with associated
![]() $\{ r_n \}$
and
$\{ r_n \}$
and
![]() $\{ s_{n,i} \}$
. We will define a subshift
$\{ s_{n,i} \}$
. We will define a subshift
![]() $X(T)$
with alphabet
$X(T)$
with alphabet
![]() $\{0,1\}$
which is measure-theoretically isomorphic to T. Define a sequence of words as follows:
$\{0,1\}$
which is measure-theoretically isomorphic to T. Define a sequence of words as follows:
![]() $B_1 = 0$
, and for every
$B_1 = 0$
, and for every
![]() $n> 1$
,
$n> 1$
,
 $$ \begin{align*} B_{n+1}=B_n1^{s_{n,0}}B_n1^{s_{n,1}}\ldots 1^{s_{n,r_n}}= \prod_{i=0}^{r_n} B_n1^{s_{n,i}}. \end{align*} $$
$$ \begin{align*} B_{n+1}=B_n1^{s_{n,0}}B_n1^{s_{n,1}}\ldots 1^{s_{n,r_n}}= \prod_{i=0}^{r_n} B_n1^{s_{n,i}}. \end{align*} $$
The motivation here should be clear;
![]() $B_n$
is a symbolic coding of the column
$B_n$
is a symbolic coding of the column
![]() $C_n$
, where
$C_n$
, where
![]() $0$
represents levels which come from the first column
$0$
represents levels which come from the first column
![]() $C_1$
, and
$C_1$
, and
![]() $1$
represents levels which are spacers. Define
$1$
represents levels which are spacers. Define
![]() $X(T)$
to consist of all bi-infinite
$X(T)$
to consist of all bi-infinite
![]() $\{0,1\}$
sequences where every subword is a subword of some
$\{0,1\}$
sequences where every subword is a subword of some
![]() $B_n$
. We note that
$B_n$
. We note that
![]() $X(T)$
is not uniquely ergodic if the spacer sequence
$X(T)$
is not uniquely ergodic if the spacer sequence
![]() $\{ s_{n,i} \}$
is unbounded (which will always be the case for us), since the sequence
$\{ s_{n,i} \}$
is unbounded (which will always be the case for us), since the sequence
![]() $1^{\infty }$
is always in
$1^{\infty }$
is always in
![]() $X(T)$
. Nevertheless, there is a ‘natural’ measure associated to
$X(T)$
. Nevertheless, there is a ‘natural’ measure associated to
![]() $X(T)$
.
$X(T)$
.
Definition 2.10. The empirical measure for a symbolic model
![]() $X(T)$
of a rank-one system T is the measure
$X(T)$
of a rank-one system T is the measure
![]() $\mu $
defined by
$\mu $
defined by
for every
![]() $\ell $
and every word w of length
$\ell $
and every word w of length
![]() $\ell $
.
$\ell $
.
It was proved in [Reference Adams, Ferenczi and PetersenAFP17, Reference DanilenkoDan16] (see [Reference Foreman, Gao, Hill, Silva and WeissFGH+21] for a more general definition of rank one which includes odometers in the symbolic setting) that a rank-one MDS T and its symbolic model
![]() $X(T)$
(with empirical measure
$X(T)$
(with empirical measure
![]() $\mu $
) are always measure-theoretically isomorphic, and so the symbolic model is measure-theoretically mixing if and only if the original rank one was. Due to this isomorphism, in the sequel we move back and forth between rank one and symbolic model terminology as needed. For simplicity, we from now on write
$\mu $
) are always measure-theoretically isomorphic, and so the symbolic model is measure-theoretically mixing if and only if the original rank one was. Due to this isomorphism, in the sequel we move back and forth between rank one and symbolic model terminology as needed. For simplicity, we from now on write
![]() $\mathcal {L}(T)$
for the language of
$\mathcal {L}(T)$
for the language of
![]() $X(T)$
, and make the definition.
$X(T)$
, and make the definition.
Definition 2.11. A mixing rank-one subshift is a symbolic model of a rank-one transformation that is mixing with respect to its empirical measure.
3 Extremely elevated staircase transformations
Definition 3.1. An extremely elevated staircase transformation is a rank-one transformation defined by cut sequence
![]() $\{ r_{n} \}$
and elevating sequence
$\{ r_{n} \}$
and elevating sequence
![]() $\{ c_{n} \}$
with spacer sequence given by
$\{ c_{n} \}$
with spacer sequence given by
![]() $s_{n,j} = c_{n} + i$
for
$s_{n,j} = c_{n} + i$
for
![]() $0 \leq i < r_{n}$
and
$0 \leq i < r_{n}$
and
![]() $s_{n,r_{n}} = 0$
. The cut sequence
$s_{n,r_{n}} = 0$
. The cut sequence
![]() $\{ r_{n} \}$
is required to be non-decreasing to infinity with
$\{ r_{n} \}$
is required to be non-decreasing to infinity with
![]() ${r_{n}^{2}}/{h_{n}} \to 0$
and the elevating sequence
${r_{n}^{2}}/{h_{n}} \to 0$
and the elevating sequence
![]() $\{ c_{n} \}$
to satisfy
$\{ c_{n} \}$
to satisfy
![]() $c_{1} \geq 1$
and
$c_{1} \geq 1$
and
![]() $c_{n+1} \geq h_{n} + 2c_{n} + 2r_{n} - 2$
and
$c_{n+1} \geq h_{n} + 2c_{n} + 2r_{n} - 2$
and
![]() $\sum ({c_{n}+r_{n}})/{h_{n}} < \infty $
.
$\sum ({c_{n}+r_{n}})/{h_{n}} < \infty $
.
Theorem 3.1. Let T be an extremely elevated staircase transformation. Then T is mixing (on a finite measure space).
The proof of Theorem 3.1 is postponed to the Appendix.
The symbolic representation of an extremely elevated staircase is
![]() $B_{1} = 0$
and
$B_{1} = 0$
and
![]() $h_{1} = 1$
, and
$h_{1} = 1$
, and
 $$ \begin{align*} B_{n+1} = \bigg( \prod_{i=0}^{r_{n}-1}B_{n}1^{c_{n}+i}\bigg) B_{n} \quad\text{and}\quad h_{n+1} = (r_{n}+1)h_{n} + r_{n}c_{n} + \frac{1}{2}r_{n}(r_{n}-1). \end{align*} $$
$$ \begin{align*} B_{n+1} = \bigg( \prod_{i=0}^{r_{n}-1}B_{n}1^{c_{n}+i}\bigg) B_{n} \quad\text{and}\quad h_{n+1} = (r_{n}+1)h_{n} + r_{n}c_{n} + \frac{1}{2}r_{n}(r_{n}-1). \end{align*} $$
3.1 Right-special words in the language of T
Proposition 3.2. Let T be an extremely elevated staircase transformation with language
![]() $\mathcal {L}(T)$
. If
$\mathcal {L}(T)$
. If
![]() $w \in \mathcal {L}(T)$
is right special then exactly one of the following statements holds:
$w \in \mathcal {L}(T)$
is right special then exactly one of the following statements holds:
-
(1)
 $w = 1^{\|{w}\|}$
; or
$w = 1^{\|{w}\|}$
; or -
(2) w is a suffix of
 $1^{c_{n}+r_{n}-1}B_{n}1^{c_{n}}$
for some n and
$1^{c_{n}+r_{n}-1}B_{n}1^{c_{n}}$
for some n and
 $\|{w}\|> c_{n}$
; or
$\|{w}\|> c_{n}$
; or -
(3) w is a suffix of
 $1^{c_{n}+i-1}B_{n}1^{c_{n}+i}$
for some n and
$1^{c_{n}+i-1}B_{n}1^{c_{n}+i}$
for some n and
 $0 < i < r_{n}$
and
$0 < i < r_{n}$
and
 $\|{w}\|> c_{n}+i$
.
$\|{w}\|> c_{n}+i$
.
Proof. If
![]() $01^{t}0 \in \mathcal {L}(T)$
then there exist
$01^{t}0 \in \mathcal {L}(T)$
then there exist
![]() $m \geq 1$
and
$m \geq 1$
and
![]() $0 \leq j < r_{m}$
such that
$0 \leq j < r_{m}$
such that
![]() $t = c_{m} + j$
as only spacer sequences can appear between
$t = c_{m} + j$
as only spacer sequences can appear between
![]() $0$
s. Since
$0$
s. Since
![]() $c_{n+1} \geq c_{n} + r_{n}$
, for any such word the choice of m is unique. Moreover, since
$c_{n+1} \geq c_{n} + r_{n}$
, for any such word the choice of m is unique. Moreover, since
![]() $01^{c_{m}+j}0$
only appears in
$01^{c_{m}+j}0$
only appears in
![]() $B_{m+1}$
, which is always preceded by
$B_{m+1}$
, which is always preceded by
![]() $1^{c_{m+1}}$
, the word
$1^{c_{m+1}}$
, the word
![]() $01^{c_{m}+j}0$
only appears as a suffix of
$01^{c_{m}+j}0$
only appears as a suffix of
![]() $1^{c_{m+1}}(\prod _{k=0}^{j}B_{m}1^{c_{m}+k})0$
.
$1^{c_{m+1}}(\prod _{k=0}^{j}B_{m}1^{c_{m}+k})0$
.
Let
![]() $w \in \mathcal {L}(T)$
be a right-special word. Since
$w \in \mathcal {L}(T)$
be a right-special word. Since
![]() $c_{1} \geq 1$
, the word
$c_{1} \geq 1$
, the word
![]() $00 \notin \mathcal {L}(T)$
so w does not end with
$00 \notin \mathcal {L}(T)$
so w does not end with
![]() $0$
. If
$0$
. If
![]() $w = 1^{\|{w}\|}$
, it is of the form (1). So we may assume that w ends with
$w = 1^{\|{w}\|}$
, it is of the form (1). So we may assume that w ends with
![]() $1$
and contains at least one
$1$
and contains at least one
![]() $0$
.
$0$
.
Let
![]() $z \in \mathbb {N}$
such that w has
$z \in \mathbb {N}$
such that w has
![]() $01^{z}$
as a suffix.
$01^{z}$
as a suffix.
Since
![]() $w0 \in \mathcal {L}(T)$
,
$w0 \in \mathcal {L}(T)$
,
![]() $01^{z}0 \in \mathcal {L}(T)$
so there exist a unique
$01^{z}0 \in \mathcal {L}(T)$
so there exist a unique
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $0 \leq i < r_{n}$
such that
$0 \leq i < r_{n}$
such that
![]() $z = c_{n} + i$
.
$z = c_{n} + i$
.
First consider when
![]() $i> 0$
. The word
$i> 0$
. The word
![]() $w0$
has
$w0$
has
![]() $01^{c_{n}+i}0$
as a suffix and that word only appears in the word
$01^{c_{n}+i}0$
as a suffix and that word only appears in the word
![]() $B_{n+1}$
, meaning that
$B_{n+1}$
, meaning that
![]() $w0$
and
$w0$
and
![]() $1^{c_{n+1}}(\prod _{j=0}^{i}B_{n}1^{c_{n}+j})0$
have a common suffix.
$1^{c_{n+1}}(\prod _{j=0}^{i}B_{n}1^{c_{n}+j})0$
have a common suffix.
If w has
![]() $01^{c_{n}+i-1}B_{n}1^{c_{n}+i}$
as a suffix then
$01^{c_{n}+i-1}B_{n}1^{c_{n}+i}$
as a suffix then
![]() $w1$
has
$w1$
has
![]() $01^{c_{n}+i-1}B_{n}1^{c_{n}+i+1}$
as a suffix but
$01^{c_{n}+i-1}B_{n}1^{c_{n}+i+1}$
as a suffix but
![]() $01^{c_{n}+i-1}B_{n}1^{c_{n}+i+1} \notin \mathcal {L}(T)$
. Therefore, w is a suffix of
$01^{c_{n}+i-1}B_{n}1^{c_{n}+i+1} \notin \mathcal {L}(T)$
. Therefore, w is a suffix of
![]() $1^{c_{n}+i-1}B_{n}1^{c_{n}+i}$
and has length
$1^{c_{n}+i-1}B_{n}1^{c_{n}+i}$
and has length
![]() $\|{w}\| \geq c_{n} + i + 1$
, so w is of the form (3).
$\|{w}\| \geq c_{n} + i + 1$
, so w is of the form (3).
We are left with the case when
![]() $i = 0$
, that is, when
$i = 0$
, that is, when
![]() $z = c_{n}$
.
$z = c_{n}$
.
The word
![]() $w0$
has
$w0$
has
![]() $01^{c_{n}}0$
as a suffix and
$01^{c_{n}}0$
as a suffix and
![]() $01^{c_{n}}0$
only appears in the word
$01^{c_{n}}0$
only appears in the word
![]() $B_{n+1}$
, and only immediately after the first
$B_{n+1}$
, and only immediately after the first
![]() $B_{n}$
in
$B_{n}$
in
![]() $B_{n+1}$
. As the word
$B_{n+1}$
. As the word
![]() $B_{n+1}$
is always preceded by
$B_{n+1}$
is always preceded by
![]() $1^{c_{n+1}}$
, it follows that
$1^{c_{n+1}}$
, it follows that
![]() $w0$
and
$w0$
and
![]() $1^{c_{n+1}}B_{n}1^{c_{n}}0$
have a common suffix.
$1^{c_{n+1}}B_{n}1^{c_{n}}0$
have a common suffix.
If w has
![]() $1^{c_{n}+r_{n}}B_{n}1^{c_{n}}$
as a suffix then
$1^{c_{n}+r_{n}}B_{n}1^{c_{n}}$
as a suffix then
![]() $w1$
has
$w1$
has
![]() $1^{c_{n} + r_{n}}B_{n}1^{c_{n}+1}$
as a suffix but
$1^{c_{n} + r_{n}}B_{n}1^{c_{n}+1}$
as a suffix but
![]() $1^{c_{n} + r_{n}}B_{n}1^{c_{n}+1} \notin \mathcal {L}(T)$
.
$1^{c_{n} + r_{n}}B_{n}1^{c_{n}+1} \notin \mathcal {L}(T)$
.
So w is a suffix of
![]() $1^{c_{n}+r_{n}-1}B_{n}1^{c_{n}}$
of length
$1^{c_{n}+r_{n}-1}B_{n}1^{c_{n}}$
of length
![]() $\|{w}\| \geq c_{n} + 1$
, meaning w is of the form (2).
$\|{w}\| \geq c_{n} + 1$
, meaning w is of the form (2).
Lemma 3.3.
![]() $1^{\ell }$
is right special for all
$1^{\ell }$
is right special for all
![]() $\ell $
.
$\ell $
.
Proof. Find n such that
![]() $\ell \leq \|{1^{c_{n}}}\|$
. Then
$\ell \leq \|{1^{c_{n}}}\|$
. Then
![]() $1^{\ell }0$
is a suffix of
$1^{\ell }0$
is a suffix of
![]() $1^{c_{n}}0$
and
$1^{c_{n}}0$
and
![]() $1^{\ell }1$
is a suffix of
$1^{\ell }1$
is a suffix of
![]() $1^{c_{n}+1}$
.
$1^{c_{n}+1}$
.
Lemma 3.4. If w is a suffix of
![]() $1^{c_{n}+r_{n}-1}B_{n}1^{c_{n}}$
then w is right special.
$1^{c_{n}+r_{n}-1}B_{n}1^{c_{n}}$
then w is right special.
Proof. Choose any such w. Observe that
![]() $B_{n+2}$
has
$B_{n+2}$
has
![]() $B_{n+1}1^{c_{n+1}}B_{n+1}$
as a subword and that has the subword
$B_{n+1}1^{c_{n+1}}B_{n+1}$
as a subword and that has the subword
![]() $B_{n+1}1^{c_{n+1}}B_{n}1^{c_{n}}B_{n}$
. That word has
$B_{n+1}1^{c_{n+1}}B_{n}1^{c_{n}}B_{n}$
. That word has
![]() $1^{c_{n}+r_{n}-1}B_{n}1^{c_{n}}0$
as a subword since
$1^{c_{n}+r_{n}-1}B_{n}1^{c_{n}}0$
as a subword since
![]() $c_{n}+r_{n}-1 < c_{n+1}$
and so
$c_{n}+r_{n}-1 < c_{n+1}$
and so
![]() $w0$
, being a suffix of
$w0$
, being a suffix of
![]() $1^{c_{n}+r_{n}-1}B_{n}1^{c_{n}}0$
, is in
$1^{c_{n}+r_{n}-1}B_{n}1^{c_{n}}0$
, is in
![]() $\mathcal {L}(T)$
. Also
$\mathcal {L}(T)$
. Also
![]() $B_{n+2}$
has
$B_{n+2}$
has
![]() $B_{n+1}1^{c_{n+1}}$
as a subword which has
$B_{n+1}1^{c_{n+1}}$
as a subword which has
![]() $1^{c_{n}+r_{n}-1}B_{n}1^{c_{n+1}}$
as a subword which then has
$1^{c_{n}+r_{n}-1}B_{n}1^{c_{n+1}}$
as a subword which then has
![]() $1^{c_{n}+r_{n}-1}B_{n}1^{c_{n}}1$
as a subword. As
$1^{c_{n}+r_{n}-1}B_{n}1^{c_{n}}1$
as a subword. As
![]() $w1$
is a suffix of that word,
$w1$
is a suffix of that word,
![]() $w1 \in \mathcal {L}(T)$
.
$w1 \in \mathcal {L}(T)$
.
Lemma 3.5. If w is a suffix of
![]() $1^{c_{n}+i-1}B_{n}1^{c_{n}+i}$
for
$1^{c_{n}+i-1}B_{n}1^{c_{n}+i}$
for
![]() $0 < i < r_{n}$
then w is right special.
$0 < i < r_{n}$
then w is right special.
Proof. Choose any such w. Since
![]() $B_{n+1}$
has
$B_{n+1}$
has
![]() $1^{c_{n}+i-1}B_{n}1^{c_{n}+i}B_{n}$
as a subword,
$1^{c_{n}+i-1}B_{n}1^{c_{n}+i}B_{n}$
as a subword,
![]() $1^{c_{n}+i-1} B_{n} 1^{c_{n}+i}0 \in \mathcal {L}(T)$
. When
$1^{c_{n}+i-1} B_{n} 1^{c_{n}+i}0 \in \mathcal {L}(T)$
. When
![]() $i < r_{n} - 1$
,
$i < r_{n} - 1$
,
![]() $B_{n+1}$
has
$B_{n+1}$
has
![]() $1^{c_{n}+i}B_{n}1^{c_{n}+i+1}$
as a subword, which gives
$1^{c_{n}+i}B_{n}1^{c_{n}+i+1}$
as a subword, which gives
![]() $11^{c_{n}+i-1}B_{n}1^{c_{n}+i}1$
; when
$11^{c_{n}+i-1}B_{n}1^{c_{n}+i}1$
; when
![]() $i = r_{n}-1$
,
$i = r_{n}-1$
,
![]() $B_{n+2}$
has
$B_{n+2}$
has
![]() $1^{c_{n}+r_{n}-1}B_{n}1^{c_{n+1}}$
as a subword, which gives
$1^{c_{n}+r_{n}-1}B_{n}1^{c_{n+1}}$
as a subword, which gives
![]() $11^{c_{n} + r_{n} - 2}B_{n}1^{c_{n}+r_{n}-1}1$
as
$11^{c_{n} + r_{n} - 2}B_{n}1^{c_{n}+r_{n}-1}1$
as
![]() $r_{n} < c_{n+1}$
. As w is a suffix of
$r_{n} < c_{n+1}$
. As w is a suffix of
![]() $1^{c_{n}+i-1}B_{n}1^{c_{n}+i}$
, it is right special.
$1^{c_{n}+i-1}B_{n}1^{c_{n}+i}$
, it is right special.
Lemma 3.6. Let T be an extremely elevated staircase transformation. For
![]() $w \in \mathcal {L}(T)$
, let n be the unique integer such that w has
$w \in \mathcal {L}(T)$
, let n be the unique integer such that w has
![]() $1^{c_{n}}$
as a subword and does not have
$1^{c_{n}}$
as a subword and does not have
![]() $1^{c_{n+1}}$
as a subword.
$1^{c_{n+1}}$
as a subword.
Then w is right special if and only if exactly one of the following statements holds:
-
(1)
 $w = 1^{\|{w}\|}$
and
$w = 1^{\|{w}\|}$
and
 $c_{n} \leq \ell < c_{n+1}$
; or
$c_{n} \leq \ell < c_{n+1}$
; or -
(2) w is a suffix of
 $1^{c_{n}+i-1}B_{n}1^{c_{n}+i}$
and
$1^{c_{n}+i-1}B_{n}1^{c_{n}+i}$
and
 $\|{w}\|> c_{n}+i$
for some
$\|{w}\|> c_{n}+i$
for some
 $0 \leq i < r_{n}$
; or
$0 \leq i < r_{n}$
; or -
(3) w is a suffix of
 $1^{c_{n}+r_{n}-1}B_{n}1^{c_{n}}$
and
$1^{c_{n}+r_{n}-1}B_{n}1^{c_{n}}$
and
 $\|{w}\| \geq h_{n} + 2c_{n}$
.
$\|{w}\| \geq h_{n} + 2c_{n}$
.
Proof. The only words in Proposition 3.2 which have
![]() $1^{c_{n}}$
as a subword,
$1^{c_{n}}$
as a subword,
![]() $1^{c_{n+1}}$
not a subword and at least one
$1^{c_{n+1}}$
not a subword and at least one
![]() $0$
are of the stated forms, and Lemmas 3.3, 3.4 and 3.5 state that these words are right special. The restriction on
$0$
are of the stated forms, and Lemmas 3.3, 3.4 and 3.5 state that these words are right special. The restriction on
![]() $\|{w}\|$
in form (3)
$\|{w}\|$
in form (3)
![]() ${}_{n}$
prevents any overlap between forms (2)
${}_{n}$
prevents any overlap between forms (2)
![]() ${}_{n}$
and (3)
${}_{n}$
and (3)
![]() ${}_{n}$
; the requirement that
${}_{n}$
; the requirement that
![]() $\|{w}\|> c_{n} + i$
ensures no overlap with form (1)
$\|{w}\|> c_{n} + i$
ensures no overlap with form (1)
![]() ${}_{n}$
by either of the other two.
${}_{n}$
by either of the other two.
The largest length we need consider for a given n is then
![]() $h_{n} + 2c_{n} + 2(r_{n}-1) - 1$
, explaining the requirement on
$h_{n} + 2c_{n} + 2(r_{n}-1) - 1$
, explaining the requirement on
![]() $c_{n+1}$
in the definition of extremely elevated staircases and leading to the following definition.
$c_{n+1}$
in the definition of extremely elevated staircases and leading to the following definition.
Definition 3.2. The post-productive sequence is
![]() $ m_{n} = h_{n} + 2c_{n} + 2r_{n} - 2 $
.
$ m_{n} = h_{n} + 2c_{n} + 2r_{n} - 2 $
.
Proposition 3.7. For an extremely elevated staircase transformation, there is at most one right-special word of each of the forms in Lemma 3.6. Furthermore,
-
(1) there is a word of the form (1)
 ${}_{n}$
only for
${}_{n}$
only for
 $c_{n} \leq \ell < c_{n+1}$
; and
$c_{n} \leq \ell < c_{n+1}$
; and -
(2) for each
 $0 \leq i < r_{n}$
, there is a word of the form (2)
$0 \leq i < r_{n}$
, there is a word of the form (2)
 ${}_{n}$
for that value of i only for
${}_{n}$
for that value of i only for
 $c_{n} + i < \ell \leq h_{n} + 2c_{n} + 2i - 1$
; and
$c_{n} + i < \ell \leq h_{n} + 2c_{n} + 2i - 1$
; and -
(3) there is a word of the form (3)
 ${}_{n}$
only for
${}_{n}$
only for
 $h_{n} + 2c_{n} \leq \ell < h_{n} + 2c_{n} + r_{n}$
.
$h_{n} + 2c_{n} \leq \ell < h_{n} + 2c_{n} + r_{n}$
.
Proof. Every w of a form in Lemma 3.6 for a given n has length
![]() $c_{n} \leq \|{w}\| < m_{n} \leq c_{n+1}$
, so for every length
$c_{n} \leq \|{w}\| < m_{n} \leq c_{n+1}$
, so for every length
![]() $\ell $
there is exactly one n for which Lemma 3.6 could potentially give a right-special word.
$\ell $
there is exactly one n for which Lemma 3.6 could potentially give a right-special word.
![]() $1^{\ell }$
is of the form (1)
$1^{\ell }$
is of the form (1)
![]() ${}_{n}$
for
${}_{n}$
for
![]() $c_{n} \leq \ell < c_{n+1}$
.
$c_{n} \leq \ell < c_{n+1}$
.
If w is of the form (2)
![]() ${}_{n}$
, it is a suffix of
${}_{n}$
, it is a suffix of
![]() $1^{c_{n}+r_{n}-1}B_{n}1^{c_{n}}$
, so
$1^{c_{n}+r_{n}-1}B_{n}1^{c_{n}}$
, so
![]() $\|{w}\| \leq \|{1^{c_{n}+r_{n}-1}B_{n}1^{c_{n}}}\| = h_{n} + 2c_{n} + r_{n} - 1$
.
$\|{w}\| \leq \|{1^{c_{n}+r_{n}-1}B_{n}1^{c_{n}}}\| = h_{n} + 2c_{n} + r_{n} - 1$
.
If w is of the form (3)
![]() ${}_{n}$
, it is a suffix of
${}_{n}$
, it is a suffix of
![]() $1^{c_{n}+i-1}B_{n}1^{c_{n}+i}$
, so
$1^{c_{n}+i-1}B_{n}1^{c_{n}+i}$
, so
![]() $\|{w}\| \leq \|{1^{c_{n}+i-1}B_{n}1^{c_{n}+i}}\| = h_{n} + 2c_{n} + 2i - 1$
.
$\|{w}\| \leq \|{1^{c_{n}+i-1}B_{n}1^{c_{n}+i}}\| = h_{n} + 2c_{n} + 2i - 1$
.
3.2 Counting right-special words of length
 $\ell $
for extremely elevated staircases
$\ell $
for extremely elevated staircases
Lemma 3.8. If
![]() $c_n \leq \ell < c_n + r_n$
then
$c_n \leq \ell < c_n + r_n$
then
![]() $p(\ell +1)-p(\ell )=(\ell -c_n)+1$
.
$p(\ell +1)-p(\ell )=(\ell -c_n)+1$
.
Proof. Proposition 3.7 gives one word of the form (1)
![]() ${}_{n}$
and one of the form (2)
${}_{n}$
and one of the form (2)
![]() ${}_{n}$
for each
${}_{n}$
for each
![]() $0 \leq i < \ell - c_{n}$
.
$0 \leq i < \ell - c_{n}$
.
Lemma 3.9. If
![]() $c_n+r_n \leq \ell \leq h_n+2c_n+1$
then
$c_n+r_n \leq \ell \leq h_n+2c_n+1$
then
![]() $p(\ell +1)-p(\ell )=r_n+1$
.
$p(\ell +1)-p(\ell )=r_n+1$
.
Proof. Proposition 3.7 gives one word of the form (1)
![]() ${}_{n}$
and one for each
${}_{n}$
and one for each
![]() $0 \leq i < r_{n}$
of the form (2)
$0 \leq i < r_{n}$
of the form (2)
![]() ${}_{n}$
.
${}_{n}$
.
Lemma 3.10. If
![]() $h_n+2c_n+1 < \ell \leq h_n+2c_n+r_n-1$
then
$h_n+2c_n+1 < \ell \leq h_n+2c_n+r_n-1$
then
![]() $p(\ell + 1) - p(\ell ) = r_n - \lceil \tfrac 12(\ell -(h_n+2c_n+1)) \rceil + 1$
.
$p(\ell + 1) - p(\ell ) = r_n - \lceil \tfrac 12(\ell -(h_n+2c_n+1)) \rceil + 1$
.
Proof. Proposition 3.7 gives one word of the form (1)
![]() ${}_{n}$
, one word of the form (3)
${}_{n}$
, one word of the form (3)
![]() ${}_{n}$
and, for
${}_{n}$
and, for
![]() $0 \leq i < r_{n}$
, one of the form (2) for
$0 \leq i < r_{n}$
, one of the form (2) for
![]() $0 \leq i < r_{n}$
only if
$0 \leq i < r_{n}$
only if
![]() $\ell \leq h_{n} + 2c_{n} + 2i - 1$
, so only when
$\ell \leq h_{n} + 2c_{n} + 2i - 1$
, so only when
![]() $x = \ell - h_{n} - 2c_{n} - 1 \leq 2i - 2$
, so only when
$x = \ell - h_{n} - 2c_{n} - 1 \leq 2i - 2$
, so only when
![]() $i \geq \lceil (x+2)/2 \rceil $
. This gives exactly
$i \geq \lceil (x+2)/2 \rceil $
. This gives exactly
![]() $r_{n}-1 - \lceil x/2 \rceil $
words of the form (2)
$r_{n}-1 - \lceil x/2 \rceil $
words of the form (2)
![]() ${}_{n}$
.
${}_{n}$
.
Lemma 3.11. If
![]() $h_n+2c_n+r_n \leq \ell \leq h_n+2c_n+2r_n-3$
then
$h_n+2c_n+r_n \leq \ell \leq h_n+2c_n+2r_n-3$
then
![]() $p(\ell + 1) - p(\ell ) = r_n - \lceil \tfrac 12(\ell -(h_n+2c_n+1)) \rceil $
.
$p(\ell + 1) - p(\ell ) = r_n - \lceil \tfrac 12(\ell -(h_n+2c_n+1)) \rceil $
.
Proof. The proof of Lemma 3.10 holds here except that we do not get a word of the form (3)
![]() ${}_{n}$
.
${}_{n}$
.
Lemma 3.12. If
![]() $m_{n} \leq \ell < c_{n+1}$
, then
$m_{n} \leq \ell < c_{n+1}$
, then
![]() $p(\ell +1)-p(\ell )=1$
.
$p(\ell +1)-p(\ell )=1$
.
Proof. Proposition 3.7 gives only the word
![]() $1^{\ell }$
of length
$1^{\ell }$
of length
![]() $\ell \geq m_{n}$
.
$\ell \geq m_{n}$
.
3.3 Counting words in the language of extremely elevated staircases
Proposition 3.13. If T is an extremely elevated staircase transformation and
![]() $c_n<q\leq c_{n+1}$
, then
$c_n<q\leq c_{n+1}$
, then
Proof. From Lemmas 3.8–3.12, for
![]() $c_m\leq \ell < c_{m+1}$
it always holds that
$c_m\leq \ell < c_{m+1}$
it always holds that
![]() $p(\ell +1)-p(\ell ) \leq r_m+1$
, so
$p(\ell +1)-p(\ell ) \leq r_m+1$
, so
 $$ \begin{align*} p(q) = p(c_{n}) + \sum_{\ell=c_{n}}^{q-1} (p(\ell+1)-p(\ell)) \leq p(c_{n}) + (q - c_{n})(r_{n} + 1) \end{align*} $$
$$ \begin{align*} p(q) = p(c_{n}) + \sum_{\ell=c_{n}}^{q-1} (p(\ell+1)-p(\ell)) \leq p(c_{n}) + (q - c_{n})(r_{n} + 1) \end{align*} $$
and, since
![]() $r_m \leq r_n$
for all
$r_m \leq r_n$
for all
![]() $m\leq n$
,
$m\leq n$
,
 $$ \begin{align*} p(c_{n}) = \sum \limits_{\ell=1}^{c_{n}} (p(\ell+1)-p(\ell)) \leq \sum \limits_{\ell=1}^{c_{n}} (r_n+1) = c_{n}(r_n+1).\\[-46pt] \end{align*} $$
$$ \begin{align*} p(c_{n}) = \sum \limits_{\ell=1}^{c_{n}} (p(\ell+1)-p(\ell)) \leq \sum \limits_{\ell=1}^{c_{n}} (r_n+1) = c_{n}(r_n+1).\\[-46pt] \end{align*} $$
Proposition 3.14. For an extremely elevated staircase transformation,
![]() $ p(m_{n}) \geq h_{n+1}. $
$ p(m_{n}) \geq h_{n+1}. $
Proof. By Lemma 3.8,
![]() $p(c_{n}+r_{n}) - p(c_{n}) = \tfrac 12r_{n}(r_{n}+1)$
. There are
$p(c_{n}+r_{n}) - p(c_{n}) = \tfrac 12r_{n}(r_{n}+1)$
. There are
![]() $r_{n}-2+\sum _{x=0}^{2(r_{n}-2)} (r_{n} - \lceil {x}/{2}\rceil )$
words from Lemmas 3.10 and 3.11 of lengths
$r_{n}-2+\sum _{x=0}^{2(r_{n}-2)} (r_{n} - \lceil {x}/{2}\rceil )$
words from Lemmas 3.10 and 3.11 of lengths
![]() $h_{n} + 2_{n} + 2 \leq \ell \leq h_{n} + 2c_{n} + 2r_{n} - 3$
, therefore
$h_{n} + 2_{n} + 2 \leq \ell \leq h_{n} + 2c_{n} + 2r_{n} - 3$
, therefore
![]() $p(h_{n}+2c_{n}+2r_{n}-2) - p(h_{n}+2c_{n}+1) = r_{n}^{2}-4$
. By Lemma 3.9,
$p(h_{n}+2c_{n}+2r_{n}-2) - p(h_{n}+2c_{n}+1) = r_{n}^{2}-4$
. By Lemma 3.9,
![]() $p(h_{n}+2c_{n}+1) - p(c_{n}+r_{n}) = (r_{n}+1)(h_{n}+c_{n}-r_{n}+2)$
so
$p(h_{n}+2c_{n}+1) - p(c_{n}+r_{n}) = (r_{n}+1)(h_{n}+c_{n}-r_{n}+2)$
so
4 Mixing rank-one subshifts with low complexity
Theorem 4.1. Let
![]() $f : \mathbb {N} \to \mathbb {N}$
be a function such that
$f : \mathbb {N} \to \mathbb {N}$
be a function such that
![]() ${f(q)}/{q}$
is non-decreasing and
${f(q)}/{q}$
is non-decreasing and
![]() $\sum {1}/{f(q)} < \infty $
. Then there exists a (mixing) extremely elevated staircase transformation where
$\sum {1}/{f(q)} < \infty $
. Then there exists a (mixing) extremely elevated staircase transformation where
![]() $\lim\!{p(q)}/{f(q)} = 0$
.
$\lim\!{p(q)}/{f(q)} = 0$
.
Proof. The function
![]() $g(q) = \min (f(q),q^{3/2})$
is non-decreasing as it is the minimum of two non-decreasing functions and
$g(q) = \min (f(q),q^{3/2})$
is non-decreasing as it is the minimum of two non-decreasing functions and
![]() ${g(q)}/{q}$
is the minimum of
${g(q)}/{q}$
is the minimum of
![]() ${f(q)}/{q}$
and
${f(q)}/{q}$
and
![]() $q^{1/2}$
so is also non-decreasing. Replacing
$q^{1/2}$
so is also non-decreasing. Replacing
![]() $f(q)$
by
$f(q)$
by
![]() $g(q)$
if necessary, we may assume that
$g(q)$
if necessary, we may assume that
![]() $f(q) \leq q^{3/2}$
for all q.
$f(q) \leq q^{3/2}$
for all q.
Note that
![]() ${f(q)}/{q} \to \infty $
since it is non-decreasing and if
${f(q)}/{q} \to \infty $
since it is non-decreasing and if
![]() $f(q) \leq Cq$
then
$f(q) \leq Cq$
then
![]() $\sum {1}/{f(q)} \geq (1/C) \sum {1}/{q} = \infty $
.
$\sum {1}/{f(q)} \geq (1/C) \sum {1}/{q} = \infty $
.
Set
![]() $x_{1} = 1$
and choose
$x_{1} = 1$
and choose
![]() $x_{t}$
such that
$x_{t}$
such that
![]() $\sum _{q=x_{t}}^{\infty}{1}/{f(q)} \leq t^{-3}$
and
$\sum _{q=x_{t}}^{\infty}{1}/{f(q)} \leq t^{-3}$
and
![]() ${f(q)}/{q} \geq t^{2}$
for
${f(q)}/{q} \geq t^{2}$
for
![]() $q \geq x_{t}$
.
$q \geq x_{t}$
.
Set
![]() $r_{1} = 2$
and
$r_{1} = 2$
and
![]() $c_{1} = 1$
. Given
$c_{1} = 1$
. Given
![]() $r_{n}$
and
$r_{n}$
and
![]() $c_{n}$
, let
$c_{n}$
, let
![]() $t_{n}$
such that
$t_{n}$
such that
![]() $x_{t_{n}} \leq c_{n} < x_{t_{n}+1}$
and set
$x_{t_{n}} \leq c_{n} < x_{t_{n}+1}$
and set
 $$ \begin{align*} c_{n+1} = m_{n}\quad \text{and}\quad r_{n+1} = \bigg\lceil{\frac{f(c_{n+1})}{t_{n}(c_{n+1} - c_{n})}}\bigg\rceil. \end{align*} $$
$$ \begin{align*} c_{n+1} = m_{n}\quad \text{and}\quad r_{n+1} = \bigg\lceil{\frac{f(c_{n+1})}{t_{n}(c_{n+1} - c_{n})}}\bigg\rceil. \end{align*} $$
Since
![]() $r_{n+1} \geq ({f(c_{n+1}})/{c_{n+1}}) \cdot ({1}/{t_{n}}) \geq {t_{n}^{2}}/{t_{n}} \to \infty $
, we have that
$r_{n+1} \geq ({f(c_{n+1}})/{c_{n+1}}) \cdot ({1}/{t_{n}}) \geq {t_{n}^{2}}/{t_{n}} \to \infty $
, we have that
![]() $r_{n}$
non-decreasing to
$r_{n}$
non-decreasing to
![]() $\infty $
.
$\infty $
.
Let
![]() $n_{t} = \inf \{ n : c_{n} \geq x_{t} \}$
so that
$n_{t} = \inf \{ n : c_{n} \geq x_{t} \}$
so that
![]() $t_{n} = t$
for
$t_{n} = t$
for
![]() $n_{t} \leq n < n_{t+1}$
. Since f is increasing,
$n_{t} \leq n < n_{t+1}$
. Since f is increasing,
 $$ \begin{align*} \sum_{n=1}^{\infty} \frac{1}{r_{n}} &\leq \sum_{n=1}^{\infty} \frac{1}{{f(c_{n})}/({t_{n-1}(c_{n} - c_{n-1})})} = \sum_{n=1}^{\infty} \frac{t_{n-1}(c_{n} - c_{n-1})}{f(c_{n})}= \sum_{n=1}^{\infty} \sum_{\ell=c_{n-1}}^{c_{n}-1} \frac{t_{n-1}}{f(c_{n})} \\ &\leq \sum_{n=1}^{\infty} \sum_{\ell=c_{n-1}}^{c_{n}-1} \frac{t_{n-1}}{f(\ell)} = \sum_{t=1}^{\infty} \sum_{n=n_{t}+1}^{n_{t+1}} \sum_{\ell=c_{n-1}}^{c_{n}+1} \frac{t}{f(\ell)} = \sum_{t=1}^{\infty} \sum_{\ell=c_{n_{t}}}^{c_{n_{t+1}}-1} \frac{t}{f(\ell)} \nonumber \\&\leq \sum_{t=1}^{\infty} t \sum_{\ell=x_{t}}^{\infty} \frac{1}{f(\ell)} \leq \sum_{t=1}^{\infty} \frac{t}{t^{3}} < \infty. \end{align*} $$
$$ \begin{align*} \sum_{n=1}^{\infty} \frac{1}{r_{n}} &\leq \sum_{n=1}^{\infty} \frac{1}{{f(c_{n})}/({t_{n-1}(c_{n} - c_{n-1})})} = \sum_{n=1}^{\infty} \frac{t_{n-1}(c_{n} - c_{n-1})}{f(c_{n})}= \sum_{n=1}^{\infty} \sum_{\ell=c_{n-1}}^{c_{n}-1} \frac{t_{n-1}}{f(c_{n})} \\ &\leq \sum_{n=1}^{\infty} \sum_{\ell=c_{n-1}}^{c_{n}-1} \frac{t_{n-1}}{f(\ell)} = \sum_{t=1}^{\infty} \sum_{n=n_{t}+1}^{n_{t+1}} \sum_{\ell=c_{n-1}}^{c_{n}+1} \frac{t}{f(\ell)} = \sum_{t=1}^{\infty} \sum_{\ell=c_{n_{t}}}^{c_{n_{t+1}}-1} \frac{t}{f(\ell)} \nonumber \\&\leq \sum_{t=1}^{\infty} t \sum_{\ell=x_{t}}^{\infty} \frac{1}{f(\ell)} \leq \sum_{t=1}^{\infty} \frac{t}{t^{3}} < \infty. \end{align*} $$
Since
![]() $h_{n+1} \geq r_{n}(h_{n} + c_{n})$
and
$h_{n+1} \geq r_{n}(h_{n} + c_{n})$
and
![]() $2r_{n} \leq h_{n}$
,
$2r_{n} \leq h_{n}$
,
 $$ \begin{align*} \sum_{n} \frac{c_{n+1}}{h_{n+1}} \leq \sum_{n} \frac{h_{n} + 2c_{n} + 2r_{n} - 2}{r_{n}(h_{n}+c_{n})} \leq \sum_{n} \frac{2(h_{n}+c_{n})}{r_{n}(h_{n} + c_{n})} = 2\sum_{n} \frac{1}{r_{n}} \end{align*} $$
$$ \begin{align*} \sum_{n} \frac{c_{n+1}}{h_{n+1}} \leq \sum_{n} \frac{h_{n} + 2c_{n} + 2r_{n} - 2}{r_{n}(h_{n}+c_{n})} \leq \sum_{n} \frac{2(h_{n}+c_{n})}{r_{n}(h_{n} + c_{n})} = 2\sum_{n} \frac{1}{r_{n}} \end{align*} $$
and therefore
![]() $\sum ({c_{n}}/{h_{n}}) < \infty $
. Since
$\sum ({c_{n}}/{h_{n}}) < \infty $
. Since
![]() $f(q) \leq q^{3/2}$
,
$f(q) \leq q^{3/2}$
,
 $$ \begin{align*} \frac{r_{n}^{2}}{h_{n}} &\leq \frac{(f(c_{n}))^{2}}{h_{n}t_{n-1}^{2}(c_{n} - c_{n-1})^{2}} \leq \frac{(c_{n}^{3/2})^{2}}{h_{n}c_{n}^{2}}\bigg(\frac{c_{n}}{c_{n} - c_{n-1}}\bigg)^{2} \frac{1}{t_{n-1}^{2}} \\[6pt] &= \frac{c_{n}}{h_{n}} \bigg(\frac{1}{1 - {c_{n-1}}/{c_{n}}}\bigg)^{2} \frac{1}{t_{n-1}^{2}} \to 0 \end{align*} $$
$$ \begin{align*} \frac{r_{n}^{2}}{h_{n}} &\leq \frac{(f(c_{n}))^{2}}{h_{n}t_{n-1}^{2}(c_{n} - c_{n-1})^{2}} \leq \frac{(c_{n}^{3/2})^{2}}{h_{n}c_{n}^{2}}\bigg(\frac{c_{n}}{c_{n} - c_{n-1}}\bigg)^{2} \frac{1}{t_{n-1}^{2}} \\[6pt] &= \frac{c_{n}}{h_{n}} \bigg(\frac{1}{1 - {c_{n-1}}/{c_{n}}}\bigg)^{2} \frac{1}{t_{n-1}^{2}} \to 0 \end{align*} $$
as
![]() ${c_{n-1}}/{c_{n}} \leq {c_{n-1}}/{h_{n-1}} \to 0$
. Then the transformation T with cut sequence
${c_{n-1}}/{c_{n}} \leq {c_{n-1}}/{h_{n-1}} \to 0$
. Then the transformation T with cut sequence
![]() $\{ r_{n} \}$
and elevating sequence
$\{ r_{n} \}$
and elevating sequence
![]() $\{ c_{n} \}$
satisfies all the conditions required to be an extremely elevated staircase, so Theorem 3.1 gives that T is mixing on a finite measure space.
$\{ c_{n} \}$
satisfies all the conditions required to be an extremely elevated staircase, so Theorem 3.1 gives that T is mixing on a finite measure space.
Given q, choose n such that
![]() $c_{n} < q \leq c_{n+1}$
. Using the fact that
$c_{n} < q \leq c_{n+1}$
. Using the fact that
![]() ${f(q)}/{q}$
is non-decreasing (and so
${f(q)}/{q}$
is non-decreasing (and so
![]() $q> c_{n}$
implies
$q> c_{n}$
implies
![]() ${f(c_{n})}/{c_{n}} \leq {f(q)}/{q}$
) and tends to infinity, by Proposition 3.13,
${f(c_{n})}/{c_{n}} \leq {f(q)}/{q}$
) and tends to infinity, by Proposition 3.13,
 $$ \begin{align*} \frac{p(q)}{f(q)} &\leq \frac{q(r_{n} + 1)}{f(q)} \leq \frac{q}{f(q)} \bigg(\frac{f(c_{n})}{t_{n-1}(c_{n} - c_{n-1})} + 2\bigg) \\[6pt]& = \frac{q}{f(q)} \bigg(\frac{1}{t_{n-1}} \frac{f(c_{n})}{c_{n}}~\frac{1}{1 - {c_{n-1}}/{c_{n}}} + 2 \bigg) \\[6pt] &\leq \frac{q}{f(q)} \bigg(\frac{1}{t_{n-1}}\frac{f(q)}{q}~\frac{1}{1 - {c_{n-1}}/{c_{n}}} + 2 \bigg) = \frac{1}{t_{n-1}} \cdot \frac{1}{1 - {c_{n-1}}/{c_{n}}} + 2\frac{q}{f(q)} \to 0. \end{align*} $$
$$ \begin{align*} \frac{p(q)}{f(q)} &\leq \frac{q(r_{n} + 1)}{f(q)} \leq \frac{q}{f(q)} \bigg(\frac{f(c_{n})}{t_{n-1}(c_{n} - c_{n-1})} + 2\bigg) \\[6pt]& = \frac{q}{f(q)} \bigg(\frac{1}{t_{n-1}} \frac{f(c_{n})}{c_{n}}~\frac{1}{1 - {c_{n-1}}/{c_{n}}} + 2 \bigg) \\[6pt] &\leq \frac{q}{f(q)} \bigg(\frac{1}{t_{n-1}}\frac{f(q)}{q}~\frac{1}{1 - {c_{n-1}}/{c_{n}}} + 2 \bigg) = \frac{1}{t_{n-1}} \cdot \frac{1}{1 - {c_{n-1}}/{c_{n}}} + 2\frac{q}{f(q)} \to 0. \end{align*} $$
4.1 Even lower complexity
It is natural to wonder whether the hypothesis of Theorem 4.1 is necessary. This is, however, not the case: there exist mixing elevated rank ones with even lower complexity.
Theorem 4.2. There exists a (mixing) extremely elevated staircase transformation where
![]() $\sum {1}/{p(q)} = \infty $
.
$\sum {1}/{p(q)} = \infty $
.
Proof. Fix
![]() $0 < \epsilon \leq 1$
and set
$0 < \epsilon \leq 1$
and set
![]() $r_{n} = \lceil (n+1)(\log (n+1))^{1+\epsilon } \rceil - 1$
and
$r_{n} = \lceil (n+1)(\log (n+1))^{1+\epsilon } \rceil - 1$
and
![]() $c_{1} = 1$
and
$c_{1} = 1$
and
![]() ${c_{n+1} = m_{n}}$
. As
${c_{n+1} = m_{n}}$
. As
![]() $h_{n} \geq \prod _{j=1}^{n-1} r_{j} \geq \prod _{j=1}^{n-1} (j+1) = n!$
we have
$h_{n} \geq \prod _{j=1}^{n-1} r_{j} \geq \prod _{j=1}^{n-1} (j+1) = n!$
we have
![]() ${r_{n}^{2}}/{h_{n}} \to 0$
. By the integral comparison test,
${r_{n}^{2}}/{h_{n}} \to 0$
. By the integral comparison test,
![]() $\sum {1}/{r_{n}} < \infty $
. Then
$\sum {1}/{r_{n}} < \infty $
. Then
![]() $\sum {c_{n}}/{h_{n}} < \infty $
, following the same reasoning as in the proof of Theorem 4.1. So, by Theorem 3.1, the extremely elevated staircase transformation T with cut sequence
$\sum {c_{n}}/{h_{n}} < \infty $
, following the same reasoning as in the proof of Theorem 4.1. So, by Theorem 3.1, the extremely elevated staircase transformation T with cut sequence
![]() $\{ r_{n} \}$
and elevating sequence
$\{ r_{n} \}$
and elevating sequence
![]() $\{ c_{n} \}$
is mixing on a finite measure space.
$\{ c_{n} \}$
is mixing on a finite measure space.
Then
![]() $c_{n} + r_{n} \leq h_{n}$
for large n, so
$c_{n} + r_{n} \leq h_{n}$
for large n, so
![]() $c_{n} = h_{n-1} + 2c_{n-1} + 2r_{n-1} - 2 \leq 3h_{n-1}$
. Since
$c_{n} = h_{n-1} + 2c_{n-1} + 2r_{n-1} - 2 \leq 3h_{n-1}$
. Since
![]() $1/x$
is a decreasing positive function for
$1/x$
is a decreasing positive function for
![]() $x> 0$
, a Riemann sum approximation gives
$x> 0$
, a Riemann sum approximation gives
![]() $\sum _{q=a+1}^{b} {1}/{q} \geq \int _{a+1}^{b+1} ({1}/{x})\,dx = \log (b+1) - \log (a+1)$
. Employing Proposition 3.13,
$\sum _{q=a+1}^{b} {1}/{q} \geq \int _{a+1}^{b+1} ({1}/{x})\,dx = \log (b+1) - \log (a+1)$
. Employing Proposition 3.13,
 $$ \begin{align*} &\sum_{q=2}^{\infty} \frac{1}{p(q)} = \sum_{n} \sum_{q=c_{n}+1}^{c_{n+1}} \frac{1}{p(q)} \geq \sum_{n} \sum_{q=c_{n}+1}^{c_{n+1}} \frac{1}{q(r_{n}+1)} = \sum_{n} \frac{1}{r_{n}+1} \sum_{q=c_{n}+1}^{c_{n+1}} \frac{1}{q} \\[6pt] &\quad\geq \sum_{n} \frac{1}{r_{n}+1} \log\bigg(\frac{c_{n+1}+1}{c_{n}+1}\bigg) \geq \sum_{n} \frac{1}{r_{n}+1} \log\bigg(\frac{h_{n}}{3h_{n-1}}\bigg)\\[6pt] &\quad\geq \sum_{n} \frac{1}{r_{n}+1} \log\bigg(\frac{(r_{n-1}+1)h_{n-1}}{3h_{n-1}}\bigg) \\[6pt] &\quad\geq \sum_{n} \frac{1}{(n+1)(\log(n+1))^{1 + \epsilon}} \bigg(\log(n(\log(n))^{1+\epsilon}-1) - \log(3)\bigg) \\[6pt] &\quad\geq \sum_{n} \frac{1}{(n+1)(\log(n+1))^{1 + \epsilon}} \bigg(\log(n) - \log(3)\bigg) \\[6pt] &\quad= \sum_{n} \frac{1}{(n+1)(\log(n+1))^{\epsilon}}\frac{\log(n)}{\log(n+1)} - (\log(3))\sum_{n} \frac{1}{(n+1)(\log(n+1))^{1 + \epsilon}} \end{align*} $$
$$ \begin{align*} &\sum_{q=2}^{\infty} \frac{1}{p(q)} = \sum_{n} \sum_{q=c_{n}+1}^{c_{n+1}} \frac{1}{p(q)} \geq \sum_{n} \sum_{q=c_{n}+1}^{c_{n+1}} \frac{1}{q(r_{n}+1)} = \sum_{n} \frac{1}{r_{n}+1} \sum_{q=c_{n}+1}^{c_{n+1}} \frac{1}{q} \\[6pt] &\quad\geq \sum_{n} \frac{1}{r_{n}+1} \log\bigg(\frac{c_{n+1}+1}{c_{n}+1}\bigg) \geq \sum_{n} \frac{1}{r_{n}+1} \log\bigg(\frac{h_{n}}{3h_{n-1}}\bigg)\\[6pt] &\quad\geq \sum_{n} \frac{1}{r_{n}+1} \log\bigg(\frac{(r_{n-1}+1)h_{n-1}}{3h_{n-1}}\bigg) \\[6pt] &\quad\geq \sum_{n} \frac{1}{(n+1)(\log(n+1))^{1 + \epsilon}} \bigg(\log(n(\log(n))^{1+\epsilon}-1) - \log(3)\bigg) \\[6pt] &\quad\geq \sum_{n} \frac{1}{(n+1)(\log(n+1))^{1 + \epsilon}} \bigg(\log(n) - \log(3)\bigg) \\[6pt] &\quad= \sum_{n} \frac{1}{(n+1)(\log(n+1))^{\epsilon}}\frac{\log(n)}{\log(n+1)} - (\log(3))\sum_{n} \frac{1}{(n+1)(\log(n+1))^{1 + \epsilon}} \end{align*} $$
and the left sum diverges as
![]() $\epsilon \leq 1$
while the right sum converges as
$\epsilon \leq 1$
while the right sum converges as
![]() $\epsilon> 0$
.
$\epsilon> 0$
.
4.2 Even lower complexity along sequences
We are able to achieve even lower complexity for mixing subshifts along a sequence of lengths.
Theorem 4.3. For every
![]() $\epsilon> 0$
, there exists a (mixing) extremely elevated staircase transformation where
$\epsilon> 0$
, there exists a (mixing) extremely elevated staircase transformation where
![]() $\liminf {p(q)}/{q (\log q)^\epsilon }= 0$
.
$\liminf {p(q)}/{q (\log q)^\epsilon }= 0$
.
Proof. Set
![]() $\alpha = \lceil (1 + \epsilon )/\epsilon \rceil $
. Since
$\alpha = \lceil (1 + \epsilon )/\epsilon \rceil $
. Since
![]() $\alpha> 1$
, the function
$\alpha> 1$
, the function
![]() $x^{\alpha }$
is increasing, so a Riemann sum approximation gives
$x^{\alpha }$
is increasing, so a Riemann sum approximation gives
![]() $\sum _{j=1}^{n-1} j^{\alpha } \geq \int _{0}^{n-1} x^{\alpha }\,dx = (n-1)^{1+\alpha }/(1 + \alpha )$
. An easy induction argument shows
$\sum _{j=1}^{n-1} j^{\alpha } \geq \int _{0}^{n-1} x^{\alpha }\,dx = (n-1)^{1+\alpha }/(1 + \alpha )$
. An easy induction argument shows
![]() $\sum _{j=1}^{n-1} j^{\alpha } \leq n^{1 + \alpha }$
. So, writing
$\sum _{j=1}^{n-1} j^{\alpha } \leq n^{1 + \alpha }$
. So, writing
![]() $d = 1/(1 + \alpha )$
, we have
$d = 1/(1 + \alpha )$
, we have
![]() $d(n-1)^{1+\alpha } \leq \sum _{j=1}^{n-1} j^{\alpha } \leq n^{1+\alpha }$
.
$d(n-1)^{1+\alpha } \leq \sum _{j=1}^{n-1} j^{\alpha } \leq n^{1+\alpha }$
.
Construct T inductively by setting
![]() $r_1=1$
and
$r_1=1$
and
![]() $c_1=1$
and, for
$c_1=1$
and, for
![]() $n> 1$
,
$n> 1$
,
 $$ \begin{align*} r_{n} = 2^{n^{\alpha}} - 1 \quad\text{and}\quad c_{n} = \bigg{\lceil} \frac{h_{n}}{n^{1+\epsilon}} \bigg{\rceil}. \end{align*} $$
$$ \begin{align*} r_{n} = 2^{n^{\alpha}} - 1 \quad\text{and}\quad c_{n} = \bigg{\lceil} \frac{h_{n}}{n^{1+\epsilon}} \bigg{\rceil}. \end{align*} $$
Then
![]() $\sum {c_{n}}/{h_{n}} \leq \sum {1}/{n^{1+\epsilon }} + {1}/{h_{n}} < \infty $
. Since
$\sum {c_{n}}/{h_{n}} \leq \sum {1}/{n^{1+\epsilon }} + {1}/{h_{n}} < \infty $
. Since
 $$ \begin{align*} \prod_{j=1}^{n-1} (r_{j} + 1) = \prod_{j=1}^{n-1} 2^{j^{\alpha}} = 2^{\sum_{j=1}^{n-1} j^{\alpha}}, \text{ we have } 2^{d(n-1)^{1+\alpha}} \leq \prod_{j=1}^{n-1} (r_{j}+1) \leq 2^{n^{1+\alpha}}. \end{align*} $$
$$ \begin{align*} \prod_{j=1}^{n-1} (r_{j} + 1) = \prod_{j=1}^{n-1} 2^{j^{\alpha}} = 2^{\sum_{j=1}^{n-1} j^{\alpha}}, \text{ we have } 2^{d(n-1)^{1+\alpha}} \leq \prod_{j=1}^{n-1} (r_{j}+1) \leq 2^{n^{1+\alpha}}. \end{align*} $$
By Proposition 2.4, we then have that for some constant K,
![]() $ 2^{d(n-1)^{1+\alpha }} \leq h_{n} \leq K \cdot 2^{n^{1+\alpha }}$
. Then
$ 2^{d(n-1)^{1+\alpha }} \leq h_{n} \leq K \cdot 2^{n^{1+\alpha }}$
. Then
 $$ \begin{align*} \frac{r_{n}^{3}}{h_{n}} \leq \frac{2^{3n^{\alpha}}}{2^{d(n-1)^{1+\alpha}}} \to 0\quad \text{since}\quad \frac{d(n-1)^{1+\alpha}-3n^{\alpha}}{n^{\alpha}} = d\bigg(1-\frac{1}{n}\bigg)^{\alpha}(n-1) - 3 \to \infty. \end{align*} $$
$$ \begin{align*} \frac{r_{n}^{3}}{h_{n}} \leq \frac{2^{3n^{\alpha}}}{2^{d(n-1)^{1+\alpha}}} \to 0\quad \text{since}\quad \frac{d(n-1)^{1+\alpha}-3n^{\alpha}}{n^{\alpha}} = d\bigg(1-\frac{1}{n}\bigg)^{\alpha}(n-1) - 3 \to \infty. \end{align*} $$
To see that T is an extremely elevated staircase transformation (hence is mixing on a finite measure space by Theorem 3.1), we observe that
 $$ \begin{align*} \frac{m_{n}}{c_{n+1}} \leq \frac{3h_{n}}{h_{n+1}/(n+1)^{1 + \epsilon}} \leq \frac{3h_{n}(n+1)^{1 + \epsilon}}{r_{n}h_{n}} = \frac{3(n+1)^{1+\epsilon}}{r_{n}} \to 0. \end{align*} $$
$$ \begin{align*} \frac{m_{n}}{c_{n+1}} \leq \frac{3h_{n}}{h_{n+1}/(n+1)^{1 + \epsilon}} \leq \frac{3h_{n}(n+1)^{1 + \epsilon}}{r_{n}h_{n}} = \frac{3(n+1)^{1+\epsilon}}{r_{n}} \to 0. \end{align*} $$
We may apply Lemma 3.12 to get
![]() $p(c_{n+1}) = p(m_{n}) + (c_{n+1} - m_{n})$
. Then Proposition 3.13 gives
$p(c_{n+1}) = p(m_{n}) + (c_{n+1} - m_{n})$
. Then Proposition 3.13 gives
Since
![]() $\log (c_{n}) \geq \log (h_{n}) - (1+\epsilon )\log (n) \geq \log (2^{d(n-1)^{1+\alpha }}) - 2\log (n)$
, using that
$\log (c_{n}) \geq \log (h_{n}) - (1+\epsilon )\log (n) \geq \log (2^{d(n-1)^{1+\alpha }}) - 2\log (n)$
, using that
![]() $\alpha \epsilon \geq ((1+\epsilon )/\epsilon )\epsilon = \epsilon + 1$
,
$\alpha \epsilon \geq ((1+\epsilon )/\epsilon )\epsilon = \epsilon + 1$
,
 $$ \begin{align*} \liminf \frac{c_{n}(\log(c_{n}))^{\epsilon}}{h_{n}} &\geq \liminf \frac{(d(n-1)^{1+\alpha})^{\epsilon}}{n^{1+\epsilon}} \geq \liminf \frac{d^{\epsilon} (n-1)^{\epsilon + \alpha\epsilon}}{n^{1+\epsilon}} \\[6pt] & \geq \liminf \frac{d^{\epsilon}(n-1)^{1+2\epsilon}}{n^{1+\epsilon}} = \liminf d^{\epsilon}\bigg(1- \frac{1}{n}\bigg)^{1+\epsilon}(n-1)^{\epsilon} = \infty. \end{align*} $$
$$ \begin{align*} \liminf \frac{c_{n}(\log(c_{n}))^{\epsilon}}{h_{n}} &\geq \liminf \frac{(d(n-1)^{1+\alpha})^{\epsilon}}{n^{1+\epsilon}} \geq \liminf \frac{d^{\epsilon} (n-1)^{\epsilon + \alpha\epsilon}}{n^{1+\epsilon}} \\[6pt] & \geq \liminf \frac{d^{\epsilon}(n-1)^{1+2\epsilon}}{n^{1+\epsilon}} = \liminf d^{\epsilon}\bigg(1- \frac{1}{n}\bigg)^{1+\epsilon}(n-1)^{\epsilon} = \infty. \end{align*} $$
Therefore,
4.3 A lower bound on the complexity
Our constructions, however, do not attain complexity as low as
![]() $q \log (q)$
.
$q \log (q)$
.
Theorem 4.4. For every extremely elevated staircase transformation,
![]() $\limsup\!{p(q)}/ {q \log q} = \infty $
.
$\limsup\!{p(q)}/ {q \log q} = \infty $
.
Proof. Since T is extremely elevated,
![]() $\infty> \sum _{n} {c_{n+1}}/{h_{n+1}} \geq \sum _{n} {h_{n}}/({3(r_{n}+1)h_{n}}) = \tfrac 13 \sum _{n} {1}/{r_{n}} $
. By Proposition 3.14,
$\infty> \sum _{n} {c_{n+1}}/{h_{n+1}} \geq \sum _{n} {h_{n}}/({3(r_{n}+1)h_{n}}) = \tfrac 13 \sum _{n} {1}/{r_{n}} $
. By Proposition 3.14,
By Proposition 2.4 there exists a constant K such that
![]() $h_{n} \leq K\prod _{j=1}^{n-1}r_{j}$
, so
$h_{n} \leq K\prod _{j=1}^{n-1}r_{j}$
, so
![]() $\log (h_{n}/K) \leq \sum _{j=1}^{n-1} \log (r_{j})$
.
$\log (h_{n}/K) \leq \sum _{j=1}^{n-1} \log (r_{j})$
.
Consider first when
![]() $r_{n} \leq n^{2}$
for infinitely many n. Write
$r_{n} \leq n^{2}$
for infinitely many n. Write
![]() $r_{n} + 1 = (n+1) \log (n+1) z_{n}$
. Then
$r_{n} + 1 = (n+1) \log (n+1) z_{n}$
. Then
![]() $z_{n} \to \infty $
since
$z_{n} \to \infty $
since
![]() $\sum {1}/{r_{n}} < \infty $
and
$\sum {1}/{r_{n}} < \infty $
and
![]() $z_{n} \leq n+1$
as we have assumed
$z_{n} \leq n+1$
as we have assumed
![]() $r_{n} \leq n^{2}$
,
$r_{n} \leq n^{2}$
,
 $$ \begin{align*} \sum_{j=1}^{n-1} \log(r_{j}) &= \sum_{j=1}^{n-1} (\log(j+1) + \log(\log(j+1)) + \log(z_{j})) \\[6pt] &\leq \sum_{j=1}^{n-1} 3\log(j+1)\leq 3n\log(n). \end{align*} $$
$$ \begin{align*} \sum_{j=1}^{n-1} \log(r_{j}) &= \sum_{j=1}^{n-1} (\log(j+1) + \log(\log(j+1)) + \log(z_{j})) \\[6pt] &\leq \sum_{j=1}^{n-1} 3\log(j+1)\leq 3n\log(n). \end{align*} $$
So, as
![]() $z_{n} \to \infty $
,
$z_{n} \to \infty $
,
Now consider when
![]() $r_{n}> n^{2}$
for all sufficiently large n. Then as
$r_{n}> n^{2}$
for all sufficiently large n. Then as
![]() $\log (x) \leq x^{1/3}$
for large x and
$\log (x) \leq x^{1/3}$
for large x and
![]() $\log (h_{n}) \leq n\log (n+1) + \log (K)$
, as
$\log (h_{n}) \leq n\log (n+1) + \log (K)$
, as
![]() $r_{n}$
is increasing,
$r_{n}$
is increasing,
 $$ \begin{align*} \liminf \frac{r_{n}+1}{\log(h_{n})} &\geq \liminf \frac{r_{n}+1}{n\log(r_{n}+1)} \geq \liminf \frac{r_{n}}{nr_{n}^{1/3}} = \liminf \frac{r_{n}^{2/3}}{n} \\[6pt] & \geq \liminf \frac{n^{4/3}}{n} = \infty. \end{align*} $$
$$ \begin{align*} \liminf \frac{r_{n}+1}{\log(h_{n})} &\geq \liminf \frac{r_{n}+1}{n\log(r_{n}+1)} \geq \liminf \frac{r_{n}}{nr_{n}^{1/3}} = \liminf \frac{r_{n}^{2/3}}{n} \\[6pt] & \geq \liminf \frac{n^{4/3}}{n} = \infty. \end{align*} $$
In both cases, we have
![]() $\liminf ({r_{n}+1})/{\log (h_{n})} \to \infty $
. By equation
$\liminf ({r_{n}+1})/{\log (h_{n})} \to \infty $
. By equation
![]() $(\star )$
, this completes the proof.
$(\star )$
, this completes the proof.
4.4 Linear complexity is unattainable even along a sequence
Though the complexity along a sequence can be lower than
![]() $q \log (q)$
, it cannot be linear.
$q \log (q)$
, it cannot be linear.
Theorem 4.5. For every extremely elevated staircase transformation,
![]() $\lim\!{p(q)}/ {q} = \infty $
.
$\lim\!{p(q)}/ {q} = \infty $
.
Proof. Let
![]() $\epsilon> 0$
. Then there exists N such that for
$\epsilon> 0$
. Then there exists N such that for
![]() $n \geq N$
, we have
$n \geq N$
, we have
![]() $({c_{n}+r_{n}})/{h_{n}} < \epsilon $
(since T is on a finite measure space) and
$({c_{n}+r_{n}})/{h_{n}} < \epsilon $
(since T is on a finite measure space) and
![]() $r_{n} \geq 1/\epsilon $
(since
$r_{n} \geq 1/\epsilon $
(since
![]() $r_{n} \to \infty $
is necessary for T to be mixing).
$r_{n} \to \infty $
is necessary for T to be mixing).
For
![]() $q \geq m_{N-1}$
, choose
$q \geq m_{N-1}$
, choose
![]() $n \geq N$
such that
$n \geq N$
such that
![]() $m_{n-1} \leq q < m_{n}$
.
$m_{n-1} \leq q < m_{n}$
.
If
![]() $m_{n-1} \leq q < 2(c_{n} + r_{n})$
then, using Proposition 3.14,
$m_{n-1} \leq q < 2(c_{n} + r_{n})$
then, using Proposition 3.14,
For
![]() $c_{n} + r_{n} \leq q < h_{n} + 2c_{n}$
, by Lemma 3.9,
$c_{n} + r_{n} \leq q < h_{n} + 2c_{n}$
, by Lemma 3.9,
![]() $p(q) - p(c_{n}+r_{n}) \geq (q - c_{n} - r_{n})r_{n}$
. Then, for
$p(q) - p(c_{n}+r_{n}) \geq (q - c_{n} - r_{n})r_{n}$
. Then, for
![]() $2(c_{n} + r_{n}) \leq q < h_{n} + 2c_{n} + 1$
,
$2(c_{n} + r_{n}) \leq q < h_{n} + 2c_{n} + 1$
,
 $$ \begin{align*} \frac{p(q)}{q} \geq \frac{(q - c_{n} - r_{n})r_{n}}{q} \geq \bigg(1 - \frac{c_{n}+r_{n}}{q}\bigg) r_{n} \geq \frac{1}{2}r_{n}> \frac{1}{2\epsilon}. \end{align*} $$
$$ \begin{align*} \frac{p(q)}{q} \geq \frac{(q - c_{n} - r_{n})r_{n}}{q} \geq \bigg(1 - \frac{c_{n}+r_{n}}{q}\bigg) r_{n} \geq \frac{1}{2}r_{n}> \frac{1}{2\epsilon}. \end{align*} $$
For
![]() $h_{n} + 2c_{n} + 1 \leq q < m_{n}$
, we have
$h_{n} + 2c_{n} + 1 \leq q < m_{n}$
, we have
![]() $p(q) \geq p(h_{n} + 2c_{n}) \geq (h_{n} + c_{n} - r_{n})r_{n}$
. Provided
$p(q) \geq p(h_{n} + 2c_{n}) \geq (h_{n} + c_{n} - r_{n})r_{n}$
. Provided
![]() $\epsilon < 1/4$
, we have
$\epsilon < 1/4$
, we have
![]() $(1 - \epsilon )/(1+2\epsilon ) \geq 1/2$
, so for
$(1 - \epsilon )/(1+2\epsilon ) \geq 1/2$
, so for
![]() $h_{n} + 2c_{n} \leq q < m_{n}$
,
$h_{n} + 2c_{n} \leq q < m_{n}$
,
Taking
![]() $\epsilon \to 0$
then gives
$\epsilon \to 0$
then gives
![]() ${p(q)}/{q} \to \infty $
as for all sufficiently large q we have
${p(q)}/{q} \to \infty $
as for all sufficiently large q we have
![]() ${p(q)}/{q}> {1}/{2\epsilon }$
.
${p(q)}/{q}> {1}/{2\epsilon }$
.
Acknowledgements
We wish to thank the referee for helpful suggestions regarding terminology and organization of the results. The second author gratefully acknowledges the support of a Simons Foundation Collaboration Grant.
A Appendix. Mixing for extremely elevated staircase transformations
For our proof of mixing, we do not need the full strength of extremely elevated staircase transformations and so will define a more general class.
Definition A.1. A rank-one transformation is an elevated staircase transformation when it has non-decreasing cut sequence
![]() $\{ r_{n} \}$
tending to infinity with
$\{ r_{n} \}$
tending to infinity with
![]() ${r_{n}^{2}}/{h_{n}} \to 0$
, and spacer sequence given by
${r_{n}^{2}}/{h_{n}} \to 0$
, and spacer sequence given by
![]() $s_{n,i} = c_{n} + i$
for
$s_{n,i} = c_{n} + i$
for
![]() $0 \leq i < r_{n}$
and
$0 \leq i < r_{n}$
and
![]() $s_{n,r_n} = 0$
for some sequence
$s_{n,r_n} = 0$
for some sequence
![]() $\{ c_{n} \}$
such that
$\{ c_{n} \}$
such that
![]() $c_{n+1} \geq c_{n} + r_{n}$
and
$c_{n+1} \geq c_{n} + r_{n}$
and
![]() $\sum ({c_{n} + r_{n}})/{h_{n}} < \infty $
.
$\sum ({c_{n} + r_{n}})/{h_{n}} < \infty $
.
This is the same class as the more natural
![]() $s_{n,i} = e_{n} + i$
for a sequence
$s_{n,i} = e_{n} + i$
for a sequence
![]() $\{ e_{n} \}$
required to satisfy no condition beyond
$\{ e_{n} \}$
required to satisfy no condition beyond
![]() $e_{n} \geq 0$
(and
$e_{n} \geq 0$
(and
![]() $\sum ({1}/{h_{n}}) \sum _{j \leq n} e_{j} < \infty $
to ensure finite measure). In particular, traditional staircases, corresponding to
$\sum ({1}/{h_{n}}) \sum _{j \leq n} e_{j} < \infty $
to ensure finite measure). In particular, traditional staircases, corresponding to
![]() $e_{n} = 0$
, are in the class of elevated staircase transformations.
$e_{n} = 0$
, are in the class of elevated staircase transformations.
Proposition A.1. Let
![]() $\{ e_{n} \}$
be a sequence of non-negative integers. Let
$\{ e_{n} \}$
be a sequence of non-negative integers. Let
![]() $\tilde {T}$
be the rank-one transformation with cut sequence
$\tilde {T}$
be the rank-one transformation with cut sequence
![]() $\{ r_{n} \}$
and spacer sequence
$\{ r_{n} \}$
and spacer sequence
![]() $\{ \tilde {s}_{n,i} \}$
given by
$\{ \tilde {s}_{n,i} \}$
given by
![]() $\tilde {s}_{n,i} = e_{n} + i$
for
$\tilde {s}_{n,i} = e_{n} + i$
for
![]() $0 \leq i \leq r_{n}$
. Let T be the rank-one transformation with cut sequence
$0 \leq i \leq r_{n}$
. Let T be the rank-one transformation with cut sequence
![]() $\{ r_{n} \}$
and elevating sequence
$\{ r_{n} \}$
and elevating sequence
![]() $\{ c_{n} \}$
given by
$\{ c_{n} \}$
given by
![]() $c_{1} = e_{1}$
and
$c_{1} = e_{1}$
and
![]() $c_{n+1} = e_{n+1} + \sum _{j=1}^{n} (e_{j} + r_{j}) = e_{n+1} + c_{n} + r_{n}$
and spacer sequence given by
$c_{n+1} = e_{n+1} + \sum _{j=1}^{n} (e_{j} + r_{j}) = e_{n+1} + c_{n} + r_{n}$
and spacer sequence given by
![]() $s_{n,i} = c_{n}+i$
for
$s_{n,i} = c_{n}+i$
for
![]() $0 \leq i < r_{n}$
and
$0 \leq i < r_{n}$
and
![]() $s_{n,r_{n}} = 0$
. Then T and
$s_{n,r_{n}} = 0$
. Then T and
![]() $\tilde {T}$
generate the same subshift (and are measure-theoretically isomorphic).
$\tilde {T}$
generate the same subshift (and are measure-theoretically isomorphic).
Proof. If
![]() $\tilde {B}_{n}$
are the words representing the
$\tilde {B}_{n}$
are the words representing the
![]() $\tilde {s}_{n,i}$
construction and
$\tilde {s}_{n,i}$
construction and
![]() $B_{n}$
those of T, then
$B_{n}$
those of T, then
![]() $\tilde {B}_{1} = B_{1} = 0$
,
$\tilde {B}_{1} = B_{1} = 0$
,
![]() $\tilde {B}_{n+1} = \prod _{i=1}^{r_{n}} \tilde {B}_{n}1^{e_{n}+i}$
and
$\tilde {B}_{n+1} = \prod _{i=1}^{r_{n}} \tilde {B}_{n}1^{e_{n}+i}$
and
![]() $B_{n} = (\prod _{i=0}^{r_{n}-1}B_{n}1^{c_{n}+i})B_{n}$
, and we claim that
$B_{n} = (\prod _{i=0}^{r_{n}-1}B_{n}1^{c_{n}+i})B_{n}$
, and we claim that
![]() $\tilde {B}_{n+1} = B_{n+1}1^{\sum _{j=1}^{n}(e_{j}+r_{j})}$
for all
$\tilde {B}_{n+1} = B_{n+1}1^{\sum _{j=1}^{n}(e_{j}+r_{j})}$
for all
![]() $n \geq 1$
. The base case is
$n \geq 1$
. The base case is
 $$ \begin{align*} \tilde{B}_{2} = \prod_{i=0}^{r_{1}}\tilde{B}_{1}1^{e_{1}+i} = \bigg(\prod_{i=0}^{r_{1}-1}\tilde{B}_{1}1^{e_{1}+i}\bigg) \tilde{B}_{1}1^{e_{1}+r_{1}} = \bigg(\prod_{i=0}^{r_{1}-1}B_{1}1^{c_{1}+i}\bigg) B_{1}1^{e_{1}+r_{1}} \end{align*} $$
$$ \begin{align*} \tilde{B}_{2} = \prod_{i=0}^{r_{1}}\tilde{B}_{1}1^{e_{1}+i} = \bigg(\prod_{i=0}^{r_{1}-1}\tilde{B}_{1}1^{e_{1}+i}\bigg) \tilde{B}_{1}1^{e_{1}+r_{1}} = \bigg(\prod_{i=0}^{r_{1}-1}B_{1}1^{c_{1}+i}\bigg) B_{1}1^{e_{1}+r_{1}} \end{align*} $$
as claimed since
![]() $c_{1} = e_{1}$
. Assume the claim holds for n and then
$c_{1} = e_{1}$
. Assume the claim holds for n and then
 $$ \begin{align*} \tilde{B}_{n+2} &= \prod_{i=0}^{r_{n+1}}\tilde{B}_{n+1}1^{e_{n+1}+i} = \bigg(\prod_{i=0}^{r_{n+1}-1}\tilde{B}_{n+1}1^{e_{n+1}+i}\bigg) \tilde{B}_{n+1}1^{e_{n+1}+r_{n+1}} \\[6pt] &= \bigg( \prod_{i=0}^{r_{n+1}-1}B_{n+1}1^{\sum_{j=1}^{n}(e_{j}+r_{j})+e_{n+1}+i}\bigg) B_{n+1}1^{\sum_{j=1}^{n}(e_{j}+r_{j})+e_{n+1}+r_{n+1}} \\[6pt] &= \bigg(\prod_{i=0}^{r_{n+1}-1}B_{n+1}1^{c_{n+1}+i}\bigg) B_{n+1}1^{\sum_{j=1}^{n+1}(e_{j}+r_{j})} \end{align*} $$
$$ \begin{align*} \tilde{B}_{n+2} &= \prod_{i=0}^{r_{n+1}}\tilde{B}_{n+1}1^{e_{n+1}+i} = \bigg(\prod_{i=0}^{r_{n+1}-1}\tilde{B}_{n+1}1^{e_{n+1}+i}\bigg) \tilde{B}_{n+1}1^{e_{n+1}+r_{n+1}} \\[6pt] &= \bigg( \prod_{i=0}^{r_{n+1}-1}B_{n+1}1^{\sum_{j=1}^{n}(e_{j}+r_{j})+e_{n+1}+i}\bigg) B_{n+1}1^{\sum_{j=1}^{n}(e_{j}+r_{j})+e_{n+1}+r_{n+1}} \\[6pt] &= \bigg(\prod_{i=0}^{r_{n+1}-1}B_{n+1}1^{c_{n+1}+i}\bigg) B_{n+1}1^{\sum_{j=1}^{n+1}(e_{j}+r_{j})} \end{align*} $$
so the claim holds for all n. As this means every subword of
![]() $\tilde {B}_{n}$
is a subword of
$\tilde {B}_{n}$
is a subword of
![]() $B_{n}$
or
$B_{n}$
or
![]() $B_{n+1}$
and conversely (with
$B_{n+1}$
and conversely (with
![]() $\tilde {B}_{n-1}$
rather than
$\tilde {B}_{n-1}$
rather than
![]() $\tilde {B}_{n+1}$
), the languages of the transformations are the same.
$\tilde {B}_{n+1}$
), the languages of the transformations are the same.
The proof of mixing is very similar to that of [Reference Creutz and SilvaCS04] for traditional staircases; our proof is self-contained.
Theorem 3.1 is a special case of the following result.
Theorem A.2. Every elevated staircase transformation is mixing (on a finite measure space).
Remark A.3. The requirement that
![]() ${r_{n}^{2}}/{h_{n}} \to 0$
is not necessary but one would need to bring the more complicated and technical techniques of [Reference Creutz and SilvaCS10] in to prove it.
${r_{n}^{2}}/{h_{n}} \to 0$
is not necessary but one would need to bring the more complicated and technical techniques of [Reference Creutz and SilvaCS10] in to prove it.
The remainder of this appendix is devoted the proof of Theorem A.2.
Proposition A.4. Every elevated staircase transformation is on a finite measure space.
Proof. Writing
![]() $S_{n}$
for the union of the spacers added above the nth column,
$S_{n}$
for the union of the spacers added above the nth column,
 $$ \begin{align*} \mu(S_{n}) &= \bigg(c_{n}r_n+\frac{1}{2}r_{n}(r_{n}-1)\bigg)\mu(I_{n+1}) = \bigg(c_n\frac{r_n}{r_{n}+1}+\frac{1}{2}\frac{r_{n}(r_{n}-1)}{r_{n}+1}\bigg)\mu(I_{n}) \\[6pt] & \leq \frac{c_{n} + r_{n}}{h_{n}}~\mu(C_{n}), \end{align*} $$
$$ \begin{align*} \mu(S_{n}) &= \bigg(c_{n}r_n+\frac{1}{2}r_{n}(r_{n}-1)\bigg)\mu(I_{n+1}) = \bigg(c_n\frac{r_n}{r_{n}+1}+\frac{1}{2}\frac{r_{n}(r_{n}-1)}{r_{n}+1}\bigg)\mu(I_{n}) \\[6pt] & \leq \frac{c_{n} + r_{n}}{h_{n}}~\mu(C_{n}), \end{align*} $$
and therefore
![]() $\mu (C_{n+1}) = \mu (C_{n}) + \mu (S_{n}) \leq ( 1 + ({c_{n} + r_{n}})/{h_{n}}) \mu (C_{n})$
. Then
$\mu (C_{n+1}) = \mu (C_{n}) + \mu (S_{n}) \leq ( 1 + ({c_{n} + r_{n}})/{h_{n}}) \mu (C_{n})$
. Then
![]() $\mu (C_{n+1}) \leq \prod _{j=1}^{n} (1 + ({c_{j} + r_{j}})/{h_{j}}) \mu (C_{1}), $
meaning that
$\mu (C_{n+1}) \leq \prod _{j=1}^{n} (1 + ({c_{j} + r_{j}})/{h_{j}}) \mu (C_{1}), $
meaning that
![]() $\log (\mu (C_{n+1})) \leq \log (\mu (C_{1})) + \sum _{j=1}^{n} \log (1 + ( {c_{j} + r_{j}})/{h_{j}}). $
As
$\log (\mu (C_{n+1})) \leq \log (\mu (C_{1})) + \sum _{j=1}^{n} \log (1 + ( {c_{j} + r_{j}})/{h_{j}}). $
As
![]() $({c_{n} + r_{n}})/{h_{n}} \to 0$
, since
$({c_{n} + r_{n}})/{h_{n}} \to 0$
, since
![]() $\log (1+x) \approx x$
for
$\log (1+x) \approx x$
for
![]() $x \approx 0$
,
$x \approx 0$
,
![]() $ \lim _{n} \log (\mu (C_{n+1})) \lesssim \log (\mu (C_{1})) + \sum _{j=1}^{\infty } (({c_{j} + r_{j}})/{h_{j}}) < \infty $
gives that T is on a finite measure space.
$ \lim _{n} \log (\mu (C_{n+1})) \lesssim \log (\mu (C_{1})) + \sum _{j=1}^{\infty } (({c_{j} + r_{j}})/{h_{j}}) < \infty $
gives that T is on a finite measure space.
From here on, assume that all transformations T are on probability spaces.
Lemma A.5. Let T be any rank-one transformation and B be a union of levels in some column
![]() $C_{N}$
. Then for any
$C_{N}$
. Then for any
![]() $n \geq N$
,
$n \geq N$
,
![]() $0 \leq a < h_{n}$
and
$0 \leq a < h_{n}$
and
![]() $0 \leq i \leq r_{n}$
,
$0 \leq i \leq r_{n}$
,
Proof. Since B is a union of levels in
![]() $C_{N}$
, it is also a union of levels in
$C_{N}$
, it is also a union of levels in
![]() $C_{n}$
. Therefore,
$C_{n}$
. Therefore,
![]() $I_{n,a} \subseteq B$
or
$I_{n,a} \subseteq B$
or
![]() $I_{n,a} \cap B = \varnothing $
. When
$I_{n,a} \cap B = \varnothing $
. When
![]() $I_{n,a} \subseteq B$
we have
$I_{n,a} \subseteq B$
we have
![]() $\mu (I_{n,a}^{[i]} \cap B) = \mu (I_{n,a}^{[i]}) = ({1}/({r_{n}+1})) \mu (I_{n,a}) = ({1}/({r_{n}+1})) \mu (I_{n,a} \cap B)$
, and when
$\mu (I_{n,a}^{[i]} \cap B) = \mu (I_{n,a}^{[i]}) = ({1}/({r_{n}+1})) \mu (I_{n,a}) = ({1}/({r_{n}+1})) \mu (I_{n,a} \cap B)$
, and when
![]() $I_{n,a} \cap B = \varnothing $
we have
$I_{n,a} \cap B = \varnothing $
we have
![]() $\mu (I_{n,a}^{[i]} \cap B) = 0 = \mu (I_{n,a} \cap B)$
.
$\mu (I_{n,a}^{[i]} \cap B) = 0 = \mu (I_{n,a} \cap B)$
.
Lemma A.6. Let T be an elevated staircase transformation with height sequence
![]() $\{h_n\}$
. Let
$\{h_n\}$
. Let
![]() $I_{n,a}$
be the ath level in the nth column
$I_{n,a}$
be the ath level in the nth column
![]() $C_{n}$
for T. Let B be a union of levels in a column
$C_{n}$
for T. Let B be a union of levels in a column
![]() $C_{N}$
with
$C_{N}$
with
![]() $N \leq n$
. Then for k such that
$N \leq n$
. Then for k such that
![]() $ ki+\tfrac 12k(k-1) \leq a <h_n$
,
$ ki+\tfrac 12k(k-1) \leq a <h_n$
,
 $$ \begin{align*} &|\mu(T^{k(h_n+c_n)}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)| \\[6pt] & \quad \leq \int \limits_{I_{n,a}} \bigg{|}\frac{1}{r_n+1} \sum \limits_{i=0}^{r_n} \chi_{B} \circ T^{-ki-\frac{1}{2}k(k-1)}-\mu(B)\bigg{|}\,d\mu + \frac{2k+2}{r_n+1}\mu(I_{n}). \end{align*} $$
$$ \begin{align*} &|\mu(T^{k(h_n+c_n)}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)| \\[6pt] & \quad \leq \int \limits_{I_{n,a}} \bigg{|}\frac{1}{r_n+1} \sum \limits_{i=0}^{r_n} \chi_{B} \circ T^{-ki-\frac{1}{2}k(k-1)}-\mu(B)\bigg{|}\,d\mu + \frac{2k+2}{r_n+1}\mu(I_{n}). \end{align*} $$
Proof. Write
![]() $I_{n,a}$
as a disjoint union of all the sublevels of
$I_{n,a}$
as a disjoint union of all the sublevels of
![]() $I_{n,a}$
so that
$I_{n,a}$
so that
 $$ \begin{align*} |\mu(T^{k(h_n+c_n)}(I_{n,a}) \cap B) &- \mu(I_{n,a})\mu(B)| =\! \bigg|\sum \limits_{i=0}^{r_{n}} \mu(T^{k(h_n+c_n)}(I^{[i]}_{n,a}) \cap B) - \mu(I^{[i]}_{n,a})\mu(B)\bigg|. \nonumber \end{align*} $$
$$ \begin{align*} |\mu(T^{k(h_n+c_n)}(I_{n,a}) \cap B) &- \mu(I_{n,a})\mu(B)| =\! \bigg|\sum \limits_{i=0}^{r_{n}} \mu(T^{k(h_n+c_n)}(I^{[i]}_{n,a}) \cap B) - \mu(I^{[i]}_{n,a})\mu(B)\bigg|. \nonumber \end{align*} $$
Now for
![]() $i<r_n$
,
$i<r_n$
,
![]() $T^{h_n}(I_{n,a}^{[i]})=T^{-i-c_n}(I_{n,a}^{[i+1]})$
and so
$T^{h_n}(I_{n,a}^{[i]})=T^{-i-c_n}(I_{n,a}^{[i+1]})$
and so
![]() $T^{h_n+c_n}(I_{n,a}^{[i]})=T^{-i}(I_{n,a}^{[i+1]})$
. Applying this k times, for
$T^{h_n+c_n}(I_{n,a}^{[i]})=T^{-i}(I_{n,a}^{[i+1]})$
. Applying this k times, for
![]() $i < r_n-k$
, we get
$i < r_n-k$
, we get
![]() $T^{k(h_n+c_n)}(I_{n,a}^{[i]}) = T^{-i-(i+1)-\cdots -(i+k-1)} (I_{n,a}^{[i+k]})=T^{-ki-\tfrac 12k(k-1)}(I_{n,a}^{[i+k]})$
. So for
$T^{k(h_n+c_n)}(I_{n,a}^{[i]}) = T^{-i-(i+1)-\cdots -(i+k-1)} (I_{n,a}^{[i+k]})=T^{-ki-\tfrac 12k(k-1)}(I_{n,a}^{[i+k]})$
. So for
![]() $ki+\tfrac 12k(k-1) \leq a <h_n$
,
$ki+\tfrac 12k(k-1) \leq a <h_n$
,
 $$ \begin{align*} &|\mu(T^{k(h_n+c_n)}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)| = \bigg|\sum_{i=0}^{r_n}\mu(T^{k(h_n + c_n)}(I_{n,a}^{[i]}) \cap B) - \mu(I_{n,a}^{[i]})\mu(B)\bigg| \\[6pt] &\quad\leq \bigg|\sum \limits_{i=0}^{r_{n}-(k+1)} \mu(T^{-ki-\frac{1}{2}k(k-1)}(I^{[i+k]}_{n,a}) \cap B) - \mu(I^{[i+k]}_{n,a})\mu(B)\bigg| + \frac{k+1}{r_{n}+1}\mu(I_{n,a}) \\[6pt] &\quad= \bigg|\sum \limits_{i=0}^{r_{n}-(k+1)} \mu(I^{[i+k]}_{n,a-ki-\frac{1}{2}k(k-1)} \cap B) - \mu(I^{[i+k]}_{n,a-ki-\frac{1}{2}k(k-1)})\mu(B)\bigg| + \frac{k+1}{r_n+1}\mu(I_{n,a}). \end{align*} $$
$$ \begin{align*} &|\mu(T^{k(h_n+c_n)}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)| = \bigg|\sum_{i=0}^{r_n}\mu(T^{k(h_n + c_n)}(I_{n,a}^{[i]}) \cap B) - \mu(I_{n,a}^{[i]})\mu(B)\bigg| \\[6pt] &\quad\leq \bigg|\sum \limits_{i=0}^{r_{n}-(k+1)} \mu(T^{-ki-\frac{1}{2}k(k-1)}(I^{[i+k]}_{n,a}) \cap B) - \mu(I^{[i+k]}_{n,a})\mu(B)\bigg| + \frac{k+1}{r_{n}+1}\mu(I_{n,a}) \\[6pt] &\quad= \bigg|\sum \limits_{i=0}^{r_{n}-(k+1)} \mu(I^{[i+k]}_{n,a-ki-\frac{1}{2}k(k-1)} \cap B) - \mu(I^{[i+k]}_{n,a-ki-\frac{1}{2}k(k-1)})\mu(B)\bigg| + \frac{k+1}{r_n+1}\mu(I_{n,a}). \end{align*} $$
By Lemma A.5, then
 $$ \begin{align*} &|\mu(T^{k(h_n+c_n)}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)| \\[6pt] &\leq \bigg|\frac{1}{r_n+1}\sum \limits_{i=0}^{r_{n}-(k+1)}\mu(I_{n,a-ki-\frac{1}{2}k(k-1)} \cap B) - \mu(I_{n,a-ki-\frac{1}{2}k(k-1)})\mu(B) \bigg| + \frac{k+1}{r_n+1}\mu(I_{n,a}) \\[6pt] &= \bigg|\frac{1}{r_n+1} \sum \limits_{i=0}^{r_n-(k+1)}\mu(T^{-ki-\frac{1}{2}k(k-1)}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)\bigg| + \frac{k+1}{r_n+1}\mu(I_{n,a}) \\[6pt] &\leq \bigg|\frac{1}{r_n+1} \sum \limits_{i=0}^{r_n}\mu(T^{-ki-\frac{1}{2}k(k-1)}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)\bigg| + 2\frac{k+1}{r_n+1}\mu(I_{n,a}) \\[6pt] &\leq \int \limits_{I_{n,a}} \bigg{|}\frac{1}{r_n+1} \sum \limits_{i=0}^{r_n} \chi_{B} \circ T^{-ki-\frac{1}{2}k(k-1)}-\mu(B)\bigg{|}\, d\mu + \frac{2k+2}{r_n+1}\mu(I_{n,a}).\\[-46pt] \end{align*} $$
$$ \begin{align*} &|\mu(T^{k(h_n+c_n)}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)| \\[6pt] &\leq \bigg|\frac{1}{r_n+1}\sum \limits_{i=0}^{r_{n}-(k+1)}\mu(I_{n,a-ki-\frac{1}{2}k(k-1)} \cap B) - \mu(I_{n,a-ki-\frac{1}{2}k(k-1)})\mu(B) \bigg| + \frac{k+1}{r_n+1}\mu(I_{n,a}) \\[6pt] &= \bigg|\frac{1}{r_n+1} \sum \limits_{i=0}^{r_n-(k+1)}\mu(T^{-ki-\frac{1}{2}k(k-1)}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)\bigg| + \frac{k+1}{r_n+1}\mu(I_{n,a}) \\[6pt] &\leq \bigg|\frac{1}{r_n+1} \sum \limits_{i=0}^{r_n}\mu(T^{-ki-\frac{1}{2}k(k-1)}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)\bigg| + 2\frac{k+1}{r_n+1}\mu(I_{n,a}) \\[6pt] &\leq \int \limits_{I_{n,a}} \bigg{|}\frac{1}{r_n+1} \sum \limits_{i=0}^{r_n} \chi_{B} \circ T^{-ki-\frac{1}{2}k(k-1)}-\mu(B)\bigg{|}\, d\mu + \frac{2k+2}{r_n+1}\mu(I_{n,a}).\\[-46pt] \end{align*} $$
Definition A.2. A sequence
![]() $\{ t_{n} \}$
is mixing for T when, for all measurable sets A and B,
$\{ t_{n} \}$
is mixing for T when, for all measurable sets A and B,
Definition A.3. [Reference Creutz and SilvaCS04]
A sequence
![]() $\{t_n\}$
is rank-one uniform mixing for T when, for every union of levels B,
$\{t_n\}$
is rank-one uniform mixing for T when, for every union of levels B,
 $$ \begin{align*} \lim_{n \to \infty}\sum \limits_{a=0}^{h_{n}-1} |\mu(T^{t_n}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)| = 0 .\end{align*} $$
$$ \begin{align*} \lim_{n \to \infty}\sum \limits_{a=0}^{h_{n}-1} |\mu(T^{t_n}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)| = 0 .\end{align*} $$
Proposition A.7. [Reference Creutz and SilvaCS04]
If
![]() $\{t_n\}$
is rank-one uniform mixing for T, then
$\{t_n\}$
is rank-one uniform mixing for T, then
![]() $\{t_n\}$
is mixing for T.
$\{t_n\}$
is mixing for T.
Proof. Every measurable set can be arbitrarily well approximated by a union of levels.
Theorem A.8. Let T be an elevated staircase transformation with height sequence
![]() $\{h_n\}$
and
$\{h_n\}$
and
![]() $k \: \in \mathbb {N}$
such that
$k \: \in \mathbb {N}$
such that
![]() $T^k$
is ergodic. Then the sequence
$T^k$
is ergodic. Then the sequence
![]() $\{k(h_n+c_n)\}$
is rank-one uniform mixing for T.
$\{k(h_n+c_n)\}$
is rank-one uniform mixing for T.
Proof. By Lemma A.6, for a such that
![]() $ ki+\tfrac 12k(k-1)\leq a <h_n$
, since
$ ki+\tfrac 12k(k-1)\leq a <h_n$
, since
![]() $ki + \tfrac 12k(k-1) \leq kr_n + k^{2}$
,
$ki + \tfrac 12k(k-1) \leq kr_n + k^{2}$
,
 $$ \begin{align*} & \sum \limits_{a=0}^{h_{n}-1} |\mu(T^{k(h_n+c_n)}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)| \\[6pt]&{\leq{\kern-2pt}} (kr_{n}+k^2)\mu(I_n) \\[6pt] &\quad + \sum \limits_{a=kr_{n}+r_n^2}^{h_n-1} \bigg(\int_{I_{n,a}} \bigg{|}\frac{1}{r_n+1} \sum \limits_{i=0}^{r_n} \chi_{B} \circ T^{-ki-\frac{1}{2}k(k-1)}-\mu(B)\bigg{|} d\mu + \frac{2k+2}{r_n+1}\mu(I_{n,a}) \bigg) \\[6pt] &{\leq{\kern-2pt}} (kr_{n}+k^2)\mu(I_{n}) +\! \int\! \bigg{|}\frac{1}{r_n+1}\! \sum \limits_{i=0}^{r_n} \chi_{B} \circ T^{-ki-\frac{1}{2}k(k-1)}-\mu(B)\bigg{|} d\mu +h_{n}\bigg(\frac{2k+2}{r_n+1}\bigg)\mu(I_{n}), \end{align*} $$
$$ \begin{align*} & \sum \limits_{a=0}^{h_{n}-1} |\mu(T^{k(h_n+c_n)}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)| \\[6pt]&{\leq{\kern-2pt}} (kr_{n}+k^2)\mu(I_n) \\[6pt] &\quad + \sum \limits_{a=kr_{n}+r_n^2}^{h_n-1} \bigg(\int_{I_{n,a}} \bigg{|}\frac{1}{r_n+1} \sum \limits_{i=0}^{r_n} \chi_{B} \circ T^{-ki-\frac{1}{2}k(k-1)}-\mu(B)\bigg{|} d\mu + \frac{2k+2}{r_n+1}\mu(I_{n,a}) \bigg) \\[6pt] &{\leq{\kern-2pt}} (kr_{n}+k^2)\mu(I_{n}) +\! \int\! \bigg{|}\frac{1}{r_n+1}\! \sum \limits_{i=0}^{r_n} \chi_{B} \circ T^{-ki-\frac{1}{2}k(k-1)}-\mu(B)\bigg{|} d\mu +h_{n}\bigg(\frac{2k+2}{r_n+1}\bigg)\mu(I_{n}), \end{align*} $$
using that the levels are disjoint. Clearly
![]() $(kr_n + k^2)\mu (I_{n}) \leq {kr_{n}}/{h_{n}} + {k^2}/{h_{n}} \to 0$
and
$(kr_n + k^2)\mu (I_{n}) \leq {kr_{n}}/{h_{n}} + {k^2}/{h_{n}} \to 0$
and
![]() $h_{n} (({2k+2})/({r_{n}+1})) \mu (I_{n}) \leq ({2k+2})/({r_{n}+1}) \to 0$
. That T is measure-preserving and the mean ergodic theorem applied to
$h_{n} (({2k+2})/({r_{n}+1})) \mu (I_{n}) \leq ({2k+2})/({r_{n}+1}) \to 0$
. That T is measure-preserving and the mean ergodic theorem applied to
![]() $T^{k}$
give
$T^{k}$
give
 $$ \begin{align*} &\int \bigg{|} \frac{1}{r_n+1} \sum \limits_{i=0}^{r_n} \chi_{B} \circ T^{-ki-\frac{1}{2}k(k-1)}-\mu(B\bigg{|} |\, d\mu \\[6pt] &\quad \leq \int \bigg{|}\frac{1}{r_n+1} \sum \limits_{i=0}^{r_n} \chi_{B} \circ T^{-ki}-\mu(B)\bigg{|} \,d\mu\\[6pt] &\quad\leq \bigg(\int\bigg|\frac{1}{r_n+1} \sum \limits_{i=0}^{r_n} \chi_{B} \circ T^{-ki}-\mu(B)\bigg|^2\, d\mu\bigg)^{1/2} \to 0.\\[-48pt] \end{align*} $$
$$ \begin{align*} &\int \bigg{|} \frac{1}{r_n+1} \sum \limits_{i=0}^{r_n} \chi_{B} \circ T^{-ki-\frac{1}{2}k(k-1)}-\mu(B\bigg{|} |\, d\mu \\[6pt] &\quad \leq \int \bigg{|}\frac{1}{r_n+1} \sum \limits_{i=0}^{r_n} \chi_{B} \circ T^{-ki}-\mu(B)\bigg{|} \,d\mu\\[6pt] &\quad\leq \bigg(\int\bigg|\frac{1}{r_n+1} \sum \limits_{i=0}^{r_n} \chi_{B} \circ T^{-ki}-\mu(B)\bigg|^2\, d\mu\bigg)^{1/2} \to 0.\\[-48pt] \end{align*} $$
Corollary A.9. If T is an elevated staircase transformation then
![]() $T^k$
is ergodic for each fixed k.
$T^k$
is ergodic for each fixed k.
Proof. Using Theorem A.8 with
![]() $k=1$
, since T is ergodic we have that
$k=1$
, since T is ergodic we have that
![]() $\{h_n+c_n\}$
is uniform mixing, hence mixing by Proposition A.7. The existence of a mixing sequence for T implies T is weakly mixing hence each power of T is ergodic.
$\{h_n+c_n\}$
is uniform mixing, hence mixing by Proposition A.7. The existence of a mixing sequence for T implies T is weakly mixing hence each power of T is ergodic.
Lemma A.10. Let T be a rank-one transformation and
![]() $\{ c_{n} \}$
a sequence such that
$\{ c_{n} \}$
a sequence such that
![]() ${{c_{n}}/{h_{n}} \to 0}$
. If
${{c_{n}}/{h_{n}} \to 0}$
. If
![]() $q\in \mathbb {N}$
, and
$q\in \mathbb {N}$
, and
![]() $\{ q(h_{n}+c_{n}) \}$
and
$\{ q(h_{n}+c_{n}) \}$
and
![]() $\{ (q+1)(h_{n} + c_{n}) \}$
are rank-one uniform mixing, and
$\{ (q+1)(h_{n} + c_{n}) \}$
are rank-one uniform mixing, and
![]() $\{ t_{n} \}$
is a sequence such that
$\{ t_{n} \}$
is a sequence such that
![]() $q(h_{n} + c_{n}) \leq t_{n} < (q+1)(h_{n}+c_{n})$
for all n, then
$q(h_{n} + c_{n}) \leq t_{n} < (q+1)(h_{n}+c_{n})$
for all n, then
![]() $\{ t_{n} \}$
is rank-one uniform mixing.
$\{ t_{n} \}$
is rank-one uniform mixing.
Proof. For
![]() $0 \leq a < q(h_n+c_n)-t_n+h_n$
, we have
$0 \leq a < q(h_n+c_n)-t_n+h_n$
, we have
![]() $0 \leq t_n-q(h_n+c_n) \leq t_n+a-q(h_n+c_n)<h_n$
, so
$0 \leq t_n-q(h_n+c_n) \leq t_n+a-q(h_n+c_n)<h_n$
, so
For
![]() $(q+1)(h_n+c_n)-t_n \leq a < h_n$
, we have
$(q+1)(h_n+c_n)-t_n \leq a < h_n$
, we have
![]() $0 \leq t_n+a-(q+1)(h_n+c_n)<a<h_n$
, so
$0 \leq t_n+a-(q+1)(h_n+c_n)<a<h_n$
, so
For a union of levels B in
![]() $C_N$
and
$C_N$
and
![]() $n \geq N$
,
$n \geq N$
,
 $$ \begin{align*} &\sum \limits_{a=0}^{h_n-1} |\mu(T^{t_n}(I_{n,a} \cap B) - \mu(I_{n,a})\mu(B)| \\[6pt] &\quad\leq \sum \limits_{a=0}^{q(h_n+c_n)-t_n+h_n-1} |\mu(T^{q(h_n+c_n)}I_{n,t_n+a-q(h_n+c_n)} \cap B) - \mu(I_{n})\mu(B)| + c_{n}\mu(I_{n}) \\[6pt] &\qquad +\sum \limits_{a=(q+1)(h_n+c_n)-t_n}^{h_n-1} |\mu(T^{(q+1)(h_n+c_n)}I_{n,t_n+a-(q+1)(h_n+c_n)} \cap B) - \mu(I_{n})\mu(B)| \\[6pt] &\quad\leq \sum \limits_{b=0}^{h_n-1} |\mu(T^{q(h_n+c_n)}I_{n,b} \cap B) - \mu(I_{n})\mu(B)| + c_{n}\mu(I_{n}) \\[6pt] &\qquad + \sum \limits_{b=0}^{h_n-1} |\mu(T^{(q+1)(h_n+c_n)}I_{n,b} \cap B) - \mu(I_{n})\mu(B) | \to 0 \end{align*} $$
$$ \begin{align*} &\sum \limits_{a=0}^{h_n-1} |\mu(T^{t_n}(I_{n,a} \cap B) - \mu(I_{n,a})\mu(B)| \\[6pt] &\quad\leq \sum \limits_{a=0}^{q(h_n+c_n)-t_n+h_n-1} |\mu(T^{q(h_n+c_n)}I_{n,t_n+a-q(h_n+c_n)} \cap B) - \mu(I_{n})\mu(B)| + c_{n}\mu(I_{n}) \\[6pt] &\qquad +\sum \limits_{a=(q+1)(h_n+c_n)-t_n}^{h_n-1} |\mu(T^{(q+1)(h_n+c_n)}I_{n,t_n+a-(q+1)(h_n+c_n)} \cap B) - \mu(I_{n})\mu(B)| \\[6pt] &\quad\leq \sum \limits_{b=0}^{h_n-1} |\mu(T^{q(h_n+c_n)}I_{n,b} \cap B) - \mu(I_{n})\mu(B)| + c_{n}\mu(I_{n}) \\[6pt] &\qquad + \sum \limits_{b=0}^{h_n-1} |\mu(T^{(q+1)(h_n+c_n)}I_{n,b} \cap B) - \mu(I_{n})\mu(B) | \to 0 \end{align*} $$
since
![]() $\{q(h_n+c_n)\}$
,
$\{q(h_n+c_n)\}$
,
![]() $\{(q+1)(h_n+c_n)\}$
are rank-one uniform mixing and
$\{(q+1)(h_n+c_n)\}$
are rank-one uniform mixing and
![]() $c_{n}\mu (I_{n}) \leq {c_{n}}/{h_{n}} \to 0$
.
$c_{n}\mu (I_{n}) \leq {c_{n}}/{h_{n}} \to 0$
.
Proposition A.11. Let T be a rank-one transformation and
![]() $\{ c_{n} \}$
a sequence such that
$\{ c_{n} \}$
a sequence such that
![]() ${c_{n}}/{h_{n}} \to 0$
. If
${c_{n}}/{h_{n}} \to 0$
. If
![]() $k \in \mathbb {N}$
, and
$k \in \mathbb {N}$
, and
![]() $\{ q(h_{n}+c_{n}) \}$
is rank-one uniform mixing for each
$\{ q(h_{n}+c_{n}) \}$
is rank-one uniform mixing for each
![]() $q \leq k+1$
, and
$q \leq k+1$
, and
![]() $\{ t_{n} \}$
is a sequence such that
$\{ t_{n} \}$
is a sequence such that
![]() $h_{n} + c_{n} \leq t_{n} < (k+1)(h_{n}+c_{n})$
for all n, then
$h_{n} + c_{n} \leq t_{n} < (k+1)(h_{n}+c_{n})$
for all n, then
![]() $\{ t_{n} \}$
is mixing.
$\{ t_{n} \}$
is mixing.
Proof. Since
![]() $t_{n} < (k+1)(h_n+c_n)$
, there is some
$t_{n} < (k+1)(h_n+c_n)$
, there is some
![]() $q_n \leq q$
such that
$q_n \leq q$
such that
![]() $q_n(h_n+c_n) \leq t_n < (q_n+1)(h_n+c_n)$
. Let
$q_n(h_n+c_n) \leq t_n < (q_n+1)(h_n+c_n)$
. Let
![]() $\{t_{n_j}\}$
be any subsequence of
$\{t_{n_j}\}$
be any subsequence of
![]() $\{t_n\}$
. Since
$\{t_n\}$
. Since
![]() $q_n \leq k$
for all n and q is fixed, there exists a further subsequence
$q_n \leq k$
for all n and q is fixed, there exists a further subsequence
![]() $\{t_{n_{j_k}}\}$
on which
$\{t_{n_{j_k}}\}$
on which
![]() $q_{n_{j_k}}$
is constant. By Lemma A.10 and Proposition A.7,
$q_{n_{j_k}}$
is constant. By Lemma A.10 and Proposition A.7,
![]() $\{t_{n_{j_k}}\}$
is mixing. As every subsequence of
$\{t_{n_{j_k}}\}$
is mixing. As every subsequence of
![]() $\{t_n\}$
has a mixing subsequence,
$\{t_n\}$
has a mixing subsequence,
![]() $\{t_n\}$
is mixing.
$\{t_n\}$
is mixing.
Lemma A.12. Let T be a measure-preserving transformation. If for each fixed
![]() $\ell \in \mathbb {N}$
,
$\ell \in \mathbb {N}$
,
![]() $\{\ell t_n\}$
is mixing, then for any
$\{\ell t_n\}$
is mixing, then for any
![]() $\epsilon> 0$
there exist L and N such that for all
$\epsilon> 0$
there exist L and N such that for all
![]() $n \geq N$
,
$n \geq N$
,
![]() $\int | ({1}/{L}) \sum _{\ell =1}^{L} \chi _{B} \circ T^{-\ell t_n}-\mu (B)|\, d\mu < \epsilon .$
$\int | ({1}/{L}) \sum _{\ell =1}^{L} \chi _{B} \circ T^{-\ell t_n}-\mu (B)|\, d\mu < \epsilon .$
Proof. Take
![]() $L> 2/\epsilon ^{2}$
and N so that
$L> 2/\epsilon ^{2}$
and N so that
![]() $|\mu (T^{\ell t_{n}}(B) \cap B) - \mu (B)\mu (B)| < \epsilon ^{2}/2$
for
$|\mu (T^{\ell t_{n}}(B) \cap B) - \mu (B)\mu (B)| < \epsilon ^{2}/2$
for
![]() $\ell < L$
and
$\ell < L$
and
![]() $n> N$
. Then
$n> N$
. Then
 $$ \begin{align*} \int \bigg{|}\frac{1}{L} \sum \limits_{m=1}^{L} \chi_{B} \circ T^{-m t_n} - \mu(B)\bigg{|}^{2}\, d\mu &= \frac{1}{L^{2}}\sum \limits_{r,m=1}^{L} \mu(T^{(m-r)t_{n}}(B) \cap B) - \mu(B)\mu(B) \\[3pt] &\leq \frac{1}{L} + \frac{1}{L} \sum \limits_{\ell=1}^{L-1} \frac{L-\ell}{L} \mu(T^{\ell t_{n}}(B) \cap B) - \mu(B)\mu(B) \\[3pt] &< 2\epsilon^{2}/2 = \epsilon^{2} \end{align*} $$
$$ \begin{align*} \int \bigg{|}\frac{1}{L} \sum \limits_{m=1}^{L} \chi_{B} \circ T^{-m t_n} - \mu(B)\bigg{|}^{2}\, d\mu &= \frac{1}{L^{2}}\sum \limits_{r,m=1}^{L} \mu(T^{(m-r)t_{n}}(B) \cap B) - \mu(B)\mu(B) \\[3pt] &\leq \frac{1}{L} + \frac{1}{L} \sum \limits_{\ell=1}^{L-1} \frac{L-\ell}{L} \mu(T^{\ell t_{n}}(B) \cap B) - \mu(B)\mu(B) \\[3pt] &< 2\epsilon^{2}/2 = \epsilon^{2} \end{align*} $$
so, by the Cauchy–Schwarz inequality,
![]() $\int | ({1}/{L}) \sum _{\ell =1}^{L} \chi _{B} \circ T^{-\ell t_n}-\mu (B)|\,d\mu \leq \sqrt {\epsilon ^{2}} = \epsilon $
.
$\int | ({1}/{L}) \sum _{\ell =1}^{L} \chi _{B} \circ T^{-\ell t_n}-\mu (B)|\,d\mu \leq \sqrt {\epsilon ^{2}} = \epsilon $
.
Lemma A.13. (Block lemma [Reference AdamsAda98])
For T measure-preserving and
![]() $R,L,p \in \mathbb {N}$
with
$R,L,p \in \mathbb {N}$
with
![]() $pL \leq R$
,
$pL \leq R$
,
 $$\begin{align*}\int \bigg| \frac{1}{R} \sum_{r=0}^{R-1} \chi \circ T^{-r}\bigg|\, d\mu \leq \int \bigg| \frac{1}{L} \sum_{\ell=0}^{L-1} \chi \circ T^{-p\ell}\bigg|\, d\mu + \frac{pL}{R} \int |\chi|\, d\mu. \end{align*}$$
$$\begin{align*}\int \bigg| \frac{1}{R} \sum_{r=0}^{R-1} \chi \circ T^{-r}\bigg|\, d\mu \leq \int \bigg| \frac{1}{L} \sum_{\ell=0}^{L-1} \chi \circ T^{-p\ell}\bigg|\, d\mu + \frac{pL}{R} \int |\chi|\, d\mu. \end{align*}$$
Proof.
![]() $0 \leq R - pL\lfloor {R}/{pL} \rfloor \leq {pL}/{r}$
, so
$0 \leq R - pL\lfloor {R}/{pL} \rfloor \leq {pL}/{r}$
, so
 $$\begin{align*}\int \left| \frac{1}{R} \sum_{r=0}^{R-1} \chi \circ T^{-r}\right|\, d\mu \leq \frac{pL}{R} + \int \left| \frac{1}{R} \sum_{r=0}^{\lfloor {R}/{pL}\rfloor-1} \chi \circ T^{-r}\right|\, d\mu \end{align*}$$
$$\begin{align*}\int \left| \frac{1}{R} \sum_{r=0}^{R-1} \chi \circ T^{-r}\right|\, d\mu \leq \frac{pL}{R} + \int \left| \frac{1}{R} \sum_{r=0}^{\lfloor {R}/{pL}\rfloor-1} \chi \circ T^{-r}\right|\, d\mu \end{align*}$$
and
 $$ \begin{align*} &\int \bigg{|}\frac{1}{R}\sum \limits_{r=0}^{pL\lfloor {R}/{pL} \rfloor -1} \chi \circ T^{-r}\bigg{|}\, d\mu \\[3pt] &= \frac{pL\lfloor {R}/{pL} \rfloor}{R} \int \bigg{|}\frac{1}{\lfloor {R}/{pL} \rfloor}\sum \limits_{m=0}^{\lfloor {R}/{pL} \rfloor-1} \frac{1}{p}\sum \limits_{b=0}^{p-1} \frac{1}{L}\sum \limits_{\ell=0}^{L-1} \int \chi \circ T^{-p\ell} \circ T^{-b} \circ T^{-mpL}\bigg{|}\, d\mu \\[3pt] &\leq \frac{1}{\lfloor {R}/{pL} \rfloor}\sum \limits_{m=0}^{\lfloor {R}/{pL} \rfloor-1} \frac{1}{p}\sum \limits_{b=0}^{p-1} \int\bigg{|} \frac{1}{L}\sum \limits_{\ell=0}^{L-1} \chi \circ T^{-p\ell}\circ T^{-b} \circ T^{-mpL} \bigg{|}\, d\mu \\[3pt] &= \frac{1}{\lfloor {R}/{pL} \rfloor}\sum \limits_{m=0}^{\lfloor {R}/{pL} \rfloor-1} \frac{1}{p}\sum \limits_{b=0}^{p-1} \int\bigg{|} \frac{1}{L}\sum \limits_{\ell=0}^{L-1} \chi \circ T^{-p\ell} \bigg{|}\, d\mu = \int \bigg{|}\frac{1}{L}\sum \limits_{\ell=0}^{L-1} \chi \circ T^{-p\ell} \bigg{|}\, d\mu. \quad \\[-48pt] \end{align*} $$
$$ \begin{align*} &\int \bigg{|}\frac{1}{R}\sum \limits_{r=0}^{pL\lfloor {R}/{pL} \rfloor -1} \chi \circ T^{-r}\bigg{|}\, d\mu \\[3pt] &= \frac{pL\lfloor {R}/{pL} \rfloor}{R} \int \bigg{|}\frac{1}{\lfloor {R}/{pL} \rfloor}\sum \limits_{m=0}^{\lfloor {R}/{pL} \rfloor-1} \frac{1}{p}\sum \limits_{b=0}^{p-1} \frac{1}{L}\sum \limits_{\ell=0}^{L-1} \int \chi \circ T^{-p\ell} \circ T^{-b} \circ T^{-mpL}\bigg{|}\, d\mu \\[3pt] &\leq \frac{1}{\lfloor {R}/{pL} \rfloor}\sum \limits_{m=0}^{\lfloor {R}/{pL} \rfloor-1} \frac{1}{p}\sum \limits_{b=0}^{p-1} \int\bigg{|} \frac{1}{L}\sum \limits_{\ell=0}^{L-1} \chi \circ T^{-p\ell}\circ T^{-b} \circ T^{-mpL} \bigg{|}\, d\mu \\[3pt] &= \frac{1}{\lfloor {R}/{pL} \rfloor}\sum \limits_{m=0}^{\lfloor {R}/{pL} \rfloor-1} \frac{1}{p}\sum \limits_{b=0}^{p-1} \int\bigg{|} \frac{1}{L}\sum \limits_{\ell=0}^{L-1} \chi \circ T^{-p\ell} \bigg{|}\, d\mu = \int \bigg{|}\frac{1}{L}\sum \limits_{\ell=0}^{L-1} \chi \circ T^{-p\ell} \bigg{|}\, d\mu. \quad \\[-48pt] \end{align*} $$
Proposition A.14. Let T be a rank-one transformation and
![]() $\{ c_{n} \}$
a sequence such that
$\{ c_{n} \}$
a sequence such that
![]() ${c_{n}}/{h_{n}} \to 0$
. If
${c_{n}}/{h_{n}} \to 0$
. If
![]() $\{ q(h_{n}+c_{n}) \}$
is rank-one uniform mixing for each fixed q and
$\{ q(h_{n}+c_{n}) \}$
is rank-one uniform mixing for each fixed q and
![]() $k_n \to \infty $
is such that
$k_n \to \infty $
is such that
![]() $ {k_n}/{n} \leq 1$
, then
$ {k_n}/{n} \leq 1$
, then
 $$ \begin{align*} \int \bigg{|}\frac{1}{n} \sum \limits_{j=0}^{n-1} \chi \circ T^{-jk_n}\bigg{|}\, d\mu \rightarrow 0. \end{align*} $$
$$ \begin{align*} \int \bigg{|}\frac{1}{n} \sum \limits_{j=0}^{n-1} \chi \circ T^{-jk_n}\bigg{|}\, d\mu \rightarrow 0. \end{align*} $$
This condition is called power ergodic in [Reference Creutz and SilvaCS04, Reference Creutz and SilvaCS10].
Proof. For each n there exists a unique m such that
![]() $h_m+c_m \leq k_n < h_{m+1}+c_{m+1}$
. Let
$h_m+c_m \leq k_n < h_{m+1}+c_{m+1}$
. Let
![]() $p_n$
be the smallest integer such that
$p_n$
be the smallest integer such that
![]() $p_nk_n \geq h_{m+1}+c_{m+1}$
. Suppose
$p_nk_n \geq h_{m+1}+c_{m+1}$
. Suppose
![]() $p_nk_n> 2(h_{m+1}+c_{m+1})$
. Then
$p_nk_n> 2(h_{m+1}+c_{m+1})$
. Then
![]() $({p_n}/{2})k_n> h_{m+1}+c_{m+1}$
. If
$({p_n}/{2})k_n> h_{m+1}+c_{m+1}$
. If
![]() $p_n$
is even,
$p_n$
is even,
![]() $p_n> {p_n}/{2}$
, which contradicts that
$p_n> {p_n}/{2}$
, which contradicts that
![]() $p_n$
is the smallest integer such that
$p_n$
is the smallest integer such that
![]() $p_nk_n\geq h_{m+1}+c_{m+1}$
. If
$p_nk_n\geq h_{m+1}+c_{m+1}$
. If
![]() $p_n$
is odd,
$p_n$
is odd,
![]() $p_n \geq ({p_n+1})/{2}$
, which contradicts that
$p_n \geq ({p_n+1})/{2}$
, which contradicts that
![]() $p_n$
is smallest such that
$p_n$
is smallest such that
![]() $p_nk_n\geq h_{m+1}+c_{m+1}$
. In the case when
$p_nk_n\geq h_{m+1}+c_{m+1}$
. In the case when
![]() $p_n=1$
, then
$p_n=1$
, then
![]() $k_n \geq 2(h_{m+1}+c_{m+1})$
with
$k_n \geq 2(h_{m+1}+c_{m+1})$
with
![]() $k_n =h_{m+1}+c_{m+1}$
, contradicting that
$k_n =h_{m+1}+c_{m+1}$
, contradicting that
![]() $k_{n} < h_{m+1} + c_{m+1}$
. So
$k_{n} < h_{m+1} + c_{m+1}$
. So
![]() $p_nk_n < 2(h_{m+1}+c_{m+1})$
. Set
$p_nk_n < 2(h_{m+1}+c_{m+1})$
. Set
![]() $t_n=p_nk_n$
. Then
$t_n=p_nk_n$
. Then
![]() $h_{m+1}+c_{m+1} \leq t_n < 2(h_{m+1}+c_{m+1})$
. For each fixed
$h_{m+1}+c_{m+1} \leq t_n < 2(h_{m+1}+c_{m+1})$
. For each fixed
![]() $\ell $
then
$\ell $
then
![]() $(h_{m} + c_{m}) \leq \ell t_{n} < 2\ell (h_{m} + c_{m})$
, so
$(h_{m} + c_{m}) \leq \ell t_{n} < 2\ell (h_{m} + c_{m})$
, so
![]() $\{ \ell t_{n} \}$
is mixing by Proposition A.11.
$\{ \ell t_{n} \}$
is mixing by Proposition A.11.
Fix
![]() $\epsilon> 0$
. By Lemma A.12, there exist L and N such that for all
$\epsilon> 0$
. By Lemma A.12, there exist L and N such that for all
![]() $n> N$
, we have
$n> N$
, we have
![]() $ \int | ({1}/{L}) \sum _{\ell =1}^{L} \chi \circ T^{-\ell t_n}|\, d\mu < \epsilon. $
By Lemma A.13,
$ \int | ({1}/{L}) \sum _{\ell =1}^{L} \chi \circ T^{-\ell t_n}|\, d\mu < \epsilon. $
By Lemma A.13,
 $$ \begin{align*} \int \bigg{|}\frac{1}{n} \sum \limits_{j=0}^{n-1} \chi \circ T^{-jk_n}\bigg{|}\, d\mu &\leq \int \bigg{|}\frac{1}{L} \sum \limits_{\ell=0}^{L-1} \chi \circ T^{-\ell p_{n}k_n}\bigg{|}\, d\mu + \frac{p_n L}{n} \\[6pt] &= \int \bigg{|}\frac{1}{L} \sum \limits_{\ell=0}^{L-1} \chi \circ T^{-\ell t_n}\bigg{|}\, d\mu + \frac{p_n L}{n} < \epsilon +\frac{p_n L}{n}. \end{align*} $$
$$ \begin{align*} \int \bigg{|}\frac{1}{n} \sum \limits_{j=0}^{n-1} \chi \circ T^{-jk_n}\bigg{|}\, d\mu &\leq \int \bigg{|}\frac{1}{L} \sum \limits_{\ell=0}^{L-1} \chi \circ T^{-\ell p_{n}k_n}\bigg{|}\, d\mu + \frac{p_n L}{n} \\[6pt] &= \int \bigg{|}\frac{1}{L} \sum \limits_{\ell=0}^{L-1} \chi \circ T^{-\ell t_n}\bigg{|}\, d\mu + \frac{p_n L}{n} < \epsilon +\frac{p_n L}{n}. \end{align*} $$
Since
![]() ${k_{n}}/{n} \leq 1$
gives
${k_{n}}/{n} \leq 1$
gives
![]() ${r_{m}}/{n} = {r_{m}k_{n}}/{nk_{n}} \leq {r_{m}}/{k_{n}} \leq {r_{m}}/{h_{m}} \to 0$
,
${r_{m}}/{n} = {r_{m}k_{n}}/{nk_{n}} \leq {r_{m}}/{k_{n}} \leq {r_{m}}/{h_{m}} \to 0$
,
 $$ \begin{align*} \frac{p_{n}}{n} &= \frac{p_{n}k_{n}}{nk_{n}} \leq \frac{2(h_{m+1}+c_{m+1})}{n(h_{m}+c_{m})} \leq \frac{4}{n} \frac{(r_{m}+1)(h_{m} + c_{m} + r_{m})}{(h_{m}+c_{m})} \\[6pt] &= \frac{4r_{m}}{n} \bigg(1 + \frac{r_{m}}{h_{m}+c_{m}}\bigg) \to 0 \end{align*} $$
$$ \begin{align*} \frac{p_{n}}{n} &= \frac{p_{n}k_{n}}{nk_{n}} \leq \frac{2(h_{m+1}+c_{m+1})}{n(h_{m}+c_{m})} \leq \frac{4}{n} \frac{(r_{m}+1)(h_{m} + c_{m} + r_{m})}{(h_{m}+c_{m})} \\[6pt] &= \frac{4r_{m}}{n} \bigg(1 + \frac{r_{m}}{h_{m}+c_{m}}\bigg) \to 0 \end{align*} $$
so
![]() $ \limsup _{n} \int | ({1}/{n}) \sum _{j=0}^{n-1} \chi \circ T^{-jk_n}|\, d\mu \leq \epsilon. $
As this holds for all
$ \limsup _{n} \int | ({1}/{n}) \sum _{j=0}^{n-1} \chi \circ T^{-jk_n}|\, d\mu \leq \epsilon. $
As this holds for all
![]() $\epsilon> 0$
,
$\epsilon> 0$
,
 $$ \begin{align*} \int \bigg| \frac{1}{n} \sum _{j=0}^{n-1} \chi \circ T^{-jk_n}\bigg|\, d\mu \to 0. \\[-48pt] \end{align*} $$
$$ \begin{align*} \int \bigg| \frac{1}{n} \sum _{j=0}^{n-1} \chi \circ T^{-jk_n}\bigg|\, d\mu \to 0. \\[-48pt] \end{align*} $$
Theorem A.15. Let T be an elevated staircase transformation with height sequence
![]() $\{h_n\}$
such that
$\{h_n\}$
such that
![]() ${r_n^2}/{h_n}\rightarrow 0$
. Let
${r_n^2}/{h_n}\rightarrow 0$
. Let
![]() $\{t_n\}$
be a sequence such that
$\{t_n\}$
be a sequence such that
![]() $(h_n+c_n) \leq t_n < (h_{n+1}+c_{n+1})$
. Then
$(h_n+c_n) \leq t_n < (h_{n+1}+c_{n+1})$
. Then
![]() $\{t_n\}$
is mixing.
$\{t_n\}$
is mixing.
Proof. By Corollary A.9,
![]() $T^{k}$
is ergodic for each fixed k. Then by Theorem A.8, the sequence
$T^{k}$
is ergodic for each fixed k. Then by Theorem A.8, the sequence
![]() $\{ k(h_{n} + c_{n}) \}$
is rank-one uniform mixing for each fixed k. By Proposition A.11, if there exists a constant k such that
$\{ k(h_{n} + c_{n}) \}$
is rank-one uniform mixing for each fixed k. By Proposition A.11, if there exists a constant k such that
![]() $(h_n+c_n) \leq t_n < k(h_n+c_n)$
, then
$(h_n+c_n) \leq t_n < k(h_n+c_n)$
, then
![]() $\{t_n\}$
is mixing, so, writing
$\{t_n\}$
is mixing, so, writing
![]() $t_{n} = k_{n}(h_{n}+c_{n}) + z_{n}$
for
$t_{n} = k_{n}(h_{n}+c_{n}) + z_{n}$
for
![]() $0 \leq z_{n} < h_{n} + c_{n}$
, we may assume
$0 \leq z_{n} < h_{n} + c_{n}$
, we may assume
![]() $k_n \to \infty $
.
$k_n \to \infty $
.
For
![]() $0 \leq a < h_n-z_n$
we have
$0 \leq a < h_n-z_n$
we have
![]() $T^{t_n}(I_{n,a})=T^{k_n(h_n+c_n)}(I_{n,a+z_n})$
, and for
$T^{t_n}(I_{n,a})=T^{k_n(h_n+c_n)}(I_{n,a+z_n})$
, and for
![]() $h_n+c_n-z_n \leq a < h_n$
we have
$h_n+c_n-z_n \leq a < h_n$
we have
For a union of levels B in
![]() $C_N$
and
$C_N$
and
![]() $n \geq N$
,
$n \geq N$
,
 $$ \begin{align} &\sum \limits_{a=0}^{h_n-1} |\mu(T^{t_n}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)| \nonumber \\[6pt] &\quad\leq \sum \limits_{a=0}^{h_n-z_{n}-1} |\mu(T^{t_n}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)| + c_{n}\mu(I_{n}) \nonumber \\[6pt] &\qquad + \sum \limits_{a=h_{n}+c_{n}+z_{n}}^{h_n-1} |\mu(T^{t_n}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)| \nonumber \\[6pt] &\quad\leq \sum \limits_{b=0}^{h_n-1} |\mu(T^{k_n(h_n+c_n)}(I_{n,b}) \cap B) - \mu(I_{n,b})\mu(B)| + c_{n}\mu(I_{n}) \end{align} $$
$$ \begin{align} &\sum \limits_{a=0}^{h_n-1} |\mu(T^{t_n}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)| \nonumber \\[6pt] &\quad\leq \sum \limits_{a=0}^{h_n-z_{n}-1} |\mu(T^{t_n}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)| + c_{n}\mu(I_{n}) \nonumber \\[6pt] &\qquad + \sum \limits_{a=h_{n}+c_{n}+z_{n}}^{h_n-1} |\mu(T^{t_n}(I_{n,a}) \cap B) - \mu(I_{n,a})\mu(B)| \nonumber \\[6pt] &\quad\leq \sum \limits_{b=0}^{h_n-1} |\mu(T^{k_n(h_n+c_n)}(I_{n,b}) \cap B) - \mu(I_{n,b})\mu(B)| + c_{n}\mu(I_{n}) \end{align} $$
 $$ \begin{align} & +\sum \limits_{b=0}^{h_n-1} |\mu(T^{(k_n+1)(h_n+c_n)}(I_{n,b}) \cap B) - \mu(I_{n,b})\mu(B)|. \end{align} $$
$$ \begin{align} & +\sum \limits_{b=0}^{h_n-1} |\mu(T^{(k_n+1)(h_n+c_n)}(I_{n,b}) \cap B) - \mu(I_{n,b})\mu(B)|. \end{align} $$
We show that the sum
![]() $(\star )$
tends to zero:
$(\star )$
tends to zero:
 $$ \begin{align} &\sum \limits_{b=0}^{h_n-1} |\mu(T^{k_n(h_n+c_n)}(I_{n,b}) \cap B) - \mu(I_{n,b})\mu(B)| \nonumber \\[6pt] &\quad\leq \sum \limits_{b=0}^{h_n-1} \bigg|\sum \limits_{i=0}^{r_{n}-k_n}\mu(T^{k_n(h_n+c_n)}(I^{[i]}_{n,b}) \cap B) - \mu(I^{[i]}_{n,b})\mu(B)\bigg| \quad\qquad\qquad \end{align} $$
$$ \begin{align} &\sum \limits_{b=0}^{h_n-1} |\mu(T^{k_n(h_n+c_n)}(I_{n,b}) \cap B) - \mu(I_{n,b})\mu(B)| \nonumber \\[6pt] &\quad\leq \sum \limits_{b=0}^{h_n-1} \bigg|\sum \limits_{i=0}^{r_{n}-k_n}\mu(T^{k_n(h_n+c_n)}(I^{[i]}_{n,b}) \cap B) - \mu(I^{[i]}_{n,b})\mu(B)\bigg| \quad\qquad\qquad \end{align} $$
 $$ \begin{align} &\qquad + \frac{2}{r_{n}} + \sum \limits_{b=0}^{h_n-1} \bigg|\sum \limits_{i=r_{n}-k_n+2}^{r_{n}}\mu(T^{k_n(h_n+c_n)}(I^{[i]}_{n,b}) \cap B) - \mu(I^{[i]}_{n,b})\mu(B)\bigg|. \end{align} $$
$$ \begin{align} &\qquad + \frac{2}{r_{n}} + \sum \limits_{b=0}^{h_n-1} \bigg|\sum \limits_{i=r_{n}-k_n+2}^{r_{n}}\mu(T^{k_n(h_n+c_n)}(I^{[i]}_{n,b}) \cap B) - \mu(I^{[i]}_{n,b})\mu(B)\bigg|. \end{align} $$
For the sum
![]() $(\dagger )$
,
$(\dagger )$
,
 $$ \begin{align*} &\sum \limits_{b=0}^{h_n-1} \bigg|\sum \limits_{i=0}^{r_{n}-k_n}\mu(T^{k_n(h_n+c_n)}(I^{[i]}_{n,b}) \cap B) - \mu(I^{[i]}_{n,b})\mu(B)\bigg| \leq \bigg(r_nk_n+ \frac{1}{2}k_n(k_n-1)\bigg)\mu(I_n) \\[6pt] &\quad + \sum \limits_{b=r_nk_n + \frac{1}{2}k_n(k_n-1)}^{h_n-1} \bigg|\sum \limits_{i=0}^{r_{n}-k_n}\mu(T^{k_n(h_n+c_n)}(I^{[i]}_{n,b}) \cap B) - \mu(I^{[i]}_{n,b})\mu(B)\bigg|, \end{align*} $$
$$ \begin{align*} &\sum \limits_{b=0}^{h_n-1} \bigg|\sum \limits_{i=0}^{r_{n}-k_n}\mu(T^{k_n(h_n+c_n)}(I^{[i]}_{n,b}) \cap B) - \mu(I^{[i]}_{n,b})\mu(B)\bigg| \leq \bigg(r_nk_n+ \frac{1}{2}k_n(k_n-1)\bigg)\mu(I_n) \\[6pt] &\quad + \sum \limits_{b=r_nk_n + \frac{1}{2}k_n(k_n-1)}^{h_n-1} \bigg|\sum \limits_{i=0}^{r_{n}-k_n}\mu(T^{k_n(h_n+c_n)}(I^{[i]}_{n,b}) \cap B) - \mu(I^{[i]}_{n,b})\mu(B)\bigg|, \end{align*} $$
and, by Lemma A.5,
 $$ \begin{align*} &\sum \limits_{b=r_nk_n + \frac{1}{2}k_n(k_n-1)}^{h_n-1} \bigg|\sum \limits_{i=0}^{r_{n}-k_n}\mu(T^{k_{n}(h_{n}+c_{n})}(I^{[i]}_{n,b}) \cap B) - \mu(I^{[i]}_{n,b})\mu(B)\bigg| \nonumber \\&\quad= \sum \limits_{b=r_nk_n + \frac{1}{2}k_n(k_n-1)}^{h_n-1} \bigg|\frac{1}{r_n+1}\sum \limits_{i=0}^{r_{n}-k_n}\mu(T^{-ik_{n} + \frac{1}{2}k_{n}(k_{n}-1)}(I_{n,b}) \cap B) - \mu(I_{n,b})\mu(B)\bigg| \\[6pt] &\quad\leq \int \bigg{|} \frac{1}{r_n+1} \sum \limits_{i=0}^{r_{n}-k_n} \chi_{B} \circ T^{-k_ni-\frac{1}{2}k_n(k_n-1)}-\mu(B)\bigg{|}\,d\mu \to 0 \end{align*} $$
$$ \begin{align*} &\sum \limits_{b=r_nk_n + \frac{1}{2}k_n(k_n-1)}^{h_n-1} \bigg|\sum \limits_{i=0}^{r_{n}-k_n}\mu(T^{k_{n}(h_{n}+c_{n})}(I^{[i]}_{n,b}) \cap B) - \mu(I^{[i]}_{n,b})\mu(B)\bigg| \nonumber \\&\quad= \sum \limits_{b=r_nk_n + \frac{1}{2}k_n(k_n-1)}^{h_n-1} \bigg|\frac{1}{r_n+1}\sum \limits_{i=0}^{r_{n}-k_n}\mu(T^{-ik_{n} + \frac{1}{2}k_{n}(k_{n}-1)}(I_{n,b}) \cap B) - \mu(I_{n,b})\mu(B)\bigg| \\[6pt] &\quad\leq \int \bigg{|} \frac{1}{r_n+1} \sum \limits_{i=0}^{r_{n}-k_n} \chi_{B} \circ T^{-k_ni-\frac{1}{2}k_n(k_n-1)}-\mu(B)\bigg{|}\,d\mu \to 0 \end{align*} $$
by Proposition A.14 as
![]() $k_{n} \leq r_{n} + 1$
. Since
$k_{n} \leq r_{n} + 1$
. Since
![]() $k_{n} \leq r_{n}$
,
$k_{n} \leq r_{n}$
,
![]() $r_{n}k_{n} + \tfrac 12k_{n}(k_{n}-1) \leq 2r_{n}^{2}$
and since
$r_{n}k_{n} + \tfrac 12k_{n}(k_{n}-1) \leq 2r_{n}^{2}$
and since
![]() ${r_{n}^{2}}/{h_{n}} \to 0$
by assumption,
${r_{n}^{2}}/{h_{n}} \to 0$
by assumption,
![]() $(r_{n}k_{n} + \tfrac 12k_{n}(k_{n}-1))\mu (I_{n}) \to 0$
. So the sum
$(r_{n}k_{n} + \tfrac 12k_{n}(k_{n}-1))\mu (I_{n}) \to 0$
. So the sum
![]() $(\dagger )$
tends to zero.
$(\dagger )$
tends to zero.
For the sum
![]() $(\ddagger )$
, for
$(\ddagger )$
, for
![]() $r_{n} - k_{n} + 2 \leq i < r_{n} + 1$
and
$r_{n} - k_{n} + 2 \leq i < r_{n} + 1$
and
![]() $k_{n} \leq r_{n}$
, since
$k_{n} \leq r_{n}$
, since
![]() ${r_{n}^{2}}/{h_{n}} \to 0$
we have
${r_{n}^{2}}/{h_{n}} \to 0$
we have
![]() $k_{n}(h_{n}+c_{n}) + i(h_{n}+c_{n}) \geq (r_{n}+2)(h_{n}+c_{n}) \kern1.5pt{=}\kern1.5pt h_{n+1} + h_{n} + 2c_{n} - \tfrac 12r_{n}(r_{n}-1) \,{\geq} h_{n+1}$
, so
$k_{n}(h_{n}+c_{n}) + i(h_{n}+c_{n}) \geq (r_{n}+2)(h_{n}+c_{n}) \kern1.5pt{=}\kern1.5pt h_{n+1} + h_{n} + 2c_{n} - \tfrac 12r_{n}(r_{n}-1) \,{\geq} h_{n+1}$
, so
 $$ \begin{align*} T^{k_{n}(h_{n}+c_{n})}(I_{n,b}^{[i]}) &= T^{k_{n}(h_{n}+c_{n})}(I_{n+1,b + i(h_{n}+c_{n})+\frac{1}{2}i(i-1)}) \\[6pt] &= T^{k_{n}(h_{n}+c_{n})+ i(h_{n}+c_{n})+\frac{1}{2}i(i-1)}\kern-1pt(I_{n+1,b}) = T^{h_{n+1}}\kern-1pt(I_{n+1,b+h_{n}+2c_{n}-\frac{1}{2}r_{n}(r_{n}-1)}\kern-1pt). \end{align*} $$
$$ \begin{align*} T^{k_{n}(h_{n}+c_{n})}(I_{n,b}^{[i]}) &= T^{k_{n}(h_{n}+c_{n})}(I_{n+1,b + i(h_{n}+c_{n})+\frac{1}{2}i(i-1)}) \\[6pt] &= T^{k_{n}(h_{n}+c_{n})+ i(h_{n}+c_{n})+\frac{1}{2}i(i-1)}\kern-1pt(I_{n+1,b}) = T^{h_{n+1}}\kern-1pt(I_{n+1,b+h_{n}+2c_{n}-\frac{1}{2}r_{n}(r_{n}-1)}\kern-1pt). \end{align*} $$
Therefore, the sum
![]() $(\ddagger )$
satisfies
$(\ddagger )$
satisfies
 $$ \begin{align*} &\sum_{b=0}^{h_{n}-1} \bigg|\sum_{i=r_{n}-k_{n}+2}^{r_{n}} \mu(T^{k_n(h_n+c_n)}(I_{n,b}^{[i]}) \cap B) - \mu(I_{n,b}^{[i]})\mu(B)\bigg| \\[6pt] &\quad \leq \sum_{y=0}^{h_{n+1}-1} |\mu(T^{h_{n+1}}(I_{n+1,y}) \cap B) - \mu(I_{n+1,y})\mu(B)| \end{align*} $$
$$ \begin{align*} &\sum_{b=0}^{h_{n}-1} \bigg|\sum_{i=r_{n}-k_{n}+2}^{r_{n}} \mu(T^{k_n(h_n+c_n)}(I_{n,b}^{[i]}) \cap B) - \mu(I_{n,b}^{[i]})\mu(B)\bigg| \\[6pt] &\quad \leq \sum_{y=0}^{h_{n+1}-1} |\mu(T^{h_{n+1}}(I_{n+1,y}) \cap B) - \mu(I_{n+1,y})\mu(B)| \end{align*} $$
which tends to zero as
![]() $\{h_{n}\}$
is rank-one uniform mixing.
$\{h_{n}\}$
is rank-one uniform mixing.
Since
![]() $(\dagger )$
and
$(\dagger )$
and
![]() $(\ddagger )$
tend to
$(\ddagger )$
tend to
![]() $0$
, we have that
$0$
, we have that
![]() $(\star )$
tends to zero. The same argument with
$(\star )$
tends to zero. The same argument with
![]() $k_{n} + 1$
in place of
$k_{n} + 1$
in place of
![]() $k_{n}$
shows that
$k_{n}$
shows that
![]() $(\star \star )$
tends to zero. As
$(\star \star )$
tends to zero. As
![]() $c_{n}\mu (I_{n}) \leq {c_{n}}/{h_{n}} \to 0$
, this shows
$c_{n}\mu (I_{n}) \leq {c_{n}}/{h_{n}} \to 0$
, this shows
![]() $\{ t_{n} \}$
is rank-one uniform mixing.
$\{ t_{n} \}$
is rank-one uniform mixing.
Proof of Theorem A.2
By Proposition A.4, T is on a finite measure space. Let
![]() $\{t_m\}$
be any sequence. Set
$\{t_m\}$
be any sequence. Set
![]() $p_m$
such that
$p_m$
such that
![]() $h_{p_m}+c_{p_m} \leq t_m < h_{p_m+1}+c_{p_m+1}$
. Choose a subsequence
$h_{p_m}+c_{p_m} \leq t_m < h_{p_m+1}+c_{p_m+1}$
. Choose a subsequence
![]() $\{t_{m_j}\}$
of
$\{t_{m_j}\}$
of
![]() $\{t_m\}$
such that
$\{t_m\}$
such that
![]() $p_{m_j}$
is strictly increasing. Then
$p_{m_j}$
is strictly increasing. Then
![]() $\text { there exists } \{q_n\}$
with
$\text { there exists } \{q_n\}$
with
![]() $h_n+c_n \leq q < h_{n+1}+c_{n+1}$
such that
$h_n+c_n \leq q < h_{n+1}+c_{n+1}$
such that
![]() $\{t_{m_j}\}$
is a subsequence of
$\{t_{m_j}\}$
is a subsequence of
![]() $\{q_n\}$
(take
$\{q_n\}$
(take
![]() $\{q_n\}=\{t_{m_j}\} \cup \{h_n+c_n | \; n \text { such that for all } j,\ p_{m_j} \neq n \}$
). Theorem A.15 gives that
$\{q_n\}=\{t_{m_j}\} \cup \{h_n+c_n | \; n \text { such that for all } j,\ p_{m_j} \neq n \}$
). Theorem A.15 gives that
![]() $\{q_n\}$
is mixing, so
$\{q_n\}$
is mixing, so
![]() $\{t_{m_j}\}$
is. As every
$\{t_{m_j}\}$
is. As every
![]() $\{t_m\}$
has a mixing subsequence, T is mixing.
$\{t_m\}$
has a mixing subsequence, T is mixing.