The Basic Problem and a General Model

The problem that we need to address is: What is the probability that two sampled species could have a posited divergence time without one or the other having had a more recent divergence time with another sampled taxon? Every sampled species represents the tip of a lineage extending back to the origin of the clade being studied. Barring exceptional circumstances such as species-flocking (e.g., Yacobucci Reference Yacobucci, Olóriz and Rodriguez-Tovar1999), the lineages leading from the base of the clade to most species are united as single lineages that diverged at some point in the clade's history. Thus, the branch duration connecting any sampled Species X to its divergence time from the rest of the clade usually will span less time than the extended lineage leading to the base of the clade. (I use “branch duration” rather than “branch length,” because the latter term also is used for expected character change along a phylogenetic branch; e.g., Lewis Reference Lewis2001.) Similarly, the branch duration separating the node linking Species X to other sampled species usually will span less time than the remainder of that extended lineage leading to the base of the clade.

Consider two hypothetical taxa, Species A and Species I (Fig. 1). Species A appears 304 Ma and Species I appears 306 Ma. The particular phylogeny we are evaluating posits that the two species diverged from a common ancestor (here represented by Species D) at 310 Ma. The maximum branch durations preceding either species are 6 Myr for Species A and 4 Myr for Species I (i.e., the dark gray [dark blue online] bars in Fig. 1A). One evaluation of this divergence time estimate is the probability of zero finds given the branch durations (Wagner Reference Wagner1995a, Reference Wagner2000b; Huelsenbeck and Rannala Reference Huelsenbeck and Rannala1997). This assesses the probability that we failed to sample an immediate predecessor of Species A and Species I. However, Foote et al. (Reference Foote, Hunter, Janis and Sepkoski1999) make the important point that unless sampling levels are very high, most divergence times are set by sampling sister taxa rather than predecessors. Thus, if we sample any of the light gray (yellow online) lineages, then we will have a more recent divergence time and shorter branch duration for either Species A or Species I. For example, if we eventually sample Species F and correctly reconstruct the phylogeny, then we will reconstruct a divergence between Species A and Species F at 307 Ma. The branch duration leading from Species A to the rest of the clade reduces to 3 Myr; the remaining 3 Myr linking Clade A + F to the base of the clade now is the branch duration preceding the clade including Clade A + F. Thus, estimating the probability of a branch duration and divergence time requires estimating the probability of no sampled predecessors and the probability of no additional divergences leading to sampled sister taxa.

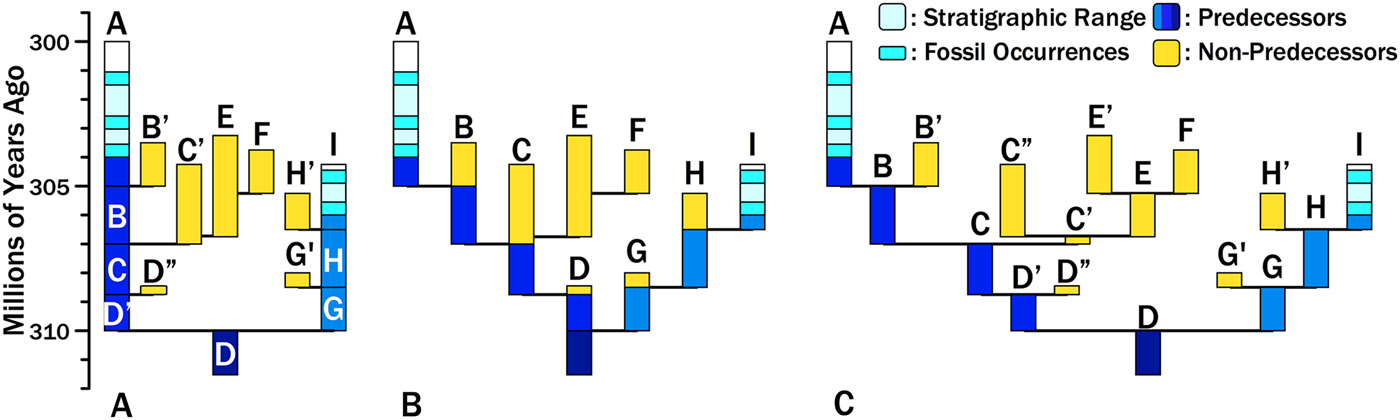
Figure 1. Hypothetical phylogeny for sampled lineages (black/light blue), unsampled predecessors (dark gray/dark blue), and unsampled sister taxa (light gray/yellow). A, Two sampled species diverged from unsampled Species D at 310 Ma, generating branch durations (and chronostratigraphic gaps) of 6 Myr for Species A and 4 Myr for Species I. Increased sampling will provide earlier divergence times and shorter branch durations/chronostratigraphic gaps in one of two ways. We might sample predecessors of A or I (dark gray/dark blue). The probability of doing so is the probability of sampling an individual lineage at any one point in time. Alternatively, we might sample sister taxa of A or I (light gray/yellow). The probability of doing so reflects origination (affecting the number of possible sister taxa and the richness of sister clades), extinction (affecting the richness of sister clades and the probability of sampling individual lineages), and sampling (affecting the probability of sampling individual lineages). B, The phylogeny re-rendered as budding speciation. Each letter represents a distinct morphospecies that we would recognize before phylogenetic analysis. Note that the predecessors of A and I now are only part of the durations of ancestors such a Species B and Species H. However, the sum of predecessors (dark gray/dark blue) and the sum of possible “sisters” (light gray/yellow) remains unchanged. C, The phylogeny re-rendered as bifurcation speciation, with ancestral morphospecies being at least slightly altered at divergence so that Species B and Species B′ have at least one character distinguishing them. Now predecessors and ancestors are nearly synonymous, save for the earliest unsampled members of Species A and I. However, the sum of predecessors and the sum of possible sisters remains unchanged.

As Bapst (Reference Bapst2013) emphasizes, the probability of any divergence time (and its implicit branch duration and stratigraphic gap within a phylogeny) reflects three rates: origination, extinction, and sampling rates. Origination and extinction both have two effects on this probability. Origination rates provide the expected number of cladogenetic events along any branch leading to the base of the tree. Both origination and extinction affect the expected number of progeny that any one cladogenetic event will ultimately generate: as origination increases and/or extinction decreases (i.e., as net diversification increases), we expect more taxa to evolve that could become sampled sister taxa. That in turn reduces the probability of deep divergences by increasing the probability of finding at least one descendant of a divergence, even if sampling rates themselves do not increase. Decreasing extinction has a similar effect, as increasing the durations of individual species increases the probability that at least one descendant of a divergence is found, even if neither origination nor sampling increase (Foote Reference Foote1996). Figure 1 illustrates how diversification affects expected branch durations and divergence times. There are three branching events leading to Species A compared with only two branching events leading to Species I; thus, all else being equal, it is more probable that subsequent sampling will add a sister taxon to Species A rather than to Species I. Moreover, one of Species A's possible sisters, the C+E+F clade, offers many more opportunities for sampling than do any of the other divergences. All else being equal, the probability of sampling some descendant of that “C” divergence is greater than the probability of sampling descendants of any other divergence.

These expectations are independent of particular speciation models. Re-rendering Fig. 1A as either a budding (Fig. 1B) or bifurcating (Fig. 1C) speciation model leaves the same branch durations leading from Species A and Species I to the base of the tree, and the same sum of durations for additional potential sister taxa. The difference is that “predecessors” and “ancestors” are basically identical given bifurcation, because ancestral morphotypes anagenetically change at cladogenesis, whereas predecessors include only those members of an ancestral species extant before cladogenesis under the budding model. (Under both models, the earliest members of Species A and Species I also are “predecessors.”) Under the latter model, the probability of sampling an ancestor is greater than the probability of sampling a predecessor (Foote Reference Foote1996). To avoid implying that ancestors necessarily become pseudoextinct at speciation, I will use the term “predecessor” for the analogues of the dark gray (dark blue online) bars in Fig. 1 throughout this paper.

Bapst (Reference Bapst2013) and Didier et al. (Reference Didier, Fau and Laurin2017) extend the work of Foote et al. (Reference Foote, Hunter, Janis and Sepkoski1999) by deriving the probability of sampling a species or any successors (i.e., a clade of unknown size) given time-homogeneous origination, extinction, and sampling. These birth–death-sampling models (= fossilized-birth–death sampling sensu Heath et al. Reference Heath, Huelsenbeck and Stadler2014; Gavryushkina et al. Reference Gavryushkina, Heath, Ksepka, Stadler, Welch and Drummond2016; Zhang et al. Reference Zhang, Stadler, Klopfstein, Heath and Ronquist2016; Stadler et al. Reference Stadler, Gavryushkina, Warnock, Drummond and Heath2018) offer great potential as tools for assessing the branch durations and divergence times implicit to rival phylogenetic hypotheses, and thus for assessing different models of anatomical evolution favoring those rival phylogenetic hypotheses. Moreover, because we have abundant paleobiological methods for estimating origination, extinction, and sampling from the fossil record, this represents a relatively rare case in which we can empirically justify the rate parameters that we need to estimate prior probabilities of branch durations and divergence times in Bayesian analyses.

The same paleobiological methods that provide us with diversification and sampling rates also indicate that all three rates all vary over time (e.g., Connolly and Miller Reference Connolly and Miller2001; Foote Reference Foote2001, Reference Foote2003; Liow and Finarelli Reference Liow and Finarelli2014; Alroy Reference Alroy2014; Finarelli and Liow Reference Finarelli and Liow2016). What we require to accommodate interval-to-interval variation in origination, extinction, and sampling is a general model that will estimate: (1) the probability of a species appearing in some interval generating any sampled specimens either of itself or some descendant species given the diversification and sampling rates of that interval and when in that interval the first species originated; (2) the probabilities that the first species sends 1…∞ successors (with the successors possibly including the first species itself) into the next interval given the origination and extinction rates of that first interval; and (3) the probability that any of those successors generate at least one sampled species given the origination, extinction, and sampling rates of subsequent intervals.

Table 1. Glossary of terms and variables of importance in this work.

The Probability of Sampling a Species or Any Successors from Any One Interval

In Figure 1, we posit that Species A and Species I are each other's closest sampled relative. The divergence time demands a branch duration and stratigraphic gap over which we failed to sample any specimens and over which no other sampled relatives diverged. If diversification and sampling rates are constant, then the expected number of sampled species or clades that should be more closely related to Species A than is Species I is Φλd, where λ is the origination rate, Φ is the proportion of branching events for which any successors are sampled (i.e., the probability of sampling a clade of unknown size sensu Bapst [2013]), and d is the branch duration leading to Species A (Table 1). Φ reflects sampling (ψ) and the summed species durations (S) expected given λ and μ (Foote et al. Reference Foote, Hunter, Janis and Sepkoski1999). For example, the C′+E + F clade (Fig. 1A) has S = 7.75 lineage million years (LMyr). Bapst (Reference Bapst2013: eq. 2) extends this logic to estimate the probability of sampling a species or any successors (i.e., a clade of unknown size) given constant λ, μ, and ψ as:

(1a)$$\; \Phi = 1-\mathop \sum \limits_{K\; = \; 1}^\infty \displaystyle{{{\rm \lambda} ^{\lpar {K-1} \rpar }{\rm \mu} ^K\left( {\matrix{ {2K-2} \cr {K-1} \cr}} \right)} \over {K{\lpar {{\rm \lambda} + {\rm \mu} + {\rm \psi}} \rpar }^{\lpar {2K-1} \rpar }}}$$

where K = 1…∞ represents the possible richness generated by any one divergence. Didier et al (Reference Didier, Fau and Laurin2017: appendix 5; see also King in Bapst Reference Bapst2016) estimate Φ using a quadratic:

(1b)$$\Phi= 1-\displaystyle{{\lpar {{\rm \lambda} + {\rm \mu} + {\rm \psi}} \rpar -\sqrt {{\lpar {{\rm \lambda} + {\rm \mu} + {\rm \psi}} \rpar }^2-4{\rm \lambda \mu}}} \over {2{\rm \lambda}}} $$

Bapst's and Didier et al.’s equations generate very similar estimates of Φ, and in both cases the probability of sampling a species or any successors increases as:

1. 1. λ increases (increasing S by generating more species);

2. 2. μ decreases (increasing S by generating longer-lived species);

3. 3. ψ increases (increasing the probability of sampling per LMyr).

To estimate Φ given shifting diversification and/or sampling, we first need to estimate Φ′, the probability of sampling a clade of unknown size over some interval i of duration T _i with its rates of λ_i, μ_i, and ψ_i. (Note that time now refers to time elapsed after a divergence, not time before a first appearance or the splitting from a common predecessor.) First, we calculate the probability that one lineage will result in K = 0…∞ lineages at any time from t = 0…T (Fig. 2). When λ ≠ μ:

(2)$$P{\rm [}K\; = \; 0\; {\rm \vert \lambda}, {\rm \mu}, t]\; = \; \displaystyle{{{\rm \mu} \times (e^{\lpar {{\rm \lambda} -{\rm \mu}} \rpar t}-1)} \over {\lpar {{\rm \lambda} \times e^{\lpar {{\rm \lambda} -{\rm \mu}} \rpar t}} \rpar -{\rm \mu}}} $$

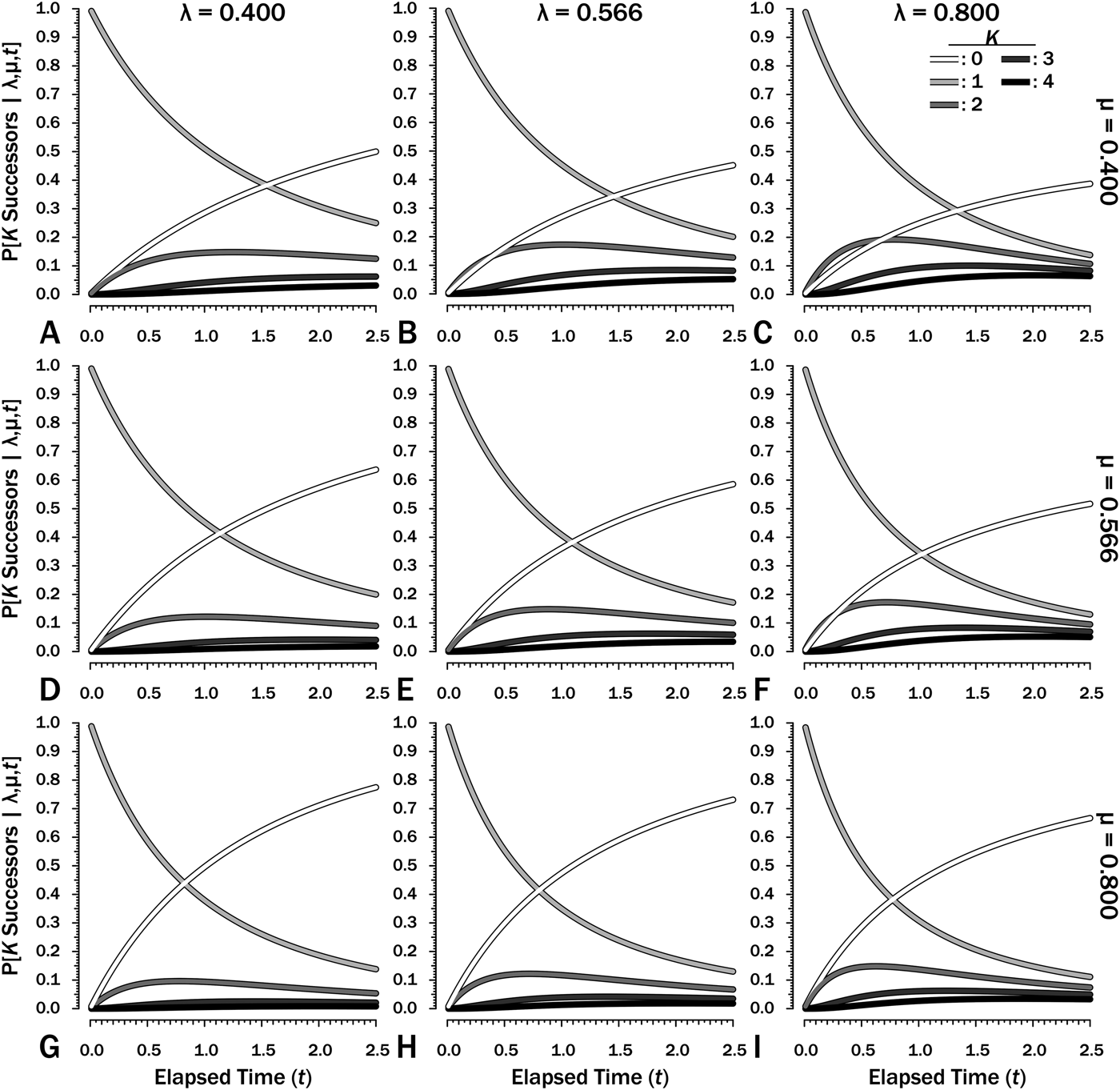
Figure 2. The probability of there being K = 0…4 successors of a species extant at time t = 0 over an interval with duration T = 2.5 given different combinations of origination (λ) and extinction (μ) rates. Note that rates increase by a factor of 1.414 (2^0.5) between adjacent frames. Note that the successors might include the original species at any point in time.

(Raup Reference Raup1985: eq. A13) and

(3)$$\eqalign{P\lsqb {K \ge 1{\rm \vert \lambda}, {\rm \mu}, t} \rsqb \; & = \; \left( {1-\displaystyle{{{\rm \mu} \times (e^{\lpar {{\rm \lambda} -{\rm \mu}} \rpar t}-1)} \over {\lpar {{\rm \lambda} \times e^{\lpar {{\rm \lambda} -{\rm \mu}} \rpar t}} \rpar -{\rm \mu}}}} \right)\; \cr & \times \left( {1-\displaystyle{{{\rm \lambda \times \mu} \times {\rm \;} (e^{\lpar {{\rm \lambda} -{\rm \mu}} \rpar t}-1)} \over {{\rm \mu} \times \lpar {\lsqb {{\rm \lambda} \times e^{\lpar {{\rm \lambda} -{\rm \mu}} \rpar t}} \rsqb -{\rm \mu}} \rpar }}} \right) \cr &\times \left( {\displaystyle{{{\rm \lambda \times \mu} \times (e^{\lpar {{\rm \lambda} -{\rm \mu}} \rpar t}-1)} \over {{\rm \mu} \times \lpar {\lsqb {{\rm \lambda} \times e^{\lpar {{\rm \lambda} -{\rm \mu}} \rpar t}} \rsqb -{\rm \mu}} \rpar }}} \right)^{K-1}} $$

(Raup Reference Raup1985: eq. A13, A17). When λ = μ:

(4)$$P{\rm [}K\; = \; 0\; {\rm \vert \lambda}, {\rm \mu}, t]\; = \; \displaystyle{{{\rm \lambda} t} \over {1 + {\rm \lambda} t}}$$

(Raup Reference Raup1985: eq. A12), and

(5)$$P{\rm [}K \ge 1\; {\rm \vert \lambda}, {\rm \mu}, t]\; = \; \displaystyle{{{\lpar {{\rm \lambda} t} \rpar }^{K-1}} \over {{\lpar {1 + {\rm \lambda} t} \rpar }^{K + 1}}}$$

(Raup Reference Raup1985: eq. A14). Figure 2 illustrates these in nine combinations of rates over some interval with T = 2.5. Both λ and μ give expectations over t = 1 (e.g., rates per million years for an interval of 2.5 Myr).

Integrating over the individual probability curves for K successors of one species gives the E[t _K], the expected amount of time within interval i in which K successors of the original species are present (Fig. 3). We can use this to estimate E[S], the expected sum of durations within an interval:

(6)$$E\lsqb S \rsqb \; = \; \mathop \sum \limits_{K\; = \; 1}^\infty \lpar {K \times E\lsqb {t_K} \rsqb } \rpar $$

that is, the number of lineages (K) times the expected time with that number of lineages (E[t _N]) summed over all possible K. (Because E[t _K] rapidly declines to very low numbers, the summation can be quickly truncated.) If we have Interval A with λ = μ = 0.4 Myr⁻¹ (Fig. 3A), then:

$$\eqalign{& {\rm E}\lsqb {S_A} \rsqb {\rm} = {\rm} (1{\rm \times} 1.250){\rm} + {\rm} (2{\rm \times} 0.625){\rm} + {\rm} (3{\rm \times} 0.313){\rm} \cr & \qquad \quad \,+ {\rm} (3{\rm \times} 0.156){\rm} + {\rm} (4{\rm \times} 0.078){\rm} \ldots \cr & = {\rm} 2.5{\rm}\ {\rm LMyr}} $$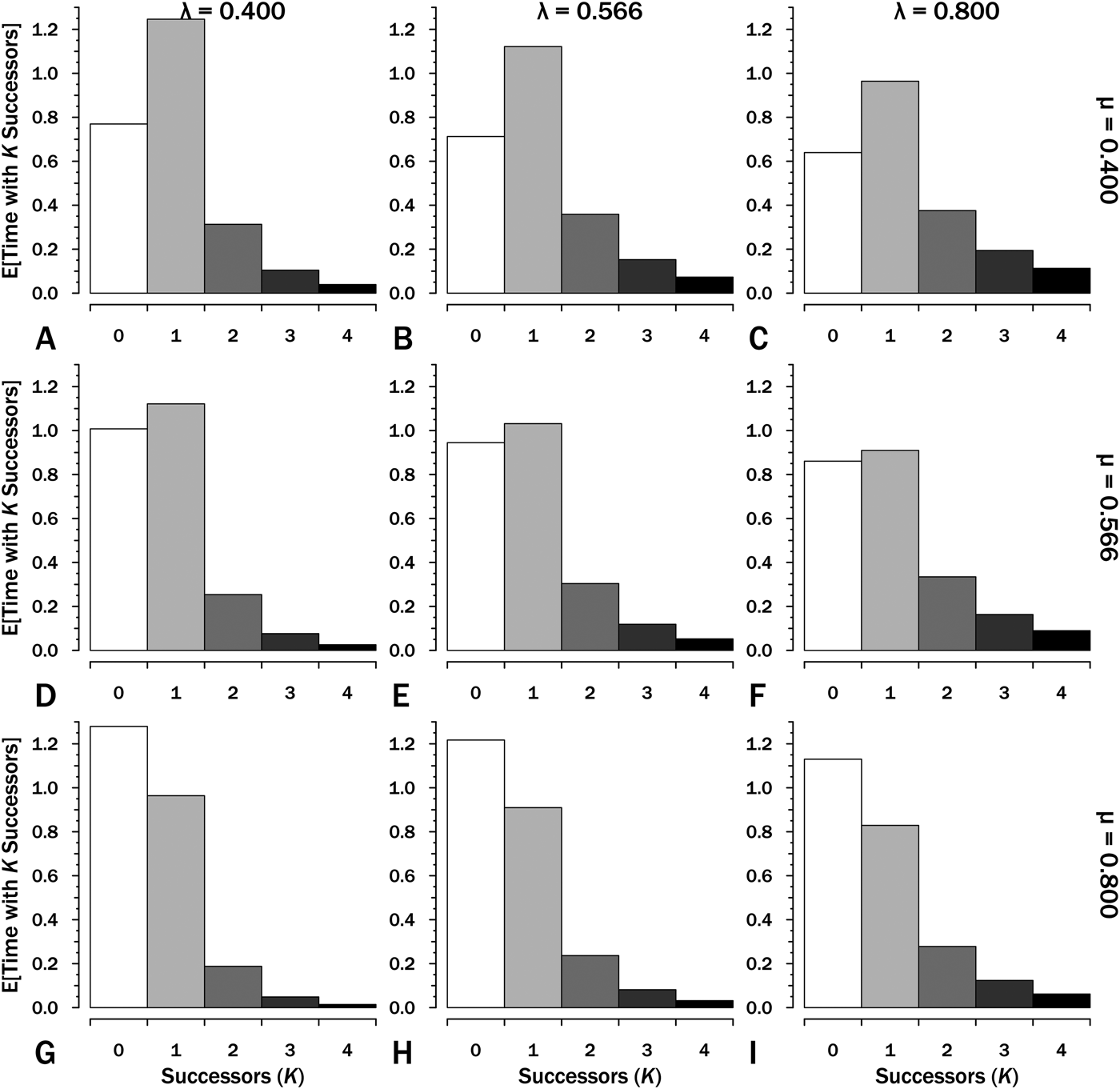

Figure 3. The expected time with K = 0…4 successors (including the original species) given interval duration T = 2.5. These are the areas under each curve for the corresponding K, origination (λ) and extinction (μ) in the corresponding panels in Fig. 2. The sum of expected lineage durations, S, is the sum of K × E[T _K]. Thus at λ = 0.4 and μ = 0.4 (A), E[S] = (1 × 1.25) + (2 × 0.313) + (3 × 0.104) + (4 × 0.039) … = 2.5 LMyr.

If we have Interval B with λ = 0.566 and μ = 0.4 (Fig. 3B), then:

$$\eqalign{ {\rm E}\lsqb {S_B} \rsqb {\rm}& = {\rm} (1{\rm \times} 1.125){\rm} + {\rm} (2{\rm \times} 0.716){\rm} + {\rm} (3{\rm \times} 0.456){\rm} \cr & \quad+ {\rm} (3{\rm \times} 0.290){\rm} + {\rm} (4{\rm \times} 0.185){\rm} \ldots \; \cr & = {\rm} 3.1{\rm} \;{\rm LMyr}} $$

A first approximation of the probability of sampling a lineage present at the outset of any interval X or any successors to that species is:

(7)$${\rm \Phi} _X^{\prime} \; = \; 1-e^{-\psi _XE\lsqb {S_X} \rsqb }$$

Therefore, if ψ_A < 1.24 × ψ_B, then we expect to sample more clades diverging at the onset of Interval B than we would for Interval A.

Simulations show that eq. (7) overestimates Φ′. At λ = μ = ψ = 0.4 and T = 2.5, eqs. (6 and 7) estimate Φ′ = 0.632, whereas simulations starting using these same parameters generate sampled species in only 53.3% of runs (see also Supplementary Fig. S1). The culprit is the failure of eq. (6) to account for total extinction within the interval eliminating any possibility of additional sampling regardless of the remaining expected S (see Supplementary Fig. S2). One solution is to divide intervals into m interval-slices so that each per-slice ψ is low and then estimate: (1) ν_i, the probability of a species extant at the outset having sampled members or successor in interval-slice i (eq. 7); and (2) ζ_i, the probability of a lineage present at the outset of interval-slice i having sampled successors in interval-slices i + 1 to m. The former parameter, ν, is the probability of finding a species and/or any successors in an interval-slice:

(7a)$${\rm \upsilon} _i\; = \; 1-e^{-{\rm \psi} _iE\lsqb {S_i} \rsqb t_i}$$

where ψ_i is the sampling rate for the interval, S _i is the expected total progeny in the interval-slice, and t _i is duration of the interval-slice. The latter parameter, ζ, is the probability of K = 1…∞ total progeny yielding at least one sampled species times given “future” λ, μ, and ψ multiplied by the probability of the initial species having K = 1…∞ successors (again, possibly including the original species) at the end of the interval-slice i given λ_i and μ_i (Fig. 4):

(8)$$ \eqalign{ \zeta _i\; = & \; \sum\nolimits_{K\; = \; 1}^\infty {\lpar {P\lsqb { \ge 1\; {\rm Finds\;} \vert K,{\rm \Phi}_{i + 1}^{\prime}} \rsqb }} \cr & \times P\lsqb {K\; Successors\; \vert {\rm \lambda}_{i.},{\rm \mu}_i} \rsqb\rpar } } $$

Figure 4. The probability of a species extant at the outset of an interval with particular origination (λ) and extinction (μ) having K = 0…4 successors extant 0.25 Myr later. The probability of the species or any successor generating a sampled species in the subsequent 0.25 Myr is conditioned on the probability of K = 0…∞ survivors going into the next interval-slice.

For the final interval-slice m, ζ_m = 0, because there are no opportunities to sample successors later in the interval. Thus, ${\rm \Phi} _m^{\prime} $ = ν_m, and we can solve ζ_{1…(m − 1)} recursively. The maximum possible value for ζ_i is the probability of any successors surviving interval-slice i: at λ = μ = 0.4 and T _i = 0.25, the probability of extinction is 0.091 (Fig. 5A) and the maximum possible ζ_i is 0.909. Now:

(9)$${\rm \Phi} _i^{\prime} \cong 1-\lpar {\lsqb {1-\upsilon_i} \rsqb \times \lsqb {1-\zeta_i} \rsqb } \rpar $$

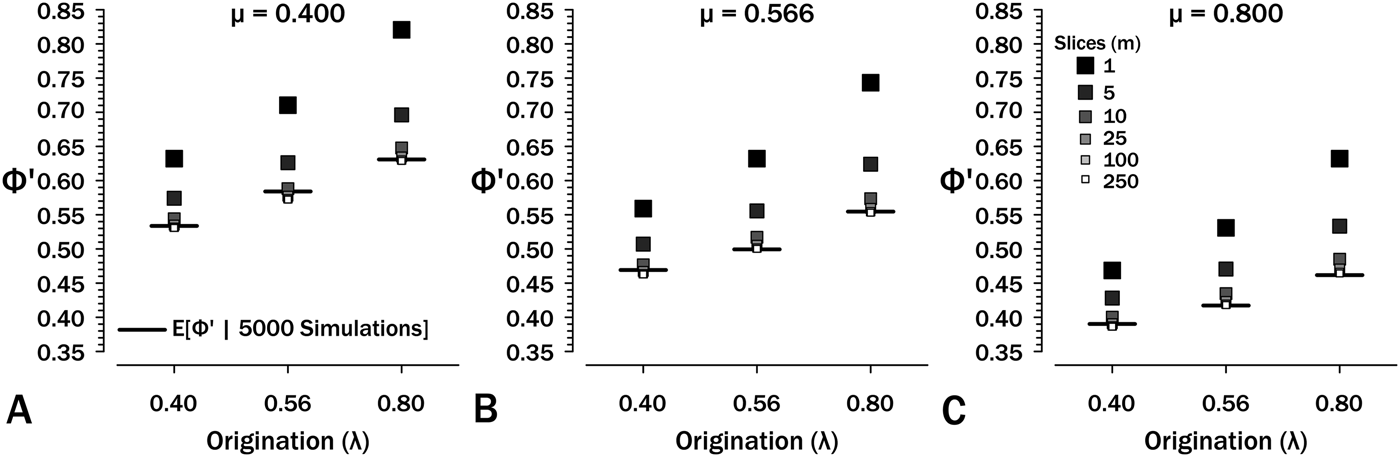
Figure 5. The effect of interval-slice length on overestimate of Φ′. Horizontal bars denote expected Φ′ given 5000 simulations at the appropriate origination (λ) and extinction (μ) rates. Intervals durations are set to T = 2.5, so at m = 250 slices, each t _i = 0.001. See also Supplementary Fig. S3.

This explicitly accommodates the probability that a lineage present at the outset of an interval is extinct with no successors by (say) the 5^th of m = 10 interval-slices.

Simulations (Fig. 5, Supplementary Fig. S1) show that eq. (9) rapidly converges to appropriate estimates of ${\rm \Phi} _1^{\prime} $ at m ≥ 10 over the range of diversification parameters used in Figures 2–5. Thus, if we typically have intervals of (say) 2.5 Myr over which we have estimates of λ, μ, and ψ, then 100 kyr interval-slices should be adequate to estimate ${\rm \Phi} _1^{\prime} $.

Another useful aspect of calculating ${\rm \Phi} _i^{\prime} $ for multiple slices within an interval is that divergences could happen at any time within an interval if origination is continuous through time. Suppose that the precision of divergence dates that we will consider are in 100 kyr increments: that is, we will ask whether a divergence happened at 450.1 Ma, 450.0 Ma, 449.9 Ma, etc. If these divergences are within a 2.5 Myr chronostratigraphic interval, then we then we need to know ${\rm \Phi} _{1 \ldots 25}^{\prime} $. ${\rm \Phi} _i^{\prime} $ will decrease as i increases: we have both less time to accrue lineage durations and less time in which to sample them. If the interval has λ = μ = ψ = 0.4 Myr⁻¹, then: ${\rm \Phi} _1^{\prime} $ = 0.536, ${\rm \Phi} _{13}^{\prime} $ = 0.383, and ${\rm \Phi} _{25}^{\prime} {\rm \;} $= 0.039. Thus, even if the probability of a divergence is the same at any point within the interval, the probability of a divergence that generates a sampled species within that interval declines over time.

The Probability of Sampling a Species or Successors over 2+ Intervals with Different Diversification and/or Sampling Rates

The exercise above applies sampling within one interval. However, this is just the particular case where all m diversification and sampling rates are the same and ν₁ = ν_2… = ν_m. We can calculate eq. (9) just as easily using ν₁ ≠ ν_2… ≠ ν_m, as will be the case if either of the diversification rates or the sampling rate varied in every interval-slice. Similarly, ζ_i is just as easy to calculate if λ_i and/or μ_i differ in every interval-slice. What I will do here is intermediate: interval-slices from different intervals will use particular values of λ, μ, and ψ so that each ν _i within an interval is identical and each ζ_i within an interval uses the same values of λ and μ. The one difference is that ζ_m will be greater than zero for all intervals save the last, and all ζ_i from those intervals will reflect subsequent shifts in diversification and/or sampling.

Suppose that we are analyzing a clade of Ordovician gastropod species known through the Katian. Suppose further that data from the Paleobiology Database coupled with an external stratigraphic database allow us to estimate separate diversification and sampling rates for gastropods as a whole for three divisions of the Katian, corresponding to Bergström et al.’s (Reference Bergström, Chen, Gutiérrez-Marco and Dronov2009) Ka1, Ka2 + Ka3 (hereafter: Ka2–3), and Ka4: λ_Ka1 = 0.269, λ_Ka2–3 = 0.348, λ_Ka4 = 0.312; μ_Ka1 = 0.293, μ_Ka2–3 = 0.495, μ_Ka4 = 0.514; and, ψ_Ka1 = 0.147, ψ_Ka2–3 = 0.155, ψ_Ka4 = 0.122 (Fig. 6). These parameters come from capture-mark-recapture analysis (Connolly and Miller Reference Connolly and Miller2001; Liow and Nichols Reference Liow, Nichols, Alroy and Hunt2010) using Paleobiology Database data, with the analysis modified to allow for log-normal distributions of sampling rates (Wagner and Marcot Reference Wagner and Marcot2013) and each ψ_Ka the median of those log-normal distributions. Each 100 kyr interval-slice within any one interval will have the same probability of a divergence in that interval-slice being sampled immediately: ν_i•Ka1 = 1.46 × 10⁻², ν_i•Ka2–3 =1.53 × 10⁻², ν_i•Ka4 = 1.20 × 10⁻² (Fig. 6A). Each 100 kyr interval-slice within an interval also shares the same probability of a species present at the outset having 0…∞ successors at the outset of the next 100 kyr interval-slice (Supplementary Fig. S3). However, ζ_i for a Ka2–3 divergence (i.e., the probability of sampling the species or successors in subsequent interval-slices) now reflects diversification and sampling in both Ka2–3 and Ka4 (Fig. 6). This in turn means that we now have Φ_i for each interval-slice within all three intervals: that is, the probability of ever sampling a descendant of a divergence occurring in that 100 kyr interval-slice at some point in the time range encompassed by our study. Simulations using the same origination, extinction, and sampling rates per interval indicate that eqs. (7a) and (8) combined generate accurate estimates of Φ_i for all interval-slices (Supplementary Fig. S4). This in turn indicates that eq. (6) is accurately estimating E[S] (expected summed durations evolving from a divergence) for different interval-slices given heterogeneous λ and μ.

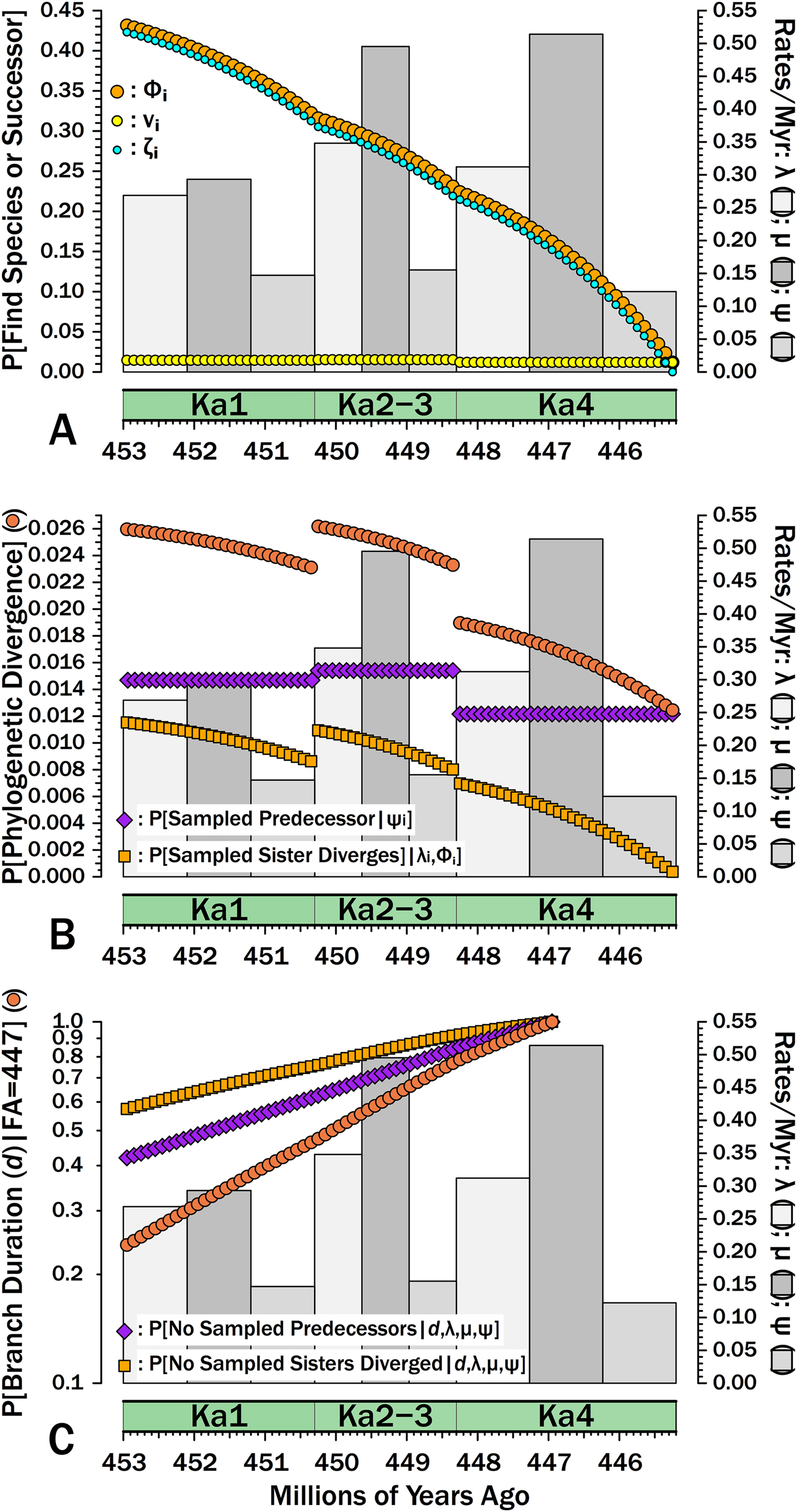
Figure 6. Breaking down estimates of branch duration probabilities given empirically estimated rates of origination (λ), extinction (μ), and sampling (ψ). Gray bars give rates for each interval (2^nd y-axis). A, The components of Φ_i, the probability of sampling a species appearing in interval-slice i or any successors of that species (i.e., a clade of unknown size). ν_i (yellow dots) gives the probability of sampling that species or any successors in interval-slice i. ζ_i (light blue dots) gives the probability of sampling any successors of that species (including the original species) in interval-slice i + 1 or any time afterward before the end of the Katian. Φ_i reflects the probability of doing either and therefore is Φ_i = 1− ([1 − ν_i] × [1 − ζ_i]). B, The exact probability of a branch duration leading to a sampled species or to a node linking sampled species starting in interval-slice i. The probability of sampling a predecessor (purple) is the probability of sampling the one predecessor of a species or node extant in interval-slice i. The probability of sampling a sister taxon (dark orange) is the probability of a divergence giving rise to a sister taxon with 1+ sampled species in interval-slice i. The probability of one or the other happening (sienna) is the probability of a phylogenetic divergence in interval-slice i given that we have some sampled species with a first occurrence after interval-slice i (or a node linking sampled species that diverges after interval-slice i). C, The probabilities of branch durations (sienna) preceding Salpingostoma richmondensis, which is first known from early in the Aphelognathus divergens conodont Zone. This is broken down into the probability of duration d with no divergences to sampled sister taxa (orange) and the probability of no sampled precursors (purple). The expected branch duration (where P[d] = 0.50) is 3.2 Myr.

The Probability of Branch Durations and Divergence Times Given Shifting Rates of Diversification and/or Sampling

We now can estimate the probability that a branch duration leading to a sampled species (or to the basal divergence of a sampled clade) diverges from the rest of the clade in any particular interval-slice. Following the gastropod example above, suppose that we are analyzing a group of bellerophontoids through the Katian. One of the species is Salpingostoma richmondensis, which is first known from rocks at the base of the Aphelognathus divergens conodont Zone in Ka4. What is the probability that S. richmondensis diverged from its closest relative before the Katian? Based on Gradstein et al. (Reference Gradstein, Ogg and Schmitz2012), we assign an earliest appearance date of 447 Ma for S. richmondensis, that is, about halfway through Ka4. (I will disregard uncertainty in the time-scale here.) Given that the Katian starts at 453 Ma, we are positing a minimum branch duration of d = 6 Myr. The probability of failing to sample a predecessor of S. richmondensis over d = 6 Myr is the probability of missing it in every interval-slice i:

(10)$$e^{-\sum\nolimits_{i\; = \; 1}^{FA-1} {{\rm \psi } _id_i}} $$

where FA-1 is the interval-slice preceding the first appearance (here, the interval-slice corresponding to 447.1 Ma), d ₁ is the time encompassed by each interval-slice (here, 100 kyr), and ψ_i is the sampling rate of that interval. (Fig. 6B gives the complement of this, i.e., the probability of sampling a predecessor per interval-slice). Given the sampling rates from above, this comes to p = 0.420.

The probability of there being no divergences leading to a sister taxon of S. richmondensis sampled in the Katian reflects the three separate origination rates and Φ_i at any given point in time:

(11)$$\mathop \prod \limits_{i\; = \; 1}^{FA-1} \mathop \sum \limits_{n\; = \; 1}^\infty \lpar {P\lsqb {n\; {\rm branchings} \vert \lambda_id_i} \rsqb \times {\lsqb {1-{\rm \Phi}_i} \rsqb }^n} \rpar $$

where P[n branchings|λ_i] is the Poisson probability of n cladogenetic events in an interval-slice given the origination rate of that interval and the duration of each interval-slice (here, 100 kyr), and [1-Φ_i]ⁿ is the probability of n divergences yielding no sampled sister taxa. Here, this generates p = 0.574. We usually will get almost identical results estimating the probability of no divergences leading to sampled sister taxa as:

$$e^{-\sum\nolimits_{i\; = \; 1}^{FA-1} {{\rm \Phi} _i{\rm \lambda} _id_i}} $$

because the probability of just one branching event is nearly equal to the probability of there being any branching events. However, at origination rates comparable to those estimated for major radiations, the probability of two branching events over even short intervals is great enough that not allowing for n = 2 yields notable underestimates of the probability of a sampled sister taxon. (Note that even with very high λ, we can truncate the summation by n = 5.)

The complement of eq. (11) is the probability that any given interval-slice includes a divergence leading to a sampled sister taxon of S. richmondensis (Fig. 6B). This increases not just as Φ increases (Fig. 6A), but also as λ increases: thus, the probability of a divergence leading to a sampled sister taxon of S. richmondensis peaks early in Ka2–3, despite the edge effect of ending the study after the next interval (Fig. 6B). Because ψ_Ka2–3 is only marginally higher than ψ_Ka1 and ψ_Ka4 is less than ψ_Ka1, this necessarily is driven by the λ_Ka2–3 being greater than λ_Ka1. The combination of elevated λ and elevated ψ in Ka2–3 also means that these interval-slices have the highest probabilities of providing S. richmondensis’s divergence from either a sampled predecessor or a sampled sister taxon.

We now calculate the probability of branch duration d as the probability of no sampled predecessors (i.e., one minus eq. 10) times the probability of no divergences leading to sampled sister taxa (i.e., one minus eq. 11). Thus, the probability that S. richmondensis has a divergence time from other bellerophontoids no later than the base of the Katian given the shifting diversification and sampling rates of the Katian (and without the possibility of sampling post-Katian sister taxa) is 0.420 × 0.574 = 0.241 (Fig. 6C). Finally, note that if we do not include any post-Katian species, then the expected branch duration for S. richmondensis (E[d]), that is, the point where the probability of the branch duration is 0.5, is 3.1 Myr.

Effects of Simple Shifts in Sampling and/or Diversification Rates on Expected Stratigraphic Gaps and Branch Durations

The specific effects of each parameter are difficult to appreciate when origination, extinction, and sampling all vary from one interval to the next, as in the Katian gastropod example. Moreover, the short span of time encompassed by the Katian data creates a major edge effect: Φ_i steadily declines throughout the Katian because no post-Katian descendants of Katian divergences can be sampled. Most studies include many more than one stage and thus might have many intervals without such an edge effect. Indeed, just how long before the conclusion of a study (or before the total extinction of a clade) we need to go before this edge effect disappears is in itself a question of interest.

Therefore, I will present simple examples in which (with one exception) two of the rate parameters are held constant while one varies over time. This will emphasize how the particular parameters affect the probabilities of branch durations and divergence times. I will first cover shifts in sampling with constant diversification. I then will cover some simplified versions of major evolutionary events given constant sampling. The latter examples are particularly important, not simply because they emphasize the strong effects of both origination and extinction rates on expected branch durations and stratigraphic gaps within a phylogeny, but because paleobiologists often target species spanning such events when conducting phylogenetic analyses. In each example, I will use 6 intervals of 2.5 Myr each, with estimates of Φ based on 100 kyr interval-slices. The “standard” diversification rates are set to 0.4 Myr⁻¹ so that we expect one event per interval. In all cases, I will use different median sampling levels that range from an expectation of one sample per interval to one sample per 100 intervals. To avoid the edge effect from the Katian gastropod example, all of the examples (save one) are followed by 12 intervals with “normal” λ, μ, and ψ.

For each combination of parameters and parameter shifts, I present the following: (1) Φ, the probability of sampling a species or any successors (= a clade of unknown size); (2) the probability of a divergence leading to a sampled sister taxon given expectation λ_iΦ_i; (3) the probability of truncating a branch duration in interval-slice i either by sampling a predecessor or from the divergence of a subsequently sampled sister taxon; and (4) the expected branch duration (E[d]) given a sampled species with that first appears in interval-slice i. The last represents the branch duration where the probability of encountering either a sampled predecessor or the divergence time of a sampled sister taxon reaches 0.5. Note that this E[d] also applies to the expected branch duration leading to a node that diverges in interval-slice i.

Finally, for Φ over time, I also include the results from 10,000 simulations (dots in Figs. 7A, 8). Each simulation begins with a single lineage, with both lifetimes and descendants per time-slice allowing for shifts in either diversification or sampling. Lifetimes and progeny of descendants are simulated the same way, albeit using rates specific to their lifetimes. Interval-specific rates of sampling are used when sampling changes. The results show the proportion of simulated lineages that generate 1+ sampled species.

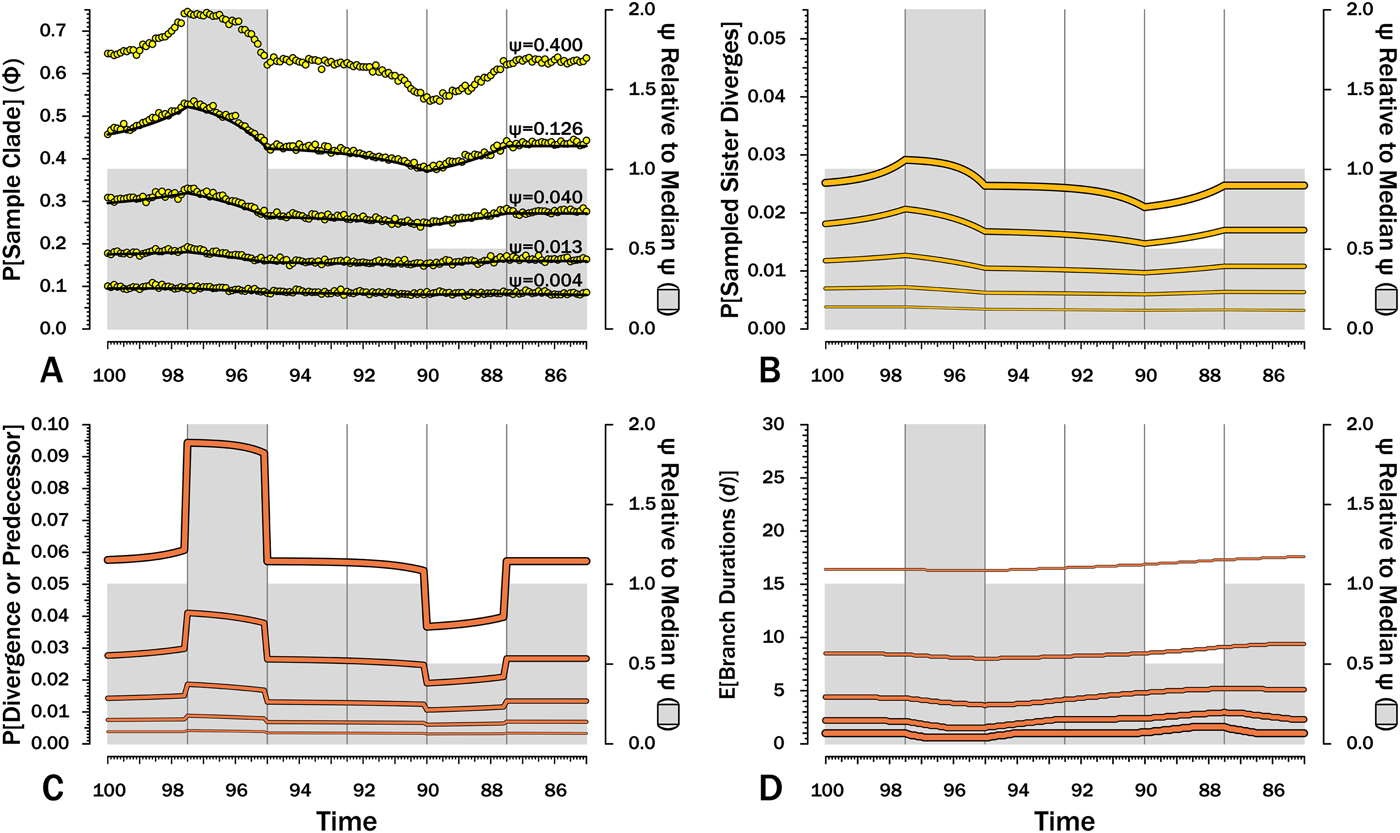
Figure 7. Effects of variable sampling over time with constant origination and extinction (λ = μ = 0.40). Five median sampling rates (ψ) are illustrated, with ψ relative to the median given on by the gray bars (2^nd y-axis). The six intervals of 2.5 Myr are preceded by six others with median ψ. A, Φ, the probability of sampling a species or any successors given that the species is extant in an interval-slice. Yellow dots give expected Φ given 10,000 simulations using ψ (and λ and μ) of the intervals of a species lifetime. B, The probability of a sampled sister species diverging in each interval-slice. C, The probability of a phylogenetic divergence in each interval-slice from either sampling a predecessor or from the divergence of a subsequently sampled sister taxon. D, Expected durations (d) for a species first appearing in each interval-slice. This also applies to a node that diverged in the same interval-slice. E[d] is the branch duration where P[no ancestors or divergences] reaches 0.50 (see Fig. 6C).

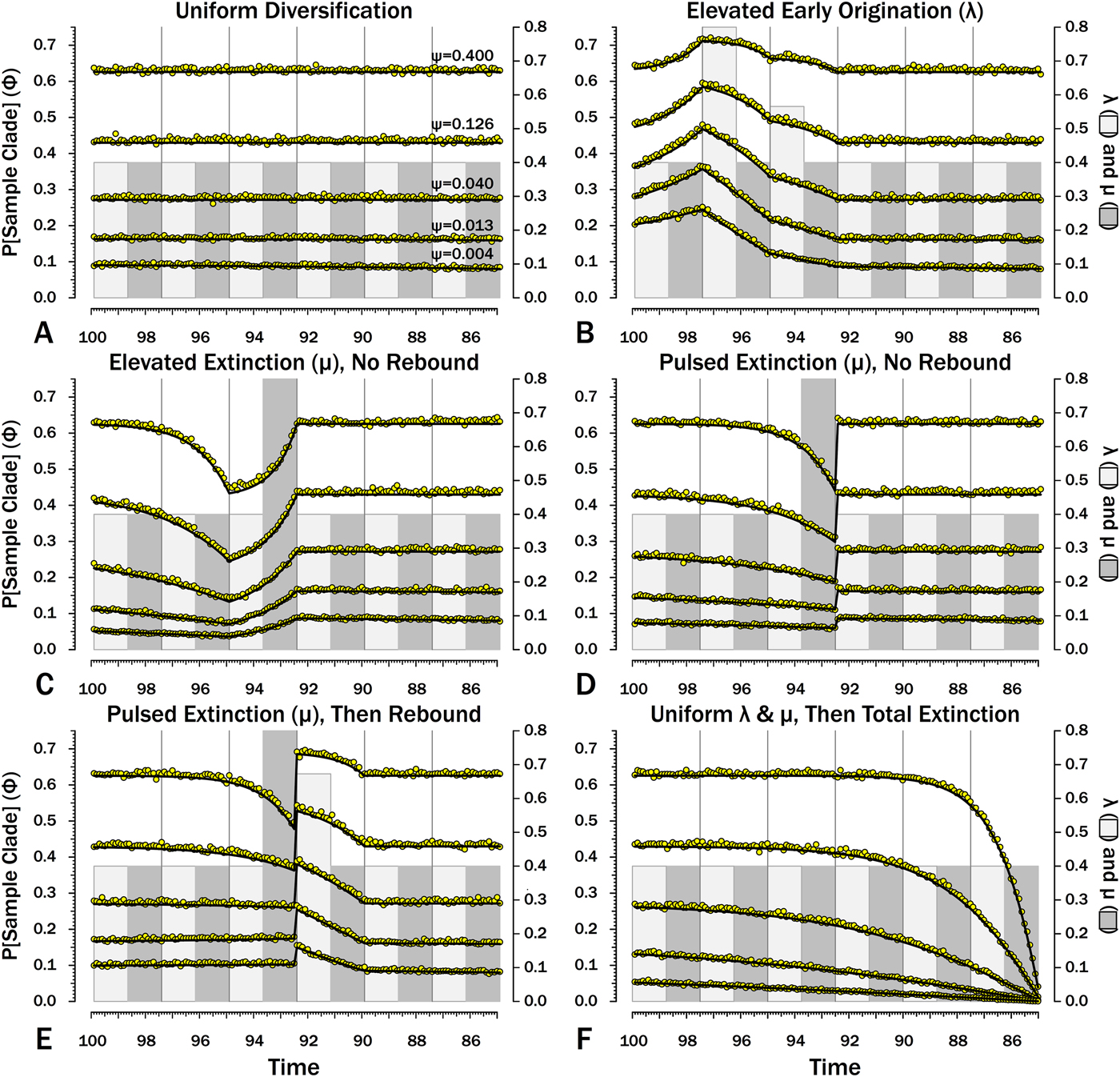
Figure 8. Probabilities of sampling clades of unknown size (Φ) under exemplar models of diversification. Origination, extinction, and sampling rates are per millions of years, with each interval 2.5 Myr long. Each Φ_i is for a 100 kyr slice. Black lines indicate Φ based on text eq. (9) and the rates of origination (λ, in light gray) and extinction (μ, in dark gray) of that time-slice and subsequent time-slices. For each curve, one of five sampling rates (ψ) is assumed for the entire duration. For pulsed extinction, the gray bar shows the average stage rate, with μ_i = 0.4 for the first 24 slices and μ_i = 10.4 for the final interval-slice, giving average μ = 0.8. Yellow dots represent the results of 10,000 simulations and give the proportion of runs in which a lineage appearing at that time ultimately generates a sampled specimen given subsequent diversification.

Effects of Shifts in Diversification Rates (λ and μ)

I use five shifts in diversification rates to stereotype five basic macroevolutionary scenarios:

1. 1. a burst of high speciation with constant extinction;

2. 2. an interval of elevated continuous extinction and constant origination;

3. 3. an interval ending with elevated pulsed extinction and constant origination;

4. 4. an interval ending with elevated pulsed extinction followed by a rebound interval of elevated origination; and

5. 5. sudden total extinction ending a clade.

I also include constant rates of λ and μ (Figs. 8A, 9A, 10A, 11A). This provides a comparison for assessing the importance of shifting rates and also allows comparison with both the Bapst (Reference Bapst2013) and Didier et al. (Reference Didier, Fau and Laurin2017) estimates of Φ (Table 2).

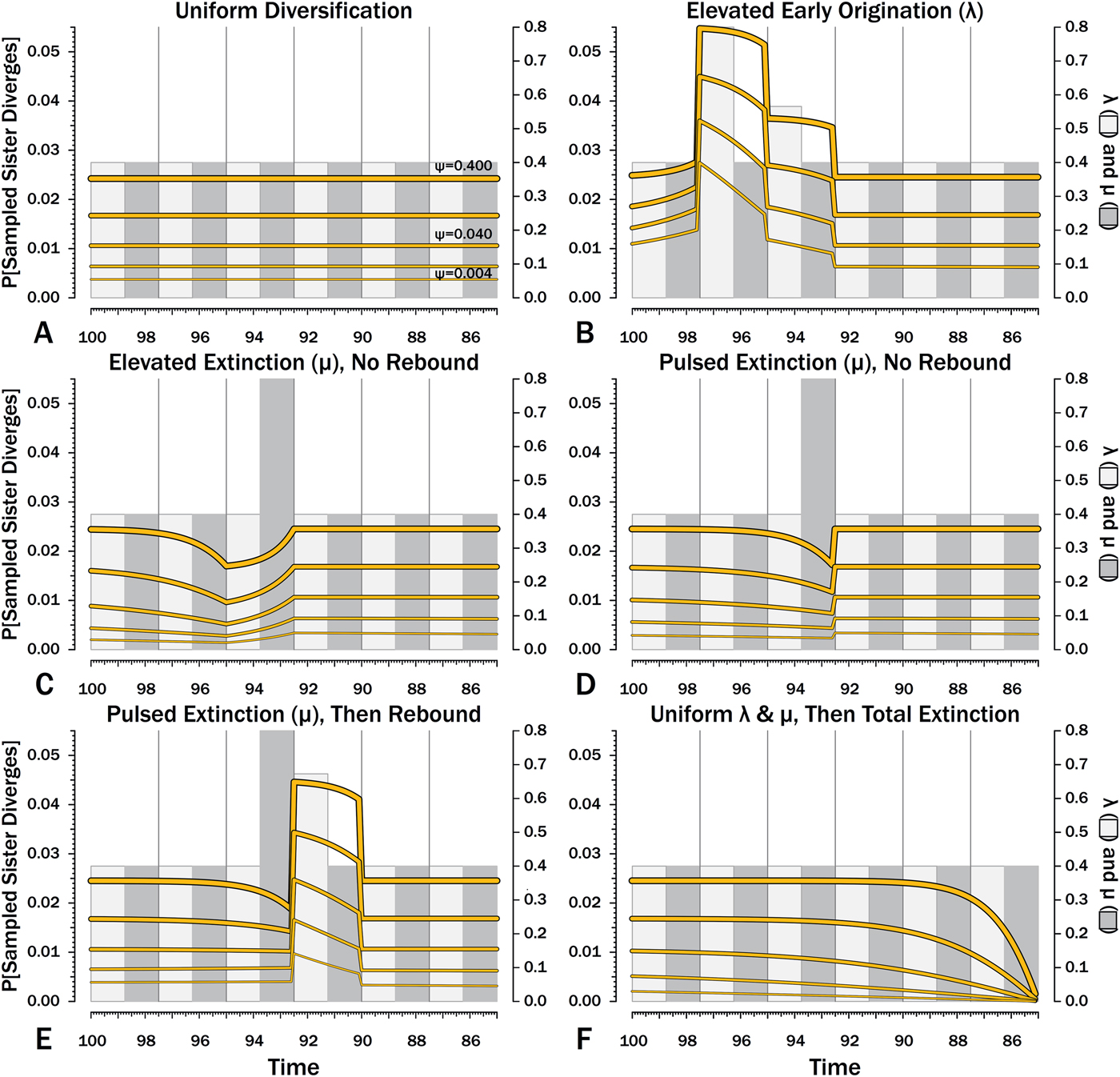
Figure 9. Probabilities of a divergence that ultimately generates a sampled species given the subsequent origination, extinction, and sampling rates.

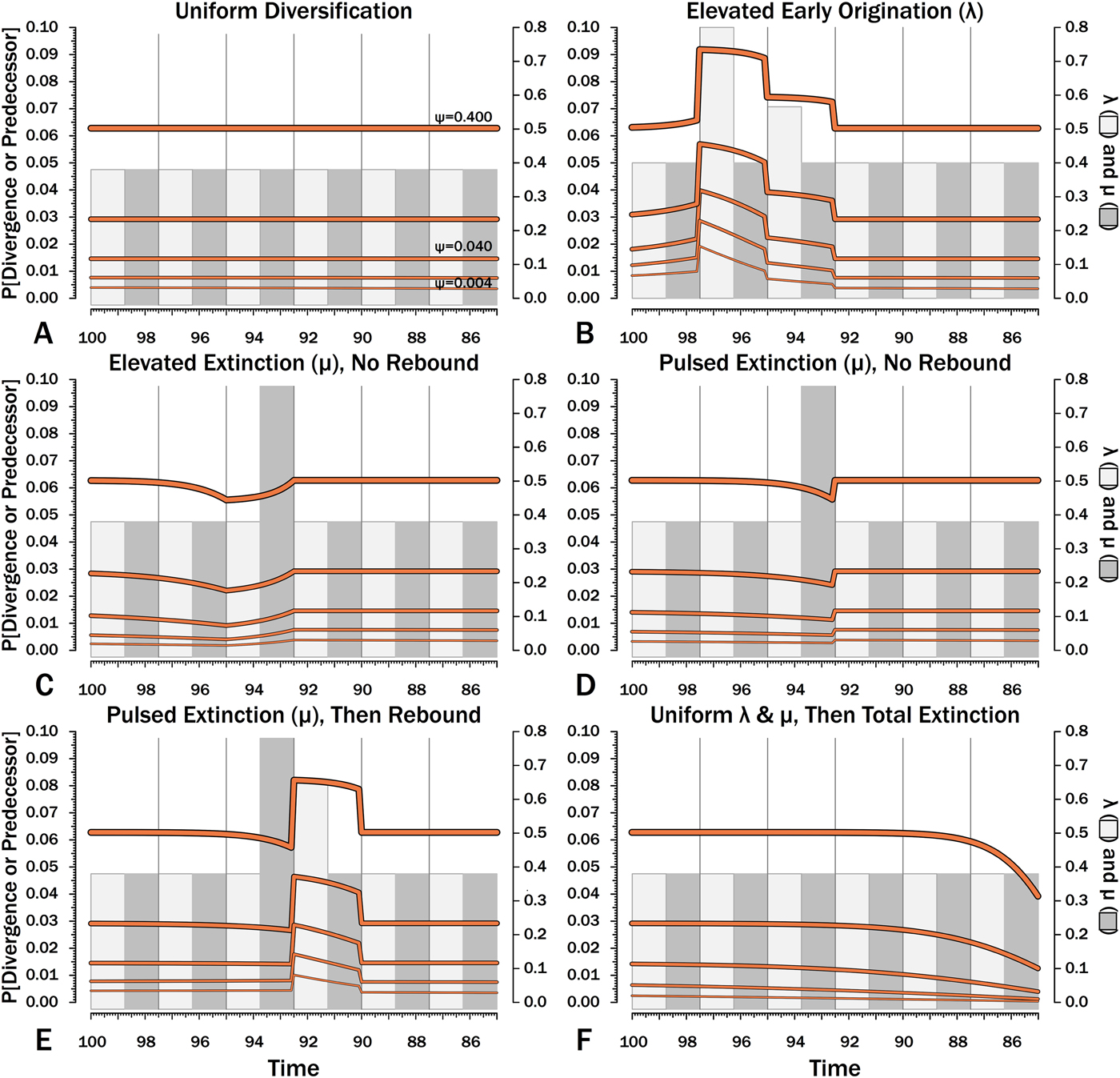
Figure 10. Probabilities of setting a phylogenetic divergence in a particular 100 kyr interval-slice, either by sampling a predecessor or by the divergence of a sister taxon that is sampled in that interval-slice or in some subsequent one. The complements of these probabilities are the probabilities of a stratigraphic gap within a phylogeny over the particular interval-slices. The product of these probabilities over any set of interval-slices gives the prior probability of a branch duration spanning that set of interval-slices.

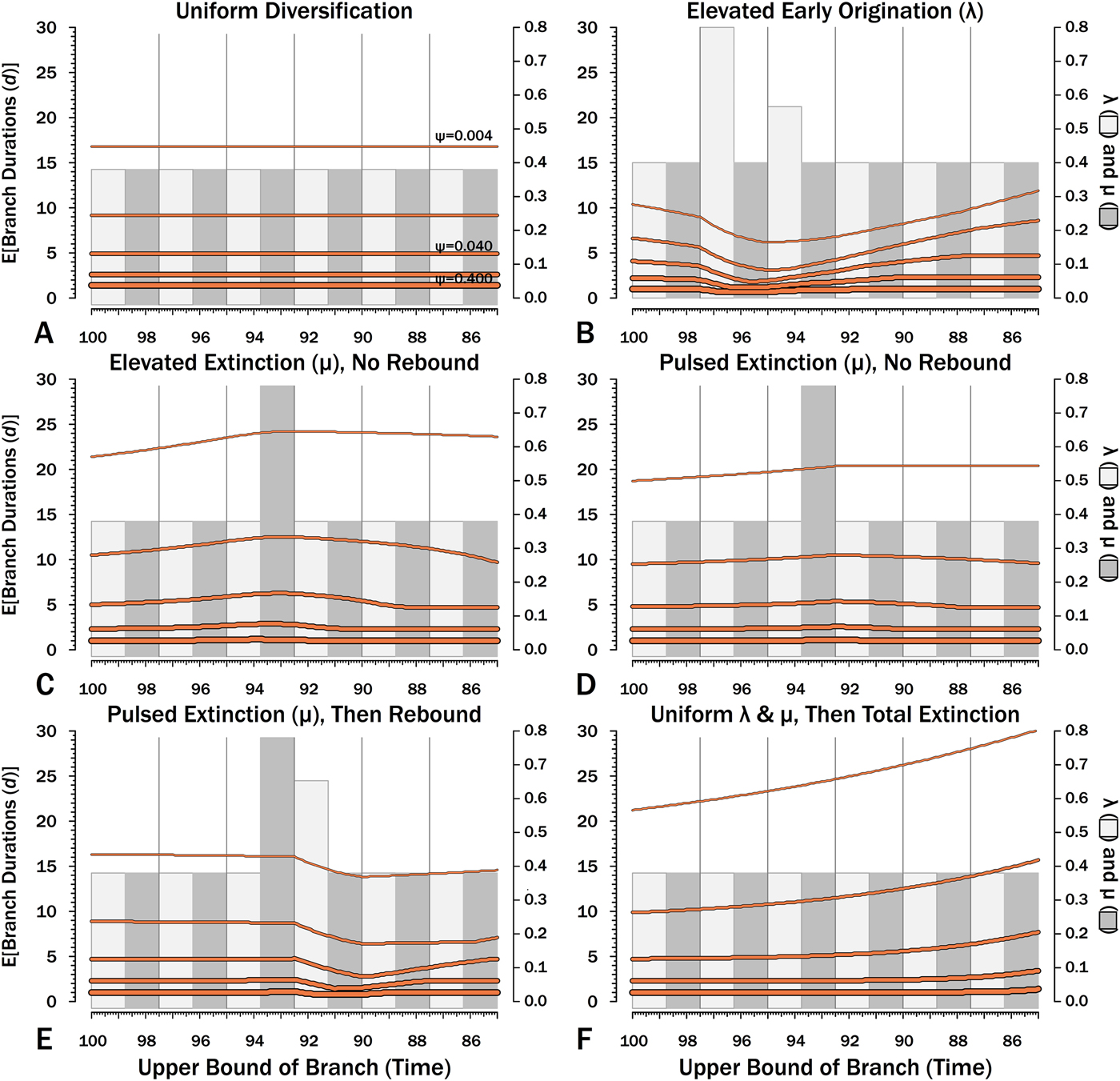
Figure 11. Expected branch durations (E[d]) for a species first appearing in an interval-slice or for an unsampled ancestor diverging in that interval-slice. E[d] is the branch duration where P[d|λ,μ,ψ] = 0.5. Note that E[d] at low ψ allows for several preceding intervals with “normal” diversification and sampling rates.

Table 2. The probability of sampling a clade of unknown size given origination and extinction = 0.4 and different levels of sampling (ψ). Φ_B gives the global estimate for a clade given Bapst (Reference Bapst2013); Φ_D gives the global estimate given Didier et al (Reference Didier, Fau and Laurin2017); and med. Φ_i gives the median 100 kyr estimate that allows for variation in diversification and sampling.

Constant Diversification and Sampling

When diversification and sampling are constant over time, the estimates of Φ that allow for temporal variation in diversification and sampling rates are nearly identical to estimates assuming constant rates (Table 2). The greatest difference is seen when ψ is very low. As discussed later, this reflects the fact that the edge effect of not allowing sampling 13+ intervals later begins to affect the probability of sampling sister taxa at very low levels of sampling.

Intervals of Elevated Origination

Here, λ doubles in the second interval, and then decreases by 1.414 times over both of the next two intervals to return to the “normal” level. Elevating λ raises Φ not just in the intervals of high λ, but also in preceding intervals (Fig. 8B). The latter effect becomes more pronounced as ψ decreases: at ψ = 0.4 (50% taxon sampling given μ = 0.4 and P[taxon sampling] = $\displaystyle{{\rm \psi} \over {{\rm \mu} + {\rm \psi}}} $; Foote Reference Foote1996), Φ at the onset of the interval preceding diversification is close to that expected given normal rates (Fig. 8A); however, given ψ = 0.004 (~0.99% taxon sampling given μ = 0.4), Φ at the onset of the preceding interval is twice that expected given normal rates. Accordingly, the probability of a sampled clade diverging in the interval preceding a radiation is greater than the probability of a sampled clade diverging after that radiation, even if the origination rates themselves are the same before and after (Fig. 9B).

The effects of elevated λ on expected branch durations and stratigraphic gaps within a tree (E[d]) also are more dramatic when ψ is low than when ψ is high (Figs. 10B, 11B). When ψ is high, expected sampled predecessors make long branch durations and stratigraphic gaps improbable given either high or low λ (see, e.g., Foote Reference Foote1996). On the other hand, when ψ is low, divergence times usually are truncated by sampled sister taxa and the increased probability of sampled sister taxa when or before λ is high reduces expected branch durations. Thus, the effect of elevated λ on E[d] is more pronounced under low ψ than under high ψ.

Interval of Continuous Elevated Extinction

Here, μ is twice normal for one interval. Elevated μ causes both Φ and expected sampled sister taxa to decrease in the intervals leading up to it (Figs. 7C, 8C). This reflects the decreased probability of a lineage having numerous and/or long-lived progeny. As ψ decreases, the effect of elevated μ on Φ extends further back in time before the extinction interval. However, Φ increases as the extinction interval progresses, reflecting the increasing probability of extant species having surviving successors that might be sampled in subsequent intervals.

Intervals of elevated extinction increase the probability of stratigraphic gaps (Fig. 9C) and thus inflate expected branch durations and stratigraphic gaps for species first appearing either before or after the interval of extinction (Figs. 10C, 11C). This reflects the increased probability of sister taxa going extinct before generating a sampled species. The effect becomes more pronounced as ψ decreases and the probability of setting a divergence time with a sampled predecessor decreases: not only is E[d] higher during the extinction interval, but E[d] is also inflated in earlier and later intervals (Fig. 8C vs. 8A at the same ψ).

Interval Ending in Pulsed Elevated Extinction

There is considerable evidence that some major extinctions occur as pulses at the end of intervals (Marshall Reference Marshall1995a; Jin et al. Reference Jin, Wang, Wang, Shang, Cao and Erwin2000; Wang and Marshall Reference Wang and Marshall2004; Wang et al. Reference Wang, Sadler, Shen, Erwin, Zhang, Wang, Wang, Crowley and Henderson2014). Therefore, I model pulsed extinction here by setting μ_i = 10.4 for the final interval-slice and μ_i = 0.4 for the first 24 interval-slices. The probability of extinction for an individual species present at the outset of the high-extinction interval is the same as in the continuous elevated-extinction example (0.86), but with the bulk of the extinction concentrated in the final interval-slice. This generates a similar decline in Φ and expected sampled divergences as we see given elevated continuous extinction (Figs. 10D, 11D vs. 10C, 11C), but with the decline in Φ now shifted so that the minimum values are at the end of the extinction interval rather than at the outset. Correspondingly, the rebound to “normal” Φ and expected sampled divergences is immediate rather than protracted. The differences in both offset and the rebound reflect species appearing in the middle of the interval not having appreciably better probabilities of having surviving successors than species appearing or existing at the outset of the interval. The amount of time with depressed Φ before the extinction also is lower with pulsed extinction than with continuous extinction of the same magnitude, particularly when ψ is low. The effect on expected branch durations and stratigraphic gaps at any given sampling level ψ is muted under pulsed extinction relative to continuous extinction (Figs. 9D vs. 9C and 10D vs. 10C). Not only are the maximum deviations from “normal” lower, but the departures from normal begin and end closer to the extinction event.

Pulsed Elevated Extinction followed by Rebound in Origination

Intervals following elevated extinction often show rebounds with elevated origination (e.g., Miller and Sepkoski Reference Miller and Sepkoski1988; Lu et al. Reference Lu, Yogo and Marshall2006; Foote et al. Reference Foote, Cooper, Crampton and Sadler2018). The probability of sister taxa evolving in the last interval and then surviving the extinction are the same as in the prior example. However, there now is a much higher probability that any species evolving before the extinction that do have surviving successors will generate a sampled descendant, which dampens the drop in Φ (Figs. 8E, 9E vs. 8D, 9D). This results in a mixing of the expected phylogenetic patterns preceding extinctions and radiations: the extinction reduces the probability of sampled sister taxa diverging before the extinction and subsequent, which offsets the preradiation decrease in expected branch durations (Figs. 10E, 11E vs. 10B, 11E); however, the elevated probability of sampling the successors of any survivors dampens the expected increase in branch durations induced by the extinction (Figs. 10E, 11E vs. 10D, 11D). As in other scenarios, low ψ results in more time elapsing after the rebound before we return to “normal” branch durations and stratigraphic gaps. In particular, E[d] decreases going back in time (Fig. 11E) until the rebound interval, and then rapidly increases. Going further back in time, E[d] increases slightly rather than decreases (as expected when there is no rebound), with the time of increase greater at low ψ than at high ψ.

Complete Extinction (or End of Study Edge Effect)

Whole clades might go extinct during pulsed extinctions, which ends the chance to sample subsequent successors. For example, in a phylogenetic analysis of nonavian dinosaurs or ammonites from the Cretaceous, there is no opportunity for an unsampled Maastrichtian species to leave Paleocene or Eocene species that would document that particular divergence. Therefore, divergences that are not sampled in the Maastrichtian are never sampled. This has strong effects on branch durations. Even if λ, μ, and ψ are static before the extinction event, Φ declines markedly before the extinction (Fig. 8F). Because divergences generating sampled sister taxa become rarer (Fig. 9F), expected branch durations increase as taxon first appearances approach the extinction (Figs. 10F, 11F).

The effect of ψ on Φ and expected sampled sister taxa seen for elevated extinction rates above becomes even more pronounced given total extinction. Under high ψ, Φ begins to decline notably only about 1.5 intervals (= 1.5 times the average species duration) before the extinction. However, at the lowest ψ, Φ is only half of “normal” (Fig. 8F vs. 8A) six intervals (again, six times the average species duration) before the extinction. We see a corresponding effect on expected branch durations (Fig. 11F). When ψ is high, E[d] is low until just before the extinction: even though we have little chance of sampling late divergences in any way, we have a high probability of sampling the predecessors of those late-appearing species that we do sample. When ψ is low and we do not expect to sample many direct predecessors, E[d] just before the extinction can be nearly twice E[d] under the same “normal” diversification and sampling rates (Fig. 11E vs. 11A), simply because of our inability to sample survivors of the extinction.

The sudden extinction scenario here is the same as edge effect that excluding post-Katian species induces on the expected branch durations for an analysis of pre-Hirnantian gastropods only. As also noted earlier, this edge effect can be seen in Table 2. At the two lowest sampling levels, median Φ given homogeneous λ, μ, and ψ is lower when we allow for temporal variation than when we do not. At the second-lowest level (where we expect to sample about 3% of taxa), Φ_i drops below the “global” estimate over 18 intervals before the end of the calculations. At the lowest ψ, Φ_i is less than the estimates assuming constant diversification and sampling at least 30 intervals before the conclusion.