1. Introduction
The joint effects of selection and migration have long been appreciated (Haldane, Reference Haldane1930; Wright, Reference Wright1931), and their importance has received considerable examinations in evolutionary theory and conservation biology. In a simple case where a balance can take place between effects of selection (soft selection) and immigration, the allele frequency in the recipient population may vary from zero (extinction) to unity (fixation), depending on the relative strengths of selection and immigration (Wright, Reference Wright1969, pp. 36–38). When the immigration rate is greater than a threshold value (the minimum migration rate required for fixing migrated alleles or genotypes), such a balance vanishes, and the immigrating allele can eventually swamp the locally dominant allele, irrespective of the adaptation or maladaptation of immigrating alleles to local habitats. This migration threshold is termed as the critical migration rate by Crow et al. (Reference Crow, Engels and Denniston1990) in addressing phase three of Wright's shifting balance theory (SBT; Wright, Reference Wright1977, pp. 443–473), and its role in impeding population fitness peak shift is extensively studied in theory (Barton, Reference Barton1992; Barton & Rouhani, Reference Barton and Rouhani1993; Rouhani & Barton, Reference Rouhani and Barton1993; Barton & Whiltlock, Reference Barton, Whiltlock, Hanski and Gilpin1997).
In flowering plants, this critical migration rate may include both haploid pollen and diploid seed flow. The existing theories are mainly developed for animal species except that Haldane (Reference Haldane1930, p. 229) indicated the necessity of generalizing the critical ratio of selection to immigration to inbreeding plants. The contribution of seed and pollen dispersal to gene flow is related to both the mode of gene inheritance and the reproductive system of species (Ennos, Reference Ennos1994). For maternally inherited organelle genomes, gene flow is mediated by seed dispersal only. This can occur for chloroplast genomes in angiosperms and mitochondrial genomes in both most angiosperms and gymnosperms (Mogenson, Reference Mogenson1996). For the nuclear and paternally inherited organelle genomes, gene flow can be mediated through both seed and pollen dispersal. Such differences in gene flow lead to unequal spreading rates in space, evidenced from differential introgression between cytonuclear genes in hybrid zones (Avise, Reference Avise1994, pp. 293–295). When combined with effects of natural selection, different critical migration rates are expected in the presence of unequal selection strengths among the three genomes, as implied from the discordance among cytonuclear clines (Hu & Li, Reference Hu and Li2002). In practical terms, the critical migration rate is of particular interest for insights into the contamination of natural forests resulting from the immigration of artificial plantations (genetically modified) with high frequencies of target genes (Ellstrand, Reference Ellstrand2003; Hu et al., Reference Hu, Zeng and Li2003). Contamination may come from genes on either nuclear or organelle genomes, or both, and the required migration rate for gene swamping in natural populations could be different through seed or pollen dispersal.
Ample evidence indicates that distinct population genetic structure, assessed using nuclear and/or organelle genome markers, exists in species of various mating systems (Ennos, Reference Ennos1994; Ennos et al., Reference Ennos, Sinclair, Hu, Langdon, Hollingsworth, Bateman and Gornall1999). A plant mating system directly affects pollen flow, and a plant population with a high outcrossing rate often receives a high immigration rate of alien pollen (Pakkad et al., Reference Pakkad, Ueno and Yoshimaru2008). For a predominantly outcrossing species, pollen dispersal often plays a dominant role in bringing about gene flow among mature forest populations (Chen et al., Reference Chen, Fan and Hu2008), enhancing the migration rate of both nuclear and paternal organelle genes. For the predominant selfing species, pollen dispersal only contributes a small portion of gene flow, enhancing comparable migration rates among nuclear, paternal and maternal organelle genes. Thus, the mating system as an important agent is involved in altering the critical migration rate through adjusting effective pollen dispersal (Haldane, Reference Haldane1930).
In addition, the joint effects of migration and the mating system facilitate interaction between nuclear and organelle genomes. Previous theories show that seed and pollen dispersal can generate cytonuclear linkage disequilibrium (LD) in the mainland–island model (Asmussen & Schnabel, Reference Asmussen and Schnabel1991; Schnabel & Asmussen, Reference Schnabel and Asmussen1992) and in hybrid zones (Arnold, Reference Arnold1993). Such an outcome can also be implied from the presence of stable LD between selective nuclear loci in structured populations (Li & Nei, Reference Li and Nei1974; Slatkin, Reference Slatkin1975). The cytonuclear LD as a biological barrier, generated by seed and pollen dispersal, can impede the spread of nuclear or organelle genes in space (Hu, Reference Hu2008, Reference Hu2010). Partial selfing reinforces the generation of cytonuclear LD in plant species (Asmussen et al., Reference Asmussen, Arnold and Avise1987, Reference Asmussen, Arnold and Avise1989; Maroof et al., Reference Maroof, Zhang, Neale and Allard1992; Asmussen & Orive, Reference Asmussen and Orive2000), similar to its function in generating LD between nuclear sites. Therefore, it is of both theoretical and practical significance to examine the similarity and differences in the critical migration rate among cytonuclear genes.
The purpose of this study is to bring together different combinations of cytonuclear systems to show how mating pattern changes the critical migration rate of seeds and pollen. This necessarily generalizes the theory to the cytonuclear system from the previous studies on the solely nuclear system where LD is negligible under the assumption of weak selection and random mating (Crow et al., Reference Crow, Engels and Denniston1990; Barton, Reference Barton1992). The cytonuclear system cannot be approximated simply by setting the recombination rate as ½ in the nuclear system, as indicated from the study of comparing two-locus LD in finite populations (Fu & Arnold, Reference Fu and Arnold1992) or from the studies on spreading neutral alleles in structured populations (Hu, Reference Hu2008, Reference Hu2010). The mixed mating system can exert distinct effects on diploid nuclear genes from on haploid organelle genes due to different modes of inheritance in addition to generating cytonuclear LD. Also, the functional epistasis between cytonuclear genes cannot be simply approximated in theory by the epistasis between nuclear sites due to the asymmetric mode of inheritance between cytonuclear genes. Cytonuclear epistasis may take place at the different levels of metabolic pathways for the products from organelle and nuclear genomes (Elo et al., Reference Elo, Lyznik, Gonzalez, Kachman and Mackenzie2003; Wolf, Reference Wolf2009), due to the long-term endosymbiotic co-evolution in a plant cell (Stoebe et al., Reference Stoebe, Hansmann, Goremykin, Kowallik, Martin, Hollingsworth, Bateman and Gornall1999; Rand et al., Reference Rand, Haney and Fry2004). Thus, it is important to consider the genetic swamping effects in shifting the fitness of the cytonuclear system.
In my analysis of the critical migration rate of seeds and pollen, three cytonuclear systems are separately addressed: the nuclear and maternally or paternally organelle genome system; the nuclear and maternal and paternal organelle genome system. In the following sections, I begin by describing the exact general model where the critical migration rates of seed and pollen can only be estimated through numerical simulations. I then separately examine each system under weak selection where the analytical approximations for critical migration rates are derived. These approximations are checked through the exact simulation results. Inferences on how the mating system shapes the critical migration rate of seeds and pollen are drawn from both analytical and simulation results under the cytonuclear system.
2. General assumptions
Consider one natural population of a hermaphrodite plant species, with constant immigration rates of pollen (m P) and seeds (m S) per generation from a source population. The source population may have either the same or different fitness from the recipient population. For simplicity, the reverse directional migration is not considered or is assumed to be not important (Fig. 1). Mutation rate is assumed to be very much smaller, and its effect is excluded. Each population size is assumed to be large so that genetic drift effect is negligible, similar to previous studies (Haldane, Reference Haldane1930; Crow et al., Reference Crow, Engels and Denniston1990; Barton, Reference Barton1992). The source population is assumed to be stable in gametic and genotypic frequencies. At the gametophyte stage, pollen and ovules are subject to natural selection (gametic selection) before combined to produce seeds. The same mating system in each population is assumed, with an arbitrary selfing rate. The plant life cycle follows a sequence of events: pollen and ovules generation, pollen flow, selection at the gametophyte stage, mixed mating, seed flow and selection at the sporophyte stage.
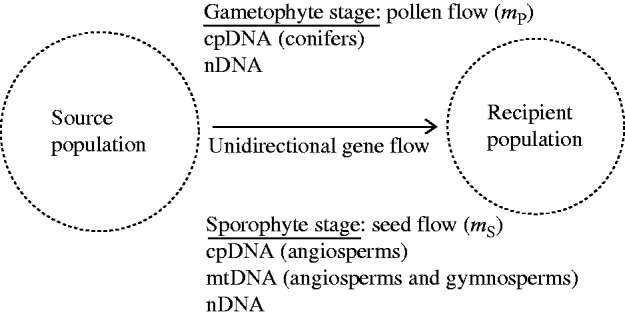
Fig. 1. A recipient population of a hermaphrodite plant species is subject to the influences of constant immigration of pollen and seeds from a source population. The source population is assumed to be stable in gametic and genotypic frequencies. At the gametophyte stage, chloroplast DNA (cpDNA) in conifers and nuclear DNA (nDNA) can be dispersed through pollen flow. At the sporophyte stage, all three genomes (mitochondrial DNA (mtDNA), cpDNA and nDNA), can be dispersed through seed flow. The present model considers the effects of unidirectional gene flow on swamping selection in the recipient population.
Consider three diallelic genes with contrasting modes of inheritance (bi-parental, paternal and maternal). Again, the three-gene cytonuclear system can naturally occur in some gymnosperms where chloroplast and mitochondrial genomes are paternally and maternally inherited, respectively (Mogenson, Reference Mogenson1996). When the effects of one organelle genome are neglected, a two-gene cytonuclear system can occur between nuclear and chloroplast genomes in angiosperms or between nuclear and mitochondrial genomes in both angiospersms and gymnosperms. Selection strength can be either strong or weak, and cytonuclear epistasis at either the gametophyte or the sporophyte stage, or both, is allowed in theory.
3. Exact simulation model
Let A 1 and A 2 be the two alleles on the diploid nuclear genomes, B 1 and B 2 be the two alleles on the haploid organelle genome with paternal inheritance, and C 1 and C 2 be the two alleles on the haploid organelle genome with maternal inheritance. These genes are selectively non-neutral, and population fitness is decided by the joint cytonuclear genes. In the recipient population, let ![]() ,
, ![]() ,
, ![]() and
and ![]() be the frequencies of cytonuclear genotype AiAjBkCl
, nuclear genotype AiAj
, organelle genotypes Bk
and Cl
(i,j,k,l=1,2; i⩽j), respectively. In order to extend the definitions of genotypic cytonuclear LD by Asmussen et al. (Reference Asmussen, Arnold and Avise1987), the genotypic cytonuclear LD in the four-gene case,
be the frequencies of cytonuclear genotype AiAjBkCl
, nuclear genotype AiAj
, organelle genotypes Bk
and Cl
(i,j,k,l=1,2; i⩽j), respectively. In order to extend the definitions of genotypic cytonuclear LD by Asmussen et al. (Reference Asmussen, Arnold and Avise1987), the genotypic cytonuclear LD in the four-gene case, ![]() , can be expressed as
, can be expressed as
where ![]() is the LD between Bk
and Cl
(=
is the LD between Bk
and Cl
(=![]() ),
), ![]() is the LD between AiAj
and Cl
(=
is the LD between AiAj
and Cl
(=![]() ) and
) and ![]() is the LD between AiAj
and Bk
(=
is the LD between AiAj
and Bk
(=![]() ). The above expression can be readily derived using Bennett's method (Bennett, Reference Bennett1954). Some properties of cytonuclear LD are
). The above expression can be readily derived using Bennett's method (Bennett, Reference Bennett1954). Some properties of cytonuclear LD are ![]() . The following relationships between gametic and genotypic cytonuclear LDs hold:
. The following relationships between gametic and genotypic cytonuclear LDs hold: ![]() ,
, ![]() and
and ![]() .
.
Similarly, let ![]() and QCl
be the frequencies of cytonuclear genotype AiAjBkCl
, nuclear genotype AiAj
, cytoplasmic genotypes Bk
and Cl
(i, j, k, l=1, 2; i⩽j) in the source population, respectively. Let
and QCl
be the frequencies of cytonuclear genotype AiAjBkCl
, nuclear genotype AiAj
, cytoplasmic genotypes Bk
and Cl
(i, j, k, l=1, 2; i⩽j) in the source population, respectively. Let ![]() ,
, ![]() and
and ![]() be the LDs between Bk
and Cl
, between AiAj
and Cl
and between AiAj
and Bk
, respectively.
be the LDs between Bk
and Cl
, between AiAj
and Cl
and between AiAj
and Bk
, respectively. ![]() and some properties about cytonuclear LD in the source population can be derived in the same way as in the recipient population.
and some properties about cytonuclear LD in the source population can be derived in the same way as in the recipient population.
In the gametophyte stage, let ![]() and
and ![]() be the fitness for gametes AiBk
in pollen and AiCl
in ovules, respectively. The average fitness in pollen and ovules, denoted by w P and w O, respectively, can be calculated using the conventional method
be the fitness for gametes AiBk
in pollen and AiCl
in ovules, respectively. The average fitness in pollen and ovules, denoted by w P and w O, respectively, can be calculated using the conventional method ![]() , where
, where ![]() and
and ![]() are the gametic frequencies after pollen dispersal. Let
are the gametic frequencies after pollen dispersal. Let ![]() ), the relative ratio of gametic fitness in pollen, and
), the relative ratio of gametic fitness in pollen, and ![]() , the relative ratio of gametic fitness in ovules. In the sporophyte stage, let
, the relative ratio of gametic fitness in ovules. In the sporophyte stage, let ![]() be the fitness for AiAjBkCl
(i, j=1, 2, i⩽j; k, l=1, 2). The average fitness in the sporophyte stage, w, can be calculated by
be the fitness for AiAjBkCl
(i, j=1, 2, i⩽j; k, l=1, 2). The average fitness in the sporophyte stage, w, can be calculated by ![]() , where
, where ![]() is the genotypic frequency after seed dispersal.
is the genotypic frequency after seed dispersal.
Let α (0⩽α⩽1) be the selfing rate. Following the life cycle mentioned above, the cytonuclear genotypic frequency after selection in the sporophyte stage, denoted by ![]() for AiAiBkCl
(i, k, l=1, 2), can be expressed as
for AiAiBkCl
(i, k, l=1, 2), can be expressed as

Similarly, the general expression for ![]() (k, l=1, 2 ) is derived as
(k, l=1, 2 ) is derived as

The above general model has several advantages. First, it allows an arbitrary level of selfing rate and can be used to assess the critical migration rate for any mating system. Second, no assumptions are imposed on the mode of joint selection for cytonuclear genotypes. Selection can be either weak or strong, or either the presence of cytonuclear epistasis or a purely linear additive–cytonuclear–viability model. Third, the general model considers natural selection at either the gametophyte or the sporophyte stage or both (Tanksley et al., Reference Tanksley, Zamir and Rick1981; Clark, Reference Clark1984). This may be of significance for some plant species where genes expressed in the sporophyte stage (~60% of structural genes) can also be expressed and potentially subject to selection in the gametophyte stage (Mulcahy et al., Reference Mulcahy, SariGorla and Mulcahy1996). Selection at the gametophyte stage can modify the critical migration rates for seeds and pollen. Finally, the model allows different cytonuclear systems, such as the system of nuclear and paternal (or maternal) organelle genomes or the system of sole organelle genomes, depending on the type of system in question.
Although the recursion expression for each allele frequency can be derived from the above general model, the migration rates of seeds and pollen are difficult to solve as the function of genotypic and allelic frequencies and selection coefficients. Given a set of parameters, the above exact model can be applied to searching for the critical migration rates of seeds and pollen in the cytonuclear system. The simulation results are not separately presented but are used to check the analytical approximations under weak selection.
4. Analytical model under weak selection
In order to derive the analytical expressions for the critical migration rates of seeds and pollen, a linear–additive–viability model with weak selection is considered. Let the gametic fitness be ![]() and
and ![]() , where
, where ![]() ,
, ![]() and
and ![]() are the selection coefficients for alleles Ai
, Bk
and Cl
, respectively. Similarly, let
are the selection coefficients for alleles Ai
, Bk
and Cl
, respectively. Similarly, let ![]() , where
, where ![]() is the selection coefficient for nuclear genotype AiAj
. Under weak selection, all terms containing the second or higher orders of the selection coefficients are neglected. The immigration rates of seeds and pollen are assumed to be small as well so that the balance between the effects of migration and selection can be attained. The terms containing the second or higher orders of the migration rate (m P2, m S2 or m Sm P or higher orders) or the products of the migration rate and selection coefficient (sm P or sm S) are neglected. For simplicity, the notation for alleles and subscripts is changed by A for A 1 and a for A 2, …, and c for C 2. The Appendix gives the recursion equations for allele frequencies and cytonuclear LD under a general mixed mating system.
is the selection coefficient for nuclear genotype AiAj
. Under weak selection, all terms containing the second or higher orders of the selection coefficients are neglected. The immigration rates of seeds and pollen are assumed to be small as well so that the balance between the effects of migration and selection can be attained. The terms containing the second or higher orders of the migration rate (m P2, m S2 or m Sm P or higher orders) or the products of the migration rate and selection coefficient (sm P or sm S) are neglected. For simplicity, the notation for alleles and subscripts is changed by A for A 1 and a for A 2, …, and c for C 2. The Appendix gives the recursion equations for allele frequencies and cytonuclear LD under a general mixed mating system.
Throughout this section, suppose that genotype AABC is fixed in the source population, and that genotype aabc is initially fixed in the recipient population. Frequencies for A, B and C are equal to unity in the source population, without cytonuclear LD, similar to the single locus case investigated by Barton (Reference Barton1992) for the nuclear system. In order to examine the swamping effects of migration, alleles A, B and C that are adaptive to the source population are assumed to be maladaptive to the recipient population although other soft selection schemes can be examined in different scenarios. Two selection schemes for the migrating nuclear genes in the recipient population are considered: heterozygote disadvantage where the heterozygotes are less fit than the homozygotes (sAA =0, sAa =−s 2, and saa =0), and directional selection where allele A is maladaptive (sAA =−2s 2, sAa =−s 2 and saa =0). Selection in the gametophyte stage is set as sA =−s 1 and sa =0 with directional selection, but is not considered in the scheme of heterozygote disadvantage. Selection coefficient for the organelle genomes is set as −sB for B and 0 for b, and −sC for C and 0 for c in both the gametophyte and sporophyte stages. The consequence for the migration swamping effects is that alleles A, B and C are fixed in the recipient population. In the following, the critical migration rates are analytically examined in three different cytonuclear systems. In each system, two specific mating systems (α=0 and 1) are firstly presented, and a mixed mating system is then examined.
(i) Nuclear and maternally inherited organelle genome system
(a) Random mating
The theory in this subsubsection is applicable to the nuclear and mitochondrial genome system in flowering plants or to the nuclear and chloroplast genome system in angiosperms with complete outcrossing (α=0). In the presence of heterozygote disadvantage, the change for the nuclear allele frequency, ΔpA =pA **−pA , is derived from eqn (A1) in the Appendix:
The change for maternal organelle allele C, ΔpC =pC **−pC , can be derived from eqn (A4) in the Appendix:
Note that 2sC in the above equation comes from selection in both the gametophyte and sporophyte stages, and it becomes sC in the absence of gametic selection. It can be seen that the frequencies of alleles A and C can consistently increase as long as their changes are greater than zero (ΔpA>0 and ΔpC>0), leading to the eventual fixation of alleles A and C in the recipient population.
Suppose that cytonuclear LD is mainly maintained by migration, the recombination rate (=1/2) and the mating system. This consideration is similar to LD between nuclear sites in the hybrid zone studies where LD can be approximated by the balance between migration and recombination (Kruuk et al., Reference Kruuk, Baird, Gale and Barton1999; Barton & Shpak, Reference Barton and Shpak2000; Hu, Reference Hu2005). Here, the mating system plays a role similar to recombination in the nuclear system in maintaining cytonuclear LD. A high selfing rate (or a high outcrossing rate) enhances (or erodes) cytonuclear LD. From eqn (A7) in the Appendix, the steady-state cytonuclear LD is approximated by DAC≈2m Sp ap c, which is of the order similar to m S.
Substituting DAC into eqn (4) at the steady state and neglecting the term with the order of migration times selection yield
The critical migration rate for joint seeds and pollen is (m S+m P/2)*=s 2/8, essentially the same as Barton's result (Barton, Reference Barton1992, p. 552) except that migration here refers to the compounded seed and pollen flow. For a given selection coefficient s 2, the sum of m S and m P is a constant. A simple complementary relationship exists between seed and pollen flow in contributing to the total critical migration rate. Similarly, substituting DAC into eqn (5) at the steady state and neglecting the term with the order of migration times selection yield
The critical migration rate for seeds is m S*=2s C, the maximum value of function 2sCpC . It can be seen that the effects of cytonuclear LD can be neglected under random mating with weak selection.
In order to check the above analytical results, exact simulations are conducted according to the general model described in the preceding section. The critical migration rates are calculated using the binary search method detailed by Barton (Reference Barton1992, p. 557). Given the settings of selection coefficients, an analytical estimate of the migration rate is used as the starting value and then adjusted by the binary search procedure. When the difference between the upper (starting fixation of migrated alleles) and lower (sufficiently close to fixation of migrated alleles) values is smaller than their average divided by 20, the average of the upper and lower values is used as the estimate, ensuring the estimate within 5% of the true value. The dynamics for allele frequency is considered to reach steady state when its changes within 10 consecutive generations are sufficiently small (<10−8; Crow et al., Reference Crow, Engels and Denniston1990).
Figure 2 a shows the comparisons between the exact simulation and analytical approximation results for the maternal organelle gene. Results indicate that slight biases exist when selection coefficients are large, but good agreement between them exists when selection coefficients are small. Figure 2 b shows the comparisons between the exact simulation and analytical approximation results for the nuclear gene. Since seed and pollen migration rates are compounded, the critical migration rates of seeds are estimated, given a migration rate of pollen, or the critical migration rates of pollen are estimated, given a migration rate of seeds. In each case, the analytical approximation performs well for the compounded migration rates of seeds and pollen (Fig. 2 b).
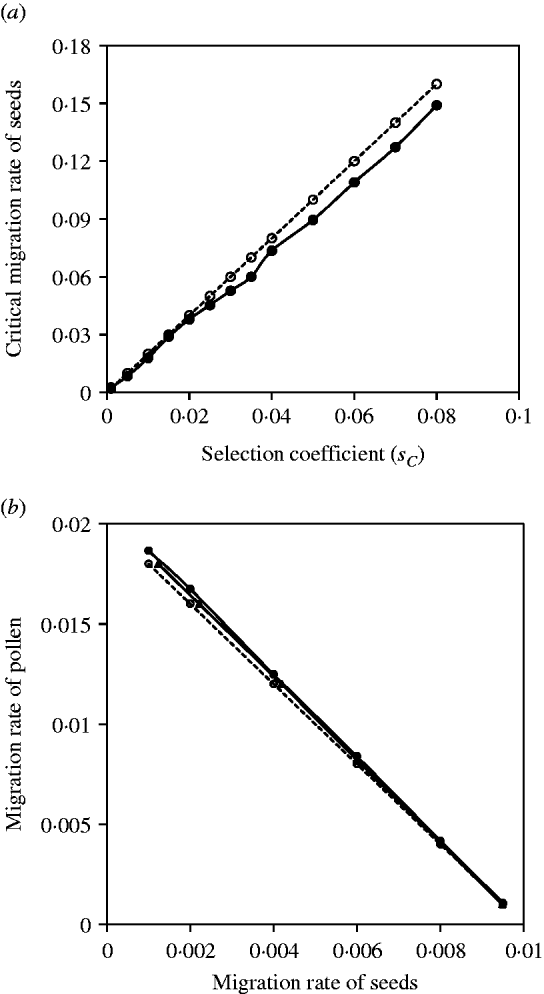
Fig. 2. (a) The critical migration rate of seeds as a function of selection strength for the maternal organelle gene. The dashed line with opened circles gives the analytic approximation, m S*=2sC from eqn (3). The solid line with closed circles is the exact simulation result. (b) A comparison of estimates of the critical migration rate from exact simulation and from analytical approximation. The dashed line with opened circles is the analytical approximation, (m S+m P/2)*=s 2/8 from eqn (4). The line with closed circles is the exact simulation result for the critical migration rate of pollen, given a set of migration rates of seeds. The line with closed triangles is the exact simulation result for the critical migration of seeds, given a set of migration rate of pollen. The selection coefficient in each case is set as s 2=−0·08.
The relationships between m S* and (m S+m P/2)* are complex in fixing the immigrated maternal and nuclear alleles. m S* for the maternal organelle gene may be smaller than (m S+m P/2)* in the presence of weaker selection against allele C than against nuclear allele A. If the migration rate of seeds for both nuclear and maternal organelle genes is equal to m S*, the migration rate of pollen may be estimated as (1/4−4γ)s 2, where γ=sC/s 2. When the selection against allele C is much stronger than selection against allele A, m S* may be greater than (m S+m P/2)*, and maternal organelle allele C is expected to be fixed earlier than nuclear allele A.
A concordance between nuclear and maternal allele frequencies is possible when certain conditions regarding selection strength, migration and the mating system are met. When a coincidence between cytonuclear allele frequencies occurs, let pA =pC =p. The recursion equation for the change of p can be approximated by combining eqns (A1) and (A4) in the Appendix. At the steady state, we obtained 2m S+m P/2=2(1+2γ−2p)ps 2. The critical value for compounded migration rate of seeds and pollen (m S+m P/4)* is derived as (1+2γ)2s 2/16, which is difficult to numerically check using the exact simulation model described in the preceding section.
With directional selection, the effects of cytonuclear LD are negligible in altering allele frequency. The steady-state equation for the frequency of maternal organelle allele remains the same as eqn (7), yielding the same critical migration rate, i.e. m S*=2sC . The steady-state equation for the nuclear allele frequency becomes
where ρ=s 1/s 2, the ratio of selection coefficients between the gametophyte and sporophyte stages. The critical migration rate for compounded seeds and pollen flow is (m S+m P/2)*=(1+ρ)s 2, greater than the results in the scheme of heterozygote disadvantage. It reduces to the result obtained by Barton (Reference Barton1992, p. 552) in the absence of gametic selection (ρ=0). Here, m S* and the critical migration rate for compounded seed and pollen flow, (m S+m P/2)*, are independently responsible for swamping maternal and nuclear alleles. m S* may be greater than (m S+m P/2)* under certain conditions. Exact simulations confirm a very good performance for the analytical estimates of critical migration rate of pollen, given a migration rate of seeds, or the analytical estimates of critical migration rate of seeds, given a migration rate of pollen (data not given here).
When a coincidence between cytonuclear allele frequencies (pA =pC =p) occurs, the steady-state equation for p can be approximated by combining eqns (A1) and (A4) in the Appendix, i.e. 2m S+m P/2=(1+ρ+2γ)ps 2. The critical migration rate for compounded seed and pollen flow becomes (m S+m P/4)*=(1+ρ+2γ)s 2/2, unequal to the results in the scheme of heterozygote disadvantage.
(b) Complete selfing
Complete selfing (α=1) removes the impacts of pollen flow. Cytonuclear LD is mainly generated by seed flow and selfing. From eqn (A7) in the Appendix, DAC is approximated by papc . In the scheme of heterozygote disadvantage, the change for the frequency of allele C is
In the above equation, the selection component comes from the selection in the sporophyte stage. From eqn (A11) in the Appendix, the genotypic cytonuclear LD can be approximated by ![]() where
where ![]() is the function of the first-order migration rate and selection coefficients. The third term on the right-hand side of eqn (9) is negligible according to the assumption of weak selection. Thus, the critical migration rate for seeds is m S*=sC
, a half value of the results under random mating due to the removal of selection effects in the gametophyte stage.
is the function of the first-order migration rate and selection coefficients. The third term on the right-hand side of eqn (9) is negligible according to the assumption of weak selection. Thus, the critical migration rate for seeds is m S*=sC
, a half value of the results under random mating due to the removal of selection effects in the gametophyte stage.
From eqn (A1) in the Appendix, the steady-state equation for the nuclear allele frequency becomes
According to eqn (A2) in the Appendix, the steady-state heterozygosity at the nuclear site can be approximated by ![]() , where
, where ![]() is the function of the first-order migration rate and selection coefficients. Substituting pAa
and DAC
in eqn (10) yields the same steady-state equation as the maternal allele frequency, with the critical migration rate for seeds, m S*=sC
, irrespective of the selection pressure at the nuclear site. This indicates the coincidence between maternal and nuclear allele frequencies, i.e. pA
=pC
=p, with approximately the same speed towards fixation.
is the function of the first-order migration rate and selection coefficients. Substituting pAa
and DAC
in eqn (10) yields the same steady-state equation as the maternal allele frequency, with the critical migration rate for seeds, m S*=sC
, irrespective of the selection pressure at the nuclear site. This indicates the coincidence between maternal and nuclear allele frequencies, i.e. pA
=pC
=p, with approximately the same speed towards fixation.
Figure 3 a shows the same trajectory for the change of migrated maternal (C) and nuclear (A) allele frequencies in the recipient population, calculated from the exact general model. The migrated alleles gradually replace the pre-existed alleles until fixation. Figure 3 b shows a good agreement between the simulation results and the analytical approximation m S* under the complete selfing.

Fig. 3. (a) A coincidence for the change of migrated maternal organelle (C) or nuclear (A) allele frequencies was observed from the exact general model in the complete selfing system, with the parameter settings sC =0·02 and m S=0·02. (b) Critical migration rate of seeds as a function of selection strength. The dashed line with opened circles gives the analytical approximation. The closed triangles are the exact simulation results.
With directional selection at the nuclear site, the steady-state equation for the maternal organelle allele frequency is different from eqn (9),
By substituting DAC into eqn (11), the critical migration rate for seeds is derived as m S*=(2+γ)s 2. The steady-state equation for the nuclear allele frequency from eqn (A1) in the Appendix after substituting DAC by papc yields the same critical migration rate. Simulation results confirm that m S*=(2+γ)s 2 is in very good agreement with the estimate from the exact model (data are not given here). Furthermore, a coincidence between maternal and nuclear allele frequencies occurs with this critical migration rate. Compared with the results for heterozygote disadvantage, a higher critical migration rate is needed for swamping selection with directional selection.
(c) Mixed mating system
From eqn (A7) in the Appendix, the steady-state cytonuclear LD can be approximated by
Equation (12) basically reflects the balance between the effects of migration and selfing that generate cytonuclear LD and the effects of recombination (1/2) that erodes cytonuclear LD, analogous to LD in the nuclear system except for the inclusion of the mating system effects (Hu, Reference Hu2005, p. 121). This is an intermediate case of the above two specific cases. In random mating (α=0), eqn (12) can be approximated by DAC≈2m Spapc . In the complete selfing case (α=1), eqn (12) can be approximated by DAC =papc . For many plant species with the mixed mating system, the condition of 1−α>>(1+α)m S is appropriate. Numerical assessment indicates that plants of wide range of selfing rates meet this condition, given that migration rate is of the order similar to weak selection. Under this case, cytonuclear LD can be further simplified as DAC≈2m Spapc/(1−α). However, the condition of 1−α<<(1+α)m S is applicable to the plant species with a predominant selfing system, and this leads to the approximation of DAC =2papc/(1+α). For a more accurate calculation, these conditions are not separately addressed.
In the scheme of heterozygote disadvantage, substitution of DAC into eqn (A4) in the Appendix yields the steady-state equation for the maternal organelle allele frequency:

The maximum value of the right-hand side of eqn (13) is (2−α)sC . The allele frequency pC consistently increases until the fixation of allele C as long as the left-hand side of eqn (13) is greater than (2−α)sC . However, the left-hand side of eqn (13) as a function of pa indicates that an array of migration rate of seeds can be generated to meet the above condition. Note that searching for the critical migration rate m S* is different from searching for the maximum m S as the function of pA and pC . Here, consider the critical migration rate of seeds at the point pa =1/4, where −pa (pa−pA ) has a maximum value of 1/8. Given the selfing rate and selection coefficients, the critical migration rate of seeds can be numerically solved (e.g., using the iterative method) from

Figure 4 a shows that the estimates of critical migration rate of seeds from the exact model with the binary search method are in good agreement with the results predicted from eqn (14) under various selfing rates.
From eqn (A1) in the Appendix and the use of the approximation for DAC , the steady-state equation for the nuclear allele frequency can be written as

This compounded critical migration rate changes with the mating system. The maximum value for the right-hand side of eqn (15) (as the function of pA
) is ![]() at pA
=1/4. The proportion of seed flow in the left-hand side of eqn (15) is the function of pc
. Thus, the critical migration rate for the compounded seed and pollen flow is expressed as
at pA
=1/4. The proportion of seed flow in the left-hand side of eqn (15) is the function of pc
. Thus, the critical migration rate for the compounded seed and pollen flow is expressed as

Given the migration rate of seeds (or pollen), the critical migration rate of pollen (or seeds) can be calculated from eqn (16). Given a mating system and selection coefficients, the right-hand side of eqn (16) is constant. Numerical analysis shows that the migration rate of pollen required to satisfy eqn (16) reduces with an increase in migration rate of seeds, i.e. a negative but not complementary relationship between seed and pollen flow. Figure 4 b shows the estimates of the critical migration rate of pollen under a fixed migration rate of seeds and various selfing rates. Estimates from the exact simulation results are slightly higher than those predicted from eqn (16) although the similar changing patterns with the selfing rate exist between them.
When eqns (14) and (16) are jointly considered, the maximum value of the right-hand side of eqn (14) may be greater than the maximum value of the right-hand side of eqn (16) except for s 2>>16sC . This strict condition s 2>>16sC is applicable to the maternal alleles whose selection coefficients are much smaller than those of nuclear alleles. The more frequent situation is that the migration rate of seeds from eqn (14) that leads to the fixation of allele C can also lead to the fixation of nuclear allele A, without the need of pollen flow, which has been confirmed through exact simulations (data not given here).

Fig. 4. (a) Critical migration rate of seeds as a function of selfing rate for the maternal organelle allele. The dashed line gives the analytical approximation from eqn (14). The line with closed circles is the exact simulation result. In each case, parameter settings are the migration rate of pollen m P=0·01, the selection coefficient sC =0·02 and s 2=0·08. (b) Critical migration rate of pollen as a function of selfing rate for the nuclear allele. The dashed curve with closed triangles gives the analytical approximation from eqn (16). The curve with closed circles is the exact simulation result. In each case, parameter settings are the migration rate of seeds m S=0·001, the selection coefficient sC =0·01 and s 2=0·04.
When a coincidence between cytonuclear allele frequencies (pA =pC =p) occurs, the steady-state equation for p can be obtained by combining eqns (A1) and (A4) in the Appendix:

where ![]() Let
Let ![]() . It can be shown that the maximum value of the right-hand side of eqn (17) is
. It can be shown that the maximum value of the right-hand side of eqn (17) is ![]() at the point p=(1+λ1)/4. Similarly, the minimum migration rate of seeds can be obtained by setting the maximum f 1max in the left-hand side of eqn (17), i.e.
at the point p=(1+λ1)/4. Similarly, the minimum migration rate of seeds can be obtained by setting the maximum f 1max in the left-hand side of eqn (17), i.e. ![]() . The critical migration rate of seeds or pollen can be numerically calculated from the following equation:
. The critical migration rate of seeds or pollen can be numerically calculated from the following equation:

With the change in the mating system and selection coefficients, a negative but not complementary relation exists between seed and pollen flow in contributing to the compounded critical migration rate. Figure 5 shows the change of the critical migration rate of pollen, predicted by the above equation, with the selfing rate. These estimates are unequal to those under the discordance case. Generally, a high critical migration rate of pollen is needed for species with a high selfing rate, given a fixed migration rate of seeds and selection strengths.
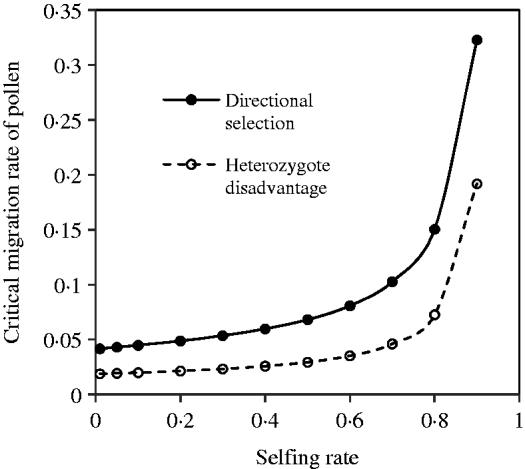
Fig. 5. Critical migration rate of pollen as a function of the selfing rate under the coincidence between the nuclear and maternal organelle allele frequencies. The curve with opened circles is the result estimated from eqn (16) in the scheme of heterozygote disadvantage, with the selection coefficients s 2=0·04, sC =0·01, and the migration rate m S=0·001. The curve with closed circles is the result estimated from eqn (21) with directional selection, with the selection coefficients s 1=s 2=0·01, sC =0·01, and the migration rate m S=0·01.
With directional selection at the nuclear site, the steady-state equation for the change of maternal organelle allele frequency is derived as

The critical migration rate for seeds, m S*, can be numerically calculated from eqn (19) by letting pa =1 and pC =1, i.e.

It can be shown that m S* is greater with directional selection than in the scheme of heterozygote disadvantage, eqn (14). Exact simulation results confirm that the analytical approximations from eqn (19) perform very well (data not shown here). The critical migration rate of seeds generally reduces with the selfing rate.
Similarly, the critical migration rate for the nuclear gene can be calculated from eqn (A1) in the Appendix,

A negative but not complementary relation exists between seed and pollen flow in contributing to the compounded critical migration rate, given a mixed mating system and selection coefficients. Figure 6 demonstrates that good analytical approximations from eqn (20) can be obtained in comparison with the exact simulation results under various selfing rates. The critical migration rate of pollen increases with the selfing rate, given a fixed migration rate of seeds.
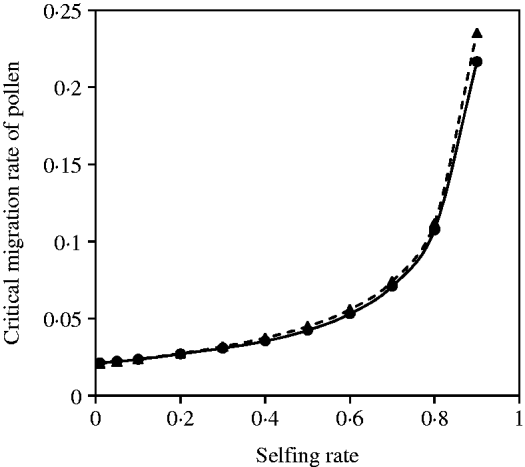
Fig. 6. Critical migration rate of pollen as a function of selfing rate for the nuclear allele. The dashed curve with closed triangles gives the analytical approximation from eqn (20). The curve with closed circles is the exact simulation result. In each case, parameter settings are the migration rate of seeds m S=0·01, the selection coefficient sC =0·01 and s 1=s 2=0·01.
When a coincidence between nuclear and maternal organelle allele frequencies occurs, the critical migration rate for the compounded seed and pollen flow can be derived by combining eqns (A1) and (A4) in the Appendix,

where
Similarly, given the migration rate of pollen (or seeds), critical migration rate of seeds (or pollen) can be estimated from the above equation. The critical migration rate of pollen may be greater with direction selection than that in the scheme of heterozygote disadvantage (e.g. Fig. 5). This critical migration rate of pollen (or seeds) is also unequal to that under the discordance between cytonuclear allele frequencies.
(ii) Nuclear and paternally inherited organelle genome system
The theory in this subsubsection is applicable to the nuclear and chloroplast genome system in conifer tree species. The difference from the preceding subsection is that both seed and pollen flow may contribute to swamping selection for the paternal organelle genes.
(a) Random mating
From eqn (A6) in the Appendix, the gametic cytonuclear LD between nuclear and paternal organelle alleles can be approximated by DAB≈2(m S+m P/2)papb , reflecting the balance between the effect of recombination (1/2) that reduces cytonuclear LD and the effect of migration that generates cytonuclear LD. In the scheme of heterozygote disadvantage, the equilibrium for the change of paternal allele frequency can be simplified from eqn (A3) in the Appendix. The effects of cytonuclear LD are negligible in altering allele frequency. The critical migration rate for the compounded seed and pollen flow is given by
A complementary relationship exists between seed and pollen flow in contributing to the critical migration rate. Given the setting of seed flow (or pollen flow), the critical migration rate of pollen (or seeds) for the paternal allele can be estimated. Exact simulations confirm that the above analytical approximation performs well in predicting critical migration rate of seeds (or pollen), given a fixed migration rate of pollen (or seeds).
Equilibrium for the change of nuclear allele frequency can be simplified from eqn (A1) in the Appendix. The critical migration rate for the compounded seed and pollen flow is the same as that derived from eqn (6), i.e. (m S+m P/2)*=s 2/8. The required migration rates of seeds and pollen may be unequal for the nuclear and paternal organelle alleles. Cytonuclear gene frequencies are basically independent due to the negligible effects of cytonuclear LD in random mating, and their alleles can be fixed at different speeds. In the condition of m S=s 2/4−2sB and m P=4sB−s 2/4, which requires s 2/16<sB <s 2/8, both the nuclear and paternal alleles can be fixed even at different speeds.
When a coincidence between the nuclear and paternal organelle allele frequencies (pA =pB =p) occurs, the critical migration rate for the compounded seed and pollen flow can be derived by combining eqns (A1) and (A3) in the Appendix: (m S+3m P/4)*=(1/2+β)2s 2/4, where β=sB/s 2, the ratio of selection coefficients between paternal organelle and nuclear alleles.
Similarly, with directional selection at the nuclear site, it can be shown that the critical migration rate for the paternal organelle allele remains the same as eqn (22). The critical migration rate for the nuclear gene is derived as (m S+m P/2)*=(1+ρ)s 2, the same as that derived from eqn (8). Cytonuclear genes are essentially independent but both can be fixed at unequal speeds when m P=2(2β−1−ρ)s 2 and m S=2(1+ρ−β)s 2. When a coincidence between cytonuclear allele frequencies (pA =pB =p) occurs, the critical migration rate for compounded seed and pollen flow becomes (m S+3m P/4)*=(1+ρ+2β)s 2/2, obtained by combining eqns (A1) and (A3) in the Appendix.
(b) Complete selfing
Pollen flow does not contribute to swamping selection. At the steady state, cytonuclear LD can be approximated by DAB≈papb
from eqn (A6) in the Appendix, which is much greater than that in random mating. From eqn (A10) in the Appendix, the genotypic cytonuclear LD can be approximated by ![]() where
where ![]() is the function of the first-order migration rate and selection coefficients. In the scheme of heterozygote disadvantage, it can be shown from eqn (A3) in the Appendix that the critical migration rate of seeds for the paternal organelle allele is m S*=βs 2.
is the function of the first-order migration rate and selection coefficients. In the scheme of heterozygote disadvantage, it can be shown from eqn (A3) in the Appendix that the critical migration rate of seeds for the paternal organelle allele is m S*=βs 2.
From eqn (A1) in the Appendix and the approximation of cytonuclear LD, the steady-state equation for the nuclear allele frequency is 0=m Spa−sBpapc , which yields the critical migration rate for seeds, m S*=βs 2, irrespective of selection pressure at the nuclear site. Exact simulation confirms that this condition also leads to a coincidence between cytonuclear allele frequencies, i.e. pA =pC =p, with the same speed towards fixation (data not presented here).
With directional selection, the steady-state equation for the paternal organelle allele frequency can be readily obtained by replacing subscript C with B in eqn (11), yielding the critical seed migration rate m S*=(2+β)s 2. This is greater than that in the scheme of heterozygote disadvantage. It can also be shown from eqn (A1) in the Appendix that m S*=(2+β)s 2 is the critical seed migration rate for the nuclear allele. Exact simulation results confirm that the analytical approximation can predict accurate results. A coincidence between paternal and nuclear allele frequencies occurs with this critical migration rate.
(c) Mixed mating system
From eqn (A6) in the Appendix, the steady-state cytonuclear LD can be approximated by

The above equation reflects the balance among the effects of migration, selfing and cytonuclear recombination. Different from eqn (12), both seed and pollen flow contribute to generating cytonuclear LD. In the random mating case (α=0), eqn (23) can be approximated by DAB≈(2m S+m P)papb . In the complete selfing case (α=1), eqn (23) can be approximated by DAB =papb .
In the scheme of heterozygote disadvantage at the nuclear site, the steady-state equation for the paternal organelle allele frequency can be derived from eqn (A3) in the Appendix:
where
which is a function of the nuclear allele frequency. The maximum value of the right-hand side of eqn (24) is (2−α)sB . When the left-hand side of eqn (24) is greater than (2−α)sB , the paternal organelle allele frequency pB increase towards the fixation. To minimize the migration rate that satisfies the above condition, the maximum f 1 is chosen at pa =1/4. The critical migration rate for the compounded seed and pollen can be derived:
where
A negative but not complementary relationship exists between seed and pollen flow in contributing to the critical migration rate of seed and pollen. Given the migration rate of seeds (or pollen), the critical migration rate of pollen (or seeds) can be numerically calculated through the iterative method. Figure 7 shows that the exact simulation results for the critical migration rate of pollen are in good agreement with the predictions from eqn (25) under various selfing rates, given a migration rate of seeds. The critical migration rate of pollen nonlinearly increases with the selfing rate when the migration rate of seeds is fixed.
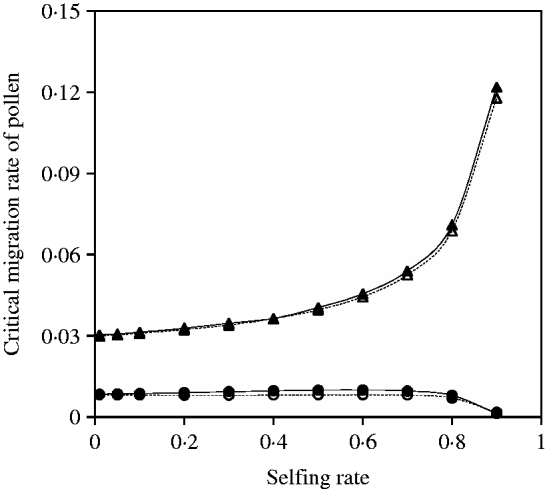
Fig. 7. Critical migration rate of pollen as a function of selfing rate in the scheme of heterozygote disadvantage. The curves with closed and opened triangles give the exact simulation results and the analytical approximation from eqn (25) for the paternal organelle allele, respectively. Parameter settings are the migration rate of seeds m S=0·01, the selection coefficient sB =0·02 and s 2=0·04. The curves with closed and opened circles give the exact simulation results and the analytical approximation from eqn (27) for the nuclear allele, respectively. Parameter settings are the migration rate of seeds m S=0·001, the selection coefficient sB =0·01 and s 2=0·04.
Similarly, the steady-state equation for the nuclear allele frequency can be derived from eqn (A1) in the Appendix

which is analogous to eqn (15) except that pollen flow is involved in changing cytonuclear LD. Following the same consideration as in deriving eqn (16), the critical migration rate for the compounded seed and pollen flow is expressed as

Figure 7 shows that the exact simulation results are slightly higher than those predicted from eqn (27) although the similar changing patterns with the selfing rate exist between them.
Equations (25) and (27) are separately applied to the paternal and nuclear alleles. Nuclear and paternal organelle genes can be fixed at different speeds due to the needs of unequal critical migration rates. When a coincidence between cytonuclear allele frequencies (pA =pB =p) occurs, the steady-state equation for p can be obtained by combining eqns (A1) and (A3) in the Appendix:

where

The function f 4 has a maximum, ![]() . Let λ2=(2−α)2β/(1−α)(2−α+α2), the critical migration rate for the compounded seeds and pollen can be numerically calculated from the following equation:
. Let λ2=(2−α)2β/(1−α)(2−α+α2), the critical migration rate for the compounded seeds and pollen can be numerically calculated from the following equation:

Figure 8 shows the change for the critical migration rate of pollen with the selfing rate, predicted by eqn (29).

Fig. 8. Critical migration rate of pollen as a function of the selfing rate under the coincidence between the nuclear and paternal organelle allele frequencies. The curve with opened circles is the result estimated from eqn (29) in the scheme of heterozygote disadvantage, with the selection coefficients s 2=0·04, sB =0·01, and the migration rate m S=0·001. The curve with closed circles is the result estimated from eqn (32) with directional selection, with the selection coefficients s 1=s 2=0·01, sB =0·01 and the migration rate m S=0·01.
With directional selection, the steady-state equation for the change of paternal organelle allele frequency is
where

The above equation is analogous to eqn (19) except for the inclusion of pollen flow. The critical migration rate for the compounded seed and pollen flow can be numerically calculated from eqn (30) by letting pa =1 and pB =1. This analytical approximation performs very well in comparison with the exact simulation results (e.g. Fig. 9).
Similarly, the critical migration rate for the nuclear gene can be calculated from eqn (A1) in the Appendix,

Given a migration rate of seeds (or pollen), the critical migration rate of pollen (or seeds) can be numerically calculated. Figure 9 demonstrates that estimates from eqn (31) are generally in good agreement with the exact simulation results.
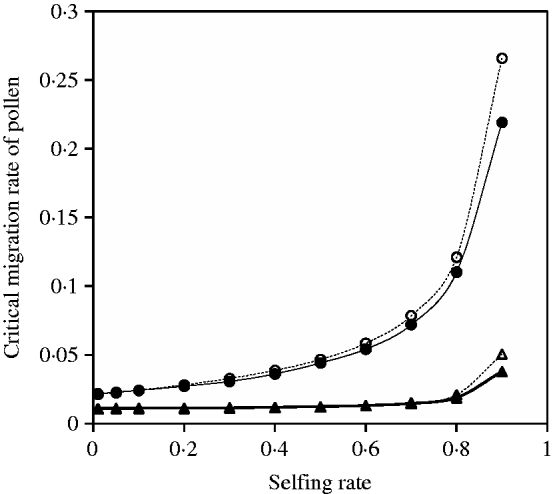
Fig. 9. Critical migration rate of pollen as a function of selfing rate with directional selection. The curves with closed and opened triangles give the exact simulation results and the analytical approximation from eqn (30) for the paternal organelle allele, respectively. Parameter settings are the migration rate of seeds m S=0·01, the selection coefficient sB =0·01 and s 1=s 2=0·01. The curves with closed and opened circles give the exact simulation results and the analytical approximation from eqn (31) for the nuclear allele, respectively. Parameter settings are the migration rate of seeds m S=0·01, the selection coefficient sB =0·01 and s 1=s 2=0·01.
Equations (30) and (31) separately address the critical migration rate for nuclear and paternal organelle alleles in the presence of cytonuclear LD. When a coincidence between nuclear and paternal organelle allele frequencies occurs, the critical migration rate for the compounded seed and pollen flow can be derived by combining eqns (A1) and (A3) in the Appendix:

The above equation is analogous to eqn (21) but has a different f function. Figure 8 shows the pattern for the change of the critical migration rate of pollen, predicted from eqn (32), with the selfing rate. The required migration rate of pollen, given a fixed rate of seed flow, is higher with directional selection than in the scheme of heterozygote disadvantage.
(iii) Nuclear and maternally and paternally inherited organelle genome system
The three-genome system, each genome with different modes of inheritance, is applicable to most conifer tree species. Theoretical deductions indicate that under weak selection, LD between paternal and maternal organelle genomes essentially does not change their allele frequencies although each of them separately interacts with the nuclear genomes (Appendix). This simplifies the analysis of the three-genome system.
(a) Random mating
In random mating, three cytonuclear genomes are essentially independent since the effects of cytonuclear LD, mainly maintained by migration and recombination, are negligible in changing cytonuclear allele frequencies. The swamping effects of migration for individual genomes have been addressed in the preceding sections. Here, only the coincidence among three genomes (pA =pB =pC =p) is presented.
In the scheme of heterozygote disadvantage, the critical migration rate for the compounded seed and pollen flow can be derived by combining eqns (A1), (A2) and (A3) in the Appendix:
With directional selection, the critical migration rate for compounded seed and pollen flow can be derived by combining eqns (A1)–(A3) in the Appendix:
In each case, the critical migration rate of seeds (or pollen) is unequal to that in the two-genome case, given the same migration rate of pollen (or seeds).
(b) Complete selfing
In the complete selfing, the critical migration rates for paternal and maternal organelle alleles remain the same as in the preceding sections. The difference from the two-genome cytonuclear system is that both paternal and maternal organelle genomes contribute to the swamping effects of migration for the nuclear allele.
In the scheme of heterozygote disadvantage, the critical migration rate of seeds for the nuclear allele is m S*=(β+γ)s 2, greater than the result at the two-genome system. When a coincidence among the three genomes occurs, the critical migration rate of seeds can be obtained by combining eqns (A1), (A3) and (A4) in the Appendix: m S*=(β+γ)s 2/3.
With directional selection, the critical migration rate of seeds for the nuclear allele is given by m S*=(2+β+γ)s 2. When a coincidence among the three genomes occurs, the critical migration rate of seeds can be obtained by combining eqns (A1), (A3) and (A4) in the Appendix: m S*=(β+γ+4)s 2/3. This critical value is greater with directional selection than in the scheme of heterozygote disadvantage.
(c) Mixed mating system
The approximations for the steady-state cytonuclear LD between the nuclear and maternal organelle alleles or between the nuclear and paternal organelle alleles remain the same as eqn (12) or (23), respectively. Expressions for the critical migration rate remain the same as eqn (13) or (19) for the seed flow for the maternal organelle gene, or the same as eqn (25) or (30) for the compounded seed and pollen flow for the paternal organelle gene.
In the scheme of heterozygote disadvantage, the critical migration rate for compounded seed and pollen flow for the nuclear gene can be derived from eqn (A1) in the Appendix:

Equation (35) is analogous to eqn (16) or (27) in the two-genome system except that effects of cytonuclear LD are linearly added to its left-hand side. Given the migration rate of seeds (or pollen), the critical migration rate of pollen (or seeds) can be numerically calculated using the iterative method. Figure 10 shows that the critical migration rate of pollen from the analytical approximation is slightly biased from the exact simulation results although a similar pattern as the function of selfing rate exists between them, similar to the results in the two-genome cases.
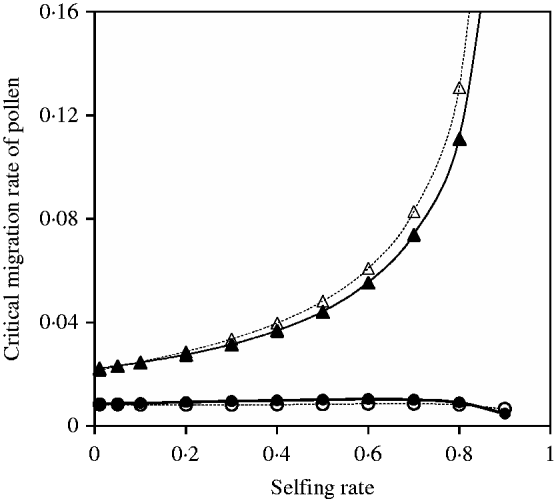
Fig. 10. Critical migration rate of pollen as a function of selfing rate for the nuclear allele. The curves with closed and opened circles give the exact simulation results and the analytical approximation from eqn (35) in the scheme of heterozygote disadvantage, respectively. Parameter settings are the migration rate of seeds m S=0·001, the selection coefficient sB =sC =0·01, s 1=0·0 and s 2=0·04. The curves with closed and opened triangles give the exact simulation results and the analytical approximation from eqn (37) with directional selection, respectively. Parameter settings are the migration rate of seeds m S=0·01, the selection coefficient sB =sC =0·01 and s 1=s 2=0·01.
When a coincidence among the three-genome allele frequencies (pA =pB =pC =p) occurs, the steady-state equation for p can be calculated by simply combining eqns (A1), (A3) and (A4) in the Appendix. The critical migration rate for the compounded seed and pollen flow can be derived:

Compared with eqns (18) and (29) in the two-genome systems, there is not a simple relationship among them. Figure 11 shows the pattern for the change of critical migration rate of pollen with the selfing rate, given a fixed migration rate of seeds. The results similar to Figs 5 and 8 can be observed.
With directional selection, the critical migration rate for compounded seed and pollen flow for the nuclear allele can be derived in the same method:

Equation (37) is analogous to eqns (20) and (31) in the two-genome system except that effects of cytonuclear LD are linearly added. Exact simulation results indicate that the analytical approximation by eqn (37) performs very well (Fig. 10). The critical migration rate of pollen increases with the selfing rate under a fixed rate of seed flow.
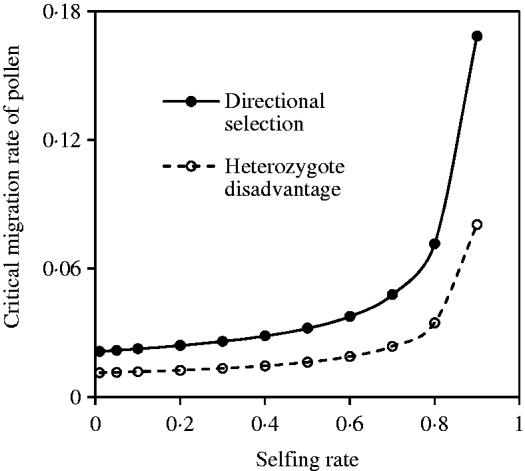
Fig. 11. Critical migration rate of pollen as a function of the selfing rate under the coincidence among nuclear, maternal and paternal organelle allele frequencies. The curve with opened circles is the result estimated from eqn (36) in the scheme of heterozygote disadvantage, with the selection coefficients s 2=0·04, sB =sC =0·01, and the migration rate m S=0·001. The curve with closed circles is the result estimated from eqn (38) with directional selection, with the selection coefficients s 1=s 2=0·01, sB =sC =0·01, and the migration rate m S=0·01.
Similarly, when a coincidence among the three-genome allele frequencies occurs, the critical migration rate for compounded seed and pollen flow is given by

Compared with the two-genome system (eqns 21 and 32), effects of cytonuclear LD are linearly added into eqn (38). Figure 11 shows the effects of the mating system on the critical migration rate of pollen, given a fixed rate of seed flow. The critical migration rate of pollen may be much greater with directional selection than in the scheme of heterozygote disadvantage.
5. Discussion
This study demonstrates how the mating system changes the critical migration rate for swamping selection for plant genomes with contrasting modes of inheritance (maternal, paternal and bi-parental inheritance), necessarily extending the previous studies to include the effects of mating systems and the joint cytonuclear system (Haldane, Reference Haldane1930; Wright, Reference Wright1969; Crow et al., Reference Crow, Engels and Denniston1990; Barton, Reference Barton1992). The analytical and simulation results demonstrate that the mating system can alter the critical migration rates of seed and pollen through changing effective pollen flow, cytonuclear LD and gametic selection for both nuclear and paternal organelle genes. Partial selfing changes the critical migration rate of seeds for the maternal organelle genes through changing gametic selection and cytonuclear LD. Both concordance and discordance between cytonuclear genes can occur during the gene swamping process due to the needs of unequal critical migration rates of seeds and pollen. These theoretical results expand our understanding of the joint effects of migration and selection in evolving natural hermaphrodite plant populations.
It is important to understand the biological significance of incorporating the mating system into the joint effects of migration and selection, the very important type of interaction that is considered as one of mechanisms for gene spread, species’ range expansion and incipient speciation (Wright, Reference Wright1931, Reference Wright1977; Fisher, Reference Fisher1937; Haldane, Reference Haldane1956; Barton & Charlesworth, Reference Barton and Charlesworth1984; Kirkpatrick & Barton, Reference Kirkpatrick and Barton1997). Complete random mating and selfing represent two extreme breeding systems, while the mixed mating system is considered as a transitional pattern (Goodwillie et al., Reference Goodwillie, Kalisz and Eckert2005; Charlesworth, Reference Charlesworth2006). Complete random mating allows a maximum probability of immigrating alien pollen and enhances differential fixation rates between cytonuclear genes. A low migration rate can swamp weak selection for the nuclear allele, but a high migration rate may be required for the maternal organelle gene. The effect of random mating has been addressed for the nuclear system (Crow et al., Reference Crow, Engels and Denniston1990; Barton, Reference Barton1992). Complete selfing does not allow immigration of alien pollen but enhances the concordant swamping process between cytonuclear genes. A typical flowering plant is hermaphroditic and self-compatible (Heilbuth, Reference Heilbuth2000), with co-sexual functions for an individual. The evolutionary stability of this reproductive system remains controversial due to the use of two contrasting strategies with different proportions of gene transmission to progeny (Maynard Smith, Reference Maynard Smith1982; Goodwillie et al., Reference Goodwillie, Kalisz and Eckert2005). The proportion of each strategy (selfing versus outcrossing) alters the relative pollen and seed flow and hence changes the swamping rate. The present theory confirms that the mixed mating system directly adjusts the contributions of alien pollen to swamping selection in a complicated non-linear way for the nuclear and paternal organelle genes.
In comparison with the nuclear system for animal species (Barton, Reference Barton1992), the expression for critical migration rate for a single nuclear gene is the same in the cytonuclear system under random mating with weak selection. The only step is to replace the critical migration rate for animal species with m S+m P/2 for plant species. However, the inclusion of cytonuclear LD, attained by selfing and migration in the mixed mating system, falsifies such simple transformation. One more likely system is the involvement of multiple nuclear sites because nuclear genomes are much larger in size and have a more number of genes than organelle genomes (Barton, Reference Barton1992; Birky, Reference Birky1995). The effects of selection on multiple nuclear sites may substantially reduce effective gene flow, which makes swamping less likely. Also, the transformation from the nuclear to the cytonuclear system becomes complicated in the mixed mating system because additional LD between nuclear sites can alter the process of nuclear gene swamping. A more sophisticated model is needed to assess the critical migration rate and the relative contributions of cytonuclear LD versus LD between nuclear sites.
Similarly, in comparison with the sole organelle genome system (not separately addressed here), the critical migration rate for maternal or paternal organelle gene remains the same as in the cytonuclear system in random mating with weak selection. The inclusion of cytonuclear LD in the mixed mating system can modify this swamping process in a non-linear way. It is speculated that such a modification can be intensified when multiple nuclear sites are jointly considered, as implied from the studies on gene spreading in structured populations (Hu, Reference Hu2008, Reference Hu2010).
Biologically, both concordant and discordant processes of gene swamping between cytonuclear genes have significantly evolutionary meanings although the proportion of nuclear or organelle genes undergoing these distinct processes is unknown. The population fitness in the sporophyte stage here is determined by cytonuclear genes rather than by the individual nuclear or organelle genes. The same swamping rate, such as in the complete selfing case, implies that the whole three-genome system approaches maximum co-evolution. The population fitness can be shifted when different population fitness exists between the source and recipient populations, the phase III of Wright's SBT (Wright, Reference Wright1977). The unequal swamping rates result in a different structure for cytonuclear genes, and leads to a lag in population adaptation between genomes.
This study assumes that genetic drift effects are negligible compared with the effects of seed and pollen flow and selection. This is plausible for a large population where a deterministic approach is approximated. For a small population, genetic drift could also cause population fitness shifting through the joint effects of drift and selection (Wright, Reference Wright1977). An important extension in a future study is to include genetic drift effects to derive the average critical migration rate of seed and pollen in the mixed mating system. Some insights into the drift and migration effects can be obtained from extensive explorations on Wright's SBT for both polygene quantitative traits and nuclear genes under random mating with classic island model (Barton & Rouhani, Reference Barton and Rouhani1993). It is likely that the average critical migration rate of seed and pollen can be further modified by genetic drift effects.
The present study only addresses the case of one-way gene flow. The general exact model can be applied to the case of two-way gene flow as well. This can be done simply by setting the migrant cytonuclear genotypes not as constants and swapping the frequency notation p and Q to get the dynamics for the other population. The results in the Appendix need not be changed and are applicable to each population. What needs changing is the analytical deduction for the critical migration rate of seed and pollen, which becomes more complicated in algebra. Early studies under random mating for nuclear genes indicate that the critical migration rates for the forward and reverse directions may be unequal when the two population fitness is different (Crow et al., Reference Crow, Engels and Denniston1990; Barton, Reference Barton1992). It is speculated that similar results might occur, given the constant mixed mating system and soft selection schemes, which remains to be explored.
The analytical results only address two selection schemes for the nuclear genes and one selection scheme for organelle genes. The migrating alleles are assumed to be maladaptive to the recipient population and cause migration loads. Such migration load is the function of the mating system (Hu & Li, Reference Hu and Li2003). Only when the migration rate exceeds a threshold can the selection effects be swamped. However, the critical migration rate also exists when migrating genes are more adaptive in the scheme of heterozygote disadvantage, as demonstrated in previous studies (Crow et al., Reference Crow, Engels and Denniston1990; Barton, Reference Barton1992). This is because an equilibrium point between 0 and 1 for the nuclear gene is unstable. Under this situation, the application of the present theory simply needs to change selection coefficient settings. When other selection schemes are employed, such as the disruptive selection with asymmetry in fitness of the homozygotes (Barton & Rouhani, Reference Barton and Rouhani1993), the analytical expression for the critical migration rate of seed and pollen needs modification under the mixed mating system.
Although the purpose of this study is to examine how the mating system changes the critical migration rate of seeds and pollen in the cytonuclear system, several implications can be deduced. One is to predict the potential impacts of the migration of genetically modified populations to natural populations through pollen (e.g. hybridization and introgression) and seed flow, an important issue recently received considerable attention in conservation biology (Ellstrand et al., Reference Ellstrand, Prentice and Hancock1999; Ellstrand, Reference Ellstrand2003). Hu et al. (Reference Hu, Zeng and Li2003) demonstrate that genetic variation and population fitness of natural populations can be altered, depending on the type of selection scheme (adaptive/maladaptive migrating genes). This result is derived for the nuclear genes under random mating. The present study furthers such impacts for both nuclear and organelle genes since the genetically modified genes may be located on organelle genomes as well (Verma & Daniell, Reference Verma and Daniell2007). The present results highlight the role of the mating system in swamping natural selection. Concerning the impacts through pollen flow, natural populations could be more seriously affected for species with a predominant outcrossing system (e.g. most conifer trees) than for species with the predominant selfing system. A small migration rate could sufficiently bring about gene swamping under weak selection, as implied from the present results. In addition, when the natural population is small, the probability of fixation of maladaptive genes from migrating pollen or seeds can be enhanced (Wright, Reference Wright1931). The joint effects of genetic drift and migration might speed up or impede gene swamping, and this remains to be explored in a future study.
The second implication is to predict the spatial variation in critical migration rate of seeds and pollen in spreading either adaptive or maladaptive genes. Empirical studies on genetic swamping are recorded, primarily in hybrid zones (Antonovics, Reference Antonovics1976; Raymond & Marquine, Reference Raymond and Marquine1994; Childs et al., Reference Childs, Echelle and Dowling1996; Avise et al., Reference Avise, Pierce, Vanden Avyle, Smith, Nelson and Asmussen1997). Ample evidence indicates the presence of population variation in the mating system since many biotic and abiotic factors can influence seed flow and pollination (Mitton, Reference Mitton1992; Goodwillie et al., Reference Goodwillie, Kalisz and Eckert2005; Charlesworth, Reference Charlesworth2006; Eckert et al., Reference Eckert, Kalisz, Geber, Sargent, Elle, Cheptou, Goodwillie, Johnston, Kelly, Moeller, Porcher, Ree, Vallejo-Marin and Winn2009). The shift between insect and wind pollination can cause variation in the migration rate of pollen among local populations (Stebbins, Reference Stebbins1970). The shift between animal and wind seed dispersal can cause variation in the migration rate of seeds among local populations (Montoya et al., Reference Montoya, Zavala, Rodríguez and Purves2008). It is commonly held that heterogeneous selection often exists among natural populations in many plant species. Such heterogeneity may be attributable to the differences in either gametic selection, or zygotic selection, or both, which purges maladaptive or enhances adaptive genes. The present analytical results show that the critical migration rate of seeds and pollen is the function of the mating system and selection coefficients. Accordingly, the critical migration rates required for swamping natural selection are expected to vary in space for cytonuclear genes.
The third implication is to predict how the mating system adjusts the relative contributions of pollen and seed flow to the critical migration rate. Ennos (Reference Ennos1994) has demonstrated the relative rates of pollen to seed flow as a function of the mating system in terms of Fst for nuclear and organelle markers. Pollen flow often dominantly contributes to gene flow for the plant species with predominant outcrossing rate (Ennos, Reference Ennos1994; Ennos et al., Reference Ennos, Sinclair, Hu, Langdon, Hollingsworth, Bateman and Gornall1999; Dick et al., Reference Dick, Hardy, Jones and Petit2008). The present study shows that a simple complementary relationship between pollen and seed flow exists in contributing to the total critical migration rate for nuclear and paternal organelle genes in random mating. However, a non-complementary relationship exists between seed and pollen flow in contributing to the total critical migration rate for a mixed mating system. Combining the present results with those obtained from F st, it is speculated that pollen flow (or seed flow) might play a dominant role in order to swamp natural selection for the predominant outcrossing (or selfing) species.
Finally, the present theory predicts how the mating system influences gene swamping for the haploid maternal organelle genes. Although there are many empirical studies on mating systems and seed dispersal, the effects of the mating system on the spread of maternal organelle genes are rarely recorded. In a pure neutral process, a mixed mating system does affect the spread of maternal organelle genes, which can be inferred from eqn (A4) in the Appendix by setting selection coefficients to zero. The neutral maternal organelle gene spreads through seed dispersal, given that the gene attains a certain level of frequency. When the maternal organelle gene is selectively not neutral, the mixed mating system influences both gametic and zygotic selection, or the completely selfing influences the gametic selection. Here, the evolutionary significance is that genetic swamping from seed dispersal is enhanced for species with a higher selfing rate, given comparable natural selection strengths. This awaits empirical verification with collections of appropriate data.
Appendix: Cytonuclear LDs in a mixed mating system
Consider three diallelic cytonuclear sites, with alleles A and a at the nuclear site, B and b at the organelle genome site of paternal inheritance, and C and c at the organelle genome site of maternal inheritance. The same assumptions as the main text are considered about the model of population structure and the life cycle of hermaphrodite plants. With weak selection, the terms containing the second or higher orders of the selection coefficients are neglected. The terms containing the second or higher orders of the immigration rate (m P2, m S2 or m Sm P or higher orders) and the products of the migration rates and selection coefficients (sm P or sm S) are neglected as well. A linear–additive–viability model is assumed between cytonuclear genes. Let the gametic fitness be wAB =1+sA +sB and wAC =1+sA +sC , where sA , sB and sC are the selection coefficients for alleles A, B and C, respectively. Let wAABC =1+sAA +sB +sC , where sAA is the selection coefficient for genotype AA. Fitness for other gametes and cytonuclear genotypes are set in the similar way.
From the general eqns (2) and (3) in the main text, the recursion equation for the nuclear allele frequency is derived as

Cytonuclear LD (DAB and DAC ) gives additional sources to change the nuclear allele frequency in addition to migration and selection. The expression for the change of nuclear heterozygosity is given by

In the absence of cytonuclear LD, the above two expressions reduce to the results of Hu & Li (Reference Hu and Li2003; eqns 5 and 6) by resetting selection coefficients.
The change for the frequency of the organelle gene with paternal inheritance is derived as

Similarly, the change for the frequency of the organelle gene with maternal inheritance is given by

A mixed mating system can modify the organelle allele frequency through cytonuclear LD. In the case of complete selfing (α=1), the selection at the nuclear site does not change the organelle gene frequency in the gametophyte stage, but does in the sporophyte stage. In the case of complete outcrossing (α=0), the genotypic cytonuclear LD does not affect organelle gene frequency, but the gametic cytonuclear LD does.
Let Δ1=(1−α)(pABpaC +paBpAC )/2+αpAaBC/4 and Δ2=(1−α)pABpAC +α(pAABC +pAaBC/4). The change for the frequency of three-allele cytonuclear combination is given by

The above equation is used for calculating three-allele cytonuclear LD as the function of migration, selection and mating system.
The change for the gametic LD between the nuclear and paternal organelle sites is given by

In random mating (α=0) and the absence of gametic selection, the above equation reduces to the result equivalent to eqn (3) of Hu & Li (Reference Hu and Li2002) .
The change for the gametic LD between the nuclear and maternal organelle sites is given by

Similarly, in random mating (α=0), the above equation reduces to the result equivalent to eqn (12a) of Hu & Li (Reference Hu and Li2002) . Pollen flow does not contribute to the change of the gametic LD between the nuclear and maternal organelle sites.
The recursion equation for the change of LD between the paternal and maternal organelle sites is derived as

In random mating (α=0), LD between the paternal and maternal organelle sites transiently exists at the current generation and is of the order similar to the migration rate of seeds or selection coefficients, essentially the same as previous studies (Hu & Li, Reference Hu and Li2002; Hu, Reference Hu2008). Partial selfing can produce stable LD between the paternal and maternal organelle genomes.
From eqns (A5)–(A8), the recursion equation for the three-allele cytonuclear LD, D ABC* (=p ABC**−p A*p B*p C*−p A*D BC*−p B*D AC*−p C*D AB*), is derived as

Like the LD between the paternal and maternal organelle sites, the three-allele cytonuclear LD, DABC , transiently exists in the case of random system due to the effects of seed migration and selection in the sporophyte stage. Note that the above expression is different from the D of Hu & Li (Reference Hu and Li2002, eqn 15) where D is a composite cytonuclear LD (here, equal to pABC−pApBpC ), and the effects of the LD between the paternal and maternal organelle alleles (DBC ) are neglected due to their magnitudes of the second order of selection coefficients or migration rates under the conditions of random mating and weak selection.
The change for genotypic cytonuclear LD is derived as

and

Selection in both the gametophyte and the sporophyte stages can affect the dynamics of genotypic cytonuclear LD. Partial selfing (α≠0) results in the involvement of higher-order disequilibrium in changing genotypic cytonuclear LD.
I sincerely appreciate Nick H. Barton and two anonymous reviewers for valuable comments and corrections that substantially improved the earlier version of this article.













