Introduction
In the transition, ice-plain, region between Whillans Ice Stream and the Ross Ice Shelf and Crary Ice Rise, West Antarctica, the surface slope and basal shear stress is almost zero (≈1 kPa) (Reference Bindschadler, King, Alley, Anandakrishnan and PadmanBindschadler and others, 2003a ,Reference Bindschadler, Vornberger, King and Padmanb). The fast motion of the ice stream is transmitted through this region in a series of stick–slip events that propagate at a mean velocity of 88ms-1 (Reference Bindschadler, King, Alley, Anandakrishnan and PadmanBindschadler and others, 2003a, Reference Bindschadler, Vornberger, King and Padmanb). Bindschadler and others observed that the transient motion events propagated downstream at a velocity of the order expected for a Stoneley wave traveling at the ice–basal-till interface or a shear wave traveling within the till. (Stoneley surface waves, which move on an interface at a velocity slightly slower than the lower shear wave velocity, do not produce slip across an interface. However, Stoneley waves should not exist at the ice–till interface. (See Equation (A4) of Appendix A.)) The magnitude of the total Burgers vector of the localized propagating dislocations must be at least 0.1m. Reference Anandakrishnan, Voigt, R.B. and KingBindschadler and others (2003a, Reference Bindschadler, King, Alley, Anandakrishnan and Padmanb) show that the periodic ocean tides under the Ross Ice Shelf are in some way triggering the slip pulses. (Tides also influence ice-stream motion far inland (Reference Anandakrishnan and AlleyAnandakrishnan and Alley, 1997; Reference Anandakrishnan, Voigt, R.B. and KingAnandakrishnan and others, 2003).)
An ice plain of very low basal shear stress (100 times smaller than that of an active glacier) presents two problems. One is to account for the stick–slip motion (the primary concern of this paper). The other is to account for the existence of the low basal shear stress. The latter problem suggests either the basal till is very weak (a possibility ignored here) or the effective friction at the till–ice interface is small. I have argued the basal water in a transition region should be broadly, but not uniformly, distributed (see Appendix B and Reference WeertmanWeertman, 2003). The downstream pressure gradient in the basal water is 100 times smaller than in glaciers. Hence the average basal water thickness is at least 100 times larger than under a glacier, and the effective basal friction should therefore be at least 100 times smaller than under a glacier. Consider next the stick–slip problem.
Ice motion in the direction from an ice stream to an ice shelf is produced when positive glide edge dislocations at the ice–till interface move downstream or negative dislocations move upstream. The former produces downstream-propagating transient motion events, and the latter upstream-propagating transient motion events. (The dislocations treated here are not crystal dislocations but are gradients in displacement. That is, the dislocation density B(x) of a smeared-out localized group of dislocations at an interface that move in the x direction is equal (identical) to –dD/dx where D(x) is the displacement across the interface at x. If the displacement is a step function, the step height is the Burgers vector usually associated with a crystal dislocation.) A localized slip pulse that travels downstream at a till–ice interface is a localized distribution of moving dislocations, all of the same sign. Where the dislocations exist, the normal pressure across the interface is increased or decreased depending on the sign of the dislocations. A decrease in normal pressure presumably facilitates slip by decreasing the friction stress when the slip rate is too fast to be accounted for by ordinary, relatively slow glacier sliding mechanisms. In the next section, the interface traction stresses arising from a dislocation distribution of gliding edge dislocations which move at a velocity V are presented.
Dislocation Solution
Consider a smeared-out localized group of gliding edge dislocations of distribution density Bx
(x), shown schematically in Figure 1, on an interface between two media A and B. The dislocations move at constant velocity V in the x direction. The shear constants of the media are GA
and GB
, the densities are ρA
and ρB
and Poisson’s ratios are νA
and νB
. The shear wave speeds in the two media are equal to ![]() the longitudinal wave speeds are
the longitudinal wave speeds are ![]() and C
LB
=
and C
LB
= ![]() The traction stresses on an interface produced by the dislocation distribution Bx
are given by the Comninou–Dundurs-type equations (Reference WeertmanWeertman 1980, Reference Weertman1996,Reference Weertman2004):
The traction stresses on an interface produced by the dislocation distribution Bx
are given by the Comninou–Dundurs-type equations (Reference WeertmanWeertman 1980, Reference Weertman1996,Reference Weertman2004):
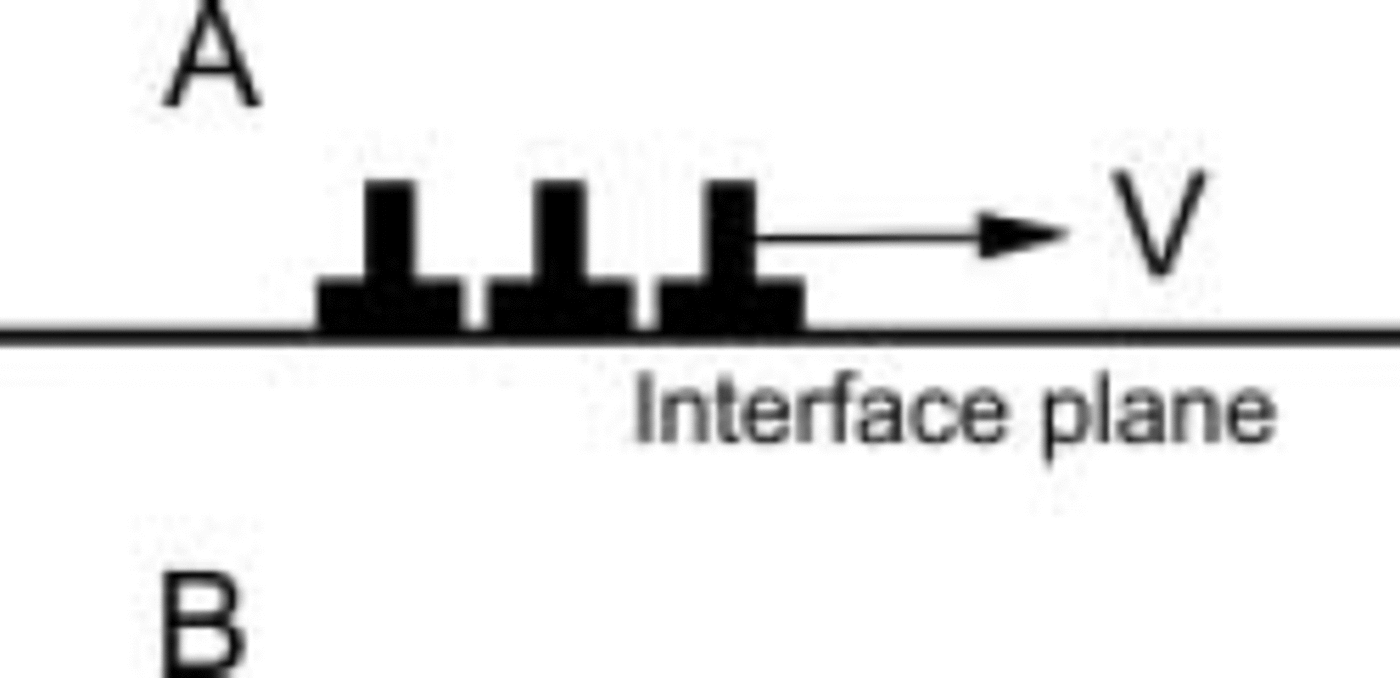
Fig. 1. Group of gliding edge dislocations.
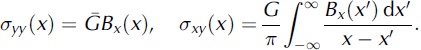
The non-traction stress σxx , which usually is of opposite sign but in general is not the same magnitude on either side of the interface, is given by
Here G
+ and G
– refer respectively to the ice and till side of the interface. Expressions for the elastic-constant-type terms ![]() are given in Appendix A.
are given in Appendix A.
Figure 2 shows a normalized plot of G/GB
, G
/GB
, G
+
/GB
, and G
–
/GB
vs V/C
SB
, where GB
is the shear modulus estimated for till, and C
SB
the shear velocity of the till (see Appendix A and the constants in Table 2). G, G, G
+ and G
- are finite at V = C
SB
. Note in Figure 2 that the normal stress σyy
(G) is negative (compressive). The signs of the stresses are reversed for negative gliding edge dislocation. G is negative in Figure 2. Consquently, the normal pressure is increased. If the frictional resistance to sliding is increased by increased normal pressure, the Figure 2 data imply that a positive gliding edge dislocation packet moves with greater difficulty, and a negative gliding edge dislocation packet moves with greater ease. The change in hydrostatic pressure ΔP in the till just beneath the dislocations is equal to ![]()
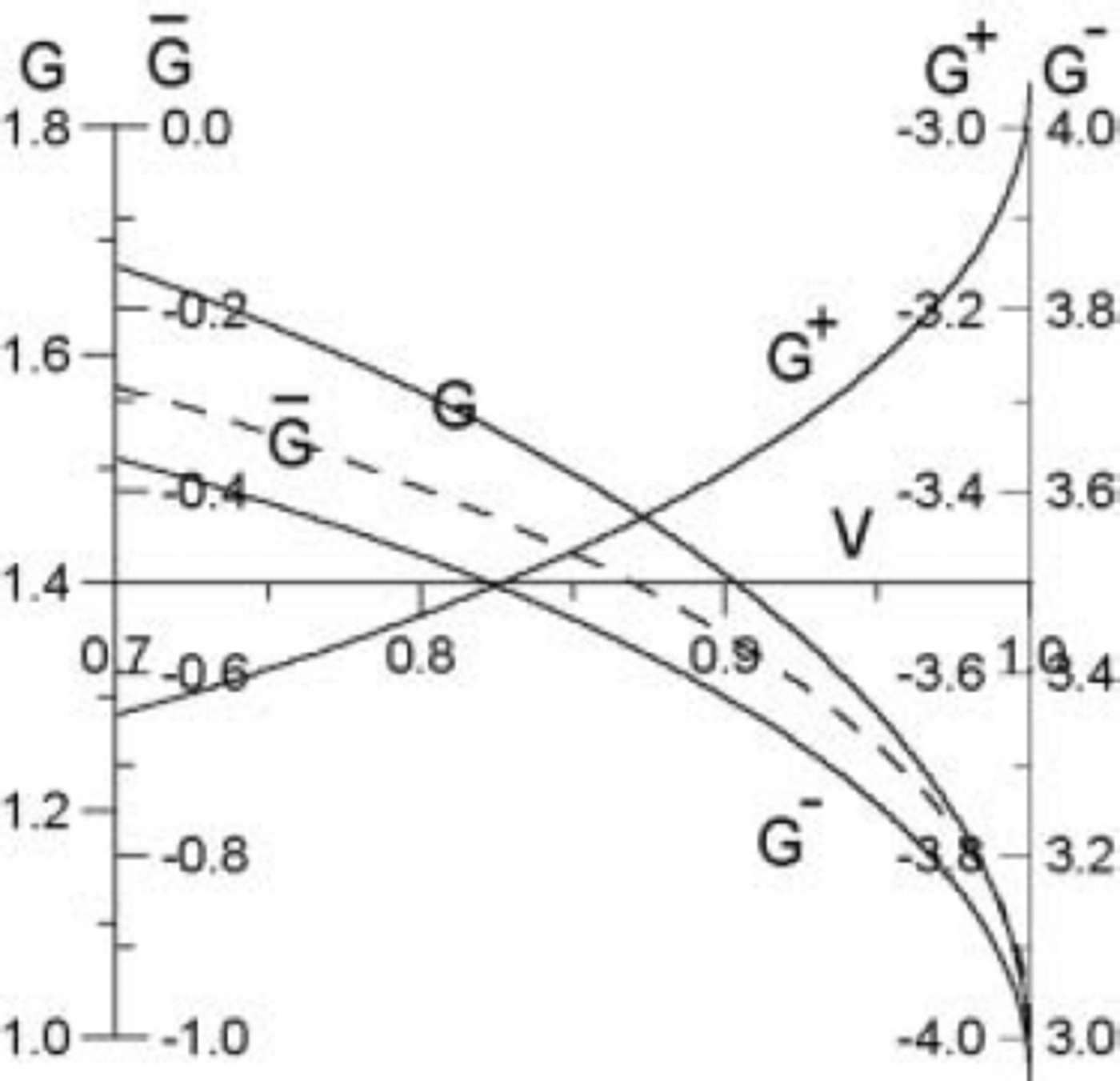
Fig. 2. Normalized plots of G, G, G + and G –, vs V.
From Figure 2 the hydrostatic pressure is reduced in the till.
When a Stoneley wave exists, the terms G, ![]() etc., in a Figure 2 type plot become infinite at a velocity somewhat smaller than the Stoneley wave velocity, which itself is slightly smaller than the slower shear wave velocity (Reference WeertmanWeertman, 2004). This is not seen in Figure 2, and therefore a Stoneley wave does not exist.
etc., in a Figure 2 type plot become infinite at a velocity somewhat smaller than the Stoneley wave velocity, which itself is slightly smaller than the slower shear wave velocity (Reference WeertmanWeertman, 2004). This is not seen in Figure 2, and therefore a Stoneley wave does not exist.
Table 1. Transonic dislocation
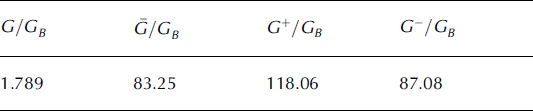
Transonic Dislocation
A gliding edge dislocation moving at the generalized Eshelby velocity V E (Reference WeertmanWeertman, 2002) has traction and non-traction stresses at the interface given by Equations (1) and (2), but with the G terms given by Equations (A5) and (A6) of Appendix A. The Eshelby velocity, when it exists, is larger than the smaller shear wave velocity but smaller than the longitudinal wave velocities. Thus the velocity V E is transonic because it lies between the slowest and fastest sound velocities. At V = V E the dislocation acts like a subsonic dislocation because it does not generate the shock waves that occur at transonic velocities when V ≠ V E.
Table 1 lists the normalized values of the terms G, G, G
+ and G
- found, using constants listed in Table 2, for a dislocation moving at the generalized Eshelby velocity. From Equation (A7) and the Table 2 constants: VE
= 9.253V
SB
= 0.816V
LB
. (When the two half-spaces are identical, the Eshelby velocity is equal to ![]()
Discussion
Bindschadler and others (2003a, b) have shown that ice motion propagates down the ice plain in front of Whillans Ice Stream in short time movements of the order of 0.1m with a propagation velocity of the order expected for the shear velocity in the underlying till. Such motion strongly implies the motion of smeared subsonic gliding edge dislocation packets at the ice–till interface. (Of course, it also could be explained by deformation within the till.) Subsonic edge glide dislocations that move in the downstream direction produce increased normal pressure across the interface but decreased hydrostatic pressure in the till next to the interface. An increase in normal pressure usually is associated with increased friction and more difficult slip. On the other hand, if the hydrostatic pressure is lowered, a small amount of water flow from the till to the interface could occur rapidly and temporarily reduce, where the dislocations are, the resistance to interface slip. This is an attractive explanation of the downstream motion of the dislocations. The water flow from the till is expected to be facilitated for the following reason. The deviatoric stress σ D = (1/2)(σxx – σyy ) within the till is approximately equal to 2GBBx (from Equations (1) and (2) and Fig. 2) Here Bx ≈ slip distance (≈0.1m) divided by width of the slip pulse. Thus σ D = 800, 80, 8 kPa respectively for slip widths of 10, 100, 1000 m. The strength of basal till under the West Antarctic ice streams seems to be of the order of 2–5 kPa (Reference HobbsKamb, 2001). Thus, any pulse width smaller than about 2–4 km will cause breakdown of till.
Table 2. Constants (A → ice, B → till)

From Table 1 it is seen that if a dislocation moves at the generalized Eshelby velocity, the normal pressure ![]() across the interface as well as the hydrostatic pressure
across the interface as well as the hydrostatic pressure ![]() is reduced. Both conditions favor downstream dislocation motion. A dislocation that moves with this velocity (close to the longitudinal wave velocity of the till), of course, moves too quickly to explain the field observations. A transonic glide edge dislocation which moves with a speed close to but faster than the till shear wave velocity, and in the process radiates seismic energy into the till, might also have reduced normal and hydrostatic pressure at the interface.
is reduced. Both conditions favor downstream dislocation motion. A dislocation that moves with this velocity (close to the longitudinal wave velocity of the till), of course, moves too quickly to explain the field observations. A transonic glide edge dislocation which moves with a speed close to but faster than the till shear wave velocity, and in the process radiates seismic energy into the till, might also have reduced normal and hydrostatic pressure at the interface.
Acknowledgements
I appreciate the helpful suggestions of an anonymous reviewer, T. Pfeiffer and S. Tulaczyk for improving the paper.
Appendix A
Terms G And G ∼
The terms G and G of Equation (1) and G + and G - of Equation (2) are equal to
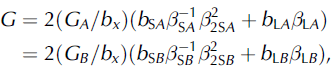
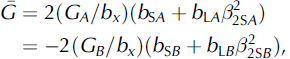
Here 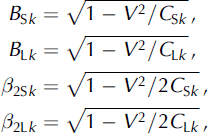
where k = A or B and bx is the Burgers vector of a discrete gliding dislocation. The sub-dislocation Burgers vectors are equal to
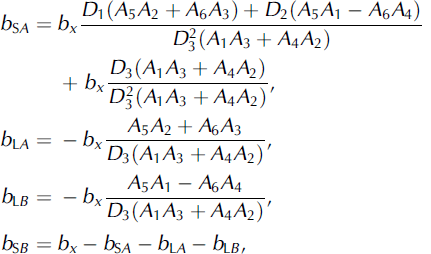
where
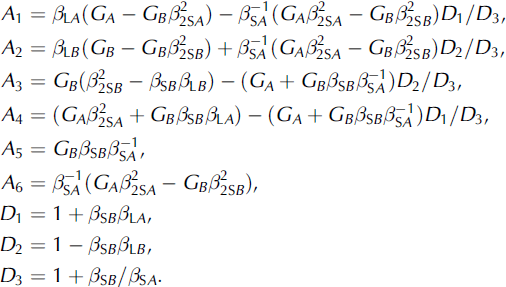
If the term A 1 A 3 + A 2 A 4 in the denominator of the expressions in Equation (A3) is zero, the constants G and G become infinite. (These equations are derived in Reference WeertmanWeertman (2004) and, in equivalent form, in Reference WeertmanWeertman (1980). The presence of a thin, non-uniform water layer between the two half-spaces A and B will not appreciably affect these equations provided that traction stress can be transmitted across the layer. Only if the bed were perfectly smooth would it not be possible to transmit a shear traction stress.)
Note that the Stoneley velocity is the velocity that satisfies the relationship (Reference AchenbachAchenbach, 1973; Reference WeertmanWeertman, 2004):
Reference Bindschadler, King, Alley, Anandakrishnan and PadmanBindschadler and others (2003a, Reference Bindschadler, Vornberger, King and Padmanb) point out that Reference Blankenship, Bentley, Rooney and AlleyBlankenship and others (1987) reported a shear wave velocity (C SB ) in till (under Whillans Ice Stream) of about 150ms–1 and a longitudinal wave speed (C LB ) of about 1700ms– 1. These velocities require the shear modulus, Poisson’s ratio and density for till (GB , νB , ρB in Fig. 1) to have the values listed in Table 2 if the till density is assumed to be twice that of ice. In Table 2 are also listed the values for these quantities for ice (Hobbs, 1974, p. 258), and C SA and C LA calculated from them. The curves of Figure 2 are calculated using the constants of Table 2. If the density of till (ρB ) lies between one and three times the density of ice (ρA =980 kgm–3) it is impossible, according to Equation (A4), for a Stoneley wave to exist at the ice–till interface if till has the wave velocities reported by Blankenship and others.
Transonic dislocation
When an Eshelby velocity V E exists in the velocity range V SB < V E < V LB , V SA , V LA the terms G, G, G +, G - are given by
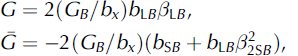
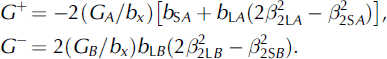
The sub-dislocation Burgers vectors are
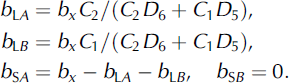
Here 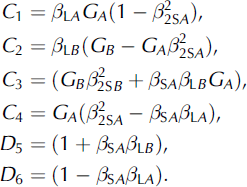
The Eshelby velocity is given by
Appendix B
Basal Water
In my review article on basal water flow (Reference WeertmanWeertman, 1972) it was pointed out that the pressure gradient driving basal water into or away from a Röthlisberger (R) tunnel depends upon the power-law creep exponent n. If n ≤ 2, water is driven into the R tunnel. If n < 2, water flows away from the tunnel. In that article it was pointed out that if a large shear stress exists at the bottom of the ice mass the effective value of n is reduced from Glen’s value of n ≈ 3 to a value of n ≈ 1. There is always a radial distance from an R tunnel beyond which n ≈ 1 and water cannot flow to an R channel. The basal shear stress, of course, is small under the ice plain (1 kPa; Bindschadler and others, 2003b) and should not cause R tunnels to leak the water. The longitudinal stress σxx , however, within the ice of the ice plain should be about the same as that in a floating ice shelf of similar thickness, that is, of order (1/2)ρ icegH(1 – ρ ice /ρ sea water) where the terms have their usual meaning. Thus σxx ≈ 110–180 kPa for an ice thickness of H ≈ 300–500 m. These values are high enough to make it difficult for most R tunnels to remain in existence under an ice plain. Thus the base of an ice plain, if it is melting, should have a broadly distributed, lubricating water layer (of variable thickness). (The anonymous reviewer points out that the Whillans Ice Plain experiences longitudinal compression and lateral extension. The argument above is not changed provided the stress levels remain at about the same magnitude.)
Surge mechanism
The tensile stress mechanism above might also cause exceptional lubrication of a surging glacier. Surging glaciers elongate at a rate of the order of 0.1a–1. This strain would require σxx to have a value of the order of 140 kPa. This longitudinal stress could lead too to a water layer (film) of variable but sufficient thickness to allow fast surge sliding motion.






