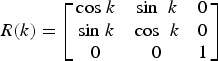1. INTRODUCTION
Glacier mass balance is a key component of glacier monitoring, which is important for assessing climatic changes, water resources and sea level (IPCC, 2013; Zemp and others, Reference Zemp2015; Slod and others, Reference Sold2016). Mass balance has been monitored around the world during the last six decades (WGMS, 2013). Traditional glaciological methods provide in situ observations of annual and sometimes seasonal mass balance (Zemp and others, Reference Zemp2013). Ablation can be derived from stake measurements, and snow pits provide accumulation (Cogley and others, Reference Cogley2011). Using the contour-line or profile method, point observations can be extrapolated to glacier-wide mass balance (Østrem and Brugman, Reference Østrem and Brugman1991; Xie and Liu, Reference Xie, Liu, Kovar and Nachtnabel1991; Kaser and others, Reference Kaser, Fountain and Jansson2003). The principles of the glaciological observation method are widely accepted. These approaches require dense spatial coverage of in situ observation, which can only be obtained through a succession of intensive measurements of field networks of stakes and snow pits. However, the densities of stake and snow pit observation vary from glacier to glacier and over time (Fountain and Vecchia, Reference Fountain and Vecchia1999; Miller and Pelto, Reference Miller and Pelto1999; Van Beusekom and others, Reference Van Beusekom, O'Neel, March, Sass and Cox2010), and, because of this and the remote location and dispersed distribution of mountain glaciers (Shangguan and others, Reference Shangguan2009) and the inaccessibility of glacier surface areas due to hazardous zones (prone to crevasses, rockfalls or avalanches) (Mehta and others, Reference Mehta2014), most glaciological mass-balance data series consist of just a few years. For the period 1946–2005, 226 glaciers worldwide have mass-balance results, with an average of 15 observation years and 39 glaciers have more than 30 years of measurements, most of the reported series being in North America (WGMS, 2008). In China, only Urumqi Glacier No. 1 has a long mass-balance data series, beginning in 1959 (Li and others, Reference Li2007).
Mass balance can be calculated by repeated mapping and differencing of multitemporal DEMs of glacier surface topography using the geodetic observation method and comparing the results with annual in situ measurements using the glaciological method (Zemp and others, Reference Zemp2013). Data sources including theodolite, total station or global navigation satellite systems (Hagen and others, Reference Hagen, Eiken, Kohler and Melvold2005), photogrammetry (Wang and others, Reference Wang, Li, Li, Wang and Yao2014), InSAR (Rankl and Braun, Reference Rankl and Braun2016) and stereo images (Berthier and others, Reference Berthier2007) mostly restrict the spatial and time resolution of geodetic mass-balance measurements (Thibert and others, Reference Thibert, Blanc, Vincent and Lane2008; Fischer and others, Reference Fischer, Huss, Kummert and Hoelzle2016). In recent years, airborne and terrestrial lidar techniques (e.g. laser scanning) have offered dense point clouds and high-resolution and -precision DEMs of the glacier surface (Joerg and others, Reference Joerg, Morsdorf and Zemp2012; Helfricht and others, Reference Helfricht, Kuhn, Keuschnig and Heilig2014; Piermattei and others, Reference Piermattei, Carturan and Guarnieri2015). Research shows that the accuracy of geodetic mass balance resulting from the accuracy of the DEMs ranges from 2 m w.e. for photogrammetric data to 0.02 m w.e. for lidar data (Fischer, Reference Fischer2011). Thus, the laborious and time-consuming glaciological method can be supplemented and validated, basal or internal melt processes can be taken into consideration, and extrapolation of point measurements over the entire glacier surface, which is an important source of uncertainty for glaciological mass balance, can be avoided.
Terrestrial laser scanner (TLS) can achieve changes of the mountain cryosphere at very high spatial and temporal resolution (Ravanel and others, Reference Ravanel, Bodin and Deline2014). We have used an ultra-long-range TLS (Riegl VZ®-6000) to monitor the net mass balance of Urumqi Glacier No. 1 at the monthly scale. This scanner can acquire high-quality surface elevation information on snow and ice cover over a large range (Gabbud and others, Reference Gabbud, Micheletti and Lane2015). Most current geodetic mass-balance research focuses on annual or multi-annual scales, while monthly scale has received little attention. This paper describes an application of TLS to monitor the monthly net mass balance and compares direct glaciological and geodetic mass balance at corresponding ablation stakes (points).
2. STUDY SITE
Urumqi Glacier No. 1 (43°06′N, 86°49′E) is a valley glacier located in the Chinese central Tien Shan (Fig. 1a) and is the source of the headwaters of the Urumqi River. It is a northeast-facing valley glacier with an area of 1.59 km2 in 2012, and elevations of the east and west branches ranging from 3743 to 4267 m a.s.l. and from 3845 to 4484 m a.s.l., respectively. The two branches became separated in 1993 because of continued glacier retreat (Li and others, Reference Li, Wang, Zhang, Wang and Li2010). Urumqi Glacier No. 1 is a summer-accumulation-type glacier (both accumulation and ablation occur during summer), so the mass balance needs to be monitored in summer (melt season). The glacier has been monitored since 1959; it is one of the reference glaciers of the World Glacier Monitoring Service (WGMS) and a representative glacier in central Asia (Li and others, Reference Li2007; Zemp and others, Reference Zemp, Hoelzle and Haeberli2009).
Fig. 1. Study site. (a) Location of Urumqi Glacier No. 1 in the Chinese Central Tien Shan. (b) Measuring point network in 2014, glacier boundary was added based on Fig. 3. (c) Overview of TLS stations at the glacier terminus (image source: Google Earth).
3. DATA AND METHODS
3.1. Riegl VZ®-6000 terrestrial laser scanner
Based on time-of-flight measurement with echo digitization and online waveform processing (RIEGL Laser Measurement Systems, 2013), the Riegl VZ®-6000 TLS can acquire dense point clouds of the glacier surface by emitting near-infrared laser signals (Fig. 2). The pulse emitted by the laser transmitter reaches the target object, from which it is reflected back to the laser receiver. A referenced point cloud results from the calculation of the two-way travel time of the pulse (t). The longitudinal (θ) and transverse (φ) scanning angles of the instantaneous survey are captured by the TLS internal measurement. The coordinates of the measured object (x, y, z) are presented according to
$$L = \displaystyle{{ct} \over 2}$$
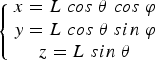$$\left\{ {\matrix{ {x = L\;cos\; \theta \; cos\; \varphi} \cr {y = L\;cos\; \theta \; sin\; \varphi} \cr {z = L\;sin\; \theta} \cr}} \right.$$
where L is the distance between the laser pulse transmitter and target object, and c is the propagation speed of the laser pulse (RIEGL Laser Measurement Systems, 2014a).
Fig. 2. TLS survey of Urumqi Glacier No. 1 with the Riegl VZ®-6000 terrestrial laser scanner on 25 April 2015. Lower right corner of the picture was a scanning station, which was fixed using reinforced concrete with a GPS-leveling point.
Traditionally, TLS uses class 1 laser beams (wavelengths ~1500 nm), with low reflectance but high absorption over snow and ice cover, and the scanning distance is limited to a few hundred meters (Deems and others, Reference Deems, Painter and Finnegan2013; Gabbud and others, Reference Gabbud, Micheletti and Lane2015). Riegl VZ®-6000 uses class 3B laser beams (wavelengths ~1064 nm), so high rates of reflection (80%) from snow- and ice- covered terrain and faster surveys (up to 222 000 measurements s−1) are possible even at long distances (up to 6000 m) with high accuracy and precision (Table 1; RIEGL Laser Measurement Systems, 2014a).
Table 1. Parameters and values of ultra-long-range Riegl VZ®-6000 terrestrial laser scanner (RIEGL Laser Measurement Systems, 2014a)
3.2. Point cloud data acquisition
In order to quantify geodetic mass balance in detail, four scanning stations with a reinforced concrete structure were installed at the terminus of the glacier (Fig. 1c). Scanning stations T1 and T4 captured the surface point clouds of the west branch and T2 and T3 those of the east branch. On 25 April and 28 May 2015, Riegl VZ®-6000 measurements of Urumqi Glacier No. 1 were performed with the same survey parameters, nearly coincident with days of direct measurements of mass balance (Table 1). To avoid ground motion and to guarantee data quality, the Riegl VZ®-6000 was always mounted on a tripod placed on stable bedrock (scanning stations) around the glacier for each scan (Figs 1c, 2). Three-dimensional (3-D) coordinates of the four scanning stations were obtained using the real-time kinematic (RTK) GPS (Unistrong E650). The horizontal and vertical accuracies of RTK survey stations were ±1 cm + 1 ppm × D and ±2 cm + 1 ppm × D, respectively, where ppm is parts per million and D is the distance (km) between base station and mobile station. The coordinated system of RTK measurement data is the World Geodetic System 1984 (WGS84) (Wang and others, Reference Wang2016).
Based on high-accuracy 3-D coordinates of the scanning stations, we can quickly and efficiently realize multi-station scanning point clouds registration (a detailed introduction is provided in Section 3.3). In fieldwork, both the data quality and acquisition time must be considered, so surveying parameters are of crucial importance (Table 1). To avoid range ambiguity and to obtain point clouds of the whole glacier surface, laser pulse repetition rates were set to 50 and 30 kHz for rough and fine scanning, respectively (Table 1). The overlap percentage of each scan was above 30%. Surveying parameters of Urumqi Glacier No. 1 are listed in Table 2.
Table 2. Riegl VZ®-6000 TLS surveying parameters of Urumqi Glacier No. 1 at the monthly scale
3.3. Point cloud data processing
Point cloud data processing was performed using RiSCAN PRO® v 1.81 software (RIEGL Laser Measurement Systems, 2014b). This includes:
-
(1) Direct georeferencing. The method uses additional sensors (navigation sensors, total station, etc.) to convert the laser scanner's system (Mukupa and others, Reference Mukupa, Roberts, Hancock and Almanasir2016). We used RTK surveying points of each scanning station to transform the Scanner's Own Coordinate System (SOCS) into a Global Coordinate System (GLCS). The principle can be described as
(3)
$$\overrightarrow {r_g} = \overrightarrow {r_0} + R(k)\overrightarrow {r_s} $$
(4)where
$$R(k) = \left[ {\matrix{ {{\rm cos}\;k} & {{\rm sin\;} \;k} & 0 \cr {{\rm sin}\;k} & {{\rm cos\;} \;k} & 0 \cr 0 & 0 & 1 \cr}} \right]$$
${\rm \;} \overrightarrow {r_g} $
is the vector of the target in the GLCS,
$\overrightarrow {r_s} $
is the vector of the same target in the SOCS,
$\overrightarrow {r_0} $
is the vector of SCOS origin in the GLCS, and k is the azimuth between scanning station and backsight target (Lichti and others, Reference Lichti, Gordon and Tipdecho2005).
-
(2) Point cloud registration (Mukupa and others, Reference Mukupa, Roberts, Hancock and Almanasir2016). The position of each scan was fixed after direct georeferencing. However, due to the influence of orientation, the point clouds of the overlapped regions cannot coincide completely. A multi-station adjustment was performed based on the iterative closest point (ICP) algorithm (Besl and McKay, Reference Besl and McKay1992; Zhang, Reference Zhang1992). The orientation of each scan was iteratively modified to calculate the best fit between the point patches based on least-squares minimization of residuals (Besl and McKay, Reference Besl and McKay1992; Gabbud and others, Reference Gabbud, Micheletti and Lane2015).
-
(3) Point cloud vacuation and filtering. An octree algorithm was applied to the registered scans to generate points with equal spacing to realize point cloud data reduction (vacuation) (Schnabel and Klein, Reference Schnabel and Klein2006; Perroy and others, Reference Perroy, Bookhagen, Asner and Chadwick2010), and a terrain filter was used to remove noise and non-ground points (RIEGL Laser Measurement Systems, 2014b).
3.4. Geodetic mass-balance method
In the ArcGIS10.2 software support, interpolation of the processed point generates regular grids (DEMs), and subtraction of the two DEMs provides glacier surface elevation changes. The geodetic observation method determines volume changes by comparing glacier surface elevations of different time periods (Zemp and others, Reference Zemp2013):
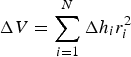$${\rm \Delta} V = \mathop \sum \limits_{i = 1}^N {\rm \Delta} h_ir_i^2 $$
where N is the number of pixels covering the glacier at the maximum extent,
$\triangle h_i{\rm \;} $
is the elevation difference of the two grids at pixel i, and r
i
is the pixel size at pixel i.
To estimate glacier mass balance (B geo), geodetic volume change must be converted to specific mass balance (m w.e.) using
$$\; B_{{\rm geo}} = \displaystyle{{{\rm \Delta} V} \over S}\displaystyle{\rho \over {\rho _{{\rm water}}}}$$
$$S = \displaystyle{{S_{t0} + S_{t1}} \over 2}$$
where ρ is the average density of volume changes, and S is the average glacier area of the two geodetic times, t0 and t1, assuming a linear change (Thibert and others, Reference Thibert, Blanc, Vincent and Lane2008; Zemp and others, Reference Zemp2013), which can be considered unchanged at the monthly scale.
3.5. In situ measurements
The mass-balance observation of Urumqi Glacier No. 1 has been implemented using measured points (ablation stakes and snow pits) (Han and others, Reference Han, Liu, Ding and Jiao2005; Xie and Liu, Reference Xie and Liu2010; Wang and others, Reference Wang, Li, Li, Wang and Yao2014). More than 40 ablation stakes were drilled into the glacier surface evenly at different elevations of the east and west branches using a steam drill (Fig. 1b). The hydrological year (mass-balance year) of Urumqi Glacier No. 1 is defined from the previous September 1 to the next August 31 (Liu and others, Reference Liu, Xie and Wang1997). The glacier is a summer-accumulation-type glacier; summer runs from the beginning of May to early September each year. A spatial distribution of single-point measurements of ablation and accumulation (snow depth and density) was determined by stakes and snow pits at intervals of a month during the summer. The measurements include the stake vertical height above the glacier surface, superimposed ice thickness and the density and thickness of each snow/firn layer at individual stakes. Stake and snow pit heights were converted into mass (w.e.) to calculate single point mass balance (the summation of snow/firn, superimposed ice and glacier ice mass balance) using measured densities of snow and ice (Xie and Liu, Reference Xie and Liu2010). For Urumqi Glacier No. 1, point mass balance can be extrapolated to glacier-wide mass balance using contour-line and isoline methods (Xie and Liu, Reference Xie, Liu, Kovar and Nachtnabel1991).
According to fieldwork in April and May, a larger amount of fresh snow covered the whole glacier surface at the time of TLS measurements (Fig. 2), so we primarily thought about snow/firn mass balance in geodetic method. In order to calculate geodetic mass balance precisely, more than 40 snow pits were dug in the glacier surface to measure the snow density, which were performed on the same days as the TLS survey (Fig. 7a). Interpolation of the snow pits produced a distributed snow density of the glacier surface, which was set as an average density of the volume changes (Eqn (6)).
3.6. Uncertainty assessment
Uncertainties in the TLS-derived geodetic mass balance include systematic or random errors (Zemp and others, Reference Zemp2013), which can be attributed to: (1) point cloud data acquisition errors, including terrain and atmospheric environment (wind and moisture); (2) data processing errors and DEM creation, i.e. registration (multi-station adjustment), point cloud filtering and interpolation of the raster DEM (smoothing terrain information) (Gabbud and others, Reference Gabbud, Micheletti and Lane2015; Hartzell and others, Reference Hartzell, Gadomski, Glennie, Finnegan and Deems2015; Fischer and others, Reference Fischer, Huss, Kummert and Hoelzle2016); and (3) spatial bias of the two DEMs and sampling density of snow and ice (Nuth and kääb, Reference Nuth and Kääb2011; Zemp and others, Reference Zemp2013).
Point clouds of the glacier were captured in sunny, windless weather, so wind- and moisture-induced errors can be minimized. The octree algorithm built the topological relationship of scattered points to reduce the point cloud, in order to preserve terrain information as much as possible. To eliminate spatial bias of the two DEMs, scanning point clouds of April were set as the reference; a relative registration selects the ground control points of the stable terrain to match the point clouds of the two periods.
The uncertainties of the average TLS-derived glacier surface elevation changes for individual glaciers were quantified based on geostatistical analysis methods (Rolstad and others, Reference Rolstad, Haug and Denby2009), and can be approximated by
$${\rm \;} \sigma _{\overline {\Delta h{\rm TLS}}} ^2 = \sigma _{\Delta h{\rm TLS}}^2 \times \displaystyle{{S_{{\rm cor}}} \over {5S}}$$
where S is the glacierized area of the subtracted DEMs, which is really the same as the S defined by Eqn (7) at the monthly scale, S cor is the area over which there are spatial correction errors in the subtraction of the two DEMs, and we conservatively estimate S cor = S (Fischer and others, Reference Fischer, Huss, Kummert and Hoelzle2016). σΔhTLS is the standard deviation for TLS-derived bedrock (stable terrain) elevation changes.
According to Huss and others (Reference Huss, Bauder and Funk2009), the uncertainty σ BTLS in the homogenized mass-balance results from errors in the geodetic mass change:
$$\sigma _{{\rm BTLS}} = \pm \sqrt {{(\overline {{\rm \Delta} h{\rm TLS}} \times \sigma _\rho )}^2 + {(\rho \times {\rm \sigma} _{\overline {\Delta h{\rm TLS}}} )}^2} $$
where σ
ρ
is the uncertainty of density.
${\rm \; \;} \overline {\Delta h{\rm TLS}} $
is the mean of TLS-derived geodetic elevation changes and the related uncertainty depends on the accuracy of the two DEMs. Resulting values are listed in Table 2 and illustrated in Section 4.3.
4. RESULTS
4.1. TLS-derived glacier area and surface elevation changes
Based on the TLS-derived high-resolution DEM and previous field surveys, we extracted the glacier boundary on 25 April 2015. As shown in Fig. 3, the area of Urumqi Glacier No. 1 was 1.558 km2, 1.018 km2 for the east branch and 0.540 km2 for the west branch. Compared with the latest surveys (GPS-RTK) in 2012 (Wang and others, Reference Wang2016), the total area decreased by 0.03 km2, at a rate of 0.01 km2 a−1. As mentioned in Section 4.3, glacier area was an important input parameter for geodetic mass-balance calculation, due to the monthly scale of measurements, so we maintained an unchanged glacier area of 1.558 km2 as the inputting area parameter.
Fig. 3. Extraction of 2015 glacier boundary based on TLS-derived high-resolution DEM and previous field surveying.
Surface elevation changes were slightly positive during the study period. Average elevation changes were 0.019 and 0.611 m for the east and west branches, respectively. The mean elevation change was 0.225 m for the total glacier surface; with a glacier volume change of 3.45 × 104 m3, the mean glacier surface elevation change was 0.007 m d−1. The west branch was more positive than the east branch, mainly because there was more accumulation in the accumulation area of the glacier, which may be related to terrain and altitude factors. The firn basin terrain is steeper in the west branch than the east branch, and the middle–lower part of the west branch has a flat terrain (Fig. 1b), giving rise to mass accumulation and consequent avalanches. An obvious accumulation area can be identified in the west branch (region in blue in Fig. 4), which may have been caused by an avalanche in the upper part (region in light red in Fig. 4). Reduced glacier surface elevation is mainly concentrated in the ablation area of the west branch and the right edge of the east branch, both of which have steeper topographies, which may be adverse to mass accumulation. So the glacial/topographical features of the two branches have important impacts on their dynamics (Xu and others, Reference Xu, Pan, Hu, Li and Liang2011). It should be mentioned that fresh snow covered the whole glacier surface during the two field measurements. According to field observations, the TLS system captures the surface of snow- and ice-covered terrain (high reflection), and the penetration effect of snow can be ignored. The surface changes therefore included ice and snow.
Fig. 4. Spatial distribution of TLS-derived monthly surface elevation changes for Urumqi Glacier No. 1 between 25 April and 28 May 2015. Black crosses show the location of ablation stakes and snow pits. Two green frames indicate areas that cloud not be detected by TLS.
4.2. Comparison with in situ measurements
Based on the location of individual ablation stakes (Fig. 4), TLS-derived geodetic elevation changes of the stakes were extracted, and were found to match closely the direct glaciological elevation changes (stake height) from in situ measurements, except for a few stakes in the ablation area (Fig. 5). The surface elevation change trends coincided for both methods (Fig. 6), and the correlation coefficient (R 2) for glaciological elevation change of the individual stakes and the TLS-derived geodetic elevation change of corresponding points was 0.85 (passing the 0.001 significance level test). Considering the uncertainties of the two measuring methods and the influence of the terrain factors, differences in surface elevation changes of the point measurements were negligible, indicating that the TLS-derived glacier surface elevation changes were valid. It should be stressed that dynamic thickening and thinning were minor for the monthly scale measurements here.
Fig. 5. Comparison between glaciological and geodetic glacier surface elevation changes; the letters represent ablation stakes (Fig. 4).
Fig. 6. Relation between glaciological elevation change and geodetic elevation change.
4.3. TLS-derived glacier monthly net mass balance
To convert glacier volume (elevation) changes to mass balance, the distributed snow density of the total glacier was generated by interpolating in situ measured densities, and then the distributed mass balance was calculated using Eqns (5)–(7) (Fig. 7a). To assess the uncertainty of TLS-derived mass balance, more than 150 stable points in the surrounding bedrock area were selected, and the mean elevation changes and standard deviation of the selected points were −0.011 m and 0.116 m, respectively. Using Eqns (8) and (9), the net mass-balance uncertainty (σ BTLS) was ± 0.018 m w.e., and the TLS-derived mass balance was 0.074 ± 0.018 m w.e., which was slightly positive in the investigated period (Table 3). Based on the two field TLS surveys, plenty of fresh snow covered the whole glacier surface (Fig. 2); the slight accumulation was probably caused by fresh snow cover, which was illustrated in detail in Section 5.2.
Fig. 7. Distributed snow densities and mass balance for the total glacier from 25 April to 28 May 2015.
Table 3. The average density (ρ) and its uncertainty (σ ρ ), TLS-derived glacier surface elevation changes (ΔhTLS), standard deviation of surface elevation changes (σΔhTLS) in stable bedrock area, and uncertainty of mass balance (σ BTLS)
Net mass balance versus altitude is important basic information in the Glacier Mass Balance Bulletin reports (WGMS, 2013); Fig. 8 shows the net balance versus altitude of Urumqi Glacier No. 1, with histograms and polylines representing glacier area and net balance in the different altitude regions, respectively. Unlike annual mass balance, the graded law of net mass balance versus altitude was not obvious in the TLS measurements; elevations of the east and west branches were under 3800 and 4000 m a.s.l., where the net mass balance increased with rising altitude. For the east branch, however, the altitude above 3800 m a.s.l. exhibited an opposite trend, potentially caused by ablation on the right side of the back wall region (Fig. 4). The west branch showed a trend relatively well above 4000 m a.s.l.
Fig. 8. Monthly net mass balance versus altitude of Urumqi Glacier No. 1.
5. DISCUSSION
5.1. Surveying precautions and point cloud data quality
Generally, the environment (terrain and atmosphere) around the glacierized area is complicated and the quality of TLS survey data is influenced by the surroundings. This paper has shown that an ultra-long-range TLS is well suited for surveying snow- and ice-covered terrain, as it provides precise detail of glacier surface elevation changes. The maximum survey distance of Riegl VZ®-6000 TLS is 6000 m, the total scanning time for the measurement on 25 April was ~46 min and for the measurement on 28 May was ~57 min. The quality of those data and acquisition time depended mainly on the following two matters:
-
(1) Visual angles of the scanning stations. All the scanning stations should have a field of view wide enough to cover the glacier surface. However, two minimal artifacts existed in the central part of west branch. Although four scans were set at the terminus of Urumqi Glacier No. 1, the artifacts were due to the flatness of the terrain and relatively high altitude of west branch surface (Fig. 1b). Here, the null value regions were filled using spatial interpolation method. Fortunately, we had two stakes (H1 and H1′) in these regions (Fig. 4) and the comparison of the interpolated and measured results was convincing (Fig. 5), indicating the filled portions were reliable. So the artifacts were taken into account to calculate the volume and mass balance.
-
(2) Atmospheric conditions. Rain, cloud and fog would absorb laser pulse and reduce the possible survey distance; wind might influence the accuracy of point cloud. However, all of those conditions are common around the glacier, so a good weather condition (dry and windless atmosphere) is pre-requisite for TLS survey and data acquisition (Fig. 2). The point cloud data quality can be guaranteed by considering all of these matters.
5.2. Glacier behavior and monthly net mass balance
As Urumqi Glacier No. 1 is located in inner Asia, precipitation and temperature of glacierized areas are the main factors controlling glacier mass balance (Li and others, Reference Li, Han, Jing, Yang and Jiao2003). In winter, the westerly circulation is affected by the dynamic action of the Tibetan Plateau, inducing cold high-pressure systems to the south of the Tien Shan, which results in a cold and dry climate, with scarce precipitation. In summer, the Tibetan Plateau becomes a thermal depression and shapes a plateau monsoon, which pulls in warm and moist air from India, which in turn produces abundant precipitation around the Plateau. The above-mentioned precipitation and temperature conditions determine Urumqi Glacier No. 1 as a summer-accumulation-type glacier. Namely, the glacier is dominated by weak accumulation from October to next March (winter); the accumulation rate from April to May is faster than in winter; strong ablation and accumulation occur simultaneously during the period June–September (Liu and others, Reference Liu, Xie and Wang1997).
It was possible that the slightly positive mass balance observed from the geodetic method was attributable to the assumption of fresh snow cover. According to daily data of Daxigou Meteorological Station (3539 m a.s.l.), at ~3 km south-east of Urumqi Glacier No. 1, the total precipitation was 138 mm and daily mean temperature was −0.3°C during the month (25 April–28 May 2015) (Fig. 9). Numerous studies have shown that air temperature is the most critical factor in determining the precipitation type (Bocchieri, Reference Bocchieri1980; Czys and others, Reference Czys, Scott, Tang, Przybylinski and Sabones1996). It was determined that 98% of the precipitation type was snowfall when temperature fell below 0° (Upadhyay, Reference Upadhyay1995). Observations indicated most of the precipitation was snow at the headwater of Urumqi River from May to September (Yang and others, Reference Yang, Kang and Blumer1992b). The precipitation of the nearest two periods (Fig. 9) all occurred before the two TLS surveys. Besides, mean temperature was below 0°C during the two periods, especially the second period (23–27 May), when the mean temperature was −1.2°C (Fig. 9) and we could conclude that the precipitation type (the total precipitation was 35.4 mm) was mainly solid. Glacier melting is directly related to air temperature, which has been well described by positive degree days (the cumulative positive temperatures in a year) (Li and others, Reference Li, Li and Chen2011). Figure 9 shows that most of the daily mean temperatures were below freezing for several continuous days and considerable amounts of precipitation fell at sub-freezing temperatures, which eventually caused the ablation in seasonal snow layer less than fresh snow derived accumulation. Therefore, the assumption was validated by the meteorological conditions and field observations.
Fig. 9. Daily precipitation and mean temperature observed at the Daxigou Meteorological Station from 16 April to 28 May 2015.
5.3. Applicability of Riegl VZ®−6000 TLS to monitor the mass balance of Urumqi Glacier No. 1
Riegl VZ®-6000 TLS, thanks to its high temporal-spatial resolution and ultra-long-range, has been proved successful in monitoring mass balance of very small glaciers in the Swiss Alps (Fischer and others, Reference Fischer, Huss, Kummert and Hoelzle2016) and surface melt of Alpine glaciers at the seasonal and hourly scales (Gabbud and others, Reference Gabbud, Micheletti and Lane2015). Furthermore, TLS can work without contact with the survey objects and in difficult environments, so allowing to measure dangerous or inaccessible regions of the glacier surface. The surface of Urumqi Glacier No. 1 has been changed with the accelerated shrinkage (Li and others, Reference Li, Li and Chen2011; Wang and others, Reference Wang2016). The firn basin and glacier tongue terrain of the west branch have become extremely steep; and the upper right edge terrain of the east branch is also precipitous (Fig. 1b). Hence, it is very difficult for us to insert ablation stakes and dig snow pits in those inaccessible regions. However, glacial terrain and insufficient spatial distribution of stakes have significant influence on extrapolating point observations to glacier-wide mass balance (Yang and others, Reference Yang, Liu, Wang, Elder and Kattelmann1992a; Dyurgerov, Reference Dyurgerov2002; Huss and others, Reference Huss, Bauder and Funk2009; Xie and Liu, Reference Xie and Liu2010). Besides, according to field observations, steep slopes in the tongue of the west branch are prone to ice avalanches in the ablation season, which cannot be quantified well using the glaciological method.
TLS technology makes it possible for us to monitor those inaccessible regions and quantify the mass loss duo to ice avalanche. In this study, the TLS system measured most of the glacier surface area (Fig. 4) and the comparison of results between TLS-derived and conventional glaciological elevation changes of individual stakes at the monthly scale was promising (Figs 5, 6). In situ measured densities were used to convert TLS-derived elevation changes to mass-balance changes, so the quality of the geodetic net mass balance was very good. We recommend the application of Riegl VZ®-6000 TLS for future mass balance monitoring of Urumqi Glacier No. 1, which will become a beneficial complement to glaciological measurements. From our current experience, although the point cloud data quality can be guaranteed when we follow the field surveying precautions given in Section 5.1, a number of recommendations need to be followed to improve the results: (1) Riegl VZ®-6000 TLS measurements should coincide closely with, and ideally on the same day as, glaciological measurements; (2) fixed scanning stations are necessary between surveys, which could minimize registration errors among the scans of the same time (e.g. on 25 April 2015) and provide better precision of glacier surface elevation changes. In this study each scanning station was fixed using reinforced concrete with a GPS-leveling point (lower right of Fig. 3); (3) the overlap percentage of each scanning station of the same period should be no <30% to achieve a perfect mosaic of multi-station adjustment; (4) plentiful and visible areas of stable bedrock terrain surrounding the whole glacier are needed to guarantee a good quality of the relative registration of different temporal point clouds; and (5) the density of the glacier surface needs to be measured in fieldwork.
At present, the average density of the glacier surface is still a fundamental issue for TLS-derived geodetic mass balance, especially when large amounts of fresh snow cover the glacier surface. Density assumptions of temperature and polythermal glaciers have been researched deeply (Huss, Reference Huss2013), but little attention has been given to this assumption by Chinese scholars. Most glaciers are cold and multi-thermal glaciers in northwest China (Xie and Liu, Reference Xie and Liu2010), so a density assumption or model based on in situ measured densities is of importance in the next step. We should note that not all glaciers in China have such detailed observations as Urumqi Glacier No. 1, and TLS surveys are ideally carried out at the end of the ablation season to reduce the influence of fresh snow. In addition, the required level of specific knowledge, skills and experience with TLS data acquisition and processing are likely higher than for the conventional glaciological method. It is necessary for us to standardize the processes of TLS measurements and point cloud processing.
6. CONCLUSION
The Riegl VZ®-6000 is specially designed for surveying snow- and ice-covered terrain, and has a ranging accuracy up to 10 mm. The TLS system can monitor surface elevation changes and the mass of mountain glaciers at high spatiotemporal resolution, so the quality of the geodetic net mass balance derived by terrestrial laser scanning is relatively good. We have presented the application of an ultra-long-range TLS to monitor monthly net mass balance. Based on the collection of field data, point cloud data processing and the principle of geodetic mass-balance calculation, we derived surface elevation changes and the geodetic mass balance of Urumqi Glacier No. 1 from 25 April to 28 May 2015.
The TLS-derived high spatial resolution DEM extracted an area of Urumqi Glacier No. 1 of 1.588 km2 on 25 April 2015. The surface elevation change was 0.225 m, and the correlation coefficient (R 2) between the glaciological elevation change of individual stakes and the TLS-derived geodetic elevation change of corresponding points was 0.85. Using the in situ measured snow density of the glacier surface, the converted geodetic mass balance was 0.074 m w.e., and slightly positive mass balance was due to recent snowfalls.
Mean uncertainty in the TLS-derived monthly net mass balance was 0.018 m w.e. (Table 3). The uncertainty is attributed to data acquisition errors, data-processing and DEM creation errors, the spatial bias of the two DEMs and the sampling density of snow and ice. The next step will be standardizing the processes of TLS measurements and point cloud processing. A density assumption is also significant for TLS-derived geodetic glacier mass balance in northwest China. Despite some uncertainties, the TLS surveying system provided accurate results and is therefore suitable for repeated net mass-balance measurement of mountain glaciers, which can become a beneficial complement to conventional glaciological mass balance.
ACKNOWLEDGEMENTS
We thank the Tien Shan Glaciological Station for field data collection. This research was supported by the National Natural Science Foundation of China (No. 41471958; No. 91425303; No. 41421061), the Key Research Program of Frontier Sciences of Chinese Academy of Sciences (No. QYZDB-SSW-SYS024) and the West Light Program for Talent Cultivation of Chinese Academy of Sciences. We also thank the two reviewers and Graham Cogley (chief editor) for their careful and constructive comments in improving the manuscript.
Open access
