Hostname: page-component-f554764f5-68cz6 Total loading time: 0 Render date: 2025-04-23T06:58:07.748Z Has data issue: false hasContentIssue false
  • English
  • Français

On conformally flat minimal Legendrian submanifolds in the unit sphere

Part of: Global differential geometry

Published online by Cambridge University Press:  10 May 2024

Cece Li Open the ORCID record for Cece Li [Opens in a new window] ,
Cheng Xing Open the ORCID record for Cheng Xing [Opens in a new window]  and
Jiabin Yin Open the ORCID record for Jiabin Yin [Opens in a new window]
Cece Li
Affiliation:
School of Mathematics and Statistics, Henan University of Science and Technology, Luoyang 471000, People's Republic of China (ceceli@haust.edu.cn)
Cheng Xing*
Affiliation:
School of Mathematical Sciences and LPMC, Nankai University, Tianjin 300071, People's Republic of China (xingcheng@nankai.edu.cn)
Jiabin Yin
Affiliation:
School of Mathematics and Statistics, Guangxi Normal University, Guilin 541001, People's Republic of China (jiabinyin@126.com)
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with the study on an open problem of classifying conformally flat minimal Legendrian submanifolds in the $(2n+1)$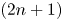-dimensional unit sphere $\mathbb {S}^{2n+1}$ admitting a Sasakian structure $(\varphi,\,\xi,\,\eta,\,g)$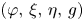 for $n\ge 3$, motivated by the classification of minimal Legendrian submanifolds with constant sectional curvature. First of all, we completely classify such Legendrian submanifolds by assuming that the tensor $K:=-\varphi h$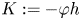 is semi-parallel, which is introduced as a natural extension of $C$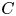-parallel second fundamental form $h$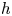. Secondly, such submanifolds have also been determined under the condition that the Ricci tensor is semi-parallel, generalizing the Einstein condition. Finally, as direct consequences, new characterizations of the Calabi torus are presented.

Keywords

Legendrian submanifoldunit sphereconformally flatsemi-parallelproduct manifoldrigidity theorem

MSC classification

Primary: 53C24: Rigidity results
Secondary: 53C25: Special Riemannian manifolds (Einstein, Sasakian, etc.) 53C40: Global submanifolds 53C42: Immersions (minimal, prescribed curvature, tight, etc.)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 30
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Antić, M., Li, H., Vrancken, L. and Wang, X.. Affine hypersurfaces with constant sectional curvature. Pacific J. Math. 310 (2021), 275–302.CrossRefGoogle Scholar
Baikoussis, C., Blair, D. E. and Koufogiorgos, T.. Integral submanifolds of Sasakian space forms $\overline {M}^7(k)$. Results Math. 27 (1995), 207–226.CrossRefGoogle Scholar
Blair, D. E.. Riemannian Geometry of Contact and Symplectic Manifolds, 2nd edn (Boston: Birkhäuser, 2010).CrossRefGoogle Scholar
Brozos-Vázquez, M., García-Río, E. and Vázquez-Lorenzo, R.. Complete locally conformally flat manifolds of negative curvature. Pacific J. Math. 226 (2006), 201–219.CrossRefGoogle Scholar
Cheng, X. and Hu, Z.. On $C$-totally real submanifolds of $\mathbb {S}^2n+1(1)$ with non-negative sectional curvature. Kodai Math. J. 46 (2023), 184–206.CrossRefGoogle Scholar
Cheng, X., Hu, Z., Moruz, M. and Vrancken, L.. On product minimal Lagrangian submanifolds in complex space forms. J. Geom. Anal. 31 (2021), 1934–1964.CrossRefGoogle Scholar
Cheng, X., He, H. and Hu, Z.. $C$-totally real submanifolds with constant sectional curvature in the Sasakian space forms. Res. Math. 76 (2021), 144.CrossRefGoogle Scholar
Dillen, F. and Vrancken, L.. $C$-totally real submanifolds of $S^7(1)$ with nonnegative sectional curvature. Math. J. Okayama Univ. 31 (1989), 227–242.Google Scholar
Dillen, F. and Vrancken, L.. $C$-totally real submanifolds of Sasakian space forms. J. Math. Pures Appl. 69 (1990), 85–93.Google Scholar
Dioos, B., Vrancken, L. and Wang, X.. Lagrangian submanifolds in the homogeneous nearly Kähler $\mathbb {S}^3\times \mathbb {S}^3$. Ann. Global Anal. Geom. 53 (2018), 39–66.CrossRefGoogle Scholar
Hu, Z., Li, H. and Vrancken, L.. On four-dimensional Einstein affine hyperspheres. Differ. Geom. Appl. 50 (2017), 20–33.CrossRefGoogle Scholar
Hu, Z., Li, M. and Xing, C.. On $C$-totally real minimal submanifolds of the Sasakian space forms with parallel Ricci tensor. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 116 (2022), 163.CrossRefGoogle Scholar
Hu, Z., Moruz, M., Vrancken, L. and Yao, Z.. On the nonexistence and rigidity for hypersurfaces of the homogeneous nearly Kähler $\mathbb {S}^3\times \mathbb {S}^3$. Differ. Geom. Appl. 75 (2021), 101717.CrossRefGoogle Scholar
Hu, Z. and Xing, C.. On the Ricci curvature of $3$-submanifolds in the unit sphere. Arch. Math. 115 (2020), 727–735.CrossRefGoogle Scholar
Hu, Z. and Xing, C.. New equiaffine characterizations of the ellipsoids related to an equiaffine integral inequality on hyperovaloids. Math. Inequal. Appl. 24 (2021), 337–350.Google Scholar
Hu, Z. and Xing, C.. New characterizations of the Whitney spheres and the contact Whitney spheres. Mediterr. J. Math. 19 (2022), 75.CrossRefGoogle Scholar
Hu, Z. and Yin, J.. An optimal inequality related to characterizations of the contact Whitney spheres in Sasakian space forms. J. Geom. Anal. 30 (2020), 3373–3397.CrossRefGoogle Scholar
Lee, J. W., Lee, C. W. and Vîlcu, G.-E.. Classification of Casorati ideal Legendrian submanifolds in Sasakian space forms. J. Geom. Phys. 155 (2020), 103768.CrossRefGoogle Scholar
Lee, J. W., Lee, C. W. and Vîlcu, G.-E.. Classification of Casorati ideal Legendrian submanifolds in Sasakian space forms II. J. Geom. Phys. 171 (2022), 104410.CrossRefGoogle Scholar
Li, C., Xing, C. and Xu, H.. Locally strongly convex affine hypersurfaces with semi-parallel cubic form. J. Geom. Anal. 33 (2023), 81.CrossRefGoogle Scholar
Li, H., Ma, H., Van der Veken, J., Vrancken, L. and Wang, X.. Minimal Lagrangian submanifolds of the complex hyperquadric. Sci. China Math. 63 (2020), 1441–1462.CrossRefGoogle Scholar
Li, H. and Wang, X.. Calabi product Lagrangian immersions in complex projective space and complex hyperbolic space. Res. Math. 59 (2011), 453–470.CrossRefGoogle Scholar
Luo, Y.. On Willmore Legendrian surfaces in $\mathbb {S}^5$ and the contact stationary Legendrian Willmore surfaces. Calc. Var. Partial Differ. Equ. 56 (2017), 86.CrossRefGoogle Scholar
Luo, Y.. Contact stationary Legendrian surfaces in $\mathbb {S}^5$. Pacific J. Math. 293 (2018), 101–120.CrossRefGoogle Scholar
Luo, Y. and Sun, L.. Rigidity of closed CSL submanifolds in the unit sphere. Ann. Inst. H. Poincaré C Anal. Non Linéaire 40 (2023), 531–555.CrossRefGoogle Scholar
Luo, Y., Sun, L. and Yin, J.. An optimal pinching theorem of minimal Legendrian submanifolds in the unit sphere. Calc. Var. Partial Differ. Equ. 61 (2022), 192.CrossRefGoogle Scholar
Mihai, I.. On the generalized Wintgen inequality for Legendrian submanifolds in Sasakian space forms. Tohoku Math. J. 69 (2017), 43–53.CrossRefGoogle Scholar
Sasahara, T.. A class of biminimal Legendrian submanifolds in Sasakian space forms. Math. Nachr. 287 (2014), 79–90.CrossRefGoogle Scholar
Sasahara, T.. Classification of biharmonic $C$-parallel Legendrian submanifolds in $7$-dimensional Sasakian space forms. Tohoku Math. J. 71 (2019), 157–169.CrossRefGoogle Scholar
Tanno, S.. Sasakian manifolds with constant $\phi$-holomorphic sectional curvature. Tohoku Math. J. 21 (1969), 501–507.CrossRefGoogle Scholar
Verstraelen, L. and Vrancken, L.. Pinching theorems for $C$-totally real submanifolds of Sasakian space forms. J. Geom. 33 (1988), 172–184.CrossRefGoogle Scholar
Xing, C. and Yin, J.. Some optimal inequalities for anti-invariant submanifolds of the unit sphere. J. Geom. Anal. 34 (2024), 38.CrossRefGoogle Scholar
Xing, C. and Zhai, S.. Minimal Legendrian submanifolds in Sasakian space forms with $C$-parallel second fundamental form. J. Geom. Phys. 187 (2023), 104790.CrossRefGoogle Scholar
Yamaguchi, S., Kon, M. and Ikawa, T.. $C$-totally real submanifolds. J. Differ. Geom. 11 (1976), 59–64.CrossRefGoogle Scholar
Yano, K. and Kon, M., CR Submanifolds of Kaehlerian and Sasakian Manifolds. Progress in Mathematics, Vol. 30 (Birkhäuser, Boston, MA, 1983).CrossRefGoogle Scholar
Yin, J. and Qi, X.. Sharp estimates for the first eigenvalue of Schrödinger operator in the unit sphere. Proc. Am. Math. Soc. 150 (2022), 3087–3101.CrossRefGoogle Scholar
Zhai, S. and Xing, C.. Classification of semi-parallel hypersurfaces of the product of two spheres. Differ. Geom. Appl. 91 (2023), 102067.CrossRefGoogle Scholar
Zhai, S. and Zhang, H.. Minimal Legendrian submanifolds of $\mathbb {S}^9$ with nonnegative sectional curvature. Turkish J. Math. 46 (2022), 2854–2866.CrossRefGoogle Scholar