Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-26T21:32:42.782Z Has data issue: false hasContentIssue false
  • English
  • Français

A Hamiltonian ∐n BO(n)-action, stratified Morse theory and the J-homomorphism

Part of: Homotopy theory Partial differential equations

Published online by Cambridge University Press:  13 September 2024

Xin Jin Open the ORCID record for Xin Jin [Opens in a new window]
Xin Jin*
Affiliation:
Math Department, Boston College, Chestnut Hill, MA 02467, USA xin.jin@bc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We use sheaves of spectra to quantize a Hamiltonian 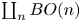$\coprod _n BO(n)$-action on 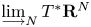$\varinjlim _{N}T^*\mathbf {R}^N$ that naturally arises from Bott periodicity. We employ the category of correspondences developed by Gaitsgory and Rozenblyum [A study in derived algebraic geometry, vol. I. Correspondences and duality, Mathematical Surveys and Monographs, vol. 221 (American Mathematical Society, 2017)] to give an enrichment of stratified Morse theory by the 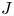$J$-homomorphism. This provides a key step in the work of Jin [Microlocal sheaf categories and the 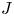$J$-homomorphism, Preprint (2020), arXiv:2004.14270v4] on the proof of a claim of Jin and Treumann [Brane structures in microlocal sheaf theory, J. Topol. 17 (2024), e12325]: the classifying map of the local system of brane structures on an (immersed) exact Lagrangian submanifold 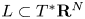$L\subset T^*\mathbf {R}^N$ is given by the composition of the stable Gauss map 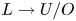$L\rightarrow U/O$ and the delooping of the 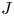$J$-homomorphism 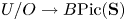$U/O\rightarrow B\mathrm {Pic}(\mathbf {S})$. We put special emphasis on the functoriality and (symmetric) monoidal structures of the categories involved and, as a byproduct, we produce several concrete constructions of (commutative) algebra/module objects and (right-lax) morphisms between them in the (symmetric) monoidal 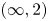$(\infty, 2)$-category of correspondences, generalizing the construction out of Segal objects of Gaitsgory and Rozenblyum, which might be of independent interest.

Keywords

microlocal sheaf theorysheaves of spectraLagrangian submanifoldsJ-homomorphismcorrespondences

MSC classification

Primary: 35A27: Microlocal methods; methods of sheaf theory and homological algebra in PDE
Secondary: 55P42: Stable homotopy theory, spectra
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 9 , September 2024 , pp. 2005 - 2099
Check for updates
Copyright
© The Author(s), 2024. The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abouzaid, M. and Kragh, T., On the immersion classes of nearby Lagrangians, J. Topol. 9 (2016), 232–244.CrossRefGoogle Scholar
Cohen, R., Jones, J. and Segal, G., Floer's infinite-dimensional Morse theory and homotopy theory, in The Floer memorial volume, Progress in Mathematics, vol. 133 (Birkhäuser, 1995), 297–325.CrossRefGoogle Scholar
Dwyer, W. and Kan, D., Function complexes in homotopical algebra, Topology 19 (1980), 427–440.CrossRefGoogle Scholar
Gaitsgory, D. and Rozenblyum, N., A study in derived algebraic geometry, vol. I. Correspondences and duality, Mathematical Surveys and Monographs, vol. 221 (American Mathematical Society, 2017).Google Scholar
Glasman, S., Day convolution for $\infty$-categories, Math. Res. Lett. 23 (2016), 1369–1385.CrossRefGoogle Scholar
Goresky, M. and MacPherson, R., Stratified Morse theory, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 14 (Springer, Berlin, 1988).CrossRefGoogle Scholar
Guillermou, S., Sheaves and symplectic geometry of cotangent bundles, Astérisque, vol. 440 (Société Mathématique de France, 2023).CrossRefGoogle Scholar
Guillermou, S., Kashiwara, M. and Schapira, P., Sheaf quantization of Hamiltonian isotopies and applications to non displaceability problems, Duke Math. J. 161 (2012), 201–245.CrossRefGoogle Scholar
Harris, B., Bott periodicity via simplicial spaces, J. Algebra 62 (1980), 450–454.CrossRefGoogle Scholar
Hinich, V., Rectification of algebras and modules, Doc. Math. 20 (2015), 879–926.CrossRefGoogle Scholar
Jin, X., Microlocal sheaf categories and the $J$-homomorphism, Preprint (2020), arXiv:2004.14270v4.Google Scholar
Jin, X. and Treumann, D., Brane structures in microlocal sheaf theory, J. Topol. 17 (2024), e12325.CrossRefGoogle Scholar
Kashiwara, M. and Schapira, P., Sheaves on manifolds. Grundlehren der Mathematischen Wissenschaften, vol. 292 (Springer, 1994). With a chapter in French by Christian Houzel.Google Scholar
Liu, Y. and Zheng, W., Enhanced six operations and base change theorem for Artin stacks, Preprint (2012), arXiv:1211.5948.Google Scholar
Lurie, J., Derived algebraic geometry II: noncommutative algebra, Preprint (2007), arXiv:math/0702299.Google Scholar
Lurie, J., Higher topos theory, Annals of Mathematics Studies, vol. 170 (Princeton University Press, 2009).CrossRefGoogle Scholar
Lurie, J., Rotation invariance in algebraic $K$-theory, Preprint (2015), https://www.math.ias.edu/~lurie/papers/Waldhaus.pdf.Google Scholar
Lurie, J., Higher algebra, Preprint (2017), https://www.math.ias.edu/~lurie/papers/HA.pdf.Google Scholar
Lurie, J., Spectral algebraic geometry, Preprint (2018), https://www.math.ias.edu/~lurie/papers/SAG-rootfile.pdf.Google Scholar
Nadler, D., Microlocal branes are constructible sheaves, Selecta Math. (N.S.) 15 (2009), 563–619.CrossRefGoogle Scholar
Nadler, D. and Shende, V., Sheaf quantization in Weinstein symplectic manifolds, Preprint (2020), arXiv:2007.10154.Google Scholar
Nadler, D. and Zaslow, E., Constructible sheaves and the Fukaya category, J. Amer. Math. Soc. 22 (2009), 233–286.CrossRefGoogle Scholar
Ramzi, M., A monoidal Grothendieck construction for $\infty$-categories, Preprint (2022), arXiv:2209.12569v1.Google Scholar
Segal, G., Categories and cohomology theories, Topology 13 (1974), 293–312.CrossRefGoogle Scholar
Seidel, P., Fukaya categories and Picard–Lefschetz theory, Zurich Lectures in Advanced Mathematics (European Mathematical Society (EMS), Zurich, 2008).CrossRefGoogle Scholar
Shende, V., Microlocal category for Weinstein manifolds via h-principle, Publ. Res. Inst. Math. Sci. 57 (2021), 1041–1048.CrossRefGoogle Scholar
Tamarkin, D., Microlocal category, Preprint (2015), arXiv:1511.08961.Google Scholar