Article contents
Faltings’ main p-adic comparison theorems for non-smooth schemes
Published online by Cambridge University Press: 12 January 2024
Abstract
To understand the p-adic étale cohomology of a proper smooth variety over a p-adic field, Faltings compared it to the cohomology of his ringed topos, by the so-called Faltings’ main p-adic comparison theorem, and then deduced various comparisons with p-adic cohomologies originating from differential forms. In this article, we generalize the former to any proper and finitely presented morphism of coherent schemes over an absolute integral closure of 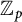 $\mathbb {Z}_p$ (without any smoothness assumption) for torsion abelian étale sheaves (not necessarily finite locally constant). Our proof relies on our cohomological descent for Faltings’ ringed topos, using a variant of de Jong’s alteration theorem for morphisms of schemes due to Gabber–Illusie–Temkin to reduce to the relative case of proper log-smooth morphisms of log-smooth schemes over a complete discrete valuation ring proved by Abbes–Gros. A by-product of our cohomological descent is a new construction of Faltings’ comparison morphism, which does not use Achinger’s results on
$\mathbb {Z}_p$ (without any smoothness assumption) for torsion abelian étale sheaves (not necessarily finite locally constant). Our proof relies on our cohomological descent for Faltings’ ringed topos, using a variant of de Jong’s alteration theorem for morphisms of schemes due to Gabber–Illusie–Temkin to reduce to the relative case of proper log-smooth morphisms of log-smooth schemes over a complete discrete valuation ring proved by Abbes–Gros. A by-product of our cohomological descent is a new construction of Faltings’ comparison morphism, which does not use Achinger’s results on 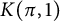 $K(\pi ,1)$-schemes.
$K(\pi ,1)$-schemes.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society
References
- 2
- Cited by



