Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T09:05:21.188Z Has data issue: false hasContentIssue false
  • English
  • Français

Assessment of GNSS Orthogonal Transformation Model

Published online by Cambridge University Press:  23 March 2012

Wantong Chen  and
Yanzhong Zhang
Wantong Chen*
Affiliation:
(School of Electronic and Information Engineering, Beihang University, Beijing)
Yanzhong Zhang
Affiliation:
(School of Electronic and Information Engineering, Beihang University, Beijing)
*
(E-mail: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

GNSS relative positioning technique is an important field of study, in which the standard ‘GNSS Baseline Model’ is often used. Differencing between observation equations is used to construct the mathematical model, since this method can eliminate some common errors in the GNSS signal measurements. The ‘Orthogonal Transformation’ method can also construct the GNSS Baseline Model. However, as is described by some scholars, this model may avoid some drawbacks of Double Differencing (DD) while maintaining all the advantages. For comparison purposes, this model is evaluated and the theoretical equivalence of both approaches is proved for the short baseline from two aspects: the Integer Ambiguity Resolution and the conditional least-squares baseline vector.

Keywords

GNSS Baseline ModelInteger Ambiguity ResolutionOrthogonal Transformation
Type
Research Article
Information
The Journal of Navigation , Volume 65 , Issue 3 , July 2012 , pp. 561 - 570
Copyright
Copyright © The Royal Institute of Navigation 2012

1. INTRODUCTION

The ‘GNSS Baseline Model’ is widely used in GNSS computations involving the relative positioning technique (Tiberius, Reference Tiberius1998; Wang, 2002; Leick, Reference Leick2003; Misra and Enge, Reference Misra and Enge2006; Hofmann-Wellenhof et al., Reference Hofmann-Wellenhof, Lichtenegger and Wasle2008). The Double Differenced (DD) method is a very common approach for constructing the GNSS Baseline Model (Strang and Borre, Reference Strang and Borre1997; Teunissen and Kleusberg, Reference Teunissen and Kleusberg1998); however, some scholars assume that there are some drawbacks in the DD method (Chang and Paige, Reference Chang and Paige2003a). For example it is numerically slightly dubious, it makes the DD measurements correlated and it gives unnecessary prominence to the reference satellite. In (Chang and Paige, Reference Chang and Paige2003b; Chang et al., Reference Chang, Paige and Yin2004), an ‘Orthogonal Transformation’ approach is presented, which can avoid the first two drawbacks, while maintaining all the advantages. Both the DD and Orthogonal Transformation can be utilized to construct the GNSS Baseline Model. In order to evaluate both models, we focus on the ‘Integer Ambiguity Resolution’ and the conditional least-squares solution. The theoretical equivalence of both models is proved for the short baseline based on those two aspects.

2. GNSS BASELINE MODEL

2.1. The Standard GNSS Baseline Model

The standard GNSS Baseline Model is the mixed integer model (Teunissen, Reference Teunissen2003, Reference Teunissen2011a). It is defined as:

(1)
$$E({\bi Y}){\bi \ = Aa} + {\bi Bb},D({\bi Y}) = {\bi Q}_{\bi Y}, {\bi a} \in Z^n, {\bi b} \in R^p $$

where:

  • Y is the given GNSS data vector.

  • a and b are the unknown parameter vectors of order n and p respectively.

  • E(·) and D(·) denote the expectation and dispersion operators, respectively.

  • A and B are the given design matrices that link the data vector to the unknown parameters.

The variance matrix of Y is given by the positive definite matrix Q Y. The n-vector a contains the integer DD ambiguities and the real-valued p-vector b contains the remaining unknown parameters, such as for instance baseline components (coordinates) and possibly atmospheric delay parameters (troposphere, ionosphere). Many relative positioning methods make use of the Least-Squares Ambiguity Decorrelation Adjustment (LAMBDA) method to estimate the integer ambiguity, as this method is known to be efficient and to maximize the ambiguity success rate (Teunissen, Reference Teunissen1995, Reference Teunissen1999; Verhagan, 2004). In order to utilize the LAMBDA method, first regardless of the integer constraint of a, the float solution ${\bi \hat a}$ and its variance–covariance (v-c) matrix ${\bi Q}_{{\bi \hat a}} $ should be obtained by the (weighted) least-squares method. The least-squares solution can be written as follows (Teunissen, Reference Teunissen2006):

(2)
$${\bi \hat a} = ({\bi \bar A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi \bar A})^{ - 1} {\bi \bar A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi Y}$$
(3)
$${\bi Q}_{{\bi \hat a}} = ({\bi \bar A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi \bar A})^{ - 1} $$

where ${\bi \bar A} = {\bi P}_{\bi B}^ \bot {\bi A}$ with the orthogonal projector P$^\bot_{\bi B}\equals{\bi I} - {\bi P}_{\bi B},{\bi P}_{\bi B} = $$ {\bi B}({\bi B}^T {\bi Q}_{\bi Y}^{ - 1} {\bi B})^{ - 1} {\bi B}^T {\bi Q}_{\bi Y}^{ - 1} $.

For the GNSS compass problem (Teunissen, Reference Teunissen2006, Reference Teunissen2010), the Constrained LAMBDA method is used since the baseline length is provided as well (Giorgi et al., Reference Giorgi, Teunissen and Verhagen2010; Teunissen et al., Reference Teunissen, Giorgi and Buist2011b). In this case, the conditional least-squares solution for b, which assumes that a is known, is also required for the estimator. The conditional least-squares solution and its v-c matrix read:

(4)
$${\bi \hat b}({\bi a}) = ({\bi B}^T {\bi Q}_{\bi Y}^{ - 1} {\bi B})^{ - 1} {\bi B}^T {\bi Q}_{\bi Y}^{ - 1} ({\bi Y} - {\bi Aa})$$
(5)
$${\bi Q}_{{\bi \hat b}({\bi a})} = ({\bi B}^T {\bi Q}_{\bi Y}^{ - 1} {\bi B})^{ - 1} $$

The notation ${\bi \hat b}({\bi a})$ emphasizes that we consider ${\bi \hat b}( \cdot )$ a function. With the fixed integer ambiguity ${\bi \breve {a}} $, the fixed baseline vector can be obtained by:

(6)
$${\bi \breve {b}} = {\bi \hat b}({\bi \breve {a}} )$$

In order to make the proof clearer, we firstly focus on the single frequency, single epoch and short baseline scenario for constructing the GNSS Baseline Model.

2.2. The Double-Differenced (DD) Model

For the short baseline and m visible satellites, with σ ϕ,i2 and σ ρ,i2 being the variance of carrier phase and code on band L i , the Single-Differenced (SD) carrier phase and code equations can be expressed in compact vector and matrix notation as (Chang et al., Reference Chang, Paige and Yin2004; Chen and Qin, Reference Chen and Qin2011)

(7)
$${\bi y}_{i,S}^\phi = \displaystyle{1 \over {\lambda _i}} {\bi E} \cdot {\bi b} - {\bi N}_{i,S} + {\bi e}_m \beta + {\bi v}_{i,S}^\phi, \quad {\bi v}_{i,S}^\phi \sim N({\bi 0},2\sigma _{\phi, i}^2 {\bi I}_m )$$
(8)
$${\bi y}_{i,S}^\rho = \displaystyle{1 \over {\lambda _i}} {\bi E} \cdot {\bi b} + {\bi e}_m \beta + {\bi v}_{i,S}^\rho, \quad {\bi v}_{i,S}^\rho \sim N({\bi 0},2\sigma _{\rho, i}^2 {\bi I}_m )$$

where:

  • yi,Sϕ and yi,Sρ are SD phase and code observations in units of cycles.

  • E is the (m−1)×3 matrix of normalized SD line-of-sight vectors.

  • vi,Sϕ and vi,Sρ are SD phase and code noise.

  • Ni ,S is the SD integer ambiguity vector.

  • λ i is the wave length.

  • em is a vector of order m for which each entry is 1 and β is the clock bias.

In order to eliminate the clock biases of all the SD equations, the (m−1)×m DD matrix operator will be defined as D=(d1d2… dm) (Teunissen, Reference Teunissen1997). This matrix can be set up in several ways, depending on the choice of reference satellite (Odijk, Reference Odijk2003). If satellite k is chosen as the reference satellite, thus the vector d k=−em− 1 where em−1 is an m−1 vector for which each entry is 1, and all the other vectors of D can be treated as Im−1. When the first satellite is selected as the reference satellite, it reads D=(−em− 1, Im−1). Pre-multiplications of Equations (7) and (8) by this operator give:

(9)
$${\bi y}_{i,D}^\phi = {\bi H}_i \cdot {\bi b} - {\bi N}_{i,D} + {\bi v}_{i,D}^\phi, \quad {\bi v}_{i,D}^\phi \sim N({\bi 0},2\sigma _{\phi, i}^2 {\bi Q})$$
(10)
$${\bi y\hskip1.5pt}_{\hskip-1pti,D} ^\rho = {\bi H}_i \cdot {\bi b} + {\bi \nu}^{\hskip1.5pt\rho}_{i,D} , \quad {\bi v}_{i,D}^{\hskip1.5pt\rho} \sim N({\bi 0},2\sigma _{\rho, i}^2 {\bi Q})$$

where:

yi,D ϕ

=Dyi,Sϕ

yi,Dρ

=Dyi,Sρ

vi,Dϕ

=Dv i,Sϕ

vi,Dρ

=Dv i,Sρ

Ni,D

=DN i,S

Hi

=1/λ iDE

Q

=DD T.

The DD model can be obtained by combining Equations (9) and (10):

(11)
$$\left[ {\matrix{ {{\bi y}_{i,D}^\phi} \cr {{\bi y}_{i,D}^\rho} \cr}} \right] = \left[ {\matrix{ {{\bi H}_i} \cr {{\bi H}_i} \cr}} \right]{\bi b} + \left[ {\matrix{ { - {\bi I}} \cr {\bi 0} \cr}} \right]{\bi N}_{i,{\bi D}} + \left[ {\matrix{ {{\bi v}_{i,D}^\phi} \cr {{\bi v}_{i,D}^\rho} \cr}} \right]$$

Thus the standard GNSS model can be obtained if each term is expressed as follows:

(12)
$$\eqalign{{\bi Y} = {\bi Y}_i = \left[ {\matrix{ {{\bi y}_{i,D}^\phi} \cr {{\bi y}_{i,D}^\rho} \cr}} \right],{\bi A = A}_0 = \left[ {\matrix{ {{\bi - I}} \cr {\bi 0} \cr}} \right],{\bi B} = {\bi B}_i {\bi =} \left[ {\matrix{ {{\bi H}_i} \cr {{\bi H}_i} \cr}} \right],{\bi Q}_{{\bi Y}_i} = \left[ {\matrix{ {2\sigma _{\phi, i}^2 {\bi Q}} & {} \cr {} & {2\sigma _{\rho, i}^2 {\bi Q}} \cr}} \right]}$$

The subscript i denotes that the item is depending on the given band and the subscript 0 denotes that its structure does nothing with the given band.

2.3. The Orthogonal Transformation Model

This model is based on an Orthogonal Transformation of single differences and the vector of DD integer ambiguities is still available (Chang and Paige, Reference Chang and Paige2003b). The main steps are re-derived as follows (Chen and Qin, Reference Chen and Qin2011). Let P∈Rm ×m be an Orthogonal Transformation such that ${\bi Pe}_m = \sqrt m {\bi u}_1 $ and the Householder transformation is used to form P as follows:

(13)
$${\bi P} = {\bi I}_m - \displaystyle{{2{\bi uu}^T} \over {{\bi u}^T {\bi u}}},{\bi u} \equiv {\bi u}_1 - \displaystyle{1 \over {\sqrt m}} {\bi e}_m $$

where u1=(1, 0,…, 0)T=(1 0)T.

By simple algebraic operations, we obtain for this matrix

(14)

where ${\bi \bar P} = \left[ {\matrix{ {\displaystyle{{{\bi e}_{m - 1}} \over {\sqrt m}}} & {{\bi I}_{m - 1} - \displaystyle{{{\bi e}_{m - 1} \cdot {\bi e}_{m - 1}^T} \over {m - \sqrt m}}} \cr}} \right]$.

In order to eliminate the clock bias, applying P to Equation (7), we obtain the initial Orthogonal Transformation of Equation (7):

(15)
$$\left[ {\matrix{ {{\bi p}_1 {\bi y}_{i,S}^\phi} \cr {{\bi \bar Py}_{i,S}^\phi} \cr}} \right] = \left[ {\matrix{ {{\bi p}_1 {\bi E}} \cr {{\bi \bar PE}} \cr}} \right]{\bi b} - \left[ {\matrix{ {{\bi p}_1 {\bi N}_{i,S}} \cr {{\bi \bar PN}_{i,S}} \cr}} \right] + \left[ {\matrix{ 1 \cr {\bi 0} \cr}} \right]\sqrt m \beta + \left[ {\matrix{ {{\bi p}_1 {\bi v}_{i,S}^\phi} \cr {{\bi \bar Pv}_{i,S}^\phi} \cr}} \right]$$

Note that only the first equation involves the clock bias term, the remaining part can be written as:

(16)
$${\bi \bar Py}_{i,S}^\phi = {\bi \bar PEb} - {\bi \bar PN}_{i,S} + {\bi \bar Pv}_{i,S}^\phi $$

Although double differencing is not used, the DD integer ambiguity vector can also be obtained by the following algebraic operations. Define the matrix F as follows:

(17)
$${\bi F} \equiv {\bi I}_{m - 1} - \displaystyle{{{\bi e}_{m - 1} {\kern 1pt} {\bi e}_{m - 1}^T} \over {m - \sqrt m}} $$

where F is nonsingular.

With Equation (14), it is easy to verify that:

(18)
${\bi \bar P} = {\bi FD}$$

where D≡[−em− 1Im−1] is the DD operator.

Thus the following formulation can be deduced:

(19)
${\bi \bar PN}_{i,S} = {\bi FDN}_{i,S} = {\bi FN}_{i,D} $$

Replacing ${\bi \bar PN}_{i,S} $ in Equations (16) by (19), we obtain

(20)
$${\bi \bar Py}_{i,S}^\phi = {\bi \bar PEb} - {\bi FN}_{i,D} + {\bi \bar Pv}_{i,S}^\phi, \quad {\bi \bar Pv}_{i,S}^\phi \sim N({\bi 0},2\sigma _{i,\phi} ^2 {\bi I}_{m - 1} )$$

where the DD integer ambiguity vector exists.

The transformed noise vector still follows the same distribution because Orthogonal Transformation will not change the statistical properties of white noise (Chang and Paige, Reference Chang and Paige2003b). Similarly, applying P to Equation (8), we obtain the following Orthogonal Transformation of SD code observation equation (Chang et al., Reference Chang, Paige and Yin2004):

(21)
$${\bi \bar Py}_{i,S}^\rho = {\bi \bar PEb} + {\bi \bar Pv}_{i,S}^\rho, \quad {\bi \bar Pv}_{i,S}^\phi \sim N({\bi 0},2\sigma _{\rho, i}^2 {\bi I}_{m - 1} )$$

The combination expression of Equations (20) and (21) reads

(22)
$$\left[ {\matrix{ {{\bi \bar y}_{i,D}^\phi} \cr {{\bi \bar y}_{i,D}^\rho} \cr}} \right] = \left[ {\matrix{ {{\bi \bar H}_i} \cr {{\bi \bar H}_i} \cr}} \right]{\bi b} + \left[ {\matrix{ { - {\bi F}} \cr {\bi 0} \cr}} \right]{\bi N}_{i,{\bi D}} + \left[ {\matrix{ {{\bi \bar v}_{i,D}^\phi} \cr {{\bi \bar v}_{i,D}^\rho} \cr}} \right]$$

where:

  • ${\bi \bar y}_{i,D}^\phi = {\bi \bar Py}_{i,S}^\phi $

  • ${\bi \bar y}_{i,D}^\rho = {\bi \bar Py}_{i,S}^\rho $

  • ${\bi \bar v}_{i,D}^\phi = {\bi \bar Pv}_{i,S}^\phi $

  • ${\bi \bar v}_{i,D}^\rho = {\bi \bar Pv}_{i,S}^\rho $

  • ${\bi N}_{i,D} = {\bi FN}_{i,S} $

  • ${\bi \bar H}_i = {1 / {\lambda _i}} {\bi \bar PE}$.

Note that both phase and code are expressed in units of cycles. This can be considered as the standard GNSS model if each term is expressed as follows:

(23)
$${{\bi Y} = {\bi Y}_i = \left[ {\matrix{ {{\bi \bar y}_{i,D}^\phi} \cr {{\bi \bar y}_{i,D}^\rho} \cr}} \right],{\bi A = A}_0 = \left[ {\matrix{ {{\bi - F}} \cr {\bi 0} \cr}} \right],{\bi B} = {\bi B}_i {\bi =} \left[ {\matrix{ {{\bi \bar H}_i} \cr {{\bi \bar H}_i} \cr}} \right],{\bi Q}_{{\bi Y}_i} = \left[ {\matrix{ {2\sigma _{\phi, i}^2 {\bi I}_{m - 1}} & {} \cr {} & {2\sigma _{\rho, i}^2 {\bi I}_{m - 1}} \cr}}} \right]$$

3. CONDITIONAL LEAST-SQUARE SOLUTION EQUIVALENCE OF BOTH MODELS

3.1. The Conditional Least-Squares Baseline Vector of the Double Difference Model

With Equations (4) and (5), the conditional least-squares solution reads

(24)
$${\bi Q}_{{\bi \hat b}\left( {\bi a} \right)} = \left( {\left( {\displaystyle{1 \over {2\sigma _{\phi, i}^2}} + \displaystyle{1 \over {2\sigma _{\rho, i}^2}}} \right)({\bi H}_i ^{\bi T} {\bi Q}^{ - 1} {\bi H}_i )} \right)^{ - 1} $$

With Hi=1/λiDE and Q=DDT, we obtain (Chen et al., Reference Chen, Qin, Zhang and Jin2012)

(25)
$${\bi Q}_{{\bi \hat b}({\bi a})} = \lambda _i^2 \omega _i^{ - 1} ({\bi E}^{\bi T} {\bi \Gamma E})^{ - 1} $$

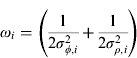where $\omega _i = \left( {\displaystyle{1 \over {2\sigma _{\phi, i}^2}} + \displaystyle{1 \over {2\sigma _{\rho, i}^2}}} \right)$ and Γ=DT(DDT)−1D.

Since Equation (5) is part of Equation (4), the conditional least-squares solution reads:

(26)
$${\bi \hat b}({\bi a}) = {\bi Q}_{{\bi \hat b}({\bi a})} \displaystyle{1 \over {\lambda _i}} \left( {\displaystyle{1 \over {2\sigma _{\phi, i}^2}} {\bi E\Gamma} ({\bi y}_{_{i,S}} ^\phi + {\bi N}_{i,S} ) + \displaystyle{1 \over {2\sigma _{\rho, i}^2}} {\bi E\Gamma y}_{_{i,S}} ^\rho} \right)$$

3.2. The Conditional Least-Squares Solution of the Orthogonal Transformation Model

In the same way, the conditional variance-covariance matrix of the Orthogonal Transformation model reads:

(27)
$$\eqalign{{\bi Q}_{{\bi \hat b}({\bi a})} = & \left( {\left( {\displaystyle{1 \over {2\sigma _{\phi, i}^2}} + \displaystyle{1 \over {2\sigma _{\rho, i}^2}}} \right)({\bi \bar H}_i ^{\bi T} {\bi \bar H}_i )} \right)^{ - 1} \cr = & \lambda _i^2 \omega _i^{ - 1} ({\bi E}^T {\bi {\rm K}E})^{ - 1}} $$

where the matrix ${\bi {\rm K}} = {\bi \bar P}^T {\bi \bar P}$.

The conditional least squares solution is expressed as the same structure of Equation (27):

(28)
$${\bi \hat b}({\bi a}) = {\bi Q}_{{\bi \hat b}({\bi a})} \displaystyle{1 \over {\lambda _i}} \left( {\displaystyle{1 \over {2\sigma _{\phi, i}^2}} {\bi E{\rm K}}({\bi y}_{_{i,S}} ^\phi + {\bi N}_{_{i,S}} ) + \displaystyle{1 \over {2\sigma _{\rho, i}^2}} {\bi E{\rm K}y}_{_{i,S}} ^\rho} \right)$$

3.3. Equivalence of the Conditional Least-Squares Solution

In order to prove the equivalence of baseline vector, we should prove the equivalence of Equations (25) and (27) and also the equivalence of Equations (26) and (28). It is worth noting that they have similar expressions and only the matrix Γ and K are different for the DD model and the Orthogonal Transformation model. In order to prove Γ =K, we should prove the following Equation (29):

(29)
$${\bi \bar P}^T {\bi \bar P} = {\bi D}^T ({\bi DD}^T )^{ - 1} {\bi D}$$

With Equation (29), we can obtain the following expression:

(30)
$${\bi \bar P}^T {\bi \bar P} = {\bi D}^T {\bi F}^T {\bi FD}$$

With Equation (17), the following equation can be verified:

(31)
$${\bi F}^T {\bi F} = {\bi I}_{m - 1} - \displaystyle{1 \over m}{\bi e}_{m - 1} {\bi e}_{m - 1}^T $$

For the DD operator, we have the same structure (Teunissen, Reference Teunissen1997) as follows:

(32)
$$({\bi DD}^T )^{ - 1} = {\bi I}_{m - 1} - \displaystyle{1 \over m}{\bi e}_{m - 1} {\bi e}_{m - 1}^T $$

With Equations (31) and (32), we have:

(33)
$${\bi F}^T {\bi F} = ({\bi DD}^T )^{ - 1} $$

With Equations (30) and (33), Equation (29) can be verified, and so we prove the conditional least-square solution equivalence of both models.

4. INTEGER AMBIGUITY RESOLUTION EQUIVALENCE OF BOTH MODELS

In order to prove the equivalence of integer ambiguity resolution, we should focus on the float ambiguity vector ${\bi \hat a}$ and its v-c matrix ${\bi Q}_{{\bi \hat a}} $, see also Equations (2) and (3). For the orthogonal projector ${\bi P}_{\bi B}^ \bot $, the following properties can be verified:

(34)
$$$${\bi Q}_{\bi Y}^{ - 1} {\bi P}_{\bi B}^ \bot = ({\bi P}_{\bi B}^ \bot )^T {\bi Q}_{\bi Y}^{ - 1} = ({\bi P}_{\bi B}^ \bot )^T {\bi Q}_{\bi Y}^{ - 1} {\bi P}_{\bi B}^ \bot $$

With Equation (34), the equivalent expression of Equation (3) is written as:

(35)
$$\eqalign{{\bi Q}_{{\bi \hat a}} = \ & ({\bi A}^T {\bi Q}_{\bi Y}^{ - 1} ({\bi P}_{\bi B}^ \bot ){\bi A})^{ - 1} \cr = \ & ({\bi A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi A} - {\bi A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi B}({\bi B}^T {\bi Q}_{\bi Y}^{ - 1} {\bi B})^{ - 1} {\bi B}^T {\bi Q}_{\bi Y}^{ - 1} {\bi A})^{ - 1} \cr = \ & ({\bi A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi A} - {\bi A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi B} \cdot {\bi Q}_{{\bi \hat b}\left( {\bi a} \right)} \cdot ({\bi A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi B})^{\rm T})^{ - 1}} $$

We may also therefore write Equation (2) as:

(36)
$$\eqalign{{\bi \hat a} = \ & {\bi Q}_{{\bi \hat a}} \cdot \left[ {\Big({\bi I} - {\bi B}({\bi B}^T {\bi Q}_{\bi Y}^{ - 1} {\bi B})^{ - 1} {\bi B}^T {\bi Q}_{\bi Y}^{ - 1}\Big) {\bi A}} \right]^T {\bi Q}_{\bi Y}^{ - 1} {\bi Y} \cr = \ & {\bi Q}_{{\bi \hat a}} \cdot \left( {{\bi A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi Y} - {\bi A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi B}({\bi B}^T {\bi Q}_{\bi Y}^{ - 1} {\bi B})^{ - 1} {\bi B}^T {\bi Q}_{\bi Y}^{ - 1} {\bi Y}} \right) \cr = \ & {\bi Q}_{{\bi \hat a}} \cdot \left( {{\bi A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi Y} - {\bi A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi B} \cdot {\bi Q}_{{\bi \hat b}({\bi a})} \cdot {\bi B}^T {\bi Q}_{\bi Y}^{ - 1} {\bi Y}} \right)} $$

4.1. Integer Ambiguity Resolution of the Double-Differenced (DD) Model

With the notations of Equation (12), the unknown matrices of Equation (35) can be calculated as follows:

(37)
$${\bi A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi A} = \displaystyle{1 \over {2\sigma _{\phi, i}^2}} ({\bi DD}^T )^{ - 1} {\rm and}\, {\bi A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi B} = - \displaystyle{1 \over {2\sigma _{\phi, i}^2 \lambda _i}} ({\bi DD}^T )^{ - 1} {\bi DE}$$

The unknown matrices of (36) read as

(38)
${\bi A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi Y} = - ({\bi DD}^T )^{ - 1} {\bi D}\displaystyle{1 \over {2\sigma _{\phi, i}^2}} {\bi y}_{_{i,S}} ^\phi \,{\rm and}\,{\bi B}^T {\bi Q}_{\bi Y}^{ - 1} {\bi Y} = \displaystyle{1 \over {\lambda _i}} {\bi E}^T {\bi \Gamma} \left( {\displaystyle{1 \over {2\sigma _{\phi, i}^2}} {\bi y}_{_{i,S}} ^\phi + \displaystyle{1 \over {2\sigma _{\rho, i}^2}} {\bi y}_{_{i,S}} ^\rho} \right)$$

4.2. Integer Ambiguity Resolution of the Orthogonal Transformation Model

With the notations of Equation (23), the matrices of Equation (35) can be calculated as follows:

(39)
$${\bi A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi A} = \displaystyle{1 \over {2\sigma _{\phi, i}^2}} {\bi F}^T {\bi F}\quad {\bi A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi B} = - \displaystyle{1 \over {2\sigma _{\phi, i}^2 \lambda _i}} {\bi F}^T ({\bi \bar PE})$$

The matrices of Equation (36) read as:

(40)
$${\bi A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi Y} = - {\bi F}^T {\bi \bar P}\displaystyle{1 \over {2\sigma _{\phi, i}^2}} {\bi y}_{_{i,S}} ^\phi \quad {\bi B}^T {\bi Q}_{\bi Y}^{ - 1} {\bi Y} = \displaystyle{1 \over {\lambda _i}} {\bi E}^T {\bi {\rm K}}\left( {\displaystyle{1 \over {2\sigma _{\phi, i}^2}} {\bi y}_{_{i,S}} ^\phi + \displaystyle{1 \over {2\sigma _{\rho, i}^2}} {\bi y}_{_{i,S}} ^\rho} \right)$$

4.3. Equivalence of Integer Ambiguity Resolution

With the derivation given in Equations (29) to (33), the equivalence of both operators is proved:

(41)
$${\bi \Gamma} = {\bi K}$$

With Equation (33), the following equations can also be verified:

(42)
$${\bi F}^T {\bi \bar P} = {\bi F}^T {\bi FD} = ({\bi DD}^T )^{ - 1} {\bi D}$$

With Equations (33) (41) and (42), the equivalence of both models can be verified for ${\bi Q}_{{\bi \hat a}} $ and ${\bi \hat a}$, can all be proved. Thus the same float solution ${\bi \hat a}$ and its variance-covariance matrix ${\bi Q}_{{\bi \hat a}} $ can be obtained for both models.

5. ASSESSMENT OF GENERAL CASES

Assume that n GNSS bands are used to construct the GNSS Baseline Model, the single epoch GNSS model can be written as

(43)
$$\hskip12pt{\bi Y} = & \left[ {\matrix{ {{\bi Y}_1} \cr {{\bi Y}_2} \cr \vdots \cr {{\bi Y}_n} \cr}} \right],\quad {\bi B} = \left[ {\matrix{ {{\bi B}_1} \cr {{\bi B}_2} \cr \vdots \cr {{\bi B}_n} \cr}} \right],\quad {\bi A =} \left[ {\matrix{ {{\bi A}_0} & {} & {} & {} \cr {} & {{\bi A}_0} & {} & {} \cr {} & {} & \ddots & {} \cr {} & {} & {} & {{\bi A}_0} \cr}} \right],\quad {\bi Q}_{\bi Y} {\bi =}\ \left[ {\matrix{ {{\bi Q}_{{\bi Y}_1}} & {} & {} & {} \cr {} & {{\bi Q}_{{\bi Y}_2}} & {} & {} \cr {} & {} & \ddots & {} \cr {} & {} & {} & {{\bi Q}_{{\bi Y}_n}} \cr}} \right]$$

The multi-frequency observation of the same GNSS constellation will bring the summation operator Σ into the computation, for example:

(44)
$${\bi Q}_{{\bi \hat b}({\bi a})} = \left( {\sum\limits_{i = 1}^n {({\bi B}_i ^{\bi T} {\bi Q}_{Y_i} ^{ - 1} {\bi B}_i )}} \right)^{ - 1} \,{\rm and}\, {\bi B}^T {\bi Q}_{\bi Y}^{ - 1} {\bi Y} = \sum\limits_{i = 1}^n {({\bi B}_i ^{\bi T} {\bi Q}_{Y_i} ^{ - 1} {\bi Y}_i )} $$

For the computation of ${\bi Q}_{{\bi \hat a}} $ and ${\bi \hat a}$, we obtain the following matrices:

(45)
$${\bi A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi A} = \left[ {\matrix{ {{\bi A}_0^T {\bi Q}_{{\bi Y}_1} {\bi A}_0} & {} & {} & {} \cr {} & {{\bi A}_0^T {\bi Q}_{{\bi Y}_2} {\bi A}_0} & {} & {} \cr {} & {} & \ddots & {} \cr {} & {} & {} & {{\bi A}_0^T {\bi Q}_{{\bi Y}_n} {\bi A}_0} \cr}} \right]\quad {\bi A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi Y} = \left[ {\matrix{ {{\bi A}_0^T {\bi Q}_{{\bi Y}_1} ^{ - 1} {\bi Y}_1} \cr {{\bi A}_0^T {\bi Q}_{{\bi Y}_2} ^{ - 1} {\bi Y}_2} \cr \vdots \cr {{\bi A}_0^T {\bi Q}_{{\bi Y}_n} ^{ - 1} {\bi Y}_n} \cr}} \right]\quad {\bi A}^T {\bi Q}_{\bi Y}^{ - 1} {\bi B} = \left[ {\matrix{ {{\bi A}_0^T {\bi Q}_{{\bi Y}_1} ^{ - 1} {\bi B}_1} \cr {{\bi A}_0^T {\bi Q}_{{\bi Y}_2} ^{ - 1} {\bi B}_2} \cr \vdots \cr {{\bi A}_0^T {\bi Q}_{{\bi Y}_n} ^{ - 1} {\bi B}_n} \cr}} \right]$$

Thus, in this case, the equivalence of both models does not alter. For k epochs, the standard GNSS model reads as follows (Giorgi et al., Reference Giorgi, Teunissen and Verhagen2010)

(46)
$${\bi Y} = \left[ {\matrix{ {{\bi Y}(1)} \cr {{\bi Y}(2)} \cr \vdots \cr {{\bi Y}(k)} \cr}} \right],{\bi A} = \left[ {\matrix{ {{\bi A}(0)} \cr {{\bi A}(0)} \cr \vdots \cr {{\bi A}(0)} \cr}} \right],{\bi B =} \left[ {\matrix{ {{\bi B}(1)} & {} & {} & {} \cr {} & {{\bi B}(2)} & {} & {} \cr {} & {} & \ddots & {} \cr {} & {} & {} & {{\bi B}(k)} \cr}} \right],\quad {\bi Q}_{\bi Y} {\bi =}\left[ {\matrix{ {{\bi Q}_{{\bi Y}(1)}} & {} & {} & {} \cr {} & {{\bi Q}_{{\bi Y}(2)}} & {} & {} \cr {} & {} & \ddots & {} \cr {} & {} & {} & {{\bi Q}_{{\bi Y}\left( k \right)}} \cr}} \right]$$

where:

  • A(0) denotes the constant A matrix for each epoch.

  • (k) denotes the corresponding matrix of the k epoch.

The multi-epoch observation will result in the Kronecker product operator (Giorgi et al., Reference Giorgi, Teunissen and Verhagen2010), and in this case the equivalence of both models is also valid, since the basic matrix of Equations (41) and (42) still remain in the derivations.

6. ASSESSMENT OF THE DRAWBACKS AND ADVANTAGES

Note that the cofactor matrix Q in Equations (9) and (10) has 2 s on the main diagonal and 1 s in all off-diagonal positions. Some scholars assume that the double differencing makes the DD measurements correlated, which is a drawback. However, this is not appropriate. Although the noise of Orthogonal Transformation model is white, the noise of DD model can still be white if an inverse-Cholesky factorization is used. The Cholesky decomposition of Q reads:

(47)
$${\bi Q = LL}^{\rm T} $$

where:

  • L is a lower triangular matrix with strictly positive diagonal entries.

  • LT denotes the conjugate transpose of L.

Pre-multiplication of Equations (9) and (10) by inverse of L gives:

(48)
$${\bi L}^{ - 1} {\bi y}_{i,D}^\phi = ({\bi L}^{ - 1} {\bi H}_i ) \cdot {\bi b} - {\bi L}^{ - 1} \cdot {\bi N}_{i,D} + {\bi L}^{ - 1} {\bi v}_{i,D}^\phi, \quad {\bi L}^{ - 1} {\bi v}_{i,D}^\phi \sim N({\bi 0},2\sigma _{\phi, i}^2 {\bi I}_{m - 1} )$$
(49)
$${\bi L}^{ - 1} {\bi y}_{i,D}^\rho = ({\bi L}^{ - 1} {\bi H}_i ) \cdot {\bi b} + {\bi L}^{ - 1} {\bi v}_{i,D}^\rho, \quad {\bi L}^{ - 1} {\bi v}_{i,D}^\rho \sim N({\bi 0},2\sigma _{\rho, i}^2 {\bi I}_{m - 1} )$$

The structure of Equations (48) and (49) are the same as Equations (20) and (21). Although the noise levels of Equations (20) and (21) seem smaller than those of Equations (9) and (10), with the use of the Orthogonal Transformation, one does not avoid the higher noise level of double differencing, due to the equivalence of both models. Finally, although Orthogonal Transformation is a numerically stable approach, double differencing is also not numerically dubious if properly implemented.

7. CONCLUSIONS

The Double Difference (DD) method and the Orthogonal Transformation approach can both construct the standard GNSS Baseline Model. Some scholars assume that the Orthogonal Transformation approach is better than the DD method. In this paper, we prove the theoretical equivalence of both approaches for the short baseline. Assessment of some views about the model drawbacks and advantages is also given and discussed.

References

REFERENCES

Chang, X. W. and Paige, C. C. (2003a). An algorithm for combined code and carrier phase based GPS positioning. BIT Numerical Mathematics, 43, 915–927.CrossRefGoogle Scholar
Chang, X. W. and Paige, C. C. (2003b). An Orthogonal Transformation Algorithm for GPS Positioning. SIAM Journal of Scientific Computing, 24(5), 1710–1732.CrossRefGoogle Scholar
Chang, X. W., Paige, C. C. and Yin, L. (2004). Code and Carrier Phase Based Short Baseline GPS Positioning, Computational Aspects. GPS Solutions, 7, 230–240.CrossRefGoogle Scholar
Chen, W. and Qin, H. (2011). New Method for Single Epoch, Single Frequency Land Vehicle Attitude Determination Using Low-End GPS Receiver. GPS Solutions. In press, doi: 10.1007/s10291-011-0234-8Google Scholar
Chen, W., Qin, H., Zhang, Y. and Jin, T. (2012). Accuracy Assessment of Single and Double Difference Models for the Single Epoch GPS Compass. Advances in Space Research, 49(4), 725–738.CrossRefGoogle Scholar
Giorgi, G., Teunissen, P. J. G., Verhagen, S. (2010). Reducing the Time-To-Fix for Stand-Alone Single-Frequency GNSS Attitude Determination. Proceedings of ION-ITM, 2010, 526–533.Google Scholar
Hofmann-Wellenhof, B., Lichtenegger, H. and Wasle, E. (2008). GNSS global navigation satellite systems. GPS, GLONASS. Galileo and More. Springer, Berlin.Google Scholar
Leick, A. (2003). GPS Satellite Surveying, 3rd edition. Wiley, New York.Google Scholar
Misra, P. and Enge, P. (2006). Global Positioning System Signals, Measurements and Performance. Ganga-Jamuna Press, Lincoln.Google Scholar
Odijk, D. (2003). Ionosphere-Free Phase Combinations for Modernized GPS. Journal of Surveying Engineering, 129(4), 165–173.CrossRefGoogle Scholar
Strang, G. and Borre, K. (1997). Linear Algebra, Geodesy, and GPS. Wellesley-Cambridge Press, Wellesley.Google Scholar
Teunissen, P. J. G. (1995). The Least-Squares Ambiguity Decorrelation Adjustment: a Method for Fast GPS Integer Ambiguity Estimation. Journal of Geodesy, 70, 65–82.CrossRefGoogle Scholar
Teunissen, P. J. G. (1997). GPS Double Difference Statistics: With and Without Using Satellite Geometry. Journal of Geodesy, 71(3), 138–148.CrossRefGoogle Scholar
Teunissen, P. J. G. and Kleusberg, A. (1998). GPS for Geodesy. Springer, Berlin, Heidelberg, New York.CrossRefGoogle Scholar
Teunissen, P. J. G. (1999). An Optimality Property of the Integer Least-Squares Estimator. Journal of Geodesy, 73, 587–593.CrossRefGoogle Scholar
Teunissen, P. J. G. (2003). Towards a Unified Theory of GNSS Ambiguity Resolution. Journal of Global Positioning Systems, 2(1), 1–12.CrossRefGoogle Scholar
Teunissen, P. J. G. (2006). The LAMBDA Method for the GNSS Compass. Artificial Satellites, 41(3), 89–103.CrossRefGoogle Scholar
Teunissen, P. J. G. (2010). Integer Least Squares Theory for the GNSS Compass. Journal of Geodesy, 84(7), 433–447.CrossRefGoogle Scholar
Teunissen, P. J. G. (2011a). A New Method for DGPS Ambiguity Resolution? Journal of Navigation, 64, 375–379.CrossRefGoogle Scholar
Teunissen, P. J. G., Giorgi, G. and Buist, P. J. (2011b). Testing of a New Single-Frequency GNSS Carrier-Phase Compass Method. Land, Ship and Aircraft Experiments. GPS Solutions, 15(1), 15–28.CrossRefGoogle Scholar
Verhagen, S. and Teunissen, P. J. G. (2006). New Global Navigation Satellite System Ambiguity Resolution Method Compared to Existing Approaches. Journal of Guidance, Control, and Dynamics, 29(4), 981–991.CrossRefGoogle Scholar
Tiberius, C. C. J. M. (1998). Recursive Data Processing for Kinematic GPS Surveying. PhD thesis, Department of Mathematical Geodesy and Positioning, Delft University of Technology.CrossRefGoogle Scholar
Wang, J., Satirapod, C. and Rizos, C. (2002). Stochastic Assessment of GPS Carrier Phase Measurements for Precise Static Relative Positioning. Journal of Geodesy, 76(2), 95–104.CrossRefGoogle Scholar