1 Introduction
With the development of laser technology[Reference Mourou, Tajima and Bulanov1–Reference Schreiber, Bolton and Parodi4], laser-driven ion beams have attracted much attention owing to potential applications such as fast ignition of inertial confinement fusion[Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason5, Reference Naumova, Schlegel, Tikhonchuk, Labaune, Sokolov and Mourou6], medical therapy[Reference Bulanov, Esirkepov, Khoroshkov, Kuznetsov and Pegoraro7–Reference Bulanov, Wilkens, Esirkepov, Korn, Kraft, Kraft, Molls and Khoroshkov9], proton imaging[Reference Borghesi, Campbell, Schiavi, Haines, Willi, MacKinnon, Patel, Gizzi, Galimberti, Clarke, Pegoraro, Ruhl and Bulanov10], neutron production[Reference Kar, Green, Ahmed, Alejo, Robinson, Cerchez, Clarke, Doria, Dorkings, Fernandez, Mirfayzi, McKenna, Naughton, Neely, Norreys, Peth, Powell, Ruiz, Swain, Willi and Borghesi11, Reference Roth, Jung, Falk, Guler, Deppert, Devlin, Favalli, Fernandez, Gautier, Geissel, Haight, Hamilton, Hegelich, Johnson, Merrill, Schaumann, Schoenberg, Schollmeier, Shimada, Taddeucci, Tybo, Wagner, Wender, Wilde and Wurden12], nuclear physics[Reference Ledingham, McKenna and Singhal13, Reference Zamfir14] and pre-accelerators for conventional acceleration devices[Reference Clark, Allott, Beg, Danson, Machacek, Malka, Najmudin, Neely, Norreys, Salvati, Santala, Tatarakis, Watts, Zepf and Dangor15].
Radiation pressure acceleration (RPA)[Reference Macchi, Cattani, Liseykina and Cornolti16–Reference Higginson, Gray, King, Dance, Williamson, Butler, Wilson, Capdessus, Armstrong, Green, Hawkes, Martin, Wei, Mirfayzi, Yuan, Kar, Borghesi, Clarke, Neely and McKenna30] is usually considered as an efficient mechanism to accelerate the whole target to gigaelectronvolts through the ‘hole-boring’ (HB)[Reference Macchi, Cattani, Liseykina and Cornolti16, Reference Robinson, Gibbon, Zepf, Kar, Evans and Bellei31] and ‘light-sail’ (LS)[Reference Yan, Lin, Sheng, Guo, Liu, Lu, Fang and Chen18, Reference Klimo, Psikal, Limpouch and Tikhonchuk20, Reference Qiao, Zepf, Borghesi and Geissler21, Reference Wang, Shen and Xu32] stages. However, the beam spectra in RPA experiments[Reference Henig, Steinke, Schnürer, Sokollik, Hörlein, Kiefer, Jung, Schreiber, Hegelich, Yan, Meyer-ter-Vehn, Tajima, Nickles, Sandner and Habs22, Reference Bin, Ma, Wang, Streeter, Kreuzer, Kiefer, Yeung, Cousens, Foster, Dromey, Yan, Ramis, Meyer-ter-Vehn, Zepf and Schreiber26, Reference Scullion, Doria, Romagnani, Sgattoni, Naughton, Symes, McKenna, Macchi, Zepf, Kar and Borghesi29] are much worse than what the theoretical results indicate[Reference Macchi, Cattani, Liseykina and Cornolti16–Reference Qiao, Zepf, Borghesi and Geissler21, Reference Bulanov, Echkina, Esirkepov, Inovenkov, Kando, Pegoraro and Korn23–Reference Yu, Pukhov, Shvets and Chen25, Reference Wan, Pai, Zhang, Li, Wu, Hua, Lu, Gu, Silva, Joshi and Mori27, Reference Shen, Qiao, Zhang, Kar, Zhou, Chang, Borghesi and He28]. One possible reason is the presence of multidimensional instabilities, such as Rayleigh–Taylor-like (RT-like) instability[Reference Robinson, Zepf, Kar, Evans and Bellei19, Reference Klimo, Psikal, Limpouch and Tikhonchuk20, Reference Pegoraro and Bulanov33–Reference Sgattoni, Sinigardi, Fedeli, Pegoraro and Macchi36] and Weibel-like instability[Reference Yan, Wu, Sheng, Chen and Meyer-Ter-Vehn37, Reference Zhang, Shen, Ji, Wang, Xu, Yu and Wang38]. Recent studies have given accurate predictions of the mode structures of the instabilities and the growth rates for a wide range of laser and plasma parameters[Reference Wan, Pai, Zhang, Li, Wu, Hua, Lu, Gu, Silva, Joshi and Mori27]. These show that the surface ripples are more likely induced by coupling between the transverse oscillating electrons and the quasistatic ions near the laser–plasma interface, although the target surface is initially flat. It indicates that instabilities are intrinsically generated as the laser irradiates the interface of the plasma. Previously, a model driven by the front or flat-top parts of the laser has been investigated[Reference Wan, Pai, Zhang, Li, Wu, Hua, Lu, Gu, Silva, Joshi and Mori27]. However, in real cases, the rear part of the laser pulse may further disturb the particle beam in RPA because it continues to interact with the laser–plasma interface. In addition, the accelerating gradient becomes lower in the LS stage, where the charge separation field is reduced due to the Doppler effects of the flying target on the driven laser, which is detrimental to controlling development of multidimensional instabilities in the relativistic region.
In this paper, the proton beam is prevented from moving together with the laser–plasma interface during the entire acceleration process, which may intrinsically reduce the development of detrimental instabilities. Here, a single reflection mechanism is used to stably accelerate the proton beam by optimally designing the multilayer target (the proton layer is set between two carbon ion layers). Such a multilayer target is totally different from previous cases[Reference Ji, Shen, Zhang, Wang, Jin, Li, Wen and Cary39, Reference Zhang, Shen, Ji, Wang, Jin, Li, Wen and Cary40], where the heavy ion layer is set between the proton layers. There, the heavy ions in the middle are accelerated together with protons at a lower velocity in a collisionless shock acceleration manner. However, in our case, the middle proton layer is separated from the heavy ions by means of a sharp-front laser, which is reflected once to hundreds of MeV with a monoenergetic spectrum only during the HB stage. Hence, the proton beam has a greatly reduced chance of moving together with the laser–plasma interface during the entire acceleration process. In this way, some multidimensional instabilities can be reduced to a certain extent. It could potentially be used to improve the beam quality for proton therapy and other applications.
2 Model and simulation
First, we review the traditional RPA process in a one-dimensional simulation to help us to design the target in the single reflection mechanism (SRM). A circularly polarized laser arrives at the target at
![]() $t=20T$
(see Figure 1(a)), where
$t=20T$
(see Figure 1(a)), where
![]() $T=\unicode[STIX]{x1D706}/c$
and
$T=\unicode[STIX]{x1D706}/c$
and
![]() $\unicode[STIX]{x1D706}=1~\unicode[STIX]{x03BC}\text{m}$
is the laser wavelength.
$\unicode[STIX]{x1D706}=1~\unicode[STIX]{x03BC}\text{m}$
is the laser wavelength.
![]() $c$
is the speed of light in vacuum. In the simulation, the laser amplitude has a triangular profile in time (linear up-ramp
$c$
is the speed of light in vacuum. In the simulation, the laser amplitude has a triangular profile in time (linear up-ramp
![]() $t_{\text{up}}=2.2T$
and linear down-ramp
$t_{\text{up}}=2.2T$
and linear down-ramp
![]() $t_{\text{down}}=2.2T$
). The pressure of the circularly polarized laser stably pushes electrons forward, such that the electrons are piled up at the front of the laser, forming a compressed electron layer. Previous simulations have demonstrated that the velocity of such a compressed electron layer is uniform because the laser has a linear front[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu24, Reference Wang, Zhang, Wang, Zhao, Xu, Yu, Yi, Shi, Zhang, Xu, Liu, Pei and Shen41]. In this case, the velocity of such an electron layer
$t_{\text{down}}=2.2T$
). The pressure of the circularly polarized laser stably pushes electrons forward, such that the electrons are piled up at the front of the laser, forming a compressed electron layer. Previous simulations have demonstrated that the velocity of such a compressed electron layer is uniform because the laser has a linear front[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu24, Reference Wang, Zhang, Wang, Zhao, Xu, Yu, Yi, Shi, Zhang, Xu, Liu, Pei and Shen41]. In this case, the velocity of such an electron layer
![]() $(v_{\text{CEL}})$
can be calculated from the balance between the laser pressure force
$(v_{\text{CEL}})$
can be calculated from the balance between the laser pressure force
![]() $(2a^{2}(1-v_{\text{CEL}})/(1+v_{\text{CEL}}))$
and electrostatic force
$(2a^{2}(1-v_{\text{CEL}})/(1+v_{\text{CEL}}))$
and electrostatic force
![]() $(2(\unicode[STIX]{x1D70B}n_{0}v_{\text{CEL}}t)^{2})$
. In the following calculations, the length, time, velocity, density, charge and field are normalized by
$(2(\unicode[STIX]{x1D70B}n_{0}v_{\text{CEL}}t)^{2})$
. In the following calculations, the length, time, velocity, density, charge and field are normalized by
![]() $\unicode[STIX]{x1D706},\unicode[STIX]{x1D706}/c,c,\unicode[STIX]{x1D714}_{\text{L}}^{2}m_{\text{e}}/4\unicode[STIX]{x1D70B}\text{e}^{2},-e$
and
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D706}/c,c,\unicode[STIX]{x1D714}_{\text{L}}^{2}m_{\text{e}}/4\unicode[STIX]{x1D70B}\text{e}^{2},-e$
and
![]() $e/m_{\text{e}}\unicode[STIX]{x1D714}_{\text{L}}c$
, respectively, for the theoretical compact calculation:
$e/m_{\text{e}}\unicode[STIX]{x1D714}_{\text{L}}c$
, respectively, for the theoretical compact calculation:
 $$\begin{eqnarray}\displaystyle v_{\text{CEL}} & = & \displaystyle \frac{1-3\unicode[STIX]{x1D705}^{2}}{3+3\unicode[STIX]{x1D705}^{2}}+\sqrt[3]{M+\sqrt{M^{2}+N^{3}}}\nonumber\\ \displaystyle & & \displaystyle +\,\sqrt[3]{M-\sqrt{M^{2}+N^{3}}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v_{\text{CEL}} & = & \displaystyle \frac{1-3\unicode[STIX]{x1D705}^{2}}{3+3\unicode[STIX]{x1D705}^{2}}+\sqrt[3]{M+\sqrt{M^{2}+N^{3}}}\nonumber\\ \displaystyle & & \displaystyle +\,\sqrt[3]{M-\sqrt{M^{2}+N^{3}}},\end{eqnarray}$$
where
![]() $M=-(27\unicode[STIX]{x1D705}^{4}-36\unicode[STIX]{x1D705}^{2}+1)/[27(1+\unicode[STIX]{x1D705}^{2})^{3}],N=(15\unicode[STIX]{x1D705}^{2}-1)/[9(1+\unicode[STIX]{x1D705}^{2})^{2}]$
and
$M=-(27\unicode[STIX]{x1D705}^{4}-36\unicode[STIX]{x1D705}^{2}+1)/[27(1+\unicode[STIX]{x1D705}^{2})^{3}],N=(15\unicode[STIX]{x1D705}^{2}-1)/[9(1+\unicode[STIX]{x1D705}^{2})^{2}]$
and
![]() $\unicode[STIX]{x1D705}=a_{0}/\unicode[STIX]{x1D70B}t_{\text{up}}n_{0}$
. Here
$\unicode[STIX]{x1D705}=a_{0}/\unicode[STIX]{x1D70B}t_{\text{up}}n_{0}$
. Here
![]() $a_{0}=eE_{\text{L}}/m_{\text{e}}\unicode[STIX]{x1D714}_{\text{L}}c\approx 94$
is the dimensionless peak amplitude of laser,
$a_{0}=eE_{\text{L}}/m_{\text{e}}\unicode[STIX]{x1D714}_{\text{L}}c\approx 94$
is the dimensionless peak amplitude of laser,
![]() $E_{\text{L}}$
is the amplitude of the laser electric field,
$E_{\text{L}}$
is the amplitude of the laser electric field,
![]() $\unicode[STIX]{x1D714}_{\text{L}}$
is the laser frequency, and
$\unicode[STIX]{x1D714}_{\text{L}}$
is the laser frequency, and
![]() $m_{\text{e}}$
and
$m_{\text{e}}$
and
![]() $e$
are the electron rest mass and charge, respectively.
$e$
are the electron rest mass and charge, respectively.
![]() $a=(a_{0}/t_{\text{up}})(t-v_{\text{CEL}}t)$
is the normalized laser amplitude at the electron layer. The foil density is
$a=(a_{0}/t_{\text{up}})(t-v_{\text{CEL}}t)$
is the normalized laser amplitude at the electron layer. The foil density is
![]() $n_{0}=50n_{\text{c}}$
and the foil thickness is
$n_{0}=50n_{\text{c}}$
and the foil thickness is
![]() $d=0.5~\unicode[STIX]{x03BC}\text{m}$
. Then
$d=0.5~\unicode[STIX]{x03BC}\text{m}$
. Then
![]() $v_{\text{CEL}}\sim 0.183c$
can be obtained according to Equation (2). Here an idealized triangular laser profile is used in the present scheme, mainly for simplicity of the calculation and simulation. For the case of a Gaussian temporal profile, the velocity of the compressed electron layer is no longer uniform, and the calculation becomes complex, but can be solved by the time-dependent model used in our previous work[Reference Wang, Shen, Zhang, Ji, Yu, Yi, Wang and Xu42].
$v_{\text{CEL}}\sim 0.183c$
can be obtained according to Equation (2). Here an idealized triangular laser profile is used in the present scheme, mainly for simplicity of the calculation and simulation. For the case of a Gaussian temporal profile, the velocity of the compressed electron layer is no longer uniform, and the calculation becomes complex, but can be solved by the time-dependent model used in our previous work[Reference Wang, Shen, Zhang, Ji, Yu, Yi, Wang and Xu42].
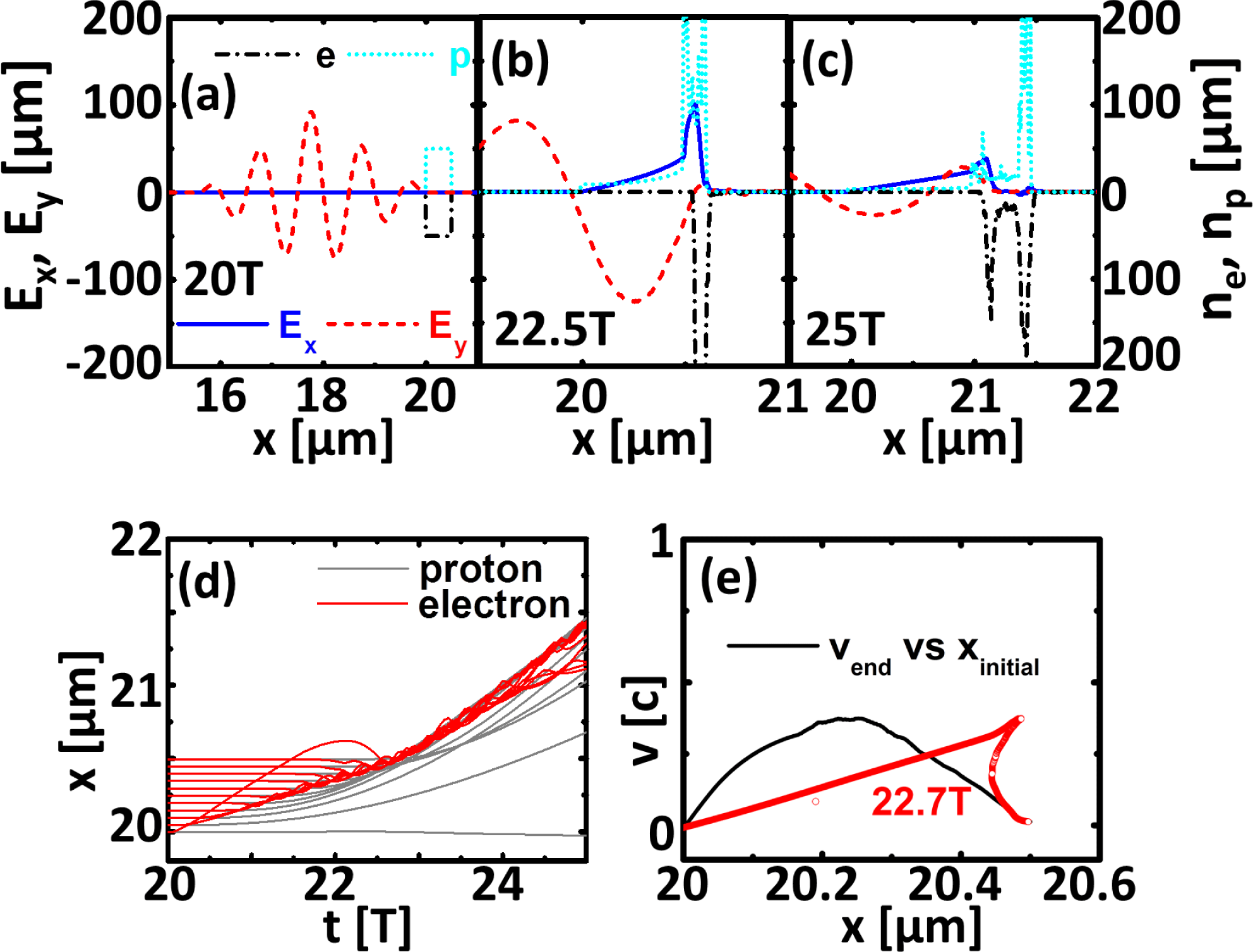
Figure 1. Electric field
![]() $E_{x}$
(blue solid line) and
$E_{x}$
(blue solid line) and
![]() $E_{y}$
(red dash line), electron density (black dash–dot line), proton density (cyan dot line) at (a)
$E_{y}$
(red dash line), electron density (black dash–dot line), proton density (cyan dot line) at (a)
![]() $t=20T$
, (b)
$t=20T$
, (b)
![]() $t=22.5T$
and (c)
$t=22.5T$
and (c)
![]() $t=25T$
. (d) Trajectories of electrons (red solid line) and protons (gray solid line) in the simulations. (e) Phase space distributions of protons at
$t=25T$
. (d) Trajectories of electrons (red solid line) and protons (gray solid line) in the simulations. (e) Phase space distributions of protons at
![]() $t=22.7T$
(red circles). The black solid line represents the velocity distribution at the end of the HB stage for protons initially at different positions of the foil (
$t=22.7T$
(red circles). The black solid line represents the velocity distribution at the end of the HB stage for protons initially at different positions of the foil (
![]() $v_{\text{end}}$
versus
$v_{\text{end}}$
versus
![]() $x_{\text{initial}}$
).
$x_{\text{initial}}$
).
Initially, the protons lag behind the compressed electron layer because the proton mass
![]() $m_{\text{i}}=1836m_{\text{e}}$
is much greater than the electron mass. At the end of HB stage, the fastest protons reach the compressed electron layer (see Figures 1(b) and 1(d))[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu24] and the LS stage starts. It should be noted that the protons initially in the target center are accelerated faster than the others at the end of the HB stage in this case[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu24]. The velocities of these protons are mainly distributed around
$m_{\text{i}}=1836m_{\text{e}}$
is much greater than the electron mass. At the end of HB stage, the fastest protons reach the compressed electron layer (see Figures 1(b) and 1(d))[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu24] and the LS stage starts. It should be noted that the protons initially in the target center are accelerated faster than the others at the end of the HB stage in this case[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu24]. The velocities of these protons are mainly distributed around
![]() $0.4c$
from
$0.4c$
from
![]() $x_{\text{initial}}=20.2~\unicode[STIX]{x03BC}\text{m}$
to
$x_{\text{initial}}=20.2~\unicode[STIX]{x03BC}\text{m}$
to
![]() $20.25~\unicode[STIX]{x03BC}\text{m}$
(see Figure 1(e)). It is also noted that a narrow energetic spectrum may be obtained if we selectively accelerate the protons in the middle layer. From Figure 1(e), it can also be seen that the spectrum of the middle proton layer becomes broadened with an increased thickness of the middle proton layer, so a thinner middle proton layer will be better.
$20.25~\unicode[STIX]{x03BC}\text{m}$
(see Figure 1(e)). It is also noted that a narrow energetic spectrum may be obtained if we selectively accelerate the protons in the middle layer. From Figure 1(e), it can also be seen that the spectrum of the middle proton layer becomes broadened with an increased thickness of the middle proton layer, so a thinner middle proton layer will be better.
Then, the multilayer target is designed to ensure that the middle proton layer can be selectively accelerated. According to Figure 1(e), a proton layer from
![]() $x=20.2~\unicode[STIX]{x03BC}\text{m}$
to
$x=20.2~\unicode[STIX]{x03BC}\text{m}$
to
![]() $x=20.25~\unicode[STIX]{x03BC}\text{m}$
is set between the carbon (
$x=20.25~\unicode[STIX]{x03BC}\text{m}$
is set between the carbon (
![]() $\text{C}^{6+}$
) layers (corresponding regions are
$\text{C}^{6+}$
) layers (corresponding regions are
![]() $20~\unicode[STIX]{x03BC}\text{m}<x<20.2~\unicode[STIX]{x03BC}\text{m}$
and
$20~\unicode[STIX]{x03BC}\text{m}<x<20.2~\unicode[STIX]{x03BC}\text{m}$
and
![]() $20.25~\unicode[STIX]{x03BC}\text{m}<x<20.5~\unicode[STIX]{x03BC}\text{m}$
). The electron density is
$20.25~\unicode[STIX]{x03BC}\text{m}<x<20.5~\unicode[STIX]{x03BC}\text{m}$
). The electron density is
![]() $n_{0}=50n_{\text{c}}$
and the densities of the proton and
$n_{0}=50n_{\text{c}}$
and the densities of the proton and
![]() $\text{C}^{6+}$
layers are
$\text{C}^{6+}$
layers are
![]() $n_{\text{p}}=50n_{\text{c}}$
and
$n_{\text{p}}=50n_{\text{c}}$
and
![]() $n_{\text{C}6+}=8.3n_{\text{c}}$
, respectively. Here, the charge-to-mass ratio of
$n_{\text{C}6+}=8.3n_{\text{c}}$
, respectively. Here, the charge-to-mass ratio of
![]() $\text{C}^{6+}$
is
$\text{C}^{6+}$
is
![]() $1/2$
, which is half of the value for the proton (that is, 1), meaning that protons can be more easily accelerated compared with
$1/2$
, which is half of the value for the proton (that is, 1), meaning that protons can be more easily accelerated compared with
![]() $\text{C}^{6+}$
ions. So, the
$\text{C}^{6+}$
ions. So, the
![]() $\text{C}^{6+}$
ions in the rear part of the target can be assumed to be at rest when the proton layer arrives. Different from the cases depicted in Figure 1, the trajectories of the protons initially at the middle of the target will cross trajectories of the
$\text{C}^{6+}$
ions in the rear part of the target can be assumed to be at rest when the proton layer arrives. Different from the cases depicted in Figure 1, the trajectories of the protons initially at the middle of the target will cross trajectories of the
![]() $\text{C}^{6+}$
ions initially at the rear of the target. Hence, the protons can be accelerated by the charge separation field
$\text{C}^{6+}$
ions initially at the rear of the target. Hence, the protons can be accelerated by the charge separation field
![]() $E_{x}=E_{0}x(t)/d$
, where
$E_{x}=E_{0}x(t)/d$
, where
![]() $E_{0}$
is the maximum charge separation field, given by
$E_{0}$
is the maximum charge separation field, given by
![]() $E_{0}=4\unicode[STIX]{x1D70B}en_{0}d$
. The proton velocity can be calculated using the following equation:
$E_{0}=4\unicode[STIX]{x1D70B}en_{0}d$
. The proton velocity can be calculated using the following equation:
where
![]() $m_{\text{p}}=1836$
is the proton mass and
$m_{\text{p}}=1836$
is the proton mass and
![]() $\unicode[STIX]{x1D6FE}_{\text{p}}(t)=1\big/\sqrt{1-v_{\text{p}}^{2}(t)}$
is the relativistic factor for the protons. In addition, the position of the protons can be calculated using the following equation:
$\unicode[STIX]{x1D6FE}_{\text{p}}(t)=1\big/\sqrt{1-v_{\text{p}}^{2}(t)}$
is the relativistic factor for the protons. In addition, the position of the protons can be calculated using the following equation:
The dynamics of the middle proton layer can be obtained from Equations (3) and (4) for
![]() $v_{\text{p}}(t=20T)=0$
and
$v_{\text{p}}(t=20T)=0$
and
![]() $x_{\text{initial}}=20~\unicode[STIX]{x03BC}\text{m}+0.5d$
. It should be noted that all these equations are related to the electron density
$x_{\text{initial}}=20~\unicode[STIX]{x03BC}\text{m}+0.5d$
. It should be noted that all these equations are related to the electron density
![]() $n_{0}$
, and the dynamics of the different ions are determined by their charge-to-mass ratios. The accelerating scheme will be totally different if their densities change.
$n_{0}$
, and the dynamics of the different ions are determined by their charge-to-mass ratios. The accelerating scheme will be totally different if their densities change.
Based on Equations (3) and (4), the middle proton layer arrives at the back surface of the target
![]() $(x_{\text{initial}}=20.5~\unicode[STIX]{x03BC}\text{m})$
at
$(x_{\text{initial}}=20.5~\unicode[STIX]{x03BC}\text{m})$
at
![]() $t\sim 22.6T$
. To start the LS stage as soon as possible, the compressed electron layer should also arrive at the back of the target simultaneously with the middle proton layer, forming a double layer. So, the velocity of the compressed electron layer should be
$t\sim 22.6T$
. To start the LS stage as soon as possible, the compressed electron layer should also arrive at the back of the target simultaneously with the middle proton layer, forming a double layer. So, the velocity of the compressed electron layer should be
![]() $v_{\text{CEL}}=d/2.6T\sim 0.2c$
. For the linearly rising-up laser front, the velocity
$v_{\text{CEL}}=d/2.6T\sim 0.2c$
. For the linearly rising-up laser front, the velocity
![]() $v_{\text{CEL}}$
during the HB stage can be calculated according to Equations (1) and (2). Considering
$v_{\text{CEL}}$
during the HB stage can be calculated according to Equations (1) and (2). Considering
![]() $a=(a_{0}/t_{\text{up}})(1-v_{\text{CEL}})t$
, the steepness of the laser front can be obtained as
$a=(a_{0}/t_{\text{up}})(1-v_{\text{CEL}})t$
, the steepness of the laser front can be obtained as
Then,
![]() $a_{0}/t_{\text{up}}\sim 48$
is obtained for
$a_{0}/t_{\text{up}}\sim 48$
is obtained for
![]() $n_{0}=50n_{\text{c}}$
and
$n_{0}=50n_{\text{c}}$
and
![]() $v_{\text{CEL}}\sim 0.2c$
, as shown in Figure 2(a). The peak amplitude
$v_{\text{CEL}}\sim 0.2c$
, as shown in Figure 2(a). The peak amplitude
![]() $a_{0}$
of the laser can be calculated as
$a_{0}$
of the laser can be calculated as
![]() ${\sim}96$
, according to
${\sim}96$
, according to
![]() $a_{0}=(a_{0}/t_{\text{up}})(1-v_{\text{CEL}})d/v_{\text{CEL}}$
and
$a_{0}=(a_{0}/t_{\text{up}})(1-v_{\text{CEL}})d/v_{\text{CEL}}$
and
![]() $t_{\text{up}}\sim 2T$
. Here, the velocity of the proton layer can increase up to
$t_{\text{up}}\sim 2T$
. Here, the velocity of the proton layer can increase up to
![]() $v_{\text{p}}\sim 0.4c$
, which is almost twice the velocity
$v_{\text{p}}\sim 0.4c$
, which is almost twice the velocity
![]() $v_{\text{CEL}}\;({\sim}0.2c)$
. This indicates that the proton layer moves faster than the compressed layer. At the same time, the remaining electrons will move together with the other
$v_{\text{CEL}}\;({\sim}0.2c)$
. This indicates that the proton layer moves faster than the compressed layer. At the same time, the remaining electrons will move together with the other
![]() $\text{C}^{6+}$
ions, because the laser intensity begins to decrease after
$\text{C}^{6+}$
ions, because the laser intensity begins to decrease after
![]() $t\sim 22.6T$
. The velocity of the
$t\sim 22.6T$
. The velocity of the
![]() $\text{C}^{6+}$
–electron double layer is lower than the velocity of the proton–electron double layer. So, the rear part of the laser can be reflected by the
$\text{C}^{6+}$
–electron double layer is lower than the velocity of the proton–electron double layer. So, the rear part of the laser can be reflected by the
![]() $\text{C}^{6+}$
–electron double layer. Only the carbon ions are heated and spread extensively, reducing the multidimensional instabilities of the proton layer to a certain extent. Ultimately, the high-quality proton bunch can be selectively accelerated to
$\text{C}^{6+}$
–electron double layer. Only the carbon ions are heated and spread extensively, reducing the multidimensional instabilities of the proton layer to a certain extent. Ultimately, the high-quality proton bunch can be selectively accelerated to
![]() $E_{\text{p}}\sim 100~\text{MeV}$
at the end of the HB stage (see Figure 2(b)). It is believed that the single reflection mechanism can be realized only during the HB stage according to Equations (3)–(5). It should be noted that Equations (3)–(5) cannot be applied for the special case
$E_{\text{p}}\sim 100~\text{MeV}$
at the end of the HB stage (see Figure 2(b)). It is believed that the single reflection mechanism can be realized only during the HB stage according to Equations (3)–(5). It should be noted that Equations (3)–(5) cannot be applied for the special case
![]() $t_{\text{up}}=0T$
, which should be specially solved by the time-dependent models[Reference Wang, Shen, Zhang, Ji, Yu, Yi, Wang and Xu42].
$t_{\text{up}}=0T$
, which should be specially solved by the time-dependent models[Reference Wang, Shen, Zhang, Ji, Yu, Yi, Wang and Xu42].
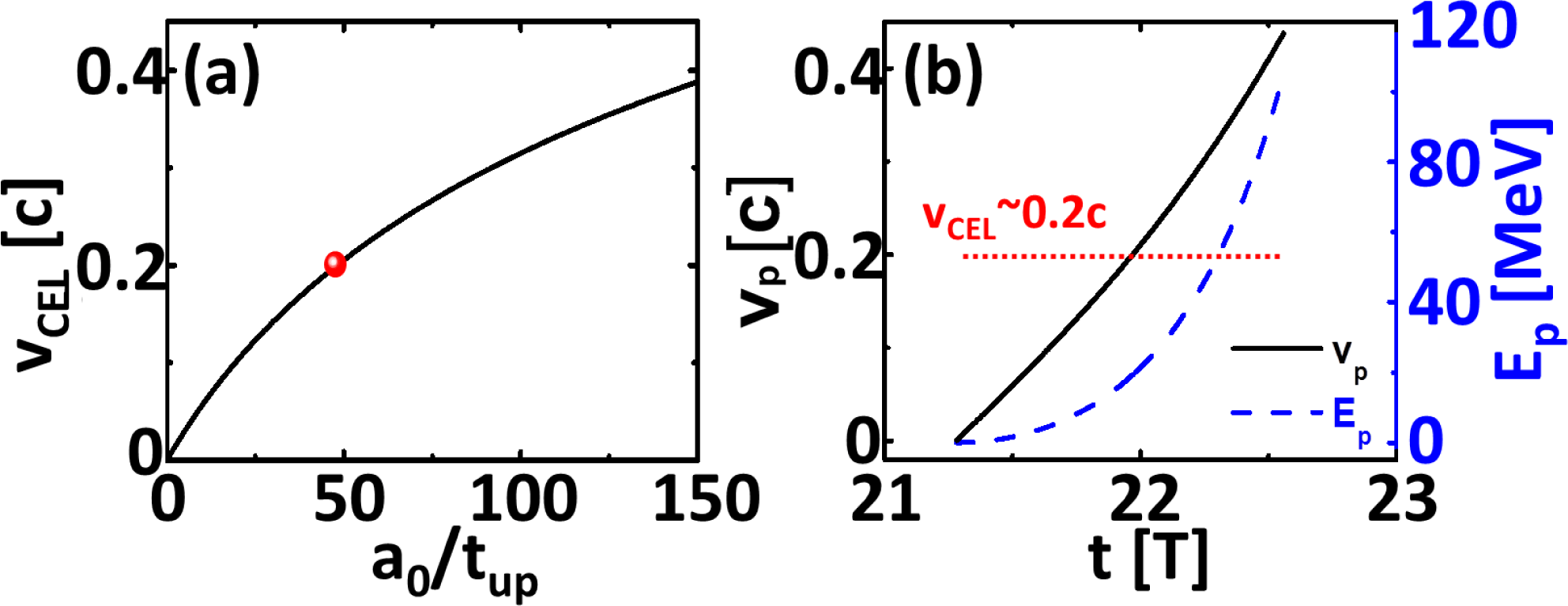
Figure 2. (a) Relation between the velocity of the compressed electron layer
![]() $v_{\text{CEL}}$
and the steepness of the laser front
$v_{\text{CEL}}$
and the steepness of the laser front
![]() $a_{0}/t_{\text{up}}$
according to Equation (5) for
$a_{0}/t_{\text{up}}$
according to Equation (5) for
![]() $n_{0}=50n_{\text{c}}$
. (b) Evolutions of the velocity,
$n_{0}=50n_{\text{c}}$
. (b) Evolutions of the velocity,
![]() $v_{\text{p}}$
(black solid line), and energy,
$v_{\text{p}}$
(black solid line), and energy,
![]() $E_{\text{p}}$
, of the proton layer during the HB stage.
$E_{\text{p}}$
, of the proton layer during the HB stage.
Two-dimensional particle-in-cell simulations are carried out to verify the theoretical expectations of the single reflection mechanism. A multilayer target is designed as shown in Figure 3. The hydrogen layer lies in the middle
![]() $(20.2~\unicode[STIX]{x03BC}\text{m}\leqslant x\leqslant 20.25~\unicode[STIX]{x03BC}\text{m})$
of the foil. The carbon layer lies in the regions
$(20.2~\unicode[STIX]{x03BC}\text{m}\leqslant x\leqslant 20.25~\unicode[STIX]{x03BC}\text{m})$
of the foil. The carbon layer lies in the regions
![]() $20~\unicode[STIX]{x03BC}\text{m}<x<20.2~\unicode[STIX]{x03BC}\text{m}$
and
$20~\unicode[STIX]{x03BC}\text{m}<x<20.2~\unicode[STIX]{x03BC}\text{m}$
and
![]() $20.25~\unicode[STIX]{x03BC}\text{m}<x<20.5~\unicode[STIX]{x03BC}\text{m}$
. The hydrogen and carbon atoms are assumed to be ionized to
$20.25~\unicode[STIX]{x03BC}\text{m}<x<20.5~\unicode[STIX]{x03BC}\text{m}$
. The hydrogen and carbon atoms are assumed to be ionized to
![]() $\text{H}^{+}$
and
$\text{H}^{+}$
and
![]() $\text{C}^{6+}$
before the main pulse is incident on the target. The electron density is
$\text{C}^{6+}$
before the main pulse is incident on the target. The electron density is
![]() $n_{0}=50n_{\text{c}}$
. The densities of the
$n_{0}=50n_{\text{c}}$
. The densities of the
![]() $\text{H}^{+}$
and
$\text{H}^{+}$
and
![]() $\text{C}^{6+}$
layers are
$\text{C}^{6+}$
layers are
![]() $n_{\text{p}}=50n_{\text{c}}$
and
$n_{\text{p}}=50n_{\text{c}}$
and
![]() $n_{\text{C}6+}=8.3n_{\text{c}}$
, respectively. The laser amplitude has a triangular profile in time (linear up-ramp
$n_{\text{C}6+}=8.3n_{\text{c}}$
, respectively. The laser amplitude has a triangular profile in time (linear up-ramp
![]() $t_{\text{up}}=2T$
and linear down-ramp
$t_{\text{up}}=2T$
and linear down-ramp
![]() $t_{\text{down}}=2T$
) with a peak value
$t_{\text{down}}=2T$
) with a peak value
![]() $a_{0}=96$
. The pulse waist is
$a_{0}=96$
. The pulse waist is
![]() $10~\unicode[STIX]{x03BC}\text{m}$
(FWHM). The simulation box size is 50
$10~\unicode[STIX]{x03BC}\text{m}$
(FWHM). The simulation box size is 50
![]() $~\unicode[STIX]{x03BC}\text{m}(x)\times 60~\unicode[STIX]{x03BC}\text{m}(y)$
, and the number of spatial grids is
$~\unicode[STIX]{x03BC}\text{m}(x)\times 60~\unicode[STIX]{x03BC}\text{m}(y)$
, and the number of spatial grids is
![]() $8000\times 9600$
. Each is filled with 20 macroelectrons and 20 macroprotons (or
$8000\times 9600$
. Each is filled with 20 macroelectrons and 20 macroprotons (or
![]() $\text{C}^{6+}$
ions).
$\text{C}^{6+}$
ions).

Figure 3. Distributions of (a)–(c) electric field
![]() $E_{y}$
, (d)–(f) electron density
$E_{y}$
, (d)–(f) electron density
![]() $n_{\text{e}}$
, (g)–(i)
$n_{\text{e}}$
, (g)–(i)
![]() $\text{C}^{6+}$
density and (j)–(l) proton density at
$\text{C}^{6+}$
density and (j)–(l) proton density at
![]() $t=21T$
(first row),
$t=21T$
(first row),
![]() $t=23T$
(second row) and
$t=23T$
(second row) and
![]() $t=25T$
(third row).
$t=25T$
(third row).
Figure 3 depicts the detailed progress from the HB to the LS stage as the CP laser irradiates the multilayer target. Initially, the electrons are stably pushed forward because there are no oscillating terms in the expression for the ponderomotive force for CP lasers[Reference Robinson, Zepf, Kar, Evans and Bellei19], as shown in Figure 3(d). The
![]() $\text{C}^{6+}$
ions lag behind the compressed electron layer initially. The charge separation field,
$\text{C}^{6+}$
ions lag behind the compressed electron layer initially. The charge separation field,
![]() $E_{x}$
, then becomes stronger with the increased distance between the electrons and the ions. Both
$E_{x}$
, then becomes stronger with the increased distance between the electrons and the ions. Both
![]() $\text{C}^{6+}$
ions and protons begin to be accelerated by
$\text{C}^{6+}$
ions and protons begin to be accelerated by
![]() $E_{x}$
. At
$E_{x}$
. At
![]() $t=23T$
, the compressed electron layer has reached the back of the target together with the proton layer, which is almost consistent with the theoretical assumption
$t=23T$
, the compressed electron layer has reached the back of the target together with the proton layer, which is almost consistent with the theoretical assumption
![]() $(t\sim 22.6T)$
according to Equation (4) (refer to Figures 3(e) and 3(k)). Based on Equation (1), the velocity of the proton layer (
$(t\sim 22.6T)$
according to Equation (4) (refer to Figures 3(e) and 3(k)). Based on Equation (1), the velocity of the proton layer (
![]() $v_{\text{p}}\sim 0.4c$
) is much higher than the velocity of the compressed electron layer
$v_{\text{p}}\sim 0.4c$
) is much higher than the velocity of the compressed electron layer
![]() $(v_{\text{CEL}}=\sim 0.2c)$
. This means the proton layer is accelerated and separated from the compressed electron layer in the LS stage. In addition, the peak decreases after
$(v_{\text{CEL}}=\sim 0.2c)$
. This means the proton layer is accelerated and separated from the compressed electron layer in the LS stage. In addition, the peak decreases after
![]() $t=22.6T$
. To maintain the balance between the laser pressure and charge separation forces again, the charge separation field,
$t=22.6T$
. To maintain the balance between the laser pressure and charge separation forces again, the charge separation field,
![]() $E_{x}$
, weakens. This is realized by the
$E_{x}$
, weakens. This is realized by the
![]() $\text{C}^{6+}$
ions reaching the compressed electron layer after
$\text{C}^{6+}$
ions reaching the compressed electron layer after
![]() $t=22.6T$
. Finally, two double layers are formed (see Figures 3(f)–3(l)). The
$t=22.6T$
. Finally, two double layers are formed (see Figures 3(f)–3(l)). The
![]() $\text{C}^{6+}$
–electron layer is heated and spreads extensively in space until the laser is totally reflected at
$\text{C}^{6+}$
–electron layer is heated and spreads extensively in space until the laser is totally reflected at
![]() $t=25T$
(see Figure 3(c)). In contrast, the proton–electron layer always moves ahead of the
$t=25T$
(see Figure 3(c)). In contrast, the proton–electron layer always moves ahead of the
![]() $\text{C}^{6+}$
–electron layer, maintaining a compact high-quality bunch, which verifies the theoretical model (Equations (3)–(5)).
$\text{C}^{6+}$
–electron layer, maintaining a compact high-quality bunch, which verifies the theoretical model (Equations (3)–(5)).

Figure 4. (a) Trajectories of the
![]() $\text{C}^{6+}$
layer (black square), the proton layer (blue triangle) and the interface between the laser and the compressed electron layer (red circle). Enlarged plots of the trajectories are shown in (b). (c) Phase space distributions of
$\text{C}^{6+}$
layer (black square), the proton layer (blue triangle) and the interface between the laser and the compressed electron layer (red circle). Enlarged plots of the trajectories are shown in (b). (c) Phase space distributions of
![]() $\text{C}^{6+}$
ions and protons at
$\text{C}^{6+}$
ions and protons at
![]() $t=25T$
. (d) Energetic spectra for the proton layer in different initial regions at
$t=25T$
. (d) Energetic spectra for the proton layer in different initial regions at
![]() $t=25T$
. Here, protons in the region
$t=25T$
. Here, protons in the region
![]() $-3~\unicode[STIX]{x03BC}\text{m}<y<3~\unicode[STIX]{x03BC}\text{m}$
are considered.
$-3~\unicode[STIX]{x03BC}\text{m}<y<3~\unicode[STIX]{x03BC}\text{m}$
are considered.
It should be noted that the proton layer has a greatly reduced probability of moving together with the laser–plasma interface in this case, as can clearly be seen from Figures 4(a) and 4(b). Initially, the laser interface moves forward and overtakes the proton layer at
![]() $t\sim 21.5T$
. At the end of the HB stage
$t\sim 21.5T$
. At the end of the HB stage
![]() $(t\sim 22.5T)$
, the proton layer overtakes the interface. After
$(t\sim 22.5T)$
, the proton layer overtakes the interface. After
![]() $t\sim 22.5T$
, the proton layer continues to move ahead of both the interface and
$t\sim 22.5T$
, the proton layer continues to move ahead of both the interface and
![]() $\text{C}^{6+}$
ions with a constant velocity, because the laser pulse is reflected by the
$\text{C}^{6+}$
ions with a constant velocity, because the laser pulse is reflected by the
![]() $\text{C}^{6+}$
–electron double layer. As depicted in Figure 4(a), the laser pulse is completely reflected away from the
$\text{C}^{6+}$
–electron double layer. As depicted in Figure 4(a), the laser pulse is completely reflected away from the
![]() $\text{C}^{6+}$
layer, and does not affect the proton layer. Here, the proton layer is just ‘slingshot-likely’ reflected once by the charge separation field only during the HB stage (refer to Figure 4(c)). Thus, instabilities of the laser–plasma interface are intrinsically reduced. A pure proton beam with a quasimonoenergetic spectrum
$\text{C}^{6+}$
layer, and does not affect the proton layer. Here, the proton layer is just ‘slingshot-likely’ reflected once by the charge separation field only during the HB stage (refer to Figure 4(c)). Thus, instabilities of the laser–plasma interface are intrinsically reduced. A pure proton beam with a quasimonoenergetic spectrum
![]() $({\sim}5\,\%)$
centered at
$({\sim}5\,\%)$
centered at
![]() ${\sim}100~\text{MeV}$
is finally generated at
${\sim}100~\text{MeV}$
is finally generated at
![]() $t=25T$
(see Figure 4(d)). From Figures 4(a) and 4(b), it can be found that the proton layer is separated from the carbon layers, and the carbon layer blocks the rear parts of the laser after
$t=25T$
(see Figure 4(d)). From Figures 4(a) and 4(b), it can be found that the proton layer is separated from the carbon layers, and the carbon layer blocks the rear parts of the laser after
![]() $t\sim 23T$
, so the spectrum of the proton beam does not change much after
$t\sim 23T$
, so the spectrum of the proton beam does not change much after
![]() $t\sim 23T$
.
$t\sim 23T$
.
The accelerations of the proton layers in the different regions are compared to verify the optimum conditions for the single reflection mechanism, shown in Figure 4(c). The center energy of the proton layer
![]() $(20.4~\unicode[STIX]{x03BC}\text{m}<x_{\text{initial}}<20.45~\unicode[STIX]{x03BC}\text{m})$
is only
$(20.4~\unicode[STIX]{x03BC}\text{m}<x_{\text{initial}}<20.45~\unicode[STIX]{x03BC}\text{m})$
is only
![]() $E_{\text{p}}=39~\text{MeV}$
. The main reason is that the proton layer, initially at rear part of the foil, is accelerated for a shorter time during the HB stage. In contrast, the proton layer initially at the front can be accelerated for a longer time to a higher maximum energy (137 MeV). However, the spectrum spread
$E_{\text{p}}=39~\text{MeV}$
. The main reason is that the proton layer, initially at rear part of the foil, is accelerated for a shorter time during the HB stage. In contrast, the proton layer initially at the front can be accelerated for a longer time to a higher maximum energy (137 MeV). However, the spectrum spread
![]() $({\sim}35\,\%)$
is much worse than the optimum case
$({\sim}35\,\%)$
is much worse than the optimum case
![]() $({\sim}5\,\%)$
. On the one hand, this is caused by the disturbed charge separation field when the falling part of the laser pulse is reflected. On the other hand, the spectrum spread is intrinsically best for the proton layer in the middle layer, as shown in Figure 1(e).
$({\sim}5\,\%)$
. On the one hand, this is caused by the disturbed charge separation field when the falling part of the laser pulse is reflected. On the other hand, the spectrum spread is intrinsically best for the proton layer in the middle layer, as shown in Figure 1(e).
3 Discussion
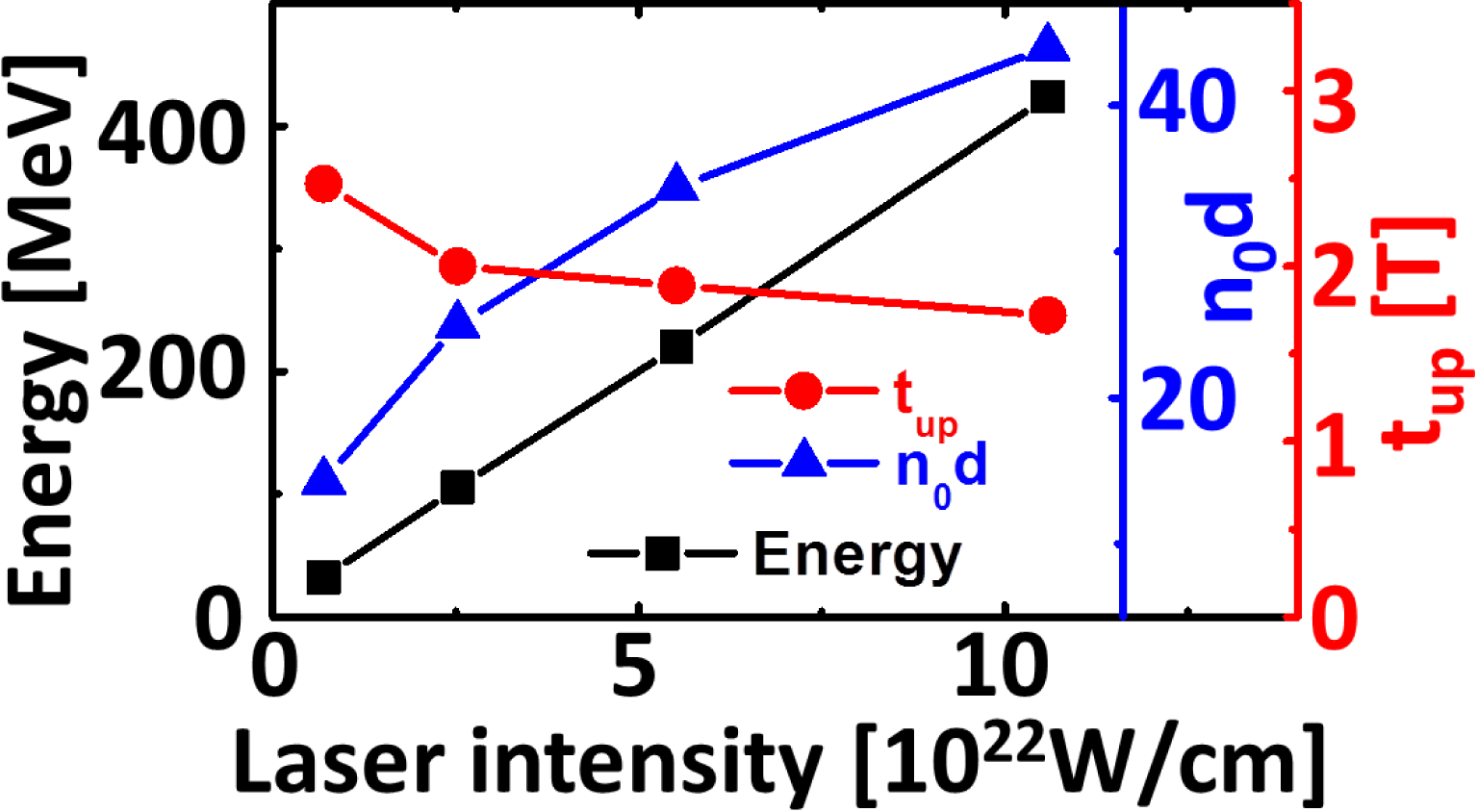
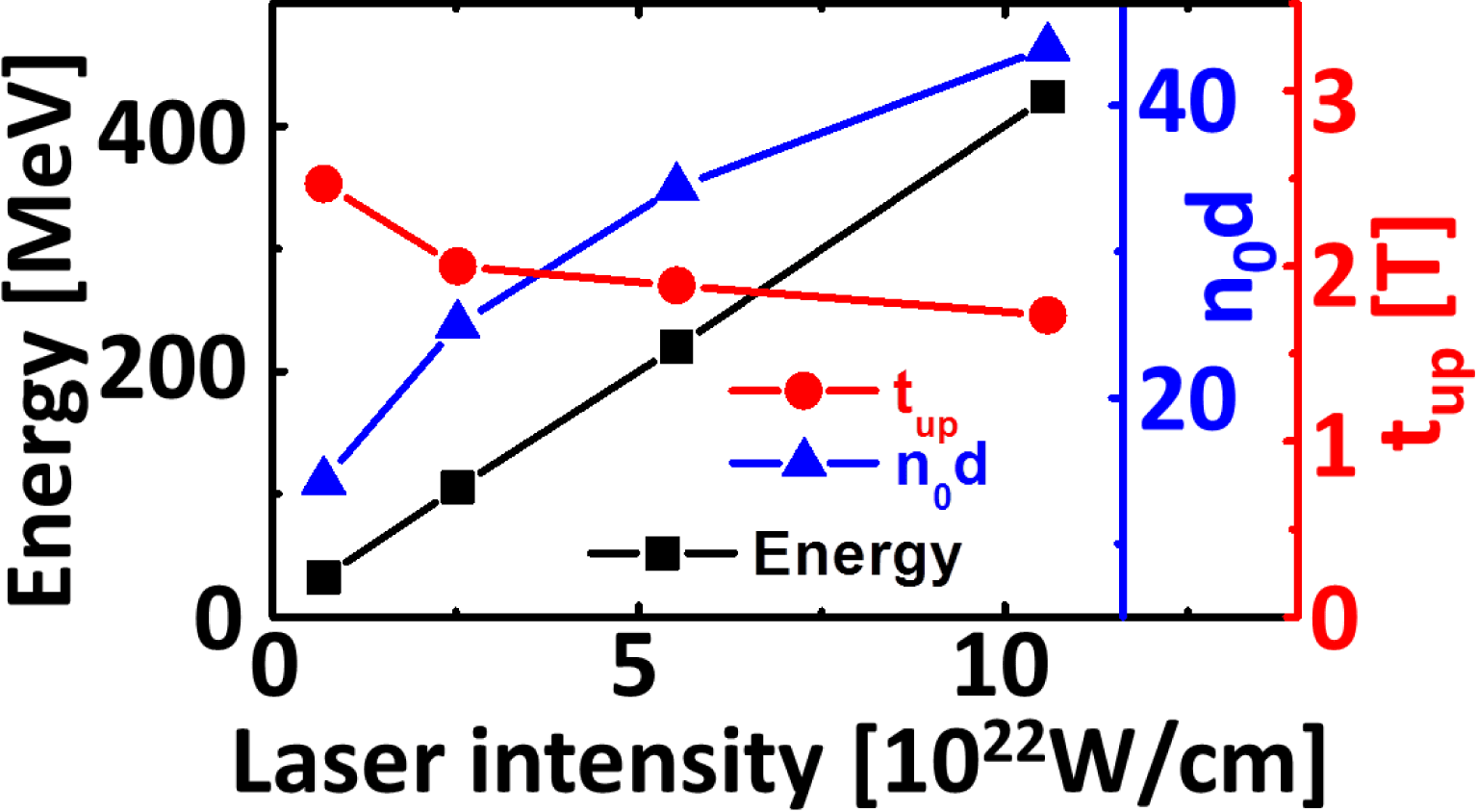
In the future, the development of 10 PW, and even 100 PW, laser systems[Reference Rus, Batysta, Čáp, Divoký, Fibrich, Griffiths, Haley, Havlíček, Hlavác, Hřebíček, Homer, Hříbek, Jand’ourek, Juha, Korn, Korouš, Košelja, Kozlová, Kramer, Krůs, Lagron, Limpouch, MacFarlane, Malý, Margarone, Matlas, Mindl, Moravec, Mocek, Nejdl, Novák, Olšovcová, Palatka, Perin, Pešlo, Polan, Prokůpek, Řídký, Rohlena, Růžička, Sawicka, Scholzová, Snopek, Strkula and Švéda43–Reference Bashinov, Gonoskov, Kim, Mourou and Sergeev46], and target fabrication[Reference Prencipe, Fuchs, Pascarelli, Schumacher, Stephens, Alexander, Briggs, Büscher, Cernaianu, Choukourov, De Marco, Erbe, Fassbender, Fiquet, Fitzsimmons, Gheorghiu, Hund, Huang, Harmand, Hartley, Irman, Kluge, Konopkova, Kraft, Kraus, Leca, Margarone, Metzkes, Nagai, Nazarov, Lutoslawski, Papp, Passoni, Pelka, Perin, Schulz, Smid, Spindloe, Steinke, Torchio, Vass, Wiste, Zaffino, Zeil, Tschentscher, Schramm and Cowan47, Reference Shavit, Ferber, Papeer, Schleifer, Botton, Zigler and Henis48] could lead to reaching laser intensities of the order of
![]() $10^{22}{-}10^{23}~\text{W}/\text{cm}^{2}$
, which can easily accelerate the proton layer to energies of hundreds of MeV (refer to Figure 5). For example,
$10^{22}{-}10^{23}~\text{W}/\text{cm}^{2}$
, which can easily accelerate the proton layer to energies of hundreds of MeV (refer to Figure 5). For example,
![]() ${\sim}400~\text{MeV}$
protons can be generated by a
${\sim}400~\text{MeV}$
protons can be generated by a
![]() ${\sim}10~\text{fs}$
, 250 J laser (
${\sim}10~\text{fs}$
, 250 J laser (
![]() ${\sim}50\,\%$
energy in a
${\sim}50\,\%$
energy in a
![]() $2\text{-}\unicode[STIX]{x03BC}\text{m}$
focal spot (FWHM), corresponding to a laser intensity of
$2\text{-}\unicode[STIX]{x03BC}\text{m}$
focal spot (FWHM), corresponding to a laser intensity of
![]() ${\sim}1\times 10^{23}~\text{W}/\text{cm}^{2}$
) irradiating the multilayer foil (areal density
${\sim}1\times 10^{23}~\text{W}/\text{cm}^{2}$
) irradiating the multilayer foil (areal density
![]() ${\sim}44n_{\text{c}}\unicode[STIX]{x1D706}$
). In proton cancer therapy, monoenergetic proton beams with a tunable energy of 50–250 MeV are required to target tumor locations, which can be realized by the single reflection mechanism proposed in this paper. It should be noted that optical components based on plasmas can provide a solution to the manipulation of the polarization state of the sharp-front laser[Reference Weng, Zhao, Sheng, Yu, Luan, Chen, Yu, Murakami, Mori and Zhang49], as well as its temporal profile[Reference Bin, Ma, Wang, Streeter, Kreuzer, Kiefer, Yeung, Cousens, Foster, Dromey, Yan, Ramis, Meyer-ter-Vehn, Zepf and Schreiber26, Reference Wang, Lin, Sheng, Liu, Zhao, Guo, Lu, He, Chen and Yan50, Reference Ji, Shen, Zhang, Wang, Jin, Xia, Wen, Wang, Xu and Yu51]. In fact, Equations (3)–(5) are general, helping us to find other optimum parameters of the laser and target under the present lab conditions.
${\sim}44n_{\text{c}}\unicode[STIX]{x1D706}$
). In proton cancer therapy, monoenergetic proton beams with a tunable energy of 50–250 MeV are required to target tumor locations, which can be realized by the single reflection mechanism proposed in this paper. It should be noted that optical components based on plasmas can provide a solution to the manipulation of the polarization state of the sharp-front laser[Reference Weng, Zhao, Sheng, Yu, Luan, Chen, Yu, Murakami, Mori and Zhang49], as well as its temporal profile[Reference Bin, Ma, Wang, Streeter, Kreuzer, Kiefer, Yeung, Cousens, Foster, Dromey, Yan, Ramis, Meyer-ter-Vehn, Zepf and Schreiber26, Reference Wang, Lin, Sheng, Liu, Zhao, Guo, Lu, He, Chen and Yan50, Reference Ji, Shen, Zhang, Wang, Jin, Xia, Wen, Wang, Xu and Yu51]. In fact, Equations (3)–(5) are general, helping us to find other optimum parameters of the laser and target under the present lab conditions.
It should be noted that the efficiency of proton acceleration only in the HB stage seems lower, compared to the previous PRA process including the LS stage[Reference Yan, Lin, Sheng, Guo, Liu, Lu, Fang and Chen18, Reference Klimo, Psikal, Limpouch and Tikhonchuk20, Reference Qiao, Zepf, Borghesi and Geissler21, Reference Wang, Shen and Xu32]. In previous works, the laser interacts with the proton beam for a longer time, so that a higher beam energy (GeV, even 10 GeV) and higher accelerating efficiency can be obtained. Especially in the LS stage, the efficiency can be near 100%. However, such good acceleration does not occur in realistic experiments. The main reason for this is that serious multidimensional instabilities develop during the laser–plasma interaction. These instabilities may arise due to intrinsic turbulence as the laser irradiates the interface of the plasma, or the unpredictable irregular shapes of the target surface and laser front. So the maximum energy of the proton beam is only
![]() ${\sim}100~\text{MeV}$
in the present experiments. Also, the spectra are not as good as what the simulations predict. In this paper, we wanted simply to use a sharp-front laser irradiating a triple-layer target to reduce the interaction time between the laser and the proton beam. In this way, the instabilities can be reduced to a certain extent, although the acceleration efficiency is lower. It is believed that proton beams with monoenergetic spectra of hundreds of MeV can potentially be applied in proton therapy.
${\sim}100~\text{MeV}$
in the present experiments. Also, the spectra are not as good as what the simulations predict. In this paper, we wanted simply to use a sharp-front laser irradiating a triple-layer target to reduce the interaction time between the laser and the proton beam. In this way, the instabilities can be reduced to a certain extent, although the acceleration efficiency is lower. It is believed that proton beams with monoenergetic spectra of hundreds of MeV can potentially be applied in proton therapy.
4 Conclusion
In conclusion, a proton layer with pure spectra can be successfully accelerated once to hundreds of MeV only during the HB stage. The proton beam has a reduced probability of moving together with the laser–plasma interface during the entire acceleration process. In this manner, some multidimensional instabilities, such as Rayleigh–Taylor-like instability and Weibel-like instability, can be reduced to a certain extent. This provides a feasible method to realize proton therapy and other applications using multi-PW laser system in the future.
Acknowledgements
This study was supported by the National Natural Science Foundation of China (No. 11575274), Strategic Priority Research Program of the Chinese Academy of Sciences (No. XDB16010600), and Ministry of Science and Technology of the People’s Republic of China (Nos. 2016YFA0401102 and 2018YFA0404803).