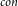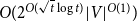1. Introduction
This paper studies the minimum connected-k-subgraph cover problem (MinCkSC) and its connected version (MinCkSC
![]() $_{con}$
).
$_{con}$
).
The MinCkSC problem was proposed because of a security consideration in a wireless sensor network (WSN, see e.g. Zhang et al. (Reference Zhang, Shi and Zhang2014): if an attacker knows at least k related information fragments in a WSN, then he can decode the full information; to protect information, we have to select some protected vertices such that each connected group on k vertices has at least one protected vertex; since protected vertices cost more, it is desired that the number of protected vertices is as small as possible. In the language of graph theory, given a graph
![]() $G=(V,E)$
and an integer k, the goal of MinCkSC is to find a minimum vertex subset C such that each connected component of
$G=(V,E)$
and an integer k, the goal of MinCkSC is to find a minimum vertex subset C such that each connected component of
![]() $G-C$
contains at most
$G-C$
contains at most
![]() $k-1$
vertices. The MinCkSC problem, under the name of the minimum k-vertex separator problem (MinkVS), was also studied for the sake of parallel computing by Guruswami et al. (2017), Lee (Reference Lee2017).
$k-1$
vertices. The MinCkSC problem, under the name of the minimum k-vertex separator problem (MinkVS), was also studied for the sake of parallel computing by Guruswami et al. (2017), Lee (Reference Lee2017).
If furthermore it is required that the connected-k-subgraph cover C induces a connected subgraph, then the problem is denoted as MinCkSC
![]() $_{con}$
. Considering connectivity in this problem is because of information sharing issues in a WSN, see e.g. Li et al. (Reference Li, Zhang and Huang2016).
$_{con}$
. Considering connectivity in this problem is because of information sharing issues in a WSN, see e.g. Li et al. (Reference Li, Zhang and Huang2016).
In this paper, we study approximation algorithms and FPT algorithms for MinCkSC and MinCkSC
![]() $_{con}$
on H-minor-free graphs, where
$_{con}$
on H-minor-free graphs, where
![]() $|V(H)|$
is upper bounded by a constant.
$|V(H)|$
is upper bounded by a constant.
1.1 Related works
Note that there is a problem which is closely related with MinCkSC: the minimum k-path vertex cover problem (MinVCP
![]() $_k$
). A vertex set C is called a VCP
$_k$
). A vertex set C is called a VCP
![]() $_k$
set if every path on k vertices has at least one vertex in C. The MinVCP
$_k$
set if every path on k vertices has at least one vertex in C. The MinVCP
![]() $_k$
problem was first proposed by Novotný (Reference Novotný2010) also because of a consideration on the security of WSNs.
$_k$
problem was first proposed by Novotný (Reference Novotný2010) also because of a consideration on the security of WSNs.
For
![]() $k=2,3$
, MinCkSC and MinVCP
$k=2,3$
, MinCkSC and MinVCP
![]() $_k$
coincide. In particular, both MinC2SC and MinVCP
$_k$
coincide. In particular, both MinC2SC and MinVCP
![]() $_2$
are the classic minimum vertex cover problem (MinVC) in Bar-Yehuda et al. (1981); Hochbaum (Reference Hochbaum1982), which still receives a lot of attention in recent years in Bar-Yehuda et al. (Reference Bar-Yehuda, Censor-Hillel and Schwartzman2017); Cabello et al. (2015); Cai et al. (Reference Cai, Li, Hou and Wang2019); Khot et al. (Reference Khot, Minzer and Safra2018); Pourhassan et al. (Reference Pourhassan, Shi and Neumann2019). Since MinCkSC and MinVCP
$_2$
are the classic minimum vertex cover problem (MinVC) in Bar-Yehuda et al. (1981); Hochbaum (Reference Hochbaum1982), which still receives a lot of attention in recent years in Bar-Yehuda et al. (Reference Bar-Yehuda, Censor-Hillel and Schwartzman2017); Cabello et al. (2015); Cai et al. (Reference Cai, Li, Hou and Wang2019); Khot et al. (Reference Khot, Minzer and Safra2018); Pourhassan et al. (Reference Pourhassan, Shi and Neumann2019). Since MinCkSC and MinVCP
![]() $_k$
and their connected variants are all NP-hard for
$_k$
and their connected variants are all NP-hard for
![]() $k\geq 2$
, most researches with theoretical guarantees focus on approximation algorithms and FPT algorithms.
$k\geq 2$
, most researches with theoretical guarantees focus on approximation algorithms and FPT algorithms.
In the following, we distinguish the weighted version and the cardinality version of these problems by whether using “W” in their abbreviations, such as MinWCkSC denotes the weighted version while MinCkSC denotes the cardinality version.
Note that both MinWCkSC and MinWVCP
![]() $_k$
are special cases of the minimum weight set cover problem (MinWSC) by Liu et al. (Reference Liu, Zhang and Huang2020); Zhang et al. (Reference Zhang, Shi and Zhang2014), so they admit k-approximation. Improvement on the ratio needs deeper exploration of graph structures. Compared with the extensive studies on the MinVCP
$_k$
are special cases of the minimum weight set cover problem (MinWSC) by Liu et al. (Reference Liu, Zhang and Huang2020); Zhang et al. (Reference Zhang, Shi and Zhang2014), so they admit k-approximation. Improvement on the ratio needs deeper exploration of graph structures. Compared with the extensive studies on the MinVCP
![]() $_k$
problem, see e.g. Bresar et al. (2011); Cabello et al. (2015); Kardoš et al. (Reference Kardoš, Katrenič and Schiermeyer2011); Ran et al. (Reference Ran, Zhang, Huang, Li and Du2019); Tu et al. (2011); Tu et al. (2011); Zhang et al. (Reference Zhang, Chen, Chen and Lin2018); Zhang et al. (Reference Zhang, Li, Shi, Nie and Zhu2017), studies on MinCkSC are relatively less. The terminology MinWCkSC was proposed in Zhang et al. (Reference Zhang, Shi and Zhang2014), and a
$_k$
problem, see e.g. Bresar et al. (2011); Cabello et al. (2015); Kardoš et al. (Reference Kardoš, Katrenič and Schiermeyer2011); Ran et al. (Reference Ran, Zhang, Huang, Li and Du2019); Tu et al. (2011); Tu et al. (2011); Zhang et al. (Reference Zhang, Chen, Chen and Lin2018); Zhang et al. (Reference Zhang, Li, Shi, Nie and Zhu2017), studies on MinCkSC are relatively less. The terminology MinWCkSC was proposed in Zhang et al. (Reference Zhang, Shi and Zhang2014), and a
![]() $(k-1)$
-approximation algorithm was designed on graphs with girth at least k. Recently, Liu et al. (Reference Liu, Zhang and Huang2020) relaxed the girth requirement from k to
$(k-1)$
-approximation algorithm was designed on graphs with girth at least k. Recently, Liu et al. (Reference Liu, Zhang and Huang2020) relaxed the girth requirement from k to
![]() $2k/3$
. For MinCkSC (the cardinality version), Lee (Reference Lee2017) presented an
$2k/3$
. For MinCkSC (the cardinality version), Lee (Reference Lee2017) presented an
![]() $O(\log k)$
-approximation algorithm which runs in time
$O(\log k)$
-approximation algorithm which runs in time
![]() $2^{O(k^3 \log k)}n^2 \log n + n^{O(1)}$
. For a more general class of problems called
$2^{O(k^3 \log k)}n^2 \log n + n^{O(1)}$
. For a more general class of problems called
![]() $\mathcal H$
-free node-deletion problem which includes both MinVCP
$\mathcal H$
-free node-deletion problem which includes both MinVCP
![]() $_k$
and MinCkSC, Li et al. (Reference Li, Shi and Huang2018) present a PTAS on disk graphs. Gupta et al. (Reference Gupta, Lee, Li and Manurangsi2019) presented a PTAS for MinCkSC on H-minor-free graphs, using a bidimensionality method. Li et al. (Reference Li, Zhang and Huang2016) were the first to study the connectivity version of the problem, and provided a k-approximation algorithm for MinCkSC
$_k$
and MinCkSC, Li et al. (Reference Li, Shi and Huang2018) present a PTAS on disk graphs. Gupta et al. (Reference Gupta, Lee, Li and Manurangsi2019) presented a PTAS for MinCkSC on H-minor-free graphs, using a bidimensionality method. Li et al. (Reference Li, Zhang and Huang2016) were the first to study the connectivity version of the problem, and provided a k-approximation algorithm for MinCkSC
![]() $_{con}$
.
$_{con}$
.
Parameterized algorithms for MinVCP
![]() $_k$
mainly focus on small k. There are a lot of works on MinVCP
$_k$
mainly focus on small k. There are a lot of works on MinVCP
![]() $_3$
, see e.g. Chang et al. (Reference Chang, Chen, Hung, Rossmanith and Su2016); Katrenič (Reference Katrenič2016); Tu (Reference Tu2015); Xiao et al. (2017) (recall that MinVCP
$_3$
, see e.g. Chang et al. (Reference Chang, Chen, Hung, Rossmanith and Su2016); Katrenič (Reference Katrenič2016); Tu (Reference Tu2015); Xiao et al. (2017) (recall that MinVCP
![]() $_3$
coincides with MinC3SC). Currently, the best known running time of FPT algorithms for MinVC and MinVCP
$_3$
coincides with MinC3SC). Currently, the best known running time of FPT algorithms for MinVC and MinVCP
![]() $_3$
in terms of solution size t are
$_3$
in terms of solution size t are
![]() $O^*(1.2738^t)$
by Chen et al. (Reference Chen, Kanj and Xia2010) and
$O^*(1.2738^t)$
by Chen et al. (Reference Chen, Kanj and Xia2010) and
![]() $O^*(1.713^t)$
by Tsur (Reference Tsur2019), respectively. For the connected version with
$O^*(1.713^t)$
by Tsur (Reference Tsur2019), respectively. For the connected version with
![]() $k=2$
, Cygan (Reference Cygan2012) presented an FPT algorithm for MinCVC with running time
$k=2$
, Cygan (Reference Cygan2012) presented an FPT algorithm for MinCVC with running time
![]() $O(2^t n^{O(1)})$
. Bai et al. (Reference Bai, Tu and Shi2019) studied parameterized algorithm in terms of treewidth
$O(2^t n^{O(1)})$
. Bai et al. (Reference Bai, Tu and Shi2019) studied parameterized algorithm in terms of treewidth
![]() $\omega$
, presenting a
$\omega$
, presenting a
![]() $3^\omega n^{O(1)}$
-time algorithm for MinVCP
$3^\omega n^{O(1)}$
-time algorithm for MinVCP
![]() $_3$
and a
$_3$
and a
![]() $4^\omega n^{O(1)}$
-time randomized algorithm for MinCVCP
$4^\omega n^{O(1)}$
-time randomized algorithm for MinCVCP
![]() $_3$
. Parameterized algorithms for MinVCP
$_3$
. Parameterized algorithms for MinVCP
![]() $_k$
with
$_k$
with
![]() $k=4,5,6,7$
are emerging recently in Červený et al. (2019); Tsur (Reference Tsur2021, Reference Tsur2019); Tu et al. (2016), but works on general k are rare. Note that MinVCP
$k=4,5,6,7$
are emerging recently in Červený et al. (2019); Tsur (Reference Tsur2021, Reference Tsur2019); Tu et al. (2016), but works on general k are rare. Note that MinVCP
![]() $_k$
and MinCkSC can be considered as special cases of a so-called graph modification problem studied by Cai (Reference Cai1996), which has been shown to have an
$_k$
and MinCkSC can be considered as special cases of a so-called graph modification problem studied by Cai (Reference Cai1996), which has been shown to have an
![]() $O^*(k^t)$
time FPT algorithm. To improve the time complexity, one has to explore graph structures of these problems. As far as we know, there is no study on parameterized algorithm for MinCkSC
$O^*(k^t)$
time FPT algorithm. To improve the time complexity, one has to explore graph structures of these problems. As far as we know, there is no study on parameterized algorithm for MinCkSC
![]() $_{con}$
or MinCVCP
$_{con}$
or MinCVCP
![]() $_k$
for general k.
$_k$
for general k.
1.2 Contribution
In this paper, we study MinCkSC and MinCkSC
![]() $_{con}$
for general constant k. The contributions are summarized as follows.
$_{con}$
for general constant k. The contributions are summarized as follows.
-
(1) Using a local search method, we present a simple but effective approximation algorithm for MinCkSC on H-minor-free graphs, where the number of vertices in H is upper bounded by a constant, achieving approximation ratio
 $(1+\varepsilon)$
in time
$(1+\varepsilon)$
in time
 $n^{O(1/\varepsilon^2)}$
, where
$n^{O(1/\varepsilon^2)}$
, where
 $\varepsilon$
is an arbitrary constant in (0,1).
$\varepsilon$
is an arbitrary constant in (0,1). -
(2) We present an
 $O(\omega(2(k-1)\omega)^{3\omega})|V|$
-time algorithm for MinCkSC
$O(\omega(2(k-1)\omega)^{3\omega})|V|$
-time algorithm for MinCkSC
 $_{con}$
, where
$_{con}$
, where
 $\omega$
is the treewidth of the graph. The algorithm is a dynamic programming, based on a nice tree-decomposition. Note that connectivity is a global feature. The challenge of designing the algorithm lies in how to extend partial solutions step by step, keeping enough information to guarantee global connectivity, while at the same time limiting the table size of the dynamic programming.
$\omega$
is the treewidth of the graph. The algorithm is a dynamic programming, based on a nice tree-decomposition. Note that connectivity is a global feature. The challenge of designing the algorithm lies in how to extend partial solutions step by step, keeping enough information to guarantee global connectivity, while at the same time limiting the table size of the dynamic programming. -
(3) Based on the above result, we prove that MinCkSC
 $_{con}$
has an
$_{con}$
has an
 $O\Big(\sqrt{t}^{O(\sqrt{t})}|V|\Big)$
-time algorithm on H-minor-free graphs, where t is an upper bound for the solution size.
$O\Big(\sqrt{t}^{O(\sqrt{t})}|V|\Big)$
-time algorithm on H-minor-free graphs, where t is an upper bound for the solution size.
The remaining parts of this paper are organized as follows. A PTAS for MinCkSC is presented in Section 2. Section 3 designs a dynamic programming for MinCkSC
![]() $_{con}$
whose running time depends on the treewidth. Section 4 obtains an FPT algorithm for MinCkSC
$_{con}$
whose running time depends on the treewidth. Section 4 obtains an FPT algorithm for MinCkSC
![]() $_{con}$
on H-minor-free graphs. And Section 5 concludes the paper with some discussion on further work.
$_{con}$
on H-minor-free graphs. And Section 5 concludes the paper with some discussion on further work.
2. Approximation Algorithm for MinC
 $\boldsymbol{k}$
SC
$\boldsymbol{k}$
SC
Before presenting the PTAS for MinCkSC, we introduce some terminologies and give some preliminary results.
Definition 1. If graph H is obtained from G via vertex deletions, edge deletions, and edge contractions, then H is a minor of G. If H is not a minor of G, then G is called an H-minor-free graph.
Definition 2. Let
![]() $\mathcal S=\{S_1,\ldots,S_q\}$
be a collection of subsets of V(G) such that
$\mathcal S=\{S_1,\ldots,S_q\}$
be a collection of subsets of V(G) such that
![]() $V(G)=S_1\cup\cdots\cup S_q$
. A vertex
$V(G)=S_1\cup\cdots\cup S_q$
. A vertex
![]() $v\in S_i$
is said to be a boundary vertex of
$v\in S_i$
is said to be a boundary vertex of
![]() $S_i$
if v also belongs to some
$S_i$
if v also belongs to some
![]() $S_j$
with
$S_j$
with
![]() $j\neq i$
. Denote by
$j\neq i$
. Denote by
![]() $B(S_i)$
the set of all boundary vertices of
$B(S_i)$
the set of all boundary vertices of
![]() $S_i$
, and
$S_i$
, and
![]() $int(S_i)=S_i\setminus B(S_i)$
the set of interior vertices of
$int(S_i)=S_i\setminus B(S_i)$
the set of interior vertices of
![]() $S_i$
. Note that
$S_i$
. Note that
![]() $int(S_i)$
is exactly the set of vertices in
$int(S_i)$
is exactly the set of vertices in
![]() $S_i$
whose neighbors are completely contained in
$S_i$
whose neighbors are completely contained in
![]() $S_i$
.
$S_i$
.
Definition 3. For a graph
![]() $G=(V,E)$
and a number
$G=(V,E)$
and a number
![]() $r>0$
, a collection
$r>0$
, a collection
![]() $\mathcal{S}=\{S_1,S_2,\ldots,S_q\}$
with
$\mathcal{S}=\{S_1,S_2,\ldots,S_q\}$
with
![]() $V(G)=S_1\cup\cdots\cup S_q$
is called an r-division of G if it satisfies the following properties:
$V(G)=S_1\cup\cdots\cup S_q$
is called an r-division of G if it satisfies the following properties:
-
(a) every edge of G is completely contained in some induced subgraph
 $G[S_i]$
;
$G[S_i]$
; -
(b)
 $|S_i|\leq r$
for every
$|S_i|\leq r$
for every
 $i=1,\ldots,q$
;
$i=1,\ldots,q$
; -
(c)
 $q\leq c_{\mathcal{S}}\frac{|V(G)|}{r}$
and
$q\leq c_{\mathcal{S}}\frac{|V(G)|}{r}$
and
 $\sum\limits_{i=1}^q|B(S_i)|\leq c_{\mathcal{S}}\frac{|V(G)|}{\sqrt{r}}$
, where
$\sum\limits_{i=1}^q|B(S_i)|\leq c_{\mathcal{S}}\frac{|V(G)|}{\sqrt{r}}$
, where
 $c_{\mathcal{S}}$
is a number related to the structure of the graph, but is independent of
$c_{\mathcal{S}}$
is a number related to the structure of the graph, but is independent of
 $|V(G)|$
and r.
$|V(G)|$
and r.
According to Alon et al. (Reference Alon, Seymour and Thomas1990) and Le et al. (2020), the following result holds.
Lemma 4. Any H-minor-free graph G has an r-division
![]() $\mathcal S$
with
$\mathcal S$
with
![]() $c_{\mathcal{S}}=$
poly
$c_{\mathcal{S}}=$
poly
![]() $(|V(H)|)$
.
$(|V(H)|)$
.
For an H-minor-free graph, which is a generalization of planar graph, if
![]() $|V(H)|$
has a constant upper bound, which is the case in this paper, then
$|V(H)|$
has a constant upper bound, which is the case in this paper, then
![]() $c_{\mathcal S}$
is a constant. Note that
$c_{\mathcal S}$
is a constant. Note that
![]() $c_{\mathcal S}$
can be computed in polynomial time by Cabello et al. (2015).
$c_{\mathcal S}$
can be computed in polynomial time by Cabello et al. (2015).
Algorithm 1 Local Search Algorithm for MinCkSC (LS-MinCkSC).

Theorem. Algorithm 1 runs in time
![]() $n^{O(\frac{1}{\varepsilon^2})}$
for an H-minor-free graph, where
$n^{O(\frac{1}{\varepsilon^2})}$
for an H-minor-free graph, where
![]() $|V(H)|$
is upper bounded by a constant.
$|V(H)|$
is upper bounded by a constant.
Proof. Since in each iteration, the size of current solution will be reduced by at least 1, the while-loop will be executed at most n rounds. By the assumption that
![]() $|V(H)|$
is upper bounded by a constant, the number
$|V(H)|$
is upper bounded by a constant, the number
![]() $c_{\mathcal S}$
is a constant. So, each round of the while-loop takes
$c_{\mathcal S}$
is a constant. So, each round of the while-loop takes
![]() $n^{O(r)}$
time to enumerate F’ and F” whose sizes are upper bounded by r, and the total time complexity is
$n^{O(r)}$
time to enumerate F’ and F” whose sizes are upper bounded by r, and the total time complexity is
![]() $n^{O(\frac{1}{\varepsilon^2})}$
. The lemma is proved.
$n^{O(\frac{1}{\varepsilon^2})}$
. The lemma is proved.
The following theorem analyzes the performance ratio of our algorithm. Let C denote the output solution of Algorithm 1,
![]() $C^*$
denote an optimal solution. The idea of the analysis is to construct an auxiliary graph
$C^*$
denote an optimal solution. The idea of the analysis is to construct an auxiliary graph
![]() $G_{a}$
and use its division to construct a feasible solution C’ such that
$G_{a}$
and use its division to construct a feasible solution C’ such that
![]() $|C|\leq|C'|\leq(1+\varepsilon)|C^*|$
.
$|C|\leq|C'|\leq(1+\varepsilon)|C^*|$
.
Theorem For any
![]() $\varepsilon\in(0,1)$
, Algorithm 1 outputs a
$\varepsilon\in(0,1)$
, Algorithm 1 outputs a
![]() $(1+\varepsilon)$
-approximate solution for MinCkSC on H-minor-free graphs, where
$(1+\varepsilon)$
-approximate solution for MinCkSC on H-minor-free graphs, where
![]() $|V(H)|$
is upper bounded by a constant.
$|V(H)|$
is upper bounded by a constant.
Proof We construct an auxiliary graph
![]() $G_{a}$
in the following way: first, let
$G_{a}$
in the following way: first, let
![]() $G_1$
be the graph obtained from
$G_1$
be the graph obtained from
![]() $G-(C\cap C^*)$
by removing all those connected components of cardinality smaller than k; then let
$G-(C\cap C^*)$
by removing all those connected components of cardinality smaller than k; then let
![]() $G_a=G[V(G_1)\cup(C\cap C^*)]$
.
$G_a=G[V(G_1)\cup(C\cap C^*)]$
.
Claim 1
![]() $|V(G_a)|\leq k|C^*|$
.
$|V(G_a)|\leq k|C^*|$
.
Let
![]() $C(G_1)$
be a connected component of
$C(G_1)$
be a connected component of
![]() $G_1$
. Then,
$G_1$
. Then,
![]() $|V(C(G_1))|\geq k$
. Since every connected component of
$|V(C(G_1))|\geq k$
. Since every connected component of
![]() $G-C$
has cardinality at most
$G-C$
has cardinality at most
![]() $k-1$
, and because
$k-1$
, and because
![]() $V(G_1)\cap (C\cap C^*)=\emptyset$
, we have
$V(G_1)\cap (C\cap C^*)=\emptyset$
, we have
![]() $V(C(G_1)\cap(C\setminus C^*)\neq\emptyset$
. Similarly,
$V(C(G_1)\cap(C\setminus C^*)\neq\emptyset$
. Similarly,
![]() $V(C(G_1))\cap(C^*\setminus C)\neq\emptyset$
. Let
$V(C(G_1))\cap(C^*\setminus C)\neq\emptyset$
. Let
![]() $C'(G_1)=C(G_1)-(V(C(G_1))\cap(C^*\setminus C))$
, then
$C'(G_1)=C(G_1)-(V(C(G_1))\cap(C^*\setminus C))$
, then
![]() $C'(G_1)\subseteq G-C^*$
, and thus,
$C'(G_1)\subseteq G-C^*$
, and thus,
![]() $ |V(C'(G_1))|\leq k-1$
. It follows that
$ |V(C'(G_1))|\leq k-1$
. It follows that
 \begin{align*}|V(G_1)|&=\sum\limits_{C(G_1):~\mbox{component of}~G_1}|V(C(G_1))|\\&\leq(k-1)\omega (G_1)+\sum\limits_{C(G_1):~\mbox{component of}~G_1}|V(C(G_1))\cap(C^*\setminus C)|\\&\leq(k-1)\omega(G_1)+|C^*\setminus C|,\end{align*}
\begin{align*}|V(G_1)|&=\sum\limits_{C(G_1):~\mbox{component of}~G_1}|V(C(G_1))|\\&\leq(k-1)\omega (G_1)+\sum\limits_{C(G_1):~\mbox{component of}~G_1}|V(C(G_1))\cap(C^*\setminus C)|\\&\leq(k-1)\omega(G_1)+|C^*\setminus C|,\end{align*}
where
![]() $\omega(G_1)$
is the number of connected components of
$\omega(G_1)$
is the number of connected components of
![]() $G_1$
. Since
$G_1$
. Since
![]() $V(C(G_1))\cap(C^*\setminus C)\neq\emptyset$
holds for any connected component
$V(C(G_1))\cap(C^*\setminus C)\neq\emptyset$
holds for any connected component
![]() $C(G_1)$
of
$C(G_1)$
of
![]() $G_1$
, we have
$G_1$
, we have
![]() $\omega (G_1)\leq|C^*\setminus C|$
. Hence,
$\omega (G_1)\leq|C^*\setminus C|$
. Hence,
It follows that
Claim 1 is proved.
Obviously,
![]() $G_{a}$
is also H-minor-free. Let
$G_{a}$
is also H-minor-free. Let
![]() $\{S_1,S_2,\ldots,S_k\}$
be an r-division of
$\{S_1,S_2,\ldots,S_k\}$
be an r-division of
![]() $G_{a}$
and let
$G_{a}$
and let
Claim 2: Every
![]() $C'_i$
is a CkSC of G.
$C'_i$
is a CkSC of G.
We prove the claim by contradiction. Suppose that there exists a connected-k-vertex subgraph G’ of G with
![]() $V(G')\cap C'_i=\emptyset$
. Since both C and
$V(G')\cap C'_i=\emptyset$
. Since both C and
![]() $C^*$
are CkSC of G, we have
$C^*$
are CkSC of G, we have
![]() $V(G')\cap C\neq\emptyset$
and
$V(G')\cap C\neq\emptyset$
and
![]() $V(G')\cap C^*\neq\emptyset$
. Suppose
$V(G')\cap C^*\neq\emptyset$
. Suppose
![]() $u\in V(G')\cap C$
and
$u\in V(G')\cap C$
and
![]() $v\in V(G')\cap C^*$
, because
$v\in V(G')\cap C^*$
, because
![]() $(C\cap C^*)\subseteq C'_i$
and
$(C\cap C^*)\subseteq C'_i$
and
![]() $B(S_i)\subseteq C'_i$
, we must have
$B(S_i)\subseteq C'_i$
, we must have
![]() $u\in \big(C\cap int(S_i)\big)\setminus C^*$
and
$u\in \big(C\cap int(S_i)\big)\setminus C^*$
and
![]() $v\in C^*\setminus(C\cup S_i)$
. Since G’ is a connected subgraph of G, there is a path
$v\in C^*\setminus(C\cup S_i)$
. Since G’ is a connected subgraph of G, there is a path
![]() $P=(u,v_1,\ldots,v_t,v)$
in G’. Since
$P=(u,v_1,\ldots,v_t,v)$
in G’. Since
![]() $u\in int(S_i)$
and
$u\in int(S_i)$
and
![]() $v\in C^*\setminus(C\cup S_i)$
is not in
$v\in C^*\setminus(C\cup S_i)$
is not in
![]() $S_i$
, there exists some index
$S_i$
, there exists some index
![]() $j\in\{1,\ldots,t\}$
with
$j\in\{1,\ldots,t\}$
with
![]() $v_j\in B(S_i)$
. But then
$v_j\in B(S_i)$
. But then
![]() $V(G')\cap C_i'\supseteq V(G')\cap B(S_i)\neq\emptyset$
, contradicting the assumption on G’. So
$V(G')\cap C_i'\supseteq V(G')\cap B(S_i)\neq\emptyset$
, contradicting the assumption on G’. So
![]() $C'_i$
is a CkSC of G. Claim 2 is proved.
$C'_i$
is a CkSC of G. Claim 2 is proved.
Note that
![]() $C_i'$
can be written as
$C_i'$
can be written as
![]() $C_i'=(C\setminus F_i')\cup F_i''$
, where
$C_i'=(C\setminus F_i')\cup F_i''$
, where
![]() $F_i'=C\cap int(S_i)$
and
$F_i'=C\cap int(S_i)$
and
![]() $F_i''=C^*\cap S_i$
. Since
$F_i''=C^*\cap S_i$
. Since
![]() $F_i'\subseteq S_i$
, we have
$F_i'\subseteq S_i$
, we have
![]() $|F_i'|\leq |S_i|\leq r$
. So, the reason why C cannot be improved to
$|F_i'|\leq |S_i|\leq r$
. So, the reason why C cannot be improved to
![]() $C_i'$
by the algorithm is because of
$C_i'$
by the algorithm is because of
![]() $|C_i'|\geq |C|$
. Combining this with
$|C_i'|\geq |C|$
. Combining this with
we have
It follows that
 \begin{align*}|C|& \leq \sum\limits_{i=1}^q|C\cap S_i|\\& \leq \sum\limits_{i=1}^q|C^*\cap S_i|+ \sum\limits_{i=1}^q|B(S_i)|\\&\leq|C^*|+2\sum\limits_{i=1}^q|B(S_i)|\\&\leq|C^*|+2c_{\mathcal{S}}\frac{k|C^*|}{\sqrt{r}}\\&=(1+2c_{\mathcal{S}}\frac{k}{\sqrt{r}})|C^*|\\&\leq(1+\varepsilon)|C^*|,\end{align*}
\begin{align*}|C|& \leq \sum\limits_{i=1}^q|C\cap S_i|\\& \leq \sum\limits_{i=1}^q|C^*\cap S_i|+ \sum\limits_{i=1}^q|B(S_i)|\\&\leq|C^*|+2\sum\limits_{i=1}^q|B(S_i)|\\&\leq|C^*|+2c_{\mathcal{S}}\frac{k|C^*|}{\sqrt{r}}\\&=(1+2c_{\mathcal{S}}\frac{k}{\sqrt{r}})|C^*|\\&\leq(1+\varepsilon)|C^*|,\end{align*}
where the first inequality holds because
![]() $V(G)=S_1\cup \cdots \cup S_q$
; the second inequality comes from (1); the third inequality holds because
$V(G)=S_1\cup \cdots \cup S_q$
; the second inequality comes from (1); the third inequality holds because
![]() $|C^*\cap S_i|=|C^*\cap int(S_i)|+|C^*\cap B(S_i)|\leq |C^*\cap int(S_i)|+|B(S_i)|$
and the sets
$|C^*\cap S_i|=|C^*\cap int(S_i)|+|C^*\cap B(S_i)|\leq |C^*\cap int(S_i)|+|B(S_i)|$
and the sets
![]() $\{int(S_i)\}_{i=1,\ldots,q}$
are mutually disjoint; the fourth inequality makes use of condition (c) in the definition of r-division and
$\{int(S_i)\}_{i=1,\ldots,q}$
are mutually disjoint; the fourth inequality makes use of condition (c) in the definition of r-division and
![]() $|V(G_a)|\leq k|C^*|$
by Claim 1; and the last inequality comes from the choice of
$|V(G_a)|\leq k|C^*|$
by Claim 1; and the last inequality comes from the choice of
![]() $r\geq \left(\frac{2c_{\mathcal{S}}k}{\varepsilon}\right)^2$
.
$r\geq \left(\frac{2c_{\mathcal{S}}k}{\varepsilon}\right)^2$
.
3. Algorithm for MinC
 $\boldsymbol{k}$
SC
$\boldsymbol{k}$
SC
 $_{\boldsymbol{con}}$
in Terms of Treewidth
$_{\boldsymbol{con}}$
in Terms of Treewidth
In this section, we provide a dynamic programming for MinCkSC
![]() $_{con}$
whose running time depends on the treewidth
$_{con}$
whose running time depends on the treewidth
![]() $\omega$
of graph G.
$\omega$
of graph G.
3.1 Basic notations
Firstly, we introduce the definition of tree decomposition.
Definition 5. (Tree decomposition) For a given graph
![]() $G=(V,E)$
, a pair
$G=(V,E)$
, a pair
![]() $(\{X_i:i\in I\},T=(I,F))$
is a tree decomposition, if the following conditions hold:
$(\{X_i:i\in I\},T=(I,F))$
is a tree decomposition, if the following conditions hold:
-
(i)
 $\bigcup_{i\in I}X_i=V$
,
$\bigcup_{i\in I}X_i=V$
, -
(ii) every edge
 $e\in E$
belongs to some
$e\in E$
belongs to some
 $G[X_i]$
,
$G[X_i]$
, -
(iii) T is a tree on vertex set I and edge set F, such that
 $X_i\cap X_k\subseteq X_j$
for any j lying on the path from i to k in T.
$X_i\cap X_k\subseteq X_j$
for any j lying on the path from i to k in T.
Each
![]() $X_i$
is called a bag. The treewidth of G is defined as
$X_i$
is called a bag. The treewidth of G is defined as
Our algorithm needs nice tree decomposition defined as follows. For the sake of clarity, we use nodes to refer to vertices of T and use vertices to refer to vertices of G.
Definition 6. (Nice tree decomposition) For a graph
![]() $G=(V,E)$
, a tree decomposition is nice if nodes in I can be partitioned into four types as follows:
$G=(V,E)$
, a tree decomposition is nice if nodes in I can be partitioned into four types as follows:
-
(i) leaf node: a node in T without children;
-
(ii) introduce node: a node i which has exactly one child j such that
 $X_j\subseteq X_i$
and
$X_j\subseteq X_i$
and
 $X_i\setminus X_j=\{v\}$
for some vertex
$X_i\setminus X_j=\{v\}$
for some vertex
 $v\in V$
;
$v\in V$
; -
(iii) forget node: a node i which has exactly one child j such that
 $X_j=X_i\cup\{v\}$
for some vertex
$X_j=X_i\cup\{v\}$
for some vertex
 $v\in V$
;
$v\in V$
; -
(iv) join node: a node i which has exactly two children j,l such that
 $X_i=X_j=X_l$
.
$X_i=X_j=X_l$
.
A nice tree decomposition is illustrated by Figure 1. Bodlaender proved in Bodlaender (Reference Bodlaender1996) that for any graph with treewidth
![]() $\omega$
, a tree decomposition can be computed in time
$\omega$
, a tree decomposition can be computed in time
![]() $O(2^{\Theta(\omega^3)}|V|)$
, and given a tree decomposition, one can transform it into a nice tree decomposition in time
$O(2^{\Theta(\omega^3)}|V|)$
, and given a tree decomposition, one can transform it into a nice tree decomposition in time
![]() $O(|V|+|E|)$
. Note that each non-leaf bag is a separator of graph G by Diestel (Reference Diestel2005).
$O(|V|+|E|)$
. Note that each non-leaf bag is a separator of graph G by Diestel (Reference Diestel2005).

Figure 1. An illustration of nice tree decomposition. The left most node is the root, and we use symbols JN,IN,FN and LN to indicate join node, introduce node, forget node, and leaf node, respectively.
3.2 MinCkSC
 $_{con}$
on bounded treewidth graphs
$_{con}$
on bounded treewidth graphs
In this section, we present a dynamic programming for the computation of MinCkSC
![]() $_{con}$
.
$_{con}$
.
For a nice tree decomposition
![]() $(\{X_i:i\in I\},T)$
, a subtree of T rooted at i which contains all descendants of i is denoted as
$(\{X_i:i\in I\},T)$
, a subtree of T rooted at i which contains all descendants of i is denoted as
![]() $T_i$
. The subgraph of G induced by all vertices of those bags corresponding to those nodes of
$T_i$
. The subgraph of G induced by all vertices of those bags corresponding to those nodes of
![]() $T_i$
is denoted as
$T_i$
is denoted as
![]() $G_i=G[\bigcup\limits_{j\in{V(T_i)}}X_j]$
.
$G_i=G[\bigcup\limits_{j\in{V(T_i)}}X_j]$
.
Status variables: For each node
![]() $i\in I$
, the dynamic programming will record a set of optimal values with respect to all possible tokens of the form
$i\in I$
, the dynamic programming will record a set of optimal values with respect to all possible tokens of the form
![]() $(F,P_F,P_{X_i\setminus F})$
, where
$(F,P_F,P_{X_i\setminus F})$
, where
![]() $F\subseteq X_i$
,
$F\subseteq X_i$
,
![]() $P_F$
is a partition of F,
$P_F$
is a partition of F,
![]() $P_{X_i\setminus F}$
consists of a partition of
$P_{X_i\setminus F}$
consists of a partition of
![]() $X_i\setminus F$
, and each part of
$X_i\setminus F$
, and each part of
![]() $P_{X_i\setminus F}$
is associated with an integer smaller than k. Define status variable
$P_{X_i\setminus F}$
is associated with an integer smaller than k. Define status variable
![]() $c(i,F,P_F,P_{X_i\setminus F})$
to be the cardinality of a minimum vertex set
$c(i,F,P_F,P_{X_i\setminus F})$
to be the cardinality of a minimum vertex set
![]() $C\subseteq V(G_i)$
which is compatible with token
$C\subseteq V(G_i)$
which is compatible with token
![]() $(F,P_F,P_{X_i\setminus F})$
, where compatible means
$(F,P_F,P_{X_i\setminus F})$
, where compatible means
-
(i)
 $C\cap X_i=F$
;
$C\cap X_i=F$
; -
(ii)
 $P_F$
is the partition of F corresponding to those connected components of
$P_F$
is the partition of F corresponding to those connected components of
 $G_i[C]$
;
$G_i[C]$
; -
(iii)
 $P_{X_i\setminus F}$
consists of the partition of
$P_{X_i\setminus F}$
consists of the partition of
 ${X_i\setminus F}$
corresponding to those connected components of
${X_i\setminus F}$
corresponding to those connected components of
 $G_i-C$
which has non-empty intersection with
$G_i-C$
which has non-empty intersection with
 $X_i$
, and for each part of the partition, the integer associated with this part is the cardinality of the connected component of
$X_i$
, and for each part of the partition, the integer associated with this part is the cardinality of the connected component of
 $G_i-C$
containing this part.
$G_i-C$
containing this part.
We shall use
![]() $P_F(v)$
(resp.
$P_F(v)$
(resp.
![]() $P_{X_i\setminus F}(v)$
) to denote the part of
$P_{X_i\setminus F}(v)$
) to denote the part of
![]() $P_F$
(resp.
$P_F$
(resp.
![]() $P_{X_i\setminus F}$
) which contains vertex v, and use
$P_{X_i\setminus F}$
) which contains vertex v, and use
![]() $k_D$
to denote the integer associated with a part D of the partition of
$k_D$
to denote the integer associated with a part D of the partition of
![]() $P_{X_i\setminus F}$
.
$P_{X_i\setminus F}$
.
Initial condition: The dynamic programming starts computing from leaf nodes. For a leaf node
![]() $i\in I$
, if F is compatible with token set
$i\in I$
, if F is compatible with token set
![]() $(F,P_F,P_{X_i\setminus F})$
, then
$(F,P_F,P_{X_i\setminus F})$
, then
![]() $c(i,F,P_F,P_{X_i\setminus F})=|F|$
, otherwise
$c(i,F,P_F,P_{X_i\setminus F})=|F|$
, otherwise
![]() $c(i,F,P_F,P_{X_i\setminus F})=\infty$
.
$c(i,F,P_F,P_{X_i\setminus F})=\infty$
.
Transition formula: We distinguish the transition formula into three cases depending on the type of the internal node.
Introduce node: Suppose i is an introduce node. Let j be the only child of i and denote by v the unique vertex in
![]() $X_i\setminus X_j$
. A triple
$X_i\setminus X_j$
. A triple
![]() $(F,P_F,P_{X_i\setminus F})$
is said to be a valid token for node i if
$(F,P_F,P_{X_i\setminus F})$
is said to be a valid token for node i if
![]() $\bf (a^{(in)})$
every part of
$\bf (a^{(in)})$
every part of
![]() $P_{X_i\setminus F}$
has cardinality at most
$P_{X_i\setminus F}$
has cardinality at most
![]() $k-1$
,
$k-1$
,
and exactly one of the following two conditions is satisfied:
![]() $\bf (b_1^{(in)})$
if
$\bf (b_1^{(in)})$
if
![]() $v\in F$
, then
$v\in F$
, then
![]() $N_G(v)\cap F\subseteq P_F(v)$
;
$N_G(v)\cap F\subseteq P_F(v)$
;
![]() $\bf (b_2^{(in)})$
if
$\bf (b_2^{(in)})$
if
![]() $v\not\in F$
, then
$v\not\in F$
, then
![]() $N_G(v)\cap (X_i\setminus F)\subseteq P_{X_i\setminus F}(v)$
.
$N_G(v)\cap (X_i\setminus F)\subseteq P_{X_i\setminus F}(v)$
.
Superscript (in) indicates that the condition is for an introduce node. Condition
![]() $(a^{(in)})$
is necessary for C to be a feasible CkSC
$(a^{(in)})$
is necessary for C to be a feasible CkSC
![]() $_{con}$
. The reason for condition
$_{con}$
. The reason for condition
![]() $(b_1^{(in)})$
is because if
$(b_1^{(in)})$
is because if
![]() $v\in F$
, then any neighbor of v in F must belong to the connected component of
$v\in F$
, then any neighbor of v in F must belong to the connected component of
![]() $G_i[C]$
containing v. Similar reason for condition
$G_i[C]$
containing v. Similar reason for condition
![]() $(b_2^{(in)})$
.
$(b_2^{(in)})$
.
Note that in the case of introduce node,
![]() $G_j=G_i-v$
due to condition (3) in the definition of tree decomposition (Definition 5). For a valid token
$G_j=G_i-v$
due to condition (3) in the definition of tree decomposition (Definition 5). For a valid token
![]() $(F,P_F,P_{X_i\setminus F})$
, we say that token
$(F,P_F,P_{X_i\setminus F})$
, we say that token
![]() $(F',P_{F'},P_{X_j\setminus F'})$
for node j is compatible with
$(F',P_{F'},P_{X_j\setminus F'})$
for node j is compatible with
![]() $(F,P_F,P_{X_i\setminus F})$
if one of the following two conditions are met:
$(F,P_F,P_{X_i\setminus F})$
if one of the following two conditions are met:
![]() $\bf (c_1^{(in)})$
If
$\bf (c_1^{(in)})$
If
![]() $v\in F$
, then
$v\in F$
, then
![]() $F'=F\setminus\{v\}$
,
$F'=F\setminus\{v\}$
,
![]() $P_F=\big(P_{F'}\setminus \{P_{F'}(u)\colon u\in F'\cap N_G(v)\}\big)\cup \{D\}$
where
$P_F=\big(P_{F'}\setminus \{P_{F'}(u)\colon u\in F'\cap N_G(v)\}\big)\cup \{D\}$
where
![]() $D=\left(\bigcup_{u\in F'\cap N_G(v)}P_{F'}(u)\right)\cup\{v\}$
, and
$D=\left(\bigcup_{u\in F'\cap N_G(v)}P_{F'}(u)\right)\cup\{v\}$
, and
![]() $P_{X_j\setminus F'}=P_{X_i\setminus F}$
.
$P_{X_j\setminus F'}=P_{X_i\setminus F}$
.
![]() $\bf (c_2^{(in)})$
If
$\bf (c_2^{(in)})$
If
![]() $v\not\in F$
, then
$v\not\in F$
, then
![]() $F'=F$
,
$F'=F$
,
![]() $P_F=P_{F'}$
, the partition of
$P_F=P_{F'}$
, the partition of
![]() $P_{X_i\setminus F}$
is
$P_{X_i\setminus F}$
is
![]() $\big(P_{X_j\setminus F'}\setminus\{P_{X_j\setminus F'}(u)\colon u\in (X_j\setminus F')\cap N_G(v)\}\big)\cup\{D'\}$
, where
$\big(P_{X_j\setminus F'}\setminus\{P_{X_j\setminus F'}(u)\colon u\in (X_j\setminus F')\cap N_G(v)\}\big)\cup\{D'\}$
, where
![]() $D'=\left(\bigcup_{u\in (X_j\setminus F')\cap N_G(v)}P_{X_j\setminus F'}(u)\right)\cup\{v\}$
, and
$D'=\left(\bigcup_{u\in (X_j\setminus F')\cap N_G(v)}P_{X_j\setminus F'}(u)\right)\cup\{v\}$
, and
![]() $k_{D'}=1+\sum_{D\in\{P_{X_j\setminus F'}(u)\colon u\in (X_j\setminus F')\cap N_G(v)\}}k_D$
must satisfy
$k_{D'}=1+\sum_{D\in\{P_{X_j\setminus F'}(u)\colon u\in (X_j\setminus F')\cap N_G(v)\}}k_D$
must satisfy
![]() $k_{D'}\leq k-1$
.
$k_{D'}\leq k-1$
.
The compatibility condition is illustrated by Fig. 2. In this figure,
![]() $P_{F'}=\{D_1,D_2,D_3\}$
(note that there are two patches in F which are both labeled
$P_{F'}=\{D_1,D_2,D_3\}$
(note that there are two patches in F which are both labeled
![]() $D_1$
since they belong to a same connected component of
$D_1$
since they belong to a same connected component of
![]() $G_j[C]$
) and the partition of
$G_j[C]$
) and the partition of
![]() $P_{X_i\setminus F'}$
is
$P_{X_i\setminus F'}$
is
![]() $\{D_4,D_5,D_6\}$
. For the case when
$\{D_4,D_5,D_6\}$
. For the case when
![]() $v\in F$
, the inclusion of vertex v merges the two connected components of
$v\in F$
, the inclusion of vertex v merges the two connected components of
![]() $G_j[C]$
containing
$G_j[C]$
containing
![]() $D_1$
and
$D_1$
and
![]() $D_2$
into one connected component of
$D_2$
into one connected component of
![]() $G_i[C]$
, the new partition
$G_i[C]$
, the new partition
![]() $P_F=\{D,D_3\}$
where
$P_F=\{D,D_3\}$
where
![]() $D=D_1\cup D_2\cup\{v\}$
. While
$D=D_1\cup D_2\cup\{v\}$
. While
![]() $P_{X_i\setminus F}$
remains the same as
$P_{X_i\setminus F}$
remains the same as
![]() $P_{X_j\setminus F'}$
. For the case when
$P_{X_j\setminus F'}$
. For the case when
![]() $v\not\in F$
, the inclusion of vertex v will not affect F and
$v\not\in F$
, the inclusion of vertex v will not affect F and
![]() $P_F$
, but may merge
$P_F$
, but may merge
![]() $D_4$
and
$D_4$
and
![]() $D_5$
into a new part
$D_5$
into a new part
![]() $D'=D_4\cup D_5\cup \{v\}$
. So the new partition of
$D'=D_4\cup D_5\cup \{v\}$
. So the new partition of
![]() $P_{X_i\setminus F}$
should be
$P_{X_i\setminus F}$
should be
![]() $\{D',D_6\}$
, and the integer associated with D’ equals
$\{D',D_6\}$
, and the integer associated with D’ equals
![]() $k_{D_4}+k_{D_5}+1$
, which is the cardinality of the merged connected component of
$k_{D_4}+k_{D_5}+1$
, which is the cardinality of the merged connected component of
![]() $G_i-C$
. It should be emphasized that if
$G_i-C$
. It should be emphasized that if
![]() $k_{D'}\geq k$
, then
$k_{D'}\geq k$
, then
![]() $G_i-C$
contains a connected subgraph of cardinality at least k, and thus C cannot be a feasible solution to the CkSC
$G_i-C$
contains a connected subgraph of cardinality at least k, and thus C cannot be a feasible solution to the CkSC
![]() $_{con}$
instance. This is why the compatibility condition in
$_{con}$
instance. This is why the compatibility condition in
![]() $\bf(c_2^{(in)})$
requires
$\bf(c_2^{(in)})$
requires
![]() $k_{D'}\leq k-1$
.
$k_{D'}\leq k-1$
.

Figure 2. An illustration of compatibility condition for introduce node. The whole figure shows
![]() $G_i$
. Solid closed curves are connected components of
$G_i$
. Solid closed curves are connected components of
![]() $G_i[C]$
, dashed closed curves are connected components of
$G_i[C]$
, dashed closed curves are connected components of
![]() $G_i-C$
.
$G_i-C$
.
The transition formula for a valid token
![]() $(F,P_F,P_{X_i\setminus F})$
of an introduce node i is
$(F,P_F,P_{X_i\setminus F})$
of an introduce node i is

where
![]() $1_{v\in F}=1$
if
$1_{v\in F}=1$
if
![]() $v\in F$
and
$v\in F$
and
![]() $1_{v\in F}=0$
if
$1_{v\in F}=0$
if
![]() $v\not\in F$
.
$v\not\in F$
.
Forget node: Suppose i is a forget node, j is the only child of i, and v is the only vertex in
![]() $X_j\setminus X_i$
. A triple
$X_j\setminus X_i$
. A triple
![]() $(F,P_F,P_{X_i\setminus F})$
is said to be a valid token for node i if
$(F,P_F,P_{X_i\setminus F})$
is said to be a valid token for node i if
![]() $\bf (a^{(for)})$
each part of
$\bf (a^{(for)})$
each part of
![]() $P_{X_i\setminus F}$
has at most
$P_{X_i\setminus F}$
has at most
![]() $k-1$
vertices,
$k-1$
vertices,
and one of the following two conditions is satisfied:
![]() $\bf (b_1^{(for)})$
all vertices in
$\bf (b_1^{(for)})$
all vertices in
![]() $N_G(v)\cap F$
belong to a same part of
$N_G(v)\cap F$
belong to a same part of
![]() $P_F$
, or
$P_F$
, or
![]() $\bf (b_2^{(for)})$
all vertices in
$\bf (b_2^{(for)})$
all vertices in
![]() $N_G(v)\cap (X_i\setminus F)$
belong to a same part of
$N_G(v)\cap (X_i\setminus F)$
belong to a same part of
![]() $P_{X_i\setminus F}$
.
$P_{X_i\setminus F}$
.
Superscript (for) indicates that the condition is for a forget node. Note that different from the case for introduce node, in which exactly one condition of
![]() $(b_1^{(in)})$
and
$(b_1^{(in)})$
and
![]() $(b_2^{(in)})$
can occur, for the case of forget node, conditions
$(b_2^{(in)})$
can occur, for the case of forget node, conditions
![]() $(b_1^{(for)})$
and
$(b_1^{(for)})$
and
![]() $(b_2^{(for)})$
can both occur.
$(b_2^{(for)})$
can both occur.
For the case of forget node,
![]() $G_i=G_j$
. For a valid token
$G_i=G_j$
. For a valid token
![]() $(F,P_F,P_{X_i\setminus F})$
, we say that a token
$(F,P_F,P_{X_i\setminus F})$
, we say that a token
![]() $(F',P_{F'},P_{X_i\setminus F'})$
for node j is compatible with
$(F',P_{F'},P_{X_i\setminus F'})$
for node j is compatible with
![]() $(F,P_F,P_{X_i\setminus F})$
if one of the following two conditions are met:
$(F,P_F,P_{X_i\setminus F})$
if one of the following two conditions are met:
![]() $\bf (c_1^{(for)})$
All vertices of
$\bf (c_1^{(for)})$
All vertices of
![]() $N_G(v)\cap F$
belong to a same part of
$N_G(v)\cap F$
belong to a same part of
![]() $P_F$
,
$P_F$
,
![]() $F'=F\cup\{v\}$
,
$F'=F\cup\{v\}$
,
![]() $P_F=\big(P_{F'}\setminus \{P_{F'}(v)\}\big)\cup \{P_{F'}(v)\setminus \{v\}\}$
, and
$P_F=\big(P_{F'}\setminus \{P_{F'}(v)\}\big)\cup \{P_{F'}(v)\setminus \{v\}\}$
, and
![]() $P_{X_i\setminus F}=P_{X_j\setminus F'}$
.
$P_{X_i\setminus F}=P_{X_j\setminus F'}$
.
![]() $\bf (c_2^{(for)})$
All vertices of
$\bf (c_2^{(for)})$
All vertices of
![]() $N_G(v)\cap (X_i\setminus F)$
belong to a same part of
$N_G(v)\cap (X_i\setminus F)$
belong to a same part of
![]() $P_{X_i\setminus F}$
,
$P_{X_i\setminus F}$
,
![]() $F'=F$
,
$F'=F$
,
![]() $P_{F'}=P_F$
,
$P_{F'}=P_F$
,
![]() $P_{X_i\setminus F}=\big(P_{X_j\setminus F'}\setminus\{P_{X_j\setminus F'}(v)\}\big)\cup \{P_{X_j\setminus F'}(v)\setminus\{v\}\}$
, and
$P_{X_i\setminus F}=\big(P_{X_j\setminus F'}\setminus\{P_{X_j\setminus F'}(v)\}\big)\cup \{P_{X_j\setminus F'}(v)\setminus\{v\}\}$
, and
![]() $k_{P_{X_j\setminus F'}(v)}\leq k-1$
.
$k_{P_{X_j\setminus F'}(v)}\leq k-1$
.
Compatibility for a forget node is illustrated by Fig. 3. For a valid token
![]() $(F,P_F,P_{X_i\setminus F})$
with
$(F,P_F,P_{X_i\setminus F})$
with
![]() $F=D_1\cup D_2$
,
$F=D_1\cup D_2$
,
![]() $P_F=\{F\}$
and
$P_F=\{F\}$
and
![]() $P_{X_i\setminus F}=\{D_3,D_4\}$
, a compatible token for node j is
$P_{X_i\setminus F}=\{D_3,D_4\}$
, a compatible token for node j is
![]() $(F',P_{F'},P_{X_j\setminus F'})$
with
$(F',P_{F'},P_{X_j\setminus F'})$
with
![]() $F'=F\cup \{v\}$
,
$F'=F\cup \{v\}$
,
![]() $P_{F'}=\{F'\}$
and
$P_{F'}=\{F'\}$
and
![]() $P_{X_j\setminus F'}=\{D_3,D_4\}$
. For a valid token
$P_{X_j\setminus F'}=\{D_3,D_4\}$
. For a valid token
![]() $(F,P_F,P_{X_i\setminus F})$
with
$(F,P_F,P_{X_i\setminus F})$
with
![]() $F=D_1\cup D_2$
,
$F=D_1\cup D_2$
,
![]() $P_F=\{D_1,D_2\}$
and
$P_F=\{D_1,D_2\}$
and
![]() $P_{X_i\setminus F}=\{D_3\cup D_4\}$
, if
$P_{X_i\setminus F}=\{D_3\cup D_4\}$
, if
![]() $k_{D_3}+k_{D_4}+1\leq k-1$
, then a compatible token for node j is
$k_{D_3}+k_{D_4}+1\leq k-1$
, then a compatible token for node j is
![]() $(F',P_{F'},P_{X_j\setminus F'})$
with
$(F',P_{F'},P_{X_j\setminus F'})$
with
![]() $F'=F$
,
$F'=F$
,
![]() $P_{F'}=P_F$
, the partition of
$P_{F'}=P_F$
, the partition of
![]() $P_{X_j\setminus F}$
is
$P_{X_j\setminus F}$
is
![]() $\{D_3\cup D_4\cup\{v\}\}$
, and the integer associated part
$\{D_3\cup D_4\cup\{v\}\}$
, and the integer associated part
![]() $D=D_3\cup D_4\cup \{v\}$
is
$D=D_3\cup D_4\cup \{v\}$
is
![]() $k_D=k_{D_3}+k_{D_4}+1$
.
$k_D=k_{D_3}+k_{D_4}+1$
.

Figure 3. An illustration of compatibility condition for forget node.
The transition formula for a valid token
![]() $(F,P_F,P_{X_i\setminus F})$
of a forget node i is
$(F,P_F,P_{X_i\setminus F})$
of a forget node i is

Join node: Suppose
![]() $i\in I$
is a join node with two children j and l. A triple
$i\in I$
is a join node with two children j and l. A triple
![]() $(F,P_F,P_{X_i\setminus F})$
is a valid token if each part of
$(F,P_F,P_{X_i\setminus F})$
is a valid token if each part of
![]() $P_{X_i\setminus F}$
has at most
$P_{X_i\setminus F}$
has at most
![]() $k-1$
vertices.
$k-1$
vertices.

Figure 4. An illustration of compatibility condition for join node. Note that
![]() $G_j-X_i$
and
$G_j-X_i$
and
![]() $G_l-X_i$
are disjoint.
$G_l-X_i$
are disjoint.
In this case,
![]() $X_i=X_j=X_l$
and
$X_i=X_j=X_l$
and
![]() $G_i=G_j\cup G_l$
. Furthermore, by condition
$G_i=G_j\cup G_l$
. Furthermore, by condition
![]() $(iii)$
of tree decomposition, it can be observed that
$(iii)$
of tree decomposition, it can be observed that
For a valid token
![]() $(F,P_F,P_{X_i\setminus F})$
of node i, we say that a token
$(F,P_F,P_{X_i\setminus F})$
of node i, we say that a token
![]() $(F',P_{F'},P_{X_i\setminus F'})$
of node j and a token
$(F',P_{F'},P_{X_i\setminus F'})$
of node j and a token
![]() $(F'',P_{F''},P_{X_i\setminus F''})$
of node l are compatible with
$(F'',P_{F''},P_{X_i\setminus F''})$
of node l are compatible with
![]() $(F,P_F,P_{X_i\setminus F})$
if the following conditions are satisfied:
$(F,P_F,P_{X_i\setminus F})$
if the following conditions are satisfied:
![]() $\bf (c^{(join)})$
$\bf (c^{(join)})$
![]() $F=F'=F''$
;
$F=F'=F''$
;
![]() $\bf (d^{(join)})$
Every part of
$\bf (d^{(join)})$
Every part of
![]() $P_{F'}$
(as well as every part of
$P_{F'}$
(as well as every part of
![]() $P_{F''}$
) is completely contained in some part of
$P_{F''}$
) is completely contained in some part of
![]() $P_F$
. Furthermore, if there are a part D’ of
$P_F$
. Furthermore, if there are a part D’ of
![]() $P_{F'}$
and a part D” of
$P_{F'}$
and a part D” of
![]() $P_{F''}$
which have non-empty intersection, then D’ and D” belong to a same part of
$P_{F''}$
which have non-empty intersection, then D’ and D” belong to a same part of
![]() $P_F$
;
$P_F$
;
![]() $\bf (e^{(join)})$
Every part of
$\bf (e^{(join)})$
Every part of
![]() $P_{X_j\setminus F'}$
(as well as every part of
$P_{X_j\setminus F'}$
(as well as every part of
![]() $P_{X_l\setminus F''}$
) is completely contained in some part of
$P_{X_l\setminus F''}$
) is completely contained in some part of
![]() $P_{X_i\setminus F}$
. If there is a part D’ of
$P_{X_i\setminus F}$
. If there is a part D’ of
![]() $P_{X_j\setminus F'}$
and a part D” of
$P_{X_j\setminus F'}$
and a part D” of
![]() $P_{X_l\setminus F''}$
with
$P_{X_l\setminus F''}$
with
![]() $D'\cap D''\neq\emptyset$
, then
$D'\cap D''\neq\emptyset$
, then
![]() $D=D'\cup D''$
is a part of
$D=D'\cup D''$
is a part of
![]() $P_{X_i\setminus F}$
, and furthermore, the integer associated with D satisfies
$P_{X_i\setminus F}$
, and furthermore, the integer associated with D satisfies
![]() $k_D=k_{D'}+k_{D''}-|D'\cap D''|\leq k-1$
.
$k_D=k_{D'}+k_{D''}-|D'\cap D''|\leq k-1$
.
The compatibility of join node is illustrated in Fig. 4. In this figure, partitions
![]() $P_F=\{D_1\cup D_2\cup D_3\}$
,
$P_F=\{D_1\cup D_2\cup D_3\}$
,
![]() $P_{F'}=\{D_1\cup D_2,D_3\}$
and
$P_{F'}=\{D_1\cup D_2,D_3\}$
and
![]() $P_{F''}=\{D_1,D_2\cup D_3\}$
satisfy condition
$P_{F''}=\{D_1,D_2\cup D_3\}$
satisfy condition
![]() $\bf (d^{(join)})$
. Note that
$\bf (d^{(join)})$
. Note that
![]() $D_1$
and
$D_1$
and
![]() $D_2$
belong to a same part of
$D_2$
belong to a same part of
![]() $P_{F'}$
, indicating that
$P_{F'}$
, indicating that
![]() $D_1$
and
$D_1$
and
![]() $D_2$
are connected in
$D_2$
are connected in
![]() $G_j$
. Since
$G_j$
. Since
![]() $G_j$
is a subgraph of
$G_j$
is a subgraph of
![]() $G_i$
, so
$G_i$
, so
![]() $D_1$
and
$D_1$
and
![]() $D_2$
are also connected in
$D_2$
are also connected in
![]() $G_i$
, and thus
$G_i$
, and thus
![]() $D_1\cup D_2$
should be completely contained in some part of
$D_1\cup D_2$
should be completely contained in some part of
![]() $P_F$
. The same is true for
$P_F$
. The same is true for
![]() $D_2\cup D_3$
by considering
$D_2\cup D_3$
by considering
![]() $G_l$
. Furthermore, the part
$G_l$
. Furthermore, the part
![]() $D_1\cup D_2\in P_{F'}$
and the part
$D_1\cup D_2\in P_{F'}$
and the part
![]() $D_2\cup D_3\in P_{F''}$
have non-empty intersection
$D_2\cup D_3\in P_{F''}$
have non-empty intersection
![]() $D_2$
, so they must belong to a same part of
$D_2$
, so they must belong to a same part of
![]() $P_F$
which contains
$P_F$
which contains
![]() $D_2$
, indicating that they are connected through
$D_2$
, indicating that they are connected through
![]() $D_2$
into a connected component of
$D_2$
into a connected component of
![]() $G_i=G_j\cup G_l$
. Similarly, partition
$G_i=G_j\cup G_l$
. Similarly, partition
![]() $P_{X_j\setminus F'}=\{D_4\}$
,
$P_{X_j\setminus F'}=\{D_4\}$
,
![]() $P_{X_l\setminus F''}=\{D_4\cup D_5\}$
, and
$P_{X_l\setminus F''}=\{D_4\cup D_5\}$
, and
![]() $P_{X_i\setminus F}=\{D_4\cup D_5\}$
satisfy
$P_{X_i\setminus F}=\{D_4\cup D_5\}$
satisfy
![]() $\bf (e^{(join)})$
as long as
$\bf (e^{(join)})$
as long as
![]() $k_{D_4}^{(j)}+k_{D_4\cup D_5}^{(l)}-|D_4|\leq k-1$
, where
$k_{D_4}^{(j)}+k_{D_4\cup D_5}^{(l)}-|D_4|\leq k-1$
, where
![]() $k_{D_4}^{(j)}$
is the integer associated with part
$k_{D_4}^{(j)}$
is the integer associated with part
![]() $D_4$
in the partition of
$D_4$
in the partition of
![]() $P_{X_j\setminus F'}$
and
$P_{X_j\setminus F'}$
and
![]() $k_{D_4\cup D_5}^{(l)}$
is the integer associated with part
$k_{D_4\cup D_5}^{(l)}$
is the integer associated with part
![]() $D_4\cup D_5$
in the partition of
$D_4\cup D_5$
in the partition of
![]() $P_{X_l\setminus F''}$
. It should be noted that if we denote by
$P_{X_l\setminus F''}$
. It should be noted that if we denote by
![]() $H_j$
the connected component of
$H_j$
the connected component of
![]() $G_j$
containing part
$G_j$
containing part
![]() $D_4\cup D_6$
, denote by
$D_4\cup D_6$
, denote by
![]() $H_l$
the connected component of
$H_l$
the connected component of
![]() $G_l$
containing part
$G_l$
containing part
![]() $D_4\cup D_5$
, then
$D_4\cup D_5$
, then
![]() $H_j$
and
$H_j$
and
![]() $H_l$
are merged into one connected component of
$H_l$
are merged into one connected component of
![]() $G_i$
, denoted as
$G_i$
, denoted as
![]() $H_i$
. Because of observation (2), we have
$H_i$
. Because of observation (2), we have
![]() $V(H_j)\cap V(H_l)=D_4$
, and thus the size of
$V(H_j)\cap V(H_l)=D_4$
, and thus the size of
![]() $H_i$
is
$H_i$
is
![]() $|H_j|+|H_l|-|D_4|=k_{D_4}^{(j)}+k_{D_4\cup D_6}^{(l)}-|D_4|$
. For the feasibility of the solution, we must require this size
$|H_j|+|H_l|-|D_4|=k_{D_4}^{(j)}+k_{D_4\cup D_6}^{(l)}-|D_4|$
. For the feasibility of the solution, we must require this size
![]() $\leq k-1$
.
$\leq k-1$
.
The transition formula for a valid token
![]() $(F,P_F,P_{X_i\setminus F})$
of a join node i is
$(F,P_F,P_{X_i\setminus F})$
of a join node i is

In the above, we only give out transition formula for valid tokens. If
![]() $(F,P_F,P_{X_i\setminus F})$
is an invalid token for node i, or there are no tokens for his child (or children) which are compatible with
$(F,P_F,P_{X_i\setminus F})$
is an invalid token for node i, or there are no tokens for his child (or children) which are compatible with
![]() $(F,P_F,P_{X_i\setminus F})$
, then set
$(F,P_F,P_{X_i\setminus F})$
, then set
Theorem Given a graph
![]() $G=(V,E)$
with treewidth
$G=(V,E)$
with treewidth
![]() $\omega$
, starting from leaf nodes of a nice tree decomposition of G, recursively use the above transition formulas in a bottom-up manner, when the dynamic programming arrives at the root node r, the minimum vertex set over all possible tokens
$\omega$
, starting from leaf nodes of a nice tree decomposition of G, recursively use the above transition formulas in a bottom-up manner, when the dynamic programming arrives at the root node r, the minimum vertex set over all possible tokens
![]() $(F,P_F,P_{X_r\setminus F})$
for r is an optimal solution for the MinCkSC
$(F,P_F,P_{X_r\setminus F})$
for r is an optimal solution for the MinCkSC
![]() $_{con}$
instance. The time complexity is
$_{con}$
instance. The time complexity is
![]() $O((2^{\Theta(\omega^3)}+(\omega+1)(2(k-1)(\omega+2))^{3\omega+3})|V|)$
.
$O((2^{\Theta(\omega^3)}+(\omega+1)(2(k-1)(\omega+2))^{3\omega+3})|V|)$
.
Proof. The correctness of the dynamic programming is already shown when we discuss compatibility for the transition formulas.
To study the time complexity, regard each node i to maintain a table
![]() $\mbox{Tab}(i)$
, which is used to record values
$\mbox{Tab}(i)$
, which is used to record values
![]() $c(i,F,P_F,P_{X_i\setminus F})$
for all tokens
$c(i,F,P_F,P_{X_i\setminus F})$
for all tokens
![]() $(F,P_F,P_{X_i\setminus F})$
. We have to estimate
$(F,P_F,P_{X_i\setminus F})$
. We have to estimate
-
(i) the number of tokens for node i, and
-
(ii) for each token
 $(F,P_F,P_{X_i\setminus F})$
, the time to compute
$(F,P_F,P_{X_i\setminus F})$
, the time to compute
 $c(i,F,P_F,P_{X_i\setminus F})$
.
$c(i,F,P_F,P_{X_i\setminus F})$
.
For task (i), it can be seen that there are at most
![]() $(2(\omega+2))^{\omega+1}$
different partitions: for each vertex
$(2(\omega+2))^{\omega+1}$
different partitions: for each vertex
![]() $v\in X_i$
, assign a label
$v\in X_i$
, assign a label
![]() $(l_1(v),l_2(v))$
to v, where
$(l_1(v),l_2(v))$
to v, where
![]() $l_1(v)$
indicates whether v belongs to F or
$l_1(v)$
indicates whether v belongs to F or
![]() $X_i\setminus F$
, and
$X_i\setminus F$
, and
![]() $l_2(v)$
indicates which part does v belongs to; there are at most
$l_2(v)$
indicates which part does v belongs to; there are at most
![]() $|X_i|$
parts for
$|X_i|$
parts for
![]() $P_F$
and at most
$P_F$
and at most
![]() $|X_i|$
parts for
$|X_i|$
parts for
![]() $P_{X_i\setminus F}$
; then the number of partitions follows from the observation that there are two choices for
$P_{X_i\setminus F}$
; then the number of partitions follows from the observation that there are two choices for
![]() $l_1(v)$
, at most
$l_1(v)$
, at most
![]() $|X_i|+1$
choices for
$|X_i|+1$
choices for
![]() $l_2(v)$
(note that either F or
$l_2(v)$
(note that either F or
![]() $X_i\setminus F$
might be empty), and
$X_i\setminus F$
might be empty), and
![]() $|X_i|\leq \omega+1$
. The set F is simply the union of those parts of
$|X_i|\leq \omega+1$
. The set F is simply the union of those parts of
![]() $P_F$
. For each part D of
$P_F$
. For each part D of
![]() $P_{X_i\setminus F}$
, there are at most
$P_{X_i\setminus F}$
, there are at most
![]() $k-1$
choices for
$k-1$
choices for
![]() $k_D$
. So, the number of different tokens for node i is at most
$k_D$
. So, the number of different tokens for node i is at most
![]() $O((2(k-1)(\omega+2))^{\omega+1})$
.
$O((2(k-1)(\omega+2))^{\omega+1})$
.
For task (ii), the time to compute
![]() $c(i,F,P_F,P_{X_i\setminus F})$
depends on the number of tokens compatible with
$c(i,F,P_F,P_{X_i\setminus F})$
depends on the number of tokens compatible with
![]() $(F,P_F,P_{X_i\setminus F})$
, which in turn is also upper bounded by the number for task (i) estimated in the above. As to checking compatibility given a token for node i’s child (or two tokens for its two children), it can be accomplished in linear time. So, the time to compute
$(F,P_F,P_{X_i\setminus F})$
, which in turn is also upper bounded by the number for task (i) estimated in the above. As to checking compatibility given a token for node i’s child (or two tokens for its two children), it can be accomplished in linear time. So, the time to compute
![]() $c(i,F,P_F,P_{X_i\setminus F})$
is
$c(i,F,P_F,P_{X_i\setminus F})$
is
![]() $O((\omega+1)(2(k-1)(\omega+2))^{2\omega+2})$
.
$O((\omega+1)(2(k-1)(\omega+2))^{2\omega+2})$
.
To sum up, for each node i in a nice tree decomposition of G, the time to compute all elements in table
![]() $\mbox{Tab}(i)$
is
$\mbox{Tab}(i)$
is
![]() $O((\omega+1)(2(k-1)(\omega+2))^{3\omega+3})$
. Since there are
$O((\omega+1)(2(k-1)(\omega+2))^{3\omega+3})$
. Since there are
![]() $O(|V|)$
nodes in a nice tree decomposition of G by Kloks (Reference Kloks1994), and the time to compute a nice tree decomposition is
$O(|V|)$
nodes in a nice tree decomposition of G by Kloks (Reference Kloks1994), and the time to compute a nice tree decomposition is
![]() $O(2^{\Theta(\omega^3)}|V|)$
in Bodlaender (Reference Bodlaender1996), the total time for the dynamic programming follows.
$O(2^{\Theta(\omega^3)}|V|)$
in Bodlaender (Reference Bodlaender1996), the total time for the dynamic programming follows.
As a consequence, we have the following result.
Corollary 7. The MinCkSC
![]() $_{con}$
problem is polynomial time solvable on a graph whose treewidth is bounded above by a constant.
$_{con}$
problem is polynomial time solvable on a graph whose treewidth is bounded above by a constant.
4. Sub-exponential FPT algorithm for MinC
 $\boldsymbol{k}$
SC
$\boldsymbol{k}$
SC
 $_{\boldsymbol{con}}$
on
$_{\boldsymbol{con}}$
on
 $\boldsymbol{H}$
-minor-free graphs
$\boldsymbol{H}$
-minor-free graphs
In this section, we present an FPT algorithm for the following parameterized version of the MinCkSC
![]() $_{con}$
problem on an H-free graph G: For a fixed graph H, given an H-free graph G and an integer t, is there a CkSC
$_{con}$
problem on an H-free graph G: For a fixed graph H, given an H-free graph G and an integer t, is there a CkSC
![]() $_{con}$
in G with size at most t? If the answer is yes, then the algorithm is able to find out an optimal solution in time f(t)p(n), where p(n) is a polynomial on the input size n, and f(t) is a function depending on t and H (but is independent of n).
$_{con}$
in G with size at most t? If the answer is yes, then the algorithm is able to find out an optimal solution in time f(t)p(n), where p(n) is a polynomial on the input size n, and f(t) is a function depending on t and H (but is independent of n).
The algorithm employs the following result which was due to Demaine and Hajiaghayi.
Lemma 8. (Demaine et al. (2008)). Any H-minor-free graph with treewidth at least
![]() $\omega$
has an
$\omega$
has an
![]() $c(H)\omega\times c(H)\omega$
grid as a minor, where c(H) is a parameter dependending on H.
$c(H)\omega\times c(H)\omega$
grid as a minor, where c(H) is a parameter dependending on H.
We could prove the following upper bound for the size of a CkSC on a
![]() $g\times g$
grid.
$g\times g$
grid.
Lemma 9. For a moderately large g (compared with k), any CkSC on a
![]() $g\times g$
grid has size larger than
$g\times g$
grid has size larger than
![]() $g^2/(2k)$
.
$g^2/(2k)$
.
Proof. Suppose C is a CkSC of a
![]() $g\times g$
grid. Note that each
$g\times g$
grid. Note that each
![]() $\lceil \sqrt{k}\rceil\times\lceil \sqrt{k}\rceil$
grid must contain a vertex of C. A
$\lceil \sqrt{k}\rceil\times\lceil \sqrt{k}\rceil$
grid must contain a vertex of C. A
![]() $g\times g$
grid has at least
$g\times g$
grid has at least
![]() $\lfloor\frac{g}{\lceil\sqrt k\rceil}\rfloor\times \lfloor\frac{g}{\lceil\sqrt k\rceil}\rfloor$
disjoint
$\lfloor\frac{g}{\lceil\sqrt k\rceil}\rfloor\times \lfloor\frac{g}{\lceil\sqrt k\rceil}\rfloor$
disjoint
![]() $\lceil k\rceil\times\lceil k\rceil$
grids. When g is moderately large,
$\lceil k\rceil\times\lceil k\rceil$
grids. When g is moderately large,
![]() $\lfloor\frac{g}{\lceil\sqrt k\rceil}\rfloor\times \lfloor\frac{g}{\lceil\sqrt k\rceil}\rfloor > \frac{g^2}{2k}$
. Then the lemma follows.
$\lfloor\frac{g}{\lceil\sqrt k\rceil}\rfloor\times \lfloor\frac{g}{\lceil\sqrt k\rceil}\rfloor > \frac{g^2}{2k}$
. Then the lemma follows.
As a consequence of Lemma 9, if the minimum CkSC
![]() $_{con}$
of graph G has at most
$_{con}$
of graph G has at most
![]() $g^2/2k$
vertices, then G cannot have
$g^2/2k$
vertices, then G cannot have
![]() $g\times g$
grid as a minor. So, for the parameterized version of the CkSC
$g\times g$
grid as a minor. So, for the parameterized version of the CkSC
![]() $_{con}$
problem with parameter t, if the answer is yes, then G is
$_{con}$
problem with parameter t, if the answer is yes, then G is
![]() $(\sqrt{2kt}\times\sqrt{2kt})$
-grid minor-free. By Lemma 8, the treewidth of G is smaller than
$(\sqrt{2kt}\times\sqrt{2kt})$
-grid minor-free. By Lemma 8, the treewidth of G is smaller than
![]() $\sqrt{2kt}/c(H)$
. Combining this with Theorem 3.2, we could find an optimal solution in time
$\sqrt{2kt}/c(H)$
. Combining this with Theorem 3.2, we could find an optimal solution in time
 $O\left(\left(2^{\Theta((\sqrt{2kt}/{c(H)})^3)}+\frac{\sqrt{2kt}}{c(H)}\left(2(k-1)\frac{\sqrt{2kt}}{c(H)}\right)^{3\frac{\sqrt{2kt}}{c(H)}}\right)|V|\right)$
. On the other hand, if the computed treewidth is larger than
$O\left(\left(2^{\Theta((\sqrt{2kt}/{c(H)})^3)}+\frac{\sqrt{2kt}}{c(H)}\left(2(k-1)\frac{\sqrt{2kt}}{c(H)}\right)^{3\frac{\sqrt{2kt}}{c(H)}}\right)|V|\right)$
. On the other hand, if the computed treewidth is larger than
![]() $\sqrt{2kt}/c(H)$
, then the answer to the instance must be no.
$\sqrt{2kt}/c(H)$
, then the answer to the instance must be no.
In particular, if
![]() $|V(H)|$
has a constant upper bound, then c(H) is a constant. Combining this with our assumption that k is a constant, we have the following result.
$|V(H)|$
has a constant upper bound, then c(H) is a constant. Combining this with our assumption that k is a constant, we have the following result.
Theorem Suppose H is a graph with a constant number of vertices and k is a constant integer. The parameterized version of the MinCkSC
![]() $_{con}$
problem on an H-minor-free graph can be solved in time
$_{con}$
problem on an H-minor-free graph can be solved in time
![]() $O\Big(\sqrt{t}^{O(\sqrt{t})}|V|\Big)$
.
$O\Big(\sqrt{t}^{O(\sqrt{t})}|V|\Big)$
.
5. Conclusion
In this paper, we designed a local search algorithm for MinCkSC on H-minor-free graph, which achieves
![]() $(1+\varepsilon)$
-approximation; presented a dynamic programming for MinCkSC
$(1+\varepsilon)$
-approximation; presented a dynamic programming for MinCkSC
![]() $_{con}$
the running time of which depends on the treewidth; and obtained an FPT algorithm for MinCkSC
$_{con}$
the running time of which depends on the treewidth; and obtained an FPT algorithm for MinCkSC
![]() $_{con}$
on H-minor-free graphs. Our results hold for general constant k.
$_{con}$
on H-minor-free graphs. Our results hold for general constant k.
Note that this paper only focuses on the cardinality version of MinCkSC and MinCkSC
![]() $_{con}$
. Studies on their weighted variants remain to be further explored.
$_{con}$
. Studies on their weighted variants remain to be further explored.
Declarations
The authors declare that they have no competing interests.