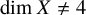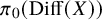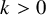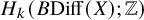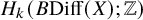1 Introduction
1.1 Main results
The purpose of this paper is to present a new special phenomenon in dimension 4 in terms diffeomorphism groups. To describe our result, let
![]() $\mathrm {Diff}(X)$
denote the diffeomorphism group equipped with the
$\mathrm {Diff}(X)$
denote the diffeomorphism group equipped with the
![]() $C^\infty $
-topology for a given a smooth manifold X. It is known that the mapping class group
$C^\infty $
-topology for a given a smooth manifold X. It is known that the mapping class group
![]() $\pi _0(\mathrm {Diff}(X))$
is finitely generated, if X is simply-connected closed and
$\pi _0(\mathrm {Diff}(X))$
is finitely generated, if X is simply-connected closed and
![]() $\dim X \neq $
4. For
$\dim X \neq $
4. For
![]() $\dim X \geq 5$
, this is due to Sullivan [Reference Sullivan33, Theorem (13.3)]. For
$\dim X \geq 5$
, this is due to Sullivan [Reference Sullivan33, Theorem (13.3)]. For
![]() $\dim X \leq 3$
, finite generation holds even dropping the simple-connectivity: In fact, even stronger finiteness is known in all dimensions
$\dim X \leq 3$
, finite generation holds even dropping the simple-connectivity: In fact, even stronger finiteness is known in all dimensions
![]() $\neq $
4 (see Subsection 5.1, including a remark for dim
$\neq $
4 (see Subsection 5.1, including a remark for dim
![]() $=$
5).
$=$
5).
We prove that analogous finite generation fails in dimension 4. Namely, we show that there exist simply-connected closed smooth 4-manifolds whose mapping class groups are infinitely generated:
Theorem 1.1. For
![]() $n \geq 2$
, set
$n \geq 2$
, set
![]() $X=E(n)\#S^2 \times S^2$
. Then
$X=E(n)\#S^2 \times S^2$
. Then
![]() $\pi _0(\mathrm {Diff}(X))$
is not finitely generated.
$\pi _0(\mathrm {Diff}(X))$
is not finitely generated.
Here,
![]() $E(n)$
denotes the simply-connected elliptic surface of degree n without multiple fiber. As is well-known,
$E(n)$
denotes the simply-connected elliptic surface of degree n without multiple fiber. As is well-known,
![]() $E(n)\#S^2 \times S^2$
can be written in terms of further basic 4-manifolds (e.g., [Reference Gompf15, Corollary 8]):
$E(n)\#S^2 \times S^2$
can be written in terms of further basic 4-manifolds (e.g., [Reference Gompf15, Corollary 8]):
 $$\begin{align*}E(n)\#S^2 \times S^2 \cong \left\{ \begin{array}{ll} 2n\mathbb{CP}^2\#10n\overline{\mathbb{CP}}^2 & \text{ for } n \text{ odd},\\ m(K3\#S^2 \times S^2) & \text{ for } n =2m \text{ even}. \end{array} \right. \end{align*}$$
$$\begin{align*}E(n)\#S^2 \times S^2 \cong \left\{ \begin{array}{ll} 2n\mathbb{CP}^2\#10n\overline{\mathbb{CP}}^2 & \text{ for } n \text{ odd},\\ m(K3\#S^2 \times S^2) & \text{ for } n =2m \text{ even}. \end{array} \right. \end{align*}$$
Remark 1.2. After completing a preprint version of this paper, the author was informed that David Baraglia [Reference Baraglia4] also proved that the mapping class groups of simply-connected 4-manifolds can be infinitely generated. Baraglia’s proof is based on essentially the same method as ours; however, we obtained our proofs completely independently.
Remark 1.3 (Topological mapping class group).
Let
![]() $\text {Homeo}(X)$
denote the homeomorphism group of X. If X is a simply-connected closed topological 4-manifold, then
$\text {Homeo}(X)$
denote the homeomorphism group of X. If X is a simply-connected closed topological 4-manifold, then
![]() $\pi _0(\text {Homeo}(X))$
is finitely generated. This follows from a result by Quinn [Reference Quinn29] and Perron [Reference Perron28]. Thus, infinite generation exhibited in Theorem 1.1 is special to the 4-dimensional smooth category.
$\pi _0(\text {Homeo}(X))$
is finitely generated. This follows from a result by Quinn [Reference Quinn29] and Perron [Reference Perron28]. Thus, infinite generation exhibited in Theorem 1.1 is special to the 4-dimensional smooth category.
Theorem 1.1 is a consequence of a more general result on the (co)homology of the moduli spaces
![]() $B\mathrm {Diff}(X)$
of 4-manifolds X. The (co)homology of
$B\mathrm {Diff}(X)$
of 4-manifolds X. The (co)homology of
![]() $B\mathrm {Diff}(X)$
is a fundamental object, since it corresponds to the set of characteristic classes of fiber bundles with fiber X. We shall prove that, for each
$B\mathrm {Diff}(X)$
is a fundamental object, since it corresponds to the set of characteristic classes of fiber bundles with fiber X. We shall prove that, for each
![]() $k\geq 0$
, there exist simply-connected closed smooth 4-manifolds X where
$k\geq 0$
, there exist simply-connected closed smooth 4-manifolds X where
![]() $H_{k}(B\mathrm {Diff}(X);\mathbb {Z})$
are infinitely generated. More strongly, we shall see that the ‘topologically trivial parts’ of
$H_{k}(B\mathrm {Diff}(X);\mathbb {Z})$
are infinitely generated. More strongly, we shall see that the ‘topologically trivial parts’ of
![]() $H_{k}(B\mathrm {Diff}(X);\mathbb {Z})$
can be infinitely generated. To state this, let
$H_{k}(B\mathrm {Diff}(X);\mathbb {Z})$
can be infinitely generated. To state this, let
![]() $i : \mathrm {Diff}(X) \hookrightarrow \text {Homeo}(X)$
denote the inclusion map into the homeomorphism group. We shall prove the following:
$i : \mathrm {Diff}(X) \hookrightarrow \text {Homeo}(X)$
denote the inclusion map into the homeomorphism group. We shall prove the following:
Theorem 1.4. For
![]() $n \geq 2$
and
$n \geq 2$
and
![]() $k \geq 1$
, set
$k \geq 1$
, set
![]() $X = E(n)\# k S^2 \times S^2$
. Then
$X = E(n)\# k S^2 \times S^2$
. Then
contains a direct summand isomorphic to
![]() $(\mathbb {Z}/2)^\infty $
. In particular,
$(\mathbb {Z}/2)^\infty $
. In particular,
![]() $H_{k}(B\mathrm {Diff}(X);\mathbb {Z})$
is not finitely generated.
$H_{k}(B\mathrm {Diff}(X);\mathbb {Z})$
is not finitely generated.
Here,
![]() $(\mathbb {Z}/2)^\infty $
denotes the countably infinite direct sum
$(\mathbb {Z}/2)^\infty $
denotes the countably infinite direct sum
![]() $\bigoplus _{\mathbb {N}}\mathbb {Z}/2$
. Rephrasing Theorem 1.4 for
$\bigoplus _{\mathbb {N}}\mathbb {Z}/2$
. Rephrasing Theorem 1.4 for
![]() $k=1$
, we have the following result, which immediately implies Theorem 1.1:
$k=1$
, we have the following result, which immediately implies Theorem 1.1:
Corollary 1.5. For
![]() $n \geq 2$
, set
$n \geq 2$
, set
![]() $X=E(n)\#S^2\times S^2$
. Then
$X=E(n)\#S^2\times S^2$
. Then
contains a direct summand isomorphic to
![]() $(\mathbb {Z}/2)^\infty $
. Here the subscript
$(\mathbb {Z}/2)^\infty $
. Here the subscript
![]() $\mathrm {ab}$
indicates the abelianization.
$\mathrm {ab}$
indicates the abelianization.
To our knowledge, Theorem 1.4 gives the first examples of simply-connected closed manifolds X where
![]() $H_k(B\mathrm {Diff}(X);\mathbb {Z})$
are confirmed to be infinitely generated for given
$H_k(B\mathrm {Diff}(X);\mathbb {Z})$
are confirmed to be infinitely generated for given
![]() $k\geq 1$
(for
$k\geq 1$
(for
![]() $k=1$
, this follows also from the aforementioned result by Baraglia [Reference Baraglia4]). It is worth noting that there are several established and expected finiteness in dim
$k=1$
, this follows also from the aforementioned result by Baraglia [Reference Baraglia4]). It is worth noting that there are several established and expected finiteness in dim
![]() $\neq 4$
(Remark 1.8). Thus, infiniteness given in Theorem 1.4 reflects a specialty of dimension 4, described in terms of characteristic classes of fiber bundles (see Remark 1.6 below).
$\neq 4$
(Remark 1.8). Thus, infiniteness given in Theorem 1.4 reflects a specialty of dimension 4, described in terms of characteristic classes of fiber bundles (see Remark 1.6 below).
Remark 1.6. In terms of cohomology, Theorem 1.4 deduces that non-topological characteristic classes may form a group isomorphic to
![]() $(\mathbb {Z}/2)^{\infty }$
for some 4-manifolds. Here, we call an element of
$(\mathbb {Z}/2)^{\infty }$
for some 4-manifolds. Here, we call an element of
a non-topological characteristic class (over
![]() $\mathbb {Z}/2$
). This
$\mathbb {Z}/2$
). This
![]() $(\mathbb {Z}/2)^{\infty }$
-subgroup is generated by gauge-theoretic characteristic classes we shall introduce (Subsection 1.3). In contrast, the Mumford–Morita–Miller classes, the most basic characteristic class of manifold bundles, are topological over a field of characteristic 2 or 0 [Reference Ebert and Randal-Williams11].
$(\mathbb {Z}/2)^{\infty }$
-subgroup is generated by gauge-theoretic characteristic classes we shall introduce (Subsection 1.3). In contrast, the Mumford–Morita–Miller classes, the most basic characteristic class of manifold bundles, are topological over a field of characteristic 2 or 0 [Reference Ebert and Randal-Williams11].
It is worth noting a consequence about stabilization. Recently, Lin and the author [Reference Konno and Lin20] proved that the moduli spaces
![]() $B\mathrm {Diff}(X)$
of 4-manifolds X do not satisfy homological stability with respect to connected sums of
$B\mathrm {Diff}(X)$
of 4-manifolds X do not satisfy homological stability with respect to connected sums of
![]() $S^2 \times S^2$
, unlike what happens in dimension
$S^2 \times S^2$
, unlike what happens in dimension
![]() $\neq 4$
[Reference Harer16, Reference Galatius and Randal-Williams14]. The proof of Theorem 1.4 shows also that the unstable part of
$\neq 4$
[Reference Harer16, Reference Galatius and Randal-Williams14]. The proof of Theorem 1.4 shows also that the unstable part of
![]() $H_\ast (B\mathrm {Diff}(X))$
may be infinitely generated. To state this precisely, given a closed 4-manifold X, take a smoothly embedded 4-disk
$H_\ast (B\mathrm {Diff}(X))$
may be infinitely generated. To state this precisely, given a closed 4-manifold X, take a smoothly embedded 4-disk
![]() $D^4$
in X, and set
$D^4$
in X, and set
![]() $\mathring {X} = X \setminus \mathrm {Int}(D^4)$
. Let
$\mathring {X} = X \setminus \mathrm {Int}(D^4)$
. Let
![]() $\mathrm {Diff}_\partial (\mathring {X})$
denote the group of diffeomorphisms that are the identity near
$\mathrm {Diff}_\partial (\mathring {X})$
denote the group of diffeomorphisms that are the identity near
![]() $\partial \mathring {X}$
. Form the (inner) connected sum
$\partial \mathring {X}$
. Form the (inner) connected sum
![]() $\mathring {X}\#S^2 \times S^2$
by
$\mathring {X}\#S^2 \times S^2$
by
![]() $\mathring {X}\cup _{S^3} ((S^3 \times [0,1])\#S^2 \times S^2)$
. Then one can define the stabilization map
$\mathring {X}\cup _{S^3} ((S^3 \times [0,1])\#S^2 \times S^2)$
. Then one can define the stabilization map
by extending by the identity on
![]() $(S^3 \times [0,1])\#S^2 \times S^2$
. We shall prove the following:
$(S^3 \times [0,1])\#S^2 \times S^2$
. We shall prove the following:
Theorem 1.7. For
![]() $n \geq 2$
and
$n \geq 2$
and
![]() $k \geq 1$
, set
$k \geq 1$
, set
![]() $X = E(n)\# k S^2 \times S^2$
. Then the kernel of the induced map
$X = E(n)\# k S^2 \times S^2$
. Then the kernel of the induced map
contains a direct summand isomorphic to
![]() $(\mathbb {Z}/2)^\infty $
.
$(\mathbb {Z}/2)^\infty $
.
1.2 Related results
The following remarks list related results in more detail:
Remark 1.8 (Other finiteness in
 $\dim \neq 4$
).
$\dim \neq 4$
).
Let us compare infinite generation of
![]() $H_k(B\text {Diff}(X);\mathbb {Z})$
in Theorem 1.4 with other dimensions. For a manifold X of even
$H_k(B\text {Diff}(X);\mathbb {Z})$
in Theorem 1.4 with other dimensions. For a manifold X of even
![]() $\dim \geq 6$
and with finite
$\dim \geq 6$
and with finite
![]() $\pi _1(X)$
, Bustamante–Krannich–Kupers proved that
$\pi _1(X)$
, Bustamante–Krannich–Kupers proved that
![]() $H_k(B\mathrm {Diff}(X);\mathbb {Z})$
is finitely generated for each k [Reference Bustamante, Krannich and Kupers9, Corollary B]. Also, in his earlier paper, Kupers [Reference Kupers22, Corollary C] has proved an analogous statement for a 2-connected manifold X of
$H_k(B\mathrm {Diff}(X);\mathbb {Z})$
is finitely generated for each k [Reference Bustamante, Krannich and Kupers9, Corollary B]. Also, in his earlier paper, Kupers [Reference Kupers22, Corollary C] has proved an analogous statement for a 2-connected manifold X of
![]() $\dim \neq 4,5,7$
. As mentioned in [Reference Bustamante, Krannich and Kupers9], there is an expectation that finiteness may hold even dropping the 2-connectivity. For finiteness of mapping class groups in dimension
$\dim \neq 4,5,7$
. As mentioned in [Reference Bustamante, Krannich and Kupers9], there is an expectation that finiteness may hold even dropping the 2-connectivity. For finiteness of mapping class groups in dimension
![]() $\neq 4$
, see Subsection 5.1.
$\neq 4$
, see Subsection 5.1.
Remark 1.9 (Infiniteness of the Torelli group).
Given a smooth closed oriented 4-manifold X, let
![]() $\text {TDiff}(X)$
denote the Torelli diffeomorphism group (i.e., the group of diffeomorphisms acting trivially on
$\text {TDiff}(X)$
denote the Torelli diffeomorphism group (i.e., the group of diffeomorphisms acting trivially on
![]() $H_\ast (X;\mathbb {Z})$
). Ruberman [Reference Ruberman31, Theorem A] proved that
$H_\ast (X;\mathbb {Z})$
). Ruberman [Reference Ruberman31, Theorem A] proved that
![]() $\pi _0(\text {TDiff}(X))$
are infinitely generated for
$\pi _0(\text {TDiff}(X))$
are infinitely generated for
![]() ${X=E(n)\#\mathbb {CP}^2\#k\overline {\mathbb {CP}}^2}$
with
${X=E(n)\#\mathbb {CP}^2\#k\overline {\mathbb {CP}}^2}$
with
![]() $k \geq 2$
. Note that infinite generation of
$k \geq 2$
. Note that infinite generation of
![]() $\pi _0(\mathrm {Diff}(X))$
does not necessarily follow from that of
$\pi _0(\mathrm {Diff}(X))$
does not necessarily follow from that of
![]() $\pi _0(\text {TDiff}(X))$
. For example,
$\pi _0(\text {TDiff}(X))$
. For example,
![]() $\pi _0(\text {TDiff}(X))$
is infinitely generated if one takes X to be the genus 2 surface, whereas
$\pi _0(\text {TDiff}(X))$
is infinitely generated if one takes X to be the genus 2 surface, whereas
![]() $\pi _0(\mathrm {Diff}(X))$
is finitely generated [Reference McCullough and Miller26]. This phenomenon may occur since the index of
$\pi _0(\mathrm {Diff}(X))$
is finitely generated [Reference McCullough and Miller26]. This phenomenon may occur since the index of
![]() $\pi _0(\text {TDiff}(X))$
in
$\pi _0(\text {TDiff}(X))$
in
![]() $\pi _0(\mathrm {Diff}(X))$
is infinite (also for X in Theorem 1.4), and an infinite index subgroup of a finitely generated group is not necessarily finitely generated.
$\pi _0(\mathrm {Diff}(X))$
is infinite (also for X in Theorem 1.4), and an infinite index subgroup of a finitely generated group is not necessarily finitely generated.
Remark 1.10 (Other infiniteness in
 $\dim =4$
).
$\dim =4$
).
Baraglia [Reference Baraglia3] and Lin [Reference Lin24] proved that
![]() $\pi _1(\mathrm {Diff}(X))$
have infinite-rank summands for some simply-connected (irreducible) 4-manifolds X. Further, Auckly–Ruberman [Reference Auckly and Ruberman1] announced that, for each
$\pi _1(\mathrm {Diff}(X))$
have infinite-rank summands for some simply-connected (irreducible) 4-manifolds X. Further, Auckly–Ruberman [Reference Auckly and Ruberman1] announced that, for each
![]() $k>0$
, there are simply-connected 4-manifolds X such that
$k>0$
, there are simply-connected 4-manifolds X such that
![]() $\pi _k(\mathrm {Diff}(X))$
have infinite-rank summands. They prove an analogous result also for
$\pi _k(\mathrm {Diff}(X))$
have infinite-rank summands. They prove an analogous result also for
![]() $H_{k}(B\text {TDiff}(X);\mathbb {Z})$
.
$H_{k}(B\text {TDiff}(X);\mathbb {Z})$
.
Remark 1.11 (Non-simply-connected manifolds).
For non-simply-connected manifolds of
![]() $\dim \geq 4$
, it has been known that the mapping class group may be infinitely generated. For instance, Hatcher [Reference Hatcher18, Theorem 4.1] proved that the mapping class groups of the tori
$\dim \geq 4$
, it has been known that the mapping class group may be infinitely generated. For instance, Hatcher [Reference Hatcher18, Theorem 4.1] proved that the mapping class groups of the tori
![]() $T^n$
for
$T^n$
for
![]() $n \geq 5$
are infinitely generated. In dimension 4, Budney–Gabai [Reference Budney and Gabai7] and Watanabe [Reference Watanabe36] gave examples of non-simply-connected 4-manifolds whose mapping class groups are infinitely generated. Budney–Gabai [Reference Budney and Gabai8] also proved that their infinitely generated subgroups of mapping class groups are nontrivial also in the topological category.
$n \geq 5$
are infinitely generated. In dimension 4, Budney–Gabai [Reference Budney and Gabai7] and Watanabe [Reference Watanabe36] gave examples of non-simply-connected 4-manifolds whose mapping class groups are infinitely generated. Budney–Gabai [Reference Budney and Gabai8] also proved that their infinitely generated subgroups of mapping class groups are nontrivial also in the topological category.
1.3 Scheme of the proof
Now we describe the idea of proofs of our results given in Subsection 1.1. We shall introduce an infinite family of characteristic classes
using Seiberg–Witten theory for families. Here,
![]() $\mathcal {S}$
are
$\mathcal {S}$
are
![]() $\mathrm {Diff}^+(X)$
-invariant subsets of the set of spin
$\mathrm {Diff}^+(X)$
-invariant subsets of the set of spin
![]() $^c$
structures
$^c$
structures
![]() $\mathrm {Spin}^{c}(X,k)$
on X with Seiberg–Witten formal dimension
$\mathrm {Spin}^{c}(X,k)$
on X with Seiberg–Witten formal dimension
![]() $-k$
, divided by the charge conjugation (see Subsection 3.1 for the precise definition).
$-k$
, divided by the charge conjugation (see Subsection 3.1 for the precise definition).
A characteristic class for families of 4-manifolds using Seiberg–Witten theory was introduced by the author [Reference Konno19], under the assumption that the monodromies of families preserve a given spin
![]() $^c$
structure. Later, Lin and the author [Reference Konno and Lin20] defined a version without the assumption on monodromy. The classes (1) are refinements of the characteristic class defined in [Reference Konno and Lin20].
$^c$
structure. Later, Lin and the author [Reference Konno and Lin20] defined a version without the assumption on monodromy. The classes (1) are refinements of the characteristic class defined in [Reference Konno and Lin20].
Using the characteristic classes (1), we can define a homomorphism
The above results follow by seeing that this homomorphism has infinitely generated image in
![]() $\bigoplus _{\mathcal {S}} \mathbb {Z}/2$
for some class of 4-manifolds X, including
$\bigoplus _{\mathcal {S}} \mathbb {Z}/2$
for some class of 4-manifolds X, including
![]() $X=E(n)\#kS^2\times S^2$
. More precisely, we shall see that
$X=E(n)\#kS^2\times S^2$
. More precisely, we shall see that
![]() $\langle \mathbb {SW}_{\mathrm {half}\text {-}\mathrm {tot}}^k(X,\mathcal {S}), -\rangle $
are nontrivial for infinitely many orbits
$\langle \mathbb {SW}_{\mathrm {half}\text {-}\mathrm {tot}}^k(X,\mathcal {S}), -\rangle $
are nontrivial for infinitely many orbits
![]() $\mathcal {S}$
for the action of
$\mathcal {S}$
for the action of
![]() $\mathrm {Diff}^+(X)$
on
$\mathrm {Diff}^+(X)$
on
![]() $\mathrm {Spin}^{c}(X,k)$
, which are distinguished by divisibilities of the first Chern classes.
$\mathrm {Spin}^{c}(X,k)$
, which are distinguished by divisibilities of the first Chern classes.
1.4 Structure of the paper
The following is an outline of the sections of the paper. In Section 2, we construct infinitely many homology classes of
![]() $B\mathrm {Diff}(X)$
for some class of 4-manifolds X, which will be shown to be linearly independent over
$B\mathrm {Diff}(X)$
for some class of 4-manifolds X, which will be shown to be linearly independent over
![]() $\mathbb {Z}/2$
. The most general statement is given as Theorem 2.7, which implies all results explained above. In Section 3, we construct characteristic classes (1) and compute them in Section 4 to prove Theorem 2.7.
$\mathbb {Z}/2$
. The most general statement is given as Theorem 2.7, which implies all results explained above. In Section 3, we construct characteristic classes (1) and compute them in Section 4 to prove Theorem 2.7.
2 Construction of homology classes
In this section, we construct infinitely many homology classes of
![]() $B\mathrm {Diff}(X)$
for 4-manifolds X with certain conditions, which will be shown to be linearly independent over
$B\mathrm {Diff}(X)$
for 4-manifolds X with certain conditions, which will be shown to be linearly independent over
![]() $\mathbb {Z}/2$
.
$\mathbb {Z}/2$
.
2.1 Mod 2 basic classes in
 $H^2(M;\mathbb {Z})/\operatorname {\mathrm {Aut}}(H^2(M;\mathbb {Z}))$
$H^2(M;\mathbb {Z})/\operatorname {\mathrm {Aut}}(H^2(M;\mathbb {Z}))$
A building block of the construction of homology classes of
![]() $B\mathrm {Diff}^+(X)$
is a 4-manifold M that admits infinitely many exotic structures. This is inspired by Ruberman’s argument [Reference Ruberman31] in his work on Torelli groups. (See also Auckly’s recent work [Reference Auckly2] for one version of Ruberman’s argument in a Seiberg–Witten context.) Compared with [Reference Ruberman31, Reference Auckly2], what we newly need to require is that those exotic structures are distinguished by mod 2 basic classes that are distinct in
$B\mathrm {Diff}^+(X)$
is a 4-manifold M that admits infinitely many exotic structures. This is inspired by Ruberman’s argument [Reference Ruberman31] in his work on Torelli groups. (See also Auckly’s recent work [Reference Auckly2] for one version of Ruberman’s argument in a Seiberg–Witten context.) Compared with [Reference Ruberman31, Reference Auckly2], what we newly need to require is that those exotic structures are distinguished by mod 2 basic classes that are distinct in
![]() $H^2(M;\mathbb {Z})/\operatorname {\mathrm {Aut}}(H^2(M;\mathbb {Z}))$
, the quotient of
$H^2(M;\mathbb {Z})/\operatorname {\mathrm {Aut}}(H^2(M;\mathbb {Z}))$
, the quotient of
![]() $H^2(M;\mathbb {Z})$
by the automorphism group of the intersection form. This is a reflection that we shall consider the whole diffeomorphism group, rather than the Torelli diffeomorphism group.
$H^2(M;\mathbb {Z})$
by the automorphism group of the intersection form. This is a reflection that we shall consider the whole diffeomorphism group, rather than the Torelli diffeomorphism group.
To formulate this precisely, let us introduce some notation. Let M be a smooth simply-connected closed oriented 4-manifold with
![]() $b^+(M) \geq 2$
. Since
$b^+(M) \geq 2$
. Since
![]() $H^2(M;\mathbb {Z})$
has no torsion, we can identify a spin
$H^2(M;\mathbb {Z})$
has no torsion, we can identify a spin
![]() $^c$
structure on M with a characteristic element in
$^c$
structure on M with a characteristic element in
![]() $H^2(M;\mathbb {Z})$
. Recall that a characteristic element
$H^2(M;\mathbb {Z})$
. Recall that a characteristic element
![]() ${c \in H^2(M;\mathbb {Z})}$
is called a basic class if
${c \in H^2(M;\mathbb {Z})}$
is called a basic class if
![]() $SW(M,c)$
, the Seiberg–Witten invariant, is nonzero. If
$SW(M,c)$
, the Seiberg–Witten invariant, is nonzero. If
![]() $SW(M,c) \neq 0$
mod
$SW(M,c) \neq 0$
mod
![]() $2$
, we say that c is a mod 2 basic class. For simplicity, whenever we say that c is a (mod 2) basic class, we further impose that the formal dimension of c is zero (see (5)). We denote by
$2$
, we say that c is a mod 2 basic class. For simplicity, whenever we say that c is a (mod 2) basic class, we further impose that the formal dimension of c is zero (see (5)). We denote by
![]() $\mathcal {B}_2(M)$
the set of mod 2 basic classes of M. Note that
$\mathcal {B}_2(M)$
the set of mod 2 basic classes of M. Note that
![]() $\mathcal {B}_2(M)$
is preserved under the
$\mathcal {B}_2(M)$
is preserved under the
![]() $\mathbb {Z}/2$
-action on
$\mathbb {Z}/2$
-action on
![]() $H^2(M;\mathbb {Z})$
via multiplication by
$H^2(M;\mathbb {Z})$
via multiplication by
![]() $-1$
. For a nonzero cohomology class
$-1$
. For a nonzero cohomology class
![]() $x \in H^2(M;\mathbb {Z})$
, let
$x \in H^2(M;\mathbb {Z})$
, let
![]() $\mathrm {div}(x)$
denote the divisibility of x – namely,
$\mathrm {div}(x)$
denote the divisibility of x – namely,
For the zero element, we formally set
![]() $\mathrm {div}(0)=0$
in this paper. For a characteristic element
$\mathrm {div}(0)=0$
in this paper. For a characteristic element
![]() $c \in H^2(M;\mathbb {Z})$
, define
$c \in H^2(M;\mathbb {Z})$
, define
where
![]() $x^2$
denotes the self-intersection of x. In this section, we consider a 4-manifold M to satisfy the following assumption:
$x^2$
denotes the self-intersection of x. In this section, we consider a 4-manifold M to satisfy the following assumption:
Assumption 2.1. Let M be an indefinite smooth simply-connected closed oriented 4-manifold with
![]() $b^+(M) \geq 2$
. Assume that there exist smooth 4-manifolds
$b^+(M) \geq 2$
. Assume that there exist smooth 4-manifolds
![]() $\{M_i\}_{i=1}^\infty $
that satisfy the following three properties:
$\{M_i\}_{i=1}^\infty $
that satisfy the following three properties:
-
(i) Each
 $M_i$
is homeomorphic to M.
$M_i$
is homeomorphic to M. -
(ii) For every i,
 $M_i\#S^2\times S^2$
is diffeomorphic to
$M_i\#S^2\times S^2$
is diffeomorphic to
 $M\#S^2\times S^2$
.
$M\#S^2\times S^2$
. -
(iii) For every i, there exists a mod 2 basic class
 $c_i$
on
$c_i$
on
 $M_i$
with
$M_i$
with
 $N(M_i;c_i)$
odd, and the sequence
$N(M_i;c_i)$
odd, and the sequence
 $\{c_i\}_{i=1}^\infty $
satisfies that
$\{c_i\}_{i=1}^\infty $
satisfies that
 $\mathrm {div}(c_i) \to +\infty $
as
$\mathrm {div}(c_i) \to +\infty $
as
 $i \to +\infty $
.
$i \to +\infty $
.
It is worth adding notes on the last property (iii) of Assumption 2.1. The principal intention of (iii) is to ensure that the mod 2 basic classes are distinct even in the quotient
![]() $H^2(M;\mathbb {Z})/\operatorname {\mathrm {Aut}}(H^2(M;\mathbb {Z}))$
(after passing to a subsequence, if necessary). For most 4-manifolds, increasing either divisibilities or self-intersections is the only possible way to get infinitely many characteristics distinct in
$H^2(M;\mathbb {Z})/\operatorname {\mathrm {Aut}}(H^2(M;\mathbb {Z}))$
(after passing to a subsequence, if necessary). For most 4-manifolds, increasing either divisibilities or self-intersections is the only possible way to get infinitely many characteristics distinct in
![]() $H^2(M;\mathbb {Z})/\operatorname {\mathrm {Aut}}(H^2(M;\mathbb {Z}))$
(cf. Proposition 4.5). The reason why we suppose
$H^2(M;\mathbb {Z})/\operatorname {\mathrm {Aut}}(H^2(M;\mathbb {Z}))$
(cf. Proposition 4.5). The reason why we suppose
![]() $N(M_i; c_i)$
is odd is that we want to control sums of mod 2 Seiberg–Witten invariants over some class of spin
$N(M_i; c_i)$
is odd is that we want to control sums of mod 2 Seiberg–Witten invariants over some class of spin
![]() $^c$
structures.
$^c$
structures.
As a series of examples of M satisfying Assumption 2.1, we have the following:
Lemma 2.2. For
![]() $n\geq 1$
,
$n\geq 1$
,
![]() $M=E(n)$
satisfies Assumption 2.1.
$M=E(n)$
satisfies Assumption 2.1.
To see Lemma 2.2, let us consider logarithmic transformations. For
![]() $n \geq 2$
and
$n \geq 2$
and
![]() $i \geq 1$
, let
$i \geq 1$
, let
![]() $E(n;i)$
denote the logarithmic transformation of order
$E(n;i)$
denote the logarithmic transformation of order
![]() $i>0$
performed on
$i>0$
performed on
![]() $E(n)$
(i.e.,
$E(n)$
(i.e.,
![]() $E(n;i)$
is the elliptic surface of degree n with a single multiple fiber of order i). (Note that
$E(n;i)$
is the elliptic surface of degree n with a single multiple fiber of order i). (Note that
![]() $E(n;1)=E(n)$
.) The Seiberg–Witten invariants of
$E(n;1)=E(n)$
.) The Seiberg–Witten invariants of
![]() $E(n;i)$
were computed by Fintushel–Stern [Reference Fintushel and Stern12]. For readers’ convenience, we recall the result following their survey [Reference Fintushel and Stern13, Lecture 2].
$E(n;i)$
were computed by Fintushel–Stern [Reference Fintushel and Stern12]. For readers’ convenience, we recall the result following their survey [Reference Fintushel and Stern13, Lecture 2].
In general, let Z be an oriented closed smooth 4-manifold with
![]() $b^+(Z) \geq 2$
, without torsion in
$b^+(Z) \geq 2$
, without torsion in
![]() $H^2(Z;\mathbb {Z})$
. Consider the Laurent polynomial
$H^2(Z;\mathbb {Z})$
. Consider the Laurent polynomial
Here,
![]() $c \in H^2(Z;\mathbb {Z})$
are characteristic elements and
$c \in H^2(Z;\mathbb {Z})$
are characteristic elements and
![]() $t_c$
are formal variables in
$t_c$
are formal variables in
![]() $\mathbb {Z}[H^2(Z;\mathbb {Z})]$
corresponding to c. Note that
$\mathbb {Z}[H^2(Z;\mathbb {Z})]$
corresponding to c. Note that
![]() $t_{c}t_{c'}=t_{c+c'}$
– in particular,
$t_{c}t_{c'}=t_{c+c'}$
– in particular,
![]() $t_c^m=t_{mc}$
for
$t_c^m=t_{mc}$
for
![]() $m \in \mathbb {Z}$
.
$m \in \mathbb {Z}$
.
Now consider
![]() $Z=E(n;i)$
. Let
$Z=E(n;i)$
. Let
![]() $F \in H_2(E(n;i);\mathbb {Z})$
be the class that represents a generic fiber of the elliptic fibration. The multiple fiber of
$F \in H_2(E(n;i);\mathbb {Z})$
be the class that represents a generic fiber of the elliptic fibration. The multiple fiber of
![]() $E(n;i)$
represents a primitive homology class, which is given by
$E(n;i)$
represents a primitive homology class, which is given by
![]() $F/i$
. Let
$F/i$
. Let
![]() $F_i$
denote the Poincaré dual of
$F_i$
denote the Poincaré dual of
![]() $F/i$
and set
$F/i$
and set
![]() $t = t_{F_i}$
. Then the Seiberg–Witten polynomial for
$t = t_{F_i}$
. Then the Seiberg–Witten polynomial for
![]() $E(n;i)$
is given by
$E(n;i)$
is given by
Lemma 2.3. The classes
![]() $\pm (ni-i-1)F_i \in H^2(E(n;r);\mathbb {Z})$
are mod 2 basic classes of
$\pm (ni-i-1)F_i \in H^2(E(n;r);\mathbb {Z})$
are mod 2 basic classes of
![]() $E(n;i)$
. Further, we have
$E(n;i)$
. Further, we have
![]() $\mathrm {div}((ni-i-1)F_i)=ni-i-1$
, and there is no mod 2 basic class of
$\mathrm {div}((ni-i-1)F_i)=ni-i-1$
, and there is no mod 2 basic class of
![]() $\mathrm {div}=ni-i-1$
other than
$\mathrm {div}=ni-i-1$
other than
![]() $\pm (ni-i-1)F_i$
.
$\pm (ni-i-1)F_i$
.
Proof. Since the right-hand side of (2) is a polynomial only in t, all basic classes of
![]() $E(n;i)$
lie in the set
$E(n;i)$
lie in the set
![]() $\{kF_i \in H^2(E(n;i);\mathbb {Z}) \mid k \in \mathbb {Z}\}$
. Thus, for each
$\{kF_i \in H^2(E(n;i);\mathbb {Z}) \mid k \in \mathbb {Z}\}$
. Thus, for each
![]() $d \geq 1$
, we have at most two basic classes of
$d \geq 1$
, we have at most two basic classes of
![]() $\mathrm {div}=d$
, related by multiplication by
$\mathrm {div}=d$
, related by multiplication by
![]() $-1$
if exist. However, the top degree term of the right-hand side of (2) is given by
$-1$
if exist. However, the top degree term of the right-hand side of (2) is given by
![]() $t^{(n-2)i}t^{i-1}=t_{(ni-i-1)F_i}$
. Thus,
$t^{(n-2)i}t^{i-1}=t_{(ni-i-1)F_i}$
. Thus,
![]() $\pm (ni-i-1)F_i$
are mod 2 basic classes. The assertion of the lemma follows from this by recalling that
$\pm (ni-i-1)F_i$
are mod 2 basic classes. The assertion of the lemma follows from this by recalling that
![]() $F_i$
is a primitive class.
$F_i$
is a primitive class.
Proof of Lemma 2.2.
Set
![]() $M_i=E(n;i)$
. Here, i runs over the natural numbers, but we restrict i to be odd if n is spin, so that the spinness of
$M_i=E(n;i)$
. Here, i runs over the natural numbers, but we restrict i to be odd if n is spin, so that the spinness of
![]() $M_{i}$
is the same as that of M. Then
$M_{i}$
is the same as that of M. Then
![]() $M_i$
satisfies the properties (i) and (ii) of Assumption 2.1 by [Reference Gompf15]. To check the property (iii), set
$M_i$
satisfies the properties (i) and (ii) of Assumption 2.1 by [Reference Gompf15]. To check the property (iii), set
![]() $c_i=(ni-i-1)F_i$
. Then it follows from Lemma 2.3 that
$c_i=(ni-i-1)F_i$
. Then it follows from Lemma 2.3 that
![]() $\mathrm {div}(c_i) \to +\infty $
as
$\mathrm {div}(c_i) \to +\infty $
as
![]() $i \to +\infty $
, and
$i \to +\infty $
, and
![]() $N(M_i;c_i)=1$
for all
$N(M_i;c_i)=1$
for all
![]() $i \geq 1$
. Hence, the property (iii) is satisfied. This completes the proof.
$i \geq 1$
. Hence, the property (iii) is satisfied. This completes the proof.
2.2 Families over the torus
Fix
![]() $k>0$
, and let us take a 4-manifold M satisfying Assumption 2.1. Fix a diffeomorphism
$k>0$
, and let us take a 4-manifold M satisfying Assumption 2.1. Fix a diffeomorphism
![]() $M_i\# S^2 \times S^2 \to M\# S^2 \times S^2$
and identify
$M_i\# S^2 \times S^2 \to M\# S^2 \times S^2$
and identify
![]() $M_i\# kS^2 \times S^2$
with X for every i. Set
$M_i\# kS^2 \times S^2$
with X for every i. Set
![]() $X = M\#kS^2 \times S^2$
.
$X = M\#kS^2 \times S^2$
.
We recall a construction of a smooth fiber bundle over
![]() $T^k$
with fiber X considered in [Reference Konno19, Reference Konno and Lin20]. Define an orientation-preserving diffeomorphism
$T^k$
with fiber X considered in [Reference Konno19, Reference Konno and Lin20]. Define an orientation-preserving diffeomorphism
![]() $f_0 : S^2 \times S^2 \to S^2 \times S^2$
by
$f_0 : S^2 \times S^2 \to S^2 \times S^2$
by
![]() $f_0(x,y) = (r(x), r(y))$
, where
$f_0(x,y) = (r(x), r(y))$
, where
![]() $r : S^2 \to S^2$
is the reflection about the equator. By isotoping
$r : S^2 \to S^2$
is the reflection about the equator. By isotoping
![]() $f_0$
, we can obtain a diffeomorphism
$f_0$
, we can obtain a diffeomorphism
![]() $f : S^2 \times S^2 \to S^2 \times S^2$
that fixes a disk
$f : S^2 \times S^2 \to S^2 \times S^2$
that fixes a disk
![]() $D^4 \subset S^2 \times S^2$
pointwise. Take copies
$D^4 \subset S^2 \times S^2$
pointwise. Take copies
![]() $f_1, \ldots , f_k$
of f, and implant them into
$f_1, \ldots , f_k$
of f, and implant them into
![]() $M_i\# kS^2\times S^2$
for each i, by extending by the identity. Thus, we obtain diffeomorphisms
$M_i\# kS^2\times S^2$
for each i, by extending by the identity. Thus, we obtain diffeomorphisms
![]() $f_1, \ldots , f_k : M_i\# kS^2\times S^2 \to M_i\# kS^2\times S^2$
. Since the supports of
$f_1, \ldots , f_k : M_i\# kS^2\times S^2 \to M_i\# kS^2\times S^2$
. Since the supports of
![]() $f_1, \ldots , f_k$
are mutually disjoint, and
$f_1, \ldots , f_k$
are mutually disjoint, and
![]() $f_1, \ldots , f_k$
commute each other. Using these commuting diffeomorphisms, we can form the multiple mapping torus
$f_1, \ldots , f_k$
commute each other. Using these commuting diffeomorphisms, we can form the multiple mapping torus
![]() $E_i \to T^k$
, which is a smooth fiber bundle with fiber
$E_i \to T^k$
, which is a smooth fiber bundle with fiber
![]() $M_i\# kS^2\times S^2$
. Using the fixed identification between
$M_i\# kS^2\times S^2$
. Using the fixed identification between
![]() $M_i\# kS^2\times S^2$
and X, we obtain smooth fiber bundles (denoted by the same notation)
$M_i\# kS^2\times S^2$
and X, we obtain smooth fiber bundles (denoted by the same notation)
![]() $X \to E_i \to T^k$
with fiber X. Since f is orientation-preserving, the resulting fiber bundles
$X \to E_i \to T^k$
with fiber X. Since f is orientation-preserving, the resulting fiber bundles
![]() $E_i$
are oriented (i.e., the structure group reduces to
$E_i$
are oriented (i.e., the structure group reduces to
![]() $\mathrm {Diff}^+(X)$
, the orientation-preserving diffeomorphism group).
$\mathrm {Diff}^+(X)$
, the orientation-preserving diffeomorphism group).
For each
![]() $i\geq 1$
, regard
$i\geq 1$
, regard
![]() $E_i$
as a continuous map
$E_i$
as a continuous map
![]() $E_i : T^k \to B\mathrm {Diff}^+(X)$
. Now we set
$E_i : T^k \to B\mathrm {Diff}^+(X)$
. Now we set
This construction of the homology class
![]() $\alpha _i$
is the same as the one in [Reference Konno and Lin20, Proof of Theorem 3.10], except only for a condition on the Seiberg–Witten invariants of 4-manifolds. The origin of this construction is the first examples of exotic diffeomorphisms of 4-manifolds due to Ruberman [Reference Ruberman30].
$\alpha _i$
is the same as the one in [Reference Konno and Lin20, Proof of Theorem 3.10], except only for a condition on the Seiberg–Witten invariants of 4-manifolds. The origin of this construction is the first examples of exotic diffeomorphisms of 4-manifolds due to Ruberman [Reference Ruberman30].
Let us observe a few properties of
![]() $\alpha _i$
:
$\alpha _i$
:
Lemma 2.4. The homology class
![]() $\alpha _i$
lies in
$\alpha _i$
lies in
Proof. Since
![]() $M_1$
and
$M_1$
and
![]() $M_i$
are homeomorphic,
$M_i$
are homeomorphic,
![]() $E_1$
and
$E_1$
and
![]() $E_i$
are isomorphic as topological bundles. The assertion follows from this.
$E_i$
are isomorphic as topological bundles. The assertion follows from this.
For each i, fix a smoothly embedded 4-disk
![]() $D^4_i \subset M_i$
and similarly take
$D^4_i \subset M_i$
and similarly take
![]() $D^4 \subset M$
. Set
$D^4 \subset M$
. Set
![]() $\mathring {M}_i = M_i \setminus \mathrm {Int}(D^4_i)$
and
$\mathring {M}_i = M_i \setminus \mathrm {Int}(D^4_i)$
and
![]() $\mathring {M} = M \setminus \mathrm {Int}(D^4)$
. We can find a diffeomorphism
$\mathring {M} = M \setminus \mathrm {Int}(D^4)$
. We can find a diffeomorphism
![]() $\psi _i : M_i\#S^2\times S^2 \to M\#S^2\times S^2$
with
$\psi _i : M_i\#S^2\times S^2 \to M\#S^2\times S^2$
with
![]() $\psi _i(D^4_i)=D^4$
that respect parametrizations of
$\psi _i(D^4_i)=D^4$
that respect parametrizations of
![]() $D^4_i$
and
$D^4_i$
and
![]() $D^4$
. Thus, we can identify
$D^4$
. Thus, we can identify
![]() $\mathring {M}_i\#S^2 \times S^2$
with
$\mathring {M}_i\#S^2 \times S^2$
with
![]() $\mathring {M}\#S^2 \times S^2$
. Using these identifications, the construction of
$\mathring {M}\#S^2 \times S^2$
. Using these identifications, the construction of
![]() $E_i$
can be carried out with fixing the 4-disks, so we also have a homology class
$E_i$
can be carried out with fixing the 4-disks, so we also have a homology class
![]() $\mathring {\alpha }_i \in H_k(B\mathrm {Diff}_\partial (\mathring {X});\mathbb {Z})$
defined similarly to
$\mathring {\alpha }_i \in H_k(B\mathrm {Diff}_\partial (\mathring {X});\mathbb {Z})$
defined similarly to
![]() $\alpha _i$
– namely,
$\alpha _i$
– namely,
where
![]() $E_i$
are regarded as maps
$E_i$
are regarded as maps
![]() $E_i : T^k \to B\text {Diff}_\partial (\mathring {X})$
. Letting
$E_i : T^k \to B\text {Diff}_\partial (\mathring {X})$
. Letting
![]() $\rho : \mathrm {Diff}_\partial (\mathring {X}) \to \mathrm {Diff}^+(X)$
be the extension map by the identity, we have that
$\rho : \mathrm {Diff}_\partial (\mathring {X}) \to \mathrm {Diff}^+(X)$
be the extension map by the identity, we have that
![]() $\alpha _i$
is the image of
$\alpha _i$
is the image of
![]() $\mathring {\alpha }_i$
under the induced map
$\mathring {\alpha }_i$
under the induced map
Lemma 2.5. The homology class
![]() $\mathring {\alpha }_i$
lies in the kernel of
$\mathring {\alpha }_i$
lies in the kernel of
Proof. Let
![]() $E_S \to T^k$
denote the trivialized bundle with fiber
$E_S \to T^k$
denote the trivialized bundle with fiber
![]() $(S^2 \times S^2) \setminus \mathrm {Int}(D^4)$
. Since
$(S^2 \times S^2) \setminus \mathrm {Int}(D^4)$
. Since
![]() $M_1 \# S^2 \times S^2$
and
$M_1 \# S^2 \times S^2$
and
![]() $M_i\# S^2 \times S^2$
are diffeomorphic, the stabilized bundles
$M_i\# S^2 \times S^2$
are diffeomorphic, the stabilized bundles
![]() $E_1\#_{\mathrm {fib}}E_S$
and
$E_1\#_{\mathrm {fib}}E_S$
and
![]() $E_i\#_{\mathrm {fib}}E_S$
are smoothly isomorphic; here,
$E_i\#_{\mathrm {fib}}E_S$
are smoothly isomorphic; here,
![]() $\#_{\mathrm {fib}}$
denotes the fiberwise connected sum along the trivial sphere bundle
$\#_{\mathrm {fib}}$
denotes the fiberwise connected sum along the trivial sphere bundle
![]() $T^k \times S^3 \to T^k$
. This implies the assertion of the lemma.
$T^k \times S^3 \to T^k$
. This implies the assertion of the lemma.
Lemma 2.6. We have
![]() $2\mathring {\alpha }_i=0$
and
$2\mathring {\alpha }_i=0$
and
![]() $2\alpha _i=0$
.
$2\alpha _i=0$
.
Proof. It follows from [Reference Konno and Lin20, Lemma 3.6] that
![]() $(E_i)_\ast ([T^k])$
is 2-torsion for every i. Thus,
$(E_i)_\ast ([T^k])$
is 2-torsion for every i. Thus,
![]() $\mathring {\alpha _i}$
is also 2-torsion. Since
$\mathring {\alpha _i}$
is also 2-torsion. Since
![]() $\alpha _i=\rho _\ast (\mathring {\alpha _i})$
, we have
$\alpha _i=\rho _\ast (\mathring {\alpha _i})$
, we have
![]() $\alpha _i$
is 2-torsion as well.
$\alpha _i$
is 2-torsion as well.
The following is the most general statement of this paper:
Theorem 2.7. Let
![]() $k>0$
and let M be a smooth simply-connected closed oriented 4-manifold that satisfies Assumption 2.1. Set
$k>0$
and let M be a smooth simply-connected closed oriented 4-manifold that satisfies Assumption 2.1. Set
![]() $X=M\# kS^2\times S^2$
. Then we have the following:
$X=M\# kS^2\times S^2$
. Then we have the following:
-
(i) The set
 $\{\alpha _i \mid i\geq 2 \}$
generates a direct summand of isomorphic to
$\{\alpha _i \mid i\geq 2 \}$
generates a direct summand of isomorphic to $$\begin{align*}\ker(i_\ast : H_k(B\mathrm{Diff}^+(X);\mathbb{Z}) \to H_k(B\mathrm{Homeo}^+(X);\mathbb{Z})) \end{align*}$$
$$\begin{align*}\ker(i_\ast : H_k(B\mathrm{Diff}^+(X);\mathbb{Z}) \to H_k(B\mathrm{Homeo}^+(X);\mathbb{Z})) \end{align*}$$
 $(\mathbb {Z}/2)^\infty $
.
$(\mathbb {Z}/2)^\infty $
.
-
(ii) The set
 $\{\mathring {\alpha }_i \mid i\geq 2\}$
generates a direct summand of isomorphic to
$\{\mathring {\alpha }_i \mid i\geq 2\}$
generates a direct summand of isomorphic to $$\begin{align*}\ker(s_\ast : H_k(B\mathrm{Diff}_\partial(\mathring{X});\mathbb{Z}) \to H_k(B\mathrm{Diff}_\partial(\mathring{X}\# S^2 \times S^2);\mathbb{Z})) \end{align*}$$
$$\begin{align*}\ker(s_\ast : H_k(B\mathrm{Diff}_\partial(\mathring{X});\mathbb{Z}) \to H_k(B\mathrm{Diff}_\partial(\mathring{X}\# S^2 \times S^2);\mathbb{Z})) \end{align*}$$
 $(\mathbb {Z}/2)^\infty $
.
$(\mathbb {Z}/2)^\infty $
.
To prove Theorem 2.7, due to Lemmas 2.4 to 2.6, it suffices to show that there is a homomorphism
that restricts to a surjection
We shall prove this remaining part in the subsequent sections.
Assuming Theorem 2.7, we obtain the proofs of results exhibited in Section 1:
3 Characteristic classes from Seiberg–Witten theory
3.1 Output
The proof of Theorem 2.7 uses characteristic classes defined by using Seiberg–Witten theory. Fix
![]() $k\geq 0$
, and let X be a smooth closed oriented 4-manifold with
$k\geq 0$
, and let X be a smooth closed oriented 4-manifold with
![]() $b^+(X) \geq k+2$
. Lin and the author [Reference Konno and Lin20] defined a characteristic class
$b^+(X) \geq k+2$
. Lin and the author [Reference Konno and Lin20] defined a characteristic class
which we called the half-total Seiberg–Witten characteristic class. This was inspired by Ruberman’s total Seiberg–Witten invariant of diffeomorphisms [Reference Ruberman32], together with a gauge-theoretic construction of characteristic classes by the author [Reference Konno19]. We introduce generalizations of the characteristic class (4) to prove Theorem 2.7 as follows.
Let
![]() $\mathrm {Spin}^{c}(X,k)$
denote the set of isomorphism classes of spin
$\mathrm {Spin}^{c}(X,k)$
denote the set of isomorphism classes of spin
![]() $^c$
structures
$^c$
structures
![]() $\mathfrak {s}$
with
$\mathfrak {s}$
with
![]() $d(\mathfrak {s})=-k$
, where
$d(\mathfrak {s})=-k$
, where
![]() $d(\mathfrak {s})$
is the formal dimension of the Seiberg–Witten moduli space:
$d(\mathfrak {s})$
is the formal dimension of the Seiberg–Witten moduli space:
The group
![]() $\mathbb {Z}/2$
acts on
$\mathbb {Z}/2$
acts on
![]() $\mathrm {Spin}^{c}(X,k)$
by the charge conjugation, which flips the sign of the first Chern class of a spin
$\mathrm {Spin}^{c}(X,k)$
by the charge conjugation, which flips the sign of the first Chern class of a spin
![]() $^c$
structure. Let
$^c$
structure. Let
![]() $\mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
denote the quotient of
$\mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
denote the quotient of
![]() $\mathrm {Spin}^{c}(X,k)$
under this
$\mathrm {Spin}^{c}(X,k)$
under this
![]() $\mathbb {Z}/2$
-action. However,
$\mathbb {Z}/2$
-action. However,
![]() $\mathrm {Diff}^+(X)$
acts on
$\mathrm {Diff}^+(X)$
acts on
![]() $\mathrm {Spin}^{c}(X,k)$
via pull-back. Since the charge conjugation commutes with and the action of
$\mathrm {Spin}^{c}(X,k)$
via pull-back. Since the charge conjugation commutes with and the action of
![]() $\mathrm {Diff}^+(X)$
on
$\mathrm {Diff}^+(X)$
on
![]() $\mathrm {Spin}^{c}(X,k)$
, we have an action of
$\mathrm {Spin}^{c}(X,k)$
, we have an action of
![]() $\mathrm {Diff}^+(X)$
on
$\mathrm {Diff}^+(X)$
on
![]() $\mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
.
$\mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
.
Let
![]() $\mathcal {S}$
be a subset of
$\mathcal {S}$
be a subset of
![]() $\mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
which is setwise preserved under the action of
$\mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
which is setwise preserved under the action of
![]() $\mathrm {Diff}^+(X)$
. We suppose that
$\mathrm {Diff}^+(X)$
. We suppose that
![]() $\mathcal {S}$
does not contain the coset of a self-conjugate spin
$\mathcal {S}$
does not contain the coset of a self-conjugate spin
![]() $^{c}$
structure, which is needed to ensure a families perturbation can be taken to be nonzero and transverse. We shall define a cohomology class
$^{c}$
structure, which is needed to ensure a families perturbation can be taken to be nonzero and transverse. We shall define a cohomology class
by repeating the construction in [Reference Konno and Lin20] only for spin
![]() $^c$
structures
$^c$
structures
![]() $\mathfrak {s}$
whose cosets
$\mathfrak {s}$
whose cosets
![]() $[\mathfrak {s}]$
under the
$[\mathfrak {s}]$
under the
![]() $\mathbb {Z}/2$
-action lie in
$\mathbb {Z}/2$
-action lie in
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
Before explaning the construction of
![]() $\mathbb {SW}_{\mathrm {half}\text {-}\mathrm {tot}}^k(X,\mathcal {S})$
, it is worth looking at the lowest degree case to see which spin
$\mathbb {SW}_{\mathrm {half}\text {-}\mathrm {tot}}^k(X,\mathcal {S})$
, it is worth looking at the lowest degree case to see which spin
![]() $^c$
structures involve: suppose
$^c$
structures involve: suppose
![]() $k=0$
, and take a section
$k=0$
, and take a section
![]() $\tau : \mathrm {Spin}^{c}(X,0)/\mathrm {Conj} \to \mathrm {Spin}^{c}(X,k)$
of the quotient map
$\tau : \mathrm {Spin}^{c}(X,0)/\mathrm {Conj} \to \mathrm {Spin}^{c}(X,k)$
of the quotient map
![]() $\mathrm {Spin}^{c}(X,0) \to \mathrm {Spin}^{c}(X,0)/\mathrm {Conj}$
. Then
$\mathrm {Spin}^{c}(X,0) \to \mathrm {Spin}^{c}(X,0)/\mathrm {Conj}$
. Then
![]() $\mathbb {SW}_{\mathrm {half}\text {-}\mathrm {tot}}^0(X,\mathcal {S})$
is given by
$\mathbb {SW}_{\mathrm {half}\text {-}\mathrm {tot}}^0(X,\mathcal {S})$
is given by
Note that this number in
![]() $\mathbb {Z}/2$
is independent of
$\mathbb {Z}/2$
is independent of
![]() $\tau $
, determined only by
$\tau $
, determined only by
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
The characteristic class (6) is a generalization of the characteristic class (4) given in [Reference Konno and Lin20]: by setting
![]() $\mathcal {S}=\mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
, we obtain (4) – namely,
$\mathcal {S}=\mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
, we obtain (4) – namely,
3.2 Construction of the characteristic classes
We explain the construction of
![]() $\mathbb {SW}_{\mathrm {half}\text {-}\mathrm {tot}}^k(X,\mathcal {S})$
below. We omit some details which are completely analogous to arguments in [Reference Konno and Lin20]: see [Reference Konno and Lin20, Section 2] for the full treatment. First, let us recall the basics of the Seiberg–Witten equations. To write down the (perturbed) Seiberg–Witten equations, we need to fix a spin
$\mathbb {SW}_{\mathrm {half}\text {-}\mathrm {tot}}^k(X,\mathcal {S})$
below. We omit some details which are completely analogous to arguments in [Reference Konno and Lin20]: see [Reference Konno and Lin20, Section 2] for the full treatment. First, let us recall the basics of the Seiberg–Witten equations. To write down the (perturbed) Seiberg–Witten equations, we need to fix a spin
![]() $^c$
structure
$^c$
structure
![]() $\mathfrak {s}$
on X, a Riemannian metric g on X and an imaginary-valed self-dual 2-form
$\mathfrak {s}$
on X, a Riemannian metric g on X and an imaginary-valed self-dual 2-form
![]() $\mu \in i\Omega ^+_g(X)$
on X. Here,
$\mu \in i\Omega ^+_g(X)$
on X. Here,
![]() $\Omega ^+_g(X)$
denotes the set of self-dual 2-forms for the metric g. The Seiberg–Witten equations perturbed by
$\Omega ^+_g(X)$
denotes the set of self-dual 2-forms for the metric g. The Seiberg–Witten equations perturbed by
![]() $\mu $
are of the form
$\mu $
are of the form
 $$ \begin{align} \left\{ \begin{array}{ll} F_A^+=\sigma(\Phi, \Phi)+\mu,\\ D_A\Phi=0. \end{array} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{array}{ll} F_A^+=\sigma(\Phi, \Phi)+\mu,\\ D_A\Phi=0. \end{array} \right. \end{align} $$
Here, A is a
![]() $U(1)$
-connection of the determinant line bundle for
$U(1)$
-connection of the determinant line bundle for
![]() $\mathfrak {s}$
,
$\mathfrak {s}$
,
![]() $\Phi $
is a positive spinor for
$\Phi $
is a positive spinor for
![]() $\mathfrak {s}$
,
$\mathfrak {s}$
,
![]() $\sigma (-,-)$
is a certain quadratic form, and
$\sigma (-,-)$
is a certain quadratic form, and
![]() $D_A$
is the spin
$D_A$
is the spin
![]() $^c$
Dirac operator associated with A. The Seiberg–Witten equations is
$^c$
Dirac operator associated with A. The Seiberg–Witten equations is
![]() $\operatorname {\mathrm {Map}}(X,U(1))$
-equivariant, and we define the moduli space of solutions to the Seiberg–Witten equations by
$\operatorname {\mathrm {Map}}(X,U(1))$
-equivariant, and we define the moduli space of solutions to the Seiberg–Witten equations by
Next, let us recall the charge conjugation symmetry on the Seiberg–Witten equations. Let
![]() $\bar {\mathfrak {s}}$
denote the conjugate spin
$\bar {\mathfrak {s}}$
denote the conjugate spin
![]() $^c$
structure to
$^c$
structure to
![]() $\mathfrak {s}$
, which satisfies
$\mathfrak {s}$
, which satisfies
![]() $c_{1}(\bar {\mathfrak {s}})=-c_{1}(\mathfrak {s})$
. Then there is a bijection
$c_{1}(\bar {\mathfrak {s}})=-c_{1}(\mathfrak {s})$
. Then there is a bijection
called the charge conjugation symmetry, which becomes a diffeomorphism between the moduli spaces if the perturbation
![]() $\mu $
is generic so that
$\mu $
is generic so that
![]() $\mathcal {M}(X,\mathfrak {s},g,\mu )$
is a smooth manifold (then so is
$\mathcal {M}(X,\mathfrak {s},g,\mu )$
is a smooth manifold (then so is
![]() $\mathcal {M}(X,\bar {\mathfrak {s}},g,-\mu )$
automatically).
$\mathcal {M}(X,\bar {\mathfrak {s}},g,-\mu )$
automatically).
Let
![]() $\mathscr {R}(X)$
denote the space of Riemannian metrics. Set
$\mathscr {R}(X)$
denote the space of Riemannian metrics. Set
 $$\begin{align*}\Pi(X) = \bigcup_{g \in \mathscr{R}(X)}i\Omega^+_g(X). \end{align*}$$
$$\begin{align*}\Pi(X) = \bigcup_{g \in \mathscr{R}(X)}i\Omega^+_g(X). \end{align*}$$
We think of
![]() $\Pi (X)$
as a vector bundle over the Frechet manifold
$\Pi (X)$
as a vector bundle over the Frechet manifold
![]() $\mathscr {R}(X)$
and then take a fiberwise completion with respect to a suitable Sobolev norm. Let us use the same notation
$\mathscr {R}(X)$
and then take a fiberwise completion with respect to a suitable Sobolev norm. Let us use the same notation
![]() $\Pi (X) \to \mathscr {R}(X)$
also for the Hilbert bundle obtained by this completion. Let
$\Pi (X) \to \mathscr {R}(X)$
also for the Hilbert bundle obtained by this completion. Let
![]() $\mathring {\Pi }(X)$
be the subset of
$\mathring {\Pi }(X)$
be the subset of
![]() $\Pi (X)$
consisting of perturbations
$\Pi (X)$
consisting of perturbations
![]() $\mu $
such that:
$\mu $
such that:
-
•
 $\|\mu \|\leq 1$
for the Sobolev norm on
$\|\mu \|\leq 1$
for the Sobolev norm on
 $\Omega ^+_g(X)$
, and
$\Omega ^+_g(X)$
, and -
• there is no reducible solution for
 $\mu $
.
$\mu $
.
The space
![]() $\mathring {\Pi }(X)$
is
$\mathring {\Pi }(X)$
is
![]() $(b^+(X)-2)$
-connected, and
$(b^+(X)-2)$
-connected, and
![]() $\mathring {\Pi }(X)$
is invariant under the fiberwise
$\mathring {\Pi }(X)$
is invariant under the fiberwise
![]() $(-1)$
-multiplication on the Hilbert bundle
$(-1)$
-multiplication on the Hilbert bundle
![]() $\Pi (X) \to \mathscr {R}(X)$
.
$\Pi (X) \to \mathscr {R}(X)$
.
What makes the construction of the half-total Seiberg–Witten characteristic class complicated is the fact that the charge conjugation acts on the space of perturbations nontrivially; the action is given as (fiberwise) multiplication by
![]() $-1$
. Because of this, to implement a construction equivariantly under the charge conjugation, we need a ‘multi-valued perturbation’ when we form a collection of moduli spaces over a set of spin
$-1$
. Because of this, to implement a construction equivariantly under the charge conjugation, we need a ‘multi-valued perturbation’ when we form a collection of moduli spaces over a set of spin
![]() $^c$
structures, not just a copy of a common families self-dual 2-form. This is formulated as follows.
$^c$
structures, not just a copy of a common families self-dual 2-form. This is formulated as follows.
Let
![]() $\varpi : \mathrm {Spin}^{c}(X,k) \to \mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
be the quotient map. Define
$\varpi : \mathrm {Spin}^{c}(X,k) \to \mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
be the quotient map. Define
![]() $\tilde {\mathcal {S}} := \varpi ^{-1}(\mathcal {S}) \subset \mathrm {Spin}^{c}(X,k)$
. Since
$\tilde {\mathcal {S}} := \varpi ^{-1}(\mathcal {S}) \subset \mathrm {Spin}^{c}(X,k)$
. Since
![]() $\mathcal {S}$
is invariant under the
$\mathcal {S}$
is invariant under the
![]() $\mathrm {Diff}^+(X)$
-action,
$\mathrm {Diff}^+(X)$
-action,
![]() $\tilde {\mathcal {S}}$
is also
$\tilde {\mathcal {S}}$
is also
![]() $\mathrm {Diff}^+(X)$
-invariant. Define
$\mathrm {Diff}^+(X)$
-invariant. Define
where
![]() $\mathbb {Z}/2$
acts on
$\mathbb {Z}/2$
acts on
![]() $\tilde {\mathcal {S}}$
via the charge conjugation and on
$\tilde {\mathcal {S}}$
via the charge conjugation and on
![]() $\mathring {\Pi }(X)$
via the (fiberwise)
$\mathring {\Pi }(X)$
via the (fiberwise)
![]() $(-1)$
-multiplication. (To make our notation consistent with that in [Reference Konno and Lin20], let us use the notation
$(-1)$
-multiplication. (To make our notation consistent with that in [Reference Konno and Lin20], let us use the notation
![]() $\mathring {\Pi }(X,\mathcal {S})'$
with prime, not like
$\mathring {\Pi }(X,\mathcal {S})'$
with prime, not like
![]() $\mathring {\Pi }(X,\mathcal {S})$
. This remark applies throughout this section.)
$\mathring {\Pi }(X,\mathcal {S})$
. This remark applies throughout this section.)
Now we consider a family of 4-manifolds. Let
![]() $X \to E \to B$
be a fiber bundle with structure group
$X \to E \to B$
be a fiber bundle with structure group
![]() $\mathrm {Diff}^+(X)$
over a CW complex B. For
$\mathrm {Diff}^+(X)$
over a CW complex B. For
![]() $b \in B$
, we denote by
$b \in B$
, we denote by
![]() $E_b$
the fiber of E over b. Associated with E, we have several natural fiber bundles. For instance, since
$E_b$
the fiber of E over b. Associated with E, we have several natural fiber bundles. For instance, since
![]() $\mathrm {Diff}^+(X)$
acts on
$\mathrm {Diff}^+(X)$
acts on
![]() $\mathcal {S}$
via pull-back, we obtain an associated fiber bundle over B with fiber
$\mathcal {S}$
via pull-back, we obtain an associated fiber bundle over B with fiber
![]() $\mathcal {S}$
. We denote it by
$\mathcal {S}$
. We denote it by
Similarly, we get a fiber bundle with fiber
![]() $\mathring {\Pi }(X,\mathcal {S})'$
, denoted by
$\mathring {\Pi }(X,\mathcal {S})'$
, denoted by
This has underlying families of spaces of metrics, denoted by
A section of
![]() $\mathscr {R}(E) \to B$
is a fiberwise metric on E. Note that the forgetful map
$\mathscr {R}(E) \to B$
is a fiberwise metric on E. Note that the forgetful map
![]() $\mathring {\Pi }(X,\mathcal {S})' \to \mathcal {S}$
induces a surjection
$\mathring {\Pi }(X,\mathcal {S})' \to \mathcal {S}$
induces a surjection
which commutes with the projections onto B.
It could be worth unpackaging the data
![]() $\mathring {\Pi }(E,\mathcal {S})'$
. Let
$\mathring {\Pi }(E,\mathcal {S})'$
. Let
![]() $\vec {\mu }$
be a point in
$\vec {\mu }$
be a point in
![]() $\mathring {\Pi }(E,\mathcal {S})'$
. Let
$\mathring {\Pi }(E,\mathcal {S})'$
. Let
![]() $b \in B$
and
$b \in B$
and
![]() $g \in \mathscr {R}(E_b)$
be the images of
$g \in \mathscr {R}(E_b)$
be the images of
![]() $\vec {\mu }$
under the projections
$\vec {\mu }$
under the projections
![]() $\mathring {\Pi }(E,\mathcal {S})' \to B$
and
$\mathring {\Pi }(E,\mathcal {S})' \to B$
and
![]() $\mathring {\Pi }(E,\mathcal {S})' \to \mathscr {R}(E)$
. Let
$\mathring {\Pi }(E,\mathcal {S})' \to \mathscr {R}(E)$
. Let
![]() $\mathcal {S}(E)_b$
be the fiber of
$\mathcal {S}(E)_b$
be the fiber of
![]() $\mathcal {S}(E) \to B$
over b. Picking a representative
$\mathcal {S}(E) \to B$
over b. Picking a representative
![]() $\mathfrak {s}$
of each coset
$\mathfrak {s}$
of each coset
![]() $[\mathfrak {s}] \in \mathcal {S}(E)_b$
, we can express
$[\mathfrak {s}] \in \mathcal {S}(E)_b$
, we can express
![]() $\vec {\mu }$
as a collection of a self-dual 2-forms
$\vec {\mu }$
as a collection of a self-dual 2-forms
![]() $\{\mu _{\mathfrak {s}} \in \Omega ^+_{g}(E_b)\}_{[\mathfrak {s}] \in \mathcal {S}(E)_b}$
. We set
$\{\mu _{\mathfrak {s}} \in \Omega ^+_{g}(E_b)\}_{[\mathfrak {s}] \in \mathcal {S}(E)_b}$
. We set
If all
![]() $\mu _{[\mathfrak {s}]}$
are generic,
$\mu _{[\mathfrak {s}]}$
are generic,
![]() $\mathcal {M}(E_b, \mathcal {S}, \vec {\mu })$
is a smooth manifold. Further, as an unoriented manifold,
$\mathcal {M}(E_b, \mathcal {S}, \vec {\mu })$
is a smooth manifold. Further, as an unoriented manifold,
![]() $\mathcal {M}(E_b, \mathcal {S}, \vec {\mu })$
is independent of choice of representatives
$\mathcal {M}(E_b, \mathcal {S}, \vec {\mu })$
is independent of choice of representatives
![]() $\mathfrak {s}$
of
$\mathfrak {s}$
of
![]() $[\mathfrak {s}]$
. Indeed, if we choose the other representative
$[\mathfrak {s}]$
. Indeed, if we choose the other representative
![]() $\bar {\mathfrak {s}}$
of
$\bar {\mathfrak {s}}$
of
![]() $[\mathfrak {s}]$
, the chosen perturbation becomes
$[\mathfrak {s}]$
, the chosen perturbation becomes
![]() $\mu _{\bar {\mathfrak {s}}} = -\mu _{\mathfrak {s}}$
, so we can use the diffeomorphism (8).
$\mu _{\bar {\mathfrak {s}}} = -\mu _{\mathfrak {s}}$
, so we can use the diffeomorphism (8).
Now let us take a fiberwise metric
![]() $\tilde {g} : B \to \mathscr {R}(E)$
, and pick a section
$\tilde {g} : B \to \mathscr {R}(E)$
, and pick a section
![]() $\sigma ' : \mathcal {S} \to \mathring {\Pi }(E,\mathcal {S})'$
that makes the following diagram commutative:
$\sigma ' : \mathcal {S} \to \mathring {\Pi }(E,\mathcal {S})'$
that makes the following diagram commutative:

Define the half-total moduli space for
![]() $\sigma '$
by
$\sigma '$
by
(This was denoted by
![]() $\mathcal {M}_{\sigma ',\mathrm {half}}$
in [Reference Konno and Lin20, Definition 2.11], but let us use the notation
$\mathcal {M}_{\sigma ',\mathrm {half}}$
in [Reference Konno and Lin20, Definition 2.11], but let us use the notation
![]() $\mathcal {M}_{\mathrm {half}}(E,\mathcal {S}, \sigma ')$
to keep track of E and
$\mathcal {M}_{\mathrm {half}}(E,\mathcal {S}, \sigma ')$
to keep track of E and
![]() $\mathcal {S}$
.) If B is a comapct manifold, by choosing generic
$\mathcal {S}$
.) If B is a comapct manifold, by choosing generic
![]() $\sigma '$
,
$\sigma '$
,
![]() $\mathcal {M}_{\mathrm {half}}(E, \mathcal {S}, \sigma ')$
becomes a compact manifold too (cf. Lemma 3.1), and the dimension of
$\mathcal {M}_{\mathrm {half}}(E, \mathcal {S}, \sigma ')$
becomes a compact manifold too (cf. Lemma 3.1), and the dimension of
![]() $\mathcal {M}_{\mathrm {half}}(E, \mathcal {S}, \sigma ')$
is given by
$\mathcal {M}_{\mathrm {half}}(E, \mathcal {S}, \sigma ')$
is given by
![]() $\dim {B}-k$
. In particular, for
$\dim {B}-k$
. In particular, for
![]() $\dim {B}=k$
, we can define a
$\dim {B}=k$
, we can define a
![]() $\mathbb {Z}/2$
-valued invariant by counting the zero dimensional compact manifold
$\mathbb {Z}/2$
-valued invariant by counting the zero dimensional compact manifold
![]() $\mathcal {M}_{\mathrm {half}}(E, \mathcal {S}, \sigma ')$
.
$\mathcal {M}_{\mathrm {half}}(E, \mathcal {S}, \sigma ')$
.
For a general case where B is neither compact nor a manifold, we define a cochain
as follows, where
![]() $C^k(B)$
denotes the
$C^k(B)$
denotes the
![]() $\mathbb {Z}/2$
-coefficient cellular cochain group. Loosely speaking, for each k-cell e of B with a characteristic map
$\mathbb {Z}/2$
-coefficient cellular cochain group. Loosely speaking, for each k-cell e of B with a characteristic map
![]() $\varphi _e : D^k \to B$
, we define
$\varphi _e : D^k \to B$
, we define
Here, the right-hand side is a finite sum (cf. Lemma 3.1), and we can justify the necessary transversality by using a virtual neighborhood technique, just as in [Reference Konno19, Reference Konno and Lin20]. Using the assumption that
![]() $b^+(X) \geq k+2$
, we can prove that
$b^+(X) \geq k+2$
, we can prove that
![]() $\mathcal {SW}_{\mathrm {half}\text {-}\mathrm {tot}}^k(E, \mathcal {S}, \sigma ')$
is a cocycle, and that the cohomology class
$\mathcal {SW}_{\mathrm {half}\text {-}\mathrm {tot}}^k(E, \mathcal {S}, \sigma ')$
is a cocycle, and that the cohomology class
is independent of the choice of
![]() $\sigma '$
([Reference Konno and Lin20, Propositions 2.22, 2.23]). We set
$\sigma '$
([Reference Konno and Lin20, Propositions 2.22, 2.23]). We set
3.3 Finiteness
Here, we record some finiteness result, which was used in Subsection 3.2 and is necessary in a subsequent argument too.
First, let us recall the following well-known finiteness of Seiberg–Witten moduli spaces (see, for example, [Reference Morgan27]). Fix a metric g and
![]() $k \in \mathbb {Z}$
. Then there are only finitely many spin
$k \in \mathbb {Z}$
. Then there are only finitely many spin
![]() $^c$
structures
$^c$
structures
![]() $\mathfrak {s}$
with
$\mathfrak {s}$
with
![]() $d(\mathfrak {s})=k$
for which the moduli space
$d(\mathfrak {s})=k$
for which the moduli space
![]() $\mathcal {M}(X,\mathfrak {s},g,\mu )$
for the perturbed equations (7) are nonempty for some
$\mathcal {M}(X,\mathfrak {s},g,\mu )$
for the perturbed equations (7) are nonempty for some
![]() $\mu \in \Omega ^+_g(X)$
with
$\mu \in \Omega ^+_g(X)$
with
![]() $\|\mu \| \leq 1$
. Here,
$\|\mu \| \leq 1$
. Here,
![]() $\|-\|$
denotes a suitable Sobolev norm. Moreover, for a fixed pair
$\|-\|$
denotes a suitable Sobolev norm. Moreover, for a fixed pair
![]() $(g,\mu )$
, the moduli space
$(g,\mu )$
, the moduli space
![]() $\mathcal {M}(X,\mathfrak {s},g,\mu )$
is compact. A families generalization of this fact in our context is as follows.
$\mathcal {M}(X,\mathfrak {s},g,\mu )$
is compact. A families generalization of this fact in our context is as follows.
As in Subsection 3.2, fix
![]() $k\geq 0$
, let X be a smooth closed oriented 4-manifold with
$k\geq 0$
, let X be a smooth closed oriented 4-manifold with
![]() $b^+(X) \geq k+2$
, and let
$b^+(X) \geq k+2$
, and let
![]() $X \to E \to B$
be a fiber bundle with structure group
$X \to E \to B$
be a fiber bundle with structure group
![]() $\mathrm {Diff}^+(X)$
over a CW complex B.
$\mathrm {Diff}^+(X)$
over a CW complex B.
Lemma 3.1. Suppose that B is compact. If we pick a section
![]() $\sigma '$
as in Subsection 3.2, then the half-total moduli space
$\sigma '$
as in Subsection 3.2, then the half-total moduli space
is compact.
Proof. This follows from that we used perturbations with
![]() $\|\mu \| \leq 1$
in the definition of
$\|\mu \| \leq 1$
in the definition of
![]() $\mathring {\Pi }(X)$
.
$\mathring {\Pi }(X)$
.
For our purpose, an important case is that
![]() $\mathcal {S}$
is an orbit of the action of
$\mathcal {S}$
is an orbit of the action of
![]() $\mathrm {Diff}^+(X)$
on
$\mathrm {Diff}^+(X)$
on
![]() $\mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
. Set
$\mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
. Set
and let
![]() $\mathbb {S}(X,k)$
denote the orbit space for the
$\mathbb {S}(X,k)$
denote the orbit space for the
![]() $\mathrm {Diff}^+(X)$
-action on
$\mathrm {Diff}^+(X)$
-action on
![]() $\mathrm {Spin}^{c}(X,k)^{\vee }/\mathrm {Conj}$
,
$\mathrm {Spin}^{c}(X,k)^{\vee }/\mathrm {Conj}$
,
As an analog of the notion of a basic class, we call
![]() $\mathcal {S} \in \mathbb {S}(X,k)$
a basic orbit of E if
$\mathcal {S} \in \mathbb {S}(X,k)$
a basic orbit of E if
![]() $\mathbb {SW}_{\mathrm {half}\text {-}\mathrm {tot}}^k(E,\mathcal {S}) \neq 0$
. Let
$\mathbb {SW}_{\mathrm {half}\text {-}\mathrm {tot}}^k(E,\mathcal {S}) \neq 0$
. Let
![]() $\mathcal {B}_{\mathrm {half}}(E,k)$
denote the set of basic orbits:
$\mathcal {B}_{\mathrm {half}}(E,k)$
denote the set of basic orbits:
Then we have the following:
Lemma 3.2. Suppose that B is compact. Then
![]() $\mathcal {B}_{\mathrm {half}}(E,k)$
is a finite set.
$\mathcal {B}_{\mathrm {half}}(E,k)$
is a finite set.
Proof. Fix a section
![]() $\sigma '$
. Lemma 3.1 implies that there are only finitely many
$\sigma '$
. Lemma 3.1 implies that there are only finitely many
![]() $\mathfrak {s} \in \mathrm {Spin}^{c}(X,k)$
such that there is
$\mathfrak {s} \in \mathrm {Spin}^{c}(X,k)$
such that there is
![]() $b \in B$
with
$b \in B$
with
![]() $\mathcal {M}(E_b, \mathfrak {s}, g_b, \sigma '(b)) \neq \emptyset $
, where
$\mathcal {M}(E_b, \mathfrak {s}, g_b, \sigma '(b)) \neq \emptyset $
, where
![]() $g_b$
is the underlying metric of
$g_b$
is the underlying metric of
![]() $\sigma '(b)$
on
$\sigma '(b)$
on
![]() $E_b$
. Since
$E_b$
. Since
![]() $\#\mathcal {B}_{\mathrm {half}}(E,k)$
is bounded above by the number of such
$\#\mathcal {B}_{\mathrm {half}}(E,k)$
is bounded above by the number of such
![]() $\mathfrak {s}$
, the assertion follows.
$\mathfrak {s}$
, the assertion follows.
4 Computing the invariant
In this section, we prove Theorem 2.7 by evaluating the Seiberg–Witten characteristic classes
![]() $\mathbb {SW}_{\mathrm {half}\text {-}\mathrm {tot}}^k(X,\mathcal {S})$
introduced in Section 3 at homology classes
$\mathbb {SW}_{\mathrm {half}\text {-}\mathrm {tot}}^k(X,\mathcal {S})$
introduced in Section 3 at homology classes
![]() $\alpha _i$
defined in (3).
$\alpha _i$
defined in (3).
Precisely, we shall consider the homomorphism
We shall show that this homomorphism has infinitely generated image in
![]() $\bigoplus _{\mathcal {S} \in \mathbb {S}(X,k)} \mathbb {Z}/2$
for 4-manifolds X considered in Theorem 2.7.
$\bigoplus _{\mathcal {S} \in \mathbb {S}(X,k)} \mathbb {Z}/2$
for 4-manifolds X considered in Theorem 2.7.
4.1 Reducing to the monodromy invariant part
The characteristic class
![]() $\mathbb {SW}_{\mathrm {half}\text {-}\mathrm {tot}}^k(X, \mathcal {S})$
involves spin
$\mathbb {SW}_{\mathrm {half}\text {-}\mathrm {tot}}^k(X, \mathcal {S})$
involves spin
![]() $^c$
structures that are not invariant under the monodromies of the families that we consider. Adapting an argument in [Reference Konno and Lin20, Section 3.1] to our setup, we shall see that such spin
$^c$
structures that are not invariant under the monodromies of the families that we consider. Adapting an argument in [Reference Konno and Lin20, Section 3.1] to our setup, we shall see that such spin
![]() $^c$
structures do not contribute to the final computation.
$^c$
structures do not contribute to the final computation.
To describe it, let us recall the numerical families Seiberg–Witten invariant. Let B be a closed smooth manifold of dimension
![]() $k \geq 0$
, X be a smooth oriented closed 4-manifold of
$k \geq 0$
, X be a smooth oriented closed 4-manifold of
![]() $b^+(X) \geq k+2$
, and
$b^+(X) \geq k+2$
, and
![]() $X \to E \to B$
be a fiber bundle with structure group
$X \to E \to B$
be a fiber bundle with structure group
![]() $\mathrm {Diff}^+(X)$
over B. Given a spin
$\mathrm {Diff}^+(X)$
over B. Given a spin
![]() $^c$
structure
$^c$
structure
![]() $\mathfrak {s}$
on X of formal dimension
$\mathfrak {s}$
on X of formal dimension
![]() $-k$
, suppose that the monodromy of E fixes the isomorphism class of
$-k$
, suppose that the monodromy of E fixes the isomorphism class of
![]() $\mathfrak {s}$
. Then the numerical families Seiberg–Witten invariant
$\mathfrak {s}$
. Then the numerical families Seiberg–Witten invariant
can be defined. If the structure of E lifts to the automorphism group of the spin
![]() $^c$
4-manifold
$^c$
4-manifold
![]() $(X,\mathfrak {s})$
, this is the invariant defined by Li–Liu [Reference Li and Liu23]. However, even if E does not admit such a lift, one can still define
$(X,\mathfrak {s})$
, this is the invariant defined by Li–Liu [Reference Li and Liu23]. However, even if E does not admit such a lift, one can still define
![]() $SW(E,\mathfrak {s})$
[Reference Konno19, Reference Baraglia and Konno5].
$SW(E,\mathfrak {s})$
[Reference Konno19, Reference Baraglia and Konno5].
Pick an orbit
![]() $\mathcal {S} \in \mathbb {S}(X,k)$
. We regard
$\mathcal {S} \in \mathbb {S}(X,k)$
. We regard
![]() $\mathcal {S}$
also as a subset of
$\mathcal {S}$
also as a subset of
![]() $\mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
. Let
$\mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
. Let
![]() $\tau : \mathrm {Spin}^{c}(X,k)/\mathrm {Conj} \to \mathrm {Spin}^{c}(X,k)$
be a section of the quotient map
$\tau : \mathrm {Spin}^{c}(X,k)/\mathrm {Conj} \to \mathrm {Spin}^{c}(X,k)$
be a section of the quotient map
![]() $\mathrm {Spin}^{c}(X,k) \to \mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
. For mutually commuting diffeomorphisms
$\mathrm {Spin}^{c}(X,k) \to \mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
. For mutually commuting diffeomorphisms
![]() $f_1, \ldots , f_k$
of X, we denote by
$f_1, \ldots , f_k$
of X, we denote by
![]() $X_{f_1, \ldots , f_k} \to T^k$
the multiple mapping torus of
$X_{f_1, \ldots , f_k} \to T^k$
the multiple mapping torus of
![]() $f_1, \ldots , f_k$
.
$f_1, \ldots , f_k$
.
Proposition 4.1 (cf. [Reference Konno and Lin20, Corollary 3.4]).
Let
![]() $f_1, \dots , f_k : X \to X$
be mutually commuting orientation-preserving diffeomorphisms. Suppose that they satisfy the following conditions:
$f_1, \dots , f_k : X \to X$
be mutually commuting orientation-preserving diffeomorphisms. Suppose that they satisfy the following conditions:
-
(i) For each
 $i = 1, \ldots , k$
,
$i = 1, \ldots , k$
,
 $f_i$
preserves
$f_i$
preserves
 $\tau (\mathcal {S})$
setwise.
$\tau (\mathcal {S})$
setwise. -
(ii) For each i, there exists a smooth isotopy
 $(F_i^t)_{t \in [0,1]}$
from
$(F_i^t)_{t \in [0,1]}$
from
 $f_i^2$
to
$f_i^2$
to
 $\mathrm {id}_X$
. For
$\mathrm {id}_X$
. For
 $i\neq j$
,
$i\neq j$
,
 $F_i^t$
commutes with
$F_i^t$
commutes with
 $f_j$
for any
$f_j$
for any
 $t \in [0,1]$
.
$t \in [0,1]$
.
Then we have
 $$\begin{align*}\langle \mathbb{SW}_{\mathrm{half}\text{-}\mathrm{tot}}^k(X_{f_1, \dots, f_k}, \mathcal{S}), [T^k] \rangle = \sum_{\substack{\mathfrak{s} \in \tau(\mathcal{S}), \\ f_i^\ast \mathfrak{s} = \mathfrak{s}\ (1 \leq i \leq k)}} SW(X_{f_1, \dots, f_k},\mathfrak{s}) \end{align*}$$
$$\begin{align*}\langle \mathbb{SW}_{\mathrm{half}\text{-}\mathrm{tot}}^k(X_{f_1, \dots, f_k}, \mathcal{S}), [T^k] \rangle = \sum_{\substack{\mathfrak{s} \in \tau(\mathcal{S}), \\ f_i^\ast \mathfrak{s} = \mathfrak{s}\ (1 \leq i \leq k)}} SW(X_{f_1, \dots, f_k},\mathfrak{s}) \end{align*}$$
in
![]() $\mathbb {Z}/2$
.
$\mathbb {Z}/2$
.
Proof. The proof is obtained by repeating the proof of [Reference Konno and Lin20, Corollary 3.4] with replacing
![]() $\mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
with
$\mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
with
![]() $\mathcal {S}$
. We just give a slight comment on how to do the modification.
$\mathcal {S}$
. We just give a slight comment on how to do the modification.
If the actions of all
![]() $f_i$
on
$f_i$
on
![]() $\tau (\mathcal {S})$
are trivial, there is nothing to prove. To treat the other case, first note that we have a modification of [Reference Konno and Lin20, Lemma 3.3] obtained by replacing
$\tau (\mathcal {S})$
are trivial, there is nothing to prove. To treat the other case, first note that we have a modification of [Reference Konno and Lin20, Lemma 3.3] obtained by replacing
![]() $\mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
with
$\mathrm {Spin}^{c}(X,k)/\mathrm {Conj}$
with
![]() $\mathcal {S}$
. Let us consider a
$\mathcal {S}$
. Let us consider a
![]() $(\mathbb {Z}/2)^k$
-action on
$(\mathbb {Z}/2)^k$
-action on
![]() $\tau (\mathcal {S})$
generated by
$\tau (\mathcal {S})$
generated by
![]() $f_1, \dots , f_k$
. For
$f_1, \dots , f_k$
. For
![]() $\mathfrak {s} \in \tau (\mathcal {S})$
, if there is i with
$\mathfrak {s} \in \tau (\mathcal {S})$
, if there is i with
![]() $f_i^\ast \mathfrak {s}\neq \mathfrak {s}$
, we may use the modified [Reference Konno and Lin20, Lemma 3.3] to conclude that the sum of the counts of the moduli spaces for the
$f_i^\ast \mathfrak {s}\neq \mathfrak {s}$
, we may use the modified [Reference Konno and Lin20, Lemma 3.3] to conclude that the sum of the counts of the moduli spaces for the
![]() $(\mathbb {Z}/2)^k$
-orbit of
$(\mathbb {Z}/2)^k$
-orbit of
![]() $\mathfrak {s}$
is zero over
$\mathfrak {s}$
is zero over
![]() $\mathbb {Z}/2$
. Thus, in any case,
$\mathbb {Z}/2$
. Thus, in any case,
![]() $\langle \mathbb {SW}_{\mathrm {half}\text {-}\mathrm {tot}}^k(X_{f_1, \dots , f_k}, \mathcal {S}), [T^k] \rangle $
is computed from the counts of the moduli spaces only for the monodromy invariant spin
$\langle \mathbb {SW}_{\mathrm {half}\text {-}\mathrm {tot}}^k(X_{f_1, \dots , f_k}, \mathcal {S}), [T^k] \rangle $
is computed from the counts of the moduli spaces only for the monodromy invariant spin
![]() $^c$
structures, and it ends up with the assertion of Proposition 4.1.
$^c$
structures, and it ends up with the assertion of Proposition 4.1.
4.2 Gluing result
Another thing we need is a gluing result proven by Baraglia and the author [Reference Baraglia and Konno5]. We recall the statement for readers’ convenience. In general, let Z be an oriented smooth closed 4-manifold, and
![]() $Z \to E \to B$
be an oriented smooth fiber bundle with fiber Z. Then we get an associated vector bundle
$Z \to E \to B$
be an oriented smooth fiber bundle with fiber Z. Then we get an associated vector bundle
by considering maximal-dimensional positive-definite subspaces of the second cohomology fiberwise. The isomorphism class of
![]() $H^+(E)$
is determined only by E.
$H^+(E)$
is determined only by E.
The gluing result we need is formulated as follows. Let
![]() $k>0$
, and let M, N be closed oriented smooth 4-manifolds with
$k>0$
, and let M, N be closed oriented smooth 4-manifolds with
![]() $b^+(M) \geq 2$
and
$b^+(M) \geq 2$
and
![]() $b^+(N)=k$
, and with
$b^+(N)=k$
, and with
![]() $b_1(M)=b_1(N)=0$
. Set
$b_1(M)=b_1(N)=0$
. Set
![]() $X=M\#N$
. Let
$X=M\#N$
. Let
![]() $\mathfrak {t} \in \mathrm {Spin}^{c}(M,0)$
and
$\mathfrak {t} \in \mathrm {Spin}^{c}(M,0)$
and
![]() $\mathfrak {t}' \in \mathrm {Spin}^{c}(N,k+1)$
. Then we have
$\mathfrak {t}' \in \mathrm {Spin}^{c}(N,k+1)$
. Then we have
![]() $d(\mathfrak {t}\#\mathfrak {t}')=-k$
. Let B be a closed smooth manifold of dimension k, and
$d(\mathfrak {t}\#\mathfrak {t}')=-k$
. Let B be a closed smooth manifold of dimension k, and
![]() $M \to E_M \to B$
and
$M \to E_M \to B$
and
![]() $N \to E_N \to B$
be oriented smooth fiber bundles. Fix sections
$N \to E_N \to B$
be oriented smooth fiber bundles. Fix sections
![]() $\iota _M : B \to E_M$
,
$\iota _M : B \to E_M$
,
![]() $\iota _N : B \to E_N$
whose normal bundles are isomorphic via a fiberwise orientation-reversing isomorphism, so that we can form the fiberwise connected sum
$\iota _N : B \to E_N$
whose normal bundles are isomorphic via a fiberwise orientation-reversing isomorphism, so that we can form the fiberwise connected sum
![]() $X \to E_X \to B$
of
$X \to E_X \to B$
of
![]() $E_M$
and
$E_M$
and
![]() $E_N$
along
$E_N$
along
![]() $\iota _M, \iota _N$
. Then we have the following:
$\iota _M, \iota _N$
. Then we have the following:
Theorem 4.2 [Reference Baraglia and Konno5, Theorem 1.1].
If
![]() $w_{b^+(N)}(H^+(E_N)) \neq 0$
, then we have
$w_{b^+(N)}(H^+(E_N)) \neq 0$
, then we have
in
![]() $\mathbb {Z}/2$
.
$\mathbb {Z}/2$
.
Now we apply Theorem 4.2 to the multiple mapping torus
![]() $E_i \to T^k$
constructed in Subsection 2.2 for
$E_i \to T^k$
constructed in Subsection 2.2 for
![]() $i \geq 1$
. For each
$i \geq 1$
. For each
![]() $j=1, \dots , k$
, recall that
$j=1, \dots , k$
, recall that
![]() $f_j$
acts on the j-th copy of
$f_j$
acts on the j-th copy of
![]() $H^+(S^2 \times S^2) \subset H^2(S^2\times S^2)$
via multiplication by
$H^+(S^2 \times S^2) \subset H^2(S^2\times S^2)$
via multiplication by
![]() $-1$
. We can see that the vector bundle
$-1$
. We can see that the vector bundle
associated to the multiple mapping torus
![]() $(kS^2\times S^2)_{f_1, \dots , f_k} \to T^k$
satisfies
$(kS^2\times S^2)_{f_1, \dots , f_k} \to T^k$
satisfies
Let
![]() $\mathfrak {s}_S$
denote the unique spin structure on
$\mathfrak {s}_S$
denote the unique spin structure on
![]() $kS^2\times S^2$
. Then we have
$kS^2\times S^2$
. Then we have
![]() $\mathfrak {s}_S \in \mathrm {Spin}^{c}(kS^2\times S^2,k+1)$
.
$\mathfrak {s}_S \in \mathrm {Spin}^{c}(kS^2\times S^2,k+1)$
.
Lemma 4.3. Let
![]() $\mathfrak {t} \in \mathrm {Spin}^{c}(M_i,0)$
. Then we have
$\mathfrak {t} \in \mathrm {Spin}^{c}(M_i,0)$
. Then we have
in
![]() $\mathbb {Z}/2$
.
$\mathbb {Z}/2$
.
4.3 Completion of the proof
As in Section 2, fix
![]() $k>0$
, take a 4-manifold M satisfying Assumption 2.1. We shall use
$k>0$
, take a 4-manifold M satisfying Assumption 2.1. We shall use
![]() $M_i$
and
$M_i$
and
![]() $c_i$
that appear in Assumption 2.1, and we shall use the notation
$c_i$
that appear in Assumption 2.1, and we shall use the notation
![]() $E_i$
and
$E_i$
and
![]() $\alpha _i$
for
$\alpha _i$
for
![]() $i\geq 1$
introduced in Subsection 2.2. Set
$i\geq 1$
introduced in Subsection 2.2. Set
![]() $X = M\#kS^2 \times S^2$
and
$X = M\#kS^2 \times S^2$
and
![]() $X_i = M_i\#kS^2\times S^2$
.
$X_i = M_i\#kS^2\times S^2$
.
For each
![]() $i\geq 1$
, we fix a section
$i\geq 1$
, we fix a section
of the quotient map
![]() $\mathrm {Spin}^{c}(M_i) \to \mathrm {Spin}^{c}(M_i)/\mathrm {Conj}$
. Using
$\mathrm {Spin}^{c}(M_i) \to \mathrm {Spin}^{c}(M_i)/\mathrm {Conj}$
. Using
![]() $\tau ^0_i$
, we define a section
$\tau ^0_i$
, we define a section
as follows: for
![]() $\mathfrak {s} \in \mathrm {Spin}^{c}(X_i)$
, we define
$\mathfrak {s} \in \mathrm {Spin}^{c}(X_i)$
, we define
![]() $\tau ([\mathfrak {s}])$
to be the spin
$\tau ([\mathfrak {s}])$
to be the spin
![]() $^c$
structure
$^c$
structure
![]() $\mathfrak {s}'$
with
$\mathfrak {s}'$
with
![]() $[\mathfrak {s}] = [\mathfrak {s}']$
in
$[\mathfrak {s}] = [\mathfrak {s}']$
in
![]() $\mathrm {Spin}^{c}(X_i)/\mathrm {Conj}$
such that
$\mathrm {Spin}^{c}(X_i)/\mathrm {Conj}$
such that
![]() $\mathfrak {s}'|_{M_i} = \tau _0([\mathfrak {s}|_{M_i}])$
. Restricting this, we obtain a section (denoted by the same notation)
$\mathfrak {s}'|_{M_i} = \tau _0([\mathfrak {s}|_{M_i}])$
. Restricting this, we obtain a section (denoted by the same notation)
As in Subsection 4.2, let
![]() $\mathfrak {s}_S$
denote the unique spin structure on
$\mathfrak {s}_S$
denote the unique spin structure on
![]() $kS^2\times S^2$
. For each
$kS^2\times S^2$
. For each
![]() $i \geq 1$
, we define
$i \geq 1$
, we define
![]() $\mathcal {S}_i \in \mathbb {S}(X_i,k)$
to be the
$\mathcal {S}_i \in \mathbb {S}(X_i,k)$
to be the
![]() $\mathrm {Diff}^+(X_i)$
-orbit that contains
$\mathrm {Diff}^+(X_i)$
-orbit that contains
![]() $[c_i\#\mathfrak {s}_S] \in \mathrm {Spin}^{c}(X_i,k)/\mathrm {Conj}$
.
$[c_i\#\mathfrak {s}_S] \in \mathrm {Spin}^{c}(X_i,k)/\mathrm {Conj}$
.
Proposition 4.4. For
![]() $E_i \to T^k$
constructed in Subsection 2.2, we have
$E_i \to T^k$
constructed in Subsection 2.2, we have
in
![]() $\mathbb {Z}/2$
.
$\mathbb {Z}/2$
.
Proof. First, the naturality of the characteristic class implies that
To compute the right-hand side of (10), we shall apply Proposition 4.1 to the families
![]() $E_i$
. Recall that
$E_i$
. Recall that
![]() $E_i$
was constructed by using a diffeomorphism
$E_i$
was constructed by using a diffeomorphism
![]() $f \in \mathrm {Diff}_\partial (S^2 \times S^2 \setminus \mathrm {Int}(D^4))$
. This diffemorphism f is order 2 in
$f \in \mathrm {Diff}_\partial (S^2 \times S^2 \setminus \mathrm {Int}(D^4))$
. This diffemorphism f is order 2 in
![]() $\pi _0(\mathrm {Diff}_\partial (S^2 \times S^2 \setminus \mathrm {Int}(D^4)))$
. Thus, for the diffeomorphisms
$\pi _0(\mathrm {Diff}_\partial (S^2 \times S^2 \setminus \mathrm {Int}(D^4)))$
. Thus, for the diffeomorphisms
![]() $f_1, \dots , f_k$
on
$f_1, \dots , f_k$
on
![]() $X_i$
, of which the multiples mapping torus is
$X_i$
, of which the multiples mapping torus is
![]() $E_i$
, we can find isotopies
$E_i$
, we can find isotopies
![]() $(F_i^t)_{t \in [0,1]}$
that satisfy the assumption (ii) of Proposition 4.1. Since
$(F_i^t)_{t \in [0,1]}$
that satisfy the assumption (ii) of Proposition 4.1. Since
![]() $f_j$
act trivially on
$f_j$
act trivially on
![]() $M_i$
, by the construction of
$M_i$
, by the construction of
![]() $\tau _i$
, it follows that
$\tau _i$
, it follows that
![]() $\tau _i(\mathcal {S}_i)$
is setwise preserved under the actions of
$\tau _i(\mathcal {S}_i)$
is setwise preserved under the actions of
![]() $f_j$
. Thus, we may apply Proposition 4.1 to the families
$f_j$
. Thus, we may apply Proposition 4.1 to the families
![]() $E_i$
and obtain the equality
$E_i$
and obtain the equality
 $$ \begin{align} \langle \mathbb{SW}_{\mathrm{half}\text{-}\mathrm{tot}}^k(E_i, \mathcal{S}_i), [T^k] \rangle = \sum_{\substack{\mathfrak{s} \in \tau_i(\mathcal{S}_i), \\ f_j^\ast \mathfrak{s} = \mathfrak{s}\ (1 \leq j \leq k)}} SW(E_i,\mathfrak{s}) \end{align} $$
$$ \begin{align} \langle \mathbb{SW}_{\mathrm{half}\text{-}\mathrm{tot}}^k(E_i, \mathcal{S}_i), [T^k] \rangle = \sum_{\substack{\mathfrak{s} \in \tau_i(\mathcal{S}_i), \\ f_j^\ast \mathfrak{s} = \mathfrak{s}\ (1 \leq j \leq k)}} SW(E_i,\mathfrak{s}) \end{align} $$
in
![]() $\mathbb {Z}/2$
.
$\mathbb {Z}/2$
.
We shall compute the right-hand side of (11). Since
![]() $f_j$
acts on the j-th copy of
$f_j$
acts on the j-th copy of
![]() $H^2(S^2\times S^2)$
via multiplication by
$H^2(S^2\times S^2)$
via multiplication by
![]() $-1$
, a spin
$-1$
, a spin
![]() $^c$
structure
$^c$
structure
![]() $\mathfrak {s} \in \mathrm {Spin}^{c}(X_i)$
is
$\mathfrak {s} \in \mathrm {Spin}^{c}(X_i)$
is
![]() $f_j$
-invariant for all j if and only if
$f_j$
-invariant for all j if and only if
![]() $\mathfrak {s}$
is of the form
$\mathfrak {s}$
is of the form
![]() $\mathfrak {t} \# \mathfrak {s}_S$
, where
$\mathfrak {t} \# \mathfrak {s}_S$
, where
![]() $\mathfrak {t} \in \mathrm {Spin}^{c}(M_i)$
. It is easy to see that, if
$\mathfrak {t} \in \mathrm {Spin}^{c}(M_i)$
. It is easy to see that, if
![]() $d(\mathfrak {t} \# \mathfrak {s}_S)=-k$
, then
$d(\mathfrak {t} \# \mathfrak {s}_S)=-k$
, then
![]() $d(\mathfrak {t})=0$
. Thus, we get from Lemma 4.3 that
$d(\mathfrak {t})=0$
. Thus, we get from Lemma 4.3 that
 $$ \begin{align} \sum_{\substack{\mathfrak{s} \in \tau_i(\mathcal{S}_i), \\ f_j^\ast \mathfrak{s} = \mathfrak{s}\ (1 \leq j \leq k)}} SW(E_i,\mathfrak{s}) = \sum_{\substack{\mathfrak{t}\#\mathfrak{s}_S \in \tau_i(\mathcal{S}_i), \\ \mathfrak{t} \in \mathrm{Spin}^{c}(M_i,0)}} SW(M_i,\mathfrak{t}) \end{align} $$
$$ \begin{align} \sum_{\substack{\mathfrak{s} \in \tau_i(\mathcal{S}_i), \\ f_j^\ast \mathfrak{s} = \mathfrak{s}\ (1 \leq j \leq k)}} SW(E_i,\mathfrak{s}) = \sum_{\substack{\mathfrak{t}\#\mathfrak{s}_S \in \tau_i(\mathcal{S}_i), \\ \mathfrak{t} \in \mathrm{Spin}^{c}(M_i,0)}} SW(M_i,\mathfrak{t}) \end{align} $$
in
![]() $\mathbb {Z}/2$
.
$\mathbb {Z}/2$
.
To compute the right-hand side of (12), let
![]() $\mathfrak {t} \in \mathrm {Spin}^{c}(M_i,0)$
be a spin
$\mathfrak {t} \in \mathrm {Spin}^{c}(M_i,0)$
be a spin
![]() $^c$
structure on
$^c$
structure on
![]() $M_i$
. We claim that
$M_i$
. We claim that
![]() $\mathfrak {t}\#\mathfrak {s}_S$
lies in
$\mathfrak {t}\#\mathfrak {s}_S$
lies in
![]() $ \tau _i(\mathcal {S}_i)$
if and only if all of the following three conditions (i)–(iii) are satisfied: (i)
$ \tau _i(\mathcal {S}_i)$
if and only if all of the following three conditions (i)–(iii) are satisfied: (i)
![]() $\mathrm {div}(c_1(\mathfrak {t})) = \mathrm {div}(c_i)$
, (ii)
$\mathrm {div}(c_1(\mathfrak {t})) = \mathrm {div}(c_i)$
, (ii)
![]() $c_1(\mathfrak {t})^2 = c_i^2$
, and (iii)
$c_1(\mathfrak {t})^2 = c_i^2$
, and (iii)
![]() $\mathfrak {t} \in \tau _i^0(\mathrm {Spin}^{c}(M_i,0)/\mathrm {Conj})$
. Noting
$\mathfrak {t} \in \tau _i^0(\mathrm {Spin}^{c}(M_i,0)/\mathrm {Conj})$
. Noting
![]() $c_1(\mathfrak {t}) = c_1(\mathfrak {t} \# \mathfrak {s}_S)$
in
$c_1(\mathfrak {t}) = c_1(\mathfrak {t} \# \mathfrak {s}_S)$
in
![]() $H^2(X_i;\mathbb {Z})$
, this claim is a direct consequence of Proposition 4.5, which we shall see later.
$H^2(X_i;\mathbb {Z})$
, this claim is a direct consequence of Proposition 4.5, which we shall see later.
By the claim of the last paragraph, we have
 $$ \begin{align} \sum_{\substack{\mathfrak{t}\#\mathfrak{s}_S \in \tau_i(\mathcal{S}_i), \\ \mathfrak{t} \in \mathrm{Spin}^{c}(M_i,0)}} SW(M_i,\mathfrak{t}) = N(M_i; c_i) \end{align} $$
$$ \begin{align} \sum_{\substack{\mathfrak{t}\#\mathfrak{s}_S \in \tau_i(\mathcal{S}_i), \\ \mathfrak{t} \in \mathrm{Spin}^{c}(M_i,0)}} SW(M_i,\mathfrak{t}) = N(M_i; c_i) \end{align} $$
in
![]() $\mathbb {Z}/2$
. Here the right-hand side of (13) was assumed to be nonzero in
$\mathbb {Z}/2$
. Here the right-hand side of (13) was assumed to be nonzero in
![]() $\mathbb {Z}/2$
in Assumption 2.1. Thus, the assertion of the proposition follows from (10), (11), (12), (13).
$\mathbb {Z}/2$
in Assumption 2.1. Thus, the assertion of the proposition follows from (10), (11), (12), (13).
Here we record a proposition that we have used above:
Proposition 4.5 (Wall [Reference Wall34, Reference Wall35]).
Let Z be a smooth closed oriented simply-connected 4-manifold. Suppose that
![]() $b_2(Z)-\sigma (Z) \geq 2$
and that Z is either indefinite or
$b_2(Z)-\sigma (Z) \geq 2$
and that Z is either indefinite or
![]() $b_2(Z) \leq 8$
. Set
$b_2(Z) \leq 8$
. Set
![]() $Z' = Z\#S^2\times S^2$
. Then, given
$Z' = Z\#S^2\times S^2$
. Then, given
![]() $x, y \in H^2(Z';\mathbb {Z})$
, there exists
$x, y \in H^2(Z';\mathbb {Z})$
, there exists
![]() $f \in \mathrm {Diff}^+(Z')$
with
$f \in \mathrm {Diff}^+(Z')$
with
![]() $f^\ast x=y$
if and only if
$f^\ast x=y$
if and only if
![]() $x, y$
have the same divisibility, self-intersection and type (i.e., characteristic or not).
$x, y$
have the same divisibility, self-intersection and type (i.e., characteristic or not).
Proof. For a unimodular lattice Q with
![]() $\mathrm {rank}(Q)-\sigma (Q) \geq 4$
, Wall [Reference Wall34, page 337] proved that
$\mathrm {rank}(Q)-\sigma (Q) \geq 4$
, Wall [Reference Wall34, page 337] proved that
![]() $\operatorname {\mathrm {Aut}}(Q)$
acts transitively on elements of given divisibility, self-intersection and type. However, each of divisibility, self-intersection and type is invariant under the action of
$\operatorname {\mathrm {Aut}}(Q)$
acts transitively on elements of given divisibility, self-intersection and type. However, each of divisibility, self-intersection and type is invariant under the action of
![]() $\operatorname {\mathrm {Aut}}(Q)$
. Thus, orbits in
$\operatorname {\mathrm {Aut}}(Q)$
. Thus, orbits in
![]() $Q/\operatorname {\mathrm {Aut}}(Q)$
one-to-one correspond to triples consisting of divisibility, self-intersection and type. The assertion of the proposition follows from this applied to the intersection form of
$Q/\operatorname {\mathrm {Aut}}(Q)$
one-to-one correspond to triples consisting of divisibility, self-intersection and type. The assertion of the proposition follows from this applied to the intersection form of
![]() $Z'$
, together with another theorem by Wall [Reference Wall35, Theorem 2] on the realizability of an automorphism of the intersection form by a diffeomorphism.
$Z'$
, together with another theorem by Wall [Reference Wall35, Theorem 2] on the realizability of an automorphism of the intersection form by a diffeomorphism.
Now we can complete the proof of the most general result in this paper:
Proof of Theorem 2.7.
As in the construction of
![]() $E_i$
, we fix diffeomorphisms
$E_i$
, we fix diffeomorphisms
![]() $\psi _i : \mathring {M_i}\#kS^2\times S^2 \to \mathring {X}$
and its extensions
$\psi _i : \mathring {M_i}\#kS^2\times S^2 \to \mathring {X}$
and its extensions
![]() $\psi _i : M_i\#kS^2\times S^2 \to X$
. Considering the pull-back of the orbits
$\psi _i : M_i\#kS^2\times S^2 \to X$
. Considering the pull-back of the orbits
![]() $\mathcal {S}_i \in \mathbb {S}(X_i,k)$
under
$\mathcal {S}_i \in \mathbb {S}(X_i,k)$
under
![]() $\psi _i$
, we obtain orbits (denoted by the same notation)
$\psi _i$
, we obtain orbits (denoted by the same notation)
![]() $\mathcal {S}_i \in \mathbb {S}(X,k)$
.
$\mathcal {S}_i \in \mathbb {S}(X,k)$
.
Passing to a subsequence if necessary, we may suppose that all
![]() $\mathrm {div}(c_i)$
are distinct by (iii) of Assumption 2.1. Thus, we may suppose that all
$\mathrm {div}(c_i)$
are distinct by (iii) of Assumption 2.1. Thus, we may suppose that all
![]() $\mathcal {S}_i$
are distinct elements in
$\mathcal {S}_i$
are distinct elements in
![]() $\mathbb {S}(X,k)$
. From this together with Lemma 3.2, by passing to a subsequence again, we may suppose that
$\mathbb {S}(X,k)$
. From this together with Lemma 3.2, by passing to a subsequence again, we may suppose that
for all
![]() $i \geq 2$
.
$i \geq 2$
.
Now it follows from Proposition 4.4 together with (3), (14) that the homomorphism
restricts to a surjection
This combined with Lemma 2.6 implies that the subgroup
![]() $\left <\mathring {\alpha }_i \mid i\geq 2\right>$
is a
$\left <\mathring {\alpha }_i \mid i\geq 2\right>$
is a
![]() $(\mathbb {Z}/2)^{\infty }$
-summand of
$(\mathbb {Z}/2)^{\infty }$
-summand of
![]() $H_k(B\mathrm {Diff}^+(X);\mathbb {Z})$
, which together with Lemma 2.4 completes the proof of (i) of Theorem 2.7.
$H_k(B\mathrm {Diff}^+(X);\mathbb {Z})$
, which together with Lemma 2.4 completes the proof of (i) of Theorem 2.7.
Since
![]() $\rho _\ast (\mathring {\alpha }_i)=\alpha _i$
, we obtain (ii) of Theorem 2.7 from (i) of Theorem 2.7 together with Lemma 2.5.
$\rho _\ast (\mathring {\alpha }_i)=\alpha _i$
, we obtain (ii) of Theorem 2.7 from (i) of Theorem 2.7 together with Lemma 2.5.
5 Addenda
5.1 Finiteness of mapping class groups in dimension
 $\neq $
4
$\neq $
4
In dimension
![]() $\neq $
4, not only finite generation, but stronger finiteness on mapping class groups is known.
$\neq $
4, not only finite generation, but stronger finiteness on mapping class groups is known.
5.1.1 dimension
 $\geq 6$
$\geq 6$
Given a simply-connected closed smooth manifold X of
![]() $\dim X\geq 6$
, Sullivan [Reference Sullivan33, Theorem (13.3)] proved that
$\dim X\geq 6$
, Sullivan [Reference Sullivan33, Theorem (13.3)] proved that
![]() $\pi _0(\mathrm {Diff}(X))$
is ‘commensurable’ with an arithmetic group. Krannich and Randal-Williams [Reference Krannich and Randal-Williams21] clarified that the term ‘commensurable’ is used in [Reference Sullivan33] in a different way from the current common usage. In summary, given a group, we have implications:
$\pi _0(\mathrm {Diff}(X))$
is ‘commensurable’ with an arithmetic group. Krannich and Randal-Williams [Reference Krannich and Randal-Williams21] clarified that the term ‘commensurable’ is used in [Reference Sullivan33] in a different way from the current common usage. In summary, given a group, we have implications:
 $$ \begin{align*} &\text{(commensurable with an arithmetic group in the current common sense)}\\ \Rightarrow& \text{(commensurable with an arithmetic group in the sense of } {[{33}])}\\ \Rightarrow & \text{(finitely presented)} \Rightarrow \text{(finitely generated)}. \end{align*} $$
$$ \begin{align*} &\text{(commensurable with an arithmetic group in the current common sense)}\\ \Rightarrow& \text{(commensurable with an arithmetic group in the sense of } {[{33}])}\\ \Rightarrow & \text{(finitely presented)} \Rightarrow \text{(finitely generated)}. \end{align*} $$
In particular, Theorem 1.1 implies that mapping class groups of simply-connected 4-manifolds need not be commensurable with arithmetic groups, even in Sullivan’s sense.
5.1.2 dimension
 $5$
$5$
While the above result by Sullivan [Reference Sullivan33, Theorem (13.3)] was stated in
![]() $\dim \geq 6$
, actually his result holds also in dimension 5. We record a way to deduce this from a recent paper [Reference Bustamante, Krannich and Kupers9]. (The author thanks Sander Kupers for informing the author of this argument.) In the proof of [Reference Bustamante, Krannich and Kupers9, Theorem 2.6], the assumption that
$\dim \geq 6$
, actually his result holds also in dimension 5. We record a way to deduce this from a recent paper [Reference Bustamante, Krannich and Kupers9]. (The author thanks Sander Kupers for informing the author of this argument.) In the proof of [Reference Bustamante, Krannich and Kupers9, Theorem 2.6], the assumption that
![]() $\dim \geq 6$
was used only in the point (i) in the proof, but it follows from Cerf’s theorem [Reference Cerf10] that
$\dim \geq 6$
was used only in the point (i) in the proof, but it follows from Cerf’s theorem [Reference Cerf10] that
![]() $\pi _0(C^{\mathrm {Diff}}(M)) = 0$
for a simply-connected 5-manifold M, and the assumption that
$\pi _0(C^{\mathrm {Diff}}(M)) = 0$
for a simply-connected 5-manifold M, and the assumption that
![]() $\dim \geq 6$
was not used in [Reference Bustamante, Krannich and Kupers9, Proposition 2.7], except for the part where [Reference Bustamante, Krannich and Kupers9, Proposition 2.6] was used.
$\dim \geq 6$
was not used in [Reference Bustamante, Krannich and Kupers9, Proposition 2.7], except for the part where [Reference Bustamante, Krannich and Kupers9, Proposition 2.6] was used.
5.1.3 dimension
 $\leq 3$
$\leq 3$
The mapping class groups of closed orientable manifolds of dim
![]() $\leq 3$
are finitely presented. See Dehn [Reference Hatcher and Thurston17] for dimension 2. In dimension 3, a more general finiteness holds for the moduli space of 3-manifolds. See Boyd–Bregman–Steinebrunner [Reference Boyd, Bregman and Steinebrunner6, Theorem 6.12].
$\leq 3$
are finitely presented. See Dehn [Reference Hatcher and Thurston17] for dimension 2. In dimension 3, a more general finiteness holds for the moduli space of 3-manifolds. See Boyd–Bregman–Steinebrunner [Reference Boyd, Bregman and Steinebrunner6, Theorem 6.12].
5.2 Questions: finiteness in other categories
We close this paper by posting questions on categories other than the smooth category.
As noted in Remark 1.3, for a simply-connected closed topological 4-manifold X, the topological mapping class group
![]() $\pi _0(\text {Homeo}(X))$
is known to be finitely generated, and so is
$\pi _0(\text {Homeo}(X))$
is known to be finitely generated, and so is
![]() $H_1(B\text {Homeo}(X);\mathbb {Z})$
.
$H_1(B\text {Homeo}(X);\mathbb {Z})$
.
However, to the best of the author’s knowledge, there is no known finiteness result on
![]() $H_k(B\text {Homeo}(X))$
for
$H_k(B\text {Homeo}(X))$
for
![]() $k>1$
for general simply-connected 4-manifolds X. However, it may be natural to hope such finiteness results in the 4-dimensional topological category, as opposed to the smooth category:
$k>1$
for general simply-connected 4-manifolds X. However, it may be natural to hope such finiteness results in the 4-dimensional topological category, as opposed to the smooth category:
Question 5.1. Let X be a simply-connected closed oriented topological 4-manifold. Is
![]() $H_k(B\text {Homeo}(X);\mathbb {Z})$
finitely generated for each k?
$H_k(B\text {Homeo}(X);\mathbb {Z})$
finitely generated for each k?
Recently, Lin and Xie [Reference Lin and Xie25] extensively studied the moduli space
![]() $\mathcal {M}^{fs}(X)$
of formally smooth 4-manifolds, which is a middle moduli space between the smooth moduli space
$\mathcal {M}^{fs}(X)$
of formally smooth 4-manifolds, which is a middle moduli space between the smooth moduli space
![]() $\mathcal {M}^{s}(X)=B\text {Diff}(X)$
and the topological moduli space
$\mathcal {M}^{s}(X)=B\text {Diff}(X)$
and the topological moduli space
![]() $\mathcal {M}^{t}(X)=B\text {Homeo}(X)$
. Lin and Xie pointed out that most exotic phenomena detected by gauge theory are relevant to the discrepancy between
$\mathcal {M}^{t}(X)=B\text {Homeo}(X)$
. Lin and Xie pointed out that most exotic phenomena detected by gauge theory are relevant to the discrepancy between
![]() $\mathcal {M}^{s}(X)$
and
$\mathcal {M}^{s}(X)$
and
![]() $\mathcal {M}^{fs}(X)$
. Since infiniteness of
$\mathcal {M}^{fs}(X)$
. Since infiniteness of
![]() $\mathcal {M}^{s}(X)$
detected in this paper comes from gauge theory, it may be natural to expect finiteness of
$\mathcal {M}^{s}(X)$
detected in this paper comes from gauge theory, it may be natural to expect finiteness of
![]() $\mathcal {M}^{fs}(X)$
:
$\mathcal {M}^{fs}(X)$
:
Question 5.2. Let X be a simply-connected closed oriented topological 4-manifold that admits a formally smooth structure. Is
![]() $H_k(\mathcal {M}^{fs}(X);\mathbb {Z})$
finitely generated for each k?
$H_k(\mathcal {M}^{fs}(X);\mathbb {Z})$
finitely generated for each k?
Acknowledgments
The author is grateful to Dave Auckly, Inanc Baykur and Danny Ruberman for enlightening conversations. Especially, the author wishes to thank Danny Ruberman for several helpful discussions during this project. The author would like to thank Sander Kupers, Jianfeng Lin, Mike Miller Eismeier, Masaki Taniguchi and Tadayuki Watanabe for their helpful comments on a draft of the paper. The author is grateful to David Baraglia for informing the author of his paper [Reference Baraglia4], as well as comments on a draft of the current paper. The author is grateful to an anonymous referee for giving several constructive comments, which greatly improved this paper. This project was prompted at SwissMAP Research Station in Les Diablerets, the conference ‘Mapping class groups: pronilpotent and cohomological approaches’, and the author wishes to thank the organizers for giving him an opportunity to join the conference. Lastly, the author wants to acknowledge the hospitality of MIT where this project was conducted.
Competing interest
The author declares that there is no competing interest.
Funding statement
The author was partially supported by JSPS KAKENHI Grant Number 21K13785 and JSPS Overseas Research Fellowship.